A Compact Polarimetric CTLR Mode Calibration Method Immune to Faraday Rotation Using Two Dihedral Reflectors

Highlights

What are the main findings?

• A novel CTLR mode calibration method using a minimum of two dihedral reflectors to estimate all system distortion parameters, significantly reducing deployment complexity.
• The method is inherently immune to Faraday rotation effects without requiring rotation angle estimation, particularly advantageous for low-frequency SAR systems.

What are the implications of the main finding?

• Clear operational guidelines are established: received crosstalk below −25 dB, SNR exceeding 35 dB, and POAS within ±1° ensure high-precision calibration performance.
• GF-3 satellite validation demonstrates excellent accuracy with amplitude, phase, and crosstalk RMSEs of 0.10 dB, 1.13°, and 0.42 dB, confirming practical applicability.

Abstract

This paper proposes a compact polarimetric CTLR mode calibration method using only two dihedral reflectors. The method leverages the property that the dihedral scattering matrix is unaffected by double-pass Faraday rotation, effectively eliminating the interference of Faraday rotation on distortion parameter estimation. By selecting any two from four dihedral reflectors rotated at 0°, 22.5°, 45°, and 67.5°, the system distortion parameters can be estimated. To resolve the two-fold solution ambiguity inherent in the estimation process, two ambiguity elimination methods are proposed: Method I selects the solution with equivalent crosstalk magnitude less than 0 dB based on the prior knowledge that the transmit antenna is dominated by right-hand circular polarization; Method II employs cross-validation using different dihedral combinations with distinct product constants, applicable when the prior knowledge does not hold. Through simulation analysis, the algorithm’s sensitivity to receive crosstalk levels, signal-to-noise ratio, and polarization orientation angle shift is evaluated. The results demonstrate that to maintain residual receive imbalance amplitude within ±1 dB, phase within ±10°, and residual equivalent crosstalk below −30 dB, the system received crosstalk must be lower than −25 dB, the signal-to-noise ratio must exceed 35 dB, and polarization orientation angle shift should be controlled within ±1°. The effectiveness of the proposed algorithm is validated using fully polarimetric calibrated GaoFen-3 satellite data, achieving root mean square errors of 0.10 dB, 1.13°, and 0.42 dB for amplitude imbalance, phase imbalance, and equivalent crosstalk amplitude, respectively. Comparative analysis demonstrates that the proposed method achieves significantly higher calibration accuracy than existing approaches, with substantial improvements in parameter estimation precision.

1. Introduction

Polarimetric synthetic aperture radar (Polarimetric SAR) can acquire the polarimetric scattering characteristics of targets and has been widely applied in land cover classification, target recognition, ocean monitoring, and other fields [1]. Fully polarimetric SAR (Full-pol SAR) obtains the complete 2 × 2 scattering matrix by alternately transmitting horizontal (H) and vertical (V) polarization states and simultaneously receiving through two orthogonal polarization channels under each transmission. However, this alternating transmission mechanism doubles the pulse repetition frequency (PRF), resulting in limited imaging swath width and difficulty in meeting the application requirements for large-scale rapid imaging [2].

Compact polarimetric SAR (CP SAR), as a compromise between fully polarimetric and single-polarization systems, acquires polarimetric information with only half the PRF of full-pol SAR by continuously transmitting a fixed polarization and receiving through dual-channel orthogonal polarization [3]. This characteristic significantly extends the imaging swath width [4], demonstrating unique advantages in application scenarios requiring high revisit frequency and large-area coverage, such as maritime vessel monitoring, crop classification, and disaster emergency response [5].

CP SAR systems mainly adopt two transmission polarization modes: the 45° linear polarization mode ($\pi$/4 mode) [3] and the circular transmit-linear receive mode (CTLR mode) [2]. The CTLR mode has become the mainstream choice for current CP SAR satellites, including Mini-RF (lunar exploration mission), RISAT-1 (India), ALOS-2 (Japan, experimental mode), and RCM (Canada) [6]. Furthermore, extensive research has been conducted on full-polarimetric reconstruction and land cover classification using CTLR mode data [1,7]. In the CTLR mode, the transmitter can employ a circularly polarized antenna or synthesize circularly polarized waves by controlling the phase difference between a pair of orthogonal linearly polarized antennas: left-handed circular polarization (LHCP) is generated when the V-polarized component leads the H-polarized component by 90°, and right-handed circular polarization (RHCP) is produced when it lags by 90° [2].

Polarimetric calibration is the foundation for quantitative applications of polarimetric SAR. Due to factors such as limited antenna port isolation and inconsistent amplitude and phase characteristics of the transmit-receive channels, actual systems exhibit distortions including cross-polarization coupling and channel imbalance. If left uncorrected, these system errors will be mixed with the true polarimetric characteristics of targets, causing deviations in subsequent applications such as polarimetric decomposition and classification. Therefore, accurate estimation and compensation of system polarimetric distortion parameters is a necessary prerequisite for polarimetric SAR data applications.

However, the calibration of CP SAR faces challenges. Unlike the four independent scattering matrix elements acquired by full-pol SAR, CP systems can only obtain two complex observations. The reduction in observation dimensions makes it more difficult to fully estimate all system distortion parameters, imposing higher requirements on calibration algorithm design. Several studies have addressed the calibration problem for CP systems. In 2008, Freeman first established a polarization distortion model for the CTLR mode [8], laying the theoretical foundation for subsequent research. Based on this model, researchers have proposed various calibration methods, each with its own limitations.

Truong et al. proposed a calibration method based on a trihedral and two dihedral reflectors [9]. This method employs ratios of observations, which can partially eliminate the influence of absolute factors. However, its core assumption is that the transmitter generates ideal circular polarization, neglecting the crosstalk and imbalance in the transmit channel. In practical systems, even if transmit crosstalk can be neglected, transmit imbalance still exists significantly, leading to systematic bias in the estimation results.

Chen et al. employed four calibrators (two active radar calibrators and two gridded trihedrals) to achieve complete estimation of all distortion parameters [10]. However, this method requires precise removal of the absolute amplitude and two-way phase of each calibrator’s scattering matrix before calibration. It should be noted that this removal must be in absolute terms rather than relative corrections between calibrators. Currently, no mature method exists to fulfill this requirement, which severely constrains the practical applicability of this algorithm.

Hou et al. proposed an iterative optimization method based on two dihedral reflectors [11]. Although this approach reduces the number of required calibrators, it fails to effectively separate Faraday rotation from system distortion in its modeling. Since Faraday rotation is coupled into the estimation of distortion parameters, the estimation accuracy degrades significantly under conditions where ionospheric effects are pronounced [12].

To address the above limitations, this paper proposes a CTLR mode calibration method using only dihedral reflectors. The main contributions of this paper are as follows:

• A minimum of only two dihedral reflectors with different rotation angles is required to complete calibration, significantly reducing the complexity and cost of field deployment.
• By exploiting the invariance property of dihedral reflector scattering matrices under double-pass Faraday rotation, the proposed method does not require estimation of the Faraday rotation angle, fundamentally circumventing the interference from ionospheric effects. This characteristic makes the method particularly suitable for low-frequency SAR systems such as L-band and P-band.
• Through the construction of observation ratios, the algorithm naturally eliminates the influence of unknown absolute factors. In contrast, methods such as Chen’s and Truong’s require prior knowledge of absolute factors before calibration, which are inherently unknowable in practice.
• Through Monte Carlo simulations, the algorithm’s sensitivity to received crosstalk, signal-to-noise ratio, and polarization orientation angle shift is systematically analyzed. A quantitative comparison with existing methods is also conducted, providing clear parameter guidelines for practical applications.

The remainder of this paper is organized as follows. Section 2 presents the materials and methods, including the Faraday rotation mechanism, CTLR-mode system model, and the proposed calibration algorithm with ambiguity elimination strategies. Section 3 presents the performance evaluation results, including sensitivity analysis under various conditions and experimental validation using GaoFen-3 satellite data. Section 4 discusses the comparative analysis with existing methods and the implications of the results. Section 5 concludes the paper.

2. Materials and Methods

2.1. Faraday Rotation

Electromagnetic waves propagating through the ionosphere interact with free electrons and the Earth’s magnetic field, causing the polarization plane of the wave to rotate. This phenomenon, known as Faraday rotation, becomes significant at L-band and lower frequencies due to its dependence on the square of the radar wavelength. For spaceborne polarimetric SAR systems operating at these frequencies, Faraday rotation can introduce polarization distortions that must be considered in the calibration process.

The Faraday rotation angle $\mathrm{\Omega }$ induced by the ionosphere can be expressed as [13]:

$$\mathrm{\Omega }=2.6\times {10}^{-13}·\mathrm{TEC}·B·{\lambda }^2·cos\theta$$

(1)

where $\mathrm{\Omega }$ is the one-way Faraday rotation angle in radians, TEC denotes the total electron content along the signal propagation path in electrons/m², B represents the Earth’s magnetic field intensity in Tesla, $\lambda$ is the radar wavelength in meters, and $\theta$ is the angle between the geomagnetic field vector and the radar line-of-sight direction.

The magnitude of Faraday rotation is primarily governed by the TEC, which exhibits significant temporal and spatial variations. In terms of diurnal variation, solar radiation dominates the ionization process, and TEC can vary by an order of magnitude between day and night, resulting in considerably larger Faraday rotation angles during daytime. Regarding latitudinal variation, the Faraday rotation angle is generally larger in tropical regions than at the poles. As for solar cycle variation, ionospheric effects are relatively minor during solar minimum, whereas during solar maximum or ionospheric storm events, Faraday rotation can become significant and affect data analysis.

Furthermore, within a single SAR image, Faraday rotation angles can vary spatially due to ionospheric inhomogeneity and incidence angle variations across the swath. Analysis of ALOS/PALSAR data over high-latitude regions [14] demonstrated that under disturbed ionospheric conditions, ionospheric irregularities cause stripe-shaped anomalies in the Faraday rotation distribution, with a maximum of 16.9°, a mean of 6.8°, and a standard deviation of 2.9°. In contrast, under quiet ionospheric conditions, the Faraday rotation distribution remains uniform with a standard deviation of only 0.18°.

Although some calibration algorithms account for the effect of Faraday rotation, they typically assume a constant Faraday rotation angle across the entire scene. However, as discussed above, the Faraday rotation angle exhibits spatial variations within a single image, causing calibrators at different locations to be affected by different levels of Faraday rotation. This inconsistency between the model assumption and the actual conditions introduces errors in Faraday rotation estimation, which subsequently degrades the accuracy of the estimated polarimetric distortion parameters.

2.2. CTLR-Mode Compact Polarimetric SAR System Model

Freeman established a compact polarimetric distortion model [8], which states that when the system generates a circularly polarized wave by controlling the phase difference between two orthogonal linear polarization signals (H and V), the polarization distortion can be characterized by two complex matrices, R and T, representing the polarization distortion at the receiving and transmitting ends, respectively, as defined below:

$$R=\left[\begin{array}{cc}{R}_{hh}\hfill & R_{hv}\hfill \\ R_{vh}\hfill & R_{vv}\hfill \end{array}\right]T=\left[\begin{array}{cc}{T}_{hh}\hfill & T_{hv}\hfill \\ T_{vh}\hfill & T_{vv}\hfill \end{array}\right]$$

Here, the subscripts $mn$ denote the polarization component m of the output signal when the input polarization is n. By normalizing the distortion matrices with $T_{hh}$ and $R_{hh}$, respectively, the polarimetric response of the CTLR system transmitting a RHCP signal can be expressed as:

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{M}_{RH}\hfill \\ M_{RV}\hfill \end{array}\right]={\displaystyle \frac{1}{\sqrt{2}}}A{e}^{j\psi }{R}_{hh}{T}_{hh}\left[\begin{array}{cc}1& {\delta }_3\\ {\delta }_4& f_2\end{array}\right]\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\hfill \\ \hfill & \left[\begin{array}{cc}{S}_{HH}\hfill & S_{HV}\hfill \\ S_{VH}\hfill & S_{VV}\hfill \end{array}\right]\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\left[\begin{array}{cc}1& {\delta }_1\\ {\delta }_2& f_1\end{array}\right]\left[\begin{array}{c}1\\ -j\end{array}\right]+\left[\begin{array}{c}{N}_1\hfill \\ N_2\hfill \end{array}\right]\hfill \end{array}$$

(2)

$M_{RH}$ and $M_{RV}$ denote the received signals in the horizontal (H) and vertical (V) channels, respectively; ${\delta }_1,{\delta }_2,{\delta }_3,{\delta }_4$ represent crosstalk terms; $f_1$ and $f_2$ indicate the imbalance of the polarization channels; $\mathrm{\Omega }$ denotes the Faraday rotation angle, describing the rotation effect of the electromagnetic wave passing through the ionosphere; $S_{HH},S_{HV},S_{VH},S_{VV}$ are the elements of the true scattering matrix; $N_1$ and $N_2$ correspond to noise components in the polarization channels; A represents the amplitude of the received signal; and $\psi$ is the two-way phase of the signal traveling from the transmitter to the target and back to the antenna.

${\delta }_c$ is termed the equivalent crosstalk. Its physical meaning represents the ratio of the LHCP component to the ideal RHCP component in the actually transmitted wave, characterizing the imperfection of the transmitter in generating an ideal RHCP wave. As shown in (3), ${\delta }_c$ completely encompasses all transmit-side distortion parameters, including transmit crosstalk ${\delta }_1$, ${\delta }_2$ and transmit imbalance $f_1$. This means that regardless of the levels of individual transmit-side distortion parameters, their combined effect on the transmitted circularly polarized wave is mathematically encapsulated within the single parameter ${\delta }_c$.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{W}{\sqrt{2}}}\left(\left[\begin{array}{c}1\\ -j\end{array}\right]+{\delta }_c\left[\begin{array}{c}1\\ j\end{array}\right]\right)={\displaystyle \frac{1}{\sqrt{2}}}\left[\begin{array}{cc}1& {\delta }_1\\ {\delta }_2& f_1\end{array}\right]\left[\begin{array}{c}1\\ -j\end{array}\right]\hfill \\ \hfill & \mathrm{where}\hfill \\ \hfill & W={\displaystyle \frac{1-{\delta }_{1}j+{\delta }_{2}j+f_1}{2}},{\delta }_c={\displaystyle \frac{1-{\delta }_{1}j-{\delta }_{2}j-f_1}{1-{\delta }_{1}j+{\delta }_{2}j+f_1}}\hfill \end{array}$$

(3)

Using this equivalent crosstalk representation, the system model (2) can be rewritten as (4), where $Y={\displaystyle \frac{R_{hh}{T}_{hh}W}{\sqrt{2}}}$ is an unknown absolute factor that cannot be neglected in polarization calibration.

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{M}_{RH}\\ M_{RV}\end{array}\right]=& A{e}^{j\psi }Y\left[\begin{array}{cc}1& {\delta }_3\\ {\delta }_4& f_r\end{array}\right]\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\left[\begin{array}{cc}{S}_{HH}& S_{HV}\\ S_{VH}& S_{VV}\end{array}\right]\hfill \\ \hfill & ·\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\left[\begin{array}{c}1+{\delta }_c\\ -j(1-{\delta }_c)\end{array}\right]+\left[\begin{array}{c}{N}_1\\ N_2\end{array}\right]\hfill \end{array}$$

(4)

2.3. Calibration Algorithm with Low Received Crosstalk Assumption

In modern polarimetric SAR systems, the crosstalk between polarization channels can be effectively controlled below −30 dB through careful system design and antenna isolation [15,16]. Under this condition, the received crosstalk can be considered negligible, and the system model can be simplified as follows:

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{M}_{RH}\\ M_{RV}\end{array}\right]=& A{e}^{j\psi }Y\left[\begin{array}{cc}1& 0\\ 0& f_r\end{array}\right]\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\left[\begin{array}{cc}{S}_{HH}& S_{HV}\\ S_{VH}& S_{VV}\end{array}\right]\hfill \\ \hfill & ·\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]\left[\begin{array}{c}1+{\delta }_c\\ -j\left(1-{\delta }_c\right)\end{array}\right]\hfill \end{array}$$

(5)

A key observation is that certain scattering matrix structures remain invariant under double-pass Faraday rotation. Specifically, consider the two basis matrices:

$${\mathbf{B}}_1=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right],{\mathbf{B}}_2=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$$

(6)

Any linear combination of these base matrices satisfies the following invariance property:

$$\mathbf{U}\left(\mathrm{\Omega }\right)\left(k_1{\mathbf{B}}_1+k_2{\mathbf{B}}_2\right)\mathbf{U}\left(\mathrm{\Omega }\right)=k_1{\mathbf{B}}_1+k_2{\mathbf{B}}_2$$

(7)

where $\mathbf{U}\left(\mathrm{\Omega }\right)=\left[\begin{array}{cc}cos\mathrm{\Omega }& sin\mathrm{\Omega }\\ -sin\mathrm{\Omega }& cos\mathrm{\Omega }\end{array}\right]$ denotes the Faraday rotation matrix. This invariance property implies that when a scattering matrix can be expressed as a linear combination of ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$, its observed response is unaffected by Faraday rotation. The dihedral reflector rotated by an arbitrary angle $\psi$ satisfies this condition, and its scattering matrix is given by:

$${\mathrm{S}}_{Di}=A_{\mathrm{Di}}(\theta ,\varphi )·e^{j{\phi }_{\mathrm{Di}}(\theta ,\varphi )}·\left[\begin{array}{cc}cos2\psi & sin2\psi \\ sin2\psi & -cos2\psi \end{array}\right]$$

(8)

$\theta$ and $\varphi$ denote the elevation and azimuth angles of the radar line of sight, respectively; $\psi$ represents the rotation angle of the dihedral reflector about the radar line of sight; $A_{\mathrm{Di}}$ is the amplitude factor; and $\phi$ denotes the two-way phase. The geometric relationship of the dihedral corner reflector is shown in Figure 1.

Unlike the methods discussed earlier that assume a constant Faraday rotation angle across the entire image, the proposed calibration method relies exclusively on dihedral reflectors. As shown in Equation (7), the dihedral scattering matrix satisfies the double-pass Faraday rotation invariance property, meaning its polarimetric response remains unchanged after undergoing any arbitrary Faraday rotation. This implies that regardless of ionospheric conditions, the observed response from a dihedral reflector depends solely on the system distortion parameters and is completely decoupled from the Faraday rotation angle. Consequently, the proposed method requires neither estimation nor compensation of the Faraday rotation angle, and is immune to its spatial variations—even when calibrators at different locations within the calibration site experience different levels of Faraday rotation, the parameter estimation results remain accurate. This inherent property makes the proposed method particularly well-suited for low-frequency SAR systems (e.g., P-band and L-band) where ionospheric effects are pronounced.

When the dihedral reflector is rotated by 0°, 45°, 22.5°, and 67.5°, respectively, and substituted into (5), the resulting observed vectors are given in (9), where I denotes an unknown absolute factor. Any two dihedral angles can be selected to obtain four complex observations, which yield four complex unknowns in the estimation equations. The estimation results for the distortion parameters are given in Equations (10)–(15) for six dihedral combinations, where each combination yields two solution pairs: Solution I (${\delta }_c^{\prime }$, $f_r^{\prime }$) and Solution II (${\delta }_c^{″}$, $f_r^{″}$).

$$\begin{array}{cc}\hfill & \left[\begin{array}{c}{M}_{RH}^{D0}\hfill \\ M_{RV}^{D0}\hfill \end{array}\right]=I_{D0}\left[\begin{array}{c}{\delta }_c+1\\ f_{r}j-{\delta }_c{f}_{r}j\end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}{M}_{RH}^{D45}\hfill \\ M_{RV}^{D45}\hfill \end{array}\right]=I_{D45}\left[\begin{array}{c}{\delta }_{c}j-1j\\ f_r+{\delta }_c{f}_r\end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}{M}_{RH}^{D22.5}\hfill \\ M_{RV}^{D22.5}\hfill \end{array}\right]=I_{D22.5}\left[\begin{array}{c}1-j+{\delta }_c(1+j)\\ f_r(1+j)+{\delta }_c{f}_r(1-j)\end{array}\right]\hfill \\ \hfill & \left[\begin{array}{c}{M}_{RH}^{D67.5}\\ M_{RV}^{D67.5}\end{array}\right]=I_{D67.5}\left[\begin{array}{c}1+j+{\delta }_c(1-j)\\ -f_r(1-j)-{\delta }_c{f}_r(1+j)\end{array}\right]\hfill \end{array}$$

(9)

Combination: 0° + 45°

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{M_{RH}^{D0}{M}_{RV}^{D45}+M_{RV}^{D0}{M}_{RH}^{D45}+2j·M_{RH}^{D0}{M}_{RH}^{D45}\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}}{M_{RH}^{D0}{M}_{RV}^{D45}-M_{RV}^{D0}{M}_{RH}^{D45}}}\\ f_r^{\prime }=-\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}\hfill \end{array}$$

(10a)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{M_{RH}^{D0}{M}_{RV}^{D45}+M_{RV}^{D0}{M}_{RH}^{D45}-2j·M_{RH}^{D0}{M}_{RH}^{D45}\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}}{M_{RH}^{D0}{M}_{RV}^{D45}-M_{RV}^{D0}{M}_{RH}^{D45}}}\\ f_r^{″}=\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}\hfill \end{array}$$

(10b)

Combination: 22.5° + 67.5°

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{-j(M_{RH}^{D22.5}{M}_{RV}^{D67.5}+M_{RV}^{D22.5}{M}_{RH}^{D67.5})+2M_{RH}^{D22.5}{M}_{RH}^{D67.5}\sqrt{-{\displaystyle \frac{M_{RV}^{D22.5}{M}_{RV}^{D67.5}}{M_{RH}^{D22.5}{M}_{RH}^{D67.5}}}}}{M_{RH}^{D22.5}{M}_{RV}^{D67.5}-M_{RV}^{D22.5}{M}_{RH}^{D67.5}}}\\ f_r^{\prime }=-\sqrt{-{\displaystyle \frac{M_{RV}^{D22.5}{M}_{RV}^{D67.5}}{M_{RH}^{D22.5}{M}_{RH}^{D67.5}}}}\hfill \end{array}$$

(11a)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{-j(M_{RH}^{D22.5}{M}_{RV}^{D67.5}+M_{RV}^{D22.5}{M}_{RH}^{D67.5})-2M_{RH}^{D22.5}{M}_{RH}^{D67.5}\sqrt{-{\displaystyle \frac{M_{RV}^{D22.5}{M}_{RV}^{D67.5}}{M_{RH}^{D22.5}{M}_{RH}^{D67.5}}}}}{M_{RH}^{D22.5}{M}_{RV}^{D67.5}-M_{RV}^{D22.5}{M}_{RH}^{D67.5}}}\\ f_r^{″}=\sqrt{-{\displaystyle \frac{M_{RV}^{D22.5}{M}_{RV}^{D67.5}}{M_{RH}^{D22.5}{M}_{RH}^{D67.5}}}}\hfill \end{array}$$

(11b)

Combination: 0° + 22.5°

$$D={\left(M_{RH}^{D0}\right)}^2{\left(M_{RV}^{D22.5}\right)}^2-6M_{RH}^{D0}{M}_{RV}^{D0}{M}_{RH}^{D22.5}{M}_{RV}^{D22.5}+{\left(M_{RV}^{D0}\right)}^2{\left(M_{RH}^{D22.5}\right)}^2$$

(12a)

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{(1-j)\sqrt{D}+(1+j)\left(M_{RH}^{D0}{M}_{RV}^{D22.5}+M_{RV}^{D0}{M}_{RH}^{D22.5}\right)}{2\left(M_{RH}^{D0}{M}_{RV}^{D22.5}-M_{RV}^{D0}{M}_{RH}^{D22.5}\right)}}\\ f_r^{\prime }={\displaystyle \frac{\sqrt{D}+M_{RH}^{D0}{M}_{RV}^{D22.5}-M_{RV}^{D0}{M}_{RH}^{D22.5}}{2M_{RH}^{D0}{M}_{RH}^{D22.5}}}\hfill \end{array}$$

(12b)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{-(1-j)\sqrt{D}+(1+j)\left(M_{RH}^{D0}{M}_{RV}^{D22.5}+M_{RV}^{D0}{M}_{RH}^{D22.5}\right)}{2\left(M_{RH}^{D0}{M}_{RV}^{D22.5}-M_{RV}^{D0}{M}_{RH}^{D22.5}\right)}}\\ f_r^{″}={\displaystyle \frac{-\sqrt{D}+M_{RH}^{D0}{M}_{RV}^{D22.5}-M_{RV}^{D0}{M}_{RH}^{D22.5}}{2M_{RH}^{D0}{M}_{RH}^{D22.5}}}\hfill \end{array}$$

(12c)

Combination: 45° + 22.5°

$$D={\left(M_{RH}^{D45}\right)}^2{\left(M_{RV}^{D22.5}\right)}^2-6M_{RH}^{D45}{M}_{RV}^{D45}{M}_{RH}^{D22.5}{M}_{RV}^{D22.5}+{\left(M_{RV}^{D45}\right)}^2{\left(M_{RH}^{D22.5}\right)}^2$$

(13a)

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{-(1+j)\sqrt{D}+(j-1)\left(M_{RH}^{D45}{M}_{RV}^{D22.5}+M_{RV}^{D45}{M}_{RH}^{D22.5}\right)}{2\left(M_{RH}^{D45}{M}_{RV}^{D22.5}-M_{RV}^{D45}{M}_{RH}^{D22.5}\right)}}\\ f_r^{\prime }={\displaystyle \frac{-\sqrt{D}+M_{RV}^{D45}{M}_{RH}^{D22.5}-M_{RH}^{D45}{M}_{RV}^{D22.5}}{2M_{RH}^{D45}{M}_{RH}^{D22.5}}}\hfill \end{array}$$

(13b)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{(1+j)\sqrt{D}+(j-1)\left(M_{RH}^{D45}{M}_{RV}^{D22.5}+M_{RV}^{D45}{M}_{RH}^{D22.5}\right)}{2\left(M_{RH}^{D45}{M}_{RV}^{D22.5}-M_{RV}^{D45}{M}_{RH}^{D22.5}\right)}}\\ f_r^{″}={\displaystyle \frac{\sqrt{D}+M_{RV}^{D45}{M}_{RH}^{D22.5}-M_{RH}^{D45}{M}_{RV}^{D22.5}}{2M_{RH}^{D45}{M}_{RH}^{D22.5}}}\hfill \end{array}$$

(13c)

Combination: 0° + 67.5°

$$D={\left(M_{RH}^{D0}\right)}^2{\left(M_{RV}^{D67.5}\right)}^2-6M_{RH}^{D0}{M}_{RV}^{D0}{M}_{RH}^{D67.5}{M}_{RV}^{D67.5}+{\left(M_{RV}^{D0}\right)}^2{\left(M_{RH}^{D67.5}\right)}^2$$

(14a)

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{(1+j)\sqrt{D}+(1-j)\left(M_{RH}^{D0}{M}_{RV}^{D67.5}+M_{RV}^{D0}{M}_{RH}^{D67.5}\right)}{2\left(M_{RH}^{D0}{M}_{RV}^{D67.5}-M_{RV}^{D0}{M}_{RH}^{D67.5}\right)}}\\ f_r^{\prime }={\displaystyle \frac{-\sqrt{D}-M_{RH}^{D0}{M}_{RV}^{D67.5}+M_{RV}^{D0}{M}_{RH}^{D67.5}}{2M_{RH}^{D0}{M}_{RH}^{D67.5}}}\hfill \end{array}$$

(14b)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{-(1+j)\sqrt{D}+(1-j)\left(M_{RH}^{D0}{M}_{RV}^{D67.5}+M_{RV}^{D0}{M}_{RH}^{D67.5}\right)}{2\left(M_{RH}^{D0}{M}_{RV}^{D67.5}-M_{RV}^{D0}{M}_{RH}^{D67.5}\right)}}\\ f_r^{″}={\displaystyle \frac{\sqrt{D}-M_{RH}^{D0}{M}_{RV}^{D67.5}+M_{RV}^{D0}{M}_{RH}^{D67.5}}{2M_{RH}^{D0}{M}_{RH}^{D67.5}}}\hfill \end{array}$$

(14c)

Combination: 45° + 67.5°

$$D={\left(M_{RH}^{D45}\right)}^2{\left(M_{RV}^{D67.5}\right)}^2-6M_{RH}^{D45}{M}_{RV}^{D45}{M}_{RH}^{D67.5}{M}_{RV}^{D67.5}+{\left(M_{RV}^{D45}\right)}^2{\left(M_{RH}^{D67.5}\right)}^2$$

(15a)

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{-(1-j)\sqrt{D}+(1+j)\left(M_{RH}^{D45}{M}_{RV}^{D67.5}+M_{RV}^{D45}{M}_{RH}^{D67.5}\right)}{2\left(M_{RH}^{D45}{M}_{RV}^{D67.5}-M_{RV}^{D45}{M}_{RH}^{D67.5}\right)}}\\ f_r^{\prime }={\displaystyle \frac{\sqrt{D}+M_{RH}^{D45}{M}_{RV}^{D67.5}-M_{RV}^{D45}{M}_{RH}^{D67.5}}{2M_{RH}^{D45}{M}_{RH}^{D67.5}}}\hfill \end{array}$$

(15b)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{(1-j)\sqrt{D}+(1+j)\left(M_{RH}^{D45}{M}_{RV}^{D67.5}+M_{RV}^{D45}{M}_{RH}^{D67.5}\right)}{2\left(M_{RH}^{D45}{M}_{RV}^{D67.5}-M_{RV}^{D45}{M}_{RH}^{D67.5}\right)}}\\ f_r^{″}={\displaystyle \frac{-\sqrt{D}+M_{RH}^{D45}{M}_{RV}^{D67.5}-M_{RV}^{D45}{M}_{RH}^{D67.5}}{2M_{RH}^{D45}{M}_{RH}^{D67.5}}}\hfill \end{array}$$

(15c)

2.3.1. Mathematical Properties of the Solution Pairs

From Equation (3), when the transmit crosstalk is negligible (${\delta }_1,{\delta }_2\approx 0$), the equivalent crosstalk simplifies to:

$${\delta }_c\approx {\displaystyle \frac{1-f_1}{1+f_1}}$$

(16)

where $f_1$ denotes the transmit channel imbalance. For $|{\delta }_c|$ to exceed 0 dB (i.e., $|{\delta }_c|>1$), the phase of $f_1$ must approach $\pm {90}^{\circ }$.

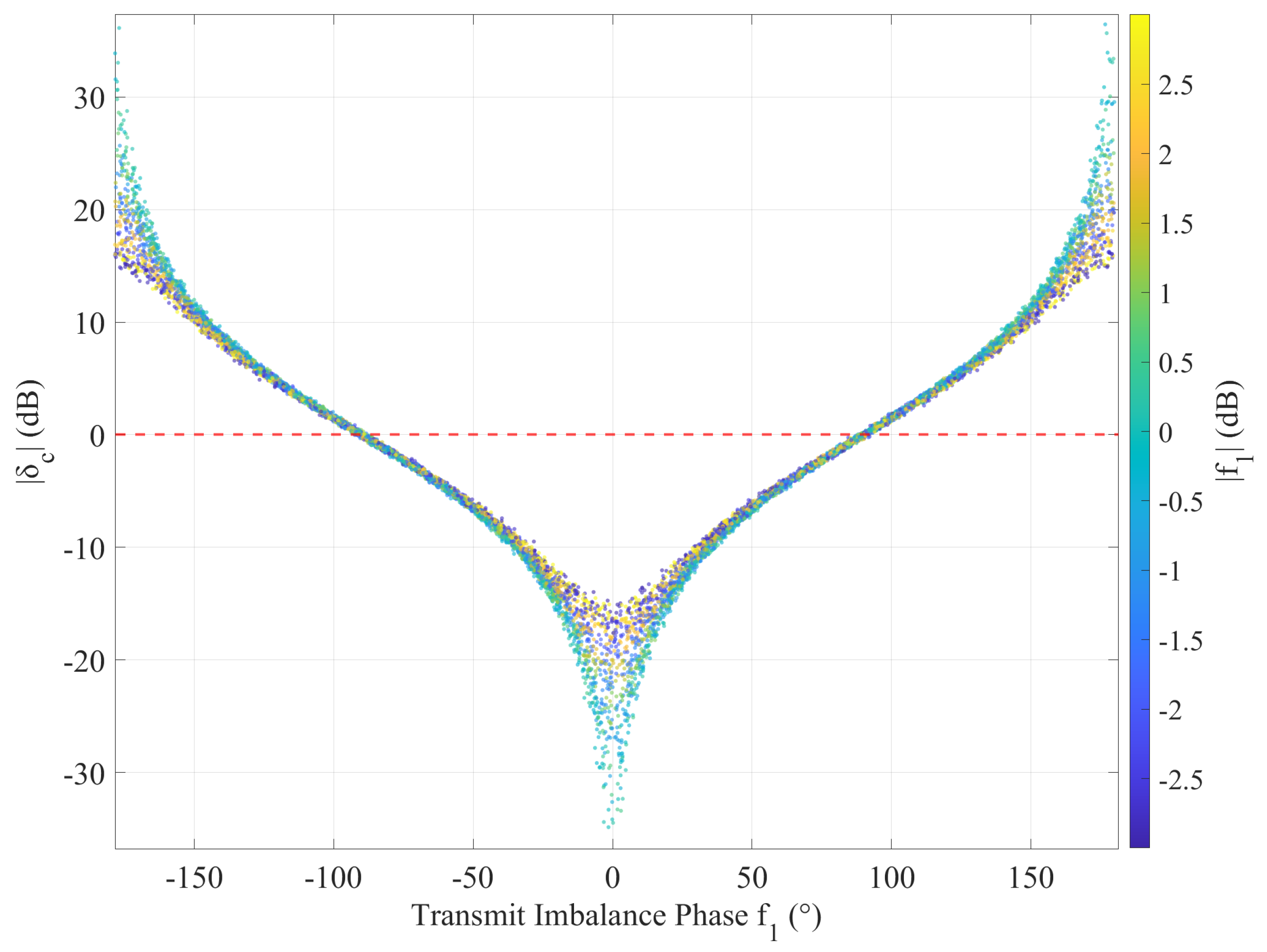
To comprehensively evaluate the range of $|{\delta }_c|$ under various distortion conditions, Monte Carlo simulations were conducted with 10,000 trials. The distortion parameters were randomly generated within the ranges specified in

Table 1. Monte Carlo Simulation Parameter Ranges.

Parameter	Range (Random)
Transmit imbalance amplitude $|f_1|$	$-3$ dB to $+3$ dB
Transmit imbalance phase $\angle f_1$	$-{180}^{\circ }$ to $+{180}^{\circ }$
Transmit crosstalk amplitude $|{\delta }_1|,|{\delta }_2|$	$-40$ dB to $-30$ dB
Transmit crosstalk phase $\angle {\delta }_1,\angle {\delta }_2$	0 to $2\pi$

, which represent realistic or even exaggerated system conditions.

The simulation results are illustrated in Figure 2. The scatter plot clearly demonstrates that the phase imbalance of $f_1$ is the dominant factor affecting $|{\delta }_c|$. Across all 10,000 random trials, $|{\delta }_c|$ exceeded 0 dB only when the phase imbalance approached the extreme values of $\pm {90}^{\circ }$.

The simulation results reveal a clear correspondence among the transmit imbalance phase $\angle f_1$, the equivalent crosstalk magnitude $|{\delta }_c|$, and the transmitted polarization state:

• When $|\angle f_1| < {90}^{\circ }$: $|{\delta }_c| < 0$ dB, RHCP component dominates, the transmitted wave is right-hand elliptically polarized
• When $|\angle f_1| = {90}^{\circ }$: $|{\delta }_c| = 0$ dB, LHCP and RHCP components have equal amplitudes, the transmitted wave degenerates into linear polarization
• When $|\angle f_1| > {90}^{\circ }$: $|{\delta }_c| > 0$ dB, LHCP component dominates, the transmitted wave becomes left-hand elliptically polarized

Therefore, $\angle f_1 = \pm {90}^{\circ }$ represents the critical point where the circular polarization sense reverses.

• Method I: Ambiguity Elimination Based on $|{\delta }_c| < 0$ dB Prior

Under normal circumstances, after adjustment in an anechoic chamber, the transmit antenna can be ensured to radiate a right-hand elliptically polarized wave, which at least will not degenerate into linear polarization or even left-hand elliptical polarization. This implies that the prior knowledge of “transmission dominated by RHCP” holds, i.e., $|{\delta }_c| < 0$ dB.

As discussed previously, each dihedral combination yields two solution pairs $({\delta }_c^{\prime },f_r^{\prime })$ and $({\delta }_c^{″},f_r^{″})$, of which only one corresponds to the true distortion parameters. To demonstrate how to eliminate the ambiguous solution using prior knowledge, Monte Carlo simulations are conducted using the 0° and 45° dihedral combination as an example. The simulation parameters are configured as shown in

Table 2. Simulation Parameter Settings for Ambiguity Elimination.

Parameter	Range
Equivalent crosstalk amplitude $|{\delta }_c|$	$-30$ dB to $-10$ dB (swept)
Equivalent crosstalk phase $\angle {\delta }_c$	0 to $2\pi$ (random)
Receive imbalance amplitude $|f_r|$	$-3$ dB to $+3$ dB (random)
Receive imbalance phase $\angle f_r$	0 to $2\pi$ (random)
Calibrator gain amplitude	0 to 1 (random)
Calibrator gain phase	0 to $2\pi$ (random)
Faraday rotation angle $\mathrm{\Omega }$	0 to $2\pi$ (random)

.

The equivalent crosstalk amplitude is swept from $-30$ dB to $-10$ dB, while all other parameters, including receive imbalance, calibrator gains, and Faraday rotation angle, are randomly generated within their respective ranges to verify the algorithm’s robustness. The simulation results are shown in Figure 3. The magnitudes of the two estimated ${\delta }_c$ values form two distinct lines symmetric about 0 dB, with the lower line corresponding to the correct solution. Therefore, the ambiguity elimination criterion is as follows: after computing ${\delta }_c^{\prime }$ and ${\delta }_c^{″}$, the solution with magnitude less than 0 dB is selected as the true estimate of the equivalent crosstalk, and the corresponding $f_r^{\prime }$ or $f_r^{″}$ is taken as the correct estimate of the receive imbalance.

• Method II: Cross-Validation with Multiple Dihedral Combinations

To make the algorithm applicable to more general scenarios, this section considers cases where the prior knowledge does not hold. When the RHCP characteristic of the transmit antenna cannot be guaranteed, and the polarization sense is severely distorted to linear polarization or even LHCP, the prior knowledge of $|{\delta }_c| < 0$ dB is no longer valid, and the ambiguity elimination criterion of Method I will fail. To address this issue, this section proposes a cross-validation-based ambiguity elimination method.

From the analysis in the previous section, we know that the magnitudes of the two ${\delta }_c$ solutions are symmetric about 0 dB, i.e., $|{\delta }_c^{\prime }|·|{\delta }_c^{″}|=1$. This section further analyzes the complex product relationship between the two solutions. Through derivation, it can be shown that solutions from different dihedral combinations satisfy ${\delta }_c^{\prime }·{\delta }_c^{″} = P$, where P is a constant related to the specific combination, as shown in

Table 3. Product Constants for Different Dihedral Combinations.

Combination	${\mathit{\delta }}_{\mathit{c}}^{\prime }·{\mathit{\delta }}_{\mathit{c}}^{″}$
0° + 45°	1
0° + 22.5°	j
0° + 67.5°	$-j$
45° + 22.5°	$-j$
45° + 67.5°	j
22.5° + 67.5°	$-1$

.

As shown in the table, different combinations have different product constants P, which forms the theoretical basis for the cross-validation method. Consider using three dihedral calibrators (e.g., 0°, 45°, and 22.5°), which can form two equation sets: Combination I (0° + 45°, $P=1$) and Combination II (0° + 22.5°, $P=j$). Since the two combinations have different P values (1 and j, respectively), the true solutions remain identical while the ambiguous solutions differ by a 90° phase. Therefore, the ambiguity elimination criterion is as follows: solve the two equation sets separately to obtain four solutions, and the two solutions that are numerically close to each other are the true solutions. This method requires at least three dihedral calibrators, and the two selected equation sets must have different product constants P. As shown in the table, combination pairs with identical P values should be avoided. For example, 0° + 22.5° and 45° + 67.5° both have $P=j$, making it impossible to distinguish between the true and ambiguous solutions through cross-validation.

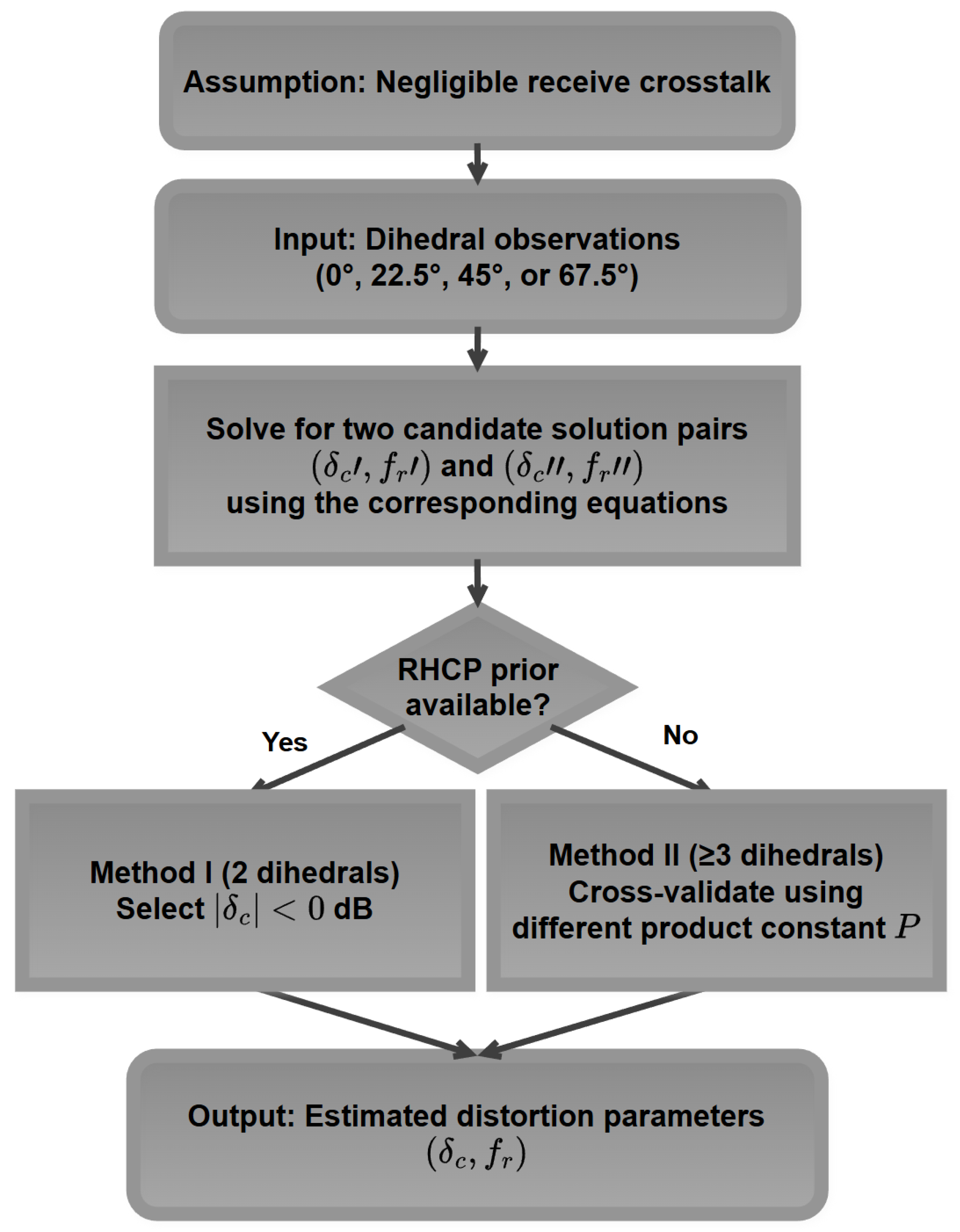
To provide a clear overview of the proposed calibration algorithm, the processing flowchart is illustrated in Figure 4. The algorithm first assumes negligible received crosstalk, then takes dihedral observations as input and solves for two candidate solution pairs using the corresponding equations. The ambiguity elimination step selects the correct solution based on either the RHCP prior (Method I, requiring only 2 dihedrals) or cross-validation with different product constants (Method II, requiring at least 3 dihedrals). Finally, the estimated distortion parameters $({\delta }_c,f_r)$ are output.

2.3.2. Extension to $\pi$/4 Mode

The proposed calibration framework can be extended to the $\pi$/4 mode by replacing the circularly polarized transmission vector with a 45° linearly polarized vector. In the $\pi$/4 mode, the ideal transmission polarization is ${[1,1]}^T$, and the equivalent crosstalk ${\delta }_c$ represents the ratio of the $-45°$ linearly polarized component to the ideal $+45°$ component.

However, mathematical analysis reveals that the solution symmetry property does not hold for all dihedral combinations in the $\pi$/4 mode. Only the 0° + 45° combination yields two solutions that are symmetric about 0 dB (i.e., $|{\delta }_c^{\prime }|·|{\delta }_c^{″}|=1$), enabling ambiguity elimination via Method I when the equivalent crosstalk is small. For other dihedral combinations, the product of the two solutions is no longer a fixed constant but depends on the observation values themselves, which is in stark contrast to the CTLR mode. In the CTLR mode, all combinations yield solution products that are fixed constants (1, $-1$, j, or $-j$), with deterministic phase differences between different combinations that can be exploited for cross-validation and ambiguity identification. The $\pi$/4 mode lacks this property; when the equivalent crosstalk exceeds 0 dB, Method II cannot be used for ambiguity elimination, and the ambiguity elimination mechanism requires further investigation. Therefore, for the $\pi$/4 mode, the proposed method is currently applicable only to the 0°+45° dihedral combination with Method I (the $|{\delta }_c| < 0$ dB prior), and the solution equations are given in (17).

$\pi$/4 Mode—Combination: 0° + 45°

$$\mathrm{Solution}\mathrm{I}:\{\begin{array}{c}\hfill {\delta }_c^{\prime }={\displaystyle \frac{M_{RH}^{D0}{M}_{RV}^{D45}-M_{RV}^{D0}{M}_{RH}^{D45}+2M_{RH}^{D0}{M}_{RH}^{D45}\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}}{M_{RH}^{D0}{M}_{RV}^{D45}+M_{RV}^{D0}{M}_{RH}^{D45}}}\\ f_r^{\prime }=-\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}\hfill \end{array}$$

(17a)

$$\mathrm{Solution}\mathrm{II}:\{\begin{array}{c}\hfill {\delta }_c^{″}={\displaystyle \frac{M_{RH}^{D0}{M}_{RV}^{D45}-M_{RV}^{D0}{M}_{RH}^{D45}-2M_{RH}^{D0}{M}_{RH}^{D45}\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}}{M_{RH}^{D0}{M}_{RV}^{D45}+M_{RV}^{D0}{M}_{RH}^{D45}}}\\ f_r^{″}=\sqrt{-{\displaystyle \frac{M_{RV}^{D0}{M}_{RV}^{D45}}{M_{RH}^{D0}{M}_{RH}^{D45}}}}\hfill \end{array}$$

(17b)

3. Results

This section analyzes the sensitivity of the proposed estimation method to various error sources, including received crosstalk, signal-to-noise ratio (SNR), and polarization orientation angle shift (POAS). Throughout this section, it is assumed that the transmit antenna radiates a right-hand elliptically polarized wave, ensuring $|{\delta }_c| < 0$ dB, such that the correct solution can be reliably selected using Method I. Under this assumption, the estimation errors arising from non-ideal system conditions are systematically evaluated through Monte Carlo simulations. Finally, experimental validation using GF-3 satellite data is presented to demonstrate the effectiveness of the proposed approach.

3.1. Sensitivity to Received Crosstalk

$${\delta }_c^{res}={\delta }_c-{\widehat{\delta }}_c{f}_r^{res}={\displaystyle \frac{f_r}{{\widehat{f}}_r}}$$

(18)

Taking the combination of the $0^{\circ }$ and ${45}^{\circ }$ dihedral reflectors as an example, the case with received crosstalk ${\delta }_r$ is considered. The crosstalk amplitude is assumed to increase from −40 dB to −20 dB, with a random phase. For each crosstalk amplitude, 200 simulations are performed to evaluate the residual estimation error (defined in (18)). The simulation parameters are set as follows, and the results are shown in Figure 5.

$$\begin{array}{cc}{\delta }_3,{\delta }_4\hfill & ={\delta }_r=[0.01-0.1]exp\left(i2\pi U(0,1)\right)\hfill \\ I_{D0},I_{D45}\hfill & =U(0,1)exp\left(i2\pi U\right(0,1\left)\right)\hfill \\ {\delta }_c\hfill & =(0.03+0.28U(0,1\left)\right)exp\left(i2\pi U\right(0,1\left)\right)\hfill \\ f_r\hfill & =(0.71+0.7U(0,1\left)\right)exp\left(i2\pi U\right(0,1\left)\right)\hfill \end{array}$$

The results show that the residual errors in estimating distortion parameters increase with the rise of the received crosstalk level. Considering the current polarization accuracy requirements—amplitude imbalance controlled within ±1 dB, phase imbalance within ±10°, and crosstalk level not exceeding −30 dB—the algorithm requires the maximum received crosstalk to be below −25 dB to meet these specifications.

3.2. Sensitivity to SNR

The proposed algorithm is particularly applicable to frequency bands significantly affected by the ionosphere, such as the P-band, where Faraday rotation is most pronounced. However, the International Telecommunication Union (ITU) regulations impose a 6 MHz bandwidth limitation on spaceborne P-band SAR systems [10]. This bandwidth constraint results in a slant-range spatial resolution of approximately 25 m, corresponding to a ground-range resolution of about 50 m at an incidence angle of 30°. The relatively coarse resolution leads to larger pixel areas, which in turn increases the integrated clutter energy and may degrade calibration accuracy [10]. To assess the impact of clutter and noise on calibration performance, or equivalently, to determine the required SNR, the algorithm’s robustness is evaluated under various SNR conditions. In practical deployments, corner reflectors should be positioned in areas with sufficiently low backscatter to maintain high SNR and minimize clutter interference.

The simulation parameters are set as follows: to study the impact of clutter on the calibration algorithm, an SNR range of 20–50 dB is chosen, with the polarization distortion parameters kept random. The simulation experiment uses a combination of 0° and 45° dihedral calibrators, and the estimated residual errors of the algorithm at different SNRs are shown in Figure 6. From Figure 6a,b, it can be seen that when the SNR exceeds 30 dB, the imbalance residual error is less than 1 dB, and the imbalance phase remains within ±10 degrees. Figure 6c shows that the residual equivalent crosstalk magnitude is linearly related to the SNR, and when the SNR exceeds 35 dB, the residual equivalent crosstalk magnitude is less than −30 dB.

3.3. Sensitivity to POAS

Due to the instability of the satellite platform attitude [17] and the terrain slope at the calibrator’s location [18], the actual scattering matrix may differ from the theoretical value. These non-ideal factors are collectively referred to as POAS. The scattering matrix affected by POAS can be expressed as follows [19], where $\theta$ denotes the POAS angle.

$$\begin{array}{cc}\hfill {\mathbf{S}}_{\theta }& =\mathbf{D}\left(\theta \right)\mathbf{S}{\mathbf{D}}^{-1}\left(\theta \right),\hfill \\ \hfill \mathrm{where}\mathbf{D}\left(\theta \right)& =\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\hfill \end{array}$$

(19)

Under the assumption of no received crosstalk, the POAS range is set to ±10° in the simulation, while other distortion parameters remain random. Taking the 0° and 45° dihedral reflectors as examples, POAS is added in two scenarios: applied to both dihedrals simultaneously (simulating overall rotation due to satellite attitude instability), and applied only to the 45° dihedral (simulating the impact of terrain slope). The corresponding residual errors are shown in Figure 7.

The results indicate that overall POAS does not affect the calibration of imbalance terms, suggesting that the imbalance estimation can be completed as long as the relative orientation between the dihedral reflectors remains unchanged. As shown in Figure 7c–f, when the relative angular error between the dihedrals is less than 5°, the residual imbalance meets the requirements of ±1 dB and ±10°. To ensure that the residual equivalent crosstalk remains below −30 dB, POAS should be controlled within ±1°.

3.4. Validation of the Proposed Method with GF-3 Data

This section validates the proposed algorithm using fully polarimetric calibrated data acquired by the GF-3 satellite. The GF-3 satellite has been extensively used for SAR calibration research [15,20]. The experimental data were acquired on 19 January 2019 at 10:00:54 (UTC) in QPSI mode, with a nominal resolution of 8 m. The data used are Single Look Complex (SLC) products, which preserve the original amplitude and phase information.

As shown in Figure 8, the calibration site is located in northern Beijing (approximately 40.14°N, 116.37°E), situated on flat bare ground with low backscatter. The site is equipped with multiple polarimetric calibrators, including trihedral corner reflectors, a 0° dihedral (D0), and two 67.5° rotated dihedrals (D67.5), with an inter-calibrator spacing of approximately 27 m. The bare ground background ensures high signal-to-clutter ratio, with measured values of approximately 35 dB. The GF-3 data have undergone full polarimetric calibration and can be considered as ideal polarimetric data, and the scattering matrices of D0 and D67.5 extracted from the data are given as follows:

$$\begin{array}{cc}\hfill S_{D0}& =\left[\begin{array}{cc}1.0000\angle 0.{00}^{\circ }& 0.0194\angle 84.{08}^{\circ }\\ 0.0133\angle -130.{13}^{\circ }& 1.0151\angle 178.{55}^{\circ }\end{array}\right]\hfill \\ \hfill S_{D67.5}& =\left[\begin{array}{cc}1.0000\angle 0.{00}^{\circ }& 1.0423\angle -177.{80}^{\circ }\\ 1.0265\angle -177.{20}^{\circ }& 1.0149\angle -179.{57}^{\circ }\end{array}\right]\hfill \end{array}$$

To validate the estimation accuracy of the proposed algorithm, the following simulation procedure is adopted. The fully polarimetric calibrated GF-3 data described above are used as ideal data, into which polarimetric distortion parameters are artificially introduced to simulate non-ideal CTLR-mode reception. Specifically, the equivalent crosstalk amplitude is randomly varied from $-30$ dB to $-10$ dB with random phase, and the receive imbalance amplitude is randomly varied from $-3$ dB to $+3$ dB with random phase. The CTLR-mode observation data are generated by right-multiplying the fully polarimetric data with the circularly polarized Jones vector. A total of 1000 sets of random distortion parameters are generated, and the estimation is performed for each set using (14). The estimation errors are then calculated, and the error statistics are presented in

Table 4. RMSE of Estimated Distortion Parameters.

Distortion Parameter	RMSE
Amplitude imbalance (dB)	0.0968
Phase imbalance (°)	1.1318
Equivalent crosstalk amplitude (dB)	0.4180

. The results show that the algorithm can achieve high precision parameter estimation, with the amplitude imbalance estimation performing the best.

According to the relevant literature, the polarimetric calibration parameters of this image are: transmit crosstalk $|{\delta }_1| = -34.2$ dB, $|{\delta }_2| = -35.8$ dB; transmit imbalance $|f_1| = 0.42$ dB, $\angle f_1 = 4.3^{\circ }$; received crosstalk $|{\delta }_3| = -35.1$ dB, $|{\delta }_4| = -34.7$ dB; receive imbalance $|f_2| = 0.51$ dB, $\angle f_2 = 5.2^{\circ }$. These distortion parameters are introduced into the calibrated GF-3 fully polarimetric data to restore the uncalibrated data, and compact polarimetric observation data are then simulated. The 0° and 67.5° dihedral reflectors in the scene are used for calibration. The true equivalent crosstalk ${\delta }_c$ is calculated from the transmit-side distortion parameters using (3). The calibration results and error analysis are presented in

Table 5. Calibration Results Based on GF-3 System Distortion Parameters.

Parameter	True Value	Estimated Value	Amp. Error	Phase Error
Equivalent crosstalk ${\delta }_c$	$-27.46$ dB	$-27.35$ dB	0.11 dB	—
Receive imbalance $f_r$	0.51 dB, $5.{20}^{\circ }$	0.54 dB, $4.{74}^{\circ }$	0.03 dB	$0.{46}^{\circ }$

.

The results demonstrate that the proposed algorithm achieves high estimation accuracy under GF-3 system conditions: the amplitude error of receive imbalance is only 0.03 dB with a phase error of $0.{46}^{\circ }$; the amplitude error of equivalent crosstalk is 0.11 dB, validating the effectiveness of the algorithm.

4. Discussion

To comprehensively evaluate the performance of the proposed algorithm, a comparative simulation study is conducted with Chen’s method [10] and Truong’s method [9]. The calibrator configurations for the three methods are as follows: Chen’s method employs the optimal calibrator combination (as specified in Equation (26) of their original paper [10]), consisting of two active radar calibrators (PARCX and PARCY) along with a vertical gridded trihedral (Gt1) and a horizontal gridded trihedral (Gt2); Truong’s method uses a trihedral, a 0° dihedral, and a 45° dihedral; the proposed method is demonstrated using the combination of 0° and 45° dihedrals. The simulation employs the Monte Carlo method with 1000 independent trials, where the distortion parameters are randomly generated within the ranges specified in

Table 6. Simulation Parameter Ranges for Algorithm Comparison.

Parameter	Range
Receive imbalance amplitude $|f_r|$	$-3$ dB to $+3$ dB
Receive imbalance phase $\angle f_r$	$-{180}^{\circ }$ to $+{180}^{\circ }$
Received crosstalk $|{\delta }_3|$, $|{\delta }_4|$	$-40$ dB to $-20$ dB
Equivalent crosstalk $|{\delta }_c|$	$-30$ dB to $-10$ dB
Faraday rotation angle $\mathrm{\Omega }$	0 to $2\pi$
Calibrator gain amplitude	$-10$ dB to $+10$ dB

, and it is assumed that all calibrators experience the same double-pass Faraday rotation.

The simulation results are presented in Figure 9 and Figure 10. Figure 9 shows the box plots of receive imbalance estimation errors for the three methods, including both amplitude and phase errors. Figure 10 displays the box plots of crosstalk estimation errors. The root mean square errors (RMSE) of the parameter estimates are summarized in

Table 7. RMSE Comparison of Distortion Parameter Estimation Among Different Calibration Methods.

Method	$|{\mathit{f}}_{\mathit{r}}|$ (dB)	$\mathit{\angle }{\mathit{f}}_{\mathit{r}}$ (°)	$|{\mathit{\delta }}_{\mathit{c}}|$ (dB)	$|{\mathit{\delta }}_3|$ (dB)	$|{\mathit{\delta }}_4|$ (dB)	$\mathrm{\Omega }$ (°)
Chen [10]	5.87	45.80	19.39	36.83	37.48	25.57
Truong [9]	1.32	8.62	—	31.69	31.69	124.31
Proposed	0.18	1.15	0.17	—	—	—

Note: “—” indicates that the parameter is not estimated by the corresponding algorithm.

, where “—” indicates that the corresponding parameter is not estimated by the algorithm.

Figure 9 illustrates the estimation performance of the three algorithms for receive imbalance parameters. The box plots clearly show that the proposed algorithm exhibits the most concentrated error distribution, closely aligned with the ideal zero-error line. Specifically, the RMSE of amplitude imbalance is 0.18 dB and the RMSE of phase imbalance is 1.15°, both significantly superior to Chen’s method (5.87 dB, 45.80°) and Truong’s method (1.32 dB, 8.62°). Truong’s method outperforms Chen’s method because its estimation formulas employ ratios of observations, partially eliminating the influence of the absolute factor. However, since it assumes ideal circular polarization at the transmitter and neglects the equivalent crosstalk, the estimation results still exhibit certain biases.

Figure 10a compares the estimation accuracy of equivalent crosstalk between the proposed algorithm and Chen’s algorithm (Truong’s method assumes ideal circular polarization transmission and does not estimate this parameter). The proposed algorithm achieves estimation results close to the ideal value with an RMSE of only 0.17 dB, while Chen’s method exhibits an RMSE as high as 19.39 dB with significant deviation.

The fundamental cause of this difference lies in the model assumptions. Chen’s method requires precise modeling to remove the amplitude gain and two-way phase of each calibrator’s scattering matrix before calibration, and this removal must be in absolute terms rather than relative corrections between calibrators. However, no mature method currently exists to precisely calculate the absolute scattering response of calibrators. Consequently, in practical calibration processes, the unknown absolute factor significantly affects the estimation accuracy of this algorithm. In contrast, the proposed algorithm incorporates the absolute factor into the unknown parameters during modeling and naturally eliminates its influence through the construction of observation ratios, resulting in more robust calibration performance.

Figure 10b,c present the estimation performance of Chen’s method and Truong’s method for receive crosstalk ${\delta }_3$ and ${\delta }_4$, respectively. The results indicate that both algorithms exhibit estimation errors exceeding 30 dB, far beyond acceptable accuracy levels and unusable in practical applications. The proposed method adopts the assumption of negligible received crosstalk based on the engineering reality that modern polarimetric SAR systems can achieve received crosstalk below $-30$ dB, thereby simplifying the system model. This assumption has been validated in the sensitivity analysis in Section 3.1: when received crosstalk is below $-25$ dB, the impact on the estimation accuracy of the proposed algorithm is acceptable.

Both Chen’s method and Truong’s method require estimation of the Faraday rotation angle, with RMSEs of 25.57° and 124.31°, respectively. Such large estimation errors will further degrade the solution accuracy of other distortion parameters through error propagation. Moreover, both methods assume uniform Faraday rotation across the entire scene in their modeling. However, as discussed in Section 2, Faraday rotation angles exhibit significant spatial variations: under disturbed ionospheric conditions, the Faraday rotation angle can differ by tens of degrees at different locations within the same image. When calibrators are distributed at different positions in the scene, the assumption of “uniform Faraday rotation” no longer holds, leading to further increased estimation errors. The proposed algorithm exploits the inherent double-pass Faraday rotation invariance property of dihedral reflector scattering matrices, fundamentally circumventing this influence factor. Regardless of ionospheric conditions, as long as the geometric accuracy and deployment precision of the calibrators are ensured, the estimation accuracy of the algorithm remains unaffected by Faraday rotation.

5. Conclusions

This paper presents a novel compact polarimetric CTLR mode calibration method that requires only dihedral reflectors to estimate polarimetric distortion parameters. The proposed method relies solely on the assumption of negligible received crosstalk and offers the following key advantages over conventional approaches.

First, the estimated distortion parameters are inherently immune to Faraday rotation effects. This is achieved by leveraging the fundamental property that dihedral reflector scattering matrices remain invariant under double-pass Faraday rotation. This characteristic makes the proposed method particularly suitable for low-frequency SAR systems (e.g., P-band and L-band) where ionospheric effects are pronounced, eliminating the need for prior knowledge or estimation of the Faraday rotation angle at the calibration site. Second, two ambiguity elimination strategies are proposed: when the transmitter distortion is small and can guarantee the transmission of a right-hand elliptically polarized wave, only two dihedral calibrators are required for ambiguity elimination; when the transmitter distortion is severe, at least three dihedrals can be used for ambiguity elimination through cross-validation.

Through comprehensive simulation analysis, the algorithm’s sensitivity to practical system imperfections has been systematically investigated, including received crosstalk, noise, and POAS. The results demonstrate that to maintain residual receive imbalance amplitude within ±1 dB, phase within ±10°, and residual equivalent crosstalk below −30 dB, the system must satisfy the following requirements: received crosstalk below −25 dB, SNR exceeding 35 dB, and POAS controlled within ±1°. The feasibility and effectiveness of the proposed algorithm have been further validated using fully polarimetric GF-3 satellite data, achieving RMSEs of 0.0968 dB, 1.1318°, and 0.4180 dB for amplitude imbalance, phase imbalance, and equivalent crosstalk amplitude, respectively. Furthermore, comparative simulations with Chen’s method and Truong’s method under identical random distortion parameters demonstrate that the proposed method achieves significantly higher calibration accuracy than existing approaches, providing clear guidelines for the practical deployment of calibration targets.