An Enhanced Three-Dimensional Wind Retrieval Method Based on Genetic Algorithm-Particle Swarm Optimization for Coherent Doppler Wind Lidar
Abstract
1. Introduction
2. Materials and Methods
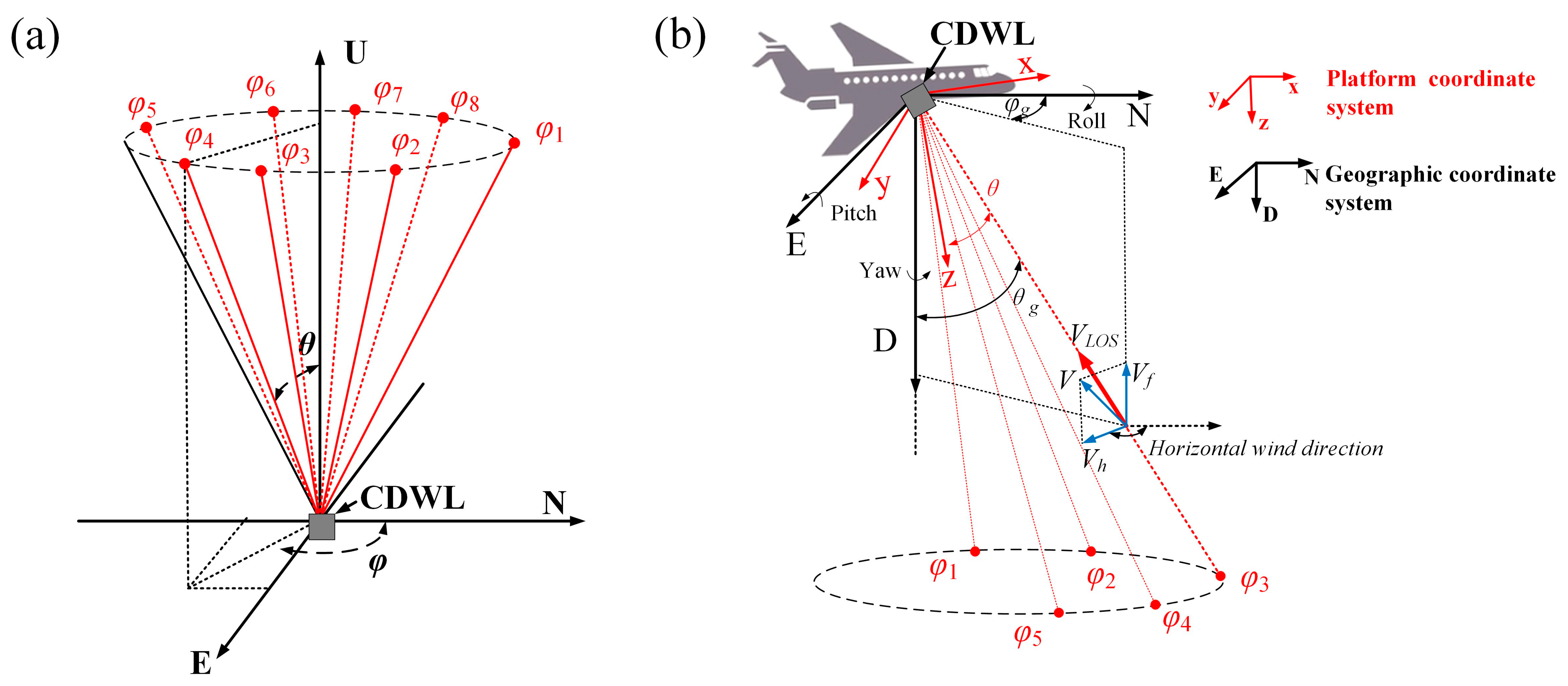
2.1. Principle of Three-Dimensional Wind Retrieval
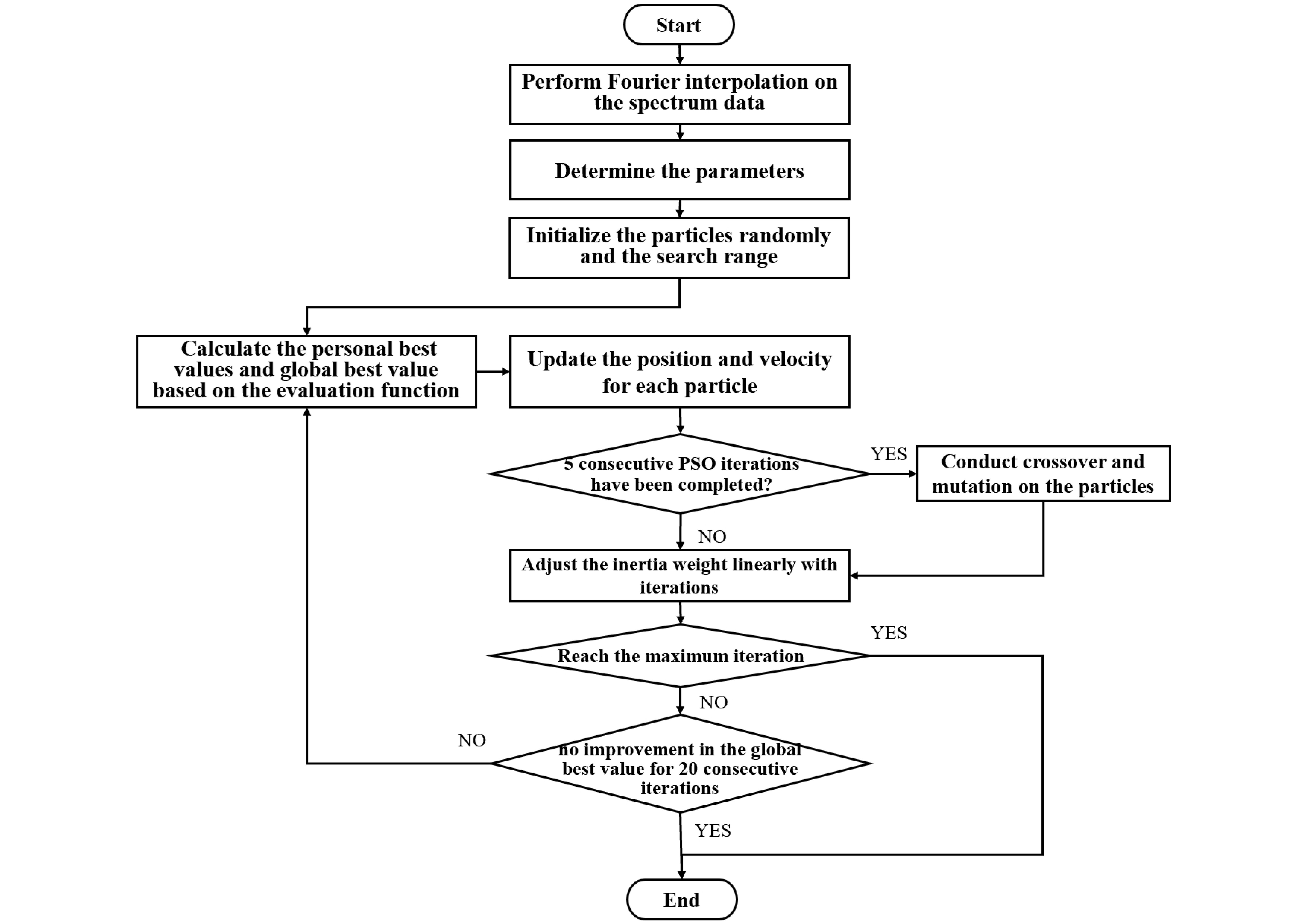
2.2. GA-PSO Algorithm
- (1)
- Experimental spectrum data often suffer from limited frequency resolution. In order to mitigate this limitation, Fourier interpolation is applied to the spectrum data, a method that has been proven effective in refining spectrum resolution [11]. After interpolation, the spectrum resolution is better than 0.05 MHz.
- (2)
- The particle swarm size is set to 50, and the maximum number of iterations is set to 200. The initial inertia weight w is set to 0.95 and decreases linearly with iterations. The cognitive learning factor c1 is set to 0.85, and the social learning factor c2 is set to 1.95. The crossover and mutation mechanisms of the genetic algorithm are introduced to enhance global search capabilities, with a crossover probability Pc of 0.2 and a mutation probability Pm of 0.35. The evaluation function is defined by Equation (5), and the total number of azimuths is set to 16. The length of the iterative evaluation register is set to 20.
- (3)
- The dimension of the problem space, d, is set to 3, corresponding to vx, vy, and vz. For the first range gate, the DSWF method is employed to compute the 3D wind speeds vx1, vy1, and vz1, which serve as the initial search center. The search range is defined as (vx1 ± 7.5 m/s, vy1 ± 7.5 m/s, vz1 ± 1 m/s), with a search step size of 0.01 m/s. The initial positions of the particle swarm are randomly assigned within the search range, and their initial velocities are also randomized. Iterative optimization is then conducted for the first range gate. By leveraging the spatial continuity of the wind field, the optimization process propagates solutions sequentially through subsequent range gates. Upon convergence at the current range gate, the optimal solution is propagated forward as the search center for the next range gate while maintaining the same search range.
- (4)
- The fitness function is applied to quantitatively evaluate each particle’s performance, simultaneously identifying both pbest and gbest solutions for the current iteration. Subsequently, particle positions and velocities are systematically updated according to Equations (6) and (7).
- (5)
- GA operations are implemented every 5 iterations to prevent premature convergence. Following the crossover probability Pc, adjacent particle pairs undergo a simple crossover operation, generating two new particle positions. Subsequently, based on the mutation probability Pm, perturbations are introduced to individual positions, effectively preventing the algorithm from falling into local optima.
- (6)
- Following each iteration, the algorithm performs a left-shift operation on the iterative evaluation register and updates it with the current gbest. Convergence is determined through gradient analysis of this register array. When the gradient becomes zero (indicating no improvement in the gbest for 20 consecutive iterations), the optimization process terminates, outputting the optimal 3D wind speed results. If the number of iterations reaches the preset maximum, the iteration is also stopped.
3. Results
3.1. Experiments Based on Simulated Signal
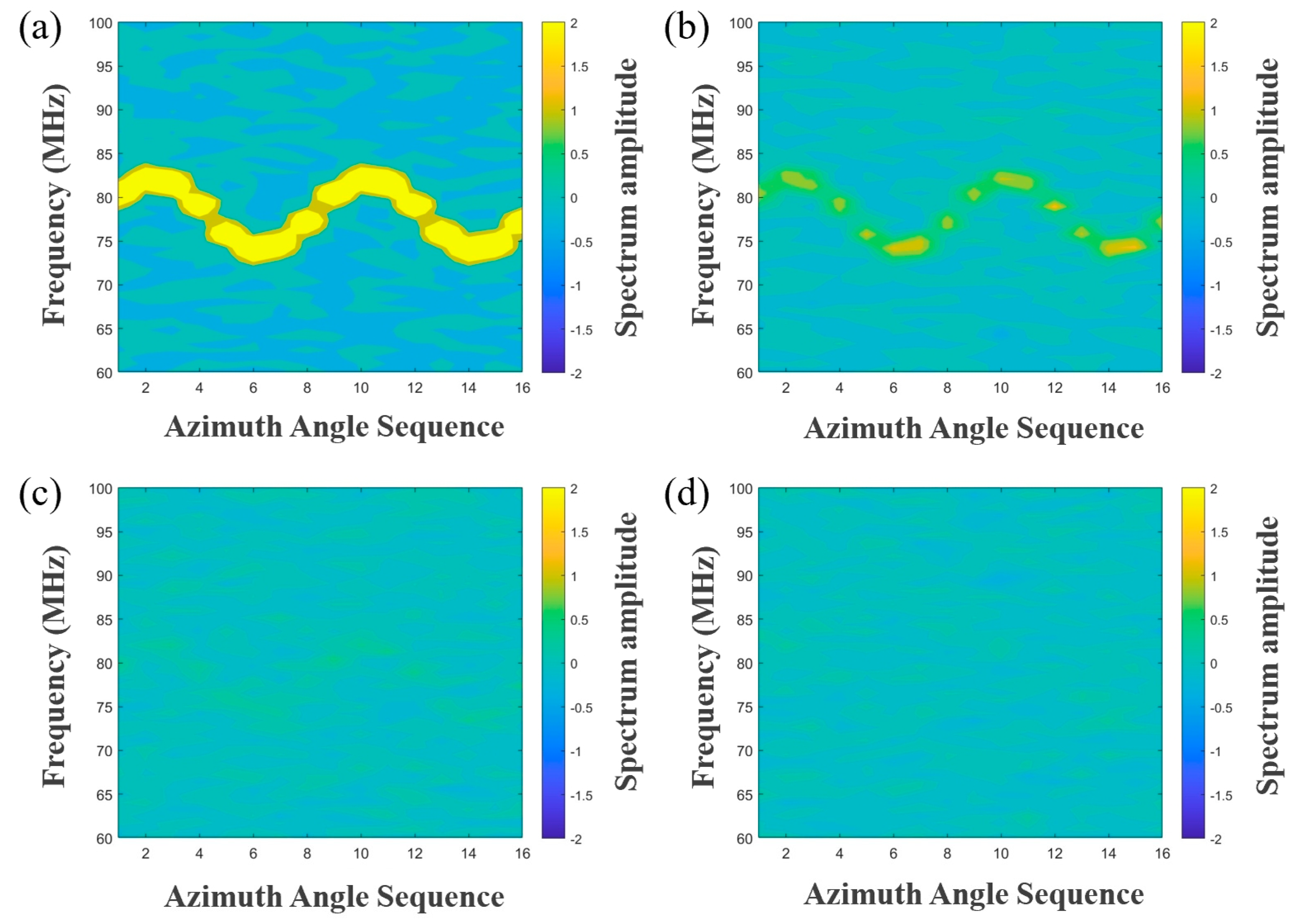
3.1.1. CDWL Signal Simulation
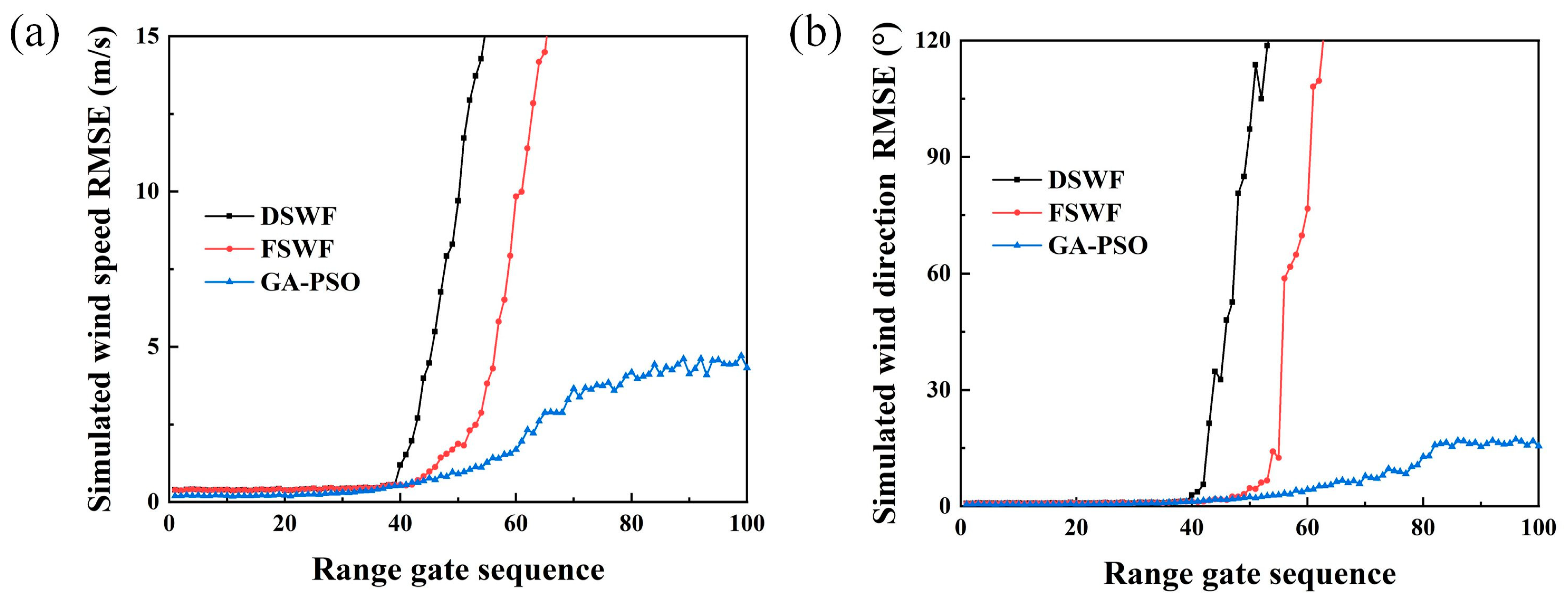
3.1.2. Performance Analysis
3.2. Field Experiments
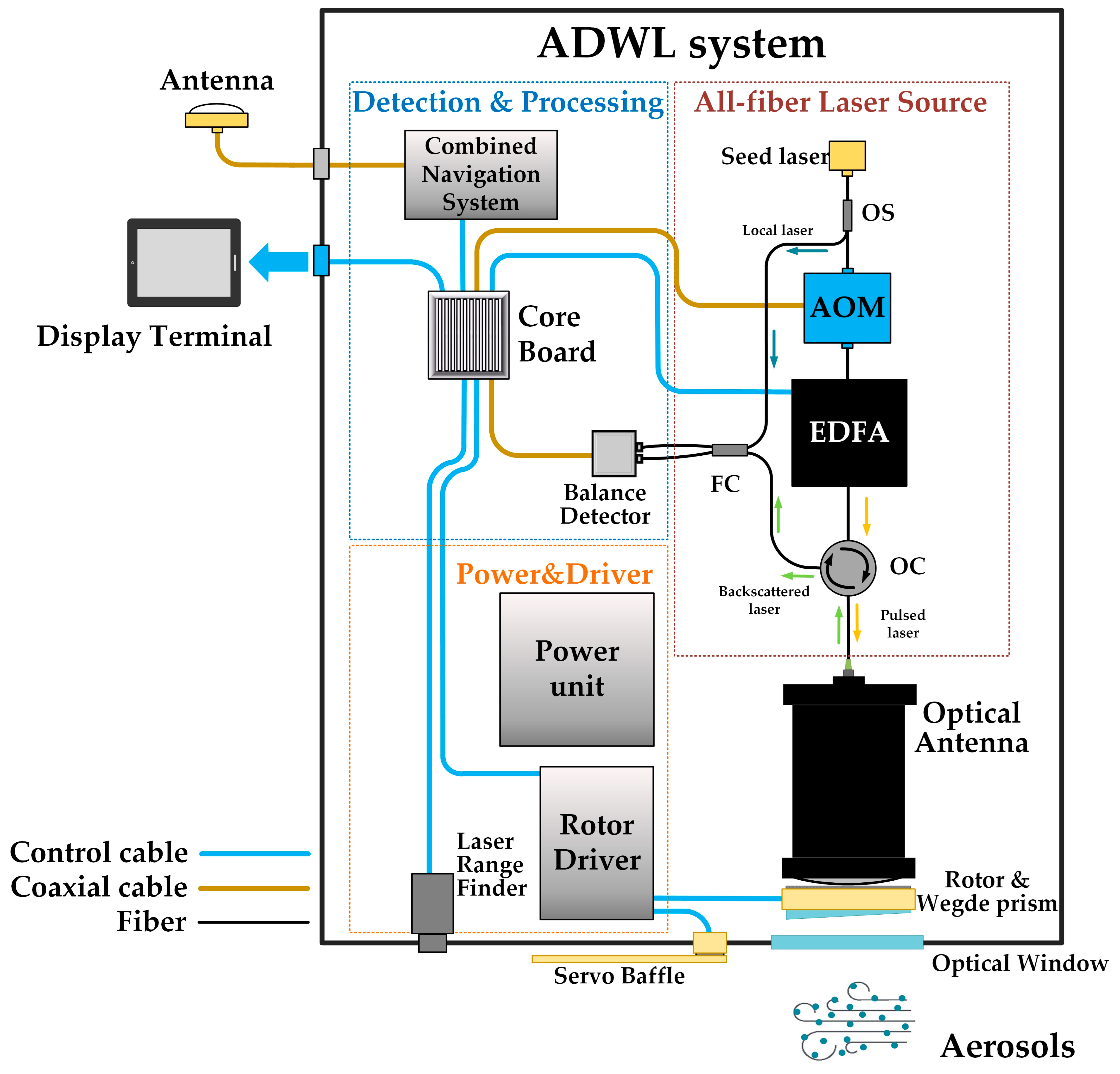
3.2.1. CDWL System
3.2.2. Ground-Based Experiments
3.2.3. Airborne Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, J.L.; Xia, H.Y.; Wei, T.W.; Wang, L.; Yue, B.; Wu, Y.B. Identifying cloud, precipitation, windshear, and turbulence by deep analysis of the power spectrum of coherent Doppler wind lidar. Opt. Express 2020, 12, 37406–37418. [Google Scholar] [CrossRef] [PubMed]
- Witschas, B.; Rahm, S.; Dörnbrack, A.; Wagner, J.; Rapp, M. Airborne Wind Lidar Measurements of Vertical and Horizontal Winds for the Investigation of Orographically Induced Gravity Waves. Atmos. Ocean. Technol. 2017, 34, 1371–1386. [Google Scholar] [CrossRef]
- Wang, L.; Wan, B.; Yang, Y.; Fan, S.; Jing, Y.; Cheng, X.; Gao, Z.; Miao, S.; Zou, H. Atmospheric Boundary Layer Stability in Urban Beijing: Insights from Meteorological Tower and Doppler Wind Lidar. Remote Sens. 2024, 16, 4246. [Google Scholar] [CrossRef]
- Liu, Z.; Barlow, J.F.; Chan, P.-W.; Fung, J.C.H.; Li, Y.; Ren, C.; Mak, H.W.L.; Ng, E. A Review of Progress and Applications of Pulsed Doppler Wind LiDARs. Remote Sens. 2019, 11, 2522. [Google Scholar] [CrossRef]
- Wang, K.X.; Gao, C.Q.; Lin, Z.F.; Wang, Q.; Gao, M.W.; Huang, S.; Chen, C.Y. 1645 nm coherent Doppler wind lidar with a single-frequency Er:YAG laser. Opt. Express 2020, 28, 14694–14704. [Google Scholar] [CrossRef]
- Bu, L.; Qiu, Z.; Gao, H.; Zhu, X.; Liu, J. All-fiber pulse coherent Doppler LIDAR and its validations. Opt. Eng. 2015, 54, 123103. [Google Scholar] [CrossRef]
- Smalikho, I. Techniques of Wind Vector Estimation from Data Measured with a Scanning Coherent Doppler Lidar. J. Atmos. Ocean. Technol. 2003, 20, 276–291. [Google Scholar] [CrossRef]
- Zhu, J.S.; Li, Z.G.; Liu, Z.S. Horizontal wind velocity retrieval using a Levenberg-Marquardt algorithm for an airborne wind lidar. J. Appl. Remote Sens. 2016, 10, 026009. [Google Scholar] [CrossRef]
- Rui, X.B.; Guo, P.; Chen, H.; Chen, S.Y.; Zhang, Y.C. Adaptive iteratively reweighted sine wave fitting method for rapid wind vector estimation of pulsed coherent Doppler lidar. Opt. Express 2019, 27, 21319–21334. [Google Scholar] [CrossRef]
- Lin, R.; Guo, P.; Chen, H.; Chen, S.; Zhang, Y. Smoothed accumulated spectra based wDSWF method for real-time wind vector estimation of pulsed coherent Doppler lidar. Opt. Express 2022, 30, 180–194. [Google Scholar] [CrossRef]
- Stephan, A.; Wildmann, N.; Smalikho, I.N. Effectiveness of the MFAS Method for Determining the Wind Velocity Vector from Windcube 200s Lidar Measurements. Atmos. Ocean. Opt. 2019, 32, 555–563. [Google Scholar] [CrossRef]
- Augere, B.; Valla, M.; Durécu, A.; Dolfi-Bouteyre, A.; Goular, D.; Gustave, F.; Planchat, C.; Fleury, D.; Huet, T.; Besson, C. Three-Dimensional Wind Measurements with the Fibered Airborne Coherent Doppler Wind Lidar LIVE. Atmosphere 2019, 10, 549. [Google Scholar] [CrossRef]
- Yuan, L.C.; Liu, H.; Liu, J.Q.; Zhu, X.P.; Hu, G.Y.; Chen, W.B. Wind vector estimation of coherent doppler wind Lidar based on genetic algorithm. Chin. J. Lasers 2020, 47, 0810004. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, L.C.; Fan, C.C.; Zhu, X.P.; Liu, J.Q.; Dai, B.; Xiao, W.G.; Zhu, X.L.; Chen, W.B. Wind retrieval for genetic algorithm-based coherent Doppler wind lidar employing airborne platform. Appl. Phys. B Lasers Opt. 2023, 129, 36. [Google Scholar] [CrossRef]
- Liu, Z.; Yuan, L.C.; Tang, J.; Zhang, Y.P.; Liu, J.Q.; Zhu, X.P.; Yang, J.X.; Shi, W.; Chen, W.B. Coherent Doppler lidar wind retrieval for a typhoon based on the genetic simulated annealing algorithm. Chin. Opt. Lett. 2024, 22, 040101. [Google Scholar] [CrossRef]
- Caya, D.; Zawadzki, I. VAD Analysis of Nonlinear Wind Fields. J. Atmos. Oceanic Technol. 1992, 9, 575–587. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, S.; Luo, K.; Wang, L.; Tang, X. Airborne Radio-Echo Sounding Data Denoising Using Particle Swarm Optimization and Multivariate Variational Mode Decomposition. Remote Sens. 2023, 15, 5041. [Google Scholar] [CrossRef]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Boeringer, D.W.; Werner, D.H. A comparison of particle swarm optimization and genetic algorithms for a phased array synthesis problem. IEEE Antennas Propag. Soc. Int. Symp. 2003, 1, 181–184. [Google Scholar] [CrossRef]
- Lima, C.A., Jr.; Lapa, C.M.; do NA Pereira, C.M.; da Cunha, J.J.; Alvim, A.C. Comparison of computational performance of GA and PSO optimization techniques when designing similar systems—Typical PWR core case. Ann. Nucl. Energy 2011, 38, 1339–1346. [Google Scholar] [CrossRef]
- Salcedo-Bosch, A.; Farré-Guarné, J.; Araújo da Silva, M.P.; Rocadenbosch, F. A Unified Formulation for the Computation of the Six-Degrees-of-Freedom-Motion-Induced Errors in Floating Doppler Wind LiDARs. Remote Sens. 2023, 15, 1478. [Google Scholar] [CrossRef]
- Kameyama, S.; Ando, T.; Asaka, K.; Hirano, Y.; Wadaka, S. Performance of discrete-Fourier-transform-based velocity estimators for a wind-sensing coherent Doppler lidar system in the Kolmogorov turbulence regime. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3560–3569. [Google Scholar] [CrossRef]
- Yoshiki, W.; Yanagisawa, T.; Kameyama, S.; Imaki, M.; Sakaizawa, D. Theoretical performance of a 1.5-µm satellite-borne coherent Doppler wind lidar using a planar waveguide optical amplifier with a demonstrated figure of merit: Simulation of signal detection probability, measurement precision, and bias. Appl. Opt. 2024, 63, 1681–1694. [Google Scholar] [CrossRef]
- Kameyama, S.; Ando, T.; Asaka, K.; Hirano, Y.; Wadaka, S. Compact all-fiber pulsed coherent Doppler lidar system for wind sensing. Appl. Opt. 2007, 46, 1953–1962. [Google Scholar] [CrossRef]
- Dabas, A.; Flamant, P.H.; Salamitou, P. Characterization of pulsed coherent Doppler LIDAR with the speckle effect. Appl. Opt. 1994, 33, 6524–6532. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, Z.; Gao, C.; Han, C.; Fan, L.; Zhao, X. Evaluation and Wind Field Detection of Airborne Doppler Wind Lidar with Automatic Intelligent Processing in North China. Atmosphere 2024, 15, 536. [Google Scholar] [CrossRef]
- Vasiljević, N.; Lea, G.; Courtney, M.; Cariou, J.-P.; Mann, J.; Mikkelsen, T. Long-Range WindScanner System. Remote Sens. 2016, 8, 896. [Google Scholar] [CrossRef]
- Smalikho, I.N.; Banakh, V.A.; Razenkov, I.A.; Sukharev, A.A.; Falits, A.V.; Sherstobitov, A.M. Comparison of Results of Joint Wind Velocity Measurements with the Stream Line and WPL Coherent Doppler Lidars. Atmos. Ocean. Opt. 2022, 35, S79–S91. [Google Scholar] [CrossRef]
- Kotake, N.; Sakamaki, H.; Imaki, M.; Miwa, Y.; Ando, T.; Yabugaki, Y.; Enjo, M.; Kameyama, S. Intelligent and compact coherent Doppler lidar with fiber-based configuration for robust wind sensing in various atmospheric and environmental conditions. Opt. Express 2022, 30, 20038–20062. [Google Scholar] [CrossRef]
| Parameters | Value |
|---|---|
| Laser wavelength | 1550 nm |
| Pulse energy | 300 μJ |
| Sampling rate | 400 MHz |
| Intermediate frequency | 80 MHz |
| Bandwidth | 200 MHz |
| Telescope diameter | 100 mm |
| Accumulated number | 5000 |
| Zenith angle | 20° |
| System efficiency | 0.193 |
| Pulse width | 600 ns |
| Parameters | Value |
|---|---|
| Laser wavelength | 1550 nm |
| Maximum pulse energy | 300 μJ |
| Pulse width | 100 ns~600 ns selectable |
| Pulse repetition frequency | 10 kHz |
| Telescope aperture | 100 mm |
| Vertical range resolution | 20 m~100 m |
| Typical accumulated number | 5000 |
| Nadir angle | 20° |
| Sampling frequency | 400 MHz |
| Data rate | ~2 Hz |
| Weight | ~20 kg |
| Size | 250 mm × 250 mm × 400 mm |
| Consumption | ≤200 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zang, X.; Sang, Y.; Lian, X.; Gao, C. An Enhanced Three-Dimensional Wind Retrieval Method Based on Genetic Algorithm-Particle Swarm Optimization for Coherent Doppler Wind Lidar. Remote Sens. 2025, 17, 1616. https://doi.org/10.3390/rs17091616
Zhang X, Zang X, Sang Y, Lian X, Gao C. An Enhanced Three-Dimensional Wind Retrieval Method Based on Genetic Algorithm-Particle Swarm Optimization for Coherent Doppler Wind Lidar. Remote Sensing. 2025; 17(9):1616. https://doi.org/10.3390/rs17091616
Chicago/Turabian StyleZhang, Xu, Xianqing Zang, Yuxuan Sang, Xinwei Lian, and Chunqing Gao. 2025. "An Enhanced Three-Dimensional Wind Retrieval Method Based on Genetic Algorithm-Particle Swarm Optimization for Coherent Doppler Wind Lidar" Remote Sensing 17, no. 9: 1616. https://doi.org/10.3390/rs17091616
APA StyleZhang, X., Zang, X., Sang, Y., Lian, X., & Gao, C. (2025). An Enhanced Three-Dimensional Wind Retrieval Method Based on Genetic Algorithm-Particle Swarm Optimization for Coherent Doppler Wind Lidar. Remote Sensing, 17(9), 1616. https://doi.org/10.3390/rs17091616






