A High Resolution Spatially Consistent Global Dataset for CO2 Monitoring
Abstract
1. Introduction
- The design of a super resolution model for atmospheric CO2 data downscaling;
- The deployment of the model on a global scale and the release of a high-resolution global CO2 dataset;
- An illustration of the usefulness of the dataset with an example test case.
2. Materials and Methods
2.1. OCO-2 L3 Dataset
2.2. Total Carbon Column Network
2.3. Land Surface Temperature Dataset
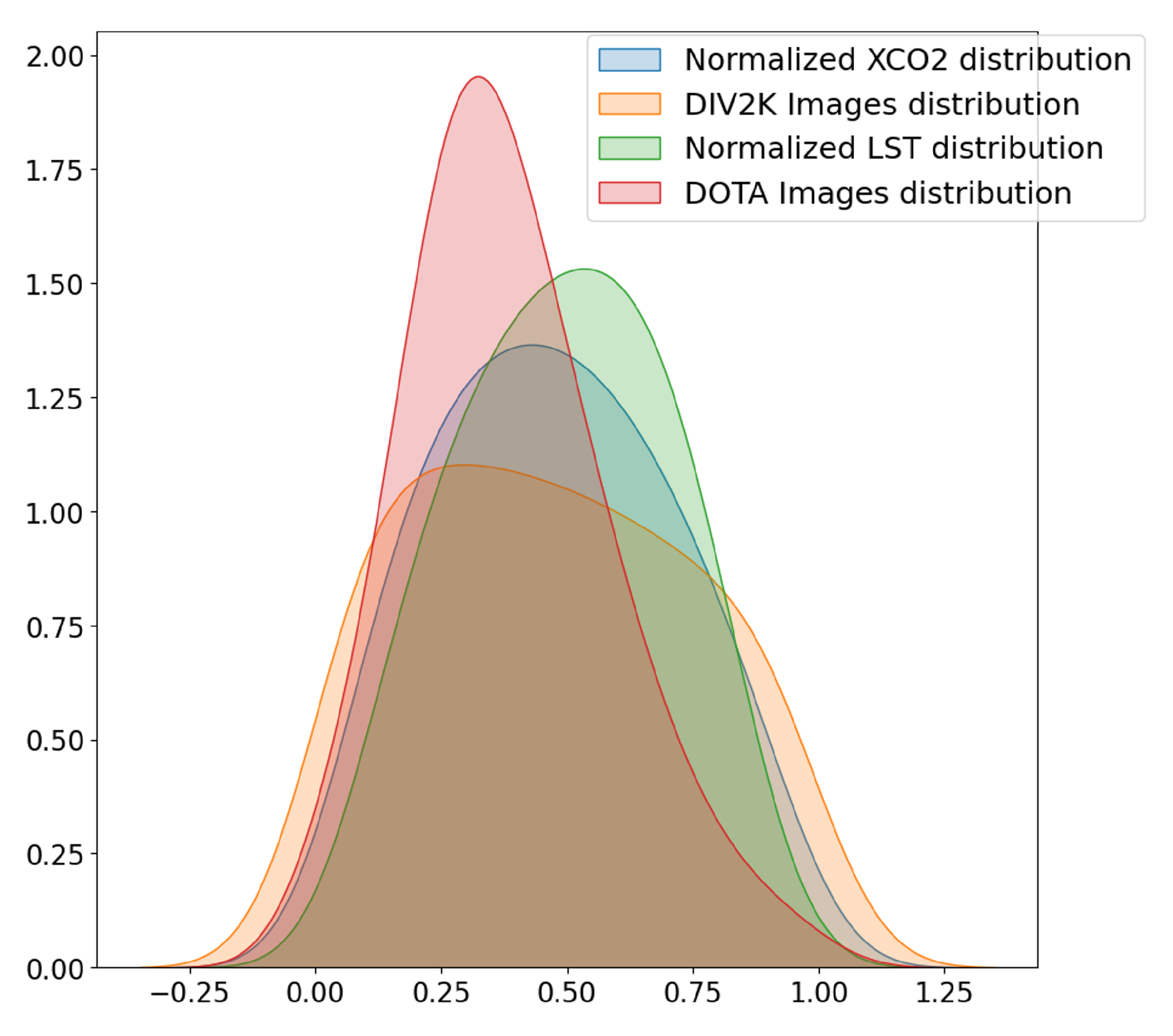
2.4. Data Pre-Analysis
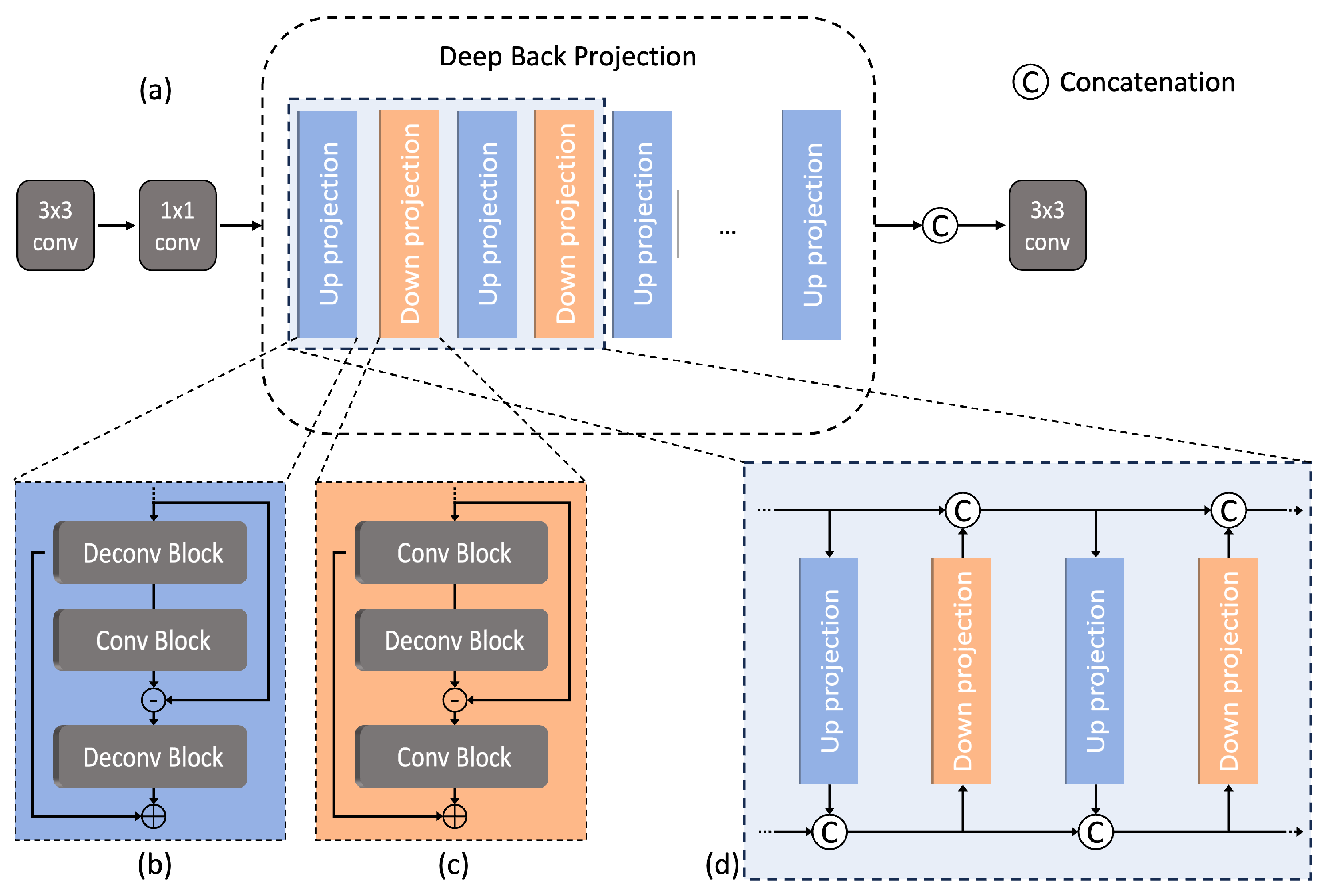
2.5. Downscaling Using Super Resolution
| Algorithm 1 Super resolution inference |
|
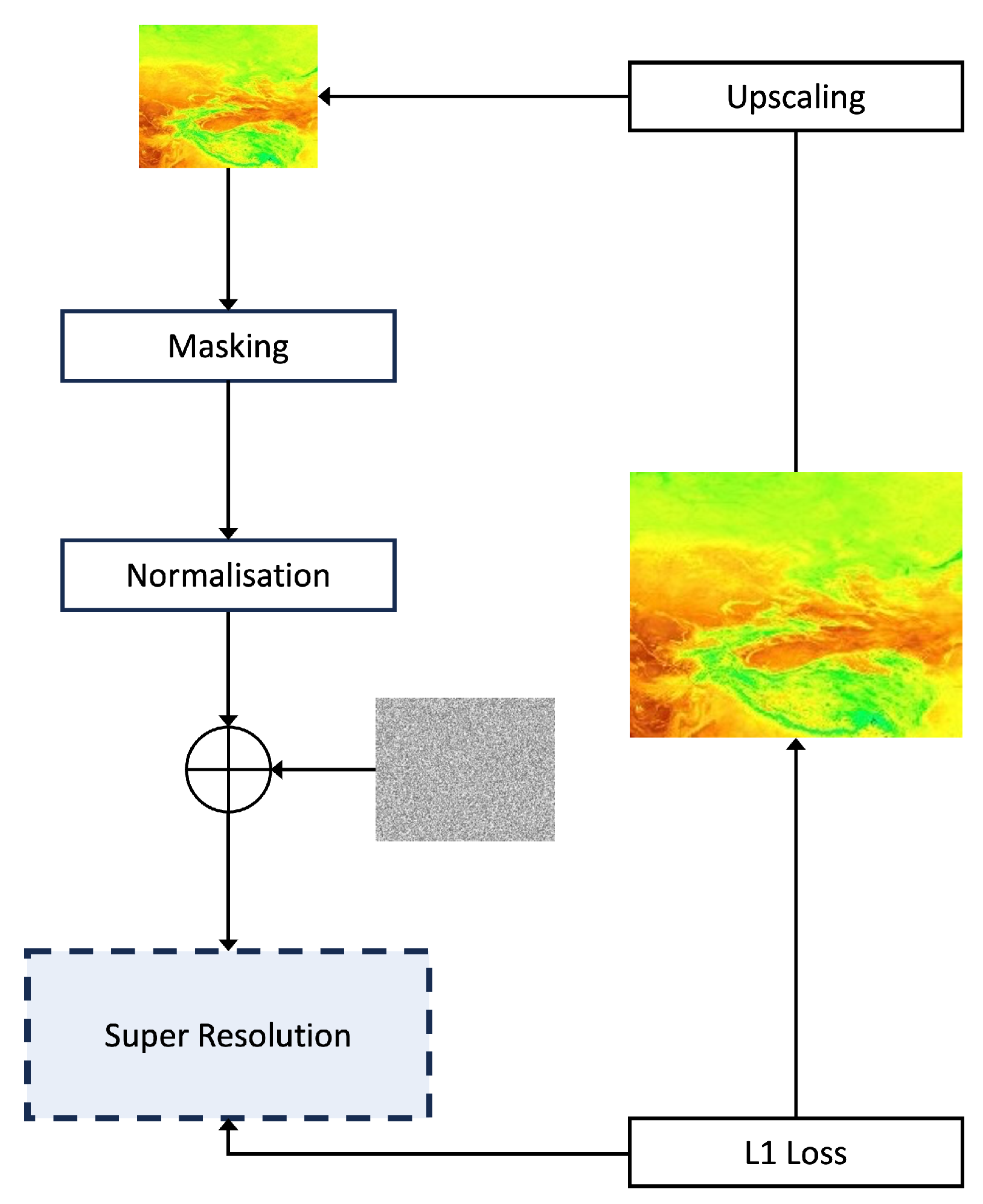
2.6. Data Preprocessing
| Algorithm 2 Supervised training with temperature LST dataset. |
|
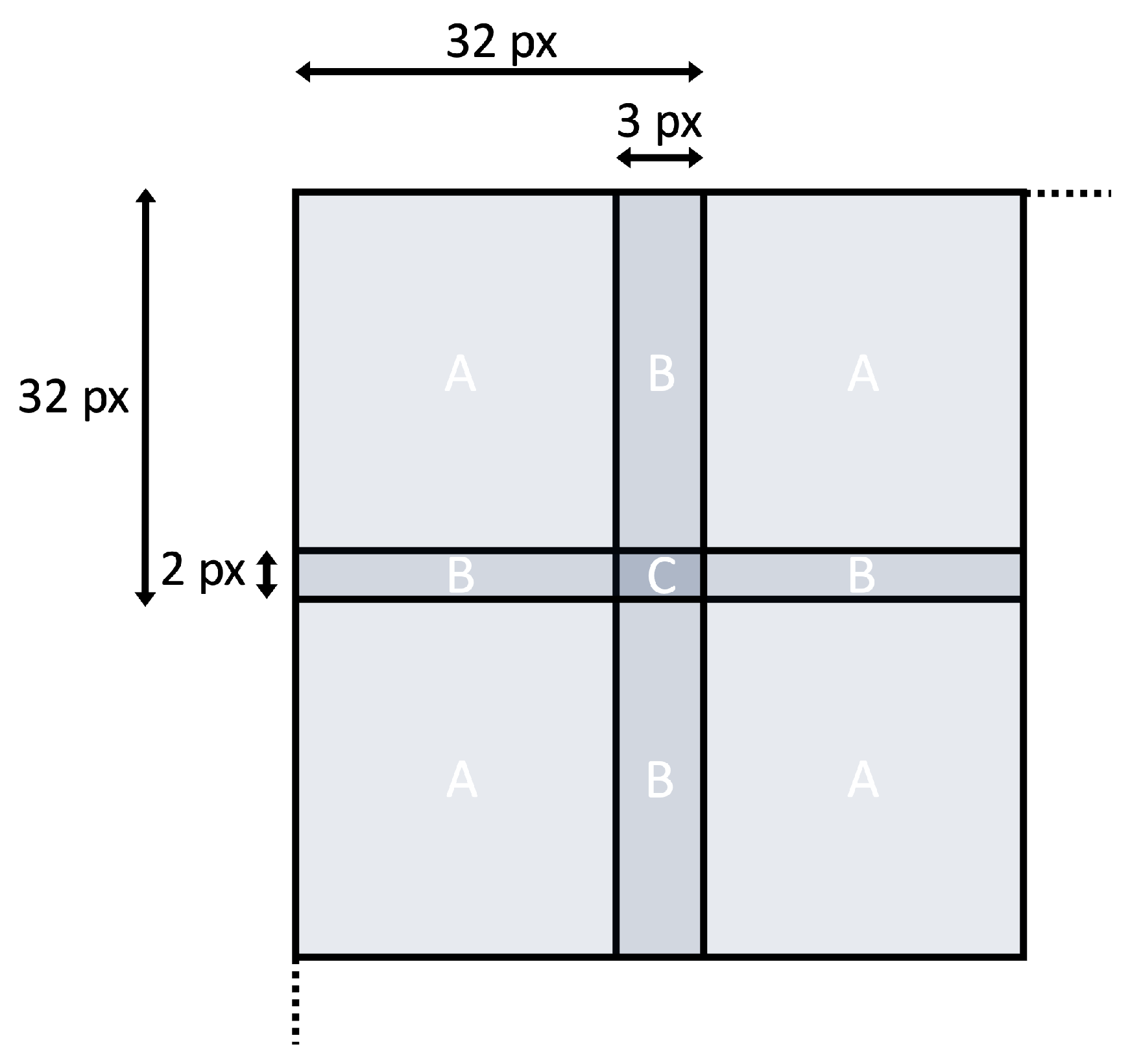
2.7. Global Maps Mosaicing
2.8. Metrics
3. Results
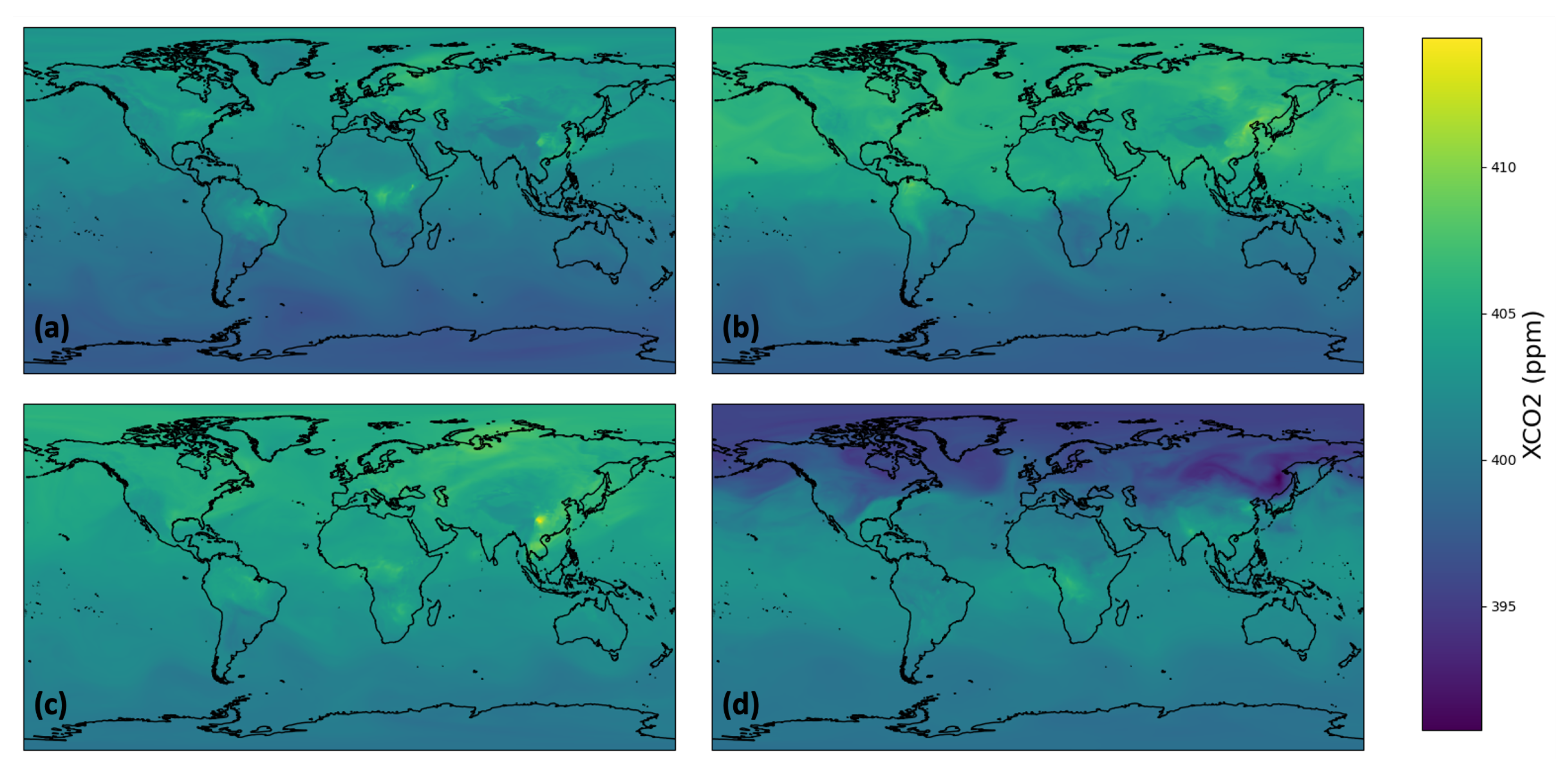
3.1. Dataset Presentation
3.2. Super-Resolved Dataset Evaluation
3.2.1. General Performance
3.2.2. Location-Specific Performance
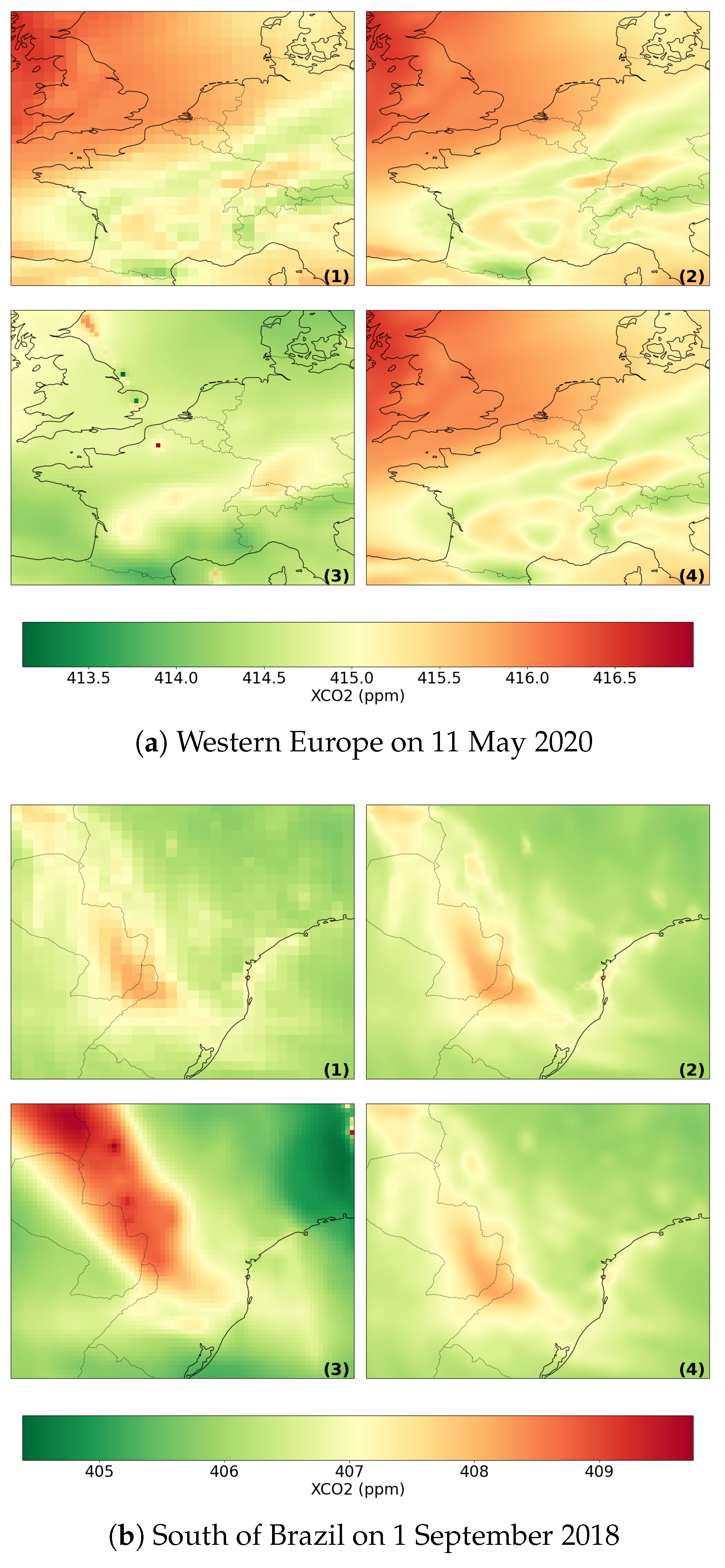
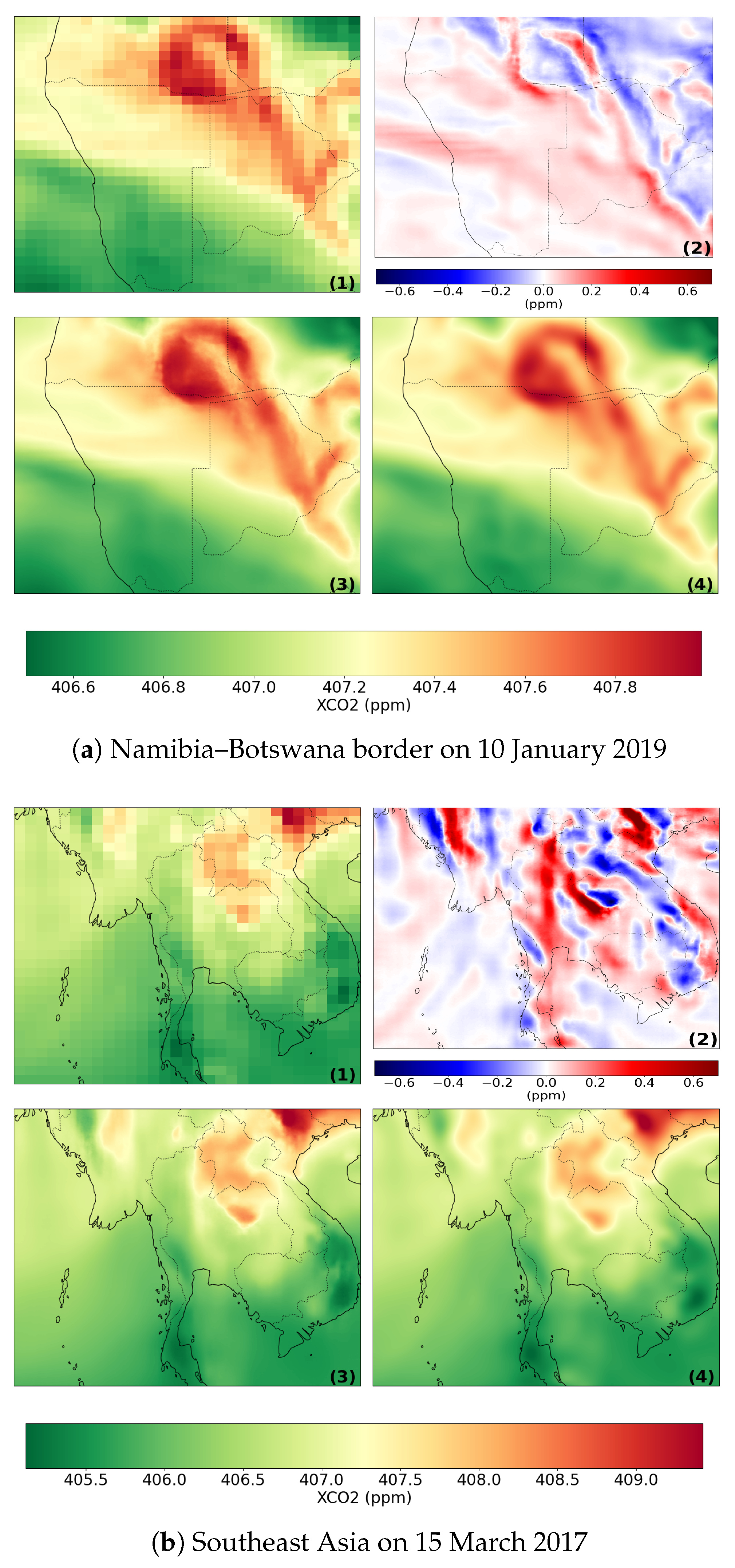
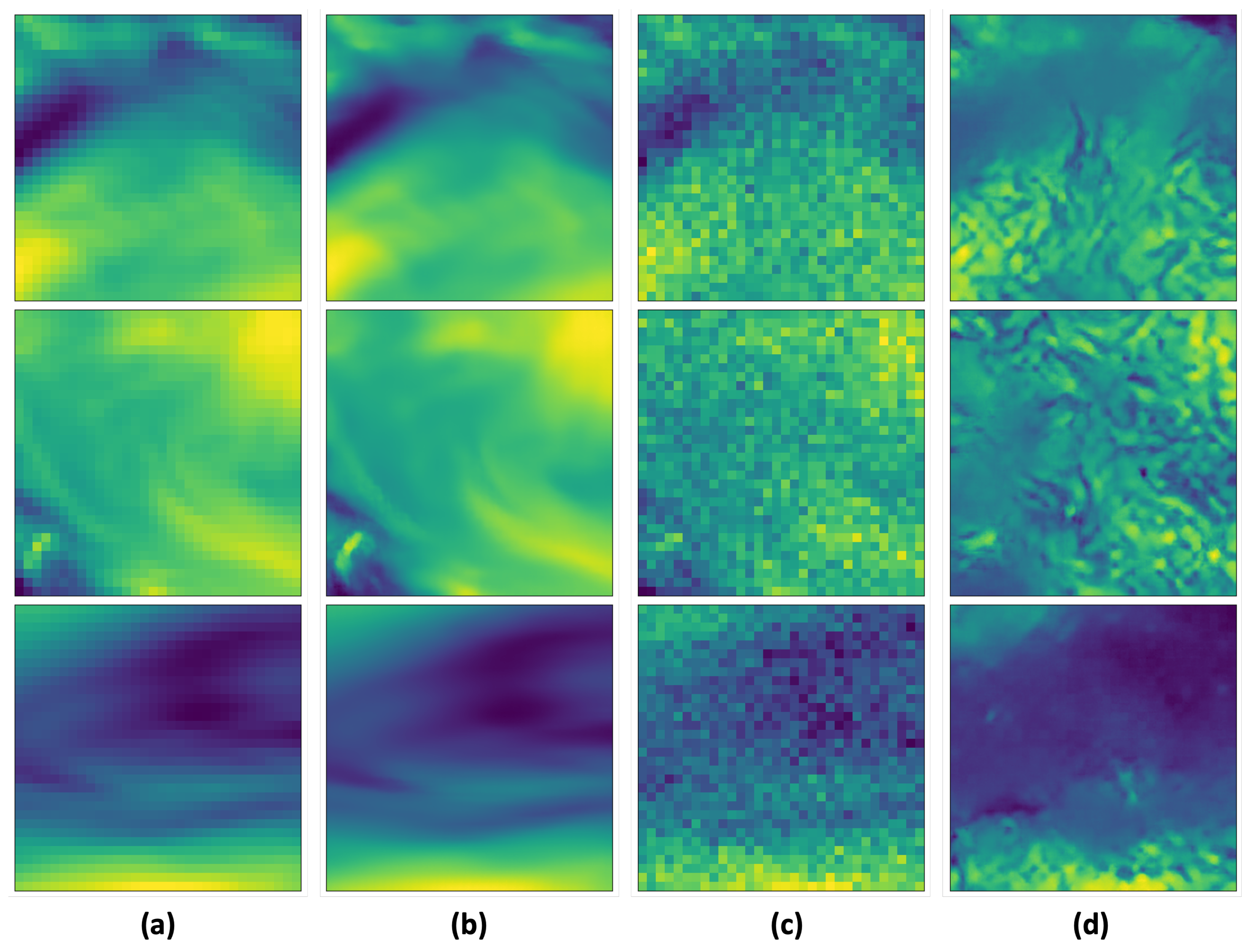
3.2.3. Visual Confirmation
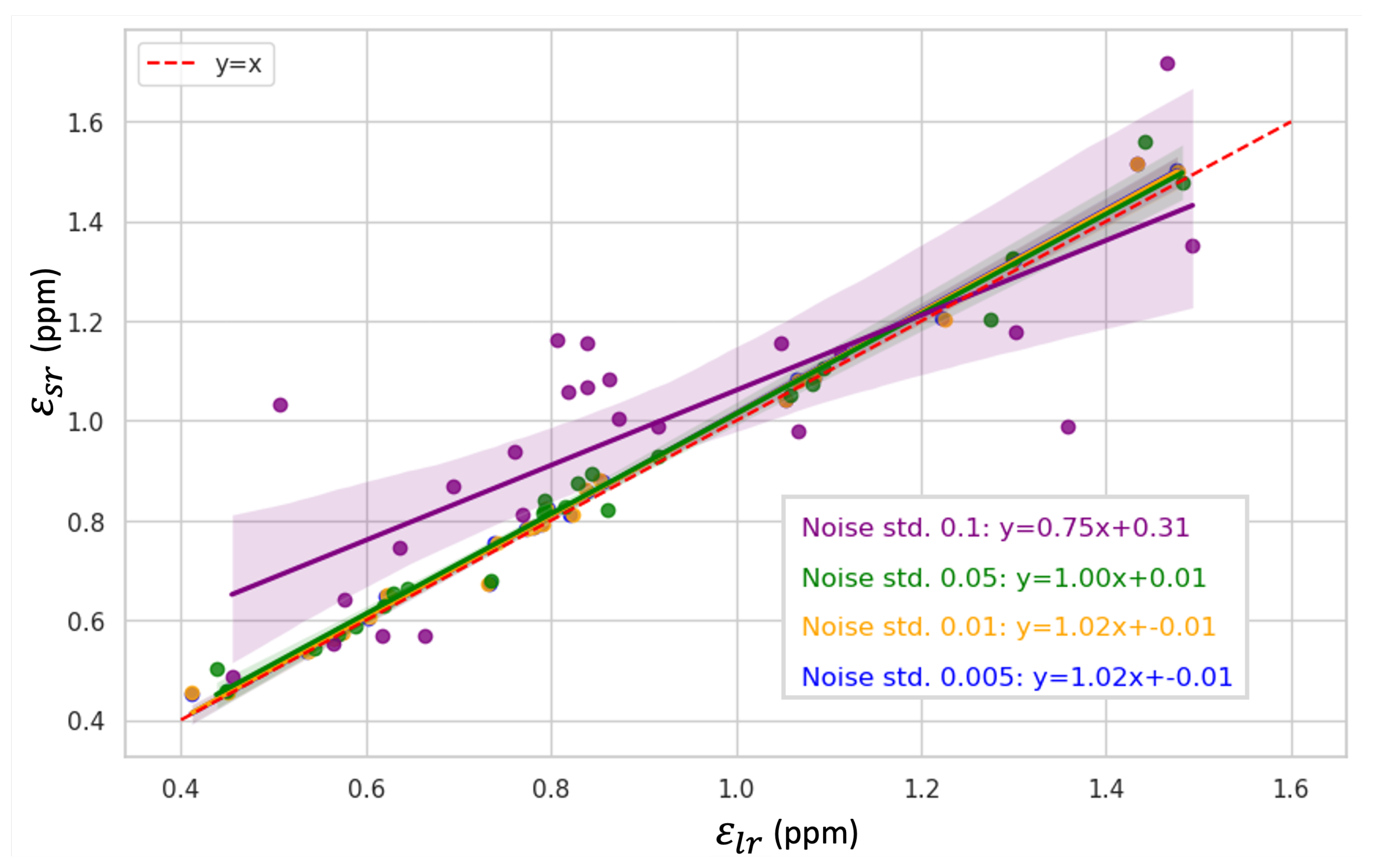
3.3. Model Uncertainty
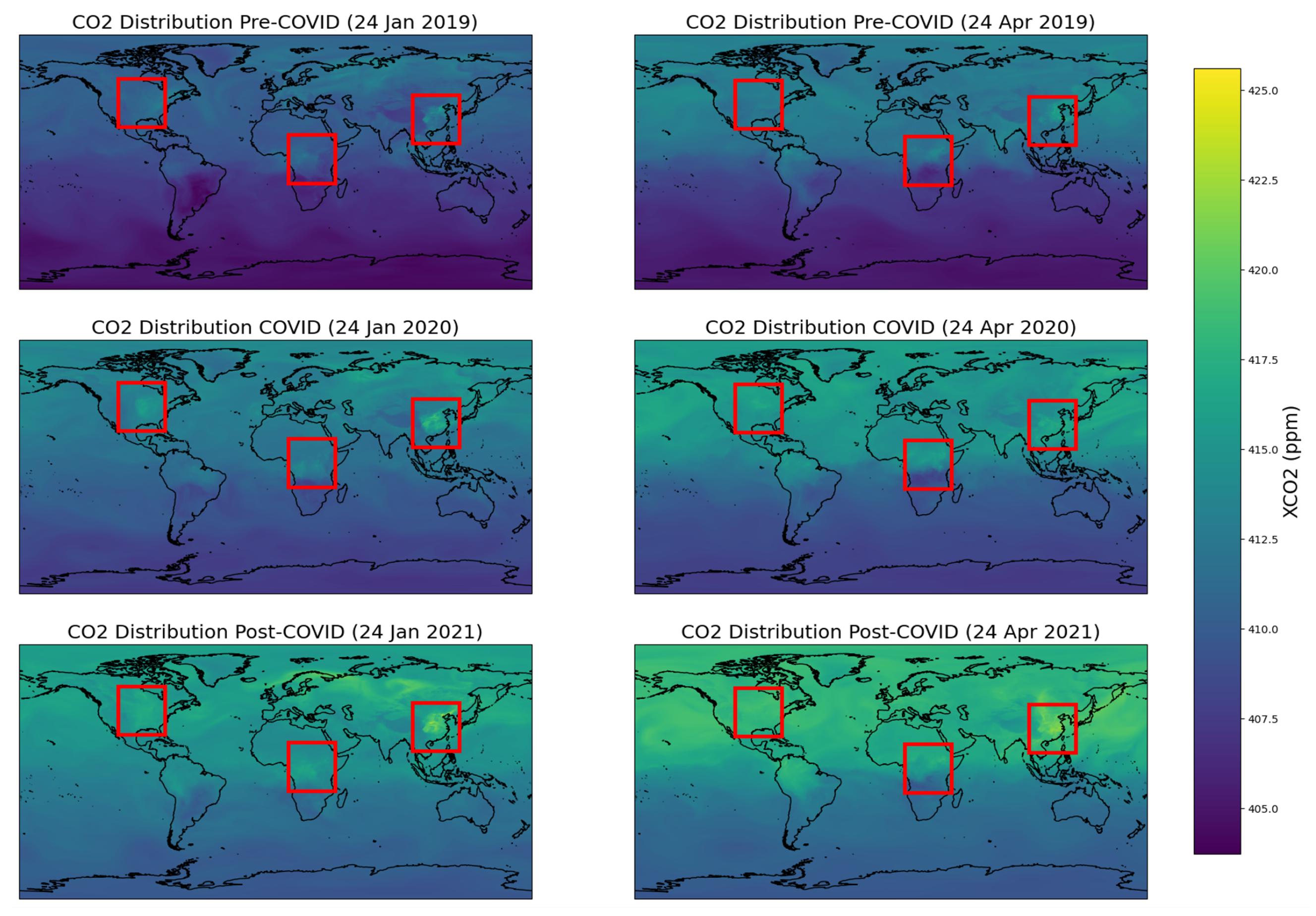
3.4. Application: Observation of Localized Changes in Pollution Through the COVID-19 Pandemic
3.4.1. Global CO2 Trends
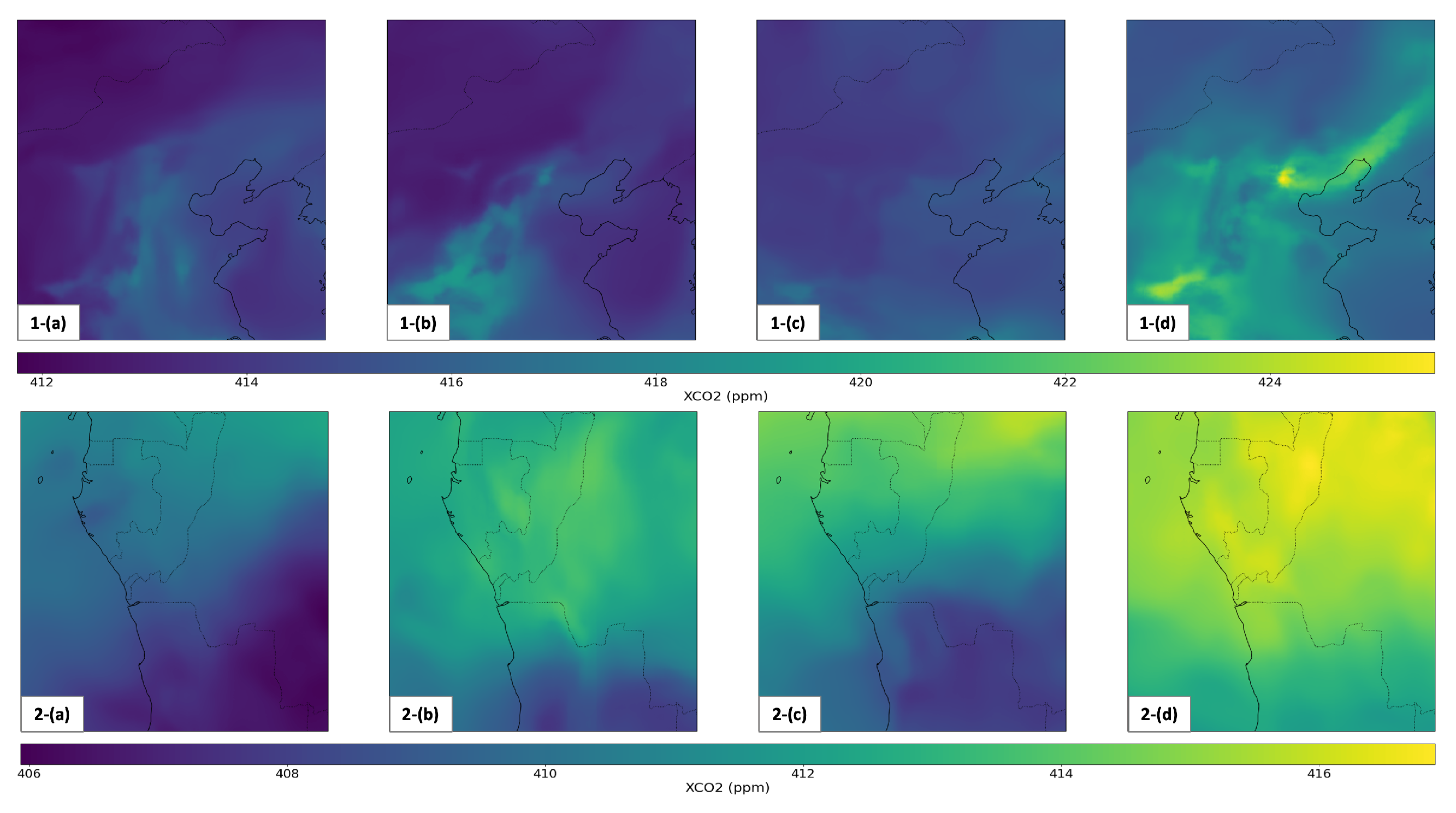
3.4.2. Local Variations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Core Writing Team; Lee, H.; Romero, J. Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. In Climate Change 2023: Synthesis Report, Proceedings of the Panel’s 58th Session, Interlaken, Switzerland, 13-19 March 2023; IPCC: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- United Nations. Paris Agreement; United Nations: New York City, NY, USA, 2015. [Google Scholar]
- United Nations Environment Programme. Global Resources Outlook 2024: Bend the Trend—Pathways to a Liveable Planet as Resource Use Spikes. International Resource Panel. Nairobi. 2024. Available online: https://www.unep.org/resources/Global-Resource-Outlook-2024 (accessed on 15 January 2025).
- Naumann, G.; Cammalleri, C.; Mentaschi, L.; Feyen, L. Increased economic drought impacts in Europe with anthropogenic warming. Nat. Clim. Change 2021, 11, 485–491. [Google Scholar] [CrossRef]
- Ou, Y.; Iyer, G.; Fawcett, A.; Hultman, N.; McJeon, H.; Ragnauth, S.; Smith, S.J.; Edmonds, J. Role of non-CO2 greenhouse gas emissions in limiting global warming. One Earth 2022, 5, 1312–1315. [Google Scholar] [CrossRef] [PubMed]
- Weiss, R.F.; Prinn, R.G. Quantifying greenhouse-gas emissions from atmospheric measurements: A critical reality check for climate legislation. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 1925–1942. [Google Scholar] [CrossRef]
- Jarnicka, J.; Żebrowski, P. Learning in greenhouse gas emission inventories in terms of uncertainty improvement over time. Mitig. Adapt. Strateg. Glob. Change 2019, 24, 1143–1168. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.; Sherlock, V.; Wennberg, P.O. The total carbon column observing network. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Kasuya, M.; Nakajima, M.; Hamazaki, T. Greenhouse gases observing satellite (GOSAT) program overview and its development status. Trans. Jpn. Soc. Aeronaut. Space Sci. Space Technol. Jpn. 2009, 7, To_4_5–To_4_10. [Google Scholar] [CrossRef]
- Eldering, A.; Boland, S.; Solish, B.; Crisp, D.; Kahn, P.; Gunson, M. High precision atmospheric CO2 measurements from space: The design and implementation of OCO-2. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–10. [Google Scholar]
- Eldering, A.; Taylor, T.E.; O’Dell, C.W.; Pavlick, R. The OCO-3 mission: Measurement objectives and expected performance based on 1 year of simulated data. Atmos. Meas. Tech. 2019, 12, 2341–2370. [Google Scholar] [CrossRef]
- Nassar, R.; Mastrogiacomo, J.P.; Bateman-Hemphill, W.; McCracken, C.; MacDonald, C.G.; Hill, T.; O’Dell, C.W.; Kiel, M.; Crisp, D. Advances in quantifying power plant CO2 emissions with OCO-2. Remote Sens. Environ. 2021, 264, 112579. [Google Scholar] [CrossRef]
- Lopez, F.P.A.; Zhou, G.; Jing, G.; Zhang, K.; Tan, Y. XCO2 and XCH4 Reconstruction Using GOSAT Satellite Data Based on EOF-Algorithm. Remote Sens. 2022, 14, 2622. [Google Scholar] [CrossRef]
- Hu, K.; Liu, Z.; Shao, P.; Ma, K.; Xu, Y.; Wang, S.; Wang, Y.; Wang, H.; Di, L.; Xia, M.; et al. A review of satellite-based CO2 data reconstruction studies: Methodologies, challenges, and advances. Remote Sens. 2024, 16, 3818. [Google Scholar] [CrossRef]
- He, Z.; Lei, L.; Zhang, Y.; Sheng, M.; Wu, C.; Li, L.; Zeng, Z.C.; Welp, L.R. Spatio-temporal mapping of multi-satellite observed column atmospheric CO2 using precision-weighted kriging method. Remote Sens. 2020, 12, 576. [Google Scholar] [CrossRef]
- Zammit-Mangion, A.; Cressie, N.; Shumack, C. On Statistical Approaches to Generate Level 3 Products from Satellite Remote Sensing Retrievals. Remote Sens. 2018, 10, 155. [Google Scholar] [CrossRef]
- Jacobson, A.R.; Schuldt, K.N.; Tans, P. CarbonTracker CT2022; NOAA Global Monitoring Laboratory: Boulder, CO, USA, 2023.
- Eastham, S.D.; Long, M.S.; Keller, C.A.; Lundgren, E.; Yantosca, R.M.; Zhuang, J.; Li, C.; Lee, C.J.; Yannetti, M.; Auer, B.M.; et al. GEOS-Chem High Performance (GCHP v11-02c): A next-generation implementation of the GEOS-Chem chemical transport model for massively parallel applications. Geosci. Model Dev. 2018, 11, 2941–2953. [Google Scholar] [CrossRef]
- Van Der Woude, A.M.; De Kok, R.; Smith, N.; Luijkx, I.T.; Botía, S.; Karstens, U.; Kooijmans, L.M.; Koren, G.; Meijer, H.A.; Steeneveld, G.J.; et al. Near-real-time CO2 fluxes from CarbonTracker Europe for high-resolution atmospheric modeling. Earth Syst. Sci. Data 2023, 15, 579–605. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, Q.; Feng, X.; Liu, Z.; Shao, P.; Xia, M.; Ye, X. An Interpolation and Prediction Algorithm for XCO2 based on Multi-source Time Series Data. Remote Sens. 2024, 16, 1907. [Google Scholar] [CrossRef]
- Rodriguez-Perez, D.; Sanchez-Carnero, N. Multigrid/multiresolution interpolation: Reducing oversmoothing and other sampling effects. Geomatics 2022, 2, 236–253. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- He, C.; Ji, M.; Li, T.; Liu, X.; Tang, D.; Zhang, S.; Luo, Y.; Grieneisen, M.L.; Zhou, Z.; Zhan, Y. Deriving Full-Coverage and Fine-Scale XCO2 Across China Based on OCO-2 Satellite Retrievals and CarbonTracker Output. Geophys. Res. Lett. 2022, 49, e2022GL098435. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Siabi, Z.; Falahatkar, S.; Alavi, S.J. Spatial distribution of XCO2 using OCO-2 data in growing seasons. J. Environ. Manag. 2019, 244, 110–118. [Google Scholar] [CrossRef]
- Taud, H.; Mas, J.F. Multilayer perceptron (MLP). In Geomatic Approaches for Modeling Land Change Scenarios; Springer: Berlin/Heidelberg, Germany, 2017; pp. 451–455. [Google Scholar]
- Moser, B.B.; Raue, F.; Frolov, S.; Palacio, S.; Hees, J.; Dengel, A. Hitchhiker’s Guide to Super-Resolution: Introduction and Recent Advances. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9862–9882. [Google Scholar] [CrossRef]
- Saharia, C.; Ho, J.; Chan, W.; Salimans, T.; Fleet, D.J.; Norouzi, M. Image Super-Resolution via Iterative Refinement. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 4713–4726. [Google Scholar] [CrossRef]
- Lever, J.; Cheng, S.; Casas, C.Q.; Liu, C.; Fan, H.; Platt, R.; Rakotoharisoa, A.; Johnson, E.; Li, S.; Shang, Z.; et al. Facing & mitigating common challenges when working with real-world data: The Data Learning Paradigm. J. Comput. Sci. 2025, 85, 102523. [Google Scholar]
- Wang, P.; Bayram, B.; Sertel, E. A comprehensive review on deep learning based remote sensing image super-resolution methods. Earth-Sci. Rev. 2022, 232, 104110. [Google Scholar] [CrossRef]
- Haris, M.; Shakhnarovich, G.; Ukita, N. Deep Back-ProjectiNetworks for Single Image Super-Resolution. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4323–4337. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Sheng, M.; Lei, L.; Zeng, Z.C.; Rao, W.; Song, H.; Wu, C. Global land 1° mapping dataset of XCO2 from satellite observations of GOSAT and OCO-2 from 2009 to 2020. Big Earth Data 2022, 7, 170–190. [Google Scholar] [CrossRef]
- Weir, B.; Ott, L.; OCO-2 Science Team. OCO-2 GEOS Level 3 Daily, 0.5 × 0.625 Assimilated CO2 V10r; Goddard Earth Sciences Data and Information Services Center (GES DISC): Severna Park, MD, USA, 2022.
- Wang, Y.; Yuan, Q.; Li, T.; Yang, Y.; Zhou, S.; Zhang, L. Seamless mapping of long-term (2010–2020) daily global XCO2 and XCH4 from the Greenhouse Gases Observing Satellite (GOSAT), Orbiting Carbon Observatory 2 (OCO-2), and CAMS global greenhouse gas reanalysis (CAMS-EGG4) with a spatiotemporally self-supervised fusion method. Earth Syst. Sci. Data 2023, 15, 3597–3622. [Google Scholar] [CrossRef]
- Li, J.; Jia, K.; Wei, X.; Xia, M.; Chen, Z.; Yao, Y.; Zhang, X.; Jiang, H.; Yuan, B.; Tao, G.; et al. High-spatiotemporal resolution mapping of spatiotemporally continuous atmospheric CO2 concentrations over the global continent. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102743. [Google Scholar] [CrossRef]
- Taylor, T.E.; O’Dell, C.W.; Baker, D.; Bruegge, C.; Chang, A.; Chapsky, L.; Chatterjee, A.; Cheng, C.; Chevallier, F.; Crisp, D.; et al. Evaluating the consistency between OCO-2 and OCO-3 XCO2 estimates derived from the NASA ACOS version 10 retrieval algorithm. Atmos. Meas. Tech. Discuss. 2023, 16, 3173–3209. [Google Scholar] [CrossRef]
- Parker, R.; Boesch, H.; Cogan, A.; Fraser, A.; Feng, L.; Palmer, P.I.; Messerschmidt, J.; Deutscher, N.; Griffith, D.W.; Notholt, J.; et al. Methane observations from the Greenhouse Gases Observing SATellite: Comparison to ground-based TCCON data and model calculations. Geophys. Res. Lett. 2011, 38, L15807. [Google Scholar] [CrossRef]
- Sha, M.K.; De Mazière, M.; Notholt, J.; Blumenstock, T.; Chen, H.; Dehn, A.; Griffith, D.W.; Hase, F.; Heikkinen, P.; Hermans, C.; et al. Intercomparison of low- and high-resolution infrared spectrometers for ground-based solar remote sensing measurements of total column concentrations of CO2, CH4, and CO. Atmos. Meas. Tech. 2020, 13, 4791–4839. [Google Scholar] [CrossRef]
- Zhou, M.; Langerock, B.; Vigouroux, C.; Sha, M.K.; Hermans, C.; Metzger, J.M.; Chen, H.; Ramonet, M.; Kivi, R.; Heikkinen, P.; et al. TCCON and NDACC X CO measurements: Difference, discussion and application. Atmos. Meas. Tech. 2019, 12, 5979–5995. [Google Scholar] [CrossRef]
- Xiong, X.; Chiang, K.; Sun, J.; Barnes, W.; Guenther, B.; Salomonson, V. NASA EOS Terra and Aqua MODIS on-orbit performance. Adv. Space Res. 2009, 43, 413–422. [Google Scholar] [CrossRef]
- Wan, Z.; Hook, S.; Hulley, G. MODIS/Terra Land Surface Temperature/Emissivity Daily L3 global 0.05 Deg CMG V061 [Data Set]; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2021.
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar]
- Haut, J.M.; Fernandez-Beltran, R.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Pla, F. A new deep generative network for unsupervised remote sensing single-image super-resolution. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6792–6810. [Google Scholar] [CrossRef]
- Wei, Y.; Gu, S.; Li, Y.; Timofte, R.; Jin, L.; Song, H. Unsupervised real-world image super resolution via domain-distance aware training. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13385–13394. [Google Scholar]
- Timofte, R.; Gu, S.; Wu, J.; Van Gool, L.; Zhang, L.; Yang, M.H.; Haris, M.; Shakhnarovich, G.; Ukita, N.; Hu, S.; et al. NTIRE 2018 Challenge on Single Image Super-Resolution: Methods and Results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 114–125. [Google Scholar]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3974–3983. [Google Scholar]
- Zhang, M.; Kafy, A.A.; Xiao, P.; Han, S.; Zou, S.; Saha, M.; Zhang, C.; Tan, S. Impact of urban expansion on land surface temperature and carbon emissions using machine learning algorithms in Wuhan, China. Urban Clim. 2023, 47, 101347. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, S.; Yang, K.; Zhu, Y.; Ma, Y. Spatio-temporal variations of CO2 emission from energy consumption in the yangtze river delta region of china and its relationship with nighttime land surface temperature. Sustainability 2020, 12, 8388. [Google Scholar] [CrossRef]
- Hong, T.; Huang, X.; Zhang, X.; Deng, X. Correlation modelling between land surface temperatures and urban carbon emissions using multi-source remote sensing data: A case study. Phys. Chem. Earth Parts A/B/C 2023, 132, 103489. [Google Scholar] [CrossRef]
- Dong, R.; Zhang, L.; Fu, H. RRSGAN: Reference-based super-resolution for remote sensing image. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5601117. [Google Scholar] [CrossRef]
- Soh, J.W.; Cho, S.; Cho, N.I. Meta-transfer learning for zero-shot super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 3516–3525. [Google Scholar]
- Dai, S.; Han, M.; Wu, Y.; Gong, Y. Bilateral back-projection for single image super resolution. In Proceedings of the 2007 IEEE International Conference on Multimedia and Expo, Beijing, China, 2–5 July 2007; pp. 1039–1042. [Google Scholar]
- Wang, W.; Zhang, H.; Yuan, Z.; Wang, C. Unsupervised real-world super-resolution: A domain adaptation perspective. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 4318–4327. [Google Scholar]
- Muthukumar, P.; Cocom, E.; Nagrecha, K.; Comer, D.; Burga, I.; Taub, J.; Calvert, C.F.; Holm, J.; Pourhomayoun, M. Predicting PM2.5 atmospheric air pollution using deep learning with meteorological data and ground-based observations and remote-sensing satellite big data. Air Qual. Atmos. Health 2022, 15, 1221–1234. [Google Scholar] [CrossRef]
- Agustí-Panareda, A.; Barré, J.; Massart, S.; Inness, A.; Aben, I.; Ades, M.; Baier, B.C.; Balsamo, G.; Borsdorff, T.; Bousserez, N.; et al. Technical note: The CAMS greenhouse gas reanalysis from 2003 to 2020. Atmos. Chem. Phys. 2023, 23, 3829–3859. [Google Scholar] [CrossRef]
- Xiang, R.; Yang, H.; Yan, Z.; Taha, A.M.M.; Xu, X.; Wu, T. Super-resolution reconstruction of GOSAT CO2 products using bicubic interpolation. Geocarto Int. 2022, 37, 15187–15211. [Google Scholar] [CrossRef]
- Hodson, T.O. Root mean square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. Discuss. 2022, 14, 5481–5487. [Google Scholar] [CrossRef]
- Biau, G.; Zorita, E.; von Storch, H.; Wackernagel, H. Estimation of precipitation by kriging in the EOF space of thesea level pressure field. J. Clim. 1999, 12, 1070–1085. [Google Scholar] [CrossRef]
- Ge, H.; Wang, X.; Yuan, X.; Xiao, G.; Wang, C.; Deng, T.; Yuan, Q.; Xiao, X. The epidemiology and clinical information about COVID-19. Eur. J. Clin. Microbiol. Infect. Dis. 2020, 39, 1011–1019. [Google Scholar] [CrossRef]
- Carvalho, T.; Krammer, F.; Iwasaki, A. The first 12 months of COVID-19: A timeline of immunological insights. Nat. Rev. Immunol. 2021, 21, 245–256. [Google Scholar] [CrossRef]
- Muhammad, S.; Long, X.; Salman, M. COVID-19 pandemic and environmental pollution: A blessing in disguise? Sci. Total Environ. 2020, 728, 138820. [Google Scholar] [CrossRef]
- Yin, S.; Wang, X.; Tani, H.; Zhang, X.; Zhong, G.; Sun, Z.; Chittenden, A.R. Analyzing temporo-spatial changes and the distribution of the CO2 concentration in Australia from 2009 to 2016 by greenhouse gas monitoring satellites. Atmos. Environ. 2018, 192, 1–12. [Google Scholar] [CrossRef]
- Li, B.; Zhang, G.; Xia, L.; Kong, P.; Zhan, M.; Su, R. Spatial and Temporal Distributions of Atmospheric CO2 in East China Based on Data from Three Satellites. Adv. Atmos. Sci. 2020, 37, 1323–1337. [Google Scholar] [CrossRef]
- Koh, D. COVID-19 lockdowns throughout the world. Occup. Med. 2020, 70, 322. [Google Scholar] [CrossRef]
- Razzak, M.T.; Mateo-García, G.; Lecuyer, G.; Gómez-Chova, L.; Gal, Y.; Kalaitzis, F. Multi-spectral multi-image super-resolution of Sentinel-2 with radiometric consistency losses and its effect on building delineation. ISPRS J. Photogramm. Remote Sens. 2023, 195, 1–13. [Google Scholar] [CrossRef]
- Ren, P.; Rao, C.; Liu, Y.; Ma, Z.; Wang, Q.; Wang, J.X.; Sun, H. PhySR: Physics-informed deep super-resolution for spatiotemporal data. J. Comput. Phys. 2023, 492, 112438. [Google Scholar] [CrossRef]
- Harder, P.; Hernandez-Garcia, A.; Ramesh, V.; Yang, Q.; Sattegeri, P.; Szwarcman, D.; Watson, C.; Rolnick, D. Hard-Constrained Deep Learning for Climate Downscaling. J. Mach. Learn. Res. 2023, 24, 1–40. [Google Scholar]
- Wiles, O.; Gowal, S.; Stimberg, F.; Alvise-Rebuffi, S.; Ktena, I.; Dvijotham, K.; Cemgil, T. A fine-grained analysis on distribution shift. arXiv 2021, arXiv:2110.11328. [Google Scholar]
- Shu, J.; Yuan, X.; Meng, D.; Xu, Z. Cmw-net: Learning a class-aware sample weighting mapping for robust deep learning. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 11521–11539. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Shen, M.; Wang, H.; Wang, X.; van Rechem, C.; Fu, T.; Wei, W. Machine learning for synthetic data generation: A review. arXiv 2023, arXiv:2302.04062. [Google Scholar]
- Zhu, D.; Cai, C.; Yang, T.; Zhou, X. A machine learning approach for air quality prediction: Model regularization and optimization. Big Data Cogn. Comput. 2018, 2, 5. [Google Scholar] [CrossRef]
- Crowley, M.A.; Stockdale, C.A.; Johnston, J.M.; Wulder, M.A.; Liu, T.; McCarty, J.L.; Rieb, J.T.; Cardille, J.A.; White, J.C. Towards a whole-system framework for wildfire monitoring using Earth observations. Glob. Change Biol. 2023, 29, 1423–1436. [Google Scholar] [CrossRef]
| Satellite | Launch | Spatial Resolution | Coverage | Public/Private |
|---|---|---|---|---|
| AIRS | 2002 | 13.5 km | Global | Public |
| IASI | 2007 | 25 km | Global | Public |
| GOSAT | 2009 | 10 km | Global | Public |
| OCO-2 | 2014 | 1.5 km | Global | Public |
| TanSat | 2016 | 2.5 km | Global | Public |
| GOSAT-2 | 2018 | 7 km | Global | Public |
| OCO-3 | 2019 | 1.5 km | Global | Public |
| DQ-1 | 2022 | - | Global | Public |
| IASI-NG | 2025 | 12 km | Global | Public |
| MicroCarb | Not before 2025 | 2 km | Global | Public |
| Source | Spatial Resolution (°/km) | Periodicity (days) | Timespan | Dataset Available |
|---|---|---|---|---|
| Sheng et al. [34] | 1°× 1°/100 km × 100 km | 3 | 2009–2020 | Yes |
| He et al. [15] | 1°× 1°/100 km × 100 km | 8 | 2003–2016 | No |
| Weir et al. [35] | 0.5°× 0.625°/50 km × 70 km | 1 | 2015–onward | Yes |
| Wang et al. [36] | 0.25°× 0.25°/25 km × 25 km | 1 | 2001–2020 | Yes |
| Li et al. [37] | 0.01°× 0.01°/1 km × 1 km | 8 | 2014–2018 | No |
| Site (Abbreviation) | Lat. | Long. | Range |
|---|---|---|---|
| Bremen, GER (br) | 53.10 N | 8.85 E | 2015–2020 |
| Burgos, PHL (bu) | 18.53 N | 120.65 E | 2017–2020 |
| Caltech, USA (ci) | 34.14 N | 118.13 W | 2015–2020 |
| Darwin, AUS (db) | 12.42 S | 130.89 E | 2015–2020 |
| Edwards, USA (df) | 34.96 N | 117.88 W | 2015–2020 |
| Saskatchewan, CAN (et) | 54.35 N | 104.99 W | 2016–2020 |
| Eureka, CAN (eu) | 80.05 N | 86.42 W | 2015–2020 |
| Garmisch, GER (gm) | 47.48 N | 11.06 E | 2015–2020 |
| Hefei, CHI (hf) | 31.91 N | 117.17 E | 2015–2018 |
| Izana, ESP (iz) | 28.30 N | 16.50 W | 2015–2020 |
| JPL, USA (jf) | 34.96 N | 117.88 W | 2015–2018 |
| Saga, JAP (js) | 33.24 N | 130.29 E | 2015–2020 |
| Karlsruhe, GER (ka) | 49.10 N | 8.44 E | 2015–2020 |
| Lauder 02, NZL (ll) | 45.04 S | 169.68 E | 2015–2018 |
| Lauder 03, NZL (lr) | 45.034 S | 169.68 E | 2018–2020 |
| Nicosia, CYP (ni) | 35.14 N | 33.38 E | 2019–2020 |
| Orleans, FRA (or) | 47.97 N | 2.11 E | 2015–2020 |
| Park Falls, USA (pa) | 45.95 N | 90.27 E | 2015–2020 |
| Paris, FRA (pr) | 48.85 N | 2.36 E | 2015–2020 |
| Reunion Isl., FRA (ra) | 20.90 S | 55.49 E | 2015–2020 |
| Rikubetsu, JAP (rj) | 43.46 N | 143.77 E | 2015–2019 |
| Sodankylä, FIN (so) | 67.37 N | 26.63 E | 2015–2020 |
| Ny Ålesund, SJM (sp) | 78.90 N | 11.90 E | 2015–2020 |
| Wollogong, AUS (wg) | 34.41 S | 150.88 E | 2015–2020 |
| Spatial Resolution (°/km) | Temporal Resolution | Coverage | Timespan |
|---|---|---|---|
| 0.03° × 0.04°/3 km × 4 km | 1 day | Global | 1 January 2015 to 28 February 2022 |
| Dataset | Spatial Resolution (°/km) | Timespan |
|---|---|---|
| OCO-2 dataset (LR) | 0.5° × 0.625°/50 km × 70 km | 1 January 2015 to 28 February 2022 |
| Bicubic interpolated dataset (BIC) | 0.03° × 0.04°/3 km × 4 km | 1 January 2015 to 28 February 2022 |
| Fusion dataset (Fus) | 0.25° × 0.25°/25 km × 25 km | 1 January 2010 to 31 December 2020 |
| Site | RMSE (↓) | R2 (↑) | MAE (↓) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SR | LR | BIC | Fus. | SR | LR | BIC | Fus. | SR | LR | BIC | Fus. | |
| eu | 1.34 | 1.36 | 1.32 | 1.98 | 0.94 | 0.94 | 0.94 | 0.87 | 1.01 | 1.03 | 0.99 | 1.60 |
| js | 0.96 | 0.97 | 0.94 | 1.21 | 0.95 | 0.95 | 0.95 | 0.92 | 0.79 | 0.80 | 0.77 | 1.02 |
| iz | 0.59 | 0.60 | 0.59 | 0.65 | 0.97 | 0.97 | 0.97 | 0.97 | 0.47 | 0.48 | 0.47 | 0.49 |
| ci | 1.26 | 1.46 | 1.50 | 1.09 | 0.93 | 0.91 | 0.91 | 0.95 | 1.00 | 1.19 | 1.20 | 0.84 |
| wg | 0.80 | 0.82 | 0.73 | 0.83 | 0.97 | 0.97 | 0.97 | 0.97 | 0.61 | 0.63 | 0.55 | 0.65 |
| lr | 0.62 | 0.62 | 0.62 | 0.77 | 0.89 | 0.88 | 0.88 | 0.82 | 0.51 | 0.52 | 0.52 | 0.61 |
| br | 0.98 | 1.00 | 0.95 | 1.23 | 0.97 | 0.96 | 0.97 | 0.95 | 0.77 | 0.79 | 0.74 | 0.94 |
| sp | 1.15 | 1.18 | 1.12 | 1.56 | 0.95 | 0.95 | 0.95 | 0.91 | 1.00 | 1.02 | 0.96 | 1.25 |
| ll | 0.50 | 0.50 | 0.51 | 0.61 | 0.96 | 0.96 | 0.96 | 0.95 | 0.38 | 0.39 | 0.39 | 0.47 |
| pa | 0.78 | 0.77 | 0.78 | 1.08 | 0.98 | 0.98 | 0.98 | 0.96 | 0.60 | 0.60 | 0.61 | 0.85 |
| hf | 1.31 | 1.48 | 1.21 | 1.74 | 0.84 | 0.79 | 0.86 | 0.71 | 1.07 | 1.21 | 0.99 | 1.44 |
| jf | 1.15 | 1.38 | 1.36 | 1.08 | 0.80 | 0.71 | 0.72 | 0.83 | 0.98 | 1.19 | 1.18 | 0.83 |
| ra | 0.60 | 0.60 | 0.60 | 0.74 | 0.98 | 0.98 | 0.98 | 0.97 | 0.46 | 0.46 | 0.46 | 0.58 |
| et | 0.80 | 0.80 | 0.82 | 1.13 | 0.97 | 0.97 | 0.97 | 0.94 | 0.63 | 0.63 | 0.65 | 0.90 |
| pr | 1.37 | 1.39 | 1.37 | 1.53 | 0.92 | 0.91 | 0.92 | 0.90 | 1.09 | 1.10 | 1.09 | 1.20 |
| gm | 0.90 | 0.91 | 1.05 | 1.11 | 0.96 | 0.96 | 0.95 | 0.95 | 0.71 | 0.71 | 0.86 | 0.86 |
| so | 0.91 | 0.91 | 0.92 | 1.46 | 0.97 | 0.97 | 0.97 | 0.93 | 0.70 | 0.71 | 0.71 | 1.15 |
| or | 1.12 | 1.12 | 1.15 | 1.19 | 0.95 | 0.95 | 0.95 | 0.94 | 0.92 | 0.92 | 0.95 | 0.94 |
| bu | 0.52 | 0.52 | 0.56 | 0.78 | 0.96 | 0.96 | 0.96 | 0.91 | 0.40 | 0.41 | 0.43 | 0.63 |
| df | 0.69 | 0.69 | 0.65 | 1.00 | 0.98 | 0.98 | 0.98 | 0.96 | 0.54 | 0.54 | 0.51 | 0.81 |
| rj | 0.89 | 0.94 | 0.83 | 1.39 | 0.96 | 0.96 | 0.97 | 0.90 | 0.66 | 0.70 | 0.62 | 1.09 |
| ka | 1.12 | 1.14 | 1.19 | 1.40 | 0.95 | 0.95 | 0.94 | 0.92 | 0.92 | 0.93 | 0.99 | 1.11 |
| ni | 0.77 | 0.79 | 0.79 | 1.06 | 0.89 | 0.89 | 0.88 | 0.79 | 0.65 | 0.67 | 0.67 | 0.87 |
| db | 0.71 | 0.70 | 0.70 | 0.93 | 0.98 | 0.98 | 0.98 | 0.96 | 0.56 | 0.56 | 0.55 | 0.72 |
| Avg. | 0.92 | 0.94 | 0.94 | 1.12 | 0.97 | 0.96 | 0.96 | 0.95 | 0.70 | 0.72 | 0.72 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rakotoharisoa, A.; Cenci, S.; Arcucci, R. A High Resolution Spatially Consistent Global Dataset for CO2 Monitoring. Remote Sens. 2025, 17, 1617. https://doi.org/10.3390/rs17091617
Rakotoharisoa A, Cenci S, Arcucci R. A High Resolution Spatially Consistent Global Dataset for CO2 Monitoring. Remote Sensing. 2025; 17(9):1617. https://doi.org/10.3390/rs17091617
Chicago/Turabian StyleRakotoharisoa, Andrianirina, Simone Cenci, and Rossella Arcucci. 2025. "A High Resolution Spatially Consistent Global Dataset for CO2 Monitoring" Remote Sensing 17, no. 9: 1617. https://doi.org/10.3390/rs17091617
APA StyleRakotoharisoa, A., Cenci, S., & Arcucci, R. (2025). A High Resolution Spatially Consistent Global Dataset for CO2 Monitoring. Remote Sensing, 17(9), 1617. https://doi.org/10.3390/rs17091617






