Geographically Weighted Random Forest Based on Spatial Factor Optimization for the Assessment of Landslide Susceptibility
Abstract
1. Introduction
2. Study Area and Materials
2.1. Study Area
2.2. Data Source
2.3. Landslide Conditioning Factors
3. Methodology
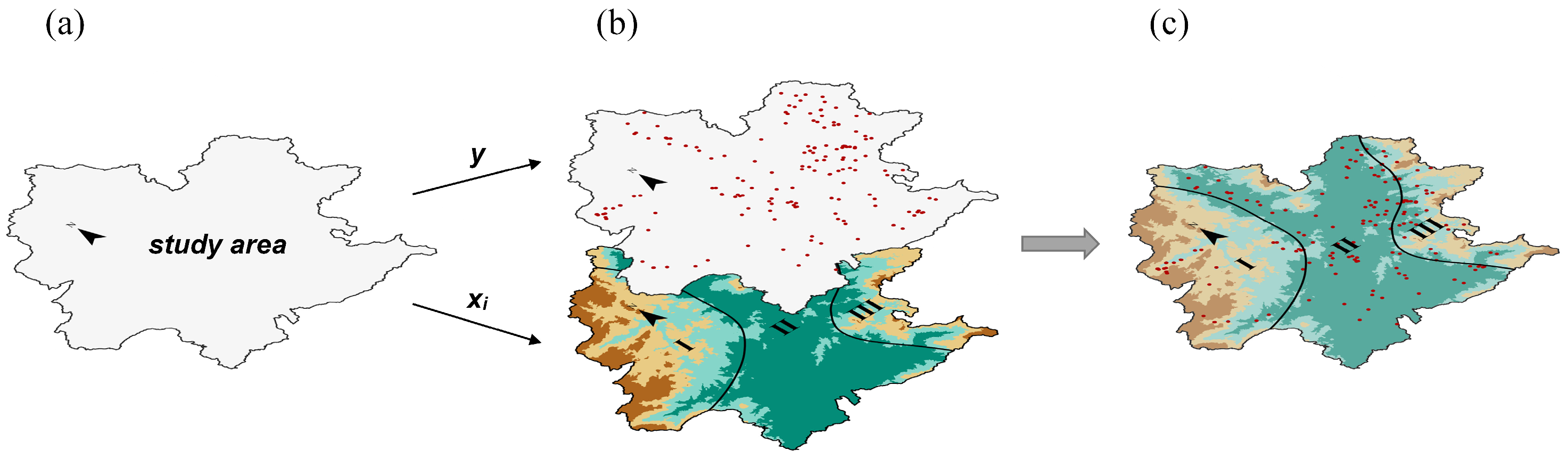
3.1. Preparation of the Sample Set
3.2. GeoDetector
3.3. Random Forest Model
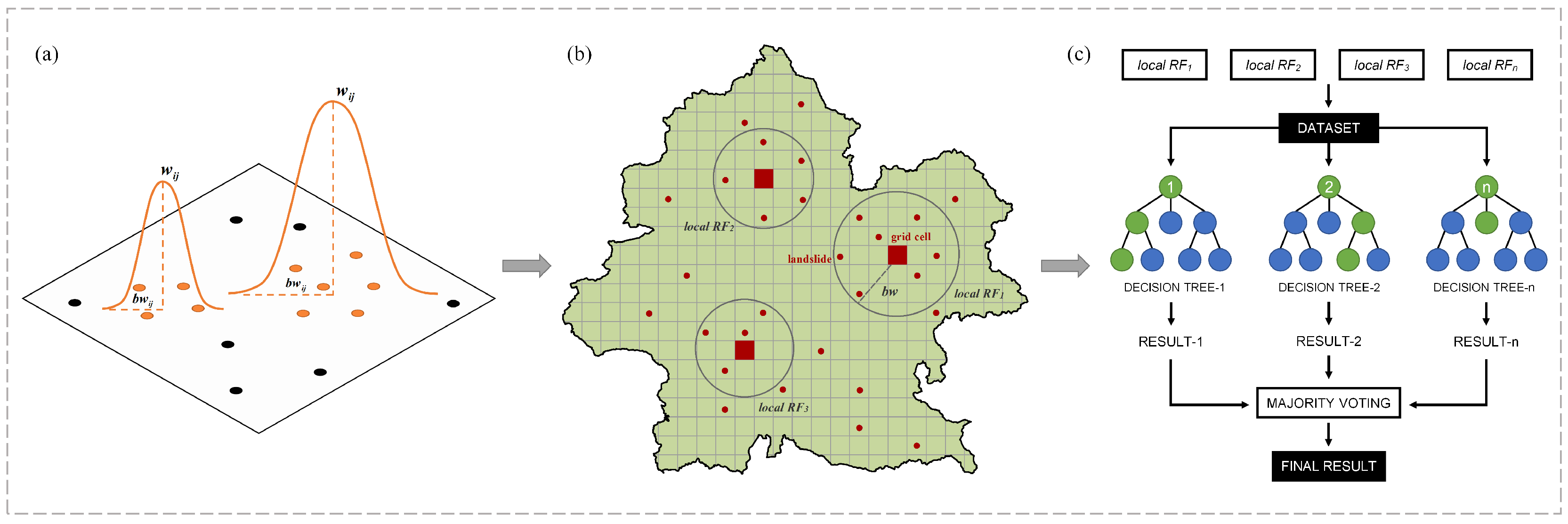
3.4. Geographical Weighted Random Forest Model
3.5. Validation of Models
4. Result
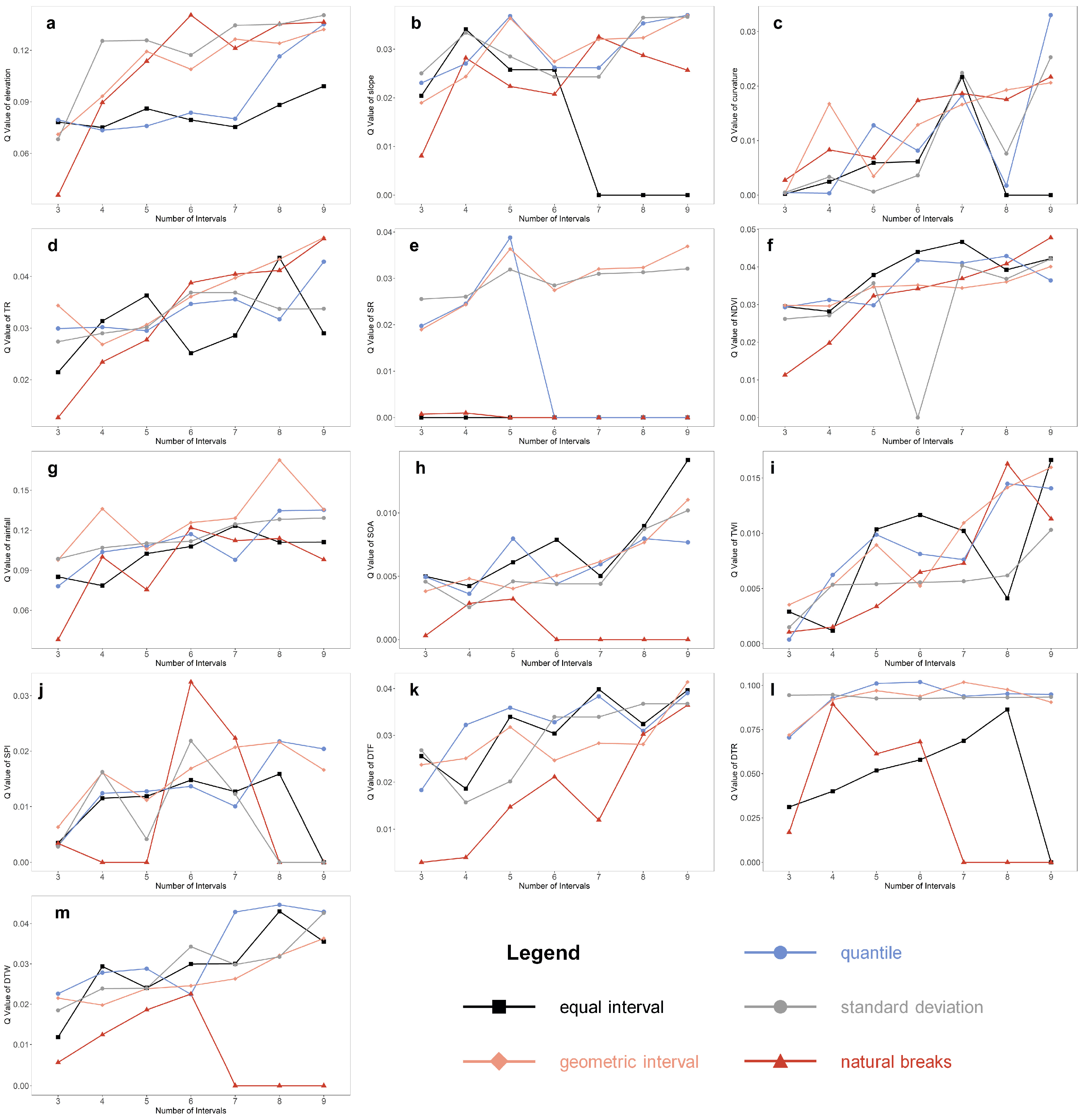
4.1. Exploration and Selection of Landslide Conditioning Factors
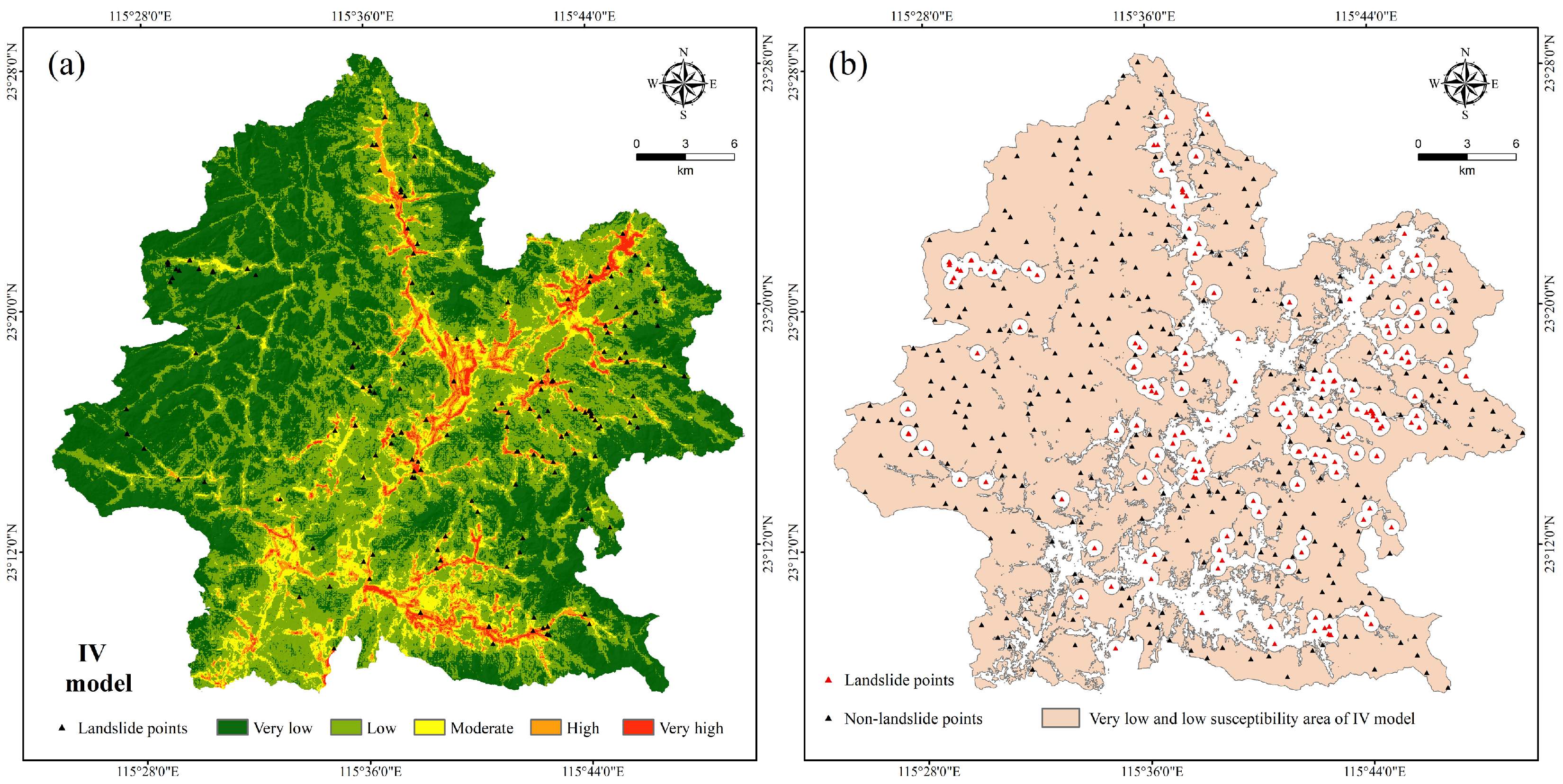
4.2. Generation of Non-Landslide Samples Based on the Information Value Model
4.3. Model Implementation and Performance Evaluation
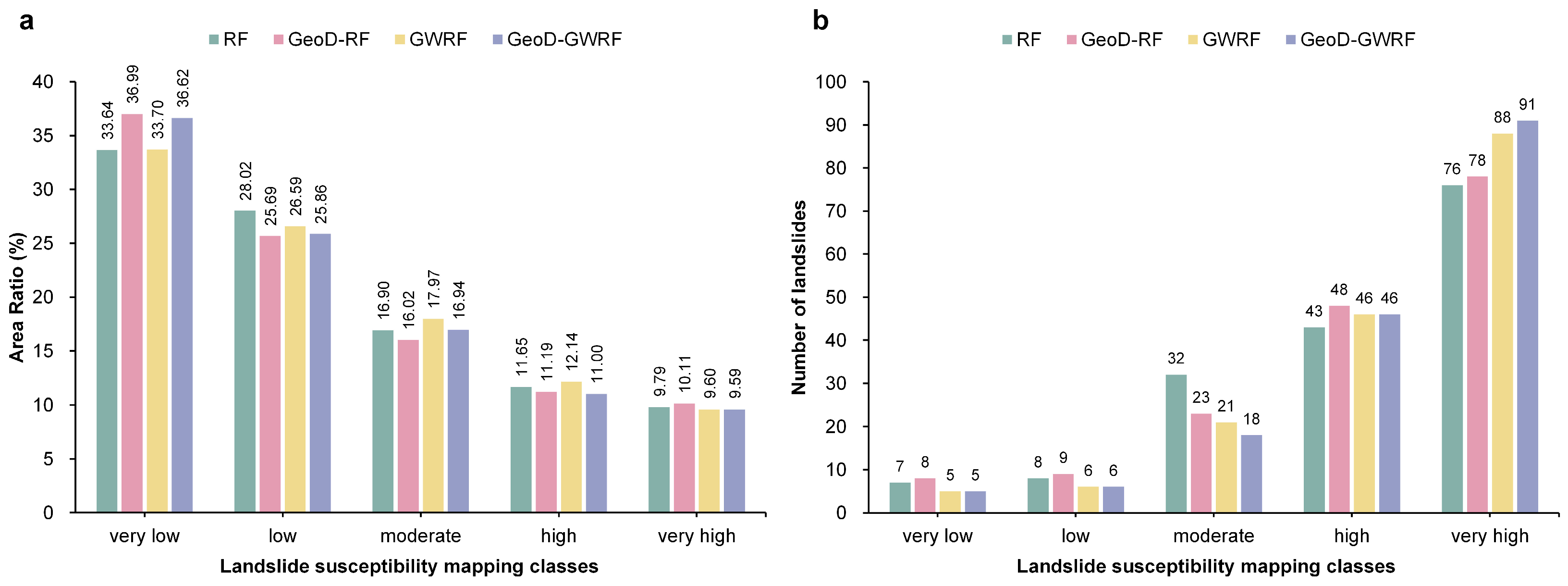
4.4. Differences in Landslide Susceptibility Mapping Across Models
5. Discussion
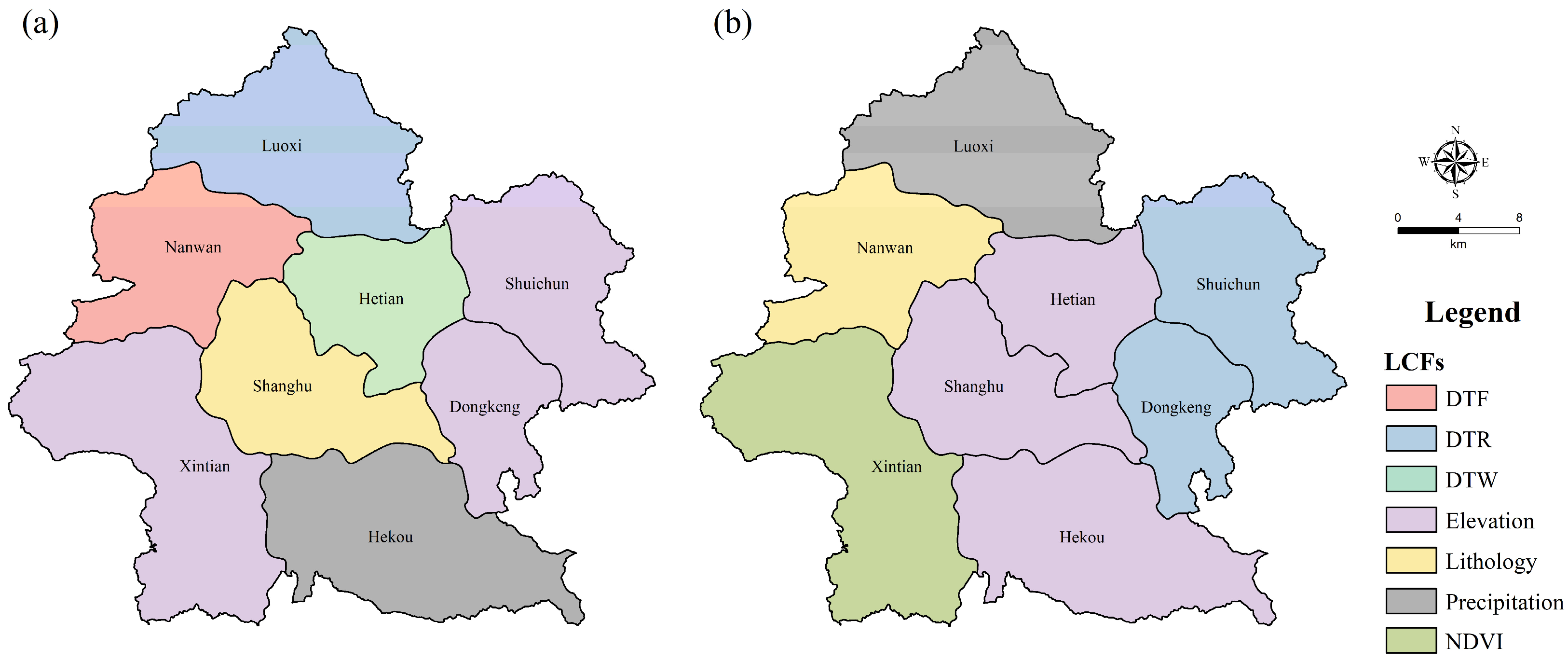
5.1. Local Interpretability of the GWRF Model
5.2. Generalizability of the Proposed Method for Landslide Susceptibility Mapping
5.3. Limitations of the Current Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Z.; Su, B.; Li, Y.; Ma, Y.; Wang, W.; Chen, G. Comprehensive analysis of landslide stability and related countermeasures: A case study of the Lanmuxi landslide in China. Sci. Rep. 2019, 9, 12407. [Google Scholar] [CrossRef]
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Kaur, R.; Gupta, V.; Chaudhary, B. Landslide susceptibility mapping and sensitivity analysis using various machine learning models: A case study of Beas valley, Indian Himalaya. Bull. Eng. Geol. Environ. 2024, 83, 228. [Google Scholar] [CrossRef]
- Panchal, S.; Shrivastava, A.K. Landslide hazard assessment using analytic hierarchy process (AHP): A case study of National Highway 5 in India. Ain Shams Eng. J. 2022, 13, 101626. [Google Scholar] [CrossRef]
- Zhang, G.; Cai, Y.; Zheng, Z.; Zhen, J.; Liu, Y.; Huang, K. Integration of the statistical index method and the analytic hierarchy process technique for the assessment of landslide susceptibility in Huizhou, China. Catena 2016, 142, 233–244. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, S.; Wang, L.; Samui, P.; Chwała, M.; He, Y. Landslide susceptibility research combining qualitative analysis and quantitative evaluation: A case study of Yunyang County in Chongqing, China. Forests 2022, 13, 1055. [Google Scholar] [CrossRef]
- Wang, Q.; Guo, Y.; Li, W.; He, J.; Wu, Z. Predictive modeling of landslide hazards in Wen County, northwestern China based on information value, weights-of-evidence, and certainty factor. Geomat. Nat. Hazards Risk 2019, 10, 820–835. [Google Scholar] [CrossRef]
- Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
- Budimir, M.; Atkinson, P.; Lewis, H. A systematic review of landslide probability mapping using logistic regression. Landslides 2015, 12, 419–436. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Yuan, R.; Chen, J. A novel method based on deep learning model for national-scale landslide hazard assessment. Landslides 2023, 20, 2379–2403. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Al-Katheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at Wadi Tayyah Basin, Asir Region, Saudi Arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Sevgen, E.; Kocaman, S.; Nefeslioglu, H.A.; Gokceoglu, C. A Novel Performance Assessment Approach Using Photogrammetric Techniques for Landslide Susceptibility Mapping with Logistic Regression, ANN and Random Forest. Sensors 2019, 19, 3940. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Chalkias, C.; Polykretis, C.; Karymbalis, E.; Soldati, M.; Ghinoi, A.; Ferentinou, M. Exploring spatial non-stationarity in the relationships between landslide susceptibility and conditioning factors: A local modeling approach using geographically weighted regression. Bull. Eng. Geol. Environ. 2020, 79, 2799–2814. [Google Scholar] [CrossRef]
- Erener, A.; Duzgun, H.S.B. Improvement of statistical landslide susceptibility mapping by using spatial and global regression methods in the case of More and Romsdal (Norway). Landslides 2010, 7, 55–68. [Google Scholar] [CrossRef]
- Gu, T.; Li, J.; Wang, M.; Duan, P. Landslide susceptibility assessment in Zhenxiong County of China based on geographically weighted logistic regression model. Geocarto Int. 2022, 37, 4952–4973. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Sameen, M.I.; Chen, W.; Xu, C. Spatial prediction of rotational landslide using geographically weighted regression, logistic regression, and support vector machine models in Xing Guo area (China). Geomat. Nat. Hazards Risk 2017, 8, 1997–2022. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, Z.; Hu, C.; Wang, K.; Ding, X. Geographically weighted neural network considering spatial heterogeneity for landslide susceptibility mapping: A case study of Yichang City, China. Catena 2024, 234, 107590. [Google Scholar] [CrossRef]
- Yang, J.; Song, C.; Yang, Y.; Xu, C.; Guo, F.; Xie, L. New method for landslide susceptibility mapping supported by spatial logistic regression and GeoDetector: A case study of Duwen Highway Basin, Sichuan Province, China. Geomorphology 2019, 324, 62–71. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Yang, B.; Liu, Z.Q.; Kwan, J.S.H.; Chen, L. Spatiotemporal modelling of rainfall-induced landslides using machine learning. Landslides 2021, 18, 2499–2514. [Google Scholar] [CrossRef]
- Popescu, M.E. Landslide causal factors and landslide remediatial options. In Proceedings of the 3rd International Conference on Landslides, Slope Stability and Safety of Infra-Structures, Singapore, 11–12 July 2002; pp. 61–81. [Google Scholar]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; Binh, T.; Dieu Tien, B.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid Integration Approach of Entropy with Logistic Regression and Support Vector Machine for Landslide Susceptibility Modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef]
- Li, L.-M.; Cheng, S.-K.; Wen, Z.-Z. Landslide prediction based on improved principal component analysis and mixed kernel function least squares support vector regression model. J. Mt. Sci. 2021, 18, 2130–2142. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W. GIS-based landslide susceptibility assessment using optimized hybrid machine learning methods. Catena 2021, 196, 104833. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Wang, Y.; Wen, H.; Sun, D.; Li, Y. Quantitative Assessment of Landslide Risk Based on Susceptibility Mapping Using Random Forest and GeoDetector. Remote Sens. 2021, 13, 2625. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, Z.; Xu, Q.; Li, W. Risk Factor Detection and Landslide Susceptibility Mapping Using Geo-Detector and Random Forest Models: The 2018 Hokkaido Eastern Iburi Earthquake. Remote Sens. 2021, 13, 1157. [Google Scholar] [CrossRef]
- Quevedo, R.P.; Velastegui-Montoya, A.; Montalvan-Burbano, N.; Morante-Carballo, F.; Korup, O.; Renno, C.D. Land use and land cover as a conditioning factor in landslide susceptibility: A literature review. Landslides 2023, 20, 967–982. [Google Scholar] [CrossRef]
- Ren, T.; Gao, L.; Gong, W. An ensemble of dynamic rainfall index and machine learning method for spatiotemporal landslide susceptibility modeling. Landslides 2024, 21, 257–273. [Google Scholar] [CrossRef]
- Xiao, T.; Zhang, L.M.; Cheung, R.W.M.; Lacasse, S. Predicting spatio-temporal man-made slope failures induced by rainfall in Hong Kong using machine learning techniques. Geotechnique 2022, 73, 749–765. [Google Scholar] [CrossRef]
- Zhu, A.X.; Miao, Y.; Wang, R.; Zhu, T.; Deng, Y.; Liu, J.; Yang, L.; Qin, C.-Z.; Hong, H. A comparative study of an expert knowledge-based model and two data-driven models for landslide susceptibility mapping. Catena 2018, 166, 317–327. [Google Scholar] [CrossRef]
- Martinello, C.; Delchiaro, M.; Iacobucci, G.; Cappadonia, C.; Rotigliano, E.; Piacentini, D. Exploring the geomorphological adequacy of the landslide susceptibility maps: A test for different types of landslides in the Bidente river basin (northern Italy). Catena 2024, 238. [Google Scholar] [CrossRef]
- Peng, L.; Niu, R.; Huang, B.; Wu, X.; Zhao, Y.; Ye, R. Landslide susceptibility mapping based on rough set theory and support vector machines: A case of the Three Gorges area, China. Geomorphology 2014, 204, 287–301. [Google Scholar] [CrossRef]
- Nefeslioglu, H.A.; Gokceoglu, C.; Sonmez, H. An assessment on the use of logistic regression and artificial neural networks with different sampling strategies for the preparation of landslide susceptibility maps. Eng. Geol. 2008, 97, 171–191. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Huang, J.; Gui, L.; Wang, P. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 2017, 223, 11–22. [Google Scholar] [CrossRef]
- Khabiri, S.; Crawford, M.M.; Koch, H.J.; Haneberg, W.C.; Zhu, Y. An Assessment of Negative Samples and Model Structures in Landslide Susceptibility Characterization Based on Bayesian Network Models. Remote Sens. 2023, 15, 3200. [Google Scholar] [CrossRef]
- Hu, Q.; Zhou, Y.; Wang, S.; Wang, F. Machine learning and fractal theory models for landslide susceptibility mapping: Case study from the Jinsha River Basin. Geomorphology 2020, 351, 106975. [Google Scholar] [CrossRef]
- Dou, H.; He, J.; Huang, S.; Jian, W.; Guo, C. Influences of non-landslide sample selection strategies on landslide susceptibility mapping by machine learning. Geomat. Nat. Hazards Risk 2023, 14, 2285719. [Google Scholar] [CrossRef]
- Wang, J.-F.; Li, X.-H.; Christakos, G.; Liao, Y.-L.; Zhang, T.; Gu, X.; Zheng, X.-Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Luo, W.; Liu, C.-C. Innovative landslide susceptibility mapping supported by geomorphon and geographical detector methods. Landslides 2018, 15, 465–474. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Sahin, E.K.; Colkesen, I.; Kavzoglu, T. A comparative assessment of canonical correlation forest, random forest, rotation forest and logistic regression methods for landslide susceptibility mapping. Geocarto Int. 2020, 35, 341–363. [Google Scholar] [CrossRef]
- Georganos, S.; Grippa, T.; Gadiaga, A.N.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Dai, X.; Zhu, Y.; Sun, K.; Zou, Q.; Zhao, S.; Li, W.; Hu, L.; Wang, S. Examining the Spatially Varying Relationships between Landslide Susceptibility and Conditioning Factors Using a Geographical Random Forest Approach: A Case Study in Liangshan, China. Remote Sens. 2023, 15, 1513. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Dou, J.; Yunus, A.P.; Dieu Tien, B.; Merghadi, A.; Sahana, M.; Zhu, Z.; Chen, C.-W.; Khosravi, K.; Yang, Y.; Binh Thai, P. Assessment of advanced random forest and decision tree algorithms for modeling rainfall-induced landslide susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. Total Environ. 2019, 662, 332–346. [Google Scholar] [CrossRef]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, G.; Wang, T.; Ye, Y.; Zhen, J.; Tu, W. Analyzing spatial non-stationarity effects of driving factors on landslides: A multiscale geographically weighted regression approach based on slope units. Bull. Eng. Geol. Environ. 2024, 83, 394. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Polykretis, C.; Grillakis, M.G.; Argyriou, A.V.; Papadopoulos, N.; Alexakis, D.D. Integrating multivariate (GeoDetector) and bivariate (IV) statistics for hybrid landslide susceptibility modeling: A case of the vicinity of Pinios artificial lake, Ilia, Greece. Land 2021, 10, 973. [Google Scholar] [CrossRef]
- Zhou, C.; Cheng, W.; Qian, J.; Bingyuan, L.I.; Zhang, B. Research on the Classification System of Digital Land Geomorphology of 1: 1,000,000 in China. Geo-Inf. Sci. 2009, 11, 707–724. [Google Scholar] [CrossRef]
- Wang, N.; Cheng, W.; Wang, B.; Liu, Q.; Zhou, C. Geomorphological regionalization theory system and division methodology of China. J. Geogr. Sci. 2020, 30, 212–232. [Google Scholar] [CrossRef]
- Cheng, W.; Zhou, C.; Chai, H.; Zhao, S.; Liu, H.; Zhou, Z. Research and compilation of the Geomorphologic Atlas of the People’s Republic of China (1:1,000,000). J. Geogr. Sci. 2011, 21, 89–100. [Google Scholar] [CrossRef]
- Yu, B.; Chen, W.; Feng, W.; Liu, K.; Ye, L. A case study of shallow landslides triggered by rainfall in Sanming, Fujian Province, China. Environ. Earth Sci. 2023, 82, 426. [Google Scholar] [CrossRef]
- Liang, X.; Segoni, S.; Yin, K.; Du, J.; Chai, B.; Tofani, V.; Casagli, N. Characteristics of landslides and debris flows triggered by extreme rainfall in Daoshi Town during the 2019 Typhoon Lekima, Zhejiang Province, China. Landslides 2022, 19, 1735–1749. [Google Scholar] [CrossRef]
- Li, Z.; Fotheringham, A.S.; Li, W.; Oshan, T. Fast Geographically Weighted Regression (FastGWR): A scalable algorithm to investigate spatial process heterogeneity in millions of observations. Int. J. Geogr. Inf. Sci. 2019, 33, 155–175. [Google Scholar] [CrossRef]
- Sheng, Y.; Xu, G.; Jin, B.; Zhou, C.; Li, Y.; Chen, W. Data-Driven Landslide Spatial Prediction and Deformation Monitoring: A Case Study of Shiyan City, China. Remote Sens. 2023, 15, 5256. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Li, Z.; Zhang, H.; Zhang, W. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on SHAP and XGBoost. Geocarto Int. 2022, 37, 13419–13450. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]








| Data Name | Data Format | Scale or Resolution | Data Source |
|---|---|---|---|
| DEM | GeoTIFF | 12.5 m | ALOS GDEM |
| Disaster points | .shp (point) | 1:50,000 | Field work and remote sensing interpretation |
| Remote sensing image | GeoTIFF | 30 m | L1T product of LANDSAT-8 |
| Road | .shp (line) | 1:50,000 | Calibration data based on Amap |
| Water body | .shp (polygon) | 1:50,000 | Calibration data based on Amap |
| Fault | .shp (line) | 1:50,000 | Zijin regional geological map |
| Land use | GeoTIFF | 30 m | GlobeLand30 |
| Conditioning Factors | Classes | Percentage of Area (%) | Percentage of Landslides (%) | IV |
|---|---|---|---|---|
| Elevation (m) | <159 | 35.534 | 57.229 | 0.477 |
| 160–329 | 23.684 | 22.892 | −0.034 | |
| 329–508 | 17.804 | 13.855 | −0.251 | |
| 508–702 | 15.457 | 4.819 | −1.165 | |
| >702 | 7.521 | 1.205 | −1.831 | |
| Slope (°) | <8 | 25.495 | 34.337 | 0.298 |
| 8–16 | 30.539 | 39.759 | 0.264 | |
| 16–24 | 23.339 | 17.470 | −0.290 | |
| 24–33 | 14.849 | 7.831 | −0.640 | |
| >33 | 5.779 | 0.602 | −2.261 | |
| Terrain relief (m) | <17 | 22.682 | 36.747 | 0.482 |
| 17–31 | 31.038 | 36.145 | 0.152 | |
| 31–45 | 26.149 | 20.482 | −0.244 | |
| 45–63 | 15.332 | 4.217 | −1.291 | |
| >63 | 4.800 | 2.410 | −0.689 | |
| Surface roughness | <1.04 | 58.636 | 74.699 | 0.242 |
| 1.04–1.13 | 28.385 | 21.084 | −0.297 | |
| 1.13–1.26 | 9.776 | 3.614 | −0.995 | |
| 1.26–1.49 | 2.837 | 0.602 | −1.550 | |
| >1.49 | 0.367 | 0.000 | −2.000 | |
| NDVI | <0.13 | 6.223 | 8.434 | 0.304 |
| 0.13–0.22 | 13.906 | 26.506 | 0.645 | |
| 0.22–0.28 | 21.117 | 22.892 | 0.081 | |
| 0.28–0.35 | 35.430 | 32.530 | −0.085 | |
| >0.35 | 23.324 | 9.639 | −0.884 | |
| Precipitation (mm) | <1603 | 39.058 | 61.446 | 0.453 |
| 1603–1622 | 21.062 | 19.277 | −0.089 | |
| 1622–1727 | 17.615 | 7.229 | −0.891 | |
| 1727–1801 | 13.904 | 8.434 | −0.500 | |
| >1801 | 8.361 | 3.614 | −0.839 | |
| Distance to fault (m) | <500 | 8.743 | 9.639 | 0.097 |
| 500–1000 | 9.368 | 10.241 | 0.089 | |
| 1000–1500 | 8.361 | 13.253 | 0.461 | |
| 1500–2000 | 6.872 | 4.819 | −0.355 | |
| >2000 | 66.655 | 62.048 | −0.072 | |
| Distance to road (m) | <50 | 19.159 | 40.964 | 0.760 |
| 50–100 | 14.258 | 24.699 | 0.549 | |
| 100–150 | 11.801 | 11.446 | −0.031 | |
| 150–200 | 9.862 | 5.422 | −0.598 | |
| >200 | 44.921 | 17.470 | −0.944 | |
| Distance to water (m) | <50 | 11.182 | 21.084 | 0.634 |
| 50–100 | 10.316 | 15.663 | 0.418 | |
| 100–150 | 9.911 | 16.265 | 0.495 | |
| 150–200 | 7.234 | 10.241 | 0.348 | |
| >200 | 61.357 | 36.747 | −0.513 | |
| Lithology | massive intrusive rock | 80.806 | 86.747 | 0.071 |
| stratified clastic rock | 14.165 | 7.831 | −0.593 | |
| single layer soil | 4.232 | 4.217 | −0.004 | |
| multilayer soil | 0.346 | 0.000 | −2.000 | |
| double layer soil | 0.451 | 1.205 | 0.982 | |
| Land use | arable land | 17.429 | 45.783 | 0.966 |
| woodland and shrubland | 76.730 | 43.976 | −0.557 | |
| grassland | 1.946 | 0.602 | −1.173 | |
| artificial surfaces | 3.304 | 8.434 | 0.937 | |
| water bodies and bare land | 0.591 | 1.205 | 0.712 |
| Model | Moran’s I | z-Score | p-Value |
|---|---|---|---|
| RF | 0.157 | 6.132 | 0.000 |
| GeoD-RF | 0.129 | 4.643 | 0.000 |
| GWRF | 0.137 | 5.498 | 0.000 |
| GeoD-GWRF | 0.106 | 4.103 | 0.000 |
| Landslide Conditioning Factors | First Round of Analysis | Second Round of Analysis | ||
|---|---|---|---|---|
| TOL | VIF | TOL | VIF | |
| Elevation | 0.06 | 15.94 | 0.74 | 1.35 |
| Slope | 0.09 | 10.88 | 0.30 | 3.37 |
| Curvature | 0.83 | 1.20 | 0.86 | 1.16 |
| Terrain relief | 0.31 | 3.24 | 0.31 | 3.20 |
| Surface roughness | 0.13 | 7.77 | - | - |
| NDVI | 0.83 | 1.20 | 0.85 | 1.18 |
| Precipitation | 0.07 | 14.58 | - | - |
| Slope of aspect | 0.81 | 1.24 | 0.82 | 1.22 |
| TWI | 0.64 | 1.55 | 0.70 | 1.42 |
| SPI | 0.74 | 1.36 | 0.76 | 1.32 |
| Distance to fault | 0.90 | 1.11 | 0.91 | 1.10 |
| Distance to road | 0.85 | 1.18 | 0.87 | 1.16 |
| Distance to water | 0.82 | 1.22 | 0.88 | 1.14 |
| Lithology | 0.95 | 1.05 | 0.95 | 1.05 |
| Land use | 0.94 | 1.06 | 0.94 | 1.06 |
| Model | Accuracy | AUC | Recall | F1 Score | ||||
|---|---|---|---|---|---|---|---|---|
| Median | Std | Median | Std | Median | Std | Median | Std | |
| Logistic | 0.740 | 0.012 | 0.815 | 0.008 | 0.560 | 0.016 | 0.589 | 0.012 |
| VIF-Logistic | 0.753 | 0.016 | 0.821 | 0.015 | 0.580 | 0.017 | 0.611 | 0.013 |
| GeoD-Logistic | 0.753 | 0.009 | 0.831 | 0.006 | 0.560 | 0.008 | 0.602 | 0.013 |
| SVM | 0.833 | 0.009 | 0.843 | 0.017 | 0.580 | 0.007 | 0.699 | 0.007 |
| VIF-SVM | 0.820 | 0.024 | 0.842 | 0.016 | 0.560 | 0.016 | 0.675 | 0.018 |
| GeoD-SVM | 0.833 | 0.025 | 0.844 | 0.010 | 0.600 | 0.018 | 0.706 | 0.016 |
| RF | 0.840 | 0.016 | 0.915 | 0.024 | 0.640 | 0.019 | 0.727 | 0.009 |
| VIF-RF | 0.833 | 0.017 | 0.909 | 0.024 | 0.620 | 0.018 | 0.713 | 0.016 |
| GeoD-RF | 0.853 | 0.017 | 0.928 | 0.015 | 0.680 | 0.016 | 0.756 | 0.018 |
| GWRF | 0.880 | 0.020 | 0.937 | 0.030 | 0.780 | 0.016 | 0.812 | 0.019 |
| VIF-GWRF | 0.867 | 0.017 | 0.928 | 0.015 | 0.740 | 0.017 | 0.787 | 0.019 |
| GeoD-GWRF | 0.880 | 0.009 | 0.942 | 0.012 | 0.780 | 0.009 | 0.812 | 0.016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, F.; Zhang, G.; Wang, T.; Ye, Y.; Zhao, Q. Geographically Weighted Random Forest Based on Spatial Factor Optimization for the Assessment of Landslide Susceptibility. Remote Sens. 2025, 17, 1608. https://doi.org/10.3390/rs17091608
Lu F, Zhang G, Wang T, Ye Y, Zhao Q. Geographically Weighted Random Forest Based on Spatial Factor Optimization for the Assessment of Landslide Susceptibility. Remote Sensing. 2025; 17(9):1608. https://doi.org/10.3390/rs17091608
Chicago/Turabian StyleLu, Feifan, Guifang Zhang, Tonghao Wang, Yumeng Ye, and Qinghao Zhao. 2025. "Geographically Weighted Random Forest Based on Spatial Factor Optimization for the Assessment of Landslide Susceptibility" Remote Sensing 17, no. 9: 1608. https://doi.org/10.3390/rs17091608
APA StyleLu, F., Zhang, G., Wang, T., Ye, Y., & Zhao, Q. (2025). Geographically Weighted Random Forest Based on Spatial Factor Optimization for the Assessment of Landslide Susceptibility. Remote Sensing, 17(9), 1608. https://doi.org/10.3390/rs17091608






