Detecting Post-Midnight Plasma Depletions Through Plasma Density and Electric Field Measurements in the Low-Latitude Ionosphere
Abstract
1. Introduction
2. Data and Methods
2.1. Data
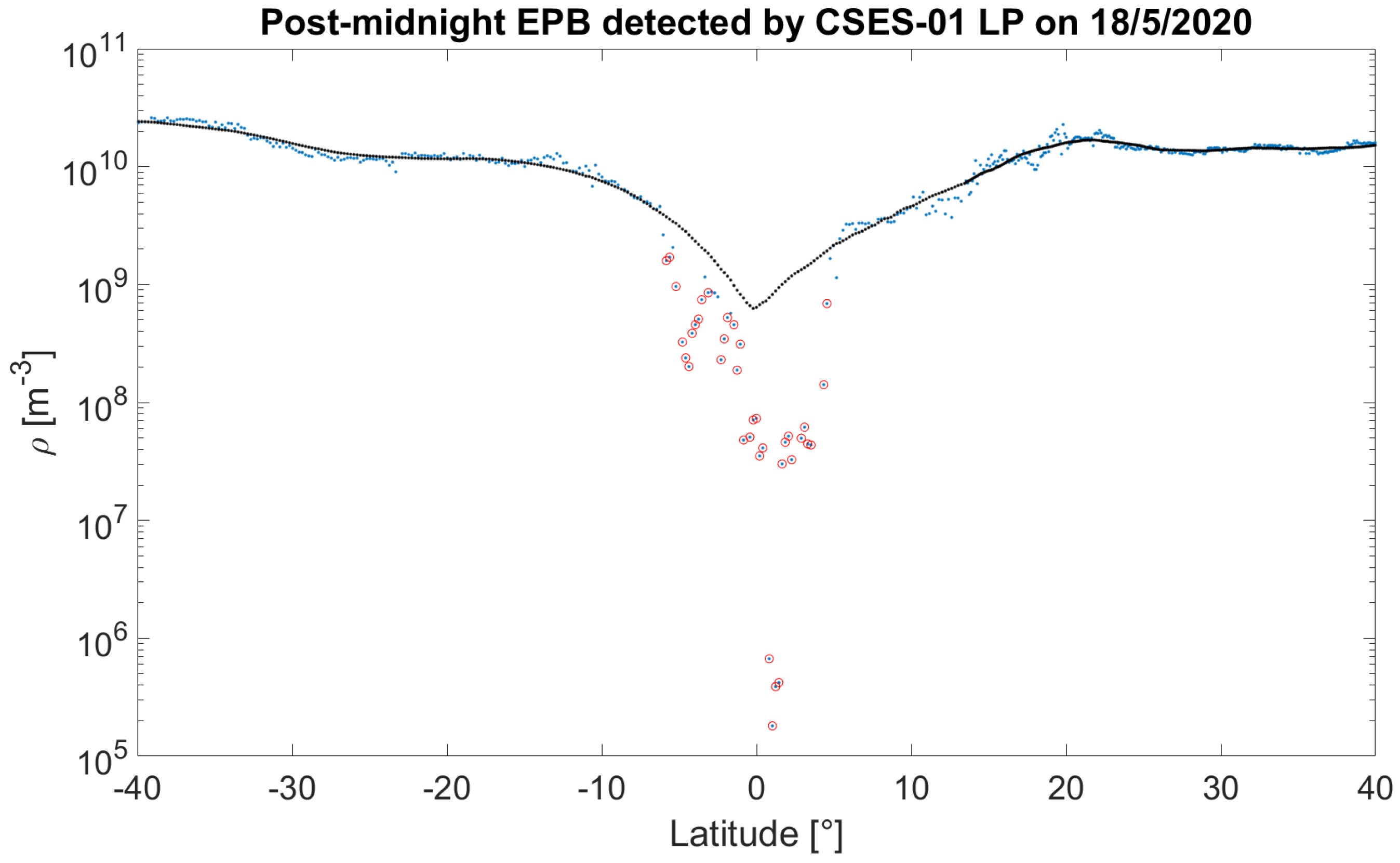
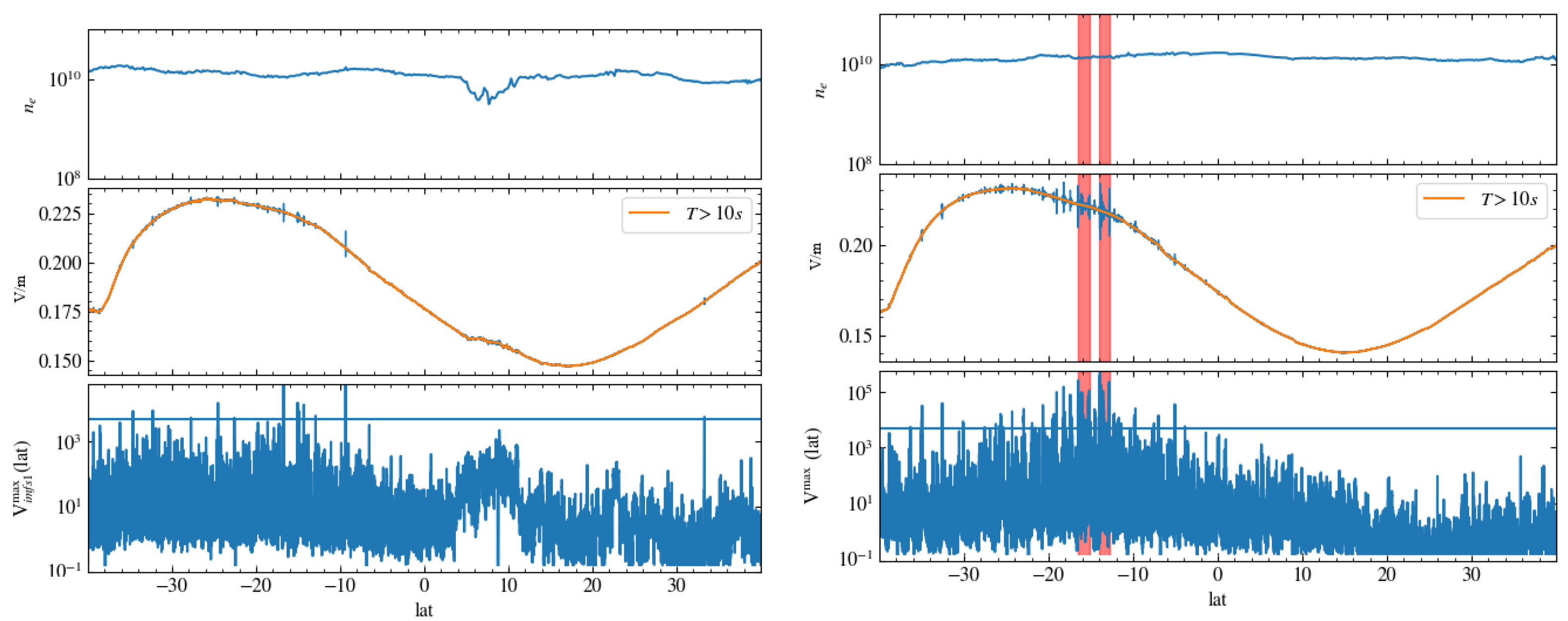
2.2. EPB Detection Based on LP Measurements of Plasma Density
- The ratio between the density measured at each point along the semiorbit and the running mean of the density is less than 1/2;
- The above condition is satisfied for at least five points along the semiorbit;
- Points whose time distance is lower than 40 s are considered as belonging to the same depletion; otherwise, they are considered as belonging to two (or more) different depletions.
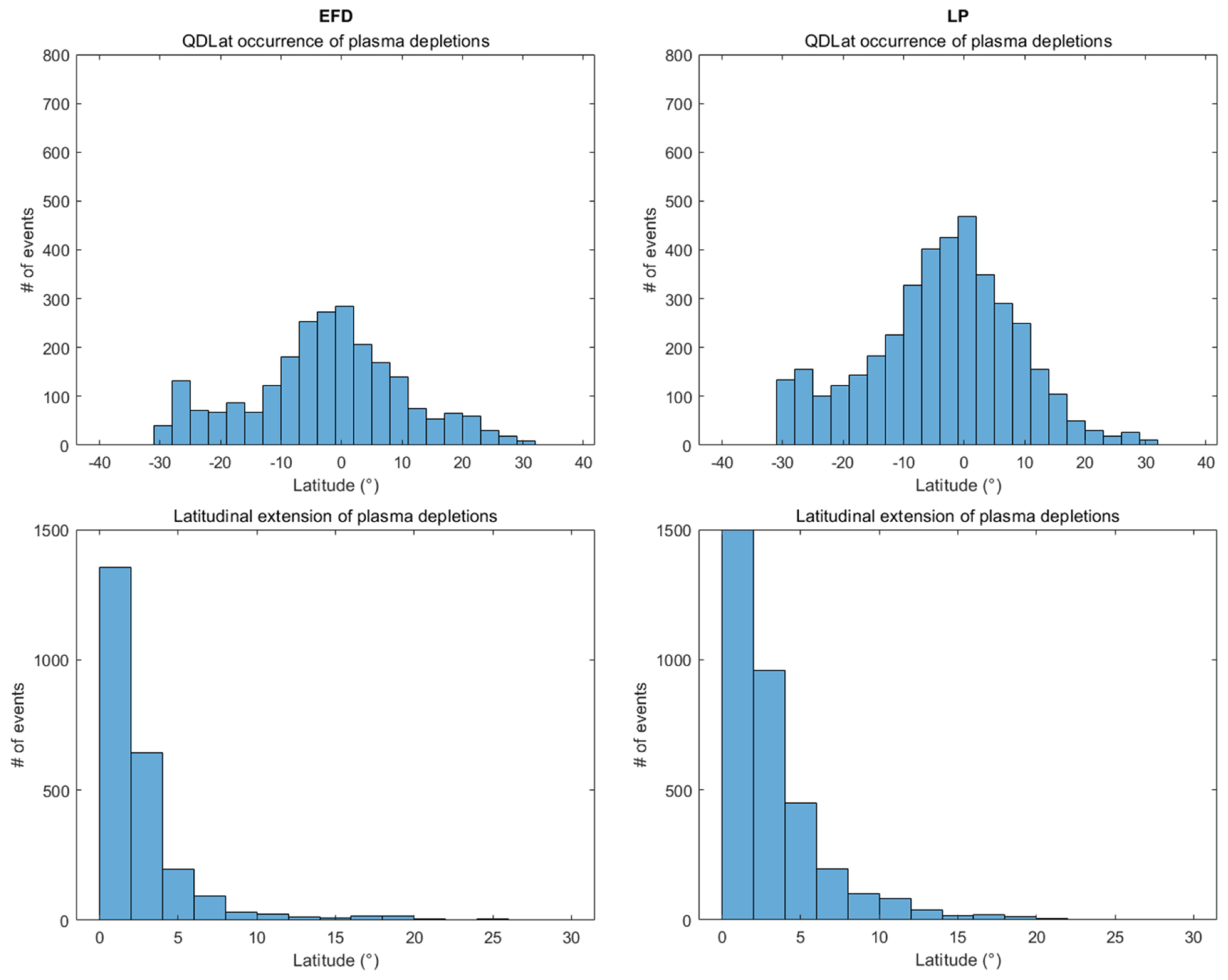
- Identified intervals are located in a latitudinal band from −30° to 30° of quasi dipole magnetic latitude [55].
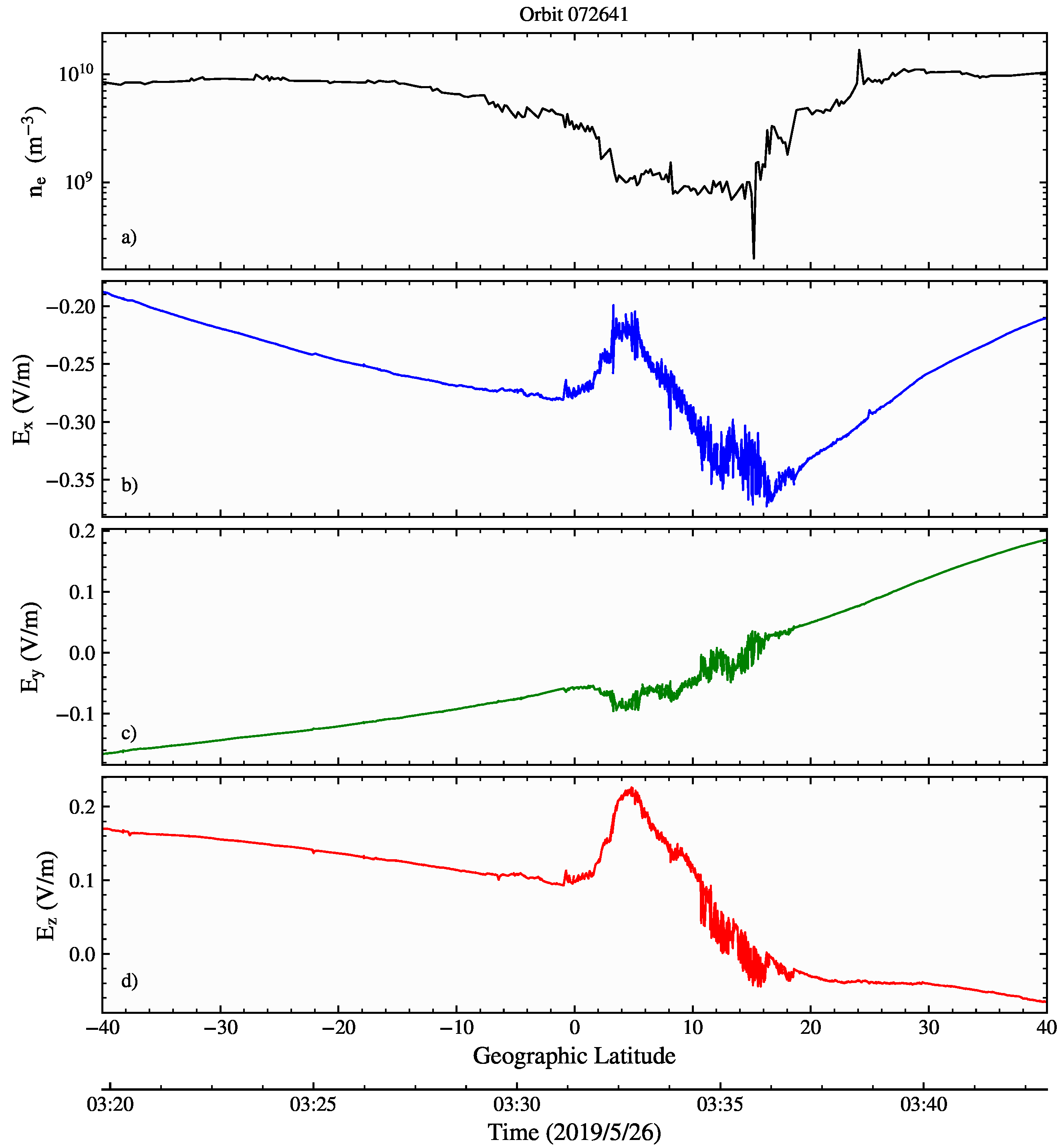
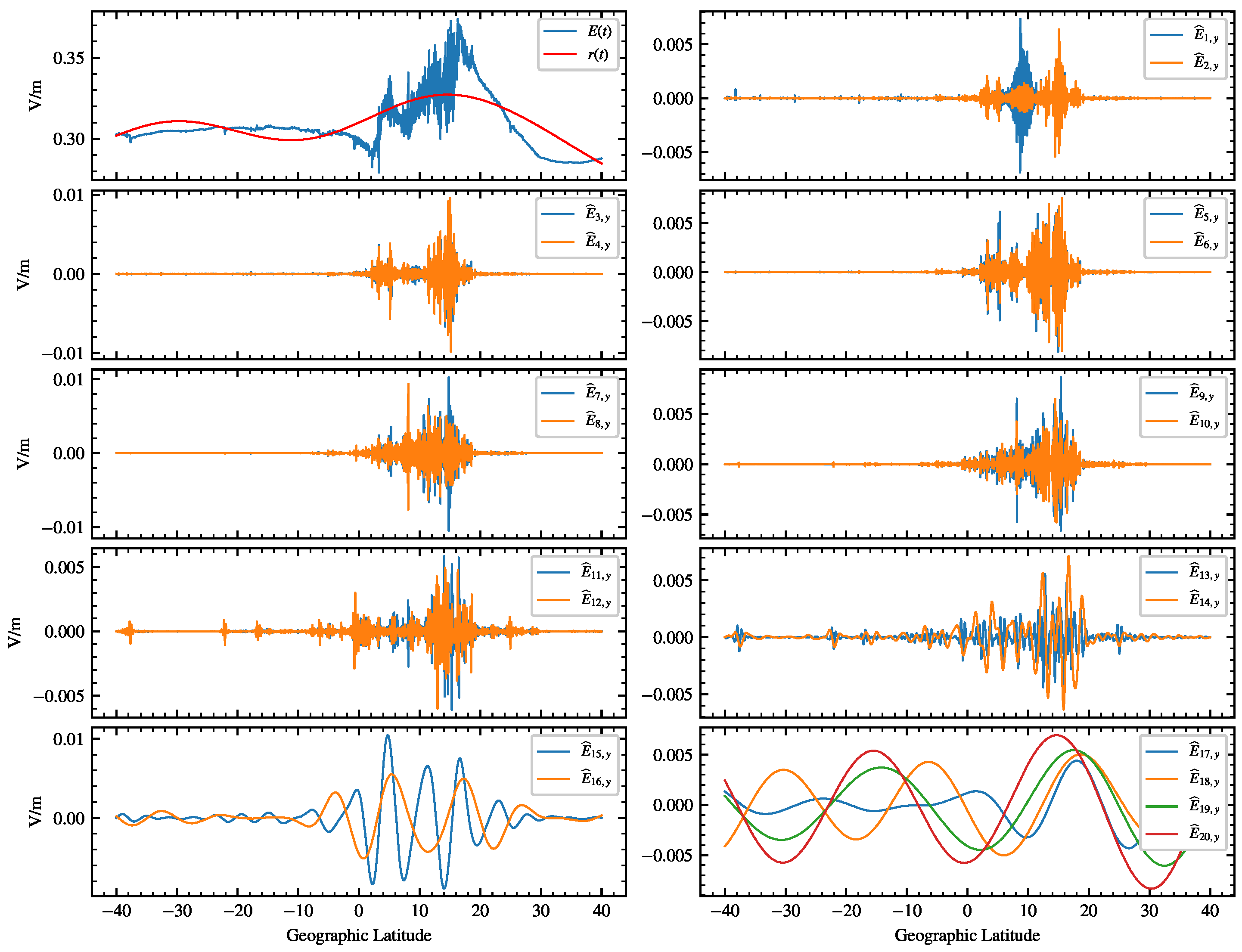
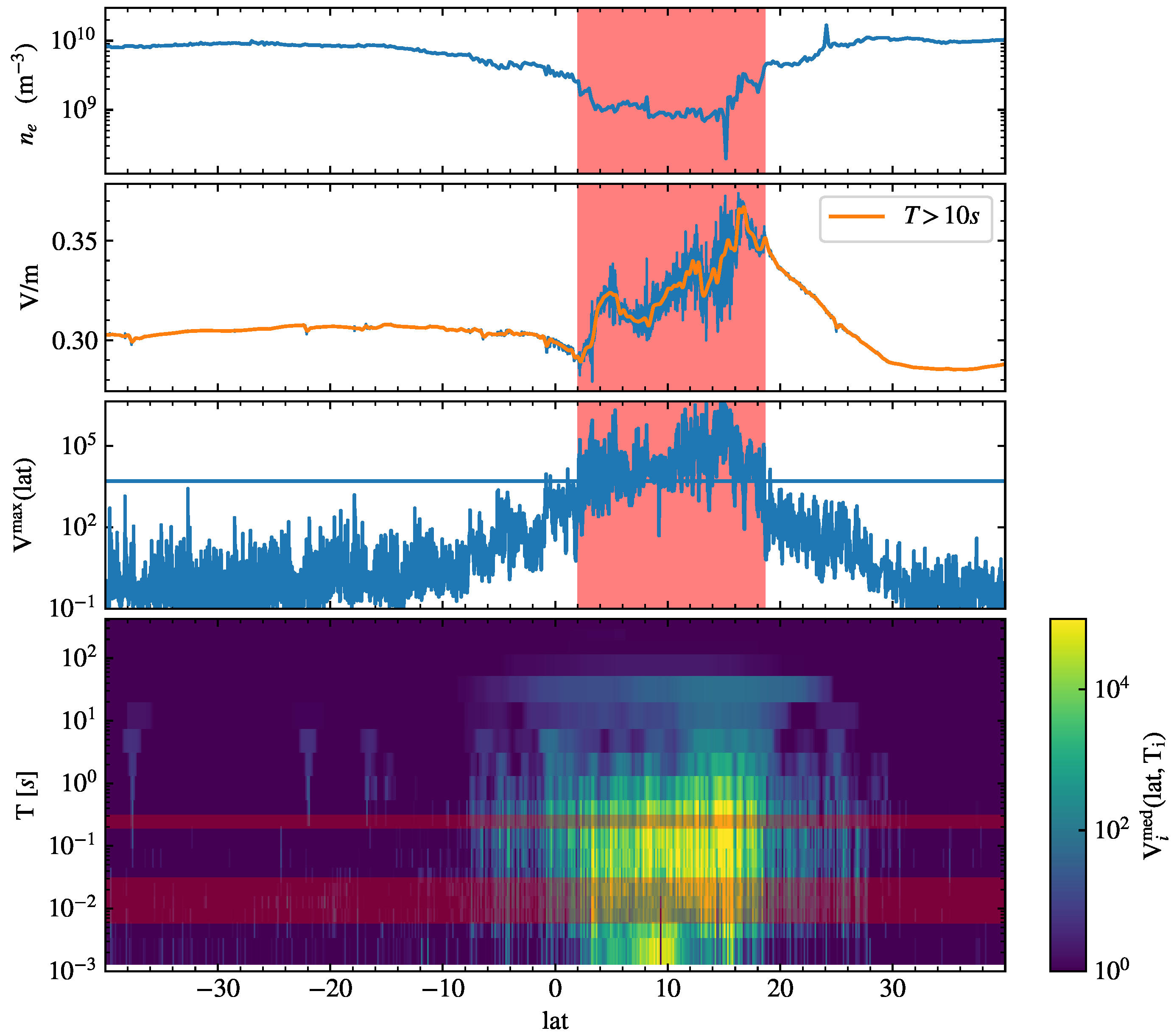
2.3. EPB Detection Based on a Local Variance Measure of the Electric Field
- A threshold of 5000 on the activity proxy ;
- A minimum latitudinal extension of for the fluctuations above the threshold;
- A minimum distance between two consecutive intervals of (below this value, intervals are merged together).
3. Results and Discussion
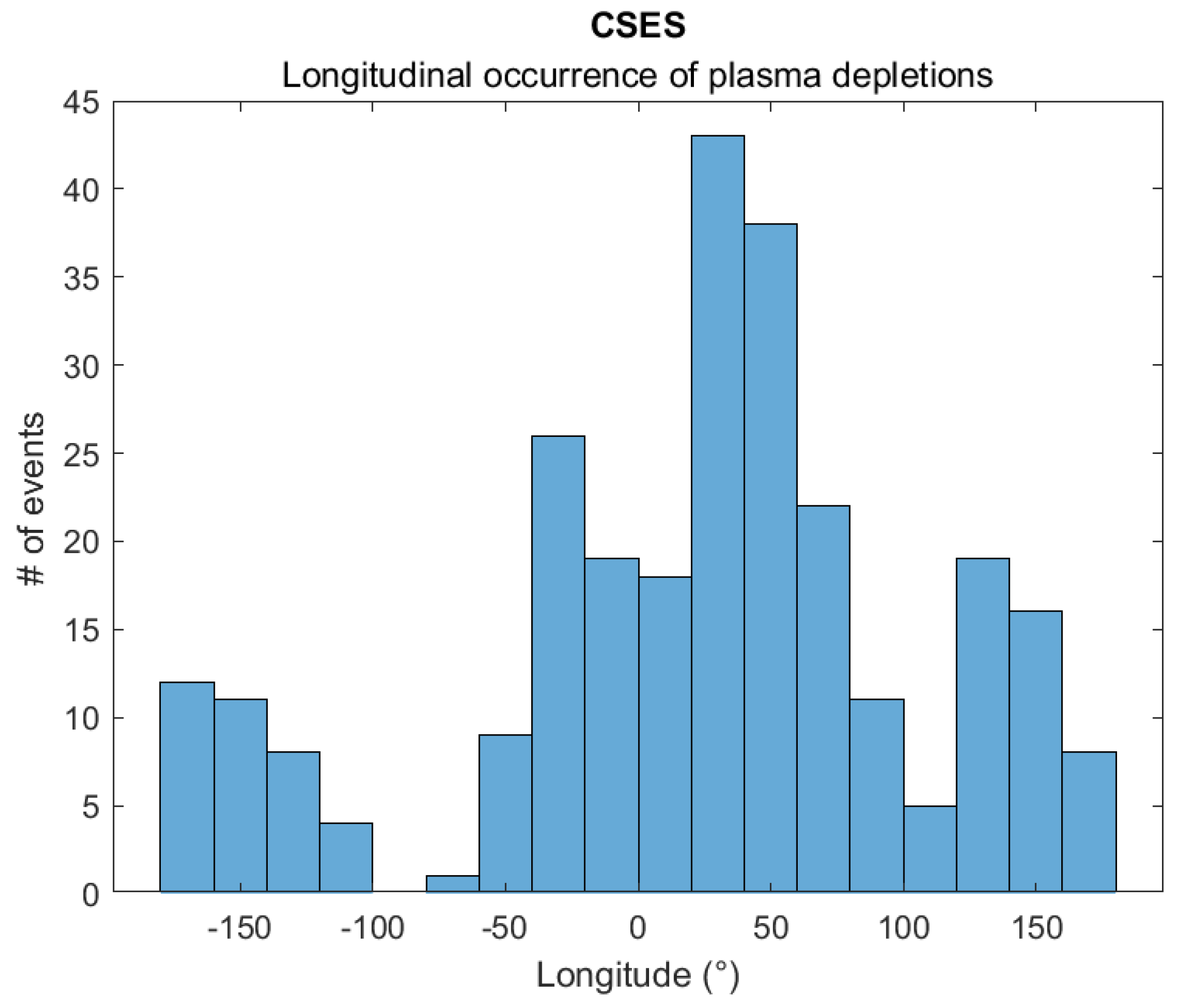
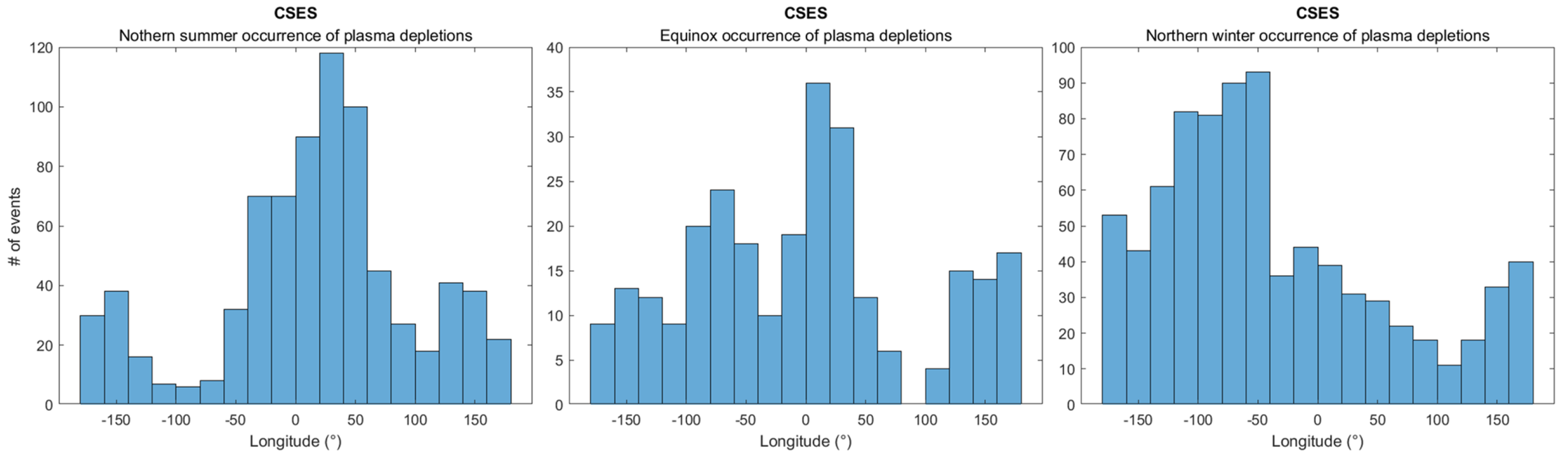
3.1. Post-Midnight EPBs from CSES-01 Observations
3.2. EPBs from Swarm B Observations
Cross-Validation Between Swarm B and CSES-01
4. Summary and Conclusions
- The detection of post-midnight EPBs using both CSES-01 and Swarm B provides valuable insights into the seasonal, latitudinal, and longitudinal characteristics of such ionospheric irregularities;
- The complementary nature of the LP and EFD algorithms enables a more comprehensive identification and characterization of EPBs.
- The observed seasonal and regional patterns of both post-sunset and post-midnight EPBs corroborate previous findings and enhance our understanding of the underlying mechanisms governing EPB formation, with many potential applications in the frame of space weather.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dungey, J. Convective diffusion in the equatorial F region. J. Atmos. Terr. Phys. 1956, 9, 304–310. [Google Scholar] [CrossRef]
- Balsley, B.; Haerendel, G.; Greenwald, R. Equatorial spread F: Recent observations and a new interpretation. J. Geophys. Res. 1972, 77, 5625–5628. [Google Scholar] [CrossRef]
- Hudson, M.K.; Kennel, C.F. Linear theory of equatorial spread F. J. Geophys. Res. 1975, 80, 4581–4590. [Google Scholar] [CrossRef]
- Ott, E. Theory of Rayleigh-Taylor bubbles in the equatorial ionosphere. J. Geophys. Res. Space Phys. 1978, 83, 2066–2070. [Google Scholar] [CrossRef]
- Tsunoda, R.T. Magnetic-field-aligned characteristics of plasma bubbles in the nighttime equatorial ionosphere. J. Atmos. Terr. Phys. 1980, 42, 743–752. [Google Scholar] [CrossRef]
- Woodman, R.F.; La Hoz, C. Radar observations of F region equatorial irregularities. J. Geophys. Res. 1976, 81, 5447–5466. [Google Scholar] [CrossRef]
- Kelley, M.; Hysell, D. Equatorial spread-F and neutral atmospheric turbulence: A review and a comparative anatomy. J. Atmos. Terr. Phys. 1991, 53, 695–708. [Google Scholar] [CrossRef]
- Hei, M.; Heelis, R.; McClure, J. Seasonal and longitudinal variation of large-scale topside equatorial plasma depletions. J. Geophys. Res. Space Phys. 2005, 110. [Google Scholar] [CrossRef]
- Pimenta, A.; Bittencourt, J.; Fagundes, P.; Sahai, Y.; Buriti, R.; Takahashi, H.; Taylor, M.J. Ionospheric plasma bubble zonal drifts over the tropical region: A study using OI 630 nm emission all-sky images. J. Atmos. Sol.-Terr. Phys. 2003, 65, 1117–1126. [Google Scholar] [CrossRef]
- Makela, J.J.; Vadas, S.; Muryanto, R.; Duly, T.; Crowley, G. Periodic spacing between consecutive equatorial plasma bubbles. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Basu, S.; Groves, K.; Basu, S.; Sultan, P. Specification and forecasting of scintillations in communication/navigation links: Current status and future plans. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1745–1754. [Google Scholar] [CrossRef]
- Nishioka, M.; Basu, S.; Basu, S.; Valladares, C.; Sheehan, R.; Roddy, P.; Groves, K. C/NOFS satellite observations of equatorial ionospheric plasma structures supported by multiple ground-based diagnostics in October 2008. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I. First observations of super plasma bubbles in Europe. Geophys. Res. Lett. 2016, 43, 11,137–11,145. [Google Scholar] [CrossRef]
- Yang, Z.; Morton, Y.J. Low-latitude GNSS ionospheric scintillation dependence on magnetic field orientation and impacts on positioning. J. Geod. 2020, 94, 59. [Google Scholar] [CrossRef]
- Pezzopane, M.; Pignalberi, A.; Coco, I.; Consolini, G.; De Michelis, P.; Giannattasio, F.; Marcucci, M.F.; Tozzi, R. Occurrence of GPS loss of lock based on a Swarm half-solar cycle dataset and its relation to the background ionosphere. Remote Sens. 2021, 13, 2209. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Pignalberi, A.; Lovati, G.; Pezzopane, M.; Tozzi, R.; Giannattasio, F.; Coco, I.; Marcucci, M.F. Ionospheric turbulence: A challenge for GPS loss of lock understanding. Space Weather 2022, 20, e2022SW003129. [Google Scholar] [CrossRef]
- Sousasantos, J.; Gomez Socola, J.; Rodrigues, F.S.; Eastes, R.W.; Brum, C.G.; Terra, P. Severe L-band scintillation over low-to-mid latitudes caused by an extreme equatorial plasma bubble: Joint observations from ground-based monitors and GOLD. Earth Planets Space 2023, 75, 41. [Google Scholar] [CrossRef]
- Booker, H.; Wells, H. Scattering of radio waves by the F-region of the ionosphere. Terr. Magn. Atmos. Electr. 1938, 43, 249–256. [Google Scholar] [CrossRef]
- Abdu, M.; De Medeiros, R.; Sobral, J.; Bittencourt, J. Spread F plasma bubble vertical rise velocities determined from spaced ionosonde observations. J. Geophys. Res. Space Phys. 1983, 88, 9197–9204. [Google Scholar] [CrossRef]
- Kelley, M.C.; McClure, J. Equatorial spread-F: A review of recent experimental results. J. Atmos. Terr. Phys. 1981, 43, 427–435. [Google Scholar] [CrossRef]
- Mendillo, M.; Baumgardner, J.; Pi, X.; Sultan, P.J.; Tsunoda, R. Onset conditions for equatorial spread F. J. Geophys. Res. Space Phys. 1992, 97, 13865–13876. [Google Scholar] [CrossRef]
- Miller, E.; Makela, J.; Groves, K.; Kelley, M.; Tsunoda, R. Coordinated study of coherent radar backscatter and optical airglow depletions in the central Pacific. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Pimenta, A.; Fagundes, P.; Bittencourt, J.; Sahai, Y.; Gobbi, D.; Medeiros, A.; Taylor, M.J.; Takahashi, H. Ionospheric plasma bubble zonal drift: A methodology using OI 630 nm all-sky imaging systems. Adv. Space Res. 2001, 27, 1219–1224. [Google Scholar] [CrossRef]
- Otsuka, Y.; Shiokawa, K.; Ogawa, T.; Wilkinson, P. Geomagnetic conjugate observations of equatorial airglow depletions. Geophys. Res. Lett. 2002, 29, 43-1–43-4. [Google Scholar] [CrossRef]
- Abdu, M.; Muralikrishna, P.; Batista, I.; Sobral, J. Rocket observation of equatorial plasma bubbles over Natal, Brazil, using a high-frequency capacitance probe. J. Geophys. Res. Space Phys. 1991, 96, 7689–7695. [Google Scholar] [CrossRef]
- Muralikrishna, P. Electron temperature variations in developing plasma bubbles–rocket observations from Brazil. Adv. Space Res. 2006, 37, 903–909. [Google Scholar] [CrossRef]
- Aggson, T.; Laakso, H.; Maynard, N.; Pfaff, R. In situ observations of bifurcation of equatorial ionospheric plasma depletions. J. Geophys. Res. Space Phys. 1996, 101, 5125–5132. [Google Scholar] [CrossRef]
- Huang, C.; Burke, W.; Machuzak, J.; Gentile, L.; Sultan, P. DMSP observations of equatorial plasma bubbles in the topside ionosphere near solar maximum. J. Geophys. Res. Space Phys. 2001, 106, 8131–8142. [Google Scholar] [CrossRef]
- Xiong, C.; Lühr, H.; Ma, S.; Stolle, C.; Fejer, B. Features of highly structured equatorial plasma irregularities deduced from CHAMP observations. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2012; Volume 30, pp. 1259–1269. [Google Scholar]
- De Michelis, P.; Consolini, G.; Alberti, T.; Pignalberi, A.; Coco, I.; Tozzi, R.; Giannattasio, F.; Pezzopane, M. Investigating Equatorial Plasma Depletions through CSES-01 Satellite Data. Atmosphere 2024, 15, 868. [Google Scholar] [CrossRef]
- Nishioka, M.; Saito, A.; Tsugawa, T. Occurrence characteristics of plasma bubble derived from global ground-based GPS receiver networks. J. Geophys. Res. Space Phys. 2008, 113. [Google Scholar] [CrossRef]
- Barros, D.; Takahashi, H.; Wrasse, C.M.; Figueiredo, C.A.O. Characteristics of equatorial plasma bubbles observed by TEC map based on ground-based GNSS receivers over South America. In Annales Geophysicae; Copernicus Publications: Göttingen, Germany, 2018; Volume 36, pp. 91–100. [Google Scholar]
- Tang, L.; Chen, G. Equatorial plasma bubble detection using vertical TEC from altimetry satellite. Space Weather 2022, 20, e2022SW003142. [Google Scholar] [CrossRef]
- Takahashi, H.; Wrasse, C.; Otsuka, Y.; Ivo, A.; Gomes, V.; Paulino, I.; Medeiros, A.; Denardini, C.; Sant’Anna, N.; Shiokawa, K. Plasma bubble monitoring by TEC map and 630 nm airglow image. J. Atmos. Sol.-Terr. Phys. 2015, 130, 151–158. [Google Scholar] [CrossRef]
- Oliveira, C.B.A.d.; Espejo, T.M.S.; Moraes, A.; Costa, E.; Sousasantos, J.; Lourenco, L.F.D.; Abdu, M.A. Analysis of plasma bubble signatures in total electron content maps of the low-latitude ionosphere: A simplified methodology. Surv. Geophys. 2020, 41, 897–931. [Google Scholar] [CrossRef]
- Mokhtar, M.; Rahim, N.; Ismail, M.; Buhari, S. Ionospheric perturbation: A review of equatorial plasma bubble in the ionosphere. In Proceedings of the 2019 6th International Conference on Space Science and Communication (IconSpace), Johor Bahru, Malaysia, 28–30 July 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 23–28. [Google Scholar] [CrossRef]
- Kil, H. The occurrence climatology of equatorial plasma bubbles: A review. J. Astron. Space Sci. 2022, 39, 23–33. [Google Scholar] [CrossRef]
- Bhattacharyya, A. Equatorial Plasma Bubbles: A Review. Atmosphere 2022, 13, 1637. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The state-of-the-art of the China Seismo-Electromagnetic Satellite mission. Sci. China E Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Yan, R.; Guan, Y.; Shen, X.; Huang, J.; Zhang, X.; Liu, C.; Liu, D. The Langmuir Probe Onboard CSES: Data inversion analysis method and first results. Earth Planet. Phys. 2018, 2, 479–488. [Google Scholar] [CrossRef]
- Liu, C.; Guan, Y.; Zheng, X.; Zhang, A.; Piero, D.; Sun, Y. The technology of space plasma in-situ measurement on the China Seismo-Electromagnetic Satellite. Sci. China E Technol. Sci. 2019, 62, 829–838. [Google Scholar] [CrossRef]
- Huang, J.; Lei, J.; Li, S.; Zeren, Z.; Li, C.; Zhu, X.; Yu, W. The Electric Field Detector (EFD) onboard the ZH-1 satellite and first observational results. Earth Planet. Phys. 2018, 2, 469–478. [Google Scholar] [CrossRef]
- Diego, P.; Huang, J.; Piersanti, M.; Badoni, D.; Zeren, Z.; Yan, R.; Rebustini, G.; Ammendola, R.; Candidi, M.; Guan, Y.B.; et al. The Electric Field Detector on Board the China Seismo Electromagnetic Satellite—In-Orbit Results and Validation. Instruments 2021, 5, 1. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm An Earth Observation Mission investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Olsen, N.; Friis-Christensen, E.; Floberghagen, R.; Alken, P.; Beggan, C.D.; Chulliat, A.; Doornbos, E.; da Encarnação, J.T.; Hamilton, B.; Hulot, G.; et al. The Swarm Satellite Constellation Application and Research Facility (SCARF) and Swarm data products. Earth Planets Space 2013, 65, 1189–1200. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.E.; Öhlen, L.; Smith, M.; Moffat, B. Thermal ion imagers and Langmuir probes in the Swarm electric field instruments. J. Geophys. Res. (Space Phys.) 2017, 122, 2655–2673. [Google Scholar] [CrossRef]
- Lomidze, L.; Knudsen, D.J.; Burchill, J.; Kouznetsov, A.; Buchert, S.C. Calibration and validation of Swarm plasma densities and electron temperatures using ground-based radars and satellite radio occultation measurements. Radio Sci. 2018, 53, 15–36. [Google Scholar] [CrossRef]
- Xiong, C.; Jiang, H.; Yan, R.; Lühr, H.; Stolle, C.; Yin, F.; Smirnov, A.; Piersanti, M.; Liu, Y.; Wan, X.; et al. Solar flux influence on the in-situ plasma density at topside ionosphere measured by Swarm satellites. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030275. [Google Scholar] [CrossRef]
- Burchill, J.K.; Lomidze, L. Calibration of Swarm ion density, drift, and effective mass measurements. Earth Space Sci. 2024, 11, e2023EA003463. [Google Scholar] [CrossRef]
- Pakhotin, I.; Burchill, J.; Förster, M.; Lomidze, L. The swarm Langmuir probe ion drift, density and effective mass (SLIDEM) product. Earth Planets Space 2022, 74, 109. [Google Scholar] [CrossRef]
- Pignalberi, A.; Pezzopane, M.; Coco, I.; Piersanti, M.; Giannattasio, F.; De Michelis, P.; Tozzi, R.; Consolini, G. Inter-calibration and statistical validation of topside ionosphere electron density observations made by cses-01 mission. Remote Sens. 2022, 14, 4679. [Google Scholar] [CrossRef]
- Smirnov, A.; Shprits, Y.; Lühr, H.; Pignalberi, A.; Xiong, C. Calibration of Swarm plasma densities overestimation using neural networks. Space Weather 2024, 22, e2024SW003925. [Google Scholar] [CrossRef]
- Rao, S.; Singh, A. Probing the upper atmosphere using GPS. In GPS and GNSS Technology in Geosciences; Elsevier: Amsterdam, The Netherlands, 2021; pp. 135–153. [Google Scholar] [CrossRef]
- Laundal, K.M.; Richmond, A.D. Magnetic coordinate systems. Space Sci. Rev. 2017, 206, 27–59. [Google Scholar] [CrossRef]
- Li, G.; Ning, B.; Otsuka, Y.; Abdu, M.A.; Abadi, P.; Liu, Z.; Spogli, L.; Wan, W. Challenges to equatorial plasma bubble and ionospheric scintillation short-term forecasting and future aspects in east and southeast Asia. Surv. Geophys. 2021, 42, 201–238. [Google Scholar] [CrossRef]
- Spicher, A.; Clausen, L.B.N.; Miloch, W.J.; Lofstad, V.; Jin, Y.; Moen, J.I. Interhemispheric study of polar cap patch occurrence based on Swarm in situ data. J. Geophys. Res. (Space Phys.) 2017, 122, 3837–3851. [Google Scholar] [CrossRef]
- Crowley, G. Critical review of ionospheric patches and blobs. In The Review of Radio Science 1992–1996; Ross Stone, W., Ed.; Oxford University Press: Oxford, UK, 1996; Volume 619. [Google Scholar]
- D’Angelo, G.; Piersanti, M.; Pignalberi, A.; Coco, I.; De Michelis, P.; Tozzi, R.; Pezzopane, M.; Alfonsi, L.; Cilliers, P.; Ubertini, P. Investigation of the physical processes involved in gnss amplitude scintillations at high latitude: A case study. Remote Sens. 2021, 13, 2493. [Google Scholar] [CrossRef]
- Rino, C.; Tsunoda, R.; Petriceks, J.; Livingston, R.; Kelley, M.; Baker, K. Simultaneous rocket-borne beacon and in situ measurements of equatorial spread F—Intermediate wavelength results. J. Geophys. Res. Space Phys. 1981, 86, 2411–2420. [Google Scholar] [CrossRef]
- Singh, M.; Szuszczewicz, E. Composite equatorial spread F wave number spectra from medium to short wavelengths. J. Geophys. Res. Space Phys. 1984, 89, 2313–2323. [Google Scholar] [CrossRef]
- Carrano, C.S.; Rino, C.L. A theory of scintillation for two-component power law irregularity spectra: Overview and numerical results. Radio Sci. 2016, 51, 789–813. [Google Scholar] [CrossRef]
- Aol, S.; Buchert, S.; Jurua, E. Ionospheric irregularities and scintillations: A direct comparison of in situ density observations with ground-based L-band receivers. Earth Planets Space 2020, 72, 164. [Google Scholar] [CrossRef]
- Papini, E.; Piersanti, M.; D’Angelo, G.; Cicone, A.; Bertello, I.; Parmentier, A.; Diego, P.; Ubertini, P.; Consolini, G.; Zhima, Z. Detecting the Auroral Oval through CSES-01 Electric Field Measurements in the Ionosphere. Remote Sens. 2023, 15, 1568. [Google Scholar] [CrossRef]
- Cicone, A.; Zhou, H. Numerical analysis for iterative filtering with new efficient implementations based on FFT. Numer. Math. 2021, 147, 1–28. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Cicone, A.; Liu, J.; Zhou, H. Adaptive local iterative filtering for signal decomposition and instantaneous frequency analysis. Appl. Comput. Harmon. Anal. 2016, 41, 384–411. [Google Scholar] [CrossRef]
- Cicone, A.; Pellegrino, E. Multivariate Fast Iterative Filtering for the Decomposition of Nonstationary Signals. IEEE Trans. Signal Process. 2022, 70, 1521–1531. [Google Scholar] [CrossRef]
- Xiong, C.; Stolle, C.; Lühr, H.; Park, J.; Fejer, B.G.; Kervalishvili, G.N. Scale analysis of equatorial plasma irregularities derived from Swarm constellation. Earth Planets Space 2016, 68, 121. [Google Scholar] [CrossRef]
- Piersanti, M.; Pezzopane, M.; Zhima, Z.; Diego, P.; Xiong, C.; Tozzi, R.; Pignalberi, A.; D’Angelo, G.; Battiston, R.; Huang, J.; et al. Can an impulsive variation of the solar wind plasma pressure trigger a plasma bubble? A case study based on CSES, Swarm and THEMIS data. Adv. Space Res. 2021, 67, 35–45. [Google Scholar] [CrossRef]
- Patra, A.; Phanikumar, D.; Pant, T. Gadanki radar observations of F region field-aligned irregularities during June solstice of solar minimum: First results and preliminary analysis. J. Geophys. Res. Space Phys. 2009, 114. [Google Scholar] [CrossRef]
- Otsuka, Y.; Ogawa, T.; Effendy. VHF radar observations of nighttime F-region field-aligned irregularities over Kototabang, Indonesia. Earth Planets Space 2009, 61, 431–437. [Google Scholar] [CrossRef]
- Yokoyama, T.; Yamamoto, M.; Otsuka, Y.; Nishioka, M.; Tsugawa, T.; Watanabe, S.; Pfaff, R. On postmidnight low-latitude ionospheric irregularities during solar minimum: 1. Equatorial Atmosphere Radar and GPS-TEC observations in Indonesia. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Rosli, N.I.M.; Hamid, N.S.A.; Abdullah, M.; Buhari, S.M.; Sarudin, I. Seasonal Variation of Post-sunset and Post-midnight Equatorial Plasma Bubble in Malaysia during Moderate Solar Activity Level. In Proceedings of the 2021 7th International Conference on Space Science and Communication (IconSpace), Selangor, Malaysia, 23–24 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 294–297. [Google Scholar]
- Heelis, R.; Stoneback, R.; Earle, G.; Haaser, R.A.; Abdu, M. Medium-scale equatorial plasma irregularities observed by Coupled Ion-Neutral Dynamics Investigation sensors aboard the Communication Navigation Outage Forecast System in a prolonged solar minimum. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef]
- Otsuka, Y.; Shiokawa, K.; Nishioka, M. VHF radar observations of post-midnight F-region field-aligned irregularities over Indonesia during solar minimum. Indian J. Radio Space Phys. 2012, 41, 199–207. [Google Scholar]
- Nishioka, M.; Otsuka, Y.; Shiokawa, K.; Tsugawa, T.; Effendy, N.; Supnithi, P.; Nagatsuma, T.; Murata, K. On post-midnight field-aligned irregularities observed with a 30.8-MHz radar at a low latitude: Comparison withF-layer altitude near the geomagnetic equator. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Recchiuti, D.; D’Angelo, G.; Papini, E.; Diego, P.; Cicone, A.; Parmentier, A.; Ubertini, P.; Battiston, R.; Piersanti, M. Detection of electromagnetic anomalies over seismic regions during two strong (MW > 5) earthquakes. Front. Earth Sci. 2023, 11, 1152343. [Google Scholar] [CrossRef]
- Yizengaw, E.; Retterer, J.; Pacheco, E.; Roddy, P.; Groves, K.; Caton, R.; Baki, P. Postmidnight bubbles and scintillations in the quiet-time June solstice. Geophys. Res. Lett. 2013, 40, 5592–5597. [Google Scholar] [CrossRef]
- Dao, E.; Kelley, M.; Roddy, P.; Retterer, J.; Ballenthin, J.; de La Beaujardiere, O.; Su, Y.J. Longitudinal and seasonal dependence of nighttime equatorial plasma density irregularities during solar minimum detected on the C/NOFS satellite. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Otsuka, Y. Review of the generation mechanisms of post-midnight irregularities in the equatorial and low-latitude ionosphere. Prog. Earth Planet. Sci. 2018, 5, 57. [Google Scholar] [CrossRef]
- Stolle, C.; Lühr, H.; Rother, M.; Balasis, G. Magnetic signatures of equatorial spread F as observed by the CHAMP satellite. J. Geophys. Res. Space Phys. 2006, 111. [Google Scholar] [CrossRef]
- Burke, W.; Gentile, L.; Huang, C.; Valladares, C.; Su, S. Longitudinal variability of equatorial plasma bubbles observed by DMSP and ROCSAT-1. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R.; Pignalberi, A.; Pezzopane, M.; Coco, I.; Giannattasio, F.; Marcucci, M.F. Ionospheric turbulence and the equatorial plasma density irregularities: Scaling features and RODI. Remote Sens. 2021, 13, 759. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Alberti, T.; Tozzi, R.; Giannattasio, F.; Coco, I.; Pezzopane, M.; Pignalberi, A. Magnetic field and electron density scaling properties in the equatorial plasma bubbles. Remote Sens. 2022, 14, 918. [Google Scholar] [CrossRef]
- Tsunoda, R.T. Control of the seasonal and longitudinal occurrence of equatorial scintillations by the longitudinal gradient in integrated E region Pedersen conductivity. J. Geophys. Res. Space Phys. 1985, 90, 447–456. [Google Scholar] [CrossRef]


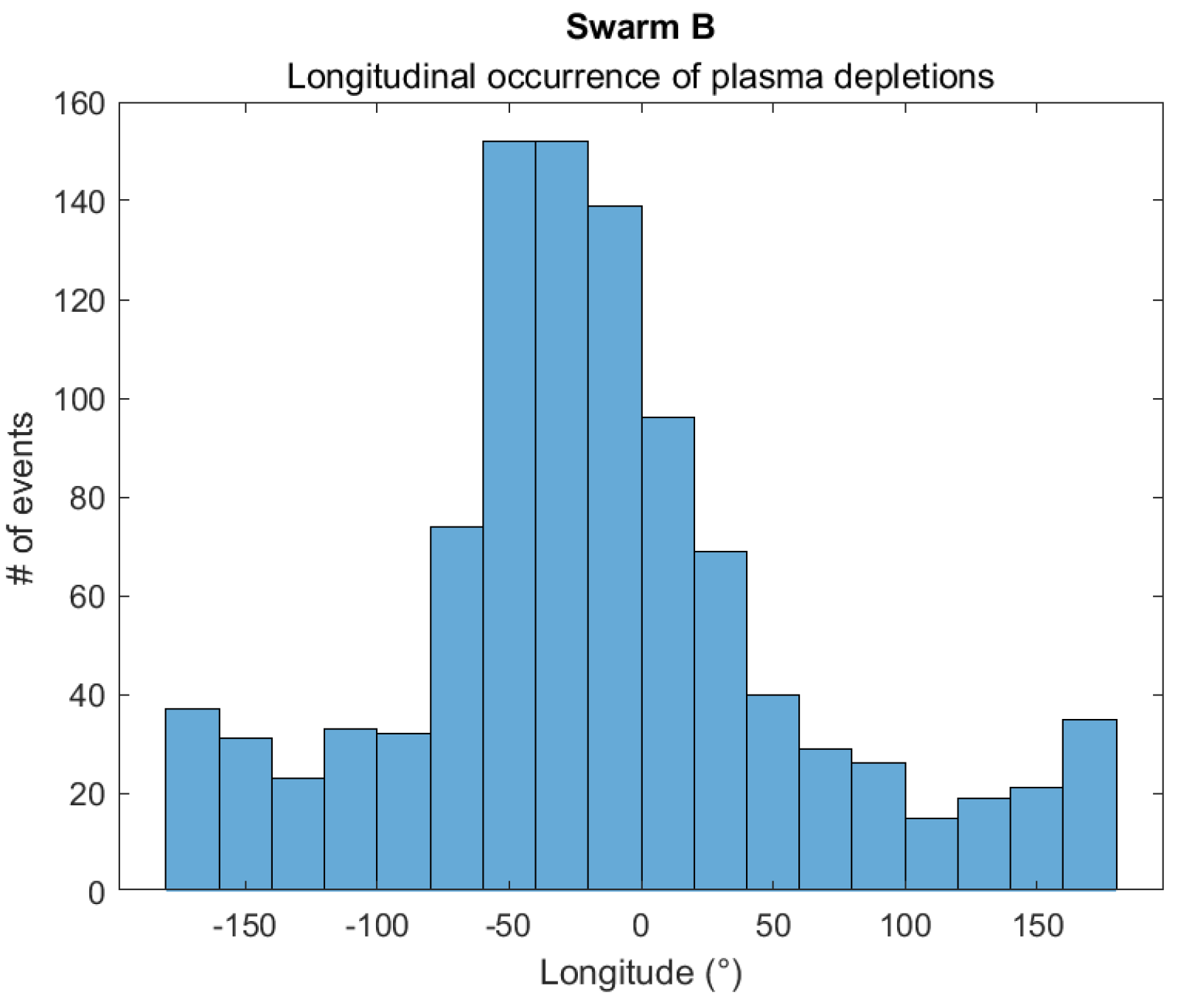

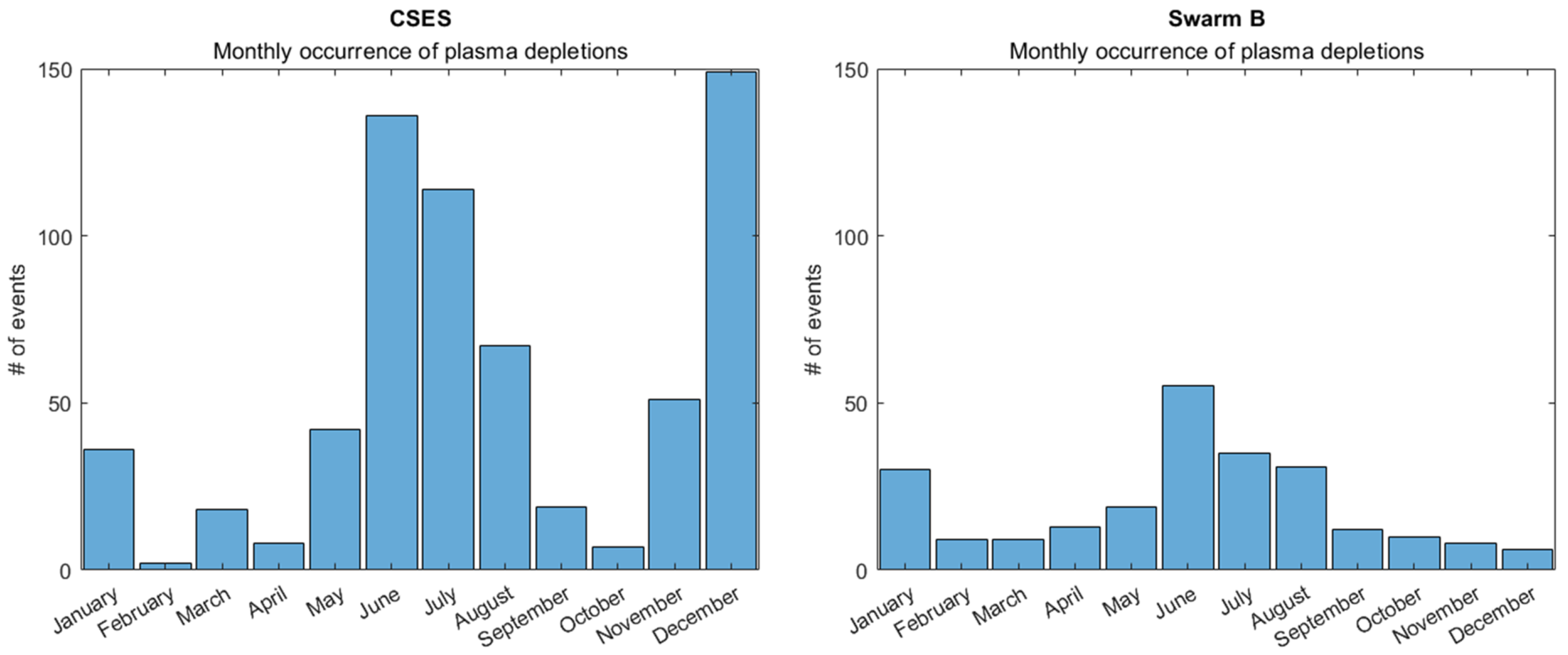
| Instrument | Number of Detected EPBs | Number of Semiorbits |
|---|---|---|
| LP | 3973 | 1937 |
| EFD | 2411 | 1598 |
| LP ∩ EFD | 1658 | 800 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Angelo, G.; Papini, E.; Pignalberi, A.; Recchiuti, D.; Diego, P. Detecting Post-Midnight Plasma Depletions Through Plasma Density and Electric Field Measurements in the Low-Latitude Ionosphere. Remote Sens. 2025, 17, 1529. https://doi.org/10.3390/rs17091529
D’Angelo G, Papini E, Pignalberi A, Recchiuti D, Diego P. Detecting Post-Midnight Plasma Depletions Through Plasma Density and Electric Field Measurements in the Low-Latitude Ionosphere. Remote Sensing. 2025; 17(9):1529. https://doi.org/10.3390/rs17091529
Chicago/Turabian StyleD’Angelo, Giulia, Emanuele Papini, Alessio Pignalberi, Dario Recchiuti, and Piero Diego. 2025. "Detecting Post-Midnight Plasma Depletions Through Plasma Density and Electric Field Measurements in the Low-Latitude Ionosphere" Remote Sensing 17, no. 9: 1529. https://doi.org/10.3390/rs17091529
APA StyleD’Angelo, G., Papini, E., Pignalberi, A., Recchiuti, D., & Diego, P. (2025). Detecting Post-Midnight Plasma Depletions Through Plasma Density and Electric Field Measurements in the Low-Latitude Ionosphere. Remote Sensing, 17(9), 1529. https://doi.org/10.3390/rs17091529







