Abstract
Deep learning has shown significant potential in multi-band Polarimetric Synthetic Aperture Radar (PolSAR) land cover classification. However, the existing methods face two main challenges: accurately modeling the complex nonlinear relationships between multiple bands and balancing classifier parameter efficiency with classification accuracy. To address these challenges, this paper proposes a novel decision-level multi-band fusion framework that leverages the synergistic optimization of the Vision Transformer (ViT) and Kolmogorov–Arnold Network (KAN). This innovative architecture effectively captures global spatial–spectral correlations through ViT’s cross-band self-attention mechanism and achieves parameter-efficient decision-level probability space mapping using KAN’s spline basis functions. The proposed method significantly enhances the model’s generalization capability across different band combinations. The experimental results on the quad-band (P/L/C/X) Hainan PolSAR dataset, acquired by the Aerial Remote Sensing System of the Chinese Academy of Sciences, show that the proposed framework achieves an overall accuracy of 96.24%, outperforming conventional methods in both accuracy and parameter efficiency. These results demonstrate the practical potential of the proposed method for high-performance and efficient multi-band PolSAR land cover classification.
1. Introduction
Polarimetric Synthetic Aperture Radar (PolSAR) has emerged as a pivotal technology for land cover classification due to its ability to capture both geometric and dielectric properties of terrain under all-weather, day-and-night conditions. However, achieving accurate land cover classification remains challenging, especially when dealing with complex terrains and multi-band SAR observations. The increasing availability of multi-frequency PolSAR data introduces new opportunities for classification but also poses challenges in terms of cross-band information fusion and model generalizability.
The existing methodologies can be broadly categorized into conventional approaches and deep-learning-based techniques. Traditional methods primarily employ statistical-probability-distribution-based classifiers, exemplified by the Wishart distribution-optimized classifier [1]. These approaches, while foundational, suffer from two inherent limitations: (1) heavy reliance on a priori assumptions about probability distributions that often mismatch real-world scattering characteristics; and (2) the inability to capture spatial–contextual patterns, leading to suboptimal performance in complex-terrain scenarios.
Another conventional paradigm involves polarimetric decomposition techniques, such as the seminal three-component scattering model by Freeman et al. [2]. Although these methods provide physically interpretable representations through target decomposition theorems, their diagnostic capability significantly degrades when handling heterogeneous landscapes with mixed scattering mechanisms.
The advent of deep learning [3], particularly convolutional neural networks (CNNs) [4], has revolutionized PolSAR interpretation. Zhou et al. [5] pioneered this transition with a shallow CNN architecture (two convolutional layers + two fully connected layers), demonstrating superior classification accuracy over conventional methods. The subsequent innovations include (1) complex-valued CNNs [6] that preserve phase information; (2) 3D convolutional operations [7] for joint spatial–polarimetric feature learning; and (3) semi-supervised [8] and adversarial learning frameworks [9,10] to address label scarcity. More recently, Wang et al. [11] achieved promising results by introducing Vision Transformers [12], leveraging self-attention mechanisms to model global contextual relationships in PolSAR imagery.
Despite these advances, two core challenges in multi-band PolSAR classification remain unresolved: (1) the existing models struggle to effectively capture nonlinear spatial–spectral interactions across different bands; and (2) the trade-off between model complexity and classification accuracy hinders deployment in practical applications. These limitations highlight a critical gap in the current research.
This study aims to bridge this gap by proposing a novel framework for efficient and accurate multi-band PolSAR land cover classification. Specifically, we introduce a decision-level fusion architecture that synergistically integrates Vision Transformer (ViT) and Kolmogorov–Arnold Network (KAN) to jointly address global contextual modeling and parameter efficiency.
The key contributions of this work are as follows:
- We design a position-encoding-enhanced cross-band ViT module that captures long-range dependencies among multi-band classification probability maps using self-attention mechanisms.
- We propose a spline-basis-expanded KAN classifier that achieves high fusion accuracy with significantly reduced parameter counts, enhancing the model’s practical applicability.
The remainder of this paper is organized as follows: Section 2 elaborates on the methodological framework, including the PolSAR feature representation, baseline single-band classification methods, and our core ViT–KAN fusion architecture. Section 3 presents the experimental results, including single- and multi-band classification performance, ablation studies, and a band combination impact analysis. Section 4 discusses the synergy between ViT’s attention mechanisms and KAN’s parameter efficiency. Section 5 concludes with a summary of the key findings and future directions.
2. Methods
In this section, we first introduce the representation and preprocessing of PolSAR images. Then, we present two single-band PolSAR image land cover classification methods based on convolutional neural networks and Transformers. Finally, we propose and elaborate on a decision-level land cover classification method for multi-band PolSAR images introduced in this paper.
2.1. Representation and Preprocessing of PolSAR Images
For fully polarized PolSAR data, the backscattering properties of a pixel can be described using the Sinclair matrix [13]:
Since is a symmetric matrix, it satisfies the condition . To facilitate the analysis of the backscattering characteristics, we introduce the Pauli vector and the polarization coherency matrix , which are defined as follows:
Here, represents temporal or spatial ensemble averaging, commonly referred to as the multilook operation. The coherency matrix is Hermitian, and its information can be compactly expressed as a nine-dimensional real-valued feature vector :
2.2. Single-Band PolSAR Image Land Cover Classification Methods
2.2.1. Typical CNN-Based Method
A single-band PolSAR land cover classification method based on convolutional neural networks (CNNs) [4] typically uses polarization features from a local pixel window as input and predicts the land cover type of each pixel. The classification of the entire image is achieved by traversing all pixels in the image using a sliding window. Due to the limited number of labeled samples, the network architecture is usually shallow, which simplifies the construction process. Although such networks generally perform averagely on complex high-resolution image problems, they are easier to train, requiring less time. Therefore, this method is adopted as a single-band PolSAR image classification approach, which serves as the input for the multi-band decision-level classification method. Figure 1 illustrates the CNN framework used in this study.
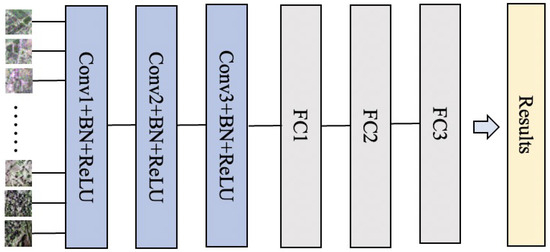
Figure 1.
The CNN framework used in this study.
2.2.2. Vision-Transformer-Based Method
The Vision Transformer (ViT) has demonstrated excellent performance in feature extraction. Another single-band land cover classification method used in this study is the model proposed by Wang et al. [11], with its framework illustrated in Figure 2. This model achieves high classification accuracy and is capable of handling complex high-resolution images. However, due to its long training time and the large amount of data required, the model is not suitable for all practical application scenarios. In this paper, it is adopted as the second single-band PolSAR image classification method and used as input for the multi-band decision-level classification method, aiming to demonstrate that the proposed approach achieves good classification performance when processing various single-band classification methods.
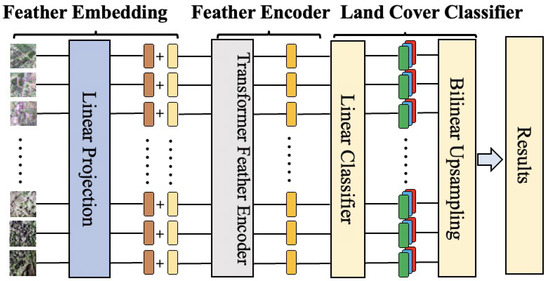
Figure 2.
The framework of the method based on Vision Transformer.
2.3. The Proposed Multi-Band Land Cover Classification Method
Traditional probability-based PolSAR classification methods often assume independence or simple linear correlations between bands, making it challenging to model the complex nonlinear relationships among them. To address this limitation, we propose a novel neural network architecture that combines Vision Transformer (ViT) and Kolmogorov–Arnold Network (KAN), as illustrated in Figure 3. The ViT module effectively captures complex dependencies between bands, while the KAN module models the underlying nonlinear structures with high precision.
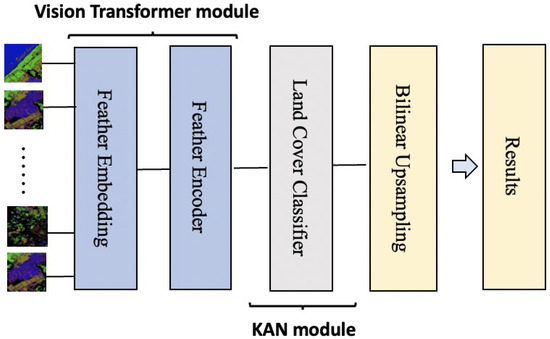
Figure 3.
The architecture of the proposed method.
Given the commonly observed class imbalance in PolSAR land cover datasets, we adopted a weighted cross-entropy loss function, where the weight for each class was set inversely proportional to its sample frequency in the training set. This strategy encourages the model to pay more attention to minority classes during training and prevents it from being overly biased towards majority classes.
To further mitigate the impact of class imbalance, we paid special attention to per-class precision metrics and the confusion matrix during evaluation, ensuring that the model performs well across all categories. We observed that the classes moss and trees, which have fewer training samples, exhibited relatively lower classification accuracy. This is primarily due to the limited number of samples and the fact that these classes typically appear as small and scattered patches in PolSAR images, which increases the difficulty of accurate classification.
Although no explicit data augmentation strategies were employed in this study, we recognize their potential value in addressing class imbalance in future work. It is important to note that, for pixel-wise classification tasks involving SAR images, conventional augmentation methods (e.g., random rotations, flips, or elastic deformations) are generally unsuitable as they may disrupt the physical consistency of spatial structures. In future work, we plan to explore more suitable class balancing strategies for PolSAR data, such as minority class sample simulation via generative models and target scattering characteristic modeling, to enhance model performance in low-sample categories.
These findings are consistent with the results shown in Table 6, where the proposed method achieves notably higher precision for the moss and trees classes compared to other methods, demonstrating its robustness and effectiveness in addressing the class imbalance problem.
The hardware device used is a high-performance server with a CPU of Intel(R) Core(TM) i9-10940X @ 3.30 GHz and a GPU of Nvidia RTX 3090 Ti, and the software implementation is based on PyTorch (version 2.1.0) with Python 3.10.
2.3.1. Vision Transformer Module
The input data for our method are derived from the output of a single-band land cover classification neural network. Specifically, for each pixel, the single-band classification network outputs a probability vector representing the likelihood of the pixel belonging to each class. For multi-band PolSAR data with B bands, the classification result of each band can be represented as a probability matrix , where H and W denote the height and width of the image, respectively, and C is the number of classes.
To fully exploit local spatial context information, the input data are divided into pixel patches. Each patch contains pixels, and the multi-band classification result for each pixel is represented as a three-dimensional tensor , where denote the row and column indices of the patch.
To adapt to the input format of the ViT model, each pixel patch is flattened into a one-dimensional vector and projected into a high-dimensional embedding space using a learnable linear projection matrix , resulting in a patch embedding vector , where L is the embedding dimension.
To preserve the spatial position information of the pixel patches, a positional embedding is assigned to each pixel patch. The positional embedding is defined using trigonometric functions, encoding the row index i (or x) and the column index j (or y) as follows:
The patch embedding vector is combined with the positional embedding to obtain the final input embedding . The embedding vectors of all pixel patches are concatenated to form a two-dimensional feature embedding , where is the number of patches.
The core component of the ViT encoder is the multi-head self-attention (MSA) mechanism, which captures dependencies between different positions in the input sequence through parallel computation of multiple attention heads. Specifically, for the input feature , MSA first projects it linearly into query (Query), key (Key), and value (Value) matrices:
where are learnable projection matrices, and is the dimension of each attention head.
The output of each attention head is computed as
The outputs of all attention heads are concatenated and projected linearly to obtain the final output of MSA:
where is the output projection matrix, and h is the number of attention heads.
Following MSA, the ViT encoder employs a multi-layer perceptron (MLP) to further enhance the nonlinear expressive power of the features. The MLP consists of two fully connected layers with a GELU activation function in between
where and are learnable weight matrices, and and are bias terms.
Each Transformer layer in the ViT encoder consists of an MSA block followed by an MLP block, with residual connections and layer normalization applied to stabilize training. The output of the l-th Transformer layer is computed as
where LayerNorm denotes layer normalization.
2.3.2. Kolmogorov–Arnold Network (KAN) Module
The Kolmogorov–Arnold representation theorem states that any multivariate continuous function can be decomposed into a finite combination of univariate functions:
where and are univariate functions.
Based on this theorem, we construct a single-layer KAN. Given the input and output , the single-layer KAN is formulated as follows:
The function follows the formulation proposed by Liu et al. [14]:
where is the SiLU (Swish) activation function, represents the spline interpolation function, and and are learnable weights.
The KAN network is constructed by stacking multiple single-layer KANs, where each layer utilizes the single-layer KAN structure to achieve nonlinear mappings from inputs to outputs. This multi-layer architecture enhances the network’s expressiveness while maintaining computational efficiency and lightweight characteristics.
3. Results
3.1. Data Description, Data Preprocessing, and Experimental Setup
This paper utilizes a multi-band PolSAR dataset acquired by the Aerial Remote Sensing System of the Chinese Academy of Sciences (ARSSCAS) in Hainan, China, covering P-, L-, C-, and X-bands. Three co-registered images with dimensions of 12,500 × 10,600 pixels are selected, with slant range and azimuth pixel spacing of 0.18 m and 0.12 m, respectively. The ground truth includes six classes: buildings, crops, moss, trees, roads, and water, manually annotated by comparing with optical imagery. Figure 4 shows examples of pseudo-Pauli images for the L-band.

Figure 4.
The Hainan dataset: the pseudo-Pauli images of L-band.
Before training, all the polarimetric SAR (PolSAR) image data were standardized and filtered. Specifically, we applied min–max normalization to scale the pixel values to the range . Considering the presence of strong speckle noise in the raw PolSAR imagery, a Gaussian filter with standard deviation was applied to each image prior to reconstruction, aiming to enhance smoothness and improve the stability of the subsequent feature extraction.
For dataset partitioning, 80% of the samples were randomly assigned to the training set, and the remaining 20% were used for testing. Cross-validation was not applied in order to maintain a streamlined training process and ensure that all the models were compared under the same data distribution.
All the models were trained using the same optimization configuration, including the optimizer, learning rate schedule, and loss function. We used the AdamW optimizer with an initial learning rate of 0.001 and a weight decay coefficient of 0.05. A half-cycle cosine annealing strategy was adopted to adjust the learning rate. The batch size was set to 64, and the total number of training epochs was 500. The cross-entropy loss function was used to supervise the pixel-wise classification.
To ensure fair comparison across the experiments, all the models shared the same hyperparameter settings and preprocessing steps. The fusion experiments focused on four selected frequency bands: P, L, C, and X.
3.2. Experimental Results
3.2.1. Single-Band Land Cover Classification
In the single-band land cover classification experiment, we compared CNN-based and ViT-based methods. The experiments used the AdamW optimizer (weight decay ) with an initial learning rate of , following a half-cycle cosine decay schedule over 100 training epochs, including a 10-epoch warmup phase. Independent training and testing were conducted on the P, L, C, and X bands.
Table 1 shows that the ViT-based method outperformed the traditional CNN approach across all six bands. These results demonstrate that ViT can better capture global contextual information in single-band images.

Table 1.
Single-band classification accuracy (unit: %).
3.2.2. Comparative Experiments
To validate the robustness of the proposed multi-band decision-level method, we compared it with the modified average approach [15], the multi-band fusion method proposed by Zhu et al. [16], a CNN-based fusion baseline, and a Support Vector Machine (SVM) classifier with a radial basis function (RBF) kernel, using single-band classification results from both CNN and ViT as inputs. All the experiments were conducted on the same four-band data (P, L, C, and X). For the baseline models, the SVM used a radial basis function (RBF) kernel and took concatenated features from multiple band-specific classifiers as input. Hyperparameters were tuned via grid search. The CNN consisted of three convolutional layers with kernels, each followed by ReLU activation and max pooling, and a fully connected layer for classification.
Table 2 and Table 3 show the multi-band classification overall accuracy comparisons based on CNN and ViT single-band inputs, respectively. Table 4 and Table 5 present the classification results (overall accuracy and Kappa coefficient) of the five fusion strategies under CNN- and ViT-based single-band input settings, respectively. The results indicate the following:
- 1.
- Robustness: The proposed method outperforms the baselines across all the band combinations regardless of whether the single-band input is from a CNN or ViT. For example, with the P + L + C + X band combination, the proposed method achieves accuracies of for CNN input, significantly higher than the modified average approach () and Zhu method ().
- 2.
- Impact of Band Number: While the baselines show significant accuracy improvements when increasing from one band to two bands, their performance gains diminish as more bands are added. For example, with the ViT input, the modified average approach and Zhu method improve accuracy by and , respectively, when increasing from two bands (L + C) to four bands (P + L + C + X), whereas the proposed method achieves a improvement. This indicates that the baselines face limitations in multi-band fusion, while the proposed method can more effectively utilize multi-band information, continuously improving classification accuracy as the number of bands increases.
 Table 2. Multi-band classification overall accuracy with CNN single-band input (unit: %).Table 2. Multi-band classification overall accuracy with CNN single-band input (unit: %).
Table 2. Multi-band classification overall accuracy with CNN single-band input (unit: %).Table 2. Multi-band classification overall accuracy with CNN single-band input (unit: %).Band Combination SVM CNN Modified Average Zhu Method Proposed Method C (Single-Band) 83.84 83.84 83.84 83.84 83.84 L + C 84.01 85.27 84.41 85.53 85.92 L + C + X 84.23 86.18 84.82 86.23 86.96 P + L + C + X 84.96 86.88 85.14 86.87 87.79  Table 3. Multi-band classification overall accuracy with ViT single-band input (unit: %).Table 3. Multi-band classification overall accuracy with ViT single-band input (unit: %).
Table 3. Multi-band classification overall accuracy with ViT single-band input (unit: %).Table 3. Multi-band classification overall accuracy with ViT single-band input (unit: %).Band Combination SVM CNN Modified Average Zhu Method Proposed Method L (Single-Band) 92.52 92.52 92.52 92.52 92.52 L + C 92.67 94.13 93.14 94.21 94.87 L + C + X 93.01 95.01 93.52 94.98 95.62 P + L + C + X 93.31 95.32 93.82 95.22 96.24  Table 4. Multi-band classification accuracy with CNN single-band input.Table 4. Multi-band classification accuracy with CNN single-band input.
Table 4. Multi-band classification accuracy with CNN single-band input.Table 4. Multi-band classification accuracy with CNN single-band input.Method OA (%) Kappa SVM (RBF kernel) 84.96 0.847 CNN 86.88 0.869 Modified Average 85.14 0.852 Zhu Method 86.87 0.869 Proposed Method 87.79 0.879  Table 5. Multi-band classification accuracy with ViT single-band input.Table 5. Multi-band classification accuracy with ViT single-band input.
Table 5. Multi-band classification accuracy with ViT single-band input.Table 5. Multi-band classification accuracy with ViT single-band input.Method OA (%) Kappa SVM (RBF kernel) 91.67 0.910 CNN 95.32 0.939 Modified Average 93.82 0.921 Zhu Method 95.22 0.934 Proposed Method 96.24 0.942
To further analyze the classification performance across different land cover classes, we provide a per-class precision comparison in Table 6. The results show that the proposed method consistently achieves the highest precision across five classes—buildings, crops, moss, trees, and water—demonstrating its robustness and superior performance in multi-class scenarios.

Table 6.
Per-class precision comparison with ViT single-band input.
It is important to note that the precision of all the methods varies across different classes. In particular, the classes moss and trees exhibit relatively lower precision compared to the other land covers across all the methods. We observed frequent misclassifications among the moss, trees, and crops classes. This is primarily due to their similar scattering characteristics in certain polarimetric channels, especially under similar environmental conditions such as moisture levels or seasonal changes. Additionally, moss typically appears in sparse and fragmented patches, making it challenging to capture distinctive structural features at the patch level. The trees class is often misclassified as crops when the tree canopy is sparse or the vertical structure is not clearly expressed in the SAR imagery. Likewise, in regions with irregular planting patterns or mixed vegetation, crops are frequently confused with trees or moss due to the ambiguity in texture and scattering mechanisms.
These patterns of misclassification suggest that, while our proposed method demonstrates strong overall performance, relying solely on spectral–spatial features may be insufficient when handling classes with highly similar scattering and spatial properties. In future work, we plan to incorporate additional auxiliary information (e.g., temporal sequences or topographic features) and explore advanced post-processing strategies (e.g., contextual refinement and spatial consistency constraints) to further mitigate such classification errors.
Since our method builds upon the results of single-band classification, its final performance inherently depends on the quality of those preliminary predictions. Nevertheless, the proposed ViT–KAN fusion approach demonstrates a remarkable ability to integrate inconsistent or uncertain predictions from different bands. For example, even when single-band classifiers struggle to recognize moss and tree regions reliably, our fusion method can leverage complementary information from multiple bands and produce more accurate predictions. This highlights the effectiveness of our architecture in resolving ambiguities and enhancing class separability in complex multi-band PolSAR data.
In terms of spatial–spectral interaction modeling, our ViT–KAN framework demonstrates clear advantages over conventional approaches such as CNNs and SVMs. Traditional CNN models primarily capture local spatial features within individual bands but lack mechanisms for effectively modeling cross-band dependencies. Similarly, SVM classifiers treat concatenated features independently and are inherently limited in capturing hierarchical or global spatial correlations. In contrast, the ViT encoder leverages self-attention mechanisms to capture long-range spatial dependencies and inter-band relationships simultaneously, enabling the model to discover subtle structural patterns shared across bands. Furthermore, the KAN classifier provides a flexible and data-adaptive decision boundary by approximating complex multi-band distributions through spline basis functions, allowing for more precise fusion of spatial–spectral cues. This synergy between ViT’s global attention and KAN’s adaptive fusion explains the consistent performance gains observed in our comparative and per-class experiments, especially for spectrally ambiguous or spatially fragmented land cover types like moss and trees.
3.2.3. Ablation Studies
To validate the effectiveness of our architectural design, we conduct systematic ablation studies using controlled variables. Taking the four bands’ outputs from the ViT-based single-band classification method as unified inputs, we evaluate the contributions of feature extractor and classifier modules (Table 7 and Table 8). All the experiments share identical training strategies and hyperparameter settings.

Table 7.
Effectiveness analysis of ViT architecture.

Table 8.
Effectiveness analysis of KAN classifier.
When replacing ViT-Base with ResNet-18 as the feature extractor, the overall accuracy decreases by 4.11 percentage points (96.24% → 92.13%), with a 5.73% reduction in the Kappa coefficient (0.942 → 0.891). Although the CNN variant reduces the parameters by 9.8% (120.5k → 108.7k), the performance degradation far outweighs the parameter benefits. This confirms the superiority of ViT’s global attention mechanism in remote sensing feature representation, particularly in capturing discriminative cross-band features through its sequential modeling capability when processing long-range spatial correlations in multi-spectral data.
Substituting a KAN with a conventional MLP classifier leads to a 3.39 percentage point accuracy drop despite a 12.2% parameter increase (120.5k → 135.2k). This demonstrates that the KAN’s adaptive combination of spline basis functions enables higher-order feature interactions within more compact parameter spaces. Notably, the absolute Kappa reduction (0.041) is 1.7× greater than the relative OA decline, proving the KAN’s enhanced robustness in classifying challenging samples with ambiguous category boundaries.
To further investigate the effectiveness of the KAN’s core components, we introduce a new ablation experiment by replacing the activation functions in the MLP classifier with B-spline functions, thus constructing a ViT-Base + MLP (B-Spline) model (Table 9). This model isolates the contribution of the B-spline basis from the KAN’s full architecture while retaining the conventional MLP structure.

Table 9.
Effectiveness analysis of B-spline-activated MLP.
The experimental results demonstrate that simply adopting B-spline activation significantly boosts the performance of the MLP classifier (OA: 92.85% → 96.11%; Kappa: 0.901 → 0.940), underscoring the effectiveness of B-spline representations in modeling nonlinear feature relationships.
Our full model (ViT-Base + KAN) achieves the highest classification performance (OA: 96.24%; Kappa: 0.942) with moderate parameter complexity (120.5k), demonstrating superior parameter efficiency. Compared with the baseline MLP variant, the KAN improves accuracy by 3.39% while reducing the parameters by 10.9%. Even when compared to the enhanced B-spline-activated MLP, which narrows the performance gap (OA: 96.11%; Kappa: 0.940), the KAN still achieves slightly better results. This demonstrates that the KAN effectively breaks the conventional “more parameters–-better performance” trade-off, offering a promising paradigm for lightweight and scalable remote sensing classification systems.
In terms of computational cost, we conduct a qualitative analysis of the training time associated with different architectural variants. Using the ResNet-18 + MLP configuration as the baseline (with an average training time of approximately 96 min), we observe that replacing the CNN with a ViT encoder moderately increases training time due to the higher computational complexity of self-attention mechanisms. Similarly, substituting the MLP classifier with the KAN module introduces an additional overhead, primarily caused by the spline-based activation and adaptive combination operations. Despite these incremental costs, the overall training time of the full ViT + KAN model remains within a practically acceptable range, especially when considering the significant gains in accuracy and parameter efficiency. This balance underscores the practicality and scalability of the proposed framework for real-world PolSAR image classification tasks.
3.2.4. Theoretical Justification of KAN’s Efficiency
The effectiveness of the Kolmogorov–Arnold Network (KAN) in our proposed method can be theoretically supported by the following approximation result [14]:
Theorem 1
(Approximation Theory, KAT). Let . Suppose a multivariate function can be written as
where each is r-times continuously differentiable. Then, there exists a constant C such that, for any grid size , there exist r-th-order B-spline functions such that
where has the same structural form, and denotes the r-th-order Sobolev norm.
This theorem indicates that a KAN can approximate any sufficiently smooth function with an error bound proportional to , independent of the input dimension d. This breaks the curse of dimensionality and highlights the parameter efficiency of the KAN: by learning structured compositions of univariate functions and utilizing B-spline representations, a KAN significantly reduces the need for large numbers of independent weights, especially compared to traditional fully connected neural networks (MLPs).
Consequently, KANs achieve strong expressivity while maintaining low parameter complexity, which is especially beneficial for remote sensing tasks with limited training data and high input dimensionality.
4. Discussion
The experimental results demonstrate three core advantages of our proposed ViT–KAN framework for multi-band PolSAR classification. First, the ViT module achieves deep feature fusion of multi-band classification results through its global attention mechanism. As shown in Table 3, when using ViT-based single-band classification outputs as inputs, our method attains 96.24% overall accuracy (OA) for the four-band (P + L + C + X) combination, outperforming the traditional fusion methods by 3.02 percentage points. This validates the exceptional capability of attention mechanisms in cross-band information integration.
Second, the KAN classifier pioneers a new parameter-efficient decision-level fusion approach. The ablation study data (Table 8) reveal a significant phenomenon: KAN achieves a 3.39 percentage point OA improvement over MLP while reducing the parameters by 10.9%. This inverse “parameter reduction–performance enhancement” relationship stems from KAN’s adaptive combination mechanism of spline basis functions, which precisely characterizes complex decision surfaces in multi-band probability spaces through local nonlinear approximation. The greater degradation in the Kappa coefficient (0.041 vs. 0.024 OA drop) in the MLP variant further proves that KAN effectively alleviates typical land cover boundary ambiguity in PolSAR imagery.
Finally, the framework exhibits unique band scalability advantages. As demonstrated in Table 2, when expanding from single-band (C) to four-band (P + L + C + X) inputs, our method with CNN inputs achieves a 3.95% accuracy improvement—1.95× greater than the Zhu method’s 2.03% enhancement. This advantage becomes more pronounced with ViT inputs, where our method maintains near-linear accuracy growth (92.52%→96.24%), while the baseline methods show evident performance saturation. This phenomenon confirms that, through the ViT–KAN cascade architecture, additional bands consistently provide complementary discriminative information rather than redundant noise.
Although our study has made significant progress in PolSAR classification, there are still some limitations. First, although the proposed ViT–KAN framework achieves high classification accuracy on the Hainan quad-band PolSAR dataset, its performance in regions with highly heterogeneous landforms—such as mountainous areas or densely urbanized regions—has not been thoroughly evaluated. Such environments may introduce significant spatial distortions and backscattering complexities that affect the quality of cross-band correlation modeling. Moreover, terrain-induced polarization effects or shadowing artifacts could reduce the effectiveness of both the ViT encoder’s global attention and the KAN classifier’s local decision surfaces. Future work will focus on evaluating model robustness in diverse terrain settings and exploring potential adaptations, such as terrain normalization or terrain-aware feature integration, to address these challenges. Second, while the ViT–KAN framework demonstrates strong performance, it comes with high computational overhead, particularly during the training phase, which limits its application in resource-constrained environments. Future work could focus on optimizing the model or utilizing more efficient computational methods to reduce the computational cost. Additionally, while our method shows good scalability with the addition of more bands, the computational cost increases as the number of bands rises, which may require a trade-off between performance improvement and computational resources in practical applications. Therefore, further research on balancing performance enhancement with computational costs, especially in large-scale datasets, remains an important direction for future work.
5. Conclusions
This paper proposes the ViT–KAN fusion architecture, a novel framework that excels in multi-band PolSAR land cover classification by combining the strengths of a Vision Transformer (ViT) and a Kernel Attention Network (KAN). By addressing long-range spatial dependencies and nonlinear cross-band relationships, the method achieves 96.24% overall accuracy, significantly outperforming the existing methods. The key innovations include the ViT encoder for cross-band interaction modeling, the KAN decision fusion module for improved accuracy and parameter efficiency, and the scalable end-to-end training architecture.
Future work could explore enhancing model scalability for large datasets and real-time applications, incorporating multi-temporal data, and improving model interpretability through explainability techniques for deep learning. These directions will further enhance the model’s adaptability and practical utility in diverse remote sensing tasks.
Author Contributions
Conceptualization, S.H., H.M., and J.Y.; methodology, S.H., D.R., and F.G.; software, S.H.; validation, S.H.; formal analysis, S.H.; investigation, S.H.; resources, S.H.; data curation, J.Y.; writing—original draft preparation, S.H.; writing—review and editing, H.M. and J.Y.; visualization, S.H.; supervision, J.Y.; project administration, J.Y.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded partly by the Major Project of Chinese High-resolution Earth Observation System (grant number: 30-H30C01-9004-19/21) and partly by the National Natural Science Foundation of China (grant number: 62171023 and grant number: 62222102).
Data Availability Statement
The Hainan dataset was obtained from the Aerospace Information Research Institute of the Chinese Academy of Sciences (AIRCAS) and is available with the permission of AIRCAS.
Acknowledgments
The authors are grateful to AIRCAS for providing the Hainan dataset.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lee, J.S.; Grunes, M.R.; Kwok, R. Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution. Int. J. Remote Sens. 1994, 15, 2299–2311. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.Q. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Zou, B. PolSAR Image Classification with Lightweight 3D Convolutional Networks. Remote Sens. 2020, 12, 396. [Google Scholar] [CrossRef]
- Xie, W.; Ma, G.; Zhao, F.; Liu, H.; Zhang, L. PolSAR image classification via a novel semi-supervised recurrent complex-valued convolution neural network. Neurocomputing 2020, 388, 255–268. [Google Scholar] [CrossRef]
- Liu, F.; Jiao, L.; Tang, X. Task-Oriented GAN for PolSAR Image Classification and Clustering. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 2707–2719. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Zhang, Z.; Zhang, T.; Guo, W.; Luo, Y. Transferable SAR Image Classification Crossing Different Satellites Under Open Set Condition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4506005. [Google Scholar] [CrossRef]
- Wang, H.; Xing, C.; Yin, J.; Yang, J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sens. 2022, 14, 4656. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is All you Need. In Advances in Neural Information Processing Systems; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Newry, UK, 2017; Volume 30. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Yong, D.; WenKang, S.; ZhenFu, Z.; Qi, L. Combining belief functions based on distance of evidence. Decis. Support Syst. 2004, 38, 489–493. [Google Scholar] [CrossRef]
- Zhu, J.; Pan, J.; Jiang, W.; Yue, X.; Yin, P. SAR image fusion classification based on the decision-level combination of multi-band information. Remote Sens. 2022, 14, 2243. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).