MSIM: A Multiscale Iteration Method for Aerial Image and Satellite Image Registration
Abstract
1. Introduction
- (1)
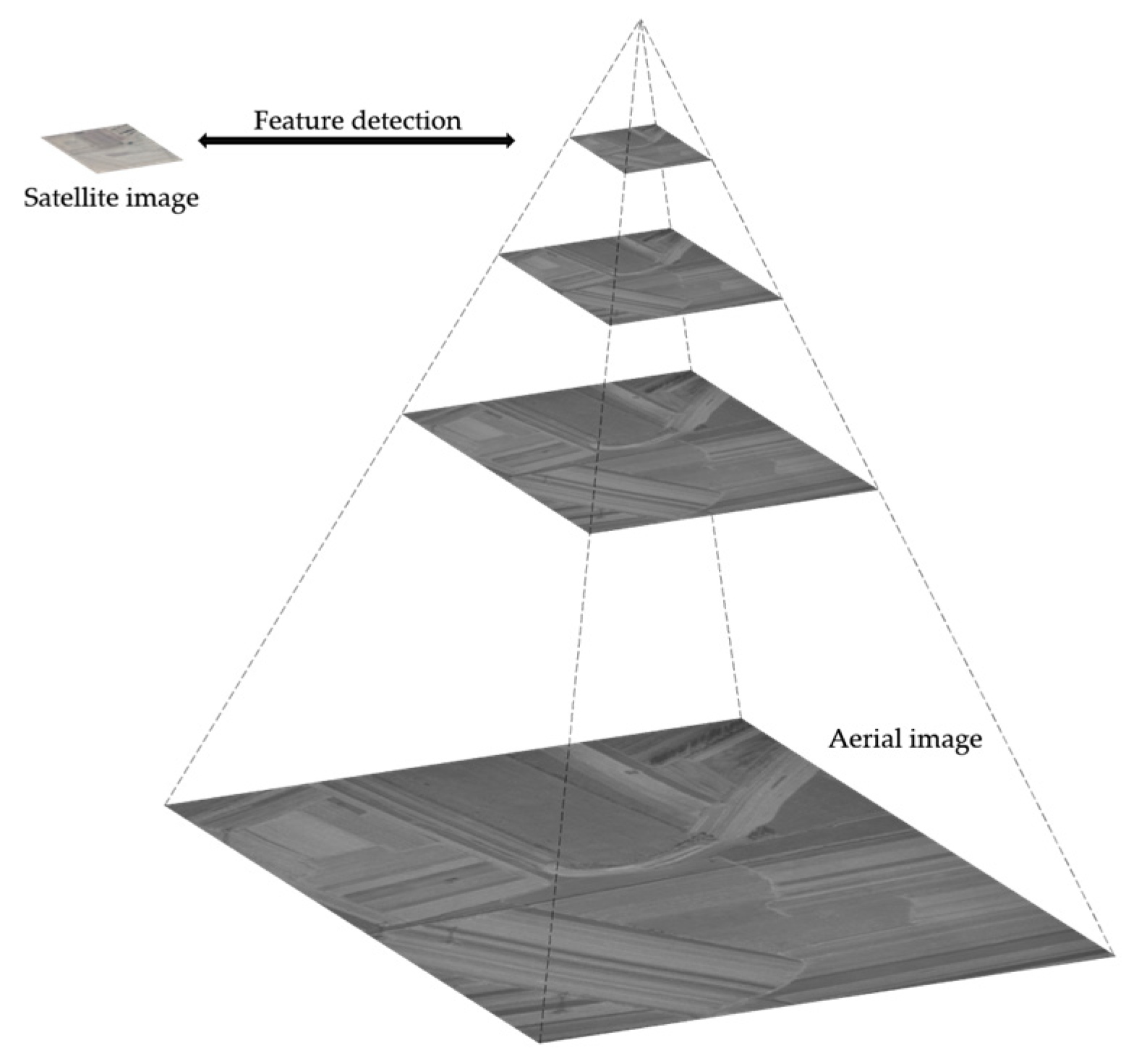
- A feature detection method based on image pyramids and phase congruency is proposed. This approach eliminates scale differences through image pyramids and enhances edge features by extracting phase congruency maps, thereby significantly increasing the number of feature points.
- (2)
- A feature descriptor is designed which takes into account the neighborhood information weights of feature points, improving the accuracy of feature point matching.
2. Method and Materials
2.1. Feature Detection Using Image Pyramid and Phase Congruency
2.2. Feature Point Descriptor and Matching
2.3. Data
3. Experiments
3.1. Metrics
3.1.1. Subjective Evaluation Metrics
3.1.2. Objective Evaluation Metrics
- Root Mean Square Error (RMSE)
- Accuracy
- Standard Deviation
- Success Rate
3.2. Parameter Study
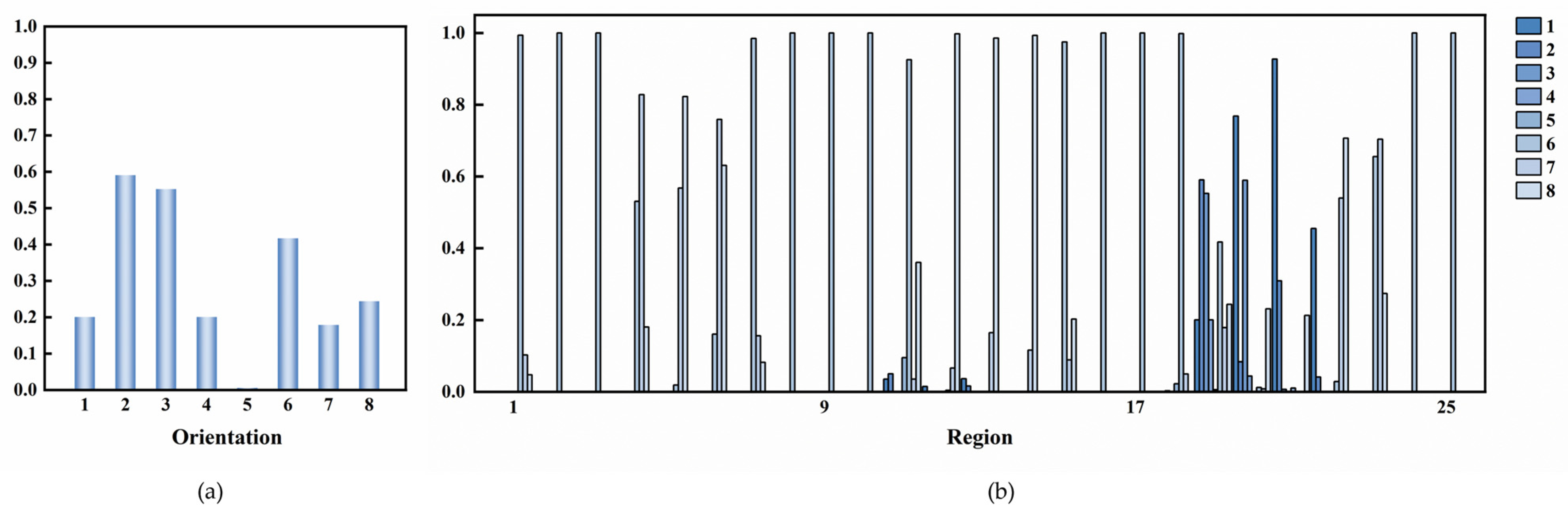
3.2.1. The Number of Directions NO
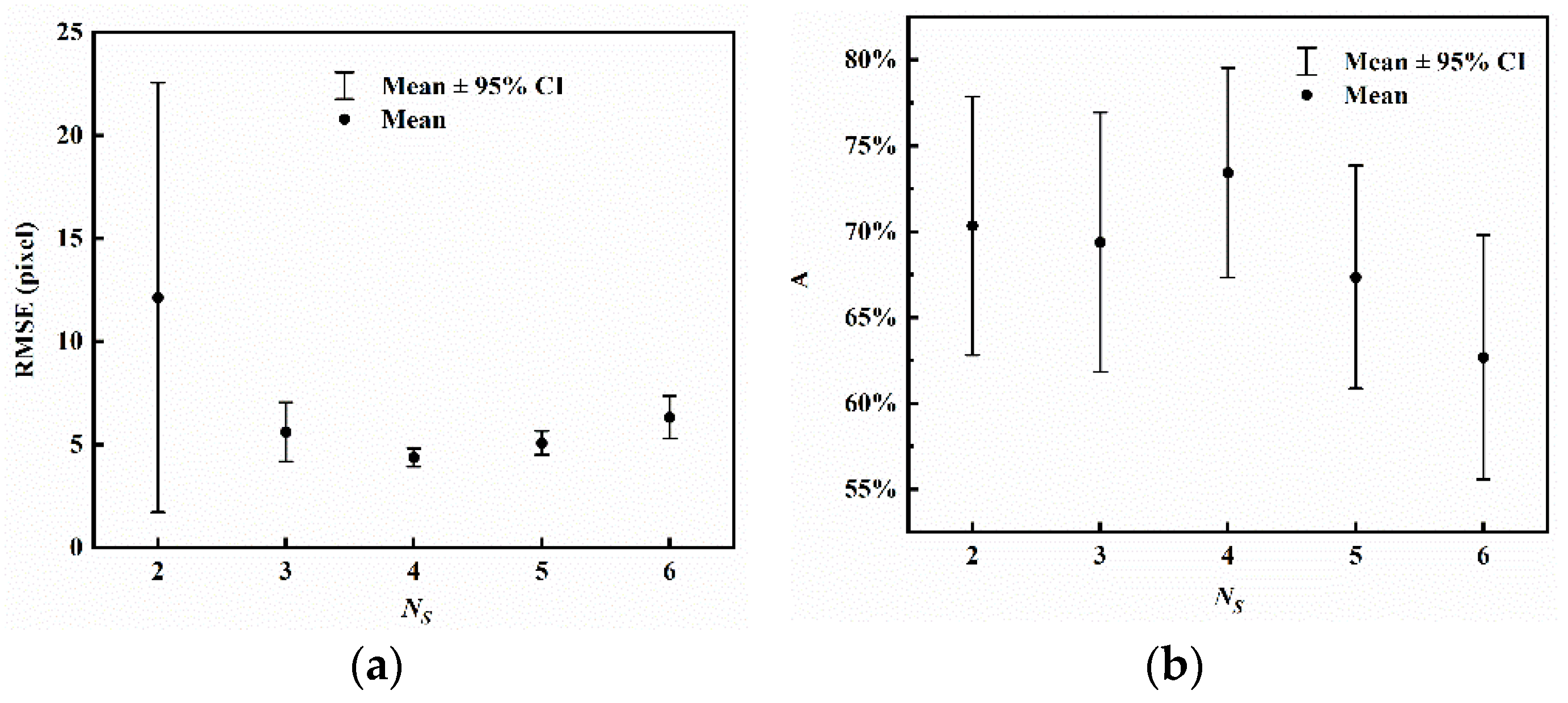
3.2.2. The Number of Scales NS
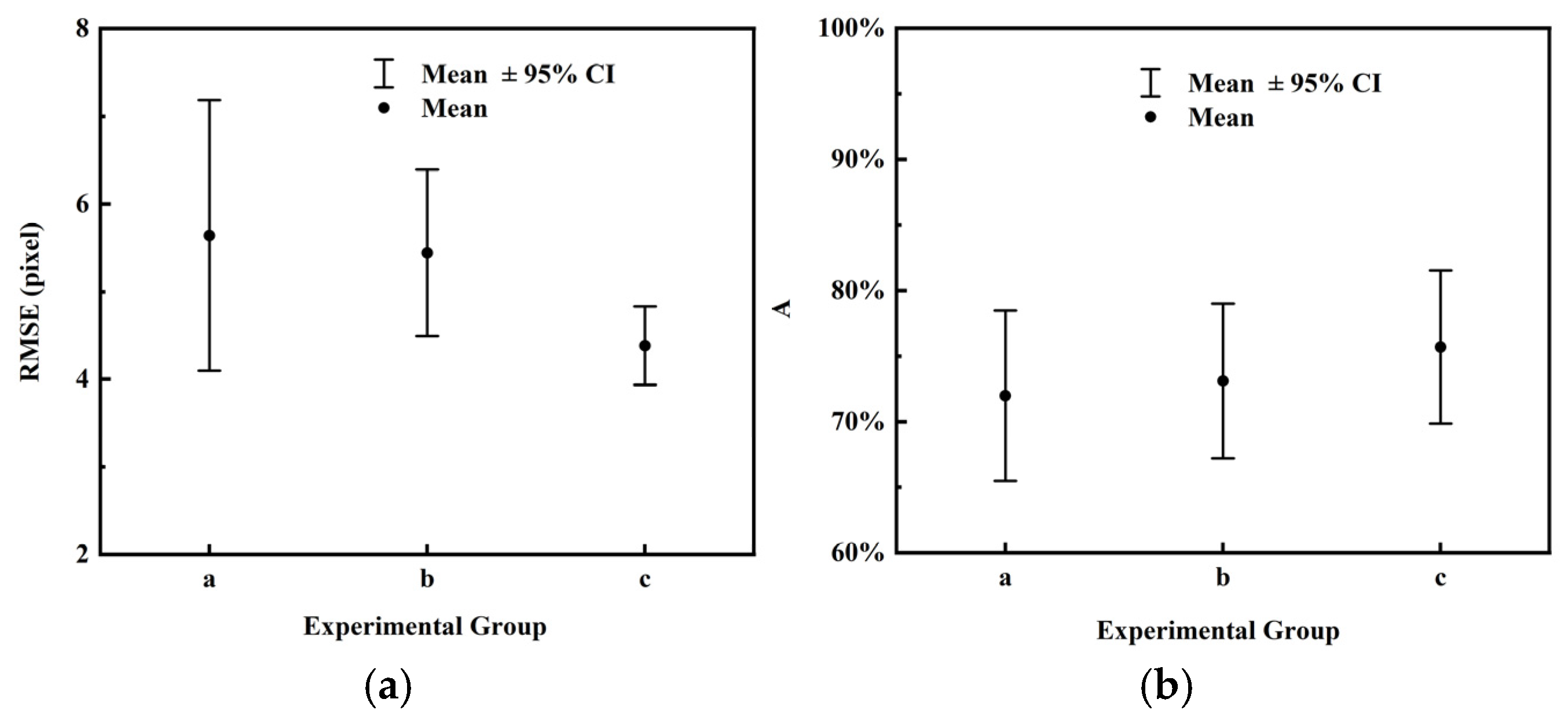
3.2.3. Moment Selection Comparison
3.2.4. Comparison of Descriptor Shapes
3.3. Comparative Experimental Results
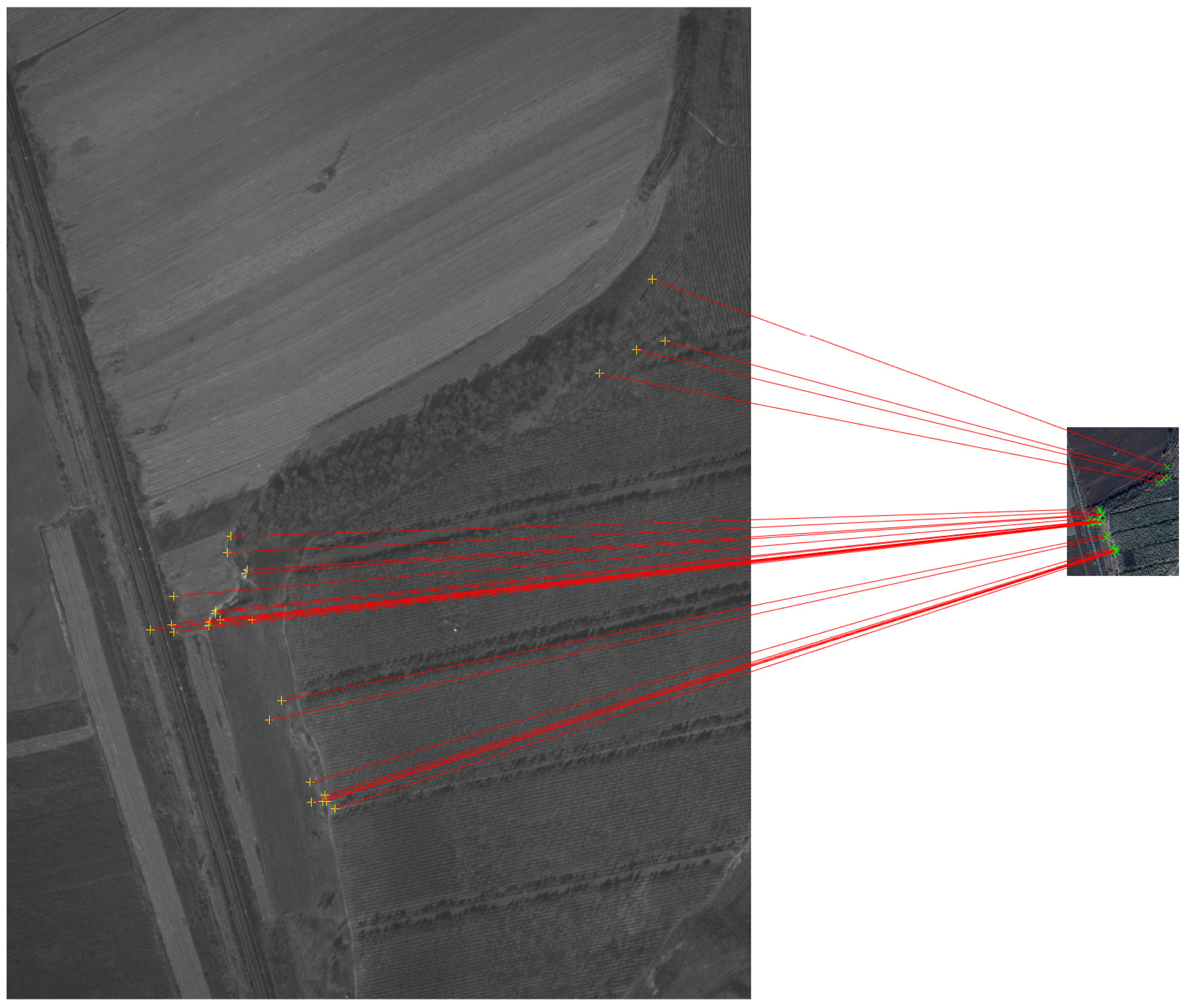
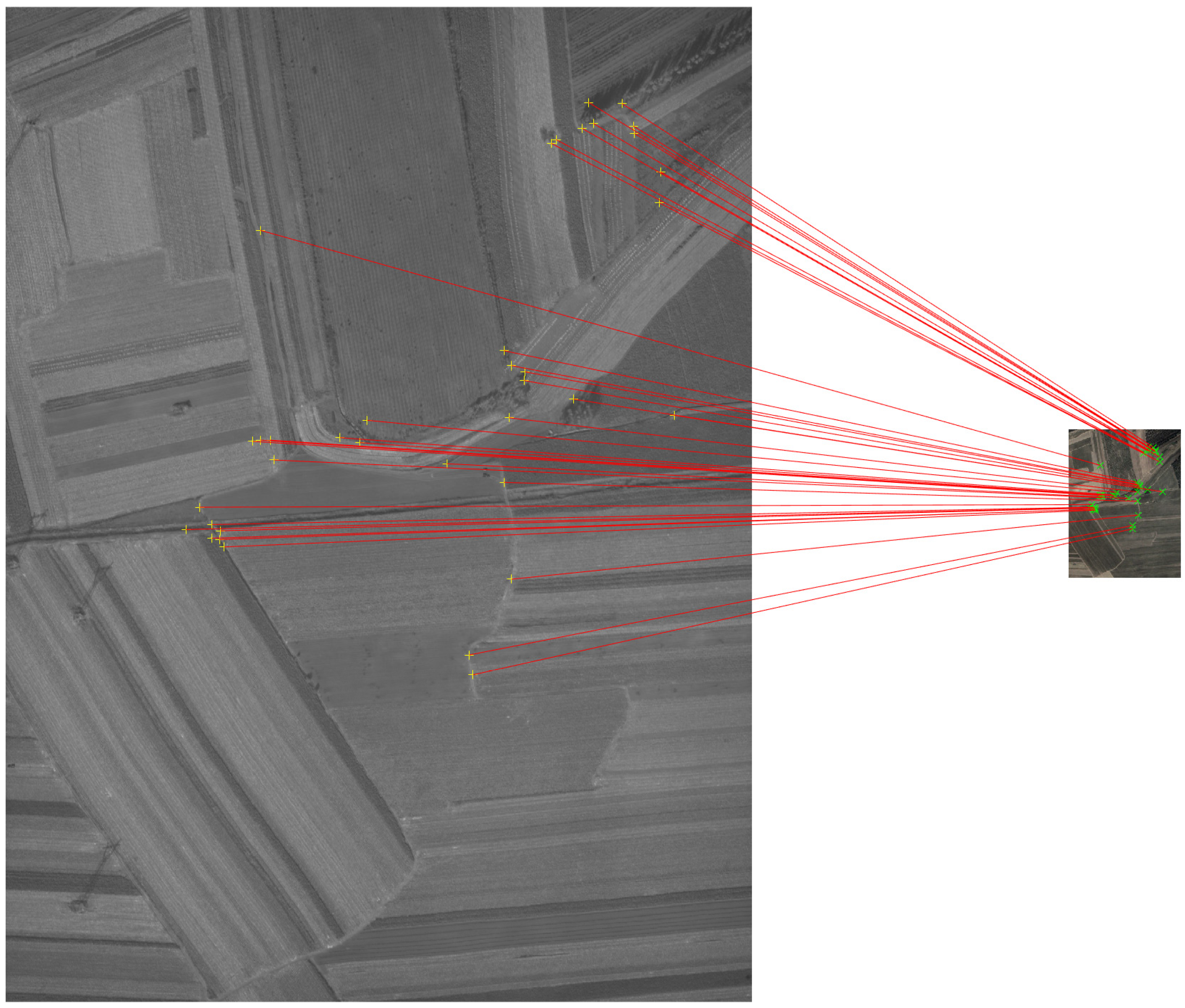
3.3.1. Subjective Evaluation
3.3.2. Objective Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, J.; Jiang, X.; Hao, Z.; Zhu, M.; Gao, W.; Liu, S. LPHOG: A Line Feature and Point Feature Combined Rotation Invariant Method for Heterologous Image Registration. Remote Sens. 2023, 15, 4548. [Google Scholar] [CrossRef]
- Zhang, X.; Leng, C.; Hong, Y.; Pei, Z.; Cheng, I.; Basu, A. Multimodal Remote Sensing Image Registration Methods and Advancements: A Survey. Remote Sens. 2021, 13, 5128. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, J.; Ma, A.; Zhong, Y.; Zheng, Z.; Zhang, L. Cross-Sensor Domain Adaptation for High Spatial Resolution Urban Land-Cover Mapping: From Airborne to Spaceborne Imagery. Remote Sens. Environ. 2022, 277, 113058. [Google Scholar] [CrossRef]
- Liu, C.; Ding, Y.; Zhang, H.; Xiu, J.; Kuang, H. Improving Target Geolocation Accuracy with Multi-View Aerial Images in Long-Range Oblique Photography. Drones 2024, 8, 177. [Google Scholar] [CrossRef]
- Zhu, B.; Ye, Y.; Dai, J.; Peng, T.; Deng, J.; Zhu, Q. VDFT: Robust Feature Matching of Aerial and Ground Images Using Viewpoint-Invariant Deformable Feature Transformation. ISPRS J. Photogramm. Remote Sens. 2024, 218, 311–325. [Google Scholar] [CrossRef]
- He, M.; Liu, J.; Gu, P.; Meng, Z. Leveraging Map Retrieval and Alignment for Robust UAV Visual Geo-Localization. IEEE Trans. Instrum. Meas. 2024, 73, 2523113. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, Q.; Mei, C.; Yang, P.; Gu, H.; Fan, Z. TROG: A Fast and Robust Scene-Matching Algorithm for Geo-Referenced Images. Int. J. Remote Sens. 2024. [Google Scholar] [CrossRef]
- He, R.; Long, S.; Sun, W.; Liu, H. A Multimodal Image Registration Method for UAV Visual Navigation Based on Feature Fusion and Transformers. Drones 2024, 8, 651. [Google Scholar] [CrossRef]
- Kovesi, P. Phase Congruency: A Low-Level Image Invariant. Psychol. Res. 2000, 64, 136–148. [Google Scholar] [CrossRef]
- Guo, H.; Xu, H.; Wei, Y.; Shen, Y. Point Pairs Optimization for Piecewise Linear Transformation of Multimodal Remote Sensing Images by the Similarity of Log-Gabor Features. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6516605. [Google Scholar] [CrossRef]
- Fan, J.; Xiong, Q.; Ye, Y.; Li, J. Combining Phase Congruency and Self-Similarity Features for Multimodal Remote Sensing Image Matching. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4001105. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-Modal Image Matching Based on Radiation-Variation Insensitive Feature Transform. IEEE Trans. Image Process. 2020, 29, 3296–3310. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Shi, P.; Hu, Q.; Zhang, Y. RIFT2: Speeding-up RIFT with A New Rotation-Invariance Technique. arXiv 2023, arXiv:2303.00319. [Google Scholar]
- Li, J.; Hu, Q.; Zhang, Y. Multimodal Image Matching: A Scale-Invariant Algorithm and an Open Dataset. ISPRS J. Photogramm. Remote Sens. 2023, 204, 77–88. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Zhao, L.; Chen, S. A Novel Coarse-to-Fine Scheme for Remote Sensing Image Registration Based on SIFT and Phase Correlation. Remote Sens. 2019, 11, 1833. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Y.; Liu, J.; Wang, S.; Zhang, C.; Liu, H. Robust Coarse-to-Fine Registration Algorithm for Optical and SAR Images Based on Two Novel Multiscale and Multidirectional Features. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5215126. [Google Scholar] [CrossRef]
- Ye, Y.; Tang, T.; Zhu, B.; Yang, C.; Li, B.; Hao, S. A Multiscale Framework with Unsupervised Learning for Remote Sensing Image Registration. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5622215. [Google Scholar] [CrossRef]
- Xiong, Z.; Li, W.; Zhao, X.; Zhang, B.; Tao, R.; Du, Q. PRF-Net: A Progressive Remote Sensing Image Registration and Fusion Network. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–14. [Google Scholar] [CrossRef]
- Tu, P.; Hu, P.; Wang, J.; Chen, X. From Coarse to Fine: Non-Rigid Sparse-Dense Registration for Deformation-Aware Liver Surgical Navigation. IEEE Trans. Biomed. Eng. 2024, 71, 2663–2677. [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, Y.; Yang, Y. University-1652: A Multi-View Multi-Source Benchmark for Drone-Based Geo-Localization. In Proceedings of the 28th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2020; pp. 1395–1403. [Google Scholar]
- Zhang, Y.; Zhang, W.; Yao, Y.; Zheng, Z.; Wan, Y.; Xiong, M. Robust Registration of Multi-Modal Remote Sensing Images Based on Multi-Dimensional Oriented Self-Similarity Features. Int. J. Appl. Earth Obs. Geoinf. 2024, 127, 103639. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector; The Plessey Company: Essex, UK, 1988; p. 6. [Google Scholar]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A Novel Point-Matching Algorithm Based on Fast Sample Consensus for Image Registration. IEEE Geosci. Remote Sens. Lett. 2015, 12, 43–47. [Google Scholar] [CrossRef]









| 4 | 6.0180 | 5.2347 | 71.62% | 0.2477 | 55.00% | 90.00% |
| 6 | 5.1652 | 3.8354 | 71.24% | 0.2941 | 66.67% | 96.67% |
| 8 | 4.3845 | 1.7209 | 73.44% | 0.2346 | 70.00% | 100.00% |
| 10 | 4.6621 | 2.1121 | 72.01% | 0.2558 | 65.00% | 98.33% |
| 12 | 6.2127 | 7.2391 | 70.93% | 0.2336 | 55.00% | 91.67% |
| 2 | 12.1344 | 40.0018 | 70.34% | 0.2891 | 56.67% | 91.67% |
| 3 | 5.6121 | 5.4839 | 69.39% | 0.2904 | 56.67% | 93.33% |
| 4 | 4.3845 | 1.7209 | 73.44% | 0.2346 | 70.00% | 100.00% |
| 5 | 5.0802 | 2.2301 | 67.35% | 0.2492 | 48.33% | 95.00% |
| 6 | 6.3275 | 3.9494 | 62.68% | 0.2731 | 41.67% | 91.67% |
| Group 1 | ||||||
|---|---|---|---|---|---|---|
| a | 11.2663 | 22.6974 | 62.97% | 0.3193 | 48.33% | 80.00% |
| b | 4.4406 | 1.8146 | 74.36% | 0.2176 | 65.00% | 98.33% |
| c | 4.8127 | 2.0770 | 71.41% | 0.2378 | 56.67% | 100.00% |
| d | 4.3845 | 1.7209 | 73.44% | 0.2346 | 70.00% | 100.00% |
| Group 1 | ||||||
|---|---|---|---|---|---|---|
| a | 5.6407 | 5.9261 | 67.01% | 0.2740 | 56.67% | 96.67% |
| b | 5.4423 | 3.6376 | 68.97% | 0.2451 | 51.67% | 95.00% |
| c | 4.3845 | 1.7209 | 73.44% | 0.2346 | 70.00% | 100.00% |
| Method | Time | ||||||
|---|---|---|---|---|---|---|---|
| SIFT | 401.4578 | 96.9894 | 0.00% | - | 0.00% | - | - |
| SRIF | 415.1512 | 175.6172 | 0.00% | - | 0.00% | - | - |
| RIFT | 273.9546 | 115.2889 | 0.00% | - | 0.00% | - | - |
| RIFT-Like | 50.3964 | 84.0021 | 28.00% | 0.3197 | 13.33% | 38.33% | 53.4476 s |
| MSIM | 4.3845 | 1.7209 | 73.44% | 0.2346 | 70.00% | 100.00% | 8.6083 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Ding, Y.; Liu, C. MSIM: A Multiscale Iteration Method for Aerial Image and Satellite Image Registration. Remote Sens. 2025, 17, 1423. https://doi.org/10.3390/rs17081423
Liu X, Ding Y, Liu C. MSIM: A Multiscale Iteration Method for Aerial Image and Satellite Image Registration. Remote Sensing. 2025; 17(8):1423. https://doi.org/10.3390/rs17081423
Chicago/Turabian StyleLiu, Xiaojia, Yalin Ding, and Chongyang Liu. 2025. "MSIM: A Multiscale Iteration Method for Aerial Image and Satellite Image Registration" Remote Sensing 17, no. 8: 1423. https://doi.org/10.3390/rs17081423
APA StyleLiu, X., Ding, Y., & Liu, C. (2025). MSIM: A Multiscale Iteration Method for Aerial Image and Satellite Image Registration. Remote Sensing, 17(8), 1423. https://doi.org/10.3390/rs17081423






