Combined L-Band Polarimetric SAR and GPR Data to Develop Models for Leak Detection in the Water Pipeline Networks
Abstract
1. Introduction
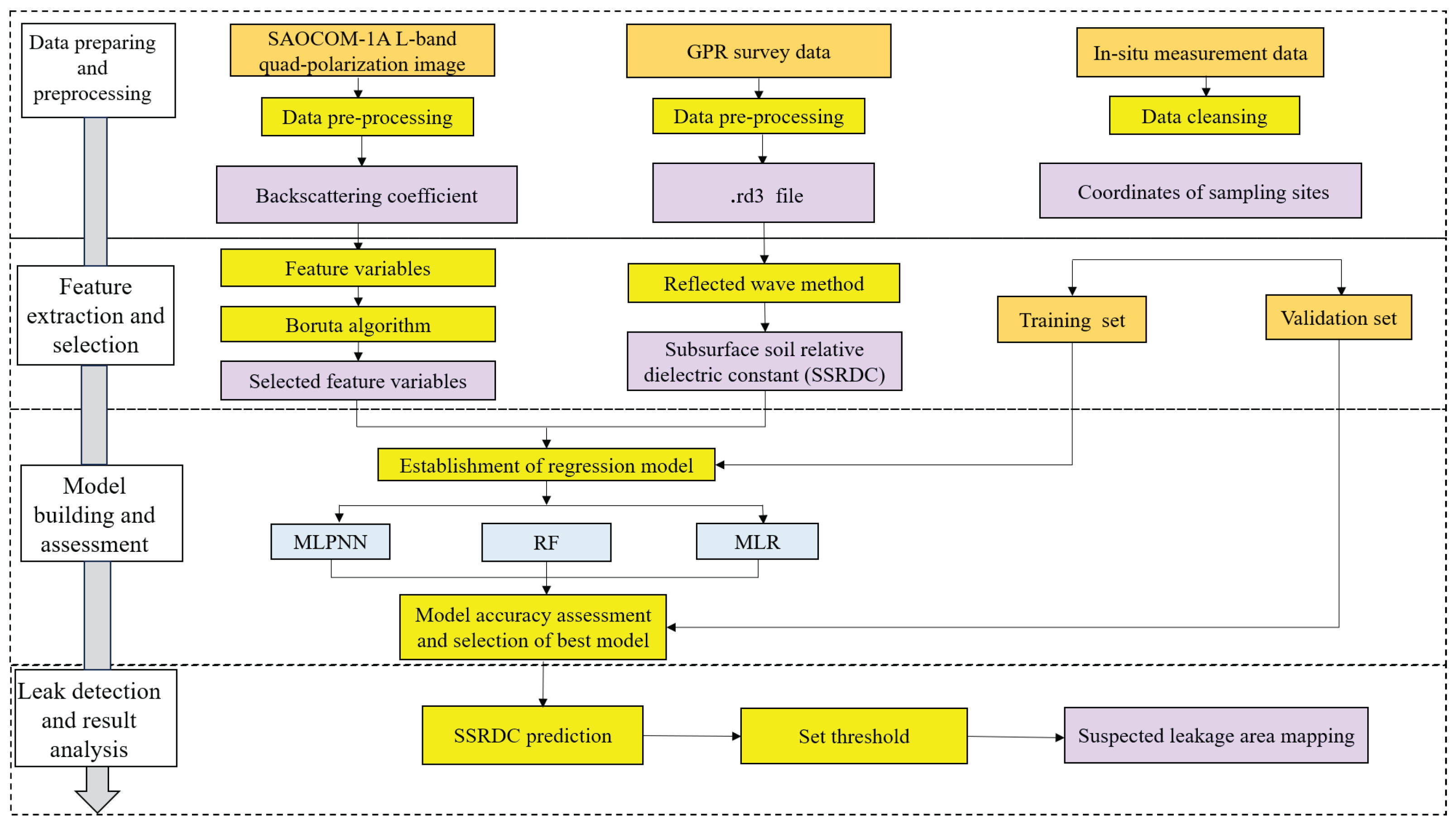
2. Materials and Models
2.1. Study Area
2.2. Data Collection and Preprocessing
2.2.1. SAOCOM-1A Data
2.2.2. GPR System
2.2.3. Measurement of SSRDC with GPR
2.3. Feature Extraction and Selection
2.3.1. Feature Variable Extraction
2.3.2. Feature Variable Selection
2.4. Models
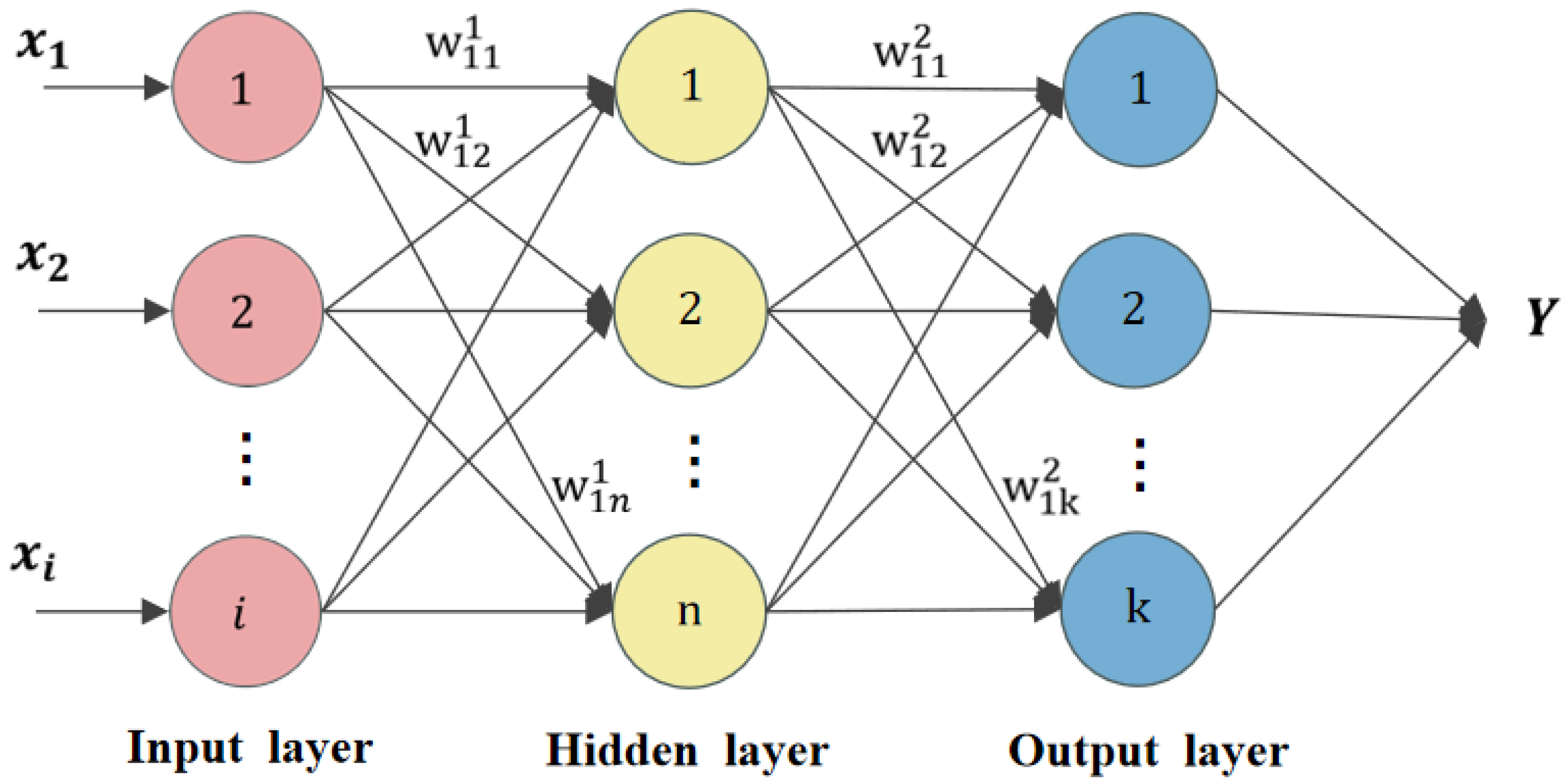
2.4.1. Machine Learning Regression Model
2.4.2. Model Evaluation
3. Results
3.1. Feature Variable Selection Result
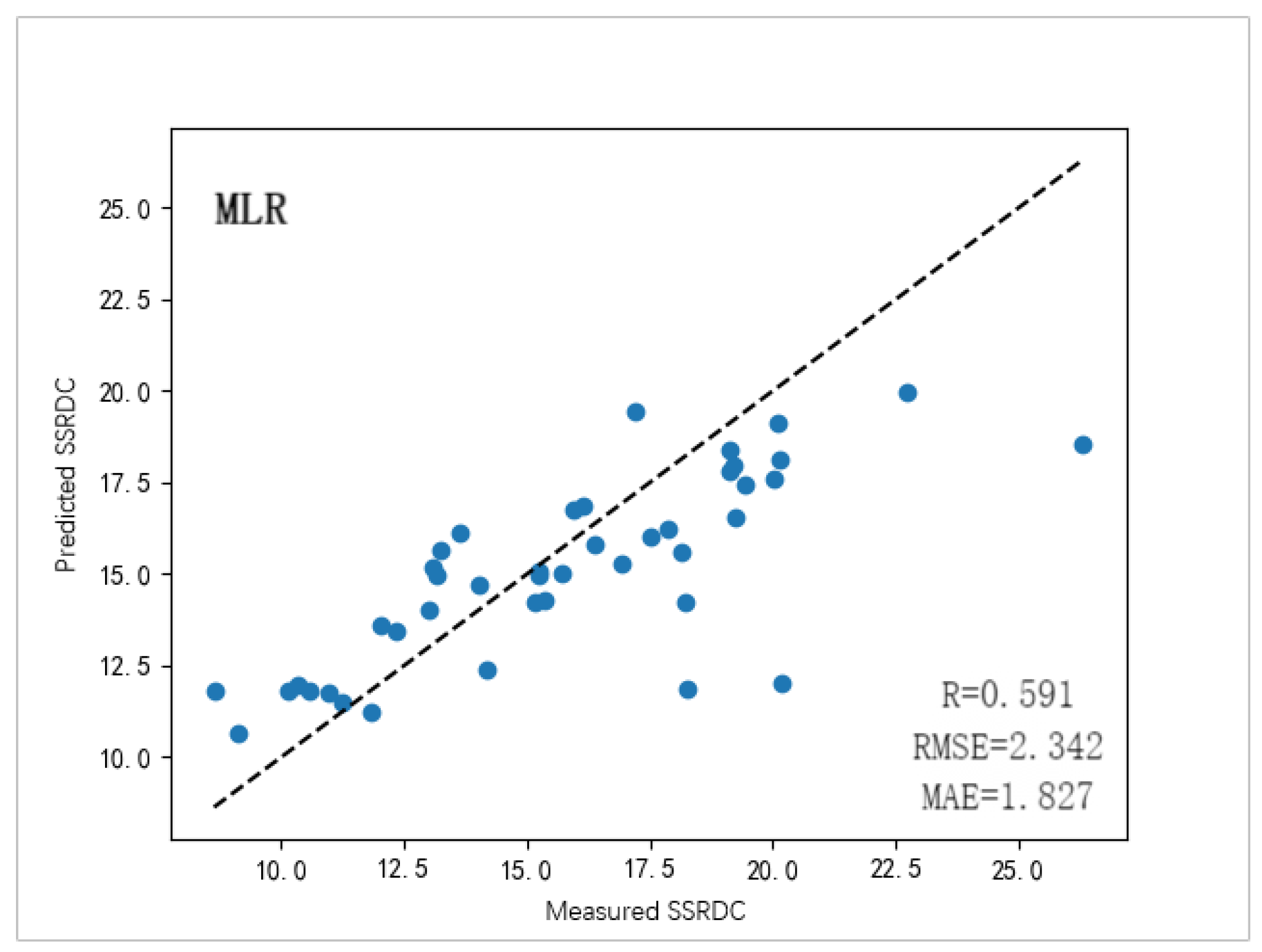
3.2. Model Training and Validation
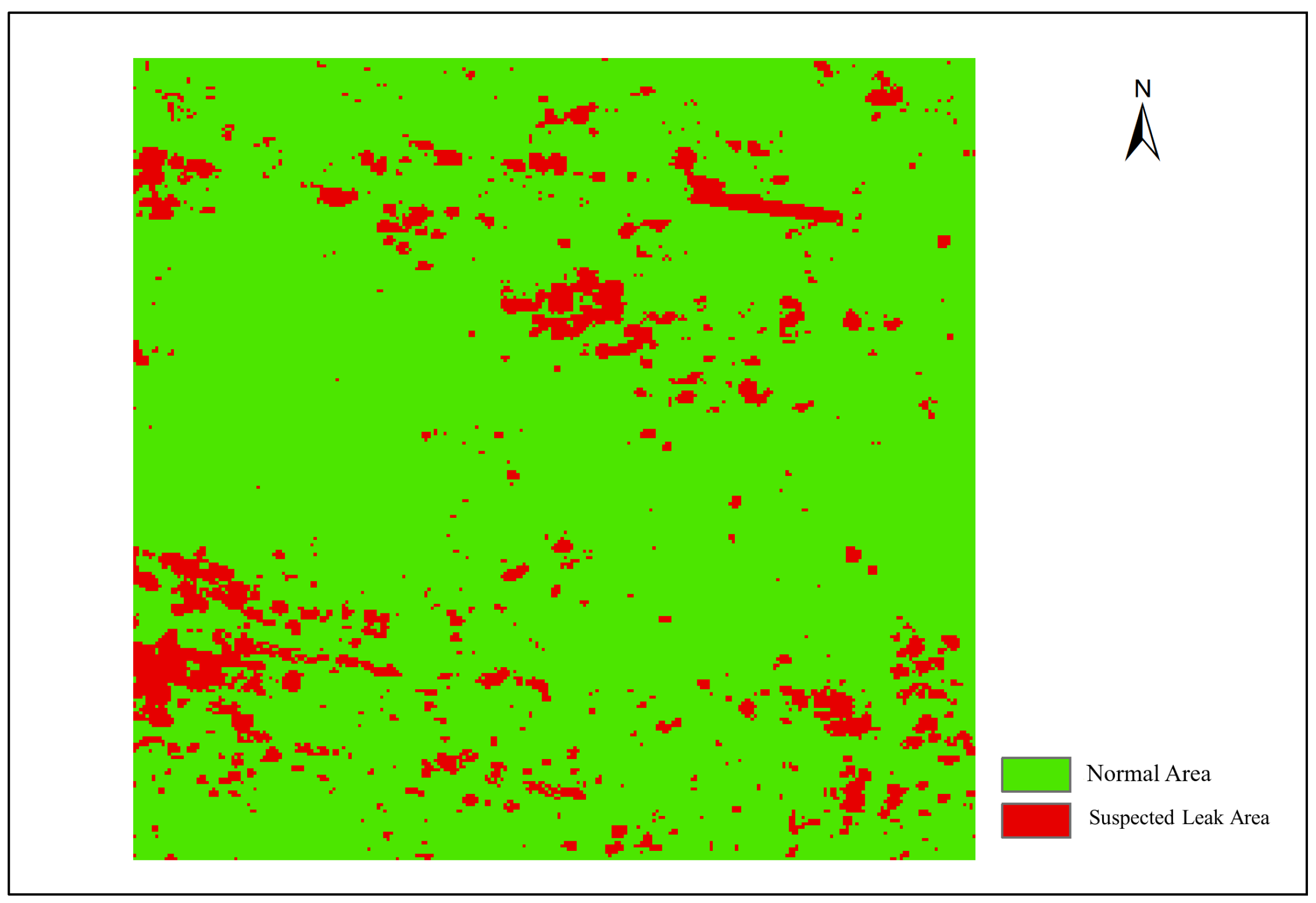
3.3. Leak Detection Result
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meng, L.; Li, Y.; Wang, W.; Fu, J. Experimental study on leak detection and location for gas pipeline based on acoustic method. J. Loss Prev. Process Ind. 2012, 25, 90–102. [Google Scholar] [CrossRef]
- Lee, S.; Kim, B. Machine learning model for leak detection using water pipeline vibration sensor. Sensors 2023, 23, 8935. [Google Scholar] [CrossRef]
- Singh, S.; Agrawal, S.; Sahu, T.; Das, D. iPipe: Water pipeline monitoring and leakage detection. In Proceedings of the 2021 IEEE International Symposium on Smart Electronic Systems (ISES), Jaipur, India, 18–22 December 2021; pp. 367–372. [Google Scholar]
- Lim, K.; Wong, L.; Chiu, W.K.; Kodikara, J. Distributed fiber optic sensors for monitoring pressure and stiffness changes in out-of-round pipes. Struct. Control Health Monit. 2016, 23, 303–314. [Google Scholar] [CrossRef]
- Chen, Q.; Shen, G.; Jiang, J.; Diao, X.; Wang, Z.; Ni, L.; Dou, Z. Effect of rubber washers on leak location for assembled pressurized liquid pipeline based on negative pressure wave method. Process Saf. Environ. Prot. 2018, 119, 181–190. [Google Scholar] [CrossRef]
- Kam, S.I. Mechanistic modeling of pipeline leak detection at fixed inlet rate. J. Pet. Sci. Eng. 2010, 70, 145–156. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Zhang, R.; Zhu, H.; Fu, J. Simulation and assessment of underwater gas release and dispersion from subsea gas pipelines leak. Process Saf. Environ. Prot. 2018, 119, 46–57. [Google Scholar]
- Gao, Y.; Liu, Y.; Ma, Y.; Cheng, X.; Yang, J. Application of the differentiation process into the correlation-based leak detection in urban pipeline networks. Mech. Syst. Signal Process. 2018, 112, 251–264. [Google Scholar] [CrossRef]
- Yin, S.; Weng, Y.; Song, Z.; Cheng, B.; Gu, H.; Wang, H.; Yao, J. Mass transfer characteristics of pipeline leak-before-break in a nuclear power station. Appl. Therm. Eng. 2018, 142, 194–202. [Google Scholar] [CrossRef]
- Cramer, R.; Shaw, D.; Tulalian, R.; Angelo, P.; van Stuijvenberg, M. Detecting and correcting pipeline leaks before they become a big problem. Mar. Technol. Soc. J. 2015, 49, 31–46. [Google Scholar] [CrossRef]
- Demirci, S.; Yigit, E.; Eskidemir, I.H.; Ozdemir, C. Ground penetrating radar imaging of water leaks from buried pipes based on back-projection method. NDT E Int. 2012, 47, 35–42. [Google Scholar] [CrossRef]
- Lai, W.W.; Chang, R.K.; Sham, J.F. A blind test of nondestructive underground void detection by ground penetrating radar (GPR). J. Appl. Geophys. 2018, 149, 10–17. [Google Scholar] [CrossRef]
- Ocaña-Levario, S.J.; Ayala-Cabrera, D.; Izquierdo, J.; Pérez-García, R. 3D model evolution of a leak based on GPR image interpretation. Water Sci. Technol. Water Supply 2015, 15, 1312–1319. [Google Scholar] [CrossRef]
- Zhao, W.; Forte, E.; Pipan, M.; Tian, G. Ground penetrating radar (GPR) attribute analysis for archaeological prospection. J. Appl. Geophys. 2013, 97, 107–117. [Google Scholar] [CrossRef]
- Atef, A.; Zayed, T.; Hawari, A.; Khader, M.; Moselhi, O. Multi-tier method using infrared photography and GPR to detect and locate water leaks. Autom. Constr. 2016, 61, 162–170. [Google Scholar] [CrossRef]
- Cataldo, A.; De Benedetto, E.; Cannazza, G.; Leucci, G.; De Giorgi, L.; Demitri, C. Enhancement of leak detection in pipelines through time-domain reflectometry/ground penetrating radar measurements. IET Sci. Meas. Technol. 2017, 11, 696–702. [Google Scholar] [CrossRef]
- Wunderlich, T.; Majchczack, B.S.; Wilken, D.; Segschneider, M.; Rabbel, W. What is beyond hyperbola detection and characterization in ground-penetrating radar data?—implications from the archaeological site of Goting, Germany. Remote Sens. 2024, 16, 4080. [Google Scholar] [CrossRef]
- Abdulraheem, M.I.; Chen, H.; Li, L.; Moshood, A.Y.; Zhang, W.; Xiong, Y.; Zhang, Y.; Taiwo, L.B.; Farooque, A.A.; Hu, J. Recent advances in dielectric properties-based soil water content measurements. Remote Sens. 2024, 16, 1328. [Google Scholar] [CrossRef]
- Guan, Y.; Grote, K. Assessing the potential of UAV-based multispectral and thermal data to estimate soil water content using geophysical methods. Remote Sens. 2023, 16, 61. [Google Scholar] [CrossRef]
- Lu, Q.; Liu, K.; Zeng, Z.; Liu, S.; Li, R.; Xia, L.; Guo, S.; Li, Z. Estimation of the soil water content using the early time signal of ground-penetrating radar in heterogeneous soil. Remote Sens. 2023, 15, 3026. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Lu, Y.; Zheng, T.; Dong, Z.; Tian, Y.; Jia, Y. In-situ recognition of moisture damage in bridge deck asphalt pavement with time-frequency features of GPR signal. Constr. Build. Mater. 2020, 244, 118295. [Google Scholar] [CrossRef]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Gururaj, P.; Umesh, P.; Shetty, A. Assessment of surface soil moisture from ALOS PALSAR-2 in small-scale maize fields using polarimetric decomposition technique. Acta Geophys. 2021, 69, 579–588. [Google Scholar] [CrossRef]
- Lasne, Y.; Paillou, P.; August-Bernex, T.; Ruffié, G.; Grandjean, G. A phase signature for detecting wet subsurface structures using polarimetric L-band SAR. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1683–1694. [Google Scholar] [CrossRef]
- Mazzarotto, G.; Tessari, G.; Pizzaia, P.; Salandin, P. Identifying pipeline leak positions potentially connected to soil deformations through SAR data analysis. J. Infrastruct. Syst. 2023, 29, 04023017. [Google Scholar] [CrossRef]
- Pongrac, B.; Gleich, D. Polarimetric SAR based water leakage detection using 3D regression neural network. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 3700–3703. [Google Scholar]
- Le, X.; Yu, H.; Wang, Y. An interpretable neural network algorithm for leaking detection in the urban water and sewer pipeline network, Tianjin, China. In Proceedings of the IGARSS 2023—2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 16–21 July 2023; pp. 2053–2056. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Liu, X.; Chen, J.; Cui, X.; Liu, Q.; Cao, X.; Chen, X. Measurement of soil water content using ground-penetrating radar: A review of current methods. Int. J. Digit. Earth 2019, 12, 95–118. [Google Scholar] [CrossRef]
- Nakashima, Y.; Zhou, H.; Sato, M. Estimation of groundwater level by GPR in an area with multiple ambiguous reflections. J. Appl. Geophys. 2001, 47, 241–249. [Google Scholar] [CrossRef]
- Huisman, J.A.; Hubbard, S.S.; Redman, J.D.; Annan, A.P. Measuring soil water content with ground penetrating radar: A review. Vadose Zone J. 2003, 2, 476–491. [Google Scholar] [CrossRef]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy 1. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Xing, M.; Chen, L.; Wang, J.; Shang, J.; Huang, X. Soil moisture retrieval using SAR backscattering ratio method during the crop growing season. Remote Sens. 2022, 14, 3210. [Google Scholar] [CrossRef]
- Haldar, D.; Das, A.; Mohan, S.; Pal, O.; Hooda, R.S.; Chakraborty, M. Assessment of L-band SAR data at different polarization combinations for crop and other landuse classification. Prog. Electromagn. Res. B 2012, 36, 303–321. [Google Scholar] [CrossRef]
- Park, N.W.; Chi, K.H. Integration of multitemporal/polarization C-band SAR data sets for land-cover classification. Int. J. Remote Sens. 2008, 29, 4667–4688. [Google Scholar] [CrossRef]
- Lee, J.S.; Grunes, M.R.; Pottier, E. Quantitative comparison of classification capability: Fully polarimetric versus dual and single-polarization SAR. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2343–2351. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef]
- Chamundeeswari, V.V.; Singh, D.; Singh, K. An analysis of texture measures in PCA-based unsupervised classification of SAR images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 214–218. [Google Scholar] [CrossRef]
- Wall, M.E.; Rechtsteiner, A.; Rocha, L.M. Singular value decomposition and principal component analysis. In A Practical Approach to Microarray Data Analysis; Springer: Berlin/Heidelberg, Germany, 2003; pp. 91–109. [Google Scholar]
- Saleem, J.; Zakar, R.; Butt, M.S.; Aadil, R.M.; Ali, Z.; Bukhari, G.M.J.; Ishaq, M.; Fischer, F. Application of the Boruta algorithm to assess the multidimensional determinants of malnutrition among children under five years living in southern Punjab, Pakistan. BMC Public Health 2024, 24, 167. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature selection with the Boruta package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, Y.; Tian, S.; Liu, D. Soil moisture and salinity inversion based on new remote sensing index and neural network at a salina-alkaline wetland. Water 2021, 13, 2762. [Google Scholar] [CrossRef]
- Wang, J.; Wu, F.; Shang, J.; Zhou, Q.; Ahmad, I.; Zhou, G. Saline soil moisture mapping using Sentinel-1A synthetic aperture radar data and machine learning algorithms in humid region of China’s east coast. Catena 2022, 213, 106189. [Google Scholar] [CrossRef]
- Yadav, V.P.; Prasad, R.; Bala, R.; Vishwakarma, A.K. An improved inversion algorithm for spatio-temporal retrieval of soil moisture through modified water cloud model using C-band Sentinel-1A SAR data. Comput. Electron. Agric. 2020, 173, 105447. [Google Scholar] [CrossRef]
- Zhang, N.; Chen, M.; Yang, F.; Yang, C.; Yang, P.; Gao, Y.; Shang, Y.; Peng, D. Forest height mapping using feature selection and machine learning by integrating multi-source satellite data in Baoding City, North China. Remote Sens. 2022, 14, 4434. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, D.; Singh, K.P.; Kumar, S. An efficient use of random forest technique for SAR data classification. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3286–3289. [Google Scholar]
- Du, P.; Samat, A.; Waske, B.; Liu, S.; Li, Z. Random forest and rotation forest for fully polarized SAR image classification using polarimetric and spatial features. ISPRS J. Photogramm. Remote Sens. 2015, 105, 38–53. [Google Scholar] [CrossRef]
- Omoniyi, T.O.; Sims, A. Enhancing the precision of forest growing stock volume in the estonian national forest inventory with different predictive techniques and remote sensing data. Remote Sens. 2024, 16, 3794. [Google Scholar] [CrossRef]
- Jin, B.; Yin, K.; Li, Q.; Gui, L.; Yang, T.; Zhao, B.; Guo, B.; Zeng, T.; Ma, Z. Susceptibility analysis of land subsidence along the transmission line in the salt lake area based on remote sensing interpretation. Remote Sens. 2022, 14, 3229. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Miller, D.M.; Kaminsky, E.J.; Rana, S. Neural network classification of remote-sensing data. Comput. Geosci. 1995, 21, 377–386. [Google Scholar] [CrossRef]
- Prost, C.; Zerger, A.; Dare, P. A multilayer feedforward neural network for automatic classification of eucalyptus forests in airborne video imagery. Int. J. Remote Sens. 2005, 26, 3275–3293. [Google Scholar] [CrossRef]
- Amini, J.; Sumantyo, J.T.S. Employing a method on SAR and optical images for forest biomass estimation. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4020–4026. [Google Scholar] [CrossRef]
- Huang, T.; Ou, G.; Wu, Y.; Zhang, X.; Liu, Z.; Xu, H.; Xu, X.; Wang, Z.; Xu, C. Estimating the aboveground biomass of various forest types with high heterogeneity at the provincial scale based on multi-source data. Remote Sens. 2023, 15, 3550. [Google Scholar] [CrossRef]
- Salazar Villegas, M.H.; Qasim, M.; Csaplovics, E.; González-Martinez, R.; Rodriguez-Buritica, S.; Ramos Abril, L.N.; Salazar Villegas, B. Examining the potential of sentinel imagery and ensemble algorithms for estimating aboveground biomass in a tropical dry forest. Remote Sens. 2023, 15, 5086. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
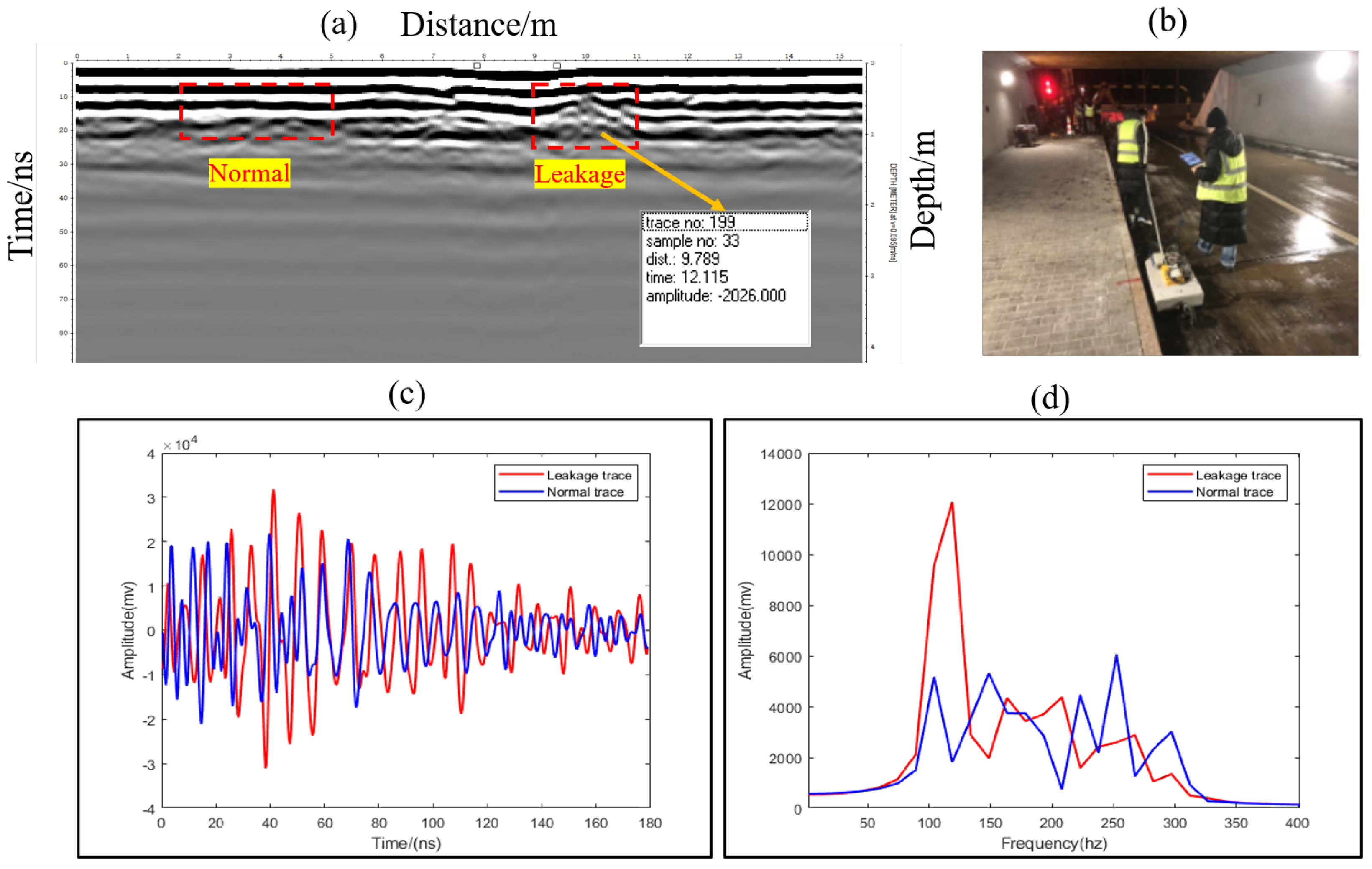
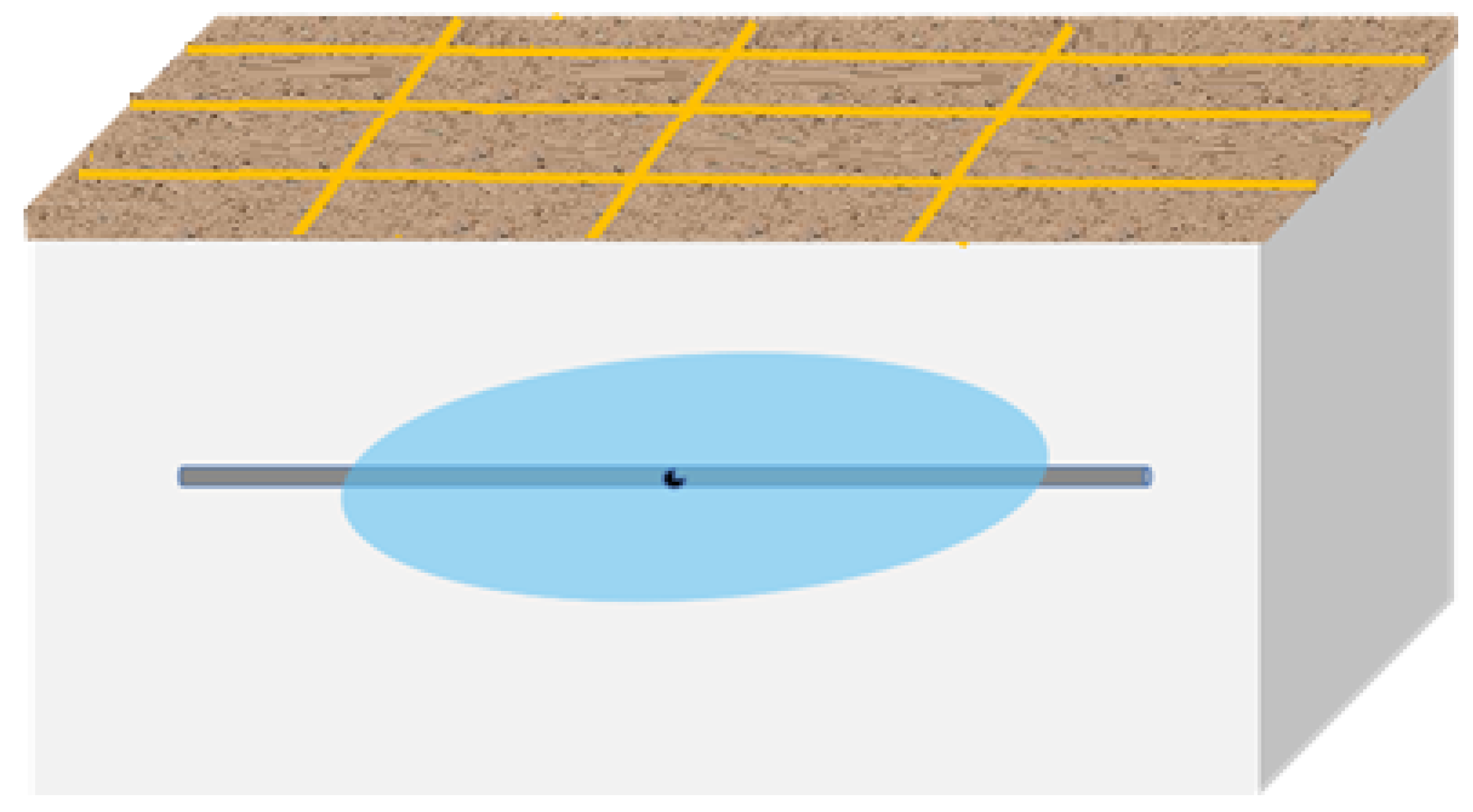
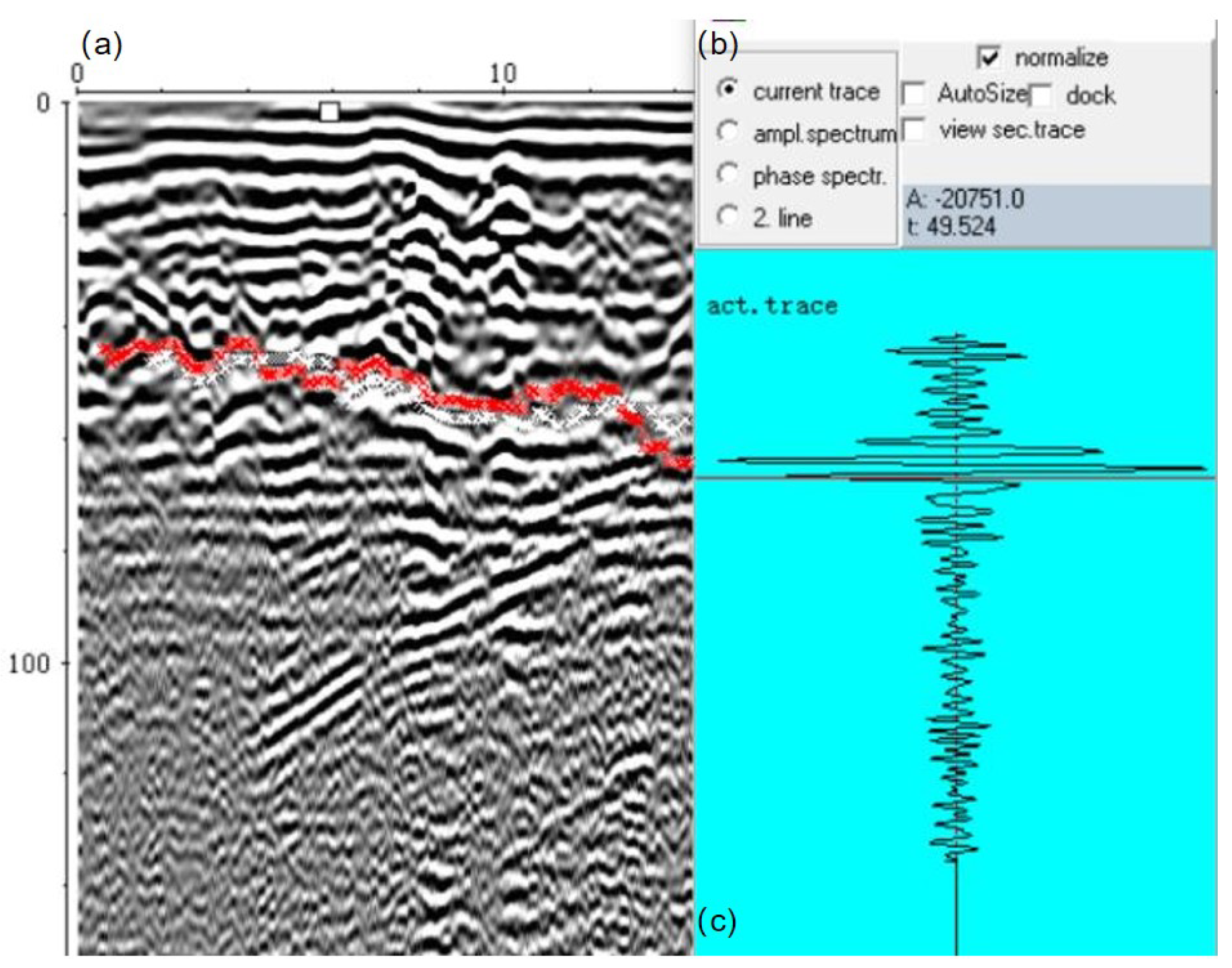






| Point | Two-Way Travel Time (ns) | Wave Speed (m/ns) | SSRDC |
|---|---|---|---|
| 1 | 39.317085 | 0.07634 | 15.44 |
| 2 | 39.695133 | 0.07562 | 15.74 |
| 3 | 40.451233 | 0.07420 | 16.35 |
| ⋯ | ⋯ | ⋯ | ⋯ |
| 58 | 41.207329 | 0.07284 | 16.96 |
| 59 | 41.585381 | 0.07218 | 17.27 |
| 60 | 41.963428 | 0.07153 | 17.59 |
| Mean Value | - | - | 16.76 |
| ID | Leakage Depth (m) | SSRDC |
|---|---|---|
| 1 | 1 | 21.51 |
| 2 | 1.2 | 10.16 |
| 3 | 1.3 | 18.02 |
| 4 | 1.2 | 17.56 |
| 5 | 0.8 | 26.51 |
| ⋯ | ⋯ | ⋯ |
| 81 | 1.5 | 13.12 |
| 82 | 1.1 | 16.50 |
| 83 | 1.2 | 16.11 |
| 84 | 1.4 | 15.72 |
| 85 | 1.2 | 20.01 |
| ID | Feature Variables | ID | Feature Variables |
|---|---|---|---|
| 1 | HH | 14 | (VV2 − HH2)/HH |
| 2 | HV | 15 | (VV2 + HH2)/(VV2 − HH2) |
| 3 | VV | 16 | ln(HH/VV) |
| 4 | VH | 17 | ln(HH) |
| 5 | HH − HV | 18 | ln(VV) |
| 6 | VV − VH | 19 | ln(HV/VH) |
| 7 | HH + VV | 20 | ln(VH/HV) |
| 8 | HH/VV | 21 | ln(VV) + ln(HH) |
| 9 | HV/VV | 22 | eln(VV) + eln(HH) |
| 10 | (VV − VH)/(VV + VH) | 23 | 10log(HH) |
| 11 | (HH − HV)/(HH + HV) | 24 | 10log(VV) |
| 12 | VH − HH | 25 | log(HV/VV) |
| 13 | VH/(HH + VV + 2VH) | 26 | 10log(HH) + 10log(VV) |
| ID | Feature Variables | ID | Feature Variables |
|---|---|---|---|
| 1 | HH | 6 | (HH − HV)/(HH + HV) |
| 2 | HH/VV | 7 | Ln(HH/VV) |
| 3 | HH − HV | 8 | Ln(VV) + Ln(HH) |
| 4 | HH − VV | 9 | 10log(HH) + 10log(VV) |
| 5 | VH − HH | 10 | (VV2 − HH2)/HH |
| Model | RMSE | MAE | |
|---|---|---|---|
| MLR | 2.342 | 1.827 | 0.591 |
| RF | 2.135 | 1.748 | 0.677 |
| MLPNN | 1.936 | 1.664 | 0.705 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Guan, H.; Duan, F. Combined L-Band Polarimetric SAR and GPR Data to Develop Models for Leak Detection in the Water Pipeline Networks. Remote Sens. 2025, 17, 1386. https://doi.org/10.3390/rs17081386
Zhang Y, Guan H, Duan F. Combined L-Band Polarimetric SAR and GPR Data to Develop Models for Leak Detection in the Water Pipeline Networks. Remote Sensing. 2025; 17(8):1386. https://doi.org/10.3390/rs17081386
Chicago/Turabian StyleZhang, Yuyao, Hongliang Guan, and Fuzhou Duan. 2025. "Combined L-Band Polarimetric SAR and GPR Data to Develop Models for Leak Detection in the Water Pipeline Networks" Remote Sensing 17, no. 8: 1386. https://doi.org/10.3390/rs17081386
APA StyleZhang, Y., Guan, H., & Duan, F. (2025). Combined L-Band Polarimetric SAR and GPR Data to Develop Models for Leak Detection in the Water Pipeline Networks. Remote Sensing, 17(8), 1386. https://doi.org/10.3390/rs17081386








