1. Introduction
Change detection is of significance in the field of remote sensing images, offering critical insights into the temporal dynamics of our environments [
1]. These changes may encompass the constructions of new infrastructures, the demolitions of existing structures and the shifts in land-use forms. The importance of change detection lies in its wide range of applications, such as urban planning, environmental monitoring, disaster management and infrastructure development [
2]. Advances in satellite technology has remarkably improved the availability and quality of satellite images, which enables more accurate monitoring of land cover types and more comprehensive analysis of land cover changes [
3,
4,
5,
6,
7]. However, as shown in
Figure 1, change detection in remote sensing images remains challenging due to the presence of pseudo changes caused by seasonal variations, varying imaging conditions and sensor noise. In light of this, mitigating pseudo change influence and thereby improving change-detection accuracy remain critical research objectives.
Traditional methods for change detection in remote sensing images such as pixel-based [
8,
9,
10,
11] and object-based approaches [
12,
13,
14,
15] have been widely studied. Pixel-based methods analyze changes between bitemporal images on a pixel-by-pixel basis, while object-based methods group pixels into homogeneous objects and analyze changes at the object level. However, both approaches are sensitive to noise and threshold selection, and their robustness to pseudo changes caused by illumination variations and seasonal changes is also limited, leading to poor change-detection performance.
Recently, with the development of deep learning (DL) techniques, DL-based methods have emerged as powerful alternatives to effectively improve change-detection performance. DL-based methods, represented by CNN-based and Transformer-based methods, leverage neural networks to effectively mine rich semantic features [
16,
17,
18,
19], enabling precise identification of changes over time in remote sensing images. For example, Daudt et al. [
20] proposed fully convolution siamese networks, marking the first integration of siamese networks with fully convolutional architectures for change detection. However, this method struggles to effectively capture deep semantic information within images, resulting in suboptimal detection performance. Since then, many efforts have been dedicated to improving the ability to reduce pseudo changes and enhancing change-detection accuracy. Specifically, Zhang et al. [
21] proposed feature difference CNN, which utilized a carefully designed loss function to learn the magnitude of changes. The learned change magnitude serves as prior knowledge to mitigate the impacts of pseudo changes. Shi et al. [
22] proposed a deeply supervised network for change detection. By incorporating a metric module and a convolutional block attention module (CBAM), this approach effectively reduced the influence of pseudo changes and enhanced change-detection performance. However, the limited size of the receptive field in CNN structures poses challenges in capturing long-range dependencies across both space and time [
23,
24], thus hindering their further advancements in change detection. To address these limitations, Transformers, introduced in 2017 [
25], have emerged as promising solutions. Unlike CNNs, Transformers excel at capturing global features and modeling long-range dependencies [
26,
27], which has contributed to their growing prominence in remote sensing image change detection. For instance, Chen et al. [
28] introduced a lightweight Transformer-based model known as BIT for change detection; BIT identified change areas by extracting a concise token set that captures high-level features, demonstrating enhanced efficiency and accuracy over purely convolutional methods. Zhao et al. [
29] introduced a hybrid network combining CNNs with a Transformer decoder. This approach employed multi-stage siamese CNNs to extract bitemporal features, which were then transformed into semantic tokens by the Transformer decoder to enhance feature interaction, demonstrating notable robustness against pseudo changes. Similarly, to mitigate the interference of pseudo changes, Xu et al. [
30] proposed a Transformer-based network that encapsulated bitemporal features into semantic tokens for effective information exchange and incorporated graph reasoning to refine the contours of change areas.
Although Transformer architectures have demonstrated strong performance in change detection tasks, their efficiency is often hindered by high computational demands and quadratic complexity. To address these limitations, Mamba was introduced, leveraging a selective state-space model [
31]. Since then, researchers have actively explored the incorporation of Mamba into change detection. For instance, Zhao et al. [
32] proposed RSMamba, an innovative framework that introduced an omnidirectional scanning technique to capture contextual information across eight directions in remote sensing images. Benefiting from the linear complexity of the space state model, this method eliminated the need for cropping of large-scale remote sensing images, reducing semantic loss while maintaining high precision and computational efficiency. Chen et al. [
33] introduced ChangeMamba, which integrated sequential, cross and parallel modeling mechanisms into a visual Mamba architecture, effectively modeling spatial-temporal relationships between bitemporal images and facilitating precise change detection. Beyond the computational challenges, Transformers also inherently face challenges due to their intrinsic sequence-based structure. While this structure allows Transformers to effectively model dependencies in sequential data, it also presents limitations when dealing with non-Euclidean data, making them less flexible for capturing complex, non-sequential relationships in remote sensing images, where interactions between different objects and landforms cannot be easily modeled as sequences. Recently, GCNs have gained traction across a wide range of domains, starting with their first proposal in [
34] for semi-supervised classification, and expanding to graph-representation learning [
35], social network analysis [
36] and bioinformatics [
37]. Compared to CNNs and Transformers, GCNs excel in feature learning on non-Euclidean data by aggregating node features based on their adjacency within the graph structure, offering a flexible and powerful approach for feature extraction and interaction in remote sensing change-detection tasks. For example, Song et al. [
38] proposed GCN-based siamese network, which integrated a hybrid backbone combining over-parameterized CNN and vision graph neural network (ViG) to reduce the number of parameters while maintaining high change-detection performance. Yu et al. [
39] proposed a multi-scale graph reasoning network for change detection. This method projected image features to graph vertices and utilized GCN for information propagation across vertices, improving feature fusion and interaction. Jiang et al [
40] proposed a hybrid method that combined GCN and Transformer. The method utilized GCN to generate a coarse change map and to mine reliable tokens extracted from bitemporal images. Cui et al. [
41] proposed a bitemporal graph semantic interaction network, which utilized soft clustering to group pixels into graph vertices and introduced a graph semantic interaction module to model bitemporal feature relationships. This method demonstrated superior performance in change detection. Wang et al. [
42] proposed a GCN-based method for change detection, which introduced two well-designed GCN-based modules: a coordinate space GCN for spatial information interaction and a feature interaction GCN for semantic information exchange. Furthermore, to alleviate the reliance on extensive annotations, GCNs have increasingly been applied to unsupervised and semi-supervised change detection, offering effective solutions for scenarios with limited labeled data. Tang et al. [
43] proposed an unsupervised change-detection method that leveraged multi-scale GCN to capture rich contextual patterns and to extract spatial-spectral features from deep difference feature maps, enabling accurate change detection in a fully unsupervised manner. Saha et al. [
44] proposed a GCN-based method for semi-supervised change detection, where bitemporal images were mapped into multi-scale parcels. Each parcel, treated as a node in the graph, encapsulates homogeneous information and spatial features. GCN was then employed to propagate information between neighboring nodes, enhancing contextual relationship modeling. Jian et al. [
45] introduced a self-supervised learning framework for hyperspectral image change detection. This method leveraged node- and edge-level data augmentations to enhance the diversity of contrastive sample pairs. It also introduced an uncertainty-aware loss function to refine the graph structures, improving the ability to capture subtle changes. These advancements highlight the potential of GCNs to enhance the accuracy and robustness of change detection. However, many existing GCN-based methods still face challenges in fully exploiting the relationships between bitemporal images. For instance, some methods mainly focus on using GCN for information propagation within individual images, while others are restricted to single-scale graph-level feature interaction, resulting in insufficient feature interaction and relationship exploitation between bitemporal images at the graph level. Therefore, there remains a need for further exploration of multi-scale and cross-temporal feature interaction to fully unlock the potential of GCNs in remote sensing change detection.
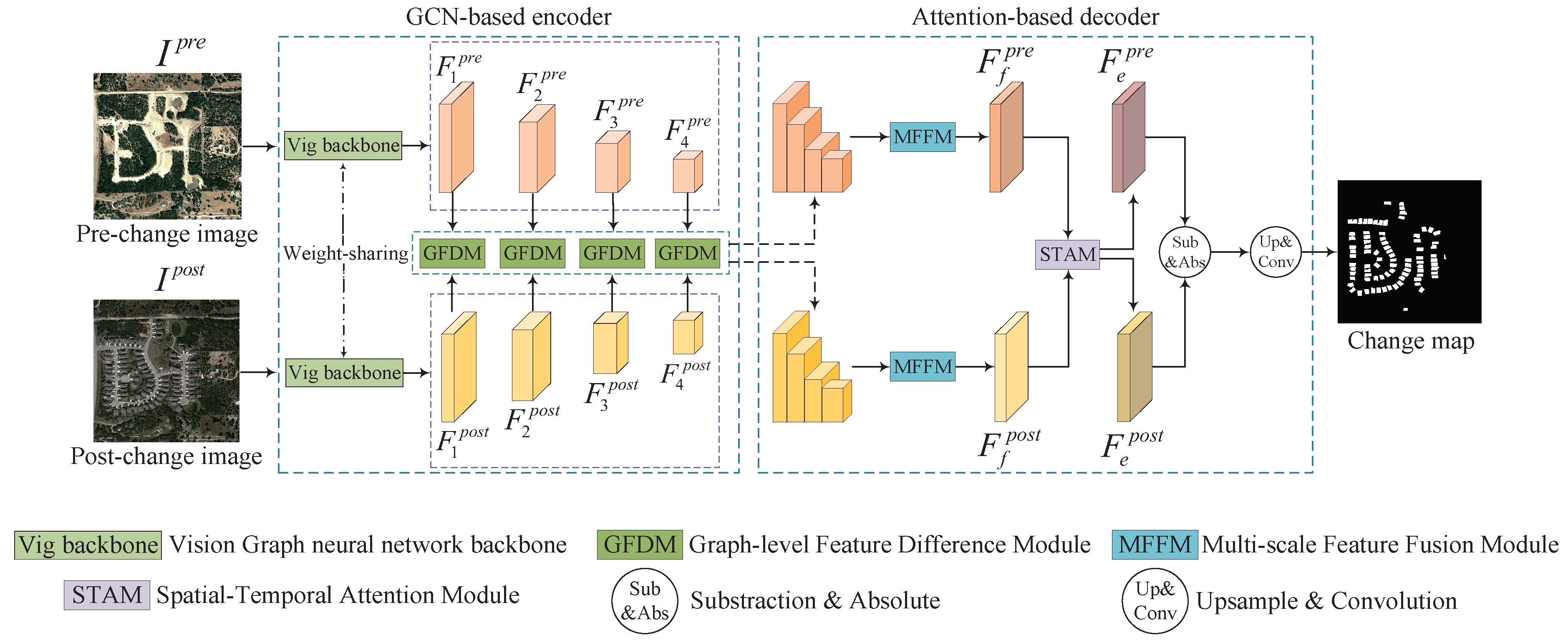
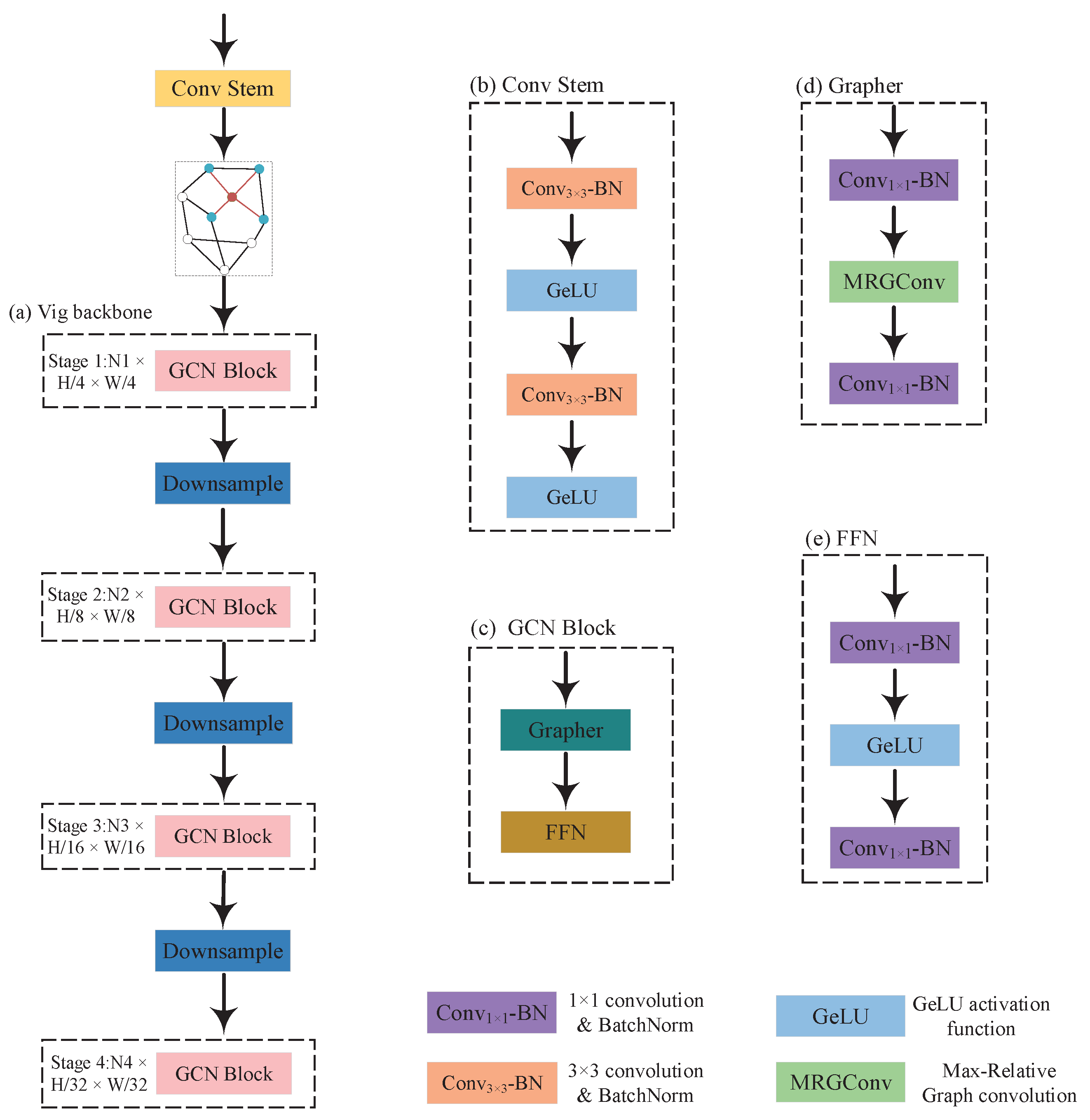
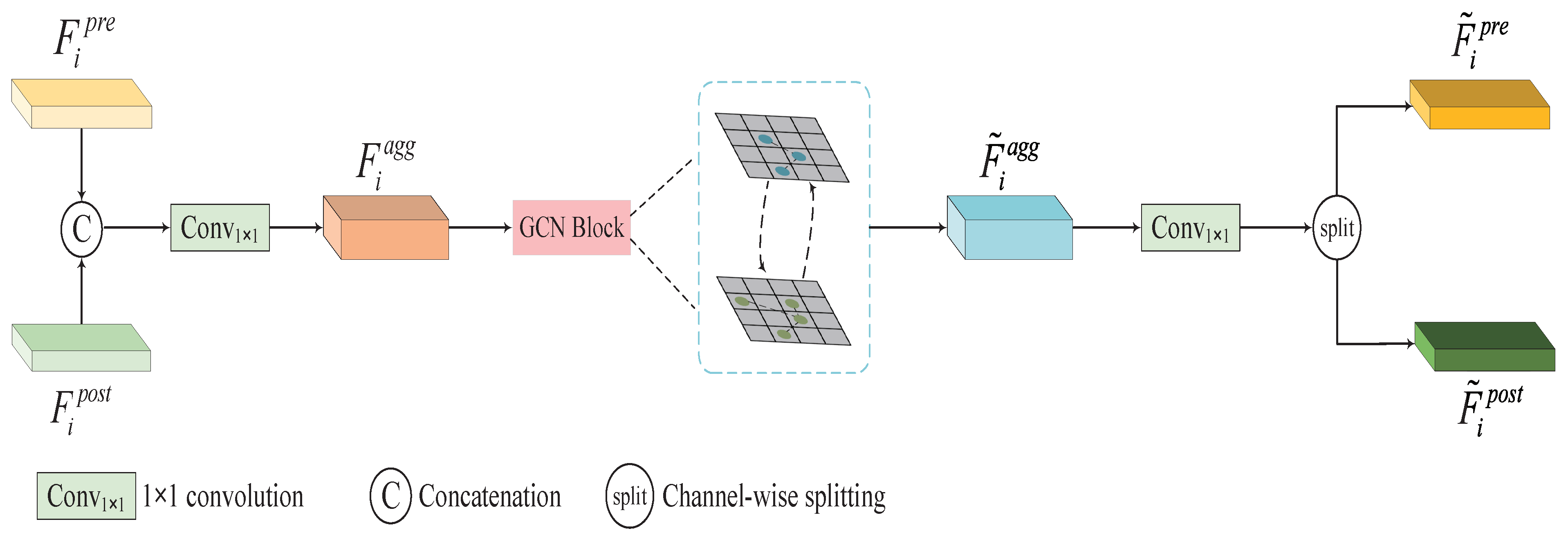
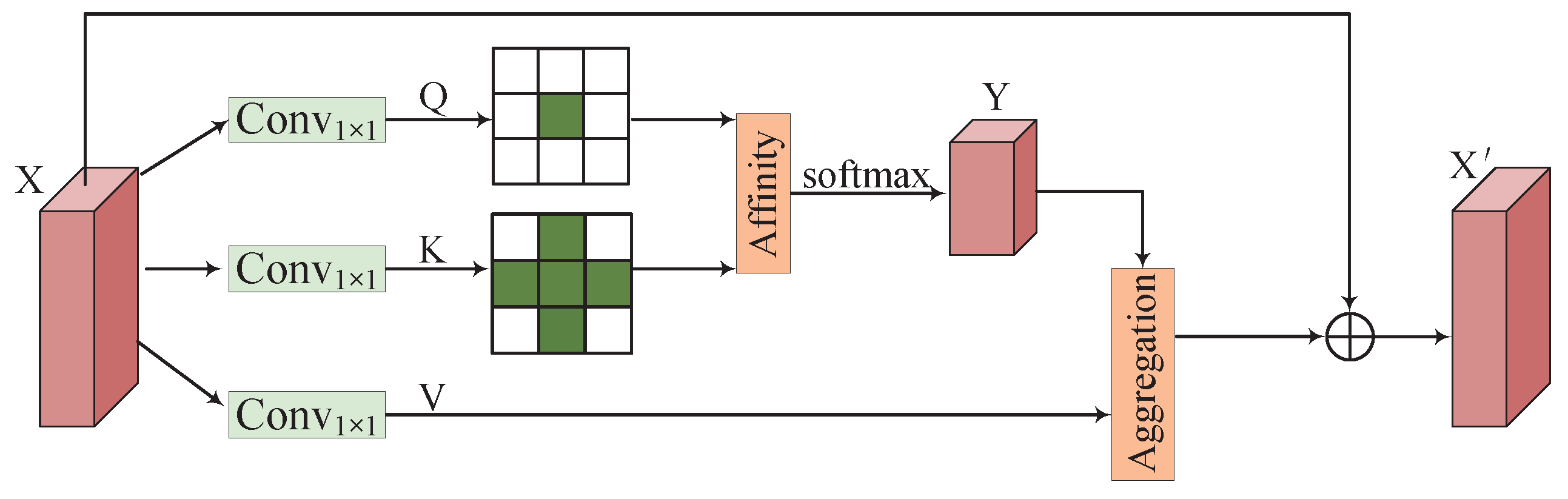
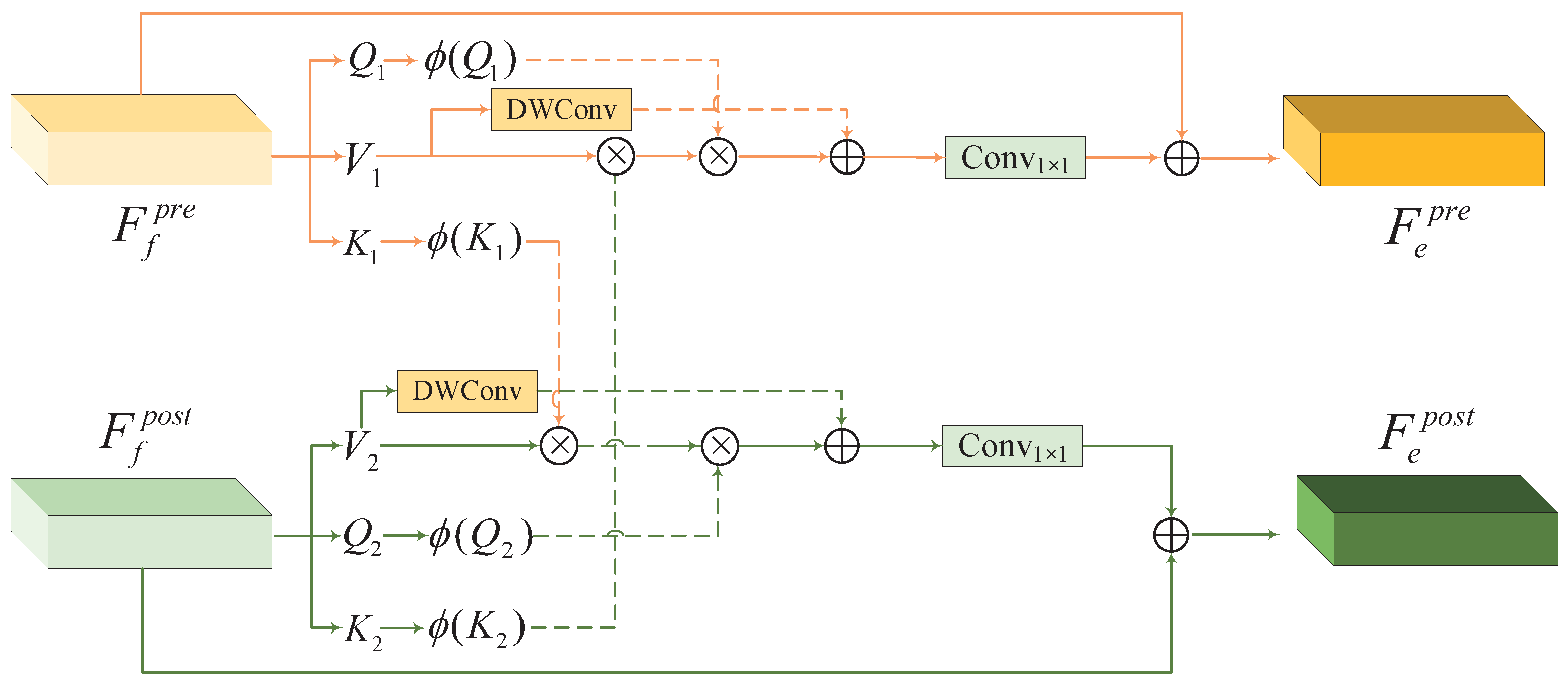
In this article, we put forward AGCD for change detection, which aims to address the challenge of pseudo changes and improve detection accuracy. The motivation for this study stems from the finding that existing methods are susceptible to pseudo changes due to two main reasons: (1) insufficient semantic understanding within individual images and (2) inadequate feature interaction between bitemporal images, which ultimately leads to suboptimal change-detection performance. To address these challenges, AGCD integrates GCN and attention mechanisms into a unified framework, with the following two core objectives: (1) Enhance semantic understanding: To capture nuanced features, AGCD leverages the hierarchical ViG backbone, enabling graph-level feature extraction for detailed representation of individual images. Additionally, MFFM is introduced to synthesize multi-scale features, facilitating comprehensive contextual understanding. (2) Improve bitemporal feature interaction: AGCD promotes effective interaction between features of bitemporal images through the proposed GFDM and STAM. GFDM facilitates multi-scale interactions at the graph level, comprehensively modeling feature similarities and disparities, while STAM employs spatial-temporal attention to enhance the identification of unchanged regions, ensuring accurate classification of changes. The core hypothesis is that our AGCD, with the integration of these modules for refined semantic understanding and enhanced feature interaction, will effectively address the problem of pseudo changes and deliver reliable change-detection results. To validate this hypothesis, extensive experiments on multiple benchmark datasets are conducted to assess both the overall performance of the AGCD and the individual contributions of each proposed module.
The main contributions of this work are summarized as follows:
- (1)
We propose a novel change-detection network, namely AGCD, which integrates a GCN-based encoder with an attention-based decoder, aiming at effectively addressing the issue of pseudo changes and enhancing change-detection precision.
- (2)
The GCN-based encoder utilizes a weight-sharing ViG backbone to extract hierarchical graph-level features, complemented by a straightforward but efficient module, GFDM, to facilitate graph-level feature interaction, improving the network’s ability to discern differential clues and alleviating the impact of pseudo changes.
- (3)
The attention-based decoder consists of MFFM and STAM. MFFM uses criss-cross attention (CCA) to refine multi-scale features, while STAM models spatial-temporal dependencies, enhancing the semantic clarity of change areas and reducing pseudo changes for accurate change detection.
3. Datasets and Experimental Settings
In this subsection, three benchmark datasets employed in our experiments are introduced first. Then, the implementation details and evaluation metrics are provided. Finally, the comparative methods are briefly described.
3.1. Dataset Descriptions
We carried out our experiments on three renowned public datasets, the LEVIR-CD dataset [
56], the WHU-CD dataset [
57], and the SYSU-CD dataset [
22].
The LEVIR-CD is composed of 637 pairs of high-resolution images, each measuring 1024 × 1024 pixels. These images, taken over a span of 5 to 14 years, illustrate a wide range of urban changes, including building construction and demolition. The dataset includes 31,333 instances of building alterations. For our study, we cropped the original image pairs to a size of 256 × 256 pixels and split the dataset into training, validation, and testing sets containing 7120, 1024, and 2048 pairs, respectively.
The WHU-CD dataset contains two high-resolution aerial images, each with a resolution of 0.075 m and dimensions of 32,507 × 15,354 pixels. These images record the urban development in Christchurch, New Zealand, from 2012 to 2016, with a focus on building structure changes. In our experiments, we extracted non-overlapping 256 × 256 patches from these images and organized the dataset into training, validation, and testing subsets, which include 6096, 762, and 762 pairs, respectively.
The SYSU-CD dataset offers a comprehensive set of 20,000 pairs of very high-resolution aerial images, each with a 0.5 m resolution and originally sized at 256 × 256 pixels. It captures a spectrum of intricate urban changes in Hong Kong between 2007 and 2014, encompassing the rise of new structures and the broadening of roadways. For our analysis, we allocated the dataset into training, validation, and testing segments, comprising 7120, 1024, and 2048 pairs, respectively.
Examples of the three datasets are shown in
Figure 8.
3.2. Implementation Details
We constructed our model utilizing the PyTorch 1.11.0 framework and trained it on a single NVIDIA Tesla V40 GPU. Standard data-augmentation techniques are employed on the input image, including random flipping and random rotating. In terms of model optimization, we employ the AdamW optimizer. The decay rates for the estimation of the first and second moments are set to their default values of 0.9 and 0.999, respectively. The weight decay is configured to 0.01. The initial learning rate is carefully chosen to be 0.0005, 0.0002, and 0.0006 for LEVIR-CD, WHU-CD, and SYSU-CD datasets, respectively. The batch size and the number of epochs for training are set to 32 and 100, respectively.
3.3. Evaluation Metrics
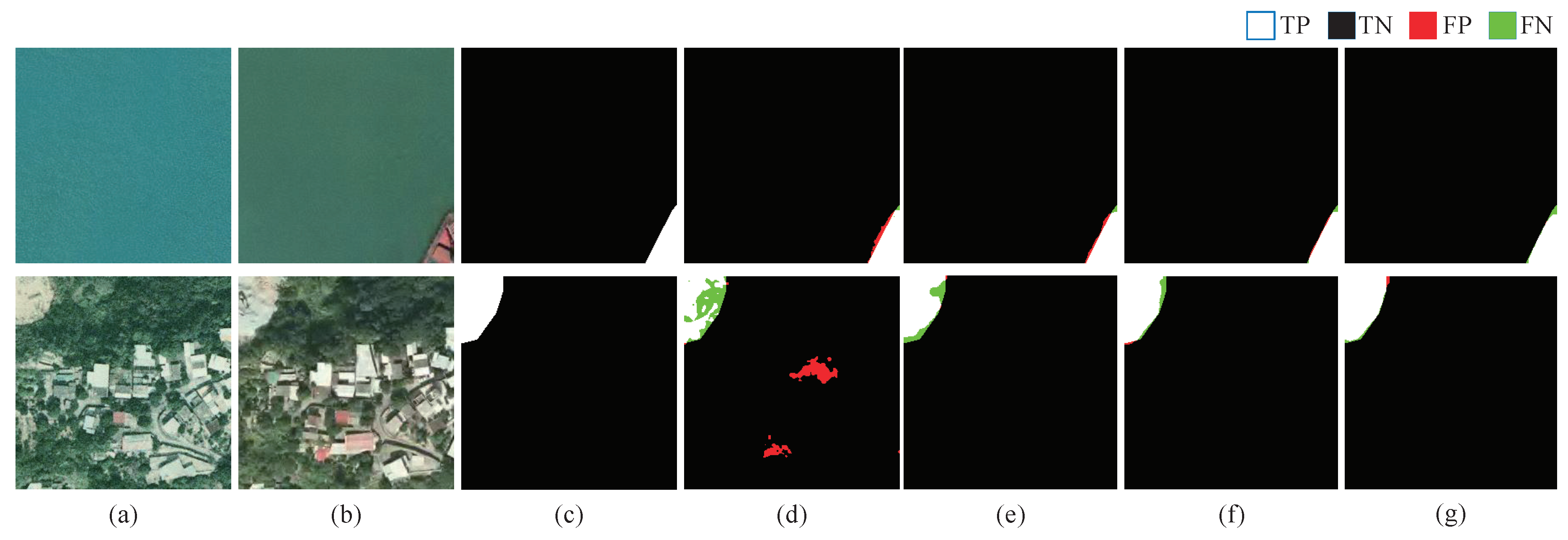
In our experiment, we selected precision (Pre), recall (Rec), F1-score (F1), overall accuracy (OA), and intersection over union (IoU) as the main evaluation indices. The definitions of these metrics are as follows:
where TP, FP, TN, and FN represent the number of true positive (TP), false positive (FP), true negative (TN), and false negative (FN), respectively.
3.4. Comparative Methods
AGCD was compared to several state-of-the-art models to verify its effectiveness, including FC-EF [
20], FC-Siam-conc [
20], FC-Siam-diff [
20], SNUNet [
58], BiT [
28], DSAMNet [
22], STNet [
59], VcT [
40], and CDMaskFormer [
60].
FC-EF, FC-Siam-conc, and FC-Siam-diff: Three variants of FCNs used for change-detection tasks. FC-EF combines bitemporal images along the channel axis before they are passed into the network. FC-Siam-conc employs a siamese network for bitemporal feature extraction, which are then fused. FC-Siam-diff, also using a siamese network, extracts bitemporal features and applies their absolute differences to capture differential clues.
SNUNet: Inspired by UNet++, SNUNet employs dense connection between bitemporal features to reduce semantic gaps and localization errors, resulting in more accurate change maps.
BiT: A lightweight network for change detection that converts bitemporal features into semantic tokens, facilitating context modeling and information exchange in a compact, token-based space–time framework.
DSAMNet: DSAMNet introduces parallel convolutional blocks to refine features, addressing feature misalignment and inefficient supervision.
STNet: STNet combines spatial and temporal features using cross-temporal and cross-scale mechanisms to recover fine spatial details, improving change-detection accuracy.
VcT: A hybrid method combining GCN and Transformer, which leverages GCN to refine token representations extracted from bitemporal images for reliable change detection.
CDMaskFormer: CDMaskFormer utilized a Transformer-based decoder for interaction of features passed from a well-designed change extractor. Change prototypes derived from this decoder are then normalized to generate the final change map.