Multi-Decision Vector Fusion Model for Enhanced Mapping of Aboveground Biomass in Subtropical Forests Integrating Sentinel-1, Sentinel-2, and Airborne LiDAR Data
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Field Data Collection
2.3. Remote Sensing Data Acquisition and Preprocessing
2.3.1. LiDAR Data Acquisition and Preprocessing
2.3.2. Satellite Image Acquisition and Preprocessing
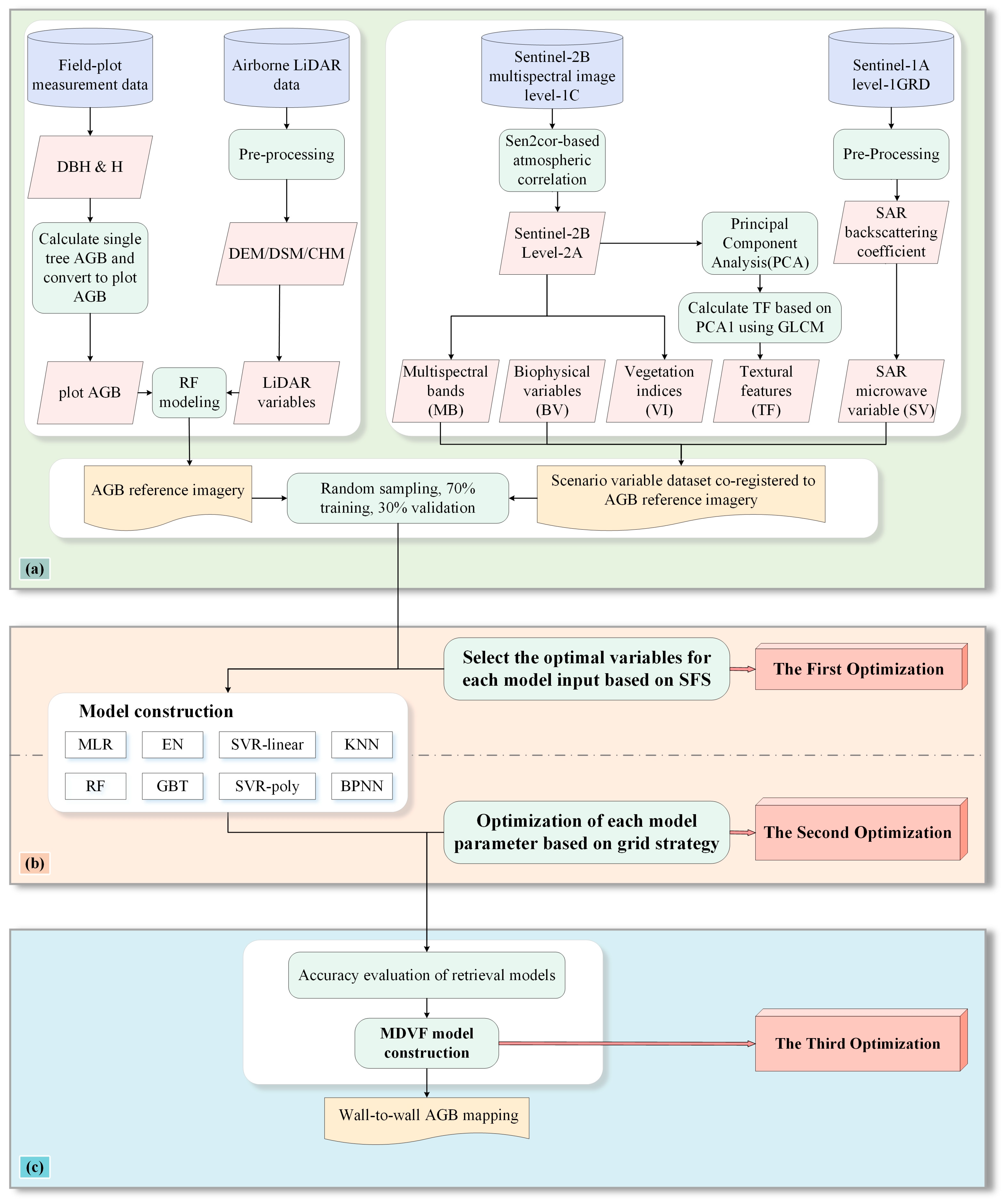
3. Methods
3.1. Extraction of Remote Sensing Variables
3.1.1. LiDAR Metrics
3.1.2. Active and Passive Remote Sensing Metrics
3.2. Generation of LiDAR-Derived AGB Reference Map
3.3. AGB Estimation Models
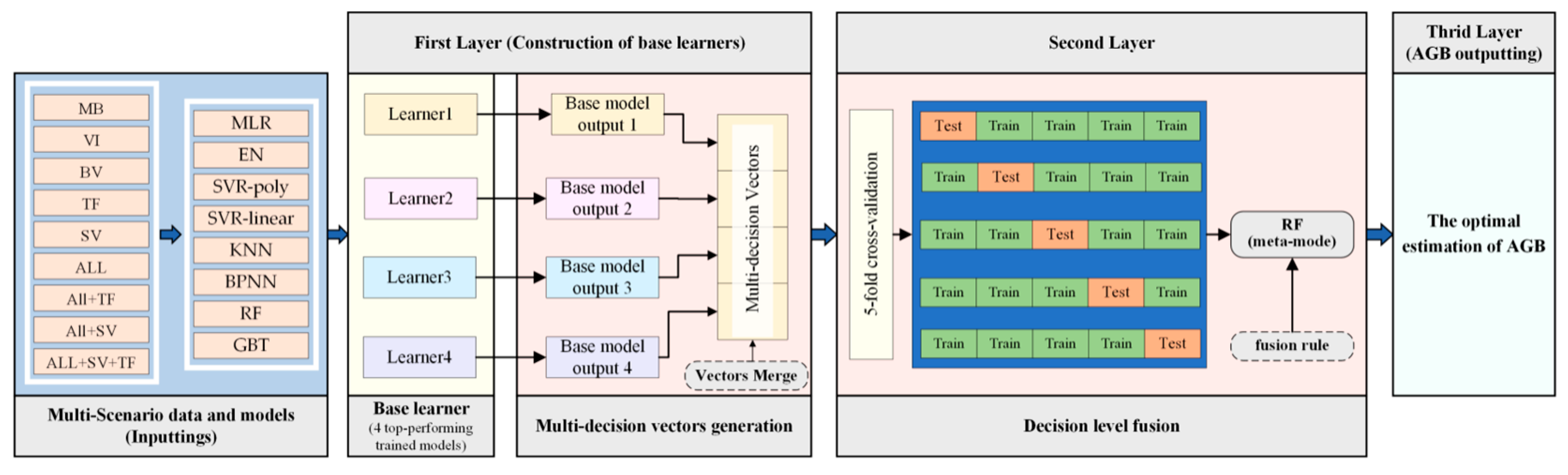
3.4. Multi-Decision Vector Fusion (MDVF) Model Construction
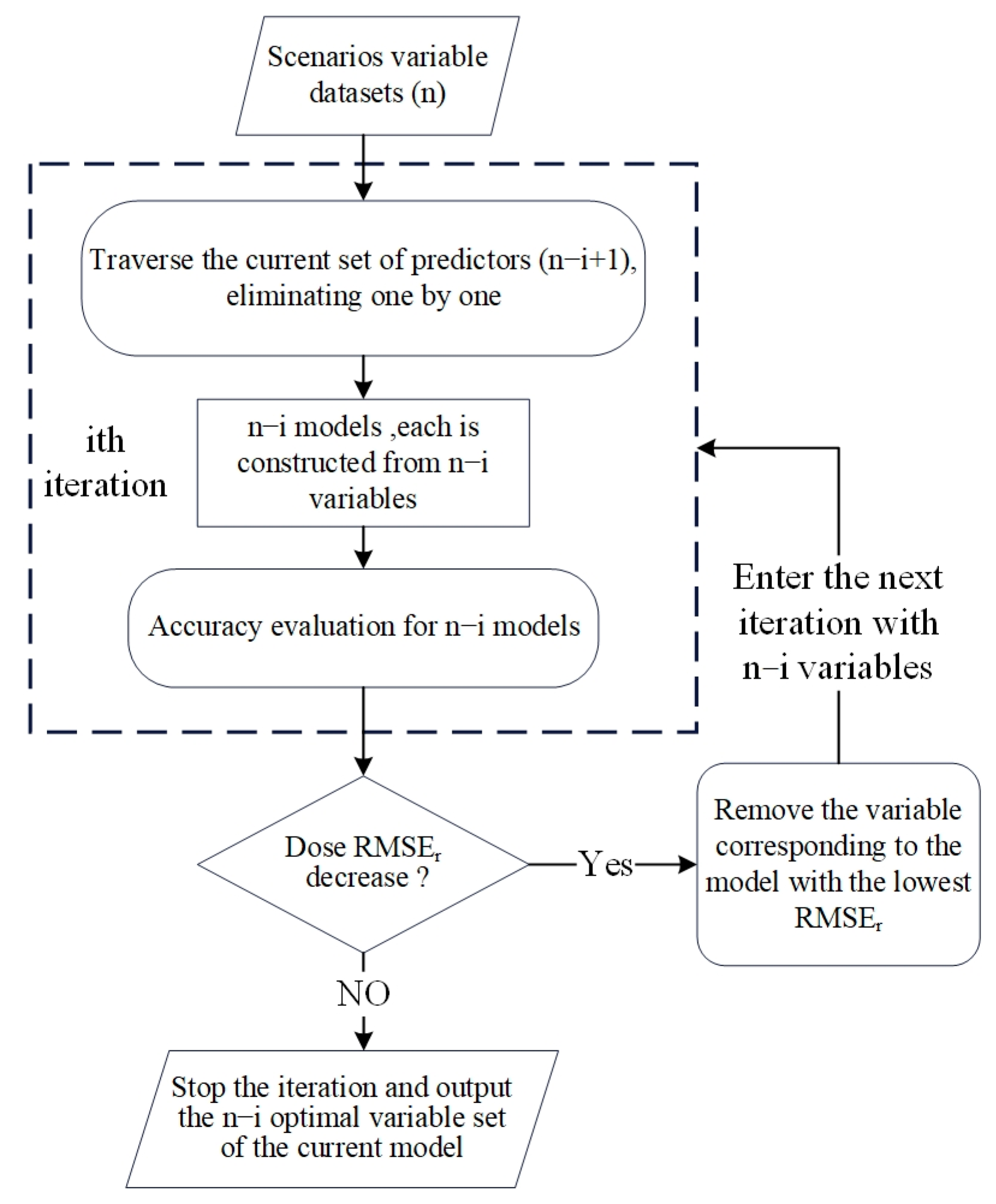
3.5. Feature Selection
3.6. Experimental Design and Accuracy Evaluation
4. Results
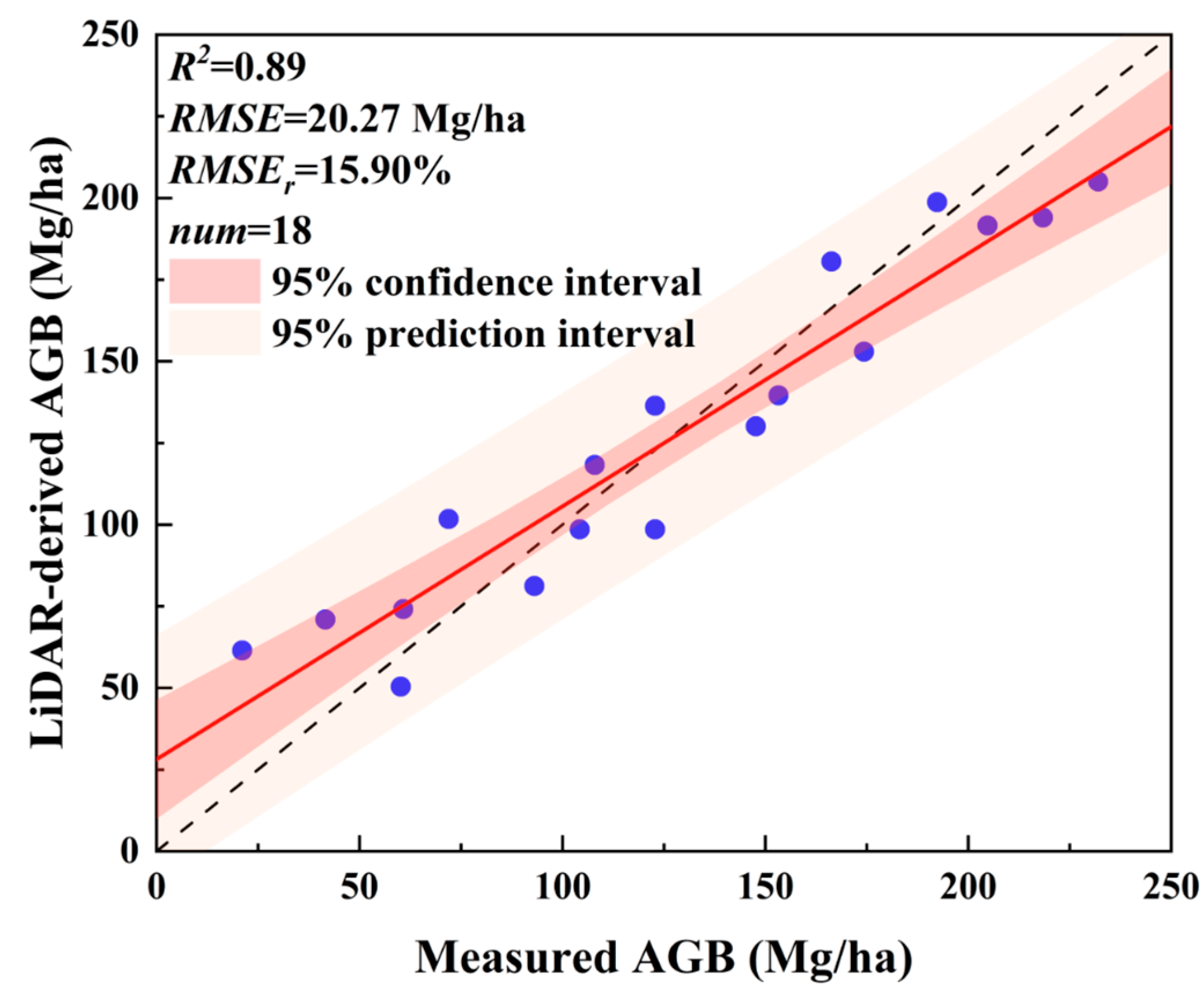
4.1. Accuracy Assessment of ABG Reference Map
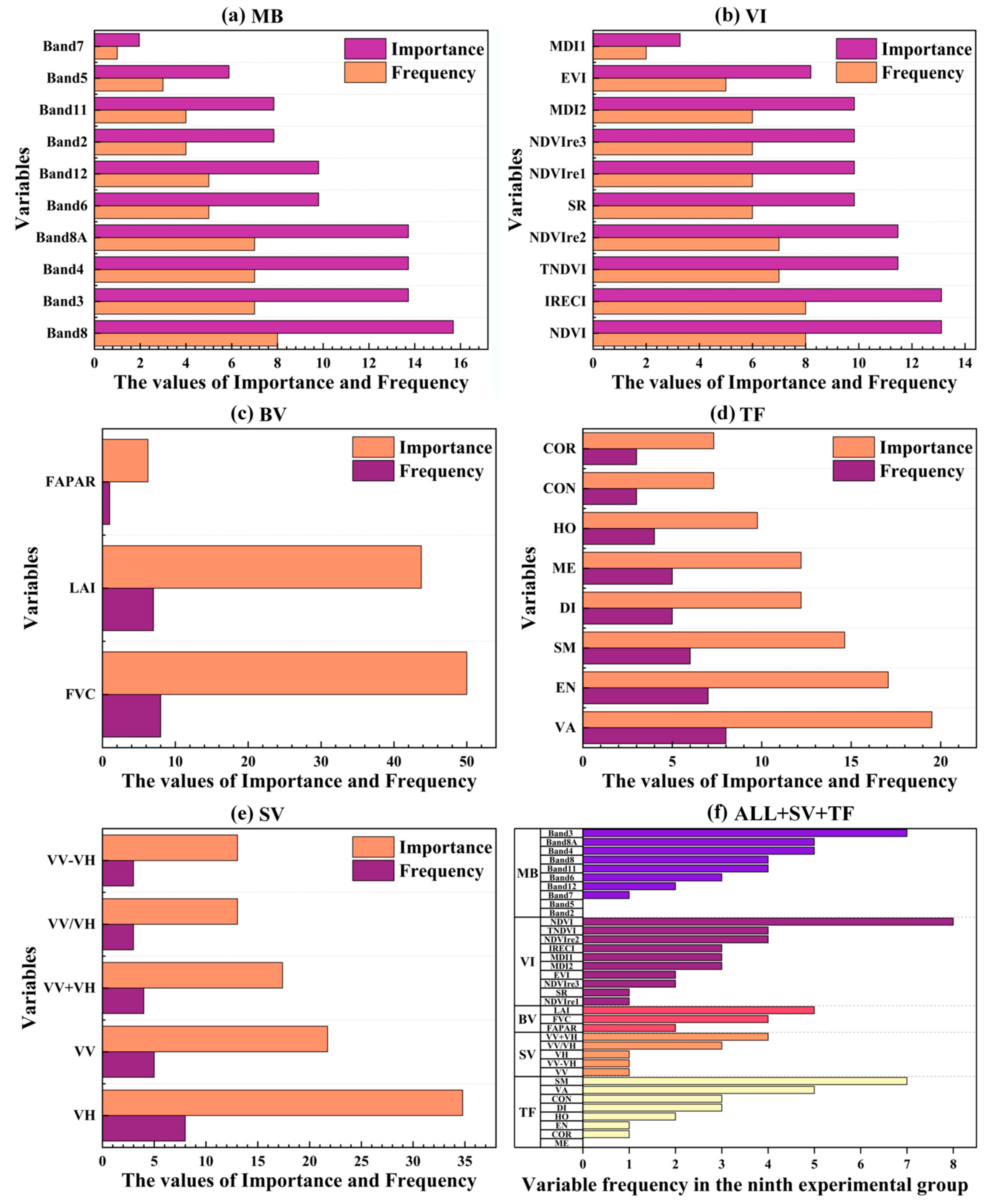
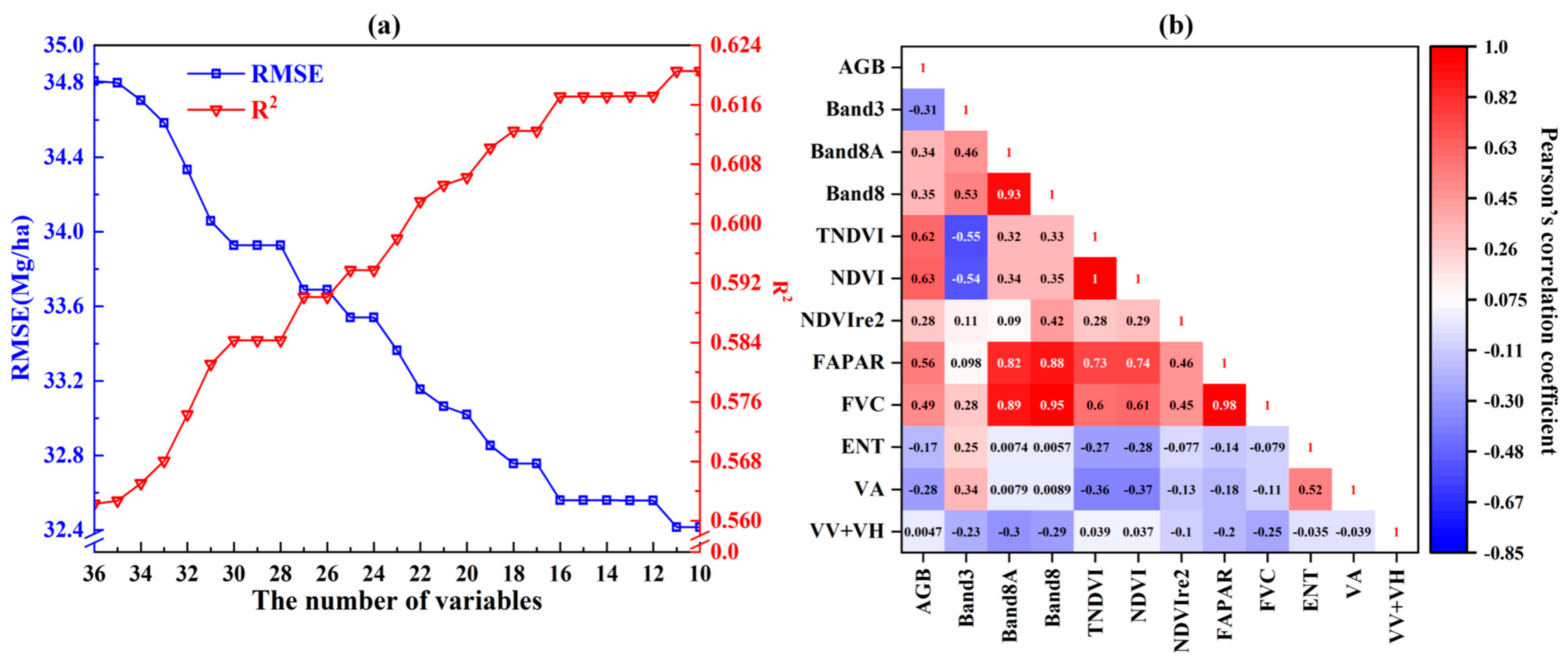
4.2. Feature Selection and First-Stage Optimization
4.2.1. Performance of Selected Predictor Sets
4.2.2. Key Variables Adaptively Identified by SFS
4.2.3. Model Performance with Optimal Feature Set
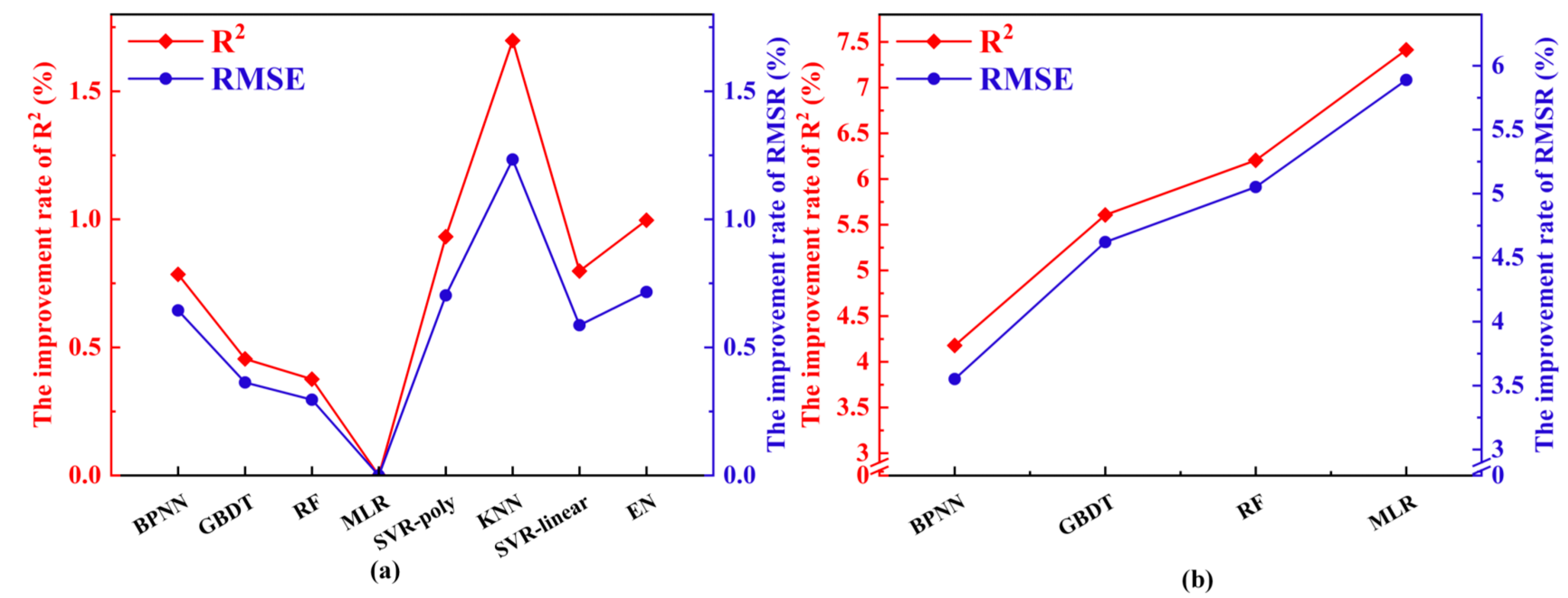
4.3. Hyperparameter Tuning and Second-Stage Optimization
4.4. MDVF Performance and Third-Stage Optimization
4.5. Forest AGB Mapping and Spatial Distribution Analysis
5. Discussion
5.1. LiDAR-Derived AGB as a Reliable Reference for Estimation
5.2. Contribution of Multi-Source Data to AGB Estimation
5.3. Effectiveness of Stepwise Feature Selection Method
5.4. Model Comparisons and the Impact of Hyperparameter Optimization
5.5. MDVF Performance and the Advantages of Three-Stage Optimization
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, Q.; Zhu, J.J.; Wang, Q.Q.; Gao, T.; Wang, G.G. Mycorrhizal type regulates trade-offs between plant and soil carbon in forests. Nat. Clim. Change 2023, 13, 1279–1281. [Google Scholar] [CrossRef]
- Heimann, M.; Reichstein, M. Terrestrial ecosystem carbon dynamics and climate feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef]
- Quegan, S.; Toan, L.T.; Chave, J.; Dall, J.; Exbrayat, J.F.; Minh, D.H.T.; Lomas, M.; D’Alessandro, M.M.; Paillou, P.; Papathanassiou, K.; et al. The European Space Agency BIOMASS mission: Measuring forest above-ground biomass from space. Remote Sens. Environ. 2019, 227, 44–60. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.J.; Guo, Q.H.; Xue, B.L.; Hu, T.Y.; Alvarez, O.; Tao, S.L.; Fang, J.Y. Spatial distribution of forest aboveground biomass in China: Estimation through combination of spaceborne lidar, optical imagery, and forest inventory data. Remote Sens. Environ. 2016, 173, 187–199. [Google Scholar] [CrossRef]
- Clark, D.B.; Kellner, J.R. Tropical forest biomass estimation and the fallacy of misplaced concreteness. J. Veg. Sci. 2012, 23, 1191–1196. [Google Scholar] [CrossRef]
- Zheng, D.L.; Rademacher, J.; Chen, J.Q.; Crow, T.; Bresee, M.; le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppa, J.; Puttonen, E. Comparison of two-dimensional multitemporal Sentinel-2 data with three-dimensional remote sensing data sources for forest inventory parameter estimation over a boreal forest. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Ramos Vieira Martins, F.d.S.; dos Santos, J.R.; Galvao, L.S.; Magalhaes Xaud, H.A. Sensitivity of ALOS/PALSAR imagery to forest degradation by fire in northern Amazon. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 163–174. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Ghulam, A.; Sidike, P.; Hartling, S.; Maimaitiyiming, M.; Peterson, K.; Shavers, E.; Fishman, J.; Peterson, J.; Kadam, S.; et al. Unmanned Aerial System (UAS)-based phenotyping of soybean using multi-sensor data fusion and extreme learning machine. ISPRS J. Photogramm. Remote Sens. 2017, 134, 43–58. [Google Scholar] [CrossRef]
- Stelmaszczuk-Górska, M.; Urbazaev, M.; Schmullius, C.; Thiel, C. Estimation of Above-Ground Biomass over Boreal Forests on Siberia Using Updated In Situ, ALOS-2 PALSAR-2, and RADARSAT-2 Data. Remote Sens. 2018, 10, 1550. [Google Scholar] [CrossRef]
- Tsui, O.W.; Coops, N.C.; Wulder, M.A.; Marshall, P.L.; McCardle, A. Using multi-frequency radar and discrete-return LiDAR measurements to estimate above-ground biomass and biomass components in a coastal temperate forest. ISPRS J. Photogramm. Remote Sens. 2012, 69, 121–133. [Google Scholar] [CrossRef]
- Hafner, S.; Ban, Y.F.; Nascetti, A. Unsupervised domain adaptation for global urban extraction using Sentinel-1 SAR and Sentinel-2 MSI data. Remote Sens. Environ. 2022, 280, 113192. [Google Scholar] [CrossRef]
- Tian, X.; Su, Z.; Chen, E.; Li, Z.; van der Tol, C.; Guo, J.; He, Q. Reprint of: Estimation of forest above-ground biomass using multi-parameter remote sensing data over a cold and arid area. Int. J. Appl. Earth Obs. Geoinf. 2012, 17, 102–110. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Wang, T.J.; Isenburg, M.; Khoshelham, K. Effect of slope on treetop detection using a LiDAR Canopy Height Model. ISPRS J. Photogramm. Remote Sens. 2015, 104, 44–52. [Google Scholar] [CrossRef]
- Falkowski, M.J.; Evans, J.S.; Martinuzzi, S.; Gessler, P.E.; Hudak, A.T. Characterizing forest succession with lidar data: An evaluation for the Inland Northwest, USA. Remote Sens. Environ. 2009, 113, 946–956. [Google Scholar] [CrossRef]
- Chirici, G.; Giannetti, F.; McRoberts, R.E.; Travaglini, D.; Pecchi, M.; Maselli, F.; Chiesi, M.; Corona, P. Wall-to-wall spatial prediction of growing stock volume based on Italian National Forest Inventory plots and remotely sensed data. Int. J. Appl. Earth Obs. Geoinf. 2020, 84, 101959. [Google Scholar] [CrossRef]
- Moghaddam, S.H.A.; Mokhtarzade, M.; Beirami, B.A. A feature extraction method based on spectral segmentation and integration of hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102097. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Xing, Y.; Hu, X.; Gong, J. Estimation of the forest stand mean height and aboveground biomass in Northeast China using SAR Sentinel-1B, multispectral Sentinel-2A, and DEM imagery. ISPRS J. Photogramm. Remote Sens. 2019, 151, 277–289. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, C.; Min, L.; Guo, Z.; Li, N. Retrieval of Farmland Surface Soil Moisture Based on Feature Optimization and Machine Learning. Remote Sens. 2022, 14, 5102. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, T.T.; Xu, H.; Liu, W.D.; Wang, J.Q.; Chen, X.D.; Liu, L.Y. GLC_FCS30D: The first global 30 m land-cover dynamics monitoring product with a fine classification system for the period from 1985 to 2022 generated using dense-time-series Landsat imagery and the continuous change-detection method. Earth Syst. Sci. Data 2024, 16, 1353–1381. [Google Scholar] [CrossRef]
- Godwin, C.; Chen, G.; Singh, K.K. The impact of urban residential development patterns on forest carbon density: An integration of LiDAR, aerial photography and field mensuration. Landsc. Urban Plan. 2015, 136, 97–109. [Google Scholar] [CrossRef]
- Fang, J.; Liu, G.; Xu, S. Biomass and Net Production of Forest Vegetation in China. Acta Ecol. Sin. 1996, 16, 497–508. [Google Scholar]
- ESA. Sentinel Application Platform (SNAP), ver. 9.0.0. European Space Agency: Paris, France, 2022. Available online: https://step.esa.int/main/download/snap-download/ (accessed on 7 July 2024).
- Warmerdam, F. The geospatial data abstraction library. In Open Source Approaches in Spatial Data Handling; Springer: Berlin/Heidelberg, Germany, 2008; pp. 87–104. [Google Scholar]
- Zhu, X.; Skidmore, A.K.; Darvishzadeh, R.; Wang, T. Estimation of forest leaf water content through inversion of a radiative transfer model from LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2019, 74, 120–129. [Google Scholar] [CrossRef]
- Majasalmi, T.; Rautiainen, M. The potential of Sentinel-2 data for estimating biophysical variables in a boreal forest: A simulation study. Remote Sens. Lett. 2016, 7, 427–436. [Google Scholar] [CrossRef]
- Murray, H.; Lucieer, A.; Williams, R. Texture-based classification of sub-Antarctic vegetation communities on Heard Island. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 138–149. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O. Investigating the robustness of the new Landsat-8 Operational Land Imager derived texture metrics in estimating plantation forest aboveground biomass in resource constrained areas. ISPRS J. Photogramm. Remote Sens. 2015, 108, 12–32. [Google Scholar] [CrossRef]
- Hudak, A.T.; Strand, E.K.; Vierling, L.A.; Byrne, J.C.; Eitel, J.U.H.; Martinuzzi, S.; Falkowski, M.J. Quantifying aboveground forest carbon pools and fluxes from repeat LiDAR surveys. Remote Sens. Environ. 2012, 123, 25–40. [Google Scholar] [CrossRef]
- Li, Y.; Chen, R.; He, B.; Veraverbeke, S. Forest foliage fuel load estimation from multi-sensor spatiotemporal features. Int. J. Appl. Earth Obs. Geoinf. 2022, 115, 103101. [Google Scholar] [CrossRef]
- Were, K.; Bui, D.T.; Dick, O.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z.; Xi, Y. Estimation of Forest Above-Ground Biomass by Geographically Weighted Regression and Machine Learning with Sentinel Imagery. Forests 2018, 9, 582. [Google Scholar] [CrossRef]
- Wang, L.a.; Zhou, X.; Zhu, X.; Dong, Z.; Guo, W. Estimation of biomass in wheat using random forest regression algorithm and remote sensing data. Crop J. 2016, 4, 212–219. [Google Scholar] [CrossRef]
- Heiskanen, J.; Rautiainen, M.; Korhonen, L.; Mottus, M.; Stenberg, P. Retrieval of boreal forest LAI using a forest reflectance model and empirical regressions. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 595–606. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Jiang, F.; Sun, H.; Chen, E.; Wang, T.; Cao, Y.; Liu, Q. Above-Ground Biomass Estimation for Coniferous Forests in Northern China Using Regression Kriging and Landsat 9 Images. Remote Sens. 2022, 14, 5734. [Google Scholar] [CrossRef]
- Shi, S.; Xu, L.; Gong, W.; Chen, B.; Chen, B.; Qu, F.; Tang, X.; Sun, J.; Yang, J. A convolution neural network for forest leaf chlorophyll and carotenoid estimation using hyperspectral reflectance. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102719. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- David, R.M.; Rosser, N.J.; Donoghue, D.N.M. Improving above ground biomass estimates of Southern Africa dryland forests by combining Sentinel-1 SAR and Sentinel-2 multispectral imagery. Remote Sens. Environ. 2022, 282, 113232. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, X.; Cai, Z. BS-Nets: An End-to-End Framework for Band Selection of Hyperspectral Image. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1969–1984. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep Learning for Geophysics: Current and Future Trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Ting, K.M.; Witten, I.H. Issues in stacked generalization. J. Artif. Intell. Res. 1999, 10, 271–289. [Google Scholar] [CrossRef]
- Peng, W.M.; Deng, H.F.; Chen, A.H. Using Hellinger and Bures metrics to construct two-dimensional quantum metric space for weather data fusion. Inform Fusion 2020, 55, 199–206. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, L.; Xiao, Q.L.; Bai, X.L.; Wu, B.H.; Wu, N.; Zhao, Y.Y.; Wang, J.M.; Feng, L. End-to-End Fusion of Hyperspectral and Chlorophyll Fluorescence Imaging to Identify Rice Stresses. Plant Phenomics 2022, 2022, 9851096. [Google Scholar] [CrossRef]
- Wang, G.; Zhai, Y.J.; Xue, Z.Z.; Xu, Y.Y. Improving Protein Subcellular Location Classification by Incorporating Three-Dimensional Structure Information. Biomolecules 2021, 11, 1607. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM Ensemble Approach Combining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Hislop, S.; Jones, S.; Soto-Berelov, M.; Skidmore, A.; Haywood, A.; Nguyen, T.H. A fusion approach to forest disturbance mapping using time series ensemble techniques. Remote Sens. Environ. 2019, 221, 188–197. [Google Scholar] [CrossRef]
- Kong, Y.; Yan, B.; Liu, Y.; Leung, H.; Peng, X. Feature-Level Fusion of Polarized SAR and Optical Images Based on Random Forest and Conditional Random Fields. Remote Sens. 2021, 13, 1323. [Google Scholar] [CrossRef]
- Healey, S.P.; Cohen, W.B.; Yang, Z.Q.; Brewer, C.K.; Brooks, E.B.; Gorelick, N.; Hernandez, A.J.; Huang, C.Q.; Hughes, M.J.; Kennedy, R.E.; et al. Mapping forest change using stacked generalization: An ensemble approach. Remote Sens. Environ. 2018, 204, 717–728. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Liang, X.; Li, Z.; Huang, N.; Gao, S.; Wang, C.; Muhammad, S. Geostatistical modeling using LiDAR-derived prior knowledge with SPOT-6 data to estimate temperate forest canopy cover and above-ground biomass via stratified random sampling. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 88–98. [Google Scholar] [CrossRef]
- Poorazimy, M.; Shataee, S.; McRoberts, R.E.; Mohammadi, J. Integrating airborne laser scanning data, space-borne radar data and digital aerial imagery to estimate aboveground carbon stock in Hyrcanian forests, Iran. Remote Sens. Environ. 2020, 240, 111669. [Google Scholar] [CrossRef]
- Tsui, O.W.; Coops, N.C.; Wulder, M.A.; Marshall, P.L. Integrating airborne LiDAR and space-borne radar via multivariate kriging to estimate above-ground biomass. Remote Sens. Environ. 2013, 139, 340–352. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Li, Z.; Wang, C.; Wu, M.; Muhammad, S. Upscaling coniferous forest above-ground biomass based on airborne LiDAR and satellite ALOS PALSAR data. J. Appl. Remote Sens. 2016, 10, 046003. [Google Scholar] [CrossRef]
- Pan, L.; Sun, Y.; Wang, Y.; Chen, L.; Cao, Y. Estimation of aboveground biomass in a Chinese fir (Cunninghamia lanceolata) forest combining data of Sentinel-1 and Sentinel-2. J. Nanjing For. Univ. Nat. Sci. Ed. 2020, 44, 149–156. [Google Scholar]
- Cao, L.; Coops, N.C.; Hermosilla, T.; Innes, J.; Dai, J.; She, G. Using Small-Footprint Discrete and Full-Waveform Airborne LiDAR Metrics to Estimate Total Biomass and Biomass Components in Subtropical Forests. Remote Sens. 2014, 6, 7110–7135. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Hyde, P.; Dubayah, R.; Walker, W.; Blair, J.B.; Hofton, M.; Hunsaker, C. Mapping forest structure for wildlife habitat analysis using multi-sensor (LiDAR, SAR/InSAR, ETM plus, Quickbird) synergy. Remote Sens. Environ. 2006, 102, 63–73. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Stark, S.C.; Leitold, V.; Wu, J.L.; Hunter, M.O.; de Castilho, C.V.; Costa, F.R.C.; McMahon, S.M.; Parker, G.G.; Shimabukuro, M.T.; Lefsky, M.A.; et al. Amazon forest carbon dynamics predicted by profiles of canopy leaf area and light environment. Ecol. Lett. 2012, 15, 1406–1414. [Google Scholar] [CrossRef]
- Rodda, S.R.; Fararoda, R.; Gopalakrishnan, R.; Jha, N.; Réjou-Méchain, M.; Couteron, P.; Barbier, N.; Alfonso, A.; Bako, O.; Bassama, P.; et al. LiDAR-based reference aboveground biomass maps for tropical forests of South Asia and Central Africa. Sci Data 2024, 11, 334. [Google Scholar] [CrossRef] [PubMed]
- Chan, E.P.Y.; Fung, T.; Wong, F.K.K. Estimating above-ground biomass of subtropical forest using airborne LiDAR in Hong Kong. Sci. Rep. 2021, 11, 1751. [Google Scholar] [CrossRef]
- Forkuor, G.; Zoungrana, J.-B.B.; Dimobe, K.; Ouattara, B.; Vadrevu, K.P.; Tondoh, J.E. Above-ground biomass mapping in West African dryland forest using Sentinel-1 and 2 datasets—A case study. Remote Sens. Environ. 2020, 236, 11496. [Google Scholar] [CrossRef]
- Georgopoulos, N.; Sotiropoulos, C.; Stefanidou, A.; Gitas, I.Z. Total Stem Biomass Estimation Using Sentinel-1 and-2 Data in a Dense Coniferous Forest of Complex Structure and Terrain. Forests 2022, 13, 2157. [Google Scholar] [CrossRef]
- Nizalapur, V.; Jha, C.S.; Madugundu, R. Estimation of above ground biomass in Indian tropical forested area using multi-frequency DLR-ESAR data. Int. J. Geomat. Geosci. 2013, 1, 167–178. [Google Scholar]
- Cartus, O.; Kellndorfer, J.; Walker, W.; Franco, C.; Bishop, J.; Santos, L.; Fuentes, J.M.M. A National, Detailed Map of Forest Aboveground Carbon Stocks in Mexico. Remote Sens. 2014, 6, 5559–5588. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Liu, L.; Li, D.; Zhu, J.; Yu, S. Forest aboveground biomass estimation in Zhejiang Province using the integration of Landsat TM and ALOS PALSAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 1–15. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics Corner: A guide to appropriate use of Correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and Evaluation of Three Methods for Estimating Forest above Ground Biomass Using TM and GLAS Data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.D.; Bui, D.T. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Araza, A.; de Bruin, S.; Hein, L.; Herold, M. Spatial predictions and uncertainties of forest carbon fluxes for carbon accounting. Sci. Rep. 2023, 13, 12704. [Google Scholar] [CrossRef]



| LiDAR Metrics | Abbreviation | Definition |
|---|---|---|
| Canopy height metric | Hmean, | Mean height above 2 m. |
| Hmax | Maximum height. | |
| Hsd | Standard deviation of height above 2 m. | |
| Hvar | Variance of height above 2 m. | |
| Hcv | Coefficient of height variation above 2 m. | |
| Hp | Percentiles (50th, 55th, 60th, …, 85th, 90th, 95th) with a 5-unit height interval distribution above 2 m. | |
| Canopy cover metric | LADa_b | The density of leaf area within the height range of a_b (2_10, 10_20, or 20_30). |
| PDa_b | Ratio of first returns within a height range of a_b (2_10, 10_20, or 20_30) to the total number of first returns. | |
| CT | Canopy thickness above 2 m, H90th–H10th. | |
| CRR | Canopy relief ratio above 2 m. | |
| CCmean | Canopy cover above the mean height above 2 m. |
| Satellite | Data Scenarios | Predictor | Formula/Definition |
|---|---|---|---|
| Sentinel-1A (27 September 2018) | SAR Variables | VV | Vertical emission–vertical receipt |
| VH | Vertical emission–horizontal receipt | ||
| VV + VH | Sum | ||
| VV − VH | Difference | ||
| VV/VH | Cross-ratio | ||
| Sentinel-2B (2 October 2018) | Multispectral Bands | Band2 | Blue; central wave length (CWL): 490 nm; spatial resolution (SP):10 m |
| Band3 | Green; CWL: 560 nm; SP:10 m | ||
| Band4 | Red (R); CWL: 660 nm; SP:10 m | ||
| Band5 | Red Edge1 (Edge1); CWL: 705 nm; SP:20 m | ||
| Band6 | Red Edge2 (Edge2); CWL: 705 nm; SP:20 m | ||
| Band7 | Red Edge3 (Edge3); CWL: 705 nm; SP:20 m | ||
| Band8 | Near infrared; CWL: 842 nm; SP:10 m | ||
| Band8A | Narrow NIR; CWL: 842 nm; SP:20 m | ||
| Band11 | SWIR1; CWL: 1610 nm; SP:20 m | ||
| Band12 | SWIR2; CWL: 2190 nm; SP:20 m | ||
| Vegetation Indices | SR | ||
| NDVI | |||
| TNDVI | |||
| EVI | |||
| IRECI | |||
| NDVIre1 | |||
| NDVIre2 | |||
| NDVIre3 | |||
| MDI1 | |||
| MDI2 | |||
| Biophysical Variables | LAI | Leaf area index | |
| FAPAR | Fraction of absorbed photosynthetically active radiation | ||
| FVC | Fraction of vegetation cover | ||
| Textural Features | Contrast (CON) | ||
| Dissimilarity (DI) | |||
| Homogeneity (HO) | |||
| Second moment (SM) | |||
| Entropy (EN) | |||
| Mean (ME) | |||
| Variance (VA) | |||
| Correlation (COR) | |||
| Experiment | Data Scenarios | Num. 1 | Data Source | Model |
|---|---|---|---|---|
| 1 | MB | 10 | Sentinel-2B | MLR |
| 2 | VI | 10 | EN | |
| 3 | BV | 3 | SVR-poly | |
| 4 | TF | 8 | SVR-linear | |
| 5 | SV | 5 | Sentinel-1A | KNN |
| 6 | ALL | 23 | Sentinel-2B +Sentinel-1A | BPNN |
| 7 | ALL + TF | 31 | RF | |
| 8 | ALL + SV | 28 | GBT | |
| 9 | ALL + SV + TF | 36 | DMVF |
| Exp. 1 | MLR | EN | SVR-Linear | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Num. 2 | R2 | RMSE | RMSEr | Num. | R2 | RMSE | RMSEr | Num. | R2 | RMSE | RMSEr | |||||
| 1 | 6/10 | 0.568 | 34.592 | 22.7 | 7/10 | 0.562 | 34.811 | 22.8 | 7/10 | 0.577 | 34.220 | 22.4 | ||||
| 2 | 8/10 | 0.567 | 34.637 | 22.7 | 8/10 | 0.551 | 35.280 | 23.1 | 9/10 | 0.561 | 34.884 | 22.9 | ||||
| 3 | 2/3 | 0.496 | 37.367 | 24.5 | 2/3 | 0.497 | 37.334 | 24.5 | 2/3 | 0.454 | 38.881 | 25.5 | ||||
| 4 | 4/8 | 0.083 | 50.384 | 33.0 | 4/8 | 0.083 | 50.393 | 33.0 | 5/8 | 0.095 | 50.060 | 32.8 | ||||
| 5 | 3/5 | 0.067 | 52.819 | 34.6 | 1/5 | 0.029 | 55.935 | 36.7 | 3/5 | 0.032 | 55.238 | 36.2 | ||||
| 6 | 10/23 | 0.603 | 33.167 | 21.7 | 10/23 | 0.586 | 33.879 | 22.2 | 5/23 | 0.591 | 33.674 | 22.1 | ||||
| 7 | 12/31 | 0.604 | 33.106 | 21.7 | 12/31 | 0.586 | 33.842 | 22.2 | 15/31 | 0.593 | 33.591 | 22.0 | ||||
| 8 | 11/28 | 0.605 | 33.062 | 21.7 | 12/28 | 0.588 | 33.774 | 22.1 | 12/28 | 0.594 | 33.539 | 22.0 | ||||
| 9 | 13/36 | 0.607 | 33.006 | 21.6 | 13/36 | 0.589 | 33.738 | 22.1 | 19/36 | 0.595 | 33.508 | 22.0 | ||||
| Exp. | SVR-Poly | KNN | BPNN | |||||||||||||
| Num. | R2 | RMSE | RMSEr | Num. | R2 | RMSE | RMSEr | Num. | R2 | RMSE | RMSEr | |||||
| 1 | 9/10 | 0.585 | 33.913 | 22.2 | 6/10 | 0.527 | 36.187 | 23.7 | 8/10 | 0.599 | 33.333 | 21.9 | ||||
| 2 | 7/10 | 0.571 | 34.476 | 22.6 | 6/10 | 0.580 | 34.105 | 22.4 | 7/10 | 0.578 | 34.169 | 22.4 | ||||
| 3 | 2/3 | 0.499 | 37.260 | 24.4 | 2/3 | 0.507 | 36.965 | 24.2 | 2/3 | 0.554 | 35.140 | 23.0 | ||||
| 4 | 5/8 | 0.135 | 48.933 | 32.1 | 4/8 | 0.103 | 49.847 | 32.7 | 7/8 | 0.121 | 49.330 | 32.3 | ||||
| 5 | 2/5 | 0.061 | 53.021 | 34.8 | 4/5 | 0.058 | 53.038 | 34.8 | 2/5 | 0.075 | 52.520 | 34.4 | ||||
| 6 | 2/23 | 0.598 | 33.380 | 21.9 | 5/23 | 0.574 | 34.330 | 22.5 | 8/23 | 0.604 | 33.098 | 21.7 | ||||
| 7 | 11/31 | 0.595 | 33.488 | 22.0 | 9/31 | 0.591 | 33.659 | 22.1 | 8/31 | 0.617 | 32.572 | 21.4 | ||||
| 8 | 8/28 | 0.600 | 33.292 | 21.8 | 8/28 | 0.574 | 34.344 | 22.5 | 8/28 | 0.610 | 32.881 | 21.6 | ||||
| 9 | 12/36 | 0.600 | 33.265 | 21.8 | 7/36 | 0.590 | 33.701 | 22.1 | 11/36 | 0.621 | 32.416 | 21.3 | ||||
| Exp. | RF | GBT | ||||||||||||||
| Num. | R2 | RMSE | RMSEr | Num. | R2 | RMSE | RMSEr | |||||||||
| 1 | 3/10 | 0.573 | 34.369 | 22.5 | 5/10 | 0.547 | 35.428 | 23.2 | ||||||||
| 2 | 6/10 | 0.566 | 34.664 | 22.7 | 8/10 | 0.589 | 33.725 | 22.1 | ||||||||
| 3 | 2/3 | 0.470 | 38.313 | 25.1 | 2/3 | 0.493 | 37.458 | 24.6 | ||||||||
| 4 | 7/8 | 0.125 | 49.227 | 32.3 | 5/8 | 0.113 | 49.561 | 32.5 | ||||||||
| 5 | 2/5 | 0.068 | 52.785 | 34.6 | 2/5 | 0.072 | 52.617 | 34.5 | ||||||||
| 6 | 8/23 | 0.604 | 33.097 | 21.7 | 5/23 | 0.598 | 33.372 | 21.9 | ||||||||
| 7 | 11/31 | 0.608 | 0.608 | 21.6 | 6/31 | 0.604 | 33.127 | 21.7 | ||||||||
| 8 | 8/28 | 0.600 | 33.279 | 21.8 | 5/28 | 0.603 | 33.176 | 21.7 | ||||||||
| 9 | 12/36 | 0.611 | 32.813 | 21.5 | 19/36 | 0.614 | 32.687 | 21.4 | ||||||||
| Model | Data Scenario | Optimized Parameter | R2 | RMSE | RMSEr |
|---|---|---|---|---|---|
| BPNN | ALL + SV + TF | max_iter = 135, activation function = logistic sigmoid, solver = stochastic gradient descent, learning rate = 0.0013, hidden_layer_sizes = 100, Alpha = 2.02 | 0.625 | 32.207 | 21.1 |
| GBT | ALL + SV + TF | Ntree = 105, max_depth = 2, min_samples_leaf = 2, min_samples_split = 6, learning rate = 0.09, subsampling rate = 0.98 | 0.617 | 32.568 | 21.4 |
| RF | ALL + SV + TF | Ntree = 350, max_depth = 16, min_samples_leaf = 1, min_samples_split = 3 | 0.613 | 32.715 | 21.4 |
| MLR | ALL + SV + TF | None | 0.607 | 33.006 | 21.6 |
| SVR-poly | ALL + SV + TF | C = 1.5, epsilon = 4.5, d = 3, r = 2 | 0.606 | 33.031 | 21.7 |
| KNN | ALL + TF | k = 15, distance function = manhattan_distance | 0.601 | 33.244 | 21.8 |
| SVR-linear | ALL + SV + TF | C = 5.5, epsilon = 0.002 | 0.599 | 33.311 | 21.8 |
| EN | ALL + SV + TF | α = 0.1, ρ = 1, max_iter = 500 | 0.595 | 33.496 | 22.0 |
| Data Scenarios | Num. 1 | Optimal Variables | Parameters of RF | R2 | RMSE | RMSEr |
|---|---|---|---|---|---|---|
| ALL + SV + TF | 21/36 | Band2, Band3, Band5, Band6, Band7, Band8a, Band11, Band12, TNDVI, EVI, NDVIre3, MDI1, LAI, DIS, EN COR, ME, VA, VV + VH, VV − VH, VV | Ntree = 30 max_depth = 12 min_samples_split = 8 min_samples_leaf = 2 | 0.652 | 31.063 | 20.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, W.; Zhang, L.; Zhang, X.; Gao, S.; Gao, H.; Sun, L.; Yan, G. Multi-Decision Vector Fusion Model for Enhanced Mapping of Aboveground Biomass in Subtropical Forests Integrating Sentinel-1, Sentinel-2, and Airborne LiDAR Data. Remote Sens. 2025, 17, 1285. https://doi.org/10.3390/rs17071285
Jiang W, Zhang L, Zhang X, Gao S, Gao H, Sun L, Yan G. Multi-Decision Vector Fusion Model for Enhanced Mapping of Aboveground Biomass in Subtropical Forests Integrating Sentinel-1, Sentinel-2, and Airborne LiDAR Data. Remote Sensing. 2025; 17(7):1285. https://doi.org/10.3390/rs17071285
Chicago/Turabian StyleJiang, Wenhao, Linjing Zhang, Xiaoxue Zhang, Si Gao, Huimin Gao, Lin Sun, and Guangjian Yan. 2025. "Multi-Decision Vector Fusion Model for Enhanced Mapping of Aboveground Biomass in Subtropical Forests Integrating Sentinel-1, Sentinel-2, and Airborne LiDAR Data" Remote Sensing 17, no. 7: 1285. https://doi.org/10.3390/rs17071285
APA StyleJiang, W., Zhang, L., Zhang, X., Gao, S., Gao, H., Sun, L., & Yan, G. (2025). Multi-Decision Vector Fusion Model for Enhanced Mapping of Aboveground Biomass in Subtropical Forests Integrating Sentinel-1, Sentinel-2, and Airborne LiDAR Data. Remote Sensing, 17(7), 1285. https://doi.org/10.3390/rs17071285







