Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests
Abstract
1. Introduction
2. Materials and Methods
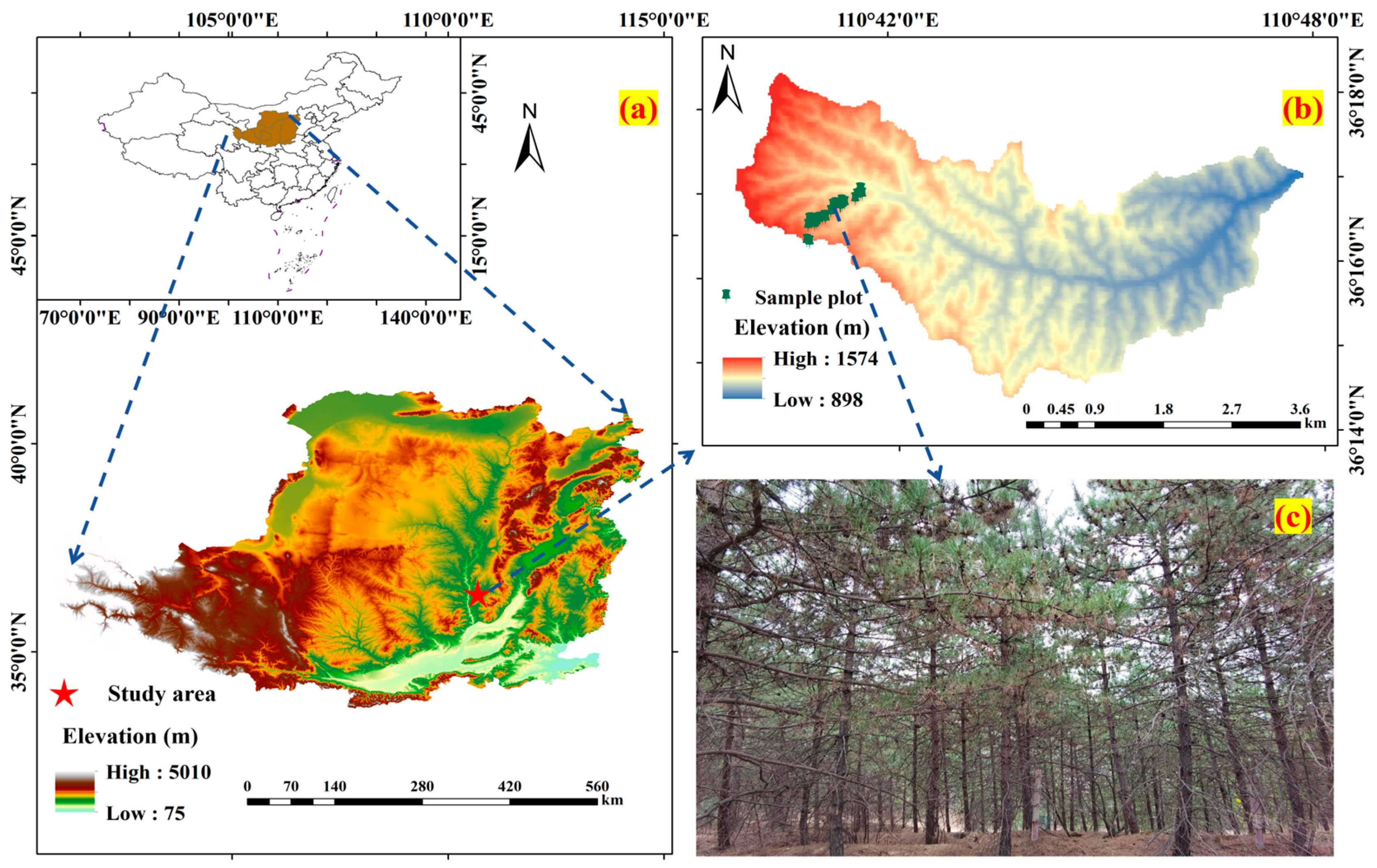
2.1. Study Area
2.2. Survey Data of Sample Plots
2.3. Standard Tree Biomass Modeling
2.4. Terrestrial Laser Scanning Data
2.4.1. Data Acquisition and Processing
2.4.2. Pre-Processing
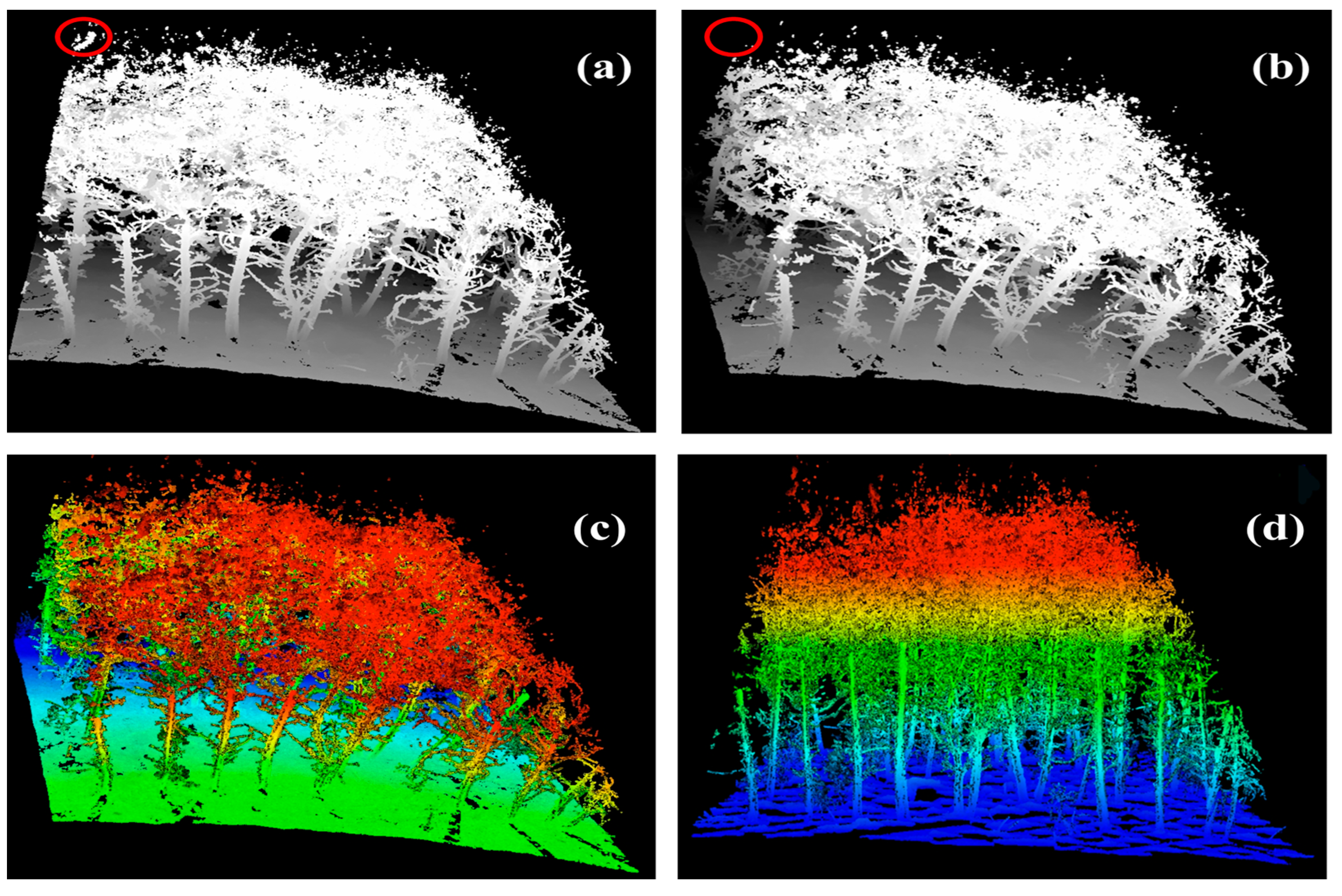
2.4.3. Individual Tree Segmentation and Accuracy Evaluation
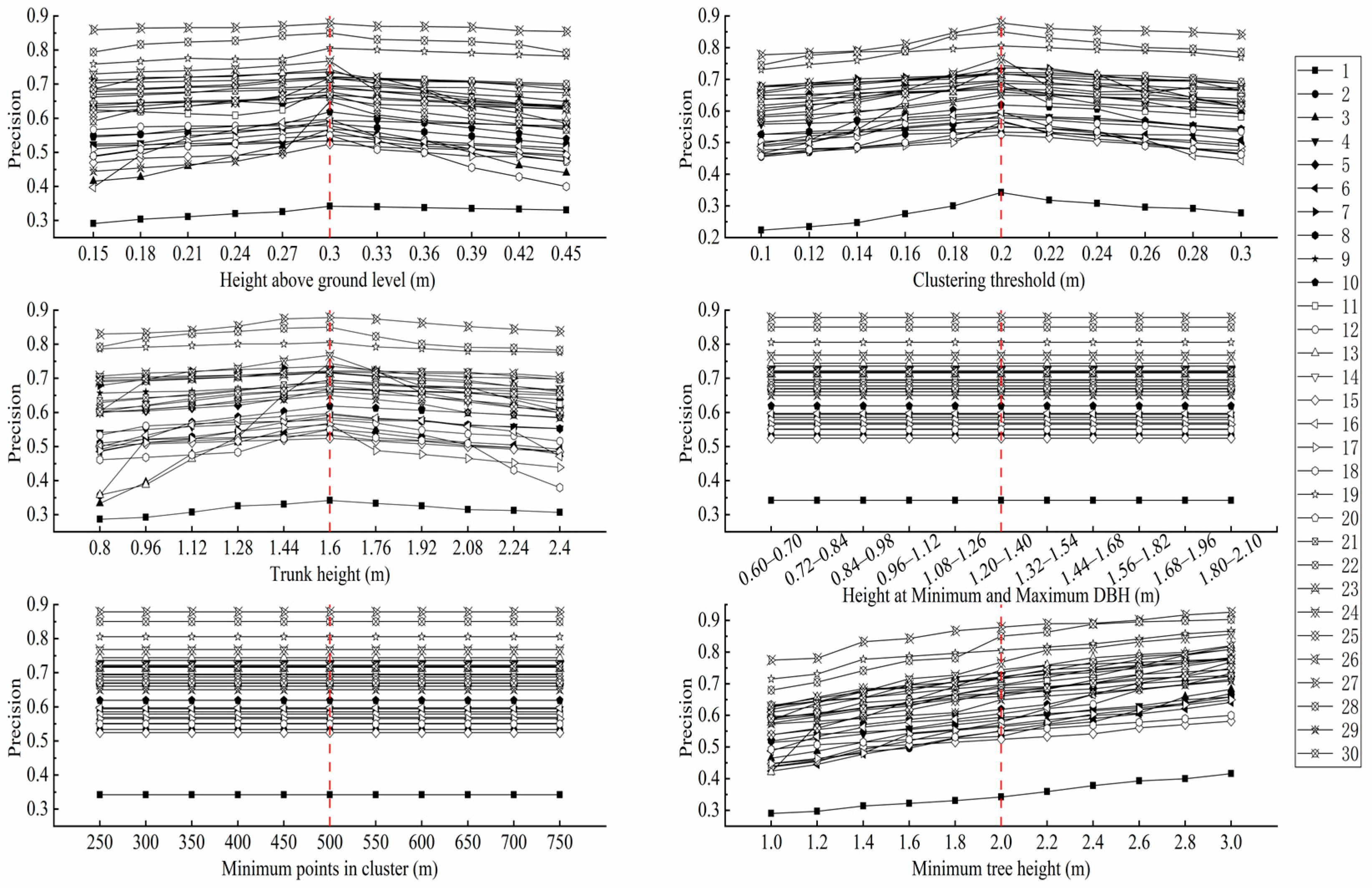
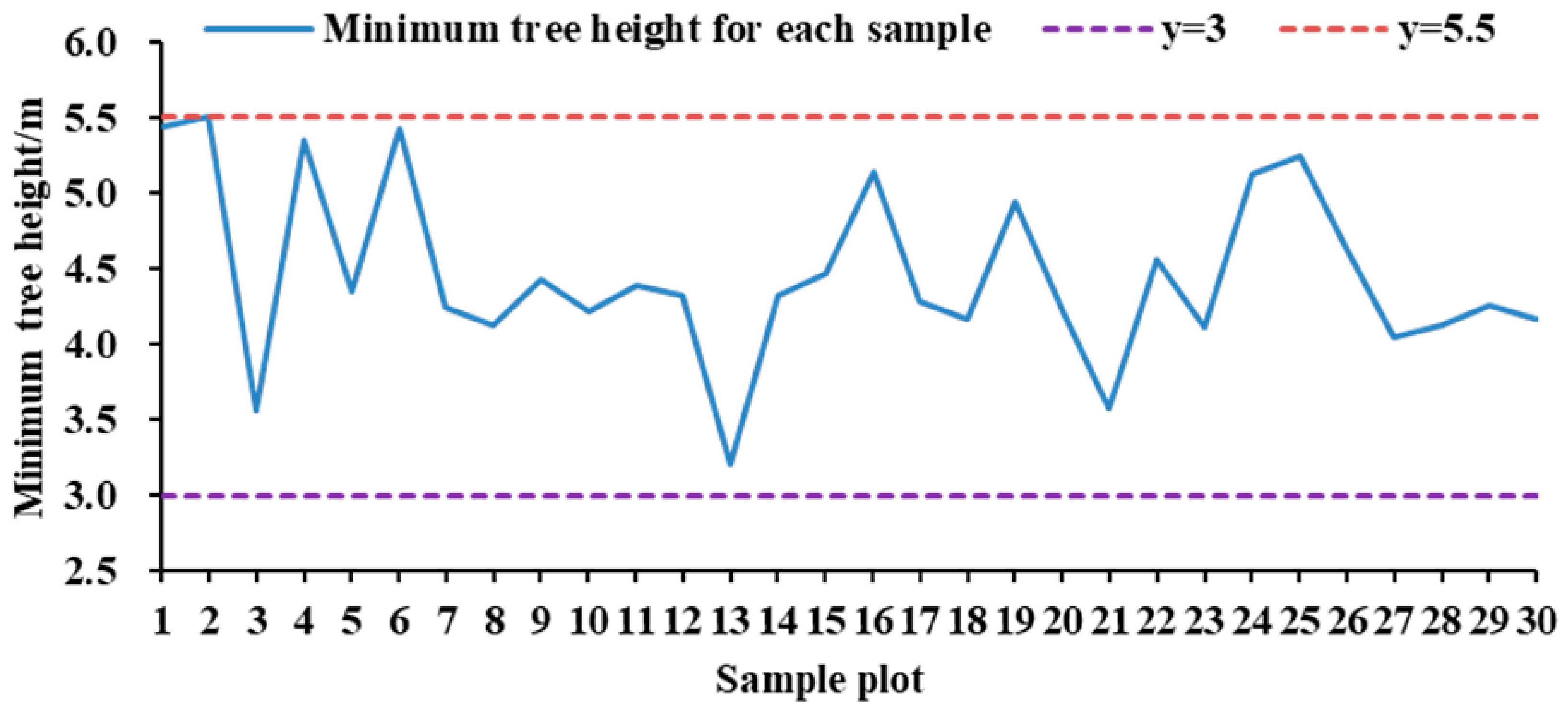
2.4.4. Sensitivity Tuning of Individual Tree Segmentation Parameters
2.4.5. Stand Parameter Extraction and Accuracy Evaluation
3. Results
3.1. Accuracy of Individual Tree Segmentation
3.2. Assessing the Accuracy of Diameter at Breast Height Extraction
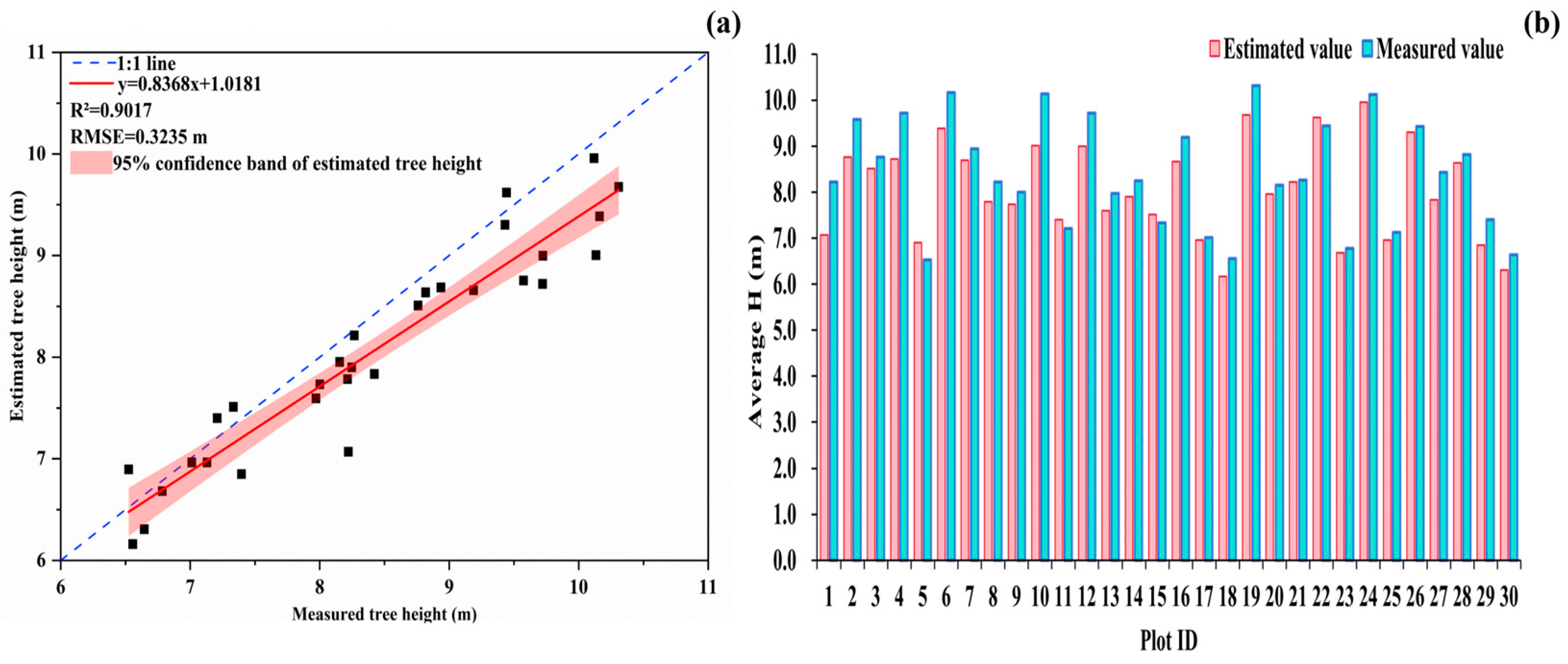
3.3. Assessing the Accuracy of Tree Height Extraction
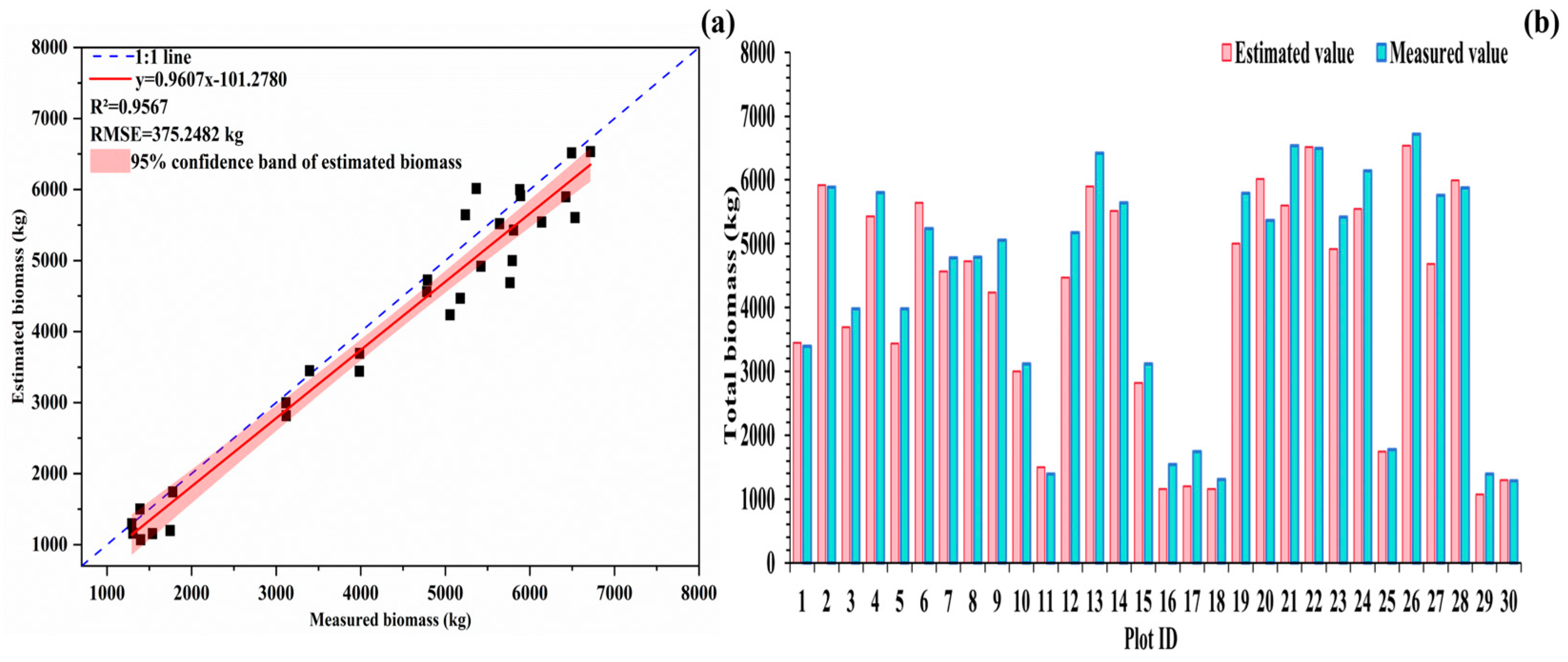
3.4. Biomass Modeling and Accuracy Evaluation
4. Discussion
4.1. Analysis of the Accuracy of Diameter at Breast Height Extraction
4.2. Analysis of the Accuracy of Tree Height Extraction
4.3. Analysis of the Accuracy of Biomass Estimation
4.4. Correlation Analysis of Factors Affecting Biomass
4.5. Research Limitations and Future Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Introduction to LiDAR360 V 5.2.2 Software
Appendix B. Detailed Methodology for Individual Tree Segmentation and Parameter Extraction
Appendix B.1. Denoising
Appendix B.2. Ground Point Classification
Appendix B.3. DEM Generation and Point Cloud Normalization
Appendix B.4. Point Cloud Segmentation Using the Comparison of Shortest Paths Algorithm

- (1)
- The case of non-intersecting tree crowns
- (2)
- Challenges of canopy intersection
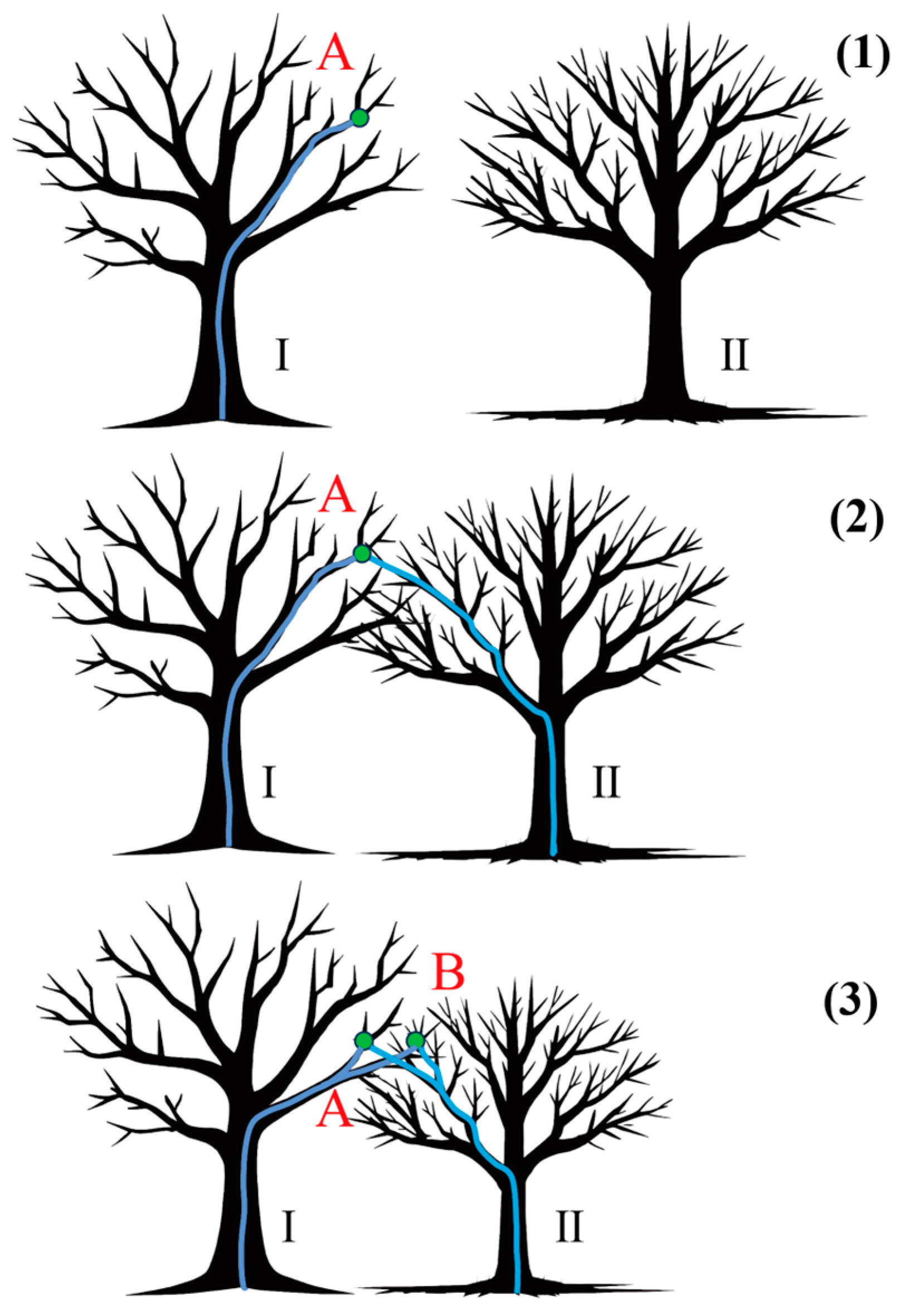
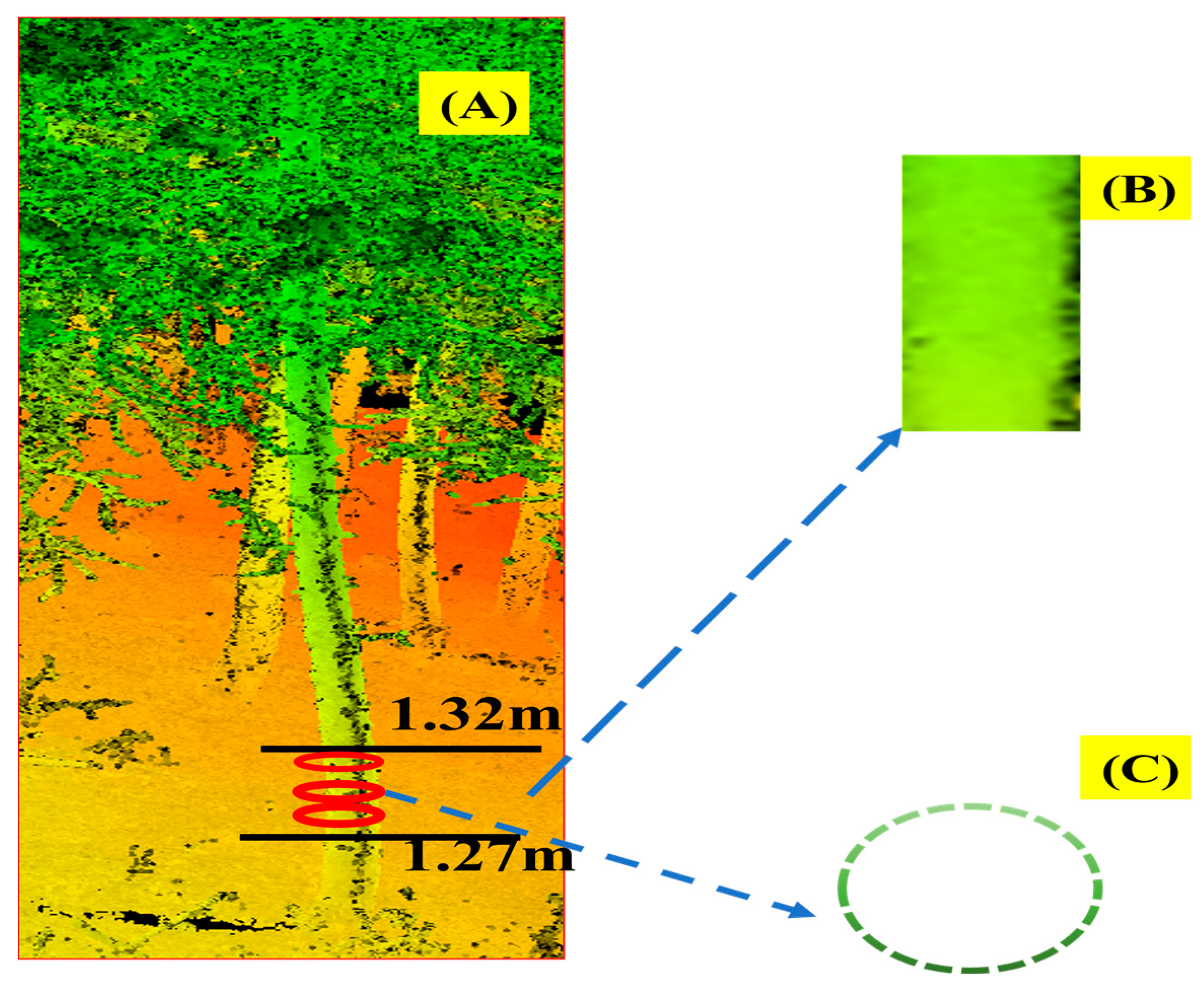
Appendix B.5. Diameter at Breast Height and Tree Height Extraction
References
- Luo, M.; Tian, Y.; Zhang, S.; Huang, L.; Wang, H.; Liu, Z.; Yang, L. Individual Tree Detection in Coal Mine Afforestation Area Based on Improved Faster RCNN in UAV RGB Images. Remote Sens. 2022, 14, 5545. [Google Scholar] [CrossRef]
- Wagner, S.; Seguin Orlando, A.; Leplé, J.C.; Leroy, T.; Lalanne, C.; Labadie, K.; Aury, J.M.; Poirier, S.; Wincker, P.; Plomion, C.; et al. Tracking population structure and phenology through time using ancient genomes from waterlogged white oak wood. Mol. Ecol. 2024, 33, e16859. [Google Scholar] [CrossRef]
- Puliti, S.; Ørka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Haq, S.M.; Waheed, M.; Khoja, A.A.; Amjad, M.S.; Bussmann, R.W.; Ali, K.; Jones, D.A. Measuring forest health at stand level: A multi-indicator evaluation for use in adaptive management and policy. Ecol. Indic. 2023, 150, 110225. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Lehtomäki, M.; Pyörälä, J.; Pfeifer, N.; Holopainen, M.; Brolly, G.; Francesco, P.; Hackenberg, J.; et al. International benchmarking of terrestrial laser scanning approaches for forest inventories. ISPRS J. Photogramm. Remote Sens. 2018, 144, 137–179. [Google Scholar]
- Li, Y.; Li, M.; Li, C.; Liu, Z. Forest aboveground biomass estimation using Landsat 8 and Sentinel-1A data with machine learning algorithms. Sci. Rep. 2020, 10, 9952. [Google Scholar]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Doblas, J.; Shimabukuro, Y.; Sant Anna, S.; Carneiro, A.; Aragão, L.; Almeida, C. Optimizing Near Real-Time Detection of Deforestation on Tropical Rainforests Using Sentinel-1 Data. Remote Sens. 2020, 12, 3922. [Google Scholar] [CrossRef]
- Montesano, P.M.; Rosette, J.; Sun, G.; North, P.; Nelson, R.F.; Dubayah, R.O.; Ranson, K.J.; Kharuk, V. The uncertainty of biomass estimates from modeled ICESat-2 returns across a boreal forest gradient. Remote Sens. Environ. 2015, 158, 95–109. [Google Scholar]
- Shennan, G.; Crabbe, R. A review of spaceborne synthetic aperture radar for invasive alien plant research. Remote Sens. Appl. 2024, 36, 101358. [Google Scholar] [CrossRef]
- Fang, F.; Im, J.; Lee, J.; Kim, K. An improved tree crown delineation method based on live crown ratios from airborne LiDAR data. GIScience Remote Sens. 2016, 53, 402–419. [Google Scholar]
- Adjovu, G.E.; Stephen, H.; James, D.; Ahmad, S. Overview of the Application of Remote Sensing in Effective Monitoring of Water Quality Parameters. Remote Sens. 2023, 15, 1938. [Google Scholar] [CrossRef]
- Du, J.; Watts, J.; Jiang, L.; Lu, H.; Cheng, X.; Duguay, C.; Farina, M.; Qiu, Y.; Kim, Y.; Kimball, J.; et al. Remote Sensing of Environmental Changes in Cold Regions: Methods, Achievements and Challenges. Remote Sens. 2019, 11, 1952. [Google Scholar] [CrossRef]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Surový, P.; Kuželka, K. Acquisition of Forest Attributes for Decision Support at the Forest Enterprise Level Using Remote-Sensing Techniques—A Review. Forests 2019, 10, 273. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S.; et al. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar]
- Picos, J.; Bastos, G.; Míguez, D.; Alonso, L.; Armesto, J. Individual Tree Detection in a Eucalyptus Plantation Using Unmanned Aerial Vehicle (UAV)-LiDAR. Remote Sens. 2020, 12, 885. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopěnka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Calders, K.; Adams, J.; Armston, J.; Bartholomeus, H.; Bauwens, S.; Bentley, L.P.; Chave, J.; Danson, F.M.; Demol, M.; Disney, M.; et al. Terrestrial laser scanning in forest ecology: Expanding the horizon. Remote Sens. Environ. 2020, 251, 112102. [Google Scholar]
- González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sens. 2018, 10, 660. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Lutz, J.A.; Chu, C.; Hu, J.; Shen, G.; Li, B.; Yang, Q.; Lian, J.; Zhang, M.; et al. Drone-acquired data reveal the importance of forest canopy structure in predicting tree diversity. For. Ecol. Manag. 2022, 505, 119945. [Google Scholar]
- Lee, H.; Coifman, B. Using LIDAR to Validate the Performance of Vehicle Classification Stations. J. Intell. Transp. Syst. 2015, 19, 355–369. [Google Scholar]
- White, J.C.; Coops, N.C.; Wulder, M.A.; Vastaranta, M.; Hilker, T.; Tompalski, P. Remote Sensing Technologies for Enhancing Forest Inventories: A Review. Can. J. Remote Sens. 2016, 42, 619–641. [Google Scholar] [CrossRef]
- Xing, J.; Sun, S.; Huang, Q.; Chen, Z.; Zhou, Z. Application of Geoinformatics in Forest Planning and Management. Forests 2024, 15, 439. [Google Scholar] [CrossRef]
- Wang, J.; Shi, K.; Hu, M. Measurement of Forest Carbon Sink Efficiency and Its Influencing Factors Empirical Evidence from China. Forests 2022, 13, 1909. [Google Scholar] [CrossRef]
- Liu, G.; Wang, J.; Dong, P.; Chen, Y.; Liu, Z. Estimating Individual Tree Height and Diameter at Breast Height (DBH) from Terrestrial Laser Scanning (TLS) Data at Plot Level. Forests 2018, 9, 398. [Google Scholar] [CrossRef]
- Latifi, H.; Fassnacht, F.E.; Müller, J.; Tharani, A.; Dech, S.; Heurich, M. Forest inventories by LiDAR data: A comparison of single tree segmentation and metric-based methods for inventories of a heterogeneous temperate forest. Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 162–174. [Google Scholar]
- Mauro, F.; Hudak, A.T.; Fekety, P.A.; Frank, B.; Temesgen, H.; Bell, D.M.; Gregory, M.J.; McCarley, T.R. Regional Modeling of Forest Fuels and Structural Attributes Using Airborne Laser Scanning Data in Oregon. Remote Sens. 2021, 13, 261. [Google Scholar] [CrossRef]
- Hastings, J.H.; Ollinger, S.V.; Ouimette, A.P.; Sanders-DeMott, R.; Palace, M.W.; Ducey, M.J.; Sullivan, F.B.; Basler, D.; Orwig, D.A. Tree Species Traits Determine the Success of LiDAR-Based Crown Mapping in a Mixed Temperate Forest. Remote Sens. 2020, 12, 309. [Google Scholar] [CrossRef]
- Li, W.; Hu, X.; Su, Y.; Tao, S.; Ma, Q.; Guo, Q. A new method for voxel-based modelling of three-dimensional forest scenes with integration of terrestrial and airborneLiDAR data. Methods Ecol. Evol. 2024, 15, 569–582. [Google Scholar]
- Aljumaily, H.; Laefer, D.F.; Cuadra, D.; Velasco, M. Point cloud voxel classification of aerial urban LiDAR using voxel attributes and random forest approach. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103208. [Google Scholar] [CrossRef]
- Parkan, M.; Tuia, D. Estimating Uncertainty of Point-Cloud Based Single-Tree Segmentation with Ensemble Based Filtering. Remote Sens. 2018, 10, 335. [Google Scholar] [CrossRef]
- Hartley, R.J.L.; Jayathunga, S.; Morgenroth, J.; Pearse, G.D. Tree Branch Characterisation from Point Clouds: A Comprehensive Review. Curr. For. Rep. 2024, 10, 360–385. [Google Scholar]
- Junger, C.; Buch, B.; Notni, G. Triangle-Mesh-Rasterization-Projection (TMRP): An Algorithm to Project a Point Cloud onto a Consistent, Dense and Accurate 2D Raster Image. Sensors 2023, 23, 7030. [Google Scholar] [CrossRef]
- Nemmaoui, A.; Aguilar, F.J.; Aguilar, M.A. Benchmarking of Individual Tree Segmentation Methods in Mediterranean Forest Based on Point Clouds from Unmanned Aerial Vehicle Imagery and Low-Density Airborne Laser Scanning. Remote Sens. 2024, 16, 3974. [Google Scholar] [CrossRef]
- Torresan, C.; Carotenuto, F.; Chiavetta, U.; Miglietta, F.; Zaldei, A.; Gioli, B. Individual Tree Crown Segmentation in Two-Layered Dense Mixed Forests from UAV LiDAR Data. Drones 2020, 4, 10. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Li, Y.; Zhao, Y. Voxel segmentation-based 3D building detection algorithm for airborne LIDAR data. PLoS ONE 2018, 13, e0208996. [Google Scholar]
- Zhang, J.; Zhao, X.; Chen, Z.; Lu, Z. A Review of Deep Learning-Based Semantic Segmentation for Point Cloud. IEEE Access 2019, 7, 179118–179133. [Google Scholar]
- Huang, M.; Wei, P.; Liu, X. An Efficient Encoding Voxel-Based Segmentation (EVBS) Algorithm Based on Fast Adjacent Voxel Search for Point Cloud Plane Segmentation. Remote Sens. 2019, 11, 2727. [Google Scholar] [CrossRef]
- Yu, J.; Lei, L.; Li, Z. Individual Tree Segmentation Based on Seed Points Detected by an Adaptive Crown Shaped Algorithm Using UAV-LiDAR Data. Remote Sens. 2024, 16, 825. [Google Scholar] [CrossRef]
- Mu, B.; Shao, F.; Xie, Z.; Chen, H.; Jiang, Q.; Ho, Y. Visual Prompt Multibranch Fusion Network for RGB-Thermal Crowd Counting. IEEE Internet Things J. 2024, 11, 31758–31775. [Google Scholar]
- Tao, S.; Wu, F.; Guo, Q.; Wang, Y.; Li, W.; Xue, B.; Hu, X.; Li, P.; Tian, D.; Li, C.; et al. Segmenting tree crowns from terrestrial and mobile LiDAR data by exploring ecological theories. ISPRS J. Photogramm. Remote Sens. 2015, 110, 66–76. [Google Scholar]
- Fan, G.; Nan, L.; Dong, Y.; Su, X.; Chen, F. AdQSM: A New Method for Estimating Above-Ground Biomass from TLS Point Clouds. Remote Sens. 2020, 12, 3089. [Google Scholar] [CrossRef]
- Palace, M.; Sullivan, F.B.; Ducey, M.; Herrick, C. Estimating Tropical Forest Structure Using a Terrestrial Lidar. PLoS ONE 2016, 11, e0154115. [Google Scholar]
- Wang, F.; Sun, Y.; Jia, W.; Zhu, W.; Li, D.; Zhang, X.; Tang, Y.; Guo, H. Development of Estimation Models for Individual Tree Aboveground Biomass Based on TLS-Derived Parameters. Forests 2023, 14, 351. [Google Scholar] [CrossRef]
- Tao, S.; Labrière, N.; Calders, K.; Fischer, F.J.; Rau, E.; Plaisance, L.; Chave, J. Mapping tropical forest trees across large areas with lightweight cost-effective terrestrial laser scanning. Ann. For. Sci. 2021, 78, 103. [Google Scholar]
- Kükenbrink, D.; Gardi, O.; Morsdorf, F.; Thürig, E.; Schellenberger, A.; Mathys, L. Above-ground biomass references for urban trees from terrestrial laser scanning data. Ann. Bot. 2021, 128, 709–724. [Google Scholar]
- Choi, H.; Song, Y. Comparing tree structures derived among airborne, terrestrial and mobile LiDAR systems in urban parks. GIScience Remote Sens. 2022, 59, 843–860. [Google Scholar]
- Mao, Z.; Hu, S.; Wang, N.; Long, Y. Precision Evaluation and Fusion of Topographic Data Based on UAVs and TLS Surveys of a Loess Landslide. Front. Earth Sci. 2021, 9, 801293. [Google Scholar]
- Li, P.; Hao, M.; Hu, J.; Gao, C.; Zhao, G.; Chan, F.K.S.; Gao, J.; Dang, T.; Mu, X. Spatiotemporal Patterns of Hillslope Erosion Investigated Based on Field Scouring Experiments and Terrestrial Laser Scanning. Remote Sens. 2021, 13, 1674. [Google Scholar] [CrossRef]
- Zhang, X.; Fu, Y.; Pei, Q.; Guo, J.; Jian, S. Study on the Root Characteristics and Effects on Soil Reinforcement of Slope-Protection Vegetation in the Chinese Loess Plateau. Forests 2024, 15, 464. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, J.; Hu, Y.; Li, Y.; Tang, P.; Gusarov, A.V.; Yu, Y. Effects of land uses and rainfall regimes on surface runoff and sediment yield in a nested watershed of the Loess Plateau, China. J. Hydrol. Reg. Stud. 2022, 44, 101277. [Google Scholar]
- Fayiah, M.; Kallon, B.F.; Dong, S.; James, M.S.; Singh, S.; Dang, Q. Species Diversity, Growth, Status, and Biovolume of Taia River Riparian Forest in Southern Sierra Leone: Implications for Community-Based Conservation. Int. J. For. Res. 2020, 2020, 2198573. [Google Scholar] [CrossRef]
- Li, Y.; Deng, X.; Huang, Z.; Xiang, W.; Yan, W.; Lei, P.; Zhou, X.; Peng, C. Development and Evaluation of Models for the Relationship between Tree Height and Diameter at Breast Height for Chinese-Fir Plantations in Subtropical China. PLoS ONE 2015, 10, e0125118. [Google Scholar]
- Rijal, B.; Sharma, M. Modelling Diameter at Breast Height Distribution for Eight Commercial Species in Natural-Origin Mixed Forests of Ontario, Canada. Forests 2024, 15, 977. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Song, W.; Xu, H. Point Cloud Denoising and Feature Preservation: An Adaptive Kernel Approach Based on Local Density and Global Statistics. Sensors 2024, 24, 1718. [Google Scholar] [CrossRef]
- Dong, Y.; Cui, X.; Zhang, L.; Ai, H. An Improved Progressive TIN Densification Filtering Method Considering the Density and Standard Variance of Point Clouds. ISPRS Int. J. Geo-Inf. 2018, 7, 409. [Google Scholar] [CrossRef]
- Hui, Z.; Hu, Y.; Yevenyo, Y.; Yu, X. An Improved Morphological Algorithm for Filtering Airborne LiDAR Point Cloud Based on Multi-Level Kriging Interpolation. Remote Sens. 2016, 8, 35. [Google Scholar] [CrossRef]
- Hahsler, M.; Piekenbrock, M.; Doran, D. dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 1–30. [Google Scholar] [CrossRef]
- Xu, Z.; Shen, X.; Cao, L. Extraction of Forest Structural Parameters by the Comparison of Structure from Motion (SfM) and Backpack Laser Scanning (BLS) Point Clouds. Remote Sens. 2023, 15, 2144. [Google Scholar] [CrossRef]
- Kattenborn, T.; Eichel, J.; Fassnacht, F.E. Convolutional Neural Networks enable efficient, accurate and fine-grained segmentation of plant species and communities from high-resolution UAV imagery. Sci. Rep. 2019, 9, 17656. [Google Scholar]
- Chen, J.; Lan, Z.; Xue, C.; Lan, J.; Liu, Z.; Yang, Y. A Wafer Pre-Alignment Algorithm Based on Weighted Fourier Series Fitting of Circles and Least Squares Fitting of Circles. Micromachines 2023, 14, 956. [Google Scholar] [CrossRef] [PubMed]
- Ritter, T.; Schwarz, M.; Tockner, A.; Leisch, F.; Nothdurft, A. Automatic Mapping of Forest Stands Based on Three-Dimensional Point Clouds Derived from Terrestrial Laser-Scanning. Forests 2017, 8, 265. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [PubMed]
- Mulindwa, D.B.; Du, S.; Liu, Q. Three-Dimensional Instance Segmentation Using the Generalized Hough Transform and the Adaptive n-Shifted Shuffle Attention. Sensors 2024, 24, 7215. [Google Scholar] [CrossRef]
- Heinzel, J.; Huber, M. Tree Stem Diameter Estimation From Volumetric TLS Image Data. Remote Sens. 2017, 9, 614. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Li, M.; Wang, Z.; Hu, C. Deep convolutional neural networks with ensemble learning and transfer learning for capacity estimation of lithium-ion batteries. Appl. Energy 2020, 260, 114296. [Google Scholar] [CrossRef]
- Michałowska, M.; Rapiński, J.; Janicka, J. Tree position estimation from TLS data using hough transform and robust least-squares circle fitting. Remote Sens. Appl. Soc. Environ. 2023, 29, 100863. [Google Scholar]
- Jiao, C.; Heitzler, M.; Hurni, L. A survey of road feature extraction methods from raster maps. Trans. GIS 2021, 25, 2734–2763. [Google Scholar]
- Zhang, F.; Zhang, X.; Xu, Z.; Dong, K.; Li, Z.; Liu, Y. Cleaning of Abnormal Wind Speed Power Data Based on Quartile RANSAC Regression. Energies 2024, 17, 5697. [Google Scholar] [CrossRef]
- Ali, Y.; Awwad, E.; Al-Razgan, M.; Maarouf, A. Hyperparameter Search for Machine Learning Algorithms for Optimizing the Computational Complexity. Processes 2023, 11, 349. [Google Scholar] [CrossRef]
- Martínez-Otzeta, J.M.; Rodríguez-Moreno, I.; Mendialdua, I.; Sierra, B. RANSAC for Robotic Applications: A Survey. Sensors 2023, 23, 327. [Google Scholar]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar]
- Winberg, O.; Pyörälä, J.; Yu, X.; Kaartinen, H.; Kukko, A.; Holopainen, M.; Holmgren, J.; Lehtomäki, M.; Hyyppä, J. Branch information extraction from Norway spruce using handheld laser scanning point clouds in Nordic forests. ISPRS Open J. Photogramm. Remote Sens. 2023, 9, 100040. [Google Scholar]
- Danson, F.M.; Gaulton, R.; Armitage, R.P.; Disney, M.; Gunawan, O.; Lewis, P.; Pearson, G.; Ramirez, A.F. Developing a dual-wavelength full-waveform terrestrial laser scanner to characterize forest canopy structure. Agric. For. Meteorol. 2014, 198–199, 7–14. [Google Scholar]
- Krishna Moorthy, S.M.; Calders, K.; Di Porcia E Brugnera, M.; Schnitzer, S.A.; Verbeeck, H. Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure. Remote Sens. 2018, 10, 810. [Google Scholar] [CrossRef]
- Swinfield, T.; Lindsell, J.A.; Williams, J.V.; Harrison, R.D.; Agustiono; Habibi; Gemita, E.; Schönlieb, C.B.; Coomes, D.A. Accurate Measurement of Tropical Forest Canopy Heights and Aboveground Carbon Using Structure From Motion. Remote Sens. 2019, 11, 928. [Google Scholar] [CrossRef]
- Wang, Y.; Lehtomäki, M.; Liang, X.; Pyörälä, J.; Kukko, A.; Jaakkola, A.; Liu, J.; Feng, Z.; Chen, R.; Hyyppä, J. Is field-measured tree height as reliable as believed—A comparison study of tree height estimates from field measurement, airborne laser scanning and terrestrial laser scanning in a boreal forest. ISPRS J. Photogramm. Remote Sens. 2019, 147, 132–145. [Google Scholar]
- Wang, P.; Li, R.; Bu, G.; Zhao, R. Automated low-cost terrestrial laser scanner for measuring diameters at breast height and heights of plantation trees. PLoS ONE 2019, 14, e0209888. [Google Scholar]
- Srinivasan, S.; Popescu, S.; Eriksson, M.; Sheridan, R.; Ku, N. Terrestrial Laser Scanning as an Effective Tool to Retrieve Tree Level Height, Crown Width, and Stem Diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef]
- Dong, Y.; Fan, G.; Zhou, Z.; Liu, J.; Wang, Y.; Chen, F. Low Cost Automatic Reconstruction of Tree Structure by AdQSM with Terrestrial Close-Range Photogrammetry. Forests 2021, 12, 1020. [Google Scholar] [CrossRef]
- Vandendaele, B.; Martin-Ducup, O.; Fournier, R.A.; Pelletier, G. Evaluation of mobile laser scanning acquisition scenarios for automated wood volume estimation in a temperate hardwood forest using quantitative structural models. Can. J. For. Res. 2024, 54, 774–792. [Google Scholar]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Z.; Zhou, G.; Qiu, Z.; Wu, Z. Site-Specific Allometric Models for Prediction of Above-and Belowground Biomass of Subtropical Forests in Guangzhou, Southern China. Forests 2019, 10, 862. [Google Scholar] [CrossRef]
- Wu, Y.; Gan, X.; Zhou, Y.; Yuan, X. Estimation of Diameter at Breast Height in Tropical Forests Based on Terrestrial Laser Scanning and Shape Diameter Function. Sustainability 2024, 16, 2275. [Google Scholar] [CrossRef]
- Yang, M.; Zhou, X.; Liu, Z.; Li, P.; Tang, J.; Xie, B.; Peng, C. A Review of General Methods for Quantifying and Estimating Urban Trees and Biomass. Forests 2022, 13, 616. [Google Scholar] [CrossRef]
- Li, Y.; Li, C.; Li, M.; Liu, Z. Influence of Variable Selection and Forest Type on Forest Aboveground Biomass Estimation Using Machine Learning Algorithms. Forests 2019, 10, 1073. [Google Scholar] [CrossRef]
- Konôpka, B.; Pajtík, J.; Šebeň, V.; Surový, P.; Merganičová, K. Woody and Foliage Biomass, Foliage Traits and Growth Efficiency in Young Trees of Four Broadleaved Tree Species in a Temperate Forest. Plants 2021, 10, 2155. [Google Scholar] [CrossRef]
- Jin, K.H.; Ye, J.C. Sparse and Low-Rank Decomposition of a Hankel Structured Matrix for Impulse Noise Removal. IEEE Trans. Image Process. 2018, 27, 1448–1461. [Google Scholar]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [PubMed]
- Yang, J.; Luo, B.; Gan, R.; Wang, A.; Shi, S.; Du, L. Multiscale Adjacency Matrix CNN: Learning on Multispectral LiDAR Point Cloud via Multiscale Local Graph Convolution. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2024, 17, 855–870. [Google Scholar]
- Jalalifar, S.A.; Soliman, H.; Sahgal, A.; Sadeghi-Naini, A. A Self-Attention-Guided 3D Deep Residual Network With Big Transfer to Predict Local Failure in Brain Metastasis After Radiotherapy Using Multi-Channel MRI. IEEE J. Transl. Eng. Health Med. JTEHM 2023, 11, 13–22. [Google Scholar]
- Chen, X.; Zhou, B.; Guo, X.; Xie, H.; Liu, Q.; Duncan, J.S.; Sinusas, A.J.; Liu, C. DuDoCFNet: Dual-Domain Coarse-to-Fine Progressive Network for Simultaneous Denoising, Limited-View Reconstruction, and Attenuation Correction of Cardiac SPECT. IEEE Trans. Med. Imaging 2024, 43, 3110–3125. [Google Scholar]
- Janga, B.; Asamani, G.; Sun, Z.; Cristea, N. A Review of Practical AI for Remote Sensing in Earth Sciences. Remote Sens. 2023, 15, 4112. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2021, 13, 77. [Google Scholar]
- Feng, Y.; Su, Y.; Wang, J.; Yan, J.; Qi, X.; Maeda, E.E.; Nunes, M.H.; Zhao, X.; Liu, X.; Wu, X.; et al. L1-Tree: A novel algorithm for constructing 3D tree models and estimating branch architectural traits using terrestrial laser scanning data. Remote Sens. Environ. 2024, 314, 114390. [Google Scholar]




| Plot ID | Altitude /m | Aspect /° | Slope /° | Density /(Tree/hm2) | H/m Avg. ± SD | DBH/cm Avg. ± SD | B/kg |
|---|---|---|---|---|---|---|---|
| 1 | 1098 | 90 | 30 | 1250 | 8.22 ± 1.07 | 14.04 ± 2.08 | 45.73 |
| 2 | 1403 | 270 | 18 | 2175 | 9.57 ± 1.86 | 14.51 ± 3.92 | 53.22 |
| 3 | 1075 | 140 | 25 | 2475 | 8.76 ± 2.04 | 10.69 ± 4.54 | 29.01 |
| 4 | 1354 | 60 | 25 | 2600 | 9.72 ± 1.52 | 13.27 ± 3.57 | 54.46 |
| 5 | 1340 | 180 | 34 | 2875 | 6.52 ± 1.41 | 9.13 ± 3.75 | 18.31 |
| 6 | 1337 | 23 | 30 | 2950 | 10.16 ± 1.76 | 11.92 ± 4.24 | 41.12 |
| 7 | 1368 | 75 | 20 | 3000 | 8.94 ± 1.74 | 10.9 ± 4.11 | 30.13 |
| 8 | 1374 | 120 | 30 | 3000 | 8.21 ± 1.57 | 10.74 ± 3.34 | 36.77 |
| 9 | 1284 | 60 | 25 | 3150 | 8.00 ± 1.61 | 10.64 ± 3.80 | 26.59 |
| 10 | 1370 | 60 | 20 | 3289 | 10.13 ± 1.79 | 11.90 ± 3.44 | 25.77 |
| 11 | 1350 | 300 | 38 | 3400 | 7.21 ± 1.86 | 10.43 ± 4.25 | 24.00 |
| 12 | 1215 | 300 | 16 | 3575 | 9.72 ± 1.74 | 10.68 ± 3.97 | 37.34 |
| 13 | 1304 | 305 | 16 | 3650 | 7.97 ± 1.39 | 11.04 ± 3.66 | 36.89 |
| 14 | 1275 | 60 | 27 | 3650 | 8.25 ± 1.59 | 10.42 ± 3.66 | 27.83 |
| 15 | 1350 | 300 | 38 | 3822 | 7.33 ± 1.63 | 9.90 ± 3.60 | 31.11 |
| 16 | 1290 | 171 | 29 | 4000 | 9.19 ± 1.26 | 10.92 ± 3.54 | 26.84 |
| 17 | 1240 | 118 | 26 | 4000 | 7.01 ± 1.31 | 10.81 ± 2.56 | 33.74 |
| 18 | 1199 | 185 | 31 | 4000 | 6.56 ± 1.33 | 9.49 ± 2.72 | 20.38 |
| 19 | 1301 | 60 | 22 | 4000 | 10.31 ± 1.79 | 11.00 ± 3.72 | 42.14 |
| 20 | 1357 | 120 | 30 | 4100 | 8.15 ± 1.66 | 9.48 ± 3.91 | 20.72 |
| 21 | 1279 | 67 | 22 | 4200 | 8.27 ± 1.47 | 10.64 ± 3.36 | 26.95 |
| 22 | 1410 | 90 | 28 | 4225 | 9.44 ± 2.25 | 10.98 ± 3.98 | 57.08 |
| 23 | 1366 | 240 | 30 | 4425 | 6.78 ± 1.58 | 8.88 ± 3.18 | 14.45 |
| 24 | 1252 | 200 | 36 | 4475 | 10.12 ± 1.99 | 10.67 ± 3.73 | 29.26 |
| 25 | 1340 | 180 | 14 | 4500 | 7.13 ± 1.36 | 10.29 ± 3.47 | 31.46 |
| 26 | 1277 | 60 | 21 | 5050 | 9.43 ± 1.56 | 10.22 ± 3.70 | 27.19 |
| 27 | 1333 | 303 | 25 | 5250 | 8.42 ± 2.37 | 8.67 ± 4.30 | 38.63 |
| 28 | 1307 | 180 | 25 | 5550 | 8.82 ± 2.09 | 8.86 ± 3.72 | 26.42 |
| 29 | 1277 | 120 | 20 | 5800 | 7.40 ± 1.26 | 7.97 ± 3.64 | 14.69 |
| 30 | 1273 | 192 | 24 | 5900 | 6.64 ± 1.17 | 7.51 ± 3.37 | 20.74 |
| Number | Equation Form | Parameters | Number | Equation Form | Parameters |
|---|---|---|---|---|---|
| 1 | 7 | ||||
| 2 | 8 | ||||
| 3 | 9 | ||||
| 4 | 10 | ||||
| 5 | 11 | ||||
| 6 | 12 |
| System Parameter | RIEGL VZ-2000i |
|---|---|
| Emission frequency | 1200 KHz |
| Wavelength | (NIR)1550 nm |
| Accuracy/repeatability | 5 mm/3 mm |
| Maximum range | 2500 m |
| Minimum distance | 1 m |
| Scanning field ofview | 100° × 360° |
| Scanning speed | 1,200,000 |
| Input voltage | 11–34 VDC |
| Power | Standard-70 W Max-87 W |
| Weight | 9.8 KG |
| Operating temperature | 0–40 °C |
| Minimum Tree Height/m | Estimated/Trees | Measured/Trees | R | P | F | |||
|---|---|---|---|---|---|---|---|---|
| Tp | Fp | SUM | Fn | |||||
| 3.0 | 3321 | 599 | 3920 | 180 | 3501 | 0.9486 | 0.8472 | 0.8950 |
| 3.5 | 3319 | 408 | 3727 | 182 | 0.9480 | 0.8905 | 0.9184 | |
| 4.0 | 3317 | 239 | 3556 | 184 | 0.9474 | 0.9328 | 0.9401 | |
| 4.5 | 3275 | 131 | 3406 | 232 | 0.9338 | 0.9615 | 0.9475 | |
| 5.0 | 3180 | 81 | 3261 | 321 | 0.9083 | 0.9752 | 0.9406 | |
| 5.5 | 3065 | 49 | 3114 | 436 | 0.8755 | 0.9843 | 0.9267 | |
| Plot ID | Minimum Tree Height/m | |||||
|---|---|---|---|---|---|---|
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |
| 1 | 0.9240 | 0.9292 | 0.9381 | 0.9554 | 0.9969 | 0.9577 |
| 2 | 0.8995 | 0.9139 | 0.9057 | 0.9615 | 0.9651 | 0.9137 |
| 3 | 0.8560 | 0.8898 | 0.9476 | 0.9993 | 0.9680 | 0.9845 |
| 4 | 0.9075 | 0.9048 | 0.9140 | 0.9202 | 0.9328 | 0.9352 |
| 5 | 0.8958 | 0.9280 | 0.9388 | 0.9556 | 0.9698 | 0.9093 |
| 6 | 0.9193 | 0.9501 | 0.9674 | 0.9903 | 0.9935 | 0.9707 |
| 7 | 0.9526 | 0.9731 | 0.9820 | 0.9909 | 0.9897 | 0.8792 |
| 8 | 0.9030 | 0.9241 | 0.9267 | 0.9499 | 0.9583 | 0.9522 |
| 9 | 0.8518 | 0.8830 | 0.9058 | 0.9233 | 0.9302 | 0.9137 |
| 10 | 0.9429 | 0.9634 | 0.9711 | 0.9711 | 0.9902 | 0.9584 |
| 11 | 0.9564 | 0.9469 | 0.9388 | 0.9388 | 0.9410 | 0.9237 |
| 12 | 0.8453 | 0.8850 | 0.9111 | 0.9069 | 0.9231 | 0.9054 |
| 13 | 0.9770 | 0.9798 | 0.9842 | 0.9994 | 0.9966 | 0.9643 |
| 14 | 0.9143 | 0.9402 | 0.9539 | 0.9623 | 0.9716 | 0.9263 |
| 15 | 0.9595 | 0.9785 | 0.9874 | 0.9874 | 0.9954 | 0.9597 |
| 16 | 0.8625 | 0.8777 | 0.9006 | 0.9006 | 0.9227 | 0.9068 |
| 17 | 0.9041 | 0.9041 | 0.9240 | 0.9240 | 0.9240 | 0.9761 |
| 18 | 0.8871 | 0.8871 | 0.9266 | 0.9021 | 0.9230 | 0.9216 |
| 19 | 0.9769 | 0.9866 | 0.9978 | 0.9918 | 0.9918 | 0.9799 |
| 20 | 0.9947 | 0.9982 | 0.9842 | 0.9843 | 0.9677 | 0.9576 |
| 21 | 0.9407 | 0.9427 | 0.9531 | 0.9558 | 0.9631 | 0.9241 |
| 22 | 0.9314 | 0.9532 | 0.9768 | 0.9840 | 0.9952 | 0.9896 |
| 23 | 0.9627 | 0.9754 | 0.9859 | 0.9995 | 0.9882 | 0.9980 |
| 24 | 0.9653 | 0.9922 | 0.9891 | 0.9858 | 0.9999 | 0.9181 |
| 25 | 0.9539 | 0.9609 | 0.9609 | 0.9722 | 0.9722 | 0.9408 |
| 26 | 0.9435 | 0.9658 | 0.9731 | 0.9776 | 0.9827 | 0.9618 |
| 27 | 0.9123 | 0.9241 | 0.9425 | 0.9619 | 0.9810 | 0.9911 |
| 28 | 0.9446 | 0.9318 | 0.9312 | 0.9280 | 0.9266 | 0.9222 |
| 29 | 0.9803 | 0.9803 | 0.9847 | 0.9918 | 0.9738 | 0.8788 |
| 30 | 0.8769 | 0.9251 | 0.9516 | 0.9606 | 0.9961 | 0.9782 |
| Average | 0.9247 | 0.9398 | 0.9518 | 0.9611 | 0.9677 | 0.9433 |
| Plot ID | Minimum Tree Height/m | |||||
|---|---|---|---|---|---|---|
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |
| 1 | 0.7372 | 0.7519 | 0.7934 | 0.8730 | 0.8600 | 0.8873 |
| 2 | 0.8468 | 0.8567 | 0.8866 | 0.9227 | 0.9145 | 0.9279 |
| 3 | 0.7760 | 0.8372 | 0.8942 | 0.9786 | 0.9714 | 0.9411 |
| 4 | 0.9006 | 0.8572 | 0.8652 | 0.8926 | 0.8973 | 0.9134 |
| 5 | 0.9596 | 0.9957 | 0.9789 | 0.9649 | 0.9430 | 0.9098 |
| 6 | 0.8291 | 0.8634 | 0.8796 | 0.9275 | 0.9238 | 0.9295 |
| 7 | 0.8704 | 0.9237 | 0.9450 | 0.9849 | 0.9721 | 0.9455 |
| 8 | 0.9234 | 0.8978 | 0.9106 | 0.9449 | 0.9477 | 0.9701 |
| 9 | 0.8584 | 0.8794 | 0.9146 | 0.9724 | 0.9665 | 0.9360 |
| 10 | 0.7860 | 0.8501 | 0.8634 | 0.8791 | 0.8886 | 0.8886 |
| 11 | 0.9048 | 0.9892 | 0.9960 | 0.9889 | 0.9734 | 0.9519 |
| 12 | 0.8255 | 0.8559 | 0.8970 | 0.9211 | 0.9255 | 0.9319 |
| 13 | 0.8889 | 0.9049 | 0.9031 | 0.9350 | 0.9529 | 0.9158 |
| 14 | 0.8775 | 0.9109 | 0.9282 | 0.9595 | 0.9581 | 0.9653 |
| 15 | 0.9085 | 0.9585 | 0.9903 | 0.9745 | 0.9756 | 0.9636 |
| 16 | 0.8106 | 0.8526 | 0.8862 | 0.9187 | 0.9424 | 0.8988 |
| 17 | 0.9482 | 0.9482 | 0.9751 | 0.9688 | 0.9931 | 0.9931 |
| 18 | 0.8759 | 0.9084 | 0.9084 | 0.9415 | 0.9398 | 0.9857 |
| 19 | 0.8804 | 0.8924 | 0.9166 | 0.9476 | 0.9386 | 0.9330 |
| 20 | 0.8491 | 0.9347 | 0.9515 | 0.9652 | 0.9754 | 0.9427 |
| 21 | 0.9849 | 0.9647 | 0.9698 | 0.9933 | 0.9936 | 0.9700 |
| 22 | 0.9742 | 0.9451 | 0.9957 | 0.9828 | 0.9811 | 0.9637 |
| 23 | 0.9346 | 0.9374 | 0.9510 | 0.9700 | 0.9851 | 0.9803 |
| 24 | 0.9204 | 0.9395 | 0.9544 | 0.9856 | 0.9844 | 0.9993 |
| 25 | 0.9392 | 0.9482 | 0.9567 | 0.9704 | 0.9769 | 0.9878 |
| 26 | 0.9110 | 0.9474 | 0.9602 | 0.9873 | 0.9865 | 0.9786 |
| 27 | 0.8473 | 0.8652 | 0.8904 | 0.9126 | 0.9304 | 0.9472 |
| 28 | 0.9144 | 0.9407 | 0.9551 | 0.9735 | 0.9796 | 0.9895 |
| 29 | 0.8477 | 0.8561 | 0.8701 | 0.9020 | 0.9262 | 0.8628 |
| 30 | 0.8436 | 0.8827 | 0.9046 | 0.9192 | 0.9492 | 0.9349 |
| Average | 0.8791 | 0.9032 | 0.9231 | 0.9486 | 0.9518 | 0.9448 |
| Equation Form | Coefficient | R2 | RMSE/kg | ||
|---|---|---|---|---|---|
| 1.1441 | 1.5462 | 0.2795 | 0.4489 | ||
| 1.2202 | 1.4134 | 0.6733 | 0.3023 | ||
| 0.5521 | 0.5962 | 0.6758 | 0.3012 | ||
| 0.7626 | 0.3260 | 1.3080 | 0.6820 | 0.2983 | |
| 7.0100 | −23.9295 | 0.1499 | 27.6950 | ||
| 7.6899 | −45.2242 | 0.8309 | 12.3530 | ||
| −1.4235 | 8.0544 | −36.1230 | 0.8321 | 12.3070 | |
| 1.8349 | 1.3941 | 0.1416 | 27.8280 | ||
| 0.3456 | 1.9373 | 0.9045 | 9.2816 | ||
| 0.1234 | 0.8089 | 0.8403 | 12.0030 | ||
| 0.7079 | 2.1299 | −0.5351 | 0.9134 | 8.8378 | |
| 0.9270 | 0.7327 | 0.9141 | 8.8055 | ||
| Plot ID | Minimum Tree Height/m | |||||
|---|---|---|---|---|---|---|
| 3.0 | 3.5 | 4.0 | 4.5 | 5.0 | 5.5 | |
| 1 | 0.9730 | 0.9808 | 0.9935 | 0.9836 | 0.8922 | 0.9973 |
| 2 | 0.9201 | 0.9384 | 0.7599 | 0.9955 | 0.9935 | 0.9841 |
| 3 | 0.8353 | 0.8670 | 0.9443 | 0.9266 | 0.8918 | 0.9405 |
| 4 | 0.9212 | 0.9171 | 0.9296 | 0.9353 | 0.9530 | 0.9966 |
| 5 | 0.8004 | 0.8310 | 0.8489 | 0.8643 | 0.8310 | 0.7587 |
| 6 | 0.9860 | 0.9755 | 0.9501 | 0.9222 | 0.9185 | 0.9497 |
| 7 | 0.9159 | 0.9326 | 0.9431 | 0.9549 | 0.9373 | 0.6662 |
| 8 | 0.9398 | 0.9607 | 0.9587 | 0.9870 | 0.9982 | 0.9650 |
| 9 | 0.7568 | 0.8043 | 0.8319 | 0.8378 | 0.8037 | 0.7716 |
| 10 | 0.9291 | 0.9533 | 0.9621 | 0.9621 | 0.9591 | 0.9448 |
| 11 | 0.9483 | 0.9235 | 0.9187 | 0.9187 | 0.9889 | 0.9470 |
| 12 | 0.7916 | 0.8467 | 0.8724 | 0.8634 | 0.8697 | 0.9344 |
| 13 | 0.9975 | 0.9712 | 0.9847 | 0.9182 | 0.8575 | 0.8000 |
| 14 | 0.9236 | 0.9553 | 0.9723 | 0.9786 | 0.9991 | 0.9687 |
| 15 | 0.8812 | 0.9031 | 0.9140 | 0.9028 | 0.8796 | 0.9676 |
| 16 | 0.7121 | 0.7280 | 0.7514 | 0.7514 | 0.7724 | 0.7526 |
| 17 | 0.6669 | 0.6669 | 0.6870 | 0.6870 | 0.6440 | 0.7915 |
| 18 | 0.8679 | 0.8679 | 0.8600 | 0.8901 | 0.9215 | 0.8854 |
| 19 | 0.8254 | 0.8376 | 0.8472 | 0.8632 | 0.8571 | 0.8715 |
| 20 | 0.9415 | 0.9376 | 0.9106 | 0.8793 | 0.8946 | 0.9777 |
| 21 | 0.8715 | 0.8718 | 0.8741 | 0.8579 | 0.8373 | 0.7985 |
| 22 | 0.9428 | 0.9742 | 0.9933 | 0.9963 | 0.9871 | 0.8385 |
| 23 | 0.8827 | 0.8987 | 0.9133 | 0.9077 | 0.8552 | 0.8289 |
| 24 | 0.8806 | 0.9261 | 0.9077 | 0.9027 | 0.9268 | 0.8512 |
| 25 | 0.9639 | 0.9711 | 0.9711 | 0.9820 | 0.9820 | 0.9853 |
| 26 | 0.9321 | 0.9577 | 0.9683 | 0.9732 | 0.9778 | 0.9519 |
| 27 | 0.8084 | 0.8217 | 0.8433 | 0.8132 | 0.7851 | 0.8261 |
| 28 | 0.8915 | 0.8973 | 0.9178 | 0.9797 | 0.9941 | 0.9753 |
| 29 | 0.7735 | 0.7735 | 0.7763 | 0.7667 | 0.7055 | 0.8292 |
| 30 | 0.9018 | 0.9667 | 0.9939 | 0.9969 | 0.9047 | 0.7382 |
| Average | 0.8794 | 0.8952 | 0.9000 | 0.9066 | 0.8939 | 0.8831 |
| Biomass | DBH | H | Number |
|---|---|---|---|
| Single-timber scale | 0.796 ** | 0.359 ** | |
| Sample scale | 0.336 ** | 0.620 ** | 0.884 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, M.; Hu, Y.; Zhao, J.; Li, Y.; Wang, B.; Zhang, J.; Noguchi, H. Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests. Remote Sens. 2025, 17, 1228. https://doi.org/10.3390/rs17071228
He M, Hu Y, Zhao J, Li Y, Wang B, Zhang J, Noguchi H. Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests. Remote Sensing. 2025; 17(7):1228. https://doi.org/10.3390/rs17071228
Chicago/Turabian StyleHe, Miaomiao, Yawei Hu, Jiongchang Zhao, Yang Li, Bo Wang, Jianjun Zhang, and Hideyuki Noguchi. 2025. "Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests" Remote Sensing 17, no. 7: 1228. https://doi.org/10.3390/rs17071228
APA StyleHe, M., Hu, Y., Zhao, J., Li, Y., Wang, B., Zhang, J., & Noguchi, H. (2025). Exploring Stand Parameters Using Terrestrial Laser Scanning in Pinus tabuliformis Plantation Forests. Remote Sensing, 17(7), 1228. https://doi.org/10.3390/rs17071228








