Two-Stage Evapotranspiration Partitioning Under the Generalized Proportionality Hypothesis Based on the Interannual Relationship Between Precipitation and Runoff
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrometeorological and Remote Sensing Data
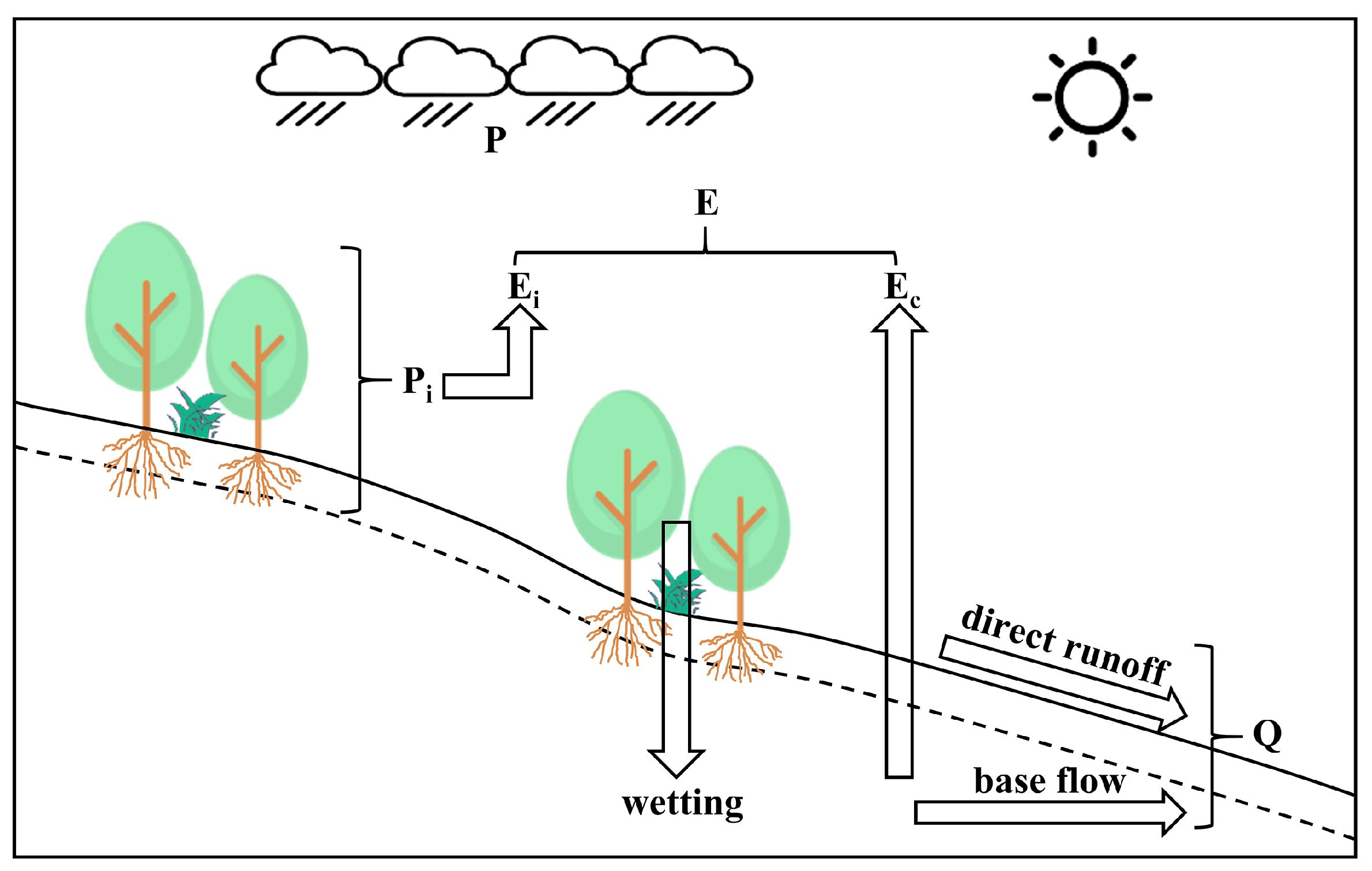
2.2. Generalized Proportionality Hypothesis and Budyko-WT Equation
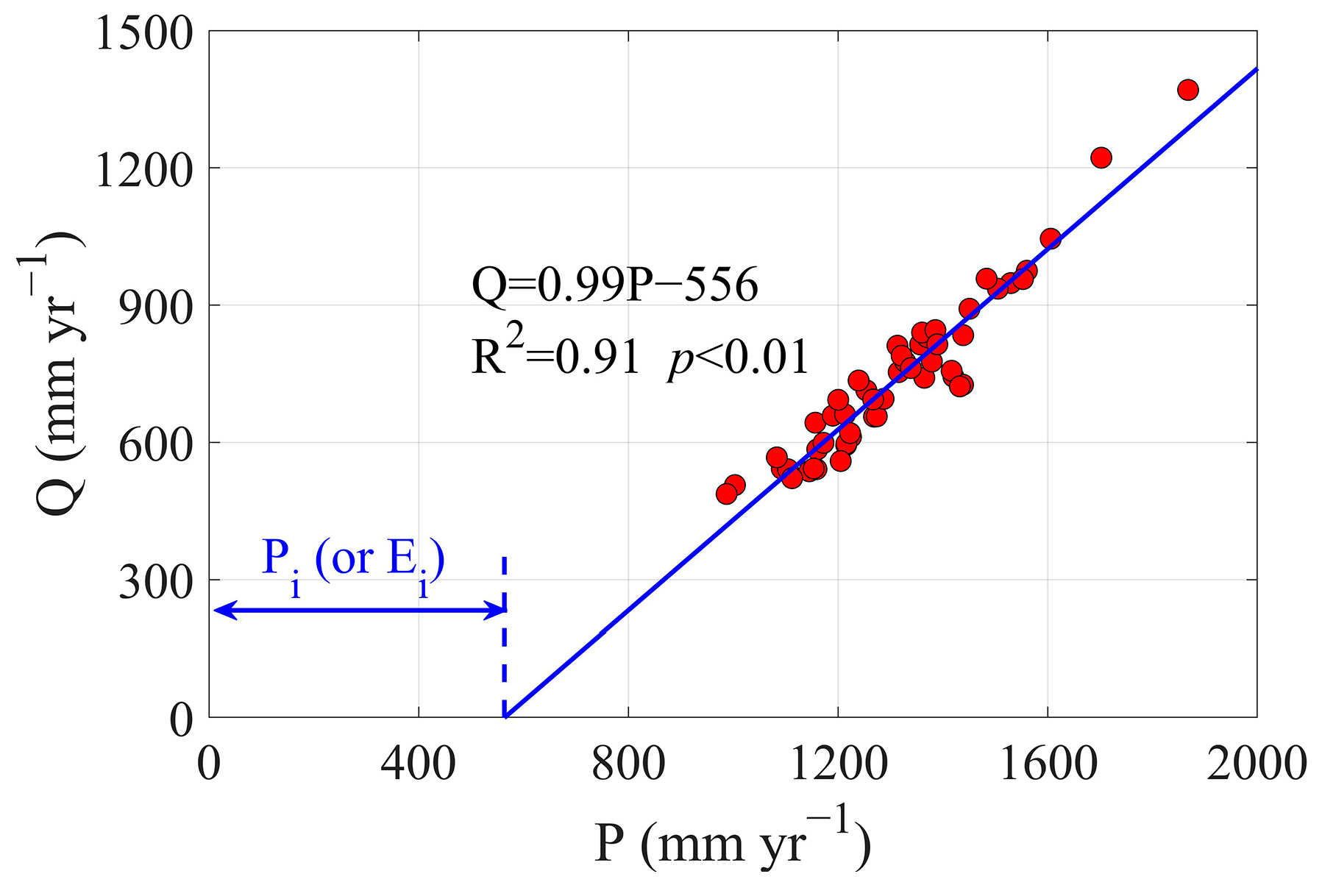
2.3. Ei Estimation Based on Catchment P-Q Relationship
2.4. Estimation of E Components Based on Penman-Monteith-Mu Algorithm
2.5. Comparison of the Inverse and Calculated Budyko-WT Model Parameter
3. Results
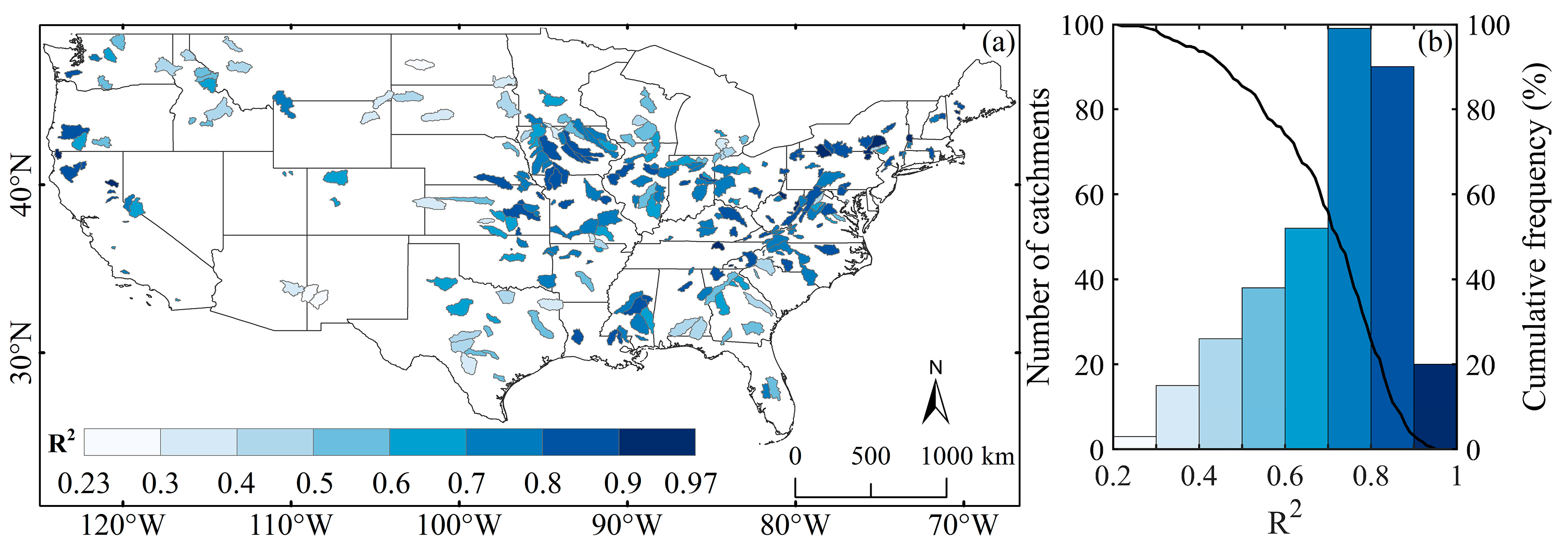
3.1. Linear Characteristics of the P-Q Relationship in MOPEX Catchments
3.2. Spatial Patterns of Ei and Ec in MOPEX Catchments
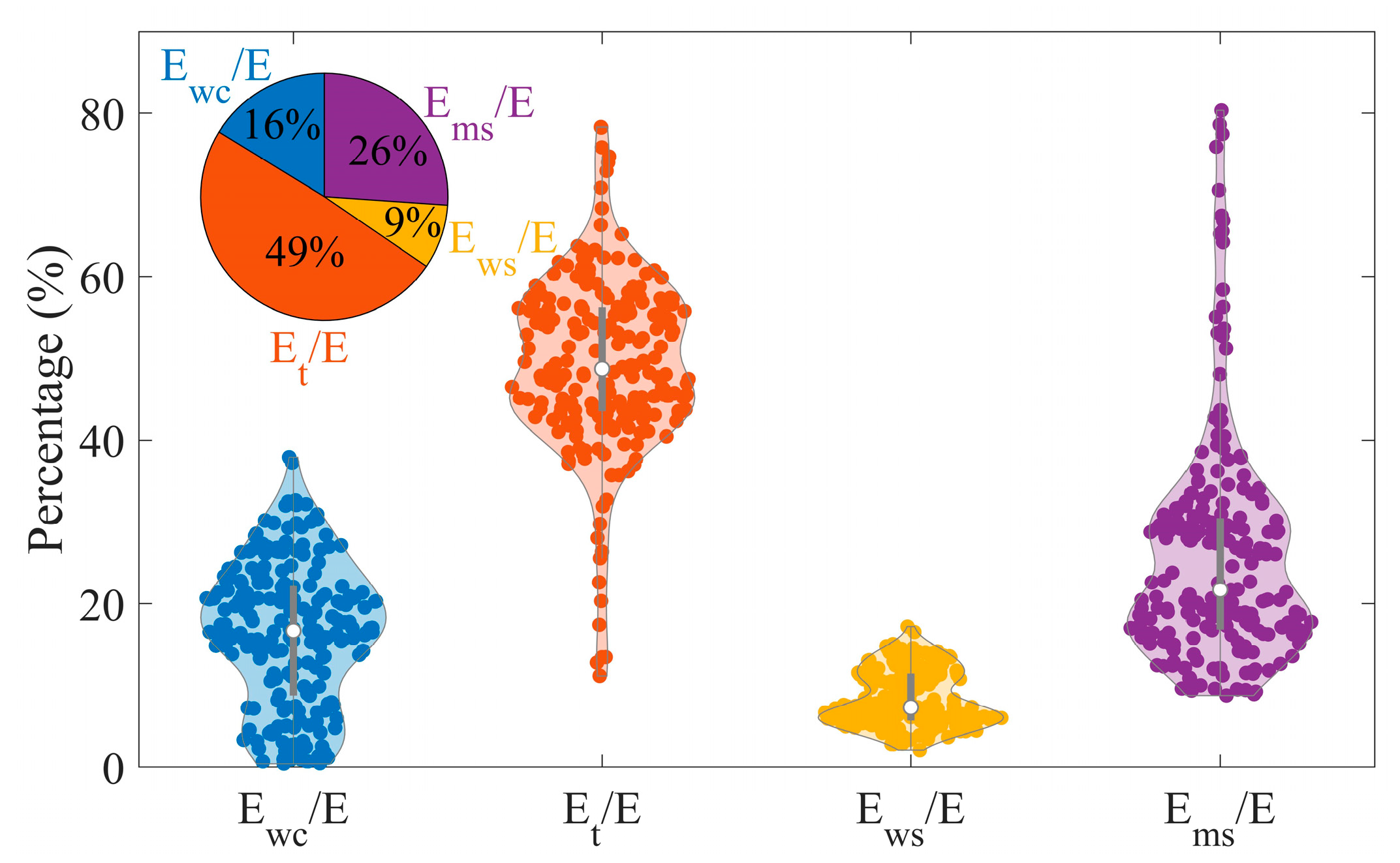
3.3. Relationship of E Components Between Two Partitioning Frameworks
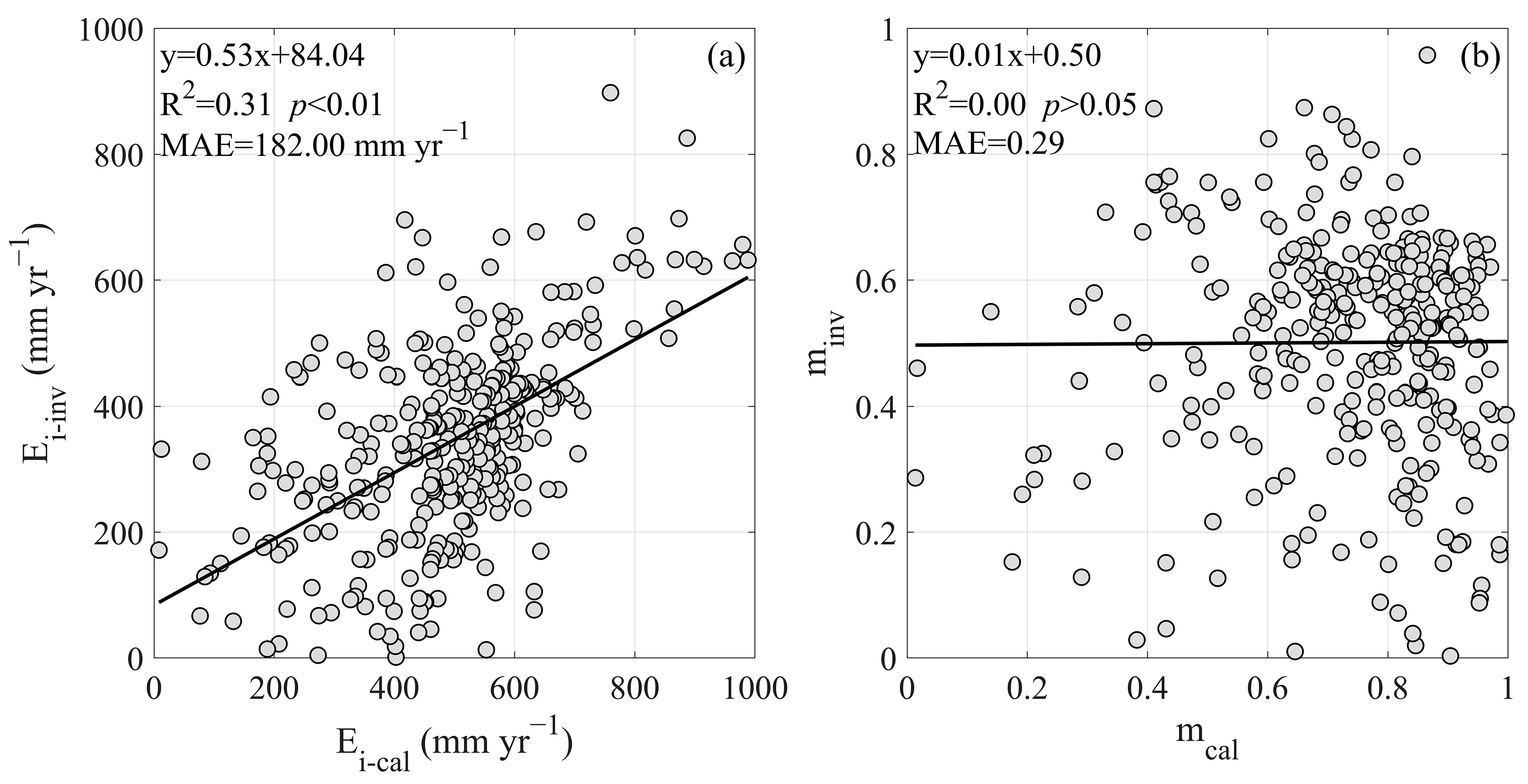
3.4. Comparison Between the Inverse and Calculated Ei/E
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brutsaert, W. Hydrology: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Chang, Y.; Ding, Y.; Zhao, Q.; Zhang, S. Attributing Evapotranspiration Changes with an Extended Budyko Framework Considering Glacier Changes in a Cryospheric-Dominated Watershed. Remote Sens. 2023, 15, 558. [Google Scholar] [CrossRef]
- Yin, L.; Wang, X.; Feng, X.; Fu, B.; Chen, Y. A comparison of SSEBop-model-based evapotranspiration with eight evapotranspiration products in the Yellow River Basin, China. Remote Sens. 2020, 12, 2528. [Google Scholar] [CrossRef]
- Yang, D.; Yang, Y.; Xia, J. Hydrological cycle and water resources in a changing world: A review. Geogr. Sustain. 2021, 2, 115–122. [Google Scholar] [CrossRef]
- Xue, Y.; Liang, H.; Zhang, B.; He, C. Vegetation restoration dominated the variation of water use efficiency in China. J. Hydrol. 2022, 612, 128257. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land–atmosphere interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project—Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef]
- Nguyen, M.N.; Hao, Y.; Baik, J.; Choi, M. Partitioning evapotranspiration based on the total ecosystem conductance fractions of soil, interception, and canopy in different biomes. J. Hydrol. 2021, 603, 126970. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Liang, X.; Lettenmaier, D.P.; Wood, E.F.; Burge, S.J. A simple hydrologically based model of land surface water and energy fluxes for general circulation models. J. Geophys. Res. 1994, 99, 14415–14428. [Google Scholar] [CrossRef]
- Yang, W.; Zhao, Y.; Guan, H.; Tang, Y.; Yang, M.; Wang, Q.; Zhao, J. Estimating spatiotemporal dynamics of evapotranspiration and assessing the cause for its increase in China. Agric. For. Meteorol. 2023, 333, 109394. [Google Scholar] [CrossRef]
- Jiang, F.; Xie, X.; Wang, Y.; Liang, S.; Zhu, B.; Meng, S.; Zhang, X.; Chen, Y.; Liu, Y. Vegetation greening intensified transpiration but constrained soil evaporation on the Loess Plateau. J. Hydrol. 2022, 614, 128514. [Google Scholar] [CrossRef]
- Niu, Z.; He, H.; Zhu, G.; Ren, X.; Zhang, L.; Zhang, K. A spatial-temporal continuous dataset of the transpiration to evapotranspiration ratio in China from 1981–2015. Sci. Data 2020, 7, 369. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, J.; Li, Y.; Bai, P.; Chen, L.; Guo, X.; Xing, Y.; Feng, A.; Yu, W.; Huang, M. Changed evapotranspiration and its components induced by greening vegetation in the Three Rivers Source of the Tibetan Plateau. J. Hydrol. 2024, 633, 130970. [Google Scholar] [CrossRef]
- L’vovich, M.I. World Water Resources and Their Future; American Geophysical Union: Washington, DC, USA, 1979; p. 415. [Google Scholar]
- Wang, D.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D. Modeling seasonal surface runoff and base flow based on the generalized proportionality hypothesis. J. Hydrol. 2015, 527, 367–379. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, D. Evaluating the role of watershed properties in long-term water balance through a Budyko equation based on two-stage partitioning of precipitation. Water Resour. Res. 2017, 53, 4142–4157. [Google Scholar] [CrossRef]
- Abeshu, G.W.; Li, H.Y. Horton Index: Conceptual framework for exploring multi-scale links between catchment water balance and vegetation dynamics. Water Resour. Res. 2021, 57, e2020WR029343. [Google Scholar] [CrossRef]
- Fang, Q.; Wang, G.; Zhang, S.; Peng, Y.; Xue, B.; Cao, Y.; Shrestha, S. A novel ecohydrological model by capturing variations in climate change and vegetation coverage in a semi-arid region of China. Environ. Res. 2022, 211, 113085. [Google Scholar] [CrossRef]
- Pellat, F.P.; Payán, J.G.; Aguilar, V.S.; Rodríguez, A.S.V.; González, M.A.B. Budyko-type models and the proportionality hypothesis in long-term water and energy balances. Water 2022, 14, 3315. [Google Scholar] [CrossRef]
- Tang, Y.; Tang, Q.; Zhang, L. Derivation of interannual climate elasticity of streamflow. Water Resour. Res. 2020, 56, e2020WR027703. [Google Scholar] [CrossRef]
- Fu, J.; Wang, W.; Shao, Q.; Xing, W.; Cao, M.; Wei, J.; Chen, Z.; Nie, W. Improved global evapotranspiration estimates using proportionality hypothesis-based water balance constraints. Remote Sens. Environ. 2022, 279, 113140. [Google Scholar] [CrossRef]
- Fu, B. On the calculation of the evaporation from land surface. Sci. Atmos. Sin. 1981, 5, 23–31. (In Chinese) [Google Scholar]
- Zhang, L.; Hickel, K.; Dawes, W.R.; Chiew, F.H.S.; Western, A.W.; Briggs, P.R. A rational function approach for estimating mean annual evapotranspiration. Water Resour. Res. 2004, 40, W02502. [Google Scholar] [CrossRef]
- Mezentsev, V.S. More on the calculation of average total evaporation. Meteorol. Gidrol. 1955, 5, 24–26. [Google Scholar]
- Choudhury, B.J. Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water-energy balance equation. Water Resour. Res. 2008, 44, W03410. [Google Scholar] [CrossRef]
- Monteith, J.I.L. Evaporation and Environment; University Press: Cambridge, UK, 1965; pp. 205–234. [Google Scholar]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Duan, Q.; Schaake, J.; Andre’assian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L.; et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef]
- Gentine, P.; D’Odorico, P.; Lintner, B.R.; Sivandran, G.; Salvucci, G. Interdependence of climate, soil, and vegetation as constrained by the Budyko curve. Geophys. Res. Lett. 2012, 39, L19404. [Google Scholar] [CrossRef]
- Greve, P.; Gudmundsson, L.; Orlowsky, B.; Seneviratne, S.I. Introducing a probabilistic Budyko framework. Geophys. Res. Lett. 2015, 42, 2261–2269. [Google Scholar] [CrossRef]
- Daly, E.; Calabrese, S.; Yin, J.; Porporato, A. Hydrological spaces of long-term catchment water balance. Water Resour. Res. 2019, 55, 10747–10764. [Google Scholar] [CrossRef]
- Krapu, C.; Borsuk, M. A differentiable hydrology approach for modeling with time-varying parameters. Water Resour. Res. 2022, 58, e2021WR031377. [Google Scholar] [CrossRef]
- Maurer, T.; Avanzi, F.; Glaser, S.D.; Bales, R.C. Drivers of drought-induced shifts in the water balance through a Budyko approach. Hydrol. Earth Syst. Sci. 2022, 26, 589–607. [Google Scholar] [CrossRef]
- Hwang, J.; Devineni, N. An improved Zhang’s dynamic water balance model using Budyko-based snow representation for better streamflow predictions. Water Resour. Res. 2022, 58, e2021WR030203. [Google Scholar] [CrossRef]
- Han, J.; Yang, Y.; Roderick, M.L.; McVicar, T.R.; Yang, D.; Zhang, S.; Beck, H.E. Assessing the steady-state assumption in water balance calculation across global catchments. Water Resour. Res. 2020, 56, e2020WR027392. [Google Scholar] [CrossRef]
- Abatzoglou, J.T. Development of gridded surface meteorological data for ecological applications and modelling. Int. J. Climatol. 2013, 33, 121–131. [Google Scholar] [CrossRef]
- Jia, K.; Yang, L.; Liang, S.; Xiao, Z.; Zhao, X.; Yao, Y.; Zhang, X.; Jiang, B.; Liu, D. Long-Term Global Land Surface Satellite (GLASS) Fractional Vegetation Cover Product Derived From MODIS and AVHRR Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 508–518. [Google Scholar] [CrossRef]
- Liang, S.; Cheng, J.; Jia, K.; Jiang, B.; Liu, Q.; Xiao, Z.; Yao, Y.; Yuan, W.; Zhang, X.; Zhao, X.; et al. The Global Land Surface Satellite (GLASS) Product Suite. Bull. Am. Meteorol. Soc. 2020, 102, E323–E337. [Google Scholar] [CrossRef]
- Cao, S.; Li, M.; Zhu, Z.; Wang, Z.; Zha, J.; Zhao, W.; Duanmu, Z.; Chen, J.; Zheng, Y.; Chen, Y.; et al. Spatiotemporally consistent global dataset of the GIMMS leaf area index (GIMMS LAI4g) from 1982 to 2020. Earth Syst. Sci. Data 2023, 15, 4877–4899. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
- SCS; U.S. Department of Agriculture Soil Conservation Service. National Engineering Handbook, Section 4, Hydrology; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Ponce, V.M.; Shetty, A.V. A conceptual model of catchment water balance: 1. Formulation and calibration. J. Hydrol. 1995, 173, 27–40. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, Y.; McVicar, T.R.; Zhang, L.; Yang, D.; Li, X. A proportionality-based multi-scale catchment water balance model and its global verification. J. Hydrol. 2020, 582, 124446. [Google Scholar] [CrossRef]
- Miao, C.; Ni, J.; Borthwick, A.G.L.; Yang, L. A preliminary estimate of human and natural contributions to the changes in water discharge and sediment load in the Yellow River. Glob. Planet. Change 2011, 76, 196–205. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, X.; Wang, X.; Fu, B. Characterizing drought in terms of changes in the precipitation–runoff relationship: A case study of the Loess Plateau, China. Hydrol. Earth Syst. Sci. 2018, 22, 1749–1766. [Google Scholar] [CrossRef]
- Avanzi, F.; Rungee, J.; Maurer, T.; Bales, R.; Ma, Q.; Glaser, S.; Conklin, M. Climate elasticity of evapotranspiration shifts the water balance of Mediterranean climates during multi-year droughts. Hydrol. Earth Syst. Sci. 2020, 24, 4317–4337. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, L.; Zhang, L.; Qin, S.; Liu, L.; Liu, P.; Liu, Y. Does non-stationarity induced by multiyear drought invalidate the paired-catchment method? Hydrol. Earth Syst. Sci. 2022, 26, 6379–6397. [Google Scholar] [CrossRef]
- Palmroth, S.; Katul, G.G.; Hui, D.; McCarthy, H.R.; Jackson, R.B.; Oren, R. Estimation of long-term basin scale evapotranspiration from streamflow time series. Water Resour. Res. 2010, 46, W10512. [Google Scholar] [CrossRef]
- Gupta, S.C.; Kessler, A.C.; Brown, M.K.; Zvomuya, F. Climate and agricultural land use change impacts on streamflow in the upper midwestern United States. Water Resour. Res. 2015, 51, 5301–5317. [Google Scholar] [CrossRef]
- Fu, G.; Chiew, F.H.; Zheng, H.; Robertson, D.E.; Potter, N.J.; Teng, J.; Post, D.A.; Charles, S.P.; Zhang, L. Statistical analysis of attributions of climatic characteristics to nonstationary rainfall-streamflow relationship. J. Hydrol. 2021, 603, 127017. [Google Scholar] [CrossRef]
- Han, J.; Gao, J.; Luo, H. Changes and implications of the relationship between rainfall, runoff and sediment load in the Wuding River basin on the Chinese Loess Plateau. Catena 2019, 175, 228–235. [Google Scholar] [CrossRef]
- Fu, J.; Wang, W.; Liu, B.; Lu, Y.; Xing, W.; Cao, M.; Zhu, S.; Guan, T.; Wei, J.; Chen, Z. Seasonal divergence of evapotranspiration sensitivity to vegetation changes—A proportionality-hypothesis-based analytical solution. J. Hydrol. 2023, 617, 129055. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Running, S.W.; Mu, Q.; Zhao, M.; Moreno, A. User’s Guide MODIS Global Terrestrial Evapotranspiration (ET) Product (MOD16A2/A3 and Year-end Gap-filled MOD16A2GF/A3GF) NASA Earth Observing System MODIS Land Algorithm (For Collection 6.1); National Aeronautics and Space Administration: Washington, DC, USA, 2021.
- Bai, P. Comparison of remote sensing evapotranspiration models: Consistency, merits, and pitfalls. J. Hydrol. 2023, 617, 128856. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X. Intercomparison and evaluation of three global high-resolution evapotranspiration products across China. J. Hydrol. 2018, 566, 743–755. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Z.; Yu, Q.; Lu, X. Estimation of global transpiration from remotely sensed solar-induced chlorophyll fluorescence. Remote Sens. Environ. 2024, 303, 113998. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Vegetation dynamics and climate seasonality jointly control the interannual catchment water balance in the Loess Plateau under the Budyko framework. Hydrol. Earth Syst. Sci. 2017, 21, 1515–1526. [Google Scholar] [CrossRef]
- Li, D.; Pan, M.; Cong, Z.; Zhang, L.; Wood, E. Vegetation control on water and energy balance within the Budyko framework. Water Resour. Res. 2013, 49, 969–976. [Google Scholar] [CrossRef]
- Kim, D.; Chun, J.A. Revisiting a two-parameter Budyko equation with the complementary evaporation principle for proper consideration of surface energy balance. Water Resour. Res. 2021, 57, e2021WR030838. [Google Scholar] [CrossRef]
- Zhang, L.; Brutsaert, W. Blending the evaporation precipitation ratio with the complementary principle function for the prediction of evaporation. Water Resour. Res. 2021, 57, e2021WR029729. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: Potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr. 2010, 20, 1–18. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D.; Tsevreni, I.; Alexandris, S.G.; Stefanidis, A.D.S.A.B.S.; Nwokolo, S.C. A thorough evaluation of 127 potential evapotranspiration models in two Mediterranean urban green sites. Remote Sens. 2023, 15, 3680. [Google Scholar] [CrossRef]
- Cheng, C.; Liu, W.; Mu, Z.; Zhou, H.; Ning, T. Lumped variable representing the integrative effects of climate and underlying surface system: Interpreting Budyko model parameter from earth system science perspective. J. Hydrol. 2023, 620, 129379. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, F.; Chen, Y.; Dixon, R.N.M. Estimating effects of plantation expansion and climate variability on streamflow for catchments in Australia. Water Resour. Res. 2011, 47, W12539. [Google Scholar] [CrossRef]
- Paschalis, A.; Fatichi, S.; Pappas, C.; Or, D. Covariation of vegetation and climate constrains present and future T/ET variability. Environ. Res. Lett. 2018, 13, 104012. [Google Scholar] [CrossRef]



| Dataset | Spatial Resolution | Temporal Resolution | Time Span | Reference | Data Access Weblink |
|---|---|---|---|---|---|
| MOPEX catchment hydrological data | Catchment scale | Daily | 1948–2003 | [33] | ftp://hydrology.nws.noaa.gov/pub/gcip/mopex/US_Data/ (accessed on 21 October 2022) |
| High-resolution meteorological data gridMET | 4 km | Daily | 1979–2021 | [41] | https://www.climatologylab.org/gridmet.html (accessed on 25 February 2023) |
| GLASS FC | 0.05° | 8 days | 1982–2020 | [42] | http://www.glass.umd.edu/Download.html (accessed on 2 June 2023) |
| GLASS albedo | 0.05° | 8 days | 1982–2020 | [43] | http://www.glass.umd.edu/Download.html (accessed on 2 June 2023) |
| GIMMS LAI | 1/12° | Half month | 1982–2020 | [44,45] | https://zenodo.org/records/8281930 (accessed on 2 June 2023) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Liu, W.; Chen, R.; Mu, Z.; Han, X. Two-Stage Evapotranspiration Partitioning Under the Generalized Proportionality Hypothesis Based on the Interannual Relationship Between Precipitation and Runoff. Remote Sens. 2025, 17, 1203. https://doi.org/10.3390/rs17071203
Cheng C, Liu W, Chen R, Mu Z, Han X. Two-Stage Evapotranspiration Partitioning Under the Generalized Proportionality Hypothesis Based on the Interannual Relationship Between Precipitation and Runoff. Remote Sensing. 2025; 17(7):1203. https://doi.org/10.3390/rs17071203
Chicago/Turabian StyleCheng, Changwu, Wenzhao Liu, Rui Chen, Zhaotao Mu, and Xiaoyang Han. 2025. "Two-Stage Evapotranspiration Partitioning Under the Generalized Proportionality Hypothesis Based on the Interannual Relationship Between Precipitation and Runoff" Remote Sensing 17, no. 7: 1203. https://doi.org/10.3390/rs17071203
APA StyleCheng, C., Liu, W., Chen, R., Mu, Z., & Han, X. (2025). Two-Stage Evapotranspiration Partitioning Under the Generalized Proportionality Hypothesis Based on the Interannual Relationship Between Precipitation and Runoff. Remote Sensing, 17(7), 1203. https://doi.org/10.3390/rs17071203










