Situation Awareness and Tracking Algorithm for Countering Low-Altitude Swarm Target Threats
Abstract
1. Introduction
- The designed digital staring radar achieves higher gain and Doppler resolution through long-term data accumulation, enabling effective separation of moving targets from clutter.
- Additional extension parameters to capture the complex extension state variations of cluster targets, building upon the original random matrix model, is introduced.
- By employing the adaptive RBPF algorithm to approximate the posterior estimation of both motion and extension states, the dimensionality of particle sampling is reduced, enhancing sampling efficiency. Compared to conventional particle filtering, RBPF results in lower estimation variance.
2. Related Works
2.1. Koch Method
2.2. Feldmann Method
2.3. Lan Method
3. Proposed Method
3.1. Improved Extended State Model of Cluster Target Tracking
3.2. Joint State Estimation Based on RBPF
3.3. Improved Resampling with Particles Segmentation Cross Summation of RBPF
3.3.1. Resampling with Particles Grid Segmentation
3.3.2. Resampling with Particles Segmentation Cross Summation of RBPF
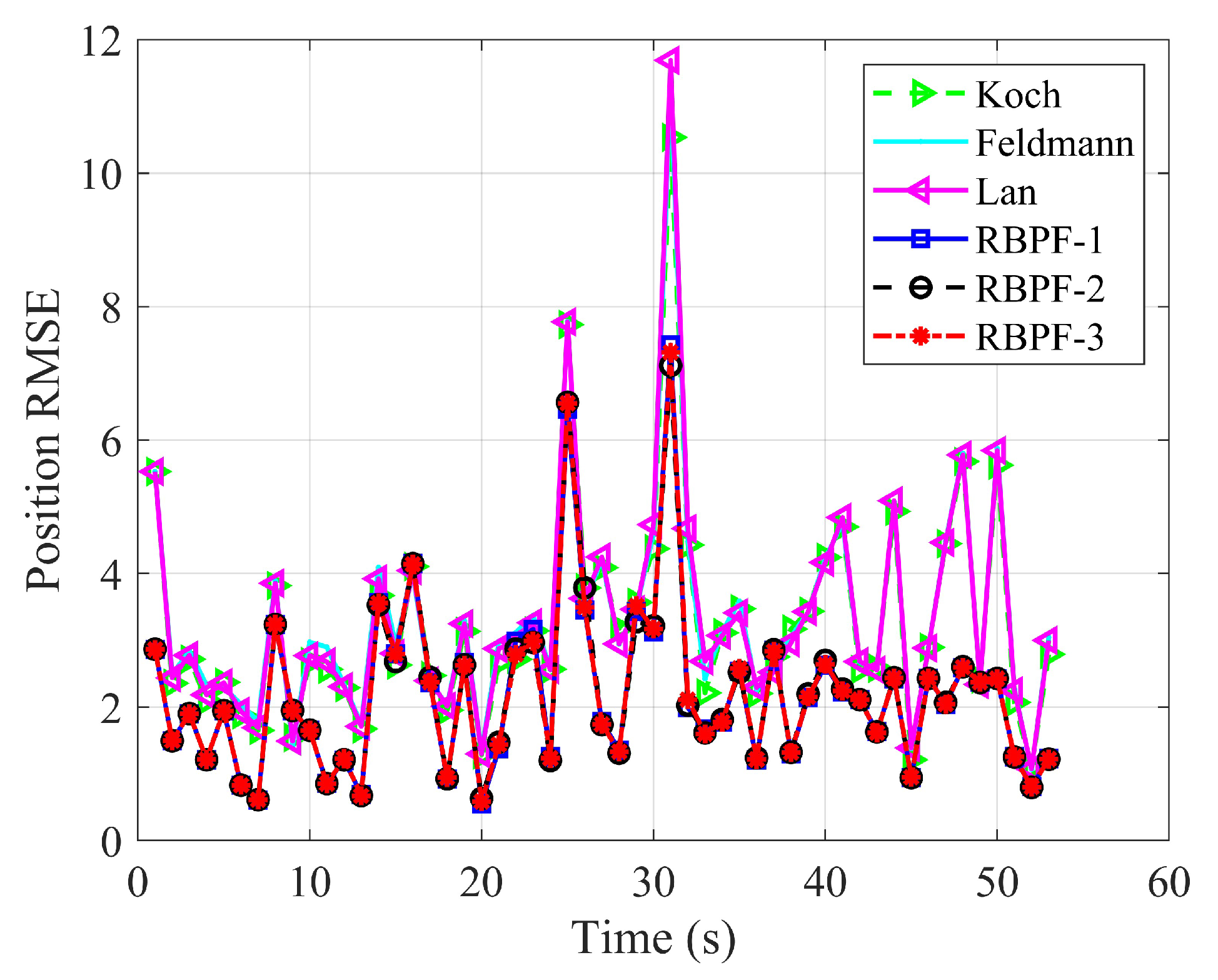
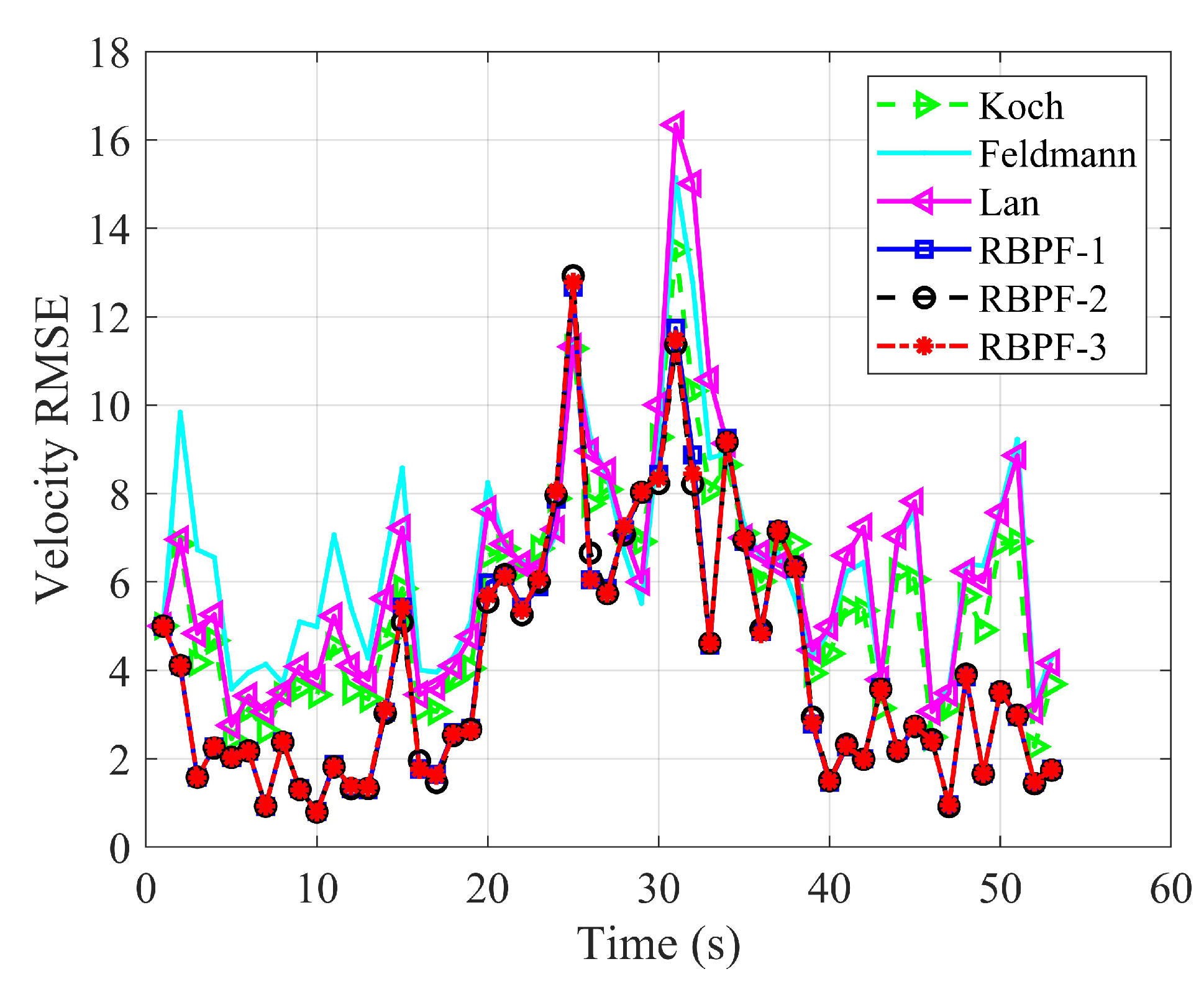
4. Experimental Results and Analysis
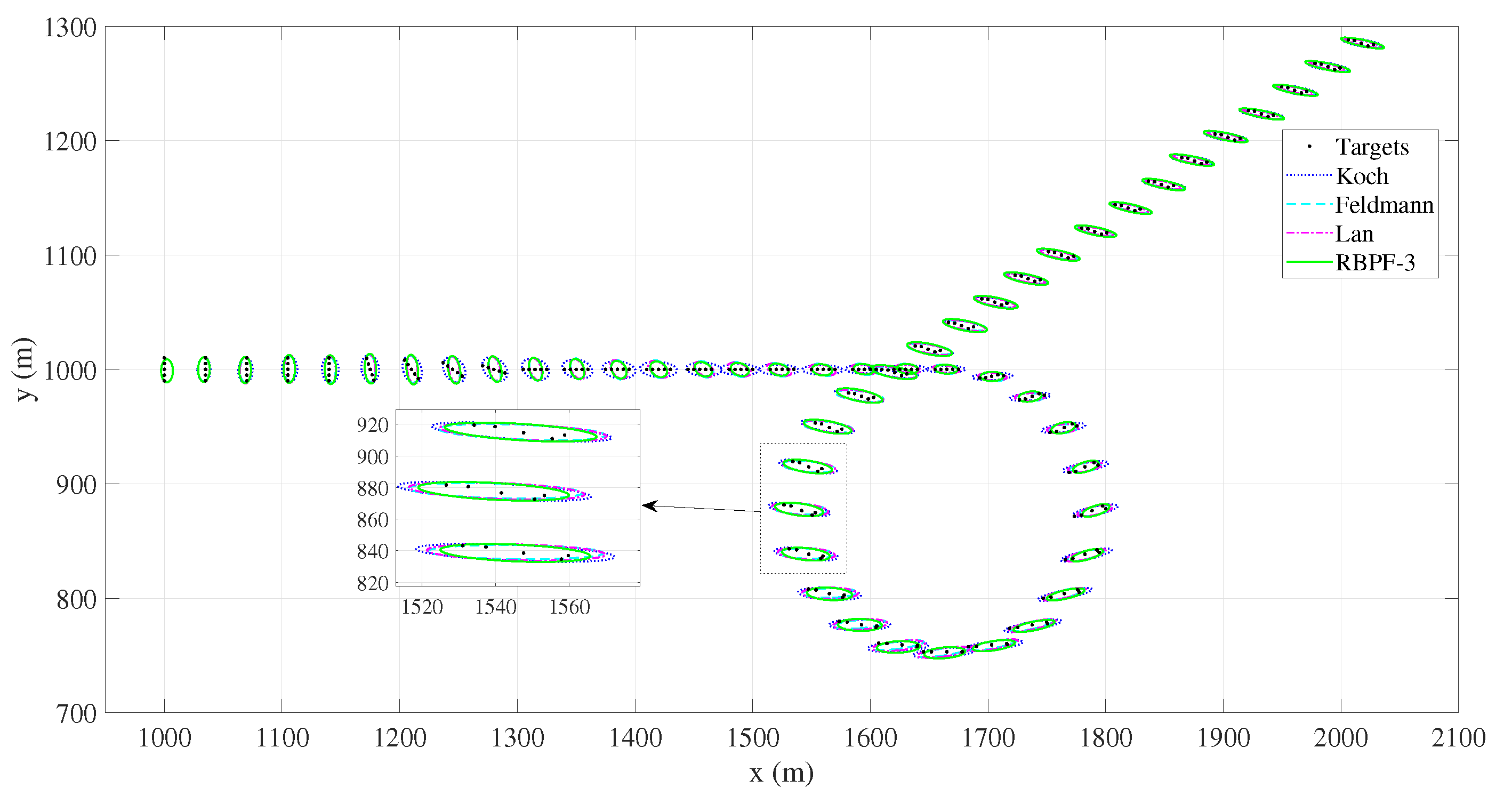
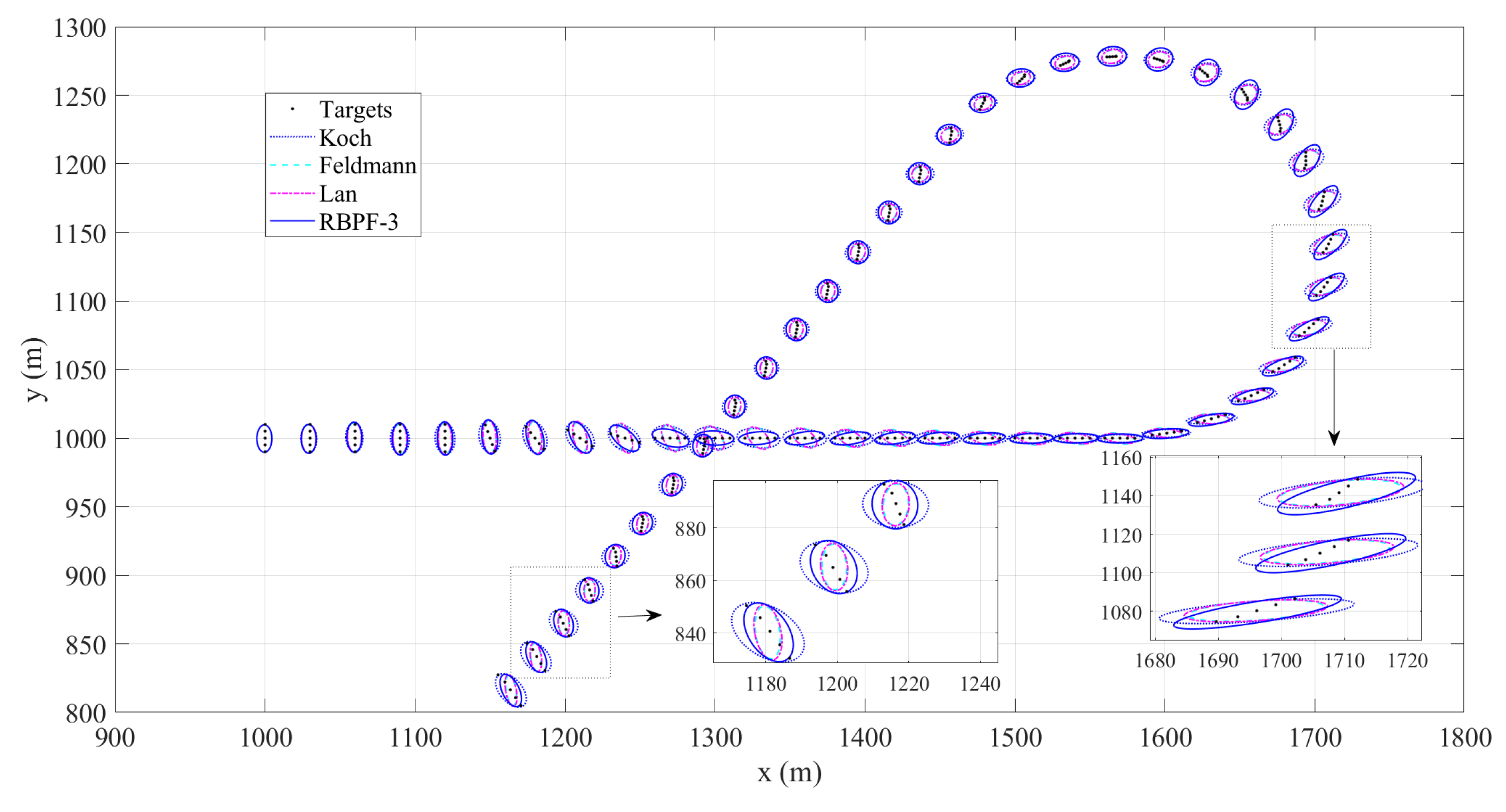
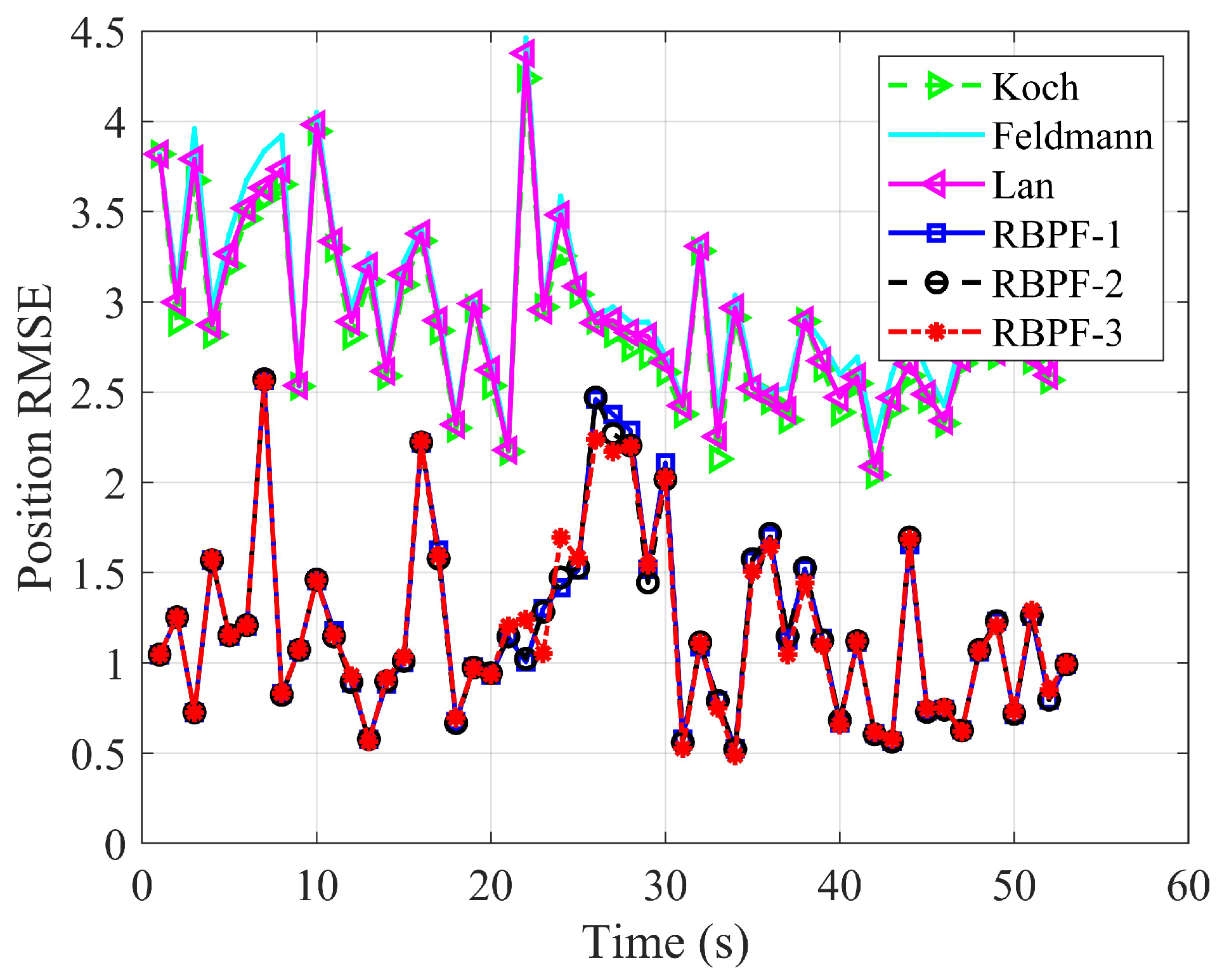
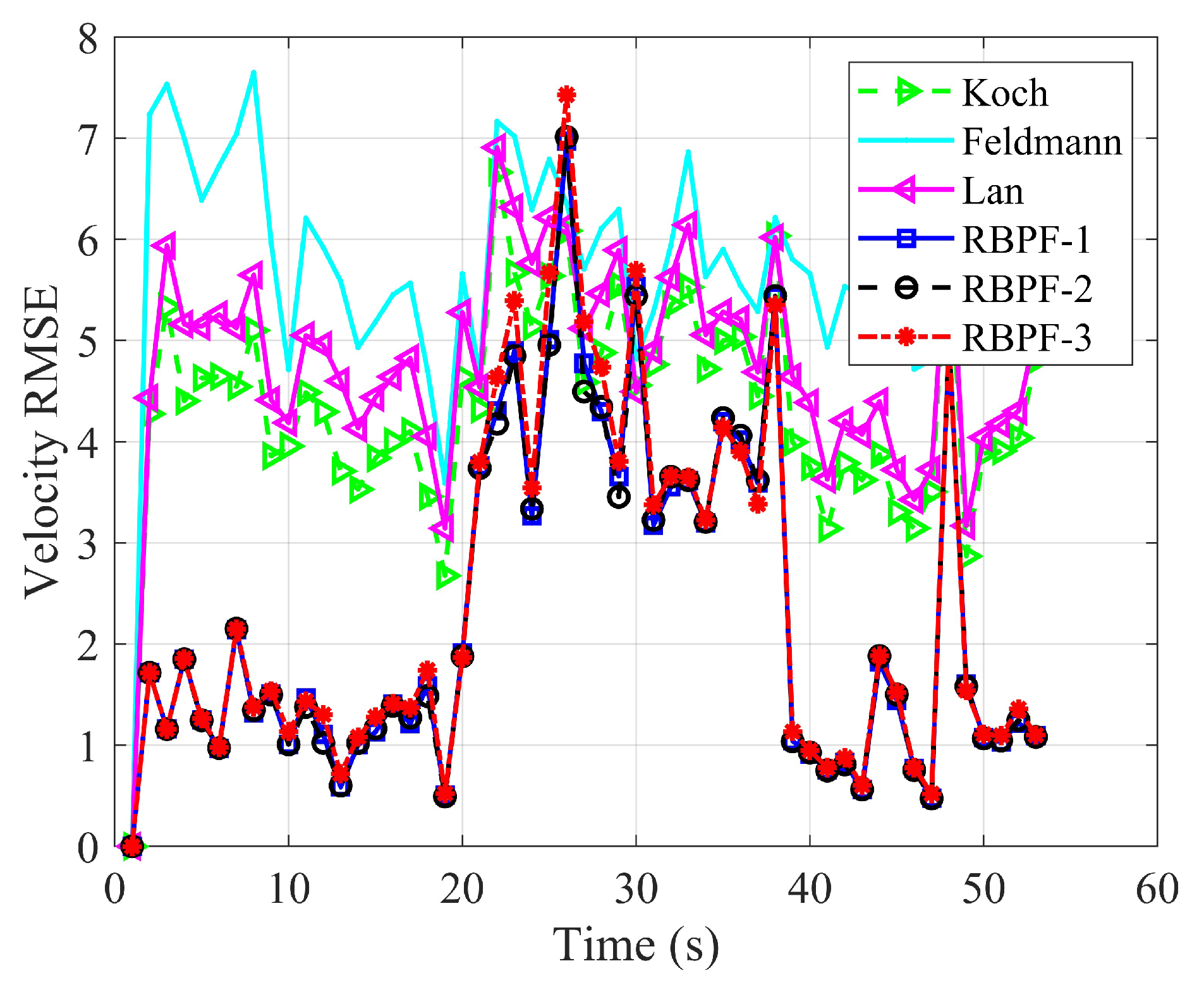
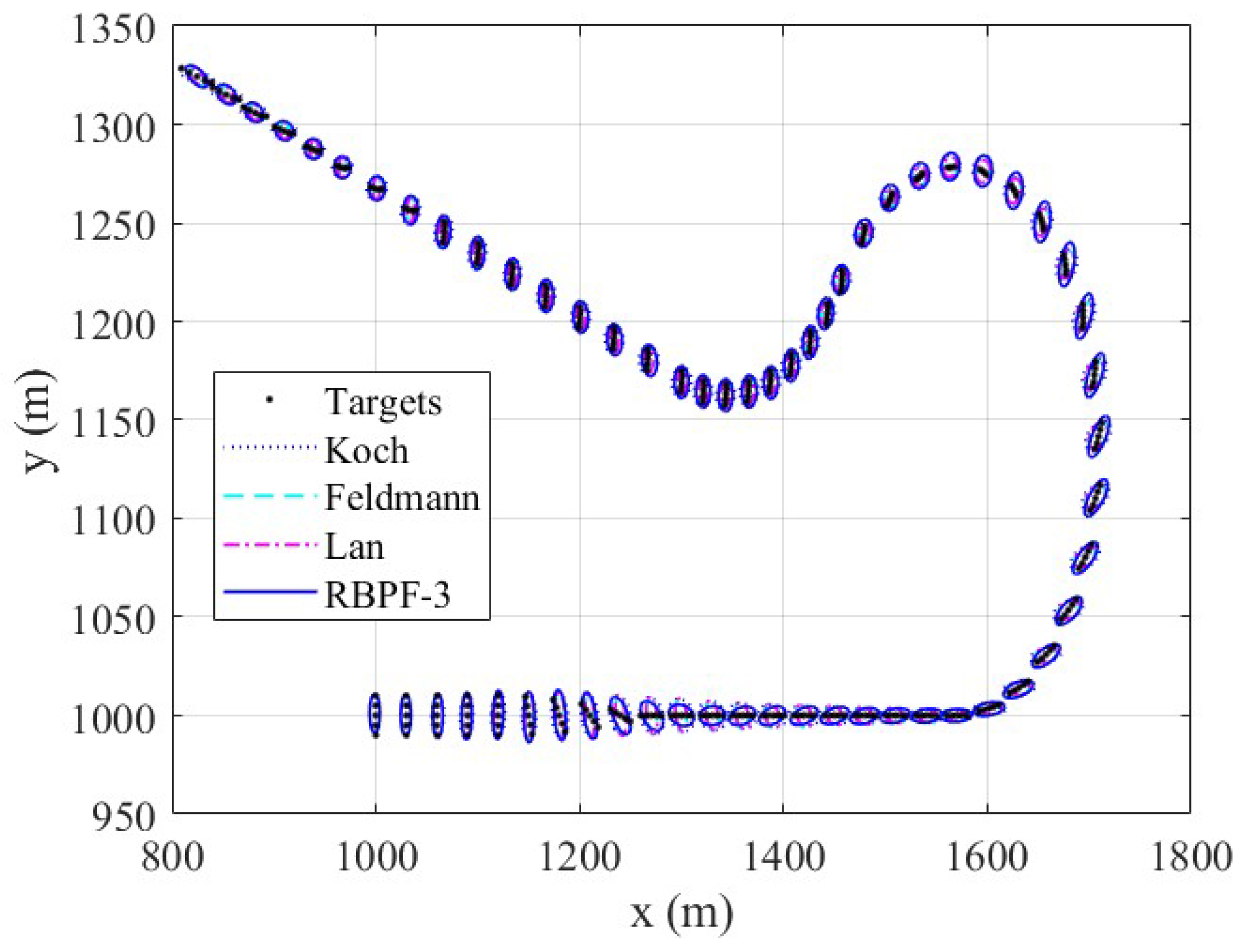
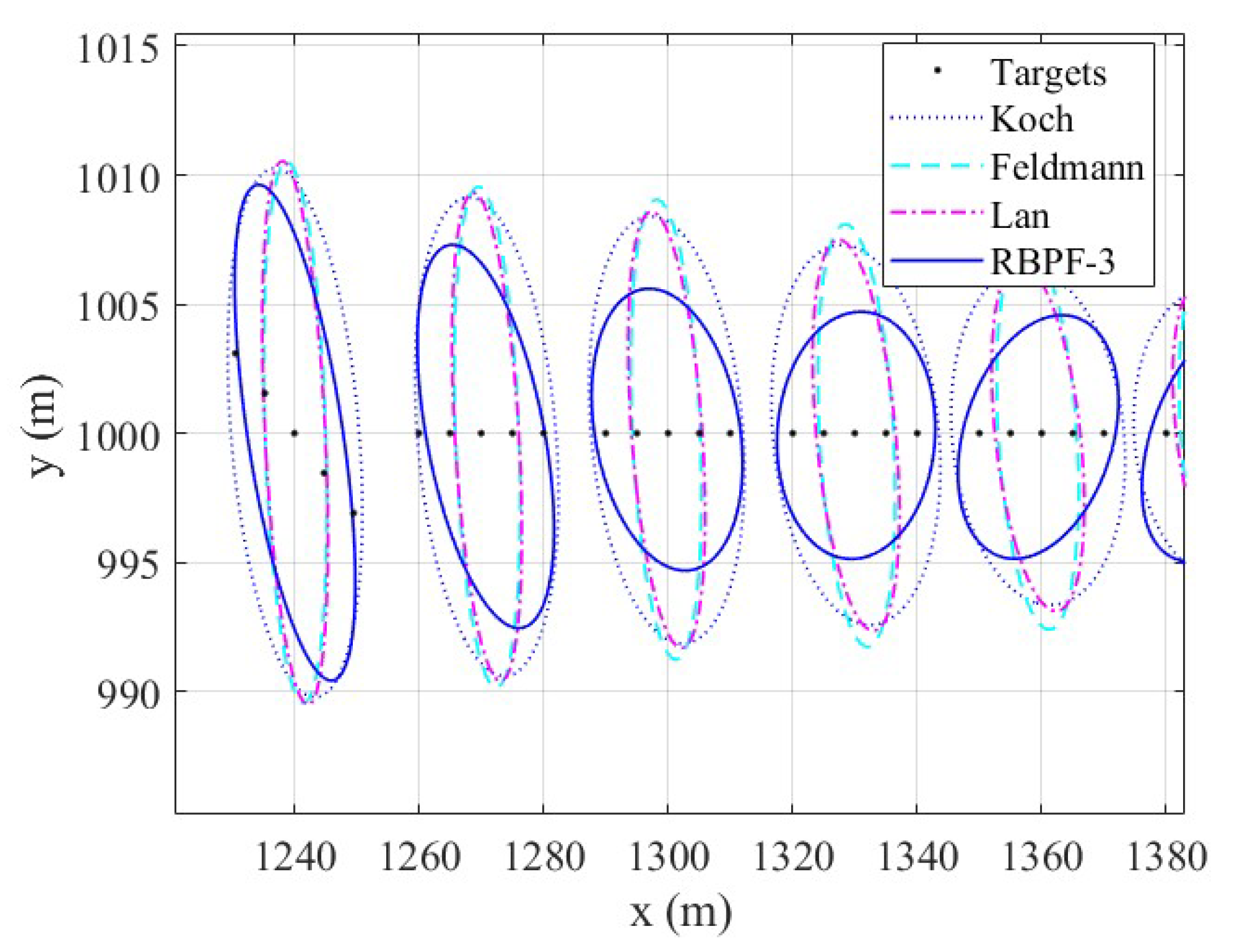
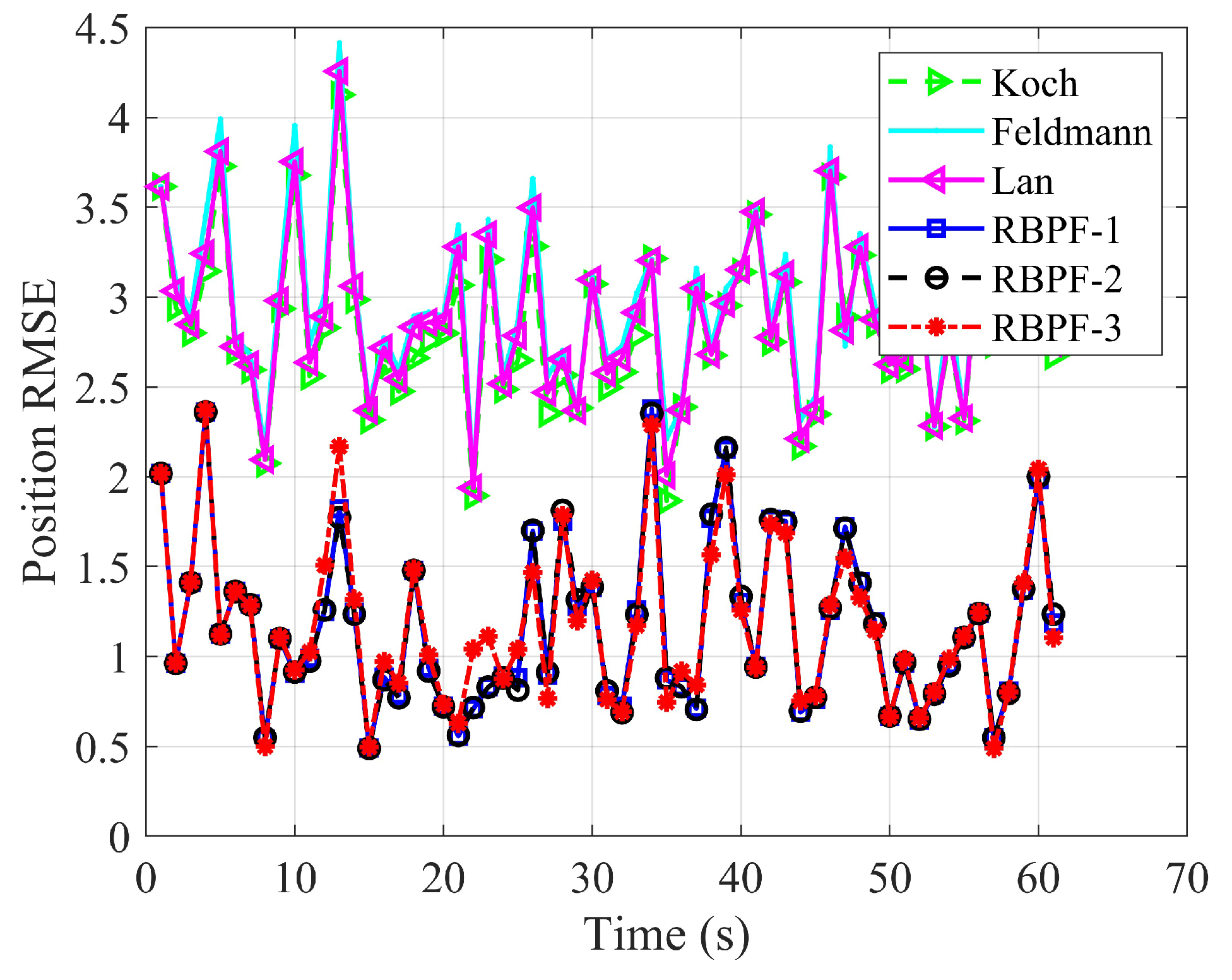
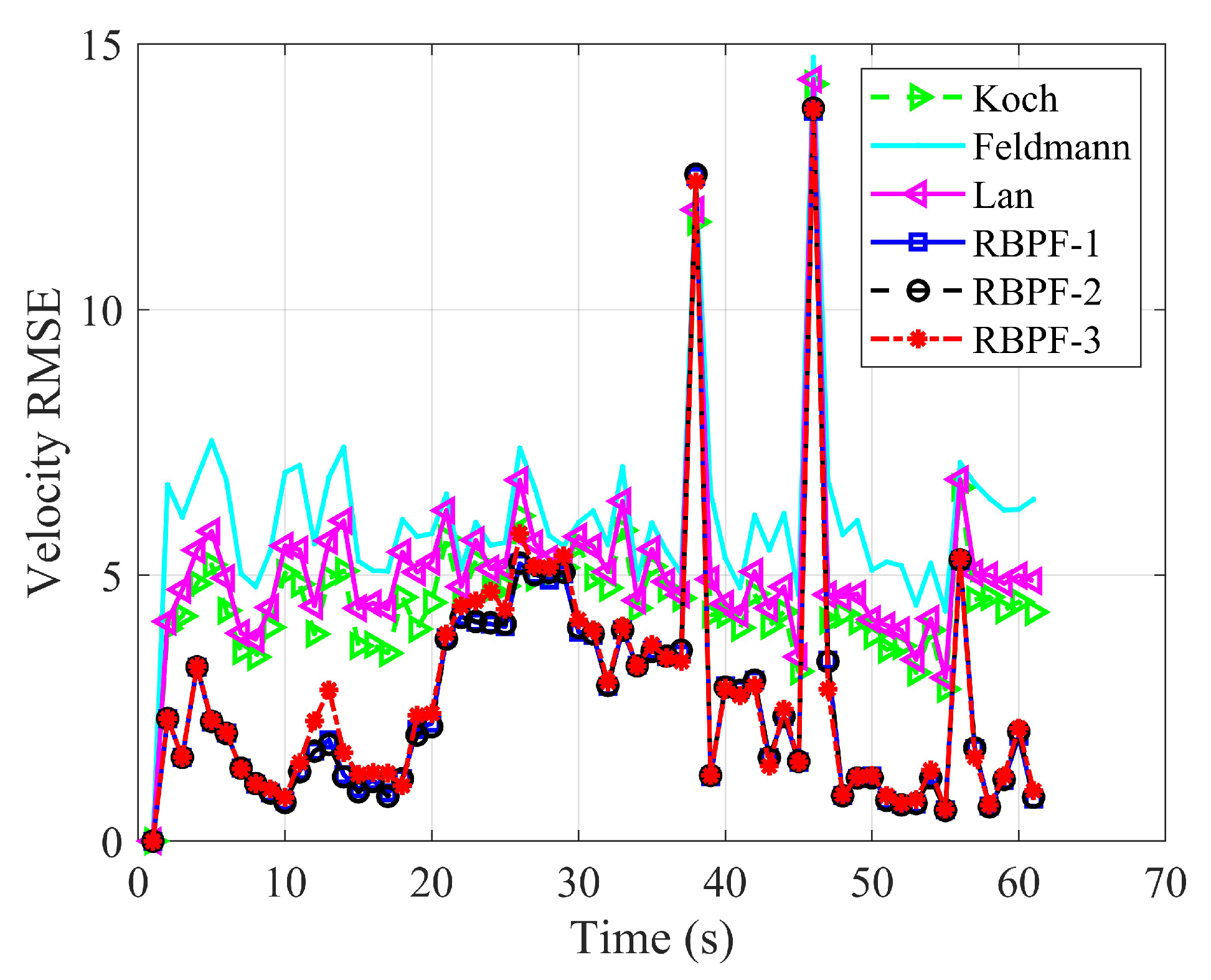
4.1. Cluster Target Tracking Test Experiment of Scenario One
4.2. Cluster Target Tracking Test Experiment of Scenario Two
4.3. Cluster Target Tracking Test Experiment of Scenario Three
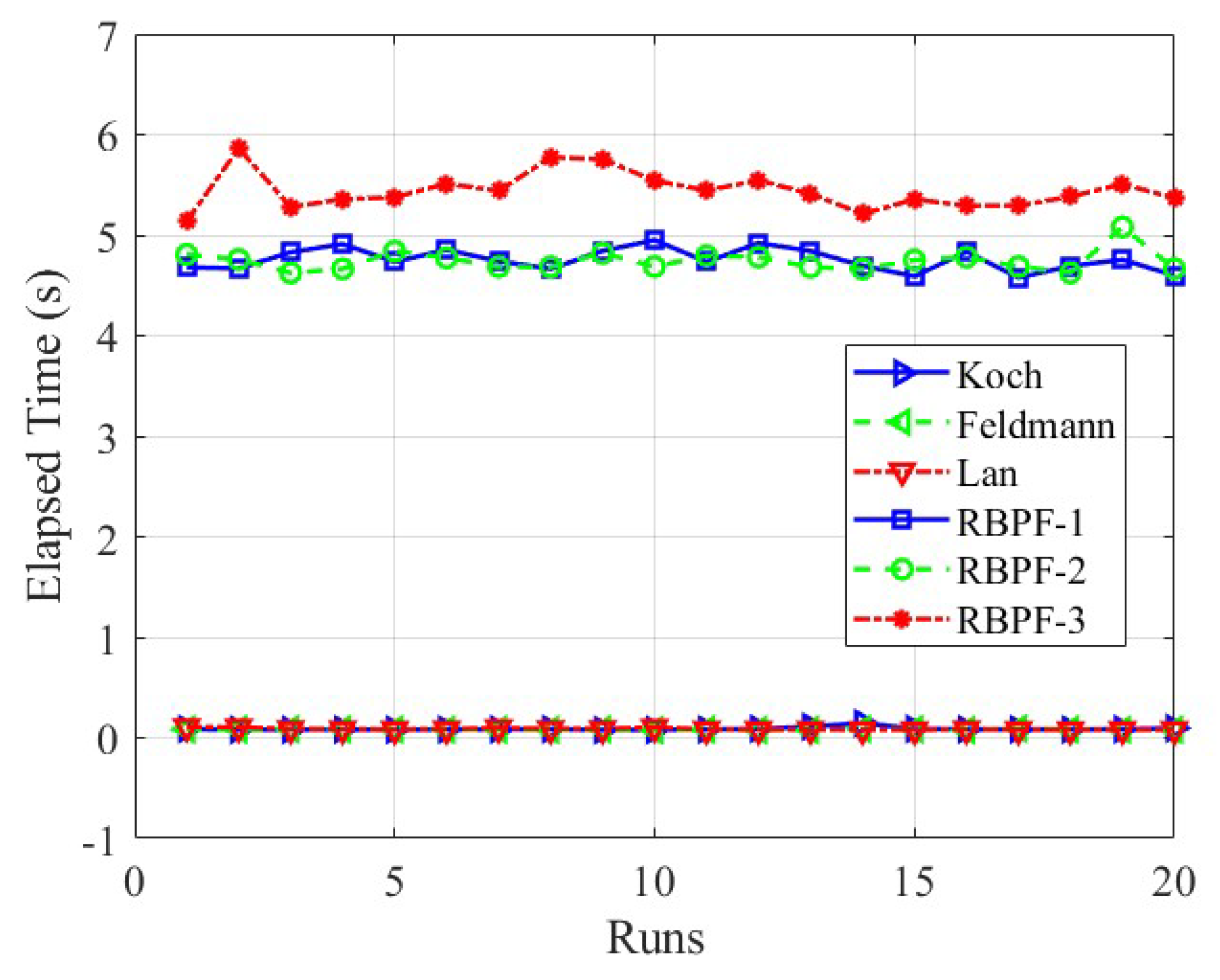
4.4. Computational Complexity Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, L.; Zhen, Z.; Tao, C.; Ding, J. Distributed Cooperative Strategy of UAV Swarm Without Speed Measurement Under Saturation Attack Mission. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4518–4529. [Google Scholar]
- Lei, Y.; Tong, X.; Qiu, C.; Sun, Y.; Tang, J.; Guo, C.; Li, H. Onboard Data Management Approach Based on a Discrete Grid System for Multi-UAV Cooperative Image Localization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar]
- Ye, X.; Xue, W.; Chen, X.; Zhang, Y.; Wang, X.; Guan, J. Cauchy Kernel-Based AEKF for UAV Target Tracking via Digital Ubiquitous Radar Under the Sea–Air Background. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar]
- Sun, Z.; Hu, C.; Cui, K.; Wang, R.; Ding, M.; Yan, Z.; Wu, D. Extracting Bird and Insect Migration Echoes From Single-Polarization Weather Radar Data Using Semi-Supervised Learning. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–12. [Google Scholar]
- Sayed, A.N.; Ramahi, O.M.; Shaker, G. In the Realm of Aerial Deception: UAV Classification via ISAR Images and Radar Digital Twins for Enhanced Security. IEEE Sens. Lett. 2024, 8, 1–4. [Google Scholar]
- Yuan, D.; Zhang, H.; Shu, X.; Liu, Q.; Chang, X.; He, Z.; Shi, G. Thermal Infrared Target Tracking: A Comprehensive Review. IEEE Trans. Instrum. Meas. 2024, 73, 1–19. [Google Scholar]
- Chen, Y.; Li, Z.; Wu, L.; Chen, P. An Efficient Multi-Object Tracking Guided by Spatial Clustering on Vision Sensors. IEEE Sens. J. 2024, 24, 19344–19351. [Google Scholar]
- Zhu, N.; Xi, Z.; Wu, C.; Zhong, F.; Qi, R.; Chen, H. Inductive Conformal Prediction Enhanced LSTM-SNN Network: Applications to Birds and UAVs Recognition. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar]
- Liu, Z.; Wang, Z.K.; Yang, Y.B.; Lu, Y. A Data-Driven Maneuvering Target Tracking Method Aided with Partial Models. IEEE Trans. Veh. Technol. 2024, 73, 414–425. [Google Scholar]
- Ming, R.; Zhou, Z.; Luo, X.; Liu, W.; Le, Z.; Song, C.; Jiang, R.; Zang, Y. Optical Tracking System for Multi-UAV Clustering. IEEE Sens. J. 2021, 21, 19382–19394. [Google Scholar]
- Liang, T.; Zhang, T.; Yang, J.; Feng, D.; Zhang, Q. UAV-Aided Positioning Systems for Ground Devices: Fundamental Limits and Algorithms. IEEE Internet Things J. 2022, 9, 13470–13485. [Google Scholar] [CrossRef]
- Ye, T.; Qin, W.; Li, Y.; Wang, S.; Zhang, J.; Zhao, Z. Dense and Small Object Detection in UAV-Vision Based on a Global-Local Feature Enhanced Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Zhu, N.; Xu, S.; Li, C.; Hu, J.; Fan, X.; Wu, W.; Chen, Z. An Improved Phase-Derived Range Method Based on High-Order Multi-Frame Track-Before-Detect for Warhead Detection. Remote Sens. 2022, 14, 29. [Google Scholar] [CrossRef]
- Song, Q.; Huang, S.; Zhang, Y.; Chen, X.; Chen, Z.; Zhou, X.; Deng, Z. Radar Target Classification Using Enhanced Doppler Spectrograms with ResNet34_CA in Ubiquitous Radar. Remote Sens. 2024, 16, 2860. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Song, J.; Guan, J.; Li, J.; He, Z. Micro-Motion Classification of Flying Bird and Rotor Drones via Data Augmentation and Modified Multi-Scale CNN. Remote Sens. 2022, 14, 1107. [Google Scholar] [CrossRef]
- Zhu, N.; Xi, Z.; Chen, H.; Xu, S.; Wang, Y.; Zhong, F. Mondrian Conformal Prediction Enhanced LSTM for Birds and Drones Recognition. In IET Conference Proceedings CP874 2023; The Institution of Engineering and Technology: Stevenage, UK, 2023; pp. 760–765. [Google Scholar]
- Zhao, Y.; Su, Y. Synchrosqueezing Phase Analysis on Micro-Doppler Parameters for Small UAVs Identification with Multichannel Radar. IEEE Geosci. Remote. Sens. Lett. 2020, 17, 411–415. [Google Scholar] [CrossRef]
- Yu, X.; Wei, S.; Fang, Y.; Sheng, J.; Zhang, L. Low-Altitude Slow Small Target Threat Assessment Algorithm by Exploiting Sequential Multi-Feature with Long-Short-Term-Memory. IEEE Sens. J. 2023, 23, 21524–21533. [Google Scholar] [CrossRef]
- Kang, K.B.; Choi, J.H.; Cho, B.L.; Lee, J.S.; Kim, K.T. Analysis of Micro-Doppler Signatures of Small UAVs Based on Doppler Spectrum. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3252–3267. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Chen, W.; Zhang, L.; Yu, X. Sparse Long-Time Coherent Integration-Based Detection Method for Radar Low-Observable Manoeuvring Target. IET Radar Sonar Navig. 2020, 14, 538–546. [Google Scholar] [CrossRef]
- White, D.; Jahangir, M.; Baker, C.J.; Antoniou, M. Urban Bird-Drone Classification with Synthetic Micro-Doppler Spectrograms. IEEE Trans. Radar Syst. 2024, 2, 167–179. [Google Scholar] [CrossRef]
- Chen, Z.; Ji, H.; Zhang, Y.; Zhu, Z.; Li, Y. High-Resolution Feature Pyramid Network for Small Object Detection on Drone View. IEEE Trans. Circuits Syst. Video Technol. 2023, 34, 475–489. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Z.; Lv, D.; Li, Z.; Lan, Z.; Zhao, S. Air-to-Air Visual Detection of Micro-UAVs: An Experimental Evaluation of Deep Learning. IEEE Robot. Autom. Lett. 2021, 6, 1020–1027. [Google Scholar]
- Zhao, Y.; Su, Y. The Extraction of Micro-Doppler Signal with EMD Algorithm for Radar-Based Small UAVs’ Detection. IEEE Trans. Instrum. Meas. 2020, 69, 929–940. [Google Scholar]
- Dugger, K. Techniques for Wildlife Investigations and Management. Condor 2007, 109, 981–983. [Google Scholar]
- Zhu, N.; Hu, J.; Xu, S.; Wu, W.; Zhang, Y.; Chen, Z. Micro-Motion Parameter Extraction for Ballistic Missile with Wideband Radar Using Improved Ensemble EMD Method. Remote Sens. 2021, 13, 3545. [Google Scholar] [CrossRef]
- Drummond, O.E.; Society of Photo-Optical Instrumentation Engineers; CREOL (Research center); SPIE Technical Symposium on Optical Engineering and Photonics in Aerospace Sensing. Signal and Data Processing of Small Targets 1990 : 16–18 April 1990, Orlando, Florida / Oliver E. Drummond, Chair/Editor; Sponsored by SPIE--The International Society for Optical Engineering; Cooperative Organization, CREOL/University of Central Florida; Society of Photo-Optical Instrumentation Engineers: Bellingham, WA, USA, 1990; Volume 1305. [Google Scholar]
- Koch, J.W. Bayesian Approach to Extended Object and Cluster Tracking Using Random Matrices. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1042–1059. [Google Scholar]
- Gupta, A.K.; Nagar, D.K. Matrix Variate Distributions; CRC Press: Boca Raton, FL, USA, 2020; pp. 13–26. [Google Scholar]
- Feldmann, M.; Fränken, D.; Koch, W. Tracking of Extended Objects and Group Targets Using Random Matrices. IEEE Trans. Signal Process. 2010, 59, 1409–1420. [Google Scholar]
- Orguner, U. A Variational Measurement Update for Extended Target Tracking with Random Matrices. IEEE Trans. Signal Process. 2012, 60, 3827–3834. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Lan, J.; Li, X.R. Tracking of Extended Object or Target Group Using Random Matrix: New Model and Approach. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2973–2989. [Google Scholar]
- Lan, J.; Li, X.R. Extended-object or Group-Target Tracking Using Random Matrix with Nonlinear Measurements. IEEE Trans. Signal Process. 2019, 67, 5130–5142. [Google Scholar]
- Mo, L.; Song, X.; Zhou, Y.; Sun, Z.K. Unbiased Converted Measurements for Tracking. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1023–1027. [Google Scholar]
- Duan, Z.; Han, C.; Li, X.R. Comments on Unbiased Converted Measurements for Tracking. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1374. [Google Scholar]
- Granström, K.; Natale, A.; Braca, P.; Ludeno, G.; Serafino, F. Gamma Gaussian Inverse Wishart Probability Hypothesis Density for Extended Target Tracking Using X-Band Marine Radar Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6617–6631. [Google Scholar]
- Doucet, A.; Godsill, S.; Andrieu, C. On Sequential Monte Carlo Sampling Methods for Bayesian Filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar]
- Mustiere, F.; Bolic, M.; Bouchard, M. Rao-Blackwellised Particle Filters: Examples of Applications. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 1196–1200. [Google Scholar]
- Cheng, L.; Sengupta, A.; Cao, S. Deep Learning-Based Robust Multi-Object Tracking via Fusion of mmWave Radar and Camera Sensors. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17218–17233. [Google Scholar]
- Huang, Y.; Guo, R.; Zhang, Y.; Chen, Z. Deep-Reinforcement-Learning-Based Radar Parameter Adaptation for Multiple-Target Tracking. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 7125–7141. [Google Scholar]
- Zhang, H.; Chen, H.; Zhang, W.; Zhang, X. Trajectory Planning for Airborne Radar in Extended Target Tracking Based on Deep Reinforcement Learning. Digit. Signal Process. 2024, 153, 104603. [Google Scholar]
- Cramér, H. Mathematical Methods of Statistics (PMS-9), Volume 9; Princeton University Press: Princeton, NJ, USA, 2016. [Google Scholar]
- Chen, R.; Liu, J.S. Mixture Kalman Filters. J. R. Stat. Soc. B 2000, 62, 493–508. [Google Scholar]
- Arulampalam, M.S.; Maskell, S.; Gordon, N.; Clapp, T. A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussian Bayesian Tracking. IEEE Trans. Signal Process. 2002, 50, 2. [Google Scholar]

| (1) Initialization |
|---|
| Initialize Kalman filter |
| Initialize particles filter |
| (2) Recursion |
| Prediction |
| Sequential sampling of particles |
| One step prediction of motion state and covariance |
| Update |
| Update particle weights |
| Update state of motion |
| Normalized weights |
| Resampling |
| Calculate the effective number of particles, and if , |
| perform the resampling step. |
| Compute the posterior estimate of the joint state. |
| , |
| Methods | Mean (Pos (m)) | STD (Pos (m)) | Mean (Vel (m/s)) | STD (Vel (m/s)) |
|---|---|---|---|---|
| Koch | 3.2602 | 1.6363 | 5.6234 | 2.3776 |
| Feldmann | 3.3579 | 1.7017 | 6.4933 | 2.4439 |
| Lan | 3.3394 | 1.7461 | 6.2769 | 2.7961 |
| RBPF-1 | 2.1864 | 1.2869 | 4.1325 | 2.8612 |
| RBPF-2 | 2.1849 | 1.2693 | 4.1088 | 2.8326 |
| RBPF-3 | 2.1846 | 1.2813 | 4.1207 | 2.8421 |
| Methods | Mean (Pos (m)) | STD (Pos (m)) | Mean (Vel (m/s)) | STD (Vel (m/s)) |
|---|---|---|---|---|
| Koch | 2.8768 | 0.4876 | 4.3638 | 1.0702 |
| Feldmann | 3.0129 | 0.5122 | 5.7570 | 1.1808 |
| Lan | 2.9282 | 0.4992 | 4.7849 | 1.0896 |
| RBPF-1 | 1.2030 | 0.5186 | 2.2970 | 1.6809 |
| RBPF-2 | 1.1992 | 0.5090 | 2.2874 | 1.6700 |
| RBPF-3 | 1.1956 | 0.4970 | 2.3914 | 1.7595 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, N.; Zhong, F.; Lei, X.; Niu, G.; Xie, H.; Zhang, Y. Situation Awareness and Tracking Algorithm for Countering Low-Altitude Swarm Target Threats. Remote Sens. 2025, 17, 1172. https://doi.org/10.3390/rs17071172
Zhu N, Zhong F, Lei X, Niu G, Xie H, Zhang Y. Situation Awareness and Tracking Algorithm for Countering Low-Altitude Swarm Target Threats. Remote Sensing. 2025; 17(7):1172. https://doi.org/10.3390/rs17071172
Chicago/Turabian StyleZhu, Nannan, Fuli Zhong, Xueyue Lei, Guo Niu, Hongtu Xie, and Yue Zhang. 2025. "Situation Awareness and Tracking Algorithm for Countering Low-Altitude Swarm Target Threats" Remote Sensing 17, no. 7: 1172. https://doi.org/10.3390/rs17071172
APA StyleZhu, N., Zhong, F., Lei, X., Niu, G., Xie, H., & Zhang, Y. (2025). Situation Awareness and Tracking Algorithm for Countering Low-Altitude Swarm Target Threats. Remote Sensing, 17(7), 1172. https://doi.org/10.3390/rs17071172







