CGD-CD: A Contrastive Learning-Guided Graph Diffusion Model for Change Detection in Remote Sensing Images
Abstract
1. Introduction
- We innovatively introduce the graph diffusion model to the field of self-supervised change detection, where the model captures objects of varying sizes and global contextual information, leading to more discriminative feature representations.
- We design a novel fused contrastive learning strategy, combining multi-view contrastive learning with graph contrastive learning to strengthen the model’s capacity to capture structural information.
- We conducted experiments on different datasets, demonstrating the feasibility and superiority of the proposed CGD-CD network.
2. Related Work
2.1. Self-Supervised Learning for CD
2.2. Graph Neural Networks
2.3. Diffusion Model
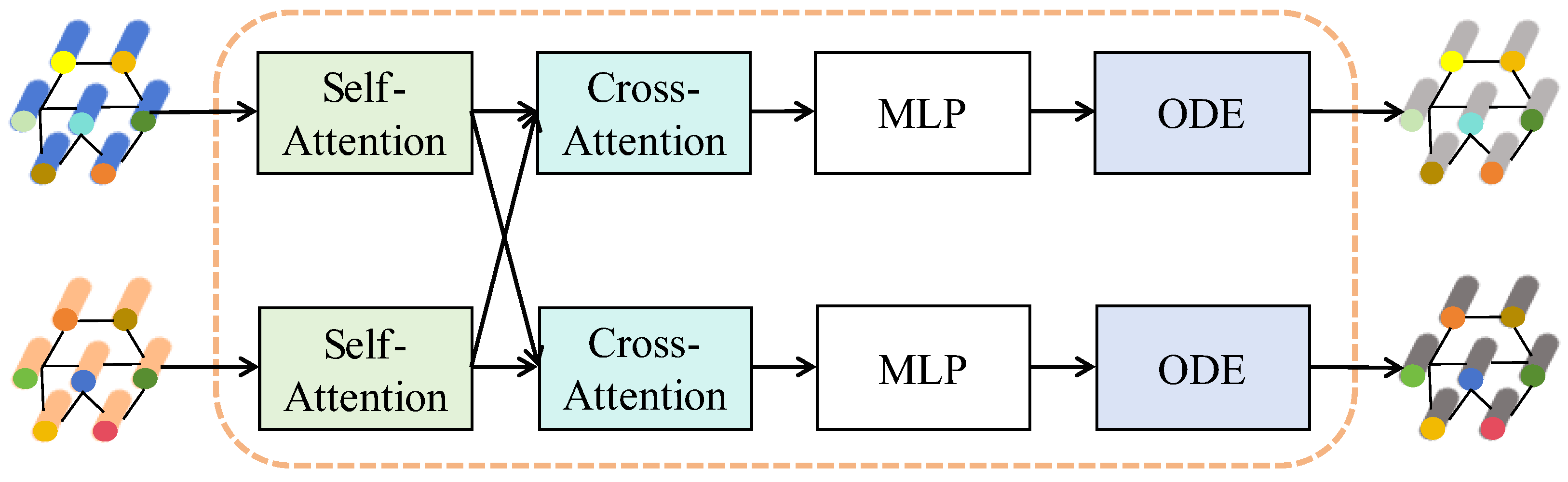
3. Methodology
3.1. Overview of the Proposed CGD-CD
| Algorithm 1 Inference process of CGD-CD |
|
3.2. Graph Construction
3.3. Graph Diffusion
3.4. Contrastive Learning
3.5. Change Detection
4. Experiments
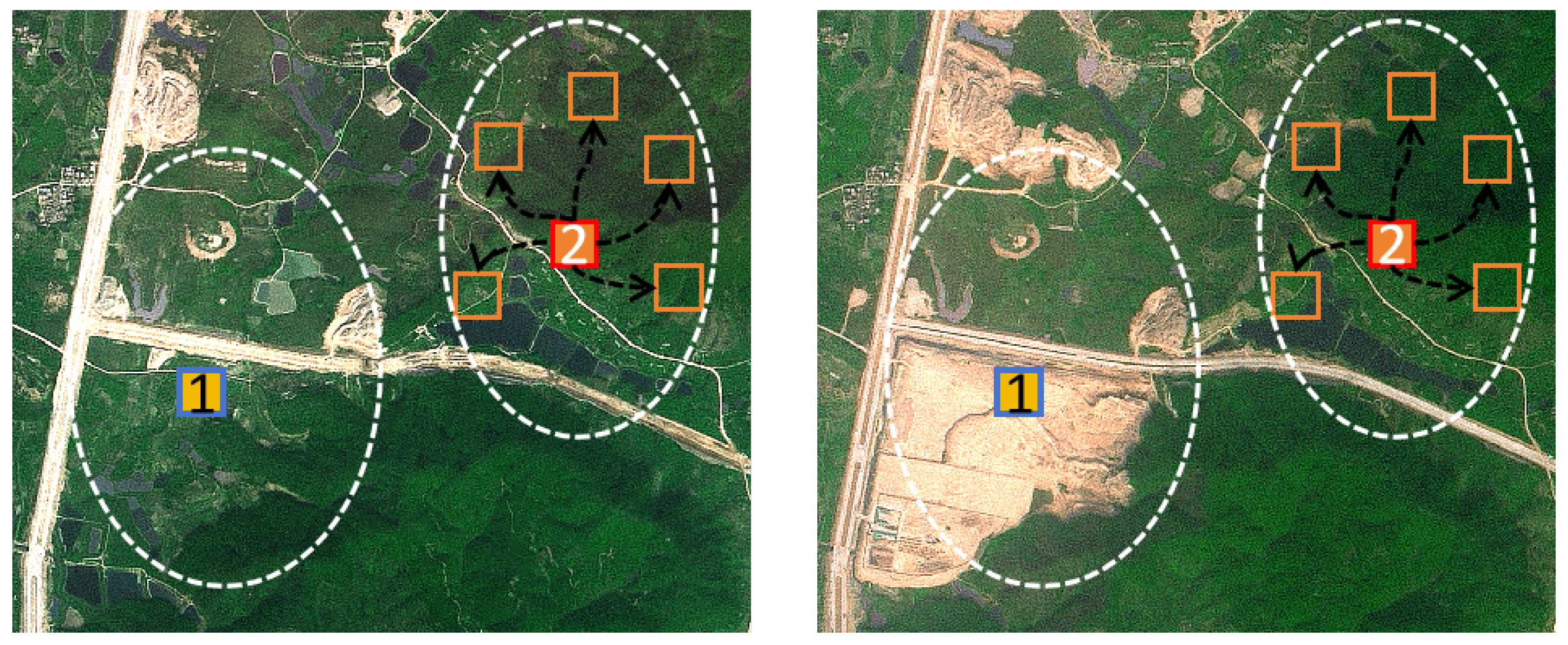
4.1. Datasets
4.1.1. Beijing Dataset
4.1.2. Guangzhou Dataset
4.1.3. Montpellier Dataset
4.2. Evaluation Metrics
4.3. Experimental Setting and Baselines
- ASEA-CD [58]: The ASEA-CD method gradually expands the adaptive region around each pixel by comparing the spectral similarity between the pixel and its eight neighboring pixels, until no pixel can be found that satisfies the similarity constraint. This method is able to adapt to the shape and size of the target and does not require parameter settings, allowing it to effectively utilize contextual information.
- HyperNet [59]: HyperNet performs full convolutional comparison of multi-temporal spatial and spectral features through a self-supervised learning model, enabling pixel-level feature representation learning. Using the designed spatial and spectral attention branches, along with the novel focal cosine loss function, HyperNet effectively detects changes in hyperspectral images.
- Patch-ssl [40]: The Patch-SSL method is a self-supervised change detection method that views different temporal samples of the same geographical location as positive examples, while samples from different locations are treated as negative examples. This method employs CL to extract informative and discriminative features for change detection.
- Net [38]: Net introduces the regional consistency principle to generate pseudo-labels for the dataset by checking if image blocks intersect, then uses the pseudo-labels to train the backbone model to generate the change map.
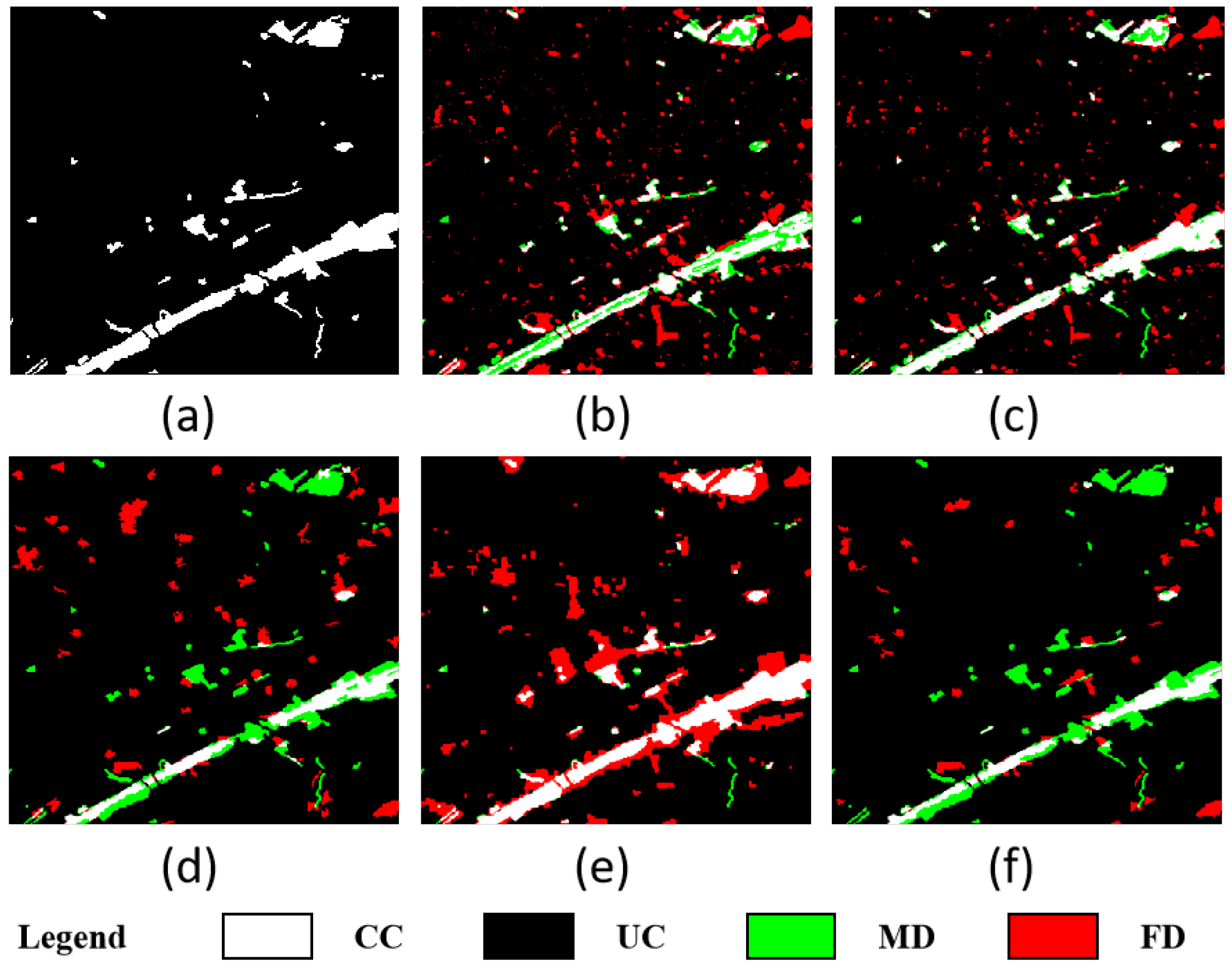
4.4. Comparison Experiments
4.4.1. Results on Beijing Dataset
4.4.2. Results on Guangzhou Dataset
4.4.3. Results on Montpellier Dataset
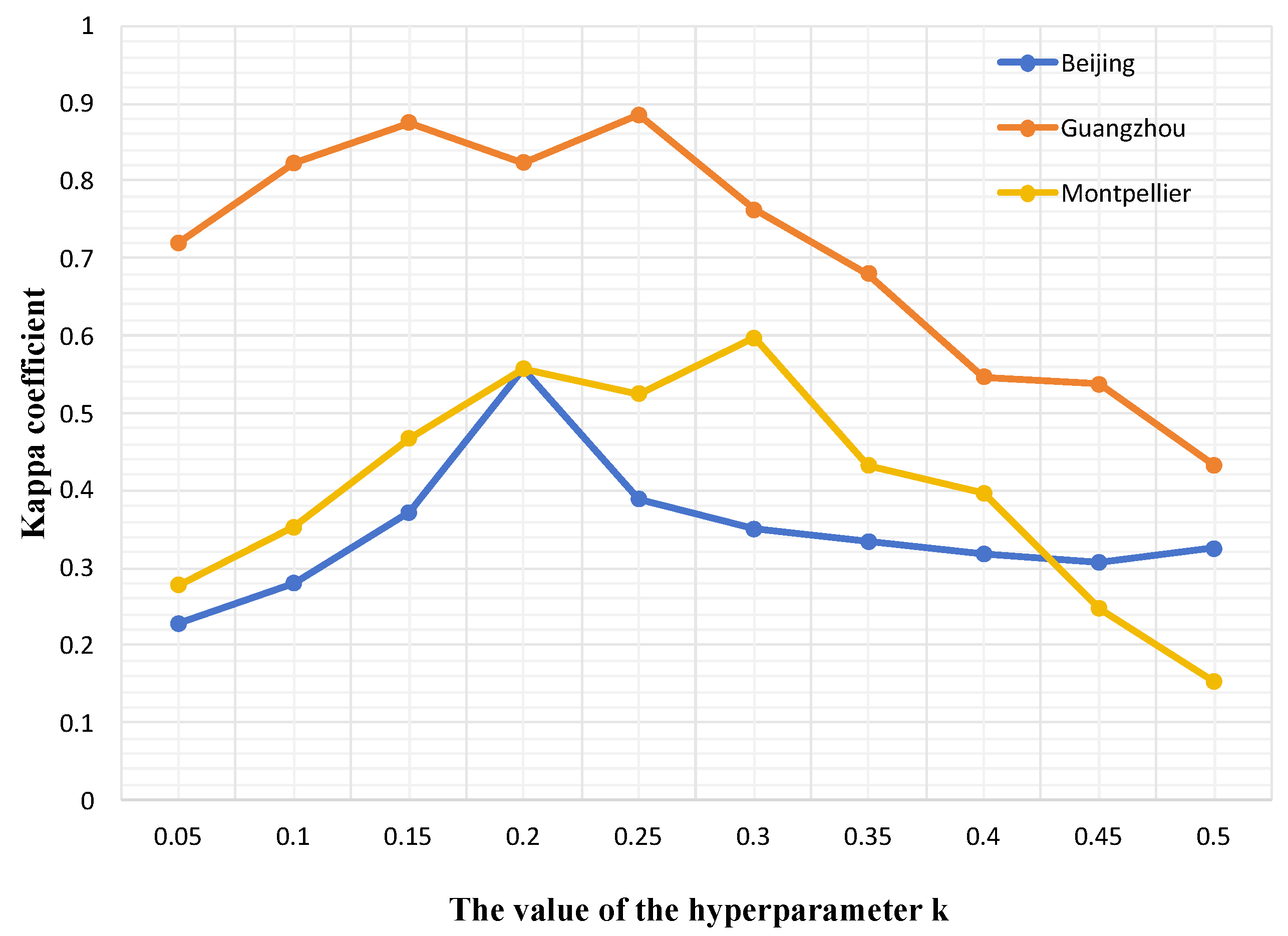
4.5. Parameters Analysis
4.6. Ablation Study
5. Discussion
5.1. Critical Considerations and Limitations
5.2. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Sun, Y.; Lei, L.; Kuang, G.; Ji, K. Change detection of multisource remote sensing images: A review. Int. J. Digit. Earth 2024, 17, 2398051. [Google Scholar]
- Cheng, G.; Huang, Y.; Li, X.; Lyu, S.; Xu, Z.; Zhao, H.; Zhao, Q.; Xiang, S. Change detection methods for remote sensing in the last decade: A comprehensive review. Remote Sens. 2024, 16, 2355. [Google Scholar] [CrossRef]
- Liu, Q.; Wan, S.; Gu, B. A review of the detection methods for climate regime shifts. Discret. Dyn. Nat. Soc. 2016, 2016, 3536183. [Google Scholar]
- Shi, S.; Zhong, Y.; Zhao, J.; Lv, P.; Liu, Y.; Zhang, L. Land-use/land-cover change detection based on class-prior object-oriented conditional random field framework for high spatial resolution remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2020, 60, 5600116. [Google Scholar]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B.; Lambin, E. Review ArticleDigital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar]
- Ridd, M.K.; Liu, J. A comparison of four algorithms for change detection in an urban environment. Remote Sens. Environ. 1998, 63, 95–100. [Google Scholar]
- Liu, Y.; Pang, C.; Zhan, Z.; Zhang, X.; Yang, X. Building change detection for remote sensing images using a dual-task constrained deep siamese convolutional network model. IEEE Geosci. Remote Sens. Lett. 2020, 18, 811–815. [Google Scholar]
- Luo, H.; Liu, C.; Wu, C.; Guo, X. Urban change detection based on Dempster–Shafer theory for multitemporal very high-resolution imagery. Remote Sens. 2018, 10, 980. [Google Scholar] [CrossRef]
- Brunner, D.; Bruzzone, L.; Lemoine, G. Change detection for earthquake damage assessment in built-up areas using very high resolution optical and SAR imagery. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3210–3213. [Google Scholar]
- Hamidi, E.; Peter, B.G.; Muñoz, D.F.; Moftakhari, H.; Moradkhani, H. Fast flood extent monitoring with SAR change detection using google earth engine. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4201419. [Google Scholar]
- He, X.; Zhang, S.; Xue, B.; Zhao, T.; Wu, T. Cross-modal change detection flood extraction based on convolutional neural network. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103197. [Google Scholar]
- Khelifi, L.; Mignotte, M. Deep learning for change detection in remote sensing images: Comprehensive review and meta-analysis. IEEE Access 2020, 8, 126385–126400. [Google Scholar] [CrossRef]
- Bai, T.; Wang, L.; Yin, D.; Sun, K.; Chen, Y.; Li, W.; Li, D. Deep learning for change detection in remote sensing: A review. Geo-Spat. Inf. Sci. 2023, 26, 262–288. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, G.; Chen, K.; Yan, M.; Sun, X. Triplet-Based Semantic Relation Learning for Aerial Remote Sensing Image Change Detection. IEEE Geosci. Remote Sens. Lett. 2019, 16, 266–270. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar]
- Lei, T.; Wang, J.; Ning, H.; Wang, X.; Xue, D.; Wang, Q.; Nandi, A.K. Difference enhancement and spatial–spectral nonlocal network for change detection in VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4507013. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, F.; Hou, Z.; Mian, L.; Wang, Z.; Zhang, J.; Tang, J. Self-supervised learning: Generative or contrastive. IEEE Trans. Knowl. Data Eng. 2021, 35, 857–876. [Google Scholar] [CrossRef]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9729–9738. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.; Buchatskaya, E.; Doersch, C.; Avila Pires, B.; Guo, Z.; Gheshlaghi Azar, M.; et al. Bootstrap your own latent-a new approach to self-supervised learning. Adv. Neural Inf. Process. Syst. 2020, 33, 21271–21284. [Google Scholar]
- Chen, X.; He, K. Exploring simple siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15750–15758. [Google Scholar]
- Saha, S.; Ebel, P.; Zhu, X.X. Self-Supervised Multisensor Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4405710. [Google Scholar] [CrossRef]
- Qu, Y.; Li, J.; Huang, X.; Wen, D. TD-SSCD: A novel network by fusing temporal and differential information for self-supervised remote sensing image change detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5407015. [Google Scholar] [CrossRef]
- Chen, Y.; Bruzzone, L. Self-supervised change detection by fusing SAR and optical multi-temporal images. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 3101–3104. [Google Scholar]
- Chen, Y.; Bruzzone, L. A self-supervised approach to pixel-level change detection in bi-temporal RS images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4413911. [Google Scholar] [CrossRef]
- Jian, P.; Ou, Y.; Chen, K. Hypergraph Self-Supervised Learning-Based Joint Spectral-Spatial-Temporal Feature Representation for Hyperspectral Image Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 741–756. [Google Scholar] [CrossRef]
- Wan, R.; Zhang, J.; Huang, Y.; Li, Y.; Hu, B.; Wang, B. Leveraging Diffusion Modeling for Remote Sensing Change Detection in Built-Up Urban Areas. IEEE Access 2024, 12, 7028–7039. [Google Scholar] [CrossRef]
- Tian, J.; Lei, J.; Zhang, J.; Xie, W.; Li, Y. SwiMDiff: Scene-Wide Matching Contrastive Learning With Diffusion Constraint for Remote Sensing Image. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5613213. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Song, Y.; Ermon, S. Generative modeling by estimating gradients of the data distribution. arXiv 2019, arXiv:1907.05600. [Google Scholar]
- Song, Y.; Sohl-Dickstein, J.; Kingma, D.P.; Kumar, A.; Ermon, S.; Poole, B. Score-based generative modeling through stochastic differential equations. arXiv 2020, arXiv:2011.13456. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Xiang, W.; Yang, H.; Huang, D.; Wang, Y. Denoising diffusion autoencoders are unified self-supervised learners. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 15802–15812. [Google Scholar]
- Chen, X.; Liu, Z.; Xie, S.; He, K. Deconstructing denoising diffusion models for self-supervised learning. arXiv 2024, arXiv:2401.14404. [Google Scholar]
- Liu, Y.; Yue, J.; Xia, S.; Ghamisi, P.; Xie, W.; Fang, L. Diffusion Models Meet Remote Sensing: Principles, Methods, and Perspectives. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4708322. [Google Scholar] [CrossRef]
- Bandara, W.G.C.; Nair, N.G.; Patel, V.M. Ddpm-cd: Remote sensing change detection using denoising diffusion probabilistic models. arXiv 2022, arXiv:2206.11892. [Google Scholar]
- Zhan, T.; Gong, M.; Jiang, X.; Zhang, E. S 3 Net: Superpixel-Guided Self-Supervised Learning Network for Multitemporal Image Change Detection. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5002205. [Google Scholar]
- Alvarez, J.L.H.; Ravanbakhsh, M.; Demir, B. S2-cGAN: Self-supervised adversarial representation learning for binary change detection in multispectral images. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2515–2518. [Google Scholar]
- Chen, Y.; Bruzzone, L. Self-Supervised Change Detection in Multiview Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5402812. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, H.; Qin, A.K.; Liu, W.; Zhao, Z. Self-paced co-training of graph neural networks for semi-supervised node classification. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 9234–9247. [Google Scholar]
- Fan, X.; Gong, M.; Xie, Y.; Jiang, F.; Li, H. Structured self-attention architecture for graph-level representation learning. Pattern Recognit. 2020, 100, 107084. [Google Scholar]
- Jian, P.; Ou, Y.; Chen, K. Uncertainty-Aware Graph Self-Supervised Learning for Hyperspectral Image Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5509019. [Google Scholar] [CrossRef]
- Liu, J.; Chen, K.; Xu, G.; Li, H.; Yan, M.; Diao, W.; Sun, X. Semi-Supervised Change Detection Based on Graphs with Generative Adversarial Networks. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 74–77. [Google Scholar] [CrossRef]
- Wu, J.; Li, B.; Qin, Y.; Ni, W.; Zhang, H.; Fu, R.; Sun, Y. A multiscale graph convolutional network for change detection in homogeneous and heterogeneous remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102615. [Google Scholar]
- Shuai, W.; Jiang, F.; Zheng, H.; Li, J. MSGATN: A superpixel-based multi-scale Siamese graph attention network for change detection in remote sensing images. Appl. Sci. 2022, 12, 5158. [Google Scholar] [CrossRef]
- Nichol, A.; Dhariwal, P.; Ramesh, A.; Shyam, P.; Mishkin, P.; McGrew, B.; Sutskever, I.; Chen, M. Glide: Towards photorealistic image generation and editing with text-guided diffusion models. arXiv 2021, arXiv:2112.10741. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Baranchuk, D.; Rubachev, I.; Voynov, A.; Khrulkov, V.; Babenko, A. Label-Efficient Semantic Segmentation with Diffusion Models. arXiv 2022, arXiv:2112.03126. [Google Scholar]
- Ma, Y.; Zhan, K. Self-Contrastive Graph Diffusion Network. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 3857–3865. [Google Scholar]
- Wen, Y.; Ma, X.; Zhang, X.; Pun, M.O. GCD-DDPM: A generative change detection model based on difference-feature guided DDPM. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5404416. [Google Scholar]
- Ding, X.; Qu, J.; Dong, W.; Zhang, T.; Li, N.; Yang, Y. Graph Representation Learning-Guided Diffusion Model for Hyperspectral Change Detection. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5506405. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar]
- Chamberlain, B.; Rowbottom, J.; Eynard, D.; Di Giovanni, F.; Dong, X.; Bronstein, M. Beltrami flow and neural diffusion on graphs. Adv. Neural Inf. Process. Syst. 2021, 34, 1594–1609. [Google Scholar]
- Chamberlain, B.; Rowbottom, J.; Gorinova, M.I.; Bronstein, M.; Webb, S.; Rossi, E. Grand: Graph neural diffusion. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 1407–1418. [Google Scholar]
- Chen, Q.; Wang, Y.; Wang, Y.; Yang, J.; Lin, Z. Optimization-induced graph implicit nonlinear diffusion. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 3648–3661. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar]
- Lv, Z.; Wang, F.; Liu, T.; Kong, X.; Benediktsson, J.A. Novel Automatic Approach for Land Cover Change Detection by Using VHR Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8016805. [Google Scholar] [CrossRef]
- Hu, M.; Wu, C.; Zhang, L. HyperNet: Self-Supervised Hyperspectral Spatial–Spectral Feature Understanding Network for Hyperspectral Change Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5543017. [Google Scholar] [CrossRef]






| Datasets | Methods | Pr | Re | F1 | OA | KC |
|---|---|---|---|---|---|---|
| Beijing | ASEA-CD | 33.5 | 72.5 | 45.8 | 89.5 | 40.9 |
| HyperNet | 30.9 | 84.6 | 45.3 | 87.6 | 39.9 | |
| Patch-ssl | 26.9 | 72.4 | 39.2 | 93.0 | 51.7 | |
| Net | 27.7 | 94.8 | 42.8 | 84.6 | 36.9 | |
| CGD-CD | 48.2 | 76.2 | 59.1 | 93.6 | 55.8 |
| Datasets | Methods | Pr | Re | F1 | OA | KC |
|---|---|---|---|---|---|---|
| Guangzhou | ASEA-CD | 95.4 | 79.7 | 86.9 | 96.4 | 84.8 |
| HyperNet | 59.6 | 78.9 | 67.9 | 88.8 | 61.3 | |
| Patch-ssl | 98.3 | 72.1 | 83.2 | 95.6 | 80.8 | |
| Net | 97.5 | 83.4 | 90.0 | 96.7 | 87.1 | |
| CGD-CD | 96.6 | 84.4 | 90.1 | 97.2 | 88.5 |
| Datasets | Methods | Pr | Re | F1 | OA | KC |
|---|---|---|---|---|---|---|
| Montpellier | ASEA-CD | 46.0 | 64.9 | 53.9 | 92.4 | 49.9 |
| HyperNet | 59.7 | 78.7 | 67.9 | 93.5 | 65.2 | |
| Patch-ssl | 42.5 | 39.7 | 41.1 | 92.3 | 36.9 | |
| Net | 43.9 | 93.7 | 59.8 | 91.4 | 55.7 | |
| CGD-CD | 62.4 | 49.3 | 70.4 | 94.2 | 59.7 |
| Datasets | GDM | OA | KC | ||
|---|---|---|---|---|---|
| Beijing | × | ✓ | ✓ | 80.9 | 27.8 |
| ✓ | × | ✓ | 85.7 | 51.2 | |
| ✓ | ✓ | × | 89.2 | 47.3 | |
| ✓ | ✓ | ✓ | 93.6 | 55.8 | |
| Guangzhou | × | ✓ | ✓ | 82.7 | 68.3 |
| ✓ | × | ✓ | 95.2 | 80.4 | |
| ✓ | ✓ | × | 87.6 | 69.5 | |
| ✓ | ✓ | ✓ | 97.2 | 88.5 | |
| Montpellier | × | ✓ | ✓ | 67.2 | 33.5 |
| ✓ | × | ✓ | 92.2 | 36.9 | |
| ✓ | ✓ | × | 74.1 | 23.5 | |
| ✓ | ✓ | ✓ | 94.2 | 59.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Lei, Z.; Chen, K.; Li, Q.; Zhao, X. CGD-CD: A Contrastive Learning-Guided Graph Diffusion Model for Change Detection in Remote Sensing Images. Remote Sens. 2025, 17, 1144. https://doi.org/10.3390/rs17071144
Shang Y, Lei Z, Chen K, Li Q, Zhao X. CGD-CD: A Contrastive Learning-Guided Graph Diffusion Model for Change Detection in Remote Sensing Images. Remote Sensing. 2025; 17(7):1144. https://doi.org/10.3390/rs17071144
Chicago/Turabian StyleShang, Yang, Zicheng Lei, Keming Chen, Qianqian Li, and Xinyu Zhao. 2025. "CGD-CD: A Contrastive Learning-Guided Graph Diffusion Model for Change Detection in Remote Sensing Images" Remote Sensing 17, no. 7: 1144. https://doi.org/10.3390/rs17071144
APA StyleShang, Y., Lei, Z., Chen, K., Li, Q., & Zhao, X. (2025). CGD-CD: A Contrastive Learning-Guided Graph Diffusion Model for Change Detection in Remote Sensing Images. Remote Sensing, 17(7), 1144. https://doi.org/10.3390/rs17071144






