Hyperspectral Target Detection Based on Masked Autoencoder Data Augmentation
Abstract
1. Introduction
- Coarse detection-based;
- Synthesis-based;
- Mask-based methods.
- A multi-scale spectral metric network is proposed; firstly, multi-scale feature vector construction is performed and a Convolutional Embedding Transformer (CET) block is proposed to extract local and global features of the feature vector and finally, the feature extraction results of multi-scale feature vector are fused to improve the ability to extract fine-grained features;
- A masked spectral data augmentation network was proposed to generate the target. The network learns spectral variability by dividing and masking the spectrum in the HSI, followed by reconstructing the spectrum. The prior spectrum is divided and masked to generate the target. The network is simple and requires adjustment of only the mask ratio to automatically learn the spectral variability for generating the target;
- Inter-class Difference Amplification Triplet Loss is proposed, based on the traditional triplet loss, to take into account the distance between the background and priori spectrum. The background information is fully utilized to enhance the discrimination between target and background.
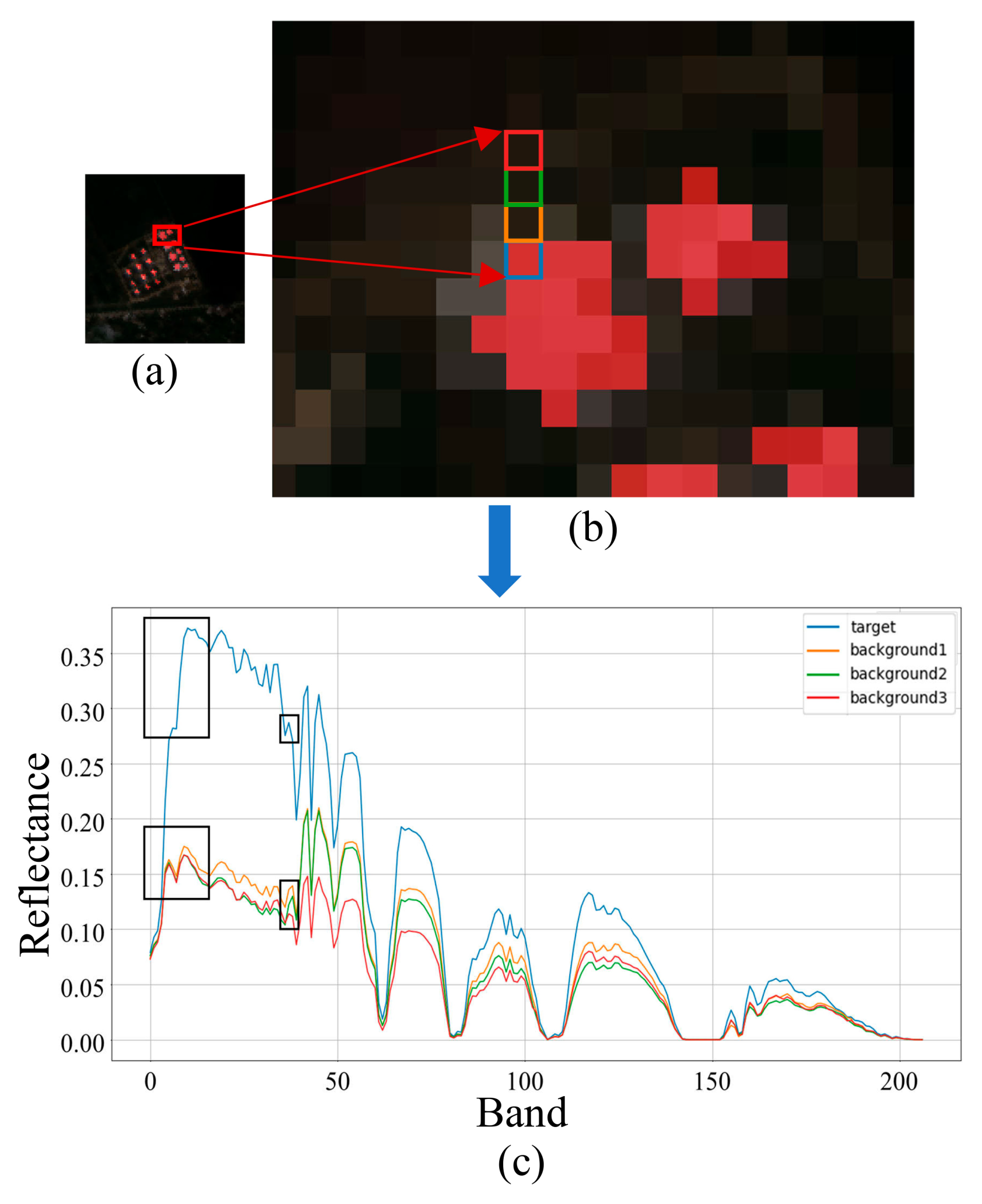
2. Materials and Methods
2.1. Materials
2.1.1. Deep Metric Learning
2.1.2. Mask-Based Data Enhancement
2.1.3. MAE Network
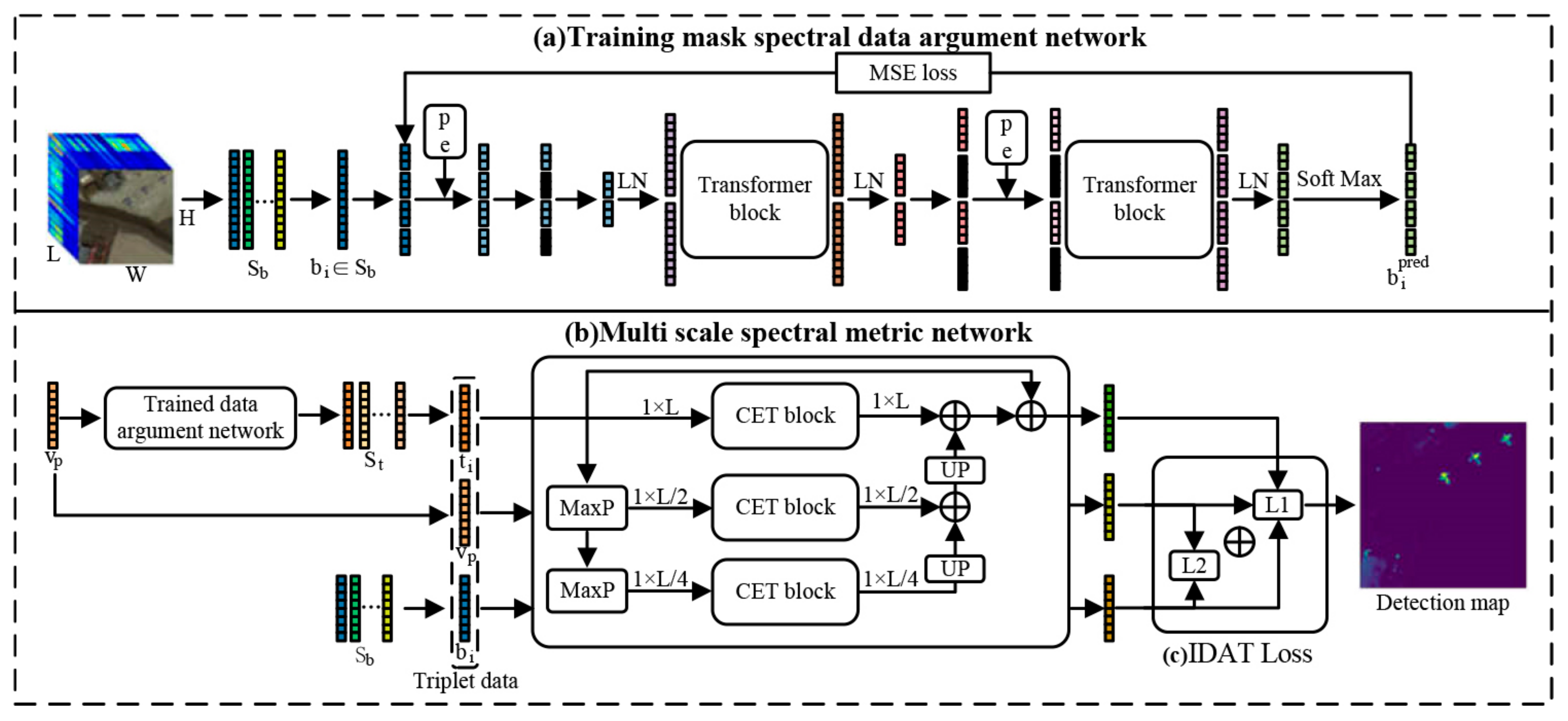
2.2. Methods
2.2.1. Masked Spectral Data Augmentation Network
2.2.2. Multi Scale Spectral Metric Network
2.2.3. Inter-Class Difference Amplification Triplet Loss
3. Results
3.1. Experimental Results
3.1.1. Datasets
3.1.2. Evaluation Indicators
3.1.3. Parameter Setting
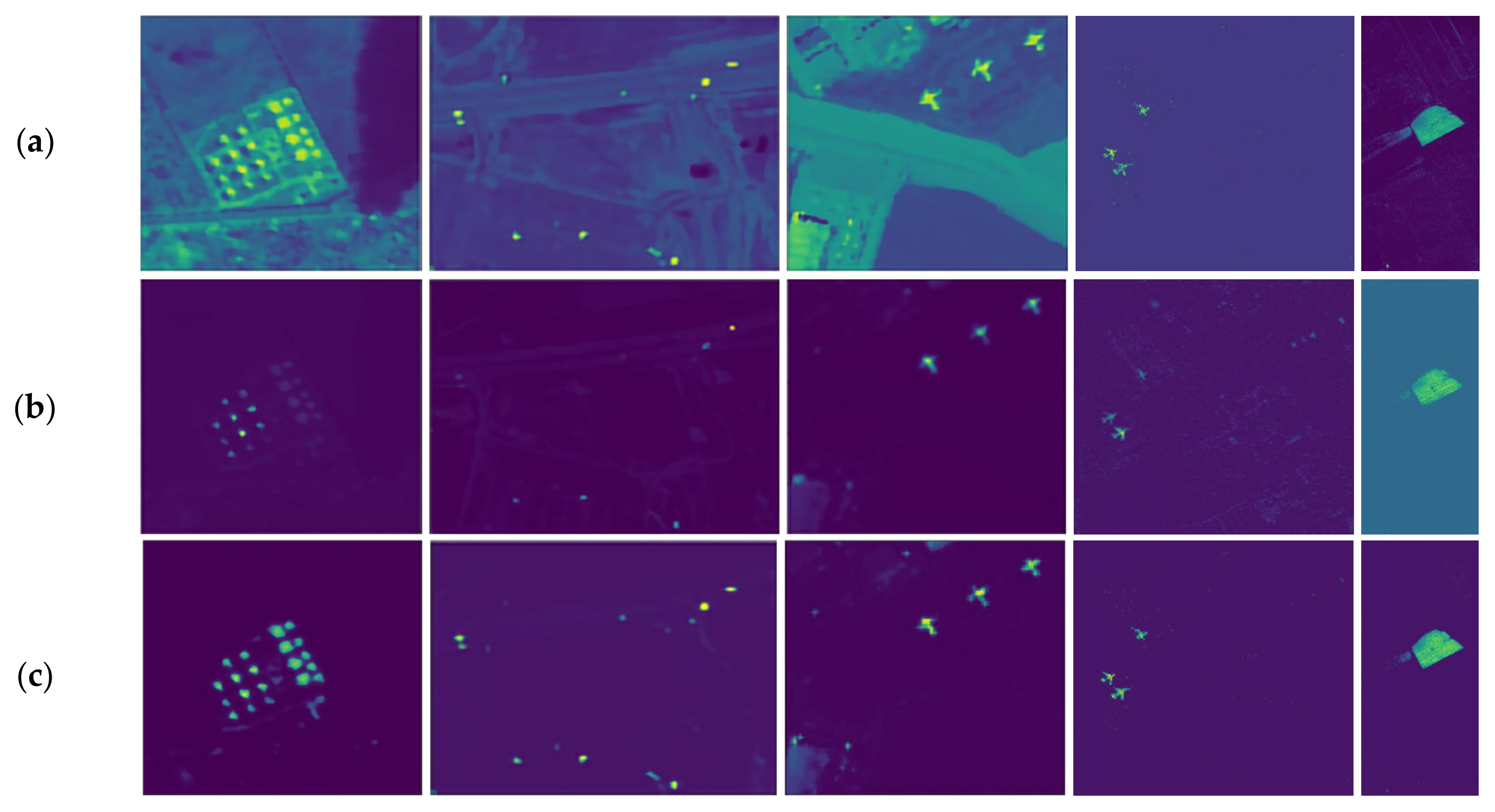
3.2. Comparison of the Experimental Results
3.3. Experimental Setup
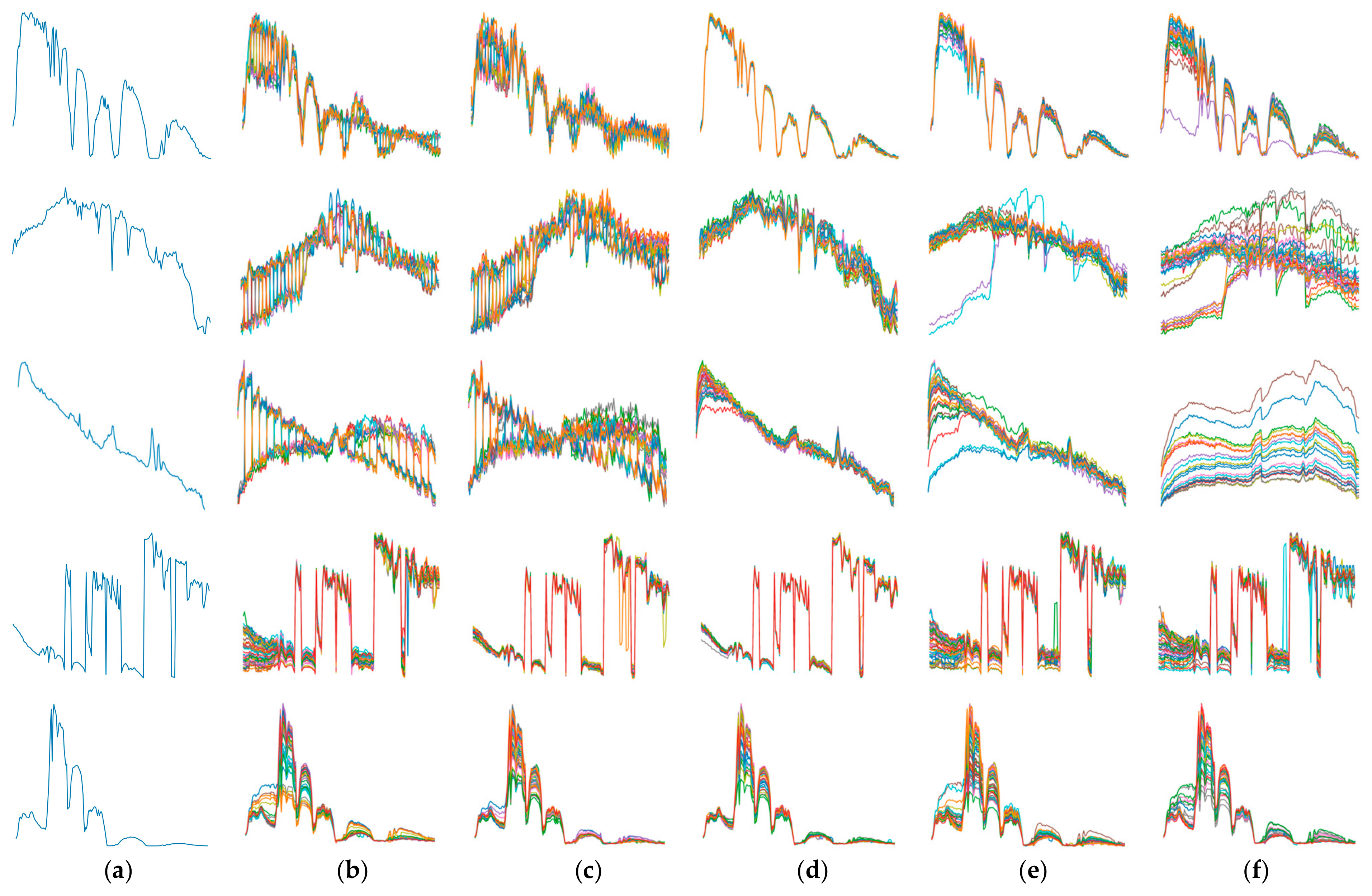
3.4. Ablation Experiments
4. Discussion
- The data amount is too large, so processing these data requires not only efficient algorithms but also powerful computational capabilities to support fast analysis;
- Factors such as light, weather, and noise are difficult to control, which challenges the robustness of the algorithm.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, B.; Dao, P.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Wang, S.; Guan, K.; Zhang, C.; Lee, D.; Margenot, A.J.; Ge, Y.; Peng, J.; Zhou, W.; Zhou, Q.; Huang, Y. Using Soil Library Hyperspectral Reflectance and Machine Learning to Predict Soil Organic Carbon: Assessing Potential of Airborne and Spaceborne Optical Soil Sensing. Remote Sens. Environ. 2022, 271, 112914. [Google Scholar] [CrossRef]
- Almeida, D.R.A.D.; Broadbent, E.N.; Ferreira, M.P.; Meli, P.; Zambrano, A.M.A.; Gorgens, E.B.; Resende, A.F.; De Almeida, C.T.; Do Amaral, C.H.; Corte, A.P.D.; et al. Monitoring Restored Tropical Forest Diversity and Structure through UAV-Borne Hyperspectral and Lidar Fusion. Remote Sens. Environ. 2021, 264, 112582. [Google Scholar] [CrossRef]
- Makki, I.; Younes, R.; Francis, C.; Bianchi, T.; Zucchetti, M. A Survey of Landmine Detection Using Hyperspectral Imaging. ISPRS J. Photogramm. Remote Sens. 2017, 124, 40–53. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, Y.; Yao, L.; Liu, X.; Wang, F. Mineral Target Detection Based on MSCPE_BSE in Hyperspectral Image. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1614–1617. [Google Scholar]
- Zhang, L.; Ma, J.; Fu, B.; Lin, F.; Sun, Y.; Wang, F. Improved Central Attention Network-Based Tensor RX for Hyperspectral Anomaly Detection. Remote Sens. 2022, 14, 5865. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection Algorithms in Hyperspectral Imaging Systems: An Overview of Practical Algorithms. IEEE Signal Process. Mag. 2014, 31, 24–33. [Google Scholar] [CrossRef]
- Chang, C.I. Spectral Information Divergence for Hyperspectral Image Analysis. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium. IGARSS’99 (Cat. No.99CH36293), Hamburg, Germany, 28 June–2 July 1999; Volume 1, pp. 509–511. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The Spectral Image Processing System (SIPS)-Interactive Visualization and Analysis of Imaging Spectrometer Data. AIP Conf. Proc. 1993, 283, 192–201. [Google Scholar]
- Zou, Z.; Shi, Z. Hierarchical Suppression Method for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 330–342. [Google Scholar] [CrossRef]
- Yang, X.; Chen, J.; He, Z. Sparse-SpatialCEM for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2184–2195. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, M.; Shi, S.; Chen, J. Deep Constrained Energy Minimization for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 8049–8063. [Google Scholar] [CrossRef]
- Chang, C.I. Orthogonal Subspace Projection (OSP) Revisited: A Comprehensive Study and Analysis. IEEE Trans. Geosci. Remote Sens. 2005, 43, 502–518. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. Two-Stream Convolutional Networks for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6907–6921. [Google Scholar] [CrossRef]
- Gao, L.; Chen, L.; Liu, P.; Jiang, Y.; Xie, W.; Li, Y. A Transformer-Based Network for Hyperspectral Object Tracking. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5528211. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, K.; Wang, J.; Hu, Z.; Wang, H.; Wang, P.; Zhao, X.; Li, W. Self-Supervised Learning with Deep Clustering for Target Detection in Hyperspectral Images with Insufficient Spectral Variation Prior. Int. J. Appl. Earth Obs. Geoinf. 2023, 122, 103405. [Google Scholar] [CrossRef]
- Koch, G.; Zemel, R.; Salakhutdinov, R. Siamese Neural Networks for One-Shot Image Recognition. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Jiao, J.; Gong, Z.; Zhong, P. Triplet Spectralwise Transformer Network for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5519817. [Google Scholar] [CrossRef]
- Qin, H.; Xie, W.; Li, Y.; Jiang, K.; Lei, J.; Du, Q. Weakly Supervised Adversarial Learning via Latent Space for Hyperspectral Target Detection. Pattern Recognit. 2023, 135, 109125. [Google Scholar] [CrossRef]
- Rao, W.; Gao, L.; Qu, Y.; Sun, X.; Zhang, B.; Chanussot, J. Siamese Transformer Network for Hyperspectral Image Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5526419. [Google Scholar] [CrossRef]
- Qin, J.; Fang, L.; Lu, R.; Lin, L.; Shi, Y. ADASR: An Adversarial Auto-Augmentation Framework for Hyperspectral and Multispectral Data Fusion. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5002705. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, Z.; Wang, X.; Gong, M.; Wu, Y.; Li, H. Features Kept Generative Adversarial Network Data Augmentation Strategy for Hyperspectral Image Classification. Pattern Recognit. 2023, 142, 109701. [Google Scholar] [CrossRef]
- Wang, W.; Chen, Y.; He, X.; Li, Z. Soft Augmentation-Based Siamese CNN for Hyperspectral Image Classification with Limited Training Samples. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5508505. [Google Scholar] [CrossRef]
- Gao, Y.; Feng, Y.; Yu, X. Hyperspectral Target Detection with an Auxiliary Generative Adversarial Network. Remote Sens. 2021, 13, 4454. [Google Scholar] [CrossRef]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked Autoencoders Are Scalable Vision Learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar]
- Wang, Y.; Chen, X.; Wang, F.; Song, M.; Yu, C. Meta-Learning Based Hyperspectral Target Detection Using Siamese Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5527913. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, K.; Wang, J.; Hu, Z.; Wang, H.; Wang, P. Siamese Network Ensembles for Hyperspectral Target Detection with Pseudo Data Generation. Remote Sens. 2022, 14, 1260. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Y.; Chen, Z.; Xu, F.; Hong, D.; Zhang, B. Hyperspectral Target Detection via Spectral Aggregation and Separation Network With Target Band Random Mask. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5515516. [Google Scholar] [CrossRef]
- Jiao, J.; Gong, Z.; Zhong, P. Dual-Branch Fourier-Mixing Transformer Network for Hyperspectral Target Detection. Remote Sens. 2023, 15, 4675. [Google Scholar] [CrossRef]
- Chen, X.; Ding, M.; Wang, X.; Xin, Y.; Mo, S.; Wang, Y.; Han, S.; Luo, P.; Zeng, G.; Wang, J. Context Autoencoder for Self-Supervised Representation Learning. Int. J. Comput. Vis. 2024, 132, 208–223. [Google Scholar] [CrossRef]
- Ly, S.T.; Lin, B.; Vo, H.Q.; Maric, D.; Roysam, B.; Nguyen, H.V. Cellular Data Extraction from Multiplexed Brain Imaging Data Using Self-Supervised Dual-Loss Adaptive Masked Autoencoder. Artif. Intell. Med. 2024, 151, 102828. [Google Scholar] [CrossRef]
- Guo, Q.; Cen, Y.; Zhang, L.; Zhang, Y.; Huang, Y. Hyperspectral Anomaly Detection Based on Spatial–Spectral Cross-Guided Mask Autoencoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9876–9889. [Google Scholar] [CrossRef]
- Boutros, F.; Damer, N.; Kirchbuchner, F.; Kuijper, A. Self-Restrained Triplet Loss for Accurate Masked Face Recognition. Pattern Recognit. 2022, 124, 108473. [Google Scholar] [CrossRef]
- Xie, W.; Wu, H.; Tian, Y.; Bai, M.; Shen, L. Triplet Loss With Multistage Outlier Suppression and Class-Pair Margins for Facial Expression Recognition. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 690–703. [Google Scholar] [CrossRef]
- Chen, J.; Lai, H.; Geng, L.; Pan, Y. Improving Deep Binary Embedding Networks by Order-Aware Reweighting of Triplets. arXiv 2018, arXiv:1804.06061. [Google Scholar]

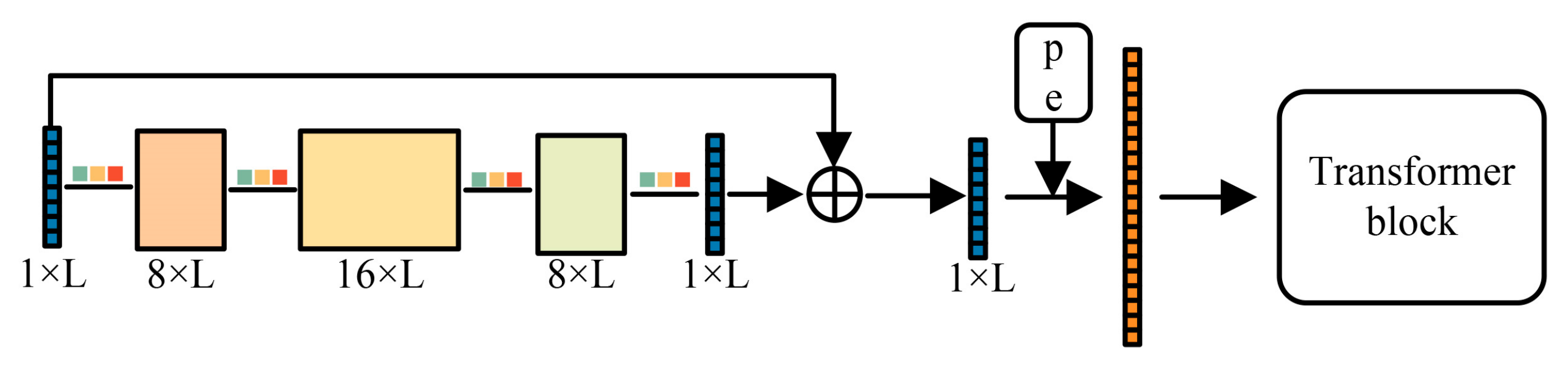





| Input | Kernel Size | Number of Convolution Kernels | Padding Size | Stride | Output Size |
|---|---|---|---|---|---|
| 1 × 5 | 8, 16, 8 | 2 | 1 | L | |
| 1 × 3 | 8, 16, 8 | 1 | 1 | L/2 | |
| 1 × 1 | 8, 16, 8 | 0 | 1 | L/4 |
| Methods | ABU | HYDICE | San Diego A | San Diego B | Salinas |
|---|---|---|---|---|---|
| CEM | 0.9842 | 0.6812 | 0.9902 | 0.4974 | 0.8853 |
| ACE | 0.7554 | 0.7103 | 0.9830 | 0.6346 | 0.9409 |
| OSP | 0.9133 | 0.7935 | 0.6735 | 0.2061 | 0.7896 |
| MF | 0.6685 | 0.9176 | 0.9753 | 0.7142 | 0.8431 |
| SFCTD | 0.9965 | 0.9972 | 0.9937 | 0.8824 | 0.9662 |
| TSCNTD | 0.9934 | 0.9499 | 0.9924 | 0.7727 | 0.9504 |
| TSTTD | 0.9935 | 0.9979 | 0.9959 | 0.9817 | 0.9685 |
| Ours | 0.9992 | 0.9998 | 0.9983 | 0.9999 | 0.9994 |
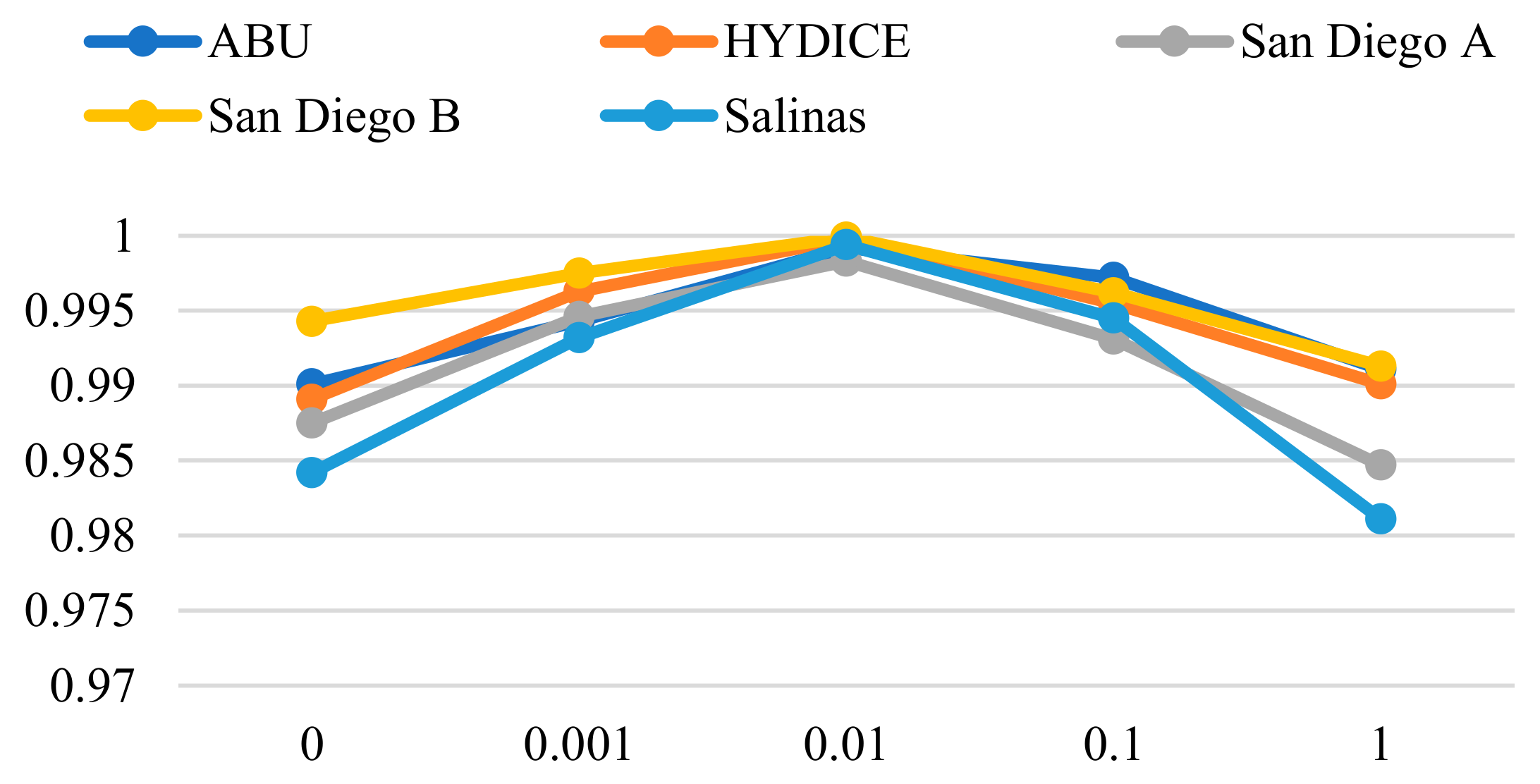
| Mask Ratio | ABU | HYDICE | San Diego A | San Diego B | Salinas |
|---|---|---|---|---|---|
| 25% | 0.8611 | 0.8731 | 0.8581 | 0.9903 | 0.9930 |
| 50% | 0.8827 | 0.8628 | 0.8603 | 0.9971 | 0.9988 |
| 75% | 0.9992 | 0.9998 | 0.9983 | 0.9999 | 0.9994 |
| 85% | 0.9951 | 0.9732 | 0.9903 | 0.9892 | 0.9941 |
| 95% | 0.9916 | 0.8755 | 0.7114 | 0.9867 | 0.9923 |
| Global | Local | ABU | HYDICE | San Diego A | San Diego B | Salinas |
|---|---|---|---|---|---|---|
| √ | 0.9982 | 0.9881 | 0.9828 | 0.9911 | 0.9855 | |
| √ | 0.9972 | 0.9994 | 0.9973 | 0.9906 | 0.9978 | |
| √ | √ | 0.9992 | 0.9998 | 0.9983 | 0.9999 | 0.9994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Z.; Lan, J.; Zeng, Y. Hyperspectral Target Detection Based on Masked Autoencoder Data Augmentation. Remote Sens. 2025, 17, 1097. https://doi.org/10.3390/rs17061097
Zhuang Z, Lan J, Zeng Y. Hyperspectral Target Detection Based on Masked Autoencoder Data Augmentation. Remote Sensing. 2025; 17(6):1097. https://doi.org/10.3390/rs17061097
Chicago/Turabian StyleZhuang, Zhixuan, Jinhui Lan, and Yiliang Zeng. 2025. "Hyperspectral Target Detection Based on Masked Autoencoder Data Augmentation" Remote Sensing 17, no. 6: 1097. https://doi.org/10.3390/rs17061097
APA StyleZhuang, Z., Lan, J., & Zeng, Y. (2025). Hyperspectral Target Detection Based on Masked Autoencoder Data Augmentation. Remote Sensing, 17(6), 1097. https://doi.org/10.3390/rs17061097







