INS/LiDAR Relative Navigation Design Based on Point Cloud Covariance Characteristics for Spacecraft Proximity Operation
Abstract
1. Introduction
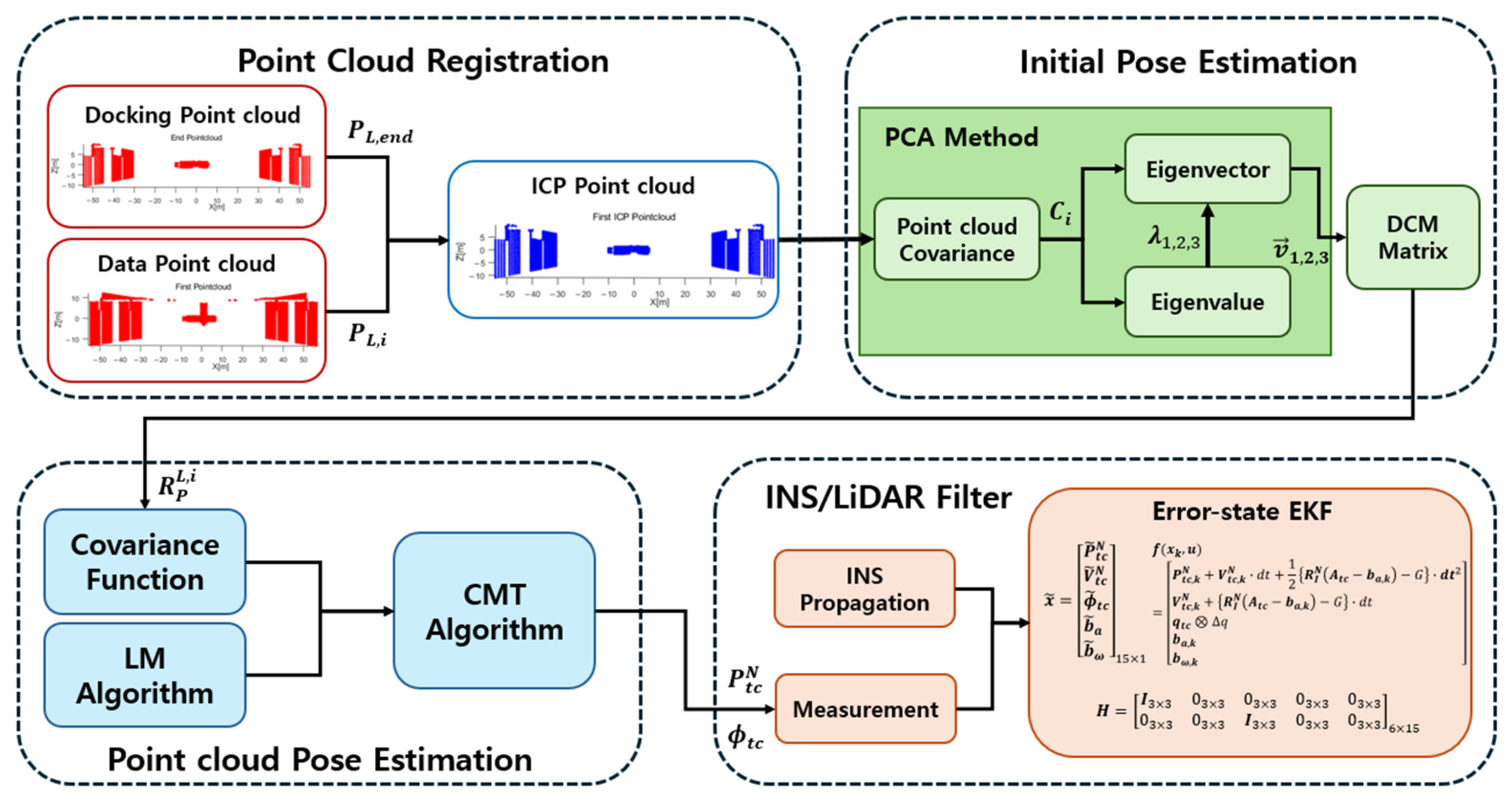
2. Background Methods
2.1. PCA Method
2.2. CMT Method
3. Point Cloud Pose Estimation
4. Simulation Study
4.1. Simulation Environment
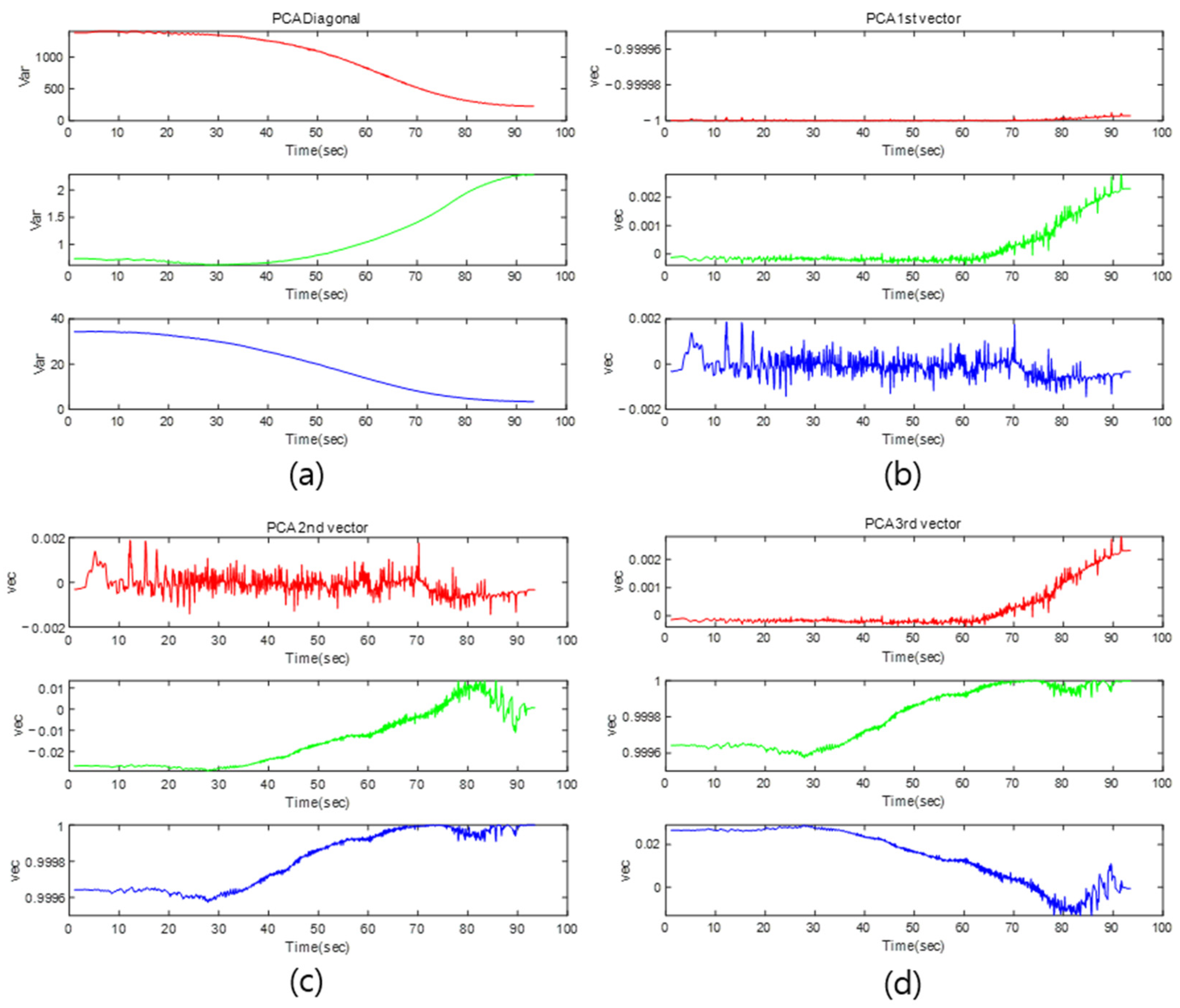
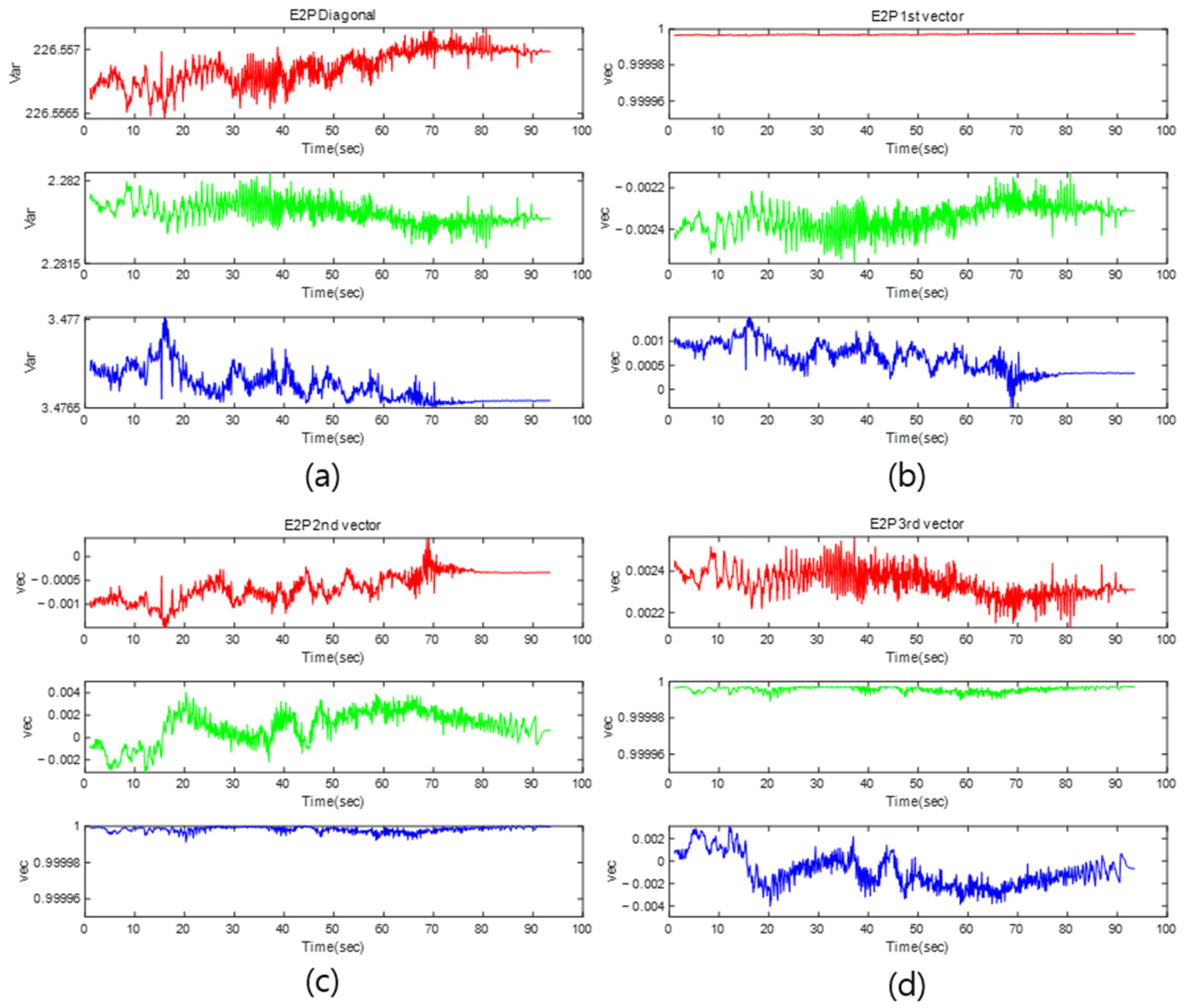
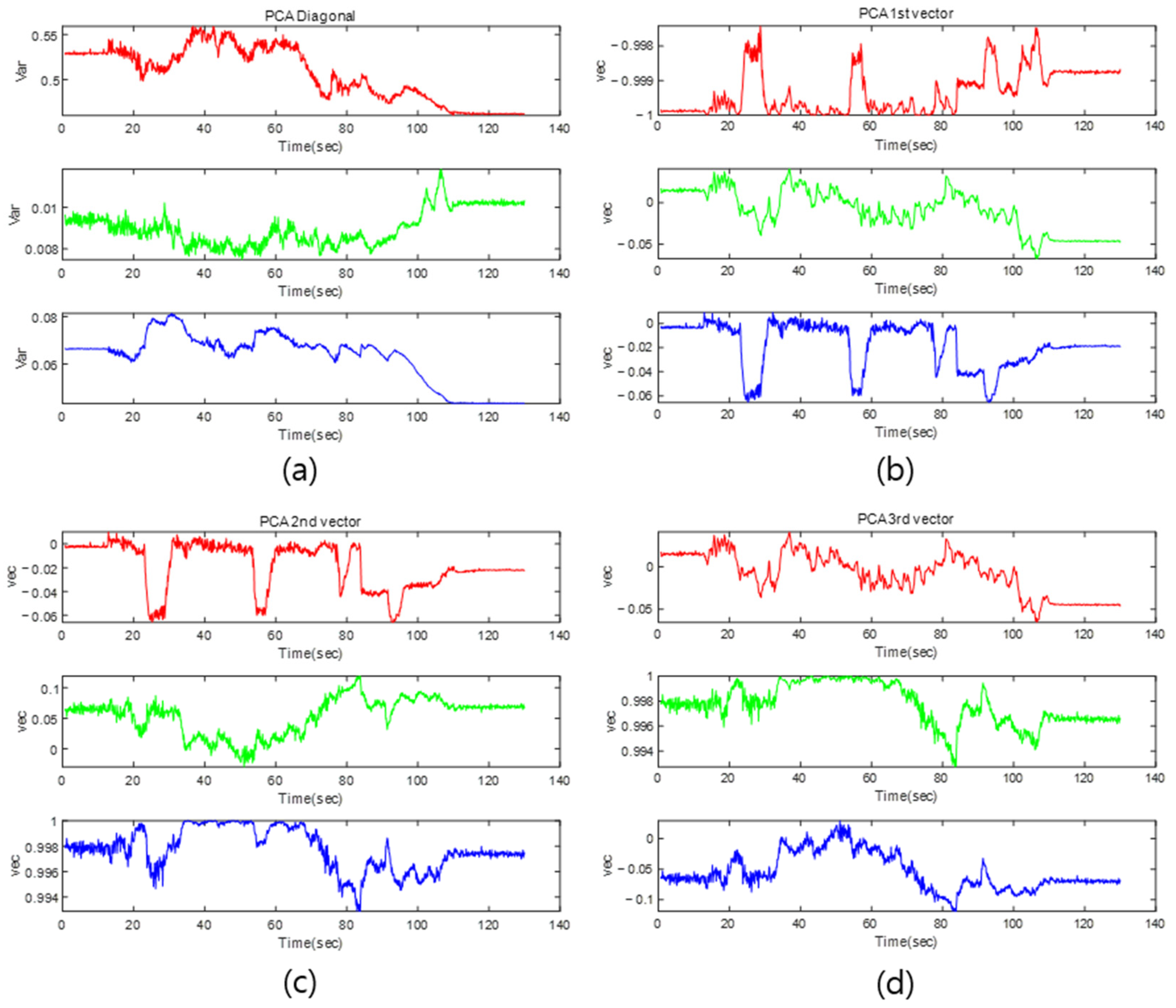
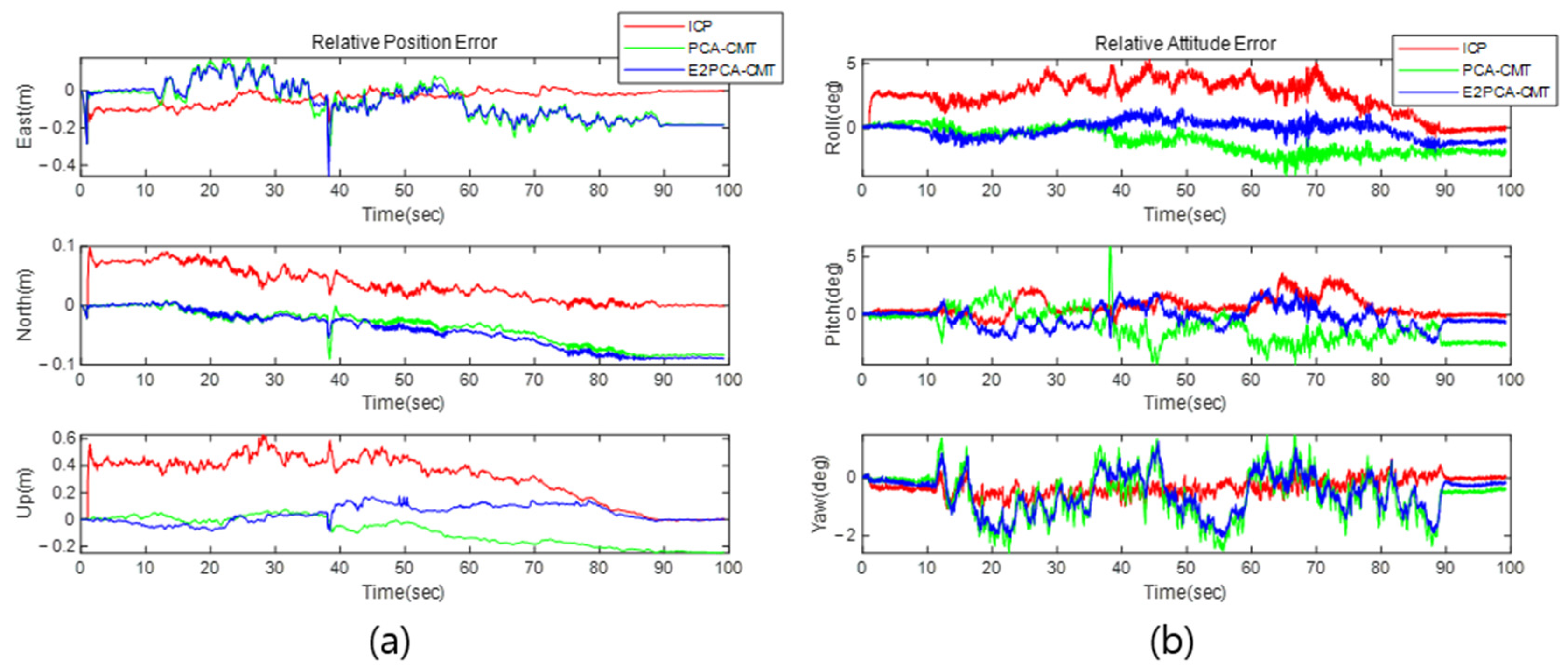
4.2. Simulation Result
5. Experiment Study
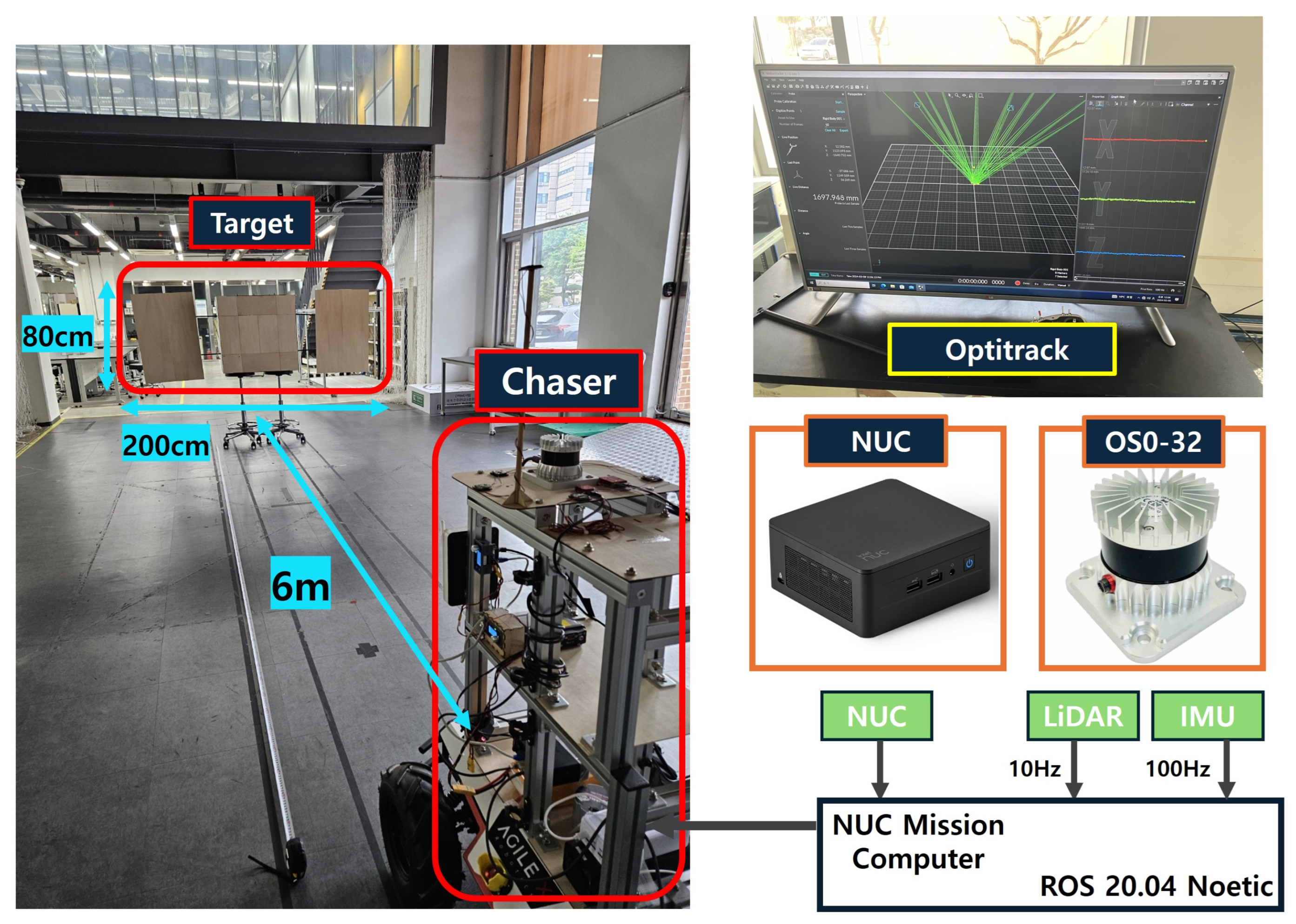
5.1. Experiment Environment
5.2. Experiment Result
6. Discussion
6.1. Performance Analysis of Algorithms Based on Point Cloud Estimation Results
6.2. Loosely Coupled EKF Filter Design Based on Measurements and the INS Model
6.3. Analysis of the Real-Time and Practical Application of Algorithms
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, X.; He, Y.; Chen, L.; Gao, S. Pose estimation of large non-cooperative spacecraft based on extended PnP model. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 413–418. [Google Scholar]
- Du, X.; Liang, B.; Xu, W.; Qiu, Y. Pose measurement of large non-cooperative satellite based on collaborative cameras. Acta Astronaut. 2011, 68, 2047–2065. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A review of cooperative and uncooperative spacecraft pose determination techniques for close-proximity operations. Prog. Aerosp. Sci. 2017, 93, 53–72. [Google Scholar] [CrossRef]
- Bezouska, W.; Barnhart, D. Decentralized cooperative localization with relative pose estimation for a spacecraft swarm. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–13. [Google Scholar]
- Martínez, H.G.; Giorgi, G.; Eissfeller, B. Pose estimation and tracking of non-cooperative rocket bodies using time-of-flight cameras. Acta Astronaut. 2017, 139, 165–175. [Google Scholar] [CrossRef]
- Perfetto, D.M.; Opromolla, R.; Grassi, M.; Schmitt, C. LIDAR-based model reconstruction for spacecraft pose determination. In Proceedings of the 2019 IEEE 5th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Turin, Italy, 19–21 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Mark, C.P.; Kamath, S. Review of active space debris removal methods. Space Policy 2019, 47, 194–206. [Google Scholar] [CrossRef]
- Woods, J.O.; Christian, J.A. Lidar-based relative navigation with respect to non-cooperative objects. Acta Astronaut. 2016, 126, 298–311. [Google Scholar]
- He, Y.; Liang, B.; He, J.; Li, S. Non-cooperative spacecraft pose tracking based on point cloud feature. Acta Astronaut. 2017, 139, 213–221. [Google Scholar]
- He, Y.; Yang, J.; Xiao, K.; Sun, C.; Chen, J. Pose tracking of spacecraft based on point cloud DCA features. IEEE Sens. J. 2022, 22, 5834–5843. [Google Scholar]
- Li, P.; Wang, M.; Zhou, D.; Lei, W. A pose measurement method of a non-cooperative spacecraft based on point cloud feature. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 4977–4982. [Google Scholar]
- Chen, Z.; Li, L.; Niu, K.; Wu, Y.; Hua, B. Pose measurement of non-cooperative spacecraft based on point cloud. In Proceedings of the 2018 IEEE CSAA Guidance, Navigation and Control Conference (CGNCC), Xiamen, China, 10–12 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. Pose estimation for spacecraft relative navigation using model-based algorithms. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 431–447. [Google Scholar] [CrossRef]
- Yuan, C.; Yu, X.; Luo, Z. 3D point cloud matching based on principal component analysis and iterative closest point algorithm. In Proceedings of the 2016 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 11–12 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 404–408. [Google Scholar]
- Zhang, G.; Huo, J.; Zhang, Z.; He, M.; Zhang, J.; Xue, M. Novel pose measurement with optimized principal component analysis for unknown spacecraft based on point cloud. In Proceedings of the 5th International Conference on Multimedia and Image Processing, Nanjing, China, 10–12 January 2020; pp. 102–108. [Google Scholar]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Proceedings of the Sensor Fusion IV: Control Paradigms and Data Structures, Boston, MA, USA, 12–15 November 1992; Volume 1611, pp. 586–606. [Google Scholar]
- Kang, G.; Zhang, Q.; Wu, J.; Zhang, H. Pose estimation of a non-cooperative spacecraft without the detection and recognition of point cloud features. Acta Astronaut. 2021, 179, 569–580. [Google Scholar]
- Gavin, H.P. The Levenberg-Marquardt Algorithm for Nonlinear Least Squares Curve-Fitting Problems; Department of Civil and Environmental Engineering, Duke University: Durham, NC, USA, 2019; Volume 3. [Google Scholar]








| LiDAR Sensor | OS0-64 |
|---|---|
| Maximum range | 0.5 m |
| Minimum range | 300 m |
| Vertical Resolution | 64 |
| Horizontal Resolution | 1024 |
| Field of View | Horizontal: 360° Vertical: −11.25°~11.25° |
| Algorithm | Position RMSE (m) | Attitude RMSE (deg) | ||||
|---|---|---|---|---|---|---|
| East | North | Up | Roll | Pitch | Yaw | |
| INS/ICP EKF | 0.0484 | 0.0122 | 0.4616 | 0.1275 | 0.0095 | 0.0050 |
| INS/PCA-CMT EKF | 0.2439 | 0.6802 | 0.4736 | 0.6331 | 0.0183 | 0.0071 |
| INS/E2PCA-CMT EKF | 0.0411 | 0.0249 | 0.0097 | 0.0177 | 0.0008 | 0.0245 |
| LiDAR Sensor | OS0–32 |
|---|---|
| Maximum range | 0.5 m |
| Minimum range | 50 m |
| Vertical Resolution | 32 |
| Horizontal Resolution | 1024 |
| Field of View | Horizontal: 360° Vertical: −45°~45° |
| Algorithm | Attitude RMSE (deg) | ||
|---|---|---|---|
| Roll | Pitch | Yaw | |
| ICP | 3.0079 | 1.0836 | 0.4075 |
| PCA-CMT | 0.4400 | 1.4324 | 1.8030 |
| E2PCA-CMT | 0.7755 | 0.9009 | 0.8739 |
| Algorithm | Position RMSE (m) | Attitude RMSE (deg) | ||||
|---|---|---|---|---|---|---|
| East | North | Up | Roll | Pitch | Yaw | |
| INS/ICP EKF | 0.0538 | 0.0386 | 0.3738 | 2.9988 | 1.0878 | 0.3847 |
| INS/PCA-CMT EKF | 0.1123 | 0.0523 | 0.0620 | 0.7746 | 1.6721 | 1.0015 |
| INS/E2PCA-CMT EKF | 0.1043 | 0.0550 | 0.0556 | 0.3445 | 0.7485 | 1.0163 |
| PC Specification | System |
|---|---|
| Processor | 13th Intel® Core i5-13600KF 3.50 GHz |
| Installed RAM | 64.0 GB DDR5 |
| Operating system | Window 11, 64 bits |
| Graphics | NVIDIA GeForce RTX 4070 Ti |
| MATLAB version | MATLAB R2023b |
| Algorithm | Simulation | Experiment | ||
|---|---|---|---|---|
| Total Time | Data Number | Total Time | Data Number | |
| ICP | 61.025 s | 925 × 10 Hz and 20,000 point | 6.47 s | 1324 × 10 Hz and 1000 point |
| E2PCA | 104.621 s | 7.488 s | ||
| E2PCA-CMT | 222.267 s | 13.97 s | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.; Shin, H.; Sung, S. INS/LiDAR Relative Navigation Design Based on Point Cloud Covariance Characteristics for Spacecraft Proximity Operation. Remote Sens. 2025, 17, 1091. https://doi.org/10.3390/rs17061091
Park D, Shin H, Sung S. INS/LiDAR Relative Navigation Design Based on Point Cloud Covariance Characteristics for Spacecraft Proximity Operation. Remote Sensing. 2025; 17(6):1091. https://doi.org/10.3390/rs17061091
Chicago/Turabian StylePark, Dongyeon, Hyeongseob Shin, and Sangkyung Sung. 2025. "INS/LiDAR Relative Navigation Design Based on Point Cloud Covariance Characteristics for Spacecraft Proximity Operation" Remote Sensing 17, no. 6: 1091. https://doi.org/10.3390/rs17061091
APA StylePark, D., Shin, H., & Sung, S. (2025). INS/LiDAR Relative Navigation Design Based on Point Cloud Covariance Characteristics for Spacecraft Proximity Operation. Remote Sensing, 17(6), 1091. https://doi.org/10.3390/rs17061091





