Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling
Abstract
1. Introduction
- To project future climate conditions under SSP (Shared Socioeconomic Pathway) scenarios.
- To use advanced modeling techniques to predict future land use and land cover changes, explicitly focusing on wetland areas.
- To forecast future changes in the distribution of wetlands under different climate change and land use pressure scenarios.
- To provide actionable insights for conservation planning and the sustainable management of aquatic ecosystems by offering accurate, high-resolution predictions for policymakers and stakeholders.
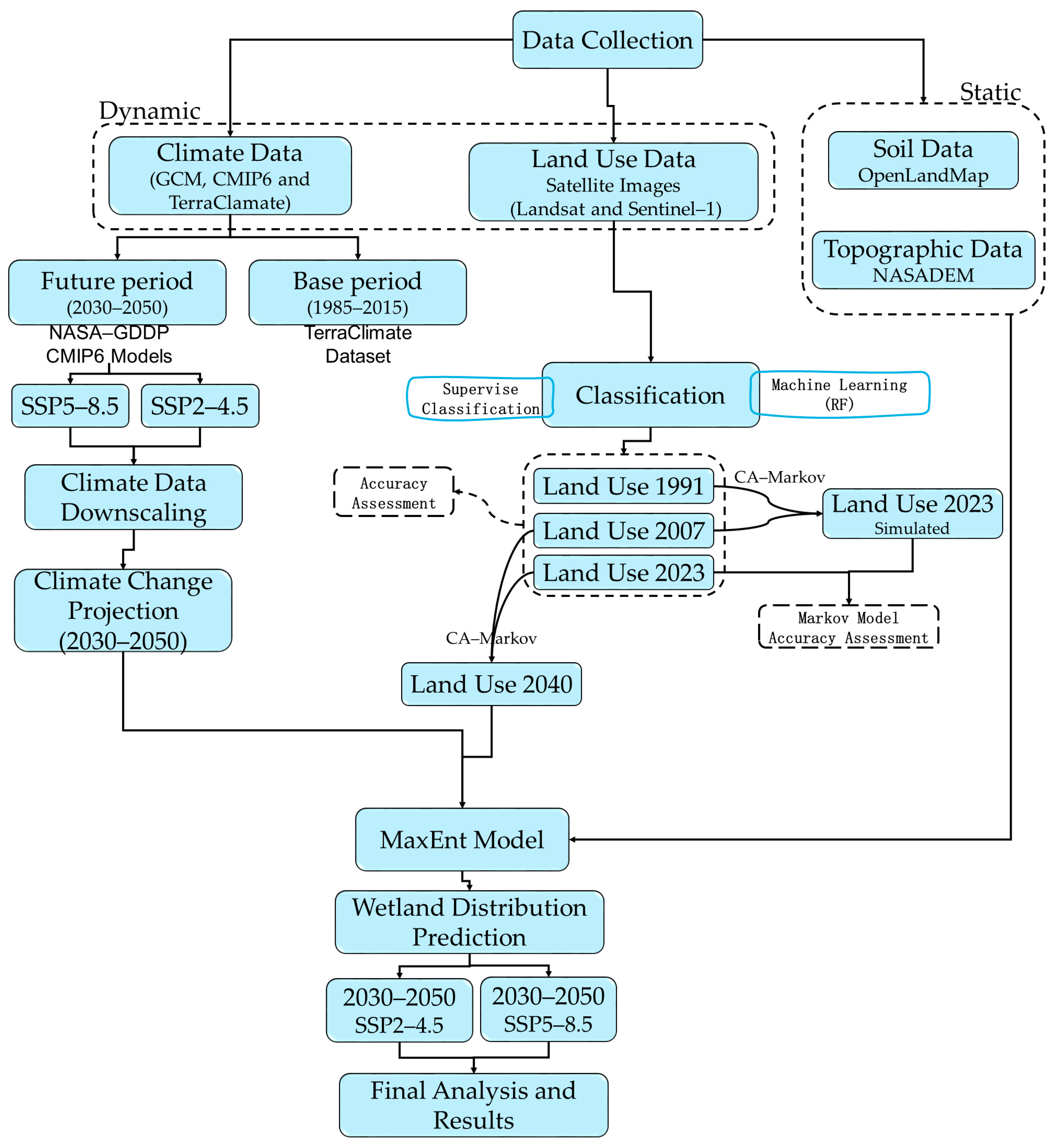
2. Materials and Methods
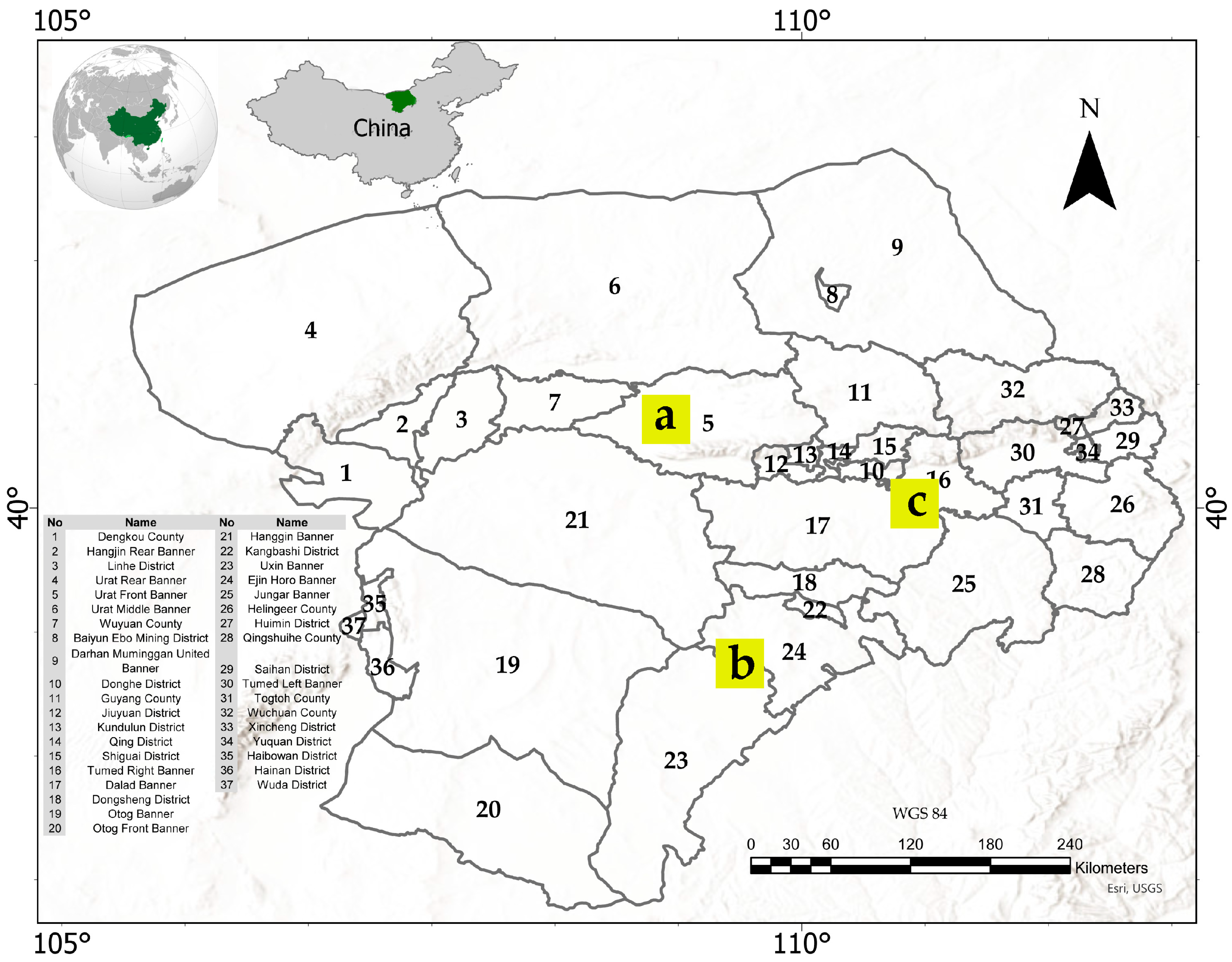
2.1. Study Area
2.2. Data Sources
2.2.1. Satellite-Based Remote Sensing Data
Remote Sensing Preprocessing (Landsat and Sentinel-1)
2.2.2. Topographic Data
2.2.3. Soil Data
2.2.4. Climate Data
2.2.5. Data Integration and Temporal Alignment
| No. | Dataset Name | Spatial Resolution | Temporal Coverage | Key Variables/Bands | Purpose | Source (Reference) |
|---|---|---|---|---|---|---|
| 1 | Copernicus Global Land Cover (2019) | 100 m | 2019 | discrete_classification | Land cover mapping and reference for classification | [29] |
| 2 | Sentinel-1 (GRD) | ~10 m | 1 January 2023–1 January 2024 | Radar bands VV, VH + derived indices | Extraction of radar backscatter features (VV, VH, and indices) for land use/cover classification | [30] |
| 3 | Landsat 8 C2 SR | 30 m | 1 January 2023–1 January 2024 | Reflective bands (B2-B7), NDVI, NDWI, NDTI | Calculation of spectral indices and time-series composites for land cover classification | [31] |
| 4 | Landsat 5 C2 SR | 30 m | 1 January 2007–1 January 2008 | Reflective bands (B1-B6), NDVI, NDWI, NDTI | Historical assessment of land surface conditions and spectral indices | [32] |
| 5 | NASADEM | ~30 m | - | Elevation | Extraction of topographic variables: elevation, slope, aspect | [22] |
| 6 | Landforms (SRTM-based) | 90 m | - | Constant (landforms) | Characterization of geomorphological landforms | [23] |
| 7 | OpenLandMap Soil Texture | 250 m | - | b0 | USDA texture classification of soils | [26] |
| 8 | TerraClimate | ~4 km | 1985–2015 (baseline) and 2023 | pr, tmmn, tmmx, srad | Baseline and annual climate variables (precipitation, temperature, radiation) | [18] |
| 9 | NASA/GDDP-CMIP6 | ~0.25° (~25 km) | 1985–2015/2030–2050 | tas, pr (under scenarios SSP2-4.5, SSP5-8.5) | Future climate projections (temperature and precipitation changes) | [19] |
2.3. Future Climate Projection and Downscaling
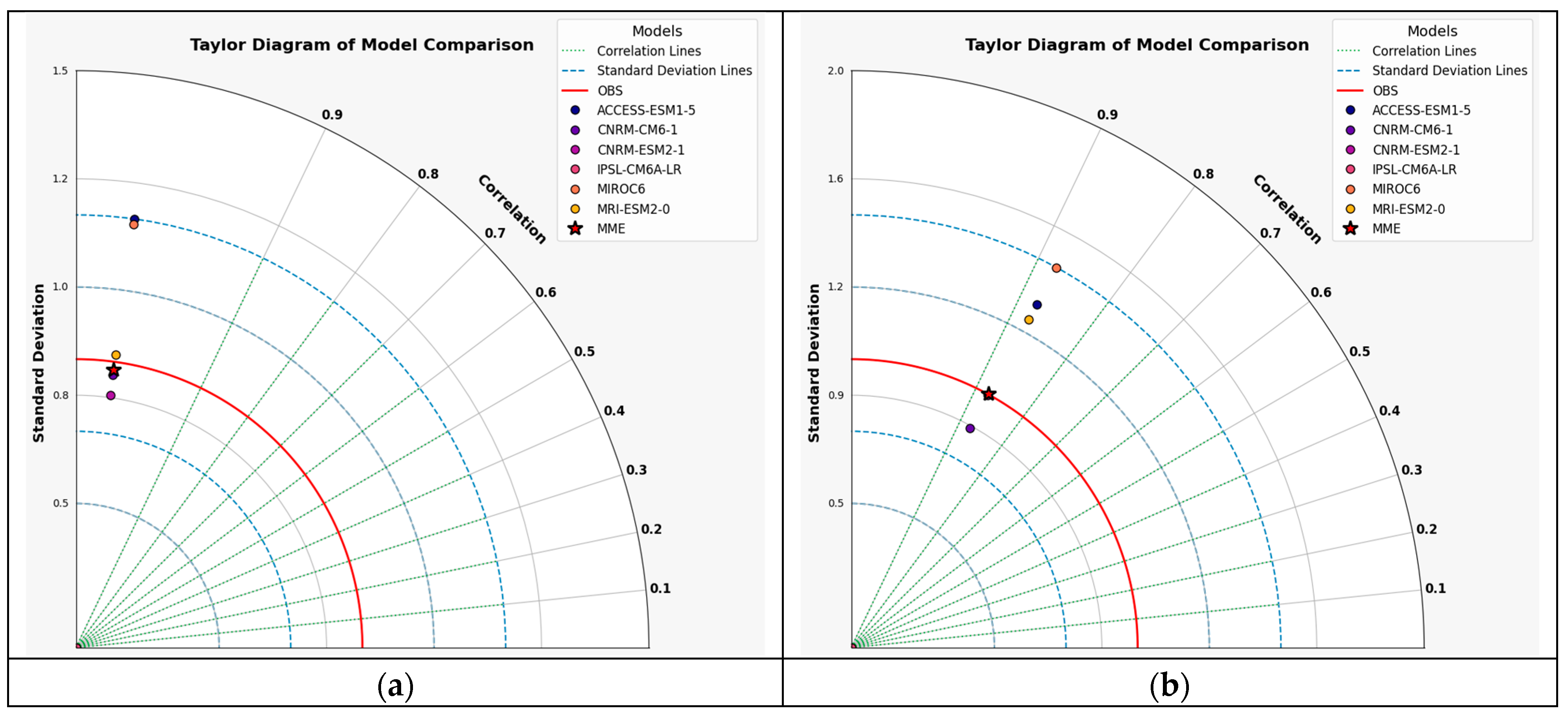
2.3.1. Model Selection via Taylor Diagrams
2.3.2. Multi-Model Mean and Scenarios (2030–2050)
2.3.3. Statistical Downscaling in the Google Earth Engine
Future Adjusted Temperature (Tadj)
Future Adjusted Precipitation (Padj)
2.3.4. GCMs Included in the Ensemble
2.4. Land Cover Mapping for 2007 and 2023
2.4.1. Land Cover Category Identification
2.4.2. Data Preprocessing and Index Computation
Normalized Difference Vegetation Index (NDVI)
Normalized Difference Water Index (NDWI)
Normalized Difference Tillage Index (NDTI)
2.4.3. Classification Using Random Forest
2.4.4. Sampling Strategy for Classification and Validation
2.4.5. Accuracy Assessment
2.5. Future Land Cover Projection in 2040
2.5.1. Markov Chain Component
Cellular Automata (CA) Transition Rules
CA–Markov Validation
2.6. MaxEnt Modeling of Wetland Presence (2023 and 2030–2050)
2.6.1. Variable Selection
2.6.2. MaxEnt Threshold Parameters
2.6.3. Future Projections
3. Results
3.1. Future Climate Projection and Downscaling
3.1.1. Selecting Best Model
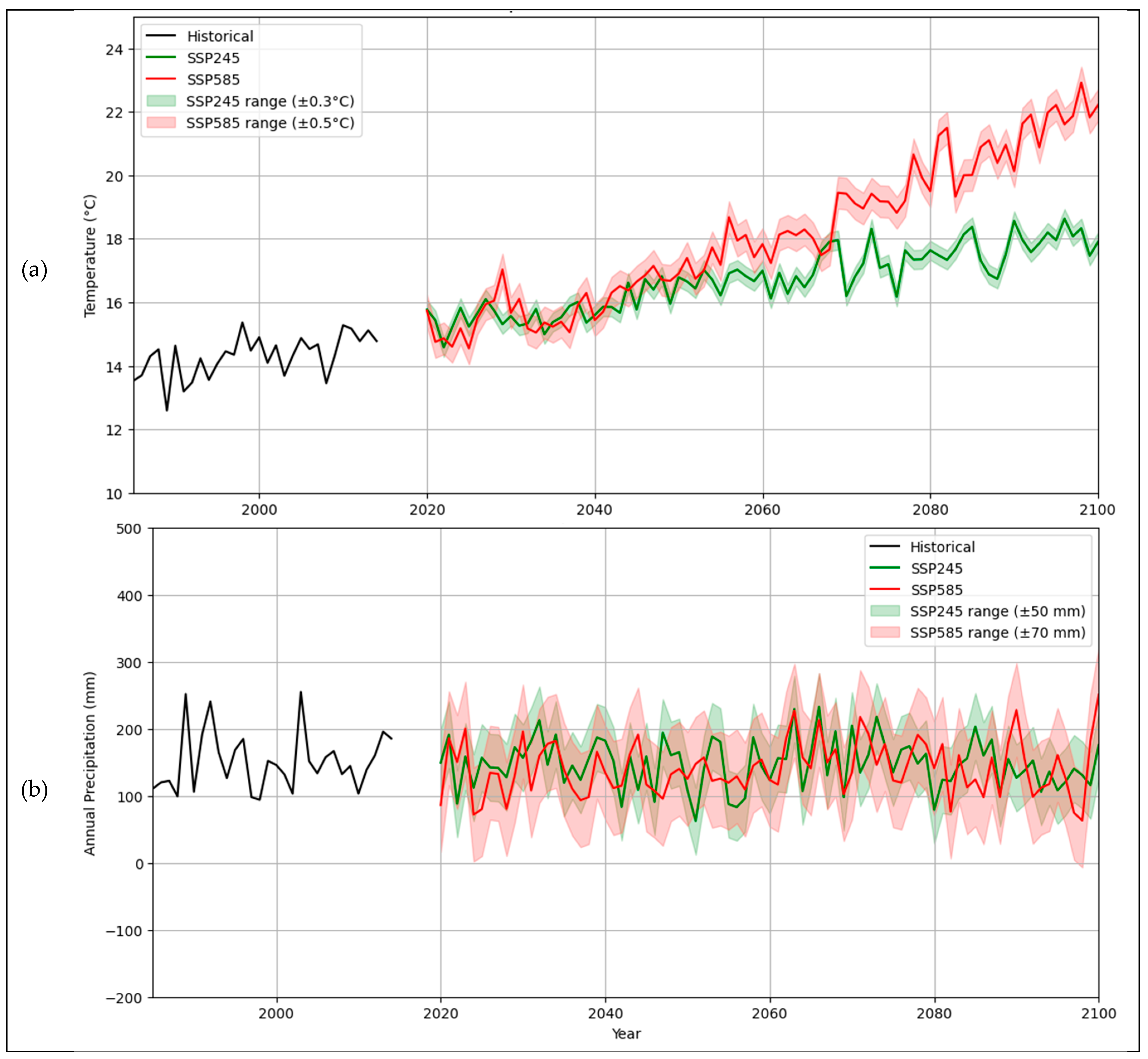
3.1.2. Projected Temperature and Precipitation Trends (1985–2100)
Temperature Trends (1985–2100)
Precipitation Trends (1985–2100)
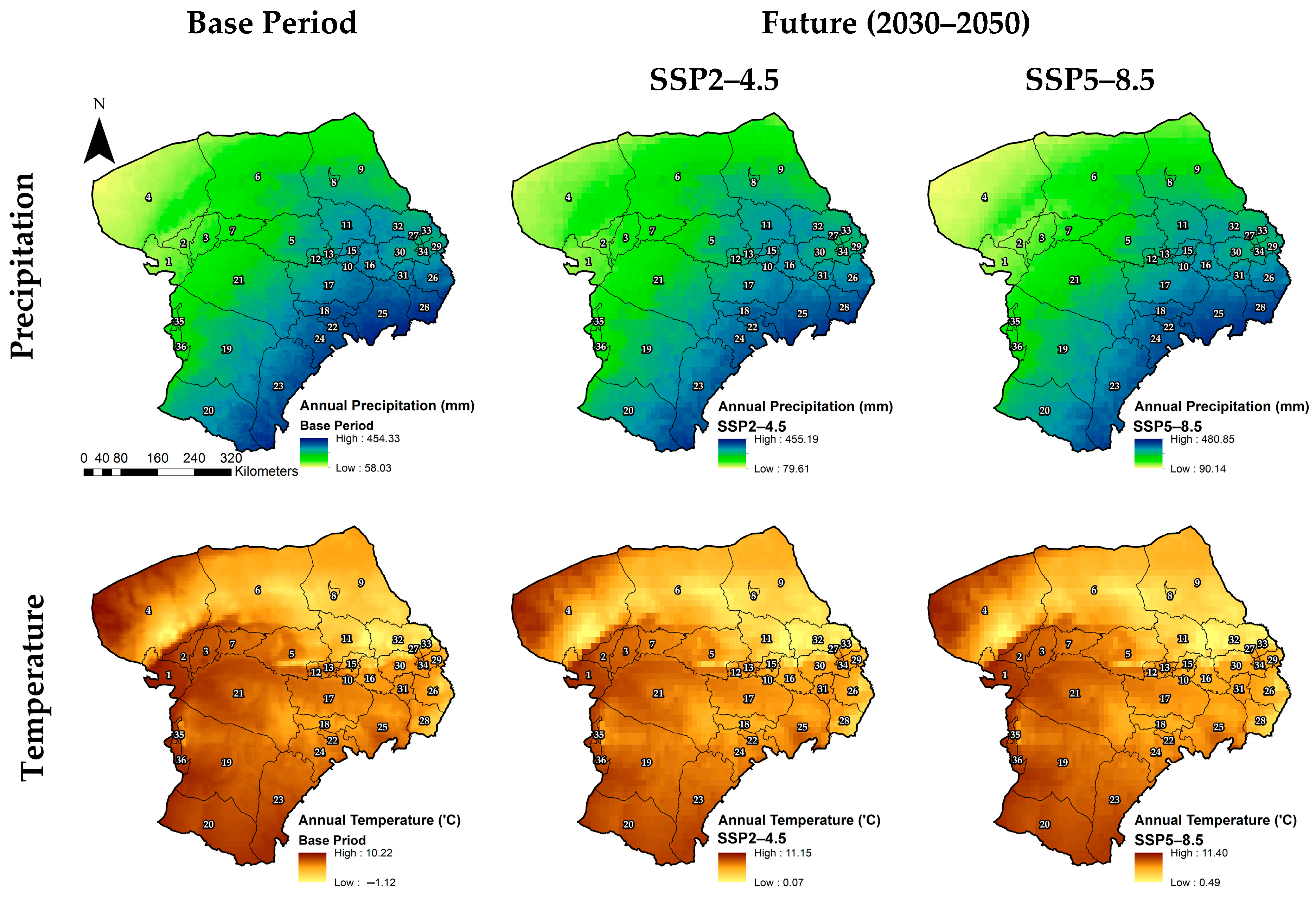
Sub-Region-Level Precipitation Changes (2030–2050)
Sub-Basin-Level Temperature Changes (2030–2050)
3.2. Land Cover Classes in the Study Area
3.3. Land Cover Mapping for 2007 and 2023
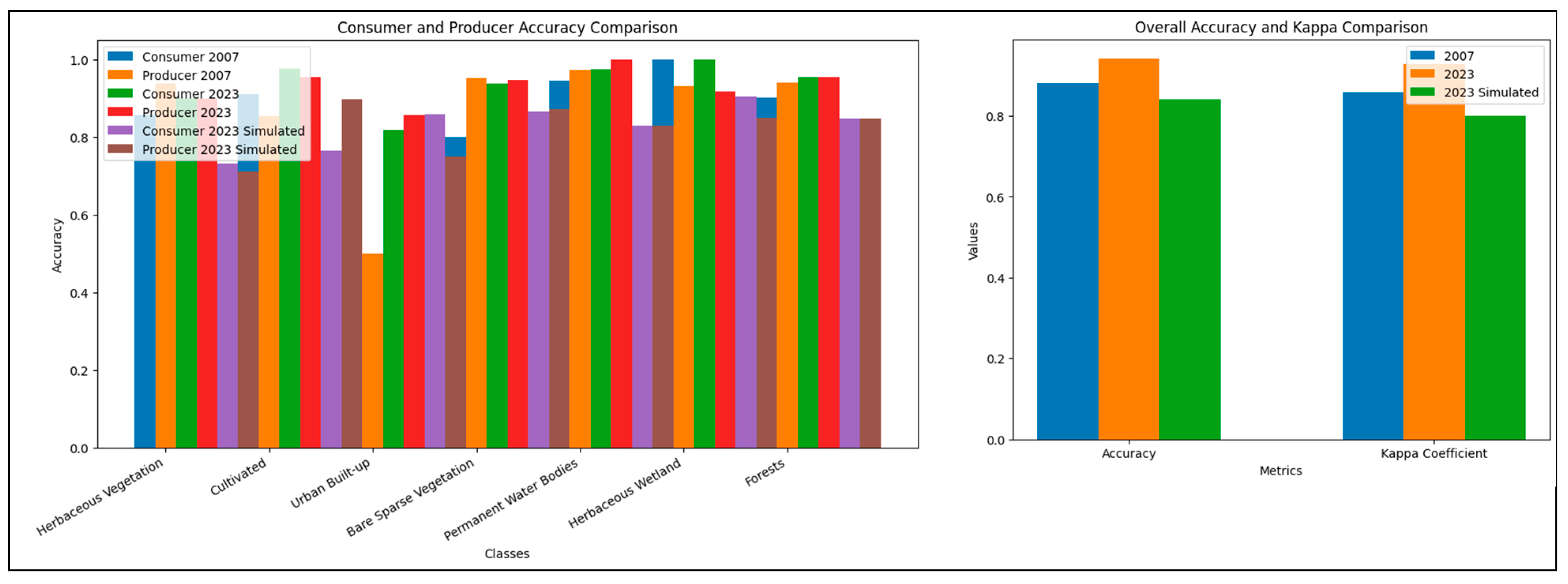
Accuracy Assessment
3.4. Future Land Cover Projection in 2040
3.5. Analysis of Land Cover Transition and Change
3.5.1. Change Analysis Between 2007 and 2023
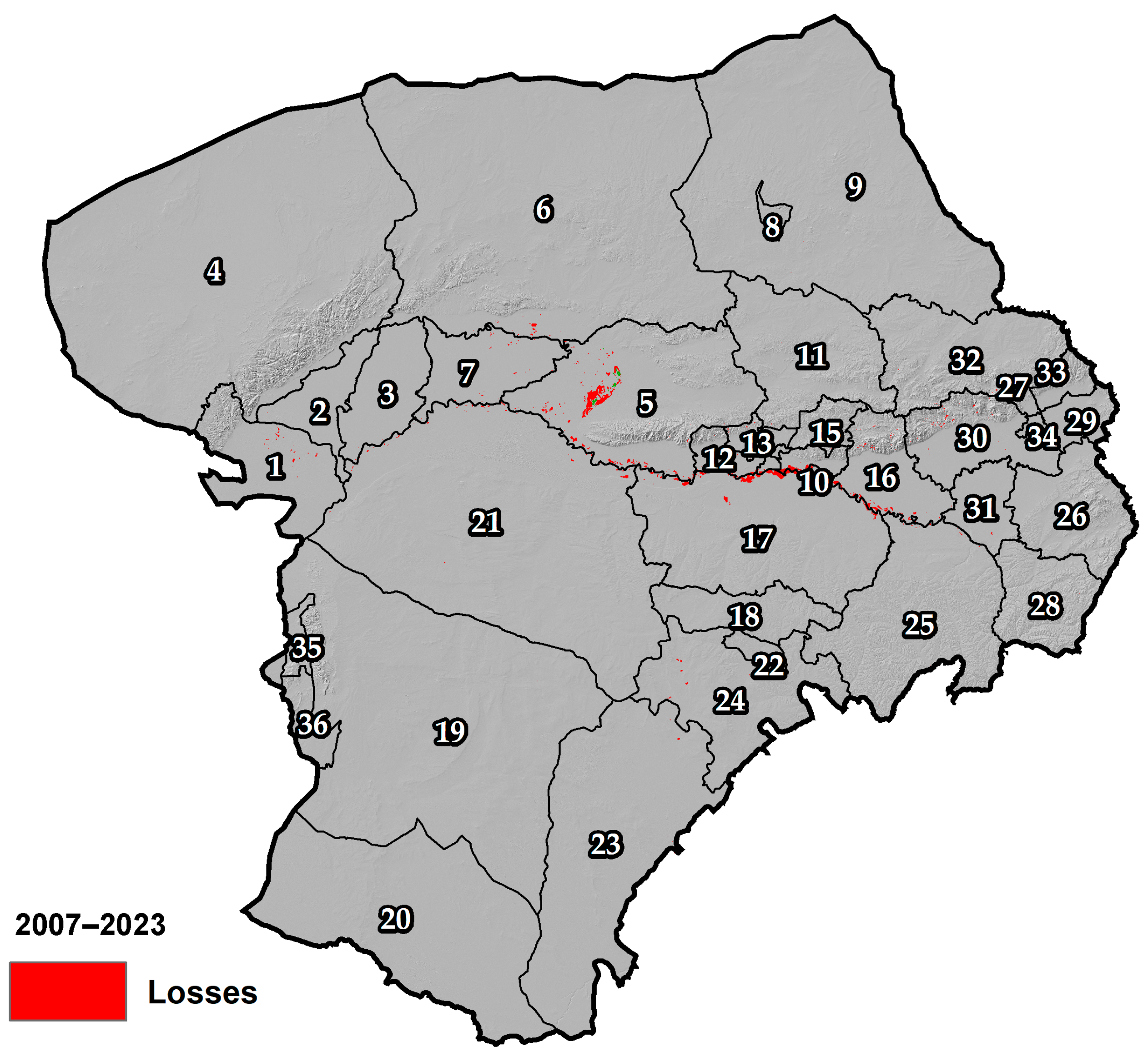
3.5.2. Gains and Losses Between 2007 and 2023
3.5.3. Gains and Losses Between 2023 and 2040
3.6. MaxEnt Modeling of Wetland Presence (2023 and 2030–2050)
3.6.1. Correlation Analysis of Environmental Variables
3.6.2. Model Performance and Variable Importance in MaxEnt
3.6.3. MaxEnt Modeling Results: Present and Future Wetland Suitability Across Administrative Subdivisions
4. Discussion
4.1. Climate Change and Wetland Hydrology
4.2. Land Use Transitions and Ecological Consequences
4.3. MaxEnt Modeling and Spatial Heterogeneity
4.4. Implications for Conservation and Policy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mitsch, W.J.; Bernal, B.; Hernandez, M.E. Ecosystem Services of Wetlands. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2015, 11, 1–4. [Google Scholar] [CrossRef]
- Zedler, J.B.; Kercher, S. Wetland Resources: Status, Trends, Ecosystem Services, and Restorability. Annu. Rev. Environ. Resour. 2005, 30, 39–74. [Google Scholar] [CrossRef]
- Ge, G.; Zhang, J.; Chen, X.; Liu, X.; Hao, Y.; Yang, X.; Kwon, S. Effects of Land Use and Land Cover Change on Ecosystem Services in an Arid Desert-Oasis Ecotone along the Yellow River of China. Ecol. Eng. 2022, 176, 106512. [Google Scholar] [CrossRef]
- Dale, V.H.; Brown, S.; Haeuber, R.A.; Hobbs, N.T.; Huntly, N.; Naiman, R.J.; Riebsame, W.E.; Turner, M.G.; Valone, T.J. Ecological Principles and Guidelines for Managing the Use of Land Sup> 1. Ecol. Appl. 2000, 10, 639–670. [Google Scholar]
- Erwin, K.L. Wetlands and Global Climate Change: The Role of Wetland Restoration in a Changing World. Wetl. Ecol. Manag. 2009, 17, 71–84. [Google Scholar] [CrossRef]
- Grimm, N.B.; Chapin, F.S., III; Bierwagen, B.; Gonzalez, P.; Groffman, P.M.; Luo, Y.; Melton, F.; Nadelhoffer, K.; Pairis, A.; Raymond, P.A. The Impacts of Climate Change on Ecosystem Structure and Function. Front. Ecol. Environ. 2013, 11, 474–482. [Google Scholar] [CrossRef]
- Sarkar, D.; Maji, N. Status and Threats of Wetland Change in Land Use Pattern and Planning: Impact of Land Use Patterns and Urbanization. In Handbook of Research on Monitoring and Evaluating the Ecological Health of Wetlands; IGI Global: Hershey, PA, USA, 2022; pp. 106–127. [Google Scholar]
- Gavrilescu, M. Water, Soil, and Plants Interactions in a Threatened Environment. Water 2021, 13, 2746. [Google Scholar] [CrossRef]
- Admas, M.; Melesse, A.M.; Tegegne, G. Predicting the Impacts of Land Use/Cover and Climate Changes on Water and Sediment Flows in the Megech Watershed, Upper Blue Nile Basin. Remote Sens. 2024, 16, 2385. [Google Scholar] [CrossRef]
- Zhou, F.; Dong, X.; Li, J.; Zhou, W.; Zhao, C.; Gang, C. Quantitative Assessment of the Individual Contribution of Climate and Human Factors to Desertification in Northwest China Using Net Primary Productivity as an Indicator. Ecol. Indic. 2014, 48, 560–569. [Google Scholar] [CrossRef]
- Kong, X.; Han, M.; Li, Y.; Kong, F.; Sun, J.; Zhu, W.; Wei, F. Spatial Differentiation and Formation Mechanism of Ecological Sensitivity in Large River Basins: A Case Study of the Yellow River Basin, China. Ecol. Indic. 2024, 158, 111571. [Google Scholar] [CrossRef]
- Mukonza, S.S.; Chiang, J.-L. Meta-Analysis of Satellite Observations for United Nations Sustainable Development Goals: Exploring the Potential of Machine Learning for Water Quality Monitoring. Environments 2023, 10, 170. [Google Scholar] [CrossRef]
- Mohanty, S.; Pandey, P.C.; Srivastava, P.K.; Srivastava, S.K. Challenges and Future Implications in Monitoring and Assessment of Aquatic Ecosystems. In Aquatic Ecosystems Monitoring; CRC Press: Boca Raton, FL, USA, 2025; pp. 297–318. [Google Scholar]
- Ozesmi, S.L.; Bauer, M.E. Satellite Remote Sensing of Wetlands. Wetl. Ecol. Manag. 2002, 10, 381–402. [Google Scholar] [CrossRef]
- Guo, M.; Li, J.; Sheng, C.; Xu, J.; Wu, L. A Review of Wetland Remote Sensing. Sensors 2017, 17, 777. [Google Scholar] [CrossRef]
- Rawat, K.S.; Kumar, S.; Garg, N. Statistical Comparison of Simple and Machine Learning Based Land Use and Land Cover Classification Algorithms: A Case Study. J. Water Manag. Model. 2024, 32, H524. [Google Scholar] [CrossRef]
- Wang, J.; Bretz, M.; Dewan, M.A.A.; Delavar, M.A. Machine Learning in Modelling Land-Use and Land Cover-Change (LULCC): Current Status, Challenges and Prospects. Sci. Total Environ. 2022, 822, 153559. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a High-Resolution Global Dataset of Monthly Climate and Climatic Water Balance from 1958–2015. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Thrasher, B.; Xiong, J.; Wang, W.; Melton, F.; Michaelis, A.; Nemani, R. Downscaled Climate Projections Suitable for Resource Management. Eos, Trans. Am. Geophys. Union 2013, 94, 321–323. [Google Scholar] [CrossRef]
- He, D.; Wang, Y.; Wang, D.; Yang, Y.; Fang, W.; Wang, Y. Analysis of Spatial and Temporal Changes in FVC and Their Driving Forces in the Inner Mongolia Section of the Yellow River Basin. Atmosphere 2024, 15, 736. [Google Scholar] [CrossRef]
- Tu, L.; Duan, L. Spatial Downscaling Analysis of GPM IMERG Precipitation Dataset Based on Multiscale Geographically Weighted Regression Model: A Case Study of the Inner Mongolia Reach of the Yellow River Basin. Front. Environ. Sci. 2024, 12, 1389587. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Theobald, D.M.; Harrison-Atlas, D.; Monahan, W.B.; Albano, C.M. Ecologically-Relevant Maps of Landforms and Physiographic Diversity for Climate Adaptation Planning. PLoS ONE 2015, 10, e0143619. [Google Scholar] [CrossRef]
- Staszel, K.; Błońska, E.; Lasota, J. Slope Aspect and Altitude Effect on Selected Soil Organic Matter Characteristics in Beskid Mountains Forest Soils. Folia For. Pol. 2021, 63, 214–224. [Google Scholar] [CrossRef]
- Vereecken, H.; Amelung, W.; Bauke, S.L.; Bogena, H.; Brüggemann, N.; Montzka, C.; Vanderborght, J.; Bechtold, M.; Blöschl, G.; Carminati, A. Soil Hydrology in the Earth System. Nat. Rev. Earth Environ. 2022, 3, 573–587. [Google Scholar] [CrossRef]
- Hengl, T. Soil Texture Classes (USDA System) for 6 Soil Depths (0, 10, 30, 60, 100 and 200 cm) at 250 m. Zenodo 2018. [Google Scholar] [CrossRef]
- Merz, B.; Aerts, J.; Arnbjerg-Nielsen, K.; Baldi, M.; Becker, A.; Bichet, A.; Blöschl, G.; Bouwer, L.M.; Brauer, A.; Cioffi, F. Floods and Climate: Emerging Perspectives for Flood Risk Assessment and Management. Nat. Hazards Earth Syst. Sci. 2014, 14, 1921–1942. [Google Scholar] [CrossRef]
- Yasuhara, M.; Cronin, T.M.; Peter, B.; Okahashi, H.; Linsley, B.K.; Yang, H.; Wang, Y.; Liu, Z.; Work Group II; Weaver, A.J.; et al. IPCC 2014. Impacts, Adaptation and Vulnerability—Europe. Clim. Dyn. 2014, 26, 661–668. [Google Scholar] [CrossRef]
- Buchhorn, M.; Smets, B.; Bertels, L.; De Roo, B.; Lesiv, M.; Tsendbazar, N.-E.; Herold, M.; Fritz, S. Copernicus Global Land Service: Land Cover 100 M: Collection 3: Epoch 2019: Globe. 2020. Available online: https://zenodo.org/record/3939050 (accessed on 30 December 2021).
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. GMES Sentinel-1 Mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Markham, B.L.; Storey, J.C.; Irons, J.R. Landsat Data Continuity Mission, Now Landsat-8: Six Months on-Orbit. In Proceedings of the Earth Observing Systems XVIII, San Diego, CA, USA, 25–29 August 2013; SPIE: Bellingham, WA, USA, 2013; Volume 8866, pp. 398–406. [Google Scholar]
- Hammer, P.D.; Valero, F.P.J.; Kinne, S. Landsat 5 Thematic Mapper (TM-6). In Proceedings of the NASA Conference Publication; [for Sale by the National Technical Information Service]. NASA: Titusville, FL, USA, 1977; p. 423. [Google Scholar]
- Wang, L.; Zhang, J.; Shu, Z.; Wang, Y.; Bao, Z.; Liu, C.; Zhou, X.; Wang, G. Evaluation of the Ability of CMIP6 Global Climate Models to Simulate Precipitation in the Yellow River Basin, China. Front. Earth Sci. 2021, 9, 751974. [Google Scholar] [CrossRef]
- Jiang, F.; Wen, S.; Gao, M.; Zhu, A. Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin. Atmosphere 2023, 14, 1497. [Google Scholar] [CrossRef]
- Wu, F.; Jiao, D.; Yang, X.; Cui, Z.; Zhang, H.; Wang, Y. Evaluation of NEX-GDDP-CMIP6 in Simulation Performance and Drought Capture Utility over China–based on DISO. Hydrol. Res. 2023, 54, 703–721. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Jian, S.; Li, X. Assessment of Rainfall and Temperature Trends in the Yellow River Basin, China from 2023 to 2100. Water 2024, 16, 1441. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Althalaj, T.D.A.; Al-Shibli, F.M.; Alassaf, A.A. Assessment of Rainfed Wheat Productivity in a Changing Climate in Irbid, Jordan Using Statistical Downscaling and Random Forest Regression Prediction under RCP4. 5 & 8.5 Pathways. Environ. Sustain. Indic. 2025, 25, 100545. [Google Scholar]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Wilby, R.L.; Wigley, T.M.L. Downscaling General Circulation Model Output: A Review of Methods and Limitations. Prog. Phys. Geogr. 1997, 21, 530–548. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS Monthly High-Resolution Gridded Multivariate Climate Dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking Climate Change Modelling to Impacts Studies: Recent Advances in Downscaling Techniques for Hydrological Modelling. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Duan, H.; Zhang, G.; Wang, S.; Fan, Y. Robust Climate Change Research: A Review on Multi-Model Analysis. Environ. Res. Lett. 2019, 14, 33001. [Google Scholar] [CrossRef]
- Murphy, J.M.; Sexton, D.M.H.; Barnett, D.N.; Jones, G.S.; Webb, M.J.; Collins, M.; Stainforth, D.A. Quantification of Modelling Uncertainties in a Large Ensemble of Climate Change Simulations. Nature 2004, 430, 768–772. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Klein, W.H.; Lewis, B.M.; Enger, I. Objective Prediction of Five-Day Mean Temperatures during Winter. J. Atmos. Sci. 1959, 16, 672–682. [Google Scholar] [CrossRef]
- Gutmann, E.; Pruitt, T.; Clark, M.P.; Brekke, L.; Arnold, J.R.; Raff, D.A.; Rasmussen, R.M. An Intercomparison of Statistical Downscaling Methods Used for Water Resource Assessments in the United States. Water Resour. Res. 2014, 50, 7167–7186. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.; O’farrell, S.; Sullivan, A.; Bodman, R.; Law, R.; Harman, I.; Srbinovsky, J.; Rashid, H.A. Configuration and Spin-up of ACCESS-CM2, the New Generation Australian Community Climate and Earth System Simulator Coupled Model. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 225–251. [Google Scholar] [CrossRef]
- Voldoire, A. CNRM-CERFACS CNRM-ESM2-1 Model Output Prepared for CMIP6 ScenarioMIP ssp245. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.ScenarioMIP.CNRM-CERFACS.CNRM-ESM2-1.ssp245 (accessed on 16 March 2025).
- Séférian, R.; Nabat, P.; Michou, M.; Saint-Martin, D.; Voldoire, A.; Colin, J.; Decharme, B.; Delire, C.; Berthet, S.; Chevallier, M. Evaluation of CNRM Earth System Model, CNRM-ESM2-1: Role of Earth System Processes in Present-day and Future Climate. J. Adv. Model. Earth Syst. 2019, 11, 4182–4227. [Google Scholar] [CrossRef]
- Jungclaus, J.; Mikolajewicz, U.; Kapsch, M.-L.; D’Agostino, R.; Wieners, K.-H.; Giorgetta, M.; Reick, C.; Esch, M.; Bittner, M.; Legutke, S. MPI-M MPIESM1. 2-LR Model Output Prepared for CMIP6 PMIP. 2019. Available online: https://www.wdc-climate.de/ui/entry?acronym=C6_5166396 (accessed on 16 March 2025).
- Yukimoto, S.; Koshiro, T.; Kawai, H.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M. MRI MRI-ESM2. 0 Model Output Prepared for CMIP6 ScenarioMIP. 2019. Available online: https://www.wdc-climate.de/ui/cmip6?input=CMIP6.PMIP.MPI-M.MPI-ESM1-2-LR.lgm (accessed on 16 March 2025).
- Sellar, A.A.; Jones, C.G.; Mulcahy, J.P.; Tang, Y.; Yool, A.; Wiltshire, A.; O’connor, F.M.; Stringer, M.; Hill, R.; Palmieri, J. UKESM1: Description and Evaluation of the UK Earth System Model. J. Adv. Model. Earth Syst. 2019, 11, 4513–4558. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gao, B.-C. NDWI—A Normalized Difference Water Index for Remote Sensing of Vegetation Liquid Water from Space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Van Deventer, A.P.; Ward, A.D.; Gowda, P.H.; Lyon, J.G. Using Thematic Mapper Data to Identify Contrasting Soil Plains and Tillage Practices. Photogramm. Eng. Remote Sens. 1997, 63, 87–93. [Google Scholar]
- Liu, Y.; Wang, Y.; Zhang, J. New Machine Learning Algorithm: Random Forest. In Proceedings of the Information Computing and Applications: Third International Conference, ICICA 2012, Chengde, China, 14–16 September 2012; Proceedings 3. Springer: Berlin/Heidelberg, Germany, 2012; pp. 246–252. [Google Scholar]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An Assessment of the Effectiveness of a Random Forest Classifier for Land-Cover Classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Story, M.; Congalton, R.G. Accuracy Assessment: A User’s Perspective. Photogramm. Eng. Remote Sens. 1986, 52, 397–399. [Google Scholar]
- Silakhori, E.; Maleki, S.; Pourghasemi, H.R. Spatiotemporal Variations in Land Use of Mahvelat Plain in Iran Using Google Earth Engine from 2011 to 2030. In Advanced Tools for Studying Soil Erosion Processes; Elsevier: Amsterdam, The Netherlands, 2024; pp. 413–433. [Google Scholar]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Calderón-Loor, M.; Hadjikakou, M.; Bryan, B.A. High-Resolution Wall-to-Wall Land-Cover Mapping and Land Change Assessment for Australia from 1985 to 2015. Remote Sens. Environ. 2021, 252, 112148. [Google Scholar] [CrossRef]
- Eastman, J.R. TerrSet. Geospatial Monitoring and Modelling System. Manual; Clark University: Worcester, MA, USA, 2016; 393p. [Google Scholar]
- Mansour, S.; Al-Belushi, M.; Al-Awadhi, T. Monitoring Land Use and Land Cover Changes in the Mountainous Cities of Oman Using GIS and CA-Markov Modelling Techniques. Land Use Policy 2020, 91, 104414. [Google Scholar] [CrossRef]
- Gidey, E.; Dikinya, O.; Sebego, R.; Segosebe, E.; Zenebe, A. Cellular Automata and Markov Chain (CA_Markov) Model-Based Predictions of Future Land Use and Land Cover Scenarios (2015–2033) in Raya, Northern Ethiopia. Model. Earth Syst. Environ. 2017, 3, 1245–1262. [Google Scholar] [CrossRef]
- Fu, X.; Wang, X.; Yang, Y.J. Deriving Suitability Factors for CA-Markov Land Use Simulation Model Based on Local Historical Data. J. Environ. Manage. 2018, 206, 10–19. [Google Scholar] [CrossRef]
- Song, J.; He, X.; Zhang, F.; Ma, X.; Jim, C.Y.; Johnson, B.A.; Chan, N.W. Analyzing and Predicting LUCC and Carbon Storage Changes in Xinjiang’s Arid Ecosystems Under the Carbon Neutrality Goal. Remote Sens. 2024, 16, 4439. [Google Scholar] [CrossRef]
- Soares-Filho, B.S.; Cerqueira, G.C.; Pennachin, C.L. DINAMICA—A Stochastic Cellular Automata Model Designed to Simulate the Landscape Dynamics in an Amazonian Colonization Frontier. Ecol. Modell. 2002, 154, 217–235. [Google Scholar] [CrossRef]
- Pontius, G.R.; Malanson, J. Comparison of the Structure and Accuracy of Two Land Change Models. Int. J. Geogr. Inf. Sci. 2005, 19, 243–265. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Schapire, R.E. A Maximum Entropy Approach to Species Distribution Modeling. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 83. [Google Scholar]
- Hao, L.; He, S.; Zhou, J.; Zhao, Q.; Lu, X. Prediction of the Landscape Pattern of the Yancheng Coastal Wetland, China, Based on XGBoost and the MCE-CA-Markov Model. Ecol. Indic. 2022, 145, 109735. [Google Scholar] [CrossRef]
- Yang, Z.; Dai, X.; Lu, H.; Liu, C.; Nie, R.; Zhang, M.; Ma, L.; Li, N.; Liu, T.; He, Y. Evaluation and Prediction of Water Conservation of the Yellow River Basin in Sichuan Province, China, Based on Google Earth Engine and CA-Markov. Heliyon 2023, 9, e17903. [Google Scholar] [CrossRef]
- Yang, C.; Zhai, H.; Fu, M.; Zheng, Q.; Fan, D. Multi-Scenario Simulation of Land System Change in the Guangdong–Hong Kong–Macao Greater Bay Area Based on a Cellular Automata–Markov Model. Remote Sens. 2024, 16, 1512. [Google Scholar] [CrossRef]
- Zhu, Y.; Ling, G.H.T. Driving Forces and Prediction of Urban Open Spaces Morphology: The Case of Shanghai, China Using Geodetector and CA-Markov Model. Ecol. Inform. 2024, 82, 102763. [Google Scholar] [CrossRef]
- Jawarneh, R.N.; Abulibdeh, A.; Hashem, N.; Awawdeh, M.; Al-Awadhi, T.; Abdullah, M.M.; El Kenawy, A.M. Assessing and Predicting Land Cover Dynamics for Environmental Sustainability in Jordan’s Arid Ecosystems Using CA-Markov Model. Remote Sens. Appl. Soc. Environ. 2024, 35, 101262. [Google Scholar] [CrossRef]
- Scafetta, N. Impacts and Risks of “realistic” Global Warming Projections for the 21st Century. Geosci. Front. 2024, 15, 101774. [Google Scholar] [CrossRef]
- Domrös, M.; Peng, G. The Climate of China; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 3642733336. [Google Scholar]
- Zhang, X.; Srinivasan, R.; Hao, F. Predicting Hydrologic Response to Climate Change in the Luohe River Basin Using the SWAT Model. Trans. ASABE 2013, 50, 901–910. [Google Scholar] [CrossRef]
- Zhang, L.; Zhen, Q.; Cheng, M.; Ouyang, Z. The Main Drivers of Wetland Changes in the Beijing-Tianjin-Hebei Region. Int. J. Environ. Res. Public Health 2019, 16, 2619. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Huang, F.; Barton, A.; Perera, B.J.C. Statistical Downscaling of General Circulation Model Outputs to Precipitation-Part 2: Bias-Correction and Future Projections. Int. J. Climatol. 2014, 34, 3282–3303. [Google Scholar] [CrossRef]
- Sannigrahi, S.; Bhatt, S.; Rahmat, S.; Paul, S.K.; Sen, S. Estimating Global Ecosystem Service Values and Its Response to Land Surface Dynamics during 1995–2015. J. Environ. Manag. 2018, 223, 115–131. [Google Scholar] [CrossRef]
- Elafri, A.; Belhamra, M.; Houhamdi, M. Comparing Habitat Preferences of a Set of Waterbird Species Wintering in Coastal Wetlands of North Africa: Implication for Management. Ekológia (Bratislava) 2017, 36, 158–171. [Google Scholar] [CrossRef]
- Wu, Z.; Cheng, S.; Xu, K.; Qian, Y. Ecological Network Resilience Evaluation and Ecological Strategic Space Identification Based on Complex Network Theory: A Case Study of Nanjing City. Ecol. Indic. 2024, 158, 111604. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z.; Han, T.; Quan, W.; Wang, J.; Zhou, H.; He, D.; Dong, F. Long-Term Declining in Carbon Monoxide (CO) at a Rural Site of Beijing during 2006–2018 Implies the Improved Combustion Efficiency and Effective Emission Control. J. Environ. Sci. 2022, 115, 432–442. [Google Scholar] [CrossRef]
- Valavi, R.; Guillera-Arroita, G.; Lahoz-Monfort, J.J.; Elith, J. Predictive Performance of Presence-only Species Distribution Models: A Benchmark Study with Reproducible Code. Ecol. Monogr. 2022, 92, e01486. [Google Scholar] [CrossRef]
- Elith, J.; Phillips, S.J.; Hastie, T.; Dudík, M.; Chee, Y.E.; Yates, C.J. A Statistical Explanation of MaxEnt for Ecologists. Divers. Distrib. 2011, 17, 43–57. [Google Scholar] [CrossRef]
- Arnold, C.A. Social-Ecological Resilience of an Eastern Urban-Suburban Watershed: The Anacostia River Basin. Idaho L. Rev. 2014, 51, 29. [Google Scholar] [CrossRef][Green Version]
- Conlisk, E.; Chamberlin, L.; Vernon, M.; Dybala, K.E. Evidence for the Multiple Benefits of Wetland Conservation in North America: Carbon, Biodiversity, and Beyond; Point Blue: Petaluma, CA, USA, 2023. [Google Scholar]
- Burgess, M.; Gregory, R.; Wilson, J.; Gillings, S.; Evans, A.; Chisholm, K.; Southern, A.; Eaton, M. A New Framework of Spatial Targeting for Single-Species Conservation Planning. Landsc. Ecol. 2019, 34, 2765–2778. [Google Scholar] [CrossRef]






| Model | Institution | Nominal Resolution | Primary Reference |
|---|---|---|---|
| ACCESS-CM2 | Commonwealth Scientific and Industrial Research Organisation (CSIRO), Australia | ~1.875° × 1.25° | [48] |
| CNRM-CM6-1 | Centre National de Recherches Météorologiques (CNRM), France | ~1.4° × 1.4° | [49] |
| CNRM-ESM2-1 | Centre National de Recherches Météorologiques (CNRM), France | ~1.4° × 1.4° | [50] |
| MPI-ESM1-2-HR | Max Planck Institute for Meteorology (MPI), Germany | ~0.9° × 0.9° | [51] |
| MRI-ESM2-0 | Meteorological Research Institute (MRI), Japan | ~1.125° × 1.125° | [52] |
| UKESM1-0-LL | Met Office Hadley Centre, UK | ~1.25° × 1.875° | [53] |
| Class | Land Use Type | Description |
|---|---|---|
| 1 | Herbaceous vegetation | Plants without persistent stems or shoots above ground and lacking a definite firm structure. Tree and shrub cover is less than 10%. |
| 2 | Cultivated and managed vegetation/agriculture | Lands covered with temporary crops followed by harvest and a bare soil period (e.g., single and multiple cropping systems). |
| 3 | Urban/built-up | Land covered by buildings and other man-made structures. |
| 4 | Bare/sparse vegetation | Lands with exposed soil, sand, or rocks that never have a vegetated cover of more than 10% during any time of the year. |
| 5 | Permanent water bodies | Lakes, reservoirs, and rivers. Can be either fresh or salt water bodies. |
| 6 | Herbaceous wetland | Lands with a permanent mixture of water and herbaceous or woody vegetation. The vegetation can be present in either salt, brackish, or fresh water. |
| 7 | Forest | Includes all forest types (evergreen and deciduous, needleleaf and broadleaf, open and closed). These areas have tree canopies ranging from 15% to >70%. |
| Land_Cover | NDVI | Landform | Elevation | Humidity | Precipitation | Radiation | Slope | Mean_Temp | Max_Temp | Min_Temp | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Land_Cover | 1 | −0.52 | 0.12 | −0.21 | −0.62 | −0.59 | 0.25 | 0.08 | 0.07 | 0.08 | 0.06 |
| NDVI | −0.52 | 1 | −0.13 | 0.11 | 0.63 | 0.72 | −0.3 | 0.1 | 0.05 | −0.03 | 0.13 |
| Landform | 0.12 | −0.13 | 1 | −0.15 | −0.18 | −0.17 | 0.03 | −0.13 | 0 | −0.01 | 0.02 |
| Elevation | −0.21 | 0.11 | −0.15 | 1 | 0.18 | 0.21 | 0.05 | 0.35 | −0.52 | −0.51 | −0.52 |
| Humidity | −0.62 | 0.63 | −0.18 | 0.18 | 1 | 0.9 | −0.66 | 0.09 | −0.28 | −0.33 | −0.22 |
| Precipitation | −0.59 | 0.72 | −0.17 | 0.21 | 0.9 | 1 | −0.37 | 0.1 | −0.01 | −0.07 | 0.05 |
| Radiation | 0.25 | −0.3 | 0.03 | 0.05 | −0.66 | −0.37 | 1 | 0.01 | 0.55 | 0.6 | 0.49 |
| Slope | 0.08 | 0.1 | −0.13 | 0.35 | 0.09 | 0.1 | 0.01 | 1 | −0.19 | −0.19 | −0.18 |
| Mean_Temp | 0.07 | 0.05 | 0 | −0.52 | −0.28 | −0.01 | 0.55 | −0.19 | 1 | 0.99 | 0.99 |
| Max_Temp | 0.08 | −0.03 | −0.01 | −0.51 | −0.33 | −0.07 | 0.6 | −0.19 | 0.99 | 1 | 0.96 |
| Min_Temp | 0.06 | 0.13 | 0.02 | −0.52 | −0.22 | 0.05 | 0.49 | −0.18 | 0.99 | 0.96 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, P.; Su, R.; Wu, G.; Xue, L.; Zhang, Z.; Fang, H.; Gao, R.; Zhang, W.; Zhang, D. Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling. Remote Sens. 2025, 17, 1089. https://doi.org/10.3390/rs17061089
Ji P, Su R, Wu G, Xue L, Zhang Z, Fang H, Gao R, Zhang W, Zhang D. Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling. Remote Sensing. 2025; 17(6):1089. https://doi.org/10.3390/rs17061089
Chicago/Turabian StyleJi, Penghao, Rong Su, Guodong Wu, Lei Xue, Zhijie Zhang, Haitao Fang, Runhong Gao, Wanchang Zhang, and Donghui Zhang. 2025. "Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling" Remote Sensing 17, no. 6: 1089. https://doi.org/10.3390/rs17061089
APA StyleJi, P., Su, R., Wu, G., Xue, L., Zhang, Z., Fang, H., Gao, R., Zhang, W., & Zhang, D. (2025). Projecting Future Wetland Dynamics Under Climate Change and Land Use Pressure: A Machine Learning Approach Using Remote Sensing and Markov Chain Modeling. Remote Sensing, 17(6), 1089. https://doi.org/10.3390/rs17061089








