Estimations of Dynamic Water Depth and Volume of Global Lakes Using Machine Learning
Abstract
1. Introduction
2. Materials
2.1. Global Surface Water Maps and Lake Extents
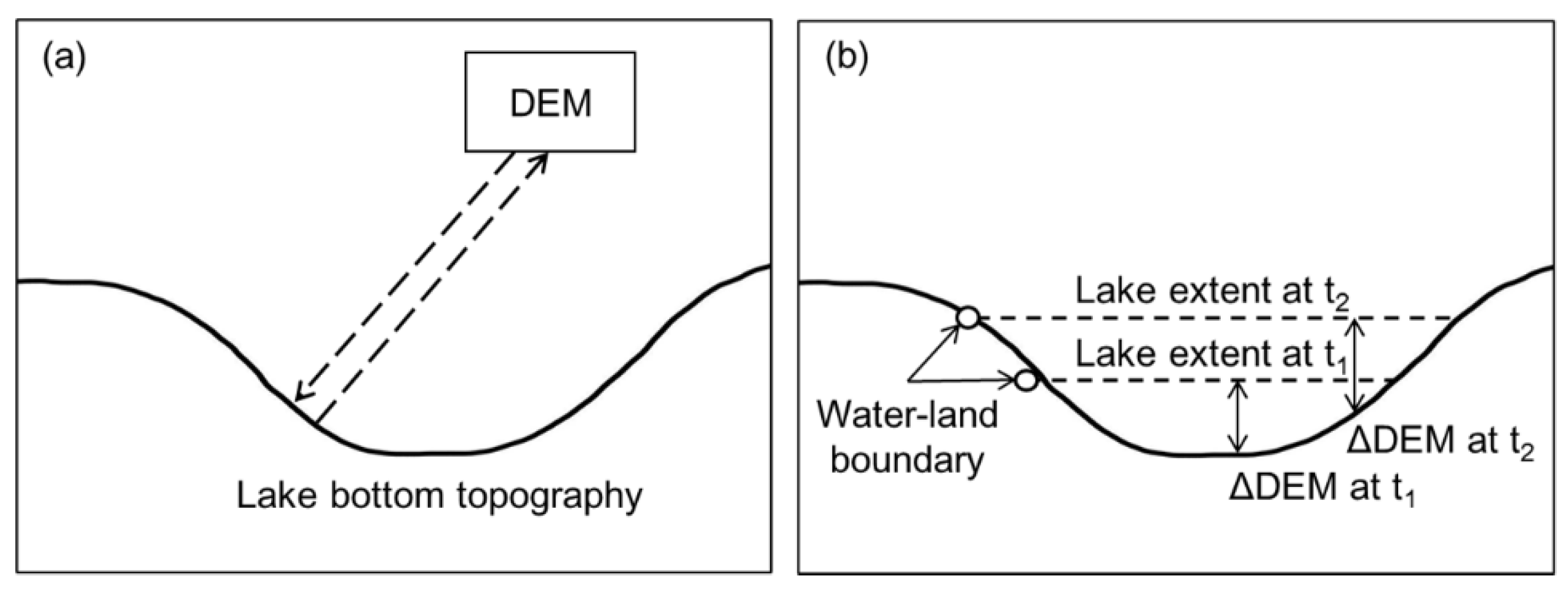
2.2. DEM Data
2.3. Available Datasets
2.4. ICESat/ICESat-2
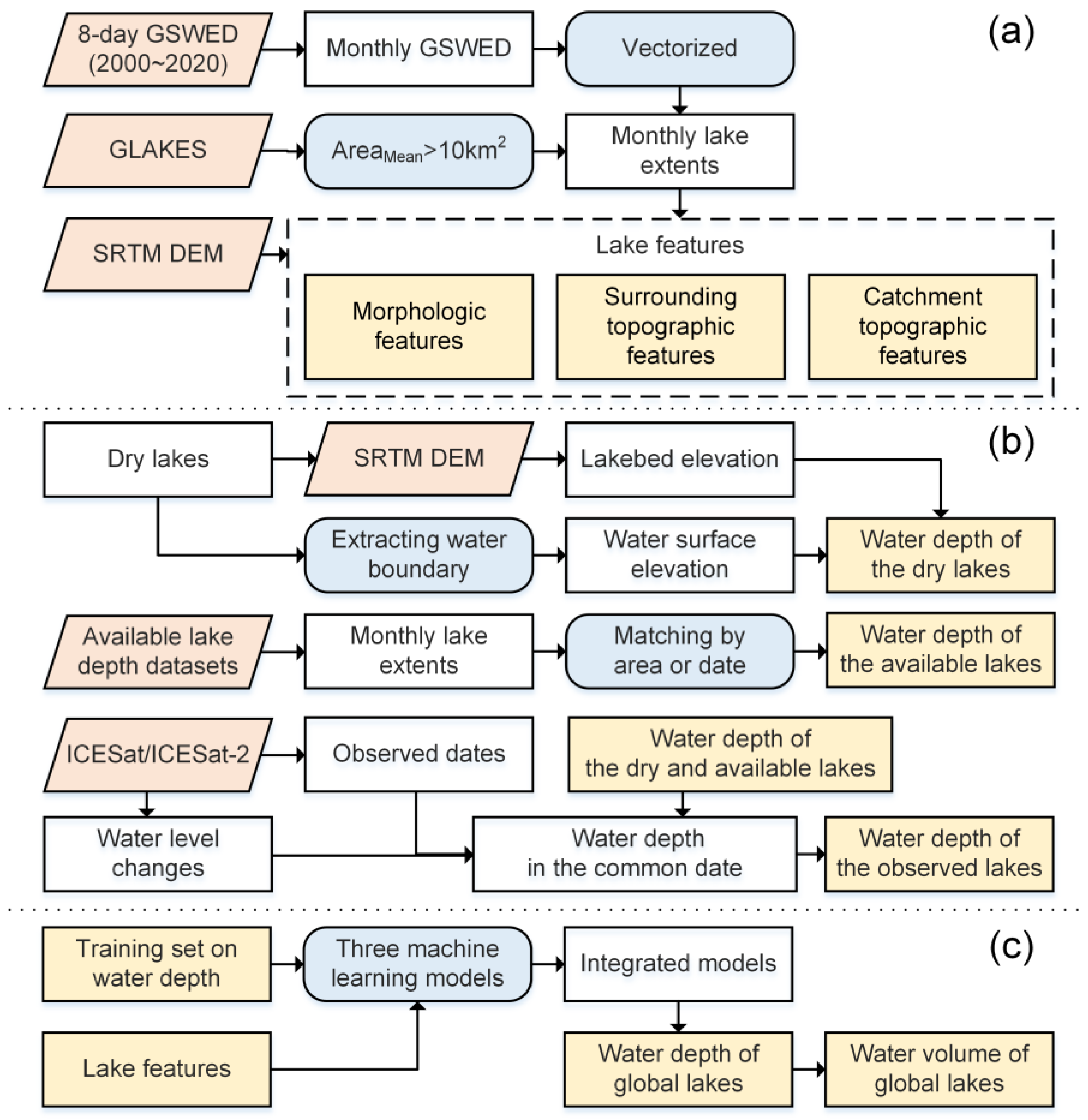
3. Methodology
3.1. Machine Learning Models
3.2. Monthly Global Lake Extents
3.3. Lake Features
3.4. Training Sets on Water Depth
3.4.1. Training Set on the Dry Lakes
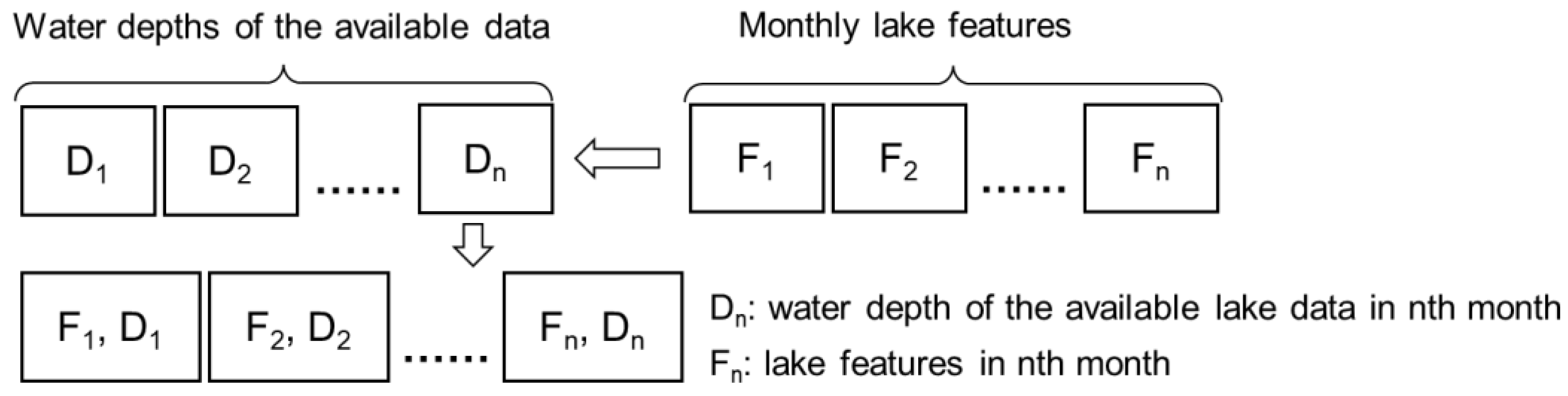
3.4.2. Training Set on the Available Lakes
- (1)
- extract the mean surface area and water depth of the target lake (At, Dt);
- (2)
- determine the monthly lake area from the lake extent data (A1, A2, … An);
- (3)
- identify the mth month where the lake area (Am) most closely matches the mean area (At);
- (4)
- use the lake features and corresponding water depth for the mth month as a training sample (Fm, Dt).

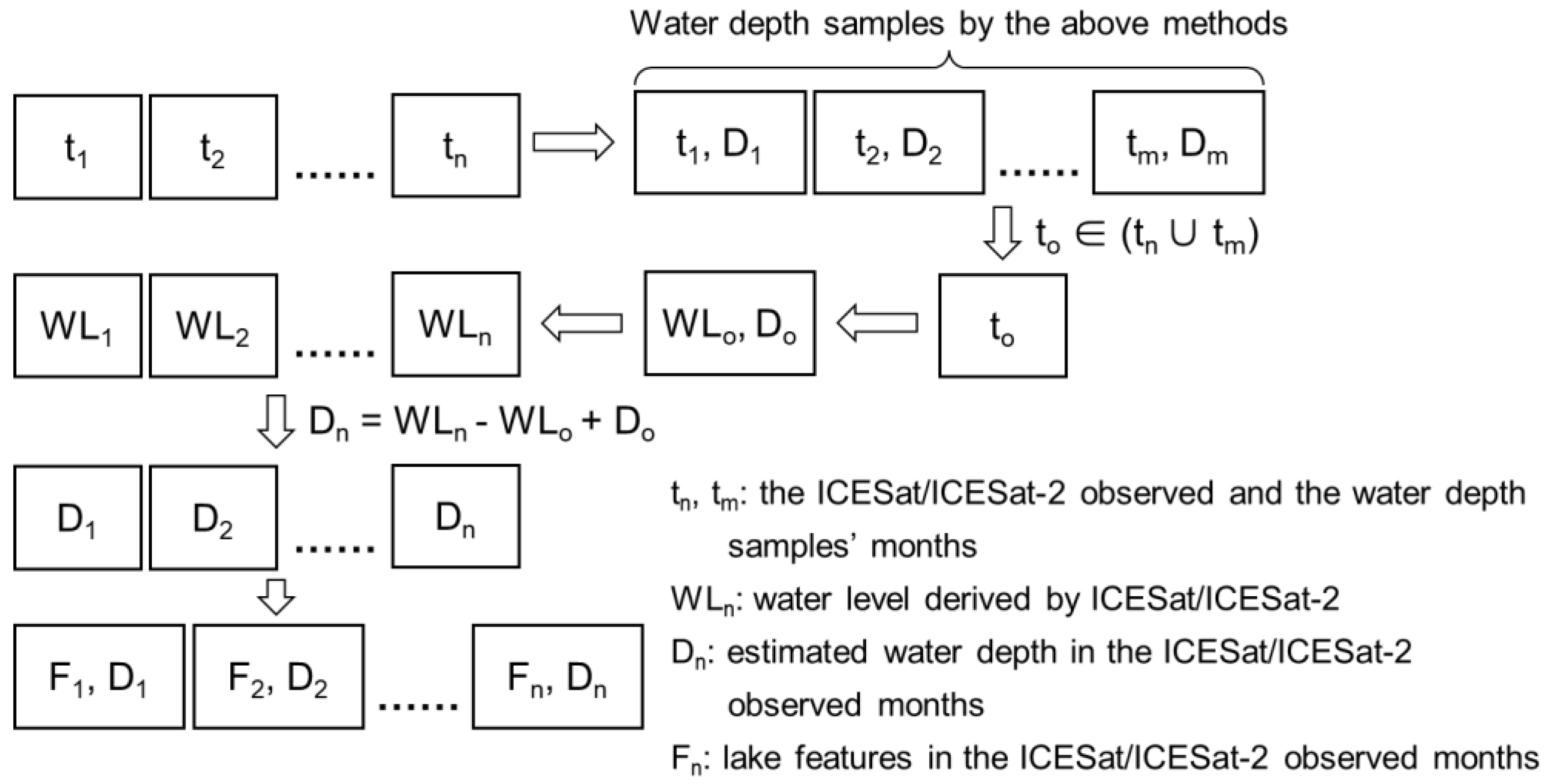
3.4.3. Training Set on the Lakes Observed by ICESat/ICESat-2
- (1)
- determine in which months (tn) the water level of a given lake was observed by ICESat/ICESat-2;
- (2)
- compare the observed months with the training sample months (tm) generated by the previous methods, and identify the coincident months (to);
- (3)
- establish the corresponding water level from ICESat/ICESat-2 measurements and the water depth from the training sample for the coincident month (WLo, Do);
- (4)
- convert the ICESat/ICESat-2 water levels into water depths as a baseline (WLo, Do);
- (5)
- integrate the lake features (listed in Table 1) and water depths according to their timestamps to create new training samples (Fn, Dn).
4. Results and Analysis
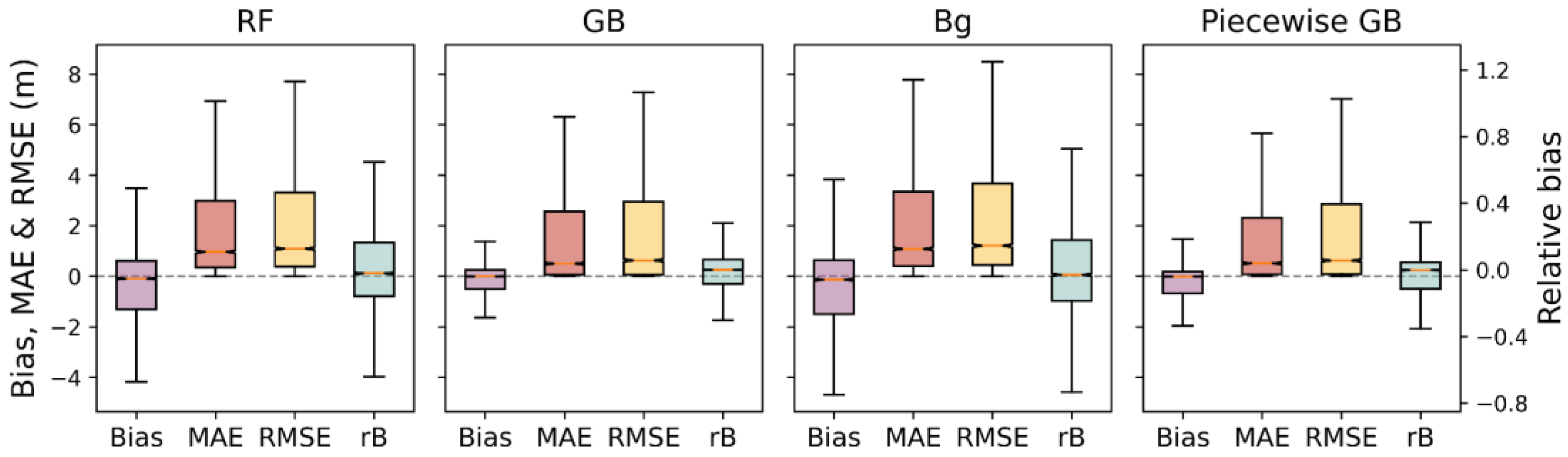
4.1. Model Performance
4.1.1. Water Depth of the Global Dry Lakes
4.1.2. Lake Training Samples
4.1.3. Reliability of ML Models
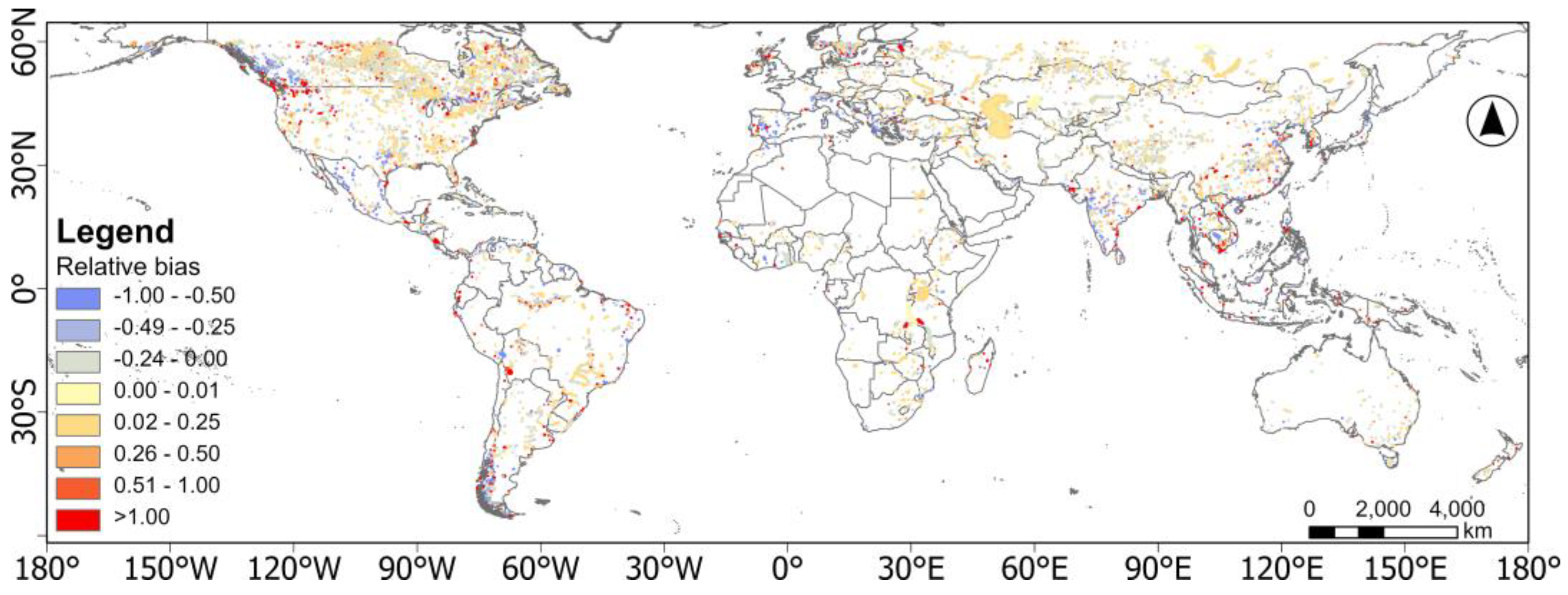
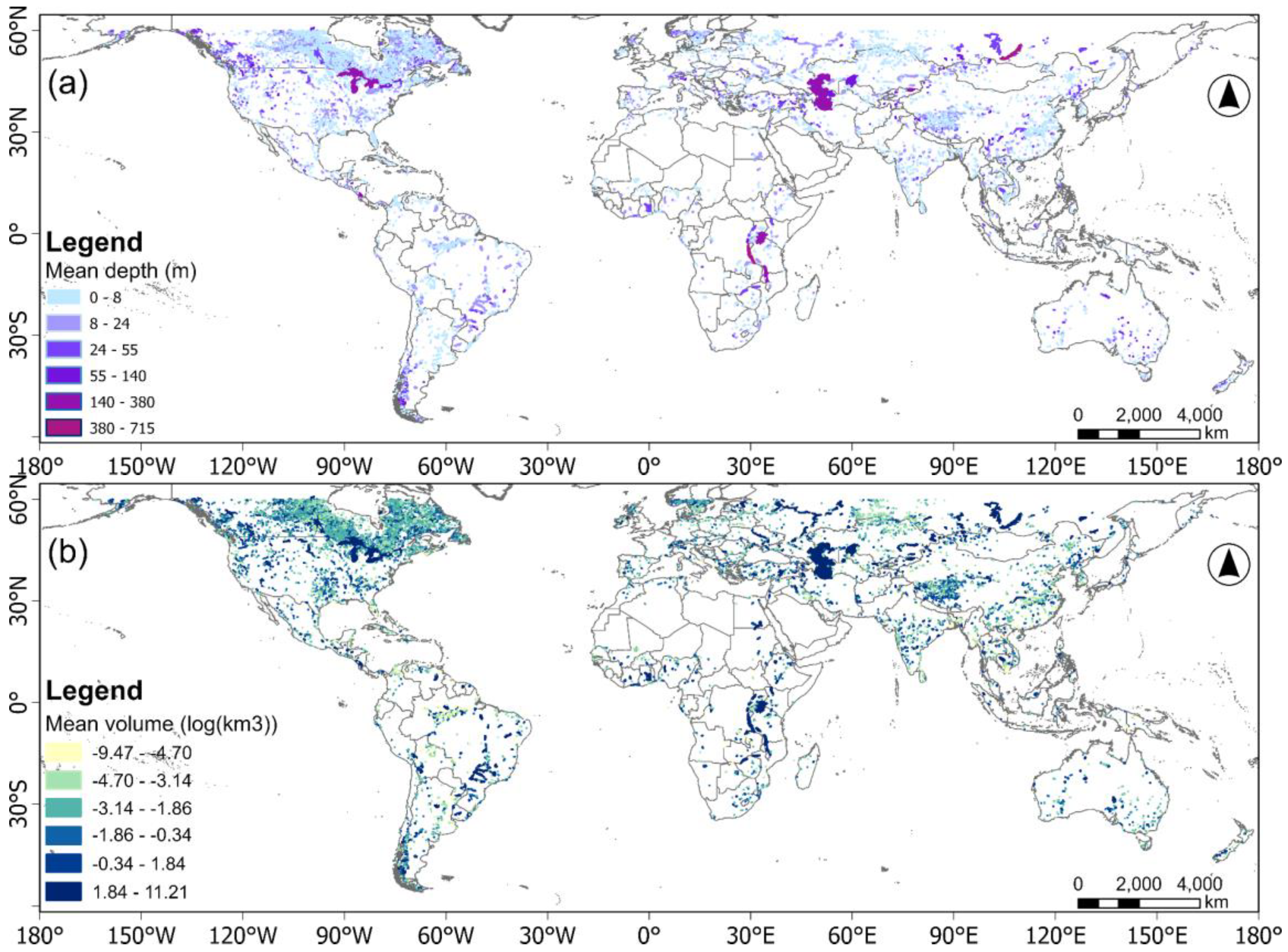
4.2. Results and Assessment
4.2.1. Assessment of the Individual Lakes
4.2.2. Estimated Water Depth
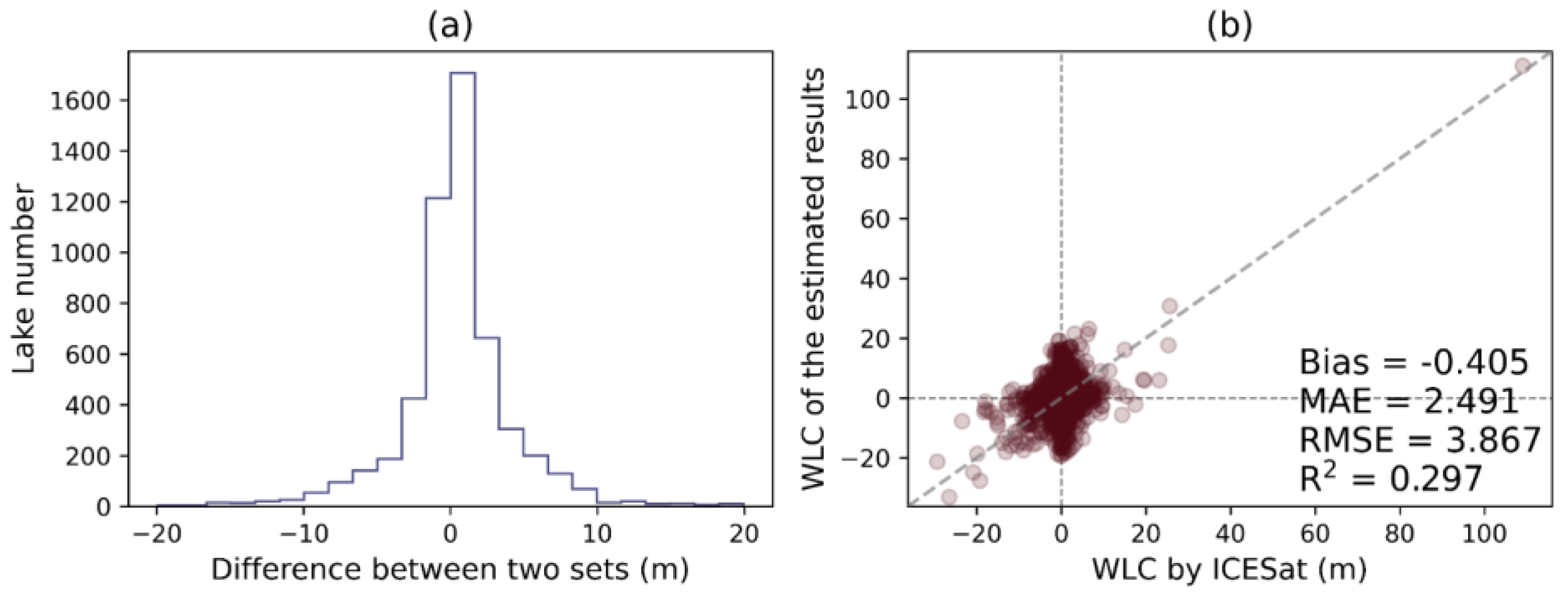
4.2.3. Comparison with the ICESat/ICESat-2 Observations
4.3. Lake Feature Analysis
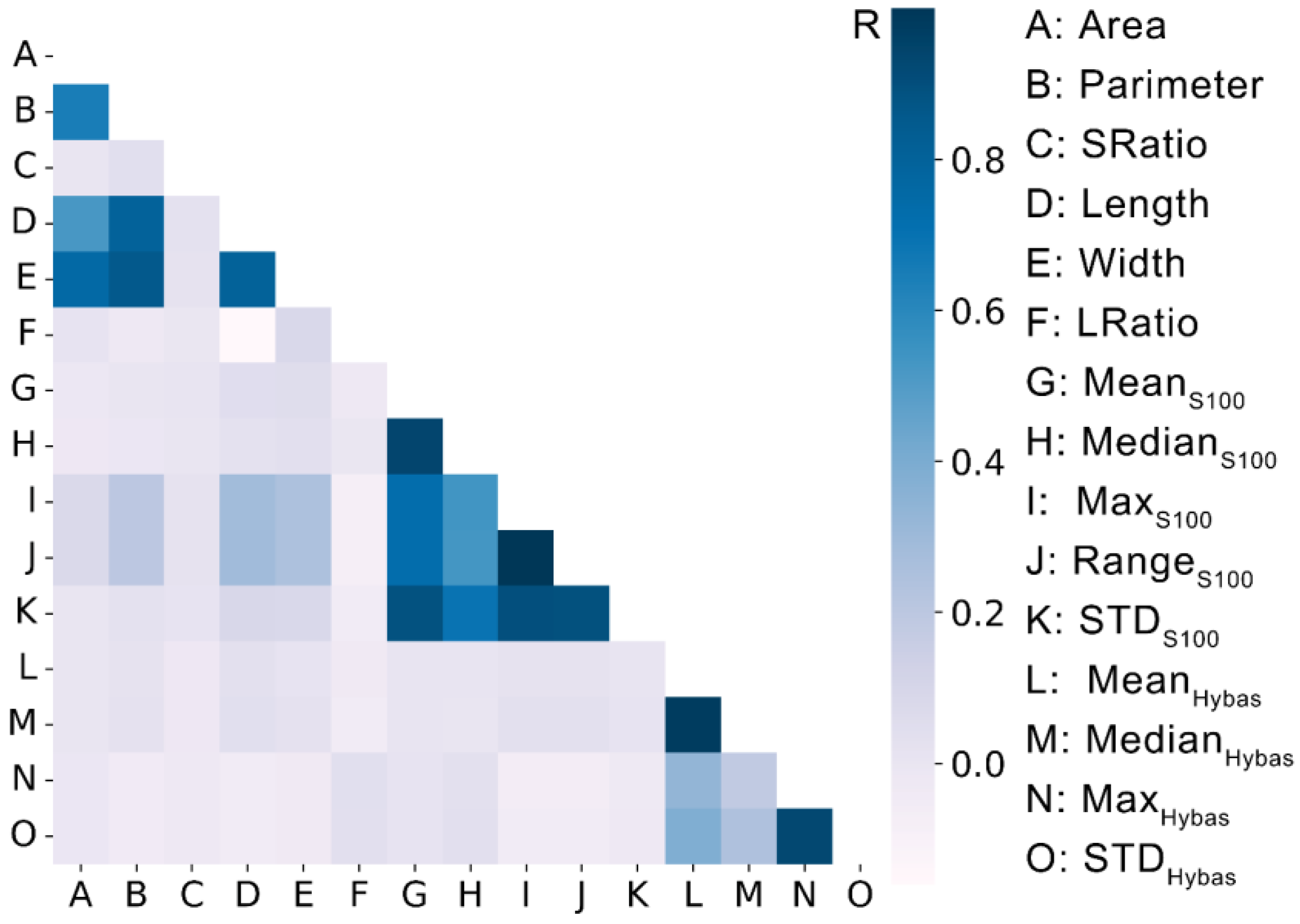
4.3.1. Feature Pairwise Correlations
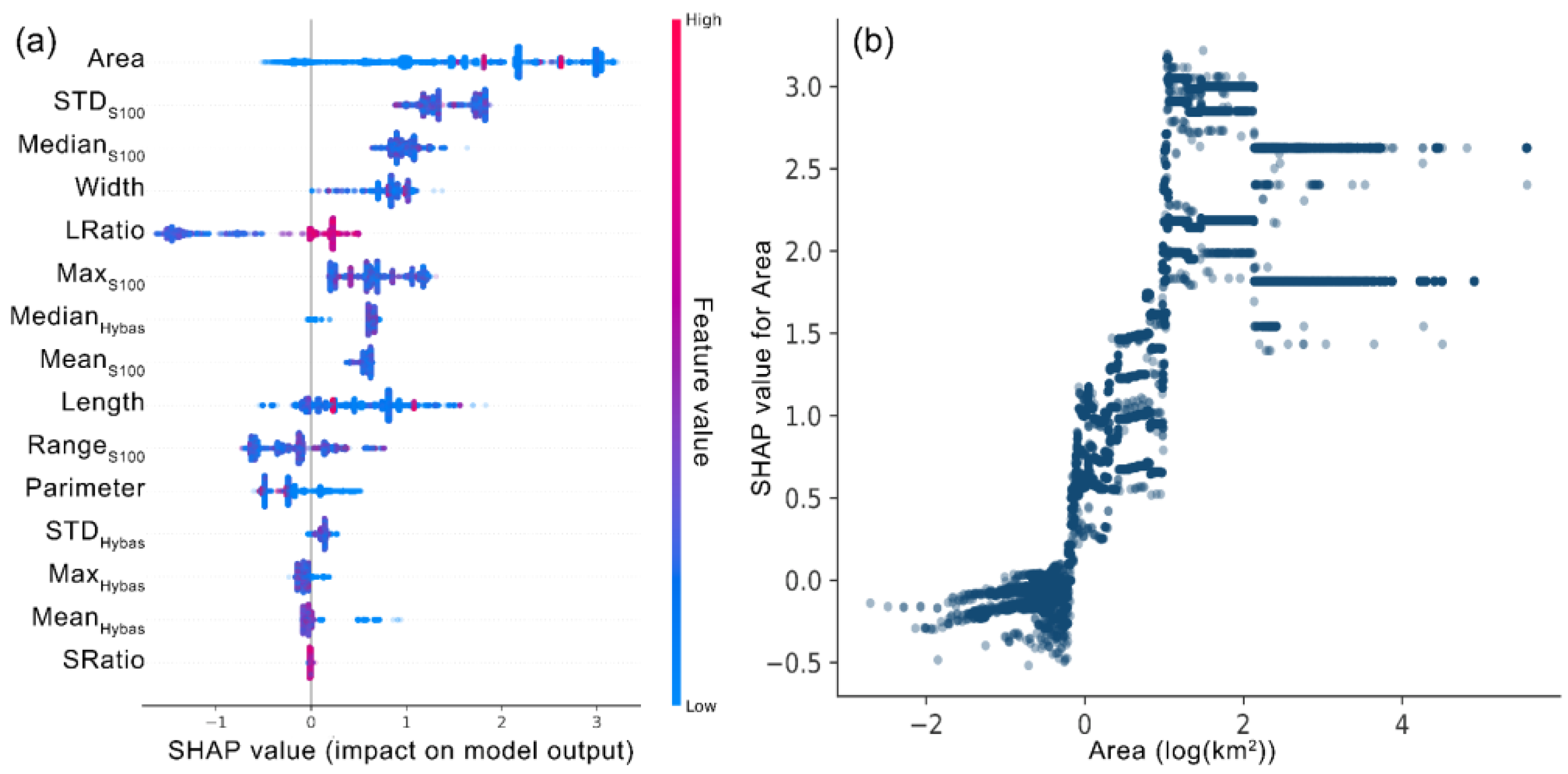
4.3.2. Feature Importance
5. Discussion
5.1. Uncertainty in Small Lakes
5.2. Limitations of Surface Water Maps
5.3. Applicability of the Methodology
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yigzaw, W.; Li, H.Y.; Demissie, Y.; Hejazi, M.I.; Leung, L.R.; Voisin, N.; Payn, R. A New Global Storage-Area-Depth Data Set for Modeling Reservoirs in Land Surface and Earth System Models. Water Resour. Res. 2018, 54, 10372–10386. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global extent of rivers and streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef]
- Sobek, S. Predicting the depth and volume of lakes from map-derived parameters. Inland Waters 2011, 1, 177–184. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H.; Cai, X. Estimating lake temperature profile and evaporation losses by leveraging MODIS LST data. Remote Sens. Environ. 2020, 251, 112104. [Google Scholar] [CrossRef]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef]
- Obertegger, U.; Flaim, G.; Braioni, M.G.; Sommaruga, R.; Corradini, F.; Borsato, A. Water residence time as a driving force of zooplankton structure and succession. Aquat. Sci. 2007, 69, 575–583. [Google Scholar] [CrossRef]
- Feng, Y.; Zhang, H.; Tao, S.; Ao, Z.; Song, C.; Chave, J.; Le Toan, T.; Xue, B.; Zhu, J.; Pan, J.; et al. Decadal Lake Volume Changes (2003–2020) and Driving Forces at a Global Scale. Remote Sens. 2022, 14, 1032. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Pittock, J.; Davis, R.; Williams, J.; Fu, G.; Warburton, M.; Udall, B.; McKenzie, R.; Yu, X.; Che, N.; et al. Global insights into water resources, climate change and governance. Nat. Clim. Change 2012, 3, 315–321. [Google Scholar] [CrossRef]
- Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
- Luo, S.; Song, C.; Ke, L.; Zhan, P.; Fan, C.; Liu, K.; Chen, T.; Wang, J.; Zhu, J. Satellite Laser Altimetry Reveals a Net Water Mass Gain in Global Lakes with Spatial Heterogeneity in the Early 21st Century. Geophys. Res. Lett. 2022, 49, e2021GL096676. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.; Zhan, P.; Luo, S.; Fan, C. A Low-Cost Approach for Lake Volume Estimation on the Tibetan Plateau: Coupling the Lake Hypsometric Curve and Bottom Elevation. Front. Earth Sci. 2022, 10, 925944. [Google Scholar] [CrossRef]
- Li, J.; Knapp, D.E.; Lyons, M.; Roelfsema, C.; Phinn, S.; Schill, S.R.; Asner, G.P. Automated Global Shallow Water Bathymetry Mapping Using Google Earth Engine. Remote Sens. 2021, 1, 1469. [Google Scholar] [CrossRef]
- Pi, X.; Luo, Q.; Feng, L.; Xu, Y.; Tang, J.; Liang, X.; Ma, E.; Cheng, R.; Fensholt, R.; Brandt, M.; et al. Mapping global lake dynamics reveals the emerging roles of small lakes. Nat. Commun. 2022, 13, 5777. [Google Scholar] [CrossRef]
- Pickens, A.H.; Hansen, M.C.; Hancher, M.; Stehman, S.V.; Tyukavina, A.; Potapov, P.; Marroquin, B.; Sherani, Z. Mapping and sampling to characterize global inland water dynamics from 1999 to 2018 with full Landsat time-series. Remote Sens. Environ. 2020, 243, 111792. [Google Scholar] [CrossRef]
- Han, Q.; Niu, Z. Construction of the Long-Term Global Surface Water Extent Dataset Based on Water-NDVI Spatio-Temporal Parameter Set. Remote Sens. 2020, 12, 2675. [Google Scholar] [CrossRef]
- Ma, S.; Liao, J.; Jing, R.; Chen, J. A dataset of lake level changes in China between 2002 and 2023 using multi-altimeter data. Big Earth Data 2024, 8, 166–188. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhang, W.; Wang, X.H. Surface-Water-Level Changes During 2003–2019 in Australia Revealed by ICESat/ICESat-2 Altimetry and Landsat Imagery. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1129–1133. [Google Scholar] [CrossRef]
- Luo, S.; Song, C.; Zhan, P.; Liu, K.; Chen, T.; Li, W.; Ke, L. Refined estimation of lake water level and storage changes on the Tibetan Plateau from ICESat/ICESat-2. Catena 2021, 200, 105177. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, W.; Xie, H. Tibetan Plateau’s Lake Level and Volume Changes from NASA’s ICESat/ICESat-2 and Landsat Missions. Geophys. Res. Lett. 2019, 46, 13107–13118. [Google Scholar] [CrossRef]
- Qiao, B.; Zhu, L.; Wang, J.; Ju, J.; Ma, Q.; Huang, L.; Chen, H.; Liu, C.; Xu, T. Estimation of lake water storage and changes based on bathymetric data and altimetry data and the association with climate change in the central Tibetan Plateau. J. Hydrol. 2019, 578, 124052. [Google Scholar] [CrossRef]
- Fang, Y.; Li, H.; Wan, W.; Zhu, S.; Wang, Z.; Hong, Y.; Wang, H. Assessment of Water Storage Change in China’s Lakes and Reservoirs over the Last Three Decades. Remote Sens. 2019, 11, 1467. [Google Scholar] [CrossRef]
- Xie, J.; Li, B.; Jiao, H.; Zhou, Q.; Mei, Y.; Xie, D.; Wu, Y.; Sun, X.; Fu, Y. Water Level Change Monitoring Based on a New Denoising Algorithm Using Data from Landsat and ICESat-2: A Case Study of Miyun Reservoir in Beijing. Remote Sens. 2022, 14, 4344. [Google Scholar] [CrossRef]
- Mateo-Pérez, V.; Corral-Bobadilla, M.; Ortega-Fernández, F.; Vergara-González, E.P. Port Bathymetry Mapping Using Support Vector Machine Technique and Sentinel-2 Satellite Imagery. Remote Sens. 2020, 12, 2069. [Google Scholar] [CrossRef]
- Yang, H.; Guo, H.; Dai, W.; Nie, B.; Qiao, B.; Zhu, L. Bathymetric mapping and estimation of water storage in a shallow lake using a remote sensing inversion method based on machine learning. Int. J. Digit. Earth 2022, 15, 789–812. [Google Scholar] [CrossRef]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.; et al. High-resolution mapping of the world’s reservoirs and dams for sustainable river-flow management. Front. Ecol. Environ. 2011, 9, 494–502. [Google Scholar] [CrossRef]
- Caballero, I.; Stumpf, R.P. Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuar. Coast. Shelf Sci. 2019, 226, 106277. [Google Scholar] [CrossRef]
- Tsolakidis, I.; Vafiadis, M. Comparison of Hydrographic Survey and Satellite Bathymetry in Monitoring Kerkini Reservoir Storage. Environ. Process. 2019, 6, 1031–1049. [Google Scholar] [CrossRef]
- Wan, J.; Ma, Y. Shallow Water Bathymetry Mapping of Xinji Island Based on Multispectral Satellite Image using Deep Learning. J. Indian Soc. Remote Sens. 2021, 49, 2019–2032. [Google Scholar] [CrossRef]
- Yang, N.; Li, J.H.; Mo, W.B.; Luo, W.J.; Wu, D.; Gao, W.C.; Sun, C.H. Water depth retrieval models of East Dongting Lake, China, using GF-1 multi-spectral remote sensing images. Glob. Ecol. Conserv. 2020, 22, e01004. [Google Scholar] [CrossRef]
- Qi, M.; Liu, S.; Wu, K.; Zhu, Y.; Xie, F.; Jin, H.; Gao, Y.; Yao, X. Improving the accuracy of glacial lake volume estimation: A case study in the Poiqu basin, central Himalayas. J. Hydrol. 2022, 610, 127973. [Google Scholar] [CrossRef]
- Qiao, B.; Ju, J.; Zhu, L.; Chen, H.; Kai, J.; Kou, Q. Improve the Accuracy of Water Storage Estimation—A Case Study from Two Lakes in the Hohxil Region of North Tibetan Plateau. Remote Sens. 2021, 13, 293. [Google Scholar] [CrossRef]
- Gu, Z.; Zhang, Y.; Fan, H. Mapping inter- and intra-annual dynamics in water surface area of the Tonle Sap Lake with Landsat time-series and water level data. J. Hydrol. 2021, 601, 126644. [Google Scholar] [CrossRef]
- Haakanson, L.; Peters, R.H. Predictive Limnology: Methods for Predictive Modelling; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Håkanson, L.; Karlsson, B. On the Relationship between Regional Geomorphology and Lake Morphometry—A Swedish Example. Geogr. Ann. Ser. A Phys. Geogr. 1984, 66, 103–119. [Google Scholar] [CrossRef]
- Heathcote, A.J.; del Giorgio, P.A.; Prairie, Y.T.; Brickman, D. Predicting bathymetric features of lakes from the topography of their surrounding landscape. Can. J. Fish. Aquat.Sci. 2015, 72, 643–650. [Google Scholar] [CrossRef]
- Cai, X.; Gan, W.; Ji, W.; Zhao, X.; Wang, X.; Chen, X. Optimizing Remote Sensing-Based Level–Area Modeling of Large Lake Wetlands: Case Study of Poyang Lake. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 471–479. [Google Scholar] [CrossRef]
- Hollister, J.W.; Milstead, W.B.; Urrutia, M.A. Predicting maximum lake depth from surrounding topography. PLoS ONE 2011, 6, e25764. [Google Scholar] [CrossRef]
- Hollister, J.; Milstead, W.B. Using GIS to estimate lake volume from limited data. Lake Reserv. Manag. 2010, 26, 194–199. [Google Scholar] [CrossRef]
- Lehner, B.; Döll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Delaney, C.; Li, X.; Holmberg, K.; Wilson, B.; Heathcote, A.; Nieber, J. Estimating Lake Water Volume with Regression and Machine Learning Methods. Front. Water 2022, 4, 886964. [Google Scholar] [CrossRef]
- Muñoz, R.; Huggel, C.; Frey, H.; Cochachin, A.; Haeberli, W. Glacial lake depth and volume estimation based on a large bathymetric dataset from the Cordillera Blanca, Peru. Earth Surf. Process. Landf. 2020, 45, 1510–1527. [Google Scholar] [CrossRef]
- Fair, Z.; Flanner, M.; Brunt, K.M.; Fricker, H.A.; Gardner, A. Using ICESat-2 and Operation IceBridge altimetry for supraglacial lake depth retrievals. Cryosphere 2020, 14, 4253–4263. [Google Scholar] [CrossRef]
- Weekley, D.; Li, X. Tracking lake surface elevations with proportional hypsometric relationships, Landsat imagery, and multiple DEMs. Water Resour. Res. 2021, 57, e2020WR027666. [Google Scholar] [CrossRef]
- Weekley, D.; Li, X. Tracking Multidecadal Lake Water Dynamics with Landsat Imagery and Topography/Bathymetry. Water Resour. Res. 2019, 55, 8350–8367. [Google Scholar] [CrossRef]
- Yang, H.; Qiao, B.; Huang, S.; Fu, Y.; Guo, H. Fitting profile water depth to improve the accuracy of lake depth inversion without bathymetric data based on ICESat-2 and Sentinel-2 data. Int. J. Appl. Earth Obs. Geoinf. 2023, 119, 103310. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhou, H.; Zhang, W.; Zhang, Z.; Wang, X.H. A Method to Derive Bathymetry for Dynamic Water Bodies Using ICESat-2 and GSWD Data Sets. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, Y.; Gao, H.; Zhao, G.; Tseng, K.-H. A high-resolution bathymetry dataset for global reservoirs using multi-source satellite imagery and altimetry. Remote Sens. Environ. 2020, 244, 111831. [Google Scholar] [CrossRef]
- Armon, M.; Dente, E.; Shmilovitz, Y.; Mushkin, A.; Cohen, T.J.; Morin, E.; Enzel, Y. Determining Bathymetry of Shallow and Ephemeral Desert Lakes Using Satellite Imagery and Altimetry. Geophys. Res. Lett. 2020, 47, e2020GL087367. [Google Scholar] [CrossRef]
- Fang, C.; Lu, S.; Li, M.; Wang, Y.; Li, X.; Tang, H.; Odion Ikhumhen, H. Lake water storage estimation method based on similar characteristics of above-water and underwater topography. J. Hydrol. 2023, 618, 129146. [Google Scholar] [CrossRef]
- Liu, K.; Song, C. Modeling lake bathymetry and water storage from DEM data constrained by limited underwater surveys. J. Hydrol. 2022, 604, 127260. [Google Scholar] [CrossRef]
- Bemmelen, C.W.T.; Mann, M.; Ridder, M.P.; Rutten, M.M.; Giesen, N.C. Determining water reservoir characteristics with global elevation data. Geophys. Res. Lett. 2016, 43, 1–11. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.; Zhao, S.; Wang, J.; Chen, T.; Zhan, P.; Fan, C.; Zhu, J. Mapping inundated bathymetry for estimating lake water storage changes from SRTM DEM: A global investigation. Remote Sens. Environ. 2024, 301, 113960. [Google Scholar] [CrossRef]
- Lv, Y.; Jia, L.; Menenti, M.; Zheng, C.; Jiang, M.; Lu, J.; Zeng, Y.; Chen, Q.; Bennour, A. A novel remote sensing method to estimate pixel-wise lake water depth using dynamic water-land boundary and lakebed topography. Int. J. Digit. Earth 2024, 17, 2440443. [Google Scholar] [CrossRef]
- O’Loughlin, F.E.; Paiva, R.C.D.; Durand, M.; Alsdorf, D.E.; Bates, P.D. A multi-sensor approach towards a global vegetation corrected SRTM DEM product. Remote Sens. Environ. 2016, 182, 49–59. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A high-accuracy map of global terrain elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Zhan, P.; Song, C.; Luo, S.; Liu, K.; Ke, L.; Chen, T. Lake Level Reconstructed from DEM-Based Virtual Station: Comparison of Multisource DEMs with Laser Altimetry and UAV-LiDAR Measurements. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Demiriz, A.; Bennett, K.P.; Shawe-Taylor, J. Linear Programming Boosting via Column Generation. Mach. Learn. 2002, 46, 225–254. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Breiman, L. Bagging Predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Zou, F.; Tenzer, R.; Jin, S. Water Storage Variations in Tibet from GRACE, ICESat, and Hydrological Data. Remote Sens. 2019, 11, 1103. [Google Scholar] [CrossRef]
- Aas, K.; Jullum, M.; Løland, A. Explaining individual predictions when features are dependent: More accurate approximations to Shapley values. Artif. Intell. 2021, 298, 103502. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 22 May 2017. [Google Scholar]
- Shen, C.; Jia, L.; Ren, S. Inter- and Intra-Annual Glacier Elevation Change in High Mountain Asia Region Based on ICESat-1&2 Data Using Elevation-Aspect Bin Analysis Method. Remote Sens. 2022, 14, 1630. [Google Scholar] [CrossRef]
- Huang, T.; Jia, L.; Menenti, M.; Lu, J.; Zhou, J.; Hu, G. A New Method to Estimate Changes in Glacier Surface Elevation Based on Polynomial Fitting of Sparse ICESat-GLAS Footprints. Sensors 2017, 17, 1803. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H. On typical range, sensitivity, and normalization of Mean Squared Error and Nash-Sutcliffe Efficiency type metrics. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]







| Data | Format | Source | URLs | Description |
|---|---|---|---|---|
| GSWED | Raster image | Big Data for Sustainable Development Goals | https://data.casearth.cn/thematic/GWRD_2023/275 (accessed on 14 March 2025) | Global surface water maps |
| GLAKES | Shapefile | Pi et al., 2022 [16] | https://zenodo.org/records/7016548 (accessed on 14 March 2025) | Global lake extents |
| Bare-Earth SRTM DEM | Raster image | O’Loughlin et al., 2015 [57] | https://data.bris.ac.uk/data/dataset/10tv0p32gizt01nh9edcjzd6wa (accessed on 14 March 2025) | DEM |
| BathybaseDb | Raster image | Open contribution and access | http://bathybase.org/ (accessed on 14 March 2025) | Lake bathymetric data |
| HydroLAKES | Shapefile | HydroSHEDS project | https://www.hydrosheds.org/products/hydrolakes (accessed on 14 March 2025) | Global lake data |
| GLWD | Shapefile | WWF and the Center for Environmental Systems Research, University of Kassel, Germany | https://worldwildlife.org/pages/global-lakes-and-wetlands-database (accessed on 14 March 2025) | Global lakes and wetlands database |
| GRanD | Shapefile | Global Water System Project [28] | https://www.globaldamwatch.org/grand (accessed on 14 March 2025) | Global Reservoir and Dam database |
| ReGeom | Shapefile | Yigzaw et al., 2018 [1] | https://zenodo.org/records/1322884 (accessed on 14 March 2025) | Global Reservoir and Dam database |
| LWPED | Table | Big Earth Data Center | https://data.casearth.cn/dataset/65387d82819aec0f26f0adc0 (accessed on 14 March 2025) | Lake field-observed data |
| WDFT | Table | Texas Water Development Board | https://waterdatafortexas.org/reservoirs/statewide (accessed on 14 March 2025) | Monitored water supply reservoirs |
| HydroBASINS | Shapefile | HydroSHEDS project | https://hydrosheds.org/products/hydrobasins (accessed on 14 March 2025) | Global sub-basin boundaries |
| ICESat-2/ATLAS | HDF5 | NASA National Snow and Ice Data Center | https://nsidc.org/data/glah14/versions/34 (accessed on 14 March 2025) https://nsidc.org/data/atl13/versions/5 (accessed on 14 March 2025) | Ice, cloud, and land elevation |
| Features | Type | Unit | Description |
|---|---|---|---|
| Area | Morphologic features | km2 | The surface area of a lake |
| Perimeter | km | The perimeter of a lake | |
| SRatio | \ | The ratio of the surface area and perimeter | |
| Length | km | The range (maximum–minimum) of the longitude of a lake | |
| Width | km | The range (maximum–minimum) of the latitude of a lake | |
| LRatio | \ | The ratio of the length and width | |
| MeanS100 | Surrounding topographic features | % | The mean slope in the 100 m buffer zone around a lake |
| Median S100 | % | The median slope in the 100 m buffer zone around a lake | |
| MaxS100 | % | The maximum slope in the 100 m buffer zone around a lake | |
| RangeS100 | % | The range (maximum–minimum) of the slope in the 100 m buffer zone around a lake | |
| STDS100 | % | The standard deviation of the slope in the 100 m buffer zone around a lake | |
| MeanHybas | Catchment topographic features | meter | The mean elevation in the hydrological basin where a lake is located |
| MedianHybas | meter | The median elevation in the hydrological basin where a lake is located | |
| MaxHybas | meter | The maximum elevation in the hydrological basin where a lake is located | |
| STDHybas | meter | The standard deviation of elevation in the hydrological basin where a lake is located |
| Number | Bias (m) | MAE (m) | RMSE (m) | R2 | KGE | |
|---|---|---|---|---|---|---|
| ICESat | 497 | 0.91 | 2.41 | 3.12 | 0.999 | 0.997 |
| ICESat-2 | 266 | 2.10 | 3.35 | 5.35 | 0.999 | 0.996 |
| Total | 763 | 1.33 | 2.74 | 4.04 | 0.999 | 0.997 |
| Number | Sample | Bias (m) | MAE (m) | RMSE (m) | R2 | KGE | |
|---|---|---|---|---|---|---|---|
| RF | 76,030 | train | 0.01 | 0.45 | 1.99 | 0.99 | 0.97 |
| test | 0.03 | 1.19 | 4.74 | 0.95 | 0.94 | ||
| GB | 76,030 | train | −0.06 | 0.12 | 1.45 | 0.99 | 0.98 |
| test | −0.03 | 1.12 | 5.20 | 0.95 | 0.96 | ||
| Bg | 76,030 | train | 0.02 | 0.57 | 2.42 | 0.99 | 0.97 |
| test | 0.06 | 1.24 | 4.77 | 0.95 | 0.94 | ||
| Piecewise GB | 76,030 | train | −0.02 | 0.19 | 1.17 | 0.99 | 0.96 |
| test | −0.08 | 1.09 | 4.78 | 0.96 | 0.95 | ||
| Piecewise GB (0~1 km2) | 6672 | train | −0.02 | 0.05 | 0.18 | 0.99 | 0.97 |
| test | 0.01 | 0.44 | 0.81 | 0.39 | 0.51 | ||
| Piecewise GB (1~10 km2) | 26,251 | train | −0.08 | 0.14 | 2.13 | 0.91 | 0.84 |
| test | −0.06 | 0.58 | 3.07 | 0.54 | 0.65 | ||
| Piecewise GB (10~102 km2) | 34,847 | train | −0.09 | 0.17 | 1.74 | 0.97 | 0.94 |
| test | −0.10 | 1.22 | 4.97 | 0.76 | 0.82 | ||
| Piecewise GB (102~103 km2) | 6366 | train | −0.09 | 0.16 | 1.07 | 0.99 | 0.97 |
| test | 0.01 | 2.15 | 6.82 | 0.88 | 0.91 | ||
| Piecewise GB (103~104 km2) | 1502 | train | −0.32 | 0.58 | 1.77 | 0.99 | 0.98 |
| test | −0.38 | 2.96 | 9.25 | 0.97 | 0.97 | ||
| Piecewise GB (~104 km2) | 392 | train | −3.38 | 5.89 | 10.16 | 0.99 | 0.95 |
| test | −1.81 | 10.38 | 22.60 | 0.99 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Jia, L.; Menenti, M.; Zheng, C.; Lu, J.; Jiang, M.; Chen, Q.; Zhang, Y. Estimations of Dynamic Water Depth and Volume of Global Lakes Using Machine Learning. Remote Sens. 2025, 17, 1052. https://doi.org/10.3390/rs17061052
Lv Y, Jia L, Menenti M, Zheng C, Lu J, Jiang M, Chen Q, Zhang Y. Estimations of Dynamic Water Depth and Volume of Global Lakes Using Machine Learning. Remote Sensing. 2025; 17(6):1052. https://doi.org/10.3390/rs17061052
Chicago/Turabian StyleLv, Yunzhe, Li Jia, Massimo Menenti, Chaolei Zheng, Jing Lu, Min Jiang, Qiting Chen, and Yiqing Zhang. 2025. "Estimations of Dynamic Water Depth and Volume of Global Lakes Using Machine Learning" Remote Sensing 17, no. 6: 1052. https://doi.org/10.3390/rs17061052
APA StyleLv, Y., Jia, L., Menenti, M., Zheng, C., Lu, J., Jiang, M., Chen, Q., & Zhang, Y. (2025). Estimations of Dynamic Water Depth and Volume of Global Lakes Using Machine Learning. Remote Sensing, 17(6), 1052. https://doi.org/10.3390/rs17061052









