Synthetic Aperture Radar Processing Using Flexible and Seamless Factorized Back-Projection
Abstract
1. Introduction
2. Signal Model and Conventional Time-Domain Focusing Schemes
2.1. Time-Domain Back-Projection
2.2. Fast Factorized Back-Projection
3. Flexible and Seamless Factorized Back-Projection
- Fast Factorized Back-Projection: First, the sub-apertures are focused on a coarse grid, then the low-resolution images are merged hierarchically until the full-resolution image is obtained. This is the well-known approach developed in [20].
- Flexible & Seamless: The coarse-resolution images are merged l-wise (e.g., couple-wise) recursively until a criterion based on the computational cost is met. More precisely, at the end of each iteration step, this algorithm chooses to proceed further into the hierarchical merging or to merge all the images left into the Cartesian reference system. This approach represents our contribution described in this article.
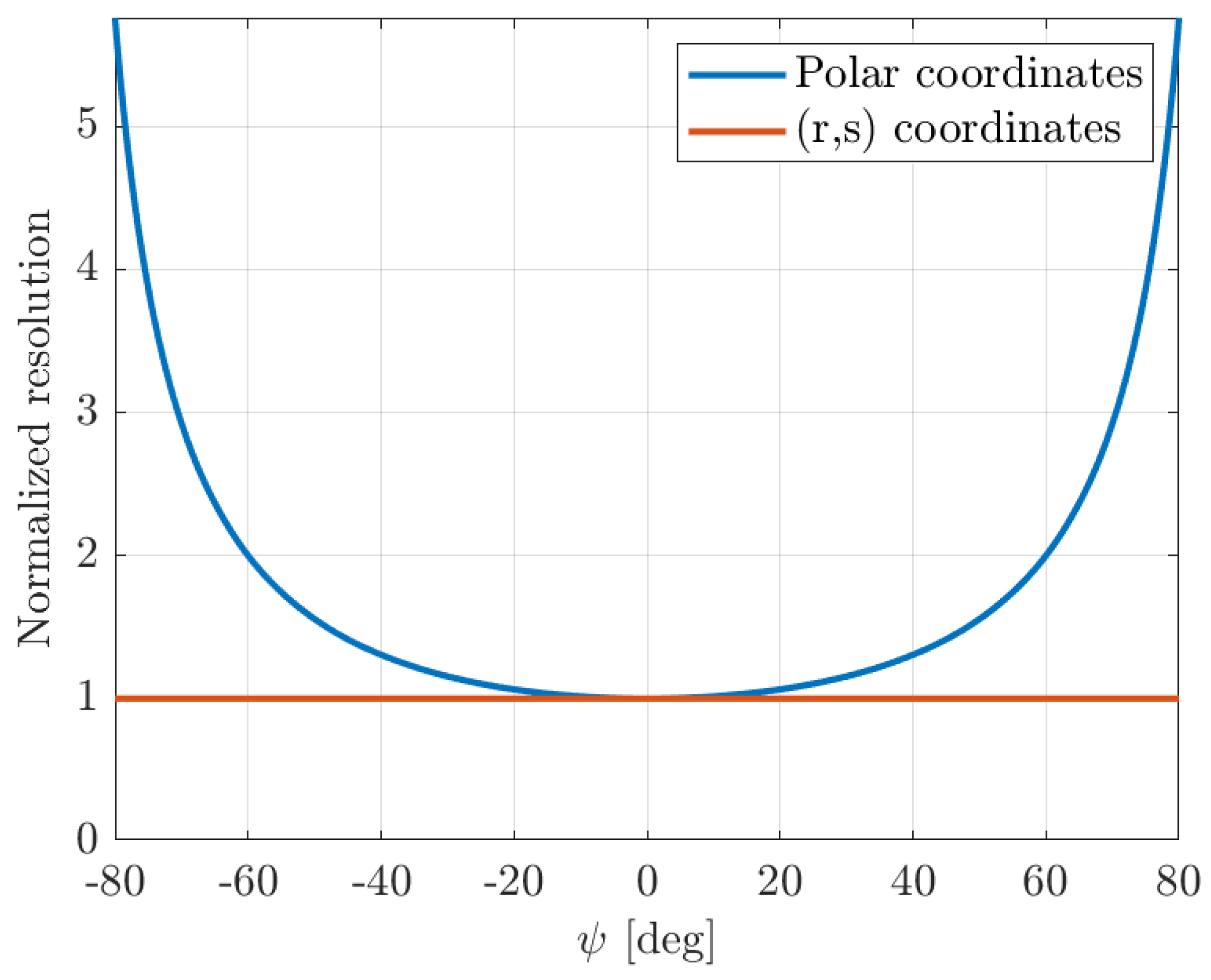
3.1. The (r,s) Reference System
- represents the position of the radar along the axis at time ;
- represents the coordinates of the target.
3.2. Flexible and Seamless Factorized Back-Projection
3.3. Computational Cost Analysis
3.4. Algorithm Implementation
4. Numerical Analysis
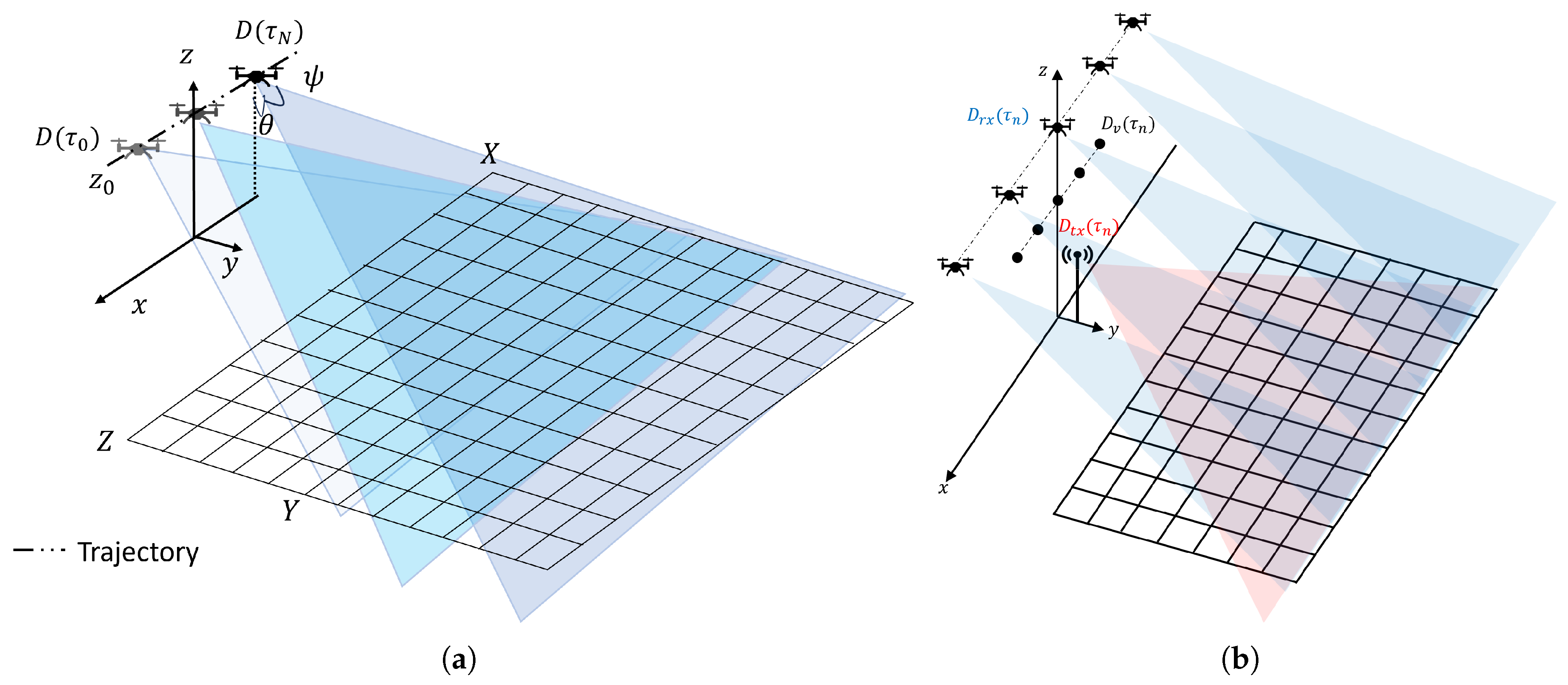
4.1. UAV Scenarios
4.2. Ground-Based-like Scenario
4.3. Stripmap Scenario
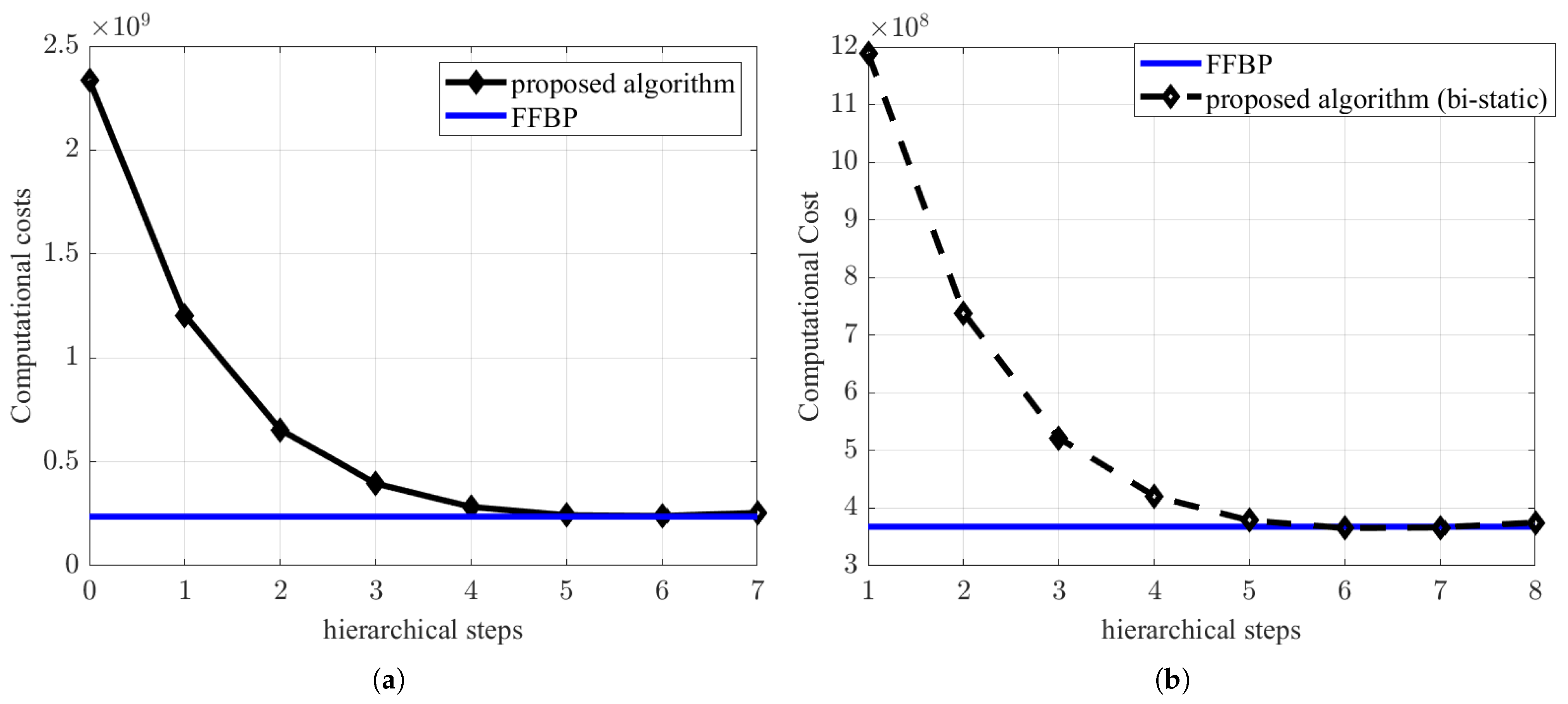
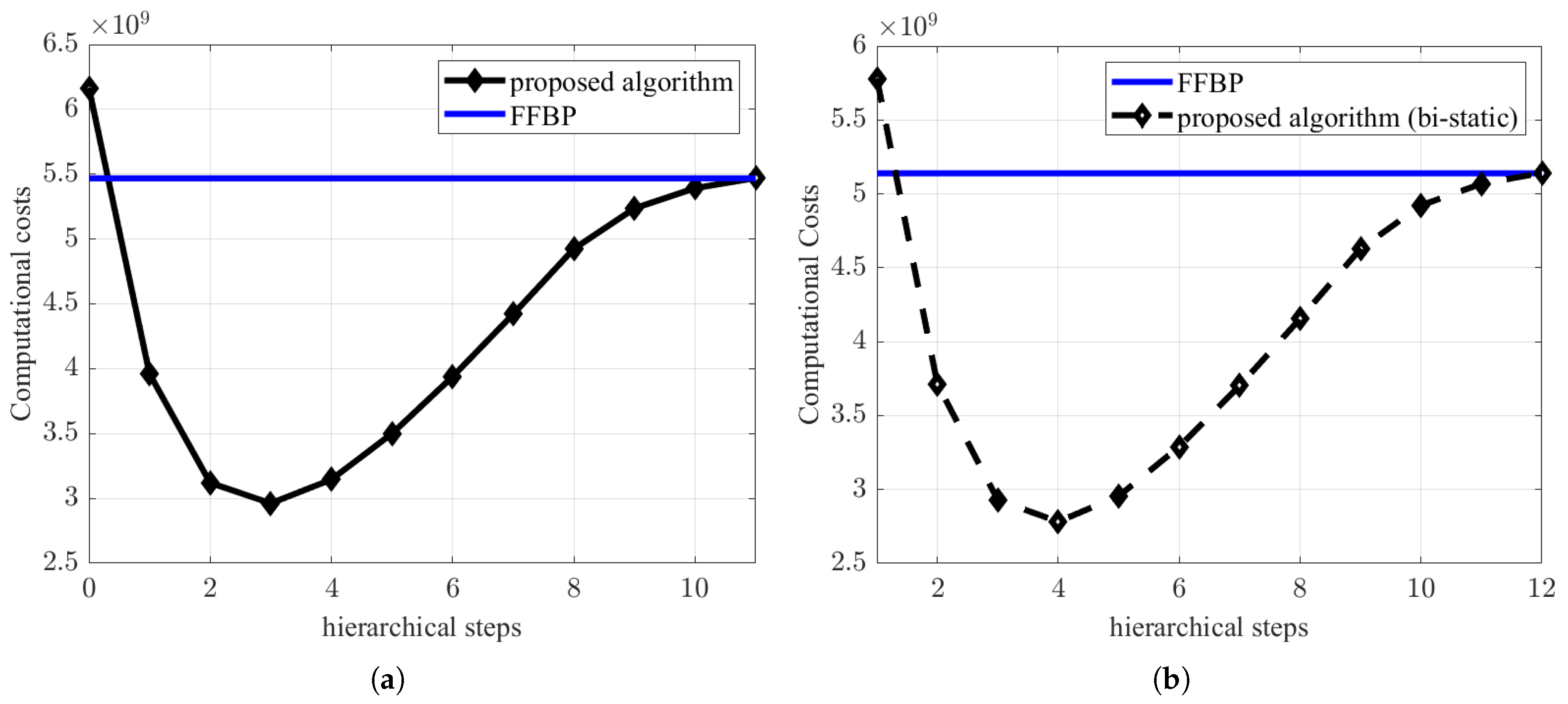
4.4. A Computational Cost Comparison Between Large-Scale FFBP and Flexible & Seamless
5. Numerical Simulation
6. Real Data
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| SAR | Synthetic Aperture Radar |
| FFBP | Fast Factorized Back-Projection |
| GBL | Ground-Based-Like |
| TDBP | Time-Domain Back-Projection |
| VPC | Virtual Antenna Phase Center |
References
- Petritoli, E.; Leccese, F.; Ciani, L. Reliability assessment of UAV systems. In Proceedings of the 2017 IEEE International Workshop on Metrology for AeroSpace (MetroAeroSpace), Padua, Italy, 21–23 June 2017; pp. 266–270. [Google Scholar]
- Meng, K.; Wu, Q.; Xu, J.; Chen, W.; Feng, Z.; Schober, R.; Swindlehurst, A.L. UAV-enabled integrated sensing and communication: Opportunities and challenges. IEEE Wirel. Commun. 2023, 31, 97–104. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, R.; Lim, T.J. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Schreiber, E.; Heinzel, A.; Peichl, M.; Engel, M.; Wiesbeck, W. Advanced buried object detection by multichannel, UAV/drone carried synthetic aperture radar. In Proceedings of the 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; pp. 1–5. [Google Scholar]
- Romero, I.; Walter, T.; Mariager, S. Performance Analysis and Simulation of a Continious Wave Metal Detector for UAV Applications. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7222–7225. [Google Scholar]
- Angelliaume, S.; Castet, N.; Dupuis, X. SAR-Light: The new ONERA SAR sensor on-board UAV. IET Conf. Proc. 2022, 17, 66–70. [Google Scholar] [CrossRef]
- Lort, M.; Aguasca, A.; Lopez-Martinez, C.; Marín, T.M. Initial evaluation of SAR capabilities in UAV multicopter platforms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 127–140. [Google Scholar] [CrossRef]
- Brigui, F.; Angelliaume, S.; Castet, N.; Dupuis, X.; Martineau, P. Sar-light-first sar images from the new onera sar sensor on uav platform. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7721–7724. [Google Scholar]
- Linsalata, F.; Albanese, A.; Sciancalepore, V.; Roveda, F.; Magarini, M.; Costa-Perez, X. OTFS-superimposed PRACH-aided localization for UAV safety applications. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Manzoni, M.; Moro, S.; Linsalata, F.; Polisano, M.G.; Monti-Guarnieri, A.V.; Tebaldini, S. Evaluation of UAV-Based ISAC SAR Imaging: Methods and Performances. In Proceedings of the 2024 IEEE Radar Conference (RadarConf24), Denver, CO, USA, 6–10 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Denbina, M.; Towfic, Z.J.; Thill, M.; Bue, B.; Kasraee, N.; Peacock, A.; Lou, Y. Flood mapping using UAVSAR and convolutional neural networks. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 3247–3250. [Google Scholar]
- Cafforio, C.; Prati, C.; Rocca, F. SAR data focusing using seismic migration techniques. IEEE Trans. Aerosp. Electron. Syst. 1991, 27, 194–207. [Google Scholar] [CrossRef]
- Bamler, R. A comparison of range-Doppler and wavenumber domain SAR focusing algorithms. IEEE Trans. Geosci. Remote Sens. 1992, 30, 706–713. [Google Scholar] [CrossRef]
- Frey, O.; Meier, E.H.; Nüesch, D.R. Processing SAR data of rugged terrain by time-domain back-projection. In Proceedings of the SAR Image Analysis, Modeling, and Techniques VII, Bruges, Belgium, 19–22 September 2005; Volume 5980, pp. 71–79. [Google Scholar]
- Frey, O.; Magnard, C.; Rüegg, M.; Meier, E. Non-linear SAR data processing by time-domain back-projection. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Frey, O.; Magnard, C.; Ruegg, M.; Meier, E. Focusing of airborne synthetic aperture radar data from highly nonlinear flight tracks. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1844–1858. [Google Scholar] [CrossRef]
- Frey, O.; Werner, C.L.; Wegmuller, U. GPU-based parallelized time-domain back-projection processing for agile SAR platforms. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1132–1135. [Google Scholar]
- Frey, O.; Werner, C.L.; Coscione, R. Car-borne and UAV-borne mobile mapping of surface displacements with a compact repeat-pass interferometric SAR system at L-band. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 8 July–2 August 2019; pp. 274–277. [Google Scholar]
- Bonfert, C.; Ruopp, E.; Waldschmidt, C. Improving SAR Imaging by Superpixel-Based Compressed Sensing and Backprojection Processing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5209212. [Google Scholar] [CrossRef]
- Ulander, L.M.; Hellsten, H.; Stenstrom, G. Synthetic-aperture radar processing using fast factorized back-projection. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 760–776. [Google Scholar] [CrossRef]
- Ponce, O.; Prats, P.; Rodriguez-Cassola, M.; Scheiber, R.; Reigber, A. Processing of circular SAR trajectories with fast factorized back-projection. In Proceedings of the 2011 IEEE international geoscience and remote sensing symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3692–3695. [Google Scholar]
- Ulander, L.M.; Froelind, P.O.; Gustavsson, A.; Murdin, D.; Stenstroem, G. Fast factorized back-projection for bistatic SAR processing. In Proceedings of the 8th European Conference on Synthetic Aperture Radar, Aachen, Germany, 7–10 June 2010; pp. 1–4. [Google Scholar]
- Manzoni, M.; Tebaldini, S.; Monti-Guarnieri, A.V.; Prati, C.M.; Russo, I. A comparison of processing schemes for automotive MIMO SAR imaging. Remote Sens. 2022, 14, 4696. [Google Scholar] [CrossRef]
- Rodriguez-Cassola, M.; Prats, P.; Krieger, G.; Moreira, A. Efficient time-domain image formation with precise topography accommodation for general bistatic SAR configurations. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2949–2966. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Vu, V.T.; Sjögren, T.K.; Pettersson, M.I. SAR imaging in ground plane using fast backprojection for mono-and bistatic cases. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 184–189. [Google Scholar]
- Vu, V.T.; Sjogren, T.K.; Pettersson, M.I. Fast time-domain algorithms for UWB bistatic SAR processing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1982–1994. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, L.; Cao, Y.; Yeo, T.S.; Lu, J.; Han, J.; Peng, Z. High-resolution Bistatic Spotlight SAR Imagery with General Configuration and Accelerated Track. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5213218. [Google Scholar] [CrossRef]
- Vu, V.T.; Pettersson, M.I. Fast backprojection algorithms based on subapertures and local polar coordinates for general bistatic airborne SAR systems. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2706–2712. [Google Scholar] [CrossRef]
- Polisano, M.G.; Manzoni, M.; Tebaldini, S.; Monti-Guarnieri, A.; Prati, C.M.; Russo, I. Very high resolution automotive SAR imaging from burst data. Remote Sens. 2023, 15, 845. [Google Scholar] [CrossRef]
- Wu, R.S.; Toksöz, M.N. Diffraction tomography and multisource holography applied to seismic imaging. Geophysics 1987, 52, 11–25. [Google Scholar] [CrossRef]
- Tebaldini, S. Single and multipolarimetric SAR tomography of forested areas: A parametric approach. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2375–2387. [Google Scholar] [CrossRef]
- Tebaldini, S.; Rocca, F. Multistatic wavenumber tessellation: Ideas for high resolution P-band SAR missions. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2412–2415. [Google Scholar]
- Polisano, M.G.; Manzoni, M.; Tebaldin, S.; Monti-Guarnieri, A.V.; Prati, C.M.; Russo, I. Automotive MIMO-SAR Imaging from Non-continuous Radar Acquisitions. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; pp. 578–587. [Google Scholar] [CrossRef]
- Ding, Y.; Munson, D.J. A fast back-projection algorithm for bistatic SAR imaging. In Proceedings of the International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 2. [Google Scholar]
- Willis, N.J. Bistatic Radar; SciTech Publishing: Raleigh, NC, USA, 2005; Volume 2. [Google Scholar]
- Polisano, M.G.; Grassi, P.; Manzoni, M.; Tebaldini, S. Signal Processing Methods for Long-Range UAV-SAR Focusing with Partially Unknown Trajectory. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 1959–1963. [Google Scholar]
- Grassi, P.; Manzoni, M.; Tebaldini, S. Low Complexity Geometrical Autofocusing Based on Subsequent Sub-Apertures Calibration. In Proceedings of the 2024 IEEE Radar Conference (RadarConf24), Denver, CO, USA, 6–10 May 2024; pp. 1–6. [Google Scholar]


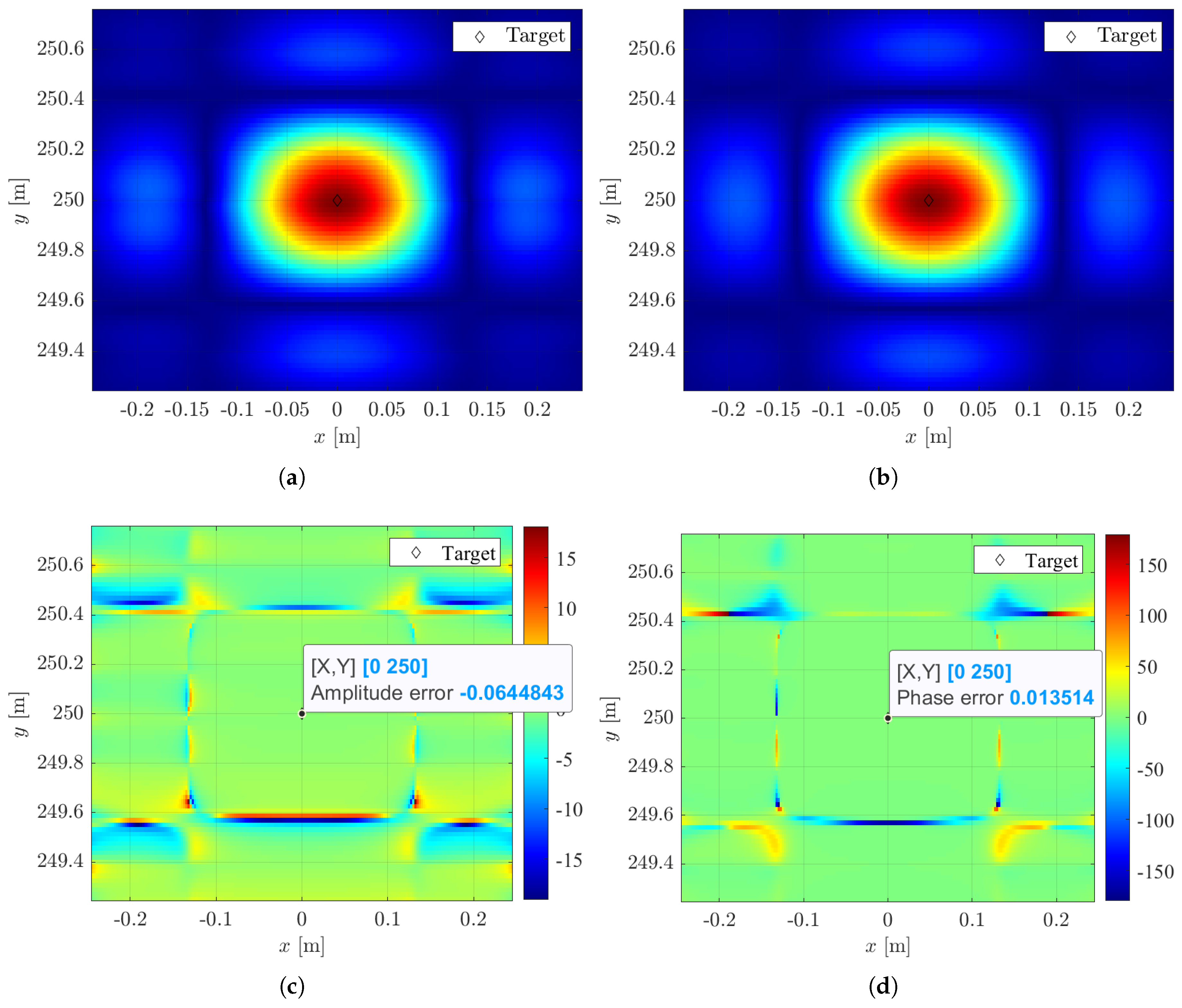
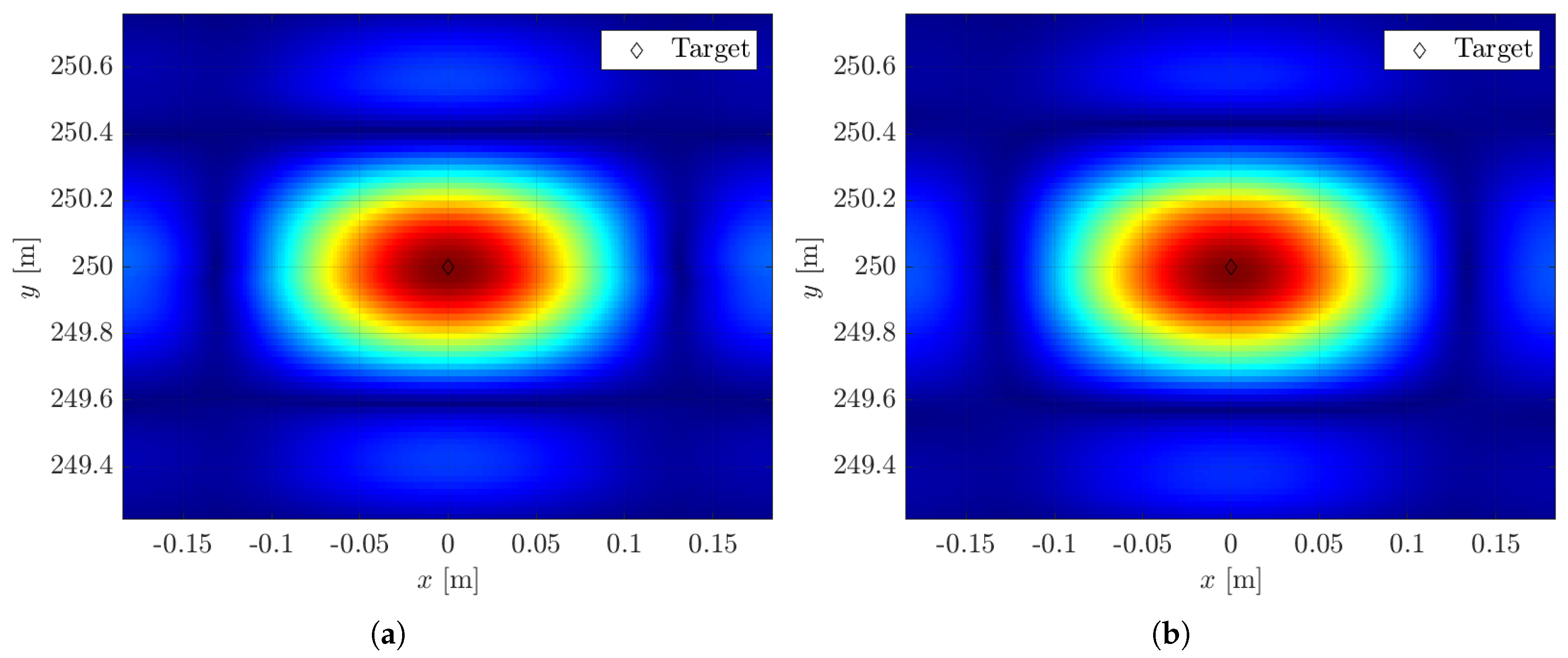
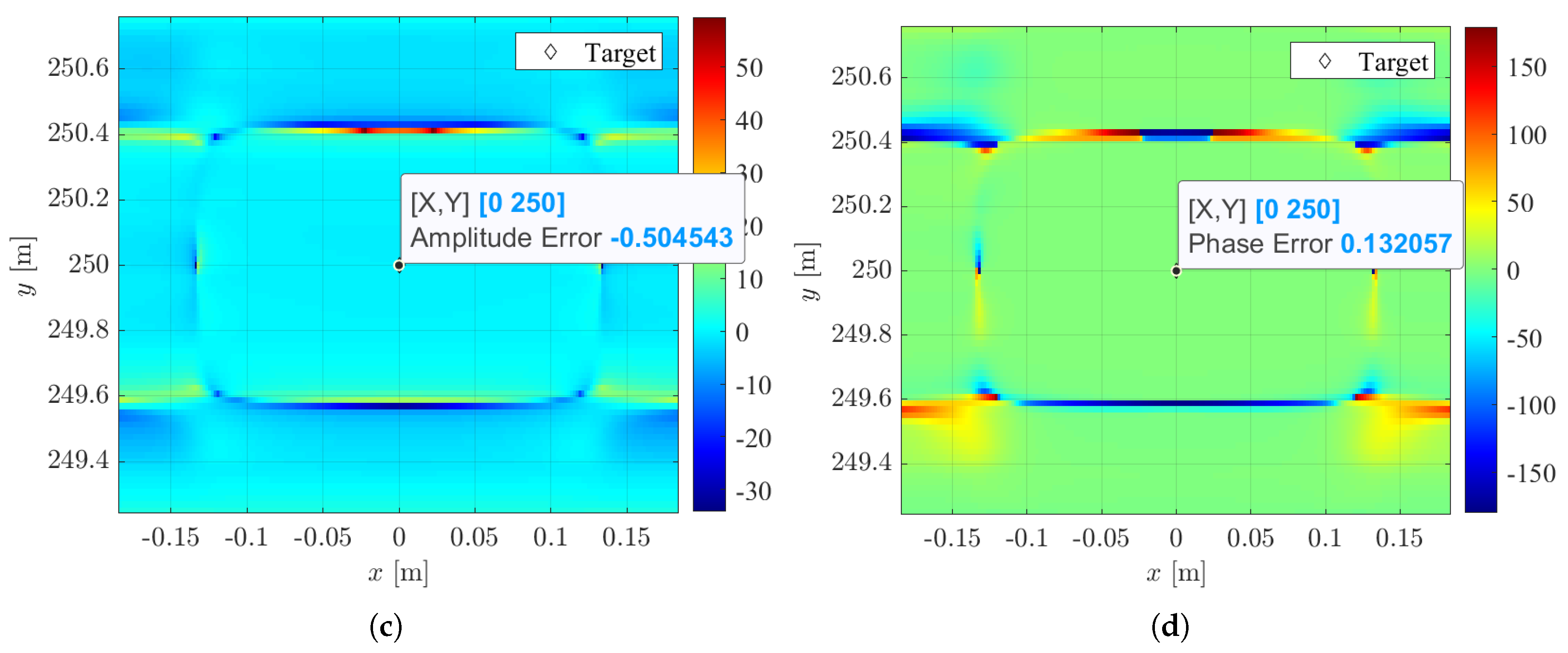
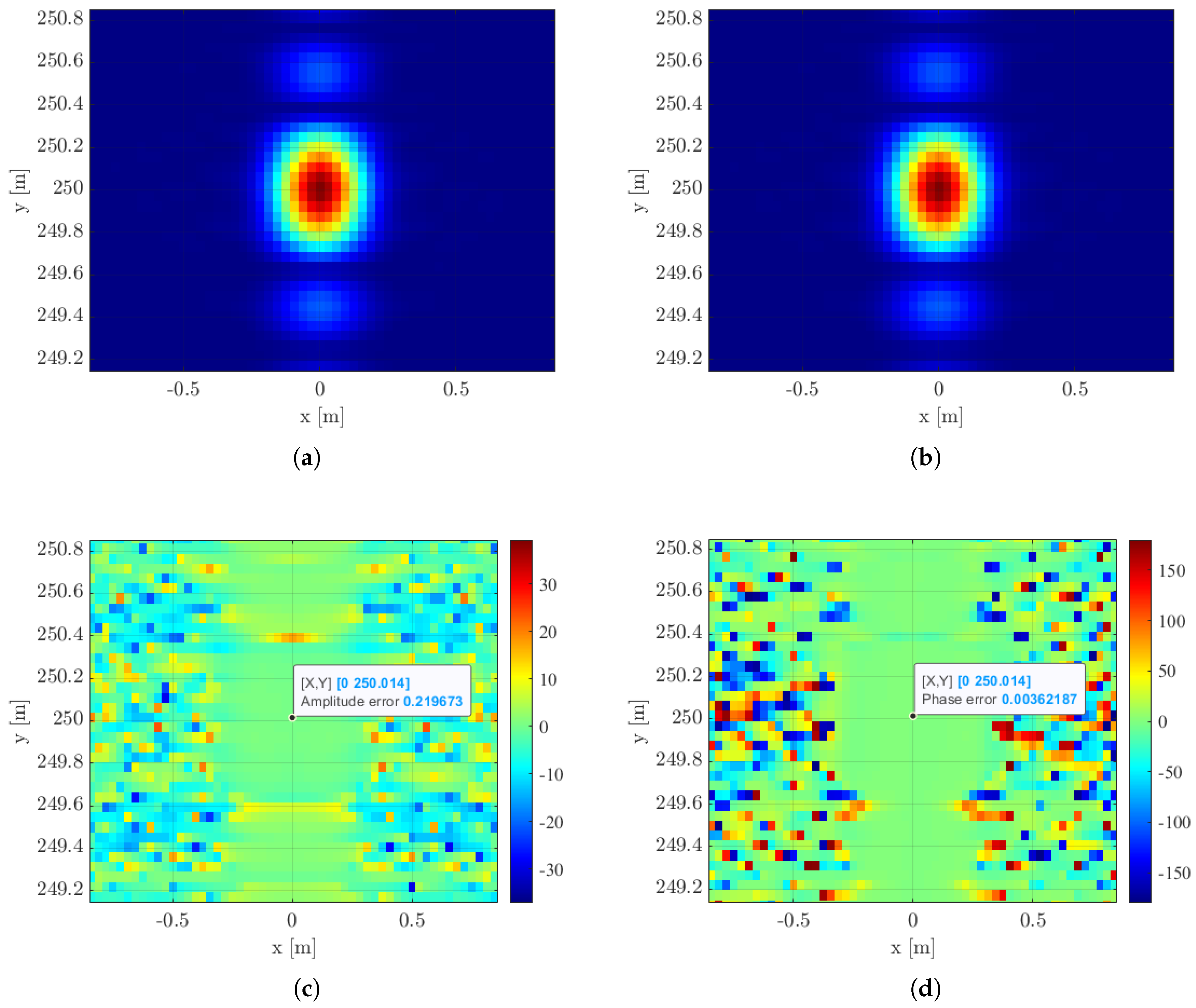
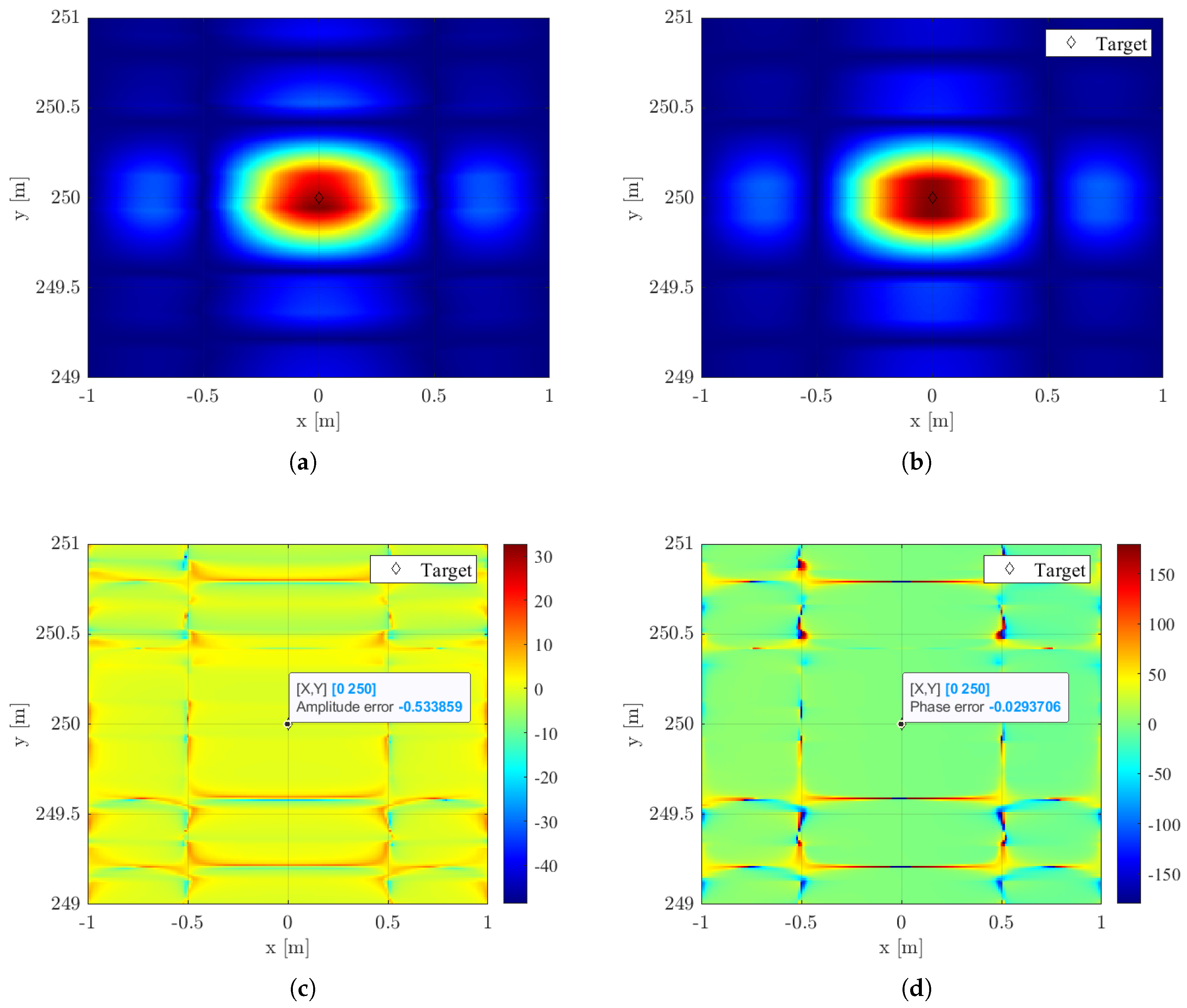
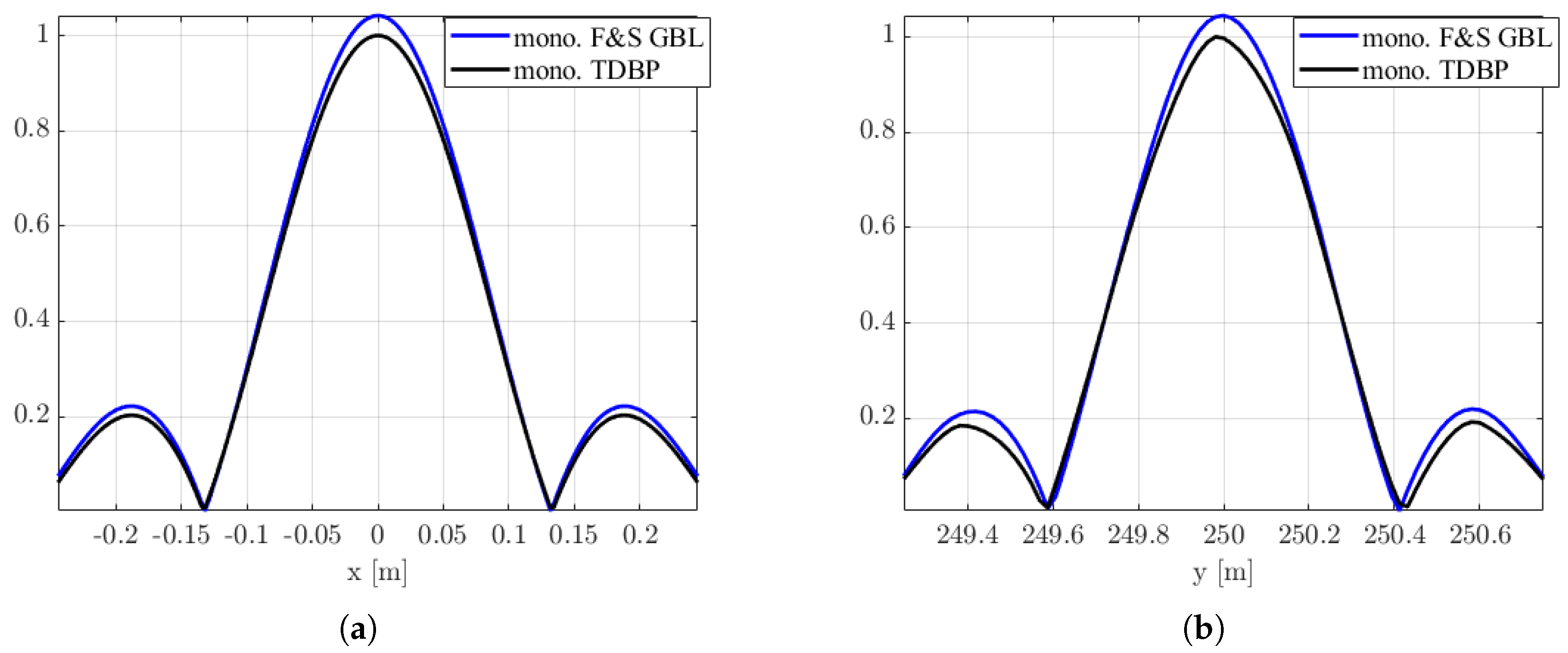



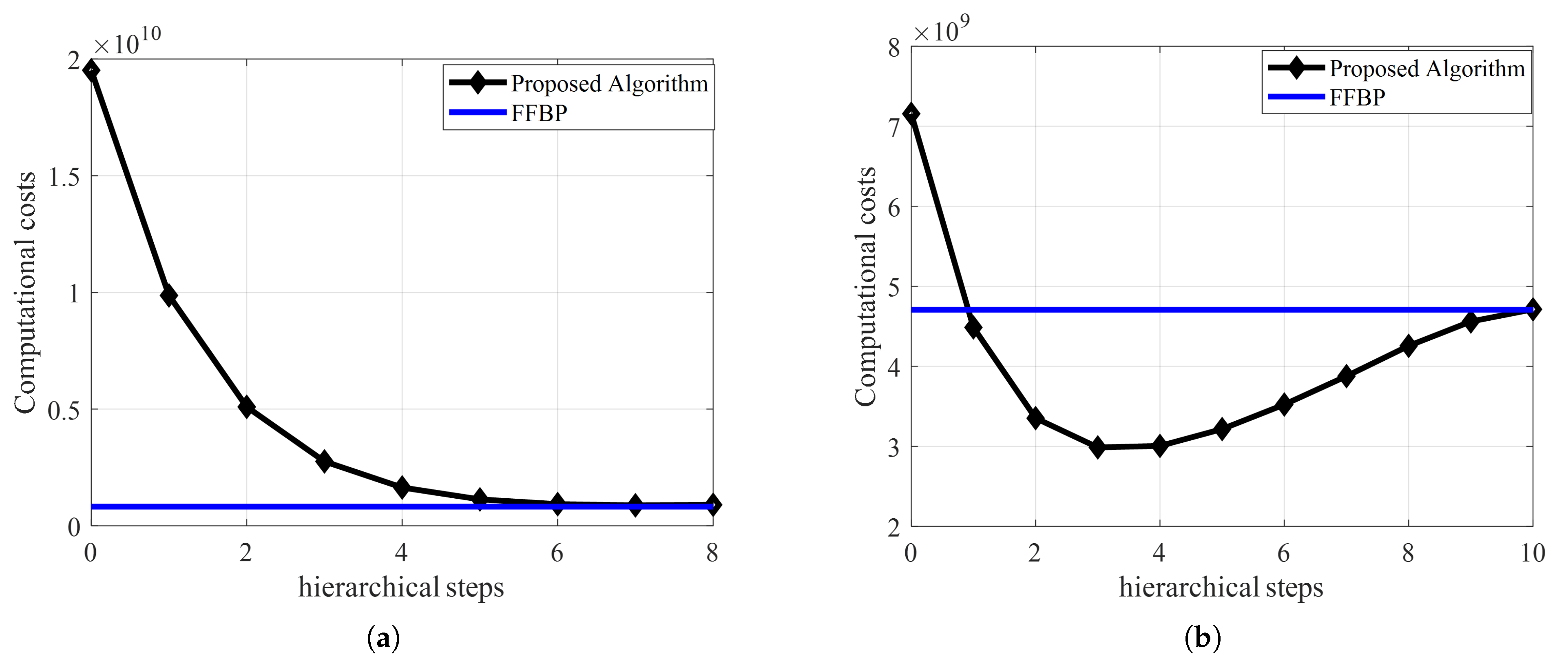

| Parameter | Symbol | Value |
|---|---|---|
| Central frequency | 9.45 GHz | |
| Bandwidth | B | 400 MHz |
| Lambda | 0.0317 m | |
| Range resolution | 0.4 m | |
| Area dimensions | (120 m, 500 m) |
| Parameter | Mono-Static | Bi-Static |
|---|---|---|
| Tx trajectory | 15 m | 0 m |
| Rx trajectory | 15 m | 15 m |
| Tx altitude | 30 m | 30 m |
| Rx altitude | 30 m | 30 m |
| Parameter | Mono-Static | Bi-Static |
|---|---|---|
| Tx trajectory | 250 m | 250 m |
| Rx trajectory | 250 m | 250 m |
| Tx altitude | 30 m | 30 m |
| Rx altitude | 30 m | 30 m |
| Bi-static baseline | ˜ | 40 m |
| Azimuth resolution | 0.25 m | 0.5 m |
| Parameter | Symbol | Value |
|---|---|---|
| Area dimensions | (4 km, 2 km) | |
| Range resolution | 0.4 m | |
| Azimuth resolution | 0.2 m | |
| Trajectory length | ˜ | 4 km |
| Flying height | 30 m |
| Parameters | GBL | Stripmap |
|---|---|---|
| Carrier frequency | 5 GHz | GHz |
| Bandwidth | 400 MHz | 400 MHz |
| Aperture | 32 m | 120 m |
| Altitude | 30 m | 30 m |
| Area | m | m |
| Azimuth resolution | ˜ | m |
| Range resolution | m | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polisano, M.G.; Manzoni, M.; Tebaldini, S. Synthetic Aperture Radar Processing Using Flexible and Seamless Factorized Back-Projection. Remote Sens. 2025, 17, 1046. https://doi.org/10.3390/rs17061046
Polisano MG, Manzoni M, Tebaldini S. Synthetic Aperture Radar Processing Using Flexible and Seamless Factorized Back-Projection. Remote Sensing. 2025; 17(6):1046. https://doi.org/10.3390/rs17061046
Chicago/Turabian StylePolisano, Mattia Giovanni, Marco Manzoni, and Stefano Tebaldini. 2025. "Synthetic Aperture Radar Processing Using Flexible and Seamless Factorized Back-Projection" Remote Sensing 17, no. 6: 1046. https://doi.org/10.3390/rs17061046
APA StylePolisano, M. G., Manzoni, M., & Tebaldini, S. (2025). Synthetic Aperture Radar Processing Using Flexible and Seamless Factorized Back-Projection. Remote Sensing, 17(6), 1046. https://doi.org/10.3390/rs17061046







