The Bright Feature Transform for Prominent Point Scatterer Detection and Tone Mapping

Abstract

Detecting bright point scatterers plays an important role in assessing the quality of many sonar, radar, and medical ultrasound imaging systems, especially for characterizing the resolution. Traditionally, prominent scatterers, also known as coherent scatterers, are usually detected by employing thresholding techniques alongside statistical measures in the detection processing chain. However, these methods can perform poorly in detecting point-like scatterers in relatively high levels of speckle background and can distort the structure of the scatterer when visualized. This paper introduces a fast image-processing method to visually identify and detect point scatterers in synthetic aperture imagery using the bright feature transform (BFT). The BFT is analytic, computationally inexpensive, and requires no thresholding or parameter tuning. We derive this method by analyzing an ideal point scatterer’s response with respect to pixel intensity and contrast around neighboring pixels and non-adjacent pixels. We show that this method preserves the general structure and the width of the bright scatterer while performing tone mapping, which can then be used for downstream image characterization and analysis. We then modify the BFT to present a difference of trigonometric functions to mitigate speckle scatterers and other random noise sources found in the imagery. We evaluate the performance of our methods on simulated and real synthetic aperture sonar and radar images, and show qualitative results on how the methods perform tone mapping on reconstructed input imagery in such a way to highlight the bright scatterer, which is insensitive to seafloor textures and high speckle noise levels.

1. Introduction

Detecting prominent scatterers in sonar [1,2,3], radar [4,5,6], and medical ultrasound [7,8,9] imagery has had many successes to date for several important applications. In the fields of synthetic aperture sonar (SAS) and synthetic aperture radar (SAR), bright point scatterers are typically used to assess image quality in terms of resolution [1,2,10,11,12,13,14,15]. Image resolution plays a critical role in synthetic aperture imaging techniques due to the ability of these modalities to yield range-independent cross-track resolution with high area coverage rates [16], unlike standard remote sensing imaging systems. Prominent scatterers identified in synthetic aperture imagery find additional practical applications in remote sensing research, such as estimating the point spread function (PSF) of the imaging system [17,18], detecting small ground vehicles in SAR imagery [19], and are used as reference reflectors for synthetic aperture calibration research [20,21]. Further, in the medical field, prominent scatterers are used for detecting breast microcalcifications, kidney stones, and lesions, which all appear like coherent targets when visualized in medical ultrasound imagery [7,8,9].

Traditionally, in SAS and SAR, prominent scatterers are usually identified using approaches based on thresholding from a statistical framework [1,2,3,4]. Pate et al. [1] identified prominent scatterers using dual thresholding integrated with a Hoshen–Kopelman connected-component labeling technique and then fitted ellipses to the half-power contour of top candidate scatterers. Prater et al. [2] detected point-like objects of opportunity by assuming that the entire image was Gaussian-distributed and the scatterers had intensities in the upper bound of the distribution. Sanjuan-Ferrer [4] applied a generalized likelihood ratio test on the sublooks of an image and tested the pixels against the Neyman–Pearson criterion. The advantage of these methods in detecting point scatterers is that they can be generalized to different imaging modalities by adjusting the thresholds as appropriate. However, these methods require further analysis to discriminate between the actual prominent scatter, peaks caused by strong speckle reflectors [22,23,24], and other noise sources [13] for scenes with high noise levels, which can also increase the computational cost.

In this work, we introduce a fast and robust image-processing method, labeled the Bright Feature Transform (BFT), to detect prominent scatterers in SAS and SAR imagery using (1) the difference between sine and cosine functions designed to capture strong changes between bright and dark pixels in the input imagery, and (2) a Hadamard operation with the original image to suppress the speckle background. We derive this method by analyzing an ideal point scatterer’s response in relation to both the contrast and pixel intensity of neighboring pixels via (1) and (2). Thus, instead of implementing a costly spatial filter to compare each pixel in an image to a threshold, we use tone mapping to highlight the bright point-like features in the imagery. The main advantage of this approach compared to traditional remote sensing thresholding methods is its ability to preserve the overall shape of the prominent scatterer, whereas applying a threshold can distort the features of the scatterer, leading to inaccurate downstream analyses.

To validate our method, we quantitatively and qualitatively evaluate the detection performance and robustness of our method on simulated data. Further, we show qualitative results on how the method performs dynamic range compression on real measured reconstructed SAS and SAR imagery while simultaneously filtering out the high-frequency features related to speckle reflectors and other noise artifacts related to rough texture. Finally, we report the latency of our method compared to other statistical methods as baselines. We plan to release both the code and data to ensure reproducibility and hope to inspire future work into non-thresholding-based point detection and characterization.

Our specific contributions for this area of remote sensing research include: (1) new tone mapping approaches for detecting prominent scatterers in synthetic aperture imagery; and (2) a novel application of sinusoidal functions for synthetic aperture characterization, particularly, speckle noise mitigation in reconstructed imagery. The significance of this work is that our method can be easily integrated in a deep learning pipeline to reduce speckle noise and boost the features of the prominent scatterer, which may aid to reduce false alarms. The paper is organized as follows: Section 2 covers the complete derivation of the BFT as well as the transformations used to mitigate the speckle noise, which we express as the trig difference (TD) and the modified trig difference (MTD) functions. Section 3 describes the problem of detecting a prominent scatterer buried in speckle noise, which we utilize throughout our experiments as a case study to evaluate the performance of our methods against the baseline approaches. The section also presents the metrics used to measure the effectiveness of the methods. Section 4 provides details of the synthetic aperture sonar and synthetic aperture radar datasets used to validate our experiments. The section also offers specific details on how to simulate a prominent scatterer in Rayleigh noise. Section 5 covers the experimental results qualitatively and quantitatively. Qualitatively, the section highlights the visual comparison of our methods against the baseline approaches and quantitatively, presents the detection performance, utilizing the metrics described in Section 3. Finally, the work is summarized in Section 6, considering the limitations of our method and future research directions.

2. Method

In this section, we derive an intensity transformation for enhancing bright features, such as point-like scatterers buried in speckle background noise, from first-principles. We begin the derivation by assuming that the point scatterers can be modeled as unit impulses when visualized in the spatial domain after deconvolving the input image with the imaging system’s PSF. As a result, this leads us to deriving a sinc function in the intensity domain from proposing that the transformation can be expressed as a sum of shifted complex exponentials. Following this, we introduce the bright feature transform and show that it is free of parameters, and then demonstrate that the BFT achieves the same level of transformation as a sinc function. We then present our proposed trigonometric (trig) difference filter designed for mitigating the scattering impact of background noise, with a particular emphasis on visual saturation caused by speckle reflectors, to improve the visual detection and interpretation of bright prominent features after tone mapping. We also present a fast version of this filter and then show that these proposed transformations can be applied at the feature extraction stage before generating binary masks in a bright scatterer detection pipeline.

2.1. Theoretical Formulation and Analysis of the Bright Feature Transform

Given an N×M single-look complex (SLC) synthetic aperture image, where N is the number of rows and M is the number of columns, the intensity value of a single pixel from the SLC imagery can be represented as $I(n,m)=x_{n,m}{e}^{j{\theta }_{n,m}}$, where $x_{n,m}$ is the amplitude, ${\theta }_{n,m}$ is the phase, and $(n,m)$ is the pixel location. We discard the phase information in this paper and only focus on the normalized version of the amplitude data such that $x_{n,m}\in [0,1]$, which allows us to make the assumption that the point-like scatterers can be modeled as unit impulses. Following this, the tone mapped imagery that highlights the bright features can be defined as,

$$\begin{array}{c}\hfill \mathbf{y}\left(\mathbf{x}\right)=\left|\mathbf{h}\left(\mathbf{x}\right)\right|\odot \mathbf{x},\end{array}$$

(1)

where $\mathbf{x}\in {\mathbb{R}}^{\mathrm{N}\times \mathrm{M}}$ is the normalized input amplitude image containing the unit impulses, $\mathbf{h}\left(\mathbf{x}\right)\in {\mathbb{C}}^{\mathrm{N}\times \mathrm{M}}$ is the tone mapping filter, and ⊙ refers to the Hadamard element-wise multiplication [25].

We use a complex intensity-based transformation to design the tone mapping filter $\mathbf{h}\left(\mathbf{x}\right)$ analogous to the inverse discrete Fourier transform of a complex exponential or unit rectangle function (when considering $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$) so that the output $\mathbf{y}\left(\mathbf{x}\right)$ boosts the contrast of the bright scatterers relative to the background in preparation for downstream image characterization or processing. Further, this transformation can either be applied globally to every pixel or defined for a specific region of the image, depending upon the application of the operation. Here, we show the derivation for the single pixel $x_{n,m}$ and then generalize the operation to be applied globally across the entire image $\mathbf{x}$. We express the transformation as a linear combination of shifted complex exponentials, where the shift captures the difference between the brightest pixel value in the image/region to the current pixel value $x_{n,m}$,

$$\begin{array}{c}\hfill \left|h_{n,m}\right|={\displaystyle \frac{1}{L}}\left|\sum _{k=-\infty }^{\infty }{c}_k{e}^{j{\displaystyle \frac{2\pi }{L}}k{x}_{n,m}}\right|,\end{array}$$

(2)

where $c_k=e^{-j{\displaystyle \frac{2\pi }{L}}k\tau }$, L is the number of classes for classification, k is the class label, and $\tau$ is the pixel intensity to highlight; for this derivation, $\tau =max\left(\mathbf{x}\right)=1$, assuming the prominent scatterers are the brightest features in the image and are unit impulses. Intuitively, Equation (2) is a filter that measures the phase shift $e^{-j{\displaystyle \frac{2\pi }{L}}k(\tau -x_{n,m})}$ between the maximum pixel and the current pixel $x_{n,m}$. When there is no shift, $x_{n,m}=\tau$, the operation leaves the current pixel unaltered when applied in Equation (1) and when a shift is detected, $x_{n,m}\ne \tau$, the current pixel gets re-scaled to a value closer to zero when applied in Equation (1). When Equation (2) is applied on the full image $\mathbf{x}$, the operation visually accentuates the prominent scatters and other bright features in the imagery.

Further, we truncate the infinite series for one period, in our case L, for first quadrant support such that no two class labels, k, share the same complex value $e^{-j{\displaystyle \frac{2\pi }{L}}k}$. Thus, we express the transformation as a finite sum ranging from 0 to $L-1$,

$$\begin{array}{c}\hfill \left|h_{n,m}\right|={\displaystyle \frac{1}{L}}\left|\sum _{k=0}^{L-1}{e}^{-j{\displaystyle \frac{2\pi }{L}}k(1-x_{n,m})}\right|.\end{array}$$

(3)

As the finite version of this series converges, it can be expressed in closed-form as follows:

$$\begin{array}{c}\hfill \left|h_{n,m}\right|={\displaystyle \frac{1}{L}}{\displaystyle \frac{sin\left(\pi (1-x_{n,m})\right)}{sin\left(\frac{\pi }{L}(1-x_{n,m})\right)}},\end{array}$$

(4)

which is the intensity domain version of a sinc function for multi-class detection $L>2$. Equation (4) can be understood as the filter’s response to unit impulses in the intensity domain, assuming that the pixels of the prominent scatterers are unit valued. In practice, the prominent scatterer can have pixel values that include unity and values close to 1 in the blurred version of the imagery (before deconvolution is performed). This effect is due to the PSF smearing or distorting the return energy of the scatterer across multiple neighboring pixels. Therefore, in the limit that the pixel value $x_{n,m}$ is close to unity in Equation (4) such that the sine arguments are $ϵ$ close to zero, the sine functions in the numerator and denominator can be approximated as the zero-order term in their Taylor series expansions i.e., $\left|h_{n,m}\right|\approx {\displaystyle \frac{1}{L}}{\displaystyle \frac{\pi (1-x_{n,m})}{\frac{\pi }{L}(1-x_{n,m})}}=1$. When $x_{n,m}=0$, Equation (4) becomes ${\displaystyle \frac{1}{L}}{\displaystyle \frac{sin\left(\pi \right)}{sin\left(\frac{\pi }{L}\right)}}=0$, which shows that dark pixels are mapped to zero and bright features in $\mathbf{x}$ are highlighted as candidate point-objects of opportunity. Also, it is worth mentioning that Equation (4) is useful for visually detecting unit impulses when the deblurred or deconvolved version of $\mathbf{x}$ is presented. For this paper, we assume that $\mathbf{x}$ is reconstructed synthetic aperture imagery that has been blurred by the imaging system’s PSF. Therefore, our objective is to exploit the properties presented in deriving Equation (4) by modifying two assumptions, such as the following: (1) the point scatterer is unit valued, and (2) we are operating in the multiclass setting where $L>2$.

Therefore, we can consider only two classes, $L=2$, where $k=0:c_0=1$ is the signal, and $k=1:c_1=-1$ is the background noise labeled as clutter, which fully describes the problem at hand, a signal buried in speckle noise. As a result, Equation (3) provides the first-order term which gives,

$$\begin{array}{cc}\hfill \left|h_{n,m}\right|& =\left|{\displaystyle \frac{1}{2}}(1+e^{-j{\displaystyle \frac{2\pi }{2}}(1-x_{n,m})})\right|\hfill \\ \hfill & =\left|e^{-j{\displaystyle \frac{\pi }{2}}(1-x_{n,m})}({\displaystyle \frac{e^{j\frac{\pi }{2}(1-x_{n,m})}+e^{-j\frac{\pi }{2}(1-x_{n,m})}}{2}})\right|\hfill \\ \hfill & =cos({\displaystyle \frac{\pi }{2}}(1-x_{n,m}))\hfill \\ \hfill & =sin({\displaystyle \frac{\pi }{2}}{x}_{n,m}),\hfill \end{array}$$

(5)

a sine function with first-quadrant support, $|h_{n,m}|\in [0,1]$. Implementing Equation (5) over Equation (4) serves three purposes: (1) it is computationally faster, (2) it is free of parameters such as L and $\tau$, and (3) there are no division by zero issues in the denominator. Also, Equation (5) assumes that the pixels of the signal can be spread across many neighboring pixels due to the smearing of the PSF after capturing the data, where again, Equation (4) assumes that pixels of the bright scatterer are represented as unit impulses in the data product. These two effects are captured in the parameter $\tau$, where Equation (5) removes the assumption that the prominent scatterer is only captured by the brightest pixel in the imagery. 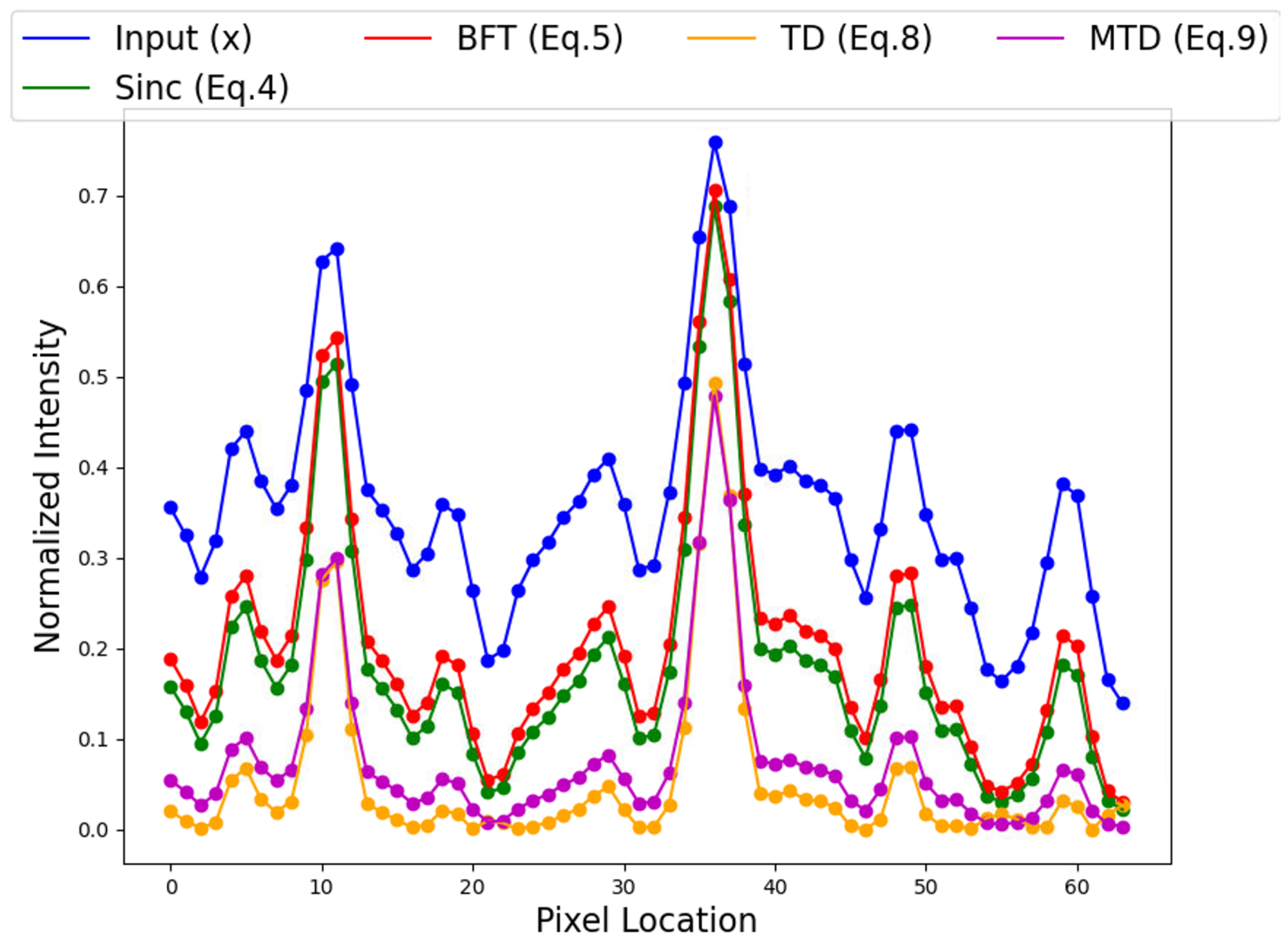Thus, we use Equation (5) in our experiments as the bright feature transform (BFT) and Figure 1 shows the line intensity profile of the BFT against the input and the sinc function, as well as two other methods that are introduced later in the paper, for a simulated prominent scatterer. What is observed in the figure is that both the BFT and the sinc function produce nearly identical transformations in the region of the scatterer, with the trade-off being that the BFT enhances sidelobe peaks slightly stronger than the sinc function.

2.2. Bright Feature Transform Enhancement for Noise Mitigation and Processing Efficiency

Continuing with our analysis, a similar transformation can be derived for filtering dark features by reversing the sign of every other term in Equation (3). This is performed by rearranging the transformation to include the factor ${(-1)}^k$ such that it is an alternating series,

$$\begin{array}{cc}\hfill \left|h_{n,m}\right|& ={\displaystyle \frac{1}{L}}\left|\sum _{k=0}^{L-1}{(-1)}^k{e}^{-j{\displaystyle \frac{2\pi }{L}}k(1-x_{n,m})}\right|.\hfill \end{array}$$

(6)

again, assuming only two classes provide the first-order term,

$$\begin{array}{cc}\hfill \left|h_{n,m}\right|& =\left|{\displaystyle \frac{1}{2}}(1-e^{-j{\displaystyle \frac{2\pi }{2}}(1-x_{n,m})})\right|\hfill \\ \hfill & =\left|e^{-j{\displaystyle \frac{\pi }{2}}(1-x_{n,m})}({\displaystyle \frac{e^{j\frac{\pi }{2}(1-x_{n,m})}-e^{-j\frac{\pi }{2}(1-x_{n,m})}}{2}})\right|\hfill \\ \hfill & =sin({\displaystyle \frac{\pi }{2}}(1-x_{n,m}))\hfill \\ \hfill & =cos({\displaystyle \frac{\pi }{2}}{x}_{n,m}),\hfill \end{array}$$

(7)

which is a cosine function with first-quadrant support. This function highlights dark regions in the imagery, such as shadows and other low-intensity prominent features, as well as the background noise. Applying a negative sign to Equation (7) inverts the image and places $\left|h_{n,m}\right|$ in the range of $[-1,0]$ vs. $[0,1]$. This transformation states that dark pixels are mapped to more negative values, while bright pixels are mapped to zero. We can exploit this property to reduce the background noise, particularly scenes saturated by speckle reflectors and other noise scatterers, to enhance the point scatterer.

Therefore, to suppress the intensity levels related to background noise which are highlighted in Equation (7), we introduce a trig difference (TD) function by subtracting Equation (7) from Equation (5),

$$\begin{array}{c}\hfill \left|h_{n,m}\right|=sin({\displaystyle \frac{\pi }{2}}{x}_{n,m})-cos({\displaystyle \frac{\pi }{2}}{x}_{n,m}).\end{array}$$

(8)

Equation (8) maximizes the distance between the noise and prominent scatterer pixels by expanding the dynamic range from $[0,1]$ to $[-1,1]$. Applying Equation (8) on $\mathbf{x}$ in Equation (1) yields a $\mathbf{y}\left(\mathbf{x}\right)$ with minimal noise and small sidelobes, as shown in Figure 1, when comparing the line profile of a scatterer against the input, BFT, and sinc function. Further, the benefit of implementing Equation (8) over Equation (5) is that it suppresses the background noise by clipping the intensity values to $-ϵ$, which, in turn, makes the prominent scatterer’s features more profound due to having a steeper drop off and narrower peak. The trade-off is that some of the low-intensity pixels at the tail-end of the prominent scatterer intensity profile may get suppressed, and Equation (8) has a longer computational processing time due to having two terms in the filter.

To reduce the TD filter’s computational speed to the same order as Equation (5), we set $x_{n,m}=1$ in the first term in Equation (8),

$$\begin{array}{c}\hfill \left|h_{n,m}\right|=1-cos({\displaystyle \frac{\pi }{2}}{x}_{n,m}),\end{array}$$

(9)

to produce a fast method to visually detect possible bright scatterers of opportunity when used in Equation (1),

$$\begin{array}{c}\hfill \mathbf{y}\left(\mathbf{x}\right)=(1-cos({\displaystyle \frac{\pi }{2}}\mathbf{x}))\odot \mathbf{x}.\end{array}$$

(10)

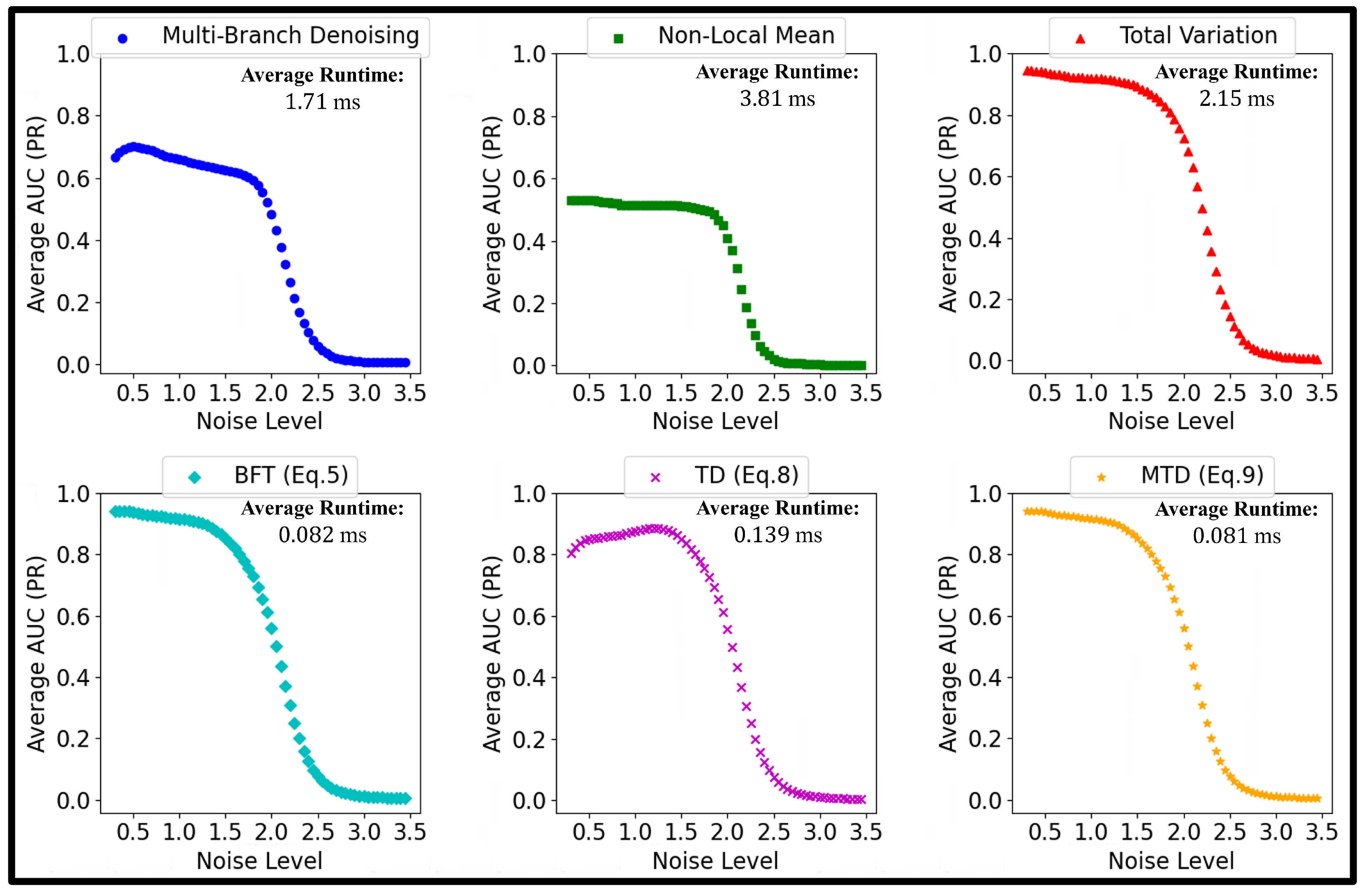
Moreover, Equation (10) is a useful technique for characterizing synthetic aperture imagery; specifically, image resolution estimation, image sharpness enhancement, and deconvolution using prominent scatterers to estimate the PSF in the presence of strong speckle noise and other bright reflectors, as shown in Figure 2. We label this method as the modified trig difference (MTD) filter, which is a shifted version of the inverted representation of Equation (7), with the data in the range of $[0,1]$ instead of $[-1,0]$. Figure 1 illustrates the typical shape of the derived transformations after taking a 1D intensity profile across a simulated prominent scatterer. The TD filter (Equation (8)) produces the narrowest and most profound main peak width out of all the transformations, with the sidelobes being reduced the steepest. The MTD filter (Equation (9)) produces a sharper main lobe than the BFT and the sinc function with smaller sidelobes, which could be correlated with speckle noise, making it an ideal filter for enhancing visual detection of bright features in synthetic aperture imagery in the presences of noise.

2.3. Bright Feature Transform for Prominent Scatterer Detection

Further, in this paper, we are not only concerned with visually identifying and analyzing prominent scatterers in the synthetic aperture imagery saturated with speckle noise but also interested in applying $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$ in a bright scatterer detection pipeline to localize the scatterers. The BFT (Equation (5)), TD (Equation (8)), and MTD (Equation (9)) can be applied at the segmentation stage before generating binary masks in the pipeline to enhance the downstream localization and classification tasks. Implementing the BFT task would effectively select the bright features and implementing the TD and MTD would effectively reduce the intensity of the visual noise in a way to highlight the prominent scatterer. This is performed by converting $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$ to a binary representation of the function,

$$\begin{array}{c}\hfill \mathbf{D}\left(\mathbf{x}\right)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}\left|\mathbf{h}\left(\mathbf{x}\right)\right|<T\hfill \\ 1\hfill & \mathrm{if}\mathbf{h}\left(\mathbf{x}\right)\ge T\hfill \end{array}\right.,\end{array}$$

(11)

where T is a specified intensity threshold such that values above the threshold are considered to be pixels belonging to the region of the prominent scatterer and values below are noise and background pixels. For our experiments, we apply a threshold in Equation (11) with BFT, TD, and MTD filters only to evaluate the detection performance against the ground truth location of the scatterer. However, these filters do not require the application of a threshold to localize the prominent scatterer as traditional thresholding techniques. For this reason, we stress the importance of designing a filter that cannot only visually identify the bright scatterer through tone mapping but does not require modulating the threshold in the processing chain to perform the task, while minimizing the false alarms and preserving the fidelity of the scatterer.

3. Implementation and Metrics

Detecting point scatterers buried in noise can be described as a binary detection problem. In simulation, we study a single point scatterer located randomly in speckle noise, as described by Thon et al. [7], where we use the Rayleigh model to simulate the speckle scenes [28]. To evaluate the detection performance, we use the area of the curve (AUC) of the Precision-Recall (PR) curve, which is a typical performance metric for binary decision problems, especially when dealing with skewed class distributions [29]. The advantage of the AUC (PR) is that it evaluates the precision and recall across a range of thresholds and quantifies the results with a single score. The precision measures the accuracy of positive predictions and the recall is the true positives predicted. We also use the the Matthews Correlation Coefficient (MCC) [30,31] and the F1-score [32,33] metrics where the MCC captures the model robustness for situations with imbalanced classes and the F1-score provides a more informative measure of false positives.

Further, we consider knowing the ground truth locations of coherent pixels belonging to a simulated prominent scatterer and the locations of incoherent noise pixels in the original imagery. We utilize Equation (11) set at $0.5$ on $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ for each method (BFT, TD, MTD) when utilizing the F1-score and the MCC metrics. Thus, performance is evaluated by aligning pixels from the mask created from the binary representation of the tone mapped imagery against pixels belonging to the scatterer from the ground truth mask. If alignment occurs, then a true positive is counted, and if misalignment occurs, false positives are counted.

To measure how well the method tone maps (suppresses) the noise intensities around the scatterer while maintaining the quality of the scatterer from distortion, we use the peak signal-to-noise (PSNR) ratio [34,35],

$$\begin{array}{c}\hfill \mathrm{PSNR}=20{log}_{10}{\displaystyle \frac{\tau }{\mathrm{MSE}}},\end{array}$$

(12)

where $\tau$ is the maximum value in the region of the scatterer ($\tau =1$) and MSE is the mean squared error between the input and processed imageries. We also leverage the structural similarity index (SSIM) [36] to measure the perceptual quality of the bright scatterer after being processed through the transformations and to gauge how well each method preserves the overall structure of the scatterer. The output of the SSIM metric is bounded between −1 and 1, where 1 indicates perfect similarity between the processed image and the original.

Further, we clock the computational processing time of our proposed methods and compare this against the computational processing time of two conventional threshold methods, a hard threshold set to 85% of the maximum and a hard threshold method set to ${\displaystyle \frac{3\mu }{\sigma }}$ defined by Prater et al. [2]. We run these experiments on an 16.04.7 LTS (Xenial Xerus) operating system that has an Intel(R) Core(TM) i7-6850K processor (Intel, Santa Clara, CA, USA) with 64 GB of memory using Python 3.7.10.

4. Datasets

4.1. SASSED and SARscope Datasets

We leverage the Synthetic Aperture Sonar Seabed Environment Dataset (SASSED) [26] and the SARscope [27], which are two real-measured synthetic aperture datasets designed for computer vision image segmentation tasks, alongside our simulated data, to validate our experiments. SASSED is a single-channel high-frequency SAS dataset curated by researchers from the Naval Surface Warfare Center Panama City Division, containing 129 complex-valued images of different classes of seafloor texture, such as sand, mud, sea grass, rock, and sand ripples [27]. SARscope is a SAR dataset featuring a diverse set of maritime images of ships and ship ports. The dataset contains 6735 instances of different ships captured out at sea or stationed by the port and was designed for object detection tasks as well as segmentation.

For the tone mapping experiments, we resize both the SASSED and SARscode to $512\times 512$ and normalize them from zero to unity for processing the raw amplitude and log-compressed version of the images. Further, we add Rayleigh-distributed noise to the scenes and render in a simulated bright scatterer. The log-compression function is applied after the noise and scatterer are added in the synthetic aperture scenes.

4.2. Simulated Data

For simulating 8-bit grayscale SAS images, we use the Python Imaging Library (PIL) version 8.2.0 to render in a $4\times 4$ bright scatterer with pixel values set at 255 into the scene imagery using the ellipse() method of ImageDraw to draw the scatterer. We then add Rayleigh-distributed random noise to the scene with the mode value set to unity. The noise was normalized from 0 to $p255$, where p was set to $1.7$, such that the noise level is comparable to the signal in the blurred version of the imagery. We then apply a $2\times 2$ smoothing filter to reduce the noise level and to increase the physical realism of a seafloor scene. Finally, we apply a $5\times 5$ Gaussian blur kernel with unit variance to each image to model the PSF and then normalize each image from 0 to 1 for processing.

5. Experimental Results

In this section, we cover the main results for detecting bright scatterers in simulated and real data. We compare the qualitative results from the tone mapped processed imagery and also compare quantitative results from using the PSNR and the SSIM to measure the distortion from the original and the tone mapping filter version of the scatterer. We also present the detection performance using the AUC (PR), MCC, and F1-score and highlight results from varying the noise level in the scenes. Finally, the computational processing time of the BFT (Equation (5)), TD filter (Equation (8)), and the MTD filter (Equation (9)) are compared against the OpenCV hard threshold method set at $85\%$ of the maximum pixel and a statistical approach described in [2] to demonstrate that our method is as fast as thresholding.

5.1. Tone Mapping for Prominent Scatterer Enhancement and Identification

Qualitative Comparison: Figure 2 highlights how the BFT, TD, and the MTD filters perform tone mapping to visually enhance bright features when applied on normalized amplitude simulated, SAS, and SAR data described by Equation (1) with a single bright scatterer located in the images specified by the red circle. Line intensity profiles of cross-sectional cuts across the simulated scatterer are used to illustrate how the shape and structure of the scatterer change with each method.

Significant Features of Methods: The BFT method applied in Equation (1) as $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$ stands out from all the other methods at minimizing the distortion and preserving the general shape of the scatterer, as shown in the green boxes. The TD and MTD excel at reducing the noise that was captured in the BFT imagery and highlighting only pixels pertaining to the scatter. However, the trade-off is that these methods slightly distort the structure by clipping the low-intensity pixels of the scatterer to zero, as shown in the light blue and green boxes. The OpenCV thresholding method and Prater et al. [2] statistical method clip significant low-intensity pixels that define the overall shape of the scatterer, as shown in the dark blue boxes for the SAS data, and failed to capture the bright scatterer in the SAR imagery due to a nearby bright target being presented in the imagery. These results show that the threshoding methods are specifically designed for detecting bright scatterers in synthetic aperture imagery when there are no other bright feature in the scene and are not applicable for detecting targets with higher intensity than the scatterer, as opposed to the BFT, TD, MTD methods that detect the target and the scatterer.

Significant Similarities Between Methods: Further, when comparing all methods in Figure 2, there is noticeable similarity in the absence of other bright features or objects, as in the case of the simulated image; all of the approaches are very good at detecting the brightest pixel in the imagery. This would be excellent if the assumption is that the bright scatterer only possesses the pixel with the maximum intensity. However, in practical remote sensing scenarios, the bright scatterer can hold low-intensity pixels in its intensity distribution, as in the case of the SAS and SAr images, where the proposed methods excel at capturing these low-intensity pixels over the threshold-based approaches.

Further, Figure 3 shows the five detection strategies applied on log-compressed simulated and real synthetic aperture images. The significant observation from this figure is that the BFT, TD, and MTD filters all effectively preserve the shape of the scatterer highlighted in green when other secondary bright features are present in the imagery, as shown in the zoomed-in snippet to the left of the zoomed-in image clip of the scatterer. The figure also shows that the OpenCV thresholding and Prater et al. [2] are not as robust as the other methods when other bright clutter features are present in the image scene and can distort the shape of the scatterer highlighted in red. The meaningful contribution of the BFT is that the function is robust at detecting the prominent scatterer and other bright features in the scene even when the intensity distribution is uniform, as in the case of log-compressing the data. As observed in Figure 3, the BFT filter is able to perform noise reduction on log-compressed imagery despite the BFT performing its own dynamic range compression (or normalization) to highlight the bright features in the imagery. However, the BFT does not standout at suppressing the background noise, as in the case of the TD and MTD filters, where these two functions perform a better task at highlighting the salient features of the scatterer while mitigating noise. The TD function is by far the best at mitigating the noise but the trade-off is that the function clips low-intensity pixels belonging to the scatterer. The MTD method is the function that suppresses the noise pixels while maintaining the fidelity of the scatterer, i.e., it does not clip the low-intensity edge pixels.

Moreover, zoomed-in snippets of a secondary scatterer are positioned to the left of the image clip of the bright scatterer in Figure 3 to show how the methods perform qualitatively to identify the target when other bright features are presented in the image. What is observed is that using the statistical assumption that the bright scatterers pixels are placed on the tail of an intensity distribution has limitations when the distribution is compressed, as shown from the Prater et al. [2] detection method, which was unsuccessful at detecting the scatterer in the SAR image. An explanation for why this method was ineffective at capturing the scatterer when the data were log-compressed could be due to the limitations of the method, which assumes the intensity of the scatterer is far above the mean of the background intensity, which may hold for raw synthetic aperture imagery and has limitations when applied to log-compressed data.

Further, Figure 3 also shows that OpenCV thresholding, which operates under the assumption that the scatterer is the brightest feature in the imagery, also has limits when trying to capture the prominent scatterer when other bright targets are present in the synthetic aperture imagery. In contrast, the transformations we propose are robust in detecting the bright scatterer in the simulated, SAS, and SAR data and can be applied to the raw amplitude or the log-compressed representations of the images. The limitation we observed with our proposed transformations is that the data have to be normalized in the range of $[0,1]$ and the method is not suited for unnormalized raw amplitude or complex data. However, using the normalized version of the data is useful for many computer vision tasks, such as deep learning-based automatic target recognition (ATR) applications. Another limitation is that the method cannot isolate the bright scatterer in the imagery from the other bright features, where additional processing would also be needed to produce an image with only the scatterer in the scene imagery.

Quantitative Comparison: Figure 4 shows the PSNR variation when applying the different $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$ filters on six simulated $64\times 64$ scenes. The figure shows that the MTD method provides the highest PSNR when comparing the output region with the bright scatterer against the input and outperforms all other methods in terms of preserving the shape and structure of the prominent scatterer. This is beneficial because this allows the tone mapping filter to be used as a bright feature extraction filter in a detection processing pipeline without thresholding (additional analysis would be needed to compare performance against the ground truth location without employing a threshold). Further, the OpenCV thresholding function provides the lowest PSNR and performs the worst at preserving the edge features of the scatterer.

Table 1. Average PSNR and SSIM for the different detection methods across 500 simulated images.

Method	Average PSNR	Average SSIM
cv2.threshold	11.09 ± 1.31	0.38 ± 0.08
BFT	32.57 ± 1.11	0.87 ± 0.04
TD	22.44 ± 3.08	0.74 ± 0.09
MTD	35.16 ± 1.67	0.93 ± 0.01

shows the average PSNR and SSIM across 500 simulated images for the filters. On average, MTD methods outperform all the other filters in terms of measuring the PSNR and SSIM. This indicates that the MTD is very effective at preserving the overall structure and quality of the scatterer after being processed through the function. The Prater et al. [2] method is not presented here due to the need for repeated adjustment of a parameter, resulting in inconsistent performance when averaging across 500 simulated images.

5.2. Tone Mapping for Prominent Scatterer Detection

Table 2. Average performance metrics across 500 simulated images.

Detection Strategy	AUC (PR) ± Std	MCC ± Std	F1 ± Std
cv2.threshold	0.685 ± 0.146	0.629 ± 0.139	0.582 ± 0.138
Prater et al. [2]	0.537 ± 0.111	0.183 ± 0.248	0.147 ± 0.216
BFT	0.769 ± 0.181	0.553 ± 0.195	0.511 ± 0.222
TD	0.769 ± 0.180	0.714 ± 0.150	0.693 ± 0.150
MTD	0.769 ± 0.181	0.714 ± 0.181	0.697 ± 0.157

presents the average results obtained from evaluating the AUC-PR, the MCC, and F1-score across 500 simulated images. The BFT, TD, and MTD methods demonstrate the same performance according to the AUC (PR) and outperform the cv2.threshold and Prater et al. methods. From Figure 2, the BFT is less effective at mitigating noise compared to the TD and MTD filters, which is captured by the F1-score and the MCC values, where BFT underperforms these methods based on these measures by raising more false alarms. The MTD method outperforms all the methods as per the F1-score. Further, the key takeaway from Table 2 is that the TD and MTD filters are highly accurate at detecting the location of the prominent scatterer through tone mapping, producing results in alignment with using OpenCV thresholding without distorting the pixels of the scatterer, which could be useful for downstream analysis, such as estimating the imaging system’s PSF.

5.3. Tone Mapping for Multiple Scatterer Detection

In this section, we compare the average performance of detecting 10 bright scatterers placed randomly in 500 simulated $64\times 64$ images with our proposed methods against traditional thresholding methods and state-of-the-art deep learning segmentation algorithms, such as U-Net, fully connected network (FCN) [37], DeepLabV3+ [38,39], and a multi-branch denoising algorithm [40].

Comparison with Traditional Thresholding Techniques: 

Table 3. Average performance metrics across 500 simulated images with 10 bright scatterers.

Detection Strategy	AUC (PR) ± Std	MCC ± Std	F1 ± Std
cv2.threshold	0.695 ± 0.025	0.536 ± 0.054	0.594 ± 0.025
Prater et al. [2]	0.525 ± 0.015	0.005 ± 0.046	0.006 ± 0.054
BFT	0.884 ± 0.030	0.199 ± 0.063	0.250 ± 0.074
TD	0.884 ± 0.030	0.765 ± 0.024	0.769 ± 0.022
MTD	0.884 ± 0.030	0.786 ± 0.030	0.779 ± 0.032

shows the average AUC (PR), MCC, and F1-score for 500 simulated images with 10 prominent scatterers placed randomly in the imagery. From the table, we find the MTD outperforming all methods in terms of the MCC and F1-score and no difference in performance in terms of the AUC (PR) when comparing the BFT, TD, and MTD. This experiment shows that the MTD method is robust at detecting multiple scatterers when buried in Rayleigh noise compared to applying a threshold and the key takeaway is that if the goal is to detect multiple prominent scatterers to estimate the imaging system’s PSF for downstream characterization then the MTD is a reliable and stable method to implement.

Figure 5 shows $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ and $\mathbf{y}\left(\mathbf{x}\right)$ for the five detection strategies. Small snippets of each method for around two prominent scatterers have been presented. The thresholding methods distort the edge features of the scatterers, which was already confirmed in the single scatterer case for both $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ and $\mathbf{y}\left(\mathbf{x}\right)$. The BFT in $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ enhances all bright features presented in the input imagery, including the background noise. However, when the BFT is transformed to $\mathbf{y}\left(\mathbf{x}\right)$, the bright features of the prominent scatterer are preserved. The TD mitigates the noise in $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ found in the BFT and the MTD method further reduced the noise. The best filter that preserves the features of the scatterer is the MTD method. Here, the Prater et al. method was modified to show the scatterer when performed under the method.

Comparison with Deep Learning Methods For this part of the study, we compare the BFT, TD, and MTD bright scatterer detection methods against state-of-the-art deep learning approaches. The deep learning approaches used to evaluate the effectiveness of our methods included U-net, FCN [37], DeepLabV3+ [38,39], and a multi-branch denoising algorithm [40]. Each model was trained for 500 epochs on 500 simulated images sized $64\times 64$, with ground truth binary images generated by applying (11) with a threshold of $0.85$ on the input imagery.

Table 4. Average performance metrics across 500 simulated images with 10 bright scatterers.

Detection Strategy	AUC (PR) ± Std	MCC ± Std	F1 ± Std
U-Net	0.547 ± 0.042	0.587 ± 0.039	0.529 ± 0.053
FCN [37]	0.714 ± 0.025	0.585 ± 0.039	0.525 ± 0.052
DeepLabV3+ [39]	0.400 ± 0.069	0.385 ± 0.071	0.402 ± 0.070
Multi-Branch Denoising [40]	0.663 ± 0.031	0.556 ± 0.039	0.487 ± 0.052
BFT	0.884 ± 0.030	0.256 ± 0.072	0.202 ± 0.063
TD	0.884 ± 0.030	0.622 ± 0.102	0.597 ± 0.120
MTD	0.884 ± 0.030	0.780 ± 0.030	0.787 ± 0.028

shows the average performance in terms of the AUC (PR), MCC, and F1-score evaluated on 500 simulated test images with 10 bright scatterers placed randomly in the scene. In terms of the AUC (PR), the BFT, TD, and MTD outperform the deep learning approaches. In terms of the MCC and F1-score, the MTD method yields the highest performance.

5.4. Analysis on Denoising for Different Noise Levels

Detecting prominent scatterers either visually or algorithmically can be a challenge, especially in high noise environments. In this section, we compare the BFT, TD, and MTD methods applied in Equation (9) against known denoising methods, such as the non-local mean denoising algorithm [41], the total variation (TV) regularization method [42] for denoising, and against a multi-branch denoising algorithm [40]. We vary the parameter p described in Section 4.2 from 0 to $3.5$ in steps of $0.05$ for 500 simulated images set at each of the noise levels, then apply each denoising method on the blurred simulated input images. Next, we use Equation (11) to generate binary images on the denoised versions of the input imagery and evaluate the performance using the AUC (PR) to quantify how well each method preserves the prominent scatterer while performing denoising.

Further, Figure 6 shows the average AUC (PR) measured across 500 denoised simulated images after applying the six denoising methods at various noise levels p. What is observed from comparing the performance curves is that the BFT, TD, MTD methods behave similarly to the TV denoising method with MTD behaving the closest. What is also observed is that when varying the noise level from low to high, the BFT, TD, MTD filters outperform the non-local mean denoising method and the multi-branch denoising algorithm [40]. Further,

Table 5. Denoising methods with average times and standard deviations.

Method $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$	Average Time (ms)
Multi-Branch Denoising [40]	$1.71\pm 0.24$
Non-Local Mean	$3.81\pm 0.23$
Total Variation	$2.15\pm 0.13$
BFT	$0.082\pm 0.006$
TD	$0.139\pm 0.012$
MTD	0.081 ± 0.005

Denoising methods $\left|\mathbf{h}\right(\mathbf{x}\left)\right|$ applied on $\mathbf{x}$ to produce $\mathbf{y}\left(\mathbf{x}\right)$.

shows the computational runtime to denoise a single $64\times 64$ simulated image. The MTD is not only comparable to the TV denoising method in terms of AUC (PR) but also requires roughly $30\times$ less processing time than the TV denoising algorithm and $21\times$ less processing than the multi-branch denoising algorithm even though it was processed on a GPU node.

5.5. Runtime Experiments

To evaluate the latency of our methods, we measure the mean computational processing of $\left|\mathbf{h}\left(\mathbf{x}\right)\right|$ and $\mathbf{D}\left(\mathbf{x}\right)$ across 1000 simulated images sizes ($1024\times 1024$) and compare it to the OpenCV thresholding method and Prater et al. [2].

Table 6. Mean runtime of 1000 simulated images ($1024\times 1024$) averaged over 100 trials (milliseconds).

Detection Strategy	$\left|\mathbf{h}\right(\mathbf{x}\left)\right|$	$\mathbf{D}\left(\mathbf{x}\right)$
cv2.threshold	$1.93\pm 0.14$	$5.36\pm 0.36$
Prater et al. [2]	$4.73\pm 0.20$	$8.17\pm 0.34$
BFT	$2.62\pm 0.27$	$7.70\pm 0.72$
TD	$6.02\pm 0.62$	$10.93\pm 1.07$
MTD	$3.24\pm 0.33$	$8.02\pm 0.69$

shows that the BFT and MTD methods are comparable to the OpenCV thresholding method in tone mapping and in detection latencies. The computational complexity for all of the methods is $O\left(N\right)$, where N is the number of pixels. Thus, the number of operations for a $1024\times 1024$ simulated image with a bright scatterer placed in the scene would require $O(1,048,576)$ for the average case when using each of the methods.

6. Conclusions

Summary: In this paper, we introduced a bright feature transform (BFT), a trig difference (TD) function, and a modified trig difference (MTD) function to visually detect prominent scatterers in noisy environments. More specifically, we considered the problem of detecting a single prominent scatterer buried in Rayleigh speckle noise and illustrated qualitatively that performing a Hadamard multiplication on the data with the BFT method outputs imagery that highlights the prominent scatterer and other bright features in the scene. We showed that the BFT could be modified to reduce the background noise levels with the TD and MTD functions. We also showed quantitatively that the MTD method preserves the general structure of the scatterer by producing high PSNR values, as opposed to applying a traditional thresholding-based method on the imagery, which produced low PSNR from distorting the edge feature of the scatterer. Following this, we presented the detection results by converting the tone mapping filters to binary images and compared the predicted regions against the ground truth location of the scatterer. What was found was that BFT, TD, and MTD filters were more robust at detecting the bright scatterer in background noise than the OpenCV thresholding method and Prater et al. [2], with the MTD filter being distinguished from the others in terms of the F1-score measure. What was also observed from the results was that the F1-score and MCC metrics captured the false positives that were induced by the BFT method after applying it in Equation (1) but had lower values in terms of the AUC (PR) results. What was concluded from the detection experiment was that the BFT, TD, and MTD methods can be used to detect bright scatterers, producing results comparable to OpenCV thresholding, and the TD and MTD methods are robust against high background noise levels and other strong noise scatterers. This facilitates tone mapping and can be used as an alternative to thresholding to detect or visually highlight prominent scatterers in synthetic aperture imagery.

Further, we also analyzed the detection performance of the method against the TV and non-local mean denoising methods for various noise levels and found that the BFT, TD, and MTD filters follow the same performance as applying TV denoising, with the filters being orders of magnitude faster and the MTD method being roughly $30\times$ faster. Lastly, we showed that our methods have the same processing time as when applying the OpenCV thresholding. Thus, the main benefits of the methods are as follows: (1) they require no thresholding for visual detection; (2) they preserve the general structure of the scatterer in noisy environments; (3) the TD and MTD methods mitigate noise and preserve the fidelity of the scatterer for downstream characterization; (4) they are fast and invertible.

Limitations: Additionally, we observed a few limitations with applying the BFT, TD, and MTD methods, such as the following: (1) the methods are not suited for unnormalizedraw amplitude or complex data. The input data have to be normalized from 0 to 1 in order for the methods to perform effectively within the first quadrant of the unit circle; (2) the TD and MTD methods cannot discriminate between different noise classes, such as multipath and inference noise, which is commonly found in sonar imagery;(3) we observed that when implementing the proposed methods, further processing would have to be performed on the output imagery when there are other bright targets in the scene after applying (1), as shown in Figure 2 and Figure 3, to solely isolate the prominent scatterer. Further, the authors do not anticipate that the proposed functions would perform equally as well on natural images or RGB data. The design of the functions is specifically intended for detecting bright scatterers for remote sensing image characterization. A future direction to overcome these limitations would possibly be to integrate the methods with edge detection filters, such as the canny edge algorithm or the Sobel filter, in a detection pipeline, as there appears to be a relationship when taking the difference between the sine and cosine pixel-wise to detect the scatterer where both are derivatives of each other.

Contributions: Further, the aim of this work was to develop a fast threshold free method to detect prominent scatterers in reconstructed synthetic aperture scenes with high noise, particularly related to speckle noise. To address the challenge of computational speed up, tone mapping was leveraged via the Hadamard operation with the original image and the BFT was designed to detect the prominent scatterer while maintaining high fidelity. The TD and MTD functions were designed as robust methods to suppress the speckle background and highlight the bright scatterer. Thus, the specific contributions of this work for synthetic aperture image processing include the following: (1) new tone mapping functions designed for remote sensing applications, and (2) novel image-processing functions utilizing sinusoidal operations to mitigate speckle noise.

Significance: The BFT, TD, and MTD methods are significant contributions in the field of remote sensing research in the era of deep learning and generative AI. In this work, the goal was to design a method that could rapidly detect and characterize prominent scatterers without the need of thresholding such that the detected bright features could then later be used for either deconvolution or another important synthetic aperture downstream image-processing task. Implementing a deep learning-based approach to achieve this goal could possibly introduce additional challenges, such as the following: (1) requiring GPU resources; (2) requiring sufficiently sized training datasets to train the neural network to generalize well across new synthetic aperture scenes where training data may be limited; (3) possibly requiring a preprocessing method to reduce the high intensity speckle noise before network processing; and (4) requiring the user to determine and assume a threshold for capturing the pixels belonging to the prominent scatterer. The BFT, TD, and MTD methods are simple and fairly straightforward to implement as preprocessing steps that can either aid deep learning models or be used as fixed tone mapping functions to visually highlight the bright scatterers in the scene imagery.

Future Work: There are multiple directions for future research. Currently, future work is centered around using the detected prominent scatterers to perform blind deconvolution, where the scatterers are used to estimate the imaging system’s PSF in the presence of strong speckle noise. However, another avenue of research would be to apply the BFT, TD, and MTD methods to characterize synthetic aperture imagery, specifically, image resolution or image sharpness, depending on the application. Additionally, another application for the transformations is in the area of shape analysis or shape classification.