The Improved MNSPI Method for MODIS Surface Reflectance Data Small-Area Restoration
Abstract
1. Introduction
- To address the limitations of the MNSPI algorithm in MODIS data, this study improves the MNSPI algorithm by leveraging the stability and invariance of land cover over short periods. The auxiliary information includes adjacent temporal phases before and after the missing phase, as well as data from the same period in the previous and following years. Based on the spectral similarity characteristics of the temporal information, different weights are assigned to the auxiliary temporal phases, and a comprehensive use of spatial–temporal–spectral information is made to achieve the reconstruction of missing MODIS data.
- To ensure the algorithm’s broad adaptability and reliability in handling diverse missing scenarios in practical applications, this study designs experiments with rectangular missing regions of different sizes. Simulated missing and real missing experiments are conducted in two scenarios with varying surface complexities. The experimental results show that the proposed method demonstrates strong robustness across different surface complexities, effectively restoring missing image regions. Additionally, this method outperforms the comparison algorithms in both qualitative and quantitative results. Moreover, to address the issue in existing algorithms where restoration effectiveness declines as the missing region expands, this study explicitly defines the optimal restoration range of the proposed method, specifically for small missing regions. This provides clear guidance for the practical application of the algorithm, ensuring more accurate reconstruction results across various missing scenarios.
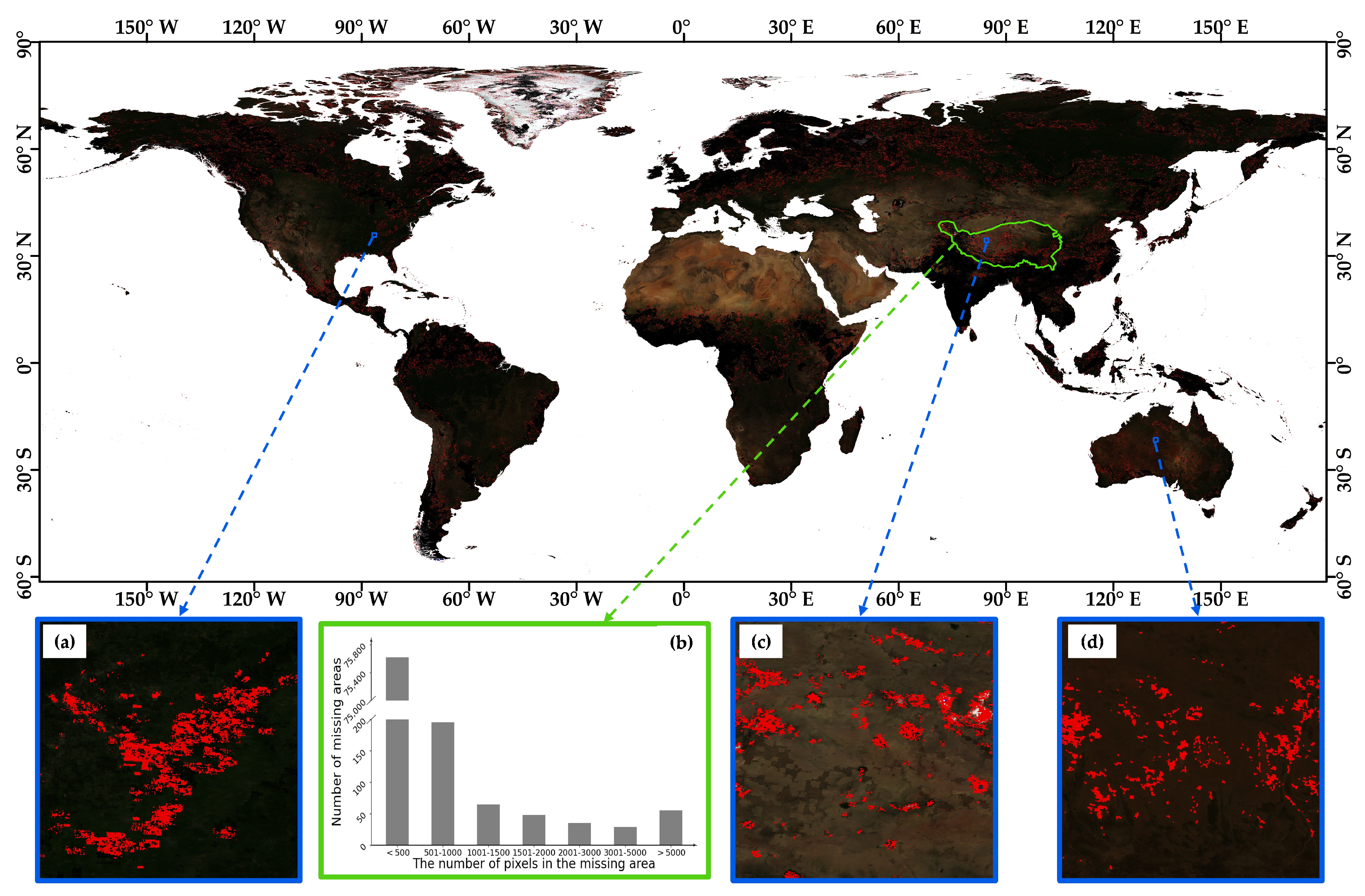
- To validate the algorithm’s reliability across different geographic regions, climate conditions, and land cover types, we apply the proposed algorithm to the global MODIS data restoration. The experimental results show that the method effectively restores small missing region data and maintains high reconstruction accuracy under diverse environmental conditions.
2. Methods
2.1. Overal Framework
2.2. MNSPI
2.3. Improved MNSPI
3. Experimental Data and Design
3.1. Experimental Data
3.2. Data Processing
3.2.1. Anomalous Pixel Identification
3.2.2. Efficient Data Layer Extraction
3.3. Experimental Design
3.3.1. Simulated Experiment Design
3.3.2. Real Experiment Design
3.3.3. Comparative Studies
3.3.4. Quantitative Evaluation
4. Experiment
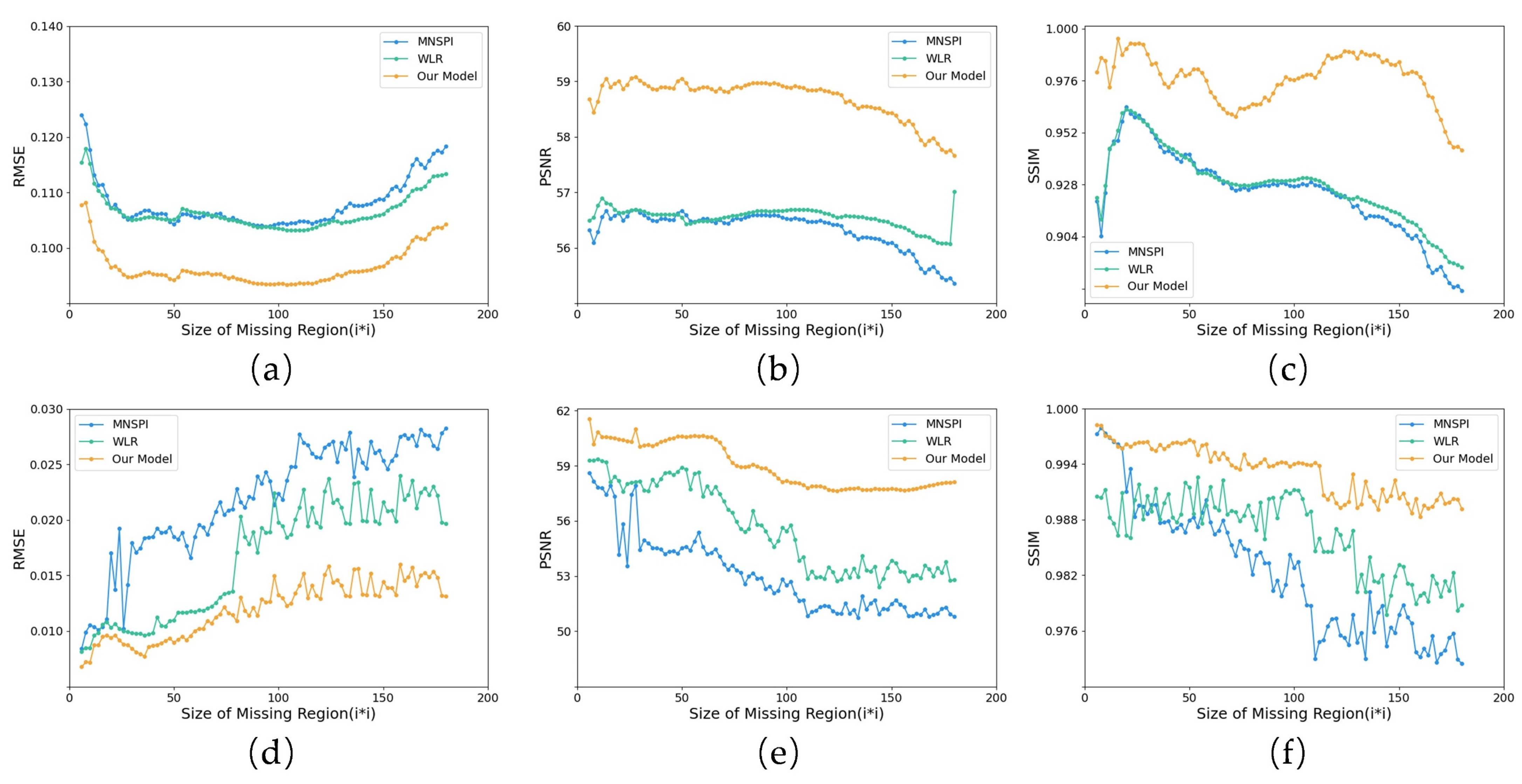
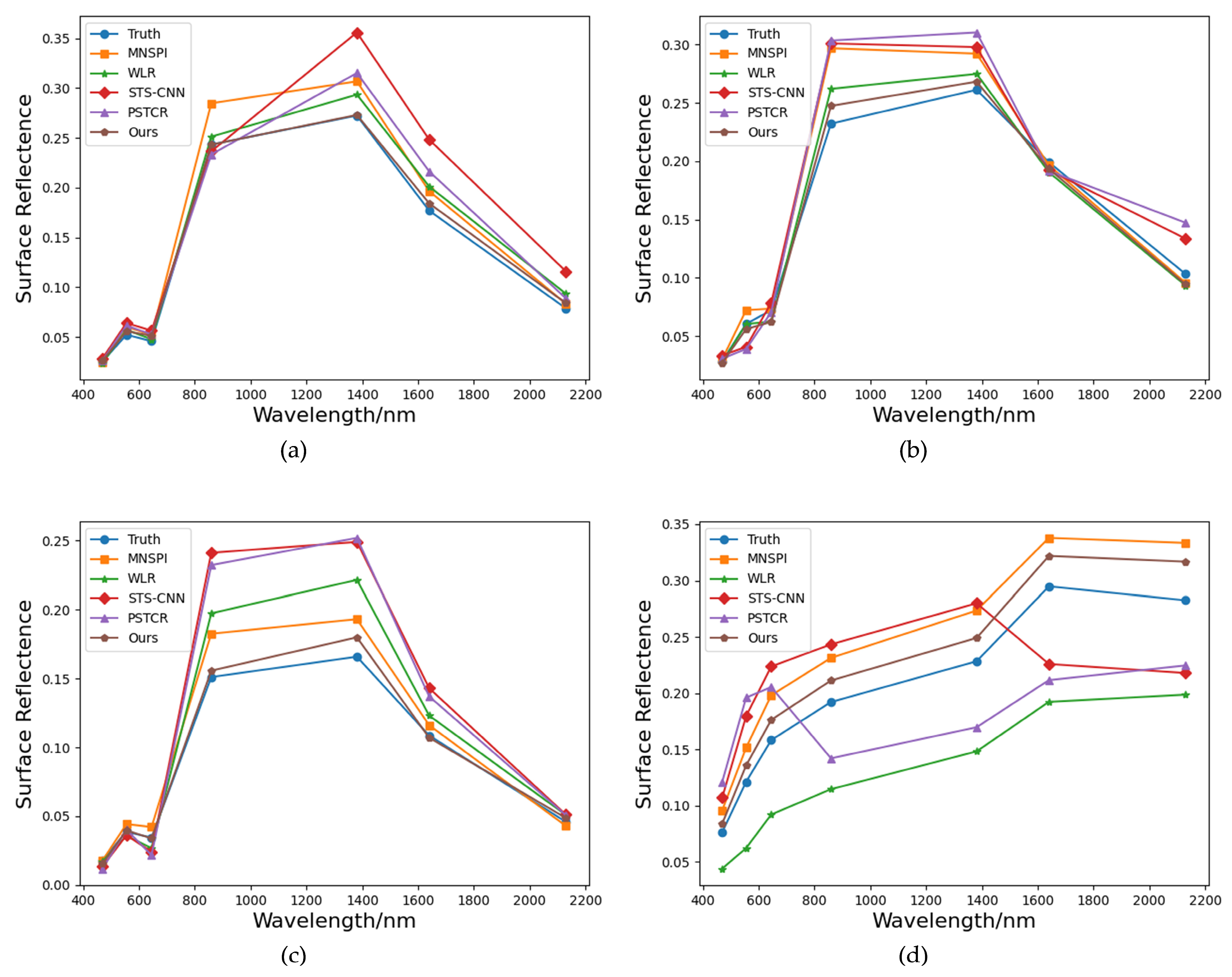
4.1. Simulated Experiment
4.2. Real Experiment
4.3. Model Efficiency Analysis
4.4. Globalization Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Zuo, X.; Tian, J.; Li, S.; Cai, K.; Zhang, W. Research on generic optical remote sensing products: A review of scientific exploration, technology research, and engineering application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3937–3953. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of water clarity in large lakes and reservoirs across China observed from long-term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
- Zhao, X.; Hong, D.; Gao, L.; Zhang, B.; Chanussot, J. Transferable deep learning from time series of Landsat data for national land-cover mapping with noisy labels: A case study of China. Remote Sens. 2021, 13, 4194. [Google Scholar] [CrossRef]
- Youssefi, F.; Zoej, M.J.V.; Hanafi-Bojd, A.A.; Dariane, A.B.; Khaki, M.; Safdarinezhad, A.; Ghaderpour, E. Temporal monitoring and predicting of the abundance of malaria vectors using time series analysis of remote sensing data through Google Earth Engine. Sensors 2022, 22, 1942. [Google Scholar] [CrossRef]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Liu, Q.; Gao, X.B.; He, L.H. Haze removal for a single visible remote sensing image. Signal Process. 2017, 137, 33–43. [Google Scholar] [CrossRef]
- Duan, C.; Pan, J.; Li, R. Thick cloud removal of remote sensing images using temporal smoothness and sparsity regularized tensor optimization. Remote Sens. 2020, 12, 3446. [Google Scholar] [CrossRef]
- Xia, M.; Jia, K. Reconstructing missing information of remote sensing data contaminated by large and thick clouds bas ed on an improved multitemporal dictionary learning method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5605914. [Google Scholar] [CrossRef]
- Yu, W.K.; Zhang, X.K.; Pun, M.O. Cloud removal in optical remote sensing imagery using multiscale distortion-aware networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5512605. [Google Scholar] [CrossRef]
- Yu, X.Y.; Pan, J.; Wang, M. A curvature-driven cloud removal method for remote sensing images. Geo-Spat. Inf. Sci. 2023, 26, 1–22. [Google Scholar] [CrossRef]
- He, B.J.; Fu, X.C.; Zhao, Z.Q.; Chen, P.X.; Sharifi, A.; Li, H. Capability of LCZ scheme to differentiate urban thermal environments in five megacities of China: Implications for integrating LCZ system into heat-resilient planning and design. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 18800–18817. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; p. 5605914. [Google Scholar]
- Zhou, J.; Jia, L.; Menenti, M.; Gorte, B. On the performance of remote sensing time-series reconstruction methods-A spatial comparison. Remote Sens. Environ. 2016, 187, 367–384. [Google Scholar] [CrossRef]
- Alvaro, M.M.; Emma, I.V.; Marco, P.; Gustau, C.V.; Nathaniel, R.; Jordi, M.M.; Fernando, S.; Nicholas, C.; Steven, W. Multispectral high resolution sensor fusion for smoothing and gap-filling in the cloud. Remote Sens. Environ. 2020, 247, 11901. [Google Scholar]
- Mikhail, S.; Eduard, K.; Nikolay, O.; Anna, V. A machine learning approach for remote sensing data gap-filling with open-source implementation: An example regarding land surface temperature, surface Albedo and NDVI. Remote Sens. 2020, 12, 3865. [Google Scholar] [CrossRef]
- Yao, R.; Wang, L.C.; Huang, X.; Sun, L.; Chen, R.Q.; Wu, X.J.; Zhang, W.; Niu, Z.G. A robust method for filling the gaps in MODIS and VIRS land surface temperature data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10738–10752. [Google Scholar] [CrossRef]
- Shi, B.B.; He, H.Q.; You, Q. A method of multi-scale total convolution network driven remote sensing image repair. J. Geomat. 2018, 43, 124–126. (In Chinese) [Google Scholar]
- Tang, W.; He, F.Z. EAT: Multi-Exposure image fusion with adversarial learning and focal transformer. IEEE Trans. Multimedia. 2025, 27, 1–12. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Field, C.B.; Behrenfeld, M.J.; Randerson, J.T.; Falkowski, P. Primary production of the biosphere: Integrating terrestrial and oceanic components. Science 1998, 281, 237–240. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, Y.; Zhao, B.; Chanussot, J.; Hong, D.; Yao, J.; Gao, L. Progress and challenges in intelligent remote sensing satellite systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1814–1822. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, B.; Zhang, W.; Hong, D.; Zhao, B.; Li, Z. Cloud Removal With SAR-Optical data fusion using a unified spatial-spectral residual network. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–20. [Google Scholar] [CrossRef]
- Chu, D.; Shen, H.; Guan, X.; Chen, J.M.; Li, X.; Li, J.; Zhang, L. Long time-series NDVI reconstruction in cloud-prone regions via spatio-temporal tensor completion. Remote Sens. Environ. 2021, 264, 112632. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Ao, Z.; Xiao, K.; Yan, C.; Xin, Q. Gap-Filling and Missing Information Recovery for Time Series of MODIS Data Using Deep Learning-Based Methods. Remote Sens. 2022, 14, 4692. [Google Scholar] [CrossRef]
- Chen, H.; Chen, R.; Li, N.N. Attentive generative adversarial network for removing thin cloud from a single sensing image. IET Image Process. 2021, 15, 856–867. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhang, W.J.; Zhen, L. Cloud removal with SAR-Optical data fusion and graph-based feature aggregation network. Remote Sens. 2022, 14, 3374. [Google Scholar] [CrossRef]
- Xu, M.; Deng, F.; Jia, S.; Jia, X.; Plaza, A.J. Attention mechanism-based generative adversarial networks for cloud removal in Landsat images. Remote Sens. Environ. 2022, 271, 112902. [Google Scholar] [CrossRef]
- Shen, H.F.; Li, X.H.; Cheng, Q. Missing information reconstruction of remote sensing data: A technical review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Chen, S.J.; Zhang, W.J.; Zhang, B.; Kang, Q.; Xu, X. Research on method of surface reflectance reconstruction in the Tibetan Plateau based on MODIS data. Optics Precis. Eng. 2023, 31, 429–441. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.D.; Wu, W.; Zhang, Z.C.; Li, Z.M.; Zhang, F.; Xin, Q.C. A temporal attention-based multi-scale generative adversarial network to fill gaps in time series of MODIS data for land surface phenology extraction. Remote Sens. Environ. 2025, 318, 114546. [Google Scholar] [CrossRef]
- Guillemot, C.; Le Meur, O. Image inpainting: Overview and recent advances. IEEE Signal Process. Mag. 2014, 31, 127–144. [Google Scholar] [CrossRef]
- Hou, J.L.; Huang, C.L.; Wang, H.W. The cloud-removal method of MODIS fractional snow cover product based on kriging spatial interpolation. Remote Sens. Technol. Appl. 2014, 29, 1001–1007. (In Chinese) [Google Scholar]
- Zhang, J.; Tan, Z.H.; Liu, M. Estimating land surface temperature under the cloud cover with spatial interpolation. Geogr. Geo-Inf. Sci. 2011, 27, 45–49+115. (In Chinese) [Google Scholar]
- Tu, L.L.; Tan, Z.H.; Zhang, J. Estimation and error analysis of land surface temperature under the cloud based on spatial interpolation. Remote Sens. Inf. 2011, 4, 59–63+106. (In Chinese) [Google Scholar]
- Tang, Z.; Wang, J.; Li, H.; Yan, L. Spatiotemporal changes of snow cover on the Tibetan Plateau based on cloud-removed moderate resolution imaging spectroradiometer fractional snow cover product from 2001 to 2011. J. Appl. Remote Sens. 2013, 7, 073582. [Google Scholar] [CrossRef]
- Jing, Y.; Shen, H.; Li, X.; Guan, X. A two stage fusion framework to generate a spatiotemporally continuous MODIS NDSI product over the Tibetan Plateau. Remote Sens. 2019, 11, 2261. [Google Scholar] [CrossRef]
- Scaramuzza, P.; Barsi, J. Landsat 7 scan line corrector-off gap-filled product development. In Proceedings of the Pecora, Sioux Falls, SD, USA, 23–27 October 2005; pp. 23–27. [Google Scholar]
- Gerber, F.; de Jong, R.; Schaepman, M.E.; Schaepman-Strub, G.; Furrer, R. Predicting missing values in spatio-temporal remote sensing data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2841–2853. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Chai, L.; Wang, D.; Liu, J. Estimation of 1-km all-weather remotely sensed land surface temperature based on reconstructed spatial-seamless satellite passive microwave brightness temperature and thermal infrared Data. ISPRS J. Photogramm. Remote Sens. 2020, 167, 321–344. [Google Scholar] [CrossRef]
- Shen, H.; Wu, J.; Cheng, Q.; Aihemaiti, M.; Zhang, C.; Li, Z. A spatiotemporal fusion-based cloud removal method for remote sensing images with land cover changes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 862–874. [Google Scholar] [CrossRef]
- Li, X.; Wang, L.; Cheng, Q.; Wu, P.; Gan, W.; Fang, L. Cloud removal in remote sensing images using nonnegative matrix factorization and error correction. ISPRS J. Photogramm. Remote Sens. 2019, 148, 103–113. [Google Scholar] [CrossRef]
- Li, M.; Zhu, X.; Li, N.; Pan, Y. Gap-Filling of a MODIS normalized difference snow index product based on the similar pixel selecting algorithm: A case study on the Qinghai-Tibetan Plateau. Remote Sens. 2020, 12, 1077. [Google Scholar] [CrossRef]
- Xing, D.; Hou, J.; Huang, C.; Zhang, W. Spatiotemporal reconstruction of MODIS normalized difference snow index products using U-Net with partial convolutions. Remote Sens. 2022, 14, 1795. [Google Scholar] [CrossRef]
- Zhu, X.; Gao, F.; Liu, D.; Chen, J. A modified neighborhood similar pixel interpolator approach for removing thick clouds in Landsat images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 521–525. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Vogelmann, J.E.; Gao, F.; Jin, S. A simple and effective method for filling gaps in Landsat ETM+ SLC-Off images. Remote Sens. Environ. 2011, 115, 1053–1064. [Google Scholar] [CrossRef]
- Qin, Y.; Guo, F.; Ren, Y.; Wang, X.; Gu, J.; Ma, J.; Zou, L.; Shen, X. Decomposition of mixed pixels in MODIS data using Bernstein basis functions. Appl. Remote Sens. 2019, 13, 046509. [Google Scholar] [CrossRef]
- Zeng, C.; Shen, H.F.; Zhang, L.P. Recovering missing pixels for Landsat ETM+ SLC-off imagery using multi-temporal regression analysis and a regularization method. Remote Sens. Environ. 2013, 131, 182–194. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.Q.; Zeng, C.; Li, X.H.; Wei, Y.C. Missing data reconstruction in remote sensing image with a unified spatial-temporal-spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.Q.; Li, J.; Li, Z.W.; Shen, H.F.; Zhang, L.P. Thick cloud and cloud shadow removal in multitemporal imagery using progressively spatio-temporal patch group deep learning. ISPRS J. Photogramm. Remote Sens. 2020, 162, 148–160. [Google Scholar] [CrossRef]









| Data Product | Data Layer | Wavelength Range | Spatial Resolution | Temporal Resolution | Projected Coordinate System |
|---|---|---|---|---|---|
| MOD09A1 | Surf_refl_b01 | 0.620–0.670 μm | 500 m | 8 days | Sinusoidal Projection |
| Surf_refl_b02 | 0.841–0.876 μm | ||||
| Surf_refl_b03 | 0.459–0.479 μm | ||||
| Surf_refl_b04 | 0.545–0.565 μm | ||||
| Surf_refl_b05 | 1.230–1.250 μm | ||||
| Surf_refl_b06 | 1.628–1.652 μm | ||||
| Surf_refl_b07 | 2.105–2.155 μm |
| Dataset | Target Image Acquisition Date | Date of Auxiliary Data Acquisition | |||
|---|---|---|---|---|---|
| 8 Days Ago | 8 Days After | Same Day the Year Before | Same Day the Year Later | ||
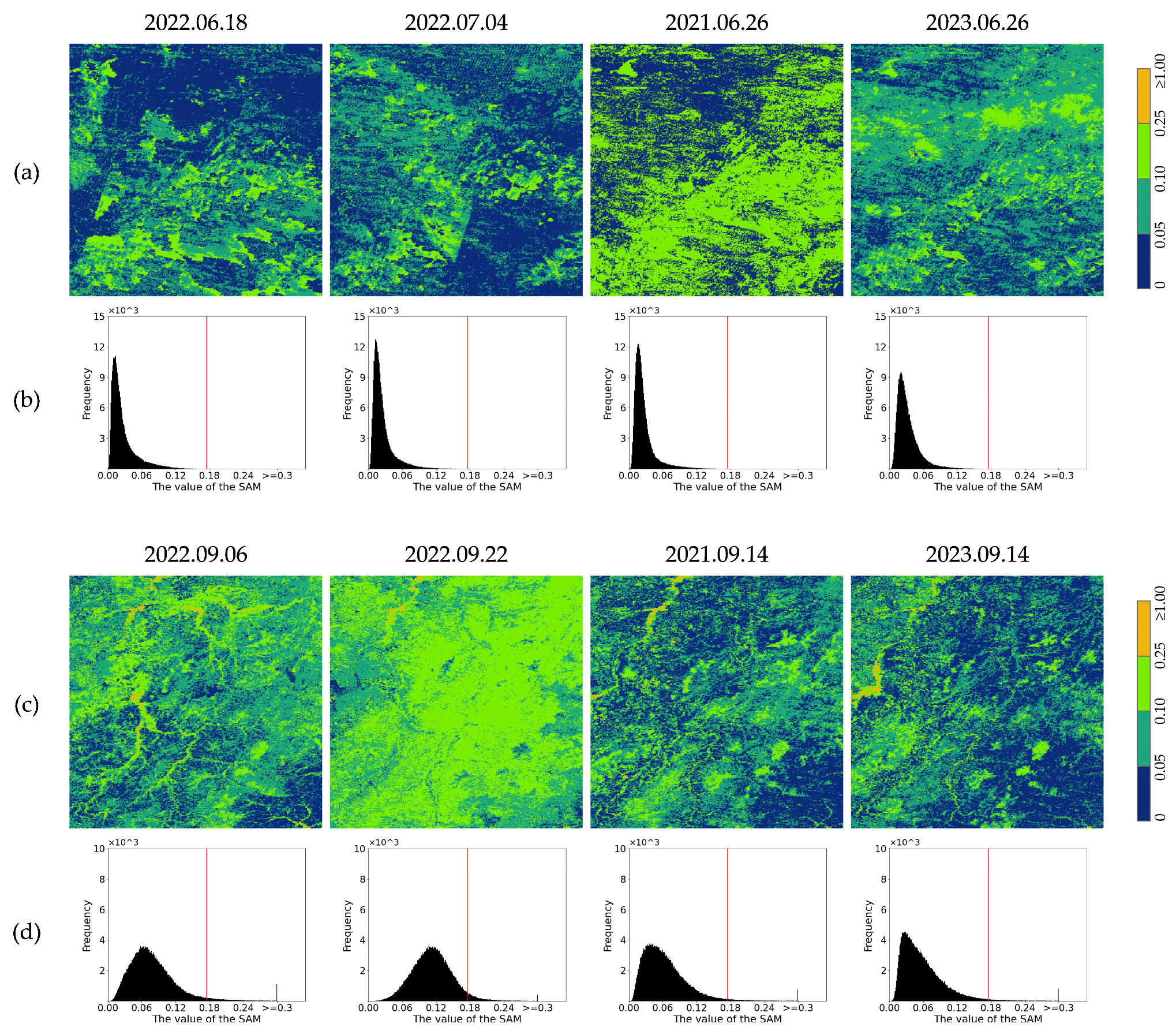
| Dataset1 (Single Surface) | 2022.06.26 | 2022.06.18 | 2022.07.04 | 2021.06.26 | 2023.06.26 |
| Dataset2 (Complex Surface) | 2022.09.14 | 2022.09.06 | 2022.09.22 | 2021.09.14 | 2023.09.14 |
| Date Layer Name | Parameter Name | Bit Comb. | Pixel Processing Rules |
|---|---|---|---|
| Surf_refl_qc_500m | MODLAND QA bits | 00 | Retain |
| Others | −28,672 | ||
| Surf_refl_state_500m | Cloud state | 00 | Retain |
| Others | −28,672 | ||
| Cloud shadow | 0 | Retain | |
| 1 | −28,672 | ||
| Aerosol quantity: level of uncertainty in aerosol correction | 00 | Retain | |
| 01 | Retain | ||
| Others | −28,672 | ||
| Cirrus detected | 00 | Retain | |
| Others | −28,672 | ||
| Internal cloud algorithm flag | 0 | Retain | |
| 1 | −28,672 | ||
| Pixel is adjacent to cloud | 0 | Retain | |
| 1 | −28,672 |
| Method | Single Surface | Complex Surface | ||||
|---|---|---|---|---|---|---|
| RMSE | PSNR | SSIM | RMSE | PSNR | SSIM | |
| MNSPI | 0.229 | 49.735 | 0.989 | 0.130 | 56.748 | 0.994 |
| 0.051 | 52.760 | 0.997 | 0.142 | 55.314 | 0.993 | |
| 0.132 | 54.463 | 0.996 | 0.128 | 56.961 | 0.994 | |
| 0.136 | 54.321 | 0.995 | 0.115 | 58.074 | 0.995 | |
| 0.169 | 52.413 | 0.995 | 0.133 | 56.571 | 0.994 | |
| WLR | 0.121 | 55.273 | 0.996 | 0.118 | 58.590 | 0.997 |
| 0.134 | 54.064 | 0.996 | 0.127 | 56.657 | 0.995 | |
| 0.132 | 54.589 | 0.987 | 0.111 | 57.908 | 0.995 | |
| 0.156 | 53.073 | 0.993 | 0.124 | 59.417 | 0.997 | |
| 0.186 | 51.524 | 0.990 | 0.126 | 57.791 | 0.996 | |
| STS-CNN | 0.150 | 54.655 | 0.995 | 0.169 | 54.923 | 0.995 |
| 0.196 | 53.585 | 0.995 | 0.252 | 53.787 | 0.993 | |
| 0.176 | 54.044 | 0.996 | 0.217 | 54.276 | 0.994 | |
| 0.189 | 51.970 | 0.994 | 0.283 | 53.696 | 0.992 | |
| 0.212 | 49.6580 | 0.989 | 0.349 | 52.537 | 0.988 | |
| PSTCR | 0.054 | 52.536 | 0.997 | 0.029 | 56.335 | 0.996 |
| 0.081 | 57.788 | 0.998 | 0.143 | 58.314 | 0.995 | |
| 0.129 | 54.347 | 0.996 | 0.162 | 52.112 | 0.994 | |
| 0.209 | 53.681 | 0.996 | 0.113 | 50.463 | 0.994 | |
| 0.282 | 50.964 | 0.993 | 0.234 | 57.039 | 0.995 | |
| Ours | 0.103 | 56.989 | 0.996 | 0.091 | 59.347 | 0.997 |
| 0.045 | 53.877 | 0.999 | 0.114 | 57.685 | 0.996 | |
| 0.119 | 54.728 | 0.997 | 0.107 | 58.026 | 0.996 | |
| 0.122 | 54.792 | 0.997 | 0.110 | 59.319 | 0.997 | |
| 0.143 | 53.638 | 0.996 | 0.111 | 57.948 | 0.996 | |
| Method | Model Training Time/h | Model Predicting Time/s | Adopted Equipment |
|---|---|---|---|
| MNSPI | / | 33.59 | CPU |
| WLR | / | 26.04 | CPU |
| STS-CNN | 4.59 | 12.78 | NVIDIA GeForce RTX 3090 GPU |
| PSTCR | 6.22 | 15.27 | NVIDIA GeForce RTX 3090 GPU |
| Ours | / | 21.96 | CPU |
| Tibetan Plateau | Amazon Rainforest | Congo Basin | Average | |
|---|---|---|---|---|
| RMSE | 0.0101 | 0.0188 | 0.0271 | 0.0187 |
| MAE | 0.0064 | 0.0132 | 0.0185 | 0.0127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, W.; Wang, B.; Ma, X.; Qi, P.; Zhou, Z. The Improved MNSPI Method for MODIS Surface Reflectance Data Small-Area Restoration. Remote Sens. 2025, 17, 1022. https://doi.org/10.3390/rs17061022
Wang M, Zhang W, Wang B, Ma X, Qi P, Zhou Z. The Improved MNSPI Method for MODIS Surface Reflectance Data Small-Area Restoration. Remote Sensing. 2025; 17(6):1022. https://doi.org/10.3390/rs17061022
Chicago/Turabian StyleWang, Meixiang, Wenjuan Zhang, Bowen Wang, Xuesong Ma, Peng Qi, and Zixiang Zhou. 2025. "The Improved MNSPI Method for MODIS Surface Reflectance Data Small-Area Restoration" Remote Sensing 17, no. 6: 1022. https://doi.org/10.3390/rs17061022
APA StyleWang, M., Zhang, W., Wang, B., Ma, X., Qi, P., & Zhou, Z. (2025). The Improved MNSPI Method for MODIS Surface Reflectance Data Small-Area Restoration. Remote Sensing, 17(6), 1022. https://doi.org/10.3390/rs17061022






