Reconstruction of Effective Cross-Sections from DEMs and Water Surface Elevation
Abstract
1. Introduction
2. Methods
- —time; —coordinate along the river centerline, —vertical coordinate;
- —set of time instants;
- —set of spatial nodes;
- —the water surface elevation, counted along the -axis, at node and time instant ;
- —the cross-section width as a function of at node ;
- —the discharge at node and time instant ;
- —the lowest water surface elevation observed at node ;
- —the highest water surface elevation observed at node ;
- —the cross-section bottom elevation at node ;
- —the cross-section bottom width at node , ;
- —the base of a rectangular cross-section;
- —the cross-section top elevation at node ;
- —the cross-section top width at node , .
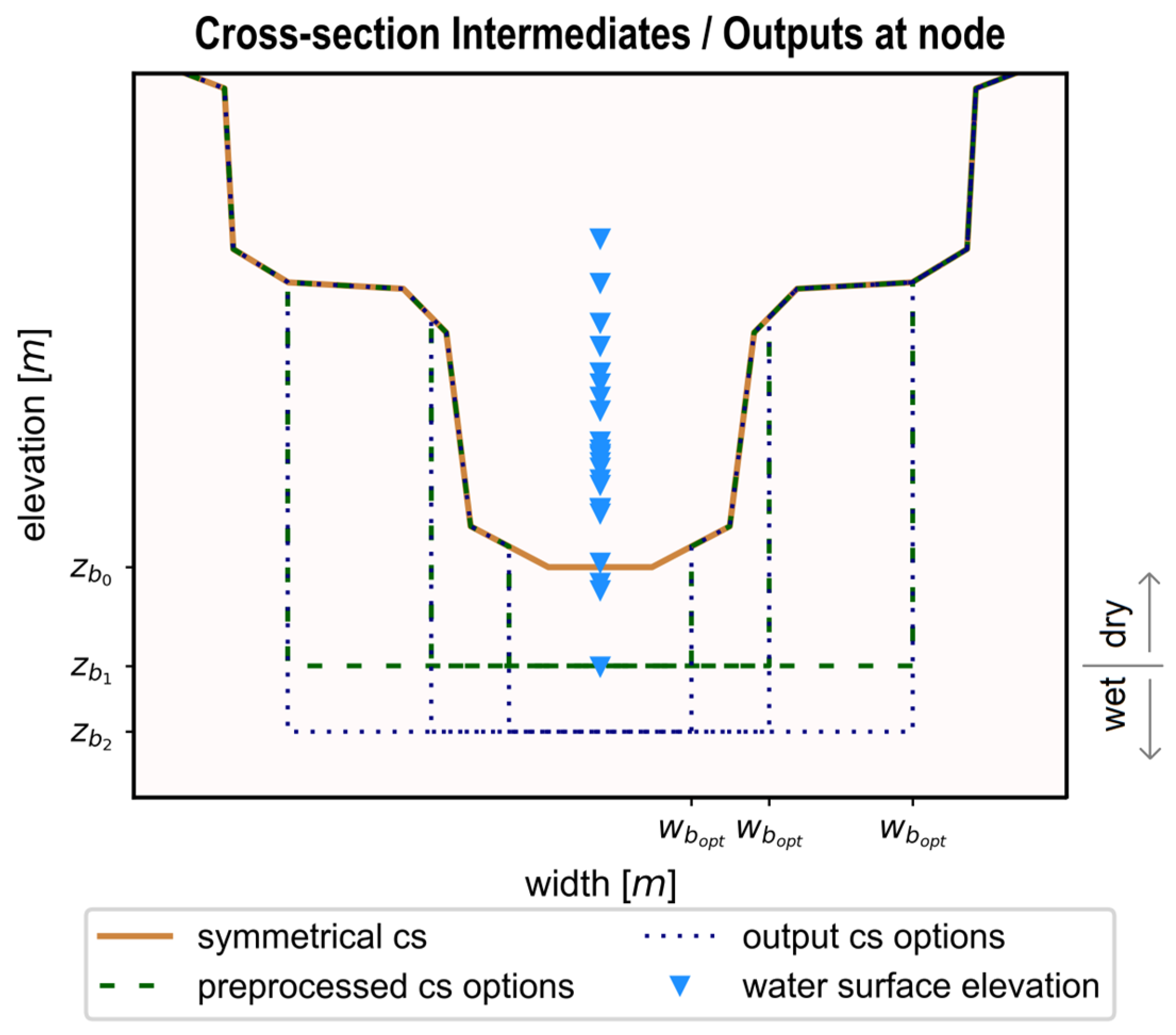
2.1. Cross-Section Definition and Extraction
2.2. Cross-Section Burning
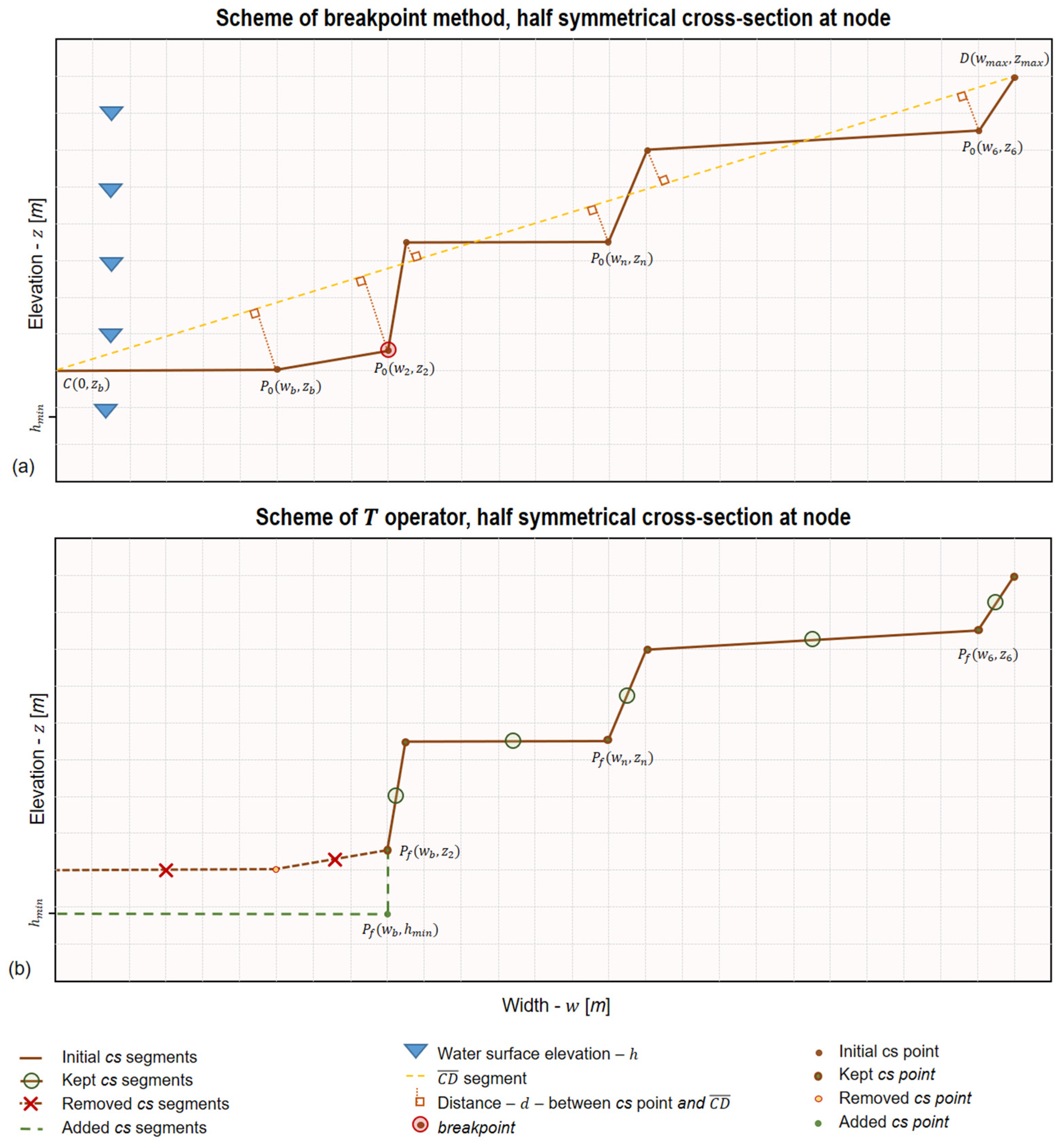
2.2.1. The Breakpoint Method
2.2.2. The Continuity Method
2.3. Discharge Estimation
2.4. Evaluation Metrics
3. Datasets
3.1. Global Remotely Sensed Digital Elevation Models (DEMs)
3.2. Water Surface Elevation from Virtual Stations
4. Study Areas
4.1. The Garonne River
4.2. The Po River
5. Results
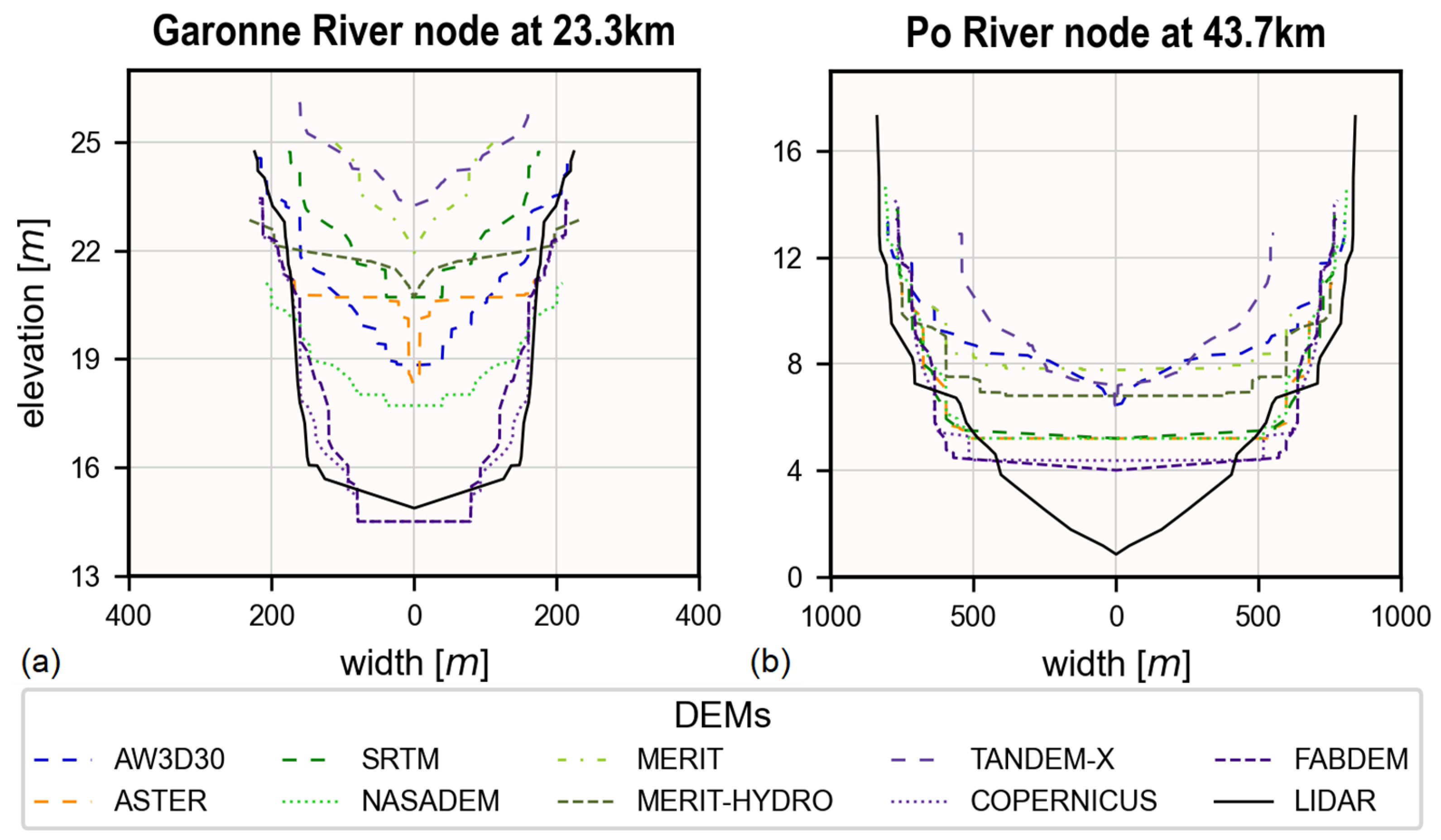
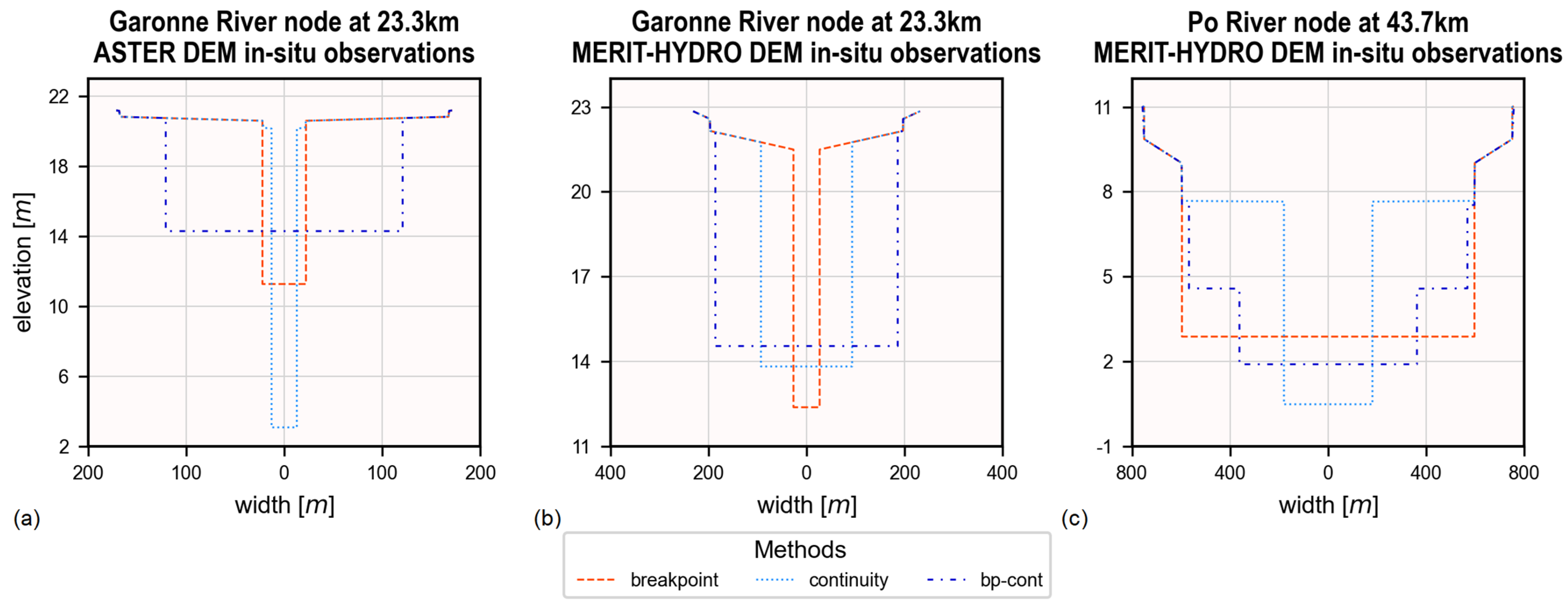
5.1. Impact of DEMs on the Dry Bathymetry
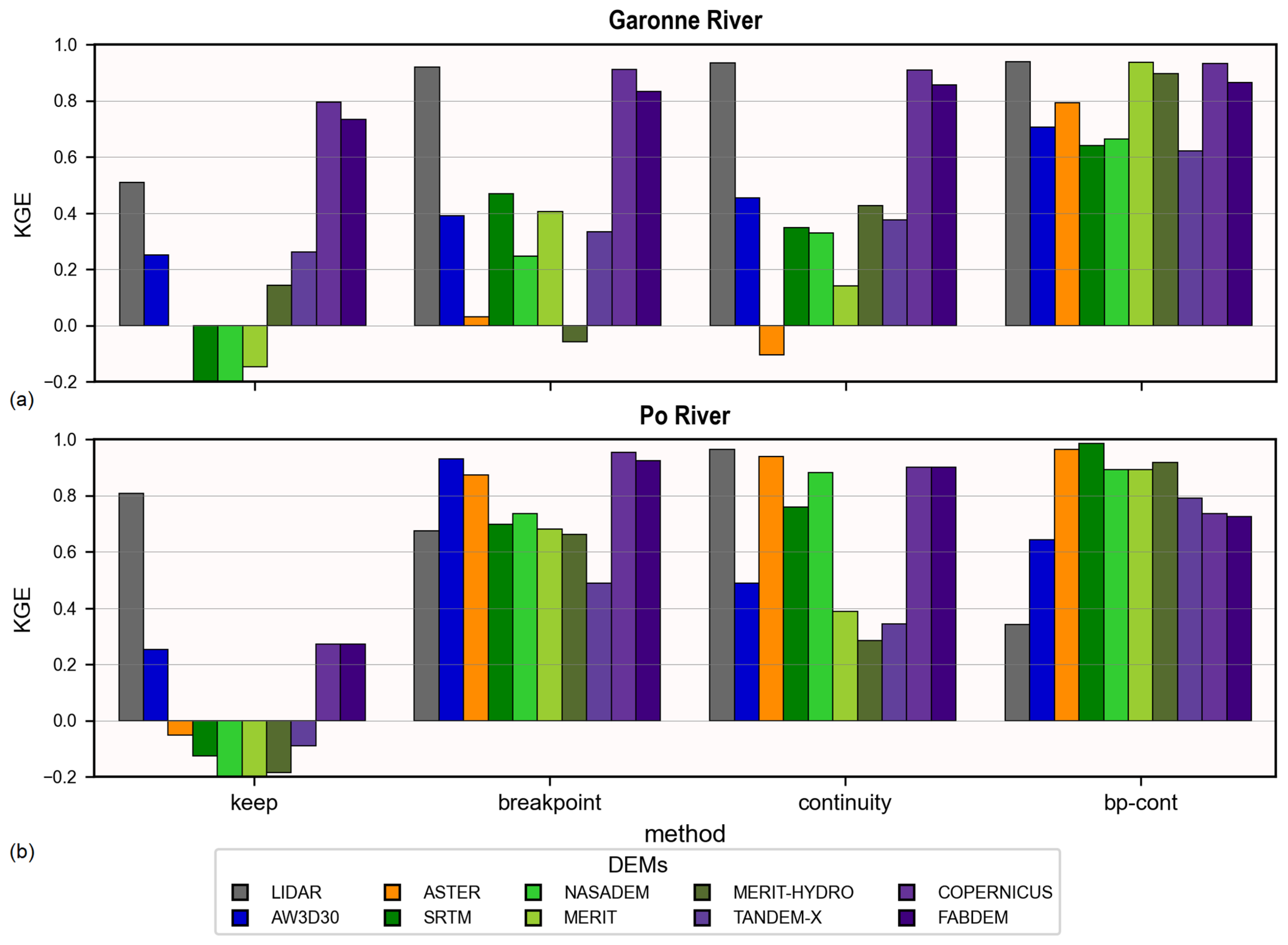
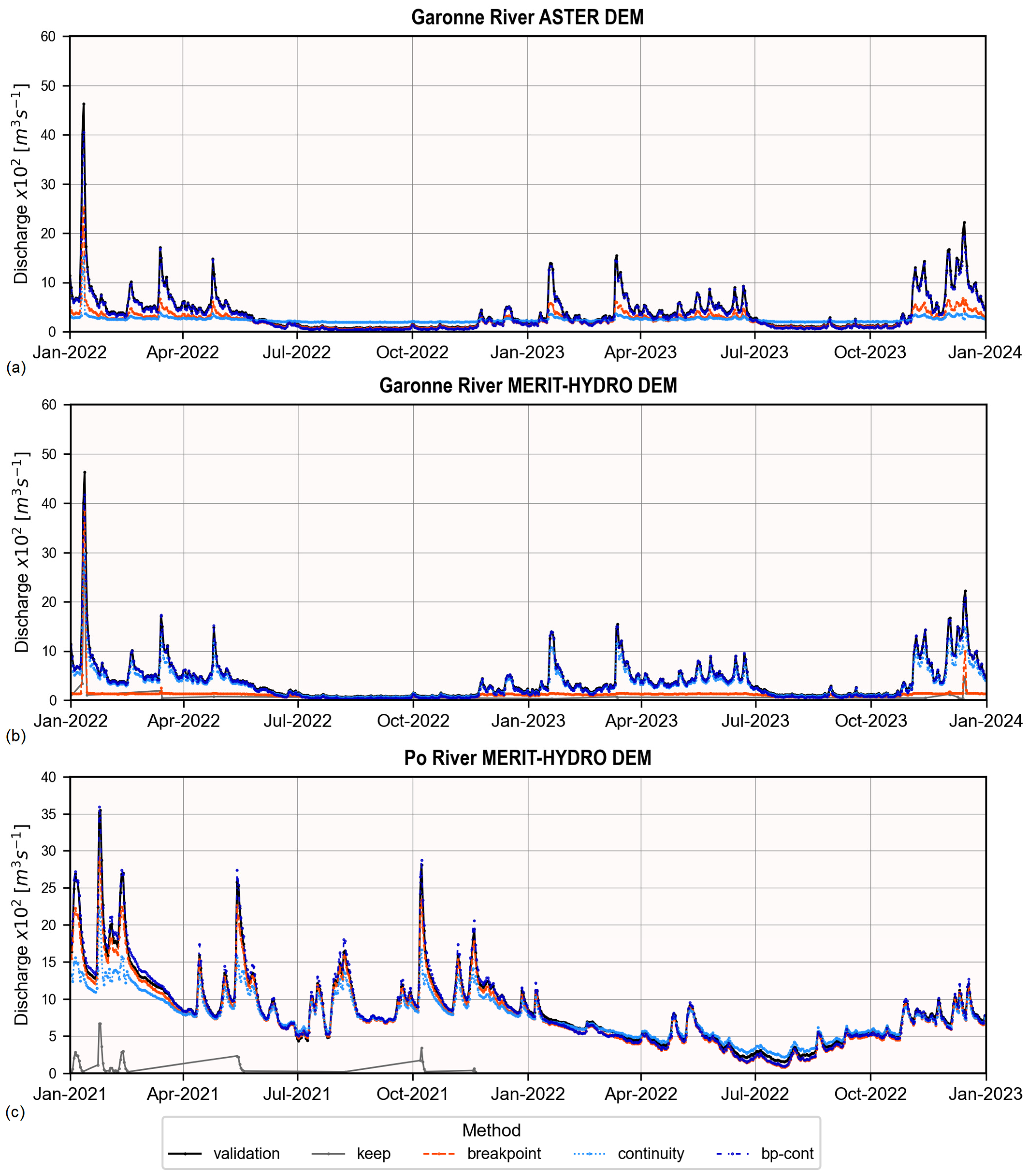
5.2. Impact of DEMs and Cross-Section Burning on the Discharge Estimate
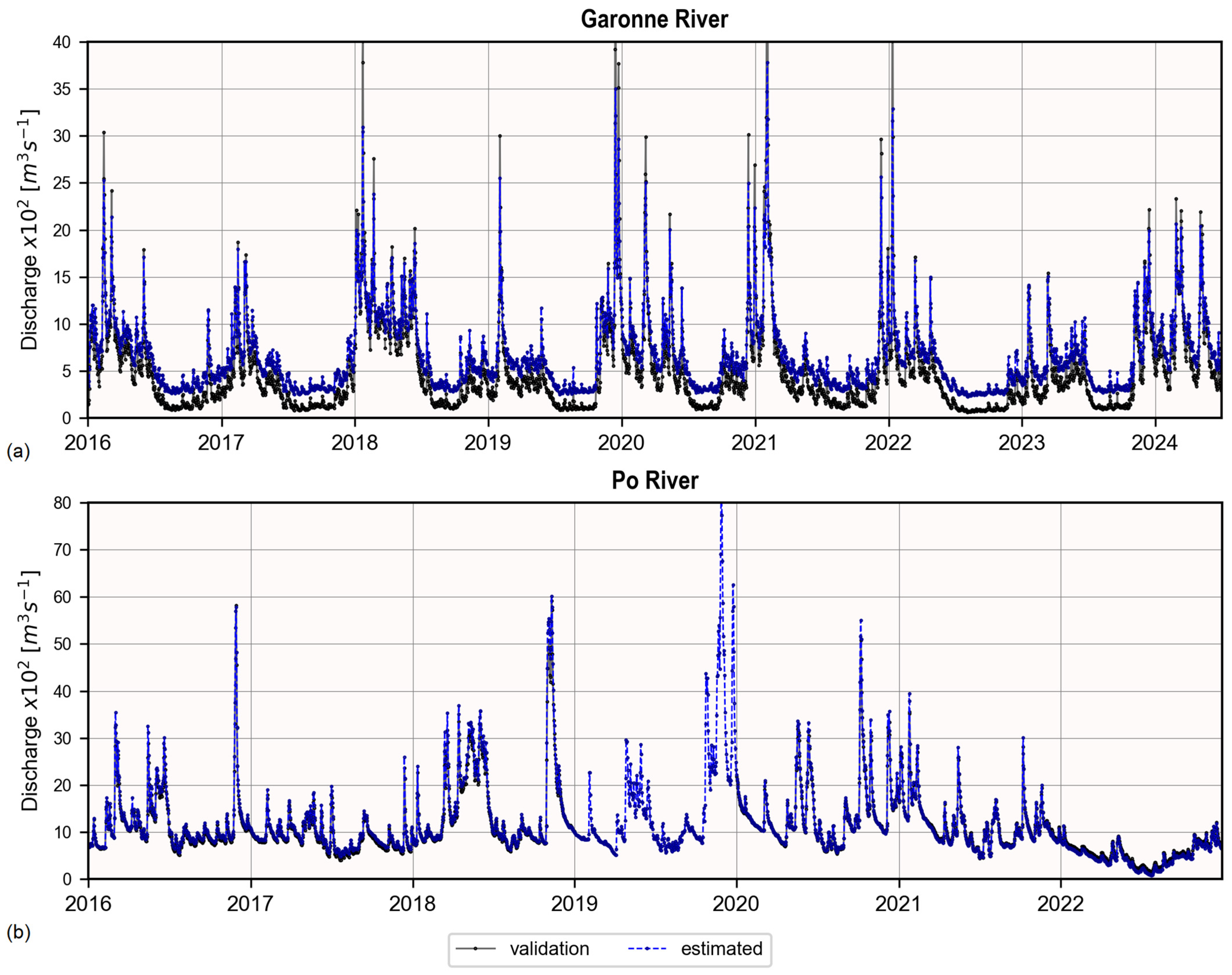
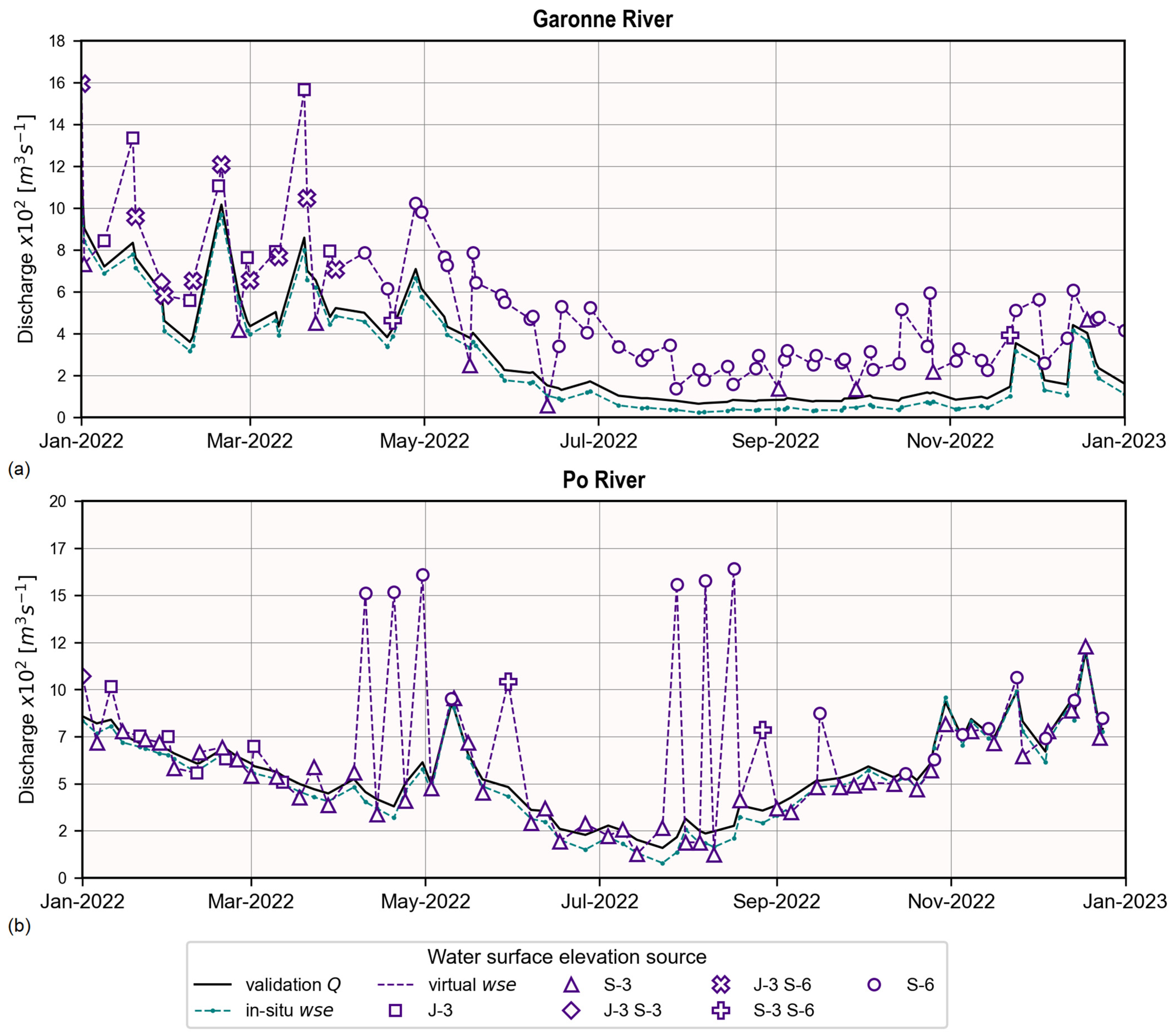
5.3. Impact of Water Surface Elevation Sources on the Discharge Estimate
5.4. Impact on the Effective Bathymetry
6. Discussion
6.1. Impact of DEMs on the Dry Bathymetry
6.2. Impact of DEMs and Cross-Section Burning on the Discharge Estimate
6.3. Impact of Water Surface Elevation Source on the Discharge Estimate
6.4. Impacts on the Effective Bathymetry
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Continuity Method
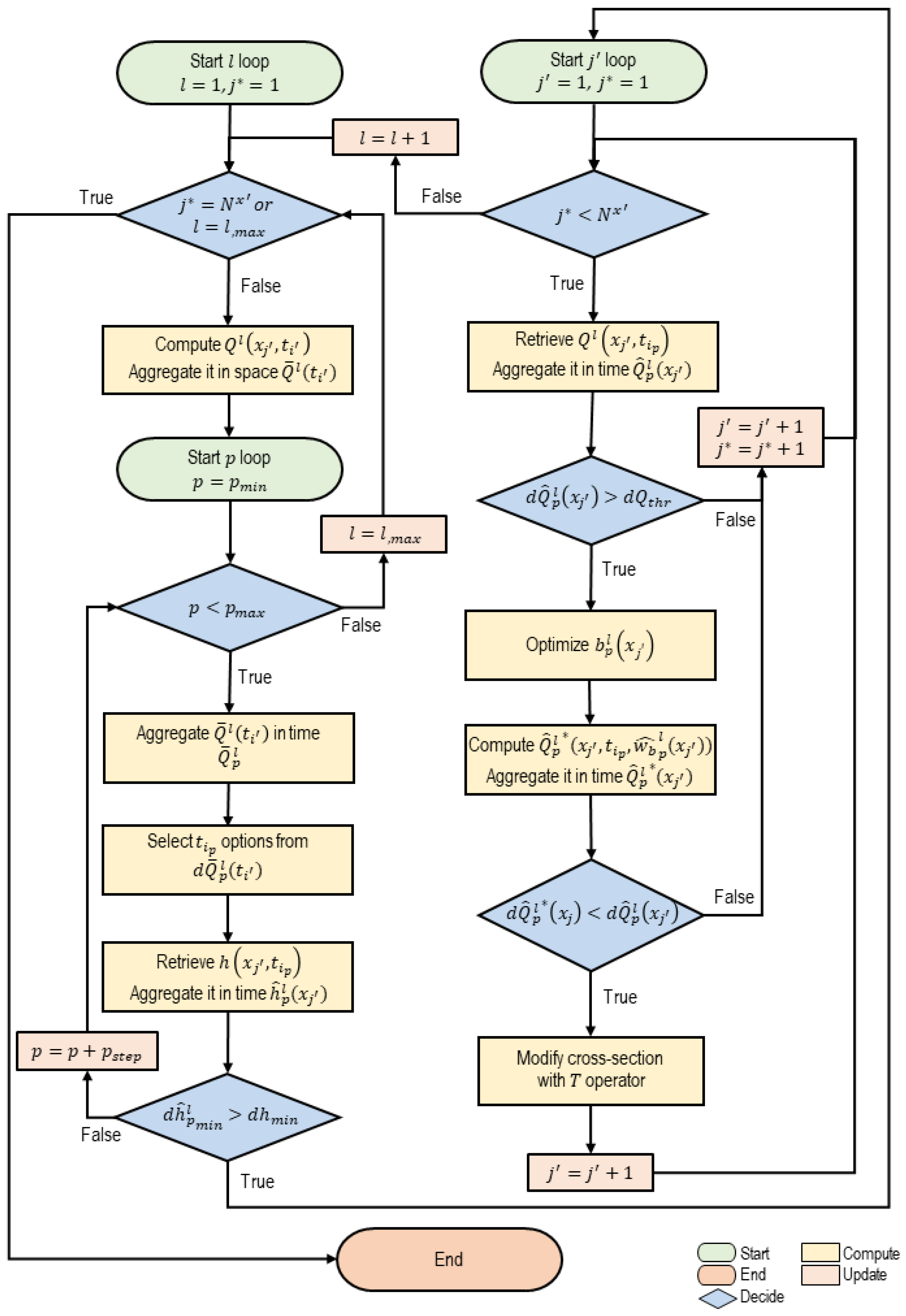
- —the number of iterations to modify the width;
- —the percentiles for temporal aggregation;
- —a subset of the spatial nodes ;
- —a subset of the spatial nodes that were not modified;
- —a subset of the time instances ;
- —a subset of the time instances ;
- —base of a rectangular cross-section,
- —the maximum top width ;
- , constant roughness coefficient for the river reach considered; and
- the initial bathymetry approximation, obtained from the DEMs for the first step and from the previous step for the second and third steps.
| Algorithm A1: Core Algorithm of the continuity method | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| - | ||||
| (A1) | ||||
| - | ||||
| - | ||||
References
- Gleason, C.J.; Durand, M.T. Remote Sensing of River Discharge: A Review and a Framing for the Discipline. Remote Sens. 2020, 12, 1107. [Google Scholar] [CrossRef]
- Schumann, G.J.-P.; Bates, P. The Need for a High-Accuracy, Open-Access Global Digital Elevation Model. Front. Earth Sci. Front. Environ. Sci. Front. Ecol. Evol. 2021, 544, 618194. [Google Scholar]
- Neal, J.; Hawker, L.; Savage, J.; Durand, M.; Bates, P.; Sampson, C. Estimating River Channel Bathymetry in Large Scale Flood Inundation Models. Water Resour. Res. 2021, 57, e2020WR028301. [Google Scholar] [CrossRef]
- Oubanas, H.; Gejadze, I.; Malaterre, P.O.; Durand, M.; Wei, R.; Frasson, R.P.M.; Domeneghetti, A. Discharge Estimation in Ungauged Basins Through Variational Data Assimilation: The Potential of the SWOT Mission. Water Resour. Res. 2018, 54, 2405–2423. [Google Scholar] [CrossRef]
- Scherer, D.; Schwatke, C.; Dettmering, D.; Seitz, F. Long-Term Discharge Estimation for the Lower Mississippi River Using Satellite Altimetry and Remote Sensing Images. Remote Sens. 2020, 12, 2693. [Google Scholar] [CrossRef]
- Durand, M.; Dai, C.; Moortgat, J.; Yadav, B.; Frasson, R.P.d.M.; Li, Z.; Wadkwoski, K.; Howat, I.; Pavelsky, T.M. Using River Hypsometry to Improve Remote Sensing of River Discharge. Remote Sens. Environ. 2024, 315, 114455. [Google Scholar] [CrossRef]
- Domeneghetti, A. On the Use of SRTM and Altimetry Data for Flood Modeling in Data-Sparse Regions. Water Resour. Res. 2016, 52, 2901–2918. [Google Scholar] [CrossRef]
- Lewis, L.A. The Adjustments of Some Hydraulic Variables at Discharges Less than One Cfs. Prof. Geogr. 1966, 18, 230–234. [Google Scholar] [CrossRef]
- Mersel, M.K.; Smith, L.C.; Andreadis, K.M.; Durand, M.T. Estimation of River Depth from Remotely Sensed Hydraulic Relationships. Water Resour. Res. 2013, 49, 3165–3179. [Google Scholar] [CrossRef]
- Schaperow, J.R.; Li, D.; Margulis, S.A.; Lettenmaier, D.P. A Curve-Fitting Method for Estimating Bathymetry From Water Surface Height and Width. Water Resour. Res. 2019, 55, 4288–4303. [Google Scholar] [CrossRef]
- Leopold, L.B.; Maddock, T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications; US Government Printing Office: Washington, DC, USA, 1953.
- Fleischmann, A.; Paiva, R.; Collischonn, W. Can Regional to Continental River Hydrodynamic Models Be Locally Relevant? A Cross-Scale Comparison. J. Hydrol. X 2019, 3, 100027. [Google Scholar] [CrossRef]
- Hilton, J.E.; Grimaldi, S.; Cohen, R.C.Z.; Garg, N.; Li, Y.; Marvanek, S.; Pauwels, V.R.N.; Walker, J.P. River Reconstruction Using a Conformal Mapping Method. Environ. Model. Softw. 2019, 119, 197–213. [Google Scholar] [CrossRef]
- Zakharova, E.; Nielsen, K.; Kamenev, G.; Kouraev, A. River Discharge Estimation from Radar Altimetry: Assessment of Satellite Performance, River Scales and Methods. J. Hydrol. 2020, 583, 124561. [Google Scholar] [CrossRef]
- Scherer, D.; Schwatke, C.; Dettmering, D.; Seitz, F. Monitoring River Discharge from Space: An Optimization Approach with Uncertainty Quantification for Small Ungauged Rivers. Remote Sens. Environ. 2024, 315, 114434. [Google Scholar] [CrossRef]
- Durand, M.; Rodríguez, E.; Alsdorf, D.E.; Trigg, M. Estimating River Depth From Remote Sensing Swath Interferometry Measurements of River Height, Slope, and Width. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 20–31. [Google Scholar] [CrossRef]
- Gleason, C.; Garambois, P.-A.; Durand, M. Tracking River Flows from Space. Eos Earth Space Sci. News 2017, 98, 1–9. [Google Scholar] [CrossRef]
- Durand, M.; Andreadis, K.M.; Alsdorf, D.E.; Lettenmaier, D.P.; Moller, D.; Wilson, M. Estimation of Bathymetric Depth and Slope from Data Assimilation of Swath Altimetry into a Hydrodynamic Model. Geophys. Res. Lett. 2008, 35, 1. [Google Scholar] [CrossRef]
- Gejadze, I.; Malaterre, P. Discharge Estimation under Uncertainty Using Variational Methods with Application to the Full Saint-Venant Hydraulic Network Model. Int. J. Numer. Methods Fluids 2017, 83, 405–430. [Google Scholar] [CrossRef]
- Brêda, J.P.L.F.; Paiva, R.C.D.; Bravo, J.M.; Passaia, O.A.; Moreira, D.M. Assimilation of Satellite Altimetry Data for Effective River Bathymetry. Water Resour. Res. 2019, 55, 7441–7463. [Google Scholar] [CrossRef]
- Larnier, K.; Monnier, J.; Garambois, P.A.; Verley, J. River Discharge and Bathymetry Estimation from SWOT Altimetry Measurements. Inverse Probl. Sci. Eng. 2021, 29, 759–789. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Legleiter, C.J.; Bovolo, F. River Bathymetry Retrieval from Landsat-9 Images Based on Neural Networks and Comparison to SuperDove and Sentinel-2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5250–5260. [Google Scholar] [CrossRef]
- Liang, C.Y.; Merwade, V. Predicting River Bathymetry in Data Sparse Regions Using a Generative Deep Learning Model. ESS Open Arch. 2024; preprint. [Google Scholar] [CrossRef]
- European Space Agency [ESA]. Copernicus DEM—Global and European Digital Elevation Model (COP-DEM). Available online: https://dataspace.copernicus.eu/explore-data/data-collections/copernicus-contributing-missions/collections-description/COP-DEM (accessed on 12 March 2024).
- Guth, P.L.; Geoffroy, T.M. LiDAR Point Cloud and ICESat-2 Evaluation of 1 Second Global Digital Elevation Models: Copernicus Wins. Trans. GIS 2021, 25, 2245–2261. [Google Scholar] [CrossRef]
- Meadows, M.; Jones, S.; Reinke, K. Vertical Accuracy Assessment of Freely Available Global DEMs (FABDEM, Copernicus DEM, NASADEM, AW3D30 and SRTM) in Flood-Prone Environments. Int. J. Digit. Earth 2024, 17, 2308734. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River Discharge Estimation at Daily Resolution from Satellite Altimetry over an Entire River Basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Altenau, E.H.; Pavelsky, T.M.; Durand, M.T.; Yang, X.; Frasson, R.P.d.M.; Bendezu, L. The Surface Water and Ocean Topography (SWOT) Mission River Database (SWORD): A Global River Network for Satellite Data Products. Water Resour. Res. 2021, 57, e2021WR030054. [Google Scholar] [CrossRef]
- Pekel, J.F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-Resolution Mapping of Global Surface Water and Its Long-Term Changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef]
- Chen, Q.; Mudd, S.M.; Attal, M.; Hancock, S. Extracting an Accurate River Network: Stream Burning Re-Revisited. Remote Sens. Environ. 2024, 312, 114333. [Google Scholar] [CrossRef]
- Lindsay, J.B. The Practice of DEM Stream Burning Revisited. Earth Surf. Process. Landf. 2016, 41, 658–668. [Google Scholar] [CrossRef]
- Gejadze, I.; Malaterre, P.O.; Oubanas, H.; Shutyaev, V. A New Robust Discharge Estimation Method Applied in the Context of SWOT Satellite Data Processing. J. Hydrol. 2022, 610, 127909. [Google Scholar] [CrossRef]
- Scherer, D.; Schwatke, C.; Dettmering, D.; Seitz, F. ICESat-2 River Surface Slope (IRIS): A Global Reach-Scale Water Surface Slope Dataset. Sci. Data 2023, 10, 359. [Google Scholar] [CrossRef] [PubMed]
- Malaterre, P.O.; Baume, J.P.; Dorchies, D. Simulation and Integration of Control for Canals Software (SIC2), for the Design and Verification of Manual or Automatic Controllers for Irrigation Canals. In Proceedings of the USCID Conference on Planning, Operation and Automation of Irrigation Delivery Systems, Phoenix, AZ, USA, 2–5 December 2014; pp. 377–382. [Google Scholar]
- Douglas, D.H.; Peucker, T.K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Cartogr. Int. J. Geogr. Inf. Geovis. 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Allen, G.H.; Pavelsky, T.M. Global Extent of Rivers and Streams. Science 2018, 361, 585–588. [Google Scholar] [CrossRef] [PubMed]
- Frasson, R.P.d.M.; Durand, M.T.; Larnier, K.; Gleason, C.; Andreadis, K.M.; Hagemann, M.; Dudley, R.; Bjerklie, D.; Oubanas, H.; Garambois, P.A.; et al. Exploring the Factors Controlling the Error Characteristics of the Surface Water and Ocean Topography Mission Discharge Estimates. Water Resour. Res. 2021, 57, e2020WR028519. [Google Scholar] [CrossRef]
- Tuozzolo, S.; Langhorst, T.; de Moraes Frasson, R.P.; Pavelsky, T.; Durand, M.; Schobelock, J.J. The Impact of Reach Averaging Manning’s Equation for an in-Situ Dataset of Water Surface Elevation, Width, and Slope. J. Hydrol. 2019, 578, 123866. [Google Scholar] [CrossRef]
- Chow, V. Te Open-Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; ISBN 007085906X/9780070859067. [Google Scholar]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; US Geological Survey: Reston, VA, USA, 1989.
- Rodríguez, E.; Morris, C.S.; Eric Belz, J. A Global Assessment of the SRTM Performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration Jet Propulsion Laboratory [NASA JPL] NASA Shuttle Radar Topography Mission Global 1 Arc Second 2013. Available online: https://lpdaac.usgs.gov/products/nasadem_hgtv001/ (accessed on 12 March 2024).
- Gesch, D.; Oimoen, M.; Danielson, J.; Meyer, D. Validation of the ASTER Global Digital Elevation Model Version 3 over the Conterminous United States. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. ISPRS Arch. Int. Soc. Photogramm. Remote Sens. 2016, 41, 143–148. [Google Scholar]
- NASA; METI; AIST; Japan Spacesystems; U.S./Japan ASTER Science Team ASTER Global Digital Elevation Model V003 2019. Available online: https://lpdaac.usgs.gov/products/astgtmv003/ (accessed on 12 March 2024).
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy Assessment of the Global TanDEM-X Digital Elevation Model with GPS Data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- German Aerospace Center [DLR] TanDEM-X-Digital Elevation Model (DEM)-Global, 90 m 2018. Available online: https://download.geoservice.dlr.de/TDM90/ (accessed on 12 March 2024).
- Takaku, J.; Tadono, T.; Tsutsui, K.; Ichikawa, M. Validation of “AW3D” Global DSM Generated from ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 25–31. [Google Scholar]
- Japan Aerospace Exploration Agency [JAXA] ALOS Global Digital Surface Model “ALOS World 3D-30 m (AW3D30)” 2023, 4.0. Available online: https://www.eorc.jaxa.jp/ALOS/en/dataset/aw3d30/aw3d30_e.htm (accessed on 12 March 2024).
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A High-Accuracy Map of Global Terrain Elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Yamazaki, D.; Ikeshima, D.; Sosa, J.; Bates, P.D.; Allen, G.H.; Pavelsky, T.M. MERIT Hydro: A High-Resolution Global Hydrography Map Based on Latest Topography Dataset. Water Resour. Res. 2019, 55, 5053–5073. [Google Scholar] [CrossRef]
- AIRBUS. Copernicus DEM Copernicus Digital Elevation Model Validation Report; Airbus Defence and Space—Intelligence: Potsdam, Germany, 2020. [Google Scholar]
- National Aeronautics and Space Administration Jet Propulsion Laboratory [NASA JPL] NASADEM Merged DEM Global 1 Arc Second V001 2020. Available online: https://lpdaac.usgs.gov/products/nasadem_hgtv001/ (accessed on 12 March 2024).
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m Global Map of Elevation with Forests and Buildings Removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Neal, J.; Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C. FABDEM V1-2 2023. Available online: https://data.bris.ac.uk/data/dataset/s5hqmjcdj8yo2ibzi9b4ew3sn (accessed on 12 March 2024).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Crippen, R.; Buckley, S.; Agram, P.; Belz, E.; Gurrola, E.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.; Neumann, M.; et al. Nasadem Global Elevation Model: Methods and Progress. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. ISPRS Arch. Int. Soc. Photogramm. Remote Sens. 2016, 41, 125–128. [Google Scholar]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Borla Tridon, D.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and Performance Assessment of the Global TanDEM-X Digital Elevation Model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Abrams, M.; Crippen, R.; Fujisada, H. ASTER Global Digital Elevation Model (GDEM) and ASTER Global Water Body Dataset (ASTWBD). Remote Sens. 2020, 12, 1156. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise Global DEM Generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 71–76. [Google Scholar] [CrossRef]
- Zebker, H.A.; Goldstein, R.M. Topographic Mapping From Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Ferretti, A.; Monti-Guarnieri, A.; Prati, C.; Rocca, F.; Massonnet, D. InSAR Principles: Guidelines for SAR Interferometry Processing and Interpretation; Fletcher, K., Ed.; ESA Publications: Noordwijk, The Netherlands, 2007; ISBN 92-9092-233-8. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodríguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Ackermann, F. Digital Image Correlation: Performance and Potential Application in Photogrammetry. Photogramm. Rec. 1984, 11, 429–439. [Google Scholar] [CrossRef]
- Bobtad, P.V.; Stowe, T. An Evaluation of DEM Accuracy: Elevation, Slope, and Aspect. Photogramm. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- Lang, H.R.; Welch, R. Algorithm Theoretical Basis Document for: ASTER Digital Elevation Models 1999, 1–73. Available online: https://lpdaac.usgs.gov/documents/68/AST_07_ATBD.pdf (accessed on 12 March 2024).
- Abrams, M.; Tsu, H.; Hulley, G.; Iwao, K.; Pieri, D.; Cudahy, T.; Kargel, J. The Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) after Fifteen Years: Review of Global Products. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 292–301. [Google Scholar] [CrossRef]
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Generation of the 30 M-MESH Global Digital Surface Model by Alos Prism. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. ISPRS Arch. Int. Soc. Photogramm. Remote Sens. 2016, 41, 157–162. [Google Scholar]
- Yin, T.; Montesano, P.M.; Cook, B.D.; Chavanon, E.; Neigh, C.S.R.; Shean, D.; Peng, D.; Lauret, N.; Mkaouar, A.; Morton, D.C.; et al. Modeling Forest Canopy Surface Retrievals Using Very High-Resolution Spaceborne Stereogrammetry: (I) Methods and Comparisons with Actual Data. Remote Sens. Environ. 2023, 298, 113825. [Google Scholar] [CrossRef]
- Wessel, B. TanDEM-X Ground Segment—DEM Products Specification Document; German Aerospace Center (DLR): Oberpfaffenhofen, Germany, 2018.
- AIRBUS. Copernicus DEM Copernicus Digital Elevation Model Product Handbook. 2022. Available online: https://dataspace.copernicus.eu/sites/default/files/media/files/2024-06/geo1988-copernicusdem-spe-002_producthandbook_i5.0.pdf (accessed on 12 March 2024).
- AIRBUS. WorldDEMTM Technical Product Specification. 2020. Available online: https://earth.esa.int/eogateway/documents/20142/37627/WorldDEM-Technical-Specification.pdf (accessed on 12 March 2024).
- Slater, J.A.; Garvey, G.; Johnston, C.; Haase, J.; Heady, B.; Kroenung, G.; Little, J. The SRTM Data “Finishing” Process and Products. Photogramm. Eng. Remote Sens. 2006, 72, 237–247. [Google Scholar] [CrossRef]
- Fujisada, H.; Urai, M.; Iwasaki, A. Technical Methodology for ASTER Global Water Body Data Base. Remote Sens. 2018, 10, 1860. [Google Scholar] [CrossRef]
- Buckley, S.M.; Agram, P.S.; Belz, J.E.; Crippen, R.E.; Gurrola, E.M.; Hensley, S.; Kobrick, M.; Lavalle, M.; Martin, J.M.; Neumann, M.; et al. NASADEM; NASA JPL: Pasadena, CA, USA, 2020. [Google Scholar]
- Takaku, J.; Tadono, T.; Tsutsui, K. Generation of High Resolution Global DSM from ALOS PRISM. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. ISPRS Arch. Int. Soc. Photogramm. Remote Sens. 2014, 40, 243–248. [Google Scholar]
- Escudier, P.; Couhert, A.; Mercier, F.; Mallet, A.; Thibaut, P.; Tran, N.; Amarouche, L.; Picard, B.; Carrere, L.; Dibarboure, G.; et al. Satellite Radar Altimetry. In Satellite Altimetry Over Oceans and Land Surfaces; Stammer, D., Cazenave, A., Eds.; CRC Press: Boca Raton, FL, USA, 2017; p. 70. [Google Scholar]
- European Space Agency (ESA). Sentinel-3 SRAL/MWR: Land User Handbook; European Space Agency: Paris, France, 2024.
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of River Level Variations with Satellite Altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Birkett, C.M. Contribution of the TOPEX NASA Radar Altimeter to the Global Monitoring of Large Rivers and Wetlands. Water Resour. Res. 1998, 34, 1223–1239. [Google Scholar] [CrossRef]
- Frappart, F.; Calmant, S.; Cauhopé, M.; Seyler, F.; Seyler, F.; Cazenave, A. Preliminary Results of ENVISAT RA-2-Derived Water Levels Validation over the Amazon Basin. Remote Sens. Environ. 2006, 100, 252–264. [Google Scholar] [CrossRef]
- Le Gac, S.; Boy, F.; Blumstein, D.; Lasson, L.; Picot, N. Benefits of the Open-Loop Tracking Command (OLTC): Extending Conventional Nadir Altimetry to Inland Waters Monitoring. Adv. Space Res. 2021, 68, 843–852. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 Mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Donlon, C.J.; Cullen, R.; Giulicchi, L.; Vuilleumier, P.; Francis, C.R.; Kuschnerus, M.; Simpson, W.; Bouridah, A.; Caleno, M.; Bertoni, R.; et al. The Copernicus Sentinel-6 Mission: Enhanced Continuity of Satellite Sea Level Measurements from Space. Remote Sens. Environ. 2021, 258, 112395. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An Innovative Approach for Estimating Water Level Time Series over Inland Waters Using Multi-Mission Satellite Altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Seitz, F. Volume Variations of Small Inland Water Bodies from a Combination of Satellite Altimetry and Optical Imagery. Remote Sens. 2020, 12, 1606. [Google Scholar] [CrossRef]
- Birkett, C.M.; Beckley, B. Investigating the Performance of the Jason-2/OSTM Radar Altimeter over Lakes and Reservoirs. Mar. Geod. 2010, 33, 204–238. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Arsen, A.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Berge-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A Lake Database to Monitor in the Near Real Time Water Level and Storage Variations from Remote Sensing Data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Tourian, M.J.; Elmi, O.; Shafaghi, Y.; Behnia, S.; Saemian, P.; Schlesinger, R.; Sneeuw, N. HydroSat: Geometric Quantities of the Global Water Cycle from Geodetic Satellites. Earth Syst. Sci. Data 2022, 14, 2463–2486. [Google Scholar] [CrossRef]
- Desjonquères, J.D.; Carayon, G.; Steunou, N.; Lambin, J. Poseidon-3 Radar Altimeter: New Modes and In-Flight Performances. Mar. Geod. 2010, 33, 53–79. [Google Scholar] [CrossRef]
- CNES; EUMETSAT; JPL. NOAA/NESDIS Jason-3 Products Handbook. 2021. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_j3.pdf (accessed on 12 March 2024).
- Syndicat Mixte d’Études et d’Aménagement de la Garonne [SMEAG] Le Bassin Versant de la Garonne. Available online: https://www.smeag.fr/le-bassin-versant-de-la-garonne.html (accessed on 30 October 2024).
- Caballero, Y.; Voirin-Morel, S.; Habets, F.; Noilhan, J.; LeMoigne, P.; Lehenaff, A.; Boone, A. Hydrological Sensitivity of the Adour-Garonne River Basin to Climate Change. Water Resour. Res. 2007, 43, W07448. [Google Scholar] [CrossRef]
- French National Institute of Geographic and Forest Information [IGN]. MNS Correl Version 1.0: Descriptif de contenu; French National Institute of Geographic and Forest Information: Paris, France, 2023. [Google Scholar]
- Zanchettin, D.; Traverso, P.; Tomasino, M. Po River Discharges: A Preliminary Analysis of a 200-Year Time Series. Clim. Change 2008, 89, 411–433. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for Changing Patterns in River Discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef]
- Po River Basin Authority [AdbPo]. Carta del Po e DTM. Available online: https://www.adbpo.it/carta-del-po-e-dtm/ (accessed on 1 February 2024).
- Garrote, J. Free Global DEMs and Flood Modelling—A Comparison Analysis for the January 2015 Flooding Event in Mocuba City (Mozambique). Water 2022, 14, 176. [Google Scholar] [CrossRef]
- Alsdorf, D.E.; Rodríguez, E.; Lettenmaier, D.P. Measuring Surface Water from Space. Rev. Geophys. 2007, 45, RG2002. [Google Scholar] [CrossRef]
- Oubanas, H.; Durand, M.; Gleason, C.; Malaterre, P.; Larnier, K. The Operational Framework of the Surface Water and Ocean Topography River Discharge. In 30 Years of Progress in Radar Altimetry Symposium; ESA: Montpellier, France, 2024. [Google Scholar]
- Egido, A.; Smith, W.H.F. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Daguzé, J.-A.; Calassou, G.; Taburet, N.; Boy, F.; Yanez, C. Exploiting the Sentinel-6MF Fully Focused SAR Waveforms over Inland Waters: Toward a New Processing Prototype for Rivers. In 30 Years of Progress in Radar Altimetry Symposium; ESA: Montpellier, France, 2024. [Google Scholar]
- Kossieris, S.; Tsiakos, V.; Tsimiklis, G.; Amditis, A. Evaluation of Sentinel-3 and Sentinel-6 Derived Water Levels Using in Situ Data Over Narrow Rivers. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: New York, NY, USA, 2024; pp. 5036–5039. [Google Scholar]
- Tourian, M.J.; Tarpanelli, A.; Elmi, O.; Qin, T.; Brocca, L.; Moramarco, T.; Sneeuw, N. Spatiotemporal Densification of River Water Level Time Series by Multimission Satellite Altimetry. Water Resour. Res. 2016, 52, 1140–1159. [Google Scholar] [CrossRef]
- Nielsen, K.; Zakharova, E.; Tarpanelli, A.; Andersen, O.B.; Benveniste, J. River Levels from Multi Mission Altimetry, a Statistical Approach. Remote Sens. Environ. 2022, 270, 112876. [Google Scholar] [CrossRef]
- Belloni, R.; Camici, S.; Tarpanelli, A. Towards the Continuous Monitoring of the Extreme Events through Satellite Radar Altimetry Observations. J. Hydrol. 2021, 603, 126870. [Google Scholar] [CrossRef]
- Blumstein, D.; Biancamaria, S.; Guérin, A.; Maisongrande, P. A Potential Constellation of Small Altimetry Satellites Dedicated to Continental Surface Waters (SMASH Mission); AGU Fall Meeting Abstracts: Chicago, IL, USA, 2019; p. H43N-2257. [Google Scholar]
- Grimaldi, S.; Li, Y.; Walker, J.P.; Pauwels, V.R.N. Effective Representation of River Geometry in Hydraulic Flood Forecast Models. Water Resour. Res. 2018, 54, 1031–1057. [Google Scholar] [CrossRef]
- Dey, S.; Saksena, S.; Merwade, V. Assessing the Effect of Different Bathymetric Models on Hydraulic Simulation of Rivers in Data Sparse Regions. J. Hydrol. 2019, 575, 838–851. [Google Scholar] [CrossRef]


| DEM | Version | Features | Pixel Size | Main Source | Acquisition Period | Accuracy |
Dataset Reference |
|---|---|---|---|---|---|---|---|
| SRTM | 3.0 | DSM | 1″ | C band SAR | February 2000 (11 days) | <9 m (LE90) [41] | [42] |
| ASTER | 3.0 | DSM | 1″ | Stereo NIR imagery | 2000–2013 | 8.5 m (RMSE) [43] | [44] |
| TanDEM-X | 1.0 | DSM | 3″ | X band SAR | 2011–2015 | <10 m (CE90) [45] | [46] |
| AW3D30 | 4.0 | DSM | 1″ | Stereo PAN imagery | 2006–2011 | <6 m (LE90) [47] | [48] |
| MERIT | 1.0.3 | DSM * | 3″ | Modified SRTM | February 2000 (11 days) | <12 m (LE90) [49] | [49] |
| MERIT-Hydro | 1.0.1 | DSM * | 3″ | Modified SRTM | February 2000 (11 days) | - | [50] |
| Copernicus | 2022_1 | DSM | 1″ | Modified Tandem-X | 2011–2015 | <3 m (LE90) [51] | [24] |
| NASADEM | 1.0 | DSM | 1″ | Reprocessed C band SAR | February 2000 (11 days) | - | [52] |
| FABDEM | 1.2 | DTM | 1″ | Modified Tandem-X | 2011–2015 | <9 m (90%) [53] | [54] |
| River | DEM | Common Depth with Reference (%) | Relative Errors in Area for Common Part (%) | ||||
|---|---|---|---|---|---|---|---|
| 25% | Median | 75% | 25% | Median | 75% | ||
| Garonne | AW3D30 | 24.79 | 38.80 | 54.16 | −61.73 | −42.18 | −28.38 |
| ASTER | 23.85 | 31.50 | 44.68 | −37.66 | −16.74 | −1.49 | |
| SRTM | 28.80 | 35.03 | 45.58 | −40.39 | −28.95 | −15.62 | |
| NASADEM | 44.74 | 54.47 | 62.99 | −29.90 | −17.45 | −7.26 | |
| MERIT | 16.96 | 23.39 | 32.26 | −48.27 | −26.08 | −15.52 | |
| MERIT-HYDRO | 22.53 | 28.98 | 37.49 | −30.43 | −16.95 | −7.79 | |
| TANDEM-X | 26.82 | 40.64 | 58.80 | −56.66 | −34.39 | −20.53 | |
| COPERNICUS | 81.27 | 91.08 | 100.00 | −4.71 | 3.40 | 9.64 | |
| FABDEM | 80.71 | 90.47 | 100.00 | −7.55 | −0.25 | 7.73 | |
| Po | AW3D30 | 35.53 | 46.03 | 57.79 | −33.41 | −21.31 | −13.73 |
| ASTER | 48.28 | 57.26 | 65.35 | −16.64 | −6.21 | −0.23 | |
| SRTM | 46.43 | 54.45 | 62.81 | −11.72 | −5.07 | 0.81 | |
| NASADEM | 43.78 | 54.03 | 61.09 | −15.75 | −7.23 | −1.75 | |
| MERIT | 28.40 | 35.55 | 41.45 | −37.51 | −23.28 | −14.22 | |
| MERIT-HYDRO | 33.97 | 40.42 | 46.89 | −32.56 | −21.28 | −12.18 | |
| TANDEM-X | 34.77 | 51.23 | 75.02 | −60.17 | −41.04 | −25.31 | |
| COPERNICUS | 50.26 | 58.92 | 66.32 | −8.82 | −3.53 | 0.10 | |
| FABDEM | 48.00 | 56.51 | 64.52 | −9.21 | −4.18 | 0.14 | |
| River | Flow | Date Distribution | RRMSE | PBIAS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| In Situ | All | In Situ | J-2 | J-3 | S-3 | S-6 | All | In Situ | J-2 | J-3 | S-3 | S-6 | All | ||
| Garonne | Min | 4.98% | 6.15% | 55.45% | nd = 0 | 138.51% | nd = 4 | 242.42% | 228.45% | −55.44% | nd = 0 | 120.25% | nd = 4 | 232.14% | 213.40% |
| Low | 19.99% | 23.26% | 38.89% | nd = 0 | 131.61% | 81.41% | 126.83% | 181.08% | −38.82% | nd = 0 | 121.35% | 39.79% | 119.36% | 145.96% | |
| Mean | 50.02% | 53.49% | 10.96% | nd = 0 | 64.64% | 35.87% | 74.86% | 106.22% | −10.68% | nd = 0 | 57.70% | −30.29% | 70.24% | 48.51% | |
| High | 19.99% | 16.45% | 5.21% | nd = 0 | 33.43% | 28.39% | 39.69% | 40.14% | −5.05% | nd = 0 | 25.96% | −20.65% | 36.22% | 27.53% | |
| Max | 5.01% | 0.66% | 5.62% | nd = 0 | nd = 1 | nd = 2 | nd = 1 | nd = 4 | −2.13% | nd = 0 | nd = 1 | nd = 2 | nd = 1 | nd = 4 | |
| All | 100.00% | 100.00% | 9.97% | nd = 0 | 58.83% | 49.51% | 71.66% | 60.38% | −8.97% | nd = 0 | 42.12% | −12.99% | 66.04% | 38.09% | |
| Po | Min | 5.02% | 5.11% | 21.09% | nd = 0 | nd = 0 | 44.69% | nd = 5 | 241.29% | −20.80% | nd = 0 | nd = 0 | −0.62% | nd = 5 | 143.75% |
| Low | 19.98% | 22.38% | 11.73% | nd = 3 | 41.68% | 36.42% | nd = 7 | 34.54% | 4.62% | nd = 3 | 3.29% | 14.43% | nd = 7 | 8.14% | |
| Mean | 50.00% | 48.42% | 6.61% | nd = 5 | 19.29% | 7.52% | nd = 6 | 14.26% | 6.16% | nd = 5 | 10.95% | −3.49% | nd = 6 | 2.36% | |
| High | 19.98% | 20.68% | 3.61% | nd = 6 | 9.86% | 10.80% | nd = 0 | 5.17% | 1.62% | nd = 6 | 0.65% | −5.85% | nd = 0 | −0.80% | |
| Max | 5.02% | 3.41% | 4.41% | nd = 1 | nd = 5 | nd = 8 | nd = 0 | 16.12% | 2.02% | nd = 1 | nd = 5 | nd = 8 | nd = 0 | −6.58% | |
| All | 100.00% | 100.00% | 6.57% | 11.03% | 29.24% | 21.67% | 124.24% | 26.23% | 3.64% | 2.93% | 6.97% | −2.35% | 84.10% | 3.23% | |
| River | Flow | Method | ALOS | ASTER | SRTM | NASADEM | MERIT | MERIT Hydro | Tandem-X | Copernicus | FABDEM |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Garonne | low | breakpoint | 293.07% | 469.26% | 500.04% | 515.76% | 489.25% | 460.48% | 516.10% | 495.03% | 509.12% |
| continuity | 564.43% | 550.87% | 610.58% | 640.18% | 603.97% | 580.42% | 639.74% | 569.67% | 556.99% | ||
| bp-cont | 362.35% | 501.42% | 545.02% | 530.21% | 519.12% | 516.38% | 543.06% | 517.87% | 544.12% | ||
| mean | breakpoint | 82.62% | 177.51% | 99.65% | 152.37% | 217.00% | 211.02% | 194.21% | 140.04% | 123.12% | |
| continuity | 63.75% | 186.48% | 120.73% | 119.35% | 154.93% | 171.06% | 140.19% | 143.52% | 140.83% | ||
| bp-cont | 110.34% | 178.98% | 124.75% | 143.98% | 215.96% | 226.94% | 202.44% | 151.86% | 140.93% | ||
| high | breakpoint | 32.44% | 61.13% | 57.78% | 51.66% | 87.01% | 89.00% | 55.02% | 45.58% | 34.53% | |
| continuity | −15.32% | 8.55% | 23.45% | 14.52% | 27.95% | 44.87% | 18.00% | 34.81% | 35.76% | ||
| bp-cont | 43.34% | 74.87% | 37.39% | 51.77% | 89.24% | 97.14% | 68.14% | 51.35% | 45.45% | ||
| Po | low | breakpoint | −14.17% | −17.19% | −19.01% | −19.45% | −17.68% | −18.83% | −16.73% | −15.85% | −14.12% |
| continuity | −19.54% | −17.96% | −21.21% | −16.88% | −17.37% | −14.94% | −16.31% | −12.39% | −12.28% | ||
| bp-cont | −17.25% | −17.63% | −16.90% | −16.05% | −13.10% | −14.33% | −15.49% | −17.45% | −16.83% | ||
| mean | breakpoint | −0.93% | −8.83% | −8.97% | −9.75% | −7.31% | −10.00% | −7.70% | −5.59% | −3.38% | |
| continuity | −20.90% | −6.39% | −15.38% | −10.40% | −16.74% | −12.82% | −21.91% | −10.08% | −8.61% | ||
| bp-cont | −1.67% | −6.56% | −6.09% | −6.68% | −0.37% | −1.79% | −5.60% | −3.78% | −3.93% | ||
| high | breakpoint | 1.56% | −6.77% | −11.34% | −9.81% | −3.88% | −7.11% | −9.14% | −1.24% | −1.08% | |
| continuity | −36.25% | −5.69% | −16.86% | −11.78% | −20.01% | −24.27% | −34.84% | −9.98% | −11.02% | ||
| bp-cont | 8.20% | −3.75% | 0.28% | 0.65% | 5.33% | 4.13% | −0.37% | 0.43% | 2.81% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezende, I.; Fatras, C.; Oubanas, H.; Gejadze, I.; Malaterre, P.-O.; Peña-Luque, S.; Domeneghetti, A. Reconstruction of Effective Cross-Sections from DEMs and Water Surface Elevation. Remote Sens. 2025, 17, 1020. https://doi.org/10.3390/rs17061020
Rezende I, Fatras C, Oubanas H, Gejadze I, Malaterre P-O, Peña-Luque S, Domeneghetti A. Reconstruction of Effective Cross-Sections from DEMs and Water Surface Elevation. Remote Sensing. 2025; 17(6):1020. https://doi.org/10.3390/rs17061020
Chicago/Turabian StyleRezende, Isadora, Christophe Fatras, Hind Oubanas, Igor Gejadze, Pierre-Olivier Malaterre, Santiago Peña-Luque, and Alessio Domeneghetti. 2025. "Reconstruction of Effective Cross-Sections from DEMs and Water Surface Elevation" Remote Sensing 17, no. 6: 1020. https://doi.org/10.3390/rs17061020
APA StyleRezende, I., Fatras, C., Oubanas, H., Gejadze, I., Malaterre, P.-O., Peña-Luque, S., & Domeneghetti, A. (2025). Reconstruction of Effective Cross-Sections from DEMs and Water Surface Elevation. Remote Sensing, 17(6), 1020. https://doi.org/10.3390/rs17061020









