An Effective Quantification of Methane Point-Source Emissions with the Multi-Level Matched Filter from Hyperspectral Imagery
Abstract
1. Introduction
2. Materials and Methods
2.1. Controlled Release Experiment
- Gaofen-5B: One scene acquired on 15 November 2022;
- Ziyuan-1F: One scene acquired on 26 October 2022;
- EnMAP: One scene acquired on 7 November 2022.
2.2. Hyperspectral Instruments
2.3. Method
2.3.1. Multi-Level Matched Filter
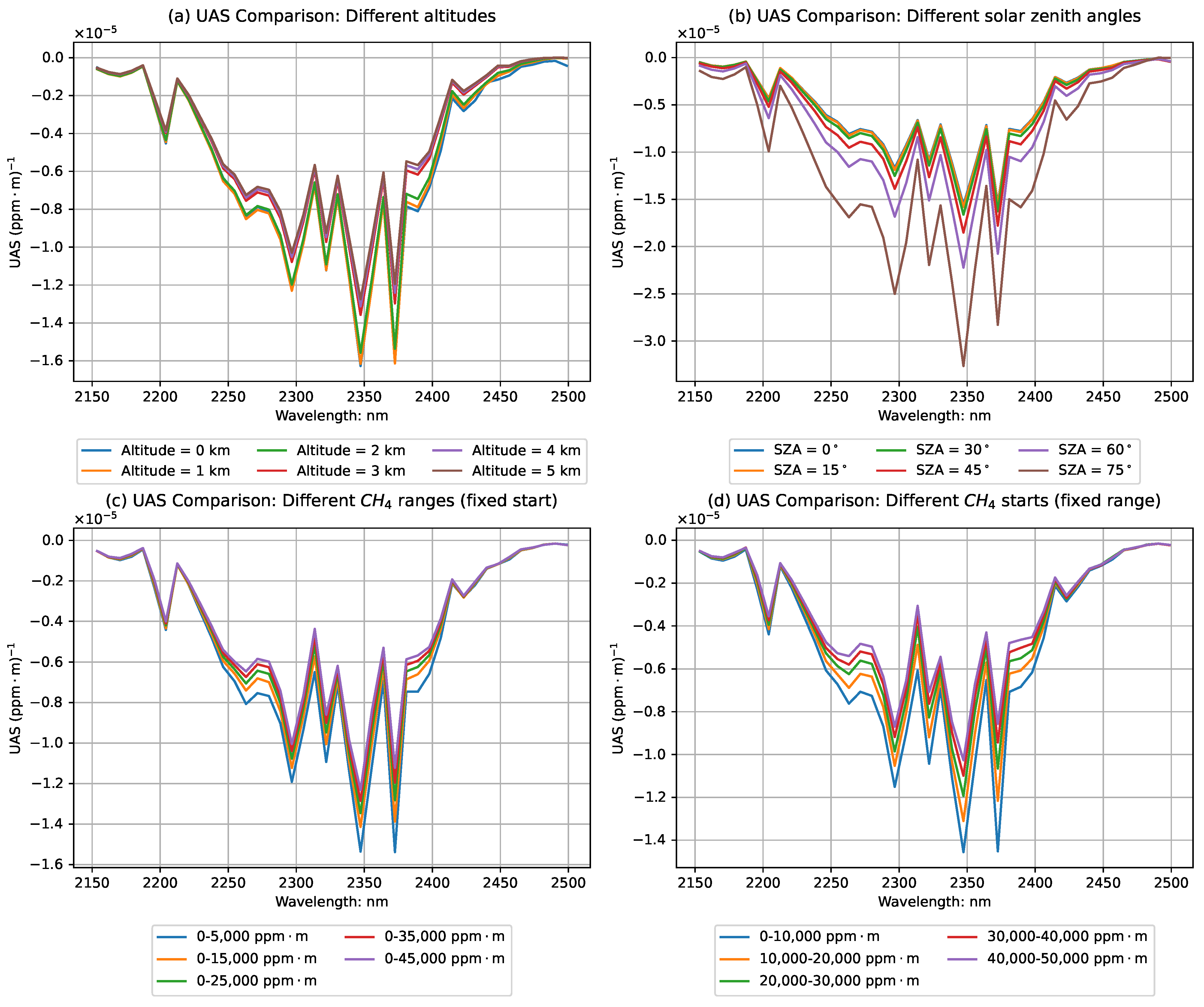
2.3.2. Unit Absorption Spectrum Construction Based on LUT
2.3.3. Detection and Quantification of Methane Plumes
3. Results
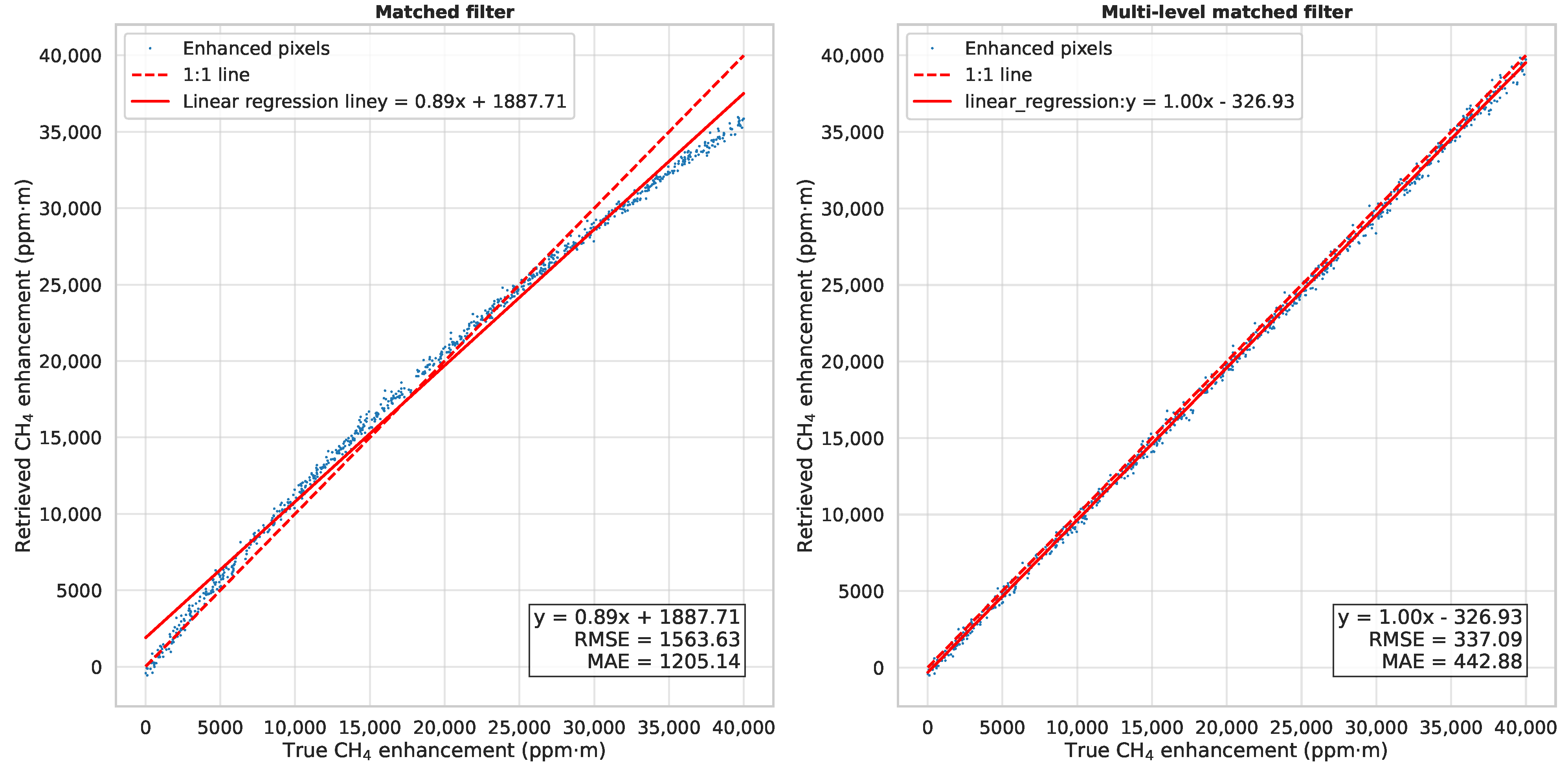
3.1. Matched Filter Variants Comparison
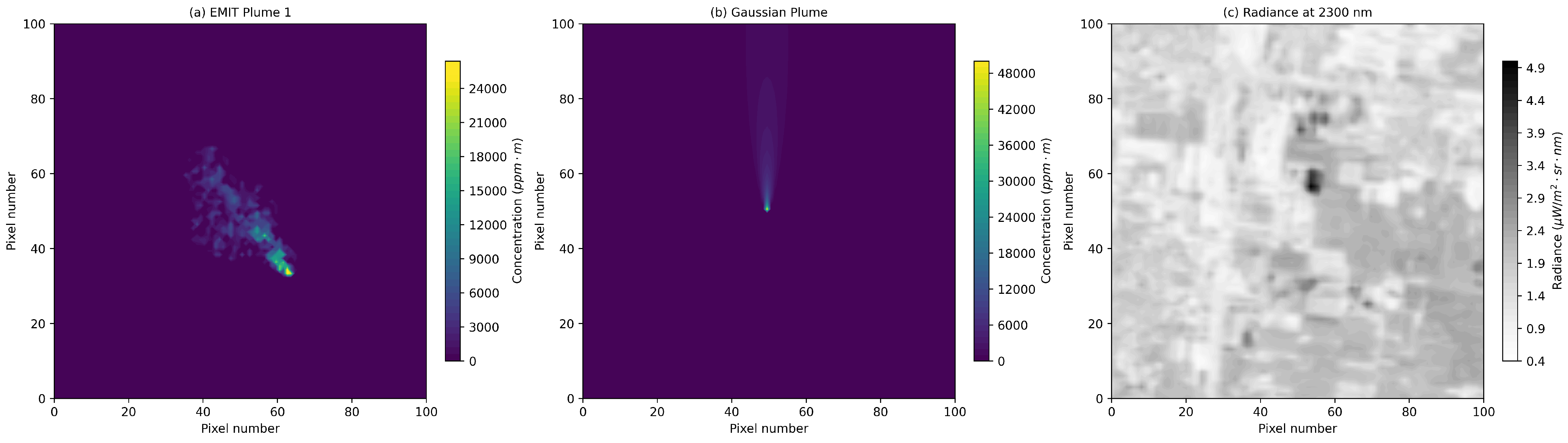
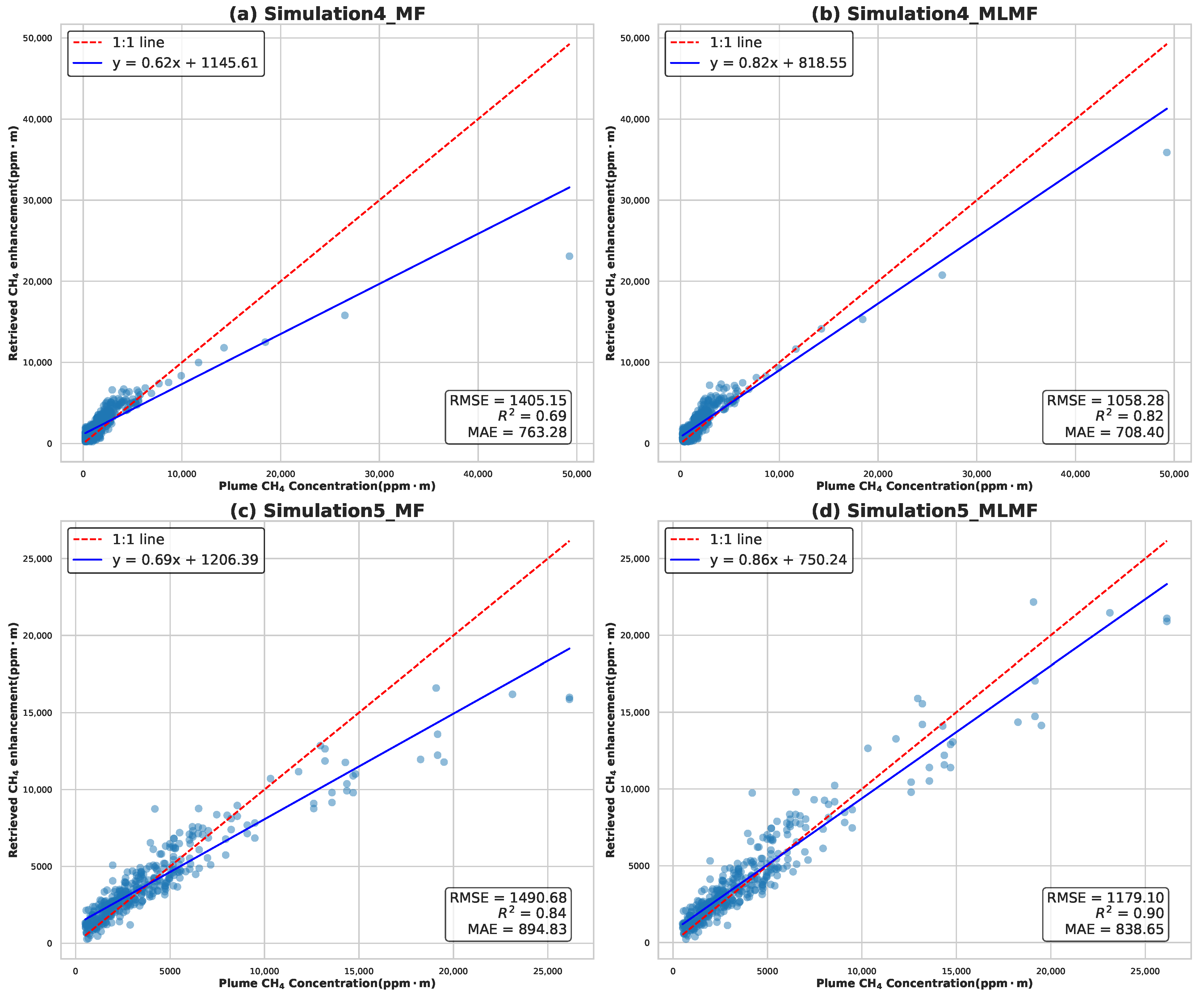
3.2. Algorithm Validation: Simulated Satellite Images with Overlaid Methane Plumes
- Gaussian plume simulation: The MLMF achieves a correlation coefficient () of 0.98, a notable improvement compared to the MF (). Furthermore, the RMSE is reduced from 746 (ppm·m) in the MF to 345 in the MLMF, representing a 53.7% reduction. Similarly, the MAE decreases from 355.27 to 279.88, highlighting the higher accuracy of the MLMF.
- EMIT plume product simulation: The MLMF achieves an even higher correlation coefficient of 0.99, demonstrating excellent fitting performance. The RMSE is reduced from 678 in the MF to 354 in the MLMF, a reduction of 47.8%. The MAE also decreases significantly, from 396.20 to 286.40, further validating the robustness of the MLMF in concentration enhancement retrieval.
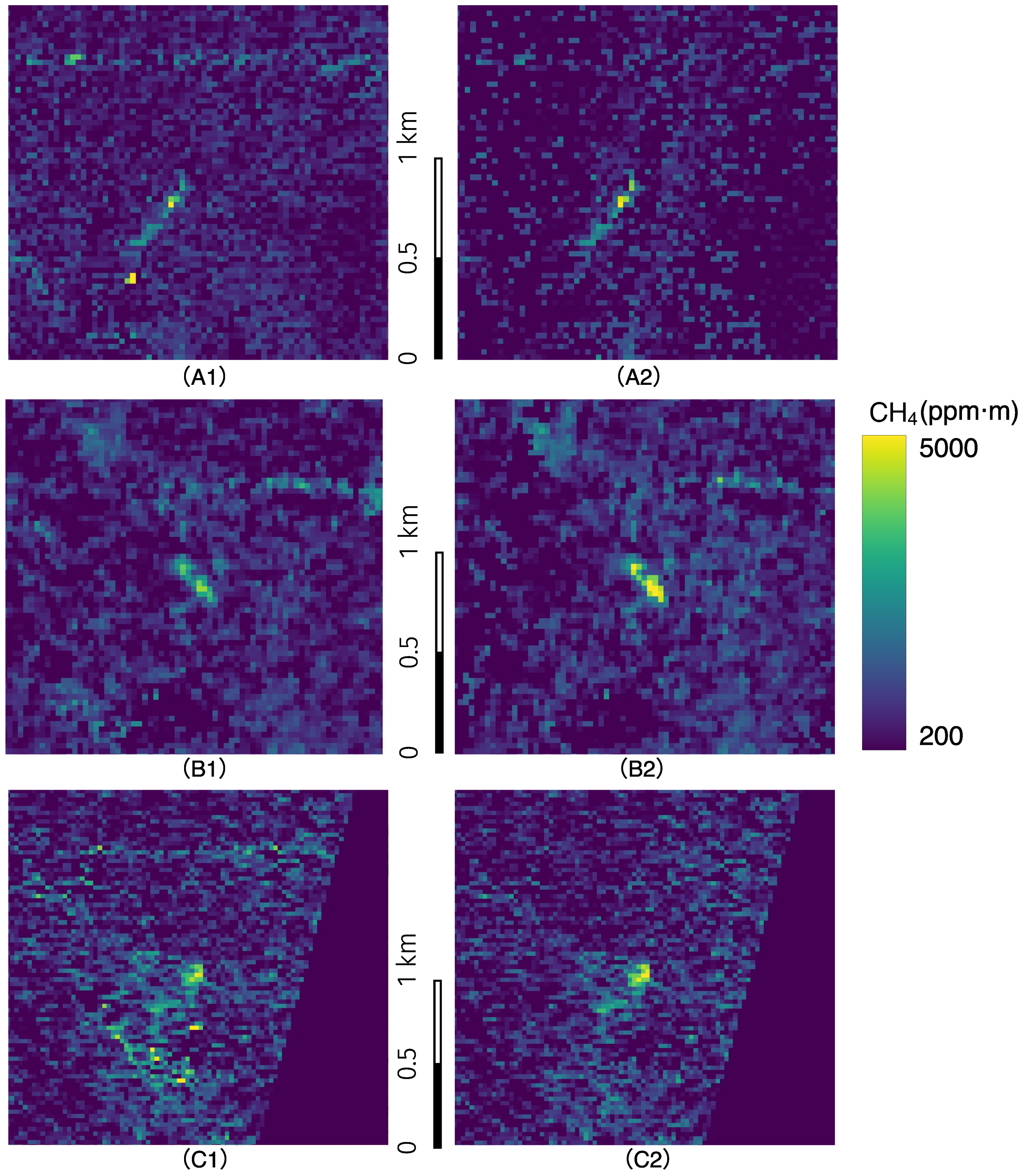
3.3. Algorithm Validation: Controlled Release Experiment
4. Discussion
- Spectral Residual Fitting: The first stage involved spectral residual fitting without considering noise or sensor spectral resolution to evaluate the MLMF’s performance. The results demonstrate that the MLMF significantly mitigates the underestimation issue for high methane concentration enhancements that arise from the linear assumptions of traditional MF algorithms. Relative errors were reduced from up to −30% to within ±5% at high concentrations, and the regression slope improved from 0.89 to 1.00, indicating the MLMF’s ability to better approximate the nonlinear relationship between methane concentration and absorption.
- Simulated Data Tests: The second stage tested the algorithm using simulated data, including randomly enhanced methane concentration pixels, synthetic Gaussian methane plumes, and EMIT plume products. The MLMF achieved better retrieval accuracy across a wide range of concentration enhancements (0–40,000 ppm·m), with RMSE reduced from 1563.63 ppm·m to 337.09 ppm·m and MAE decreased from 1205.14 ppm·m to 442.88 ppm·m compared to the MF. In plume-based simulations, the MLMF outperformed the MF, particularly in high-concentration regions, improving from 0.91 to 0.98 for Gaussian plumes and achieving an of 0.99 for EMIT plume simulations, with RMSE reductions of 53.7
- Controlled Release Experiment: The third stage involved validating the MLMF using satellite data from controlled release experiments along with ground-truth emission rate measurements. The results indicated that the MLMF provided a higher contrast between the plume and the background, resulting in more accurate methane concentration retrievals and fewer artifacts compared to the MF. These improvements led to better plume quantification and enhanced the reliability of methane emission estimates, with emission rate accuracy improving significantly. The R² value increased from 0.71 to 0.96, and RMSE reduced from 92.32 kg/h to 16.10 kg/h.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AHSI | Advanced HyperSpectral Imager |
| FWHM | Full Width at Half Maximum |
| IME | Integrated Mass Enhancement |
| LUT | Look-Up Table |
| MF | Matched Filter |
| MLMF | Multi-Level Matched Filter |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| SNR | Signal-to-Noise Ratio |
| SWIR | ShortWave InfraRed |
| SZA | Solar Zenith Angle |
References
- Xie, G.Z.; Zhang, L.P.; Li, C.Y.; Sun, W.D. Accelerated Methane Emission from Permafrost Regions since the 20th Century. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2023, 195, 103981. [Google Scholar] [CrossRef]
- Shen, L.; Jacob, D.J.; Gautam, R.; Omara, M.; Scarpelli, T.R.; Lorente, A.; Zavala-Araiza, D.; Lu, X.; Chen, Z.; Lin, J. National Quantifications of Methane Emissions from Fuel Exploitation Using High Resolution Inversions of Satellite Observations. Nat. Commun. 2023, 14, 4948. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Jacob, D.J.; Lu, X.; Maasakkers, J.D.; Scarpelli, T.R.; Sheng, J.X.; Shen, L.; Qu, Z.; Sulprizio, M.P.; Chang, J.; et al. Attribution of the Accelerating Increase in Atmospheric Methane during 2010–2018 by Inverse Analysis of GOSAT Observations. Atmos. Chem. Phys. 2021, 21, 3643–3666. [Google Scholar] [CrossRef]
- Prather, M.J.; Holmes, C.D.; Hsu, J. Reactive Greenhouse Gas Scenarios: Systematic Exploration of Uncertainties and the Role of Atmospheric Chemistry. Geophys. Res. Lett. 2012, 39, 2012GL051440. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Manning, M.R.; Dlugokencky, E.J.; Michel, S.E.; Lan, X.; Röckmann, T.; Denier Van Der Gon, H.A.C.; Schmitt, J.; Palmer, P.I.; Dyonisius, M.N.; et al. Atmospheric Methane: Comparison Between Methane’s Record in 2006–2022 and During Glacial Terminations. Glob. Biogeochem. Cycles 2023, 37, e2023GB007875. [Google Scholar] [CrossRef]
- Nisbet, E.G.; Fisher, R.E.; Lowry, D.; France, J.L.; Allen, G.; Bakkaloglu, S.; Broderick, T.J.; Cain, M.; Coleman, M.; Fernandez, J.; et al. Methane Mitigation: Methods to Reduce Emissions, on the Path to the Paris Agreement. Rev. Geophys. 2020, 58, e2019RG000675. [Google Scholar] [CrossRef]
- Isaksen, I.; Berntsen, T.; Dalsøren, S.; Eleftheratos, K.; Orsolini, Y.; Rognerud, B.; Stordal, F.; Søvde, O.; Zerefos, C.; Holmes, C. Atmospheric Ozone and Methane in a Changing Climate. Atmosphere 2014, 5, 518–535. [Google Scholar] [CrossRef]
- Kirschke, S.; Bousquet, P.; Ciais, P.; Saunois, M.; Canadell, J.G.; Dlugokencky, E.J.; Bergamaschi, P.; Bergmann, D.; Blake, D.R.; Bruhwiler, L.; et al. Three Decades of Global Methane Sources and Sinks. Nat. Geosci. 2013, 6, 813–823. [Google Scholar] [CrossRef]
- Brandt, A.R.; Heath, G.A.; Kort, E.A.; O’Sullivan, F.; Petron, G.; Jordaan, S.M.; Tans, P.; Wilcox, J.; Gopstein, A.M.; Arent, D.; et al. Methane Leaks from North American Natural Gas Systems. Science 2014, 343, 733–735. [Google Scholar] [CrossRef]
- Brandt, A.R.; Heath, G.A.; Cooley, D. Methane Leaks from Natural Gas Systems Follow Extreme Distributions. Environ. Sci. Technol. 2016, 50, 12512–12520. [Google Scholar] [CrossRef]
- Frankenberg, C.; Thorpe, A.K.; Thompson, D.R.; Hulley, G.; Kort, E.A.; Vance, N.; Borchardt, J.; Krings, T.; Gerilowski, K.; Sweeney, C.; et al. Airborne Methane Remote Measurements Reveal Heavy-Tail Flux Distribution in Four Corners Region. Proc. Natl. Acad. Sci. USA 2016, 113, 9734–9739. [Google Scholar] [CrossRef] [PubMed]
- Barré, J.; Aben, I.; Agustí-Panareda, A.; Balsamo, G.; Bousserez, N.; Dueben, P.; Engelen, R.; Inness, A.; Lorente, A.; McNorton, J.; et al. Systematic Detection of Local CH4 Anomalies by Combining Satellite Measurements with High-Resolution Forecasts. Atmos. Chem. Phys. 2021, 21, 5117–5136. [Google Scholar] [CrossRef]
- Varon, D.J.; Jervis, D.; McKeever, J.; Spence, I.; Gains, D.; Jacob, D.J. High-Frequency Monitoring of Anomalous Methane Point Sources with Multispectral Sentinel-2 Satellite Observations. Atmos. Meas. Tech. Discuss. 2020, 14, 2771–2785. [Google Scholar] [CrossRef]
- Jacob, D.J.; Turner, A.J.; Maasakkers, J.D.; Sheng, J.; Sun, K.; Liu, X.; Chance, K.; Aben, I.; McKeever, J.; Frankenberg, C. Satellite Observations of Atmospheric Methane and Their Value for Quantifying Methane Emissions. Atmos. Chem. Phys. 2016, 16, 14371–14396. [Google Scholar] [CrossRef]
- Duren, R.M.; Thorpe, A.K.; Foster, K.T.; Rafiq, T.; Hopkins, F.M.; Yadav, V.; Bue, B.D.; Thompson, D.R.; Conley, S.; Colombi, N.K.; et al. California’s Methane Super-Emitters. Nature 2019, 575, 180–184. [Google Scholar] [CrossRef]
- Jervis, D.; McKeever, J.; Durak, B.O.A.; Sloan, J.J.; Gains, D.; Varon, D.J.; Ramier, A.; Strupler, M.; Tarrant, E. The GHGSat-D Imaging Spectrometer. Atmos. Meas. Tech. 2021, 14, 2127–2140. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Duren, R.M.; Thorpe, A.K.; Pandey, S.; Maasakkers, J.D.; Aben, I.; Jervis, D.; Varon, D.J.; Jacob, D.J.; Randles, C.A.; et al. Multisatellite Imaging of a Gas Well Blowout Enables Quantification of Total Methane Emissions. Geophys. Res. Lett. 2021, 48, e2020GL090864. [Google Scholar] [CrossRef]
- Lyon, D.R.; Hmiel, B.; Gautam, R.; Omara, M.; Roberts, K.A.; Barkley, Z.R.; Davis, K.J.; Miles, N.L.; Monteiro, V.C.; Richardson, S.J.; et al. Concurrent Variation in Oil and Gas Methane Emissions and Oil Price during the COVID-19 Pandemic. Atmos. Chem. Phys. 2021, 21, 6605–6626. [Google Scholar] [CrossRef]
- Zhang, Y.; Gautam, R.; Pandey, S.; Omara, M.; Maasakkers, J.D.; Sadavarte, P.; Lyon, D.; Nesser, H.; Sulprizio, M.P.; Varon, D.J.; et al. Quantifying Methane Emissions from the Largest Oil-Producing Basin in the United States from Space. Sci. Adv. 2020, 6, eaaz5120. [Google Scholar] [CrossRef]
- Varon, D.J.; Jacob, D.J.; Jervis, D.; McKeever, J. Quantifying Time-Averaged Methane Emissions from Individual Coal Mine Vents with GHGSat-D Satellite Observations. Environ. Sci. Technol. 2020, 54, 10246–10253. [Google Scholar] [CrossRef]
- Marjani, M.; Mohammadimanesh, F.; Varon, D.J.; Radman, A.; Mahdianpari, M. PRISMethaNet: A Novel Deep Learning Model for Landfill Methane Detection Using PRISMA Satellite Data. ISPRS J. Photogramm. Remote Sens. 2024, 218, 802–818. [Google Scholar] [CrossRef]
- Frankenberg, C.; Platt, U.; Wagner, T. Iterative Maximum a Posteriori (IMAP)-DOAS for Retrieval of Strongly Absorbing Trace Gases: Model Studies for CH4 and CO2 Retrieval from near Infrared Spectra of SCIAMACHY Onboard. Atmos. Chem. Phys. 2005, 5, 9–12. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; Aan De Brugh, J.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D.; et al. Methane Retrieved from TROPOMI: Improvement of the Data Product and Validation of the First 2 Years of Measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Thorpe, A.K.; Frankenberg, C.; Thompson, D.R.; Duren, R.M.; Aubrey, A.D.; Bue, B.D.; Green, R.O.; Gerilowski, K.; Krings, T.; Borchardt, J.; et al. Airborne DOAS Retrievals of Methane, Carbon Dioxide, and Water Vapor Concentrations at High Spatial Resolution: Application to AVIRIS-NG. Atmos. Meas. Tech. 2017, 10, 3833–3850. [Google Scholar] [CrossRef]
- Thompson, D.R.; Leifer, I.; Bovensmann, H.; Eastwood, M.; Fladeland, M.; Frankenberg, C.; Gerilowski, K.; Green, R.O.; Kratwurst, S.; Krings, T.; et al. Real-Time Remote Detection and Measurement for Airborne Imaging Spectroscopy: A Case Study with Methane. Atmos. Meas. Tech. 2015, 8, 4383–4397. [Google Scholar] [CrossRef]
- Foote, M.D.; Dennison, P.E.; Thorpe, A.K.; Thompson, D.R.; Jongaramrungruang, S.; Frankenberg, C.; Joshi, S.C. Fast and Accurate Retrieval of Methane Concentration from Imaging Spectrometer Data Using Sparsity Prior. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6480–6492. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Duren, R.M.; Thorpe, A.K.; Olson-Duvall, W.; Heckler, J.; Chapman, J.W.; Eastwood, M.L.; Helmlinger, M.C.; Green, R.O.; Asner, G.P.; et al. Intermittency of Large Methane Emitters in the Permian Basin. Environ. Sci. Technol. Lett. 2021, 8, 567–573. [Google Scholar] [CrossRef]
- Thompson, D.R.; Thorpe, A.K.; Frankenberg, C.; Green, R.O.; Duren, R.; Guanter, L.; Hollstein, A.; Middleton, E.; Ong, L.; Ungar, S. Space-based Remote Imaging Spectroscopy of the Aliso Canyon CH4 Superemitter. Geophys. Res. Lett. 2016, 43, 6571–6578. [Google Scholar] [CrossRef]
- Guanter, L.; Irakulis-Loitxate, I.; Gorroño, J.; Sánchez-García, E.; Cusworth, D.H.; Varon, D.J.; Cogliati, S.; Colombo, R. Mapping Methane Point Emissions with the PRISMA Spaceborne Imaging Spectrometer. Remote Sens. Environ. 2021, 265, 112671. [Google Scholar] [CrossRef]
- Irakulis-Loitxate, I.; Guanter, L.; Liu, Y.N.; Varon, D.J.; Maasakkers, J.D.; Zhang, Y.; Chulakadabba, A.; Wofsy, S.C.; Thorpe, A.K.; Duren, R.M.; et al. Satellite-Based Survey of Extreme Methane Emissions in the Permian Basin. Sci. Adv. 2021, 7, eabf4507. [Google Scholar] [CrossRef]
- Schaum, A. A Uniformly Most Powerful Detector of Gas Plumes against a Cluttered Background. Remote Sens. Environ. 2021, 260, 112443. [Google Scholar] [CrossRef]
- Pei, Z.; Han, G.; Mao, H.; Chen, C.; Shi, T.; Yang, K.; Ma, X.; Gong, W. Improving Quantification of Methane Point Source Emissions from Imaging Spectroscopy. Remote Sens. Environ. 2023, 295, 113652. [Google Scholar] [CrossRef]
- Roger, J.; Guanter, L.; Gorroño, J.; Irakulis-Loitxate, I. Exploiting the Entire Near-Infrared Spectral Range to Improve the Detection of Methane Plumes with High-Resolution Imaging Spectrometers. Atmos. Meas. Tech. Discuss. 2023, 17, 1333–1346. [Google Scholar] [CrossRef]
- Sherwin, E.D.; El Abbadi, S.H.; Burdeau, P.M.; Zhang, Z.; Chen, Z.; Rutherford, J.S.; Chen, Y.; Brandt, A.R. Single-Blind Test of Nine Methane-Sensing Satellite Systems from Three Continents. Atmos. Meas. Tech. 2024, 17, 765–782. [Google Scholar] [CrossRef]
- Sánchez-García, E.; Gorroño, J.; Irakulis-Loitxate, I.; Varon, D.J.; Guanter, L. Mapping Methane Plumes at Very High Spatial Resolution with the WorldView-3 Satellite. Atmos. Meas. Tech. 2022, 15, 1657–1674. [Google Scholar] [CrossRef]
- Ayasse, A.K.; Dennison, P.E.; Foote, M.; Thorpe, A.K.; Joshi, S.; Green, R.O.; Duren, R.M.; Thompson, D.R.; Roberts, D.A. Methane Mapping with Future Satellite Imaging Spectrometers. Remote Sens. 2019, 11, 3054. [Google Scholar] [CrossRef]
- Li, F.; Sun, S.; Zhang, Y.; Feng, C.; Chen, C.; Mao, H.; Liu, Y. Mapping Methane Super-Emitters in China and United States with GF5-02 Hyperspectral Imaging Spectrometer. Natl. Remote Sens. Bull. 2023, 28, 986–2001. [Google Scholar] [CrossRef]
- Liu, Y.N.; Zhang, J.; Zhang, Y.; Sun, W.W.; Jiao, L.L.; Sun, D.X.; Hu, X.N.; Ye, X.; Li, Y.D.; Liu, S.F.; et al. The Advanced Hyperspectral Imager: Aboard China’s GaoFen-5 Satellite. IEEE Geosci. Remote Sens. Mag. 2019, 7, 23–32. [Google Scholar] [CrossRef]
- He, Z.; Gao, L.; Liang, M.; Zeng, Z.C. A Survey of Methane Point Source Emissions from Coal Mines in Shanxi Province of China Using AHSI on Board Gaofen-5B. Atmos. Meas. Tech. 2024, 17, 2937–2956. [Google Scholar] [CrossRef]
- Roger, J.; Irakulis-Loitxate, I.; Valverde, A.; Gorroño, J.; Chabrillat, S.; Brell, M.; Guanter, L. High-Resolution Methane Mapping with the EnMAP Satellite Imaging Spectroscopy Mission. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–12. [Google Scholar] [CrossRef]
- Foote, M.D.; Dennison, P.E.; Sullivan, P.R.; O’Neill, K.B.; Thorpe, A.K.; Thompson, D.R.; Cusworth, D.H.; Duren, R.; Joshi, S.C. Impact of Scene-Specific Enhancement Spectra on Matched Filter Greenhouse Gas Retrievals from Imaging Spectroscopy. Remote Sens. Environ. 2021, 264, 112574. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection Algorithms in Hyperspectral Imaging Systems: An Overview of Practical Algorithms. IEEE Signal Process. Mag. 2013, 31, 24–33. [Google Scholar] [CrossRef]
- Funk, C.; Theiler, J.; Roberts, D.; Borel, C. Clustering to Improve Matched Filter Detection of Weak Gas Plumes in Hyperspectral Thermal Imagery. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1410–1420. [Google Scholar] [CrossRef]
- Allen, D. Attributing Atmospheric Methane to Anthropogenic Emission Sources. Accounts Chem. Res. 2016, 49, 1344–1350. [Google Scholar] [CrossRef]
- Thorpe, A.K.; Roberts, D.A.; Bradley, E.S.; Funk, C.C.; Dennison, P.E.; Leifer, I. High Resolution Mapping of Methane Emissions from Marine and Terrestrial Sources Using a Cluster-Tuned Matched Filter Technique and Imaging Spectrometry. Remote Sens. Environ. 2013, 134, 305–318. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; Van Den Bosch, J. MODTRAN® 6: A Major Upgrade of the MODTRAN® Radiative Transfer Code. In Proceedings of the 2014 6th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lausanne, Switzerland, 24–27 June 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Yang, S.; Yang, J.; Shi, S.; Song, S.; Luo, Y.; Du, L. The Rising Impact of Urbanization-Caused CO2 Emissions on Terrestrial Vegetation. Ecol. Indic. 2023, 148, 110079. [Google Scholar] [CrossRef]
- Guanter, L.; Richter, R.; Moreno, J. Spectral Calibration of Hyperspectral Imagery Using Atmospheric Absorption Features. Appl. Opt. 2006, 45, 2360. [Google Scholar] [CrossRef]
- Lyon, D.R.; Alvarez, R.A.; Zavala-Araiza, D.; Brandt, A.R.; Jackson, R.B.; Hamburg, S.P. Aerial Surveys of Elevated Hydrocarbon Emissions from Oil and Gas Production Sites. Environ. Sci. Technol. 2016, 50, 4877–4886. [Google Scholar] [CrossRef]
- Shi, T.; Han, G.; Ma, X.; Mao, H.; Chen, C.; Han, Z.; Pei, Z.; Zhang, H.; Li, S.; Gong, W. Quantifying Factory-Scale CO2 /CH4 Emission Based on Mobile Measurements and EMISSION-PARTITION Model: Cases in China. Environ. Res. Lett. 2023, 18, 034028. [Google Scholar] [CrossRef]
- Conley, S.; Franco, G.; Faloona, I.; Blake, D.R.; Peischl, J.; Ryerson, T.B. Methane Emissions from the 2015 Aliso Canyon Blowout in Los Angeles, CA. Science 2016, 351, 1317–1320. [Google Scholar] [CrossRef]
- Varon, D.J.; Jacob, D.J.; McKeever, J.; Jervis, D.; Durak, B.O.A.; Xia, Y.; Huang, Y. Quantifying Methane Point Sources from Fine-Scale Satellite Observations of Atmospheric Methane Plumes. Atmos. Meas. Tech. 2018, 11, 5673–5686. [Google Scholar] [CrossRef]
- Zheng, B.; Chevallier, F.; Ciais, P.; Broquet, G.; Wang, Y.; Lian, J.; Zhao, Y. Observing Carbon Dioxide Emissions over China’s Cities and Industrial Areas with the Orbiting Carbon Observatory-2. Atmos. Chem. Phys. 2020, 20, 8501–8510. [Google Scholar] [CrossRef]
- Cusworth, D.H.; Duren, R.M.; Thorpe, A.K.; Tseng, E.; Thompson, D.; Guha, A.; Newman, S.; Foster, K.T.; Miller, C.E. Using Remote Sensing to Detect, Validate, and Quantify Methane Emissions from California Solid Waste Operations. Atmos. Chem. Phys. 2020, 15, 054012. [Google Scholar] [CrossRef]



| Instrument | Swath [km] | Spatial Resolution [m] | Spectral Resolution [nm] | Source |
|---|---|---|---|---|
| Gaofen 5B (GF5B) | 60 | 30 | 7.5 | [30] |
| Ziyuan 1F (ZY1F) | 60 | 30 | 7.5 | [37] |
| EnMAP | 30 | 30 | 8 | [40] |
| Part | Simulation | Methane Plume | Image Noise |
|---|---|---|---|
| Part 1 | Simulation 1 | Uniformly random enhancement | 1% |
| Part 2 | Simulation 2 | Gaussian distributed plume | 1% |
| Simulation 3 | EMIT plume product | 1% | |
| Simulation 4 | Gaussian distributed plume | True data from GF5B | |
| Simulation 5 | EMIT plume product | True data from GF5B |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, M.; Zhang, Y.; Chen, L.; Tao, J.; Fan, M.; Yu, C. An Effective Quantification of Methane Point-Source Emissions with the Multi-Level Matched Filter from Hyperspectral Imagery. Remote Sens. 2025, 17, 843. https://doi.org/10.3390/rs17050843
Liang M, Zhang Y, Chen L, Tao J, Fan M, Yu C. An Effective Quantification of Methane Point-Source Emissions with the Multi-Level Matched Filter from Hyperspectral Imagery. Remote Sensing. 2025; 17(5):843. https://doi.org/10.3390/rs17050843
Chicago/Turabian StyleLiang, Menglei, Ying Zhang, Liangfu Chen, Jinhua Tao, Meng Fan, and Chao Yu. 2025. "An Effective Quantification of Methane Point-Source Emissions with the Multi-Level Matched Filter from Hyperspectral Imagery" Remote Sensing 17, no. 5: 843. https://doi.org/10.3390/rs17050843
APA StyleLiang, M., Zhang, Y., Chen, L., Tao, J., Fan, M., & Yu, C. (2025). An Effective Quantification of Methane Point-Source Emissions with the Multi-Level Matched Filter from Hyperspectral Imagery. Remote Sensing, 17(5), 843. https://doi.org/10.3390/rs17050843







