The Spatiotemporal Evolution and Driving Forces of the Urban Heat Island in Shijiazhuang
Abstract
1. Introduction
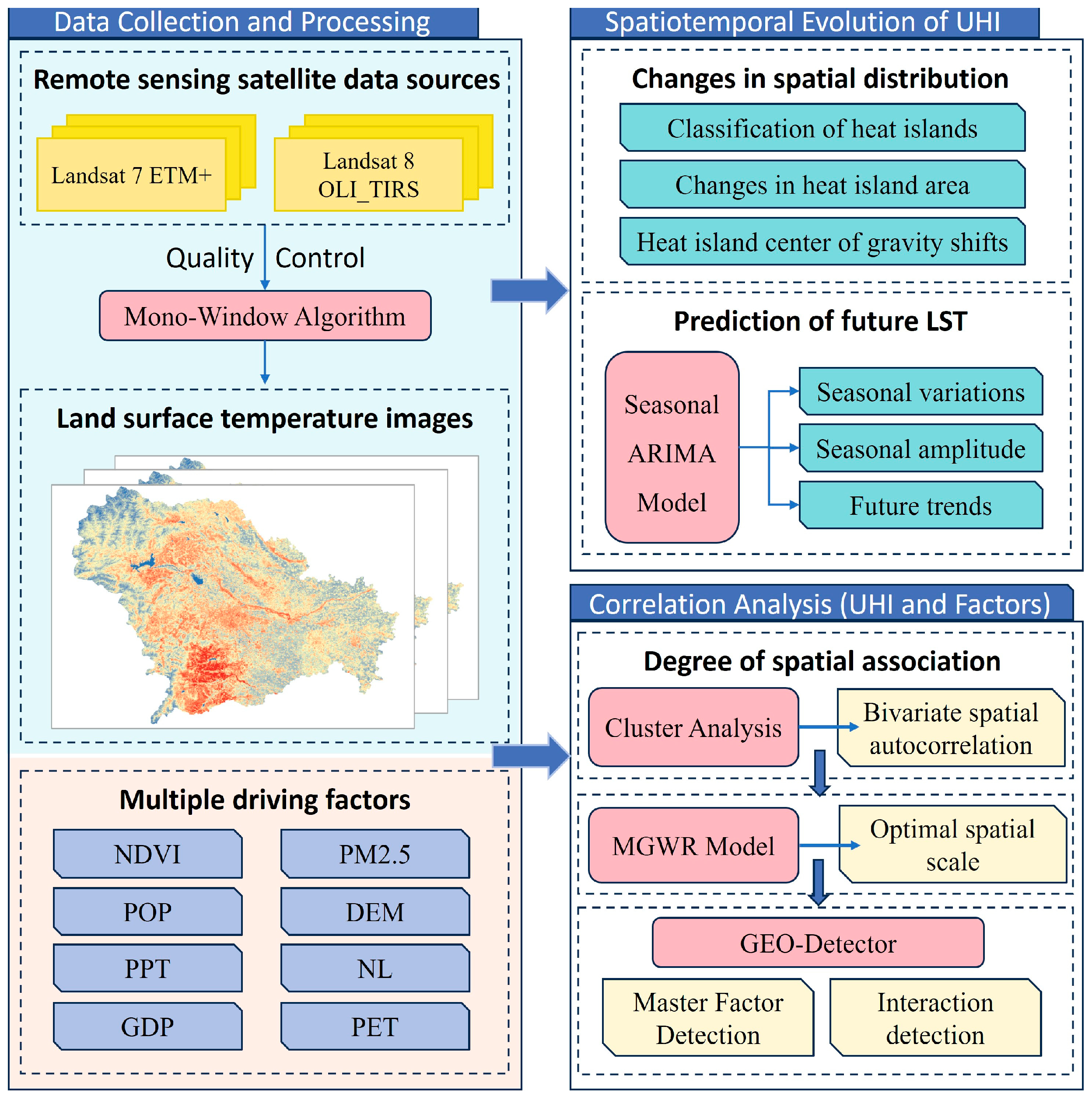
2. Materials and Methods
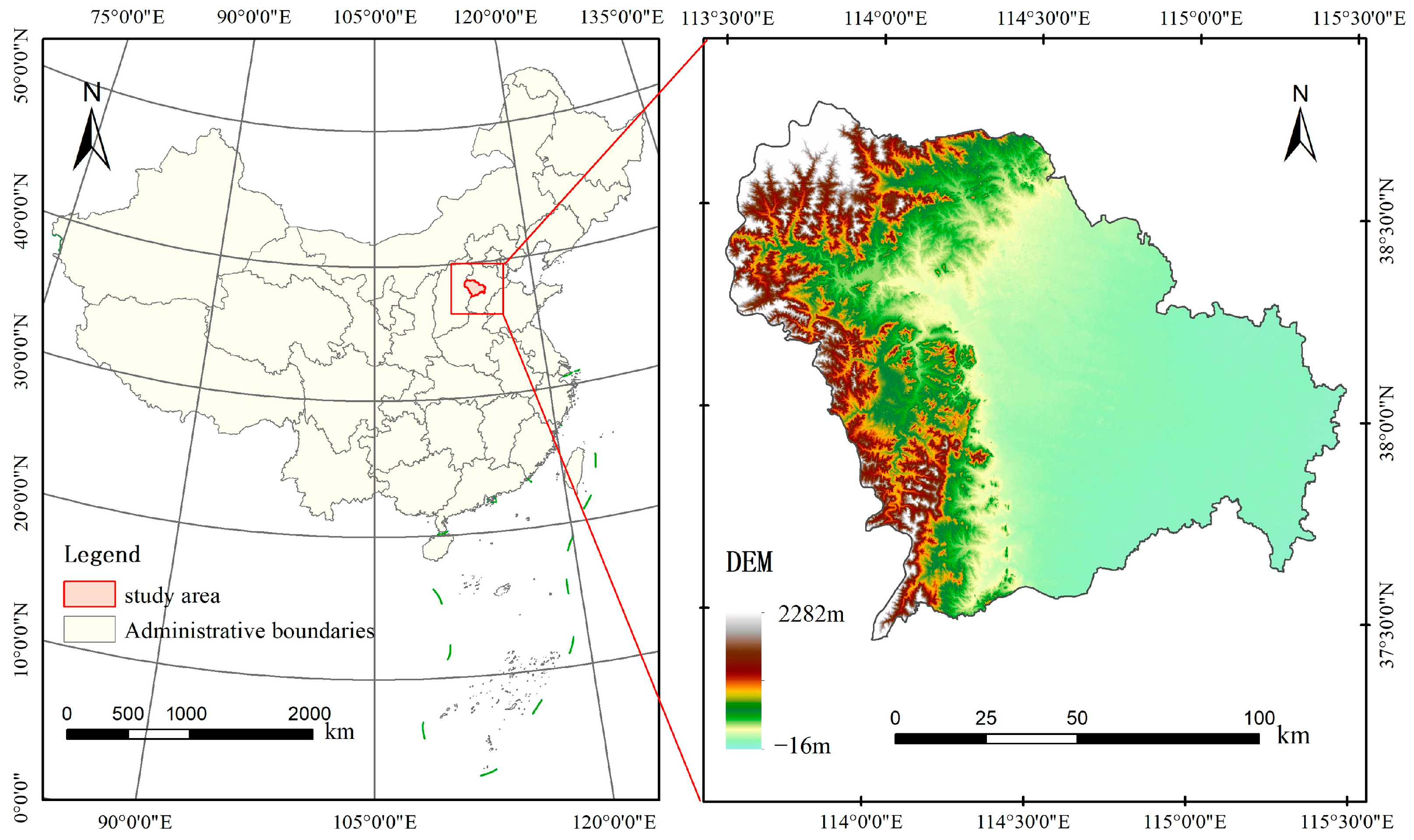
2.1. Description of the Study Area
2.2. Multi-Source Data
2.3. Methods
2.3.1. LST Retrieval and Prediction
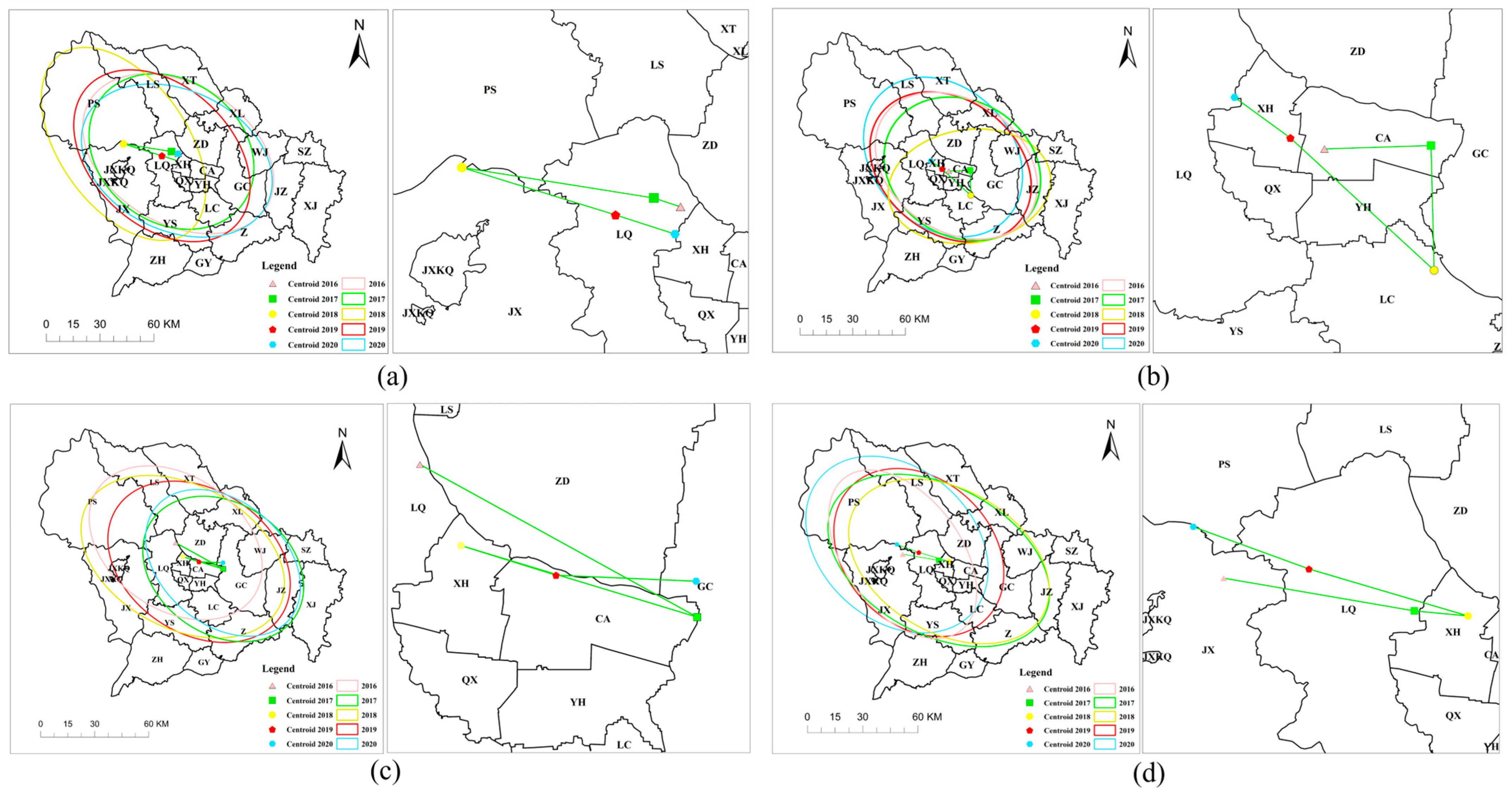
- The center point of the ellipse:
- 2.
- The direction of the ellipse:
- 3.
- The long and short semi-axes of the ellipse:
2.3.2. Spatial Autocorrelation Analysis
2.3.3. Multi-Scale Spatial and Influencing Mechanism Analysis
3. Results and Discussion
3.1. Spatial and Temporal Evolution Characteristics of UHI
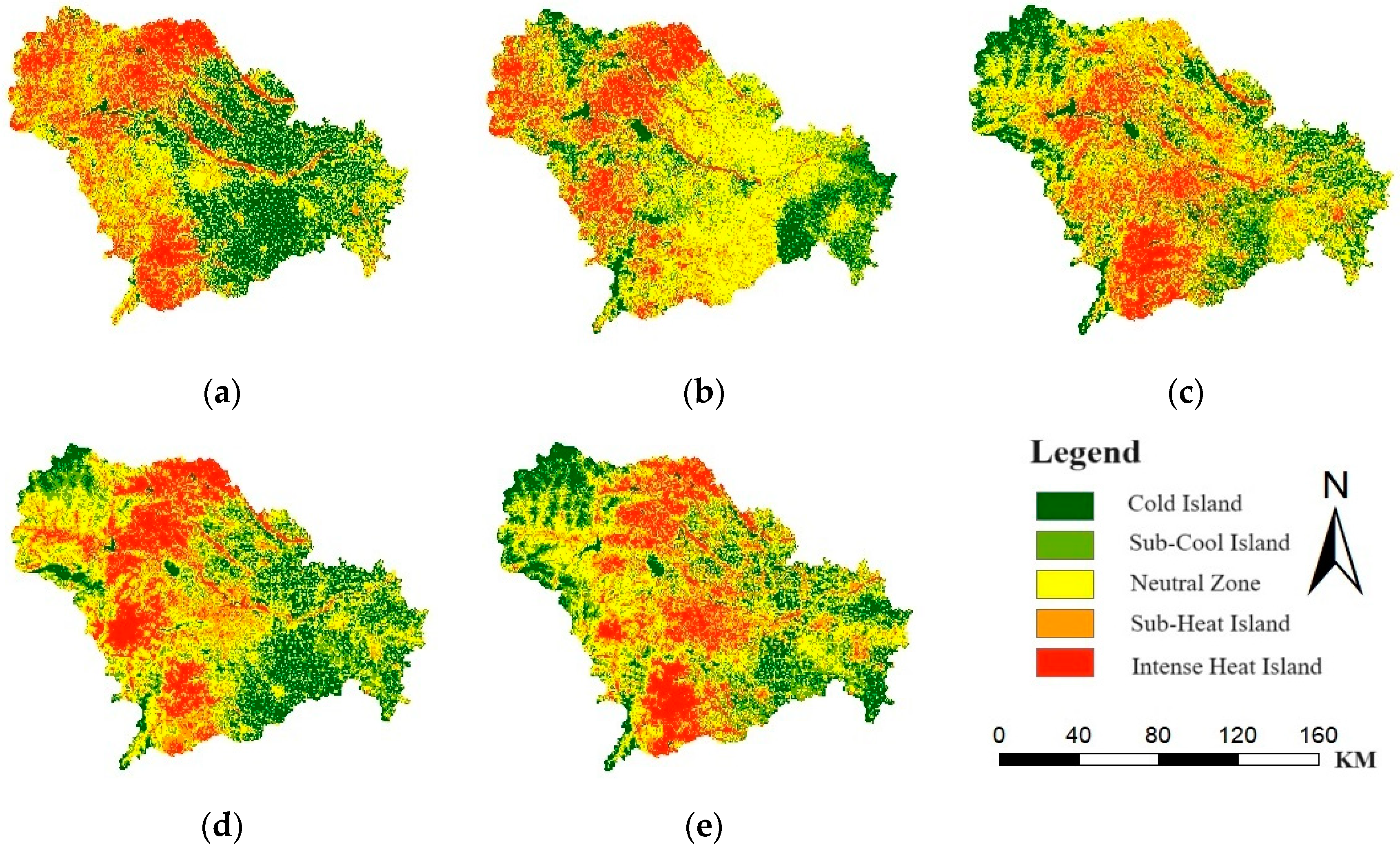
3.1.1. Classifications of UHI Pattern
3.1.2. Seasonal Variation in Spatial Pattern of UHI
3.2. Prediction of Future LST
3.3. Attribution Analysis of UHI
3.3.1. Analysis of Bivariate UHI Spatial Clustering Patterns
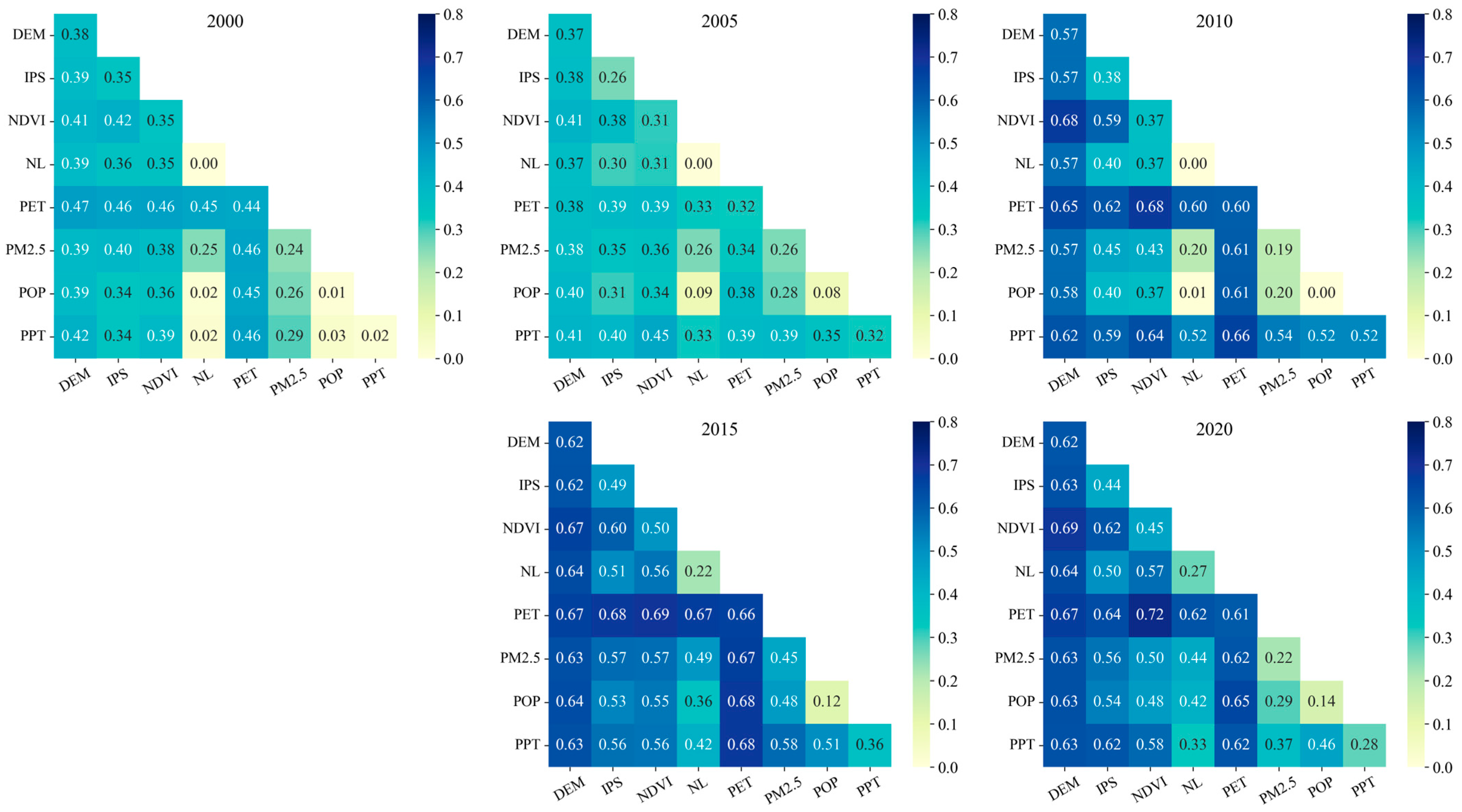
3.3.2. Analysis of Driving Factors Influencing UHI
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Howard, L. The Climate of London: Deduced from Meteorological Observations Made in the Metropolis and at Various Places Around It; W. Phillips: London, UK, 1833. [Google Scholar]
- Oke, T.R. Boundary Layer Climates; Psychology Press: East Sussex, UK, 1987. [Google Scholar]
- Grimmond, S. Urbanization and global environmental change: Local effects of urban warming. Geogr. J. 2007, 173, 83–88. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. A J. R. Meteorol. Soc. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Oke, T.R.; Cleugh, H.A.; Grimmond, S.; Schmid, H.P.; Roth, M. Evaluation of spatially-averaged fluxes of heat, mass and momentum in the urban boundary layer. Weather. Clim. 1989, 9, 14–21. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Solecki, W.; Slosberg, R. Mitigating New York City’s Heat Island with Urban Forestry, Living Roofs, and Light Surfaces; New York State Energy Research and Development Authority: Albany, NY, USA, 2006; pp. 1–5. [Google Scholar]
- Wang, Z.; Liu, M.; Liu, X.; Meng, Y.; Zhu, L.; Rong, Y. Spatio-temporal evolution of surface urban heat islands in the Chang-Zhu-Tan urban agglomeration. Phys. Chem. Earth Parts A/B/C 2020, 117, 102865. [Google Scholar] [CrossRef]
- Deng, X.; Gao, F.; Liao, S.; Liu, Y.; Chen, W. Spatiotemporal evolution patterns of urban heat island and its relationship with urbanization in Guangdong-Hong Kong-Macao greater bay area of China from 2000 to 2020. Ecol. Indic. 2023, 146, 109817. [Google Scholar] [CrossRef]
- Min, M.; Zhao, H.; Miao, C. Spatio-temporal evolution analysis of the urban heat island: A case study of Zhengzhou City, China. Sustainability 2018, 10, 1992. [Google Scholar] [CrossRef]
- Sun, L.; Hang, X.; Gao, P.; Xie, X.; Zhu, S.; Li, Y. Characteristics of summer urban heat island in Jiangsu Province by multi-year satellite observations. J. Meteorol. Sci. 2023, 43, 662–669. [Google Scholar]
- Hu, N.; Ren, Z.; Dong, Y.; Fu, Y.; Guo, Y.; Mao, Z.; Chang, X. Spatio-temporal Evolution of Heat Island Effect and Its Driving Factors in Urban Agglomerations of China. Sci. Geogr. Sin. 2022, 42, 1534–1545. [Google Scholar] [CrossRef]
- Si, M.; Li, Z.L.; Nerry, F.; Tang, B.H.; Leng, P.; Wu, H.; Zhang, X.; Shang, G. Spatiotemporal pattern and long-term trend of global surface urban heat islands characterized by dynamic urban-extent method and MODIS data. ISPRS J. Photogramm. Remote Sens. 2022, 183, 321–335. [Google Scholar] [CrossRef]
- Zhang, Z.; Paschalis, A.; Mijic, A.; Meili, N.; Manoli, G.; van Reeuwijk, M.; Fatichi, S. A mechanistic assessment of urban heat island intensities and drivers across climates. Urban Clim. 2022, 44, 101215. [Google Scholar] [CrossRef]
- Khalil, U.; Aslam, B.; Azam, U.; Khalid, H.M.D. Time series analysis of land surface temperature and drivers of urban heat island effect based on remotely sensed data to develop a prediction model. Appl. Artif. Intell. 2021, 35, 1803–1828. [Google Scholar] [CrossRef]
- He, Z.; Zhang, D.; Ye, Q.; Chen, Z.; Yang, S.; Gao, Y. Characteristics of urban heat island in Chongqing in recent 40 years and its association with weather conditions. Arid. Meteorol. 2022, 40, 683–689. [Google Scholar] [CrossRef]
- Niu, L.; Zhang, Z.; Peng, Z.; Jiang, Y.; Liu, M.; Zhou, X.; Tang, R. China’s surface urban heat island drivers and its spatial heterogeneity. China Environ. Sci. 2022, 42, 945–953. [Google Scholar]
- Liao, Y.; Shen, X.; Zhou, J.; Ma, J.; Zhang, X.; Tang, W.; Chen, Y.; Ding, L.; Wang, Z. Surface urban heat island detected by all-weather satellite land surface temperature. Sci. Total Environ. 2022, 811, 151405. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, J.; Zhang, T.; Tang, W.; Liao, Y.; Yang, M. Non-negligible clear-sky biases of satellite thermal infrared observations for analyzing surface urban heat island intensity: A case study in China. Sci. Total Environ. 2024, 949, 174928. [Google Scholar] [CrossRef] [PubMed]
- Deilami, K.; Kamruzzaman, M.; Liu, Y. Urban heat island effect: A systematic review of spatio-temporal factors, data, methods, and mitigation measures. Int. J. Appl. Earth Obs. Geoinf. 2018, 67, 30–42. [Google Scholar] [CrossRef]
- Almeida, C.R.; Teodoro, A.C.; Gonçalves, A. Study of the urban heat island (UHI) using remote sensing data/techniques: A systematic review. Environments 2021, 8, 105. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Approaches to study urban heat island–abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Rajasekar, U.; Weng, Q. Urban heat island monitoring and analysis using a non-parametric model: A case study of Indianapolis. ISPRS J. Photogramm. Remote Sens. 2009, 64, 86–96. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. A single-channel algorithm for land-surface temperature retrieval from ASTER data. IEEE Geosci. Remote Sens. Lett. 2009, 7, 176–179. [Google Scholar] [CrossRef]
- Li, H.; Liu, Q.; Zhong, B.; Du, Y.; Wang, H.; Wang, Q. A single-channel algorithm for land surface temperature retrieval from HJ-1B/IRS data based on a parametric model. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2448–2451. [Google Scholar]
- Price, J.C. Land surface temperature measurements from the split window channels of the NOAA 7 Advanced Very High Resolution Radiometer. J. Geophys. Res. Atmos. 1984, 89, 7231–7237. [Google Scholar] [CrossRef]
- Mao, K.; Qin, Z.; Shi, J.; Gong, P. The Research of Split-Window Algorithm on th e MODIS. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 703–707. [Google Scholar]
- Ulivieri, C.M.M.A.; Castronuovo, M.M.; Francioni, R.; Cardillo, A. A split window algorithm for estimating land surface temperature from satellites. Adv. Space Res. 1994, 14, 59–65. [Google Scholar] [CrossRef]
- Zheng, Z.; Xu, G.; Wang, Y.; Li, Q.; Li, J. Characteristics and Main Influence Factors of Heat Waves in Beijing–Tianjin–Shijiazhuang Cities of Northern China in Recent 50 Years. Atmos. Sci. Lett. 2020, 21, e1001. [Google Scholar] [CrossRef]
- Qin, Z.H.; Zhang, M.H.; Karnieli, A.; Berliner, P. Mono-window algorithm for retrieving land surface temperature from Landsat TM6 data. Acta Geogr. Sin. 2001, 56, 456–466. [Google Scholar]
- Yuill, R. Standard Deviational Ellipse—Updated Tool For Spatial Description. Geogr. Anal. 1971, B 53, 28–39. [Google Scholar] [CrossRef]
- Box GE, P.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Mathew, A.; Sreekumar, S.; Khandelwal, S.; Kaul, N.; Kumar, R. Prediction of land-surface temperatures of Jaipur city using linear time series model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3546–3552. [Google Scholar] [CrossRef]
- Moran, P.A. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. Local Indicators of Spatial Association—Lisa. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (Mgwr). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M. Some Notes on Parametric Significance Tests for Geographically Weighted Regression. J. Reg. Sci. 1999, 39, 497–524. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Jia, Q.; Lü, G.; Wang, X.; Zhang, Y.; Ai, J. Urban heat island intensity and its grading in Liaoning Province of Northeast China. Chin. J. Appl. Ecol. 2012, 23, 1345–1350. [Google Scholar]
- Zhang, Y.; Yu, T.; Gu, X.F.; Zhang, Y.X.; Chen, L.F. Land surface temperature retrieval from CBERS-02 IRMSS thermal infrared data and its applications in quantitative analysis of urban heat island effect. J. Remote Sens. 2006, 10, 789–797. [Google Scholar]
- Yu, C.; Hu, D.; Cao, S. Spatio-temporal pattern of heat island and multivariate modeling of impact factors of Beijing downtown from 2005 to 2016. J. Geo-Inf. Sci. 2017, 19, 1485–1494. [Google Scholar]
- Chen, S.; Wang, T. Comparison Analyses of Equal Interval Method and Mean-standard Deviation Method Used to Delimitate Urban Heat Island. J. Geo-Inf. Sci. 2009, 11, 145–150. [Google Scholar] [CrossRef]



| Sensor Types | Date | Spatial Resolution |
|---|---|---|
| Landsat7 ETM+ | 23 May 2020 22 Jun. 2005 19 May 2010 | 30 m |
| Landsat8 OLI_TIRS | 25 May 2015 03 Dec. 2015 25 Apr. 2016 12 Jun. 2016 18 Oct. 2016 22 Jan. 2017 12 Apr. 2017 01 Jul. 2017 05 Oct. 2017 24 Dec. 2017 14 Mar. 2018 20 Jul. 2018 24 Oct. 2018 11 Dec. 2018 02 Apr. 2019 20 May 2019 13 Oct. 2019 31 Jan. 2020 19 Mar. 2020 22 May 2020 13 Oct. 2020 | 30 m |
| Temperature Zone Levels | Heat Island Levels | Temperature Range |
|---|---|---|
| High-temperature zone | Intense heat island | T > u + std |
| Sub-high-temperature zone | Sub-heat island | u + 0.5 std < T < u + std |
| Medium-temperature zone | Neutral zone | u − 0.5 std < T < u + 0.5 std |
| Sub-low-temperature zone | Sub-cold island | u − std < T < u − 0.5 std |
| Low-temperature zone | Cold island | T < u − std |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Liu, Y.; Chen, R.; Si, M.; Zhang, C.; Tian, Y.; Shang, G. The Spatiotemporal Evolution and Driving Forces of the Urban Heat Island in Shijiazhuang. Remote Sens. 2025, 17, 781. https://doi.org/10.3390/rs17050781
Zhang X, Liu Y, Chen R, Si M, Zhang C, Tian Y, Shang G. The Spatiotemporal Evolution and Driving Forces of the Urban Heat Island in Shijiazhuang. Remote Sensing. 2025; 17(5):781. https://doi.org/10.3390/rs17050781
Chicago/Turabian StyleZhang, Xia, Yue Liu, Ruohan Chen, Menglin Si, Ce Zhang, Yiran Tian, and Guofei Shang. 2025. "The Spatiotemporal Evolution and Driving Forces of the Urban Heat Island in Shijiazhuang" Remote Sensing 17, no. 5: 781. https://doi.org/10.3390/rs17050781
APA StyleZhang, X., Liu, Y., Chen, R., Si, M., Zhang, C., Tian, Y., & Shang, G. (2025). The Spatiotemporal Evolution and Driving Forces of the Urban Heat Island in Shijiazhuang. Remote Sensing, 17(5), 781. https://doi.org/10.3390/rs17050781






