Next Article in Journal
PhenoCam Guidelines for Phenological Measurement and Analysis in an Agricultural Cropping Environment: A Case Study of Soybean
Next Article in Special Issue
A Mobile Triaxial Stabilized Ship-Borne Radiometric System for In Situ Measurements: Case Study of Sentinel-3 OLCI Validation in Highly Turbid Waters
Previous Article in Journal
An Optimization Method for Multi-Functional Radar Network Deployment in Complex Regions
Previous Article in Special Issue
How Useful Are Moderate Resolution Imaging Spectroradiometer Observations for Inland Water Temperature Monitoring and Warming Trend Assessment in Temperate Lakes in Poland?
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 4
10.3390/rs17040731
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Fine Estimation of Water Quality in the Yangtze River Basin Based on a Geographically Weighted Random Forest Regression Model

by
Fuliang Deng
1,
Wenhui Liu
1,
Mei Sun
1,
Yanxue Xu
2,3,*,
Bo Wang
4,
Wei Liu
1,
Ying Yuan
1 and
Lei Cui
5
1
School of Computer and Information Engineering, Xiamen University of Technology, Xiamen 361024, China
2
Chinese Academy of Environmental Planning, United Center for Eco-Environment in Yangtze River Economic Belt, Beijing 100084, China
3
Department of Hydraulic Engineering, Tsinghua University, Beijing 100041, China
4
Sichuan Academy of Environmental Policy and Planning, Chengdu 610093, China
5
Navigation College, Jimei University, Xiamen 361001, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(4), 731; https://doi.org/10.3390/rs17040731
Submission received: 18 January 2025 / Revised: 13 February 2025 / Accepted: 18 February 2025 / Published: 19 February 2025
(This article belongs to the Special Issue Applications of Remote Sensing in Water Quality Assessment of Lakes, Rivers and Reservoirs)
Browse Figures
Versions Notes

Abstract

:
Water quality evaluation usually relies on limited state-controlled monitoring data, making it challenging to fully capture variations across an entire basin over time and space. The fine estimation of water quality in a spatial context presents a promising solution to this issue; however, traditional analyses often ignore spatial non-stationarity between variables. To solve the above-mentioned problems in water quality mapping research, we took the Yangtze River as our study subject and attempted to use a geographically weighted random forest regression (GWRFR) model to couple massive station observation data and auxiliary data to carry out a fine estimation of water quality. Specifically, we first utilized state-controlled sections’ water quality monitoring data as input for the GWRFR model to train and map six water quality indicators at a 30 m spatial resolution. We then assessed various geographical and environmental factors contributing to water quality and identified spatial differences. Our results show accurate predictions for all indicators: ammonia nitrogen (NH3-N) had the lowest accuracy (R2 = 0.61, RMSE = 0.13), and total nitrogen (TN) had the highest (R2 = 0.74, RMSE = 0.48). The mapping results reveal total nitrogen as the primary pollutant in the Yangtze River basin. Chemical oxygen demand and the permanganate index were mainly influenced by natural factors, while total nitrogen and total phosphorus were impacted by human activities. The spatial distribution of critical influencing factors shows significant clustering. Overall, this study demonstrates the fine spatial distribution of water quality and provides insights into the influencing factors that are crucial for the comprehensive management of water environments.

1. Introduction

Understanding the fine spatial distribution of water quality, as well as elucidating the spatial difference in environmental factors’ influence upon it, is of considerable practical significance [1]. Although the water quality monitoring data offer an overview of the water quality at the level of the section control unit, they fail to capture its spatial distribution difference. Within the basin, there is significant spatial heterogeneity and non-stationarity in the influencing factors and water quality. In terms of modeling, global models often overlook the impact of spatial non-stationarity between variables. Analysis results obtained using this kind of model may deviate from the actual situation when interpreting the situation locally [2,3] and cannot effectively support the development of water environment governance in the local basin. The fine estimation of water quality in a spatial context is a promising solution to the above issue.
The fine estimation of water quality necessitates the development of a reliable prediction model. Such models can be broadly categorized into mechanism and empirical models. The former refers to the simulation scheme based on the hydrological process of the basin, which describes the interaction of various processes therein by establishing a model of complex nonlinear relations [4]. The CE-QUAL-W2 model is a standard mechanistic model that is primarily used for two-dimensional hydrodynamics and water quality modeling [5]. Although this model has been successfully employed to simulate the dynamics of water pollution [6,7,8], mechanism models are limited in conducting large-scale watershed water quality simulations due to the high demands for data accuracy, computational resources, and cross-scale consistency [9].
Using an empirical model with monitoring site data and relevant geographic information data may be a potential solution to the limitations of mechanism models. An empirical model is a data-driven scheme that carries out a data regression analysis on influencing factors, such as the landscape index and water quality indicator, while ignoring the physical, chemical, and hydrological processes. Empirical models have achieved rich results in various fields, including the areas of population [10,11], economy [12,13], and food production [14]. For example, the Soil and Water Assessment Tool (SWAT), developed for describing hydrological processes and water quality, is commonly applied to model the effects of anthropogenic activities and natural influences on rural and agricultural environments. The SWAT can simulate water quality on different time scales and has successfully been used to model the process of water bodies of different scales, such as rivers, reservoirs, and basins [15]. It is suitable for both watershed- and continental-scale modeling and can achieve successful calibration even in the absence of extensive data [15]. Overall, empirical models offer a more convenient approach for water quality simulation, especially for areas lacking basic monitoring data [16]. However, the empirical model often ignores the influence of spatial non-stationarity between variables on the analysis of influencing factors, leading to inaccuracies and potentially misleading conclusions [17,18].
Due to the unpredictability of natural changes and the intricate relationship between human factors and water quality, there are nonlinearities, spatial non-stationarity, and fuzziness among the relevant data, making them very challenging to address. Artificial intelligence (AI) models show significant advantages in dealing with such problems due to their robustness and reliability in tackling nonlinear data. Many studies have shown that, in water quality estimation, artificial intelligence models provide outstanding performance [19,20,21]. For instance, some studies have found that AI models can help better predict parameters for data with spatial heterogeneity and non-stationarity problems, such as water quality data [22,23,24]. For example, Georganos et al. extended the random forest regression model based on the concept of local regression and proposed a geographically weighted random forest regression (GWRFR) model to deal with spatial non-stationarity problems [25].
The GWRFR model has successfully been employed for predicting various spatial parameters. For example, Quinones et al. used this model, and others, to study the prevalence of type 2 diabetes and its influencing factors; they discovered that the GWRFR model had high potential in accounting for the spatial variability in the prevalence of type 2 diabetes and forecasting its incidence [26]. Similarly, Ren et al. utilized the GWRFR model to examine the spatial and temporal heterogeneity of samples and confirmed that carbon emissions are affected differently by control variables [27]. Khan et al. proved that, among five machine learning methods, the GWRFR model was outperformed at predicting the county-level crop yield [14]. Some researchers have applied the GWRFR model to water quality modeling [28,29]. However, water quality assessments using the GWRFR model are limited to small basins due to insufficient water quality monitoring data. Overall, the GWRFR model provides a straightforward and intuitive way to visualize spatial non-stationarity, making it a powerful tool for analyzing complex spatial data; however, computational efficiency must be taken into account when dealing with large-scale spatial data [30].
The Yangtze River basin, covering 19 provinces, is an important part of China’s history, culture, and economy [31,32,33]. The river’s water quality has always been a matter of concern, as it is closely related to the health of hundreds of millions of residents along its banks. Therefore, monitoring its water quality is vital for ensuring the well-being of the Chinese people [34,35]. Currently, many studies rely on a small amount of state-controlled section water quality monitoring data to determine water quality [36,37,38]. However, this strategy can only provide an overview of the section control unit’s water quality and fails to capture the differences within it [4]. Additionally, a tricky problem is that the water quality, in terms of temporal and spatial characteristics, is difficult to capture across the entire basin. All of these limitations of existing methods hinder our capacity to fully understand and effectively manage the water quality of the Yangtze River basin.
In this study, we attempted to carry out a fine spatial estimation of the water quality of the Yangtze River basin and adopt an analysis scheme that fully considers spatial non-stationarity. Specifically, we utilized the GWRFR model as the tool, taking water quality monitoring data from the state control section, as well as relevant geographic information data, to construct six water quality indicator models for the Yangtze River basin. These six indicators are chemical oxygen demand (CODCr), the permanganate index (CODMn), dissolved oxygen (DO), ammonia nitrogen (NH3-N), total nitrogen (TN), and total phosphorus (TP), respectively. Then, we carried out a fine estimation of the above six water quality indicators across the Yangtze River basin based on our developed models. Finally, we discussed the spatial differences of different geographical environmental variables and their contribution to the water quality according to the mapping results. Overall, our study can be a reference for managing the water environment across the Yangtze River basin.

2. Materials

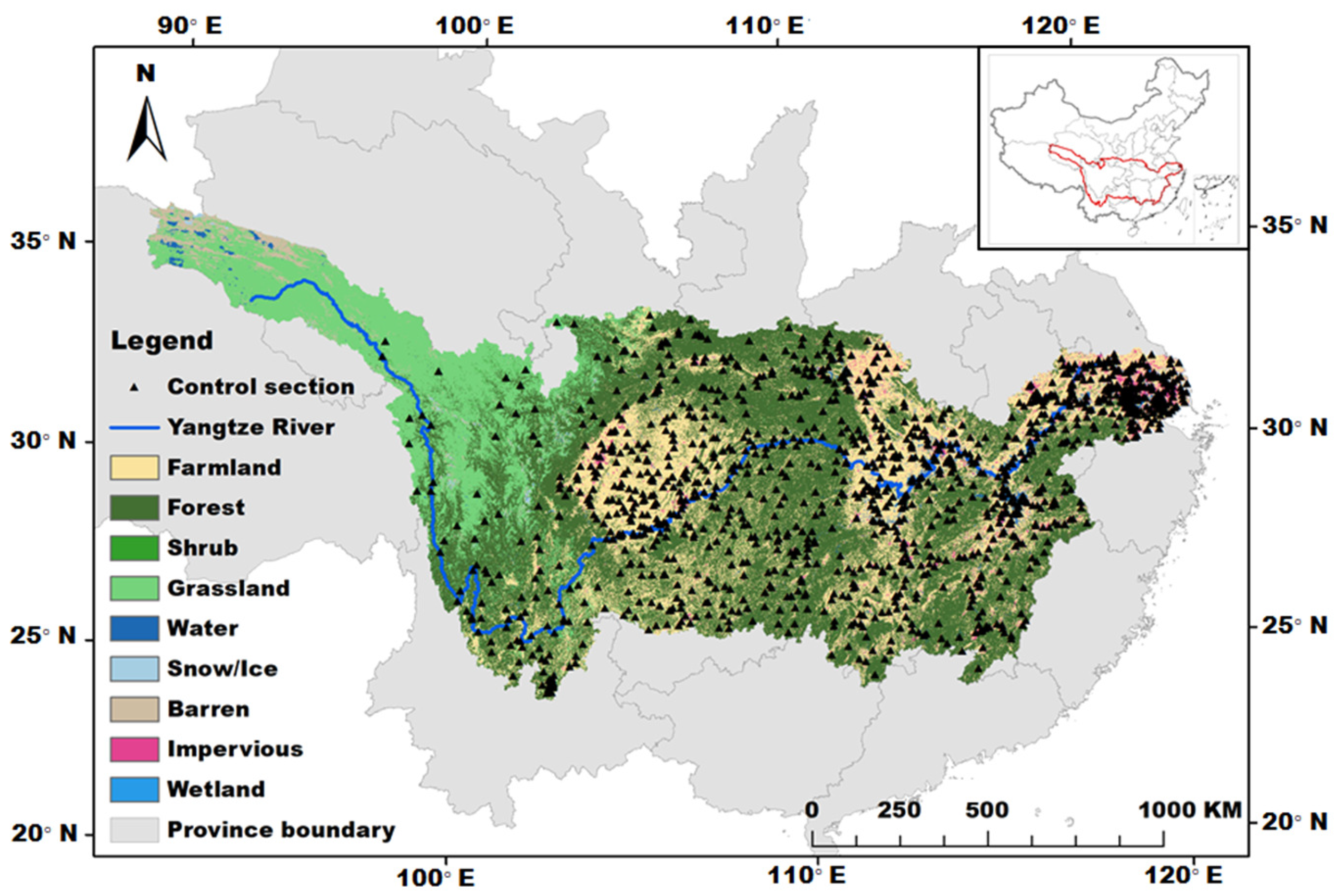
2.1. Study Area

Located in Central and Eastern China, the Yangtze River stretches 6397 km (Figure 1). The mainstream flows from the Qinghai–Tibet Plateau to Jiangsu before eventually reaching the East China Sea. The Yangtze River is nourished by numerous tributaries, which contribute to its extensive watershed, such as the Yalong and Minjiang Rivers and several others [39]. These tributaries lead to a unique ecological environment and river landform. The vast expanse of the Yangtze River basin leads to notable climatic variations between its upstream and downstream regions. The average annual precipitation in the basin varies from 300 to 2400 mm, while the average annual temperature ranges from 9 to 18 °C [40]. Specifically, the river’s source in the Qinghai–Tibet Plateau experiences an alpine climate [41]; the middle and lower reaches are mainly characterized by a subtropical monsoon climate, characterized by distinct seasonal variations and featuring hot and humid summers and warm and humid winters [42,43]. The Yangtze River basin is abundant in vegetation resources, with vast stretches of farmland spread across its fertile middle and lower plains [44].

2.2. Data

This study primarily utilizes water quality and auxiliary data; specifically, the water quality data consist of control section unit and water quality monitoring data. Section control unit data are anchored at the national control section nodes, with their spatial scope determined by multiple factors: the natural confluence characteristics of surface water, the distribution of pollution sources, and the boundaries of administrative divisions. The water quality monitoring data comprise measurements of environmental quality indicators for the control section unit, obtained from monitoring stations. The auxiliary data mainly include a digital elevation model, the population, land cover, point of interest (POI), and meteorological data (as shown in Table 1).

2.2.1. Water Quality Monitoring Data

We used water quality monitoring data from the national control sections to train the prediction model. The national control section refers to representative monitoring points selected in water environment monitoring; these are used to assess the water quality status over a long period of time. These sections usually cover different geographical areas, water types, and environmental pressures to provide comprehensive water quality information. The water quality monitoring data describe the environmental quality of water at state control sections. These data are obtained through regular sampling and monitoring at specific control sections (such as rivers, lakes, and reservoirs) across the country.
The water quality monitoring data were obtained from the Ministry of Natural Resources of China. Covering the period from January 2021 to December 2021, these data include the calculated annual average values of multiple water quality indicators of 1378 section control units across the Yangtze River basin; some of these water quality monitoring data are shown in Table A1. These data provide a representation of the water quality conditions at each monitoring point and include six key water quality indicators: the CODCr, CODMn, DO, NH3-N, TN, and TP (as shown in Table 2).
These crucial indicators for evaluating water quality were chosen because they can effectively reflect the water’s nutritional status, pollution levels, and ecological environment status. The CODCr and CODMn reflect the organic matter content and biodegradability, which are key for measuring the eutrophication and organic pollution levels. DO indicates the oxygen content and supply in water, which is crucial for aquatic organisms’ survival and reproduction and a key indicator for evaluating ecological quality. NH3-N, TN, and TP are major contributors to water eutrophication. Elevated levels lead to algae growth and eutrophication, severely impacting the water’s ecological environment [1,2].

2.2.2. Digital Elevation Model Data

Digital elevation model (DEM) data from the National Aeronautics and Space Administration (NASA) represent ground elevation through a set of ordered numerical arrays. These data provide an accurate and detailed expression of the Earth’s surface terrain features [45]. We used DEM data with a 30 m resolution as a type of auxiliary data to construct the water quality model. Its role is to characterize the possible effects of topography on water quality, mainly including elevation and slope.

2.2.3. China Land Cover Dataset

To select the land cover of the study area, we used the China Land Cover Dataset (CLCD), which is a nationwide dataset based on high-resolution remote sensing image data and generated by professional remote sensing interpretation and data processing technology. The CLCD provides a spatial resolution of a 30 m land cover product, including nine types from 1990 to 2021 (Figure 1). Each land cover type was accurately classified and labeled, allowing the researchers to accurately understand the land use situation and change trends in different regions in China [46]. We selected three land cover types (farmland, forests, and impervious surfaces) from the CLCD data. Furthermore, we used the land cover data as the input for the training model to explore its impact on water quality.

2.2.4. WorldPop Data

WorldPop is a global population and distribution project aimed at providing high-resolution, spatiotemporal population data to support research and policy-making across various disciplines [47]. This project utilizes multiple data sources, including satellite imagery, census data, geographic information system (GIS) technology, and spatial statistical models and machine learning algorithms, to estimate and forecast population distributions worldwide [48].
WorldPop data include population datasets at different spatial and temporal resolutions. These datasets cover many countries and regions around the world, providing characteristics such as population counts, age structures, gender ratios, and spatial distribution features like population density and mobility patterns [49]. Due to their high spatial resolution and spatiotemporal dynamics, WorldPop data are of significant importance in fields such as epidemiology, environmental health, disaster response, food security, urban planning, and more [50,51,52]. We used these data as input factors to train the GWRFR model and analyze the underlying cause of water pollution. In this paper, we used 2020 population grid data with a spatial resolution of 100 m.

2.2.5. Point of Interest (POI) Data

POI data serve as another important input for training the GWRFR model, providing the factory points for our study area; these were derived from Amap’s point of interest dataset. Factory point data can reflect production activities, such as the wastewater and chemicals generated and often discharged into nearby rivers and lakes. We screened out factory points of interest and performed data cleaning by screening and eliminating duplicates. Then, factory density data were obtained using nuclear density analysis [53]. These data reflect not only the spatial distribution of factories but also their degree of spatial agglomeration. In this study, we also used these data to evaluate the impact of factory distribution on water quality.

2.2.6. Meteorological Data

Meteorological data were obtained from the Resources and Environmental Science and Data Center. Based on annual meteorological data, Anusplin interpolation software v4.3 was used to generate spatial interpolation data for eight meteorological elements, such as evaporation, rainfall, and temperature, from 1960 to 2023 [54]. Considering that temperature and rainfall are dominant factors in the recycling redistribution process [55,56,57], we screened these two types of meteorological data from the dataset to estimate the water quality.

3. Methods

The workflow of this study mainly included data preprocessing, water quality estimation model training, and trained model accuracy evaluation (Figure 2). Furthermore, we analyzed the importance of the input factor for the training estimation model. Specifically, we first resampled all of the input data to a spatial resolution of 30 m. Then, we used the processed data as an input for the GWRFR model to train a water quality estimation model for the Yangtze River. Finally, we evaluated the accuracy of the training model using the collected water quality monitoring data from control sections; we also used the mean squared error reduction method to evaluate the importance of each set of input data in predicting water quality in the Yangtze River. The details of our methods can be found in the following sections.

3.1. Geographically Weighted Random Forest Model

We employed the GWRFR model to train the water quality prediction model for the Yangtze River. This method offers an advantage over traditional regression models by explaining the unbalanced distribution of dependent variables and capturing spatial variations in the relationships between dependent and independent variables [58]. The above advantage meets the needs of our research objects and has been successfully used for water quality prediction.
The geographically weighted random forest model extends the global RF regression model by incorporating the idea of local regression. Equation (1) presents a simplified expression:
S i = a ( x i , y i ) z i + e ,   i = 1 : n
Here, the statistic value at observation point i is denoted by S i , while a ( x i , y i ) z i represents the prediction from the local RF regression model calibrated at the location of the observation point i . The coordinate of observation point i is given by ( x i , y i ) , and the error term is represented by e .
Each local RF regression model only considers nearby data points for calibration and assigns different weights to them according to the weight matrix. The kernel is the region where the local RF regression model runs, and the bandwidth is the maximum distance to an observation point [30].
Based on the GWRFR model, we employed nine datasets of influencing factors as characteristic variables to construct models for six water quality indicators. In terms of the driving parameters involved in training, both temporal and spatial consistency were ensured. Temporally speaking, most data are from 2021, with the population density data sourced from 2020 due to availability constraints, thus minimizing temporal discrepancies. Spatially speaking, the data are uniformly cropped to cover the Yangtze River basin and resampled to a 30 m resolution, ensuring consistency and enabling effective model training. In the training process, each water quality indicator is trained using all of the driving parameter data, which allows for a comprehensive consideration of the interactions between different factors and indicators, aiming to enhance the performance and robustness of the models. The distance matrix between observation points was first calculated based on the Euclidean distance algorithm based on their positions. This distance matrix was then converted into a weight matrix according to the chosen bandwidth parameter and weight kernel function. Since the research object is the section control unit with significant area differences, we employed the bi-square function as the weight function and selected the variable bandwidth to establish a local model for each observation point.

3.2. The Variable Importance Measurement (VIM)

We employed the mean squared error ( M S E ) reduction method to estimate the variable importance, as recommended for permuting variables [59,60,61]. This method utilizes a reduction in M S E values from out-of-bag (OOB) data, which consist of data points not used in constructing the decision trees [62]. The process of using the M S E reduction method includes three main steps.
It first needs to calculate each decision tree’s M S E value for the out-of-bag data:
M S E t = 1 n t ∑ i = 1 n t ( b i − b ^ i , t ) 2
where n t represents the county number in the OOB data for the tree t , and b ^ i , t is the predicted dependent variable for the i th county in the tree t .
Then, the target variable m is randomly permuted, and the resulting M S E value for the newly generated tree t is calculated using Equation (3):
M S E t ( m ) = 1 n t ∑ i = 1 n t b i − b ^ i , t ( m ) 2
where b ^ i , t ( m ) represents the prediction value of the dependent variable for the i th county in the new tree t , and where the target variable m was randomly permuted.
Finally, the M S E reduction between M S E t and M S E t ( m ) is calculated, and this M S E reduction is used to determine the importance of variable m of the decision tree t . To evaluate the overall importance of variable m in the random forest model, these reductions are averaged across all n trees (Equation (4)):
V I M ( m ) = M S E ( m ) = 1 n ∑ t = 1 n M S E t − M S E t ( m )

3.3. Model Evaluation

We assessed the method’s reliability with a ten-fold cross-validation strategy, dividing the training data into ten equal subsets. In each iteration, nine subsets were used for training and one for validation. The number of matching sample points in each subset was identical, ensuring consistency in the training and validation process. This process was repeated ten times to assess the robustness of the model. We evaluated the training prediction model’s performance using the coefficient of determination ( R 2 ) and the root mean square error (RMSE); these two metrics have been widely used in the field of model evaluation [63]. The mathematical formulas for these metrics are shown below.
The coefficient of determination was
R 2 = 1 − ∑ i = 1 n ( b ^ i − b i ) 2 ∑ i = 1 n ( b ¯ i − b i ) 2
The root mean square error was
R M S E = 1 n ∑ i = 1 n ( b i − b ^ i ) 2
Here, n represents the total data count, b ^ i is the predicted value of the dependent variable, b ¯ i is the mean value of b i , and b i denotes the actual dependent variable value.

4. Results and Analysis

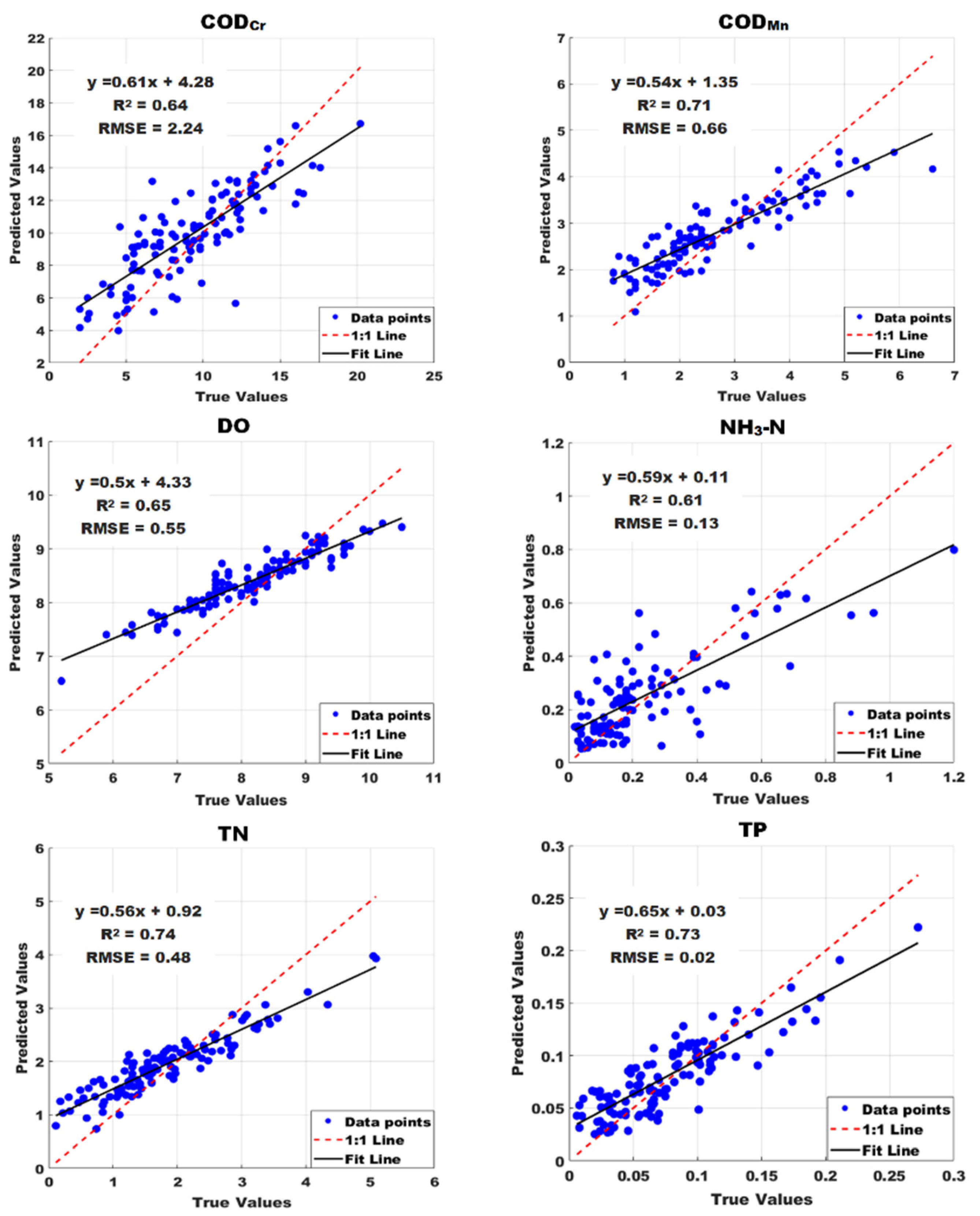
4.1. Water Quality Prediction Model Assessment

During the model training process, we first evaluated the reliability of the water quality prediction model using a ten-fold cross-validation strategy. As shown in Figure 3, all the water quality indicators can be accurately predicted based on our prediction model. For example, the indicator NH3-N has the lowest accuracy, with an R2 value of 0.61, while the indicator TN has the highest with a value of 0.74. Although all the water quality indicators can be well predicted, there is still some deviation between the predicted and true values. In other words, the prediction model may under- or overestimate certain ranges of water quality indicators. For example, the model shows that the indicators CODCr and NH3-N are overestimated in a low value range and underestimated in a high value range.

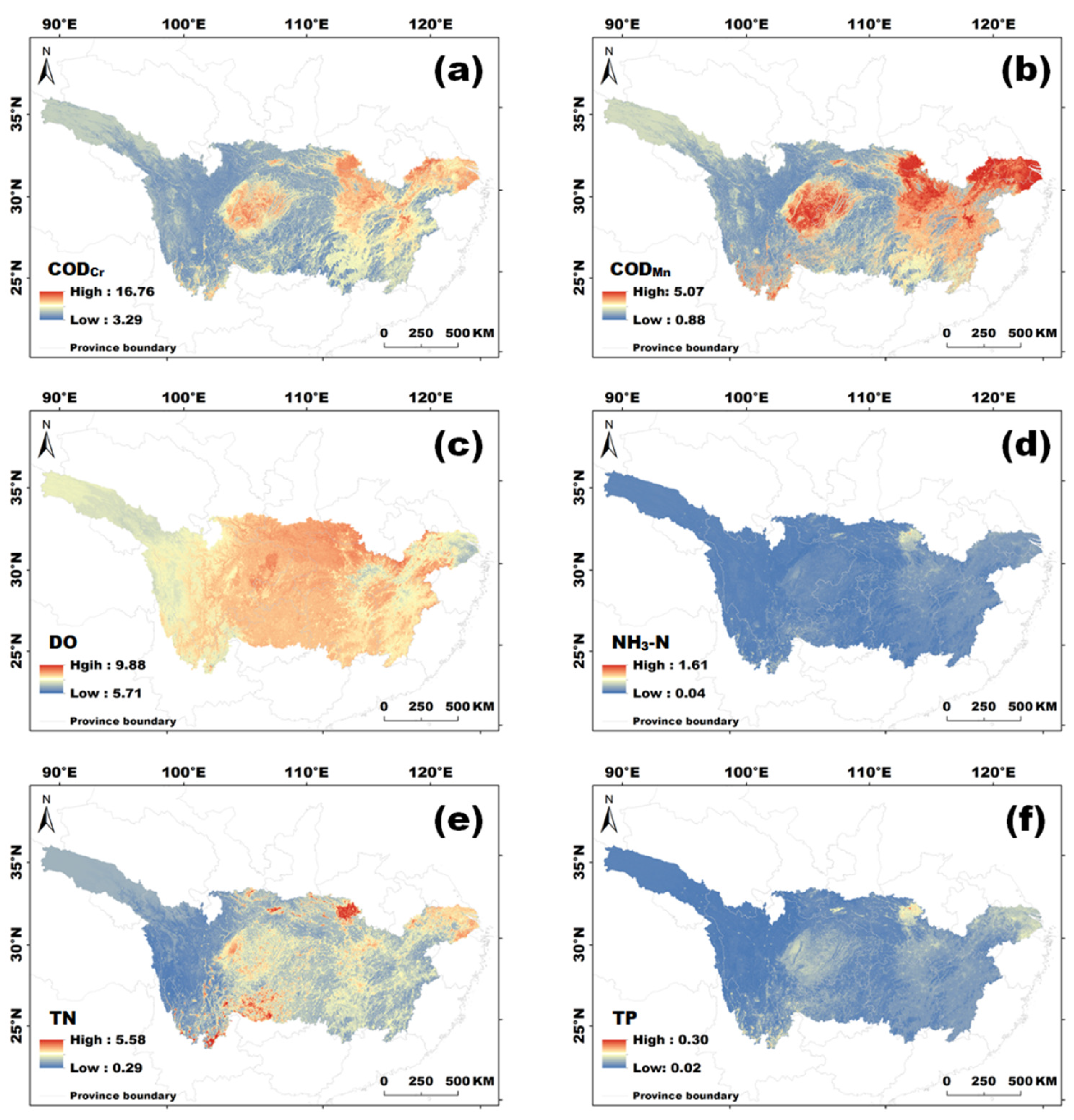
4.2. Mapping the Yangtze River Water Quality Indicators

We further used the trained water quality prediction model to map the spatial distribution of water quality in the Yangtze River, achieving a spatial resolution of 30 m. The Figure 4a–f shows the mapping results of the CODCr, CODMn, DO, NH3-N, TN, and TP in the Yangtze River basin in 2021. The variation range of the CODCr (Figure 4a) is from 3.29 mg/L to 16.76 mg/L in the Yangtze River. In terms of the CODCr distribution in the Yangtze River, higher concentrations are observed in the middle and lower reaches, as well as in the Sichuan Basin. Furthermore, it can be noted that its spatial distribution is closely related to terrain characteristics (Figure 5a).
The variation range of the CODMn (Figure 4b) is from 0.88 mg/L to 5.07 mg/L. The spatial distribution of the CODMn is similar to that of the CODCr. It can be noted that the predicted results are generally low in the mountain areas (Figure 4b and Figure 5a). This may be because of the large slope of the mountain, which is not conducive to population gathering, planting, and production, resulting in limited pollutant emissions within the purification capacity of the basin itself. The predicted variation range of the DO in the Yangtze River (Figure 4c) is from 5.71 mg/L to 9.88 mg/L. This indicator has an opposite meaning compared with the other indicators, so it shows a different pattern in the mapping results. The pattern shows higher concentrations in the middle of the Yangtze River basin with lower levels on the eastern and western sides. There are several possible explanations for the above pattern: (i) the upper reaches of the Yangtze River on the Qinghai–Tibet Plateau undergo a period of freeze when ice on the surface of the river prevents oxygen from dissolving in the water; (ii) the gentle terrain, weak hydrodynamic conditions, and salty water in the eastern part of the Yangtze River lead to the low DO content.
The variation range of the NH3-N in the Yangtze River (Figure 4d) is from 0.04 mg/L to 1.61 mg/L. Its mapping pattern is not only concentrated in the Sichuan Basin and the middle and lower reaches of the Yangtze River but is also scattered in areas with high factory and population densities (Figure 5c,d). The variation range of the TN in the Yangtze River (Figure 4e) is from 0.29 mg/L to 5.58 mg/L. It can be noted that a pattern of high values appeared in the Tangbai River, with the main streams below Shigu, the Sinan River, and the Taihu Lake basin. Furthermore, the predicted TN has the highest value in areas with frequent human activities (Figure 5d), mainly concentrated in the Jinsha and Mintuo River systems. In addition, the low values are distributed in the Yalong and Dadu River basins. Overall, TN pollution is more serious in regions with intensive human activity, while it decreases in regions with less human activity.
The variation range of the TP according to the mapping results is from 0.02 mg/L to 0.3 mg/L. According to these results, we can note that the spatial distribution trend is similar to that of TN, both of which show variation according to the intensity of human activity. However, the degree of TP pollution is lower than that of TN in the Yangtze River. The strong correlation between TP and population density is primarily observed in the lower reaches of the Yangtze River, Taihu Lake, Han River, and Jialing River systems (Figure 5d).

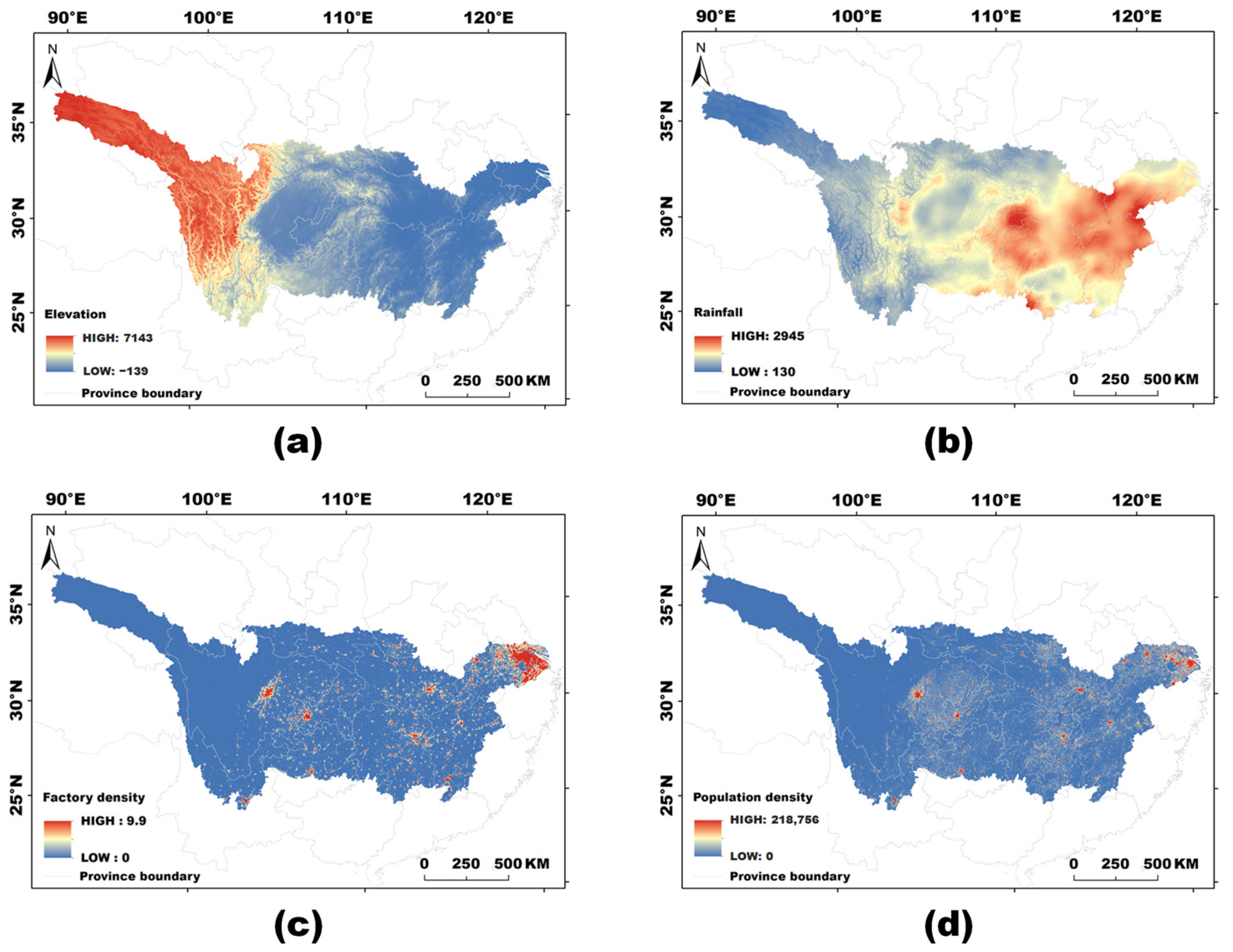
4.3. An Analysis of Factors Influencing Water Quality

4.3.1. Importance Analysis

We selected nine input variables for the GWRFR model to train the water quality prediction model. We explored the contribution of these input variables to the final training model. We quantified the contribution of influencing factors using the VIM described in Section 3.2 and defined those that may significantly affect water environmental quality as key influencing factors. For the water quality indicator CODCr, the key influencing factors included rainfall, slope, impervious water, elevation, and temperature (Figure 6a). It can be noted that the factors with higher importance ranks are mainly natural factors, while those with lower are mainly human factors. The above situation may be due to the fact that CODCr pollution in the Yangtze River basin is not serious.
In terms of the water quality indicator CODMn, the key influencing factors include rainfall, slope, temperature, and elevation (Figure 6b). Like the CODCr, the most important factors are natural variables, which may be because both CODMn and CODCr are organic matter in water. Furthermore, we can note that temperature plays a crucial role in CODMn prediction because high-temperature conditions may exacerbate the growth and degradation of algae, resulting in high CODMn [64].
For the DO, non-natural factors such as population and factory density become important (Figure 6c). For the NH3-N, it can be noted that the differences among influencing factors are very small, indicating that its levels in the Yangtze River basin are jointly affected by multiple factors (Figure 6d). Different from the above four water quality indicators, the TN is dominated by human factors, such as population and factory density, and is less influenced by natural factors, such as slope and forest cover (Figure 6e). This phenomenon shows that the Yangtze River basin has relatively serious TN pollution. TP is affected by both human and natural factors, though the former dominates (Figure 6f).

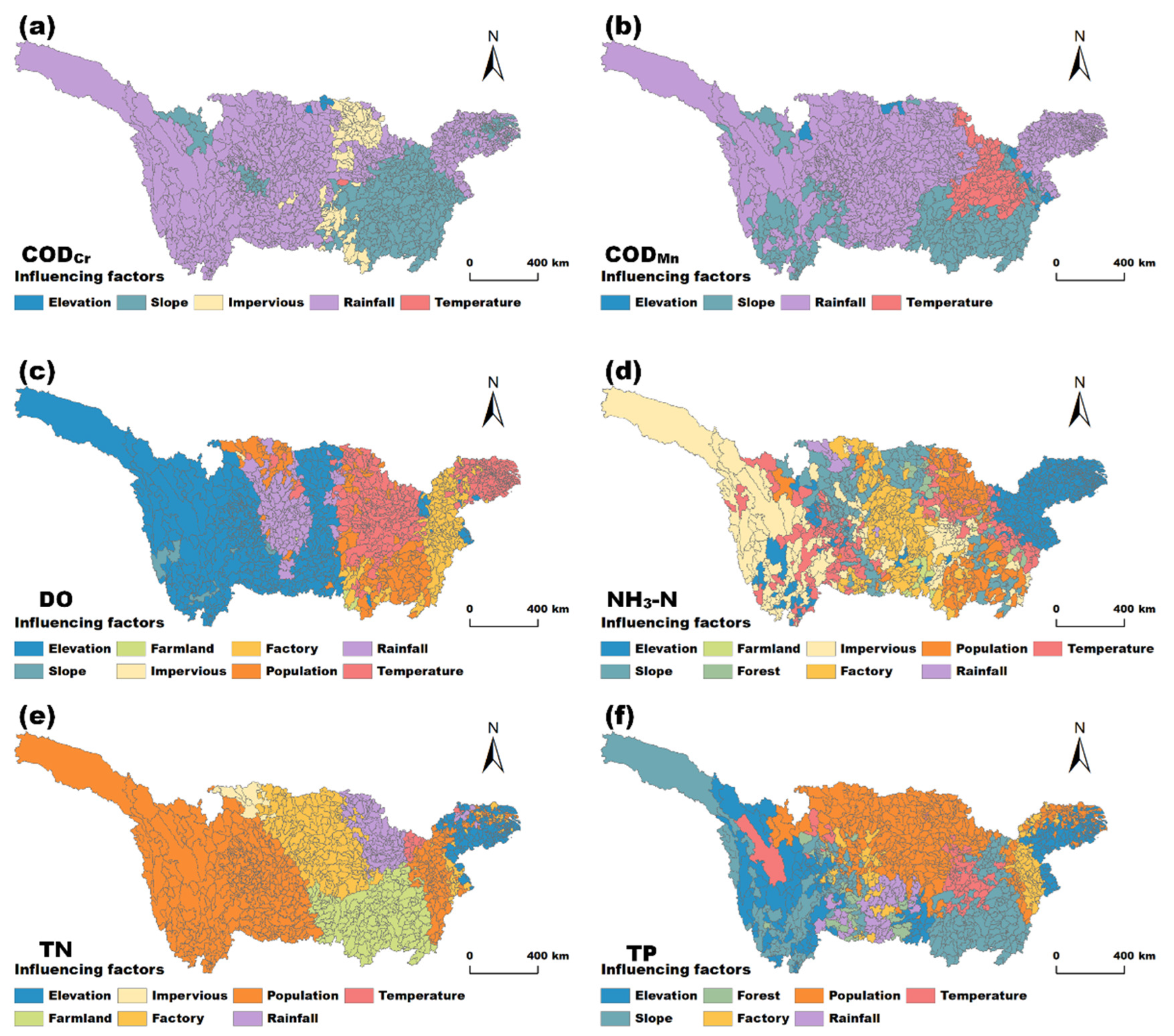
4.3.2. Spatial Distribution Analysis of Key Influencing Factors

We also map the spatial distribution of the key influencing factors for each water quality prediction model (Figure 7a). For the CODCr, rainfall and slope are the key influencing factors of most section control units, with rates of up to 61% and 31%, respectively. It can be noted that the spatial distribution of factors shows significant spatial aggregation characteristics, as well as differences. Moreover, the relationship between each influencing factor and the CODCr varies in space, and the change mode is different. The CODMn is almost the same as the CODCr—rainfall and slope are the key influencing factors for the vast majority of section control units, with rates of up to 68% and 20%, respectively, and only some regions have different key determinant factors (Figure 7b).
The DO, NH3-N, TN, and TP have relatively more determinant factors compared to the CODMn and CODCr. For the DO, there are eight main influencing factors, with temperature and elevation being key for most section control units and reaching 35% and 31%, respectively (Figure 7c). It is worth noting that the section control units where temperature is a key factor are mainly distributed in the middle reaches of the Yangtze River, Dongting Lake, and the lower reaches of the river system. For NH3-N, the nine factors involved in the construction of the water quality model are all key influencing factors (Figure 7d). The spatial distribution of the key influencing factors shows a generally checkerboard pattern with cluster distribution in local areas. TN and TP both have seven main influencing factors; some factors are the same, but they have different spatial distributions. For the TN, population density is the key influencing factor for most section control units, reaching 41% (Figure 7e). Furthermore, the spatial distribution of key factors affecting TN shows significant spatial aggregation characteristics. For the TP, population density, slope, and elevation are the key influencing factors for the majority of section control units, reaching 35%, 21%, and 21%, respectively (Figure 7f). Forest, rainfall, and temperature are the key influencing factors of individual section control units. Furthermore, the overall spatial distribution of the key influencing factors shows significant spatial aggregation characteristics.

5. Discussion

This study achieved a fine estimation of water quality indicators in the Yangtze River basin, analyzing the influence of natural and human factors upon them. Although we validated our mapping results, there are some uncertainties or limitations that could be improved in future studies.
During model verification, significant under- and overestimation issues were identified in predicting certain indicators, particularly at the extreme high and low ranges. This issue is likely attributable to the insufficient proportions of maximum and minimum values in the training samples, which causes the model to classify these extreme values as outliers during training. Consequently, the model fails to adequately learn the underlying patterns associated with these extreme values, leading to deviations between predictions and actual observations. Adjusting the bandwidth parameter in the GWRFR model presents a potential solution, as this can increase the proportional representation of extreme values within the training process. This adjustment is critical for enabling the model to better capture localized variations in and the spatial heterogeneity inherent to different geographical regions. However, it is important to recognize that excessively narrow bandwidths may reduce the number of training samples available for localized models, thereby compromising the reliability and completeness of training [65]. To solve this problem in the future, provincial and municipal water quality monitoring stations will be considered to increase the number of samples and improve the training of local models.
Through the mapped water quality results, we note that pollution is more serious in the middle and lower reaches of the Yangtze River and in the Sichuan basin. Looking at the mapping results of the pollution indicators combined with population density, we find that the spatial distribution of some pollution indicators, such as TN, TP, and NH3-N, shows obvious distribution characteristics in the center and at the edge. We also find that pollution is more serious in regions with intensive human activity and less serious in regions with less. We also note that some water pollution indicator distributions are closely related to terrain, such as the CODMn and CODCr, showing a lower estimated value in regions with plains and basins and a higher value in those with hills, mountains, and plateaus. One reason may be due to the large slope of the mountain, which is not conducive to population gathering, planting, and production, resulting in limited pollutant emissions within the purification capacity of the basin itself. The other reason may be because the area with a steep slope has a high hydrodynamic strength, meaning that pollutants in the water will quickly migrate to areas with gentler terrains [66].
From the analysis results of the training model’s input parameters, we can understand the causes of some pollution indicators in the Yangtze River to some extent. For example, we found that pollution indicators of organic matter in water, such as the CODMn and CODCr, are mainly influenced by natural factors in the basin. Taking temperature as an example, high-temperature conditions may exacerbate the growth and degradation of algae, resulting in high CODMn and CODCr [67]. Another interesting finding is that some pollution situations in the Yangtze River basin, such as the TN concentration, can be well explained by topography and human activity. Areas with a high population density produce more domestic pollution, and population concentration is accompanied by intensive and concentrated agricultural and industrial activities [68,69]. All of the above situations lead to an increase in the TN concentration in the basin. Additionally, this elevation, to a certain extent, affects the degree of aggregation of social production activities, and areas with low elevation are more conducive to social production activities and further promote their aggregation. Therefore, low-elevation areas more readily experience aggravated TN pollution than high-elevation areas. Considering the great significance of spatial heterogeneity in water quality estimation and analysis, it provides a critical basis to scientifically set control units and implement region-specific watershed management.

6. Conclusions

In this study, using the GWRFR model, we explore the feasibility of using water quality monitoring data from state-controlled sections and relevant geographic information data to map the water quality of the Yangtze River basin. We found that the relationships between various water quality indicators and influencing factors are quite different. The CODCr and CODMn are primarily influenced by natural factors such as slope and rainfall. Regarding the CODCr, the key influencing factors are the section control units of rainfall and slope, accounting for 92%; in terms of the CODMn, the same key influencing factors account for 88%. The ranking of the importance of variables shows that both natural and human factors influence the DO and NH3-N. In the Yangtze River basin, TN and TP are serious pollution indicators that are mainly affected by human factors. As a representative human factor, population density is the key influencing factor of TN in 41% and TP in 35% of section control units.
Another interesting finding is that the relationship between influencing factors and water quality indicators is spatially variable. Spatially speaking, none of the influencing factors can maintain a high variable importance score across the whole Yangtze River basin, and the relationships between all influencing factors and the water quality indicator have changed to varying degrees. By means of visualization, we found that, although population density is one of the main TN and TP influencing factors, their relationship is different in space. The strong correlation between TN and population density is primarily concentrated in the Mintuo and Jinsha River systems and is relatively weak in their regions. A strong correlation between TP and population density was found in the lower reaches of the Yangtze River, Taihu Lake, Han River, and Jialing River systems. This study highlights the complex and spatially variable relationships between natural and human factors and water quality indicators in the Yangtze River basin. Grasping these relationships is essential for developing targeted and effective water management strategies to improve and sustain water quality across various regions of the basin. Overall, the integration of water quality monitoring data and geographic information data using the GWRFR model is reliable and has significant potential for the fine estimation of water quality.

Author Contributions

Conceptualization and methodology, F.D. and Y.X.; data curation, M.S., W.L. (Wenhui Liu), B.W., W.L. (Wei Liu), Y.Y. and L.C.; formal analysis, Y.X. and F.D.; funding acquisition, F.D.; software, F.D. and Y.X.; writing—original draft, F.D., Y.X. and M.S.; writing—review and editing, F.D., Y.X., M.S., W.L. (Wenhui Liu), B.W., W.L. (Wei Liu), Y.Y. and L.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the High-Level Talent Research Initiation Project of the Xiamen University of Technology (YKJ23015R); the Natural Science Foundation of Xiamen, China (3502Z202471079 and 3502Z202473059); and the Chunhui Project Foundation of the Education Department of China (202200324).

Data Availability Statement

The data utilized in this study were primarily sourced from publicly accessible resources. Further details about the datasets are provided in Section 2.2.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Table A1. Part of the annual average of water quality monitoring data of section control units across the Yangtze River basin in 2021. We mainly present the section code and the annual average of the CODCr, CODMn, DO, NH3-N, TN, and TP of the section control units.
Table A1. Part of the annual average of water quality monitoring data of section control units across the Yangtze River basin in 2021. We mainly present the section code and the annual average of the CODCr, CODMn, DO, NH3-N, TN, and TP of the section control units.
Section CodeCODCr (mg/L)CODMn (mg/L)DO
(mg/L)		NH3-N
(mg/L)		TN
(mg/L)		TP
(mg/L)
000113.35.47.40.161.770.115
000211.43.97.90.191.920.101
0003112.27.60.141.780.092
00048.82.68.60.132.160.117
000513.53.26.50.53.010.116
00068.22.28.20.122.080.084
000713.44.28.60.182.510.068
000814.84.27.90.472.190.104
00098.427.80.072.350.088
00106.82.38.40.082.140.102
001112.846.30.151.840.102
0012112.66.50.232.010.16
001313.64.670.262.390.157
001412.437.80.262.260.16
001511.33.47.40.452.240.168
001611.72.78.30.191.930.088
001718.34.97.80.692.480.156
001810.938.30.822.430.106
001917.74.87.60.341.880.073
002011.82.510.20.111.790.087
00219.12.47.50.161.840.101
0022102.770.452.580.13
00238.22.57.20.242.330.111
00249.42.47.70.141.70.099
002518.957.80.21.240.044
002617.84.38.10.21.030.055
00277.82.18.10.341.980.074
00289.73.58.20.331.90.057
0029102.780.432.430.08
00307.22.48.20.161.340.061
00315.82.29.40.151.520.038
00329.83.290.491.80.124
003311.447.30.572.660.099
003412.32.87.90.261.830.064
00358.62.67.80.142.020.061
003612.82.38.70.091.750.064
003713.33.78.20.090.90.045
00385.81.5100.031.180.024
00398.42.58.50.040.950.037
00406.21.99.60.041.380.032

References

  1. Xiao, J.; Gao, D.; Zhang, H.; Shi, H.; Chen, Q.; Li, H.; Ren, X.; Chen, Q. Water quality assessment and pollution source apportionment using multivariate statistical techniques: A case study of the Laixi River Basin, China. Environ. Monit. Assess. 2023, 195, 287. [Google Scholar] [CrossRef] [PubMed]
  2. Chen, S.; Fang, M.; Zhuang, D. Spatial non-stationarity and heterogeneity of metropolitan housing prices: The case of Guangzhou, China. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 42008. [Google Scholar] [CrossRef]
  3. Comber, A. Hyper-local geographically weighted regression: Extending GWR through local model selection and local bandwidth optimization. J. Spat. Int. Sci. 2018, 63–84. [Google Scholar] [CrossRef]
  4. Wang, F.; Wang, Y.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef]
  5. Masoumi, F.; Afshar, A.; Palatkaleh, S.T. Selective withdrawal optimization in river-reservoir systems; trade-offs between maximum allowable receiving waste load and water quality criteria enhancement. Environ. Monit. Assess. 2016, 188, 390. [Google Scholar] [CrossRef]
  6. Jeznach, L.C.; Jones, C.; Matthews, T.; Tobiason, J.E.; Ahlfeld, D.P. A framework for modeling contaminant impacts on reservoir water quality. J. Hydrol. 2016, 537, 322–333. [Google Scholar] [CrossRef]
  7. Sadeghian, A.; Chapra, S.C.; Hudson, J.; Wheater, H.; Lindenschmidt, K. Improving in-lake water quality modeling using variable chlorophyll a/algal biomass ratios. Environ. Modell. Softw. 2018, 101, 73–85. [Google Scholar] [CrossRef]
  8. Yazdi, J.; Moridi, A. Interactive Reservoir-Watershed Modeling Framework for Integrated Water Quality Management. Water Resour. Manag. 2017, 31, 2105–2125. [Google Scholar] [CrossRef]
  9. Costa, C.M.D.S.; Leite, I.R.; Almeida, A.K.; de Almeida, I.K. Choosing an appropriate water quality model—A review. Environ. Monit. Assess. 2021, 193, 38. [Google Scholar] [CrossRef]
  10. Ye, T.; Zhao, N.; Yang, X.; Ouyang, Z.; Liu, X.; Chen, Q.; Hu, K.; Yue, W.; Qi, J.; Li, Z.; et al. Improved population mapping for China using remotely sensed and points-of-interest data within a random forests model. Sci. Total Environ. 2019, 658, 936–946. [Google Scholar] [CrossRef]
  11. You, H.; Yang, J.; Xue, B.; Xiao, X.; Xia, J.; Jin, C.; Li, X. Spatial evolution of population change in Northeast China during 1992–2018. Sci. Total Environ. 2021, 776, 146023. [Google Scholar] [CrossRef]
  12. Chen, Y.; Wu, G.; Ge, Y.; Xu, Z. Mapping Gridded Gross Domestic Product Distribution of China Using Deep Learning with Multiple Geospatial Big Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 1791–1802. [Google Scholar] [CrossRef]
  13. Zhong, L.; Liu, X.; Ao, J. Spatiotemporal dynamics evaluation of pixel-level gross domestic product, electric power consumption, and carbon emissions in countries along the belt and road. Energy 2022, 239, 121841. [Google Scholar] [CrossRef]
  14. Khan, S.N.; Li, D.; Maimaitijiang, M. A Geographically Weighted Random Forest Approach to Predict Corn Yield in the US Corn Belt. Remote Sens. 2022, 14, 2843. [Google Scholar] [CrossRef]
  15. Burigato Costa, C.M.D.S.; Da Silva Marques, L.; Almeida, A.K.; Leite, I.R.; de Almeida, I.K. Applicability of water quality models around the world—A review. Environ. Sci. Pollut. Res. 2019, 26, 36141–36162. [Google Scholar] [CrossRef]
  16. Rajaee, T.; Khani, S.; Ravansalar, M. Artificial intelligence-based single and hybrid models for prediction of water quality in rivers: A review. Chemom. Intell. Lab. Syst. 2020, 200, 103978. [Google Scholar] [CrossRef]
  17. Draidi Areed, W.; Price, A.; Arnett, K.; Mengersen, K. Spatial statistical machine learning models to assess the relationship between development vulnerabilities and educational factors in children in Queensland, Australia. Bmc Public Health. 2022, 22, 2232. [Google Scholar] [CrossRef]
  18. Lotfata, A.; Georganos, S.; Kalogirou, S.; Helbich, M. Ecological Associations between Obesity Prevalence and Neighborhood Determinants Using Spatial Machine Learning in Chicago, Illinois, USA. ISPRS Int. J. Geo-Inf. 2022, 11, 550. [Google Scholar] [CrossRef]
  19. Liao, H.; Sun, W. Forecasting and Evaluating Water Quality of Chao Lake based on an Improved Decision Tree Method. Procedia Environ. Sci. 2010, 2, 970–979. [Google Scholar] [CrossRef]
  20. Zare, A.H. Evaluation of multivariate linear regression and artificial neural networks in prediction of water quality parameters. J. Environ. Health Sci. Eng. 2014, 12, 40. [Google Scholar] [CrossRef]
  21. Liu, J.; Yu, C.; Hu, Z.; Zhao, Y.; Bai, Y.; Xie, M.; Luo, J. Accurate Prediction Scheme of Water Quality in Smart Mariculture with Deep Bi-S-SRU Learning Network. IEEE Access 2020, 8, 24784–24798. [Google Scholar] [CrossRef]
  22. Li, L.; Jiang, P.; Xu, H.; Lin, G.; Guo, D.; Wu, H. Water quality prediction based on recurrent neural network and improved evidence theory: A case study of Qiantang River, China. Environ. Sci. Pollut. Res. Int. 2019, 26, 19879–19896. [Google Scholar] [CrossRef] [PubMed]
  23. Liu, P.; Wang, J.; Sangaiah, A.; Xie, Y.; Yin, X. Analysis and Prediction of Water Quality Using LSTM Deep Neural Networks in IoT Environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef]
  24. Wang, X.; Qiao, M.; Li, Y.; Tavares, A.; Qiao, Q.; Liang, Y. Deep-Learning-Based Water Quality Monitoring and Early Warning Methods: A Case Study of Ammonia Nitrogen Prediction in Rivers. Electronics 2023, 12, 4645. [Google Scholar] [CrossRef]
  25. Georganos, S.; Grippa, T.; Niang Gadiaga, A.; Linard, C.; Lennert, M.; Vanhuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
  26. Quiñones, S.; Goyal, A.; Ahmed, Z.U. Geographically weighted machine learning model for untangling spatial heterogeneity of type 2 diabetes mellitus (T2D) prevalence in the USA. Sci. Rep. 2021, 11, 6955. [Google Scholar]
  27. Ren, Y.; Yuan, W.; Zhang, B.; Wang, S. Does improvement of environmental efficiency matter in reducing carbon emission intensity? Fresh evidence from 283 prefecture-level cities in China. J. Clean. Prod. 2022, 373, 133878. [Google Scholar] [CrossRef]
  28. Huang, J.; Huang, Y.; Pontius Jr, R.G.; Zhang, Z. Geographically weighted regression to measure spatial variations in correlations between water pollution versus land use in a coastal watershed. Ocean. Coast. Manag. 2015, 103, 14–24. [Google Scholar] [CrossRef]
  29. Mainali, J.; Chang, H.; Parajuli, R. Stream distance-based geographically weighted regression for exploring watershed characteristics and water quality relationships. Ann. Am. Assoc. Geogr. 2023, 113, 390–408. [Google Scholar] [CrossRef]
  30. Grekousis, G.; Feng, Z.; Marakakis, I.; Lu, Y.; Wang, R. Ranking the importance of demographic, socioeconomic, and underlying health factors on US COVID-19 deaths: A geographical random forest approach. Health Place 2022, 74, 102744. [Google Scholar] [CrossRef]
  31. Chen, Y.; Zang, L.; Shen, G.; Liu, M.; Du, W.; Fei, J.; Yang, L.; Chen, L.; Wang, X.; Liu, W.; et al. Resolution of the Ongoing Challenge of Estimating Nonpoint Source Neonicotinoid Pollution in the Yangtze River Basin Using a Modified Mass Balance Approach. Environ. Sci. Technol. 2019, 53, 2539–2548. [Google Scholar] [CrossRef] [PubMed]
  32. Chen, T.; Wang, Y.; Gardner, C.; Wu, F. Threats and protection policies of the aquatic biodiversity in the Yangtze River. J. Nat. Conserv. 2020, 58, 125931. [Google Scholar] [CrossRef]
  33. Li, X.; Mander, Ü.; Ma, Z.; Jia, Y. Water Quality Problems and Potential for Wetlands as Treatment Systems in the Yangtze River Delta, China. Wetlands 2009, 29, 1125–1132. [Google Scholar] [CrossRef]
  34. Di, Z.; Chang, M.; Guo, P.; Li, Y.; Chang, Y. Using Real-Time Data and Unsupervised Machine Learning Techniques to Study Large-Scale Spatio–Temporal Characteristics of Wastewater Discharges and their Influence on Surface Water Quality in the Yangtze River Basin. Water 2019, 11, 1268. [Google Scholar] [CrossRef]
  35. Liu, S.; Fu, R.; Liu, Y.; Suo, C. Spatiotemporal variations of water quality and their driving forces in the Yangtze River Basin, China, from 2008 to 2020 based on multi-statistical analyses. Environ. Sci. Pollut. Res. 2022, 29, 69388–69401. [Google Scholar] [CrossRef]
  36. Huang, J.; Zhang, Y.; Bing, H.; Peng, J.; Dong, F.; Gao, J.; Arhonditsis, G.B. Characterizing the river water quality in China: Recent progress and on-going challenges. Water Res. 2021, 201, 117309. [Google Scholar] [CrossRef]
  37. Di, Z.; Chang, M.; Guo, P. Water Quality Evaluation of the Yangtze River in China Using Machine Learning Techniques and Data Monitoring on Different Time Scales. Water 2019, 11, 339. [Google Scholar] [CrossRef]
  38. Duan, W.; He, B.; Chen, Y.; Zou, S.; Wang, Y.; Nover, D.; Chen, W.; Yang, G. Identification of long-term trends and seasonality in high-frequency water quality data from the Yangtze River basin, China. PLoS ONE 2018, 13, e0188889. [Google Scholar] [CrossRef]
  39. Lu, J.; Gu, J.; Han, J.; Xu, J.; Liu, Y.; Jiang, G.; Zhang, Y. Evaluation of Spatiotemporal Patterns and Water Quality Conditions Using Multivariate Statistical Analysis in the Yangtze River, China. Water 2023, 15, 3242. [Google Scholar] [CrossRef]
  40. Yao, R.; Wang, L.; Gui, X.; Zheng, Y.; Zhang, H.; Huang, X. Urbanization Effects on Vegetation and Surface Urban Heat Islands in China’s Yangtze River Basin. Remote Sens. 2017, 9, 540. [Google Scholar] [CrossRef]
  41. Yang, X.; Meng, F.; Fu, P.; Zhang, Y.; Liu, Y. Spatiotemporal change and driving factors of the Eco-Environment quality in the Yangtze River Basin from 2001 to 2019. Ecol. Indic. 2021, 131, 108214. [Google Scholar] [CrossRef]
  42. Yang, P.; Xia, J.; Luo, X.; Meng, L.; Zhang, S.; Cai, W.; Wang, W. Impacts of climate change-related flood events in the Yangtze River Basin based on multi-source data. Atmos. Res. 2021, 263, 105819. [Google Scholar] [CrossRef]
  43. Li, Y.; Yan, D.; Peng, H.; Xiao, S. Evaluation of precipitation in CMIP6 over the Yangtze River Basin. Atmos. Res. 2021, 253, 105406. [Google Scholar] [CrossRef]
  44. Qu, S.; Wang, L.; Lin, A.; Yu, D.; Yuan, M.; Li, C. Distinguishing the impacts of climate change and anthropogenic factors on vegetation dynamics in the Yangtze River Basin, China. Ecol. Indic. 2020, 108, 105724. [Google Scholar] [CrossRef]
  45. Smith, B.; Sandwell, D. Accuracy and resolution of shuttle radar topography mission data. Geophys. Res. Lett. 2003, 30, 1467. [Google Scholar] [CrossRef]
  46. Yang, J.; Huang, X. The 30 m annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
  47. Calka, B.; Nowak Da Costa, J.; Bielecka, E. Fine scale population density data and its application in risk assessment. Geomat. Nat. Hazards Risk 2017, 8, 1440–1455. [Google Scholar] [CrossRef]
  48. Tatem, A.J. WorldPop, open data for spatial demography. Sci. Data 2017, 4, 170004. [Google Scholar] [CrossRef]
  49. Bai, Z.; Wang, J.; Wang, M.; Gao, M.; Sun, J. Accuracy Assessment of Multi-Source Gridded Population Distribution Datasets in China. Sustainability 2018, 10, 1363. [Google Scholar] [CrossRef]
  50. Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating census data for population mapping using random forests with remotely-sensed and ancillary data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [PubMed]
  51. Trigg, M.A.; Birch, C.E.; Neal, J.C.; Bates, P.D.; Smith, A.; Sampson, C.C.; Yamazaki, D.; Hirabayashi, Y.; Pappenberger, F.; Dutra, E.; et al. The credibility challenge for global fluvial flood risk analysis. Environ. Res. Lett. 2016, 11, 94014. [Google Scholar] [CrossRef]
  52. Mohanty, M.P.; Simonovic, S.P. Understanding dynamics of population flood exposure in Canada with multiple high-resolution population datasets. Sci. Total Environ. 2021, 759, 143559. [Google Scholar] [CrossRef] [PubMed]
  53. Wang, J.; Wei, J.; Zhang, W.; Liu, Z.; Du, X.; Liu, W.; Pan, K. High-resolution temporal and spatial evolution of carbon emissions from building operations in Beijing. J. Clean. Prod. 2022, 376, 134272. [Google Scholar] [CrossRef]
  54. Guo, B.; Zhang, J.; Meng, X.; Xu, T.; Song, Y. Long-term spatio-temporal precipitation variations in China with precipitation surface interpolated by ANUSPLIN. Sci. Rep. 2020, 10, 81. [Google Scholar] [CrossRef] [PubMed]
  55. Danladi Bello, A.; Hashim, N.; Mohd Haniffah, M. Predicting Impact of Climate Change on Water Temperature and Dissolved Oxygen in Tropical Rivers. Climate 2017, 5, 58. [Google Scholar] [CrossRef]
  56. Quevedo-Castro, A.; Bustos-Terrones, Y.A.; Bandala, E.R.; Loaiza, J.G.; Rangel-Peraza, J.G. Modeling the effect of climate change scenarios on water quality for tropical reservoirs. J. Environ. Manag. 2022, 322, 116137. [Google Scholar] [CrossRef]
  57. Jerves-Cobo, R.; Forio, M.A.E.; Lock, K.; Van Butsel, J.; Pauta, G.; Cisneros, F.; Nopens, I.; Goethals, P.L.M. Biological water quality in tropical rivers during dry and rainy seasons: A model-based analysis. Ecol. Indic. 2020, 108, 105769. [Google Scholar] [CrossRef]
  58. Luo, Y.; Yan, J.; McClure, S.C.; Li, F. Socioeconomic and environmental factors of poverty in China using geographically weighted random forest regression model. Environ. Sci. Pollut. Res. 2022, 29, 33205–33217. [Google Scholar] [CrossRef]
  59. Ishwaran, H. Variable importance in binary regression trees and forests. Electron. J. Stat. 2007, 1, 519–537. [Google Scholar] [CrossRef]
  60. Strobl, C.; Boulesteix, A.L.; Zeileis, A.; Hothorn, T. Bias in random forest variable importance measures: Illustrations, sources and a solution. BMC Bioinform. 2007, 8, 25. [Google Scholar] [CrossRef]
  61. Strobl, C.; Boulesteix, A.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed]
  62. Cai, H.; Lam, N.S.N.; Qiang, Y.; Zou, L.; Correll, R.M.; Mihunov, V. A synthesis of disaster resilience measurement methods and indices. Int. J. Disaster Risk Reduct. 2018, 31, 844–855. [Google Scholar] [CrossRef]
  63. Sakaa, B.; Elbeltagi, A.; Boudibi, S.; Chaffai, H.; Islam, A.; Cimusa Kulimushi, L.; Choudhari, P.P.; HANI, A.; Brouziyne, Y.; Wong, Y.J. Water quality index modeling using random forest and improved SMO algorithm for support vector machine in Saf-Saf river basin. Environ. Sci. Pollut. Res. 2022, 29, 48491–48508. [Google Scholar] [CrossRef] [PubMed]
  64. Ren, L.; Huang, J.; Wang, B.; Wang, H.; Gong, R.; Hu, Z. Effects of temperature on the growth and competition between Microcystis aeruginosa and Chlorella pyrenoidosa with different phosphorus availabilities. Desalination Water Treat. 2021, 241, 87–111. [Google Scholar] [CrossRef]
  65. Koç, T. Bandwidth Selection in Geographically Weighted Regression Models via Information Complexity Criteria. J. Math. 2022, 2022, 1527407. [Google Scholar] [CrossRef]
  66. Xu, X.; Zhu, M.; Zhou, L.; Ma, M.; Heng, J.; Lu, L.; Qu, W.; Xu, Z. The impact of slope and rainfall on the contaminant transport from mountainous groundwater to the lowland surface water. Front. Environ. Sci. 2024, 12, 1343903. [Google Scholar] [CrossRef]
  67. Qin, B.; Xu, P.; Wu, Q.; Luo, L.; Zhang, Y. Environmental issues of Lake Taihu, China. Hydrobiologia 2007, 581, 3–14. [Google Scholar] [CrossRef]
  68. Li, S.; Peng, S.; Jin, B.; Zhou, J.; Li, Y. Multi-scale relationship between land use/land cover types and water quality in different pollution source areas in Fuxian Lake Basin. Peerj 2019, 7, e7283. [Google Scholar] [CrossRef]
  69. Shi, P.; Zhang, Y.; Song, J.; Li, P.; Wang, Y.; Zhang, X.; Li, Z.; Bi, Z.; Zhang, X.; Qin, Y.; et al. Response of nitrogen pollution in surface water to land use and social-economic factors in the Weihe River watershed, northwest China. Sustain. Cities Soc. 2019, 50, 101658. [Google Scholar] [CrossRef]
Remotesensing 17 00731 g001
Figure 1. The study area encompasses the Yangtze River basin. Highlighted on a gray base map are the provinces through which the river flows. The color map shows the extent of the basin, depicting various land cover types in detail, where different colors (from the China Land Cover Dataset) represent different types of land cover, such as farmland, forest, impervious land, etc. The blue line in the figure shows the rivers flowing through the Yangtze River basin.
Figure 1. The study area encompasses the Yangtze River basin. Highlighted on a gray base map are the provinces through which the river flows. The color map shows the extent of the basin, depicting various land cover types in detail, where different colors (from the China Land Cover Dataset) represent different types of land cover, such as farmland, forest, impervious land, etc. The blue line in the figure shows the rivers flowing through the Yangtze River basin.
Remotesensing 17 00731 g001
Remotesensing 17 00731 g002
Figure 2. A diagram of the overall flow of this paper.
Figure 2. A diagram of the overall flow of this paper.
Remotesensing 17 00731 g002
Remotesensing 17 00731 g003
Figure 3. An accuracy analysis of the water quality prediction model trained in this paper. Each chart represents a scatter plot between the predicted water quality results of each indicator and the corresponding real sample. The water quality indicators, listed from left to right and top to bottom, are CODCr, CODMn, DO, NH3-N, TN, and TP.
Figure 3. An accuracy analysis of the water quality prediction model trained in this paper. Each chart represents a scatter plot between the predicted water quality results of each indicator and the corresponding real sample. The water quality indicators, listed from left to right and top to bottom, are CODCr, CODMn, DO, NH3-N, TN, and TP.
Remotesensing 17 00731 g003
Remotesensing 17 00731 g004
Figure 4. The mapping results of the water quality in the Yangtze River basin: (a–f) represent the mapping results of the CODCr, CODMn, DO, NH3-N, TN, and TP in the Yangtze River basin.
Figure 4. The mapping results of the water quality in the Yangtze River basin: (a–f) represent the mapping results of the CODCr, CODMn, DO, NH3-N, TN, and TP in the Yangtze River basin.
Remotesensing 17 00731 g004
Remotesensing 17 00731 g005
Figure 5. Part of the influencing factors used in this paper: (a–d) represent the mapping of elevation, rainfall, factory density, and population density in the Yangtze River basin, respectively.
Figure 5. Part of the influencing factors used in this paper: (a–d) represent the mapping of elevation, rainfall, factory density, and population density in the Yangtze River basin, respectively.
Remotesensing 17 00731 g005
Remotesensing 17 00731 g006
Figure 6. Importance ranking of influencing factors of six water quality indicators: (a–f) represent diagrams of the CODCr, CODMn, DO, NH3-N, TN, and TP, respectively.
Figure 6. Importance ranking of influencing factors of six water quality indicators: (a–f) represent diagrams of the CODCr, CODMn, DO, NH3-N, TN, and TP, respectively.
Remotesensing 17 00731 g006
Remotesensing 17 00731 g007
Figure 7. Distribution of key influencing factors of six water quality indicators in each section control unit; (a–f) represent diagrams of the CODCr, CODMn, DO, NH3-N, TN, and TP, respectively.
Figure 7. Distribution of key influencing factors of six water quality indicators in each section control unit; (a–f) represent diagrams of the CODCr, CODMn, DO, NH3-N, TN, and TP, respectively.
Remotesensing 17 00731 g007
Table 1. Data used in this study, including water quality and auxiliary data.
Table 1. Data used in this study, including water quality and auxiliary data.
CategoryDataRole in Model TrainingSpatial Resolution
Water quality dataControl section unit dataSpatial range represented by water quality monitoring data/
Water quality monitoringMonitoring water quality/
Auxiliary dataDigital elevation modelCharacterizing the influence of topography on the water quality 30 m
China Land Cover DatasetFiltering out specific land cover and characterizing the land cover impact on the water quality30 m
WorldPop dataCharacterizing the influence of population on the water quality100 m
Point of interest dataCharacterizing the influence of factory distribution on the water quality30 m
Meteorological dataCharacterizing the influence of temperature and rainfall on the water quality1 km
Table 2. Water quality indicators involved in the water quality monitoring data.
Table 2. Water quality indicators involved in the water quality monitoring data.
Water Quality IndicatorUnitDescription
Chemical oxygen demand (CODCr)mg/LThe amount of oxygen needed to oxidize the organic matter in water.
Permanganate index (CODMn)mg/LAssesses the impact of organic pollutants on ecosystems and the concentration of organic pollutants in the water.
Dissolved oxygen (DO)mg/LThe oxygen content in water, obtained by assessing the biological viability of water bodies.
Ammonia nitrogen (NH3-N)mg/LAmmonia nitrogen concentration in water, obtained by assessing the eutrophication of water bodies.
Total nitrogen (TN)mg/LTotal nitrogen concentration in water, including ammonia nitrogen, nitrate nitrogen, organic nitrogen, etc.
Total phosphorus (TP)mg/LTotal phosphorus concentration in water, including dissolved and non-dissolved phosphorus.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Deng, F.; Liu, W.; Sun, M.; Xu, Y.; Wang, B.; Liu, W.; Yuan, Y.; Cui, L. Fine Estimation of Water Quality in the Yangtze River Basin Based on a Geographically Weighted Random Forest Regression Model. Remote Sens. 2025, 17, 731. https://doi.org/10.3390/rs17040731

AMA Style

Deng F, Liu W, Sun M, Xu Y, Wang B, Liu W, Yuan Y, Cui L. Fine Estimation of Water Quality in the Yangtze River Basin Based on a Geographically Weighted Random Forest Regression Model. Remote Sensing. 2025; 17(4):731. https://doi.org/10.3390/rs17040731

Chicago/Turabian Style

Deng, Fuliang, Wenhui Liu, Mei Sun, Yanxue Xu, Bo Wang, Wei Liu, Ying Yuan, and Lei Cui. 2025. "Fine Estimation of Water Quality in the Yangtze River Basin Based on a Geographically Weighted Random Forest Regression Model" Remote Sensing 17, no. 4: 731. https://doi.org/10.3390/rs17040731

APA Style

Deng, F., Liu, W., Sun, M., Xu, Y., Wang, B., Liu, W., Yuan, Y., & Cui, L. (2025). Fine Estimation of Water Quality in the Yangtze River Basin Based on a Geographically Weighted Random Forest Regression Model. Remote Sensing, 17(4), 731. https://doi.org/10.3390/rs17040731

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop