Abstract
This paper studies the performance of an interplanetary CubeSat equipped with a continuous-thrust primary propulsion system in a heliocentric mission scenario, which models a nodal flyby with a potential near-Earth asteroid. In particular, the mathematical model discussed in this work considers a small array of (commercial) miniaturized electric thrusters installed onboard a typical CubeSat, whose power-generation system is based on the use of classic solar panels. The paper also discusses the impact of the size of thrusters’ array on the nominal performance of the transfer mission by analyzing the trajectory of the CubeSat from an optimization point of view. In this context, the propulsive characteristics of a commercial electric thruster which corresponds to a iodine-fueled gridded ion-propulsion system are considered in this study, while the proposed procedure can be easily extended to a generic continuous-thrust propulsion system whose variation in thrust magnitude and specific impulse as a function of the input electric power is a known analytic function. Using an indirect approach, the paper illustrates the optimal guidance law, which allows the interplanetary CubeSat to reach a given solar distance, with the minimum flight time, by starting from a circular (ecliptic) parking orbit of assigned radius. The mission scenario is purely two-dimensional and models a rapid nodal flyby with a near-Earth asteroid whose nodal distance coincides with the solar distance to be reached.
1. Introduction
Robotic exploration of near-Earth asteroids is an important step in understanding the origin and evolution of the Solar System and is a necessary prelude to future human exploration of these fascinating minor celestial bodies, whose number continues to increase as observation techniques improve, with the additional recent help of artificial intelligence [1,2,3]. Designing and then hopefully operating and ultimately successfully completing an interplanetary space mission is usually a long and complex process [3,4,5,6], the costs of which can be significantly reduced by using a small and fairly standardized spacecraft [7,8], such as a typical CubeSat [9,10,11]. The potential of a CubeSat to support or autonomously carry out a scientific space mission in low-Earth orbit has already been demonstrated by the considerable number of space vehicles of this class successfully launched and deployed in orbit over the last two decades [12,13,14]. Compared to the application in a planetocentric (Earth) orbit, the use of a CubeSat in a heliocentric mission scenario appears rarer nowadays; this is the case despite the way in which the recent success of the Light Italian CubeSat for Imaging of Asteroids (LICIACube) within the more ambitious Double Asteroid Redirection Test (DART) mission [15,16] has highlighted the interesting performances of a CubeSat in a challenging, deep space mission scenario which involved the in situ study of a minor celestial body such as an asteroid. In fact, the scientific return of the successful LICIACube mission is only the latest, in chronological order, important result obtained thanks to the use of a small-sized spacecraft in a heliocentric environment. In this context, NASA’s Mars Cube One (MarCO) mission [17,18,19] must be considered as pioneering, both in the use of CubeSats far from circumterrestrial space and in the use of such interesting spacecraft for the exploration of the Solar System, in this specific case of Mars.
On the other hand, the use of such small space vehicle in interplanetary missions [20] poses several problems related primarily to the size of the spacecraft and its reduced payload capacity when compared to a classic interplanetary probe [21,22,23,24,25]. In this context, the difficulty (and in some cases the impossibility) of using a primary propulsion system installed on board to perform the interplanetary transfer [17,18,19] has so far been one of the factors that have limited (although not excluded) the use of CubeSats in a heliocentric mission scenario [26,27]. However, nowadays, the rapid technological progress in the realization of highly efficient miniaturized space engines [28,29,30] allows us to install on board a CubeSat a continuous-thrust propulsion system such as a classic solar electric thruster [31,32,33,34], or even a more exotic photonic solar sail [35,36,37], which uses the solar radiation pressure to produce (deep space) thrust without consuming any propellant mass. For example, in this context, the author has recently analyzed the optimal (i.e., the minimum time) transfer trajectories [38] of a CubeSat propelled by an electric thruster, modeled on the characteristics of the proposed Miniaturized Asteroid Remote Geophysical Observer (M-ARGO) spacecraft [39,40], or equipped with a hybrid propulsion system [41]; this combines a photonic solar sail in a Sun-facing configuration (i.e., a configuration where the sail mean plane is perpendicular to the direction of the radial unit vector which defines the Sun-spacecraft line) with a more conventional solar electric thruster.
The purpose of this paper is to analyze the rapid transfer performance of a CubeSat equipped with a small array of miniaturized (commercial) solar electric thrusters. This operates in a heliocentric scenario, modeling a minimum-time nodal flyby mission to a near-Earth asteroid. More precisely, the goal of the CubeSat-based interplanetary mission considered in this work is to reach, with the minimum flight time, one of the two nodal points of the heliocentric orbit of a target celestial body whose orbit around the Sun has a non-zero inclination to the Ecliptic. In particular, the target celestial body coincides with a (potential) near-Earth asteroid and the spacecraft transfer trajectory is designed by minimizing the total flight time for a given value of both the initial mass of the small spacecraft and the mass of propellant stored on board. To the best of the author’s knowledge, the concept of a nodal flyby mission for the close observation of a minor celestial body (such as an asteroid) was proposed by Perozzi et al. [42] in 2001, although the idea behind this concept could probably be older. In particular, in the interesting work of Perozzi et al. [42], a nodal flyby scenario is analyzed in detail and optimized considering a multiple-impulse trajectory which can be obtained, typically, by employing a high-thrust chemical propulsion system. Starting from the idea described in Ref. [42], Mengali et al. [43,44] have subsequently studied the optimal performance (using an indirect approach) of a photonic solar sail or an electric solar wind sail [45,46,47] in reaching the nodal distance of a series of asteroids known at the time of the preparation of the papers referred to in Refs. [43,44].
In the context of a nodal flyby heliocentric mission—by analyzing the interplanetary transfer scenario within an optimal framework and employing a simplified spacecraft mass breakdown model—this paper investigates the connection between the number of solar electric thrusters installed on board (i.e., the size of the array of the miniaturized thrusters), the payload mass that can be used to perform the scientific exploration of the target near-Earth asteroid, the (optimal) flight time, and the solar (i.e., the nodal) distance to be reached. In this regard, the paper presents and illustrates a set of graphs to quickly derive some characteristics of the CubeSat heliocentric transfer trajectory. The information obtained can be used in the first preliminary phase of the design of a nodal flyby mission for asteroid exploration when the primary propulsion system of the CubeSat is used to obtain the planned interplanetary transfer trajectory.
The technical characteristics of the generic miniaturized electric thruster of the array considered in this study are modeled on those of the commercial BIT-3 RF ion thruster engine [48,49], as declared by the manufacturer Busek co. inc. This specific RF ion thruster was recently installed aboard NASA’s Lunar IceCube [50], that is, one of the ten 6U CubeSats launched on the maiden flight of the Space Launch System [51] that successfully launched the Orion spacecraft in November 2022. The status of the CubeSat Lunar IceCube after launch appears to be unknown. The same model of miniaturized electric thruster was also installed in the Lunar Polar Hydrogen Mapper (LunaH-Map), a CubeSat designed to study the Moon’s surface and verify the potential presence of water ice. Like the Lunar IceCube, the LunaH-Map CubeSat was launched (and successfully deployed) during the first flight of the Space Launch System, although the small spacecraft was unable to successfully execute the lunar flyby maneuver due to a critical failure in the propulsion system. The performance characteristics of the BIT-3 RF ion thruster engine have been detailed in the literature; in this regard, the interesting work by Tsay et al. [49] is a nice and useful example which illustrates the analytic expressions that describe the variation in both the engine’s thrust magnitude and the specific impulse with the power-processing unit input power. These analytical (and very compact) expressions, which are originally derived for a single engine unit—which includes also the propellant tank—have been used in Section 2 to obtain a surrogate (and sufficiently simple) thrust model of the array of miniaturized electric thrusters installed on board a reference interplanetary CubeSat. In the simplified thrust model used in this paper, the total available thrust magnitude is expressed as a function of the processing unit input power, whose maximum (local) value depends on the electrical power supplied by the solar panel-based power-generation system of the interplanetary CubeSat. As for the characteristics of this power-generation system, the performances of the MMA’s High Watts per Kilogram “HaWK” solar arrays [52] were taken into consideration to model both the maximum (local) value of the electrical power and the corresponding subsystem mass, as illustrated in Section 2.
The optimal guidance law and the optimal interplanetary transfer trajectory—that is, the spacecraft trajectory that minimizes the flight time required to reach a prescribed solar distance by starting from an assigned (ecliptic and Keplerian) circular orbit—is discussed in Section 3. In particular, the classical calculus of variations [53,54,55] and the well-known Pontryagin Maximum Principle (PMP) [56] is used in the mathematical model described in that section to optimize the spacecraft trajectory during the rapid heliocentric flight. In this context, using the PMP, the optimal control law in terms of thrust vector direction and total thrust magnitude is obtained as a function of both the state variables of the CubeSat and the components of the adjoint vector [57], for a given size of the array of the miniaturized electric thrusters.
The optimization process is then used in Section 4 to simulate the optimal transfer trajectories of a set of potential CubeSat configurations as a function of the solar distance to be reached, i.e., the distance from the Sun of the node of the heliocentric orbit of the target near-Earth asteroid. In this context, a reference CubeSat configuration is assumed to obtain some sort of nominal transfer performance values for comparison purposes. In this regard, the reference CubeSat has a single BIT-3 RF ion thruster unit. In other words, the characteristics of the reference CubeSat are similar to those of NASA’s two small space satellites launched two years ago, Lunar IceCube and LunaH-Map. After estimating the performance of the reference CubeSat, the impact of a thruster array on the interplanetary transfer in the nodal flyby mission was investigated considering a number of engines equal to two or three installed inside a CubeSat, whose characteristics—in terms of initial mass—are consistent with those of the M-ARGO spacecraft [4,39,40], when the number of engine units is equal to three.
The parametric study illustrated in Section 4 was then the starting point for analyzing some applications of missions specifically related to some asteroids whose nodal distance is sufficiently close to the parking circular orbit. This part of the study is illustrated in Section 5. Finally, Section 6 contains the conclusions of the work and concludes the paper.
2. Simplified Mathematical Model for Preliminary Trajectory Analysis
This section is basically divided into three parts. The first part is dedicated to the modeling of the performances of a miniaturized electric propulsion system based on the characteristics of the BIT-3 RF ion thruster engine. The characteristics of such miniaturized thruster have been derived from the literature data. In this regard, the starting point is the analytical, simple mathematical model proposed by Tsay et al. [49] roughly 9 years ago; this is still a good approximation of the latest thruster’s performance data, which can be retrieved from the Busek website (see Ref. [58]). The second part of this section discusses a simplified thrust model of a CubeSat equipped with a propulsion system based on a small array of miniaturized electric thrusters (all identical to each other). In that case, the thrust model uses the analytical results illustrated in the first part of the section. Finally, the last part of the section discusses the mass breakdown model of the interplanetary CubeSat, which will be used in the rest of the paper to determine the transfer performance in the nodal flyby mission scenario.
2.1. Thrust Model of a Single Engine Unit Based on the BIT-3 Performance
Assume a single engine unit (which will be indicated in the rest of the paper with a subscript ), and consider the work by Tsay et al. [49], which gives the variation in the thrust magnitude and the specific impulse as a function of the (power-processing unit) input power . The latter can be selected between a minimum admissible value of and a maximum admissible value of . In other terms, according to Ref. [49], the BIT-3 electric propulsion system is “throttleable” in the range of the input power . Note that Ref. [58] indicates for the input power a range of , so that the range derived from the work by Tsay et al. [49] is substantially coincident with the latest measured performance of the BIT-3 electric propulsion system [58].
In particular, according to the graphs reported in Figure 11 of Ref. [49], the functions and can be expressed through two very simple, linear, equations as
where are four (dimensional) coefficients, most likely obtained through a classical best-fit procedure applied on a suitable set of experimental data. More specifically, Ref. [49] indicates that the values of such (best-fit) coefficients are
so that the two functions given by Equations (1) and (2) are drawn in Figure 1. Note that Equation (1) (or the graph in Figure 1) returns a maximum value of given by
which is in fact obtained when , while the data sheet retrieved from the manufacturer’s website [58] indicates a thrust magnitude up to . On the other hand, Equation (2) (or, again, the graph in Figure 1) gives a maximum value of the specific impulse of roughly , while Ref. [58] declares a value up to , i.e., a difference of about . The analytical expression of the propellant mass flow rate for a single engine unit can be easily derived from Equations (1) and (2). In this regard, if denotes the standard gravity, the variation in as a function of is obtained by the following (simple) rational equation which involves the best-fit coefficients [59]:
which is shown in Figure 2. In this case, the engine data sheet [58] indicates a (single) reference value of the propellant mass flow rate equal to , which is about lower than the average value extrapolated from Figure 2 or Equation (5). Consequently, Equations (1), (2) and (5) can be considered an acceptable (analytical) approximation of the actual latest thrust performance of the BIT-3 as declared by the manufacturer, and will be used in the rest of the paper to describe in a compact form the (single unit) thruster’s performance.
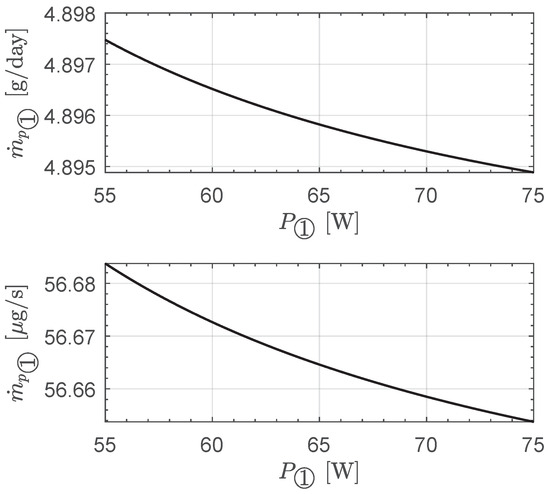
Figure 2.
Variation in the propellant mass flow rate with the input power for a single engine unit, as described by Equation (5).
In particular, observing the small variation in with as clearly described by the graphs of Figure 2, and in order to further simplify the thrust model of a single engine unit, we assume a constant value of the propellant mass flow rate in the form
The mathematical model describing the single engine unit is completed by the data regarding the dry mass of the unit and the maximum load of propellant (i.e., iodine with solid storage). According to the available data sheet [58] and assuming an engine unit with integrated gimbal, one has a dry mass and a maximum propellant mass , with a (occupied) volume equal to 1.6 U. Therefore, the maximum value of the total mass of a single engine unit (which includes the stored propellant) is .
2.2. Thrust Model of an Array of Engines
The mathematical model of a single engine unit described in the previous section is now used to obtain a simplified version of the thrust model of a (small) array of miniaturized electric thrusters. In the general case of an array with N thrusters, we denote as follows: P—the (power-processing unit) input power; T—the total thrust; —the resulting propellant mass flow rate; —the total dry mass; —the total propellant mass carried on board the small spacecraft.
2.2.1. Case of
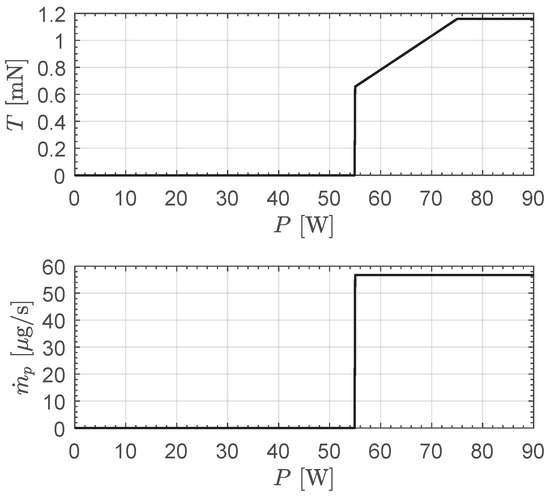
The limit case of refers to an interplanetary CubeSat with a single electric thruster, as in the case of the NASA’s Lunar IceCube and LunaH-Map [50]. Bearing in mind the admissible range of the power-processing unit input power described in the previous section, when the electric thruster is switched on, the expression of the total thrust magnitude as a function of P is given by
where and are given by Equations (1) and (4), respectively. On the other hand, using the approximation given by Equation (6), when the thruster is switched on, the propellant mass flow rate is given by the following simple equation:
Equations (7) and (8) are drawn in Figure 3 when the input power is .
Note that the power-processing unit input power P can be considered a sort of control term whose value defines both the thrust magnitude T and the propellant mass flow rate. In this context, the maximum admissible value of P depends on both the payload power and the electrical power given by the power generation subsystem, as described later in this section.
2.2.2. Case of
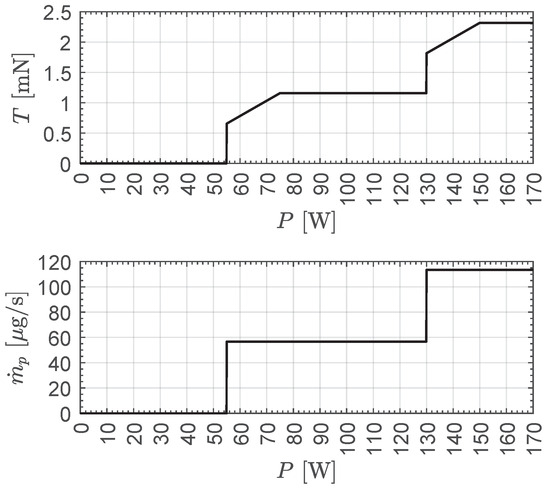
Consider now the case of , that is, the case in which the array of electric thrusters is composed of two engine units sequentially activated. When , the power-processing unit’s input power is not sufficient to activate even a single engine unit, which is instead able to operate if . On the other hand, if the value of P is greater than the sum , both the electric thrusters in the array can be turned on. In particular, when , the array of (two) engines gives the maximum allowable magnitude of the thrust, whose total value is ; see also Equation (4). For a generic value of P, bearing in mind also Equation (7), the thrust magnitude of the array of two thrusters is modeled through the following relationship:
The expression of the total propellant mass flow rate as a function of P is similar to that written in the previous equation. In particular, recalling that the propellant mass flow rate of a single engine unit is assumed to be constant (with ) and equal to given by Equation (6), one has
The variation in T and with , as modeled by the last two equations, is shown in Figure 4.
2.2.3. Case of
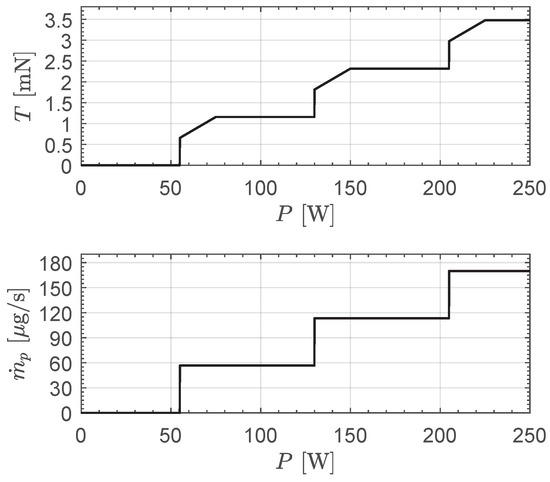
Paralleling the procedure described above for the case of , it is possible to easily obtain the thrust model for an array composed of three engine units sequentially activated, i.e., the case of . In this configuration, the result is the two following equations, which give the thrust magnitude and the propellant mass flow rate as a function of the power-processing unit input power P, viz.
and
The functions and with , when , are shown in Figure 5. Incidentally, the upper part of this specific figure is similar to that obtained by Takao et al. [60] (see, indeed, the graph in Figure 4 of that reference) in 2021; this is achieved by considering the heliocentric mission scenario of a solar power sail whose characteristics are consistent with these of the proposed Japanese mission named “Oversize Kite-craft for Exploration and Astronautics in the Outer Solar system” (OKEANOS) [61,62]. In this regard, an interesting and potential extension of the model discussed in this work could be the one that foresees the application to the fascinating concept of solar power sail like the one proposed in the scenario regarding the probe OKEANOS.
2.2.4. Case of
The analysis of the case is simple and immediate through using the results obtained in the previous subsection, but it is not detailed here because—in the author’s opinion—the use of an array composed of more than three engine units (like those modeled at the beginning of this section) would be hardly compatible with the volumetric characteristics of a potential CubeSat for interplanetary use. In fact, for example, the case would require a volume reserved for the propulsion system equal to , which would correspond to more than half of the theoretical one of an interplanetary CubeSat such as the ESA’s M-ARGO.
2.3. CubeSat Mass Breakdown and Power Model
The last part of this section describes the simplified mass breakdown and power model of the interplanetary CubeSat equipped with an array of miniaturized electric thrusters of size . The purpose of this simplified model is not to define the masses of the small spacecraft in detail, but to determine a simple and flexible analytical tool that can be used within the optimal trajectory design discussed in the next section.
In this context, the CubeSat total mass, , at the beginning of the interplanetary transfer (i.e., at the initial time instant ) is modeled as the sum of five terms (or macro-components): the total dry mass of the miniaturized electric thruster array; the total mass of the propellant stored on board the CubeSat; the mass of the power-generation system based on the use of typical high-performance solar panels; the mass of the scientific payload; and the mass of the remaining spacecraft subsystems (including the contingency factor), such as, for example, the communication system, the thermal control system, and the structure. Accordingly, the CubeSat initial mass is given by the sum
Each of the terms on the right-hand side of the previous equation is now modeled as a function of data extrapolated from the literature and also as a function of the number of miniaturized electric thrusters that form the array. In this regard, according to the model discussed at the beginning of this section, the values of and are obtained as a function of N as
where and [58]. Obviously, the mass of a small array of miniaturized electric thrusters is different from the simple sum of the mass of each (single) engine unit. However, any differences in mass can then be included in the term , which also includes an appropriate contingency factor. In order to simplify the mass breakdown model of this potential interplanetary CubeSat, the value of is assumed to be a fixed fraction of the total space vehicle’s mass, viz.
The mass of the power generation subsystem is calculated considering the electric power required by both the (N) miniaturized electric thrusters and the scientific payload, including other subsystems. In particular, considering a fixed value equal to of the electric power required by the payload (for example, in the case of the NASA’s Lunar IceCube, the payload power capability is roughly ), and denoting with the power-to-mass ratio of the power generation subsystem, one has
The value of the power-to-mass ratio depends on the design characteristics of the power generation subsystem. In this regard, the mathematical model discussed in this paper considers the performance of the MMA’s high watts per kilogram “HaWK” solar arrays [52], as declared by the manufacturer in the corresponding data sheet (see the data indicated in Ref. [63]). Accordingly, and considering a high performance solar array, the assumed value of the power-to-mass ratio is , while a value of about is consistent, for example, with a HaWK solar array with standard performance [63]. Finally, we assume a payload mass , that is, a value consistent with the payload mass installed onboard the NASA’s Lunar IceCube. In the latter case, in fact, the payload mass was with a volume of nearly 2U.
Substituting Equations (14)–(16) into Equation (13), the compact expression of the CubeSat launch mass as a function of the number N of miniaturized electric thrusters is obtained as
The value of and the masses of the other subsystems have been summarized in Table 1 and shown in Figure 6 by using a pie chart, when . Note that the reference case of has a total launch mass slightly below , that is, a value consistent with the actual launch mass of the two NASA’s CubeSats Lunar IceCube and LunaH-Map, which was about .

Table 1.
Mass breakdown model of the potential interplanetary CubeSat as a function of the number N of miniaturized electric thrusters.
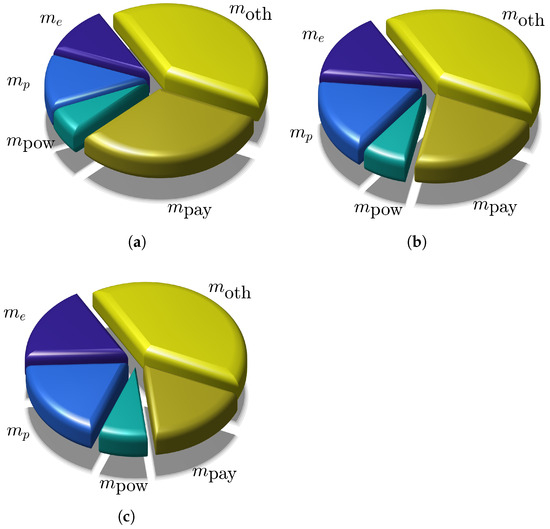
Figure 6.
CubeSat mass breakdown as a function of N. In particular, recall that is the total propellant mass stored onboard the spacecraft. (a) Case of ; (b) case of ; (c) case of .
Finally, the variation in the available electric power as a function of the distance from the Sun, i.e., the output value of the power generation subsystem as a function of the Sun–CubeSat distance r, was modeled using a simple -type relationship. In this regard, bearing in mind that the design value of the required electric power is given by the sum , one has
where is a reference distance which coincides with the semi-major axis of the Earth’s heliocentric orbit. Note that the literature presents more detailed and refined model for , which consider both the degradation of the solar array performance and the effect of the spacecraft temperature on the output power [64]. However, the simple model approximated by Equation (18), which is shown in Figure 7, is considered in this context consistent with a preliminary analysis of the CubeSat’s transfer performance.
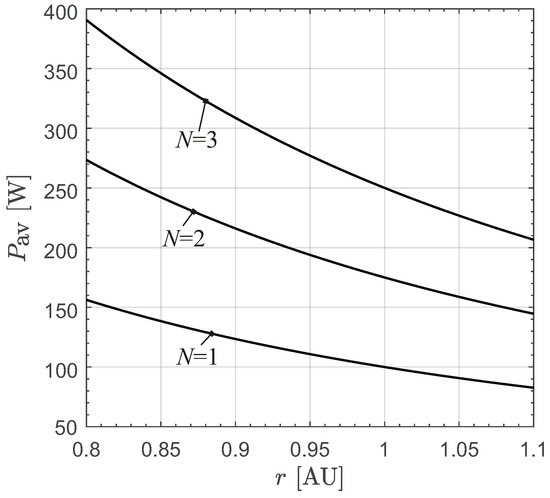
Figure 7.
Available electric power as a function of the distance from the Sun and the size N of the array of miniaturized thrusters; see Equation (18), which schematizes the simplified mathematical model used to estimate the local value of .
At a given distance r from the Sun—that is, for a given value of the available electric power given by Equation (18)—the power-processing unit input power P can be selected in the range defined by the following equation:
In other words, the available electrical energy is used first to power the payload (and other subsystems) and the remaining power is possibly diverted to the electric propulsion system.
Note that the special case of models the shutdown of the engine array, while the case of indicates an operation of the CubeSat’s electric propulsion system at maximum local thrust, when the engine units are sequentially activated.
3. Heliocentric Trajectory Design and Optimal Guidance Law
This section discusses the mathematical model used to describe the heliocentric dynamics of the interplanetary CubeSat equipped with the array of miniaturized electric thrusters. The aim is to obtain a model to determine the spacecraft heliocentric trajectory which allows the performance index
to be maximized, where is the total flight time required to reach an assigned distance from the Sun by starting from a circular parking orbit of radius . The latter is the typical approximation which is used to model an escape phase from the Earth by using a parabolic orbit. Note that the maximization of J gives the minimum-time transfer trajectory. The first step in this direction is the modeling of the spacecraft thrust vector and the temporal variation in the total mass of the small space vehicle.
In this context, the thrust vector of the spacecraft is modeled: (1) by using the results of Section 2; and (2) by assuming that the thrust direction defined through the thrust unit vector is unconstrained, as usually assumed in a spacecraft equipped with an electric propulsion system [65]. Accordingly, the CubeSat thrust vector is simply given by the following relationship:
where is the thrust magnitude which is a function of the power-processing unit input power P as described by Equations (7), (9) and (11) for , , and , respectively. On the other hand, the temporal variation in the CubeSat’s mass is related to the propellant mass flow rate as
where is given by Equations (8), (10) and (12) for , , and , respectively. Recall that the range of P is given by Equation (19) as a function of the value of the available electric power , which is, in turn, a function of the solar distance r, as described by Equation (18).
The heliocentric dynamics of the CubeSat in a two-dimensional mission scenario, where both the spacecraft trajectory and thrust vector are constrained to lie in the plane of the initial parking orbit, is studied using a classical polar reference frame where the azimuthal angle is measured from the line connecting the Sun and the CubeSat at time . In particular, according to the common approach used to obtain a preliminary trajectory design of a spacecraft in a heliocentric scenario, we consider only the gravitational attraction of the Sun (as in the typical Keplerian model) and the thrust induced by the propulsion system. Therefore, other effects such as, for example, the force due to the solar radiation pressure or the third-body gravitational effects, have been neglected in this first-order analysis. These latter (perturbative) effects can then be included in a subsequent mission analysis which refines the results obtained from the preliminary one. In the polar reference frame, the equations of motion of the spacecraft with a time-varying mass m are given by Equation (22) and the well-known
where is the gravitational parameter of the Sun, u is the radial component of the CubeSat inertial velocity, v is the transverse component of the CubeSat inertial velocity, and is the thrust angle, which defines the direction of the thrust vector in the polar reference frame. In particular, the case of indicates a thrust vector aligned with the Sun–CubeSat (radial) line, while the case is consistent with a thrust direction perpendicular to the radial line with a positive component along the direction of the CubeSat’s inertial velocity vector. Note that the two control (scalar) terms in the CubeSat’s heliocentric dynamics are as follows: (1) the power-processing unit input power P (which gives the value of the thrust magnitude), whose admissible range is given by Equation (19); and (2) the thrust angle . The equation of the mass variation (22) and the classical equations of motion (23) can be rewritten, in a more useful dimensionless form, by introducing the following (dimensionless) terms indicated through a tilde superscript
Accordingly, Equations (22) and (23) become
where the prime symbol indicate the derivative with respect to the dimensionless time , while the term is the dimensionless form of the propellant mass flow rate given by
The dimensionless form of the equations describing the CubeSat heliocentric dynamics given by Equation (25) is used in the rest of the section to study the optimal transfer trajectory. In this context, the optimal values of the two control terms are obtained by using an indirect approach to the trajectory optimization [53,66] and the classical PMP [56]. To this end, the dimensionless costate variables are introduced and the dimensionless Hamiltonian function is formed as
which gives the five Euler–Lagrange (dimensionless) differential equations
that are numerically integrated together with the CubeSat’s dimensionless equations of motion (25). The explicit expressions of the dimensionless Euler–Lagrange equations are omitted for the sake of conciseness, as usual. In particular, according to Equation (27)—and recalling that and —the part of which explicitly depends on the two control terms is
so that, according to the PMP [56], the maximization of gives the optimal value of the thrust angle . The latter, in fact, is given by the well-known relationship
Substituting the previous equation into (29), one obtains a reduced version of in which compares only the second (and last) control term, i.e., the input power P, viz.
The right hand of the previous equation gives variation with P of the reduced (dimensionless) Hamiltonian function . Again, according to the PMP, the maximization of the single-variable function gives the optimal value of the input power P and, therefore, the local (optimal) value of the thrust magnitude and the propellant mass flow rate. In this respect, the maximization of Equation (31) is numerically obtained by using a rather standard approach based on golden section search method [67].
For example, consider the case of , that is, the case of an array composed of three miniaturized electric thrusters sequentially activated. In this case, Table 1 gives an initial mass of the CubeSat equal to . Assume—just for illustrative purposes—that, in a given time instant during the transfer phase, (1) the spacecraft solar distance is , (2) the CubeSat local mass is , and (3) the value of the dimensionless adjoint variables is . In this example case, Equation (30) becomes
which gives the optimal value of the thrust angle , while Equation (18) gives an available electric power , so that the admissible range of the power-processing unit input power is . In particular, the expression of given by Equation (31) returns the graph in Figure 8. Note that the value of is greater than , which is the value of the input power that gives the maximum thrust magnitude in an array of three electric thrusters sequentially activated.
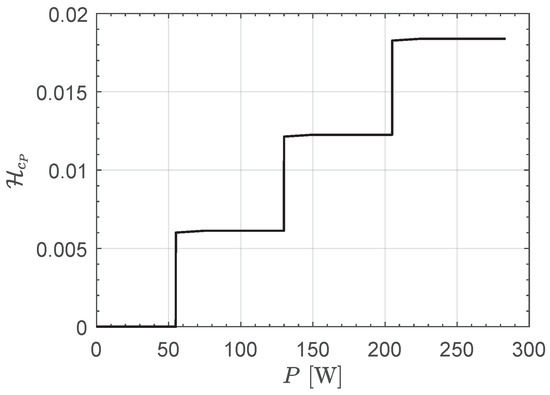
Figure 8.
Example of the variation with the input power P of the dimensionless function given by Equation (31).
According to the graph in Figure 8, the value of P that maximizes is , so that Equations (11) and (12) give the optimal value of the total thrust magnitude and the corresponding total propellant mass flow rate . The latter indicate that all three electric thrusters are activated at full throttle in that specific point of the (optimal) transfer trajectory. Of course, this is only an illustrative example of the procedure to evaluate the optimal controls, which are calculated indeed at each integration step during the simulation of the optimal CubeSat trajectory with sequentially activated engine units. In this regard, next section illustrates a set of numerical results obtained by using the procedure discussed just in this part of the paper.
It is interesting to observe that preliminary numerical simulations—that is, the optimization of a large number of heliocentric transfer trajectories—indicate that the maximization of the function defined in Equation (31) is obtained substantially when the input electric power is at the boundaries of its admissible range given by Equation (19). This is an interesting observation because it allows us to obtain a simplified and suboptimal control law for the power-processing unit input power P, in order to reduce the computational effort needed to solve the optimization problem. In this regard, a suboptimal value of the control P can be obtained by considering the value of the function at the boundaries of the admissible range of P. Bearing in mind that, when one has and , a simplified (suboptimal) expression of the control P can be written as
The suboptimal control law given by the previous equation can be used to quickly obtain a near-optimal transfer trajectory which can then be refined using the effective maximization of the function . In most scenarios, the control law given by Equation (33) determines the optimal (effective) transfer trajectory, with a reduction in computation time of about two orders of magnitude when compared to the actual (numerical) maximization of the function defined in Equation (31).
4. Numerical Results
The differential system composed of the dimensionless equations of motion (25) and the dimensionless Euler–Lagrange Equation (28) has been numerically integrated using a variable-step, variable-order PECE solver based on the classical Adams–Bashforth–Moulton algorithm [67,68], with a relative and absolute tolerance of . The (dimensionless) boundary value problem associated with the optimization process is solved using a numerical routine based on the shooting method with a final tolerance of , while the first guess of the solution has been obtained by adapting the semi-analytical procedure recently proposed by the author in Refs. [69,70]. In this context, the analytical form of the suboptimal control law given by Equation (33) allows us to significantly reduce the computation time compared to a standard approach to solving these kinds of (not so simple) optimization problems.
The optimization method and the numerical procedure illustrated above were employed to obtain the rapid transfer trajectory as a function of the number N of (sequentially activated) miniaturized electric thrusters in the array, and the target value of the solar distance to be reached by the interplanetary CubeSat, where is the final time instant which is one of the scalar outputs of the procedure. In this context, the CubeSat’s inertial velocity at the end of the flight is left free, as the spacecraft azimuthal angle and the vehicle’s total mass. In particular, at the end of the trajectory optimization the final mass of the CubeSat is compared with its minimum admissible value given by the difference , where the two terms are detailed in Table 1, in order to verify whether the obtained solution is consistent with the CubeSat mass distribution model. In fact, recall that is the total mass of the propellant stored on board the spacecraft.
The trajectory optimization was performed assuming and two distinct ranges of final (target) distance , namely and . In these two intervals, which are consistent with a sort of orbit raising (case of ) or orbit lowering (case of ), the value of used in the numerical simulations has been varied with a step of . Therefore, a total number of optimal control problems have been solved using the approach described in the previous section. Note that the numerical simulations consider a variation of of the initial Sun–CubeSat distance, which is equal to .
The results of the numerical simulations, in terms of the minimum flight time as a function of both N and , are shown in the graphs collected in Figure 9. In particular, as expected, for a given final distance the minimum flight time, decreases as the number of electric thrusters N increases. However, the difference in flight time from to is much less marked than that obtainable from a single engine () to two propulsion units (), especially for values of very different from . This is an interesting result, because it indicates that a series of thrusters with probably does not provide an appreciable performance increase (in terms of flight time reduction) compared to the case of a smaller value of N as that used in this study.
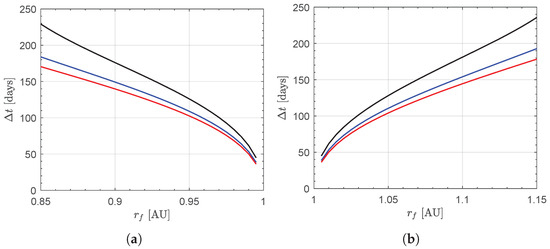
Figure 9.
Minimum flight time as a function of N and the final (target) distance . Black line →; blue line →; red line →. (a) Case of ; (b) case of .
From the point of view of propellant expenditure, i.e., from the point of view of the final mass of the spacecraft, all the 180 optimal transfer trajectories calculated during the simulation campaign are compatible with the value of the propellant mass stored on board the CubeSat (see also Table 1). This aspect emerges from Figure 10, which shows the mass of propellant required to complete the transfer as a function of N and . In fact, note that the required propellant mass is always less than when , or when , or when . As expected, to reach a given value of the target distance , the propellant mass needed to complete the transfer increases as the number N of propulsion units increases. However, the percentage impact of propellant expenditure on the total available propellant mass is a decreasing function of N, for a given value of , as shown in Figure 11. This is an important point, because the effect of an increasing number of engine units allows us to obtain a greater residual mass (in percentage terms) of propellant at the end of the heliocentric flight. Such a sort of propellant reserve can be used, for example, to further extend the interplanetary mission and to visit another target celestial body.
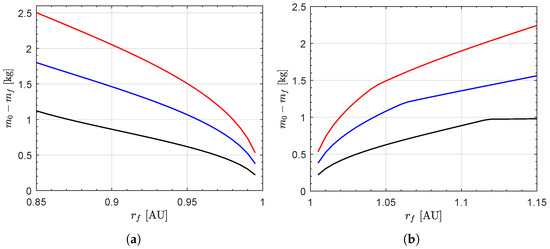
Figure 10.
Propellant expenditure , as a function of N and , for a rapid transfer. The legend is the same as in Figure 9.
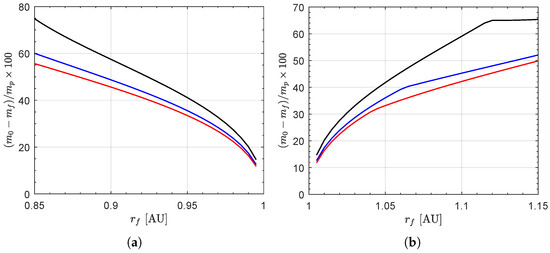
Figure 11.
Propellant expenditure percentage , as a function of N and , for a rapid transfer. The legend is the same as in Figure 9.
For example, consider the case of . In this scenario, Figure 9b gives a minimum flight time of about when , while one has a flight time of (i.e., ) if , and a flight time of (i.e., ) if . In the same scenario, Figure 10b gives a propellant expenditure of when , while the required propellant is if (i.e., with respect to the case of a single engine unit), and if (i.e., ). However, if compared with the total propellant mass stored on board the spacecraft, the required mass of propellant is about of if , or if , or if ; see the graphs sketched in Figure 11b.
In any case, it is useful to remember that the trajectories discussed in this work are optimal from the point of view of flight time, and not from the point of view of propellant consumption. In other words, it is certainly possible to obtain transfer trajectories that require a lower propellant consumption than that indicated in Figure 10, obviously at the expense of a greater flight time. In this sense, the analysis of minimum-time trajectories is the first step for a more refined study of the transfer problem [71] which, at a subsequent step, requires also the inclusion of the ephemeris constraints.
5. Potential Mission Applications
The procedure proposed in this paper to obtain the rapid transfer trajectory of an interplanetary CubeSat as a function of N and has been employed, in this section, to evaluate the performance in a nodal flyby mission towards a potential near-Earth asteroid. In this context, a catalog of these fascinating minor celestial bodies has been retrieved from Ref. [72]. In particular, this catalog contains the orbital elements of about 37,080 minor celestial objects at the end of December 2024. Using that (Keplerian) orbital data, the value of the solar distance of both the ascending node and the descending node has been obtained by using a standard astrodynamics formula [73].
Subsequently—assuming a constraint on the maximum and minimum admissible value of the distance from the Sun at the instant of the nodal flyby, i.e., assuming a distance constraint of the type —one obtains that approximately 10,320 (or 10,194) ascending (or descending) nodes are reachable, while 1870 celestial bodies have both the ascending and descending nodes at a distance compatible with the assumed range of . Therefore, there are roughly 18644 potential small celestial objects which can be reached with , which correspond to as many (potential) nodal flyby mission scenarios. Assuming that both the ascending and descending nodes are at a distance compatible with the range of —that is, considering 1870 potential mission scenarios—one obtains the graph sketched in Figure 12, which reports all the admissible pairs that can be reached by the interplanetary CubeSat.
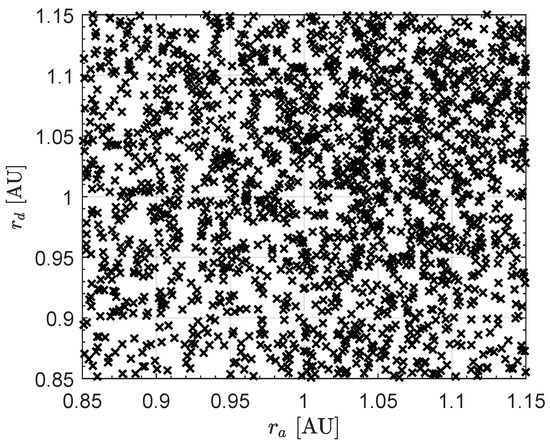
Figure 12.
Distribution of the solar distance of the ascending and descending node for the set of near-Earth asteroids listed in the catalog retrieved from Ref. [72].
In this context—that is, in the case of both and are within the range —the solution of the optimal control problem gives the minimum flight time required to reach the ascending or the descending note of each of the 1870 potential (near-Earth asteroids) targets. The numerical results, in terms of cumulative percentage, are re-assumed in Figure 13. For example, according to the graphs sketched in that figure, when the final distance is set to obtain a flyby at the ascending node of the asteroid’s orbit, one has that of the entire set of the potential targets are reachable with a flight time less than about if , while the flight time is if , or if . On the other hand, for an assigned small celestial object, one can select the more convenient (form the flight time point of view) node to be reached through a nodal flyby mission. In that case, the numerical results are given in Figure 14, showing the cumulative percentage in the best option between the ascending or descending node from the point of view of the required flight time. Note that Figure 13 and Figure 14 requires the numerical solution of 1870 optimization problems.
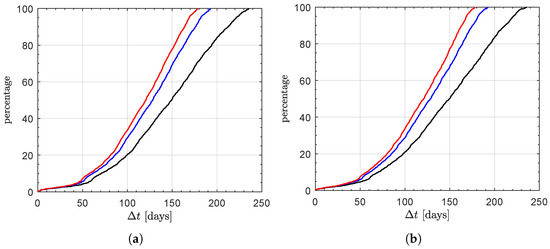
Figure 13.
Cumulative percentage of the minimum flight time in a transfer towards a potential near-Earth asteroid in which . Black line →; blue line →; red line →. (a) Case of ; (b) case of .
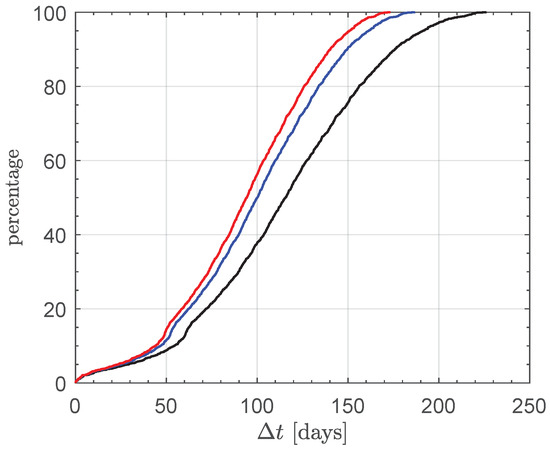
Figure 14.
Best option between the ascending or descending node from the point of view of the flight time: cumulative percentage. The legend is the same as in Figure 13.
The data summarized in Figure 14 allow the designer to quickly evaluate the impact of the value of N on the transfer performance in terms of both the minimum flight time and the number of potential targets which can be reached by the interplanetary CubeSat, whose design characteristics are indicated in Table 1. For example, consider the case of a nodal flyby with asteroid 1685 Toro, which has a solar distance of the ascending (or descending) node of (or ). In this specific mission scenario, if the number of the engine units is , then the optimization process described in this work gives a minimum flight time of (or ), while the required propellant mass is roughly (or ) of the initial mass of the CubeSat.
6. Conclusions
This paper investigated the performance of an interplanetary CubeSat in a nodal flyby mission to a near-Earth asteroid. In particular, the small spacecraft is equipped with a set of miniaturized electric thrusters whose characteristics are modeled after those of commercial propulsion systems. The proposed approach allows the designer to rapidly evaluate the impact of the number of engine units on the transfer performance, from the perspective of minimum flight time and the required propellant mass that is evaluated using a simplified mass breakdown model. The proposed approach has been applied to a recent catalog of near-Earth asteroids and a set of potential targets has been analyzed with a low computational effort. The simplified assumptions used to describe the problem from a mathematical point of view make the approach proposed in this paper suitable for a preliminary analysis of the interplanetary mission. In fact, a refinement of the results obtained could be achieved by considering both the constraints related to the planetary ephemerides and the possibility of realizing optimal transfer trajectories from the point of view of propellant consumption. Obviously, in the latter case, the availability of minimum-time transfer trajectories (such as those presented in this work) represents the necessary starting point for a correct setting of the propellant-mass optimization problem.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The author is grateful to Stacie Liu for the kind invitation and for the support during the submission of this paper. The author declares that he has not used any kind of generative artificial intelligence in the preparation of this manuscript, nor in the creation of images, graphs, tables or related captions.
Conflicts of Interest
The author declares no conflicts of interest.
Nomenclature
The following nomenclatures are used in this manuscript:
| best fit coefficients for the thrust magnitude; see Equation (1) | |
| best fit coefficients for the specific impulse; see Equation (2) | |
| standard gravity [m/s2] | |
| k | dimensionless contingency factor |
| dimensionless Hamiltonian function | |
| specific impulse [s] | |
| J | performance index [days] |
| m | mass [kg] |
| propellant mass flow rate [kg/s] | |
| N | number of miniaturized thrusters in the array |
| P | power-processing unit input power [W] |
| payload power [W] | |
| r | Sun-spacecraft distance [AU] |
| T | thrust magnitude [N] |
| thrust vector [N] | |
| t | time [days] |
| u | radial component of the spacecraft velocity [km/s] |
| v | transverse component of the spacecraft velocity [km/s] |
| Sun’s gravitational parameter [km3/s2] | |
| thrust angle [deg] | |
| reference value of the propellant mass flow rate [kg/s] | |
| total flight time [days] | |
| power-to-mass ratio [W/kg] | |
| dimensionless variable adjoint to i-th dimensionless spacecraft state | |
| azimuthal angle [deg] | |
| Subscripts | |
| referred to a single engine unit | |
| 0 | initial, parking orbit |
| ⊕ | at 1 astronomical unit from the Sun |
| available value | |
| e | electric engine dry |
| f | final, target point |
| max | maximum value |
| min | minimum value |
| other subsystems | |
| payload | |
| power generation subsystem | |
| p | propellant |
| Superscripts | |
| · | derivative with respect to t |
| ′ | derivative with respect to |
| ∼ | dimensionless version of the term |
| ∧ | unit vector |
References
- Du, Z.; Jiang, H.; Yang, X.; Cheng, H.W.; Liu, J. Deep learning-assisted near-Earth asteroid tracking in astronomical images. Adv. Space Res. 2024, 73, 5349–5362. [Google Scholar] [CrossRef]
- Assafin, M. Astrometry with PRAIA. Planet. Space Sci. 2023, 238, 105801. [Google Scholar] [CrossRef]
- Mitchell, A.M.; Panicucci, P.; Franzese, V.; Topputo, F.; Linares, R. Improved detection of a Near-Earth Asteroid from an interplanetary CubeSat mission. Acta Astronaut. 2024, 223, 685–692. [Google Scholar] [CrossRef]
- Topputo, F.; Wang, Y.; Giordano, C.; Franzese, V.; Goldberg, H.; Perez-Lissi, F.; Walker, R. Envelop of reachable asteroids by M-ARGO CubeSat. Adv. Space Res. 2021, 67, 4193–4221. [Google Scholar] [CrossRef]
- Pezent, J.; Sood, R.; Heaton, A. High-fidelity contingency trajectory design and analysis for NASA’s near-earth asteroid (NEA) Scout solar sail Mission. Acta Astronaut. 2019, 159, 385–396. [Google Scholar] [CrossRef]
- Ferrari, F.; Franzese, V.; Pugliatti, M.; Giordano, C.; Topputo, F. Preliminary mission profile of Hera’s Milani CubeSat. Adv. Space Res. 2021, 67, 2010–2029. [Google Scholar] [CrossRef]
- Johnson, L.; Castillo-Rogez, J.; Lockett, T. Near Earth asteroid Scout: Exploring asteroid 1991VG using a Smallsat. In Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Franzese, V.; Topputo, F. Celestial Bodies Far-Range Detection with Deep-Space CubeSats. Sensors 2023, 23, 4544. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, G.; Riccobono, D.; Bruno, E.; Bonariol, T.; Vigna, L.; Reverberi, G.; Fazzoletto, E.; Cotugno, B.; Vitiello, A.; Saita, G.; et al. LICIACube: Mission Outcomes of Historic Asteroid Fly-By Performed by a CubeSat. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024. [Google Scholar] [CrossRef]
- Elisabetta, D.; Angelo, Z. Impact observations of asteroid Dimorphos via Light Italian CubeSat for imaging of asteroids (LICIACube). Nat. Commun. 2023, 14, 3055. [Google Scholar] [CrossRef]
- Malphrus, B.K.; Freeman, A.; Staehle, R.; Klesh, A.T.; Walker, R. Interplanetary CubeSat missions. In CubeSat Handbook: From Mission Design to Operations; Cappelletti, C., Battistini, S., Malphrus, B.K., Eds.; Academic Press: London, UK, 2021; Chapter 4; pp. 85–121. [Google Scholar] [CrossRef]
- Zeedan, A.; Khattab, T. CubeSat Communication Subsystems: A Review of On-Board Transceiver Architectures, Protocols, and Performance. IEEE Access 2023, 11, 88161–88183. [Google Scholar] [CrossRef]
- Francisco, C.; Henriques, R.; Barbosa, S. A Review on CubeSat Missions for Ionospheric Science. Aerospace 2023, 10, 622. [Google Scholar] [CrossRef]
- Abbasy, M.; Aghayi Motaaleghi, M. Present the System Design Process and Review of Specifications of a Very Low-Cost 6U CubeSat Platform to Improve Accessibility to Space Based on Pluto Experience. Adv. Astronaut. Sci. Technol. 2023, 6, 1–18. [Google Scholar] [CrossRef]
- Dotto, E.; Deshapriya, J.; Gai, I.; Hasselmann, P.; Mazzotta Epifani, E.; Poggiali, G.; Rossi, A.; Zanotti, G.; Zinzi, A.; Bertini, I.; et al. The Dimorphos ejecta plume properties revealed by LICIACube. Nature 2024, 627, 505–509. [Google Scholar] [CrossRef]
- Deshapriya, J.; Hasselmann, P.; Gai, I.; Hirabayashi, M.; Dotto, E.; Rossi, A.; Zinzi, A.; Corte, V.D.; Bertini, I.; Ieva, S.; et al. Characterization of the DART Impact Ejecta Plume on Dimorphos from LICIACube Observations. Planet. Sci. J. 2023, 4, 231. [Google Scholar] [CrossRef]
- Klesh, A.T. MARCO: Flight results from the first interplanetary CubeSat mission. In Proceedings of the 70th Annual International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Schoolcraft, J.; Klesh, A.; Werne, T. MarCO: Interplanetary Mission Development on a CubeSat Scale. In Space Operations: Contributions from the Global Community; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; Chapter 10; pp. 221–231. [Google Scholar] [CrossRef]
- Schoolcraft, J.; Klesh, A.T.; Werne, T. MarCO: Interplanetary mission development on a cubesat scale. In Proceedings of the SpaceOps 2016 Conference, Daejeon, Republic of Korea, 16–20 May 2016. [Google Scholar] [CrossRef]
- Kulu, E. Nanosatellite Launch Forecasts - Track Record and Latest Prediction. In Proceedings of the 36th Annual Small Satellite Conference, Logan, UT, USA, 6–11 August 2022. [Google Scholar]
- Freeman, A.; Malphrus, B.K.; Staehle, R. CubeSat science instruments. In CubeSat Handbook: From Mission Design to Operations; Cappelletti, C., Battistini, S., Malphrus, B.K., Eds.; Academic Press: London, UK, 2021; Chapter 3; pp. 67–83. [Google Scholar] [CrossRef]
- Barán, B.; Martínez, B.O.; Barán, M. Multi-objective Optimization in the selection of a CubeSat PayLoad. In Proceedings of the 2021 IEEE International Conference on Aerospace and Signal Processing (INCAS 2021), Lima, Peru, 28–30 November 2021. [Google Scholar] [CrossRef]
- Aziz, M.M.; Ong, W.N.; Edwar; Fitriyanti, L.K.; Saugi, I.H.; Hidayat, F.A. Preliminary design of cubesat payload for clouds coverage detection using RGB camera. In Proceedings of the The 8th International Seminar on Aerospace Science and Technology (ISAST 2020), Bogor, Indonesia, 17 November 2021; Volume 2366. [Google Scholar] [CrossRef]
- Anderson, L.; Mork, J.; Swenson, C.; Zwolinski, B.; Mastropietro, A.J.; Sauder, J.; McKinley, I.; Mok, M. CubeSat active thermal control in support of advanced payloads: The active thermal architecture project. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 1–5 August 2021. [Google Scholar] [CrossRef]
- Garranzo, D.; Núñez, A.; Laguna, H.; Belenguer, T.; De Miguel, E.; Cebollero, M.; Ibarmia, S.; Martínez, C. APIS: The miniaturized Earth observation camera on-board OPTOS CubeSat. J. Appl. Remote Sens. 2019, 13, 032502. [Google Scholar] [CrossRef]
- Dalbins, J.; Allaje, K.; Ehrpais, H.; Iakubivskyi, I.; Ilbis, E.; Janhunen, P.; Kivastik, J.; Merisalu, M.; Noorma, M.; Pajusalu, M.; et al. Interplanetary student nanospacecraft: Development of the LEO demonstrator ESTCube-2. Aerospace 2023, 10, 503. [Google Scholar] [CrossRef]
- Staehle, R.; Blaney, D.; Hemmati, H.; Jones, D.; Klesh, A.; Liewer, P.; Lazio, J.; Wen-Yu Lo, M.; Mouroulis, P.; Murphy, N.; et al. Interplanetary CubeSat Architecture and Missions. In Proceedings of the AIAA SPACE 2012 Conference & Exposition, Pasadena, CA, USA, 11–13 September 2012. [Google Scholar] [CrossRef]
- Alnaqbi, S.; Darfilal, D.; Swei, S.S.M. Propulsion Technologies for CubeSats: Review. Aerospace 2024, 11, 502. [Google Scholar] [CrossRef]
- Kabirov, V.; Semenov, V.; Torgaeva, D.; Otto, A. Miniaturization of spacecraft electrical power systems with solar-hydrogen power supply system. Int. J. Hydrogen Energy 2023, 48, 9057–9070. [Google Scholar] [CrossRef]
- Yeo, S.H.; Ogawa, H.; Kahnfeld, D.; Schneider, R. Miniaturization perspectives of electrostatic propulsion for small spacecraft platforms. Prog. Aerosp. Sci. 2021, 126, 100742. [Google Scholar] [CrossRef]
- Wright, W.; Ferrer, P. Electric micropropulsion systems. Prog. Aerosp. Sci. 2015, 74, 48–61. [Google Scholar] [CrossRef]
- Yeo, S.H.; Gadisa, D.; Ogawa, H.; Bang, H. Multi-objective design optimization and physics-based sensitivity analysis of field emission electric propulsion for CubeSat platforms. Aerosp. Sci. Technol. 2024, 154, 109516. [Google Scholar] [CrossRef]
- Stesina, F.; Corpino, S.; Borras, E.B.; Amo, J.G.D.; Pavarin, D.; Bellomo, N.; Trezzolani, F. Environmental test campaign of a 6U CubeSat Test Platform equipped with an ambipolar plasma thruster. Adv. Aircr. Spacecr. Sci. 2022, 9, 195–215. [Google Scholar] [CrossRef]
- Bellomo, N.; Magarotto, M.; Manente, M.; Trezzolani, F.; Mantellato, R.; Cappellini, L.; Paulon, D.; Selmo, A.; Scalzi, D.; Minute, M.; et al. Design and In-orbit Demonstration of REGULUS, an Iodine electric propulsion system. CEAS Space J. 2022, 14, 79–90. [Google Scholar] [CrossRef]
- Lockett, T.R.; Castillo-Rogez, J.; Johnson, L.; Matus, J.; Lightholder, J.; Marinan, A.; Few, A. Near-Earth Asteroid Scout Flight Mission. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–29. [Google Scholar] [CrossRef]
- Heaton, A.; Miller, K.; Ahmad, N. Near earth asteroid Scout solar sail thrust and torque model. In Proceedings of the 4th International Symposium on Solar Sailing (ISSS 2017), Kyoyo, Japan, 17–20 January 2017. [Google Scholar]
- McNutt, L.; Johnson, L.; Clardy, D.; Castillo-Rogez, J.; Frick, A.; Jones, L. Near-earth asteroid scout. In Proceedings of the AIAA SPACE 2014 Conference and Exposition, San Diego, CA, USA, 4–7 August 2014. [Google Scholar]
- Quarta, A.A. Continuous-Thrust Circular Orbit Phasing Optimization of Deep Space CubeSats. Appl. Sci. 2024, 14, 7059. [Google Scholar] [CrossRef]
- Franzese, V.; Topputo, F.; Ankersen, F.; Walker, R. Deep-Space Optical Navigation for M-ARGO Mission. J. Astronaut. Sci. 2021, 68, 1034–1055. [Google Scholar] [CrossRef]
- Franzese, V.; Giordano, C.; Wang, Y.; Topputo, F.; Goldberg, H.; Gonzalez, A.; Walker, R. Target selection for M-ARGO interplanetary cubesat. In Proceedings of the 71st International Astronautical Congress, Virtual Event, 12–14 October 2020. [Google Scholar]
- Quarta, A.A. Thrust model and trajectory design of an interplanetary CubeSat with a hybrid propulsion system. Actuators 2024, 13, 384. [Google Scholar] [CrossRef]
- Perozzi, E.; Rossi, A.; Valsecchi, G.B. Basic targeting strategies for rendezvous and flyby missions to the near-Earth asteroids. Planet. Space Sci. 2001, 49, 3–22. [Google Scholar] [CrossRef]
- Mengali, G.; Bassetto, M.; Quarta, A.A. Solar Sail Optimal Performance in Heliocentric Nodal Flyby Missions. Aerospace 2024, 11, 427. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal Nodal Flyby with Near-Earth Asteroids Using Electric Sail. Acta Astronaut. 2014, 104, 450–457. [Google Scholar] [CrossRef]
- Janhunen, P. Electric sail for spacecraft propulsion. J. Propuls. Power 2004, 20, 763–764. [Google Scholar] [CrossRef]
- Janhunen, P.; Toivanen, P.K.; Polkko, J.; Merikallio, S.; Salminen, P.; Haeggström, E.; Seppänen, H.; Kurppa, R.; Ukkonen, J.; Kiprich, S.; et al. Electric solar wind sail: Toward test missions. Rev. Sci. Instruments 2010, 81, 111301. [Google Scholar] [CrossRef] [PubMed]
- Palos, M.F.; Janhunen, P.; Toivanen, P.; Tajmar, M.; Iakubivskyi, I.; Micciani, A.; Orsini, N.; Kütt, J.; Rohtsalu, A.; Dalbins, J.; et al. Electric Sail Mission Expeditor, ESME: Software Architecture and Initial ESTCube Lunar Cubesat E-sail Experiment Design. Aerospace 2023, 10, 694. [Google Scholar] [CrossRef]
- Tsay, M.; Frongillo, J.; Model, J.; Zwahlen, J.; Barcroft, C.; Feng, C. Neutralization demo and thrust stand measurement for BIT-3 RF ion thruster. In Proceedings of the 53rd AIAA/SAE/ASEE Joint Propulsion Conference, Atlanta, GA, USA, 10–12 July 2017. [Google Scholar] [CrossRef]
- Tsay, M.; Frongillo, J.; Model, J.; Zwahlen, J.; Paritsky, L. Maturation of iodine-fueled BIT-3 RF ion thruster and RF neutralizer. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar] [CrossRef]
- Malphrus, B.K.; Brown, K.Z.; Garcia, J.; Conner, C.; Kruth, J.; Combs, M.S.; Fite, N.; McNeil, S.; Clark, P.; Angkasa, K.; et al. Lunar IceCube: Pioneering technologies for interplanetary small satellite exploration. In Proceedings of the 70th International Astronautical Congress (IAC), Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Lane, R.; Ryals, C.; McLemore, C.; Hitt, D. NASA Space Launch System Cubesats: First Flight and Future Opportunities. In Proceedings of the 37th Annual Small Satellite Conference, Logan, UT, USA, 5–10 August 2023. [Google Scholar]
- McNaul, E. HaWK Solar Array Technology Advanced Deployable Satellite Power Solution. In Proceedings of the 12th Annual Summer CubeSat Developers’ Workshop, Logan, UT, USA, 8–9 August 2015. [Google Scholar]
- Betts, J.T. Survey of Numerical Methods for Trajectory Optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Chai, R.; Savvaris, A.; Tsourdos, A.; Chai, S.; Xia, Y. A review of optimization techniques in spacecraft flight trajectory design. Prog. Aerosp. Sci. 2019, 109, 100543. [Google Scholar] [CrossRef]
- Shirazi, A.; Ceberio, J.; Lozano, J.A. Spacecraft trajectory optimization: A review of models, objectives, approaches and solutions. Prog. Aerosp. Sci. 2018, 102, 76–98. [Google Scholar] [CrossRef]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control; Collegiate Publishers: San Francisco, CA, USA, 2015; Chapter 2; pp. 127–129. [Google Scholar]
- Lawden, D.F. Optimal Trajectories for Space Navigation; Butterworths & Co., Inc.: London, UK, 1963; pp. 54–60. [Google Scholar]
- Busek Co., Inc. BIT-3: Compact and Efficient Iodine Gridded Ion Thruster. 2024. Available online: https://www.busek.com/bit3 (accessed on 12 December 2024).
- Sutton, G.P. Rocket Propulsion Elements; John Wiley & Sons Inc.: Danvers, MA, USA, 2017; Chapter 2; pp. 26–31. [Google Scholar]
- Takao, Y.; Mori, O.; Matsushita, M.; Sugihara, A.K. Solar electric propulsion by a solar power sail for small spacecraft missions to the outer solar system. Acta Astronaut. 2021, 181, 362–376. [Google Scholar] [CrossRef]
- Takao, Y.; Mori, O.; Matsumoto, J.; Chujo, T.; Kikuchi, S.; Kebukawa, Y.; Ito, M.; Okada, T.; Aoki, J.; Yamada, K.; et al. Sample return system of OKEANOS–The solar power sail for Jupiter Trojan exploration. Acta Astronaut. 2023, 213, 121–137. [Google Scholar] [CrossRef]
- Berthet, M.; Schalkwyk, J.; Çelik, O.; Sengupta, D.; Fujino, K.; Hein, A.M.; Tenorio, L.; Cardoso dos Santos, J.; Worden, S.P.; Mauskopf, P.D.; et al. Space sails for achieving major space exploration goals: Historical review and future outlook. Prog. Aerosp. Sci. 2024, 150, 101047. [Google Scholar] [CrossRef]
- MMA Space. MMA HaWK Solar Arrays. 2024. Available online: https://mmadesignllc.com/next-gen-solar-arrays/ (accessed on 12 December 2024).
- Quarta, A.A.; Mengali, G. Minimum-Time Space Missions with Solar Electric Propulsion. Aerosp. Sci. Technol. 2011, 15, 381–392. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal trade studies of interplanetary electric propulsion missions. Acta Astronaut. 2008, 62, 657–667. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2020; Chapters 6 and 7; pp. 312, 378–379. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Quarta, A.A. Fast initialization of the indirect optimization problem in the solar sail circle-to-circle orbit transfer. Aerosp. Sci. Technol. 2024, 147, 109058. [Google Scholar] [CrossRef]
- Quarta, A.A. Initial costate approximation for rapid orbit raising with very low propulsive acceleration. Appl. Sci. 2024, 14, 1124. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Tradeoff performance of hybrid low-thrust propulsion system. J. Spacecr. Rocket. 2007, 44, 1263–1270. [Google Scholar] [CrossRef]
- NEODyS. Near Earth Objects—Dynamic Site. 2024. Available online: https://newton.spacedys.com/neodys/index.php?pc=5 (accessed on 27 December 2024).
- Curtis, H.D. Orbital Mechanics for Engineering Students; Elsevier: Oxford, UK, 2014; Chapter 6; pp. 298–303. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).