DHQ-DETR: Distributed and High-Quality Object Query for Enhanced Dense Detection in Remote Sensing
Abstract
1. Introduction
- We propose a groundbreaking distribution-based approach to box modeling and incorporate the distribution focus loss, which demonstrates robustness when dealing with dense multi-scale targets.
- We introduce a high-quality query selection module designed to resolve the misalignment inherent in the initialization of object queries.
- We develop a refined assignment strategy, coupled with an extra detection head, to enhance the stability and convergence speed of the DETR training process.
2. Related Work
2.1. CNN-Based Detectors
2.2. End-to-End Object Detector
3. Materials and Methods
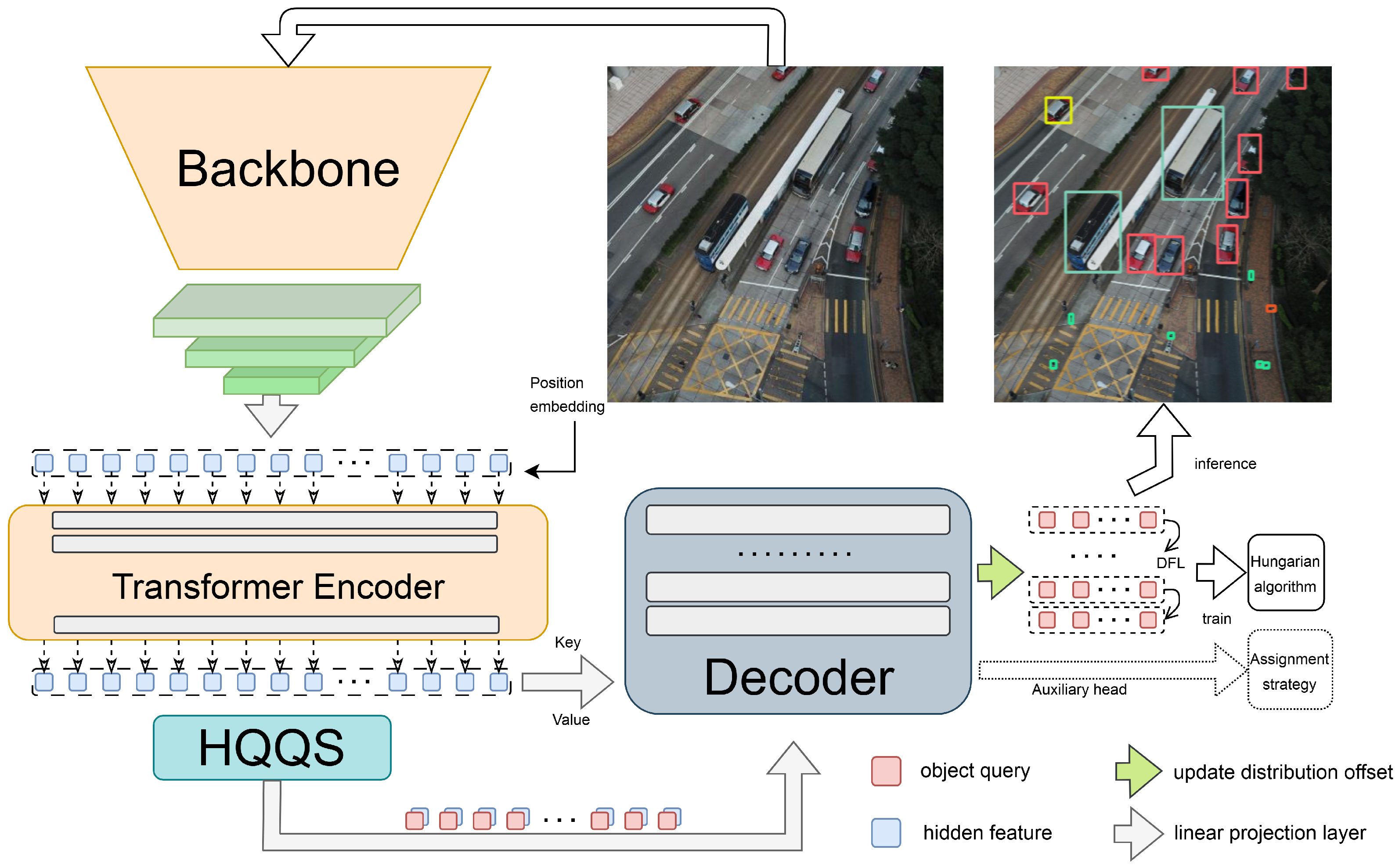
3.1. The Overall Structure
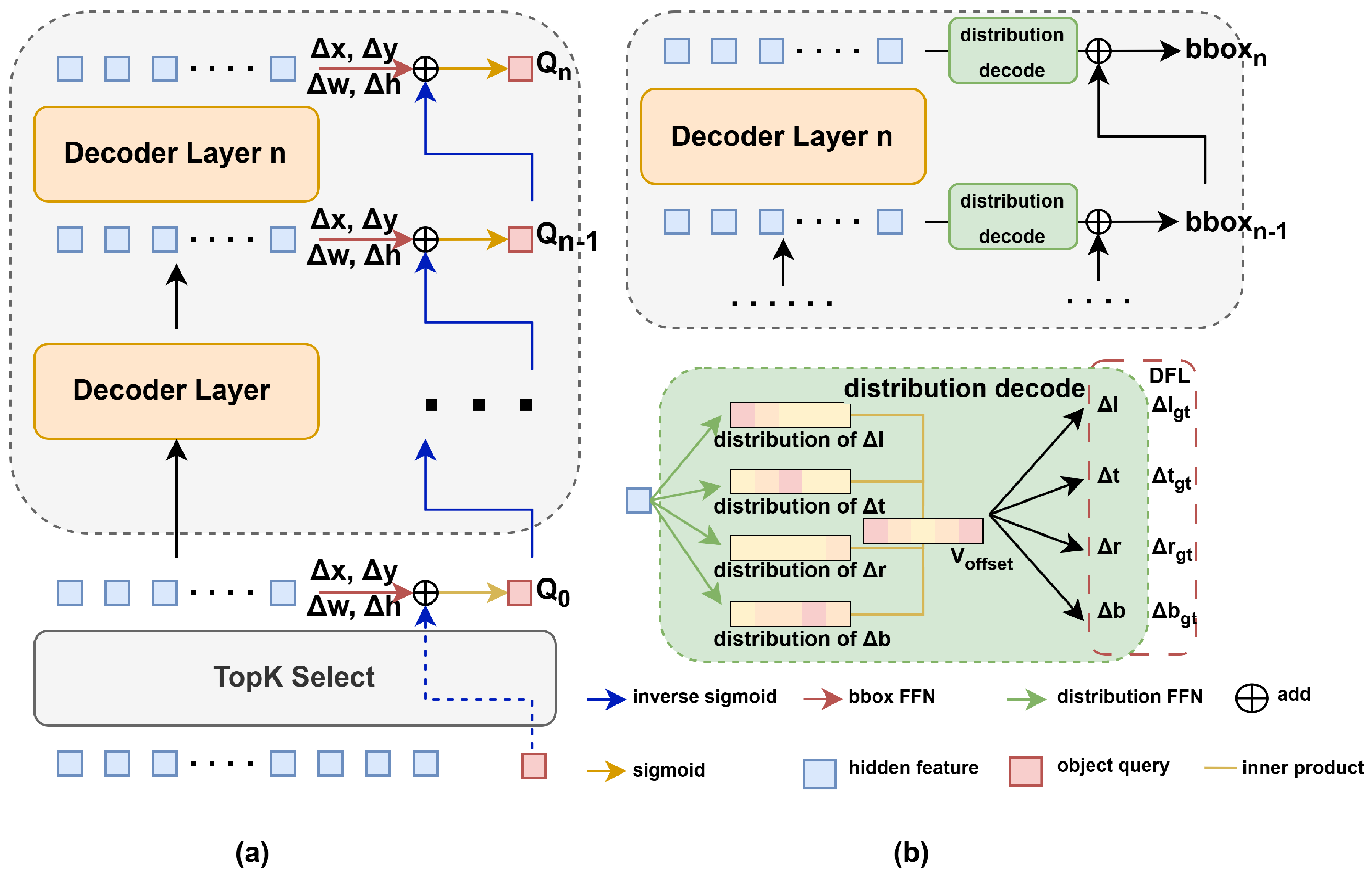
3.2. Distribution-Based Modeling
3.2.1. Basic Decoder
3.2.2. Distribution-Based Decoder
3.2.3. Distribution Focal Loss
3.3. High-Quality Query Selection Module
3.3.1. Basic Method
3.3.2. HQQS Module
3.4. Short-Circuit Training Decoder
| Algorithm 1 Task-aligned assignment algorithm |
Input:
|
| Model | Epochs | AP | AP50 | AP75 | APS | APM | APL | Params | GFLOPS |
|---|---|---|---|---|---|---|---|---|---|
| DETR-R50 [16] | 500 | 42.0 | 62.4 | 44.2 | 20.5 | 45.8 | 61.1 | 41M | 86 |
| Anchor DETR-R50 [40] | 50 | 42.1 | 63.1 | 44.9 | 22.3 | 46.2 | 60.0 | 39M | – |
| Conditional DETR-R50 [41] | 50 | 40.9 | 61.8 | 43.3 | 20.8 | 44.6 | 59.2 | 44M | 90 |
| DAB-DETR-R50 [18] | 50 | 42.2 | 63.1 | 44.7 | 21.5 | 45.7 | 60.3 | 44M | 94 |
| DN-DETR-R50 [19] | 50 | 44.1 | 64.4 | 46.7 | 22.9 | 48.0 | 63.4 | 44M | 94 |
| Align-DETR-R50 [42] | 50 | 46.0 | 64.9 | 49.5 | 25.2 | 50.5 | 64.7 | 42M | 94 |
| RT-DETR-R50 [22] | 72 | 53.1 | 71.3 | 57.7 | 34.8 | 58.0 | 70.0 | 42M | 136 |
| YOLOv5 L [10] | 300 | 49.0 | 67.3 | – | – | – | – | 46M | 109 |
| YOLOv7 L [11] | 300 | 51.2 | 69.7 | 55.5 | 35.2 | 55.9 | 66.7 | 36M | 104 |
| YOLOv8 L [12] | 300 | 52.9 | 69.8 | 57.5 | 35.3 | 58.3 | 69.8 | 43M | 165 |
| DETR-R101 [16] | 500 | 43.5 | 63.8 | 46.4 | 21.9 | 48.0 | 61.8 | 60M | 152 |
| Anchor DETR-R101 [40] | 50 | 43.5 | 64.3 | 46.6 | 23.2 | 47.7 | 61.4 | 58M | – |
| Conditional DETR-R101 [41] | 50 | 42.8 | 63.7 | 46.0 | 21.7 | 46.6 | 60.9 | 63M | 156 |
| DAB-DETR-R101 [18] | 50 | 43.5 | 63.9 | 46.6 | 23.6 | 47.3 | 61.5 | 63M | 174 |
| DN-DETR-R101 [19] | 50 | 45.2 | 65.5 | 48.3 | 24.1 | 49.1 | 65.1 | 63M | 174 |
| Align-DETR-R101 [42] | 50 | 46.9 | 65.5 | 50.9 | 25.6 | 51.9 | 66.0 | 61M | 174 |
| DETR-DC5-R50 [16] | 500 | 43.3 | 63.1 | 45.9 | 22.5 | 47.3 | 61.1 | 41M | 187 |
| Anchor DETR-DC5-R50 [40] | 50 | 44.2 | 64.7 | 47.5 | 24.7 | 48.2 | 60.6 | 39M | 151 |
| Conditional DETR-DC5-R50 [41] | 50 | 43.8 | 64.4 | 46.7 | 24.0 | 47.6 | 60.7 | 44M | 195 |
| DAB-DETR-DC5-R50 [18] | 50 | 44.5 | 65.1 | 47.7 | 25.3 | 48.2 | 62.3 | 44M | 202 |
| DN-DETR-DC5-R50 [19] | 50 | 46.3 | 66.4 | 49.7 | 26.7 | 50.0 | 64.3 | 44M | 202 |
| Align-DETR-DC5-R50 [42] | 50 | 48.3 | 66.7 | 52.5 | 29.7 | 52.8 | 65.9 | 42M | 200 |
| DETR-DC5-R101 [16] | 500 | 44.9 | 64.7 | 47.7 | 23.7 | 49.5 | 62.3 | 60M | 253 |
| Anchor DETR-DC5-R101 [40] | 50 | 45.1 | 65.7 | 48.8 | 25.8 | 49.4 | 61.6 | 58M | – |
| Conditional DETR-DC5-R101 [41] | 50 | 45.0 | 65.5 | 48.4 | 26.1 | 48.9 | 62.8 | 63M | 262 |
| DAB-DETR-DC5-R101 [18] | 50 | 45.8 | 65.9 | 49.3 | 27.0 | 49.8 | 63.8 | 63M | 282 |
| DN-DETR-DC5-R101 [19] | 50 | 47.3 | 67.5 | 50.8 | 28.6 | 51.5 | 65.0 | 63M | 282 |
| Align-DETR-DC5-R101 [42] | 50 | 49.3 | 67.4 | 53.7 | 30.6 | 54.3 | 66.4 | 61M | 280 |
| DHQ-DETR | 72 | 53.7 | 71.6 | 57.9 | 34.7 | 58.4 | 70.6 | 43M | 154 |
4. Results
| Model | Extra Data | AP | AP50 | AP75 |
|---|---|---|---|---|
| YOLOv5 (2020) [10] | × | 49.0 | 73.0 | 50.9 |
| YOLOv8 (2023) [12] | × | 52.9 | 74.5 | 56.1 |
| DETR (2020) [16] | × | 46.7 | 72.3 | 49.5 |
| DN-DETR (2022) [19] | × | 53.1 | 78.2 | 57.5 |
| RT-DETR (2023) [22] | × | 53.0 | 79.0 | 57.8 |
| DecoupleNet D2 (2024) [45] | ✓ | - | 78.0 | - |
| PP-YOLOE-R-l (2022) [46] | ✓ | - | 80.0 | - |
| MAE + MTP (2024) [47] | ✓ | - | 80.7 | - |
| LSKNet (2024) [48] | ✓ | - | 81.6 | - |
| Strip R-CNN (2025) [49] | ✓ | - | 82.3 | - |
| DHQ-DETR | × | 54.3 | 81.5 | 58.9 |
4.1. Main Results
4.2. Ablation Studies
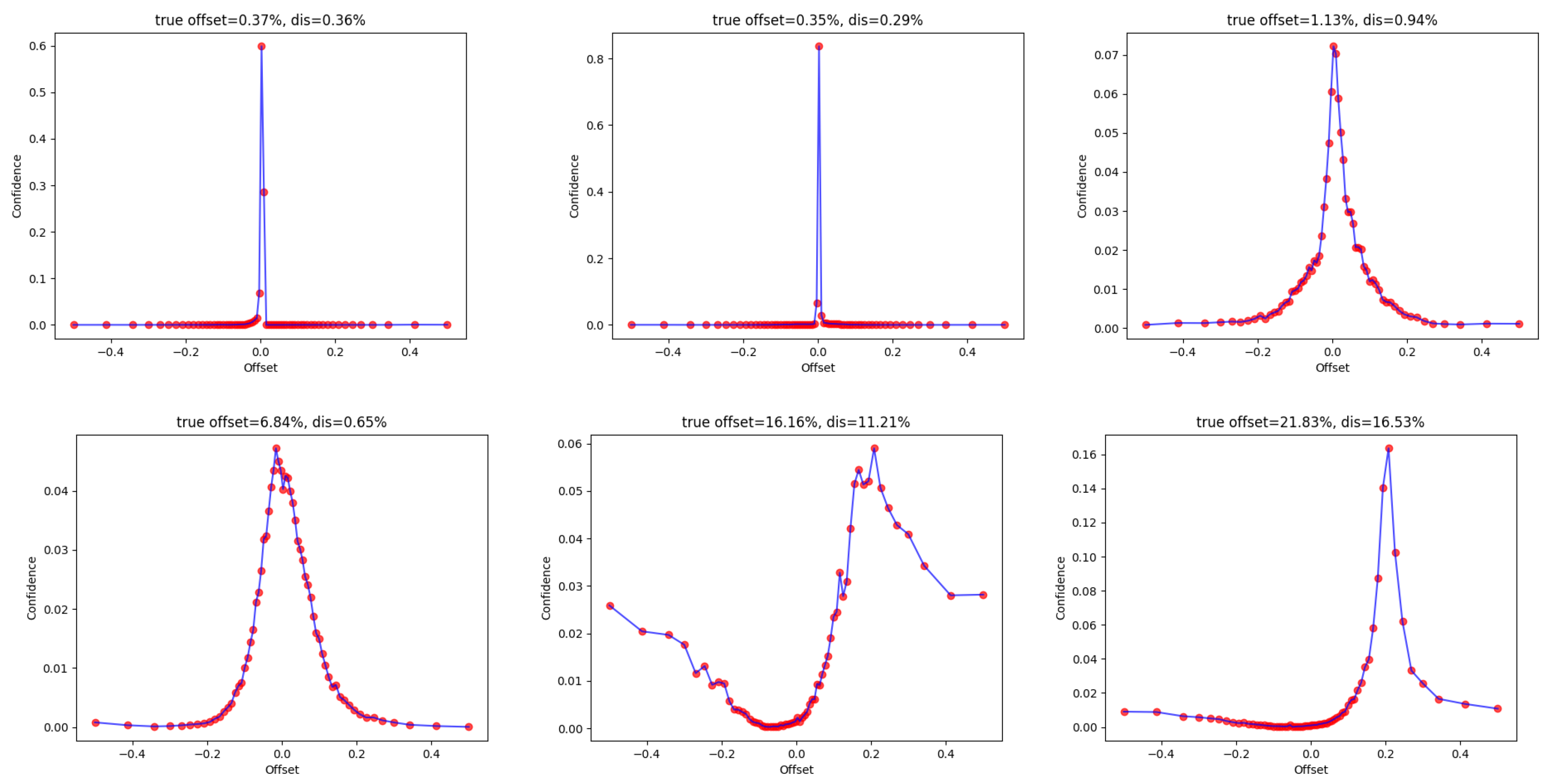
4.2.1. Distribution-Based Location Offset
4.2.2. HQQS Module
4.3. Assignment Strategies
5. Discussion
5.1. Limitations
5.2. Future Research Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DETR | Detection transformer |
| NMS | Non-Maximum Suppression |
| DHQ | Distributed and high-quality object query |
| HQQS | High-quality query selection module |
| FFN | Feedforward network |
| DFL | Distribution focus loss |
References
- Cai, Z.; Vasconcelos, N. Cascade r-cnn: Delving into high quality object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6154–6162. [Google Scholar]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; Number 1. pp. 1440–1448. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Adv. Neural Inf. Process. Syst. 2015, 28, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Ge, Z.; Liu, S.; Wang, F.; Li, Z.; Sun, J. YOLOX: Exceeding YOLO Series in 2021. arXiv 2021, arXiv:2107.08430. [Google Scholar]
- Tian, Z.; Shen, C.; Chen, H.; He, T. FCOS: Fully Convolutional One-Stage Object Detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 9627–9636. [Google Scholar]
- Long, X.; Deng, K.; Wang, G.; Zhang, Y.; Dang, Q.; Gao, Y.; Shen, H.; Ren, J.; Han, S.; Ding, E.; et al. PP-YOLO: An Effective and Efficient Implementation of Object Detector. arXiv 2020, arXiv:2007.12099. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.E.; Fu, C.; Berg, A.C. SSD: Single Shot MultiBox Detector. arXiv 2015, arXiv:1512.02325. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Jocher, G. YOLOv5 Release v7.0. 2022. Available online: https://github.com/ultralytics/yolov5/tree/v7.0 (accessed on 1 March 2023).
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.M. YOLOv7: Trainable Bag-of-Freebies Sets New State-of-the-Art for Real-time Object Detectors. arXiv 2022, arXiv:2207.02696. [Google Scholar]
- Jocher, G. YOLOv8. 2023. Available online: https://github.com/ultralytics/ultralytics/tree/main (accessed on 1 March 2023).
- Bodla, N.; Singh, B.; Chellappa, R.; Davis, L.S. Improving Object Detection With One Line of Code. arXiv 2017, arXiv:1704.04503. [Google Scholar] [CrossRef]
- Zhou, P.; Zhou, C.; Peng, P.; Du, J.; Sun, X.; Guo, X.; Huang, F. NOH-NMS: Improving Pedestrian Detection by Nearby Objects Hallucination. arXiv 2020, arXiv:2007.13376. [Google Scholar] [CrossRef]
- Liu, S.; Huang, D.; Wang, Y. Adaptive NMS: Refining Pedestrian Detection in a Crowd. arXiv 2019, arXiv:1904.03629. [Google Scholar] [CrossRef]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 1, 2, 4, 6. [Google Scholar]
- Zhu, X.; Su, W.; Lu, L.; Li, B.; Wang, X.; Dai, J. Deformable DETR: Deformable Transformers for End-to-End Object Detection. arXiv 2021, arXiv:2010.04159. [Google Scholar] [CrossRef]
- Liu, S.; Li, F.; Zhang, H.; Yang, X.; Qi, X.; Su, H.; Zhu, J.; Zhang, L. DAB-DETR: Dynamic Anchor Boxes are Better Queries for DETR. arXiv 2022, arXiv:2201.12329. [Google Scholar]
- Li, F.; Zhang, H.; Liu, S.; Guo, J.; Ni, L.M.; Zhang, L. DN-DETR: Accelerate DETR training by introducing query denoising. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2, 3, 5, 6. [Google Scholar]
- Chen, Q.; Chen, X.; Wang, J.; Zhang, S.; Yao, K.; Feng, H.; Han, J.; Ding, E.; Zeng, G.; Wang, J. Group DETR: Fast DETR Training with Group-Wise One-to-Many Assignment. arXiv 2023, arXiv:2207.13085. [Google Scholar] [CrossRef]
- Roh, B.; Shin, J.; Shin, W.; Kim, S. Sparse DETR: Efficient End-to-End Object Detection with Learnable Sparsity. arXiv 2021, arXiv:2111.14330. [Google Scholar] [CrossRef]
- Lv, W.; Zhao, Y.; Xu, S.; Wei, J.; Wang, G.; Cui, C.; Du, Y.; Dang, Q.; Liu, Y. DETRs Beat YOLOs on Real-time Object Detection. arXiv 2023, arXiv:2304.08069. [Google Scholar] [CrossRef]
- Zong, Z.; Song, G.; Liu, Y. DETRs with Collaborative Hybrid Assignments Training. arXiv 2023, arXiv:2211.12860. [Google Scholar] [CrossRef]
- Feng, C.; Zhong, Y.; Gao, Y.; Scott, M.R.; Huang, W. TOOD: Task-aligned One-stage Object Detection. arXiv 2021, arXiv:2108.07755. [Google Scholar] [CrossRef]
- Kirillov, A.; Girshick, R.; He, K.; Dollár, P. Panoptic feature pyramid networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6399–6408. [Google Scholar]
- Liu, S.; Qi, L.; Qin, H.; Shi, J.; Jia, J. Path aggregation network for instance segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8759–8768. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Hosang, J.H.; Benenson, R.; Schiele, B. A convnet for non-maximum suppression. arXiv 2015, arXiv:1511.06437. [Google Scholar] [CrossRef]
- Hosang, J.H.; Benenson, R.; Schiele, B. Learning non-maximum suppression. arXiv 2017, arXiv:1705.02950. [Google Scholar] [CrossRef]
- Solovyev, R.A.; Wang, W. Weighted Boxes Fusion: Ensembling boxes for object detection models. arXiv 2019, arXiv:1910.13302. [Google Scholar] [CrossRef]
- Choi, J.; Chun, D.; Kim, H.; Lee, H. Gaussian YOLOv3: An Accurate and Fast Object Detector Using Localization Uncertainty for Autonomous Driving. arXiv 2019, arXiv:1904.04620. [Google Scholar] [CrossRef]
- He, Y.; Zhang, X.; Savvides, M.; Kitani, K. Softer-NMS: Rethinking Bounding Box Regression for Accurate Object Detection. arXiv 2018, arXiv:1809.08545. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. arXiv 2020, arXiv:2006.04388. [Google Scholar] [CrossRef]
- Zheng, D.; Dong, W.; Hu, H.; Chen, X.; Wang, Y. Less is More: Focus Attention for Efficient DETR. arXiv 2023, arXiv:2307.12612. [Google Scholar] [CrossRef]
- Zhu, P.; Wen, L.; Du, D.; Bian, X.; Fan, H.; Hu, Q.; Ling, H. Detection and tracking meet drones challenge. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 7380–7399. [Google Scholar] [CrossRef]
- Girshick, R.B.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. arXiv 2013, arXiv:1311.2524. [Google Scholar] [CrossRef]
- Tychsen-Smith, L.; Petersson, L. Improving Object Localization with Fitness NMS and Bounded IoU Loss. arXiv 2017, arXiv:1711.00164. [Google Scholar] [CrossRef]
- Rezatofighi, S.H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.D.; Savarese, S. Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression. arXiv 2019, arXiv:1902.09630. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Yang, T.; Sun, J. Anchor detr: Query design for transformer-based detector. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 28 February–1 March 2022; pp. 2, 3, 6. [Google Scholar]
- Meng, D.; Chen, X.; Fan, Z.; Zeng, G.; Li, H.; Yuan, Y.; Sun, L.; Wang, J. Conditional detr for fast training convergence. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 2, 3, 6. [Google Scholar]
- Cai, Z.; Liu, S.; Wang, G.; Ge, Z.; Zhang, X.; Huang, D. Align-DETR: Improving DETR with Simple IoU-aware BCE loss. arXiv 2023, arXiv:2304.07527. [Google Scholar] [CrossRef]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A large-scale dataset for object detection in aerial images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3974–3983. [Google Scholar]
- Lin, T.; Maire, M.; Belongie, S.J.; Bourdev, L.D.; Girshick, R.B.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. arXiv 2014, arXiv:1405.0312. [Google Scholar] [CrossRef]
- Lu, W.; Chen, S.B.; Shu, Q.L.; Tang, J.; Luo, B. DecoupleNet: A Lightweight Backbone Network With Efficient Feature Decoupling for Remote Sensing Visual Tasks. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4414613. [Google Scholar] [CrossRef]
- Wang, X.; Wang, G.; Dang, Q.; Liu, Y.; Hu, X.; Yu, D. PP-YOLOE-R: An Efficient Anchor-Free Rotated Object Detector. arXiv 2022, arXiv:2211.02386. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, J.; Xu, M.; Liu, L.; Wang, D.; Gao, E.; Han, C.; Guo, H.; Du, B.; Tao, D.; et al. MTP: Advancing Remote Sensing Foundation Model via Multitask Pretraining. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 11632–11654. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Dai, Y.; Hou, Q.; Liu, L.; Liu, Y.; Cheng, M.M.; Yang, J. LSKNet: A Foundation Lightweight Backbone for Remote Sensing. arXiv 2024, arXiv:2403.11735. [Google Scholar] [CrossRef]
- Yuan, X.; Zheng, Z.; Li, Y.; Liu, X.; Liu, L.; Li, X.; Hou, Q.; Cheng, M.M. Strip R-CNN: Large Strip Convolution for Remote Sensing Object Detection. arXiv 2025, arXiv:2501.03775. [Google Scholar] [CrossRef]
- Chen, K.; Pang, J.; Wang, J.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Shi, J.; Ouyang, W.; et al. Hybrid Task Cascade for Instance Segmentation. arXiv 2019, arXiv:1901.07518. [Google Scholar] [CrossRef]
- Jiangmiao, P.; Kai, C.; Jianping, S.; Huajun, F.; Wanli, O.; Dahua, L. Libra R-CNN: Towards Balanced Learning for Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep High-Resolution Representation Learning for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 3349–3364. [Google Scholar] [CrossRef]
- Chen, L.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. arXiv 2016, arXiv:1606.00915. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Kang, S.; Cho, D. Patch-Level Augmentation for Object Detection in Aerial Images. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 127–134. [Google Scholar] [CrossRef]
- Chen, K.; Wang, J.; Pang, J.; Cao, Y.; Xiong, Y.; Li, X.; Sun, S.; Feng, W.; Liu, Z.; Xu, J.; et al. MMDetection: Open MMLab Detection Toolbox and Benchmark. arXiv 2019, arXiv:1906.07155. [Google Scholar]
- Chen, C.; Zhang, Y.; Lv, Q.; Wei, S.; Wang, X.; Sun, X.; Dong, J. RRNet: A Hybrid Detector for Object Detection in Drone-Captured Images. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop (ICCVW), Seoul, Republic of Korea, 27–28 October 2019; pp. 100–108. [Google Scholar] [CrossRef]
- Law, H.; Deng, J. CornerNet: Detecting Objects as Paired Keypoints. arXiv 2018, arXiv:1808.01244. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Wang, N.; Zhang, Z. Scale-Aware Trident Networks for Object Detection. arXiv 2019, arXiv:1901.01892. [Google Scholar] [CrossRef]
- Yang, B.; Xu, W.; Bi, F.; Zhang, Y.; Kang, L.; Yi, L. Multi-scale neighborhood query graph convolutional network for multi-defect location in CFRP laminates. Comput. Ind. 2023, 153, 104015. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as Points. arXiv 2019, arXiv:1904.07850. [Google Scholar]
- Meethal, A.; Granger, E.; Pedersoli, M. Cascaded Zoom-in Detector for High Resolution Aerial Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023. [Google Scholar]
- Zhang, H.; Wang, Y.; Dayoub, F.; Sünderhauf, N. VarifocalNet: An IoU-aware Dense Object Detector. arXiv 2020, arXiv:2008.13367. [Google Scholar] [CrossRef]
- Zhang, S.; Chi, C.; Yao, Y.; Lei, Z.; Li, S.Z. Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection. arXiv 2019, arXiv:1912.02424. [Google Scholar] [CrossRef]



| Model | AP | AP50 | AP75 |
|---|---|---|---|
| Cascade R-CNN [1] | 16.0 | 31.9 | 15.0 |
| HTC-drone [50] | 22.6 | 45.2 | 20.0 |
| Libra-HBR [51] | 25.6 | 48.3 | 24.0 |
| HRDet+ [52] | 28.4 | 54.5 | 26.1 |
| S + D [1,53] | 28.6 | 51.0 | 28.3 |
| ACM-OD [3,54] | 29.1 | 54.1 | 27.4 |
| DPNet [1,55] | 29.6 | 54.0 | 28.7 |
| RRNet [56] | 29.1 | 55.8 | 27.2 |
| RetinaNet [7] | 11.8 | 21.3 | 11.6 |
| CornerNet [57] | 17.4 | 34.1 | 15.8 |
| YOLOv3 [58] | 17.8 | 37.3 | 15.0 |
| TridentNet [59] | 22.5 | 43.3 | 20.5 |
| CNAnet [60] | 26.4 | 48.0 | 25.5 |
| EHR-RetinaNet [7] | 26.5 | 48.3 | 25.4 |
| CN-DhVaSa [61] | 27.8 | 50.7 | 26.8 |
| DETR (2020) [16] | 23.1 | 39.8 | 25.7 |
| DN-DETR (2022) [19] | 31.4 | 51.6 | 26.8 |
| RT-DETR (2023) [22] | 31.0 | 50.2 | 26.9 |
| CZ Det (2023) [62] | 32.2 | 54.9 | 31.2 |
| DHQ-DETR | 32.4 | 55.4 | 30.0 |
| Model | Sampling Level | DFL | Epochs | AP | AP50 |
|---|---|---|---|---|---|
| RT-DETR [22] | × | × | 36 | 48.7 | 67.1 |
| DHQ-DETR | 16 | × | 36 | 48.5 | 66.6 |
| DHQ-DETR | 32 | × | 36 | 48.8 | 67.0 |
| DHQ-DETR | 64 | × | 36 | 48.7 | 67.1 |
| DHQ-DETR | 16 | ✓ | 36 | 49.1 | 67.3 |
| DHQ-DETR | 32 | ✓ | 36 | 49.4 | 67.5 |
| DHQ-DETR | 64 | ✓ | 36 | 49.3 | 67.3 |
| Model | IoU-Aware [63] | HQQS | AP | ||
|---|---|---|---|---|---|
| RT-DETR [22] | × | × | 47.9 | 0.35 | 0.47 |
| RT-DETR [22] | ✓ | × | 48.7 | 0.82 | 0.45 |
| RT-DETR [22] | ✓ | ✓ | 49.5 | 0.79 | 0.58 |
| Assignment Strategies | Epochs | AP | |
|---|---|---|---|
| Vanilla | 36 | 48.7 | 67.1 |
| RetinaNet [7] | 36 | 49.6 | 67.9 |
| Faster R-CNN [3] | 36 | 49.9 | 68.9 |
| FCOS [5] | 36 | 50.1 | 68.6 |
| ATSS [64] | 36 | 50.4 | 68.9 |
| Ours | 36 | 50.8 | 69.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Zhang, J.; Huo, B.; Xue, Y. DHQ-DETR: Distributed and High-Quality Object Query for Enhanced Dense Detection in Remote Sensing. Remote Sens. 2025, 17, 514. https://doi.org/10.3390/rs17030514
Li C, Zhang J, Huo B, Xue Y. DHQ-DETR: Distributed and High-Quality Object Query for Enhanced Dense Detection in Remote Sensing. Remote Sensing. 2025; 17(3):514. https://doi.org/10.3390/rs17030514
Chicago/Turabian StyleLi, Chenglong, Jianwei Zhang, Bihan Huo, and Yingjian Xue. 2025. "DHQ-DETR: Distributed and High-Quality Object Query for Enhanced Dense Detection in Remote Sensing" Remote Sensing 17, no. 3: 514. https://doi.org/10.3390/rs17030514
APA StyleLi, C., Zhang, J., Huo, B., & Xue, Y. (2025). DHQ-DETR: Distributed and High-Quality Object Query for Enhanced Dense Detection in Remote Sensing. Remote Sensing, 17(3), 514. https://doi.org/10.3390/rs17030514






