A Robust Direction-of-Arrival (DOA) Estimator for Weak Targets Based on a Dimension-Reduced Matrix Filter with Deep Nulling and Multiple-Measurement-Vector Orthogonal Matching Pursuit

Abstract

In the field of target localization, improving direction-of-arrival (DOA) estimation methods for weak targets in the context of strong interference remains a significant challenge. This paper presents a robust DOA estimator for localizing weak signals of interest in an environment with strong interfering sources that improve passive sonar DOA estimation. The presented estimator combines a multiple-measurement-vector orthogonal matching pursuit (MOMP) algorithm and a dimension-reduced matrix filter with deep nulling (DR-MFDN). Strong interfering sources are adaptively suppressed by employing the DR-MFDN, and the beam-space passband robustness is improved. In addition, Gaussian pre-whitening is used to prevent noise colorization. Simulations and experimental results demonstrate that the presented estimator outperforms a conventional estimator based on a dimension-reduced matrix filter with nulling (DR-MFN) and the multiple signal classification algorithm in terms of interference suppression and localization accuracy. Moreover, the presented estimator can effectively handle short snapshots, and it exhibits superior resolution by considering the signal sparsity.

1. Introduction

Matrix filters [1,2,3,4] have been widely used in sonar and radar applications because of their exceptional data filtering and signal separation capabilities in the spatial domain. A matrix filter projects the observation space onto a subspace by linear transformation, which passes the signals in the sector of interest (passband) while suppressing the out-of-sector (stopband) interference. Vaccaro and Harrison [1] designed a conventional matrix filter (CMF) in the frequency domain. MacInnes [5] improved passband robustness in the beam space by applying the least mean square criterion and solving it using convex optimization. However, this method fails to control the stopband attenuation (SA). Yan et al. [6,7] proposed a second-order cone programming model for CMFs under the stopband constraint, a passband least-squares criterion, and passband minimax criterion. Han et al. [8] proposed three optimization problems using the Lagrange multiplier method to obtain matrix filters with adjustable SA and passband robustness. Hassanien et al. [9] proposed a dimension-reduced conventional matrix filter by constraining the stopband and minimizing the difference between actual and quiescent response matrix filters. These variants of the CMF approach can strictly control the attenuation of the stopband while maintaining the passband performance. However, data cannot be effectively filtered when strong interfering sources are present in the environment. To solve the problem of weak target direction-of-arrival (DOA) estimation in an environment with strong interfering sources, adaptive matrix filters that can provide nulls toward the direction of the interfering sources and attenuate them adaptively were proposed [9,10,11]. The presence of noise and perturbation limits the depth of the nulls in the direction of the interfering sources and degrades the passband’s robustness. Considering the effect of noise after matrix filtering, Yan [7] limited the power of the noise to reduce its impact on subsequent processing. Nevertheless, non-orthogonal matrix filters transform white noise into colored noise; therefore, the estimation of weak targets is challenging. Hassanien [9] prevented the transformation of noise into colored noise by using an orthogonal pre-whitening (OP) operation. However, this method alters the beam-space characteristics of the matrix filter, particularly by reducing the SA, leading to insufficient interference suppression. To maintain better spatial filtering performance and orthogonality of the matrix filter, Wang [12,13] achieved better performance by synthesizing a set of orthogonal eigenbeams for spatial filtering.

Moreover, the multiple signal classification (MUSIC) algorithm [14], typically employed for DOA estimation with matrix filters, has exhibited poor performance in scenarios with coherent sources or short snapshots [7,8,9,15,16,17]. Recently, sparse reconstruction techniques have demonstrated great advantages in solving signal recovery problems and have been widely used in the field of array signal processing [18,19,20,21,22,23,24,25], for example, the sparse spectrum fitting (SpSF) algorithm [26] and matching pursuit algorithms [18,19,20]. Yang [10,27] proposed estimators based on the SpSF algorithm and matrix filters. However, with these methods, noise power must be estimated. Moreover, determining the selection of the regularization parameter is challenging in practice.

This paper aims to introduce an improved DOA estimator for weak targets. First, considering that white noise at the input may be transformed into colored noise, this study utilizes a Gaussian matrix for the pre-whitening operation. The objective is to prevent the transformation of white noise into colored noise while preserving the characteristics of the beam space. Second, the DOA estimation method is presented based on matrix filters and the multiple-measurement-vector orthogonal matching pursuit (MOMP) algorithm [28]. The MOMP is an extended form of the orthogonal matching pursuit (OMP) algorithm [29] under the multiple-measurement-vector (MMV) model. Next, based on the design method of a dimension-reduced matrix filter with nulling (DR-MFN) proposed in [9], a dimension-reduced matrix filter with deep nulling (DR-MFDN) is presented for DOA estimation in this study. With a projection matrix that enhances the interference component in the array data, the presented matrix filter can provide deep nulls and a lower passband response error when the array output energy is minimized. Additionally, reducing the beam-space dimension can simplify the problem dimension, reducing the computational complexity. An estimator based on the DR-MFDN and MOMP algorithms with the Gaussian pre-whitening (GP) operations can then be obtained. An estimator based on the DR-MFN and MUSIC algorithms is used to verify the effectiveness of the pre-whitening operation. Finally, the DOA estimation performances of four combination estimators, comprising two DOA estimation algorithms (MUSIC and MOMP) and two matrix filters (DR-MFN and DR-MFDN), are compared using the preferred pre-whitening operation.

In this study, we extended our preliminary work in the conference paper [30]. Although the conference paper proposed the concept of DR-MFDN and demonstrated its preliminary performance, due to scope limitations, the paper failed to provide detailed algorithm descriptions, extensive simulation and experimental verification, and analysis of computation time. Simulations and experimental results demonstrate that the presented adaptive matrix filter exhibits greater robustness in the passband and outperforms interference suppression. Moreover, the GP operation is better adapted for processing beam-space snapshots than the OP operation. The estimator based on adaptive matrix filters and the MOMP algorithm with the GP operation can achieve high localization accuracy.

2. Materials and Methods

2.1. Signal Model and Pre-Whitening Operation

In this section, sparse models of element-space and beam-space signals are established, and a novel pre-whitening operation based on a Gaussian matrix is introduced.

2.1.1. Element-Space Signal Model

Consider K far-field signals with frequency f impinging on a uniform linear array with M elements distributed along the x direction with spacing d. The received signal at the mth element of the array can be considered as the sum of the finite plane waves as follows:

$$p_m\left(f\right)=\Delta \theta \sum _{l=1}^{L}s(f,{\theta }_j)e^{i({\displaystyle \frac{2\pi f}{c}}{x}_{m}sin{\theta }_j)}$$

(1)

where c is the velocity of sound; $s(f,{\theta }_j)$ is the plane wave amplitude in ${\theta }_j$; $\Delta \theta ={\displaystyle \frac{\pi }{J}}$, with J being the number of angular discretizations, and ${\theta }_j=(j-{\displaystyle \frac{1}{2}})\Delta \theta -{\displaystyle \frac{\pi }{2}}h,j=1,\cdots ,J$.

The wideband signals received by the array were partitioned into N segments, and an L-point FFT was applied to each segment. The array output in the frequency domain can be expressed in the discrete form shown in Equation (1) as follows:

$${\mathbf{p}}_l\left(n\right)=\mathbf{A}(f_l,\mathbf{\Theta }){\mathbf{s}}_l\left(n\right)+{\mathbf{e}}_l\left(n\right),n=1,2,\cdots ,N$$

(2)

where $\mathbf{A}(f_l,\mathbf{\Theta })\in {\mathbb{C}}^{M\times J}$ is the steering matrix, $\mathbf{\Theta }={[{\theta }_1,\cdots ,{\theta }_J]}^T$ is the vector that comprises J candidate directions, and the superscript T is the transpose operator. Moreover, ${\mathbf{p}}_l\left(n\right)\in {\mathbb{C}}^{M\times 1}$, ${\mathbf{s}}_l\left(n\right)\in {\mathbb{C}}^{J\times 1}$, and ${\mathbf{e}}_l\left(n\right)\in {\mathbb{C}}^{M\times 1}$ represent the FFT coefficients of the received data, wideband signals, and additive noise at the nth segment, respectively. The steering matrix is given by

$$\mathbf{A}(f_l,\mathbf{\Theta })=\left[\mathbf{a}(f_l,{\theta }_1),\cdots ,\mathbf{a}(f_l,{\theta }_j),\cdots ,\mathbf{a}(f_l,{\theta }_J)\right]$$

(3)

where

$$\mathbf{a}(f_l,{\theta }_j)={[1,e^{i({\displaystyle \frac{2\pi f_l}{c}}dsin{\theta }_j)},\cdots ,e^{i({\displaystyle \frac{2\pi f_l}{c}}(M-1)dsin{\theta }_j)}]}^T$$

(4)

Assuming that ${\mathbf{e}}_l$ is white noise, the array covariance matrix ${\mathbf{R}}_l{\in }^{M\times M}$ of the array output in the frequency domain is expressed as follows [14,31]:

$${\mathbf{R}}_l=\mathbb{E}\left[{\mathbf{p}}_l\left(n\right){\mathbf{p}}_l^H\left(n\right)\right]=\mathbf{A}(f_l,\mathbf{\Theta }){\mathbf{R}}_{\mathbf{s}}^l{\mathbf{A}}^H(f_l,\mathbf{\Theta })+{\mathbf{R}}_{\mathbf{e}}^l=\mathbf{A}(f_l,\mathbf{\Theta }){\mathbf{R}}_{\mathbf{s}}^l{\mathbf{A}}^H(f_l,\mathbf{\Theta })+{{\sigma }_l}^2{\mathbf{I}}_M$$

(5)

where $\mathbb{E}[·]$ denotes the expectation operation; superscript H represents the Hermitian transpose; ${\mathbf{R}}_s^l=\mathbb{E}\left[{\mathbf{s}}_l\left(n\right){\mathbf{s}}_l^H\left(n\right)\right]\in {\mathbb{C}}^{K\times K}$, ${\mathbf{R}}_{\mathbf{e}}^l=\mathbb{E}\left[{\mathbf{e}}_l\left(n\right){\mathbf{e}}_l^H\left(n\right)\right]\in {\mathbb{C}}^{M\times M}$; ${{\sigma }_l}^2$ is the variance of the white noise; and ${\mathbf{I}}_M$ is an identity matrix of dimension M.

2.1.2. Beam-Space Signal Model and Pre-Whitening Operation

Conventional array processing methods cannot effectively estimate the DOAs of weak targets under strong interfering sources. Therefore, transforming the signal into the designed beam-space is necessary. The beam-space snapshot vector ${\mathbf{z}}_l\left(n\right)\in {\mathbb{C}}^{M\times 1}$ in reduced dimensions ($M^{\prime }<M$ is the beam-space dimension) is defined as a linear transformation of the frequency-domain snapshot ${\mathbf{p}}_l\left(n\right)$ as follows:

$${\mathbf{z}}_l\left(n\right)={\mathbf{G}}_l^H{\mathbf{p}}_l\left(n\right)={\mathbf{G}}_l^H\mathbf{A}(f_l,\mathbf{\Theta }){\mathbf{s}}_l\left(n\right)+{\mathbf{G}}_l^H{\mathbf{e}}_l\left(n\right)$$

(6)

where ${\mathbf{G}}_l^H$ is the matrix filter corresponding to the frequency $f_l$.

The beam-space array covariance matrix ${\mathbf{R}}_{\mathbf{z}}$ is given by

$${\mathbf{R}}_{\mathbf{z}}=\mathrm{E}\left[{\mathbf{z}}_l\left(n\right){\mathbf{z}}_l^H\left(n\right)\right]={\mathbf{G}}_l^H{\mathbf{R}}_l{\mathbf{G}}_l={\mathbf{G}}_l^H\mathbf{A}(f_l,\mathbf{\Theta }){\mathbf{R}}_{\mathbf{s}}^l{\mathbf{A}}^H(f_l,\mathbf{\Theta }){\mathbf{G}}_l+{{\sigma }_l}^2{\mathbf{G}}_l^H{\mathbf{G}}_l$$

(7)

If ${\mathbf{G}}_l$ is not orthogonal, it transforms white noise into colored noise, which is not convenient for subsequent processing. Thus, an additional noise pre-whitening operation is required. Under a conventional OP operation, Equation (6) can be rewritten as [16,17,32]

$${\widehat{\mathbf{z}}}_l\left(n\right)={\left({\mathbf{G}}_l^H{\mathbf{G}}_l\right)}^{-1/2}{\mathbf{G}}_l^H{\mathbf{p}}_l\left(n\right)$$

(8)

The application of an OP operation alters the characteristics of the beam space. Considering that the SVD decomposition of the matrix filter is performed with ${\mathbf{G}}_l=\mathbf{u}\epsilon {\mathbf{v}}^H$ and ${\mathbf{G}}_l{\mathbf{G}}_l^H=\mathbf{u}{\epsilon }^2{\mathbf{u}}^H$, the beam-space response $h(f_l,\theta )$ by the matrix filter ${\mathbf{G}}_l$ is

$$h(f_l,\theta )={\displaystyle \frac{{∥{\mathbf{G}}_l^H\mathbf{a}(f_l,\theta )∥}_2}{{∥\mathbf{a}(f_l,\theta )∥}_2}}={[{\displaystyle \frac{1}{M}}{\mathbf{a}}^H(f_l,\theta )\mathbf{u}{\epsilon }^2{\mathbf{u}}^H\mathbf{a}(f_l,\theta )]}^{1/2}$$

(9)

With an OP operation, Equation (9) can be rewritten as

$$\widehat{h}(f_l,\theta )={\displaystyle \frac{{∥{\left({\mathbf{G}}_l^H{\mathbf{G}}_l\right)}^{-1/2}{\mathbf{G}}_l^H\mathbf{a}(f_l,\theta )∥}_2}{{∥\mathbf{a}(f_l,\theta )∥}_2}}={[{\displaystyle \frac{1}{M}}{\mathbf{a}}^H(f_l,\theta )\mathbf{u}{\mathbf{u}}^H\mathbf{a}(f_l,\theta )]}^{1/2}$$

(10)

Considering Equations (9) and (10), the OP operation normalizes the eigenvalues of the matrix ${\mathbf{G}}_l^H$, modifying the beam space. To ensure that the beam-space transformation preserves the original characteristics and prevents white noise from being transformed into colored noise, a Gaussian matrix was employed for the pre-whitening operation. The frequency-domain snapshot is transformed into

$${\tilde{\mathbf{z}}}_l\left(n\right)={\mathbf{G}}_a{\mathbf{G}}_l^H{\mathbf{p}}_l\left(n\right)$$

(11)

where ${\mathbf{G}}_a={[{\mathbf{g}}_{a1},{\mathbf{g}}_{a2},\cdots ,{\mathbf{g}}_{a{M}^{\prime }}]}^T\in {\mathbb{C}}^{M^{\prime }\times M^{\prime }}$ is a Gaussian matrix, with each vector obeying ${\mathbf{g}}_{ai}\left(m\right)\sim \mathrm{N}(0,{\sigma }_l^2),i\mid m=1,2,\cdots ,M^{\prime }$ and any two arbitrary vectors obeying $\mathrm{cov}{({\mathbf{g}}_{ai},{\mathbf{g}}_{aj})}_{(i\ne j,1\le i,j\le M^{\prime })}=0$.

With the GP operation, the beam-space response can be reformulated as follows:

$$\widehat{h}\left(f_l,\theta \right)={\displaystyle \frac{{∥{\mathbf{G}}_a{\mathbf{G}}_l^H\mathbf{a}\left(f_l,\theta \right)∥}_2}{{∥\mathbf{a}\left(f_l,\theta \right)∥}_2}}={\left[{\displaystyle \frac{1}{M}}{\mathbf{a}}^H\left(f_l,\theta \right){\mathbf{G}}_l{\mathbf{G}}_a^H{\mathbf{G}}_a{\mathbf{G}}_l^H\mathbf{a}\left(f_l,\theta \right)\right]}^{1/2}=h\left(f_l,\theta \right)$$

(12)

According to Appendix A, noise covariance matrix ${\mathbf{R}}_{\mathbf{e}}^l$ is transformed as follows [33]:

$${\mathbf{G}}_a{\mathbf{G}}_l^H{\mathbf{R}}_{\mathbf{e}}^l{\mathbf{G}}_l{\mathbf{G}}_a^H={\sigma }_l^2{\mathbf{I}}_{M^{\prime }}$$

(13)

where ${\mathbf{I}}_{M^{\prime }}$ is an identity matrix of dimension $M^{\prime }$.

It is important to note that perfectly uncorrelated Gaussian matrices do not exist in practice. However, Gaussian matrices statistically approximate this property. Therefore, extensive experimentation is needed to approach the ideal performance of a Gaussian matrix, with the average results obtained reflecting the desired outcome.

2.2. Robust DOA Estimator Based on a Matrix Filter and MOMP Algorithm

In this section, we present a robust DOA estimator based on a matrix filter and the MOMP algorithm. Referring to Equation (11), the beam-space snapshot vector with the GP operation can be further expressed as follows:

$${\tilde{\mathbf{z}}}_l\left(n\right)={\mathbf{B}}_l^H{\mathbf{p}}_l\left(n\right)={\mathbf{\Psi }}_l{\tilde{\mathbf{s}}}_l\left(n\right)+{\mathbf{B}}_l^H\mathbf{e}\left(n\right)$$

(14)

where ${\mathbf{B}}_l={\left({\mathbf{G}}_a{\mathbf{G}}_l^H\right)}^H$; ${\mathbf{\Psi }}_l={\mathbf{B}}_l^H\mathbf{A}(f_l,\mathbf{\Theta })\in {\mathbb{C}}^{M^{\prime }\times J}$ is the dictionary; ${\tilde{\mathbf{s}}}_l\left(n\right)$ is the amplitude of the plane wave in the candidate direction after filtering, and its sparsity $K^{\prime }(K^{\prime }\le K)$ is the number of residual signals after filtering.

In this study, the MOMP algorithm is an extended form of the OMP algorithm under the MMV model to solve for the column-uniform sparse matrix ${\tilde{\mathbf{s}}}_l$. The algorithm is as follows:

Algorithm 1 Multiple-Measurement-Vector Orthogonal Matching Pursuit (MOMP)
ine Step 1	Input: ${\tilde{\mathbf{z}}}_l$, ${\mathbf{\Psi }}_l$, $K^{\prime }$.
ine Step 2	Initialization: residual ${\mathbf{R}}_0={\tilde{\mathbf{z}}}_l$, subset ${\mathsf{\Lambda }}_0=\mathsf{\varnothing }$, and $i=1$.
ine Step 3	At the i-th iteration step:
	(a) Choose atom ${\mathbf{’}}_i$ satisfying ${\mathbf{’}}_i=\arg {\max }_{{\mathbf{’}}_i}{∥{\mathbf{\Psi }}_l^T{\mathbf{R}}_{i-1}∥}_{p’}$, and $p\ge 1$;
	(b) Update ${\mathsf{\Lambda }}_i=[{\mathsf{\Lambda }}_{i-1},{\mathbf{’}}_i]$, and ${\widehat{\mathbf{s}}}_l^i={\left({\mathsf{\Lambda }}_i^H{\mathsf{\Lambda }}_i\right)}^{-1}{\mathsf{\Lambda }}_i^H{\tilde{\mathbf{z}}}_l$;
	(c) Update ${\mathbf{R}}_i={\tilde{\mathbf{z}}}_l-{\mathbf{\Psi }}_l{\widehat{\mathbf{s}}}_l^i$;
	(d) If $i<{\mathrm{K}}^{\prime }$, return to step 3; if $i\ge {\mathrm{K}}^{\prime }$, terminate the iteration and switch to step 4.
ine Step 4	Output: The solution ${\tilde{\mathbf{s}}}_l={\widehat{\mathbf{s}}}_l^i$ and residual ${\mathbf{R}}_{\tilde{\mathbf{z}}}={\mathbf{R}}_{\tilde{\mathbf{z}}}^i$.
ine

After solving for the matrix ${\tilde{\mathbf{s}}}_l$ at every frequency, the final estimation of the spatial spectrum in the beam space can be calculated as follows:

$$\mathbf{s}={\displaystyle \frac{1}{N}}\sum _{l=1}^L\sum _{n=1}^N{\tilde{\mathbf{s}}}_l\left(n\right)$$

(15)

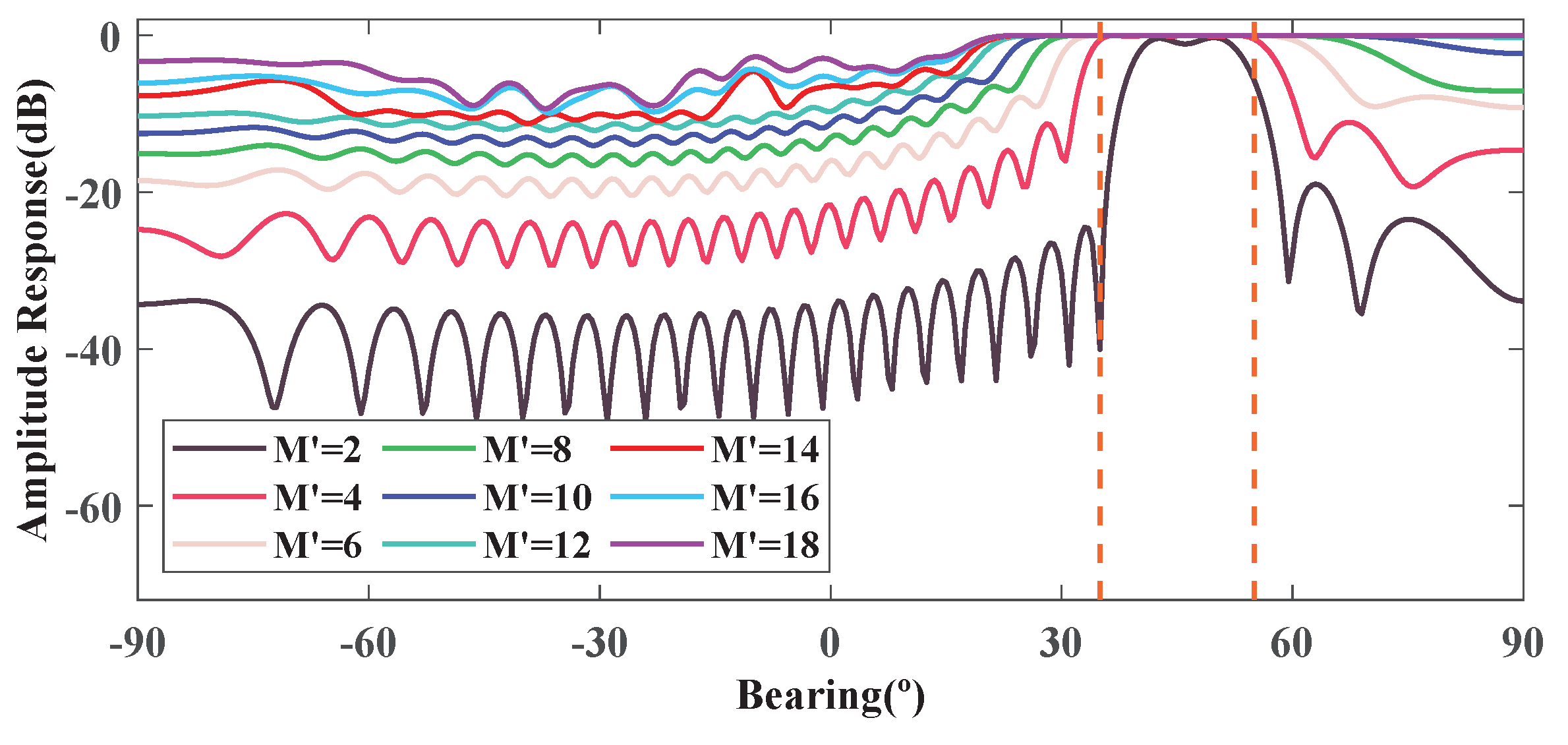
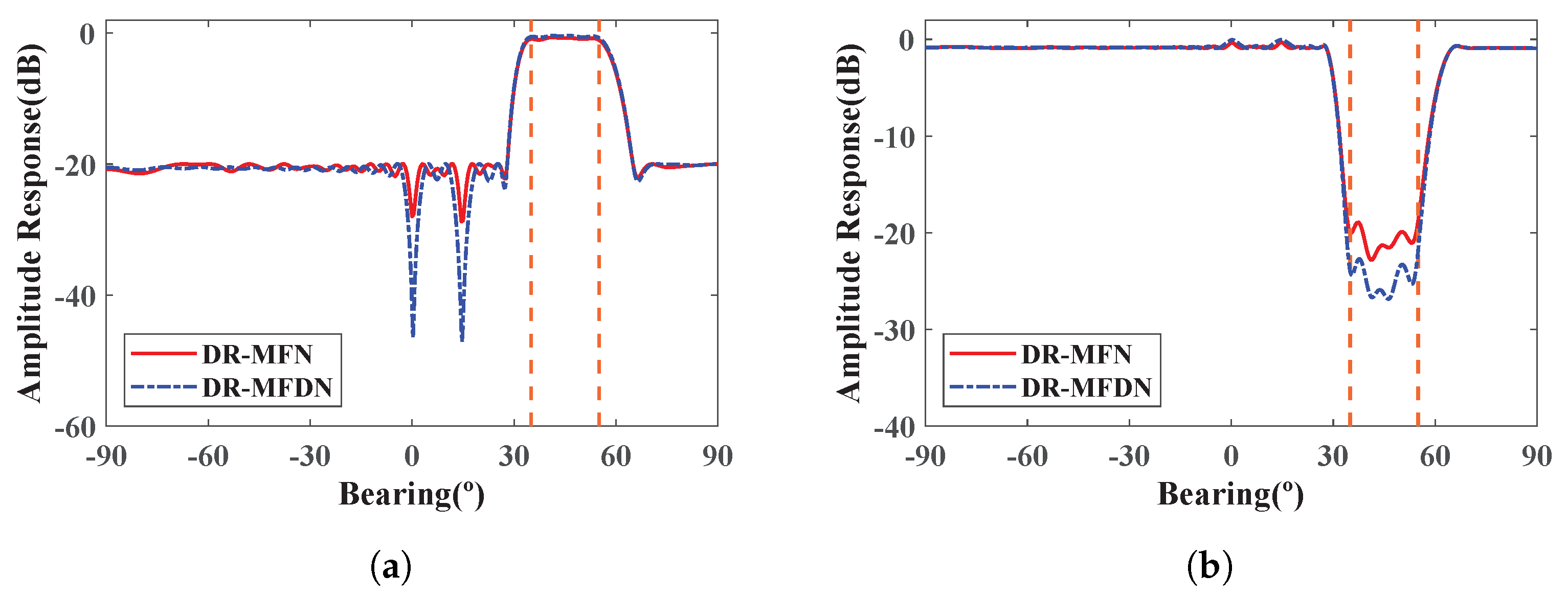
2.3. Design of Dimension-Reduced Matrix Filter with Deep Nulling

This section describes the approach to achieving high localization accuracy of the presented estimator in an environment with strong interfering sources. In particular, a dimension-reduced matrix filter with deep nulling is presented to improve interference suppression and robustness compared to a dimension-reduced matrix filter with nulling.

2.3.1. Design of Dimension-Reduced Matrix Filter with Nulling

The design of DR-MFNs based on quiescent matrix filters (QMFs) was proposed in [9]. This method uses a matrix filter, designed by the discrete prolate spheroidal sequence-based approach [34,35] as a quiescent matrix filter, to design the DR-MFN by constraining the difference between the actual response and QMF and the response of the stopband while minimizing the output power of the filtered array. The design of the MFN can be formulated as follows:

$$\begin{array}{c}\underset{{\mathbf{G}}_l}{min}tr\left\{{\mathbf{G}}_l^H{\mathbf{R}}_l{\mathbf{G}}_l\right\}\hfill \\ s.t.\left\{\begin{array}{c}{∥{\mathbf{G}}_l^H-{\mathbf{G}}_{lq}^H∥}_F\le \epsilon \hfill \\ {∥{\mathbf{G}}_l^H\mathbf{a}(f_l,{\theta }_s)∥}_2\le \delta ,{\theta }_s\in {\mathbf{\Theta }}_S,s=1,\cdots ,S\hfill \end{array}\right.\hfill \end{array}$$

(16)

where, ${\Theta }_S$ combines a continuum of all out-of-sector directions; ${\theta }_s\in {\Theta }_S(s=1,\cdots ,S)$ is the angular grid chosen (uniform or nonuniform) that properly approximates the stopband region by a finite number S of directions; ${∥•∥}_F$ is the matrix Frobenius norm; ${∥•∥}_2$ is the vector 2-norm; $\epsilon >0$ is the parameter that bounds the passband distortion of the designed matrix filter ${\mathbf{G}}_l$ with respect to ${\mathbf{G}}_{lq}$; $\delta >0$ is a parameter of the user’s choice that characterizes the worst acceptable SA; and ${\mathbf{G}}_{lq}$ is the QMF. The beam space of QMFs varies across different beam-space dimensions, as shown in Figure 1.

Figure 1 shows the beam-space amplitude response of the QMFs across various dimensions for a 32-element uniform line array with a spacing of $1 \mathrm{m}$ when the passband is set to $\left[{33}^{\circ },{55}^{\circ }\right]$ with a frequency of 600 $\mathrm{Hz}$. Note that the QMFs have a high passband response error within the preset passband for $M^{\prime }=2$. This is because of the low dimensionality, which may lead to an insufficient number of eigenvalues to adequately represent the passband space. Therefore, selecting such a low number of dimensions is not advisable when designing the DR-MFN. Moreover, the dimensions should satisfy

$$M_p\le M^{\prime }\le M$$

(17)

where $M_p$ is the minimum number of eigenvalues required to represent passband space.

Equation (16) indicates that DR-MFN is derived by imposing additional constraints based on QMF. Therefore, the beam-space characteristics of the DR-MFN are related to QMF. Applying energy constraints in noninterfering directions may lead to undesired distortions within the passband and insufficient suppression of strongly interfering sources. In particular, obtaining the desired matrix filter when QMF does not satisfy the desired SA is challenging because the stopband and energy constraints are complicated, and the parameters are difficult to establish. Therefore, the robustness of this technique for out-of-sector sources may be insufficient, making it impractical.

2.3.2. Design of Dimension-Reduced Matrix Filter with Deep Nulling

To enhance the robustness of the adaptive matrix filter with nulling, the DR-MFDN was proposed and used for the DOA estimation of the signals of interest. Assuming that all out-of-sector sources satisfy $\mathrm{INR}\ge 15\mathrm{dB}$, the design procedure is as follows:

Step 1

Input: $f_l$, ${\Theta }_P$, ${\Theta }_S$, SA, ${\mathbf{R}}_l$, $ϵ$.

Step 2

Initialization: $\delta ={10}^{(\mathrm{SA}/20)}$.

Step 3

Preprocess with MVDR algorithm [36]:

(a) Search spectral peaks in stopband and record their normalized amplitudes $[I_1,\cdots ,I_{K^{″}}]$;

(b) Record the directions $[{\theta }_1,\cdots ,{\theta }_{K^{″}}]$ corresponding to the peaks.

Step 4

Generate the projection matrix:

(a) The sector of the main lobe where each peak is located is identified; the $k^{″}$th sector of the main lobe is denoted as ${\Theta }_{k^{″}}$,

$${\Theta }_{k^{″}}=[{\theta }_{k^{″}-l_{k^{″}}},\cdots ,{\theta }_{k^{″}},\cdots ,{\theta }_{k^{″}+r_{k^{″}}}],k^{″}=1,\cdots ,K^{″}.$$

(18)

where ${\theta }_{k^{″}-l_{k^{″}}}$ and ${\theta }_{k^{″}+r_{k^{″}}}$ are the left and right boundary angulars of the main lobe corresponding to the $k^{″}$th peak, respectively.

(b) The projection matrix is constructed as follows: ${\mathbf{\Psi }}_l=[\mathbf{A}(f_l,{\mathbf{\Theta }}_1),\cdots ,\mathbf{A}(f_l,{\mathbf{\Theta }}_{K^{″}})]$ at frequency $f_l$.

Step 5

Formulate the optimization problem:

(a) Conventional form:

$$\begin{array}{c}\underset{{\mathbf{G}}_l}{min}tr\left\{{{\mathbf{G}}_l}^H{\mathbf{\Psi }}_l^H{\mathbf{R}}_l{\mathbf{\Psi }}_l{\mathbf{G}}_l\right\}\hfill \\ \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{∥{{\mathbf{G}}_l}^H-{\mathbf{G}}_{lc}^H∥}_F\le \epsilon \hfill \\ {∥{{\mathbf{G}}_l}^H\mathbf{a}\left(f_l,\theta \right)∥}_2\le \delta \hfill \end{array}\right.\hfill \end{array}$$

(19)

Step 6

Transform Equation (19) into SOCP form:

$$\begin{array}{cc}\hfill \mathrm{tr}\left\{{\mathbf{G}}_l^H{\mathbf{\Psi }}_l^H{\mathbf{R}}_l{\mathbf{\Psi }}_l{\mathbf{G}}_l\right\}& =\mathrm{tr}\left\{{\mathbf{G}}_l^H{\mathbf{\Psi }}_l^H{\mathbf{R}}_l^{1/2}{\mathbf{R}}_l^{1/2}{\mathbf{\Psi }}_l{\mathbf{G}}_l\right\}\hfill \\ \hfill & ={∥{\mathbf{G}}_l^H\left({\mathbf{\Psi }}_l^H{\mathbf{R}}_l^{1/2}\right)∥}_{\mathbf{F}}^2\hfill \\ \hfill & ={∥\mathrm{vec}\left\{{\mathbf{I}}_{M^{\prime }}{\mathbf{G}}_l^H\left({\mathbf{\Psi }}_l^H{\mathbf{R}}_l^{1/2}\right)\right\}∥}_2^2\hfill \\ \hfill & ={∥\left[{\left({\mathbf{\Psi }}_l^H{\mathbf{R}}_l^{1/2}\right)}^T\otimes {\mathbf{I}}_{M^{\prime }}\right]{\mathbf{g}}_l∥}_2^2\hfill \end{array}$$

(20)

$${∥{\mathbf{G}}_l^H-{\mathbf{G}}_{lc}^H∥}_{\mathbf{F}}={∥{\mathbf{g}}_l-{\mathbf{g}}_{lc}∥}_2$$

(21)

$${∥{\mathbf{G}}_l^H\mathbf{a}\left(f_l,{\theta }_s\right)∥}_2={∥\left[{\mathbf{a}}^T\left(f_l,{\theta }_s\right)\otimes {\mathbf{I}}_{M^{\prime }}\right]{\mathbf{g}}_l∥}_2$$

(22)

where $vec\{·\}$ denotes the vectorization operator stacking the columns of a matrix on top of each other, ${\mathbf{g}}_l=\mathrm{vec}\left({\mathbf{G}}_l^H\right)$, ${\mathbf{g}}_{lc}=\mathrm{vec}\left({\mathbf{G}}_{lc}^H\right)$, ⊗ denotes the Kronecker matrix product and ${\mathbf{I}}_{M^{\prime }}$ is an identity matrix of dimension $M^{\prime }$. Substituting Equations (20)–(22) into Equation (19), Equation (19) can be rewritten as

$$\begin{array}{cc}\hfill & \underset{{\mathbf{g}}_l}{min}{∥\left[{\left({\mathbf{\Psi }}_l^H{\mathbf{U}}_l\right)}^T\otimes {\mathbf{I}}_{M^{\prime }}\right]{\mathbf{g}}_l∥}_2\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.\left\{\begin{array}{c}{∥{\mathbf{g}}_l-{\mathbf{g}}_{lc}∥}_2\le \epsilon \hfill \\ {∥\left[{\mathbf{a}}^T\left(f_l,{\theta }_s\right)\otimes {\mathbf{I}}_{M^{\prime }}\right]{\mathbf{g}}_l∥}_2\le \delta ,{\theta }_s\in {\mathbf{\Theta }}_S,s=1,\cdots ,S.\hfill \end{array}\right.\hfill \end{array}$$

(23)

Step 7

Solve the SOCP Problem: Use an SOCP solver (e.g., mosek) to solve for ${\mathbf{g}}_l$.

Step 8

Output: Reshape ${\mathbf{g}}_l$ back to matrix form ${\mathbf{G}}_l={\left[\mathrm{mat}\left({\mathbf{g}}_l\right)\right]}^H$.

Through the above steps, a DR-MFDN ${\mathbf{G}}_l$ at frequency $f_l$ can be obtained. The enhancement principle of the projection matrix is to project all array data onto the subspace corresponding to the main lobe.

An unknown source with direction ${\theta }_u$ is projected as

$$\begin{array}{c}\mathbf{x}=I_u\mathbf{A}(f_l,{\Theta }_{k^{″}}){\mathbf{A}}^H(f_l,{\Theta }_{k^{″}})\mathbf{a}(f_l,{\theta }_u)\hfill \\ =I_u\mathbf{A}(f_l,{\Theta }_{k^{″}})[{\mathbf{a}}^H(f_l,{\theta }_{k^{″}-l_{k^{″}}});\cdots ;{\mathbf{a}}^H(f_l,{\theta }_{k^{″}+r_{k^{″}}})]\mathbf{a}(f_l,{\theta }_u)\hfill \\ ={\displaystyle \frac{I_u}{l_{k^{″}}+r_{k^{″}}+1}}[\mathbf{a}(f_l,{\theta }_{k^{″}-l_{k^{″}}}),\cdots ,\mathbf{a}(f_l,{\theta }_{k^{″}+r_{k^{″}}})]{[{\Delta }_{l_{k^{″}}},\cdots ,1,\cdots ,{\Delta }_{r_{k^{″}}}]}^T\hfill \\ =I_u{\Delta }_u\mathbf{a}({\theta }_u)\hfill \end{array}$$

(24)

where ${\Delta }_{l_{k^{″}}}={\displaystyle \frac{sin[\frac{\pi f_{l}Md}{c}(sin{\theta }_u-sin{\theta }_{k^{″}-l_{k^{″}}})]}{Msin[\frac{\pi f_{l}d}{c}(sin{\theta }_u-sin{\theta }_{k^{″}-l_{k^{″}}})]}}$; ${\Delta }_{r_{k^{″}}}={\displaystyle \frac{sin[\frac{\pi f_{l}Md}{c}(sin{\theta }_u-sin{\theta }_{k^{″}+r_{k^{″}}})]}{Msin[\frac{\pi f_{l}d}{c}(sin{\theta }_u-sin{\theta }_{k^{″}+r_{k^{″}}})]}}$; and ${\Delta }_u<1$ is the amplitude of the transformation of the unknown source into an interfering source after projection.

If ${\theta }_u={\theta }_{k^{″}}$, the spectrum estimation obtained by the MVDR algorithm provides a narrower main lobe; that is, ${\Delta }_{l_{k^{″}}}\approx {\Delta }_{r_{k^{″}}}\approx 1$, and Equation (24) can be rewritten as follows:

$$\mathbf{x}\approx {\displaystyle \frac{I_{k^{″}}}{l_{k^{″}}+r_{k^{″}}+1}}[f_l,\mathbf{a}({\theta }_{k^{″}-l_{k^{″}}}),\cdots ,\mathbf{a}(f_l,{\theta }_{k^{″}+r_{k^{″}}})]{[1,\cdots ,1]}^T\approx I_{k^{″}}\mathbf{a}(f_l,{\theta }_{k^{″}})$$

(25)

From Equations (24) and (25), it can be seen that the projection matrix retains the out-of-sector source components while concentrating the signal-of-interest components from other directions onto these out-of-sector sources, thereby directing energy toward the strong out-of-sector sources. Additionally, the interfering sources from different directions reinforce each other.

By enhancing the out-of-sector sources through the projection matrix, the DR-MFDN algorithm, which is designed based on the minimum energy criterion, effectively reduces the impact of perturbations and noise within the passband, achieving deeper nulls in the direction of strong interfering sources. As a result, the robustness of the adaptive matrix filter with nulling is significantly improved.

3. Discussion

In the simulation, a uniform linear array of 32 isotropic array elements with a spacing of 1 m was considered to analyze the effectiveness of the GP operation and DOA estimation performance of the robust estimator based on the MOMP algorithm and DR-MFDN. Three distinct received-signal scenarios were simulated.

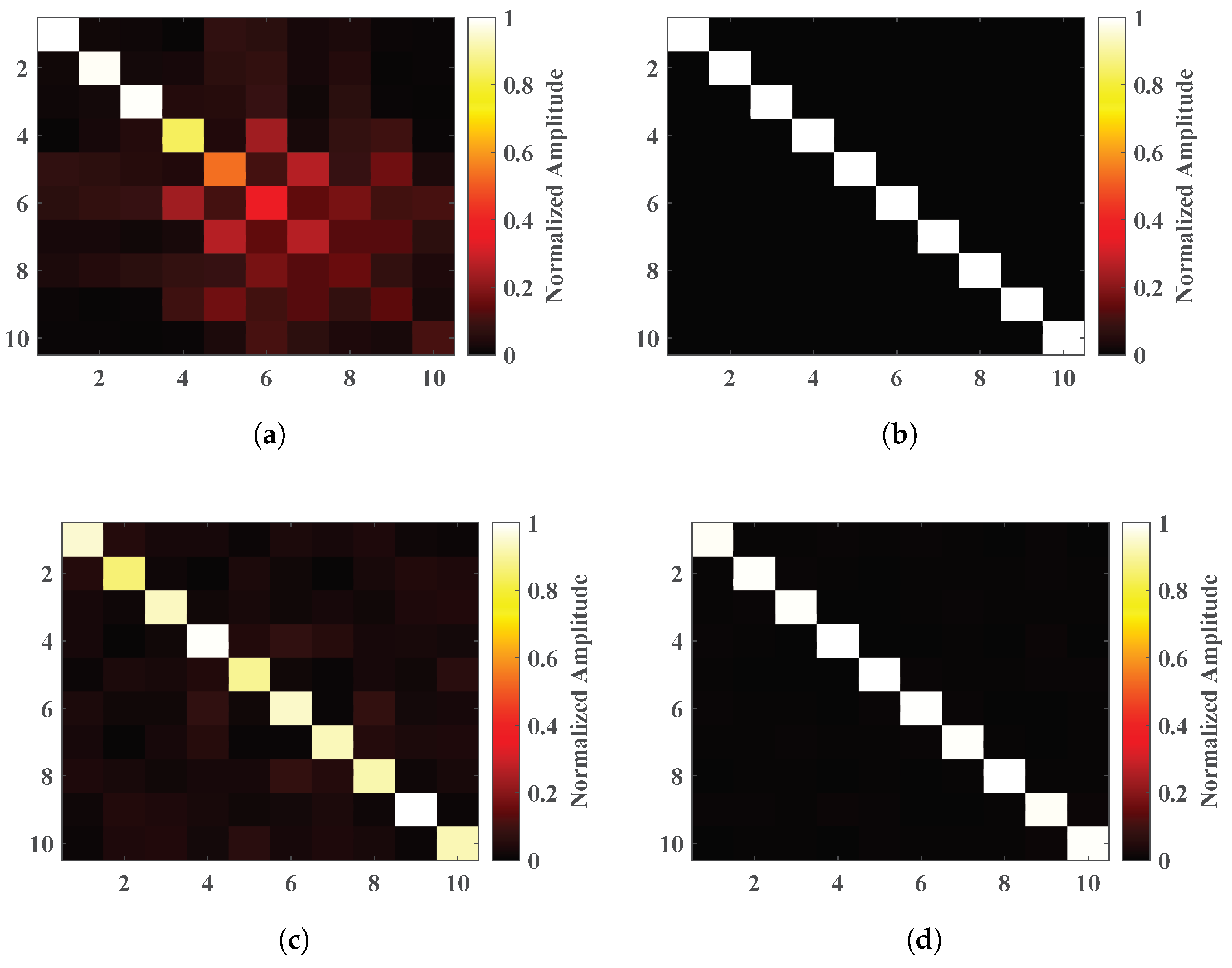
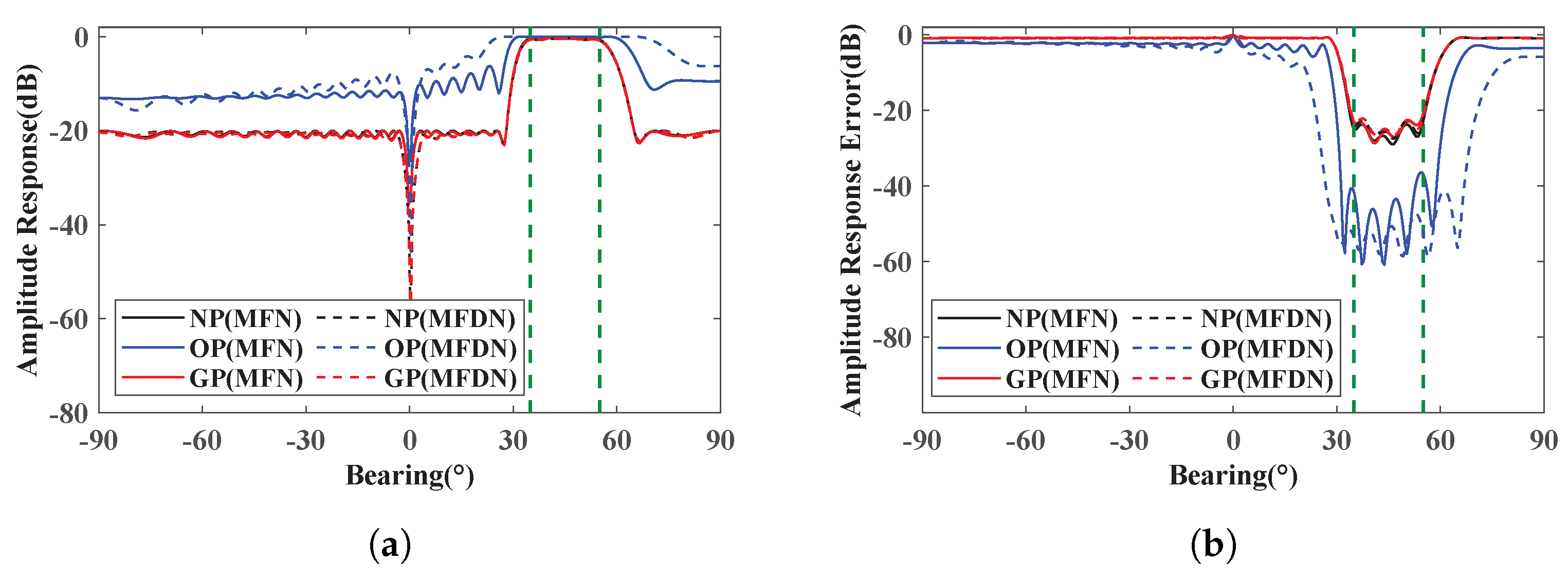
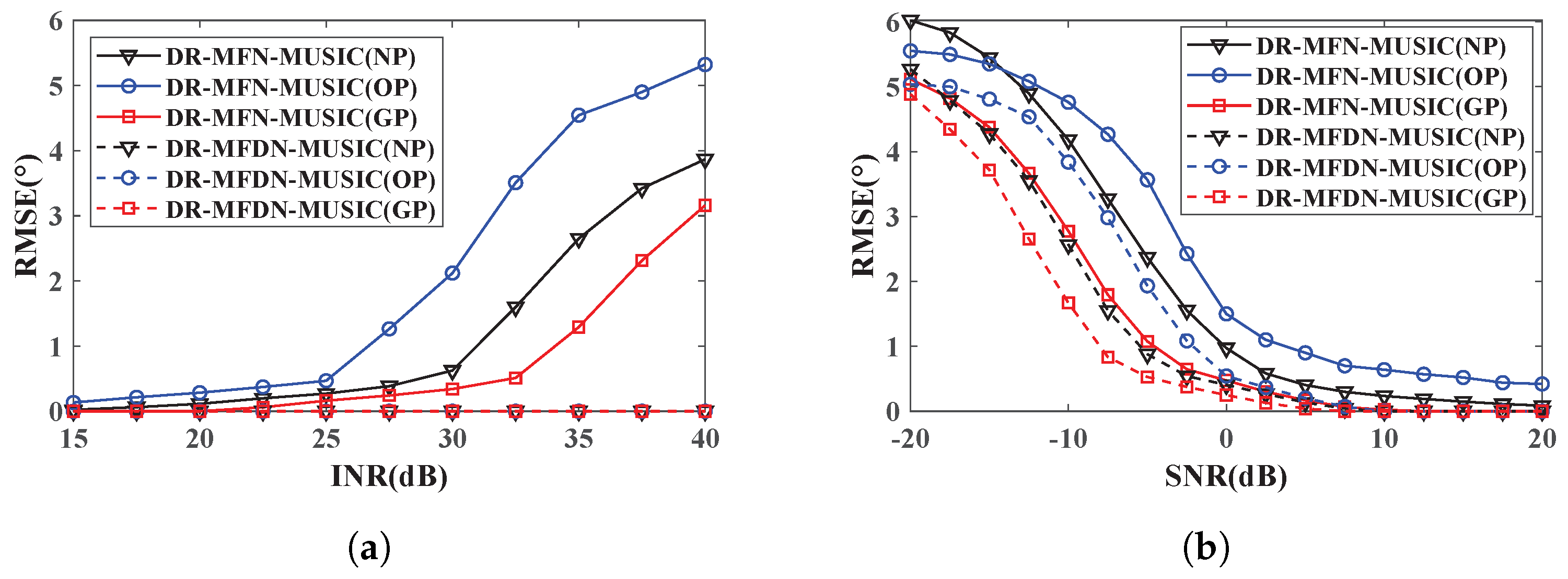
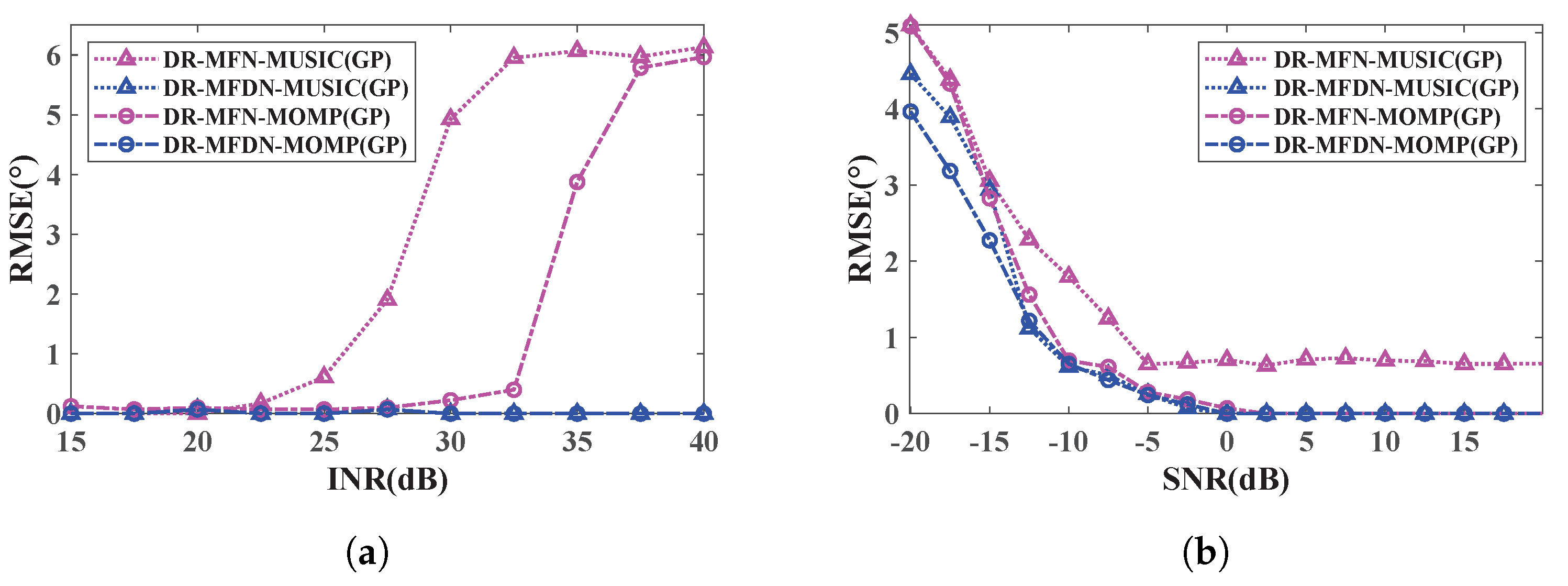
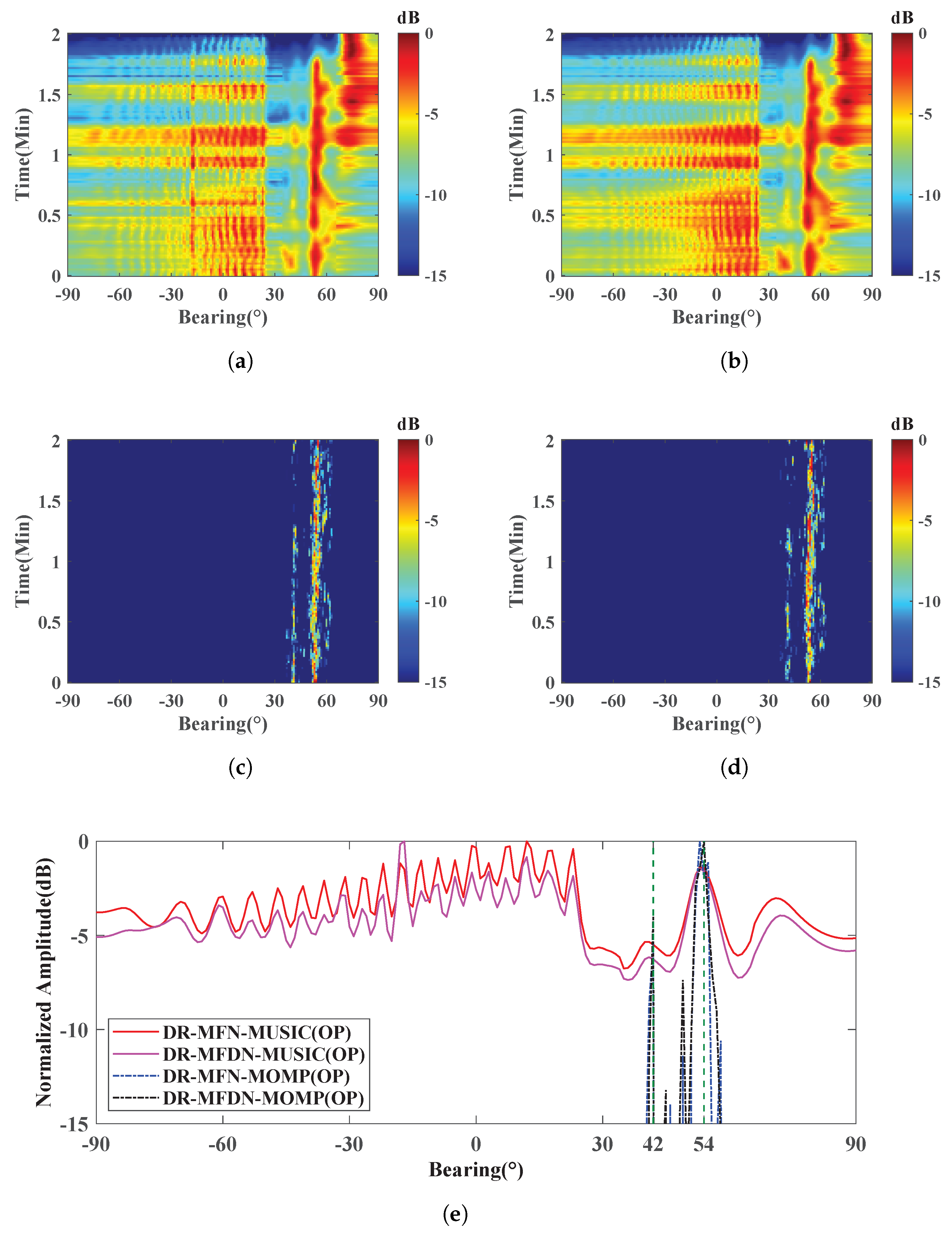
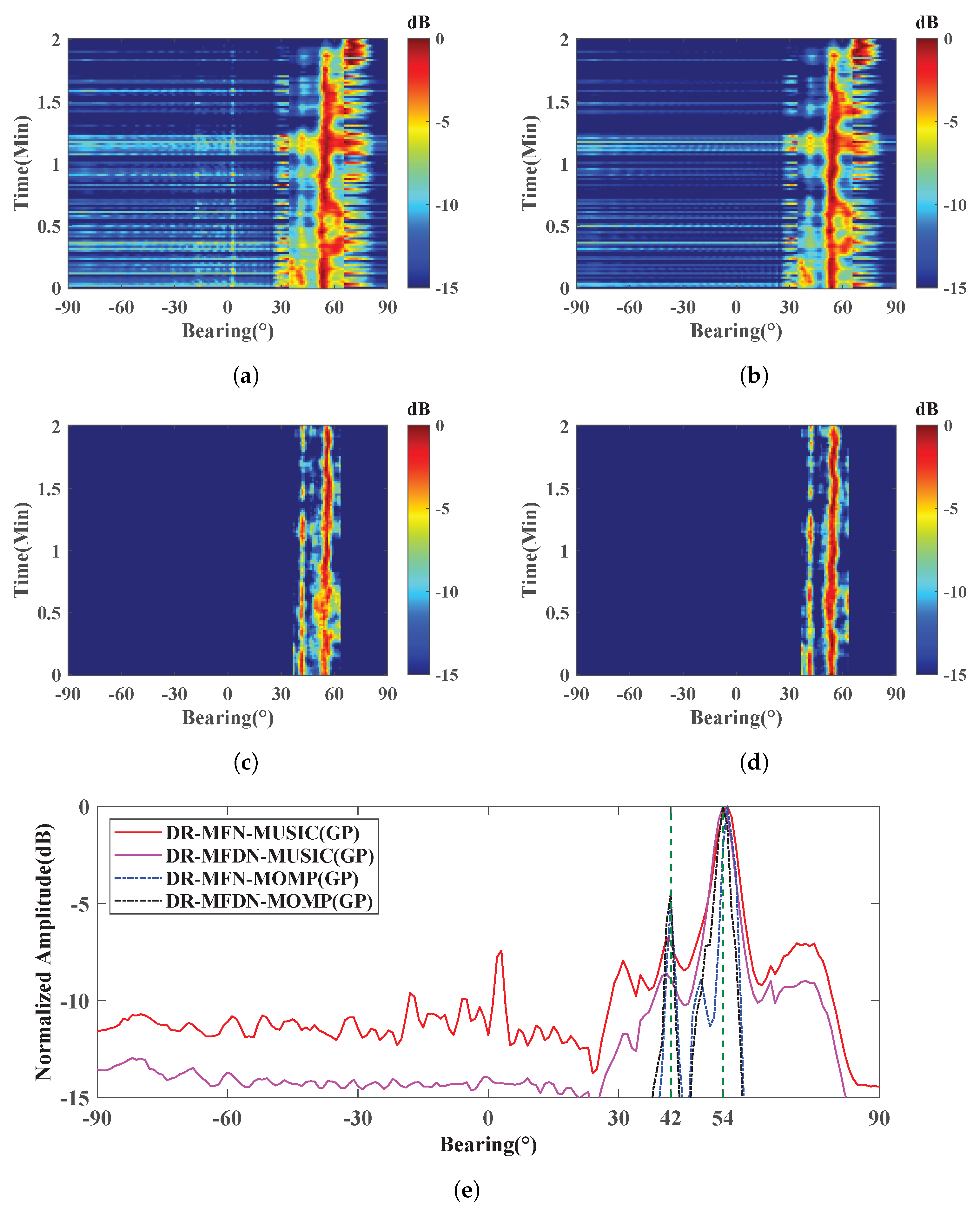
3.1. The Influence of the GP Operation

The first scenario assumed that one weak signal of interest with DOA ${\theta }_1={45}^{\circ }$ was present. Moreover, a strong out-of-sector source (interfering) located at ${\theta }_2=0^{\circ }$ (${90}^{\circ }$ was defined as the end fire direction within the frequency range of 400 to 700 $\mathrm{Hz}$. The signal-to-noise ratio (SNR) was $10\mathrm{dB}$, whereas the interference-to-noise ratio (INR) of the interference was $40\mathrm{dB}$. The data were partitioned into 10 segments, and a 512-point FFT was performed for each segment. The sector-of-interest area is ${\mathbf{\Theta }}_p=[{35}^{\circ }, {55}^{\circ }]$, the out-of-sector area is ${\mathbf{\Theta }}_s=[-{90}^{\circ }, 28.5^{\circ }]\cup [64.5^{\circ }, {90}^{\circ }]$, the beam-space dimension is $M^{\prime }=10$, and $\epsilon =0.2$, $\mathrm{SA}=-20\mathrm{dB}$. In addition, the amplitude responses and errors in the beam space were calculated as $20lg\left\{{∥{\mathbf{G}}_l^H{\mathbf{a}}_l(f_l,\theta )∥}_2/\phantom{{∥{\mathbf{G}}_l^H{\mathbf{a}}_l(f_l,\theta )∥}_2{∥{\mathbf{a}}_l(f_l,\theta )∥}_2}{∥{\mathbf{a}}_l(f_l,\theta )∥}_2\right\}$ and $20lg\left\{\left[{∥{\mathbf{G}}_l^H{\mathbf{a}}_l(f_l,\theta )∥}_2-{∥{\mathbf{a}}_l(f_l,\theta )∥}_2\right]/\phantom{\left[{∥{\mathbf{G}}_l^H{\mathbf{a}}_l(f_l,\theta )∥}_2-{∥{\mathbf{a}}_l(f_l,\theta )∥}_2\right]{∥{\mathbf{a}}_l(f_l,\theta )∥}_2}{∥{\mathbf{a}}_l(f_l,\theta )∥}_2\right\}$, respectively.

The purpose of this simulation scenario is to verify the necessity of the GP operation and to analyze the extent to which both the GP operation and the DR-MFDN affect the DOA estimation.

In the case of DR-MFN, its covariance matrix with no pre-whitening (NP) operation is shown in Figure 2a. ${\mathbf{G}}_l^H{\mathbf{G}}_l$ is not a unit matrix, which may result in the transformation of white noise into colored noise. In Figure 2b and Figure 3, when the OP operation is considered, ${\left({\mathbf{G}}_l^H{\mathbf{G}}_l\right)}^{-1/2}{\mathbf{G}}_l^H{\mathbf{G}}_l{\left({\mathbf{G}}_l^H{\mathbf{G}}_l\right)}^{-1/2}$ is the unit matrix, which prevents transforming the noise into colored noise. Meanwhile, the overall attenuation of the out-of-sector area is reduced. Moreover, changes in the beam space may lead to insufficient noise and interference suppression, which may affect the final processing results. Figure 2c,d and Figure 3 consider the case when the GP operation is performed. Note that ${\mathbf{B}}_l^H{\mathbf{B}}_l$ is a unit matrix, obtained using numerous Monte Carlo trials, which prevents transforming the noise into colored noise without significant changes in the beam space. Moreover, a Monte Carlo trial was necessary because of the randomness of the Gaussian matrix and the absence of a Gaussian matrix with uncorrelated columns. A large number of Monte Carlo trials is undoubtedly time-consuming. Therefore, determining an appropriate number of trials is necessary. This point will be discussed in the third scenario.

To clarify the difference in DOA estimation performance under different pre-whitening operations and matrix filters, Figure 4 shows the estimation results of the DR-MFN-MUSIC and DR-MFDN-MUSIC algorithms for different pre-whitening operations. The OP operation does not effectively reduce the effect of the strong interfering source, causing the energy of the signal of interest to remain lower than that of the interfering source after filtering. In contrast, the case without the pre-whitening operation shows better performance, indicating that the effect is limited at the current noise levels, even with colored noise. However, note that this trend may change under low SNR conditions. Furthermore, the GP operation significantly improves the performance of DOA estimation with matrix filters.

To analyze the impact of noise on the algorithms, Figure 5 shows the root-mean-square errors (RMSEs) of the DR-MFN-MUSIC and the DR-MFDN-MUSIC algorithms with three pre-whitening operations versus the INR and SNR. Specifically, the INR varies with a fixed $\mathrm{SNR}$ of 10 $\mathrm{dB}$, and the SNR varies with a fixed $\mathrm{INR}$ of 20 $\mathrm{dB}$. The RMSE curves were averaged over the signal sources and 500 independent simulation runs.

In Figure 5a, the following observations are made in the context of using DR-MFN: (1) RMSE increases with INR across all three pre-whitening methods. (2) The GP operation yields the lowest RMSE, while the OP operation yields the highest. This difference is likely due to the OP operation altering the beamspace characteristics (as shown in Figure 3), which weakens DR-MFN’s interference suppression. (3) RMSE without pre-whitening is generally lower than with OP. This may be because, in high-SNR conditions, changes in beamspace characteristics have a greater impact on DOA estimation than colored noise does. In the context of using DR-MFDN with sufficient suppression, noise effects in high-SNR conditions become negligible, leading to no significant performance differences among the three methods.

In Figure 5b, further analysis shows the following results. (1) For MFN, the OP operation outperforms the NP operation in the SNR range of $[-20 \mathrm{dB},-14 \mathrm{dB}]$, which is likely due to the dominant impact of colored noise in low-SNR environments. (2) For DR-MFDN, OP outperforms NP in the range of $[-20 \mathrm{dB},-18.5 \mathrm{dB}]$, and with identical pre-whitening, DR-MFDN performs better than DR-MFN. This may be attributed to DR-MFDN’s lower passband distortion, which makes it less susceptible to noise compared to DR-MFN. (3) Regardless of the filtering method, GP consistently has the smallest impact on DOA estimation, and as SNR increases, the performance differences between the three methods decrease.

In conclusion, based on Figure 4 and Figure 5, DR-MFDN’s strong interference suppression and low passband distortion significantly enhance DOA estimation performance for weak signals, while the benefits of the GP operation are relatively limited.

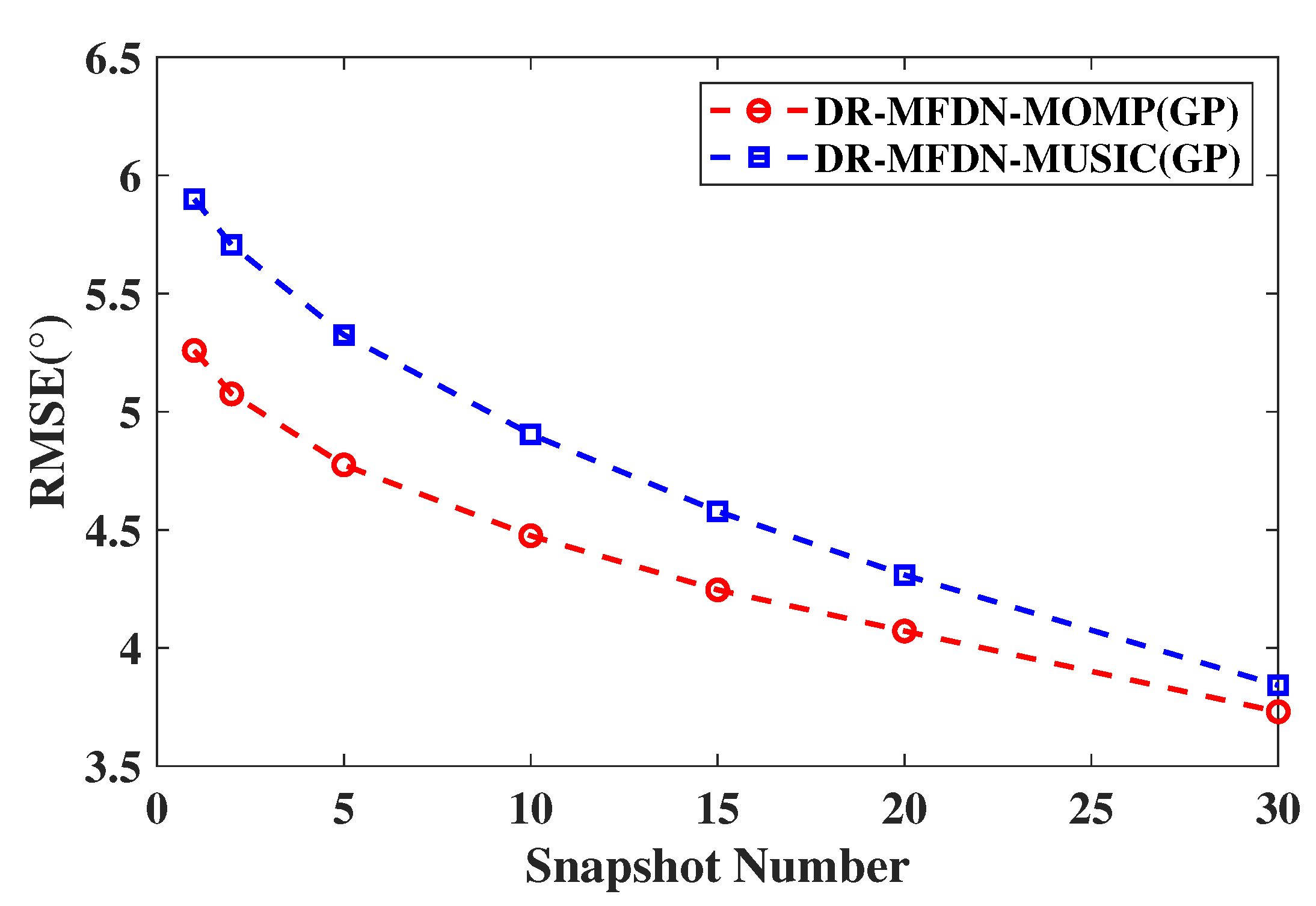
3.2. The Performance of the DR-MFDN-MOMP with the GP Operation

The second scenario assumed that two weak signals of interest with the DOAs ${\theta }_3={44}^{\circ }$ and ${\theta }_4={46}^{\circ }$ were present. Moreover, two strong out-of-sector sources (interfering) were located at ${\theta }_5=0^{\circ }$ and ${\theta }_6={15}^{\circ }$ within a frequency range of 600 to 700 $\mathrm{Hz}$. The SNR of both signals was $0\mathrm{dB}$, whereas the INR of all the interfering sources was $40\mathrm{dB}$. All the other parameters of the tested scenario were the same as those of the previous scenario. In addition, a GP operation was applied to this scenario in all the cases for simplicity.

In Figure 6, the DR-MFDN provides deeper nulls in the direction of the interfering sources and a lower passband response error in the sector of interest than the DR-MFN. Figure 7a plots estimation results of the MUSIC and MOMP without filtering, and the directions of the weak signals-of-interest cannot be distinguished. Subsequently, robust estimators based on the MUSIC or MOMP algorithm without filtering and DR-MFN or DR-MFDN, namely, DR-MFN-MUSIC, DR-MFDN-MUSIC, DR-MFN-MOMP, and DR-MFDN-MOMP estimators, with GP operations, were applied for DOA estimation, as shown in Figure 7b. The DR-MFN-MUSIC and DR-MFN-MOMP estimators with the GP operation exhibit poor estimation performance for weak targets, which can be due to the insufficient suppression of interfering sources by the DR-MFN. Comparatively, both algorithms coupled with the DR-MFDN demonstrated effective estimation of weak targets, and the DR-MFDN-MOMP estimator with the GP operation demonstrated a high resolution.

To further investigate the performance under varying conditions, the RMSEs of the DR-MFN-MUSIC(GP), DR-MFDN-MUSIC(GP), DR-MFN-MOMP(GP), and DR-MFDN-MOMP(GP) estimator are plotted with respect to INR and SNR in Figure 8. Specifically, the INR was varied for a fixed $\mathrm{SNR}$ of $0\mathrm{dB}$, and the SNR was varied for a fixed $\mathrm{INR}$ of $25\mathrm{dB}$. The RMSE curves were averaged over the signal sources and 500 independent simulation runs.

Figure 9 shows the probabilities of the source resolution with respect to INR and SNR for the same scenario and methods tested. Similar to Figure 8, all curves were averaged over the signal sources and 500 simulation runs. The signal sources are considered to be resolved in the jth run if [17]

$$\sum _{i=1}^2|{\widehat{\theta }}_i^j-{\theta }_i|<|{\theta }_1-{\theta }_2|$$

(26)

where ${\widehat{\theta }}_i^j$ is the DOA estimation for the i-th source in the j-th run.

Figure 8a and Figure 9a show that the RMSEs of the DR-MFN-MUSIC(GP) and DR-MFN-MOMP(GP) algorithms increase with increasing INR because of the insufficient suppression of strong out-of-sector sources by the DR-MFN. Conversely, the DR-MFDN provides sufficient suppression, leading to superior DOA estimation capabilities for both the DR-MFN-MUSIC(GP) and DR-MFN-MOMP(GP) estimators. Figure 8b and Figure 9b show that both the DR-MFN and DR-MFDN can sufficiently suppress strong out-of-sector sources for a fixed INR of $25\mathrm{dB}$. However, the DR-MFDN improved the performance with the same DOA estimation algorithm, indicating superior signal preservation with a lower passband response error. Figure 8 and Figure 9 show that the MOMP algorithm outperforms the MUSIC algorithm when utilizing the same matrix filter.

3.3. The Efficiency of the Presented Algorithm

In the third simulation scenario, we explore the impact of the number of GP operations on DOA estimation accuracy and algorithm runtime. Given that the GP operation processing is primarily employed to mitigate the nonlinear effects induced by colored noise, we set the SNR to $-20\mathrm{dB}$, building on the conditions established in Scenario 1. The analysis from the first two scenarios has already demonstrated the necessity of GP processing and the superior performance of the DR-MFDN-MOMP(GP) algorithm for weak-signal DOA estimation. However, the effect of GP on the runtime of different algorithms remains unclear, which is crucial for practical applications. First, we conduct a comparative study of DOA estimation performance for both the DR-MFDN-MOMP(GP) and DR-MFDN-MUSIC(GP) algorithms under varying levels of GP, as shown in Figure 10. Additionally, Figure 10 also illustrates the relationship between the degree of the beam-space response distortion and the number of Monte Carlo trials, where the tolerance is calculated as follows:

$$\mathrm{Tolerance}=\sum _{j=1}^J\left|\right|{\mathbf{G}}_l^H\mathbf{a}(f_l,{\theta }_j)-{\mathbf{B}}_l^H\mathbf{a}(f_l,{\theta }_j\left)\right|{|}_2({\theta }_j\in \mathbf{\Theta })$$

(27)

Figure 10 illustrates that as the number of the GP operations increases, the tolerance decreases. The rate of reduction progressively slows down, with convergence not being achieved until after 1000 operations. While an increased number of GP operations may yield a smaller tolerance, it also introduces a substantial computational burden. Upon evaluating the DOA estimation performance of both algorithms across varying GP operation counts, it is evident that the RMSEs for both algorithms reach convergence after approximately 100 GP operations. This phenomenon occurs because, although further increasing the GP operation count reduces the discrepancy between the pre-whitened matrix filter and the original matrix filter, the original matrix filter inherently exhibits a degree of passband distortion. After approximately 100 GP operations, the passband distortion stabilizes and ceases to exhibit significant changes. Consequently, selecting 100 GP operations effectively maximizes the performance gains from the GP processing while minimizing computational overhead.

Figure 11 shows that the RMSE decreases as the number of snapshots increases for both algorithms. This indicates that the accuracy of DOA estimation improves with more data points, leading to a reduction in estimation error. Throughout the range of snapshot numbers tested, the DR-MFDN-MOMP(GP) algorithm consistently exhibits lower RMSE values compared to the DR-MFDN-MUSIC(GP) algorithm. This suggests that DR-MFDN-MOMP(GP) provides more accurate DOA estimations under the same conditions. The rate at which RMSE decreases is relatively steep when the number of snapshots is low (e.g., between 0 and 10). As the number of snapshots continues to increase, the rate of decrease in RMSE begins to slow down, particularly noticeable after surpassing 20 snapshots. This suggests diminishing returns on increasing the number of snapshots beyond a certain point.

Based on the above conclusion, we computed the runtime of the two algorithms under different numbers of the GP operations, as shown in

Table 1. Runtime ($\mathrm{ms}$) of the DR-MFDN-MUSIC(GP) and DR-MFDN-MOMP(GP) algorithms with different numbers of GP operations.

	Times	1	5	10	20	50	100
Method
MUSIC		55.20	∖	∖	∖	∖	∖
DR-MFDN-MUSIC(GP)		8.40	39.80	79.40	158.70	392.10	779.5
MOMP		0.54	∖	∖	∖	∖	∖
DR-MFDN-MOMP(GP)		0.50	2.50	4.60	9	22.8	44.60

. These simulations were performed on a workstation equipped with an Intel Core i9-13900HX processor (24 cores), 16 GB of DDR5 memory running at 5600 MHz, and an NVIDIA GeForce RTX 4060 Laptop GPU with 8 GB of dedicated memory. The primary storage device was a 1 TB NVMe SSD (WD PC SN810), and the system was running on a Windows operating system. The algorithms were implemented in Matlab R2022b.

From Table 1, we can conclude the following. (1) The runtime of MUSIC without dimensionality reduction is significantly higher than that of DR-MFDN-MUSIC(GP), resulting in greater computational complexity. (2) DR-MFDN-MOMP(GP) with 100 GP operations runs in 44.60 ms, much more efficiently than DR-MFDN-MUSIC(GP) at 779.5 ms. While the runtime of DR-MFDN-MOMP(GP) increases with more GP operations, its computational complexity remains low, and the increase is gradual. (3) The runtime of DR-MFDN-MOMP(GP) after 100 GP operations is lower than the single execution time of MUSIC (55.20 ms), meaning it does not introduce a significant computational burden and is suitable for real-time applications.

Based on Figure 10 and Table 1, the DR-MFDN demonstrates a high cost-effectiveness ratio by effectively reducing computational burden while maintaining accuracy through dimensionality reduction. With 100 GP operations, the maximum computational accuracy benefits are achieved. Additionally, the runtime of the DR-MFDN-MOMP(GP) algorithm is significantly lower than that of DR-MFDN-MUSIC(GP), highlighting its superior performance in high GP operation counts. The lower computational time of DR-MFDN-MOMP(GP) makes it well suited for practical, real-time applications. In summary, the DR-MFDN-MOMP(GP) estimator can accurately and quickly estimate DOA for weak targets in an environment with strong interfering sources.

4. Results

In September 2019, a horizontal array detection experiment was conducted in the sea area of Laoshan Bay, Qingdao. During the experiment, the relative planar position between the horizontal array and the surface target vessel is shown in Figure 12a. The horizontal array was deployed in a region with a water depth of $18\mathrm{m}$, with 32 hydrophones uniformly spaced at $1\mathrm{m}$. The deployment depth of the horizontal array was $17.8\mathrm{m}$, and the relative positions of the array elements are illustrated in Figure 12b. The sound speed remained approximately constant at around $1530\mathrm{m}/\mathrm{s}$, as indicated by the sound speed profile shown in Figure 12c. The seabed in the experimental area was relatively flat, characterized by fine sand.

The sampling frequency was set to 6 kHz, and the duration of the processed data was 2 min. A short-time Fourier transform (STFT) was applied to the received data of a specific array element, resulting in the time-frequency spectrogram shown in Figure 13a. The STFT used a Hamming window of 4096 samples, with a $12.5\%$ overlap. The time-domain and frequency-domain information of a particular segment are illustrated in Figure 13b and Figure 13c, respectively. Figure 13b shows that the received signal appears disordered. However, multiple line spectra can be observed in Figure 13c. In the 400–700 $\mathrm{Hz}$ frequency band, background noise is relatively low compared to the spectral line intensity. To better identify the DOAs of weak targets, this frequency band was selected for the broadband DOA estimation of weak signals.

The observed space, $[-{90}^{\circ },{90}^{\circ }]$, was uniformly discretized into 181 candidate directions. The Bearing-Time Records (BTRs) of the MVDR, MUSIC and MOMP, as shown in Figure 14, reveal information about the interference source and the sector where the weak targets are located. The two interfering sources were moved to the far field of the array. One interference was in the direction of approximately $-{17}^{\circ }$, and the other was around $0^{\circ }$. A few weak targets were located at $-{47}^{\circ }$, ${42}^{\circ }$, and ${54}^{\circ }$, and the first target was clearly tracked. The DR-MFN and DR-MFDN were designed with the passband bearing sector ${\mathbf{\Theta }}_p$ at $[{35}^{\circ },{65}^{\circ }]$ and the stopband bearing sector ${\mathbf{\Theta }}_s$ at $[-{90}^{\circ },{25}^{\circ }]\cup [{80}^{\circ },{90}^{\circ }]$. The SAs were $-15\mathrm{dB}$. The received data sampled were transformed into the frequency domain by using a 512-point FFT. The sample covariance matrix was obtained by averaging 22 snapshots with a 50% overlap. The duration of each segment was $1\mathrm{s}$, and the total analysis time was $2\min$. The DR-MFN-MUSIC, DR-MFDN-MUSIC, DR-MFN-MOMP, and DR-MFDN-MOMP estimators with orthogonal or GP operations were applied to localize weak targets. The results are presented in Figure 15 and Figure 16.

Figure 15 illustrates the DOA estimation results of the four algorithms using the OP operation. Figure 15a,b,e show that the DR-MFN-MUSIC(OP) and DR-MFDN-MUSIC(OP) estimators could not obtain the DOA of a weak target with a broad main lobe. Moreover, many spurious peaks appeared outside these sectors. Figure 15c–e show that the DR-MFN-MOMP(OP) and DR-MFDN-MOMP(OP) estimators could determine the DOAs of the two weak signals. In contrast, occasional spurious peaks were present near the target. Thus, these two algorithms using the OP operation are not robust. Overall, combined with matrix filters, the MOMP algorithm demonstrated superior DOA estimation performance to the MUSIC algorithm, as shown in Figure 15. Figure 16 illustrates the DOA estimation results of the four algorithms with the GP operation. A comparison of Figure 15 and Figure 16 shows that the algorithms with the GP operation outperform those with the OP operation. Figure 15a and Figure 16b,e show that the DR-MFDN-MUSIC(GP) estimator has a smaller response than the DR-MFN-MUSIC(GP) estimator in all non-target sectors and reduces the width of the main lobe. This indicates that the DR-MFDN shows improved interference suppression performance and localization accuracy. In Figure 16c–e, the track obtained using the DR-MFDN-MOMP(GP) algorithm is clearer than that obtained using the DR-MFN-MOMP(GP) estimator. In Figure 16e, the DR-MFDN-MOMP(GP) estimator localizes two weak targets. Owing to the high passband response error of the DR-MFN, the result of the DR-MFN-MOMP(GP) estimator shows a slight but potentially misleading spurious peak. 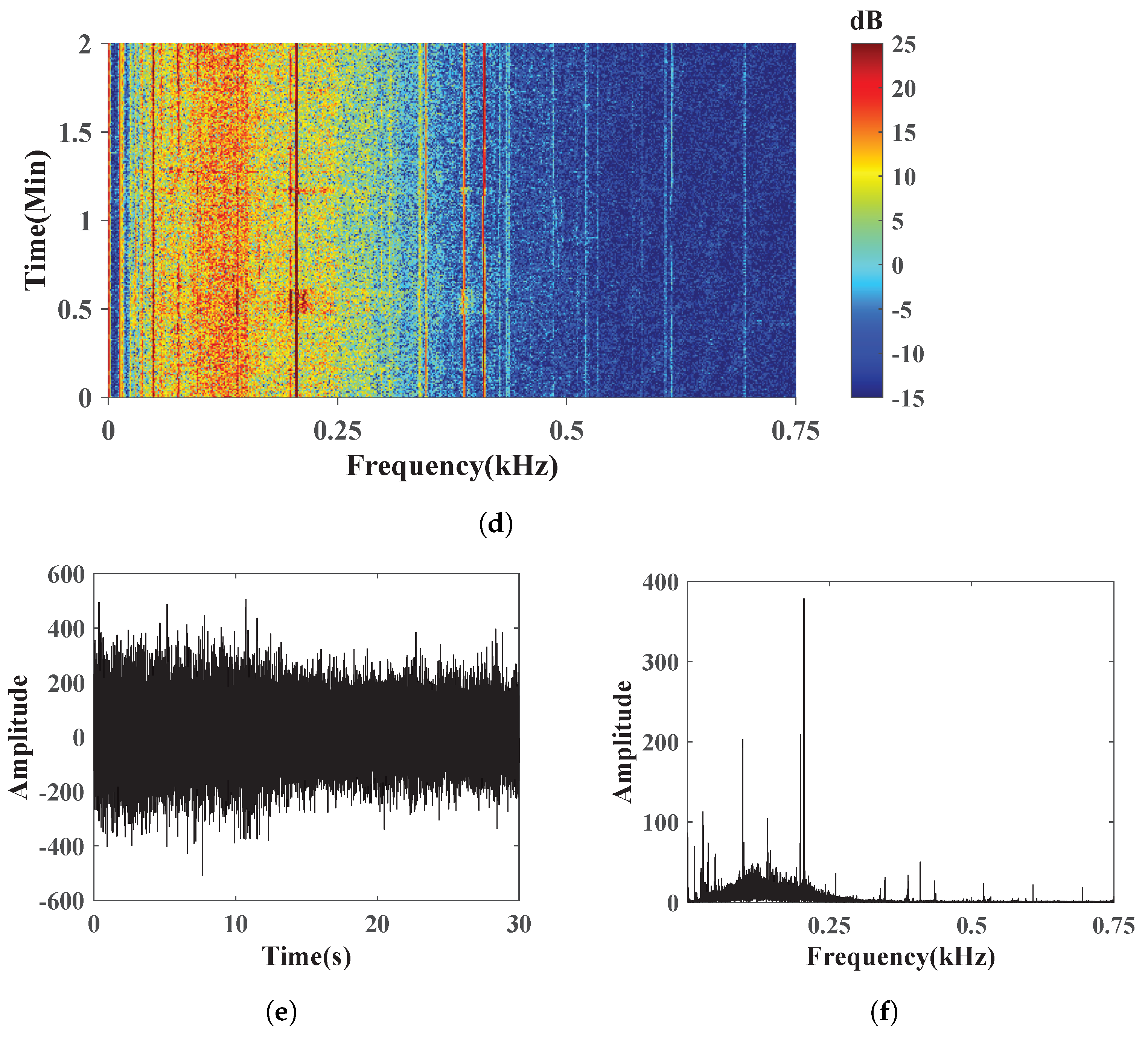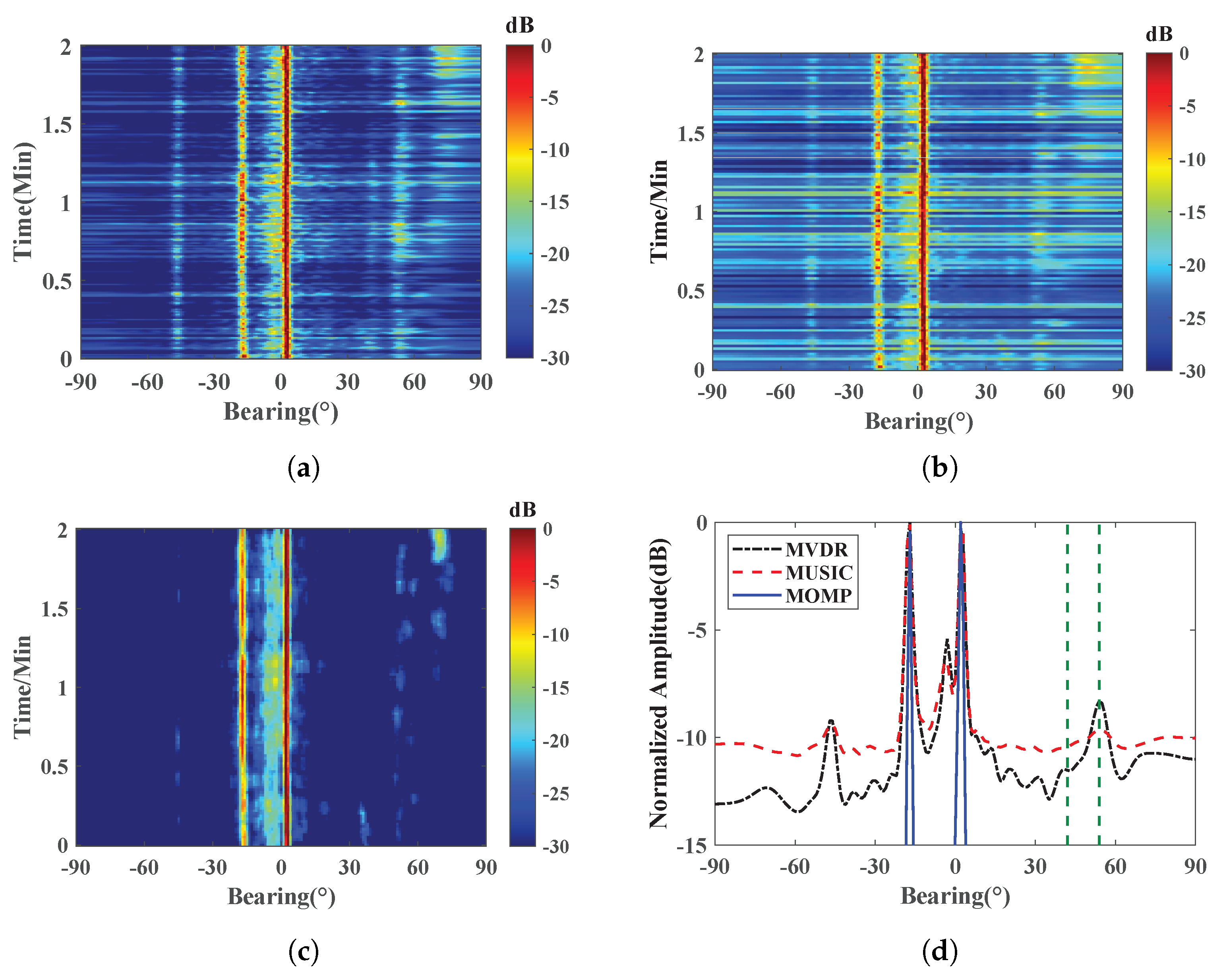Therefore, the DR-MFDN-MOMP(GP) estimator achieves superior performance in an environment with strong interfering sources.

5. Conclusions

This study presents a robust DOA estimator for weak targets based on a combination of Gaussian pre-whitening (GP), dimension-reduced matrix filter with deep nulling (DR-MFDN), and multiple-measurement-vector orthogonal matching pursuit (MOMP). The presented method demonstrates superior performance in localizing weak signals in environments with strong interfering sources. The main conclusions can be summarized as follows:

(1)

The DR-MFDN effectively suppresses strong interfering sources by forming deep nulls in their directions, thereby significantly improving interference suppression and localization accuracy compared to conventional methods like DR-MFN. This enhancement is crucial for weak target detection.

(2)

The Gaussian pre-whitening operation prevents the transformation of white noise into colored noise, preserving the beam-space characteristics and ensuring robustness in DOA estimation. This is particularly important for maintaining accuracy in high-noise environments.

(3)

The MOMP algorithm, combined with the DR-MFDN, provides higher resolution and better performance in handling short snapshots compared to traditional algorithms such as MUSIC. This makes the proposed estimator more suitable for real-time applications.

(4)

Experimental results from both simulations and sea trials demonstrate that the presented DR-MFDN-MOMP(GP) estimator outperforms existing methods in terms of interference suppression, localization accuracy, and computational efficiency. The method is highly cost-effective and suitable for practical implementation.

Future work may focus on further optimizing computational efficiency and addressing limitations in scenarios with small angular separations between targets and interference sources.