Fast Generalized Radon–Fourier Transform Based on Blind Speed Sidelobe Traction
Abstract
1. Introduction
- Dependence on Accurate Special Relationship: The algorithm heavily relies on the accuracy of the spatial relationship between the local and global optima, which cannot be adequately replaced by the known correlation between the main lobe and the center of BSSLs, especially when the BSSL peak is not centered. This reliance reduces the success probability of transitioning from “wide” BSSLs to a “narrow” main lobe.
- Premature Convergence Issues: Traditional termination criteria consider the solution final when the algorithm fails to escape from a local optimum after numerous attempts, certain time spent, and so on. However, in dealing with optimization problems in GRFT which features complex structures—such as multiple sidelobes, several sinc-shaped minor lobes, and added noise—this situation occurs too frequently. Therefore, a stricter termination criterion is needed.
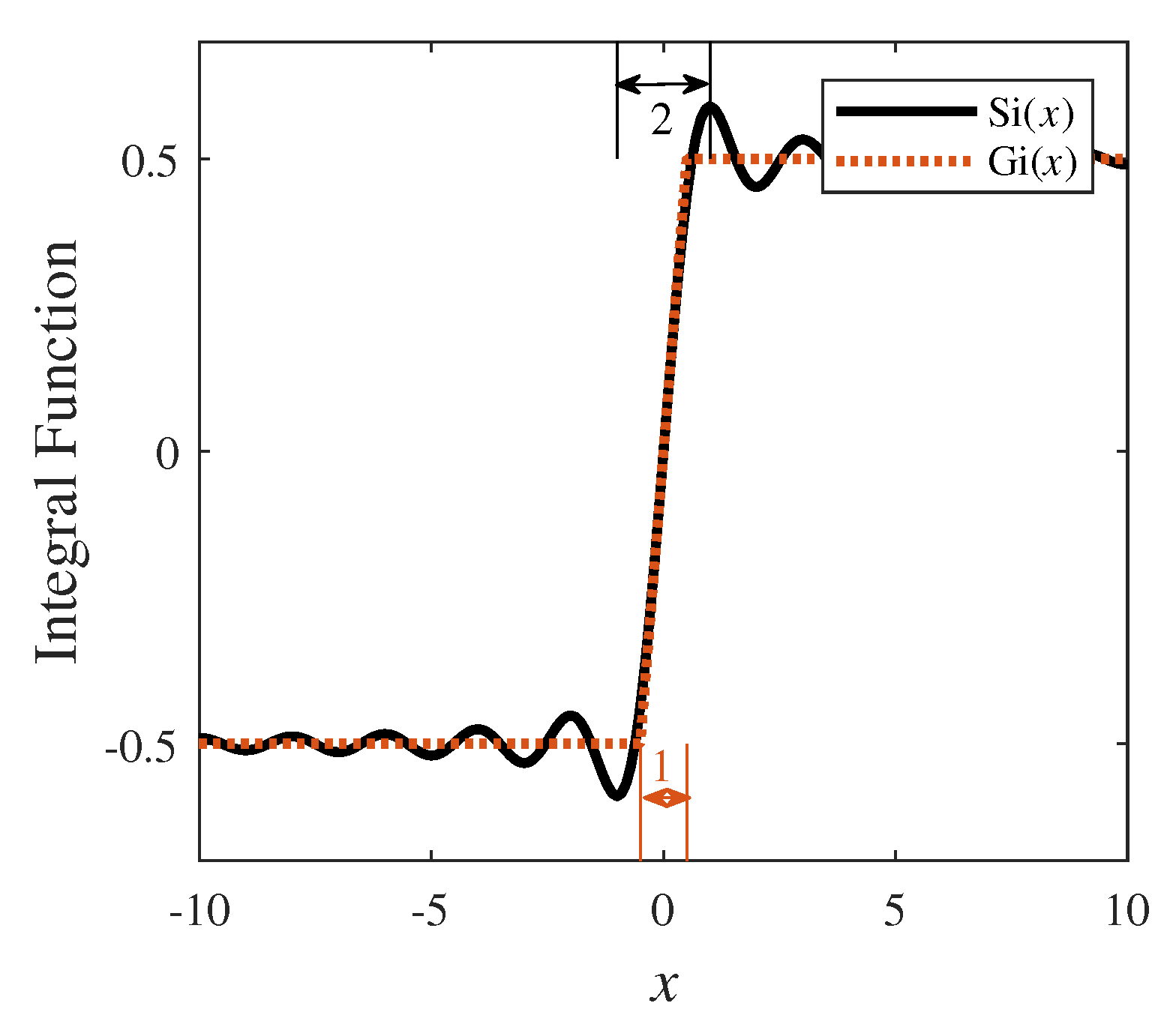
- Accurate Sidelobe Model: We employ the sine integration function method to mathematically represent the BSSLs and reveal the sidelobe plateau region phenomenon, highlighting that the optimal peak of the sidelobes is not centered.
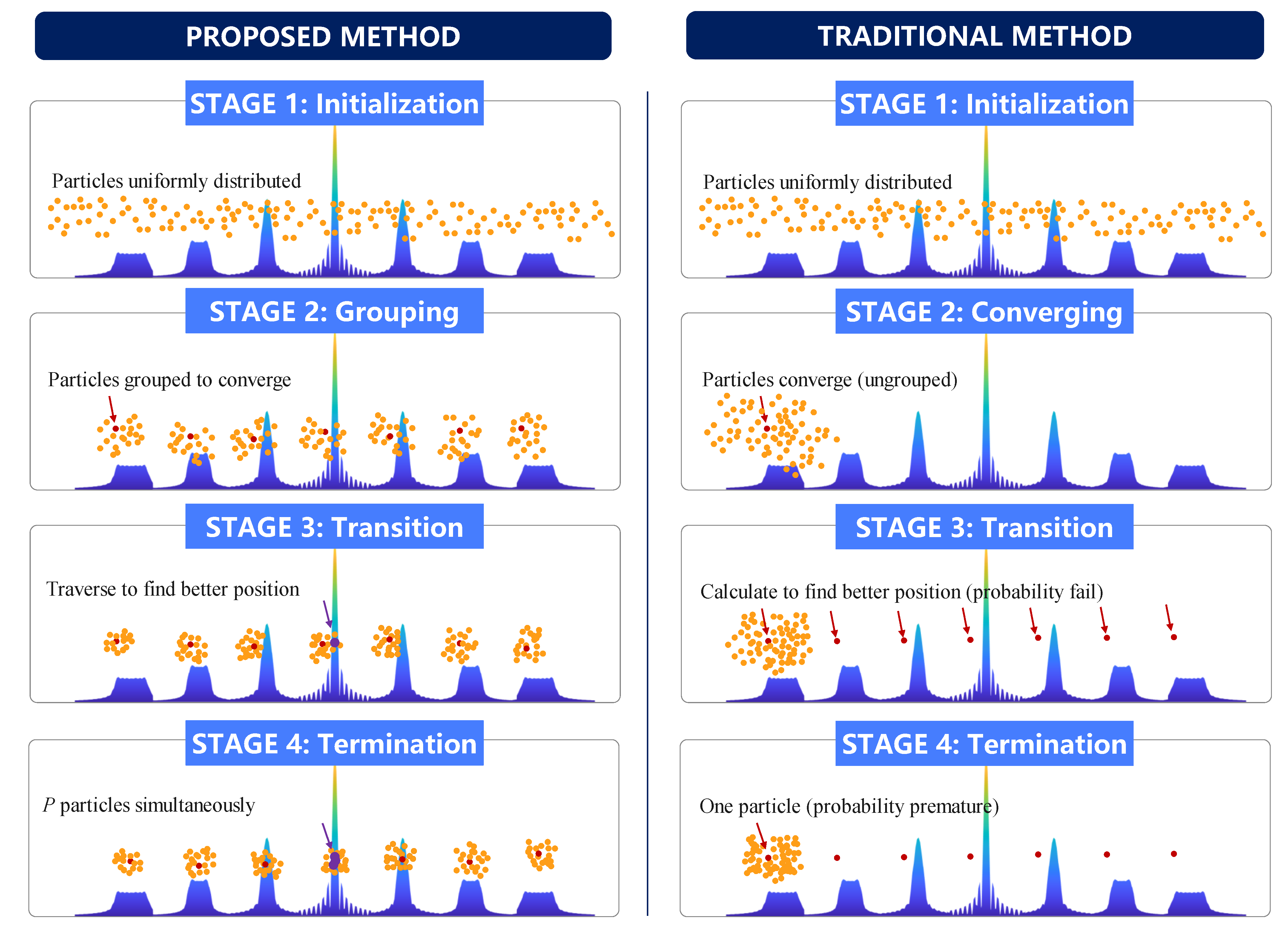
- Fast Implementation Technique: We introduce the BTPSO algorithm for GRFT, which utilizes, but does not heavily depend on, the positional relationship between the main lobe and the BSSLs. By employing group thinking, the main lobe and the sidelobes work together to attract corresponding particles to explore their nearby regions. This approach helps in finding more optimal positions when particles become trapped in local optimal sidelobes.
- Novel Termination Criterion: We consider a solution final only when multiple particles converge at the same local optimum, reducing the probability of mistakenly recognizing premature local convergence as the global optimum.
2. Principle of GRFT Theory
2.1. Algorithm Principle
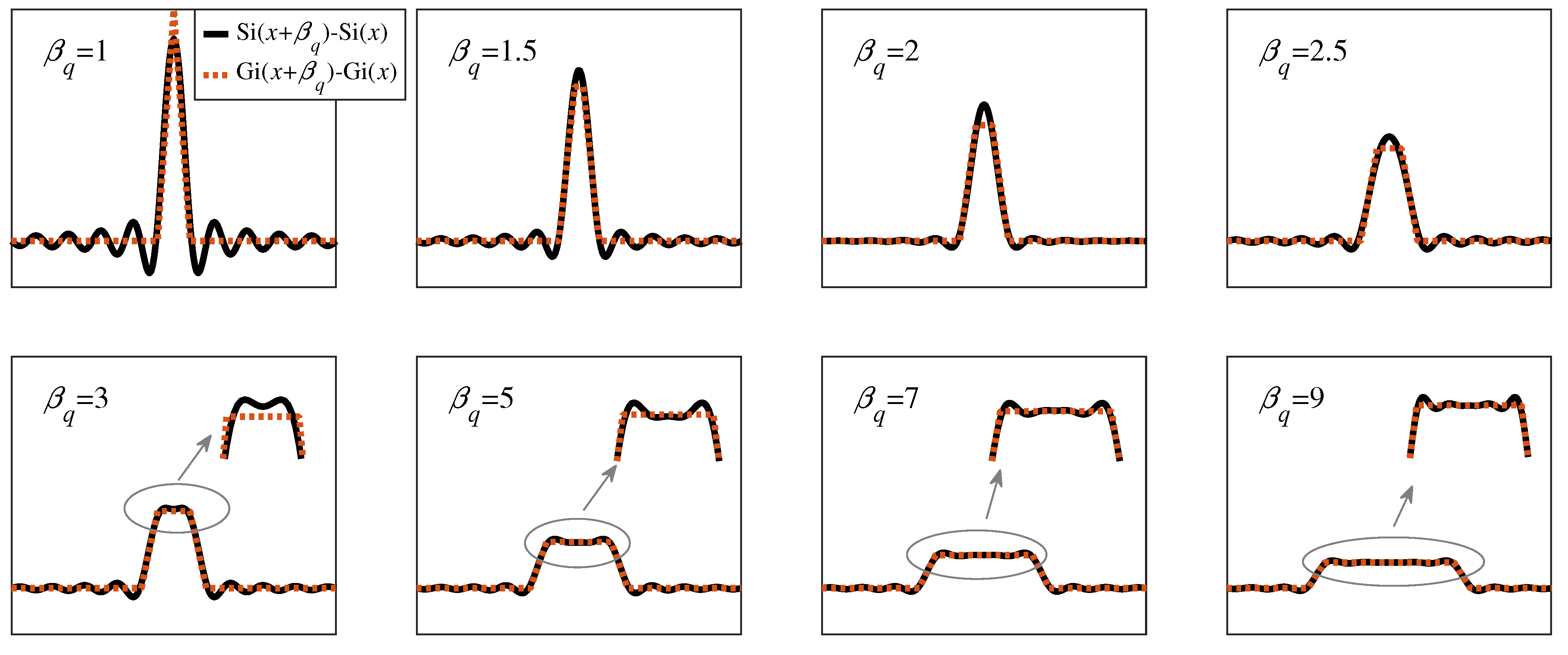
2.2. BSSL Effect and Plateau Region Phenomenon
3. BSSL Traction Particle Swarm Optimization (BTPSO)
3.1. Problems with the Existing Algorithms
3.2. BTPSO Algorithm
- The BTPSO method generates multiple values, allowing nearby particles to cluster around them. In contrast, traditional BPSO relies on a single to attract all particles, which limits its ability to explore areas surrounding the main lobe. As a result, the BTPSO can locate the main lobe more quickly and efficiently.
- The BTPSO method requires only a rough relationship in (15). In contrast, traditional BPSO needs a precise relationship to correctly identify the position within the main lobe peak. Consequently, when faced with the plateau region effect, where the sidelobe is much wider than the main lobe and the highest peak may not be centrally located, the BPSO is less effective while the BTPSO is still effective.
3.3. Enhance Termination Criterion
- Criterion 1: The number of iteration steps k exceeds the maximum number of iterations K, i.e., .
- Criterion 2: After iteration I for the optimal value of the objective function, the change is still less than the function tolerance :
- Criterion 3: The difference in objective values between the optimal particle and the Pth ranked particle is less than the specified function tolerance , referred as (18).
3.4. Execution Stages of the Algorithm
4. Simulation Experiment
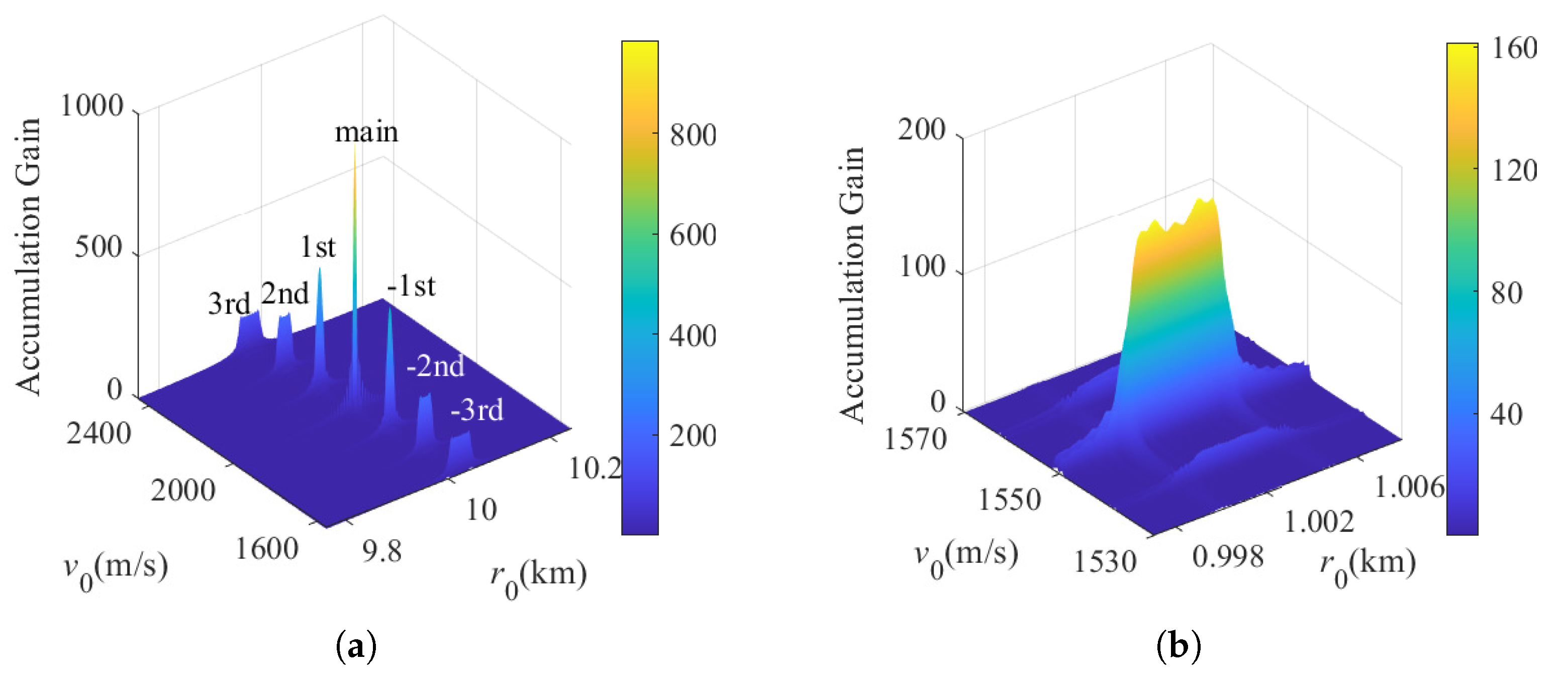
4.1. Performance of the Proposed Algorithm
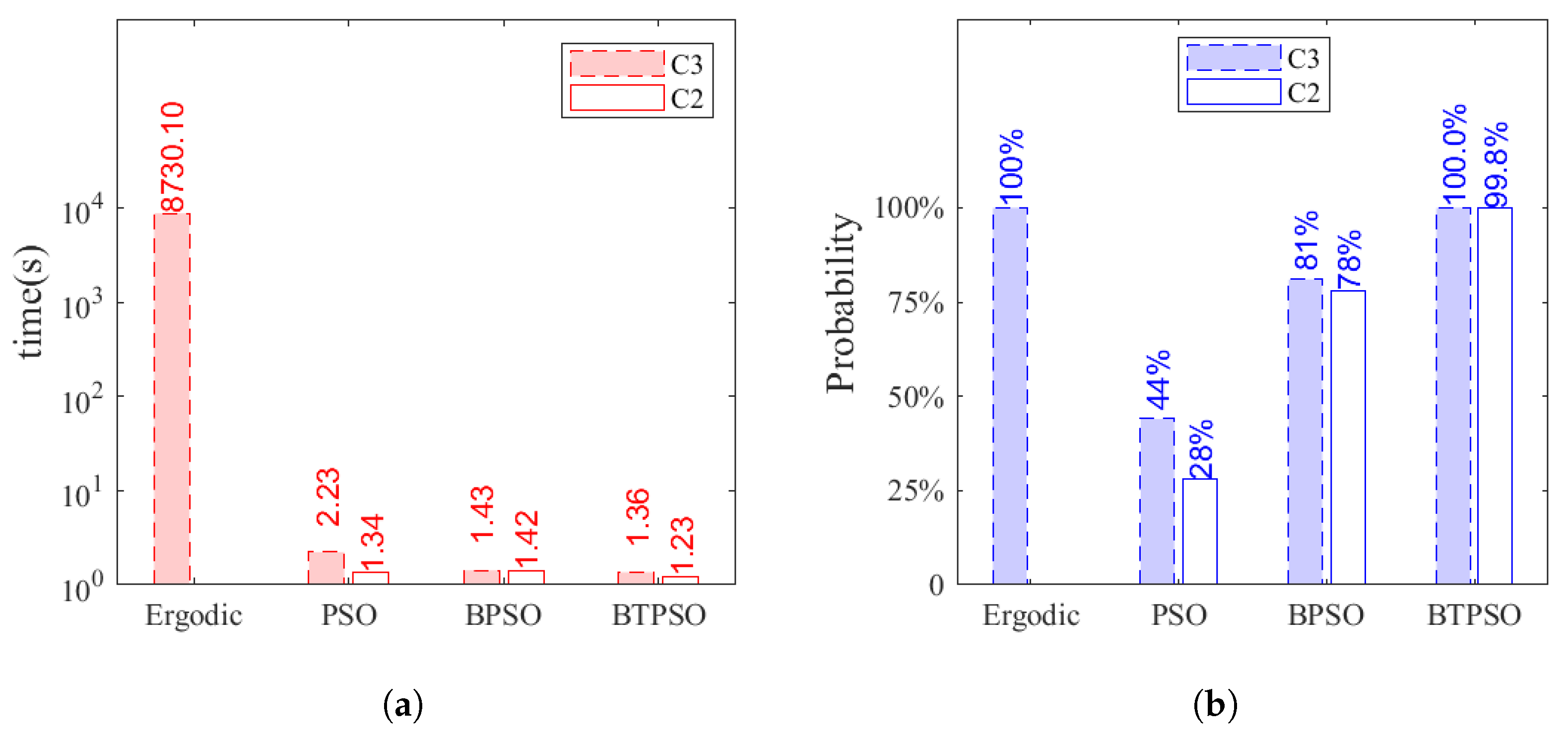
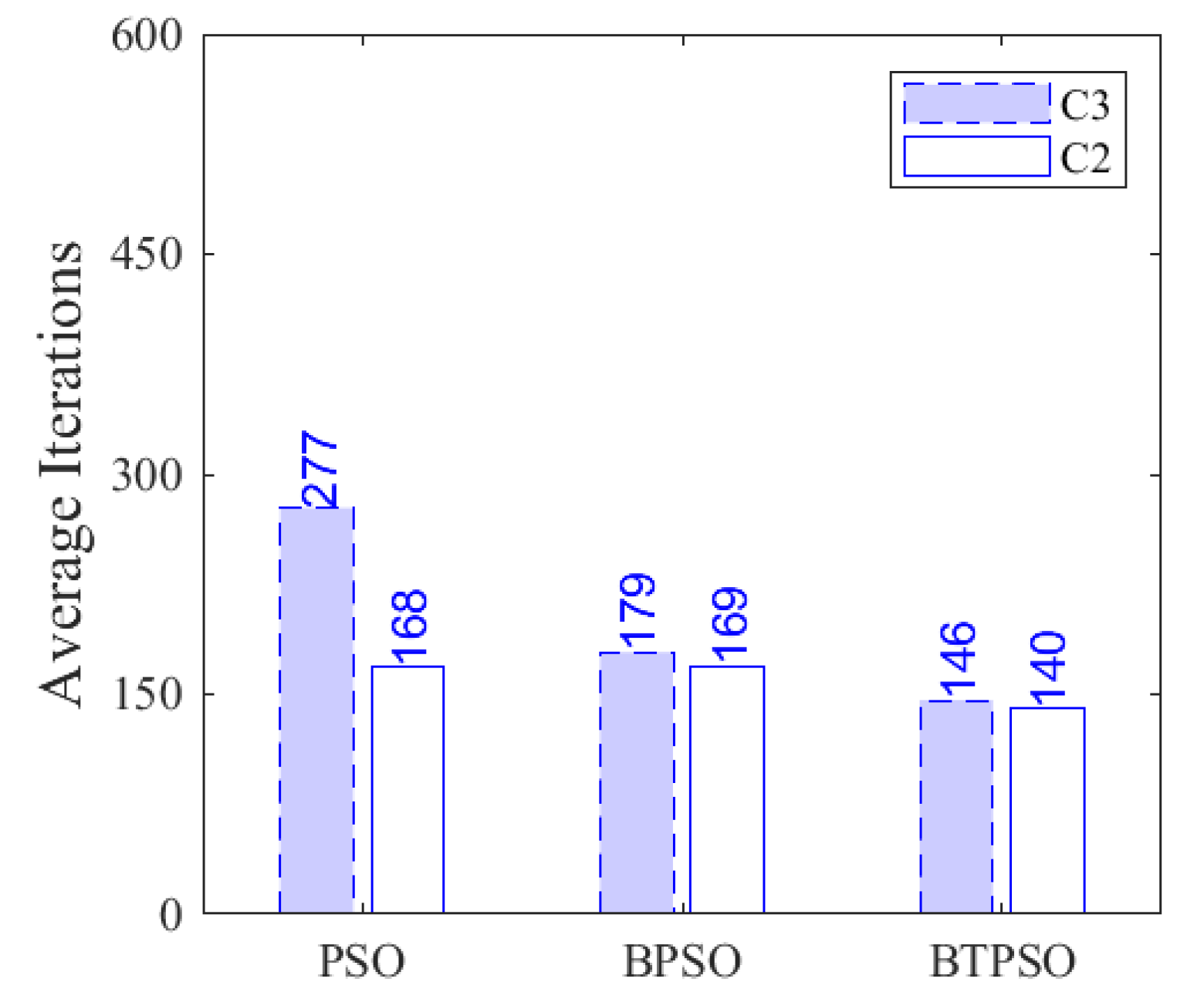
4.2. Performance of the Proposed Termination Criterion
- C2: Criterion 1 or Criterion 2
- C3: Criterion 1 or (Criterion 2 and Criterion 3)
4.3. Computation Efficiency Analysis
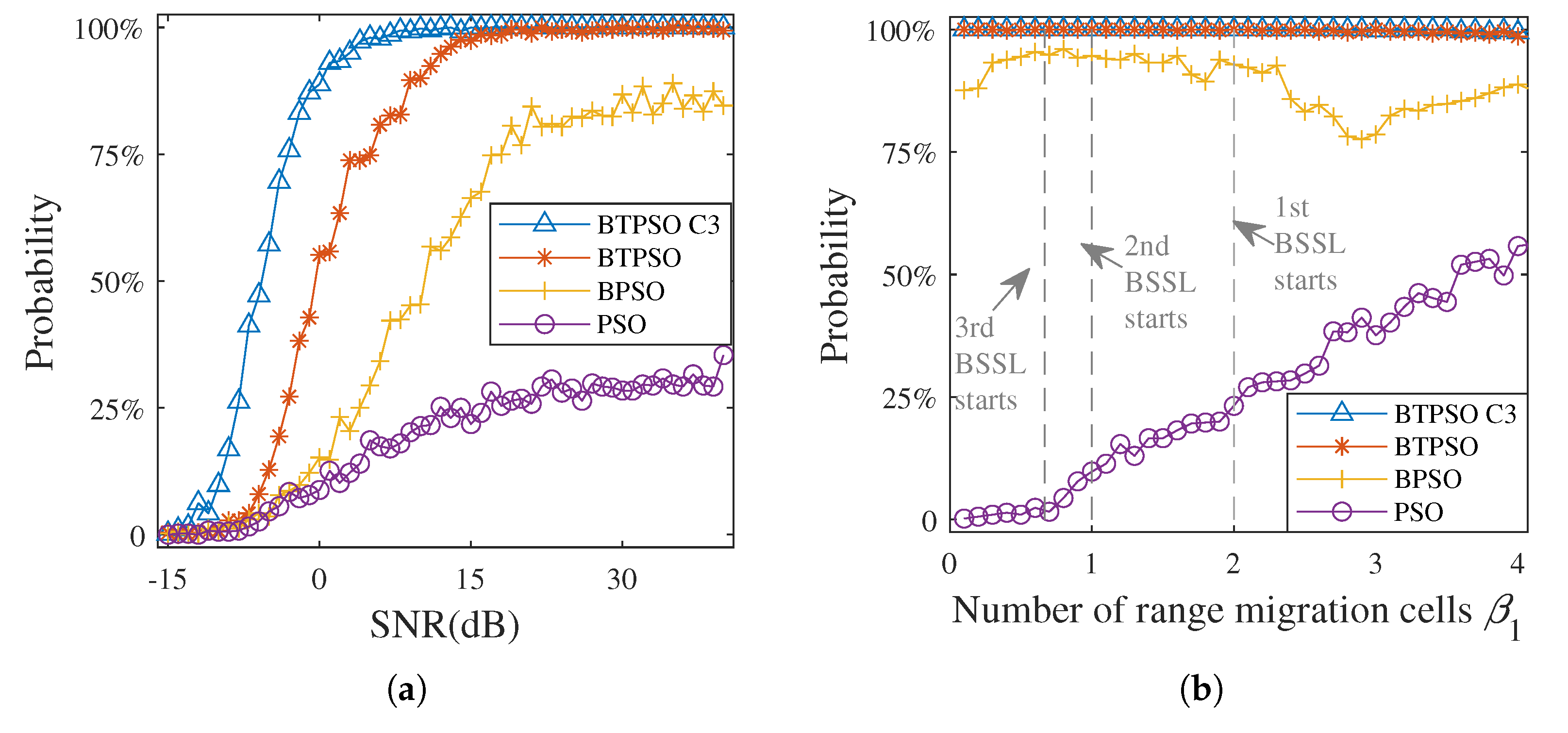
4.4. Performance Under Varying SNR
4.5. Performance Under Varying Plateau Region Size
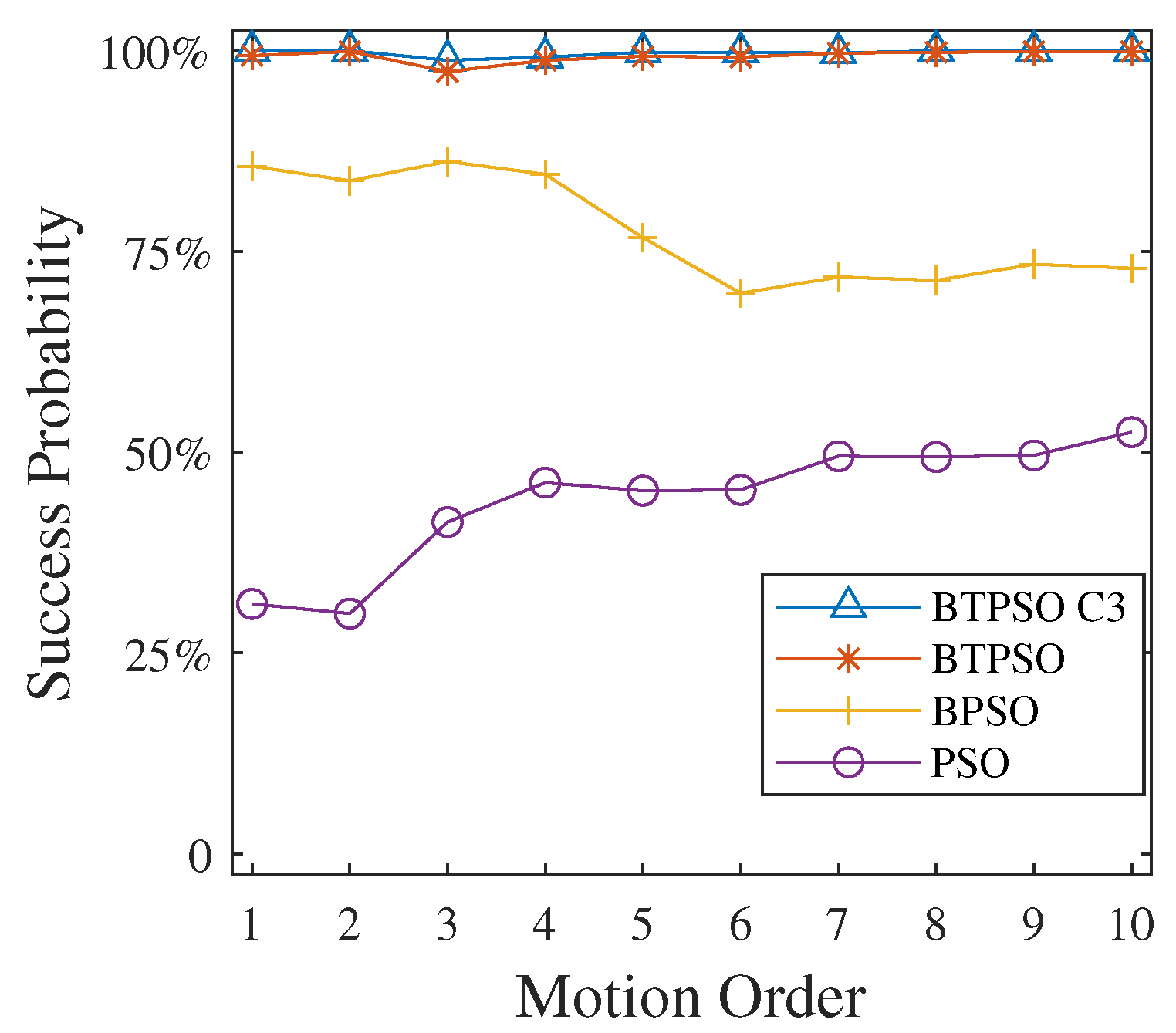
4.6. Performance Under Different Motion Order
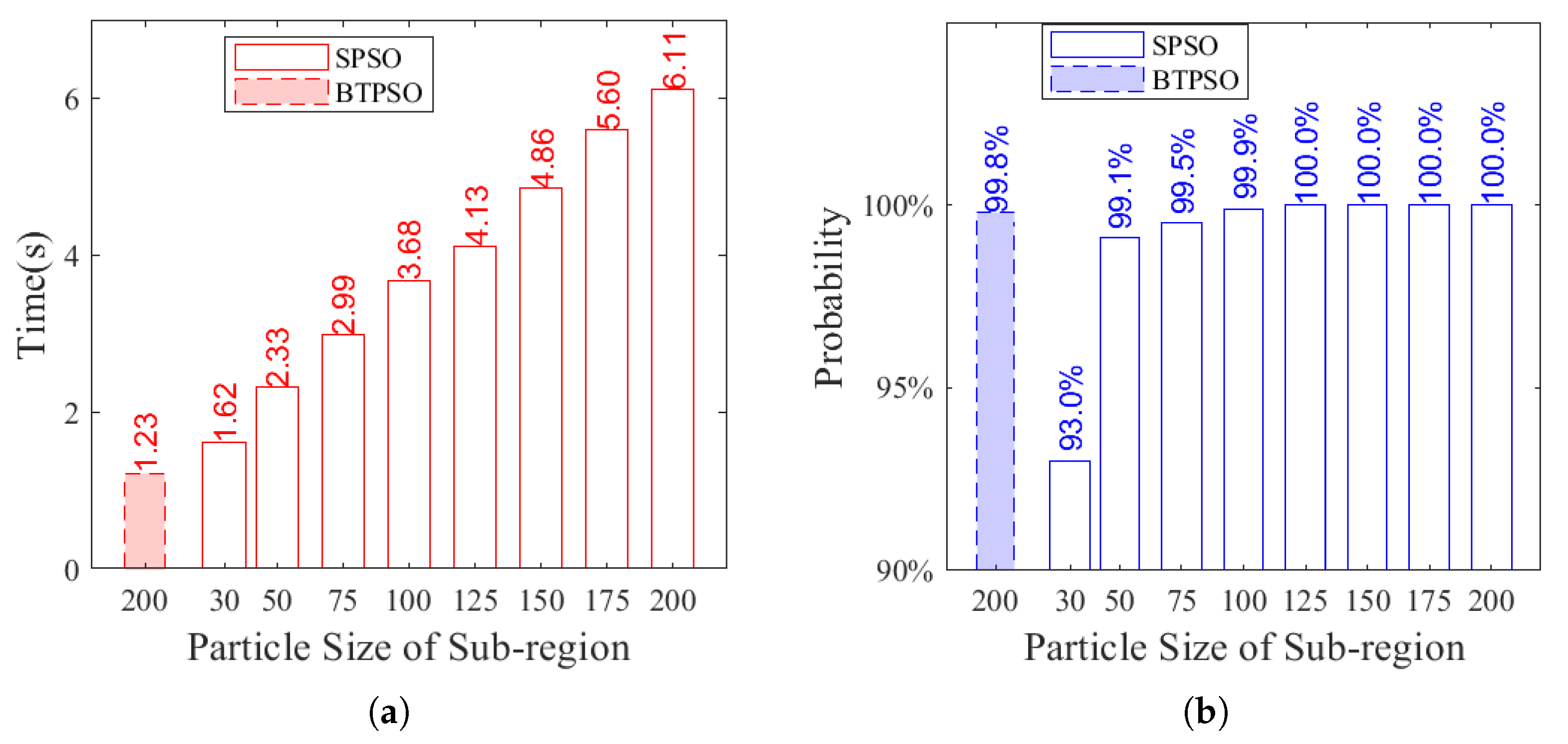
4.7. Additional Discussion for BTPSO
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Execution Steps of the Algorithm
References
- Li, X.; Sun, Z.; Yi, W.; Cui, G.; Kong, L. Radar Detection and Parameter Estimation of High-Speed Target Based on MART-LVT. IEEE Sen. J. 2019, 19, 1478–1486. [Google Scholar] [CrossRef]
- Jin, K.; Lai, T.; Zhu, S.; Li, G.; Zhao, Y. Coherent Detection and Parameter Estimation for Radar High-Speed Maneuvering Target Based on FAF–LVD. Circuits Syst. Signal Process. 2019, 39, 2600–2622. [Google Scholar] [CrossRef]
- Kong, L.; Li, X.; Cui, G.; Yi, W.; Yang, Y. Coherent Integration Algorithm for a Maneuvering Target with High-Order Range Migration. IEEE Trans. Signal Process. 2015, 63, 4474–4486. [Google Scholar] [CrossRef]
- Pei, J.; Huang, Y.; Chen, B.; Guan, J.; Cai, M.; Chen, X. Long Time Coherent Integration Method Based on Combining Pulse Compression and Radon-Fourier Transform. J. Radars 2021, 10, 956–969. [Google Scholar]
- Wang, C.; Wang, Y.; Liu, C.; Liu, B. A New Approach to Range Cell Migration Correction for Ground Moving Targets in High-resolution SAR System Based on Parameter Estimation. J. Radars 2019, 8, 64–72. [Google Scholar]
- Zhou, Y.; Xia, W.; Zhou, J.; Huang, L.; Huang, M. Coherent Integration Algorithm for Weak Maneuvering Target Detection in Passive Radar Using Digital TV Signals. In Machine Learning and Intelligent Communications; Springer: Cham, Switzerland, 2018; pp. 215–224. [Google Scholar]
- Li, X.; Yang, Y.; Sun, Z.; Cui, G.; Yeo, T.S. Multi-Frame Integration Method for Radar Detection of Weak Moving Target. IEEE Trans. Veh. Technol. 2021, 70, 3609–3624. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, R.; Yang, Y.; Bai, H.; Zhang, J.; Guo, J. ISNet: Shape Matters for Infrared Small Target Detection. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–22 June 2022. [Google Scholar]
- Zhang, M.; Zhang, R.; Zhang, J.; Guo, J.; Li, Y.; Gao, X. Dim2Clear Network for Infrared Small Target Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L.J. Coherent Integration for Maneuvering Target Detection Based on Radon-Lv’s Distribution. IEEE Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar] [CrossRef]
- Rao, X.; Tao, H.; Su, J.; Xie, J.; Zhang, X. Detection of constant radial acceleration weak target via IAR-FRFT. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3242–3253. [Google Scholar] [CrossRef]
- Suo, P.C.; Tao, S.; Tao, R.; Nan, Z. Detection of high-speed and accelerated target based on the linear frequency modulation radar. IET Radar Sonar Navig. 2014, 8, 37–47. [Google Scholar] [CrossRef]
- Zhu, D.; Li, Y.; Zhu, Z. A keystone transform without interpolation for SAR ground moving-target imaging. IEEE Geosci. Remote Sens. Lett. 2007, 4, 18–22. [Google Scholar] [CrossRef]
- Perry, R.P.; Dipietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Sun, G.; Xing, M.; Xia, X.G.; Wu, Y.; Bao, Z. Robust Ground Moving-Target Imaging Using Deramp–Keystone Processing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 966–982. [Google Scholar] [CrossRef]
- Kirkland, D. Imaging moving targets using the second-order keystone transform. Radar Sonar Navig. IET 2011, 5, 902–910. [Google Scholar] [CrossRef]
- Guo, X.; Wu, Z.; Wang, S.; Zhang, K.; Yang, X. A Maneuvering Target Compensation Algorithm Based on Third-Order Keystone Transform and Correlation Function. Radar Sci. Technol. 2022, 20, 629–634. [Google Scholar]
- Sun, Z.; Li, X.; Cui, G.; Yi, W.; Kong, L. A Fast Approach for Detection and Parameter Estimation of Maneuvering Target With Complex Motions in Coherent Radar System. IEEE Trans. Veh. Technol. 2021, 70, 10278–10292. [Google Scholar] [CrossRef]
- Tian, M.; Liao, G.; Zhu, S.; He, X.; Li, Y. An Efficient Method for Ground Maneuvering Target Refocusing and Motion Parameter Estimation Based on DPT–KT–MFP. Remote Sens. 2021, 13, 1092. [Google Scholar] [CrossRef]
- Peleg, S.; Friedlander, B. The discrete polynomial-phase transform. IEEE Trans. Signal Process. 1995, 43, 1901–1914. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, Y. Exploring Lag Diversity in the High-Order Ambiguity Function for Polynomial Phase Signals. IEEE Signal Process. Lett. 1997, 4, 240–242. [Google Scholar] [CrossRef]
- Xia, X.G. Dynamic Range of the Detectable Parameters for Polynomial Phase Signals Using Multiple-Lag Diversities in High-Order Ambiguity Functions. IEEE Trans. Inf. Theory 2001, 47, 1378–1384. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. A Fast Maneuvering Target Motion Parameters Estimation Algorithm based on ACCF. IEEE Signal Process. Lett. 2015, 22, 265–269. [Google Scholar] [CrossRef]
- Xia, X.G.; Chen, V. A Quantitative SNR Analysis for the Pseudo Wigner-Ville Distribution. IEEE Trans. Signal Process. 1999, 47, 2891–2894. [Google Scholar] [CrossRef]
- Huang, P.; Liao, G.; Yang, Z.; Xia, X.G.; Ma, J.T.; Zhang, X. A Fast SAR Imaging Method for Ground Moving Target Using a Second-Order WVD Transform. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1940–1956. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Kong, L.; Yi, W. Fast Non-Searching Method for Maneuvering Target Detection and Motion Parameters Estimation. IEEE Trans. Signal Process. 2016, 64, 2232–2244. [Google Scholar] [CrossRef]
- Lv, X.; Bi, G.; Wan, C.; Xing, M. Lv’s Distribution: Principle, Implementation, Properties, and Performance. IEEE Trans. Signal Process. 2011, 59, 3576–3591. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection (II): Blind Speed Sidelobe Suppression. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2473–2489. [Google Scholar] [CrossRef]
- Yu, J.; Xu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection (III): Optimality and Fast Implementations. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 991–1004. [Google Scholar] [CrossRef]
- Shang, Z.; Tan, X.; Qu, Z.; Wang, H. High-Speed Target Detection Based on Modified Fast RFT Algorithm. Radar Sci. Technol. 2016, 14, 184–188. [Google Scholar]
- Xu, J.; Xia, X.G.; Peng, S.B.; Yu, J.; Peng, Y.N.; Qian, L.C. Radar Maneuvering Target Motion Estimation Based on Generalized Radon-Fourier Transform. IEEE Trans. Signal Process. 2012, 60, 6190–6201. [Google Scholar]
- Qian, L.C.; Xu, J.; Xia, X.G.; Sun, W.F.; Long, T.; Peng, Y.N. Fast implementation of generalised Radon-Fourier transform for manoeuvring radar target detection. Electron. Lett. 2012, 48, 1427–1428. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, S. Parallel implementation for GRFT algorithm Based on three-order motion model. Signal Process. 2021, 37, 383–389. [Google Scholar]
- Xu, J.; Zhou, X.; Qian, L.C.; Xia, X.G.; Long, T. Hybrid integration for highly maneuvering radar target detection based on generalized radon-fourier transform. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 2554–2561. [Google Scholar] [CrossRef]
- Ma, B.; Zhang, S.; Jia, W.; Wang, W.Q. Fast Implementation of Generalized Radon-Fourier Transform. IEEE Trans. Aerosp. Electron. Syst. 2021, 3758–3767. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, H.; Jiu, B.; Zhao, Y.; Li, K.; Zhang, Y. Full-Dimensional Partial-Search Generalized Radon-Fourier Transform for High-Speed Maneuvering Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5445–5457. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; Li, Y.; Gao, X. Deep Latent Low-Rank Representation for Face Sketch Synthesis. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3109–3123. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, N.; Li, Y.; Gao, X. Neural Probabilistic Graphical Model for Face Sketch Synthesis. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 2623–2637. [Google Scholar] [CrossRef]
- Zhang, M.; Bai, H.; Zhang, J.; Zhang, R.; Wang, C.; Guo, J.; Gao, X. RKformer: Runge–Kutta Transformer with Random-Connection Attention for Infrared Small Target Detection. In MM ’22: Proceedings of the 30th ACM International Conference on Multimedia, Lisboa, Portugal, 10–14 October 2022; Association for Computing Machinery: New York, NY, USA, 2022. [Google Scholar]
- Wang, C.; Zheng, J.; Jiu, B.; Liu, H.; Shi, Y. Deep neural network-aided coherent integration method for maneuvering target detection. Signal Process. 2021, 182, 107966. [Google Scholar] [CrossRef]
- Fan, P.; Guo, Y.; Qin, K.; Yuan, H.; Zhang, X. A fast implementation algorithm of GRFT for coherent integration of high-speed maneuvering targets. In Proceedings of the IET International Radar Conference (IRC 2023), Chongqing, China, 3–5 December 2023. [Google Scholar]
- Qian, L.; Xu, J.; Sun, W.; Peng, Y. Efficient Approach of Generalized RFT Based on PSO. In Proceedings of the 2012 IEEE 12th International Conference on Computer and Information Technology, Chengdu, China, 27–29 October 2012. [Google Scholar]
- Xia, W.; Zhou, Y.; Jin, X.; Zhou, J. A Fast Algorithm of Generalized Radon-Fourier Transform for Weak Maneuvering Target Detection. Int. J. Antennas Propag. 2016, 2016, 4315616. [Google Scholar] [CrossRef]
- Yamaoka, T.; Oshima, T. Pulse Doppler radar with antenna arrays estimating angular velocity. IEICE Trans. Commun. 2024, 1–10. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Icnn95-international Conference on Neural Networks, Perth, WA, Australia, 27 November–December 1995. [Google Scholar]
- Mezura-Montes, E.; Coello Coello, C.A. Constraint-handling in nature-inspired numerical optimization: Past, present and future. Swarm Evol. Comput. 2011, 1, 173–194. [Google Scholar] [CrossRef]
- Pedersen, M.E.H. Good Parameters for Particle Swarm Optimization. 2010. Available online: https://www.researchgate.net/publication/355913207_Good_Parameters_for_Particle_Swarm_Optimization (accessed on 26 January 2025).
- Rosen, P.; Hensley, S.; Joughin, I. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–73. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Purshouse, R.C. Multi-Objective Optimization using Evolutionary Algorithms. SIAM Rev. 2002, 509. [Google Scholar]
- Li, X.; Kong, L.; Cui, G.; Yi, W. CLEAN-based coherent integration method for high-speed multi-targets detection. IET Radar Sonar Navig. 2016, 10, 1671–1682. [Google Scholar] [CrossRef]
| Radar Parameters | |
|---|---|
| Carrier Frequency () | 10 GHz |
| Frequency Bandwidth (B) | 25 MHz |
| Pulse Width () | 20 s |
| Pulse Repetition Period (T) | 100 s |
| Accumulation Time () | 100 ms |
| Pulse Number (M) | 1000 |
| Target Parameters | |
| Initial Range () | 10 km |
| Initial Velocity () | 2000 m/s |
| Acceleration (a) | −100 m/s2 |
| Initial Range Interval | [10 km − 250 m, 10 km + 250 m] |
| Initial Velocity Interval | [1500 m/s, 2500 m/s] |
| Acceleration Interval | [−200 m/s2, 200 m/s2] |
| Algorithm Parameters | |
| Swarm Size (S) | 200 |
| Inertia Range () | [0.3, 1.1] |
| Self Adjustment Weight () | 2 |
| Social Adjustment Weight () | 0.5 |
| Max Iterations (K) | 600 |
| Max Stall Iterations (I) | 20 |
| Min Convergent Particles (P) | 3 |
| Function Tolerance () | 10−6 |
| Method | Time Cost | Approximate Time Cost |
|---|---|---|
| PSO 1 | ||
| BPSO | ||
| BTPSO | ||
| BTPSO-C3 1 | ||
| Ergodic |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Xu, H.; Li, J.; Wu, Z.; Yang, J.; Wu, Y.; Zhang, B.; Cheng, Q.; Li, J. Fast Generalized Radon–Fourier Transform Based on Blind Speed Sidelobe Traction. Remote Sens. 2025, 17, 475. https://doi.org/10.3390/rs17030475
Sun D, Xu H, Li J, Wu Z, Yang J, Wu Y, Zhang B, Cheng Q, Li J. Fast Generalized Radon–Fourier Transform Based on Blind Speed Sidelobe Traction. Remote Sensing. 2025; 17(3):475. https://doi.org/10.3390/rs17030475
Chicago/Turabian StyleSun, Difeng, He Xu, Jin Li, Zutang Wu, Jun Yang, Youcao Wu, Baoguo Zhang, Qianqian Cheng, and Jianbing Li. 2025. "Fast Generalized Radon–Fourier Transform Based on Blind Speed Sidelobe Traction" Remote Sensing 17, no. 3: 475. https://doi.org/10.3390/rs17030475
APA StyleSun, D., Xu, H., Li, J., Wu, Z., Yang, J., Wu, Y., Zhang, B., Cheng, Q., & Li, J. (2025). Fast Generalized Radon–Fourier Transform Based on Blind Speed Sidelobe Traction. Remote Sensing, 17(3), 475. https://doi.org/10.3390/rs17030475






