Generalization Enhancement Strategies to Enable Cross-Year Cropland Mapping with Convolutional Neural Networks Trained Using Historical Samples
Abstract
1. Introduction
2. Materials and Methods
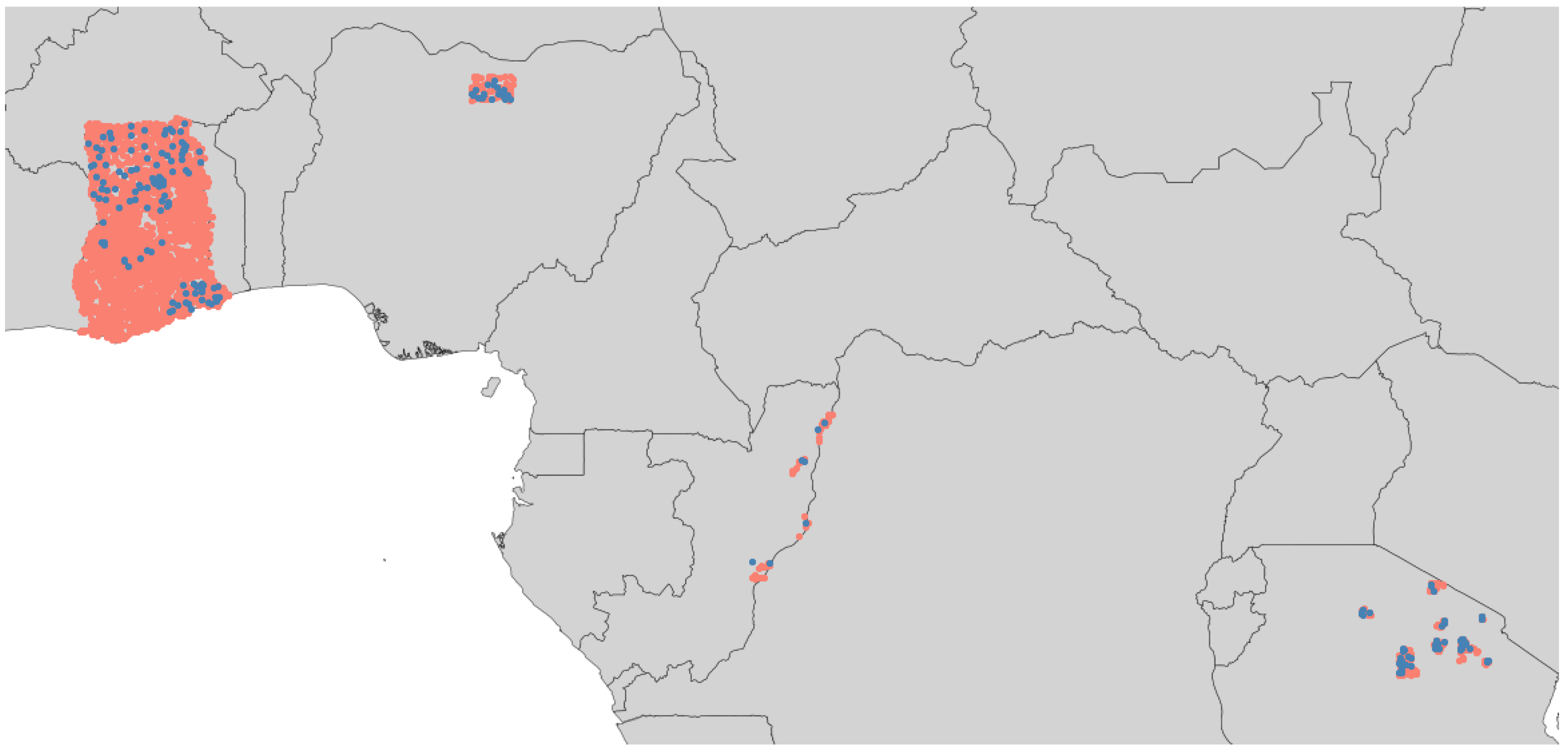
2.1. Data and Study Area
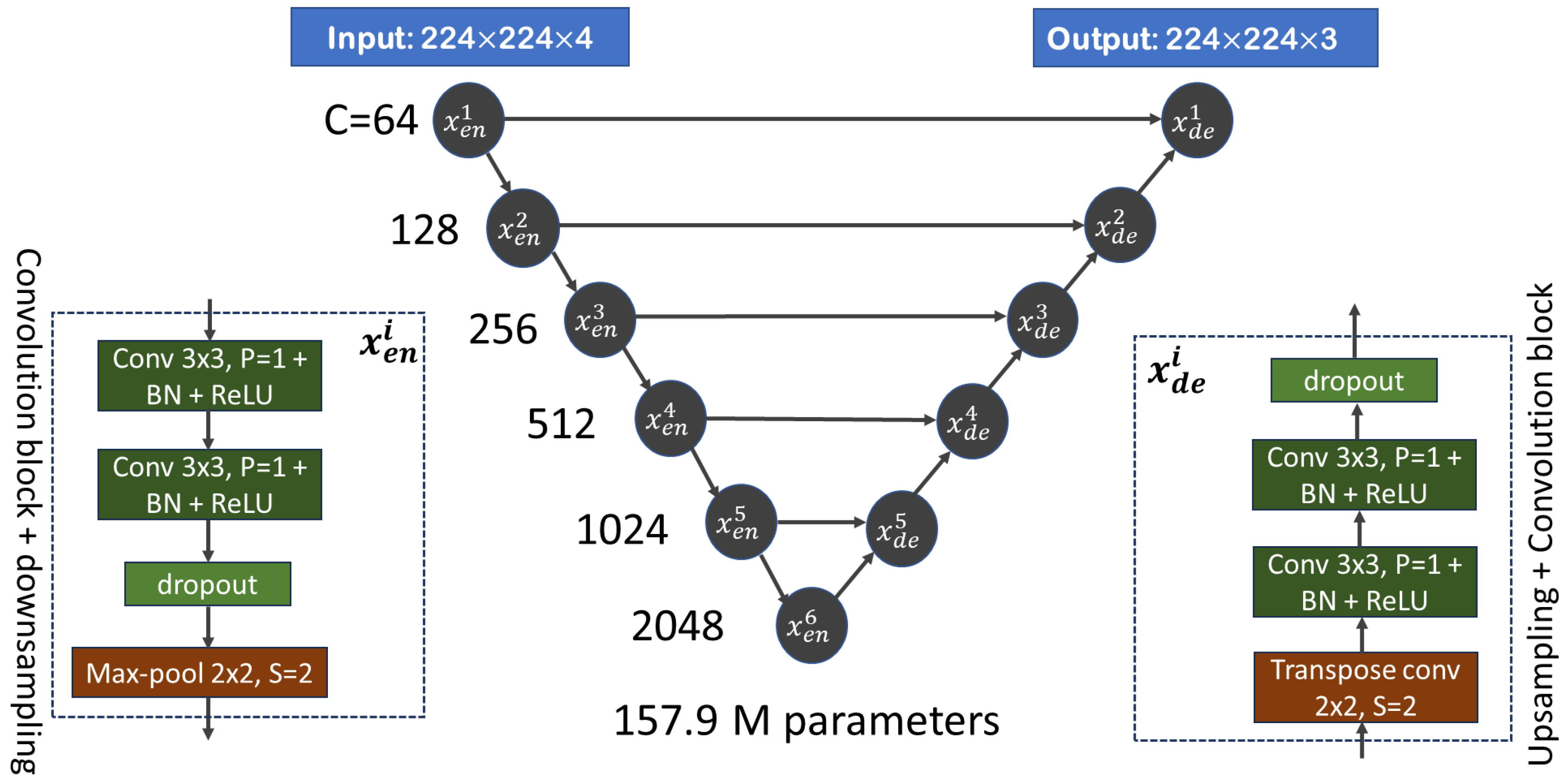
2.2. Method
3. Results
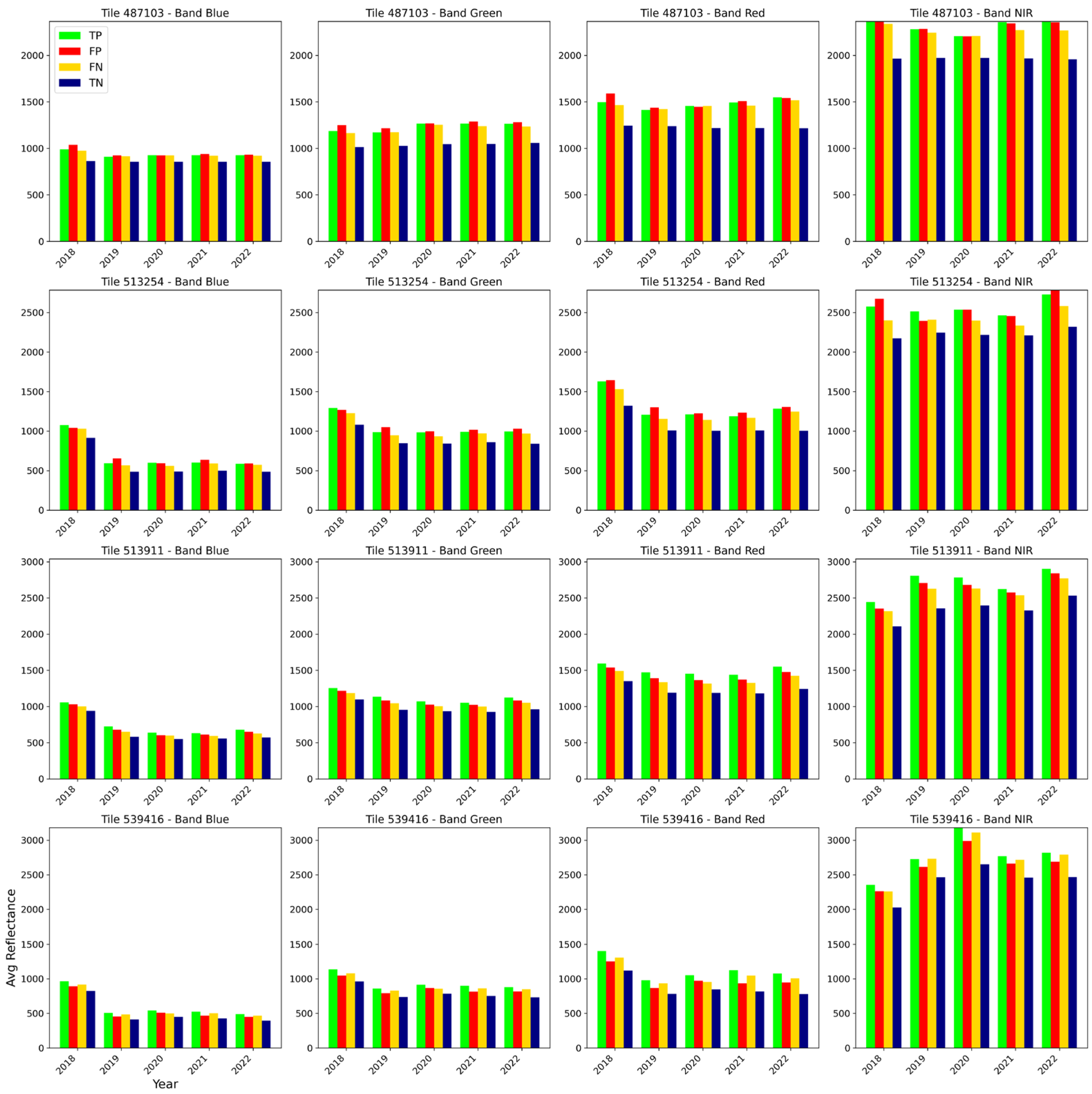
3.1. Input Normalization
3.2. Investigating the Effects of Photometric Augmentation, MC-Dropout, Loss Function, and Model Capacity on Model Performance
3.3. Investigating the Spatio-Temporal Consistency
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A





References
- Ajadi, O.A.; Barr, J.; Liang, S.-Z.; Ferreira, R.; Kumpatla, S.P.; Patel, R.; Swatantran, A. Large-scale crop type and crop area mapping across Brazil using synthetic aperture radar and optical imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 97, 102294. [Google Scholar] [CrossRef]
- Bhosle, K.; Musande, V. Evaluation of Deep Learning CNN Model for Land Use Land Cover Classification and Crop Identification Using Hyperspectral Remote Sensing Images. J. Indian Soc. Remote Sens. 2019, 47, 1949–1958. [Google Scholar] [CrossRef]
- Burkhard, B.; Kroll, F.; Nedkov, S.; Müller, F. Mapping ecosystem service supply, demand and budgets. Ecol. Indic. 2012, 21, 17–29. [Google Scholar] [CrossRef]
- Akbari, M.; Shalamzari, M.J.; Memarian, H.; Gholami, A. Monitoring desertification processes using ecological indicators and providing management programs in arid regions of Iran. Ecol. Indic. 2020, 111, 106011. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, H.; Wang, G.; Sun, H.; Fu, J. Mapping Paddy Rice Using a Convolutional Neural Network (CNN) with Landsat 8 Datasets in the Dongting Lake Area, China. Remote Sens. 2018, 10, 1840. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Chawla, I.; Mishra, A.K. A review of remote sensing applications in agriculture for food security: Crop growth and yield, irrigation, and crop losses. J. Hydrol. 2020, 586, 124905. [Google Scholar] [CrossRef]
- Mazzia, V.; Comba, L.; Khaliq, A.; Chiaberge, M.; Gay, P. UAV and Machine Learning Based Refinement of a Satellite-Driven Vegetation Index for Precision Agriculture. Sensors 2020, 20, 2530. [Google Scholar] [CrossRef]
- Khan, S.; Tufail, M.; Khan, M.T.; Khan, Z.A.; Anwar, S. Deep learning-based identification system of weeds and crops in strawberry and pea fields for a precision agriculture sprayer. Precis. Agric. 2021, 22, 1711–1727. [Google Scholar] [CrossRef]
- Lambert, M.-J.; Traoré, P.C.S.; Blaes, X.; Baret, P.; Defourny, P. Estimating smallholder crops production at village level from Sentinel-2 time series in Mali’s cotton belt. Remote Sens. Environ. 2018, 216, 647–657. [Google Scholar] [CrossRef]
- Jin, Z.; Azzari, G.; You, C.; Di Tommaso, S.; Aston, S.; Burke, M.; Lobell, D.B. Smallholder maize area and yield mapping at national scales with Google Earth Engine. Remote Sens. Environ. 2019, 228, 115–128. [Google Scholar] [CrossRef]
- Estes, L.D.; Ye, S.; Song, L.; Luo, B.; Eastman, J.R.; Meng, Z.; Zhang, Q.; McRitchie, D.; Debats, S.R.; Muhando, J.; et al. High Resolution, Annual Maps of Field Boundaries for Smallholder-Dominated Croplands at National Scales. Front. Artif. Intell. 2022, 4, 744863. [Google Scholar] [CrossRef] [PubMed]
- Salmon, J.M.; Friedl, M.A.; Frolking, S.; Wisser, D.; Douglas, E.M. Global rain-fed, irrigated, and paddy croplands: A new high resolution map derived from remote sensing, crop inventories and climate data. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 321–334. [Google Scholar] [CrossRef]
- Waldner, F.; Fritz, S.; Di Gregorio, A.; Defourny, P. Mapping Priorities to Focus Cropland Mapping Activities: Fitness Assessment of Existing Global, Regional and National Cropland Maps. Remote Sens. 2015, 7, 7959–7986. [Google Scholar] [CrossRef]
- Brown, C.F.; Brumby, S.P.; Guzder-Williams, B.; Birch, T.; Hyde, S.B.; Mazzariello, J.; Czerwinski, W.; Pasquarella, V.J.; Haertel, R.; Ilyushchenko, S.; et al. Dynamic World, Near real-time global 10 m land use land cover mapping. Sci. Data 2022, 9, 251. [Google Scholar] [CrossRef]
- Wang, S.; Waldner, F.; Lobell, D.B. Unlocking Large-Scale Crop Field Delineation in Smallholder Farming Systems with Transfer Learning and Weak Supervision. Remote Sens. 2022, 14, 5738. [Google Scholar] [CrossRef]
- Jakubik, J.; Roy, S.; Phillips, C.E.; Fraccaro, P.; Godwin, D.; Zadrozny, B.; Szwarcman, D.; Gomes, C.; Nyirjesy, G.; Edwards, B.; et al. Foundation Models for Generalist Geospatial Artificial Intelligence. arXiv 2023, arXiv:2310.18660. [Google Scholar]
- Tseng, G.; Cartuyvels, R.; Zvonkov, I.; Purohit, M.; Rolnick, D.; Kerner, H. Lightweight, Pre-Trained Transformers for Remote Sensing Timeseries. arXiv 2023, arXiv:2304.14065. [Google Scholar]
- Xie, B.; Zhang, H.K.; Xue, J. Deep Convolutional Neural Network for Mapping Smallholder Agriculture Using High Spatial Resolution Satellite Image. Sensors 2019, 19, 2398. [Google Scholar] [CrossRef]
- Sharifi, A.; Mahdipour, H.; Moradi, E.; Tariq, A. Agricultural Field Extraction with Deep Learning Algorithm and Satellite Imagery. J. Indian Soc. Remote Sens. 2022, 50, 417–423. [Google Scholar] [CrossRef]
- Tetteh, G.O.; Schwieder, M.; Erasmi, S.; Conrad, C.; Gocht, A. Comparison of an Optimised Multiresolution Segmentation Approach with Deep Neural Networks for Delineating Agricultural Fields from Sentinel-2 Images. PFG J. Photogramm. Remote Sens. Geoinf. Sci. 2023, 91, 295–312. [Google Scholar] [CrossRef]
- Du, Z.; Yang, J.; Ou, C.; Zhang, T. Smallholder Crop Area Mapped with a Semantic Segmentation Deep Learning Method. Remote Sens. 2019, 11, 888. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P.; Wu, C. ResUNet-a: A deep learning framework for semantic segmentation of remotely sensed data. ISPRS J. Photogramm. Remote Sens. 2020, 162, 94–114. [Google Scholar] [CrossRef]
- Xie, D.; Xu, H.; Xiong, X.; Liu, M.; Hu, H.; Xiong, M.; Liu, L. Cropland Extraction in Southern China from Very High-Resolution Images Based on Deep Learning. Remote Sens. 2023, 15, 2231. [Google Scholar] [CrossRef]
- Wang, H.; Chen, X.; Zhang, T.; Xu, Z.; Li, J. CCTNet: Coupled CNN and Transformer Network for Crop Segmentation of Remote Sensing Images. Remote Sens. 2022, 14, 1956. [Google Scholar] [CrossRef]
- Wang, Y.; Ding, W.; Zhang, R.; Li, H. Boundary-Aware Multitask Learning for Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 951–963. [Google Scholar] [CrossRef]
- Shunying, W.; Ya’nan, Z.; Xianzeng, Y.; Li, F.; Tianjun, W.; Jiancheng, L. BSNet: Boundary-semantic-fusion network for farmland parcel mapping in high-resolution satellite images. Comput. Electron. Agric. 2023, 206, 107683. [Google Scholar] [CrossRef]
- Long, J.; Li, M.; Wang, X.; Stein, A. Delineation of agricultural fields using multi-task BsiNet from high-resolution satellite images. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102871. [Google Scholar] [CrossRef]
- Xu, L.; Yang, P.; Yu, J.; Peng, F.; Xu, J.; Song, S.; Wu, Y. Extraction of cropland field parcels with high resolution remote sensing using multi-task learning. Eur. J. Remote Sens. 2023, 56, 2181874. [Google Scholar] [CrossRef]
- Luo, W.; Zhang, C.; Li, Y.; Yan, Y. MLGNet: Multi-Task Learning Network with Attention-Guided Mechanism for Segmenting Agricultural Fields. Remote Sens. 2023, 15, 3934. [Google Scholar] [CrossRef]
- Li, M.; Long, J.; Stein, A.; Wang, X. Using a semantic edge-aware multi-task neural network to delineate agricultural parcels from remote sensing images. ISPRS J. Photogramm. Remote Sens. 2023, 200, 24–40. [Google Scholar] [CrossRef]
- Persello, C.; Tolpekin, V.A.; Bergado, J.R.; De By, R.A. Delineation of agricultural fields in smallholder farms from satellite images using fully convolutional networks and combinatorial grouping. Remote Sens. Environ. 2019, 231, 111253. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Wang, X.; Zhang, L.; Zhong, Y. E2EVAP: End-to-end vectorization of smallholder agricultural parcel boundaries from high-resolution remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2023, 203, 246–264. [Google Scholar] [CrossRef]
- Mei, W.; Wang, H.; Fouhey, D.; Zhou, W.; Hinks, I.; Gray, J.M.; Van Berkel, D.; Jain, M. Using Deep Learning and Very-High-Resolution Imagery to Map Smallholder Field Boundaries. Remote Sens. 2022, 14, 3046. [Google Scholar] [CrossRef]
- Schmitt, M.; Hughes, L.H.; Qiu, C.; Zhu, X.X. SEN12MS—A Curated Dataset of Georeferenced Multi-Spectral Sentinel-1/2 Imagery for Deep Learning and Data Fusion. arXiv 2019, arXiv:1906.07789. [Google Scholar] [CrossRef]
- Fu, Y.; Shen, R.; Song, C.; Dong, J.; Han, W.; Ye, T.; Yuan, W. Exploring the effects of training samples on the accuracy of crop mapping with machine learning algorithm. Sci. Remote Sens. 2023, 7, 100081. [Google Scholar] [CrossRef]
- Lesiv, M.; Laso Bayas, J.C.; See, L.; Duerauer, M.; Dahlia, D.; Durando, N.; Hazarika, R.; Kumar Sahariah, P.; Vakolyuk, M.; Blyshchyk, V.; et al. Estimating the global distribution of field size using crowdsourcing. Glob. Chang. Biol. 2019, 25, 174–186. [Google Scholar] [CrossRef] [PubMed]
- Kou, W.; Shen, Z.; Liu, D.; Liu, Z.; Li, J.; Chang, W.; Wang, H.; Huang, L.; Jiao, S.; Lei, Y.; et al. Crop classification methods and influencing factors of reusing historical samples based on 2D-CNN. Int. J. Remote Sens. 2023, 44, 3278–3305. [Google Scholar] [CrossRef]
- Hao, P.; Di, L.; Zhang, C.; Guo, L. Transfer Learning for Crop classification with Cropland Data Layer data (CDL) as training samples. Sci. Total Environ. 2020, 733, 138869. [Google Scholar] [CrossRef]
- Van Den Broeck, W.A.J.; Goedemé, T.; Loopmans, M. Multiclass Land Cover Mapping from Historical Orthophotos Using Domain Adaptation and Spatio-Temporal Transfer Learning. Remote Sens. 2022, 14, 5911. [Google Scholar] [CrossRef]
- Antonijević, O.; Jelić, S.; Bajat, B.; Kilibarda, M. Transfer learning approach based on satellite image time series for the crop classification problem. J. Big Data 2023, 10, 54. [Google Scholar] [CrossRef]
- Pandžić, M.; Pavlović, D.; Matavulj, P.; Brdar, S.; Marko, O.; Crnojević, V.; Kilibarda, M. Interseasonal transfer learning for crop mapping using Sentinel-1 data. Int. J. Appl. Earth Obs. Geoinf. 2024, 128, 103718. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2024, 301, 113924. [Google Scholar] [CrossRef]
- Jiang, D.; Chen, S.; Useya, J.; Cao, L.; Lu, T. Crop Mapping Using the Historical Crop Data Layer and Deep Neural Networks: A Case Study in Jilin Province, China. Sensors 2022, 22, 5853. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Huang, H.; Wang, J.; Liu, C.; Liang, L.; Li, C.; Gong, P. The migration of training samples towards dynamic global land cover mapping. ISPRS J. Photogramm. Remote Sens. 2020, 161, 27–36. [Google Scholar] [CrossRef]
- Waldner, F.; Canto, G.S.; Defourny, P. Automated annual cropland mapping using knowledge-based temporal features. ISPRS J. Photogramm. Remote Sens. 2015, 110, 1–13. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L.; Yu, Y.; Xi, X.; Ren, T.; Zhao, Y.; Zhu, D.; Zhu, A. Cross-Year Reuse of Historical Samples for Crop Mapping Based on Environmental Similarity. Front. Plant Sci. 2022, 12, 761148. [Google Scholar] [CrossRef] [PubMed]
- Ge, S.; Zhang, J.; Pan, Y.; Yang, Z.; Zhu, S. Transferable deep learning model based on the phenological matching principle for mapping crop extent. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102451. [Google Scholar] [CrossRef]
- Diakogiannis, F.I.; Waldner, F.; Caccetta, P. Looking for Change? Roll the Dice and Demand Attention. Remote Sens. 2021, 13, 3707. [Google Scholar] [CrossRef]
- Li, L.; Zhang, W.; Zhang, X.; Emam, M.; Jing, W. Semi-Supervised Remote Sensing Image Semantic Segmentation Method Based on Deep Learning. Electronics 2023, 12, 348. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training DNNs: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef]
- Pelletier, C.; Webb, G.; Petitjean, F. Temporal Convolutional Neural Network for the Classification of Satellite Image Time Series. Remote Sens. 2019, 11, 523. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Hoang, T.D.; Pham, M.T.; Vu, T.T.; Nguyen, T.H.; Huynh, Q.-T.; Jo, J. Monitoring agriculture areas with satellite images and deep learning. Appl. Soft Comput. 2020, 95, 106565. [Google Scholar] [CrossRef]
- Tuli, S.; Dasgupta, I.; Grant, E.; Griffiths, T.L. Are Convolutional Neural Networks or Transformers more like human vision? arXiv 2021, arXiv:2105.07197. [Google Scholar]
- Schwonberg, M.; Bouazati, F.E.; Schmidt, N.M.; Gottschalk, H. Augmentation-based Domain Generalization for Semantic Segmentation. In Proceedings of the 2023 IEEE Intelligent Vehicles Symposium (IV), Anchorage, AK, USA, 4–7 June 2023. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Baldi, P.; Sadowski, P. The dropout learning algorithm. Artif. Intell. 2014, 210, 78–122. [Google Scholar] [CrossRef]
- Tompson, J.; Goroshin, R.; Jain, A.; LeCun, Y.; Bregler, C. Efficient object localization using Convolutional Networks. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; IEEE: Boston, MA, USA, 2015; pp. 648–656. [Google Scholar]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 1050–1059. [Google Scholar]
- Shridhar, K.; Laumann, F.; Liwicki, M. A Comprehensive Guide to Bayesian Convolutional Neural Network with Variational Inference. arXiv 2019, arXiv:1901.02731. [Google Scholar]
- Kendall, A.; Badrinarayanan, V.; Cipolla, R. Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding. arXiv 2016, arXiv:1511.02680. [Google Scholar]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? Adv. Neural Inf. Process. Syst. 2017, 30, 5574–5584. [Google Scholar]
- Dechesne, C.; Lassalle, P.; Lefèvre, S. Bayesian U-Net: Estimating Uncertainty in Semantic Segmentation of Earth Observation Images. Remote Sens. 2021, 13, 3836. [Google Scholar] [CrossRef]
- Mukhoti, J.; Gal, Y. Evaluating Bayesian Deep Learning Methods for Semantic Segmentation. arXiv 2018, arXiv:1811.12709. [Google Scholar]
- Peng, L.; Wang, H.; Li, J. Uncertainty Evaluation of Object Detection Algorithms for Autonomous Vehicles. Automot. Innov. 2021, 4, 241–252. [Google Scholar] [CrossRef]
- Song, X.; Zhou, H.; Liu, G.; Sheng-Xian Teo, B. Study of Multiscale Fused Extraction of Cropland Plots in Remote Sensing Images Based on Attention Mechanism. Comput. Intell. Neurosci. 2022, 2022, 2418850. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.J.; Nongmeikapam, K. Semantic Segmentation of Satellite Images Using Deep-Unet. Arab. J. Sci. Eng. 2023, 48, 1193–1205. [Google Scholar] [CrossRef]
- Waldner, F.; De Abelleyra, D.; Verón, S.R.; Zhang, M.; Wu, B.; Plotnikov, D.; Bartalev, S.; Lavreniuk, M.; Skakun, S.; Kussul, N.; et al. Towards a set of agrosystem-specific cropland mapping methods to address the global cropland diversity. Int. J. Remote Sens. 2016, 37, 3196–3231. [Google Scholar] [CrossRef]
- Potapov, P.; Turubanova, S.; Hansen, M.C.; Tyukavina, A.; Zalles, V.; Khan, A.; Song, X.-P.; Pickens, A.; Shen, Q.; Cortez, J. Global maps of cropland extent and change show accelerated cropland expansion in the twenty-first century. Nat. Food 2021, 3, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Sova, C.A.; Thornton, T.F.; Zougmore, R.; Helfgott, A.; Chaudhury, A.S. Power and influence mapping in Ghana’s agricultural adaptation policy regime. Clim. Dev. 2017, 9, 399–414. [Google Scholar] [CrossRef]
- Kansanga, M.; Andersen, P.; Kpienbaareh, D.; Mason-Renton, S.; Atuoye, K.; Sano, Y.; Antabe, R.; Luginaah, I. Traditional agriculture in transition: Examining the impacts of agricultural modernization on smallholder farming in Ghana under the new Green Revolution. Int. J. Sustain. Dev. World Ecol. 2019, 26, 11–24. [Google Scholar] [CrossRef]
- Sainte Fare Garnot, V.; Landrieu, L.; Giordano, S.; Chehata, N. Satellite Image Time Series Classification With Pixel-Set Encoders and Temporal Self-Attention. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; IEEE: Seattle, WA, USA, 2020; pp. 12322–12331. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–October 2015; pp. 234–241. [Google Scholar]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel 2 and deep learning. In Proceedings of the in 2021 IEEE international geoscience and remote sensing symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4704–4707. [Google Scholar]
- Anagnostis, A.; Tagarakis, A.C.; Kateris, D.; Moysiadis, V.; Sørensen, C.G.; Pearson, S.; Bochtis, D. Orchard Mapping with Deep Learning Semantic Segmentation. Sensors 2021, 21, 3813. [Google Scholar] [CrossRef]
- Liu, Z.; Li, N.; Wang, L.; Zhu, J.; Qin, F. A multi-angle comprehensive solution based on deep learning to extract cultivated land information from high-resolution remote sensing images. Ecol. Indic. 2022, 141, 108961. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Abraham, N.; Khan, N.M. A Novel Focal Tversky loss function with improved Attention U-Net for lesion segmentation. In Proceedings of the In 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI), Venice, Italy, 8–11 April 2019; pp. 683–687. [Google Scholar]
- Garcia-Pedrero, A.; Lillo-Saavedra, M.; Rodriguez-Esparragon, D.; Gonzalo-Martin, C. Deep Learning for Automatic Outlining Agricultural Parcels: Exploiting the Land Parcel Identification System. IEEE Access 2019, 7, 158223–158236. [Google Scholar] [CrossRef]
- Foret, P.; Kleiner, A.; Mobahi, H.; Neyshabur, B. Sharpness-Aware Minimization for Efficiently Improving Generalization. arXiv 2020, arXiv:2010.01412. [Google Scholar]
- Frazier, A.E.; Hemingway, B.L. A Technical Review of Planet Smallsat Data: Practical Considerations for Processing and Using PlanetScope Imagery. Remote Sens. 2021, 13, 3930. [Google Scholar] [CrossRef]
- Syrris, V.; Hasenohr, P.; Delipetrev, B.; Kotsev, A.; Kempeneers, P.; Soille, P. Evaluation of the Potential of Convolutional Neural Networks and Random Forests for Multi-Class Segmentation of Sentinel-2 Imagery. Remote Sens. 2019, 11, 907. [Google Scholar] [CrossRef]
- Jeon, E.-I.; Kim, S.; Park, S.; Kwak, J.; Choi, I. Semantic segmentation of seagrass habitat from drone imagery based on deep learning: A comparative study. Ecol. Inform. 2021, 66, 101430. [Google Scholar] [CrossRef]
- Khan, A.H.; Zafar, Z.; Shahzad, M.; Berns, K.; Fraz, M.M. Crop Type Classification using Multi-temporal Sentinel-2 Satellite Imagery: A Deep Semantic Segmentation Approach. In Proceedings of the International Conference on Robotics and Automation in Industry (ICRAI), Peshawar, Pakistan, 3–5 March 2023; pp. 1–6. [Google Scholar]
- Wang, Z.; Zhang, H.; He, W.; Zhang, L. Phenology Alignment Network: A Novel Framework for Cross-Regional Time Series Crop Classification. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 19–25 June 2021; IEEE: Nashville, TN, USA, 2021; pp. 2934–2943. [Google Scholar]
- Zhang, L.; Liu, Z.; Liu, D.; Xiong, Q.; Yang, N.; Ren, T.; Zhang, C.; Zhang, X.; Li, S. Crop Mapping Based on Historical Samples and New Training Samples Generation in Heilongjiang Province, China. Sustainability 2019, 11, 5052. [Google Scholar] [CrossRef]
- Montazerolghaem, M.; Sun, Y.; Sasso, G.; Haworth, A. U-Net Architecture for Prostate Segmentation: The Impact of Loss Function on System Performance. Bioengineering 2023, 10, 412. [Google Scholar] [CrossRef] [PubMed]
- Anaya-Isaza, A.; Mera-Jimenez, L.; Cabrera-Chavarro, J.M.; Guachi-Guachi, L.; Peluffo-Ordonez, D.; Rios-Patino, J.I. Comparison of Current Deep Convolutional Neural Networks for the Segmentation of Breast Masses in Mammograms. IEEE Access 2021, 9, 152206–152225. [Google Scholar] [CrossRef]
- Gannod, M.; Masto, N.; Owusu, C.; Highway, C.; Brown, K.; Blake-Bradshaw, A.; Feddersen, J.; Hagy, H.; Talbert, D.; Cohen, B. Semantic Segmentation with Multispectral Satellite Images of Waterfowl Habitat. In Proceedings of the International FLAIRS Conference Proceedings, Clearwater Beach, FL, USA, 14–17 May 2023; Volume 36. [Google Scholar] [CrossRef]
- Celikkan, E.; Saberioon, M.; Herold, M.; Klein, N. Semantic Segmentation of Crops and Weeds with Probabilistic Modeling and Uncertainty Quantification. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision Workshops (ICCVW), Paris, France, 2–6 October 2023; IEEE: Paris, France, 2023; pp. 582–592. [Google Scholar]
- Zhang, Z.; Dalca, A.V.; Sabuncu, M.R. Confidence Calibration for Convolutional Neural Networks Using Structured Dropout. arXiv 2019, arXiv:1906.09551. [Google Scholar]
- Wyatt, M.; Radford, B.; Callow, N.; Bennamoun, M.; Hickey, S. Using ensemble methods to improve the robustness of deep learning for image classification in marine environments. Methods Ecol. Evol. 2022, 13, 1317–1328. [Google Scholar] [CrossRef]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. Adv. Neural Inf. Process. Syst. 2017, 30, 6402–6413. [Google Scholar]
- Yun, S.; Han, D.; Chun, S.; Oh, S.J.; Yoo, Y.; Choe, J. CutMix: Regularization Strategy to Train Strong Classifiers With Localizable Features. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; IEEE: Seoul, Republic of Korea, 2019; pp. 6022–6031. [Google Scholar]
- Zhang, H.; Cisse, M.; Dauphin, Y.N.; Lopez-Paz, D. mixup: Beyond Empirical Risk Minimization. arXiv 2018, arXiv:1710.09412. [Google Scholar]
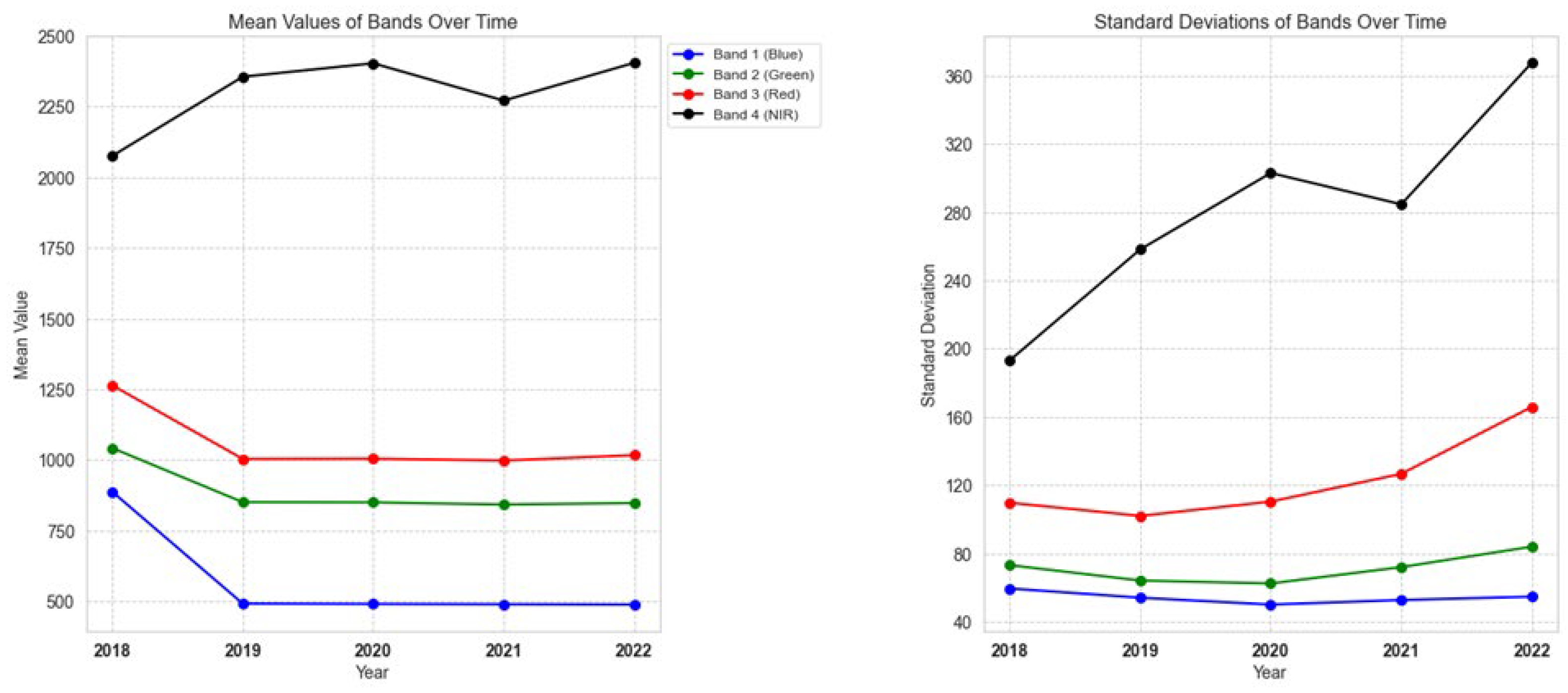
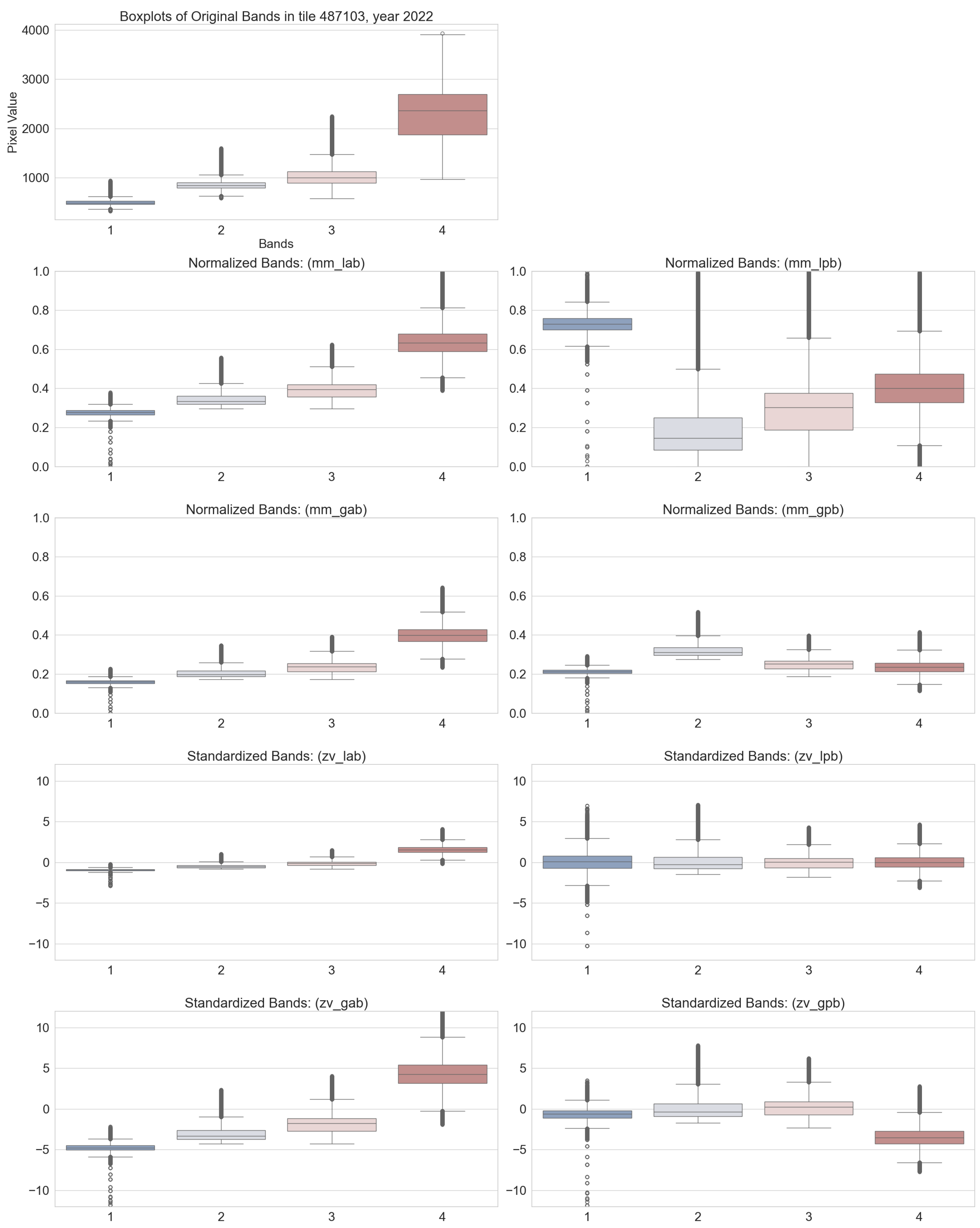
| (a) Accuracy metric of field interior class using different normalization procedures over the multi-temporal test dataset | ||||||
| Normalization type | Precision | Recall | F1-score | IoU | ||
| mm-lab | 74.94% | 50.01% | 59.99% | 42.84% | ||
| mm-lpb | 63.89% | 52.22% | 57.47% | 40.32% | ||
| mm-gab | 71.60% | 51.53% | 59.93% | 42.79% | ||
| mm-gpb | 83.01% | 41.32% | 55.18% | 38.10% | ||
| zv-lab | 85.42% | 38.84% | 53.40% | 36.42% | ||
| zv-lpb | 77.33% | 35.73% | 48.87% | 32.34% | ||
| zv-gab | 50.78% | 56.45% | 53.47% | 36.49% | ||
| zv-gpb | 59.21% | 53.96% | 56.46% | 39.33% | ||
| (b) Accuracy metric of the field interior class using different normalization procedures over the multi-temporal test dataset, separated by year | ||||||
| Normalization type | 2018 | 2019 | 2020 | 2021 | 2022 | |
| mm-lab | IoU | 51.77% | 42.76% | 34.02% | 41.44% | 44.15% |
| F1 | 68.22% | 59.89% | 50.77% | 58.57% | 61.26% | |
| mm-lpb | IoU | 49.65% | 48.49% | 32.06% | 37.81% | 36.16% |
| F1 | 66.36% | 65.31% | 48.55% | 54.87% | 53.12% | |
| mm-gab | IoU | 50.32% | 44.08% | 37.69% | 44.33% | 38.82% |
| F1 | 66.95% | 61.19% | 54.75% | 61.43% | 55.93% | |
| mm-gpb | IoU | 50.58% | 34.15% | 29.74% | 39.29% | 36.24% |
| F1 | 67.18% | 50.91% | 45.84% | 56.41% | 53.20% | |
| zv-lab | IoU | 48.99% | 36.09% | 22.38% | 36.45% | 36.68% |
| F1 | 65.76% | 53.04% | 36.58% | 53.43% | 53.67% | |
| zv-lpb | IoU | 46.98% | 35.39% | 17.38% | 30.67% | 31.18% |
| F1 | 63.93% | 52.28% | 29.61% | 46.95% | 47.54% | |
| zv-gpb | IoU | 48.44% | 42.57% | 31.20% | 41.15% | 36.56% |
| F1 | 65.26% | 59.72% | 47.56% | 58.31% | 53.54% | |
| zv-gab | IoU | 45.75% | 36.68% | 31.54% | 35.91% | 35.39% |
| F1 | 62.78% | 53.67% | 47.96% | 52.85% | 52.27% | |
| (c) Accuracy metric for the field interior class using different normalization procedures over the multi-temporal test dataset, separated by geography | ||||||
| Normalization type | Tile 1 (id: 487103) | Tile 2 (id: 513911) | Tile 3 (id: 513254) | Tile 4 (id: 539416) | ||
| mm-lab | IoU | 45.70% | 46.56% | 43.31% | 36.37% | |
| F1 | 62.73% | 63.53% | 60.44% | 53.34% | ||
| mm-lpb | IoU | 29.52% | 47.61% | 37.54% | 37.04% | |
| F1 | 45.59% | 64.51% | 54.59% | 54.05% | ||
| mm-gab | IoU | 39.92% | 46.47% | 39.58% | 46.47% | |
| F1 | 57.06% | 63.45% | 56.71% | 63.45% | ||
| mm-gpb | IoU | 40.44% | 38.86% | 36.73% | 36.71% | |
| F1 | 57.59% | 55.97% | 53.73% | 53.70% | ||
| zv-lab | IoU | 41.80% | 35.36% | 35.28% | 35.36% | |
| F1 | 58.96% | 52.25% | 52.16% | 52.25% | ||
| zv-lpb | IoU | 37.29% | 28.10% | 34.12% | 28.10% | |
| F1 | 54.32% | 43.88% | 50.88% | 43.88% | ||
| zv-gpb | IoU | 29.41% | 45.68% | 35.28% | 37.45% | |
| F1 | 45.45% | 62.71% | 52.15% | 54.49% | ||
| zv-gab | IoU | 27.08% | 46.40% | 36.90% | 28.23% | |
| F1 | 42.62% | 63.39% | 53.90% | 44.02% | ||
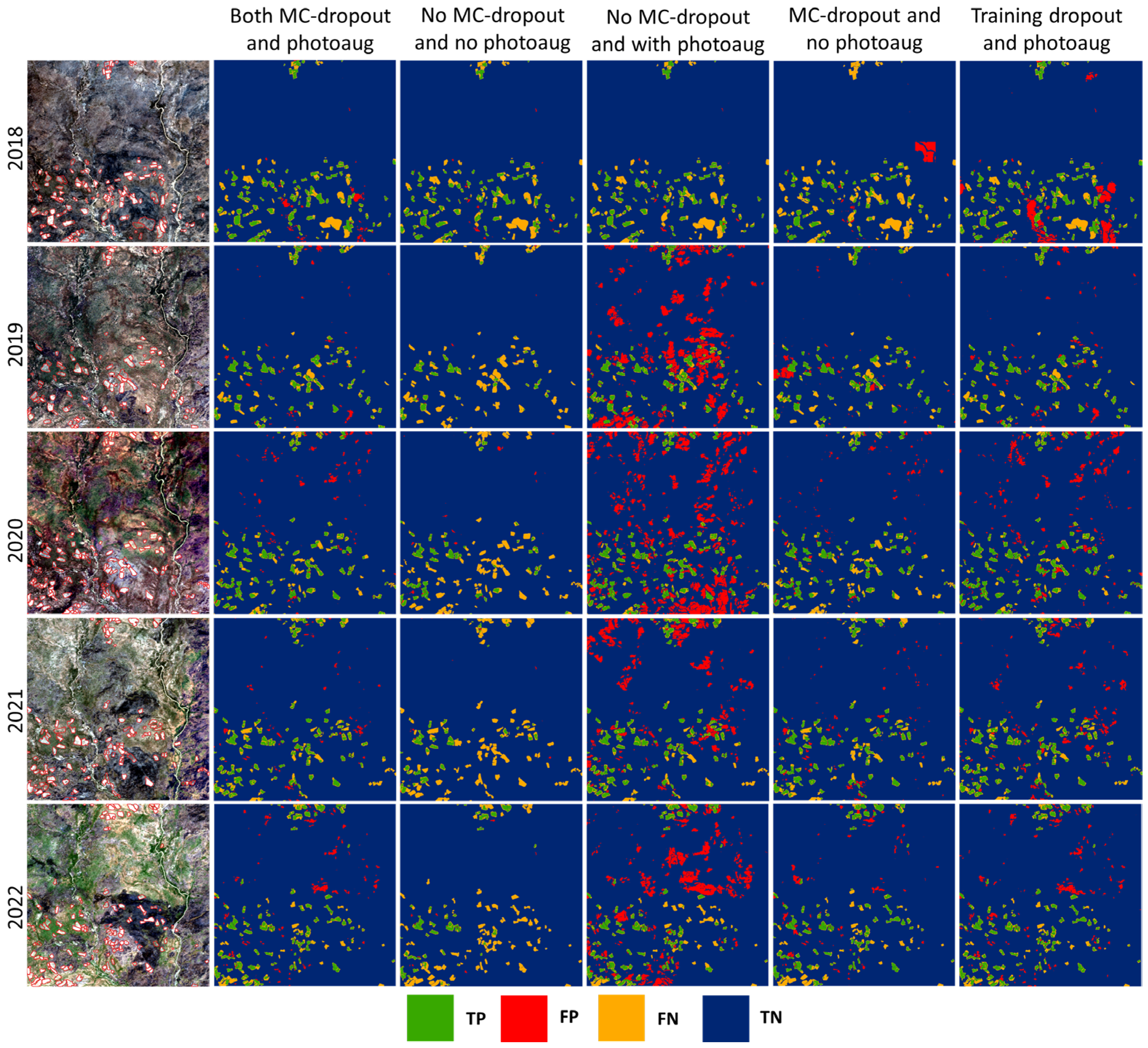
| Experiment | 2018 | 2019 | 2020 | 2021 | 2022 | Across All Years | |
|---|---|---|---|---|---|---|---|
| No MC-dropout, no photoaug. | IoU | 51.71% | 23.83% | 11.73% | 17.70% | 23.42% | 25.41% |
| F1 | 68.17% | 38.49% | 21.01% | 30.08% | 37.96% | 40.52% | |
| MC-dropout, no photoaug. | IoU | 53.38% (44.71) | 39.01% (18.23) | 24.78% (8.12) | 33.07% (14.96) | 41.09% (18.82) | 38.45% (20.75) |
| F1 | 69.60% (61.79) | 56.12% (30.84) | 39.72% (15.03) | 49.70% (26.03) | 58.24% (31.68) | 55.54% (34.37) | |
| No MC-dropout, photoaug. | IoU | 54.39% | 32.23% | 28.11% | 31.13% | 33.29% | 34.03% |
| F1 | 70.46% | 48.75% | 43.88% | 47.48% | 49.96% | 50.79% | |
| Only train dropout, photoaug. | IoU | 51.80% | 41.52% | 35.45% | 39.61% | 43.87% | 42.33% |
| F1 | 68.25% | 58.68% | 52.35% | 56.74% | 60.98% | 59.48% | |
| Both MC-dropout, photoaug. | IoU | 51.77% (50.26) | 42.76% (36.08) | 34.02% (25.70) | 41.41% (32.72) | 44.15% (40.0) | 42.84% (36.97) |
| F1 | 68.22% (66.89) | 59.89% (53.02) | 50.77% (40.90) | 58.57% (49.31) | 61.26% (57.1) | 59.99% (53.98) | |
| Both MC-dropout (conventional), photoaug. | IoU | 53.39% | 34.03% | 24.46% | 32.87% | 39.80% | 36.65% |
| F1 | 69.62% | 50.78% | 39.31% | 49.48% | 56.94% | 53.64% |
| Experiments | Precision | Recall | F1-Score | IoU |
|---|---|---|---|---|
| Best model | 74.94% | 50.01% | 59.99% | 42.84% |
| Half capacity (width) | 75.73% | 48.88% | 59.41% | 42.26% |
| TFL + global weight | 81.80% | 32.49% | 46.51% | 30.30% |
| CE + local weight | 67.88% | 26.33% | 37.94% | 23.41% |
| Histogram matching | 58.47% | 55.13% | 56.75% | 39.62% |
| Tile ID | Model | Category | Precision | Recall | F1-Score | IoU |
|---|---|---|---|---|---|---|
| 487103 | With MC-dropout, photoaug. | Persistent crop | 87.69% | 29.26% | 43.87% | 28.10% |
| Persistent non-crop | 93.82% | 96.75% | 95.26% | 90.95% | ||
| All categories and their subcategories | 23.63% | 17.18% | 19% | 12.05% | ||
| W/O MC-dropout, photoaug. | Persistent crop | 93.59% | 11.69% | 20.78% | 11.60% | |
| Persistent non-crop | 91.50% | 99.58% | 95.37% | 91.14% | ||
| All categories and their subcategories | 15.76% | 7.09% | 9.87% | 5.93% | ||
| 513254 | With MC-dropout, photoaug. | Persistent crop | 81.39% | 21.95% | 34.58% | 20.90% |
| Persistent non-crop | 89.51% | 97.43% | 93.30% | 87.45% | ||
| All categories and their subcategories | 19.22% | 13.89% | 14.62% | 9.18% | ||
| W/O MC-dropout, photoaug. | Persistent crop | 0 | 0 | 0 | 0 | |
| Persistent non-crop | 85.30% | 99.76% | 91.97% | 85.13% | ||
| All categories and their subcategories | 11.45% | 5.23% | 9.32% | 3.39% | ||
| 513911 | With MC-dropout, photoaug. | Persistent crop | 79.53% | 17.62% | 28.84% | 16.85% |
| Persistent non-crop | 63.35% | 94.76% | 75.93% | 61.20% | ||
| All categories and their subcategories | 29.98% | 18.68% | 21.23% | 12.55% | ||
| W/O MC-dropout, photoaug. | Persistent crop | 89.35% | 3.01% | 5.82% | 3% | |
| Persistent non-crop | 51.45% | 96.41% | 67.09% | 50.48% | ||
| All categories and their subcategories | 22.64% | 6.79% | 6.62% | 3.83% | ||
| 539416 | With MC-dropout, photoaug. | Persistent crop | 72.65% | 15.52% | 25.57% | 14.66% |
| Persistent non-crop | 82.08% | 81.75% | 81.92% | 69.38% | ||
| All categories and their subcategories | 17.5% | 13.20% | 13.14% | 7.91% | ||
| W/O MC-dropout, photoaug. | Persistent crop | 63.62% | 19.97% | 30.40% | 17.93% | |
| Persistent non-crop | 79.21% | 60.57% | 68.65% | 52.26% | ||
| All categories and their subcategories | 17.47% | 13.82% | 13.47% | 7.78% | ||
| Overall | With MC-dropout, photoaug. | Persistent crop | 79.85% | 19.72% | 31.63% | 18.78% |
| Persistent non-crop | 84.17% | 93.06% | 88.39% | 79.20% | ||
| All categories and their subcategories | 24.21% | 16.92% | 18.67% | 11.30% | ||
| W/O MC-dropout, photoaug. | Persistent crop | 70.25% | 8.17% | 14.63% | 7.89% | |
| Persistent non-crop | 78.35% | 89.81% | 83.96% | 71.95% | ||
| All categories and their subcategories | 17.18% | 8.75% | 9.31% | 5.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khallaghi, S.; Abedi, R.; Abou Ali, H.; Alemohammad, H.; Dziedzorm Asipunu, M.; Alatise, I.; Ha, N.; Luo, B.; Mai, C.; Song, L.; et al. Generalization Enhancement Strategies to Enable Cross-Year Cropland Mapping with Convolutional Neural Networks Trained Using Historical Samples. Remote Sens. 2025, 17, 474. https://doi.org/10.3390/rs17030474
Khallaghi S, Abedi R, Abou Ali H, Alemohammad H, Dziedzorm Asipunu M, Alatise I, Ha N, Luo B, Mai C, Song L, et al. Generalization Enhancement Strategies to Enable Cross-Year Cropland Mapping with Convolutional Neural Networks Trained Using Historical Samples. Remote Sensing. 2025; 17(3):474. https://doi.org/10.3390/rs17030474
Chicago/Turabian StyleKhallaghi, Sam, Rahebeh Abedi, Hanan Abou Ali, Hamed Alemohammad, Mary Dziedzorm Asipunu, Ismail Alatise, Nguyen Ha, Boka Luo, Cat Mai, Lei Song, and et al. 2025. "Generalization Enhancement Strategies to Enable Cross-Year Cropland Mapping with Convolutional Neural Networks Trained Using Historical Samples" Remote Sensing 17, no. 3: 474. https://doi.org/10.3390/rs17030474
APA StyleKhallaghi, S., Abedi, R., Abou Ali, H., Alemohammad, H., Dziedzorm Asipunu, M., Alatise, I., Ha, N., Luo, B., Mai, C., Song, L., Wussah, A. O., Xiong, S., Yao, Y.-T., Zhang, Q., & Estes, L. D. (2025). Generalization Enhancement Strategies to Enable Cross-Year Cropland Mapping with Convolutional Neural Networks Trained Using Historical Samples. Remote Sensing, 17(3), 474. https://doi.org/10.3390/rs17030474






