A Self-Supervised Feature Point Detection Method for ISAR Images of Space Targets

Abstract

Feature point detection in inverse synthetic aperture radar (ISAR) images of space targets is the foundation for tasks such as analyzing space target motion intent and predicting on-orbit status. Traditional feature point detection methods perform poorly when confronted with the low texture and uneven brightness characteristics of ISAR images. Due to the nonlinear mapping capabilities, neural networks can effectively learn features from ISAR images of space targets, providing new ideas for feature point detection. However, the scarcity of labeled ISAR image data for space targets presents a challenge for research. To address the issue, this paper introduces a self-supervised feature point detection method (SFPD), which can accurately detect the positions of feature points in ISAR images of space targets without true feature point positions during the training process. Firstly, this paper simulates an ISAR primitive dataset and uses it to train the proposed basic feature point detection model. Subsequently, the basic feature point detection model and affine transformation are utilized to label pseudo-ground truth for ISAR images of space targets. Eventually, the labeled ISAR image dataset is used to train SFPD. Therefore, SFPD can be trained without requiring ground truth for the ISAR image dataset. The experiments demonstrate that SFPD has better performance in feature point detection and feature point matching than usual algorithms.

1. Introduction

By observing space targets, ISAR can obtain high-resolution ISAR images. Because ISAR imaging is not affected by observing time and weather conditions, it has mainly become an observation tool in space target surveillance [1,2,3]. In ISAR imaging, the transmitted signal’s bandwidth and the accumulating angles affect the radial resolution and cross-range resolution of ISAR images. ISAR images reflect the scattering characteristics and contour shape of the target on the ISAR imaging plane [4,5,6,7,8,9]. Therefore, feature point detection in ISAR images is critical, as it provides essential technical support for subsequent tasks such as space target pose estimation and 3D reconstruction [10,11].

However, the imaging mechanisms of ISAR images result in characteristics such as weak texture and uneven brightness [12,13,14], all of which increase the difficulty of detecting feature points in ISAR images. Considering these challenges, various ISAR feature extraction methods have emerged, which include two classes. One class of methods applies the improved optical handcrafted features to ISAR images [15,16,17,18]. Di et al. [19] employed the speeded-up robust features (SURF) algorithm to detect and correlate feature points in ISAR images, and designed corresponding experiments. In experiments, the detection and correlation of feature points between adjacent frame images performed well. However, when there was a significant difference in perspective between ISAR images, the performance of the algorithm decreased noticeably. Wang et al. [20] proposed an improved SIFT algorithm combined with the RANSAC algorithm, which enhanced the detection effectiveness of feature points in ISAR images. However, there is a problem with mismatches in the feature point matching process. Shapo et al. [21] presented a feature point detection method based on the constant false alarm rate (CFAR) algorithm. However, the performance of this method will drastically decline when the primary scatterers are absent. Wang et al. [22] proposed a feature point detection and correlation method for ISAR images based on the Kanade–Lucas–Tomasi (KLT) algorithm [23,24]. However, the KLT algorithm assumed that the radar cross-section of each scatterer remained constant, which did not align with the practical situation of ISAR imaging. In summary, ISAR images have significant differences in image quality and texture features compared to optical images. Feature extraction and correlation methods of optical images are not suitable for ISAR images.

The second class of methods utilizes the nonlinear mapping capability of neural networks to extract features from ISAR images [10,25,26,27,28]. By learning complex image feature representations, neural networks can effectively capture detailed information in ISAR images, thereby enhancing the accuracy of feature point detection. In [25], Xie et al. proposed an ISAR image key point extraction network (KPEN), which can detect sail corner points and main body endpoints from ISAR images. The effectiveness of the key point extraction was validated through pose estimation experiments. Wang et al. [10] proposed a multi-scale feature extraction network, which can extract key points from ISAR images, enhancing the reliability of ISAR feature extraction. Zhou et al. [26] proposed a structural key point extraction method for ISAR images based on deep learning. Nevertheless, using neural networks to extract feature points still has some limitations. As indicated above, current research efforts mainly focus on extracting structural key points from ISAR images, without covering all feature points presented in the images. Consequently, these researchers may not be applicable to downstream tasks such as 3D reconstruction. There are two main reasons for this phenomenon. Firstly, ISAR imaging is based on the backscattering of microwaves by the target. It appears as a series of discrete scatterers on the ISAR image, resulting in discontinuous changes in the image grayscale and gradient and a lack of sufficient texture information. Meanwhile, due to the mutual occlusion among target components and the anisotropy of scatterers [29,30], the feature points in ISAR images may exhibit phenomena such as uneven brightness and sudden disappearance, which lead to difficulties in feature point detection. Secondly, using deep learning to detect feature points from ISAR images has some problems. Different from the structural key points of space targets, the feature points in ISAR images do not have clear semantics. The accuracy of the labeling results cannot be guaranteed even with manual labeling. Therefore, traditional supervised neural networks have poor applicability in ISAR image feature point detection.

To solve the aforementioned problems, this paper proposes a self-supervised feature point detection method for ISAR images, demonstrating superior performance. We simulate an ISAR image dataset of space targets containing the pseudo-ground truth of feature points, which is subjected to self-supervised training by the proposed method, without the need for manual labeling. In addition, the proposed method can output the corresponding feature descriptors while detecting feature points from ISAR images, providing support for subsequent tasks such as feature point matching. In general, the proposed method has the following several innovations:

1.

A pseudo-ground truth labeling method for feature points in ISAR images of space targets is proposed. Firstly, a fully convolutional neural network named BasicPoint is trained on the simulated ISAR primitive dataset. All the images in this dataset are simple primitive images, which have no ambiguity in the positions of the feature points. Despite the cross-domain feature differences, BasicPoint also demonstrates good feature point detection performance on the ISAR images of space targets. We combine the affine transformation with BasicPoint to assist it in observing ISAR images of space targets from multiple perspectives and sizes, improve the feature point detection performance, and generate the pseudo-ground truth of feature points.

2.

A feature point detection network named SFPD is proposed, which does not require the feature point truth of ISAR images of space targets during the training stage. It can conduct self-supervised training based on the pseudo-ground truth of feature points labeled by BasicPoint, demonstrating good performance. In addition, we introduce a decoder parameter-sharing mechanism, enabling SFPD to obtain both the locations of feature points in ISAR images and their corresponding feature descriptors. The experiments indicate that the feature point detection performance and the matching performance of this method surpass those of existing approaches.

The remaining content of this paper is organized as follows. Section 2 first introduces the ISAR imaging model. Section 3 introduces the key steps, including the basic feature point detection model, pseudo-ground truth labeling, and the structure of the SFPD model. In Section 4, we present the experimental details, which validate the efficacy of the proposed method. Finally, we conclude this paper in Section 5.

2. ISAR Imaging Model

The distance between the observed target and the radar is extremely large in ISAR imaging, with the target being very small relative to this distance, thus satisfying the far-field condition. Therefore, the electromagnetic waves received from the target can be treated as planar waves. Under this assumption, the space target motion can be decomposed into rotation, translation, and circular motion, as shown in Figure 1. In Figure 1, the space target takes three steps to move from A to C. Firstly, the space target rotates around its geometric center, causing different Doppler effects for each scatter point on the target. Secondly, there is a translational motion from A to B, during which the distance change between each scatter point and the radar is consistent, resulting in a uniform Doppler effect that can be corrected through translational compensation. Finally, from B to C, the space target rotates around the radar center in a circular motion, resulting in no Doppler effect.

Figure 2 depicts the ISAR observation and imaging model, where $O-XYZ$ represents the body coordinate system (BCS) of the space target. The red line stands for the line of sight (LOS) of the radar, which can be expressed as follows:

$$\mathit{r}\left(t\right)={[-cos\varphi \left(t\right)cos\theta \left(t\right),-cos\varphi \left(t\right)sin\theta \left(t\right),-sin\varphi \left(t\right)]}^T$$

(1)

where $\theta \left(t\right)$ and $\varphi \left(t\right)$ represent the azimuth and pitch at the observation time, respectively. $p_k={(x_k,y_k,z_k)}^T$ represents a scatter point on the target, and the distance between $p_k$ and the radar is as follows:

$$r_p\left(t\right)=r_0\left(t\right)+\mathit{r}{\left(t\right)}^T{p}_k$$

(2)

where $r_0\left(t\right)$ is the distance between the target and the radar. Taking the derivative of $r_p\left(t\right)$ yields the instantaneous velocity of $p_k$; then we obtain the following:

$${\dot{r}}_p\left(t\right)={\dot{r}}_0\left(t\right)+\mathit{r}{\left(t\right)}^T{\dot{p}}_k+\dot{\mathit{r}}\left(t\right)p_k$$

(3)

where ${\dot{r}}_p\left(t\right)$ represents the derivative of $r_p\left(t\right)$, and the remaining symbols follow the same logic. In BCS, the position and orientation of the scatter points do not change with the rotation of the target. Therefore, Equation (3) can be rewritten as follows:

$${\dot{r}}_p\left(t\right)={\dot{r}}_0\left(t\right)+{p_k}^T[{\mathit{\omega }}_{\mathrm{radar}}\left(t\right)\times \mathit{r}\left(t\right)]$$

(4)

where ${\mathit{\omega }}_{\mathrm{radar}}\left(t\right)$ denotes the rotational angular velocity of the radar. ${\mathit{\omega }}_{\mathrm{radar}}\left(t\right)$ can be decomposed into ${\mathit{\omega }}_n\left(t\right)$ and ${\mathit{\omega }}_r\left(t\right)$, where ${\mathit{\omega }}_n\left(t\right)$ is perpendicular to $LOS$, and ${\mathit{\omega }}_r\left(t\right)$ is parallel to $LOS$. ${\mathit{\omega }}_r\left(t\right)$ does not affect the computation results. Therefore, Equation (4) can be rewritten as follows:

$$\begin{array}{cc}\hfill {\dot{r}}_p\left(t\right)& ={\dot{r}}_0\left(t\right)+{p_k}^T[{\mathit{\omega }}_n\left(t\right)\times \mathit{r}\left(t\right)]=r_0\left(t\right)+{p_k}^T·{∥{\mathit{\omega }}_n\left(t\right)∥}_2·{\displaystyle \frac{{\mathit{\omega }}_n\left(t\right)\times \mathit{r}\left(t\right)}{{∥{\mathit{\omega }}_n\left(t\right)\times \mathit{r}\left(t\right)∥}_2}}\hfill \end{array}$$

(5)

Combining the above analysis, we can obtain the imaging plane, as follows:

$$\left\{\begin{array}{c}{\mathit{\rho }}_r=\mathit{r}\left(t\right)\hfill \\ {\mathit{\rho }}_a={\displaystyle \frac{{\mathit{\omega }}_n\left(t\right)\times \mathit{r}\left(t\right)}{{∥{\mathit{\omega }}_n\left(t\right)\times \mathit{r}\left(t\right)∥}_2}}\hfill \end{array}\right.$$

(6)

where ${\mathit{\rho }}_a$ denotes the projection vector in the cross-range direction, ${\mathit{\rho }}_r$ denotes the projection vector in the range direction, and ${\mathit{\omega }}_n\left(t\right)$ is the normal vector of the imaging plane. Therefore, the projection coordinates of $p_k$ can be expressed as follows:

$$\left[\begin{array}{c}{r}_k\\ a_k\end{array}\right]=\left[\begin{array}{c}{\mathit{\rho }}_r^T\\ {\mathit{\rho }}_a^T\end{array}\right]·p_k=\left[\begin{array}{c}{r}_p\left(t\right)-r_0\left(t\right)\\ \\ {\displaystyle \frac{{\dot{r}}_p\left(t\right)-{\dot{r}}_0\left(t\right)}{{∥{\mathit{\omega }}_n\left(t\right)∥}_2}}\end{array}\right]·p_k$$

(7)

Figure 3 depicts the projection mechanism of the ISAR image.

3. Self-Supervised Feature Point Detection Method

As shown in Figure 4, the proposed method can be divided into three parts. Firstly, the basic feature point detection model named BasicPoint is trained on the space target primitive dataset. Subsequently, we label the pseudo-ground truth of the ISAR image dataset of space targets by combining affine transformation with BasicPoint. Finally, the proposed fully convolutional neural network is trained on the labeled ISAR image dataset.

3.1. BasicPoint

It is worth noting that there is currently no large-scale dataset with labeled feature points for ISAR images of space targets. To train BasicPoint, we establish an ISAR primitive image dataset. Firstly, we generate a diverse set of space target primitives such as cylinders, cubes, and planes. Subsequently, we use physical optics methods [31] to simulate these primitives, generating their corresponding ISAR images, which collectively constitute the ISAR primitive image dataset. To ensure that the model trained on the ISAR primitive image dataset possesses strong data generalization capabilities and can learn feature representations of targets of various sizes, we design and introduce multi-scale space target primitives. Additionally, we label the ground truth feature point locations in the ISAR primitive images during the simulation process. Figure 5 shows examples of ISAR primitive images.

After generating the ISAR primitive image dataset, we train BasicPoint on this dataset. BasicPoint can efficiently detect feature point positions in ISAR-primitive images. As shown in Figure 6, BasicPoint only accepts single-channel images as input. During training, it is necessary to convert the images from the ISAR primitive dataset into grayscale images before feeding them into BasicPoint. Traditional dense prediction networks typically adopt an encoder–decoder structure, where the encoder reduces the dimensions of the data using convolutional or pooling operations, and then the decoder restores the data to their original dimension through upsampling operations. However, upsampling operations significantly increase computational complexity, which is detrimental to model training. Therefore, BasicPoint employs an explicit decoder structure to restore data dimensions, reducing the computational complexity of the model. Firstly, BasicPoint uses the encoder with a VGG [32] structure, encoding an ISAR primitive image of size $M\times N$ into a feature map of size $M/8\times N/8$. Each point on the feature map contains 65 channels. The feature map is then converted into probabilities through a softmax layer.

The interpretation of the channels within the feature map is illustrated in Figure 7. The first 64 channels of the feature map correspond to the probability of each pixel being a feature point within an 8 × 8 local pixel region of the input image. The 65th channel is a dropout channel, indicating that no feature point is detected in that local pixel area. To restore the data to its original dimensions, BasicPoint discards the 65th channel in the feature map. Then, through a reshape layer, the $64\times M/8\times N/8$ feature map is transformed into an $M\times N$ feature map, which represents the probability distribution of the feature point in the input image. The feature map is displayed as a heatmap, where detected feature points exhibit pronounced red characteristics on the feature point response image, forming a stark contrast against the surrounding points. BasicPoint is a fully convolutional network using 3 × 3 convolution kernels, with batch normalization employed for data normalization. The final fully connected convolutional layer uses 1 × 1 convolution kernels. In terms of the loss function, BasicPoint employs cross-entropy as its loss function, as follows:

$${\mathcal{L}}_b=-{\displaystyle \frac{1}{MN}}\sum _{m=1}^M\sum _{n=1}^N{p}_{m,n}log{q}_{m,n}$$

(8)

where $p_{m,n}$ represents the ground truth probability distribution of feature points, $q_{m,n}$ denotes the feature point probability distribution detected by BasicPoint, and M, N are the dimensions of the input image.

3.2. Pseudo-Ground Truth Labeling

To provide training data for SFPD, we use BasicPoint to label pseudo-ground truth for the ISAR image dataset of space targets. Since the image features of ISAR primitive images and ISAR images of space targets are not completely the same, it is difficult for BasicPoint to detect all feature points from ISAR images of space targets, which has an adverse effect on the pseudo-ground truth labeling. Consequently, it affects the training of SFPD, leading to suboptimal feature point detection performance. To address this issue, we combine BasicPoint and the affine transformation [33] to label the pseudo-ground truth of ISAR images of space targets. Affine transformation is a type of geometric transformation, composed of linear transformation and translation, including operations such as translation, rotation, and scaling. Applying affine transformation to ISAR images of space targets multiple times can help BasicPoint see the image from many different scales and perspectives. It is worth noting that affine transformation does not change the original geometric relationships within the image, which means that the positions of feature points in the original image can be calculated through inverse affine transformation. Subsequently, we can obtain the pseudo-ground truth of ISAR images of space targets by aggregating these feature points, as shown in Figure 8. In summary, combining affine transformation to label the pseudo-ground truth of ISAR images of space targets has the following two advantages. On the one hand, performing pseudo-ground truth labeling on the image after the affine transformation can effectively avoid the omission of feature points. On the other hand, the pseudo-ground truth labeling of a single ISAR image may contain misdetected feature points, which can be effectively removed during the aggregation process.

Assuming $f\left(·\right)$ is the BasicPoint detection function, the input of $f\left(·\right)$ is the ISAR image, and the output is the feature point set, which can be represented as follows:

$$P=f\left(I\right)$$

(9)

Applying an affine transformation to the input image, Equation (9) can be rewritten as follows:

$$\mathit{A}P=f\left(\mathit{A}\left(I\right)\right)$$

(10)

where $\mathit{A}$ represents the affine transformation matrix, and $\mathit{A}\left(I\right)$ represents the ISAR image after the affine transformation. By left-multiplying both sides of Equation (10) by ${\mathit{A}}^{-1}$, we obtain an alternative representation of P, as follows:

$$P={\mathit{A}}^{-1}f\left(\mathit{A}\left(I\right)\right)$$

(11)

therefore, by accumulating and summing over a large number of images after the affine transformation, we can obtain a more effective feature point detection function, as follows:

$$F\left(I\right)={\displaystyle \frac{1}{N_a}}\sum _{i=1}^{N_a}{\mathit{A}}_i^{-1}f\left({\mathit{A}}_i\left(I\right)\right)$$

(12)

where $N_a$ denotes the number of affine transformations, and ${\mathit{A}}_i$ represents the affine transformation matrix for the i-th transformation.

It is worth noting that not all 3 × 3 matrices are suitable for use as affine transformation matrices. To select appropriate affine transformation matrices, we decompose the affine transformation, performing simple transformations such as rotation, translation, and scaling within predetermined ranges. These simple transformations are then combined with the initial cropping center, as shown in Figure 9.

3.3. SFPD

This section introduces the proposed self-supervised feature point detection (SFPD) model. As shown in Figure 10, SFPD has a shared encoder and two separate decoders, which are adapted for different downstream tasks. Traditional feature point detection algorithms typically follow a pipelined process, where feature point detection is first performed followed by the generation of corresponding descriptors. However, these algorithms suffer from insufficient decoupling between tasks during processing. In contrast, SFPD does not suffer from this problem. The SFPD design allows the two decoders to share most of the network parameters.

3.3.1. Shared Encoder

The SFPD employs an encoder with a VGG [32] architecture to reduce the data dimensions. The size of the convolutional kernels that the shared encoder utilizes is $3\times 3$, and three $2\times 2$ downsampling pooling layers are used to reduce the input data dimensions from $H\times W$ to $H/8\times W/8$. In summary, the encoder maps $I\in {\mathbb{R}}^{H\times W}$ to $\mathcal{T}\in {\mathbb{R}}^{8/H\times 8/W\times 128}$ with smaller dimensions but greater channel depth.

3.3.2. Decoder

The feature point detection decoder outputs the probability distribution of the feature point in the ISAR image. Typical network architectures often reduce the data dimensions at the encoder and then restore the data dimensions through the decoder. However, the upsampling operations in traditional decoders can significantly increase the computational load, affecting the network’s convergence speed. Therefore, the feature point detection decoder adopts the same architecture as BasicPoint. The 65 channels in the input tensor of the feature point detection decoder are the same as those in BasicPoint, and will not be detailed further here. Then, the final channel is discarded through the softmax layer, and the tensor with dimensions $H/8\times W/8\times 64$ is reshaped into a feature point probability image with dimensions $H\times W$.

The input of the descriptor decoder is $\mathcal{D}\in {\mathbb{R}}^{8/H\times 8/W\times D}$, and the output is a descriptor with dimensions $H\times W\times D$. To reduce computational complexity, the feature point descriptor decoder first uses a UCN [34] network to generate sparse descriptors for every 8 pixels. Then, bicubic interpolation and L2 normalization are applied to obtain unit-length descriptors for each pixel.

3.3.3. Loss Function

The loss function of SFPD is composed of the loss functions of the detection decoder and descriptor decoder. These two different loss functions are balanced by a weight coefficient $\lambda$, formulated as follows:

$$\mathcal{L}={\mathcal{L}}_s+\lambda {\mathcal{L}}_d$$

(13)

where ${\mathcal{L}}_s$ is the loss function of the detection decoder as follows:

$$\begin{array}{cc}& {\mathcal{L}}_s(\mathcal{X},{\mathcal{X}}^{{⠀}^{\prime }};Y,Y^{{⠀}^{\prime }})={\displaystyle \frac{64}{H\times W}}\sum _{h=1,w=1}^{H/8,W/8}{l}_s({\mathbf{x}}_{h,w};y_{h,w})+l_s({\mathbf{x}}_{h,w}^{{⠀}^{\prime }};y_{h,w}^{{⠀}^{\prime }})\hfill \end{array}$$

(14)

where $\mathcal{X}$ is the ISAR image, ${\mathcal{X}}^{{⠀}^{\prime }}$ is the image obtained by applying an affine transformation to $\mathcal{X}$, and Y and $Y^{{⠀}^{\prime }}$ are the pseudo-ground truths for $\mathcal{X}$ and ${\mathcal{X}}^{{⠀}^{\prime }}$, respectively. $l_s(·)$ represents the cross-entropy loss, which can be expressed as follows:

$$l_s({\mathbf{x}}_{hw};y)=-log\left({\displaystyle \frac{exp\left({\mathbf{x}}_{h,w,y}\right)}{{\displaystyle \sum _{k=1}^{65}}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathbf{x}}_{h,w,k}\right)}}\right)$$

(15)

where ${\mathbf{x}}_{h,w}\in \mathcal{X}$, $y_{h,w}\in Y$.

The loss ${\mathcal{L}}_d$ of the descriptor decoder is defined as follows:

$$\begin{array}{cc}& {\mathcal{L}}_d(\mathcal{D},{\mathcal{D}}^{{⠀}^{\prime }};S)={\left({\displaystyle \frac{64}{H\times W}}\right)}^2\times \sum _{h=1,w=1}^{H/8,W/8}\sum _{h^{{⠀}^{\prime }}=1,w^{{⠀}^{\prime }}=1}^{H/8,W/8}{l}_d\left({\mathit{d}}_{h,w},{\mathit{d}}_{h^{{⠀}^{\prime }},w^{{⠀}^{\prime }}}^{{⠀}^{\prime }};s\left(h,h^{{⠀}^{\prime }},w,w^{{⠀}^{\prime }}\right)\right)\hfill \end{array}$$

(16)

where $\mathcal{D}$ and ${\mathcal{D}}^{{⠀}^{\prime }}$ are the descriptors of the input image pair, ${\mathit{d}}_{h,w}\in \mathcal{D}$, ${\mathit{d}}_{h^{{⠀}^{\prime }},w^{{⠀}^{\prime }}}^{{⠀}^{\prime }}\in {\mathcal{D}}^{{⠀}^{\prime }}$, and S represents the correspondence between the image pair. $l_d(·)$ is the hinge loss, which can be represented as follows:

$$\begin{array}{cc}\hfill l_d\left(\mathit{d},{\mathit{d}}^{{⠀}^{\prime }};s\right)& ={\lambda }_d\times s\times max\left(0,m_p-{\mathit{d}}^T{\mathit{d}}^{{⠀}^{\prime }}\right)+(1-s)\times max\left(0,{\mathit{d}}^T{\mathit{d}}^{{⠀}^{\prime }}-m_n\right)\hfill \end{array}$$

(17)

where ${\lambda }_d$ is used to balance samples, and $m_p$ and $m_n$ represent the pivotal losses for the positive and negative margins of the network, respectively. s represents the correspondence between descriptors, utilized to determine whether $\mathit{d}$ and ${\mathit{d}}^{{⠀}^{\prime }}$ are associated as follows:

$$s\left(h,h^{\prime },w,w^{\prime }\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{otherwise}\hfill \\ 1,\hfill & ∥\mathit{A}{p}_{h,w}-p_{h^{\prime },w^{\prime }}∥\le 6\hfill \end{array}\right.$$

(18)

where $p_{h,w}$ and $p_{h^{\prime },w^{\prime }}$ are the pixel grid center coordinates corresponding to point $(h,w)$ and point $(h^{\prime },w^{\prime })$, respectively. $\mathit{A}{p}_{h,w}$ represents the coordinates of $p_{h,w}$ after the affine transformation $\mathit{A}$. If the Euclidean distance between $\mathit{A}{p}_{h,w}$ and $p_{h^{\prime },w^{\prime }}$ is less than 6 pixels, the two points are considered to be associated.

4. Experiment Analysis

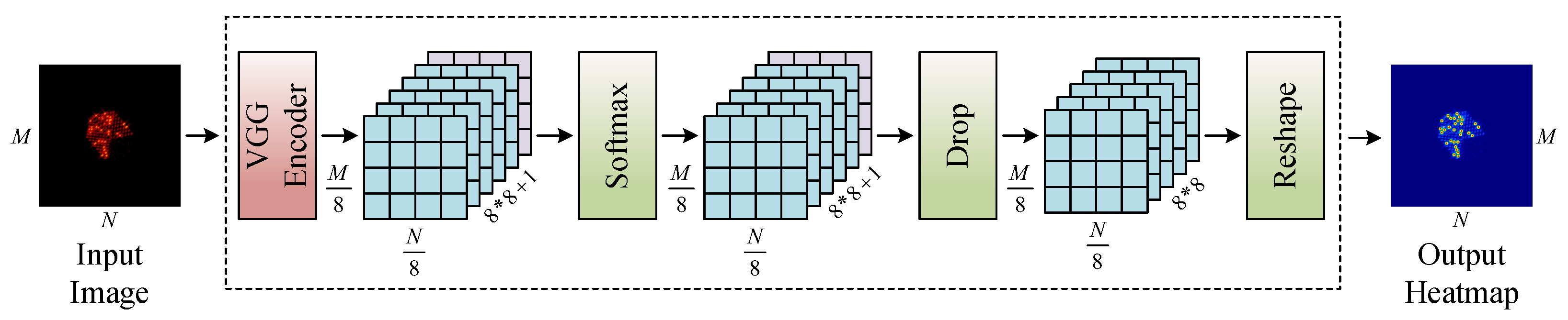
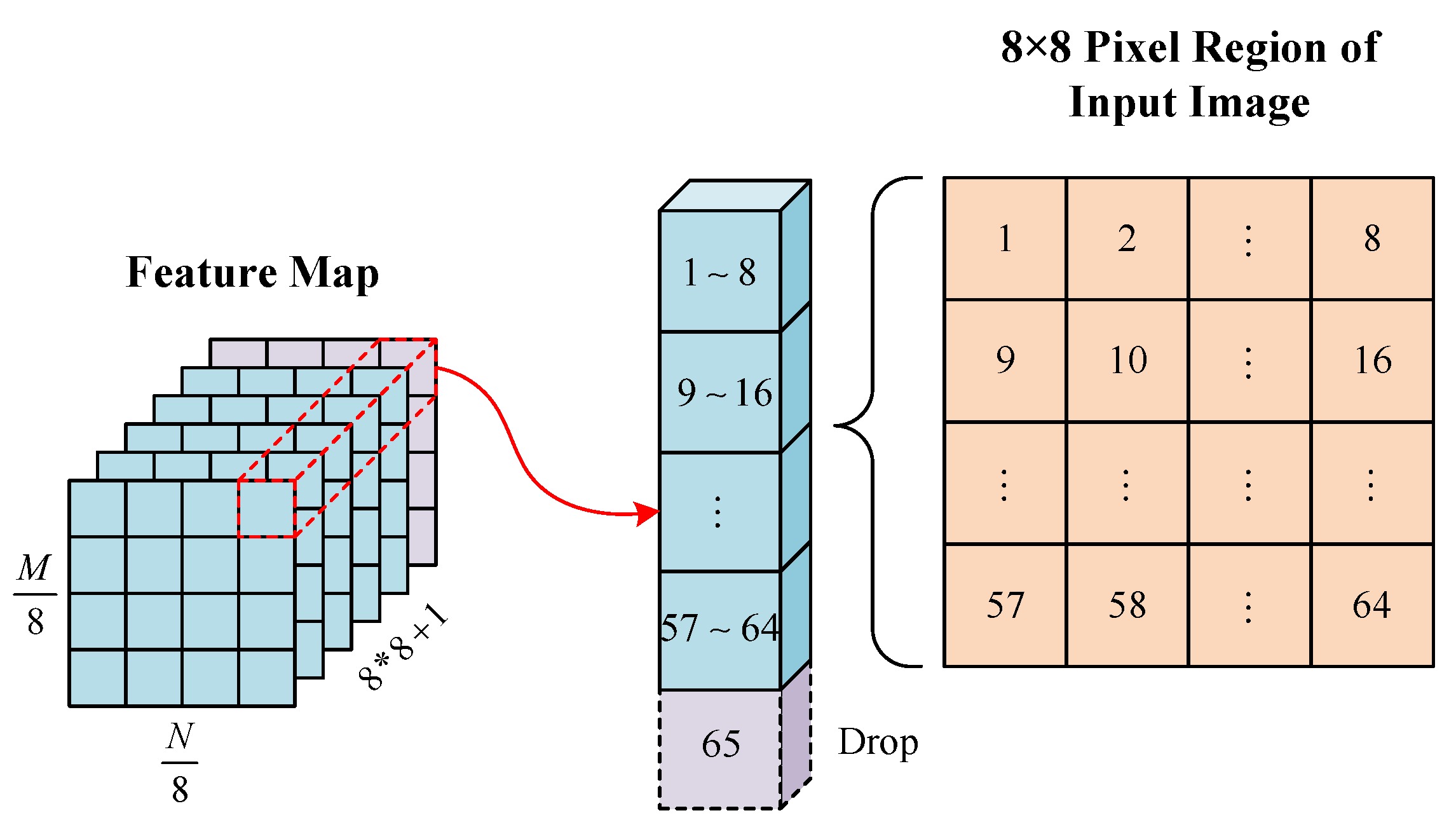
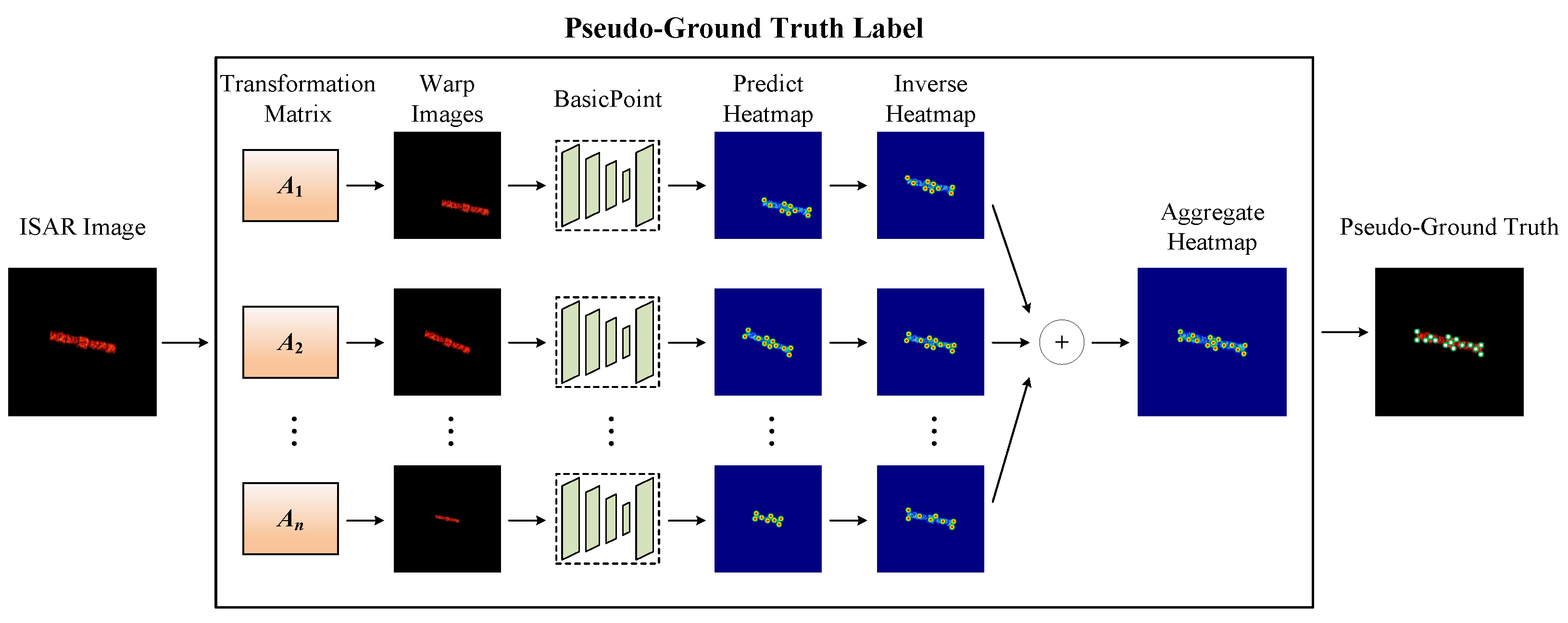
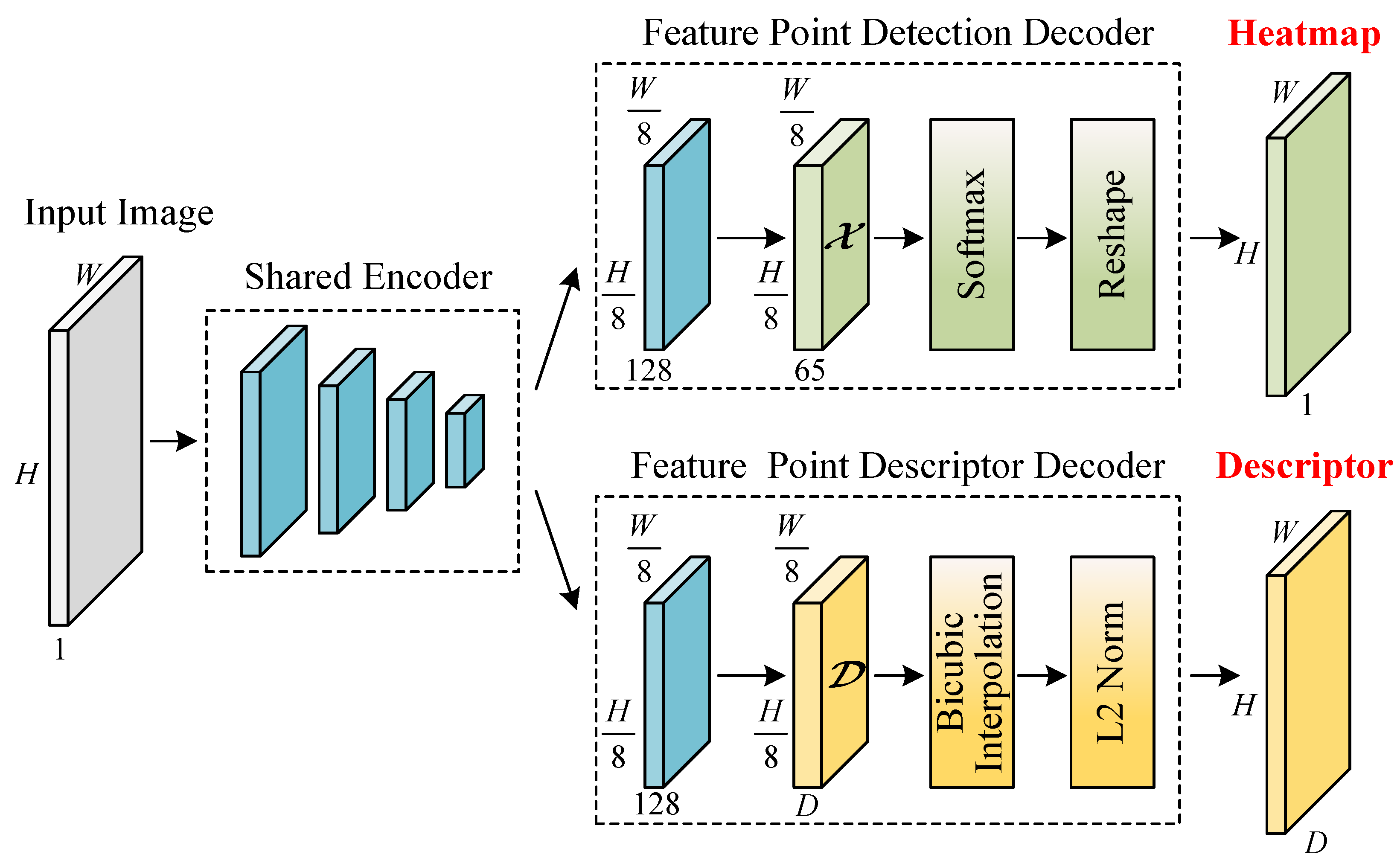
The experiment analysis can be divided into the following three parts: In the first part, we simulate a real on-orbit scenario of space targets to obtain the corresponding ISAR images. The second part analyzes the feature point detection performance. Finally, we examine the feature point matching performance in the third part.

4.1. Experiment Configuration

To simulate ISAR images, we set the satellite orbit to a commonly used sun-synchronous orbit for remote sensing satellites, with the orbit parameters shown in

Table 1. Orbital parameters of the target.

Orbital Eccentricity	Argument of Periapsis (°)	Orbital Inclination (°)	Ascending Node (°)	Average Velocity (°/s)
$1.721\times {10}^{-4}$	14.191	98.717	292.785	$5.916\times {10}^{-2}$

. The observing radar is positioned at 114 degrees east longitude and 30 degrees north latitude, with an operating bandwidth of 1.8 GHz. The observation scenario is shown in Figure 11a. Subsequently, based on this observation scenario, we simulate the wideband echoes of the target within the imaging interval using the physical optics method. After applying pulse compression and translational compensation to the wideband echoes of the target, we perform ISAR imaging using the range-Doppler algorithm. As shown in Figure 11b, We choose the Chang’e-I satellite as the target. The satellite body size of Chang’e-I is 2 m × 1.72 m × 2.2 m, and the maximum span of the solar panel is 18.1 m. To calculate the electromagnetic echoes using the physical optics method, we set the material of these models as the perfect electric conductor (PEC) and dissect these models into uniform triangular facets. Meanwhile, inspired by reference [35], we add surface roughness to the electromagnetic grid model to make the properties of the simulated images closer to those of the real ISAR data. By adding a certain perturbation to the coordinates of the subdivided triangular facets of the target, the normal vectors of these facets are slightly offset, thus obtaining a target surface with undulations. Therefore, the simulated ISAR images can be made more continuous and closer to the real ISAR data. Based on the aforementioned setup, we simulate 100 ISAR images within the imaging interval. According to the orbital motion parameters, cross-range scaling is performed on the simulated images. After cross-range scaling, the range and cross-range resolutions are both 0.08 m. Figure 12 presents the ISAR simulated images at two different time segments.

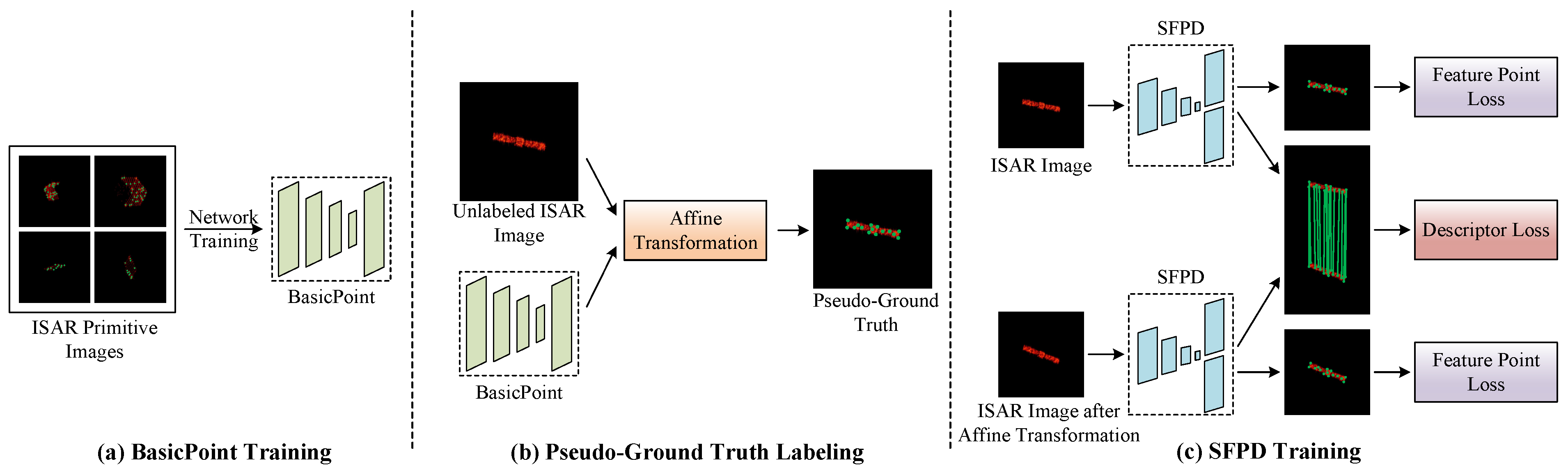
To train BasicPoint, we randomly initialize the space target primitive within the observable size and simulate the space target primitive image dataset, yielding 20,000 ISAR primitive images. In the experiment, these ISAR primitive images are divided into the training and test sets at a ratio of 8:2.

Table 2. The training parameters of BasicPoint.

Epoch	Optimizer	Batch Size	Learning Rate
100	Adam [36]	64	0.001

shows the training parameters.

To obtain the ISAR images, we utilize the physical optics algorithm and the range-Doppler algorithm to simulate 10,000 ISAR images of Chang’e-I spacecraft in different attitudes within the aforementioned observation scenario. Subsequently, we use BasicPoint to label the pseudo-ground truth of these ISAR images. In the same way, these ISAR images are divided into training and test sets at a ratio of 8:2. During the training process of SFPD, the hyperparameters of the loss function play a crucial role in optimizing performance. The key hyperparameters of the loss function used in the training process are shown in

Table 3. The hyperparameters of the loss function used in SFPD.

$\mathit{\lambda }$	${\mathit{\lambda }}_{\mathit{d}}$	${\mathit{m}}_{\mathit{p}}$	${\mathit{m}}_{\mathit{n}}$
1.0	800	1.0	0.5

, which are determined through a series of experiments. Furthermore, the training parameters of SFPD are shown in

Table 4. The training parameters of SFPD.

Epoch	Optimizer	Batch Size	Learning Rate
200	Adam [36]	64	0.0001

. The experimental platform consists of an i9-13900K CPU and two 4090 GPUs (24 GB), with the operating system being Ubuntu 20.04.

4.2. Feature Point Detection

To evaluate the feature point detection performance of SFPD, we use the number of correctly detected feature points and the feature point detection accuracy as evaluation metrics. If the Euclidean distance between the detected feature point and the ground truth is less than 2 pixels, this feature point can be regarded as correctly detected. Therefore, the number of correctly detected feature points can reflect the effectiveness of feature point detection, which can be represented as follows:

$$\begin{array}{c}\hfill N_{\mathrm{correct}}={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}\left\{\begin{array}{cc}1,& ∥p_i-g_j∥\le 2\\ 0,& \mathrm{otherwise}\end{array}\right.\end{array}$$

(19)

where $p_i$ is the ith detected feature point, and $g_j$ is the ground truth of the jth feature point. The feature point detection accuracy can reflect the reliability of feature point detection, and its equation can be represented as the ratio of $N_{\mathrm{correct}}$ to $N_{\mathrm{all}}$, where $N_{\mathrm{all}}$ is the number of all detected feature points.

$$\begin{array}{c}\hfill P_{\mathrm{accuracy}}={\displaystyle \frac{N_{\mathrm{correct}}}{N_{\mathrm{all}}}}\end{array}$$

(20)

The hyperparameters involved in the proposed method influence the feature point detection significantly. To determine the optimal values of the hyperparameters, we test the proposed method under different experimental settings and select the best-performing hyperparameters. As previously mentioned, the number of affine transformations $N_a$ affects the pseudo-ground truth labeling, which in turn impacts the training performance of SFPD. 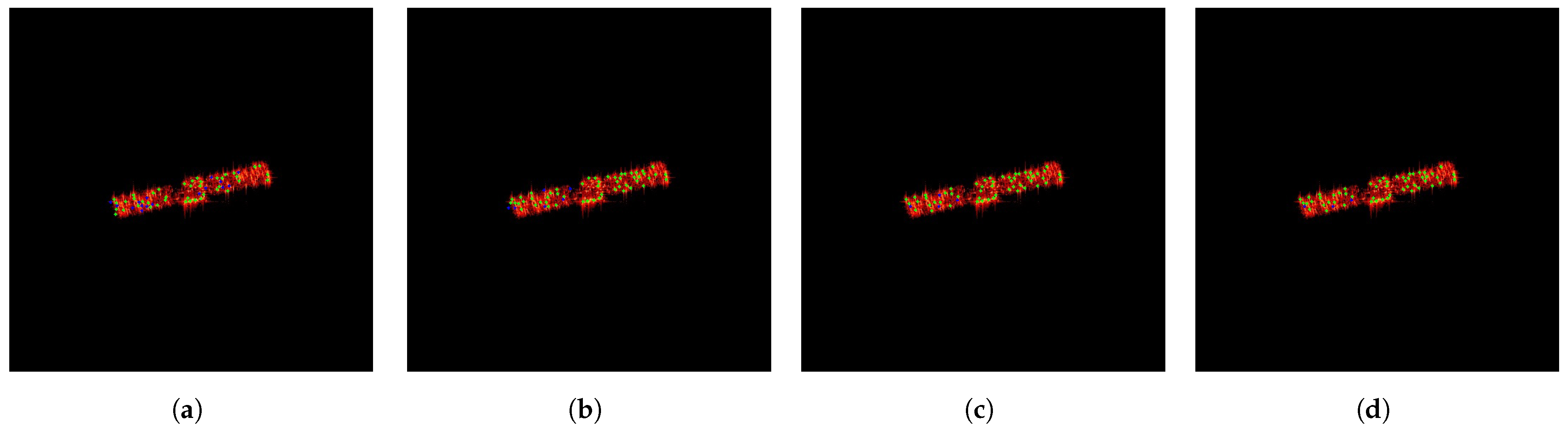Figure 13 shows an example of pseudo-ground truth labeling for ISAR images of space targets under different numbers of affine transformations. In the figure, green points represent correctly labeled feature points, while blue points represent incorrectly labeled feature points. As seen in Figure 13, the quality of the pseudo-ground truth labeling gradually improves as the number of affine transformations increases. As the pseudo-ground truth labeling becomes more accurate, SFPD can learn more precise feature mapping relationships. Its convolutional layers can better capture the image features related to the feature points, while the pooling layers can more effectively retain the key information in the image. Therefore, $N_a$ is an important hyperparameter for SFPD.

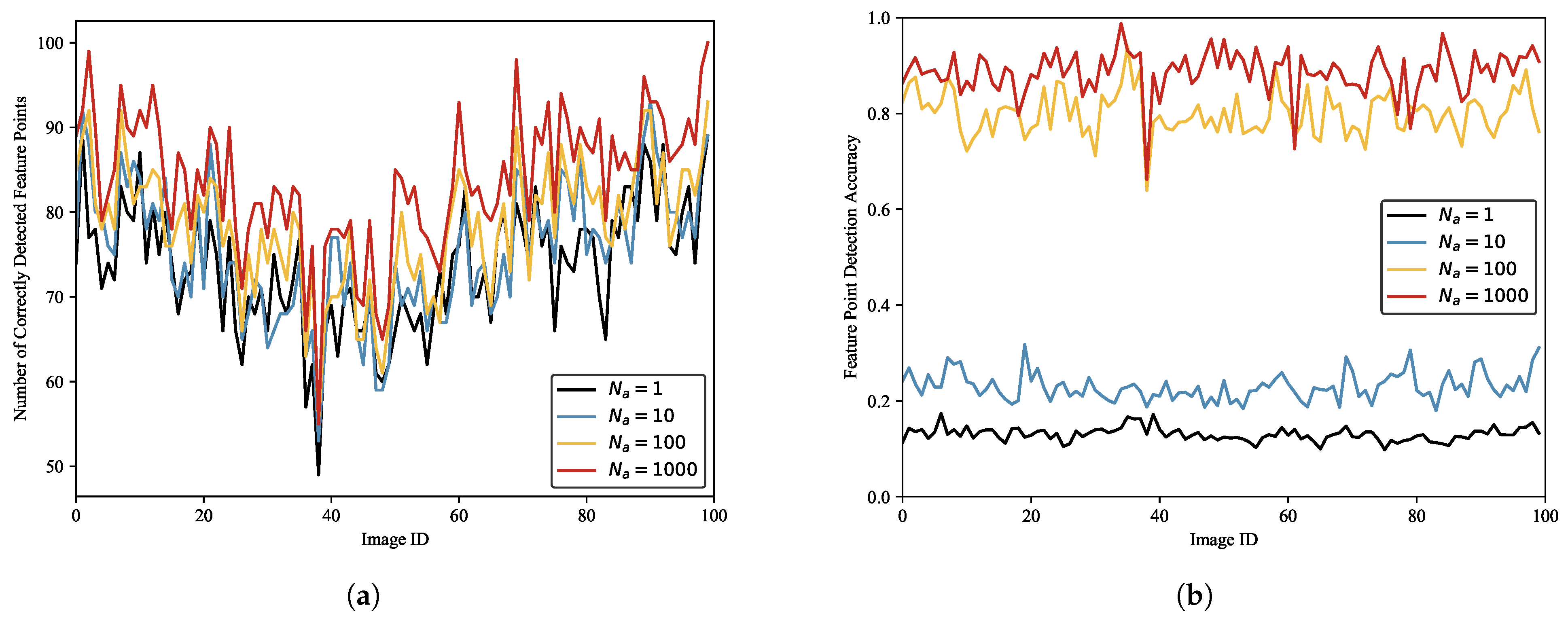
We label the ISAR image dataset of space targets using different numbers of affine transformations and train SFPD with these datasets. Then, we use these models to detect 100 randomly selected test images. Figure 14 depicts the results. As shown in Figure 14, the number of correctly detected feature points increases with the number of affine transformations. Figure 14b presents the detection accuracy under different numbers of affine transformations. Similarly, the feature point detection accuracy also increases with the number of affine transformations. The statistical results are presented in

Table 5. The statistical results of the feature point detection performance under different numbers of affine transformations.

	${\mathit{N}}_{\mathit{a}}=1$	${\mathit{N}}_{\mathit{a}}=10$	${\mathit{N}}_{\mathit{a}}=100$	${\mathit{N}}_{\mathit{a}}=1000$
Number of correctly detected feature points	73.52	75.25	78.27	83.70
Feature point detection accuracy	0.1302	0.2301	0.8004	0.8865

. It can be observed that when $N_a=1$ and $N_a=10$, the detection accuracy of SFPD is only around 0.15. When $N_a=100$ and $N_a=1000$, the detection accuracy is around 0.8. Therefore, the detection performance of SFPD is better when $N_a=100$ and $N_a=1000$. This is because when labeling the pseudo-ground truth of the ISAR image dataset of space targets, too few affine transformations can lead to errors in the pseudo-ground truth, affecting the subsequent training of SFPD. When the number of affine transformations exceeds 100, the labeled results of the pseudo-ground truth tend to stabilize, allowing SFPD to extract the correct feature point positions in the ISAR images of space targets.

In ISAR images of space targets, feature points are manifested as pixel clusters rather than individual discrete pixels. Image features within the same pixel cluster exhibit high consistency, allowing feature point detection algorithms to detect the same feature points multiple times in neighboring locations. To solve this problem, we introduce the non-maximum suppression (NMS) [37] algorithm into the feature point detection process to eliminate redundantly detected feature points. 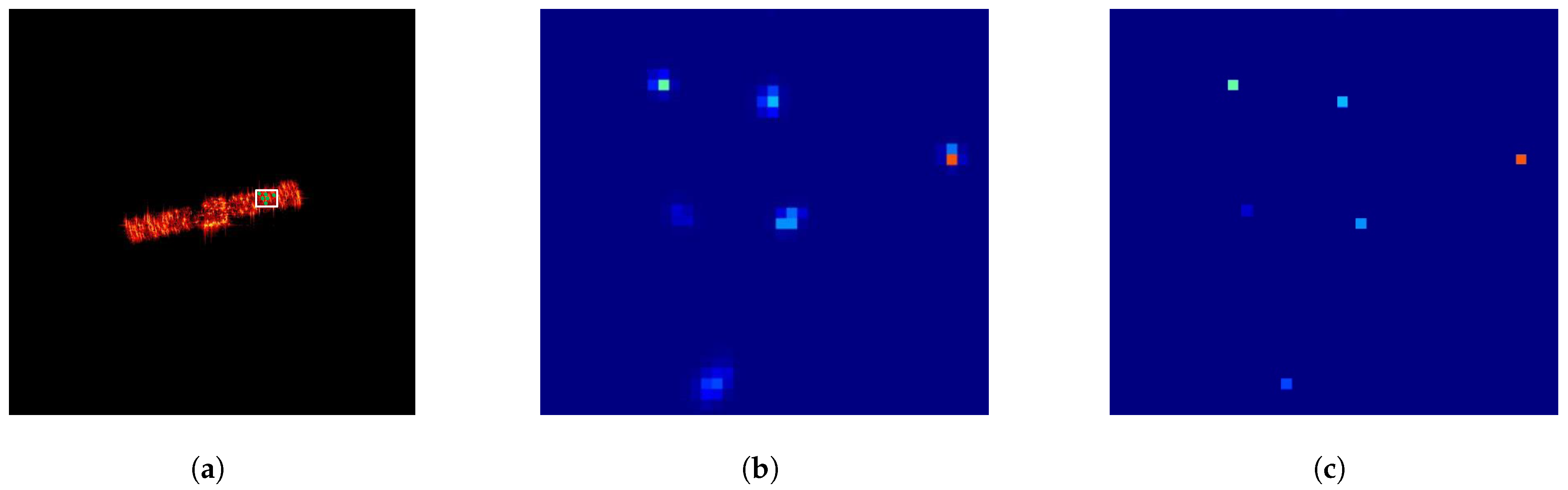Figure 15 shows an example of the feature map output by SFPD after being processed by the non-maximum suppression algorithm. For better observation, we present a local region of the feature map. From Figure 15, we can see that the feature map output by SFPD contains a large number of feature point responses. This is because, in SFPD, different convolutional kernels may extract similar features from local regions of the image, leading to overlapping responses on the feature map. The non-maximum suppression algorithm compares the intensities of these responses and retains only the strongest feature points, effectively removing redundant responses and preventing repeated processing of the same feature points. Therefore, the suppression threshold, which is a key parameter in the non-maximum suppression algorithm, also serves as a core hyperparameter in the proposed method.

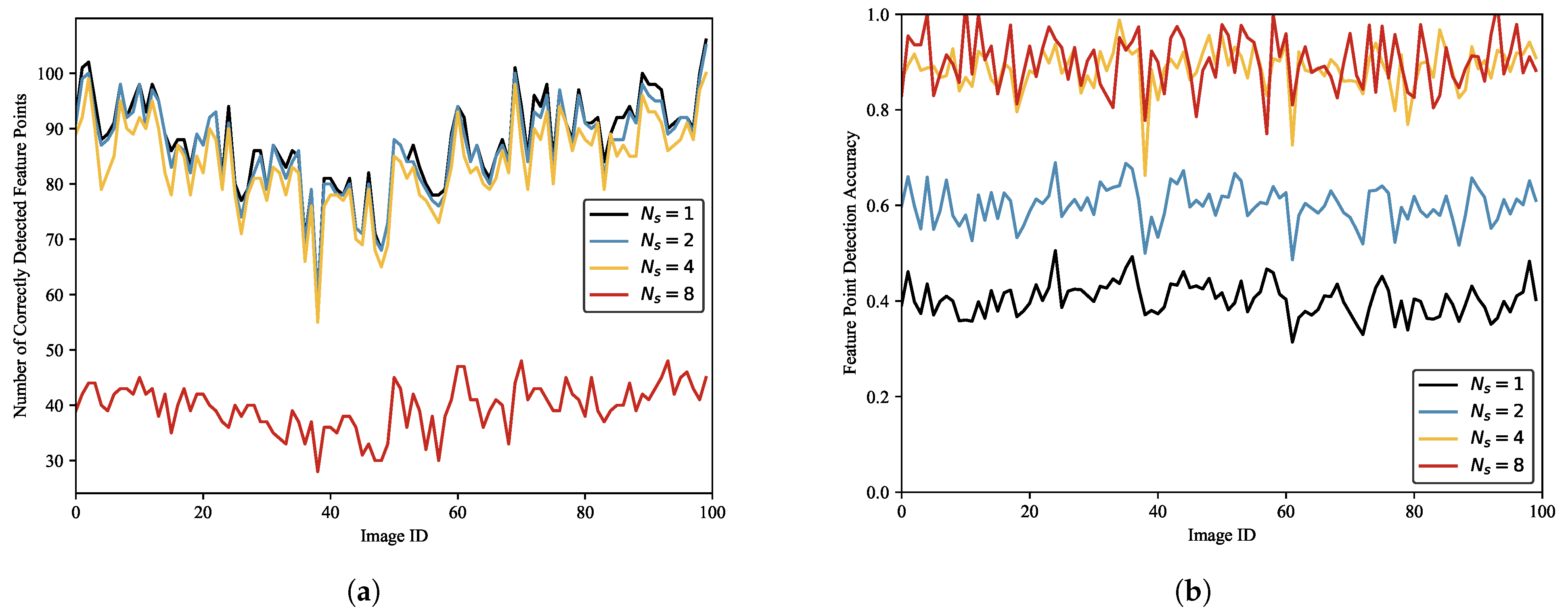
To select the optimal suppression threshold, we use SFPD to detect feature points in 100 randomly selected images from the test dataset under different suppression thresholds. Figure 16a shows the number of correctly detected feature points under different suppression thresholds. It can be observed that when the suppression threshold is maximum, SFPD detects the fewest correct feature points. This is because an excessively large suppression threshold causes the NMS algorithm to overperform, thus erroneously removing some correct feature points and, consequently, affecting feature point detection performance. Figure 16b illustrates the relationship between the detection accuracy and $N_s$. The detection accuracy increases as the suppression threshold increases. When $N_s=4$ and $N_s=8$, the detection accuracies are almost identical, suggesting that when $N_s=4$, the NMS algorithm is already capable of effectively eliminating the majority of redundant feature points. The statistical results are shown in

Table 6. The statistical results of the feature point detection performance under different suppression thresholds.

	${\mathit{N}}_{\mathit{s}}=1$	${\mathit{N}}_{\mathit{s}}=2$	${\mathit{N}}_{\mathit{s}}=4$	${\mathit{N}}_{\mathit{s}}=8$
Number of correct detected feature points	87.61	86.51	83.70	39.62
Feature point detection accuracy	0.4036	0.6011	0.8865	0.9019

. We observe that when the suppression thresholds are $N_s=1$ and $N_s=2$, SFPD detects the most correct feature points, but the feature point detection accuracy is only around 0.5, which is due to the low suppression threshold and the inability to remove redundant feature points. When $N_s=8$, the feature point detection accuracy improves by 1.54% compared to $N_s=4$, yet the number of correct feature points is only 47.34% of that achieved at $N_s=4$. Therefore, to balance the impact of the non-maximum suppression algorithm on feature point detection effectiveness, we set the suppression threshold to 4 pixels.

Since SFPD is a self-supervised network and the input labels of SFPD are the pseudo-ground truth labeled by BasicPoint, we designed corresponding experiments to verify the impact of the pseudo-ground truth on the feature point detection performance. During the experiment, we used BasicPoint and SFPD to detect feature points in 100 randomly selected test images. The experimental results are depicted in Figure 17. We can observe that the performance of SFPD is better than that of BasicPoint, which indicates that the feature point detection performance of SFPD has been significantly improved after self-supervised training. Furthermore, it also validates the effectiveness of the proposed pseudo-ground truth labeling method.

Table 7. The statistical results of the feature point detection performance of BasicPoint and SFPD.

	BasicPoint	SFPD
Number of correct detected feature points	56.13	83.70
Feature point detection accuracy	0.3280	0.8865

presents the statistical results of the experiment. From Table 7, it can be observed that compared to BasicPoint, SFPD achieves a 49.12% increase in the number of correctly detected feature points and a 55.85% enhancement in the feature point detection accuracy. This is because BasicPoint inevitably results in missed detections and false detections when labeling the ISAR images of space targets, leading to poor feature point detection performance. However, the correctly detected feature points in the labeling results share similarities in their features, while the features of false detections exhibit randomness. Therefore, during the training process, SFPD can learn the correct features of feature points, thereby enhancing the detection performance.

The existing research studies on extracting features from ISAR images using neural networks focus on semantic features, which have clear semantics and are different from the feature points detected by SFPD. Therefore, these research studies have not been used for comparison with SFPD. We compare SFPD with the commonly used feature point detection algorithm, referred to as speeded-up robust features (SURF) [38], to investigate the performance of SFPD. Additionally, we also compare our algorithm with the improved SIFT algorithm specifically designed for ISAR images in [20] and the improved Kanade–Lucas–Tomasi (KLT) algorithm designed for ISAR images in [22]. For the convenience of subsequent elaboration and comparison, these two algorithms are referred to as SIFT-ISAR and KLT-ISAR, respectively. The test data consist of 100 randomly selected ISAR images of space targets from the test dataset. 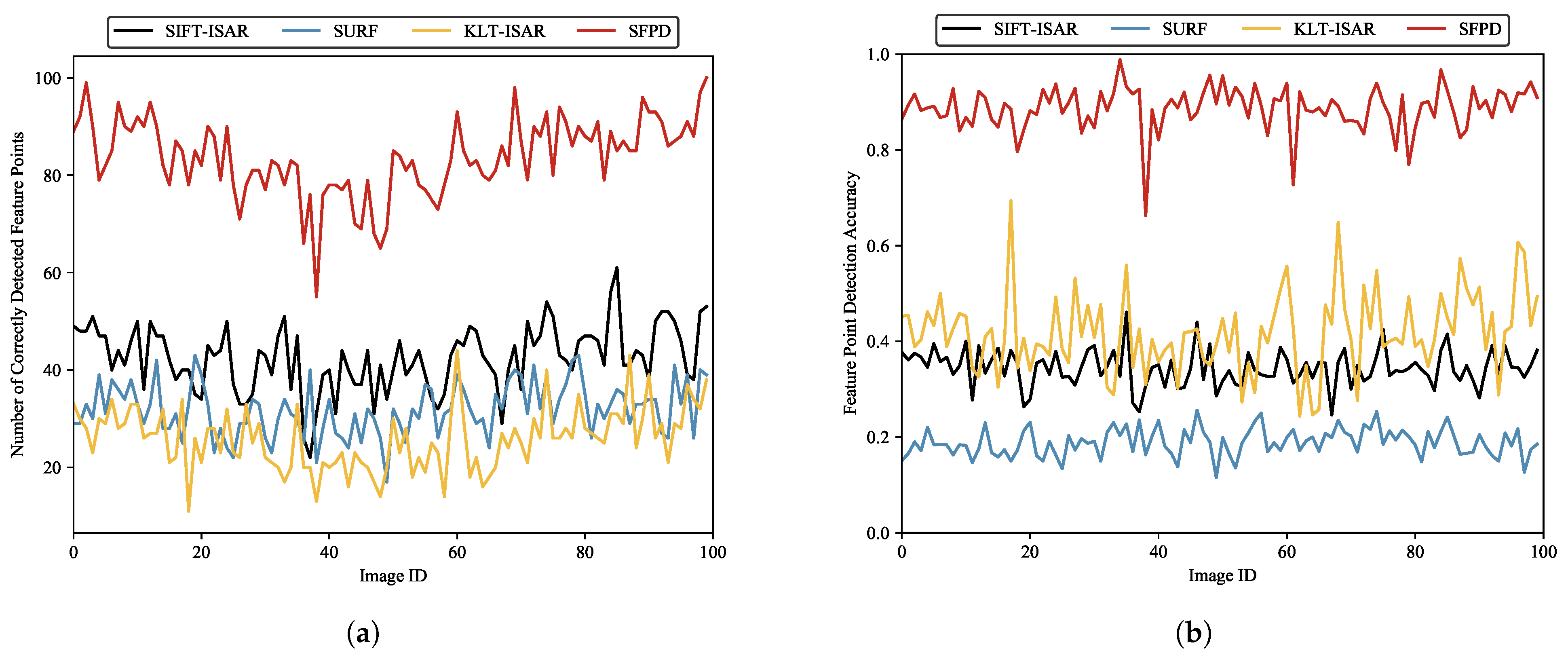As shown in Figure 18, SFPD outperforms the other three methods, which fully demonstrates the effectiveness of SFPD. Furthermore, we can observe that SURF has a lower number of correctly detected feature points and a lower feature point detection accuracy. This is because of the significant difference in the imaging mechanisms between optical images and ISAR images, leading to substantial differences in their image features. This results in a higher likelihood of false detections and missed detections during the feature point detection process. In contrast, although KLT-ISAR detects fewer feature points correctly, it has a higher detection accuracy than both SIFT-ISAR and SURF. This indicates that the detection performance of KLT-ISAR is superior to those of SIFT-ISAR and SURF, as false detections have a greater impact than missed detections. The statistics for the four aforementioned algorithms are presented in

Table 8. The feature point detection performance statistics of SIFT-ISAR, SURF, KLT-ISAR, and SFPD.

	SIFT-ISAR	SURF	KLT-ISAR	SFPD
Number of correct detected feature points	42.53	31.90	25.91	83.70
Feature point detection accuracy	0.3440	0.1885	0.4177	0.8865

. Compared to the other three methods, SFPD demonstrates an improvement of over 96.8% in the number of correctly detected feature points and an increase of over 47.48% in feature point detection accuracy. Additionally, we present examples of feature point detection using SIFT-ISAR, SURF, KLT-ISAR, and SFPD in Figure 19.

In addition to the number of correctly detected feature points and the detection accuracy, the running time is also an important evaluation metric. The running time can reflect computational efficiency, which is particularly crucial in practical applications, especially in scenarios where real-time processing is required. For a fair comparison, we measure the running times of SIFT-ISAR, SURF, KLT-ISAR, and SFPD using the same set of 100 ISAR images of space targets. The experiments were conducted on a computing platform equipped with an i9-13900K CPU and two 4090 GPUs. To reduce the uncertainty of the experimental results, we conducted 100 Monte Carlo experiments.

Table 9. The running times of SIFT-ISAR, SURF, KLT-ISAR, and SFPD.

	SIFT-ISAR	SURF	KLT-ISAR	SFPD
Running Time (s)	2.7059	2.0469	0.4962	0.1922

presents the experimental results. The experimental results show that the running time of SFPD processing 100 ISAR images of space targets is only 0.1922 s, outperforming the other three algorithms. This is because SFPD has stronger parallel computing capabilities. In contrast, SIFT-ISAR needs to construct a multi-scale Gaussian pyramid, resulting in a relatively long running time. While SURF improves computational efficiency through Hessian matrix approximation, its processing speed is still slower compared to SFPD. Although KLT-ISAR detects fewer feature points, its computational efficiency is superior to that of SURF and SIFT-ISAR because it mainly relies on the optical flow calculation of local images. Overall, SFPD not only exhibits excellent feature point detection performance but also exhibits high computational efficiency, making it suitable for the task of feature point detection in ISAR images of space targets.

In addition, we simulate the ISAR images of space targets with other structures by using the physical optics method to verify the robustness of SFPD for different model structures. We selected Tiangong-I as the target, which represents one type of space target composed of a cylindrical main body plus solar panels. Its electromagnetic grid model is shown in Figure 20a. We used SFPD to detect feature points from 100 simulated ISAR images of Tiangong-I and calculate the feature point detection accuracy for each image. The mean value of the feature point detection accuracy is 0.8759. In the above experimental results, the feature point detection accuracy of SFPD on the simulated images of Chang’e-I is 0.8865, which is consistent with that of Tiangong-I. This demonstrates that SFPD has strong robustness across different types of model structures. The satellite size of Tiangong-I is 18 m × 10.4 m × 3.35 m, and its main body is larger than that of Chang’e-I. Therefore, there are also significant differences in the main body sizes of Chang’e-I and Tiangong-I in the simulated images. Facing these two targets with significant differences in both structure and size, SFPD still demonstrates similar performance in feature point detection, which indicates that the feature point detection performance of SFPD is less affected by the model size and structure. Figure 20b shows an example of feature point detection in the simulated image of Tiangong-I.

4.3. Feature Point Matching

In space target surveillance tasks, the purpose of feature point detection is often to provide prerequisites for downstream tasks such as feature point matching and 3D reconstruction [39,40,41]. As mentioned above, SFPD not only detects the positions of feature points in ISAR images of space targets but also generates feature descriptors corresponding to the feature point positions, facilitating subsequent feature point matching. To validate the feature description performance, we selected 50 test images and employed random affine transformations for each image to generate 50 pairs of matched images. Then, we used the proposed method and the three aforementioned algorithms to perform feature point matching on these 50 pairs of images. The evaluation metrics used in the experiment are precision [42], recall [43], and F1 score [44]. Furthermore, to assess whether the feature point matching is correct, we designed the following evaluation criteria:

$$\left\{\begin{array}{c}∥\mathit{A}p-p^{\prime }∥\le threshold,Ture\hfill \\ ∥\mathit{A}p-p^{\prime }∥>threshold,False\hfill \end{array}\right.$$

(21)

where p and $p^{\prime }$ represent the detected feature points in the original image and affine transformed image, respectively. $\mathit{A}$ is the affine transformation matrix between the two images. When the Euclidean distance between $\mathit{A}p$ and $p^{\prime }$ is less than the matching threshold, we consider it a correct match. We conducted feature point matching experiments under matching thresholds of 1 pixel, 3 pixels, and 5 pixels. These results are depicted in Figure 21, Figure 22 and Figure 23.

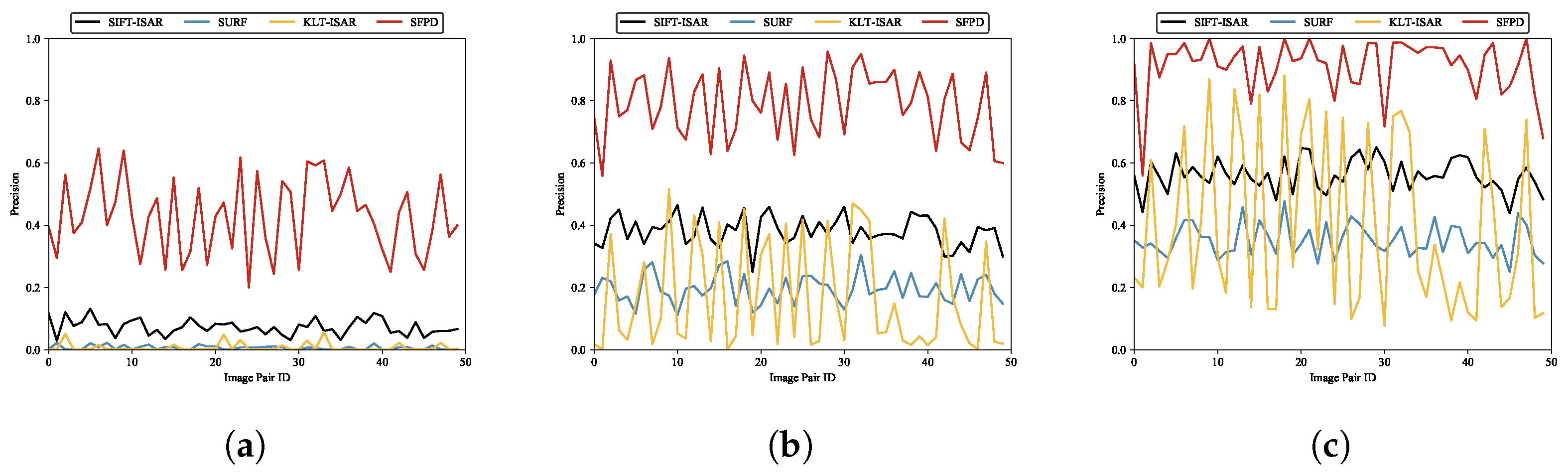
According to the experimental results, SFPD demonstrates good feature point matching performance across different matching thresholds. The experiments indicate that as the matching threshold decreases, the performance improvement of SFPD compared to the other three methods becomes more significant, which indicates that the feature descriptors generated by SFPD can accurately describe the image features of feature points, leading to higher precision in feature point matching. As the matching threshold increases, the requirement for matching accuracy becomes more relaxed, resulting in a relatively smaller performance improvement of SFPD. From Figure 21, Figure 22 and Figure 23, the curves for SIFT-ISAR and SURF are more stable, while both KLT-ISAR and SFPD exhibit larger fluctuations in performance. What is particularly notable for KLT-ISAR is its peak F1 score reaching around 0.9 but with troughs dipping below 0.2. The main cause of this phenomenon is that random affine transformations lead to significant viewpoint differences between some pairs of matching images. When there are large viewpoint differences, the feature point features in the images change, affecting the performance of the feature point matching algorithm.

Table 10. The feature point matching performance statistics of SIFT-ISAR, SURF, KLT-ISAR, and SFPD.

	Precision			Recall			F1 Score
	$\mathbf{ϵ}=\mathbf{1}$	$\mathbf{ϵ}=\mathbf{3}$	$\mathbf{ϵ}=\mathbf{5}$	$\mathbf{ϵ}=\mathbf{1}$	$\mathbf{ϵ}=\mathbf{3}$	$\mathbf{ϵ}=\mathbf{5}$	$\mathbf{ϵ}=\mathbf{1}$	$\mathbf{ϵ}=\mathbf{3}$	$\mathbf{ϵ}=\mathbf{5}$
SIFT-ISAR	0.0730	0.3808	0.5613	0.1033	0.4504	0.6051	0.0855	0.4124	0.5819
SURF	0.0064	0.1951	0.3512	0.0145	0.1889	0.2839	0.0087	0.1917	0.3135
KLT-ISAR	0.0075	0.1678	0.3975	0.0183	0.2356	0.4640	0.0105	0.1957	0.4279
SFPD	0.4308	0.7901	0.9131	0.7152	0.6665	0.6394	0.5349	0.7156	0.7435

presents the performance statistics of feature point matching experiments. When $ϵ=5$, the F1 score of SFPD shows an improvement of over 15% compared to the other three algorithms, once again validating the feature point matching performance of SFPD. To provide a more intuitive demonstration of the feature point matching performance, we present the feature point matching examples of SIFT-ISAR, SURF, KLT-ISAR, and SFPD when the matching threshold is 3 pixels in Figure 24.

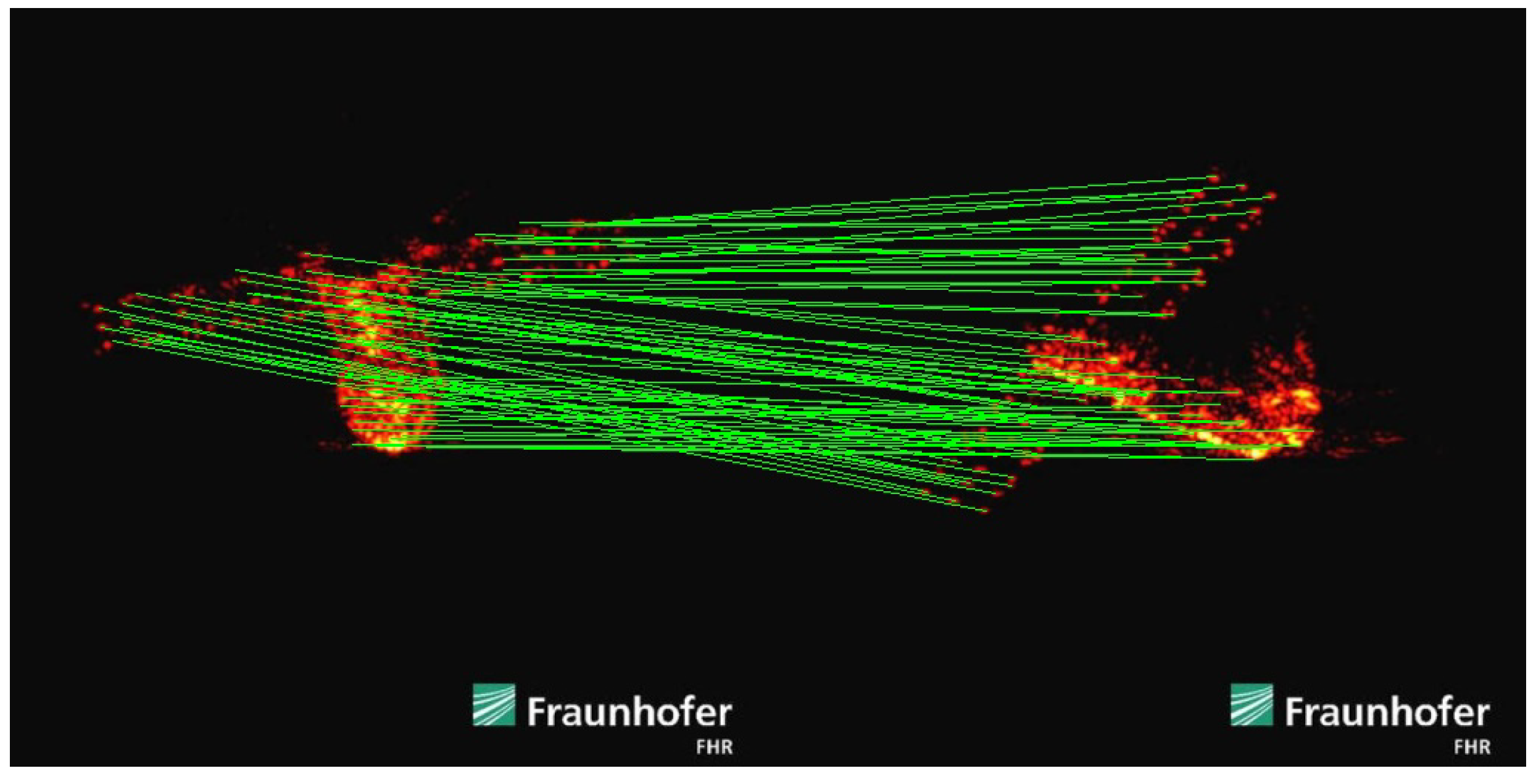
To verify the feature point detection and matching performance of SFPD more comprehensively, we process the real ISAR images using SFPD. These images were obtained by the Fraunhofer Institute for High-Frequency Physics and Radar Techniques FHR in 2018 when they used tracking and imaging radar (TIRA) to observe the fallen Tiangong-I. The experimental results are shown in Figure 25. As shown in Figure 25, the low texture and uneven brightness in the real ISAR images are more pronounced, presenting a greater challenge for feature point detection. It is worth noting that due to the complexity of the real ISAR images as well as the limitations of observation conditions and other factors, the ground truth of feature points is lacking, which makes it impossible to quantitatively analyze the performances of SFPD on the real data. However, by comparing and analyzing the experimental results, we can find that the feature point matching result of the two real ISAR images is highly consistent with the intuitive judgment made based on professional knowledge and experience. This is because SFPD can extract hierarchical features from the real ISAR images through a deep learning architecture based on self-supervised learning. Even in the case of low texture and uneven brightness, it can adaptively capture the latent features in the images, enabling it to accurately detect and match the feature points in the real ISAR images. In contrast, algorithms based on handcrafted descriptors, such as SIFT-ISAR, SURF, and KLT-ISAR, are not suitable for processing real ISAR images. SIFT-ISAR and SURF detect feature points through scale-space extrema and Hessian matrix approximation, which will fail when the images lack clear textures or have significant brightness variations. KLT-ISAR relies on local image information such as optical flow and gradients. The brightness changes in the real ISAR images can affect the calculation of local image information, resulting in poor performance in feature point detection and matching. This experiment indicates that SFPD also has good performance in feature point detection and matching when processing real ISAR images with severe degradation, further verifying the robustness of SFPD.

5. Conclusions

In this paper, we propose a self-supervised feature point detection method for the ISAR images of space targets. This method first constructs an ISAR primitive dataset and then trains a basic feature point detection model on this dataset, which is used to label the pseudo-ground truth. To improve the precision of pseudo-ground truth labeling, the affine transformation is introduced into the labeling process. Feature points are detected in images after applying affine transformations, and their positions are then inverse-transformed back to the original image. By aggregating feature point positions through multiple transformations, the accuracy of feature point position labeling is significantly improved. Subsequently, SFPD is trained on the labeled dataset. Experiments demonstrate that SFPD achieves higher detection accuracy compared to existing methods. Moreover, the detection results are also applicable to subsequent tasks such as feature point matching. However, this paper is a preliminary attempt at feature point detection in the ISAR images of space targets based on self-supervised learning. In the future, we plan to use more interpretable and efficient physical information neural networks, as described in [45,46], to replace traditional encoders for handling more complex feature point detection tasks.