Abstract
The Heifangtai Loess terrace in northwest China is frequently affected by landslides due to hydrological factors, establishing it as a significant research area for loess landslides. Advanced time-series InSAR technology facilitates the retrieval of surface deformation information, thereby aiding in the monitoring of landslide deformation status. However, existing methods that analyze deformation patterns do not fully exploit the displacement time series derived from InSAR, which hampers the exploration of potentially coexisting deformation patterns within the area. This study integrates InSAR with time-series clustering methods to reveal the surface deformation patterns and their spatial distribution characteristics in Heifangtai. Initially, utilizing the Sentinel-1 ascending and descending SAR data stack from January 2020 to June 2023, we optimize the interferometric phase based on distributed scatterer characteristics to reduce noise levels and obtain higher spatial density of measurement points. Subsequently, by combining the differential interferometric datasets from both ascending and descending orbits, the multidimensional small baseline subsets technique is employed to calculate the two-dimensional deformation time series. Finally, time-series clustering methods are utilized to extract the deformation patterns present and their spatial distribution from all measurement point time series. The results indicate that the deformation of the Heifangtai is primarily distributed around the surrounding area of the platform, with subsidence deformation being more intense than horizontal deformation. The entire terrace exhibits five deformation patterns: eastward subsidence, westward subsidence, vertical subsidence, westward movement, and eastward movement. The spatial distribution of these patterns suggests that the areas beneath the platform, namely Yanguoxia Town and Dangchuan Village, may be more susceptible to landslide threats in the future. Furthermore, wavelet analysis reveals the response relationship between rainfall and various deformation patterns, further enhancing the interpretability of these patterns. These findings hold significant implications for subsequent landslide monitoring, early warning, and risk prevention.
1. Introduction
China possesses the largest and most well-developed loess plateau in the world, which is currently accumulating [1]. The extreme water sensitivity and unique strength decay characteristics of loess make loess slopes prone to frequent landslide disasters [2]. The Heifangtai landslide in northwest China serves as a notable example, having triggered over a hundred loess landslide events in the past three decades due to extensive agricultural irrigation, which has severely endangered the safety of local residents’ lives and property [3,4].
Many scholars have conducted comprehensive research on the Heifangtai landslide, such as landslide distribution [5,6,7], sliding pattern analysis and failure mechanisms [8,9,10,11], contributing valuable data for landslide early warning systems and disaster risk reduction efforts. Surface deformation, a critical indicator for landslide development monitoring, has rendered continuous observation through both ground-based and remote sensing techniques indispensable for landslide monitoring. Current ground-based monitoring technologies, such as global navigation satellite system (GNSS) and extensometers, provide near-real-time monitoring of surface and subsurface deformations. Notably, monitoring efforts in the Heifangtai region, initiated in 2012, have resulted in multiple early warnings before landslide events, effectively preventing casualties [12]. However, these ground-based monitoring efforts rely on surface instruments, leading to low spatial resolution, which hampers a comprehensive understanding of regional deformation patterns. In contrast, remote sensing techniques, particularly interferometric synthetic aperture radar (InSAR), offer wide coverage, high spatial resolution, and high precision surface deformation information, though their temporal resolution is lower than that of ground-based methods [13,14]. Moreover, the availability of long-term archived data enables retrospective analysis of historical deformation in areas of interest, aiding in the understanding of regional-scale surface deformation.
Numerous efforts have been made to utilize InSAR technology for monitoring the Heifangtai terraces, particularly focusing on the period prior to 2019 when large-scale agricultural irrigation was prevalent. Most of these studies employed the small baseline subset (SBAS) technique to extract surface deformation time series along the line of sight (LOS) from sufficiently redundant interferograms, highlighting the unique advantages of InSAR for surface deformation monitoring. Furthermore, the integration of multi-track SAR satellites has facilitated the reconstruction of multi-dimensional deformations and improved the temporal resolution of monitoring [15,16], significantly enhancing the interpretability of the results. Notably, Liu et al. [17,18] and Shi et al. [19] conducted detailed analyses of key landslides and regions within the Heifangtai terraces, including joint analyses of deformation processes and hydrological factors. However, to the best knowledge of the authors, there remains a paucity of studies exploring the deformation patterns within the Heifangtai region directly using all InSAR-derived deformation information. In general, analyzing time-series information solely from key points or profiles does not fully exploit the spatiotemporal deformation data provided by InSAR, hindering the identification of potentially coexisting deformation patterns and limiting our understanding of surface deformation development in the Heifangtai terraces. More importantly, comprehending the deformation patterns within a region facilitates the identification of high-risk areas for the formulation of targeted risk management strategies. Additionally, it allows for the prediction of future trends, thereby enabling the development of scientifically sound disaster prevention and mitigation approaches.
InSAR can generate time-series deformation information for tens of thousands to millions of measurement points (MPs), which presents a significant challenge in extracting potential deformation patterns from such a vast dataset. Statistical dimensionality reduction methods and time-series clustering techniques can provide significant support in addressing this challenge [20,21,22]. Statistical dimensionality reduction aids in identifying the principal components of extensive spatiotemporal deformation data, whereas time-series clustering is utilized to identify potentially coexisting deformation patterns. The integration of these methods enables the automated, unsupervised data mining of large volumes of surface deformation information, providing data-driven support for disaster prevention and mitigation efforts within the region [23]. Therefore, this study first utilizes publicly available Sentinel-1 data to obtain spatiotemporal surface deformation information in the Heifangtai terrace and subsequently applies time-series clustering methods at a regional scale to identify surface deformation patterns. The primary contributions of this research can be summarized as follows: (1) optimizing the interferometric phase based on distributed scatterer characteristics to increase MP density; (2) combining ascending and descending SAR data to derive two-dimensional deformation information with enhanced temporal resolution; (3) utilizing principal component analysis (PCA, [24]) and K-Means to extract surface deformation patterns from the deformation time series of all MPs. This research fully leverages the spatiotemporal deformation information provided by InSAR, thereby enhancing the interpretability and dissemination of InSAR displacement data, and providing important reference data for landslide monitoring, early warning, and prevention efforts.
2. Methodology
This study reveals surface deformation patterns utilizing InSAR and time-series clustering, comprising four primary steps: (1) Processing ascending and descending SAR data based on the characteristics of distributed scatterers; (2) using the multidimensional small baseline subset (MSBAS) technique to obtain 2-D surface displacement time series and deformation rates; (3) conducting dimensionality reduction on the displacement time series of all MPs using PCA to identify the principal components of surface deformation; (4) implementing K-Means clustering on the time series of all MPs. The detailed processing flow is illustrated in Figure 1.
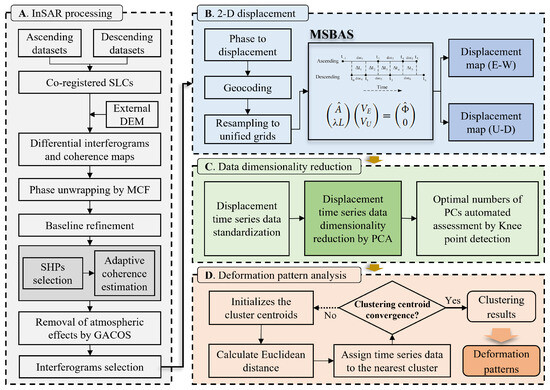
Figure 1.
Flowchart for revealing surface deformation patterns based on InSAR and time series clustering.
2.1. Interference Processing Based on Distributed Scatterers
Ground targets can be categorized into permanent scatterers (PSs) and distributed scatterers (DSs). The former consists of dominant sub-scatterer units within a single SAR pixel. However, in landslide scenarios predominantly characterized by natural terrain, PS points are often sparse, and the density of MPs may not sufficiently represent the deformation state of the landslide. Therefore, we conduct interference processing on ascending and descending SAR data based on DSs. The phase characteristics of DSs are generally associated with higher noise levels, rendering the optimization of interferometric phases a primary task. Common InSAR software, such as GAMMA software (https://www.gamma-rs.ch/, accessed on 20 November 2024) and SNAP (https://step.esa.int/main/download/snap-download/, accessed on 20 November 2024 ), employs regular grids to estimate coherence between two SAR images. This indiscriminate averaging can result in the loss of spatial resolution in coherence and may introduce estimation biases, thereby diminishing monitoring precision [25,26]. To address this issue, we first select statistically homogeneous pixels (SHPs) based on SAR intensity data. We then adaptively estimate coherence using the information from the selected SHPs and the differential interferogram, which aids in reducing the noise level of interferometric phases while preserving the spatial resolution of the SAR images.
The entire interferometric processing is conducted using GAMMA software (v2.1 4-Mar-2016) and open-source DSIPro (v2.0) program (http://mijiang.org.cn/index.php/software/, accessed on 20 November 2024 ), with the main steps outlined as follows: (1) Registering SAR data and utilizing external digital elevation model (DEM) to remove topographic phases and generate differential interferograms; (2) Employing the minimum cost flow (MCF) method for phase unwrapping; (3) Refining the baseline; (4) Selecting SHPs and conducting adaptive coherence estimation; (5) Utilizing generic atmospheric correction online service for InSAR (GACOS) to remove atmospheric delays from the differential interferograms [27,28,29]; (6) Selecting high-quality interferograms for subsequent inversion of deformation time series.
2.2. Calculating 2-D Displacement Using MSBAS
The MSBAS technique is a method used to derive multidimensional deformation time series from SAR images with varying geometric characteristics. Compared to deformations along the LOS direction, multidimensional deformation results provided improved interpretability. As SAR satellites exhibit limited sensitivity to north–south directional deformations, this study disregards deformations in that direction.
Figure 2 illustrates a simplified case that includes both ascending and descending differential InSAR (D-InSAR) datasets. Each dataset comprises three SAR images: the ascending track captures images at , , and , while the descending track captures images at , , and . Two interferograms are calculated for each dataset. Since the first ascending image is acquired before the first descending image, the first ascending interferogram is adjusted using . Similarly, the last descending interferogram is adjusted using . This adjustment synchronizes the initial acquisition times of the two datasets from to . The entire time span is divided into three intervals corresponding to continuous ascending and descending acquisitions: . In this case, each coherent pixel in all interferograms can be taken in the following form:
where represents the D-InSAR displacement observations, geocoded and resampled onto a common grid. The prime symbol indicates that time corrections at the boundaries have been applied. and denote the eastward and vertical velocities to be estimated, respectively. and represent the eastward and vertical components of the LOS vector, where and indicate the azimuth and incidence angles, respectively, with superscripts referring to ascending and descending geometries.

Figure 2.
Schematic diagram of MSBAS. The ascending and descending SAR acquisitions are represented by orange upward triangles and bright blue downward triangles, respectively. The horizontal solid line between the two triangles represents the differential interferogram, labeled as . The vertical dashed line divides the consecutive acquisitions into time intervals .
Equation (1) represents an underdetermined linear system that can be solved using Tikhonov regularization, as detailed by [15]. In this study, zero-order Tikhonov regularization is employed to estimate the velocity parameters. Finally, the velocities over the time period are integrated to reconstruct the 2-D displacement time series, as expressed in Equation (2).
The 2-D displacement time series derived from the MSBAS technique exhibits higher temporal resolution compared to the 1-D LOS time series, as it incorporates all image acquisitions from both ascending and descending orbits.
2.3. Dimensionality Reduction in Time Series Using PCA
The 2-D displacement time series dataset can consist of tens of thousands to millions of MPs, each corresponding to a displacement time series, which makes it extremely challenging to directly analyze various unknown surface deformation patterns from such a vast amount of data. In this study, we apply PCA to reduce the dimensionality of the 2-D displacement time series data, extracting the principal components (PCs) that capture the maximum variance. This method enables the understanding of the main deformation patterns hidden within the 2-D displacement time series without any prior knowledge, thereby providing valuable insights for subsequent analyses of surface deformation pattern distributions [30].
PCA is a powerful tool for data dimensionality reduction and feature extraction, and numerous software packages and code implementations are readily available. For this study, we employed the Scikit-learn library in Python [31] to perform our analysis. It is crucial to note that large time series datasets often exhibit significant variations in numerical ranges; therefore, standardizing the time series is necessary before applying PCA to avoid bias in the estimation of PCs. Furthermore, in this study, PCA was separately applied to both the east–west and vertical displacement datasets.
Each PC extracted from PCA accounts for a specific proportion of the variance, with higher variance proportions indicating that the PC more effectively captures essential structures and features in the data, thereby better representing the core information of the dataset. These PCs with significant contributions help reveal the primary variation patterns in the displacement time series, encompassing the rate of displacement changes, long-term trends, and periodic behaviors. Generally, the PCs with the highest variance proportions are retained as the primary features representing the data. We applied the Knee-Locator algorithm [32] to automatically determine the optimal number of PCs to retain, achieving a balance between minimizing information loss and preserving critical features.
2.4. Analyzing Surface Deformation Patterns Using K-Means
PCA aids in identifying the primary features of variability within the displacement time series dataset. We subsequently apply K-Means clustering to discern the various hidden deformation patterns in the dataset and assign each MP to its corresponding deformation pattern. As a widely used unsupervised clustering algorithm, K-Means requires only the specification of the number of clusters to efficiently categorize large datasets. In this study, the number of clusters is determined by the optimal number of retained PCs. This method operates on the premise that the global solution of K-Means clustering is contained within the PCA sub-space [33]. Utilizing PCA to guide K-Means clustering helps reduce Euclidean distance expansion and improves computational efficiency.
K-means clustering iteratively groups m time series x into n clusters (c), primarily involving four steps: (1) randomly initializing the centroids of n clusters; (2) assigning each time series to the nearest cluster based on Euclidean distance; (3) updating the cluster centroids; (4) repeating steps 2 and 3 until the cluster centroids convergence. Given two time series, and , their Euclidean distance D is defined as follows:
The main objective of the K-Means is to minimize the sum of distances between each time series and its respective cluster centroid:
where represents the centroid of the cluster, which is the average of all time series within the cluster.
3. Study Area and Datasets
3.1. Study Area
The Heifangtai terrace is situated in Yanguoxia Town, Yongjing County, approximately 60 km west of Lanzhou, Gansu Province, China. The Heifangtai terrace is divided into two terraces, Heitai and Fangtai, by the Hulang Gully, with Heitai being approximately seven times larger than Fangtai. The Heifangtai terrace is relatively flat, bordered by steep slopes of about 60 degrees at its edges. Its geological composition mainly consists of Malan loess, clay, gravel, and bedrock [12]. The top layer of loess is highly water-sensitive, making it prone to wet collapse and liquefaction when exposed to water. Additionally, the terrace experiences arid conditions with low annual rainfall, where the annual evaporation rate is 5.4 times higher than the precipitation. Local residents heavily extract water from the Yellow River for agricultural irrigation, which has triggered numerous loess landslides along the edges of the terrace [3], with the distribution of historical landslides shown in Figure 3b.
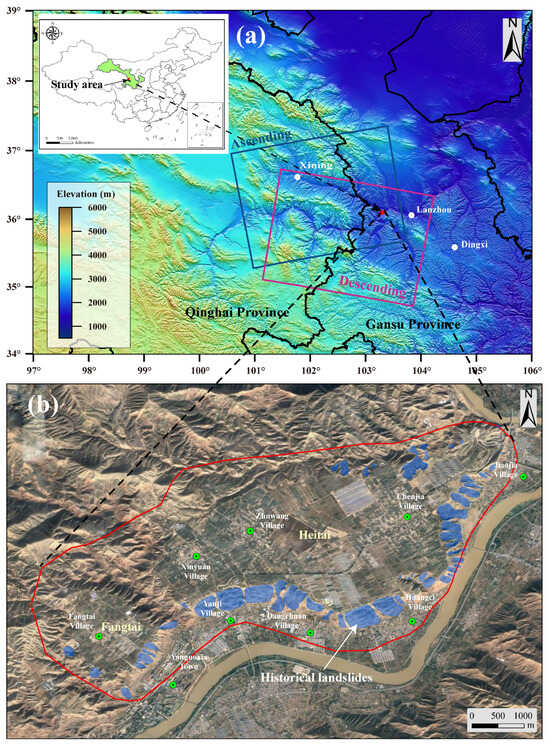
Figure 3.
Study area and SAR datasets coverage. (a) Location of the study area indicated by the red polygon. The blue and pink rectangles show the coverage of the ascending and descending Sentinel-1 data. (b) Heifangtai Google satellite image and the distribution of historical landslides (revised after [17]).
Several villages surround the terrace. In 2019, the government suspended large-scale flood irrigation to ensure the safety of residents’ lives and property and initiated the promotion of water-saving irrigation practices to achieve sustainable industrial development. Combining real-time surface monitoring with regular inspections has effectively reduced the losses caused by landslide disasters. However, due to the inherent limitations of the technology, these efforts have mainly concentrated on a limited number of key ground points. Therefore, it is essential to investigate the recent deformation patterns of Heifangtai on a regional scale to provide guidance for continuous surface monitoring and risk management.
3.2. Datasets
To acquire surface deformation information for the Heifangtai terrace, a dataset of C-band Sentinel-1 SAR images was collected from the European Space Agency. A total of 98 ascending and 97 descending SAR images from January 2020 to June 2023 were utilized, covering the area depicted in Figure 3a, with the basic parameters listed in Table 1. During data processing, the Copernicus 30 m DEM was utilized to remove the topographic phase, while GACOS was employed to correct for tropospheric delays.

Table 1.
Basic parameters of the Sentinel-1 SAR datasets used in this study.
4. Results
4.1. Interference Processing Results Based on Distributed Scatterers
For interferometric processing, the acquired SAR images are first co-registered and cropped to the study area. In this study, a 90-day temporal baseline and a 200 m spatial baseline are utilized to generate the interferogram. An external Copernicus DEM is employed to remove the topographic phase from the interferogram, producing the differential interferogram. Following phase unwrapping using the MCF method, the baseline is refined, and the resulting differential interferogram is utilized for selecting SHPs and estimating adaptive coherence. A ratio of 5 azimuth to 1 range is applied for multi-looking, with statistical tests conducted using a Baumgartner–Weiss–Schindler (BWS) within a 5-pixel by 5-pixel window to select SHPs from the intensity image sequence. Figure 4c,d illustrates the results of adaptive coherence estimation based on SHPs. In comparison to the regular grid coherence estimation (Figure 4a,b), the adaptive coherence estimation demonstrates improved spatial resolution, thereby enhancing the signal-to-noise ratio of the interferometric signal. The optimized interferogram is then used for subsequent processing.

Figure 4.
Average coherence of ascending and descending SAR datasets. (a) Coherent regular grid estimation of ascending SAR datasets. (b) Coherent regular grid estimation of descending SAR datasets. (c) Adaptive coherence estimation of ascending SAR datasets based on distributed scatterers. (d) Adaptive coherence estimation of descending SAR datasets based on distributed scatterers.
We then employ the GACOS to correct the tropospheric delay in the optimized differential interferograms. After masking pixels with low coherence (less than 0.3) and carefully examining each interferogram, we retained only those of higher quality for subsequent deformation inversion. The ascending dataset comprises 564 interferometric pairs, while the descending dataset consists of 554 interferometric pairs. Figure 5 illustrates the temporal and spatial baseline distribution of the ascending and descending interferometric pairs, demonstrating a good connection.
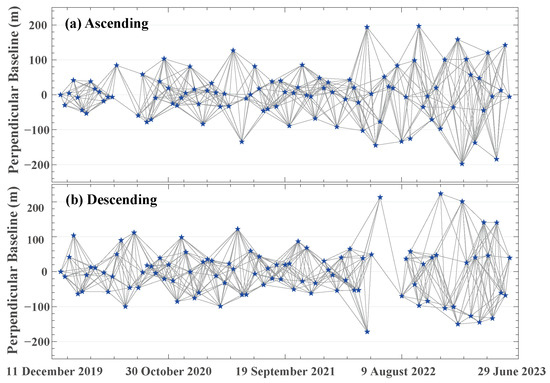
Figure 5.
Spatio-temporal baseline distribution of interferogram. (a) Ascending. (b) Descending.
Additionally, we generated the mean velocity map along the LOS for the Heifangtai terrace using the SBAS technique (Figure 6), with positive values indicating motion towards the satellite and negative values representing motion away from it. It is evident that both the ascending and descending datasets exhibit significant deformation signals along the edges of Heitai and Fangtai. Furthermore, the deformation signs are consistent across the ascending and descending tracks, indicating that the deformation in the Heifangtai terrace is predominantly characterized by subsidence. In the central region of the terrace, there is a scarcity of MPs, primarily due to the decoherence caused by local engineering and production activities. The average deformation rates along the LOS derived from the conventional SBAS reach a maximum of mm/year for the ascending track and mm/year for the descending track, while the DS-based SBAS shows mm/year and mm/year, respectively.

Figure 6.
Mean velocity maps of Heifangtai terrace along LOS directions. (a) Ascending. (b) Descending. (c) Ascending based on DS. (d) Descending based on DS.
The MPs obtained from the DS-based SBAS are significantly more numerous than those from the conventional SBAS, primarily due to the reduced noise level in the DS interferometric phase. A greater number of MPs enables a more comprehensive and detailed representation of surface deformation, which is particularly evident in the ascending dataset. Statistically, the MP density derived from the DS-based SBAS reached 3708 MPs/km2, indicating an increase of 53.9% compared to the MP density obtained from the conventional SBAS.
Figure 7a,b presents the standard deviation maps of LOS velocity derived from conventional SBAS processing, with average values of 0.9 mm/year and 0.7 mm/year for ascending and descending orbits, respectively. Figure 7c,d shows the standard deviation maps of LOS velocity obtained from DS-based SBAS, with average values of 0.8 mm/year and 0.6 mm/year for ascending and descending orbits, respectively. These improvements are primarily attributed to phase optimization based on DS characteristics (Figure 4). Both methods demonstrate millimeter-level precision in time series InSAR, but the DS-based SBAS provides a larger number of MPs, thereby offering abundant and reliable displacement data for further investigation of regional surface deformation patterns.

Figure 7.
Standard deviation maps of LOS deformation velocity. (a) Ascending. (b) Descending. (c) Ascending based on DS. (d) Descending based on DS.
4.2. Two-Dimensional Deformation Velocity Maps
In contrast to deformation along the LOS direction, two-dimensional deformation is more intuitive and easier to interpret. We first convert the retained high-quality interferograms into displacements and geocode them in the WGS-84 geographic coordinate system. Next, we sample measurements onto a common grid and input them into the MSBAS software (https://insar.ca/multidimensional-small-baseline-subset-msbas/, accessed on 20 November 2024), employing zero-order regularization to solve Equation (1). This process results in a higher temporal resolution two-dimensional surface displacement time series and deformation velocities (Figure 8). Note that positive deformation velocities in the east–west direction indicate eastward movement, while negative values indicate westward movement. In the vertical direction, positive values indicate uplift, and negative values denote subsidence. Additionally, since both ascending and descending orbit data share the same start and end dates, we calculate the mean 2-D displacement value for both acquisition times (e.g., 11:00 and 23:00) on the same date to ensure a consistent daily temporal resolution for the displacement time series.

Figure 8.
Two-dimensional deformation velocity maps of Heifangtai terrace. (a) Horizontal east–west deformation velocity map. (b) Vertical deformation velocity map.
As shown in Figure 8a, the Heifangtai terrace exhibits distinct horizontal deformation signals. A significant westward movement signal is apparent on the southwestern side of Heitai, with a deformation velocity reaching 18.5 mm/year, while the maximum eastward movement in the entire terrace reaches 20.1 mm/year. These movement directions generally align with the slope orientation of the terrace edge. Compared to the east–west deformation, the Heifangtai terrace exhibits a broader and more pronounced range of vertical deformation. Except for the eastern side of Heifangtai, significant subsidence signals are observed around Heitai and Fangtai, with a maximum subsidence velocity of mm/year. Overall, the subsidence velocity is more pronounced than the horizontal east–west deformation. The two-dimensional average velocity map aids in identifying key deformation areas within the terrace; however, it remains challenging to delineate the overall deformation pattern across the entire area clearly. In total, 77,292 MPs are available, each associated with its own deformation time series. Extracting potential deformation patterns from this wealth of spatiotemporal deformation information is both meaningful and exciting.
4.3. Principal Components of the Displacement Time Series
Figure 9 presents the PCA results for the two-dimensional displacement time series dataset. Figure 9a,b shows the first four PCs of the east–west horizontal displacement time series and the vertical displacement time series, respectively. These four orthogonal components capture the maximum variance in the displacement dataset and exhibit similar characteristics. The first PC (PC1) indicates a fundamentally stable behavior during the monitoring period, explaining 77.01% and 88.66% of the variance in the east–west and vertical directions, respectively. This corresponds to the deformation velocity observed at Heifangtai (Figure 8), indicating that most MPs are stable. The remaining three PCs (PC2, PC3, and PC4) demonstrate fluctuating characteristics, exhibiting either increases or decreases. In the horizontal displacement dataset, PC2 accounts for 5.08% of the total variance, indicating a negative trend in deformation (i.e., relative westward movement), while PC3 captures 3.36% and indicates a positive trend in deformation (i.e., relative eastward movement). In the vertical displacement dataset, PC2 explains 3.19% of the total variance and indicates a negative trend in deformation (i.e., subsidence), whereas PC3 oscillates around zero, exhibiting stronger fluctuations during the year 2020. Both PC4 in the two datasets also show oscillatory behavior near zero; however, their temporal variations are not synchronized.

Figure 9.
The PCs obtained from PCA and the results of the knee point detection. (a) First four PCs of horizontal displacement. (b) First four PCs of vertical displacement. (c) Knee point detection results of horizontal displacement. (d) Knee point detection results of vertical displacement.
Considering the proportion of total variance explained by each PC, the optimal number of PCs to retain was determined using the Knee-Locator method. The horizontal displacement dataset retained three PCs (Figure 9c), whereas the vertical displacement dataset retained two PCs (Figure 9d). Furthermore, the number of retained PCs guided the selection of cluster numbers in K-Means clustering for the time series, resulting in three clusters for the horizontal displacement time series and two clusters for the vertical displacement time series.
4.4. Revealing Deformation Patterns Using K-Means Clustering
Figure 10 presents the clustering results for the horizontal and vertical displacement datasets, including the series of cluster centroid, the 10th percentile series, and the 90th percentile series. Cluster 1 for the east–west horizontal displacement exhibits characteristics of stable eastward movement, whereas Cluster 2 displays a subtle deformation signal near zero, indicating stability in the horizontal direction. Cluster 3 demonstrates stable westward movement; however, the range of its 10th to 90th percentile series is broader than that of Cluster 1. This observation corresponds with the earlier finding that the variance explained by PC2 is slightly greater than that explained by PC3.

Figure 10.
Clustering time series of horizontal and vertical displacement datasets. (a–c) Three clustering time series of horizontal east–west displacement. (d,e) Two clustering time series of vertical displacement.
In contrast, Cluster 1 for vertical displacement indicates a stable state, whereas Cluster 2 exhibits a pronounced downward trend, indicating subsidence deformation. The range of changes between the 10th and 90th percentile series is broader, suggesting that K-Means has grouped MPs within the Heifangtai region exhibiting varying magnitudes of subsidence deformation while displaying similar stable subsidence trends. The centroid series of the clusters indicate that vertical deformation is more pronounced than horizontal deformation, highlighting the dominance of subsidence deformation in the Heifangtai terrace.
By integrating the clustering results for both horizontal and vertical displacements, we generated a geographic distribution map of the deformation patterns for 77,292 MPs in the Heifangtai area (Figure 11). This region encompasses five deformation patterns formed by the combination of three horizontal movement modes and two vertical movement modes: vertical subsidence, westward subsidence, eastward subsidence, westward movement, and eastward movement.
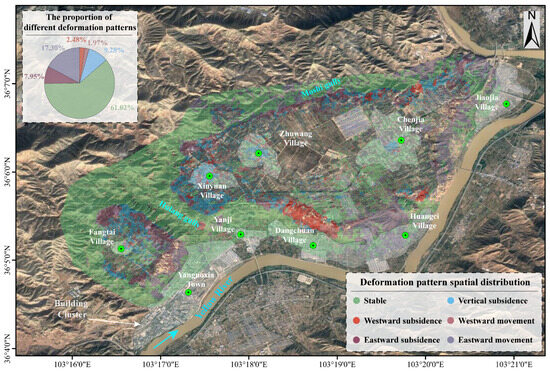
Figure 11.
Geographic distribution map of deformation patterns of Heifangtai terrace combined with horizontal and vertical displacement clustering results.
A percentage of 61.02% of the MPs are in a stable state, primarily located around Heitai and Fangtai, with a few stable points in the central part of the terrace. The remaining MPs encompass five different deformation patterns, predominantly distributed across the terrace areas of Heitai and Fangtai; 17.30% of the MPs exhibit eastward movement, found in regions along the edge and just below the terrace, with a higher concentration near Heitai compared to Fangtai; 9.28% of the MPs exhibit subsidence, mainly located on Fangtai and the western side of Heitai; 7.95% of MPs display eastward subsidence, primarily along the edge of Fangtai and north of Heitai. Westward movement accounts for 1.97% and westward subsidence accounts for 2.48% of the total MPs, predominantly found in the southwestern region of Heitai. The geographic distribution map of deformation patterns clearly illustrates the various deformation modes present in the Heifangtai terrace. In contrast to the deformation velocity map (Figure 8) and individual MP time series, this map offers richer and more intuitive information, including trends and magnitudes of deformation, as it utilizes time series data from 77,292 MPs.
The towns and villages located below the Heifangtai terrace, including Yanguoxia Town, Yanji Village, Dangchuan Village, Huangci Village, and Jiaojia Village, are generally in a stable state. Although some areas near Huangci Village and Jiaojia Village exhibit eastward movement, this does not significantly expose residents and their buildings to immediate, life-threatening hazards. The primary risks to these communities arise from landslides induced by the deformation of the adjacent terrace slopes, particularly in Yanguoxia Town and Dangchuan Village, where extensive areas of terrace slopes exhibit downward deformation patterns. While these slopes have demonstrated a state of uniform deformation up to June 2023, they may enter an accelerated deformation phase or even failure due to potential extreme weather events or seismic activity in the future. Therefore, it is recommended to enhance slope monitoring in these areas and develop corresponding disaster prevention and mitigation strategies. Moreover, the four villages situated on the terrace platform—Fangtai Village, Xinyuan Village, Zhuwang Village, and Chenjia Village—are experiencing vertical subsidence, with Xinyuan Village and Fangtai Village displaying more extensive subsidence. The primary cause of this ground subsidence is likely a decline in groundwater levels. This necessitates the integration of additional surface monitoring data and field investigations to ascertain the specific causes of deformation, thereby assisting local government decision-makers in formulating appropriate response measures.
5. Discussion
5.1. Response Relationship Between Deformation Patterns and Rainfall
Landslide surface displacements can be understood as comprising two components: a trend component and a fluctuation component. The former is defined as the trend deformation primarily controlled by the geological conditions of the landslide body, while the latter is regarded as the fluctuation displacement influenced by external environmental or anthropogenic factors. Considering that rainfall is a well-known triggering factor for landslides and that loess is sensitive to water, we aim to identify the relationship between the deformation patterns of the Heifangtai terrace and rainfall to enhance our understanding of the developmental processes of surface deformation in this region. The rainfall data utilized in this study are sourced from the global precipitation measurement (GPM) mission, which has a spatial resolution of . The value from the grid closest to Heifangtai is taken as the actual rainfall value. We employ cross wavelet transform (XWT) and wavelet coherence (WTC) as analytical tools to examine the relationship between deformation patterns and rainfall, enabling us to identify the common power and relative phase between two time-series in the time-frequency domain [34,35].
Initially, the linear trends in the east–west deformation and vertical deformation patterns were removed through linear regression to isolate the fluctuation component of the displacements. Both the fluctuation component and the rainfall time series were standardized and normalized to serve as inputs for the wavelet analysis tools, as shown in the last row of subplots in Figure 12 and Figure 13, where the blue bars represent rainfall and the orange solid line denotes the fluctuation component displacement. As illustrated in Figure 12, the fluctuation component displacement of the subsidence deformation pattern exhibits significant power at a 365-day period in the XWT analysis, covering the entire monitoring period. The WTC results also indicate continuity similar to that of the XWT at the 365-day period, suggesting a more reliable estimation of the time lag between the two time-series.

Figure 12.
Cross wavelet transform and wavelet coherence of the fluctuation component of vertical deformation displacement and rainfall.

Figure 13.
Cross wavelet transform and wavelet coherence of the fluctuation component of horizontal deformation displacement and rainfall.
The relative phase relationship between the two time-series is represented by arrows, where an arrow pointing to the right indicates a positive correlation and an arrow pointing to the left indicates a negative correlation. When the arrows point vertically upwards or downwards, the latter time series leads or lags by 1/4 of a period. However, it is important to note that there may be non-uniqueness issues when converting arrow angles into lag days, necessitating careful visual inspection in conjunction with the time series [35]. Figure 12 shows that the average phase angle for the 365-day period is approximately 45° to the right. Here, the intensification of subsidence deformation is reflected in the decrease in the standardized fluctuation displacement values. Therefore, we interpret this observation as indicating a negative correlation between rainfall and subsidence fluctuation displacement over the course of a one-year period, with rainfall leading by approximately 45 days.
Similarly, Figure 13 presents the results of the XWT and WTC for the fluctuation components of eastward and westward movements in relation to rainfall. The XWT results indicate that the fluctuation components of eastward and westward movements exhibit significantly high common power with rainfall in the 365-day period. However, the WTC does not exhibit the same continuity as the XWT, instead displaying relative phase relationships with different periods. This suggests that there are additional common powers in those periods between rainfall and the fluctuation components of eastward or westward movements. Overall, the Heifangtai terrace primarily exhibits subsidence deformation, showing significant common power with rainfall over the 3.5-year period and approximately 45 days of lag, reflecting the infiltration process of rainfall from the surface to the subsurface layers.
5.2. Prospects and Limitations
This study presents a method that combines InSAR with time-series clustering to reveal surface deformation patterns, which constitutes a significant contribution to the use of remote sensing for investigating and monitoring surface conditions. The method is based on openly available Sentinel-1 data and an unsupervised data mining approach that requires no prior knowledge. It aids both InSAR experts and non-expert users in understanding surface deformation patterns in regions of interest, significantly enhancing the interpretability and usability of InSAR-derived surface deformation information, with great potential for widespread application.
Compared to the 1-D LOS deformation results obtained through InSAR technology (Figure 6), the proposed method demonstrates clear advantages (Figure 10), which illustrate the types of surface deformation patterns and their spatial heterogeneity in the Heifangtai region. This leads to a significant improvement in the interpretability and usability of the extensive deformation dataset: (1) The combined use of more densely distributed LOS measurements based on DS enables the generation of horizontal and vertical deformation time series, thereby enhancing the interpretability of surface displacements; (2) the clustering of numerous MPs into a few clusters helps local decision-makers and other users quickly grasp regional deformation patterns; (3) the decomposition of centroid sequences for different deformation patterns into trend and fluctuation components deepens the understanding of the relationship between regional deformation and external factors.
The accuracy of revealed surface deformation patterns primarily depends on the InSAR-derived displacement measurements, as clustering merely groups similar time-series data. This study demonstrates the advantages of the proposed method in the Heifangtai Loess landslide area, characterized by relatively gentle terrain and sparse vegetation. However, data acquisition and the inherent limitations of InSAR technology present ongoing challenges. Due to satellite revisit periods and the maximum detectable deformation gradient [36], InSAR struggles to provide timely and accurate surface displacement information when encountering rapid short-term deformation events. Additionally, in regions with complex topography and dense vegetation, geometric distortions and decorrelation due to SAR imaging hinder the acquisition of reliable displacement data. Furthermore, the polar orbit of SAR satellites renders InSAR less sensitive to north–south deformation. Although 2-D deformation is obtained through MSBAS, identifying surface deformation patterns dominated by north–south movement remains difficult. The common pixel sampling in MSBAS may also result in the loss of some MPs and relies on both ascending and descending acquisitions for 2-D deformation data. These limitations may hinder the acquisition of sufficient and accurate surface displacement information in certain scenarios, thereby affecting the understanding of surface deformation patterns. Future work could incorporate joint processing techniques such as PS and DS from single-look images [37] and use SAR data from additional orbits to obtain three-dimensional deformation information, such as from NISAR, an L-band SAR that offers enhanced deformation detection capabilities in dense vegetation areas [38]. Overall, the proposed method remains effective and advantageous with currently available data.
6. Conclusions
This study proposes a method that combines InSAR and unsupervised time-series clustering to extract surface deformation patterns. Unlike previous approaches that rely solely on deformation velocity maps or key points and profile deformation time series, this method fully utilizes the two-dimensional deformation time series information of all MPs, enabling a comprehensive understanding of the surface deformation pattern at a regional scale, thereby aiding subsequent work such as real-time monitoring and disaster prevention and warning. Based on this method, the surface deformation patterns of the Heifangtai terrace have been revealed, and the main conclusions are summarized as follows:
- (1)
- Based on the characteristics of DSs, the spatial resolution of coherence can be effectively improved to reduce the noise level of differential interferometric phases, thereby increasing the density of MPs. In the Heifangtai area, the deformation signals are primarily distributed along the edges of the Heitai and Fangtai terraces. Compared to conventional SBAS, DS-based SBAS provides more comprehensive deformation information, particularly enhancing the density of MPs by 53.9% in the ascending SAR dataset.
- (2)
- A total of 77,292 two-dimensional deformation time series MPs for the Heifangtai terrace were calculated using MSBAS. Further analysis using PCA and K-Means revealed five coexisting deformation patterns: eastward subsidence, westward subsidence, vertical subsidence, eastward movement, and westward movement, with subsidence deformation signals being notably stronger than horizontal movements. The spatial distribution of deformation patterns indicates that continuous monitoring of the slopes near Yanguoxia Town and Dangchuan Village should be strengthened in the future.
- (3)
- Wavelet tools were employed to analyze the response relationships between rainfall and various deformation patterns, further deepening the understanding of surface deformation patterns. The fluctuation displacements of different deformation patterns exhibited significant common power within a one-year period, with subsidence deformation showing a negative correlation with rainfall, lagging approximately 45 days behind the rainfall. In contrast, the east–west horizontal deformation did not exhibit such a strong relative phase relationship with rainfall.
This proposed method enables the automatic and unsupervised extraction of coexisting surface deformation patterns from extensive time series deformation data. Not only does this enhance the interpretability of InSAR-derived deformation information, but it also supports future efforts in surface monitoring and decision-making for disaster prevention and mitigation.
Author Contributions
Conceptualization, H.X. and B.S.; methodology, H.X.; software, H.X.; validation, H.X., B.S. and G.X.; formal analysis, H.X.; investigation, H.X.; resources, Q.Z. and L.W.; data curation, L.W.; writing—original draft preparation, H.X.; writing—review and editing, B.S. and L.W.; visualization, H.X.; supervision, L.W.; funding acquisition, L.W. and Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is funded by National Natural Science Foundation of China (42127802), the Fundamental Research Funds for the Central Universities, CHD (300102263202) and the innovation team of ShaanXi Provincial Tri-Qin Scholars with Geoscience Big Data and Geohazard Prevention (2022).
Data Availability Statement
The Sentinel-1A data used in this study were provided by the European Space Agency (ESA), https://search.asf.alaska.edu/#/ (accessed on 20 November 2024); POD Precise Orbit Ephemerides used in this study were provided by the ESA, https://s1qc.asf.alaska.edu/aux_poeorb/ (accessed on 20 November 2024); the SRTM DEM was freely downloaded from the website http://dwtkns.com/srtm30m/ (accessed on 20 November 2024) and the GPM rainfall data were freely downloaded from the website https://gpm1.gesdisc.eosdis.nasa.gov/data/GPM_L3/ (accessed on 20 November 2024).
Acknowledgments
The authors are thankful to European Space Agency (ESA) for providing Sentinel-1 SAR satellite imagery, Generic Atmospheric Correction Online Service for InSAR (GACOS) for providing the tropospheric delay maps, and Google for the satellite maps. The graphics were drawn using ArcMap 10.8 software and Generic Mapping Tools (GMT).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Derbyshire, E. Geological hazards in loess terrain, with particular reference to the loess regions of China. Earth-Sci. Rev. 2001, 54, 231–260. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, X.; Zhang, Q.; PENG, J.; XU, Q. Research on loess landslide identification, monitoring and failure mode with InSAR technique in Heifangtai, Gansu. Geomat. Inf. Sci. Wuhan Univ. 2019, 44, 996–1007. [Google Scholar]
- Cui, S.h.; Pei, X.j.; Wu, H.y.; Huang, R.q. Centrifuge model test of an irrigation-induced loess landslide in the Heifangtai loess platform, Northwest China. J. Mt. Sci. 2018, 15, 130–143. [Google Scholar] [CrossRef]
- Zhou, Q.; Xu, Q.; Peng, D.; Fan, X.; Ouyang, C.; Zhao, K.; Li, H.; Zhu, X. Quantitative spatial distribution model of site-specific loess landslides on the Heifangtai terrace, China. Landslides 2021, 18, 1163–1176. [Google Scholar] [CrossRef]
- Yang, D.; Qiu, H.; Hu, S.; Zhu, Y.; Cui, Y.; Du, C.; Liu, Z.; Pei, Y.; Cao, M. Spatiotemporal distribution and evolution characteristics of successive landslides on the Heifangtai tableland of the Chinese Loess Plateau. Geomorphology 2021, 378, 107619. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.; Tu, X.; Tham, L.G.; Zhou, Y.; Iqbal, J. Landslides in a loess platform, North-West China. Landslides 2014, 11, 993–1005. [Google Scholar] [CrossRef]
- Kong, J.; Zhuang, J.; Peng, J.; Ma, P.; Zhan, J.; Mu, J.; Wang, J.; Zhang, D.; Zheng, J.; Fu, Y.; et al. Failure mechanism and movement process of three loess landslides due to freeze-thaw cycle in the Fangtai village, Yongjing County, Chinese Loess Plateau. Eng. Geol. 2023, 315, 107030. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, G.; Peng, J. Initiation and mobility of recurring loess flowslides on the Heifangtai irrigated terrace in China: Insights from hydrogeological conditions and liquefaction criteria. Eng. Geol. 2022, 302, 106619. [Google Scholar] [CrossRef]
- Qi, X.; Xu, Q.; Liu, F. Analysis of retrogressive loess flowslides in Heifangtai, China. Eng. Geol. 2018, 236, 119–128. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, G. Effect of irrigation-induced densification on the post-failure behavior of loess flowslides occurring on the Heifangtai area, Gansu, China. Eng. Geol. 2018, 236, 111–118. [Google Scholar] [CrossRef]
- Xu, Q.; Peng, D.; Zhang, S.; Zhu, X.; He, C.; Qi, X.; Zhao, K.; Xiu, D.; Ju, N. Successful implementations of a real-time and intelligent early warning system for loess landslides on the Heifangtai terrace, China. Eng. Geol. 2020, 278, 105817. [Google Scholar] [CrossRef]
- Cigna, F.; Bianchini, S.; Casagli, N. How to assess landslide activity and intensity with Persistent Scatterer Interferometry (PSI): The PSI-based matrix approach. Landslides 2013, 10, 267–283. [Google Scholar] [CrossRef]
- Bürgmann, R.; Rosen, P.A.; Fielding, E.J. Synthetic aperture radar interferometry to measure Earth’s surface topography and its deformation. Annu. Rev. Earth Planet. Sci. 2000, 28, 169–209. [Google Scholar] [CrossRef]
- Samsonov, S.V.; d’Oreye, N. Multidimensional small baseline subset (MSBAS) for two-dimensional deformation analysis: Case study Mexico City. Can. J. Remote Sens. 2017, 43, 318–329. [Google Scholar] [CrossRef]
- Samsonov, S.; Dille, A.; Dewitte, O.; Kervyn, F.; d’Oreye, N. Satellite interferometry for mapping surface deformation time series in one, two and three dimensions: A new method illustrated on a slow-moving landslide. Eng. Geol. 2020, 266, 105471. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhang, Q.; Peng, J.; Zhu, W.; Lu, Z. Multi-temporal loess landslide inventory mapping with C-, X-and L-band SAR datasets—A case study of Heifangtai Loess Landslides, China. Remote Sens. 2018, 10, 1756. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, C.; Zhang, Q.; Yang, C.; Zhu, W. Heifangtai loess landslide type and failure mode analysis with ascending and descending Spot-mode TerraSAR-X datasets. Landslides 2020, 17, 205–215. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Q.; Zhang, L.; Zhao, K.; Dong, J.; Jiang, H.; Liao, M. Surface displacements of the Heifangtai terrace in Northwest China measured by X and C-band InSAR observations. Eng. Geol. 2019, 259, 105181. [Google Scholar] [CrossRef]
- Rygus, M.; Novellino, A.; Hussain, E.; Syafiudin, F.; Andreas, H.; Meisina, C. A clustering approach for the analysis of InSAR Time Series: Application to the Bandung Basin (Indonesia). Remote Sens. 2023, 15, 3776. [Google Scholar] [CrossRef]
- Wang, G.; Li, P.; Li, Z.; Liang, C.; Wang, H. Coastal subsidence detection and characterization caused by brine mining over the Yellow River Delta using time series InSAR and PCA. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103077. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, X.; Sun, Q.; Wang, H.; Hu, J. Characterizing spatiotemporal patterns of land deformation in the Santa Ana Basin, Los Angeles, from InSAR time series and independent component analysis. Remote Sens. 2022, 14, 2624. [Google Scholar] [CrossRef]
- Festa, D.; Novellino, A.; Hussain, E.; Bateson, L.; Casagli, N.; Confuorto, P.; Del Soldato, M.; Raspini, F. Unsupervised detection of InSAR time series patterns based on PCA and K-means clustering. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103276. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Jiang, M.; Yong, B.; Tian, X.; Malhotra, R.; Hu, R.; Li, Z.; Yu, Z.; Zhang, X. The potential of more accurate InSAR covariance matrix estimation for land cover mapping. ISPRS J. Photogramm. Remote Sens. 2017, 126, 120–128. [Google Scholar] [CrossRef]
- Jiang, M.; Guarnieri, A.M. Distributed scatterer interferometry with the refinement of spatiotemporal coherence. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3977–3987. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of real-time mode high-resolution water vapor fields from GPS observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic atmospheric correction model for interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Chaussard, E.; Farr, T.G. A new method for isolating elastic from inelastic deformation in aquifer systems: Application to the San Joaquin Valley, CA. Geophys. Res. Lett. 2019, 46, 10800–10809. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Satopaa, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “kneedle” in a haystack: Detecting knee points in system behavior. In Proceedings of the 2011 31st International Conference on Distributed Computing Systems Workshops, Minneapolis, MN, USA, 20–24 June 2011; pp. 166–171. [Google Scholar]
- Xu, Q.; Ding, C.; Liu, J.; Luo, B. PCA-guided search for K-means. Pattern Recognit. Lett. 2015, 54, 50–55. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2016, 13, 437–450. [Google Scholar] [CrossRef]
- Dai, K.; Chen, Y.; Xu, Q.; Hancock, C.; Jiang, M.; Deng, J.; Zhuo, G. A functional model for determining maximum detectable deformation gradients of InSAR considering the topography in mountainous areas. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5211211. [Google Scholar] [CrossRef]
- Mirzaee, S.; Amelung, F.; Fattahi, H. Non-linear phase linking using joined distributed and persistent scatterers. Comput. Geosci. 2023, 171, 105291. [Google Scholar] [CrossRef]
- Manjusree, P.; Roy, A.; Martha, T.; Rajkumar, R.; Bhatwdekar, S. The NISAR Mission for Enhanced Disaster Monitoring. In Proceedings of the 2021 IEEE International India Geoscience and Remote Sensing Symposium (InGARSS), Virtual, 6–10 December 2021; pp. 332–335. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).