Pyramid Fine and Coarse Attentions for Land Cover Classification from Compact Polarimetric SAR Imagery
Abstract
1. Introduction
- Our proposed method simultaneously utilizes fine- and coarse-grained spatial dependencies, enabling the model to extract more discriminative and detailed features by capturing spatial relationships at different scales. This attribute effectively addresses spatial heterogeneity present in land covers, ultimately leading to more accurate land cover classification.
- Our proposed method incorporates the outputs of different stages and leverages information across multiple scales, resulting in enhanced accuracy for land cover classification. By addressing the challenges of signature ambiguity, this integration of low- and high-level features improves the accuracy of land cover classification.
- The potential of state-of-the-art (SOTA) DL methods in generating accurate land cover maps using CP SAR data are evaluated and compared with that of the proposed method. This thorough assessment not only advances the understanding of DL techniques in this domain but also provides valuable insights for decision makers and researchers aiming to utilize SOTA DL method for land cover classification and monitoring in CP SAR data.
2. Background
2.1. Land Cover Classification Using CP SAR Data
2.2. Land Cover Classification Using CNNs
2.3. Land Cover Classification Using Transformers
3. Compact Polarimetric SAR Basics
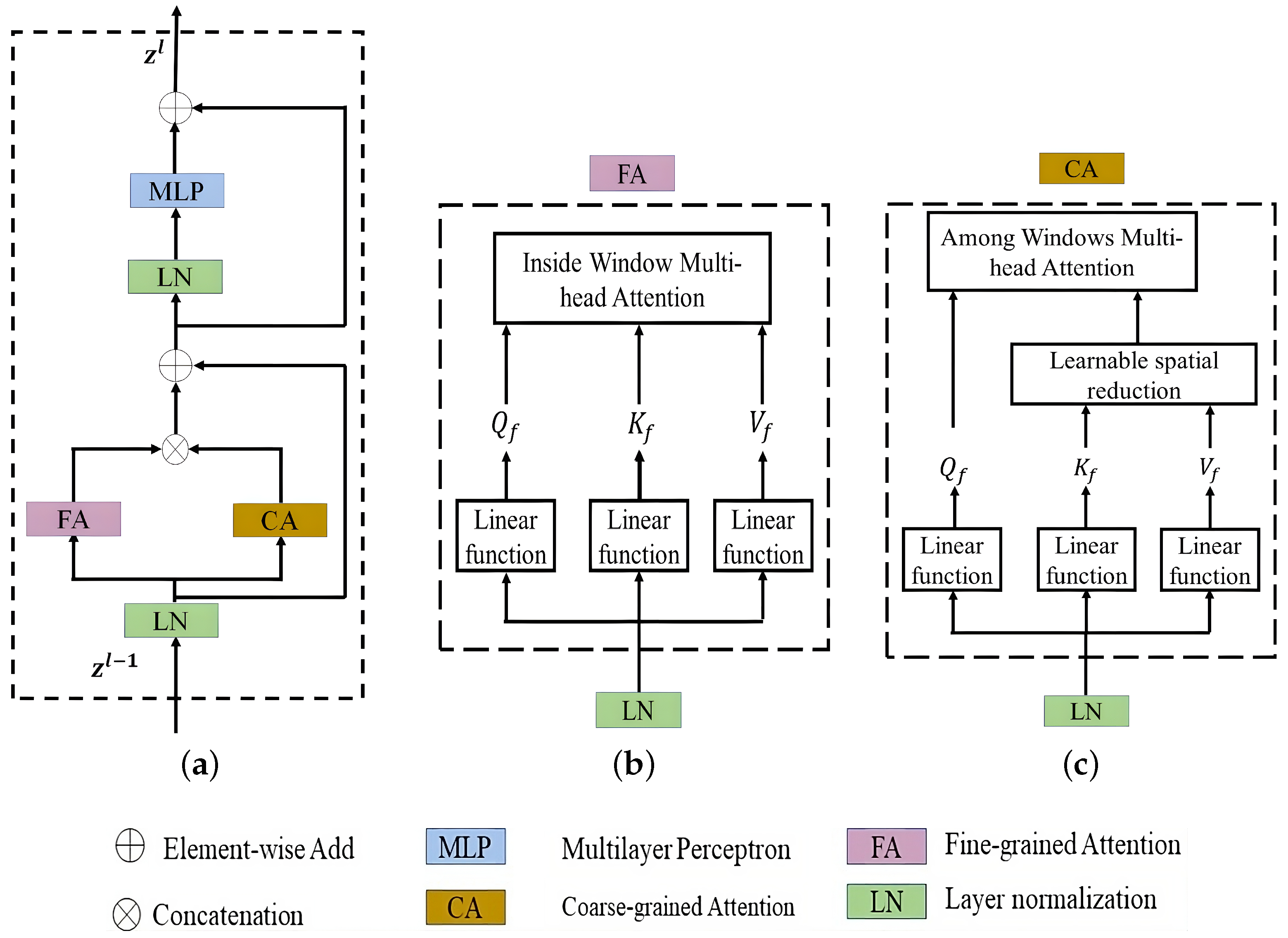
4. Methodology
4.1. Linear Embedding
4.2. FC Transformer Block
4.2.1. Fine-Grained Attention
4.2.2. Coarse-Grained Attention
4.2.3. Combining Fine- and Coarse-Grained Attentions
4.3. Downsampling
4.4. Fusion
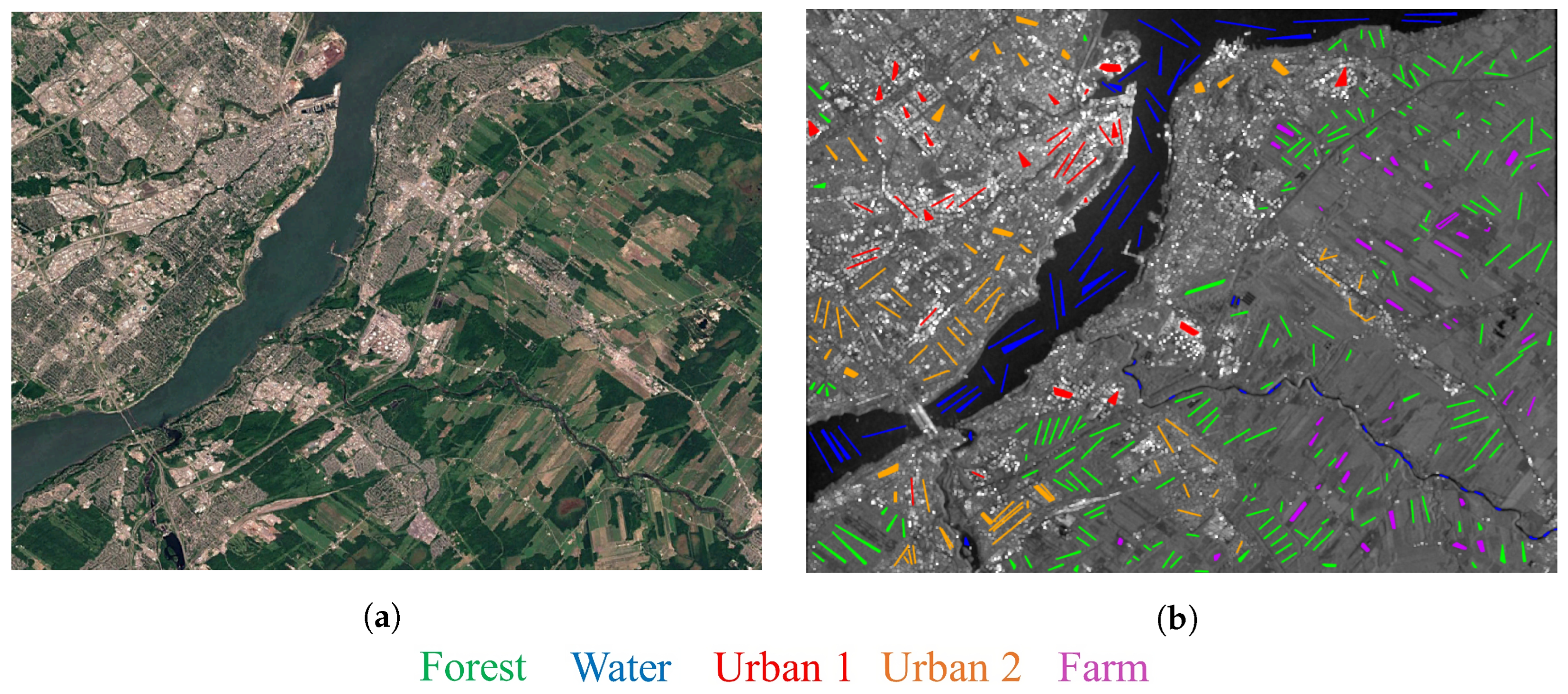
5. Study Area and Dataset
6. Experiments
- Fine-grained + coarse-grained attention (FC transformer): This configuration evaluates the combination of fine-grained and coarse-grained attention mechanisms without the incorporation of feature fusion.
- Full model (PFC transformer): This configuration includes all three core components, integrating fine-grained attention, coarse-grained attention, and fusion of features from different levels (the pyramid of features).
6.1. Training and Testing
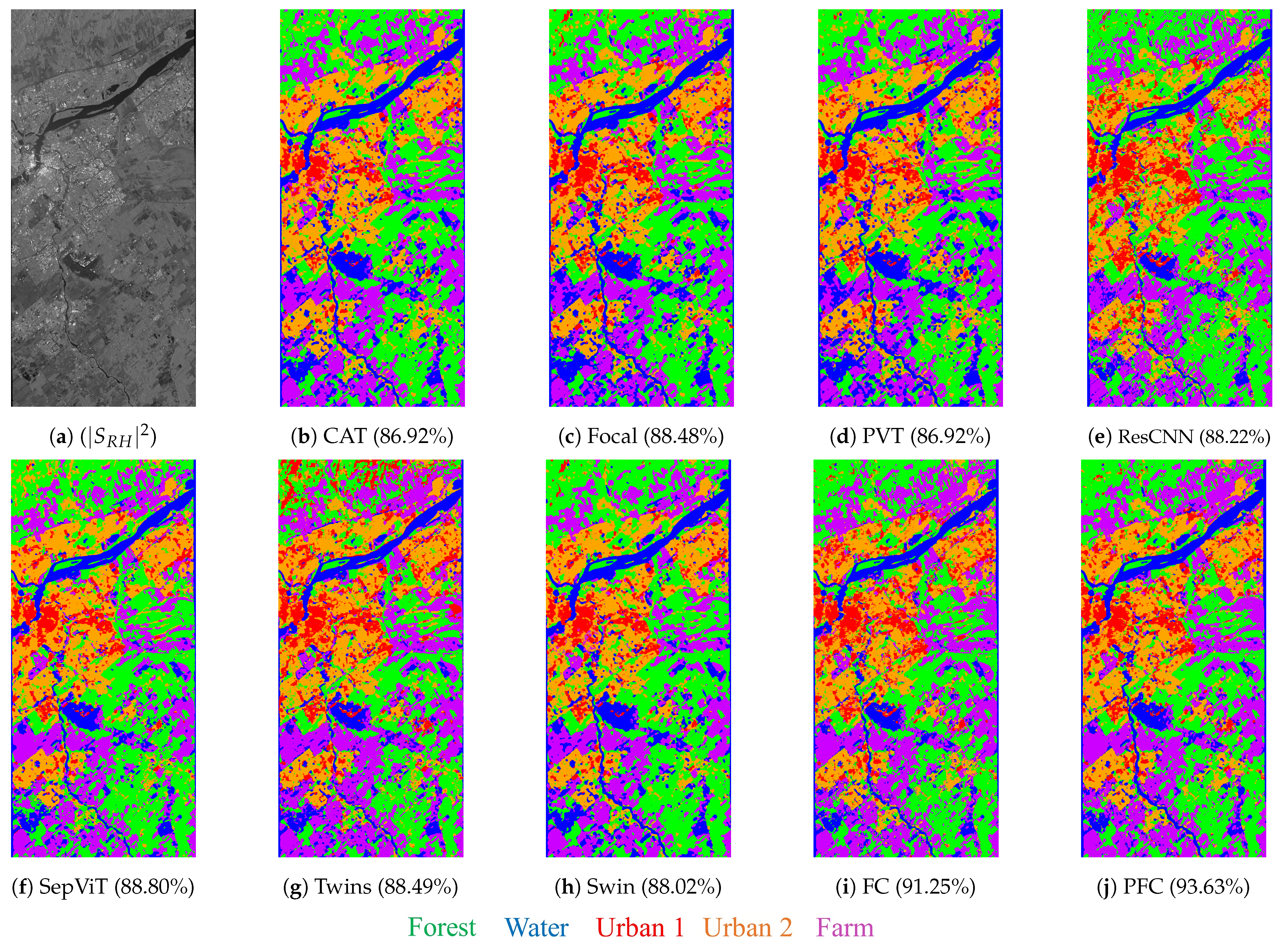
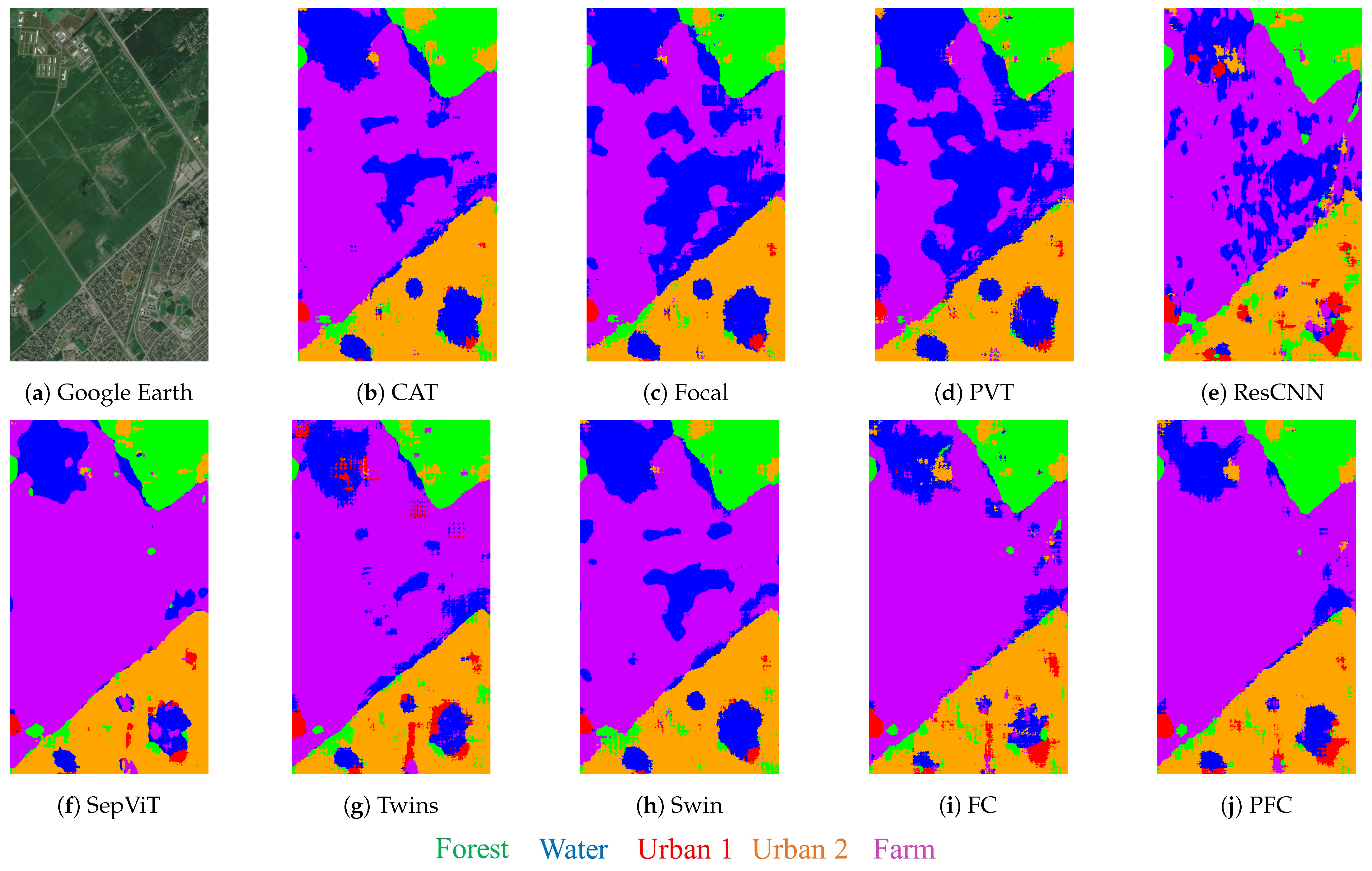
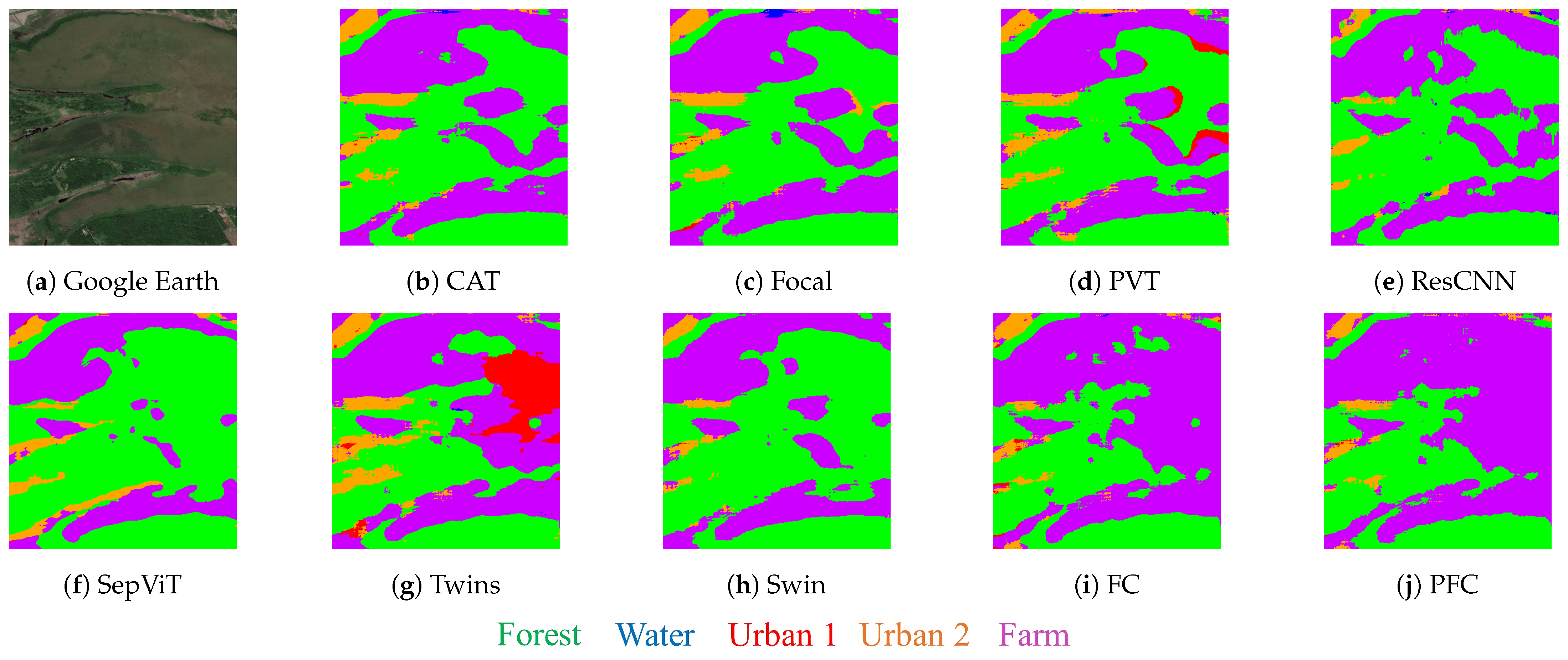
6.2. Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dabboor, M.; Iris, S.; Singhroy, V. The RADARSAT Constellation Mission in Support of Environmental Applications. Proceedings 2018, 2, 323. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Lin, Z. A Novel Algorithm for Land Use and Land Cover Classification Using RADARSAT-2 Polarimetric SAR Data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Li, X.; Lei, L.; Sun, Y.; Li, M.; Kuang, G. Multimodal Bilinear Fusion Network with Second-Order Attention-Based Channel Selection for Land Cover Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1011–1026. [Google Scholar] [CrossRef]
- Wang, Y.; He, C.; Liu, X.; Liao, M. A Hierarchical Fully Convolutional Network Integrated with Sparse and Low-Rank Subspace Representations for PolSAR Imagery Classification. Remote Sens. 2018, 10, 342. [Google Scholar] [CrossRef]
- Liu, X.; He, C.; Zhang, Q.; Liao, M. Statistical Convolutional Neural Network for Land-Cover Classification from SAR Images. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1548–1552. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Gill, E. Full and Simulated Compact Polarimetry SAR Responses to Canadian Wetlands: Separability Analysis and Classification. Remote Sens. 2019, 11, 516. [Google Scholar] [CrossRef]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support Vector Machines. IEEE Intell. Syst. Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Gao, W.; Huang, D.; Ma, Z.; Liotta, A.; Perra, C. Automatic Sea-Ice Classification of SAR Images Based on Spatial and Temporal Features Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9887–9901. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Gill, E.; Molinier, M. A New Fully Convolutional Neural Network for Semantic Segmentation of Polarimetric SAR Imagery in Complex Land Cover Ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- Ma, X.; Fu, A.; Wang, J.; Wang, H.; Yin, B. Hyperspectral Image Classification Based on Deep Deconvolution Network with Skip Architecture. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4781–4791. [Google Scholar] [CrossRef]
- Taleghanidoozdoozan, S.; Xu, L.; Clausi, D.A. Region-Based Sea Ice Mapping Using Compact Polarimetric Synthetic Aperture Radar Imagery with Learned Features and Contextual Information. Remote Sens. 2023, 15, 3199. [Google Scholar] [CrossRef]
- Taleghanidoozdoozan, S.; Xu, L.; Clausi, D.A. Sea Ice Mapping from Compact Polarimetric SAR Imagery Using Contextual Information and Learned Features. J. Comput. Vis. Imaging Syst. 2023, 8, 64–66. [Google Scholar]
- Stokholm, A.; Buus-Hinkler, J.; Wulf, T.; Korosov, A.; Saldo, R.; Pedersen, L.T.; Arthurs, D.; Dragan, I.; Modica, I.; Pedro, J.; et al. The AutoICE Challenge. Cryosphere 2024, 18, 3471–3494. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Miller, J. Contextual Land-Cover Classification: Incorporating Spatial Dependence in Land-Cover Classification Models Using Random Forests and the Getis Statistic. Remote Sens. Lett. 2010, 1, 45–54. [Google Scholar] [CrossRef]
- Peng, Z.; Guo, Z.; Huang, W.; Wang, Y.; Xie, L.; Jiao, J.; Tian, Q.; Ye, Q. Conformer: Local Features Coupling Global Representations for Recognition and Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 9454–9468. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. 2017, arXiv:1706.03762. [Google Scholar]
- Yang, J.; Li, C.; Zhang, P.; Dai, X.; Xiao, B.; Yuan, L.; Gao, J. Focal Self-Attention for Local-Global Interactions in Vision Transformers. arXiv 2021, arXiv:2107.00641. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.-P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid Vision Transformer: A Versatile Backbone for Dense Prediction without Convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Chu, X.; Tian, Z.; Wang, Y.; Zhang, B.; Ren, H.; Wei, X.; Xia, H.; Shen, C. Twins: Revisiting the Design of Spatial Attention in Vision Transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 9355–9366. [Google Scholar]
- Li, W.; Wang, X.; Xia, X.; Wu, J.; Xiao, X.; Zheng, M.; Wen, S. Sepvit: Separable Vision Transformer. arXiv 2022, arXiv:2203.15380. [Google Scholar]
- Zhang, P.; Dai, X.; Yang, J.; Xiao, B.; Yuan, L.; Zhang, L.; Gao, J. Multi-Scale Vision Longformer: A New Vision Transformer for High-Resolution Image Encoding. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Xing, H.; Zhu, L.; Feng, Y.; Wang, W.; Hou, D.; Meng, F.; Ni, Y. An Adaptive Change Threshold Selection Method Based on Land Cover Posterior Probability and Spatial Neighborhood Information. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2021, 14, 11608–11621. [Google Scholar] [CrossRef]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Lin, H.; Cheng, X.; Wu, X.; Shen, D. CAT: Cross Attention in Vision Transformer. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 21–26 July 2016. [Google Scholar]
- Robertson, L.D.; McNairn, H.; McNairn, C.; Ihuoma, S.; Jiao, X. Compact Polarimetry for Operational Crop Inventory. In Proceedings of the IGARSS IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Roy, S.; Das, A.; Omkar, S.N. A Distributed Land Cover Classification of FP and CP SAR Observation Using MapReduce-Based Multi-Layer Perceptron Algorithm over the Mumbai Mangrove Region of India. Int. J. Remote Sens. 2023, 44, 1510–1532. [Google Scholar] [CrossRef]
- Ghanbari, M.; Xu, L.; Clausi, D.A. Local and Global Spatial Information for Land Cover Semi-Supervised Classification of Complex Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 20, 4004205. [Google Scholar]
- Wang, H.; Xing, C.; Yin, J.; Yang, J. Land Cover Classification for Polarimetric SAR Images Based on Vision Transformer. Remote Sens. 2022, 14, 4656. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y.-Q. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Chen, S.-W.; Tao, C.-S. PolSAR Image Classification Using Polarimetric-Feature-Driven Deep Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2018, 15, 627–631. [Google Scholar] [CrossRef]
- Yang, C.; Hou, B.; Ren, B.; Hu, Y.; Jiao, L. CNN-Based Polarimetric Decomposition Feature Selection for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8796–8812. [Google Scholar] [CrossRef]
- Xie, W.; Ma, G.; Zhao, F.; Liu, H.; Zhang, L. PolSAR Image Classification via a Novel Semi-Supervised Recurrent Complex-Valued Convolution Neural Network. Neurocomputing 2020, 388, 255–268. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Zou, B. PolSAR Image Classification with Lightweight 3D Convolutional Networks. Remote. Sens. 2020, 12, 396. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A Hybrid MLP-CNN Classifier for Very Fine Resolution Remotely Sensed Image Classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, L.; Zou, B. Exploring Vision Transformers for Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote. Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Wu, W.; Li, H.; Li, X.; Guo, H.; Zhang, L. PolSAR Image Semantic Segmentation Based on Deep Transfer Learning—Realizing Smooth Classification with Small Training Sets. IEEE Geosci. Remote. Sens. Lett. 2019, 16, 977–981. [Google Scholar] [CrossRef]
- Henry, C.; Azimi, S.M.; Merkle, N. Road Segmentation in SAR Satellite Images with Deep Fully Convolutional Neural Networks. IEEE Geosci. Remote. Sens. Lett. 2018, 15, 1867–1871. [Google Scholar] [CrossRef]
- Mullissa, A.G.; Persello, C.; Tolpekin, V. Fully Convolutional Networks for Multi-Temporal SAR Image Classification. In Proceedings of the IGARSS IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Mullissa, A.G.; Persello, C.; Stein, A. PolSARNet: A Deep Fully Convolutional Network for Polarimetric SAR Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5300–5309. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Liu, G.; Jiao, L. A Novel Deep Fully Convolutional Network for PolSAR Image Classification. Remote Sens. 2018, 10, 1984. [Google Scholar] [CrossRef]
- Jamali, A.; Roy, S.K.; Bhattacharya, A.; Ghamisi, P. Local Window Attention Transformer for Polarimetric SAR Image Classification. IEee Geosci. Remote. Sens. Lett. 2023. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Liang, W.; Cao, Y.; Li, M. High Resolution SAR Image Classification Using Global-Local Network Structure Based on Vision Transformer and CNN. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 4505405. [Google Scholar] [CrossRef]
- Cai, J.; Zhang, Y.; Guo, J.; Zhao, X.; Lv, J.; Hu, Y. ST-PN: A Spatial Transformed Prototypical Network for Few-Shot SAR Image Classification. Remote Sens. 2022, 14, 2019. [Google Scholar] [CrossRef]
- Wang, C.; Huang, Y.; Liu, X.; Pei, J.; Zhang, Y.; Yang, J. Global in Local: A Convolutional Transformer for SAR ATR FSL. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yang, Z.-A.; Zheng, N.-R.; Wang, F. SAR Image Classification by Combining Transformer and Convolutional Neural Networks. In Proceedings of the 8th China High Resolution Earth Observation Conference (CHREOC 2022), High Resolution Earth Observation: Wide Horizon, High Accurac, Singapore, 30 November 2022. [Google Scholar]
- Ramathilagam, A.B.; Natarajan, S.; Kumar, A. TransCropNet: A Multichannel Transformer with Feature-Level Fusion for Crop Classification in Agricultural Smallholdings Using Sentinel Images. J. Appl. Remote Sens. 2023, 17, 024501. [Google Scholar] [CrossRef]
- Li, X.; Lei, L.; Sun, Y.; Li, M.; Kuang, G. Collaborative Attention-Based Heterogeneous Gated Fusion Network for Land Cover Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3829–3845. [Google Scholar] [CrossRef]
- Wang, Y.; Albrecht, C.M.; Zhu, X. Self-Supervised Vision Transformers for Joint SAR-Optical Representation Learning. In Proceedings of the IGARSS IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022. [Google Scholar]
- Li, K.; Zhao, W.; Peng, R.; Ye, T. Multi-Branch Self-Learning Vision Transformer (MSViT) for Crop Type Mapping with Optical-SAR Time-Series. Comput. Electron. Agric. 2022, 203, 107497. [Google Scholar] [CrossRef]
- Wang, H.; Chen, X.; Zhang, T.; Xu, Z.; Li, J. CCTNet: Coupled CNN and Transformer Network for Crop Segmentation of Remote Sensing Images. Remote Sens. 2022, 14, 1956. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Hu, Q. Transfuse: Fusing Transformers and CNNs for Medical Image Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI, 24th International Conference, Strasbourg, France, 27 September–1 October 1 2021. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Jafari, M.; Maghsoudi, Y.; Zoej, M.J.V. A New Method for Land Cover Characterization and Classification of Polarimetric SAR Data Using Polarimetric Signatures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3595–3607. [Google Scholar] [CrossRef]
- Cloude, S. Polarisation: Applications in Remote Sensing; OUP Oxford: Oxford, UK, 2009. [Google Scholar]
- Raney, R.K. Hybrid-Polarity SAR Architecture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3397–3404. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled Weight Decay Regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Bahri, A.; Majelan, S.G.; Mohammadi, S.; Noori, M.; Mohammadi, K. Remote Sensing Image Classification via Improved Cross-Entropy Loss and Transfer Learning Strategy Based on Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1087–1091. [Google Scholar] [CrossRef]




| Output | PFC Attention Method | |
|---|---|---|
| Stage 1 | 32 × 32 × 16 | Linear Embedding, LN |
| Stage 2 | 16 × 16 × 32 | Downsampling, LN |
| Stage 3 | 8 × 8 × 64 | Downsampling, LN |
| Stage 4 | 4 × 4 × 128 | Downsampling, LN |
| Global Average | 1 × 1 × 128 | 4 × 4 average pool |
| Classification | 5 | 128 × 5 fully connected |
| Softmax | 5 |
| Model Name | Number of Parameters | Training Time | Efficiency Metric |
|---|---|---|---|
| (Millions) | (Hours) | (Hours/Million Params) | |
| CAT [26] | 1.45 M | 7.64 | 5.26 |
| Focal [18] | 0.59 M | 2.99 | 5.06 |
| PVT [19] | 0.69 M | 0.98 | 1.42 |
| ResCNN [27] | 0.70 M | 0.67 | 0.95 |
| SepViT [22] | 0.72 M | 1.37 | 1.91 |
| Twins [21] | 0.67 M | 1.02 | 1.52 |
| Swin [20] | 0.76 M | 1.25 | 1.64 |
| FC | 0.78 M | 1.61 | 2.06 |
| PFC | 0.78 M | 1.61 | 2.06 |
| Class | # of Train | # of Test |
|---|---|---|
| Forest | 15,381 | 11,690 |
| Water | 14,853 | 8093 |
| Urban 1 | 12,032 | 11,263 |
| Urban 2 | 15,098 | 10,206 |
| Farm | 10,773 | 20,022 |
| Name | OA (%) | Forest | Water | Urban1 | Urban2 | Farm | ||
|---|---|---|---|---|---|---|---|---|
| CAT | 86.92 | 0.8343 | 0.8696 | 0.9116 | 0.7723 | 0.8843 | 0.9234 | 0.8574 |
| Focal | 88.48 | 0.8544 | 0.8852 | 0.9248 | 0.7812 | 0.9208 | 0.8715 | |
| PVT | 86.92 | 0.8351 | 0.8694 | 0.9218 | 0.7596 | 0.8955 | 0.9138 | 0.8561 |
| ResCNN | 88.22 | 0.8500 | 0.8780 | 0.8835 | 0.8246 | 0.8820 | 0.8984 | |
| SepViT | 88.80 | 0.8579 | 0.8850 | 0.9049 | 0.8219 | 0.9046 | 0.8971 | 0.8970 |
| Twins | 88.49 | 0.8538 | 0.8788 | 0.9181 | 0.8153 | 0.8531 | 0.8931 | 0.9144 |
| Swin | 87.14 | 0.8372 | 0.8707 | 0.9049 | 0.7881 | 0.9076 | 0.8866 | 0.8661 |
| FC | 91.25 | 0.8885 | 0.9054 | 0.9346 | 0.8564 | 0.9087 | 0.8844 | 0.9428 |
| PFC | 0.9191 | 0.9179 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taleghanidoozdoozan, S.; Xu, L.; Clausi, D.A. Pyramid Fine and Coarse Attentions for Land Cover Classification from Compact Polarimetric SAR Imagery. Remote Sens. 2025, 17, 367. https://doi.org/10.3390/rs17030367
Taleghanidoozdoozan S, Xu L, Clausi DA. Pyramid Fine and Coarse Attentions for Land Cover Classification from Compact Polarimetric SAR Imagery. Remote Sensing. 2025; 17(3):367. https://doi.org/10.3390/rs17030367
Chicago/Turabian StyleTaleghanidoozdoozan, Saeid, Linlin Xu, and David A. Clausi. 2025. "Pyramid Fine and Coarse Attentions for Land Cover Classification from Compact Polarimetric SAR Imagery" Remote Sensing 17, no. 3: 367. https://doi.org/10.3390/rs17030367
APA StyleTaleghanidoozdoozan, S., Xu, L., & Clausi, D. A. (2025). Pyramid Fine and Coarse Attentions for Land Cover Classification from Compact Polarimetric SAR Imagery. Remote Sensing, 17(3), 367. https://doi.org/10.3390/rs17030367







