Dual-Function Radar Communications: A Secure Optimization Approach Using Partial Group Successive Interference Cancellation
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution and Paper Organization
- Starting from the security of integrating radar and communication systems, we investigate a physical layer security issue in the dual-function radar communication scenario where the base station simultaneously performs radar target detection and communicates with multiple users. The target of interest has the potential to eavesdrop on the communication between the base station and legitimate users. By jointly considering the radar target echo SNR and increase in the legitimate transmission rate increment, we effectively optimize the radar target detection performance and secrecy performance of the system.
- Different from the existing security design and performance enhancement schemes, this paper fully takes into account the characteristics of the dual-function base station and legitimate users. By leveraging the split messages at the base station, we propose a secure design based on PGSIC that the legitimate user decodes the desired message in a partial and sequential way. Together with an optimized beamformer, our secure design can achieve further increments in the secure transmission rate of the DFRC system.
- In order to maximize the radar echo SNR, we formulate an optimization problem under the transmit power constraints and the legitimate rate increments and eavesdropping rate constraints, which guarantee the physical layer security requirement. To solve the non-convexity of the problem, we reformulate the optimization problem, introduce new variables, and relax the problem. Then, we propose a joint secure beamforming and rate increment optimization algorithm to iteratively optimize the rate increments of the legitimate users and the secure beamforming.
2. System Model
3. Radar Sensing and Secure Transmission Design
3.1. Radar Sensing Requirement
3.2. Eavesdropping Performance
3.3. Secure Design
4. Problem Formulation and Optimization Algorithm
4.1. Problem Formulation
4.2. Problem Relaxation
4.3. Joint Secure Beamforming and Rate Optimization Algorithm
| Algorithm 1 Joint secure beamforming and rate optimization algorithm |
|
5. Results and Discussion
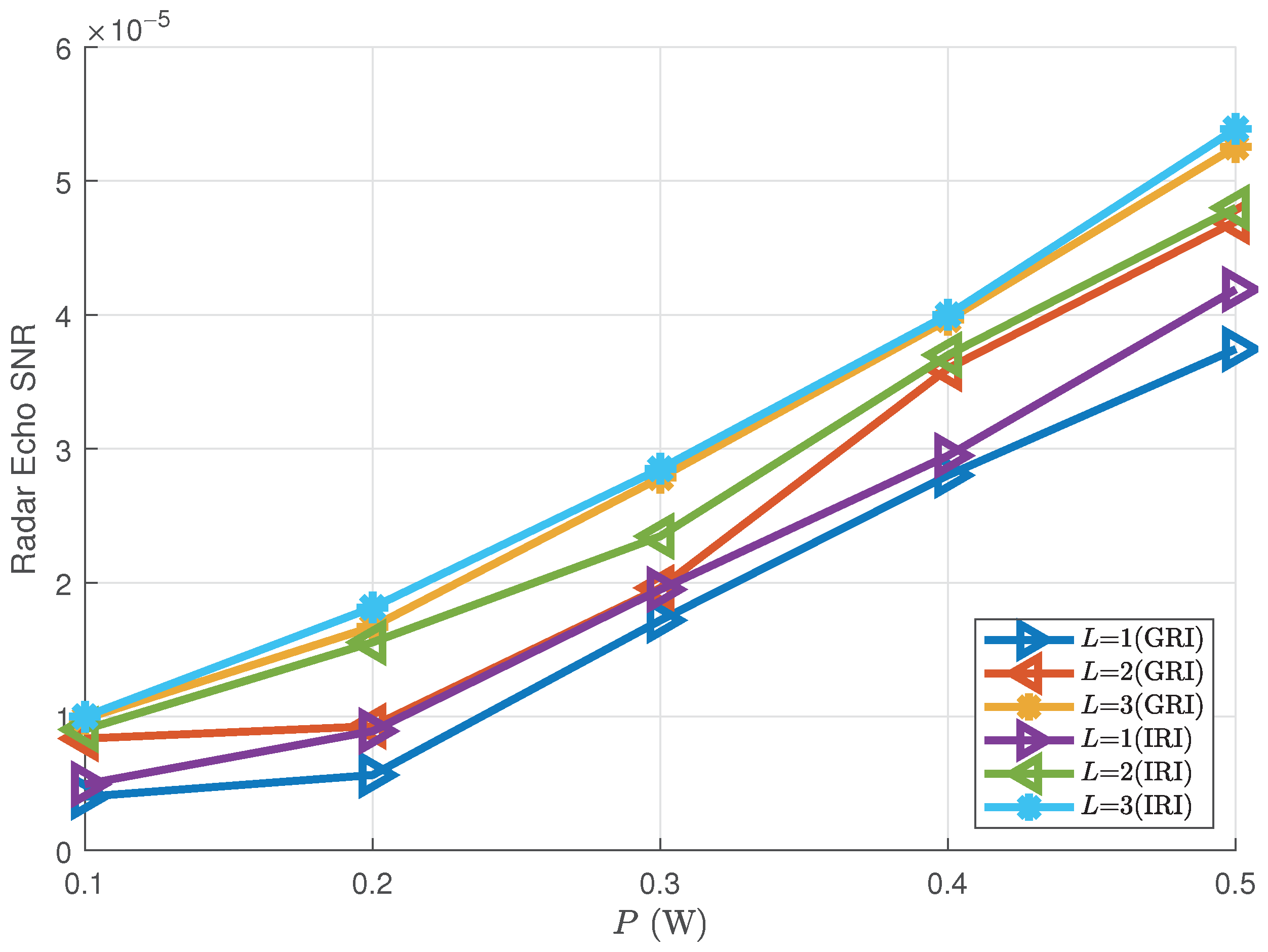
5.1. Radar Performance
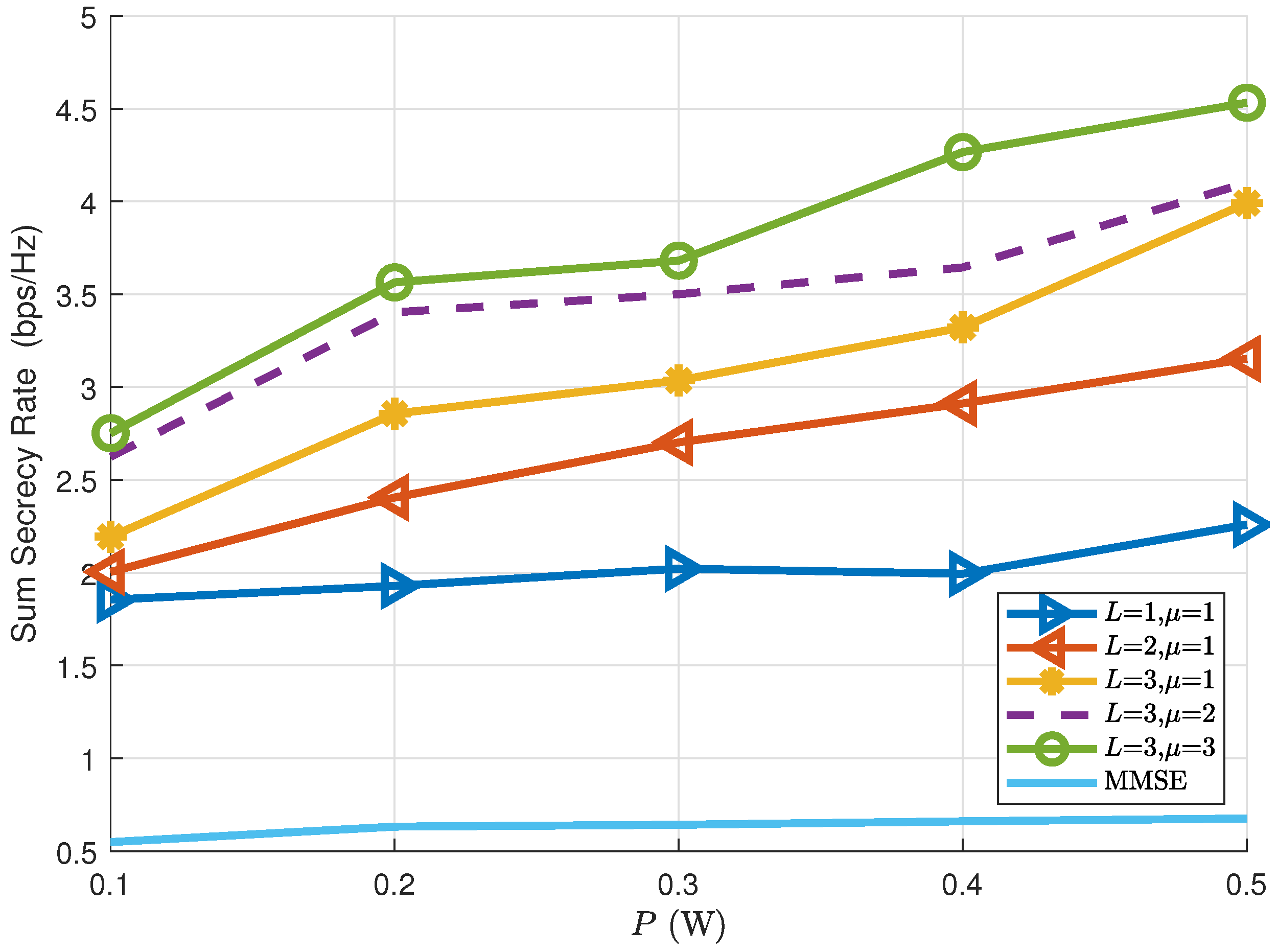
5.2. System Level Secrecy Performance
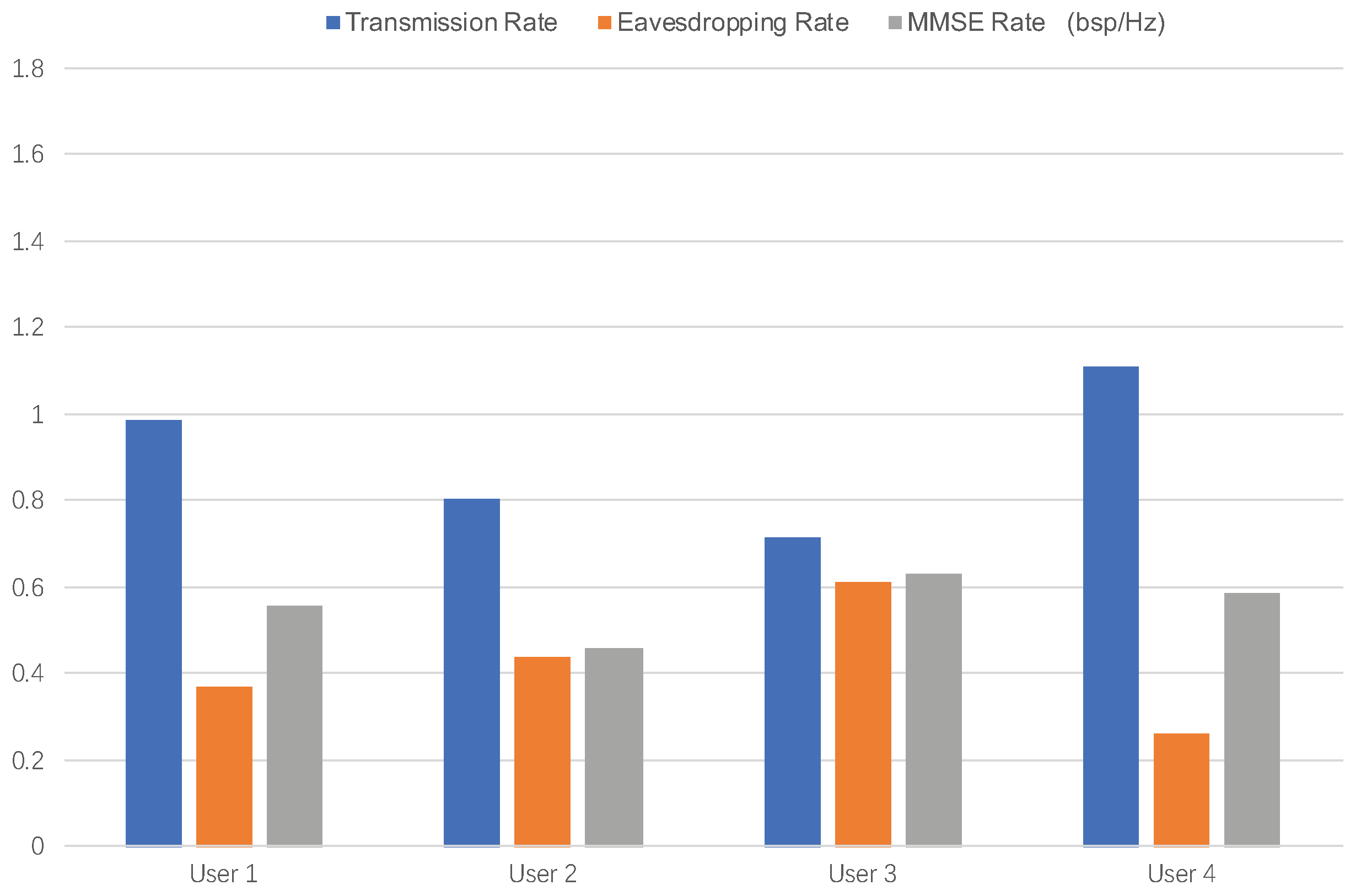
5.3. User Level Secrecy Performance
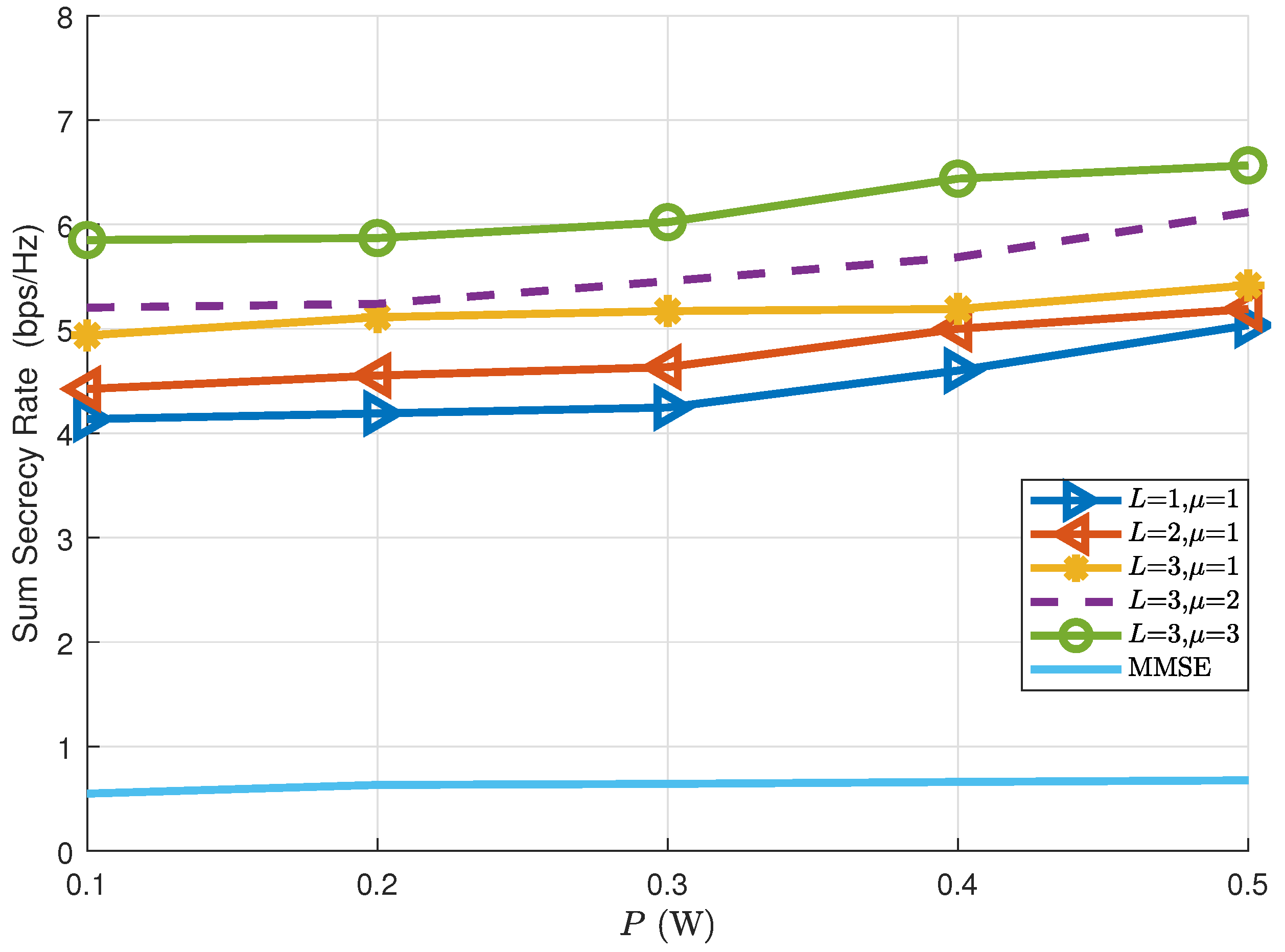
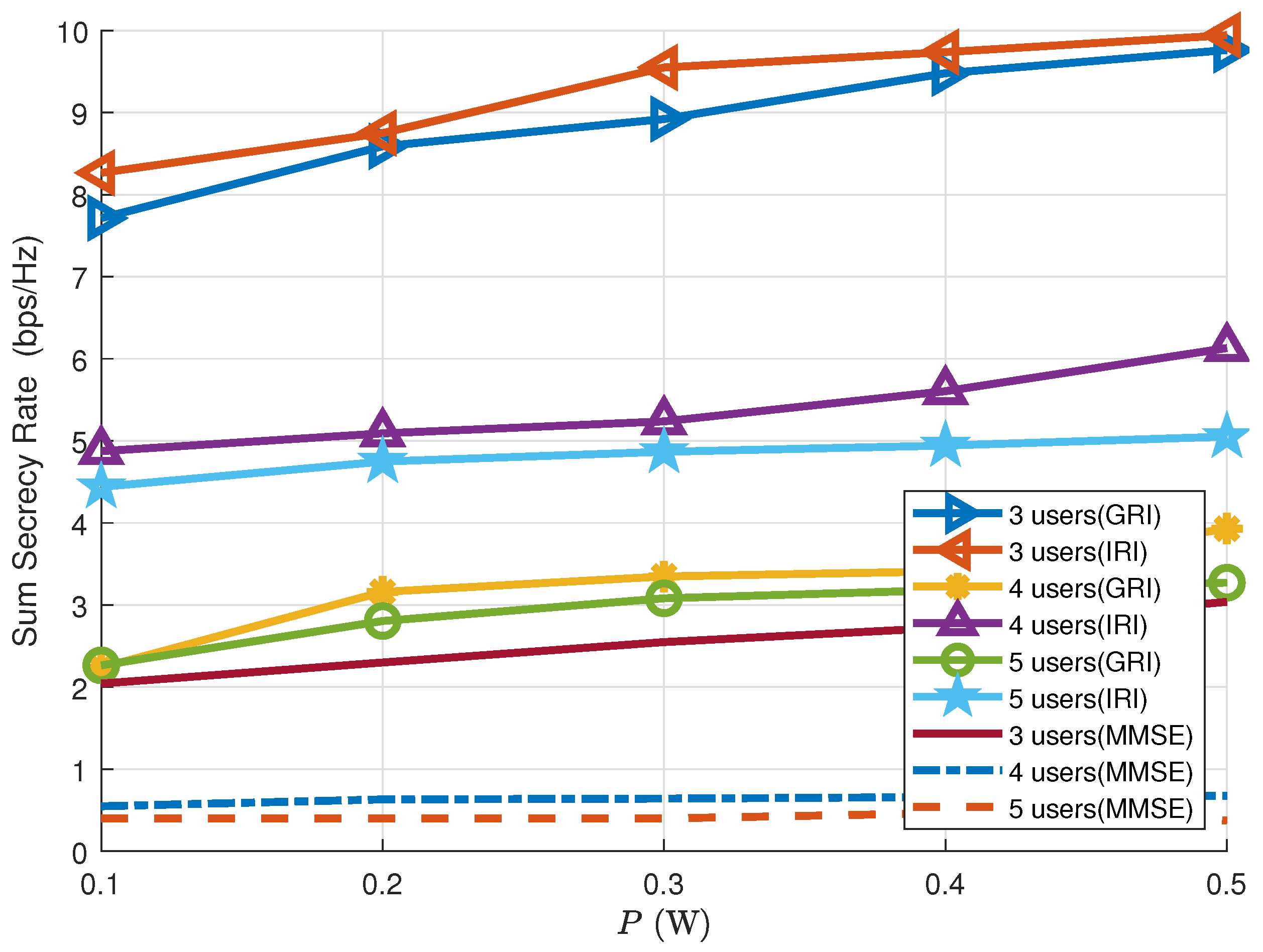
5.4. Secrecy Performance with Different Numbers of Legitimate Users
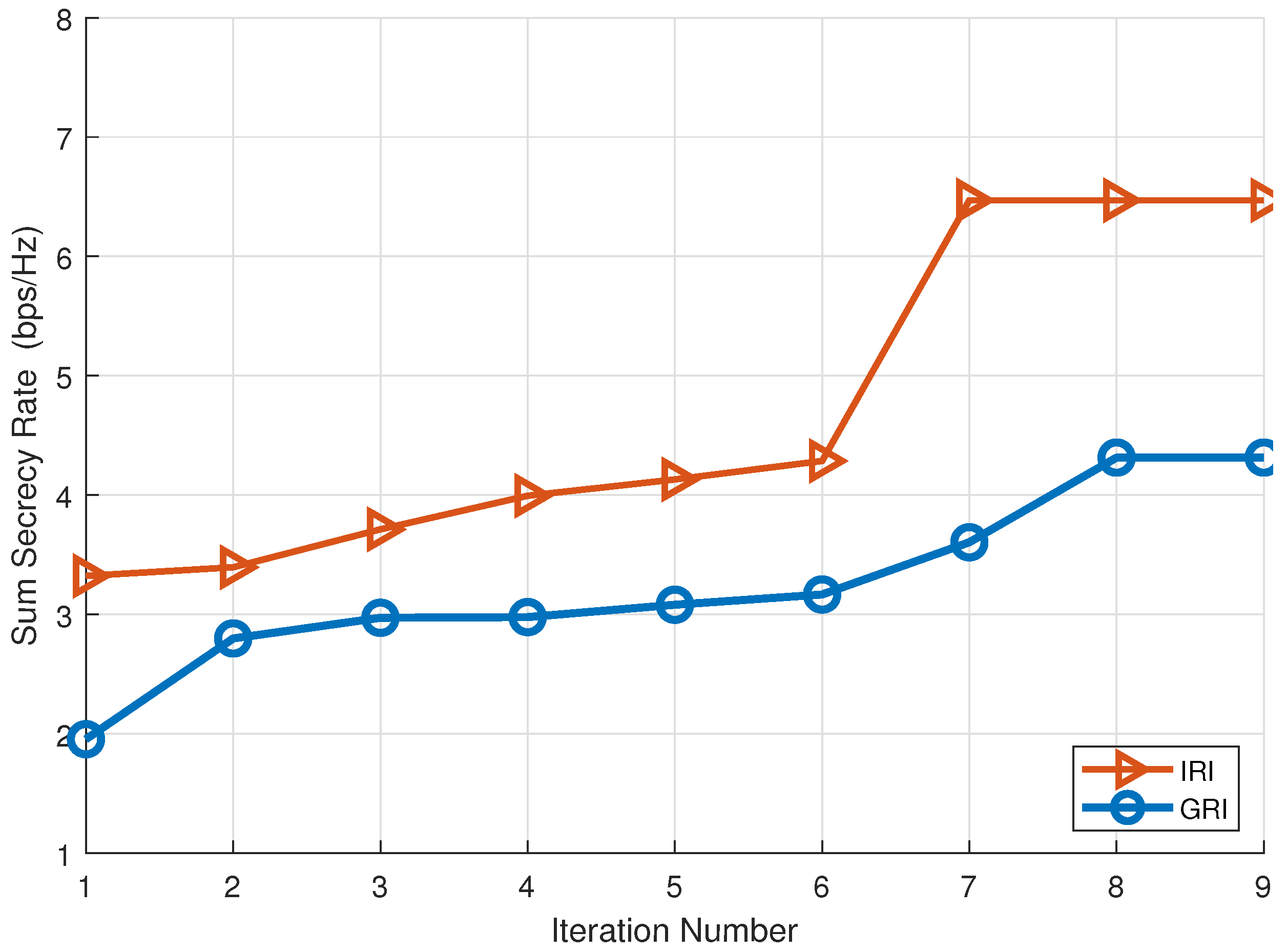
5.5. Convergence Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Partial Group Successive Interference Cancellation
| Algorithm A1 PGSIC—the optimal partition for the legitimate user (OP) |
|
| Algorithm A2 PGSIC—global rate increment assignment (GRI) |
|
| Algorithm A3 PGSIC—iterative rate increment assignment (IRI) |
|
References
- Binetti, M.S.; Campanale, C.; Massarelli, C.; Uricchio, V.F. The Use of Weather Radar Data: Possibilities, Challenges and Advanced Applications. Earth 2022, 3, 157–171. [Google Scholar] [CrossRef]
- Steiner, M.; Grebner, T.; Waldschmidt, C. Millimeter-Wave SAR-Imaging with Radar Networks Based on Radar Self-Localization. IEEE Trans. Microw. Theory Tech. 2020, 68, 4652–4661. [Google Scholar] [CrossRef]
- Hakobyan, G.; Yang, B. High-Performance Automotive Radar: A Review of Signal Processing Algorithms and Modulation Schemes. IEEE Signal Process. Mag. 2019, 36, 32–44. [Google Scholar] [CrossRef]
- Aydogdu, C.; Keskin, M.F.; Carvajal, G.K.; Eriksson, O.; Hellsten, H.; Herbertsson, H.; Nilsson, E.; Rydstrom, M.; Vanas, K.; Wymeersch, H. Radar Interference Mitigation for Automated Driving: Exploring Proactive Strategies. IEEE Signal Process. Mag. 2020, 37, 72–84. [Google Scholar] [CrossRef]
- Liu, Y.; Han, F.; Zhao, S. Flexible and Reliable Multiuser SWIPT IoT Network Enhanced by UAV-Mounted Intelligent Reflecting Surface. IEEE Trans. Reliab. 2022, 71, 1092–1103. [Google Scholar] [CrossRef]
- Koukiou, G. SAR Features and Techniques for Urban Planning—A Review. Remote Sens. 2024, 16, 1923. [Google Scholar] [CrossRef]
- Liu, F.; Zheng, L.; Cui, Y.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Eldar, Y.C. Seventy Years of Radar and Communications: The road from separation to integration. IEEE Signal Process. Mag. 2023, 40, 106–121. [Google Scholar] [CrossRef]
- Rojhani, N.; Shaker, G. Comprehensive Review: Effectiveness of MIMO and Beamforming Technologies in Detecting Low RCS UAVs. Remote Sens. 2024, 16, 1016. [Google Scholar] [CrossRef]
- Zhang, L.; Liang, Y.C.; Xiao, M. Spectrum Sharing for Internet of Things: A Survey. IEEE Wirel. Commun. 2019, 26, 132–139. [Google Scholar] [CrossRef]
- Feng, Z.; Fang, Z.; Wei, Z.; Chen, X.; Quan, Z.; Ji, D. Joint radar and communication: A survey. China Commun. 2020, 17, 1–27. [Google Scholar] [CrossRef]
- Zheng, L.; Lops, M.; Eldar, Y.C.; Wang, X. Radar and Communication Coexistence: An Overview: A Review of Recent Methods. IEEE Signal Process. Mag. 2019, 36, 85–99. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Luong, N.C.; Feng, S.; Nguyen, T.H.; Elbassioni, K.; Niyato, D.; Kim, D.I. Joint Rate Allocation and Power Control for RSMA-Based Communication and Radar Coexistence Systems. IEEE Trans. Veh. Technol. 2023, 72, 14673–14687. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, S.; Han, F.; Chai, M.; Jiang, H.; Zhang, H. Data Collection for Target Localization in Ocean Monitoring Radar-Communication Networks. Remote Sens. 2023, 15, 5126. [Google Scholar] [CrossRef]
- Ji, W.; Liu, T.; Song, Y.; Yin, H.; Tian, B.; Zhu, N. Modified Hybrid Integration Algorithm for Moving Weak Target in Dual-Function Radar and Communication System. Remote Sens. 2024, 16, 3601. [Google Scholar] [CrossRef]
- Luong, N.C.; Lu, X.; Hoang, D.T.; Niyato, D.; Kim, D.I. Radio Resource Management in Joint Radar and Communication: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2021, 23, 780–814. [Google Scholar] [CrossRef]
- Lou, X.; Xia, W.; Wong, K.K.; Zhao, H.; Quek, T.Q.S.; Zhu, H. Power Optimization for Integrated Active and Passive Sensing in DFRC Systems. IEEE Trans. Commun. 2024, 72, 3365–3377. [Google Scholar] [CrossRef]
- Xu, H.; Wang, H.; Liao, K.; Ouyang, S.; Gong, Y. Spatial Spectrum Estimation of Co-Channel Direct Signal in Passive Radar Based on Coprime Array. Remote Sens. 2022, 14, 5308. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, M.; Gao, Y.; Feng, Z. MIMO Radar Aided mmWave Time-Varying Channel Estimation in MU-MIMO V2X Communications. IEEE Trans. Wirel. Commun. 2021, 20, 7581–7594. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, Z.; Tong, F.; Sun, P.; Feng, X.; Zhao, Z. Joint Design of Transmitting Waveform and Receiving Filter via Novel Riemannian Idea for DFRC System. Remote Sens. 2023, 15, 3548. [Google Scholar] [CrossRef]
- Jiang, Z.M.; Rihan, M.; Deng, Q.; Mohamed, E.M.; Khallaf, H.S.; Wang, X.; Omar, R. On the Physical Layer Security of Automotive Dual-Function Radar-Communication Systems. IEEE Internet Things J. 2024, 11, 5090–5104. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.C.; Li, Z.; Ng, D.W.K.; Wong, K.K.; Al-Dhahir, N.; Niyato, D. STAR-RIS-Enabled Secure Dual-Functional Radar-Communications: Joint Waveform and Reflective Beamforming Optimization. IEEE Trans. Inf. Forensics Secur. 2023, 18, 4577–4592. [Google Scholar] [CrossRef]
- Su, Y.; Dai, Z.; Peng, Z.; Weng, R.; Ren, H.; Pan, C. Secure Transmission Optimization for RIS-Aided DFRC Systems with Artificial Noise. IEEE Commun. Lett. 2024, 28, 1780–1784. [Google Scholar] [CrossRef]
- Li, D.; Tang, B.; Xue, L. Waveform Design for MIMO DFRC Systems: Finer Sensing and Safer Communications. IEEE Trans. Signal Process. 2024, 72, 4509–4524. [Google Scholar] [CrossRef]
- Bazzi, A.; Chafii, M. Secure Full Duplex Integrated Sensing and Communications. IEEE Trans. Inf. Forensics Secur. 2024, 19, 2082–2097. [Google Scholar] [CrossRef]
- Mukherjee, A.; Fakoorian, S.A.A.; Huang, J.; Swindlehurst, A.L. Principles of Physical Layer Security in Multiuser Wireless Networks: A Survey. IEEE Commun. Surv. Tutor. 2014, 16, 1550–1573. [Google Scholar] [CrossRef]
- Chai, M.; Zhao, S.; Liu, Y. A Novel Secure Routing Design Based on Physical Layer Security in Millimeter-Wave VANET. Electronics 2023, 12, 4704. [Google Scholar] [CrossRef]
- Bai, L.; Zhu, L.; Liu, J.; Choi, J.; Zhang, W. Physical layer authentication in wireless communication networks: A survey. J. Commun. Inf. Netw. 2020, 5, 237–264. [Google Scholar] [CrossRef]
- Xie, N.; Zhang, J.; Zhang, Q. Security Provided by the Physical Layer in Wireless Communications. IEEE Netw. 2023, 37, 42–48. [Google Scholar] [CrossRef]
- Mitev, M.; Chorti, A.; Poor, H.V.; Fettweis, G.P. What Physical Layer Security Can Do for 6G Security. IEEE Open J. Veh. Technol. 2023, 4, 375–388. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Li, A.; Sun, H.; Hanzo, L. MU-MIMO Communications with MIMO Radar: From Co-Existence to Joint Transmission. IEEE Trans. Wirel. Commun. 2018, 17, 2755–2770. [Google Scholar] [CrossRef]
- Yao, X.; Pan, B.; Fan, T.; Yu, X.; Cui, G.; Nie, X. MIMO DFRC Signal Design in Signal-Dependent Clutter. Remote Sens. 2023, 15, 3256. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Ratnarajah, T.; Petropulu, A. On Range Sidelobe Reduction for Dual-Functional Radar-Communication Waveforms. IEEE Wirel. Commun. Lett. 2020, 9, 1572–1576. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C. A Tutorial on Joint Radar and Communication Transmission for Vehicular Networks—Part II: State of the Art and Challenges Ahead. IEEE Commun. Lett. 2021, 25, 327–331. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, W.; Masouros, C.; Yuan, J. Radar-Assisted Predictive Beamforming for Vehicular Links: Communication Served by Sensing. IEEE Trans. Wirel. Commun. 2020, 19, 7704–7719. [Google Scholar] [CrossRef]
- Yang, J.; Tan, Y.; Yu, X.; Cui, G.; Zhang, D. Waveform Design for Watermark Framework Based DFRC System with Application on Joint SAR Imaging and Communication. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, Q.; Huang, Z.; Li, Z.; Xu, Y.; Zhang, J. Unimodular Waveform Design for the DFRC System with Constrained Communication QoS. Remote Sens. 2023, 15, 5350. [Google Scholar] [CrossRef]
- Janjua, M.B.; Memişoğlu, E.; Qaraqe, K.A.; Arslan, H. Secure Pilot Allocation for Integrated Sensing and Communication. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; pp. 1466–1471. [Google Scholar] [CrossRef]
- Su, N.; Liu, F.; Masouros, C. Sensing-Assisted Eavesdropper Estimation: An ISAC Breakthrough in Physical Layer Security. IEEE Trans. Wirel. Commun. 2024, 23, 3162–3174. [Google Scholar] [CrossRef]
- Jia, H.; Li, X.; Ma, L. Physical Layer Security Optimization With Cramér–Rao Bound Metric in ISAC Systems Under Sensing-Specific Imperfect CSI Model. IEEE Trans. Veh. Technol. 2024, 73, 6980–6992. [Google Scholar] [CrossRef]
- Su, N.; Liu, F.; Wei, Z.; Liu, Y.F.; Masouros, C. Secure Dual-Functional Radar-Communication Transmission: Exploiting Interference for Resilience Against Target Eavesdropping. IEEE Trans. Wirel. Commun. 2022, 21, 7238–7252. [Google Scholar] [CrossRef]
- Han, T.; Kobayashi, K. A new achievable rate region for the interference channel. IEEE Trans. Inf. Theory 1981, 27, 49–60. [Google Scholar] [CrossRef]
- Chai, M.; Zhao, S.; Han, F.; Liu, Y. Beamforming Design with Partial Group Successive Interference Cancelation for ISAC Systems. IEEE Internet Things J. 2024, 11, 29511–29522. [Google Scholar] [CrossRef]
- Xu, C.; Clerckx, B.; Chen, S.; Mao, Y.; Zhang, J. Rate-Splitting Multiple Access for Multi-Antenna Joint Radar and Communications. IEEE J. Sel. Top. Signal Process. 2021, 15, 1332–1347. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, W.; Wu, Q.; Yuan, J.; Zhang, S.; Li, Z.; Li, J. Rate-Splitting Multiple Access for Transmissive Reconfigurable Intelligent Surface Transceiver Empowered ISAC Systems. IEEE Internet Things J. 2024, 11, 27245–27259. [Google Scholar] [CrossRef]
- Yin, L.; Clerckx, B. Rate-Splitting Multiple Access for Dual-Functional Radar-Communication Satellite Systems. In Proceedings of the 2022 IEEE Wireless Communications and Networking Conference (WCNC), Austin, TX, USA, 10–13 April 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Z.; Li, D.; Zhao, N.; Wu, Z.; Li, Y.; Niyato, D. Secure Precoding Optimization for NOMA-Aided Integrated Sensing and Communication. IEEE Trans. Commun. 2022, 70, 8370–8382. [Google Scholar] [CrossRef]
- Hua, M.; Wu, Q.; Chen, W.; Dobre, O.A.; Swindlehurst, A.L. Secure Intelligent Reflecting Surface-Aided Integrated Sensing and Communication. IEEE Trans. Wirel. Commun. 2024, 23, 575–591. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Ma, W.K.; So, A.M.C.; Ye, Y.; Zhang, S. Semidefinite Relaxation of Quadratic Optimization Problems. IEEE Signal Process. Mag. 2010, 27, 20–34. [Google Scholar] [CrossRef]
- Cao, Y.; Zhao, N.; Pan, G.; Chen, Y.; Fan, L.; Jin, M.; Alouini, M.S. Secrecy Analysis for Cooperative NOMA Networks with Multi-Antenna Full-Duplex Relay. IEEE Trans. Commun. 2019, 67, 5574–5587. [Google Scholar] [CrossRef]
- Li, D.; Yang, Z.; Zhao, N.; Wu, Z.; Quek, T.Q.S. NOMA Aided Secure Transmission for IRS-ISAC. IEEE Trans. Wirel. Commun. 2024, 23, 10911–10925. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, M.; Zhao, S.; Liu, Y. Dual-Function Radar Communications: A Secure Optimization Approach Using Partial Group Successive Interference Cancellation. Remote Sens. 2025, 17, 364. https://doi.org/10.3390/rs17030364
Chai M, Zhao S, Liu Y. Dual-Function Radar Communications: A Secure Optimization Approach Using Partial Group Successive Interference Cancellation. Remote Sensing. 2025; 17(3):364. https://doi.org/10.3390/rs17030364
Chicago/Turabian StyleChai, Mengqiu, Shengjie Zhao, and Yuan Liu. 2025. "Dual-Function Radar Communications: A Secure Optimization Approach Using Partial Group Successive Interference Cancellation" Remote Sensing 17, no. 3: 364. https://doi.org/10.3390/rs17030364
APA StyleChai, M., Zhao, S., & Liu, Y. (2025). Dual-Function Radar Communications: A Secure Optimization Approach Using Partial Group Successive Interference Cancellation. Remote Sensing, 17(3), 364. https://doi.org/10.3390/rs17030364





