Research on Multi-Source Precipitation Fusion Based on Classification and Regression Machine Learning Methods—A Case Study of the Min River Basin in the Eastern Source of the Qinghai–Tibet Plateau

Highlights

What are the main findings?

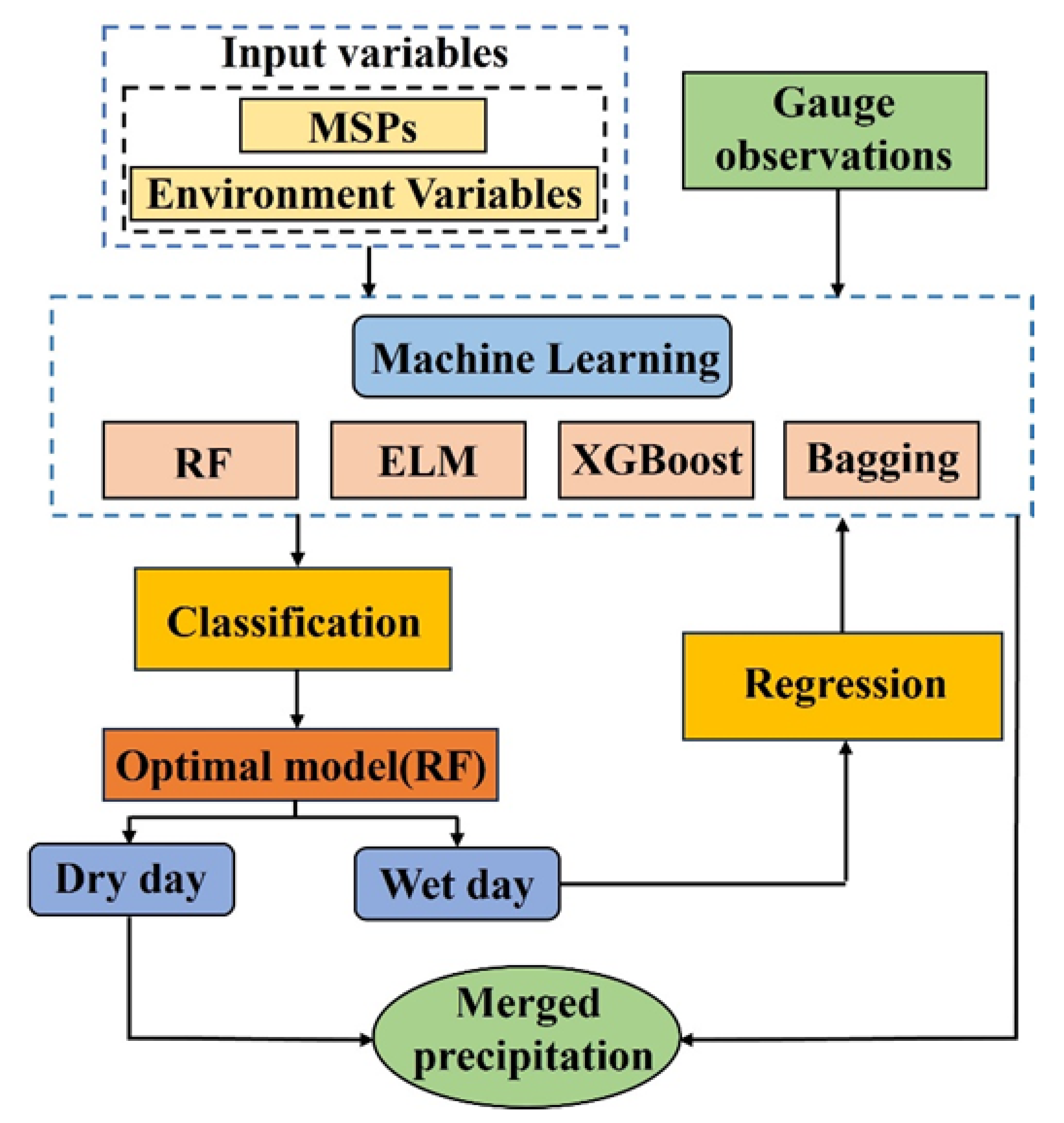
• A two-step machine learning fusion framework integrating precipitation event identification and quantitative intensity estimation is proposed, addressing the inaccuracy of satellite precipitation products in complex terrain like the MRB.
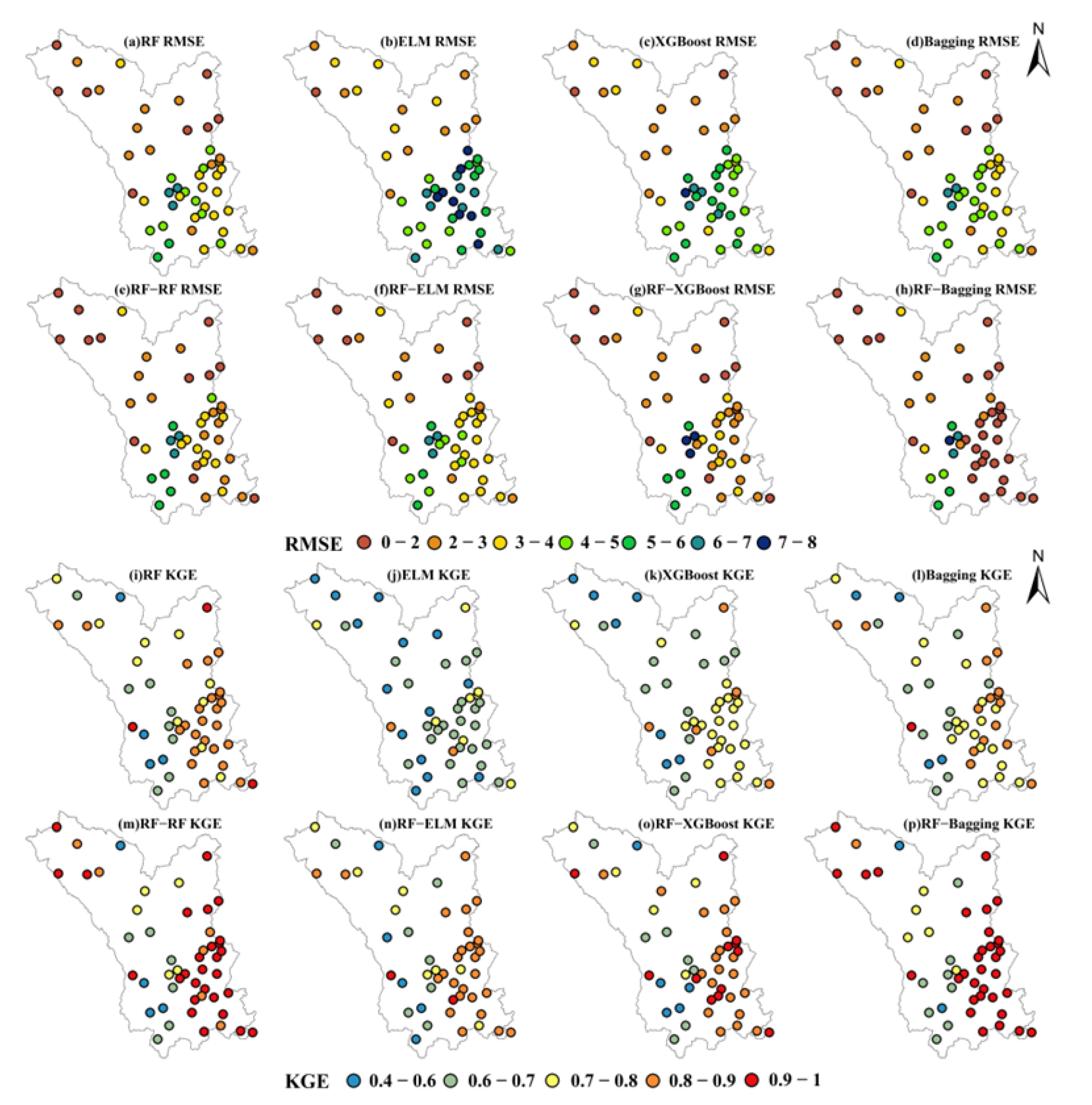
• Double Machine Learning (DML) models outperform Single Machine Learning (SML) models and original products, with RF-Bagging being the optimal model—daily-scale Correlation Coefficient (CC) is over 50% higher than original data, while RMSE and MAE are reduced by more than 40% and 35%, respectively.

What are the implications of the main findings?

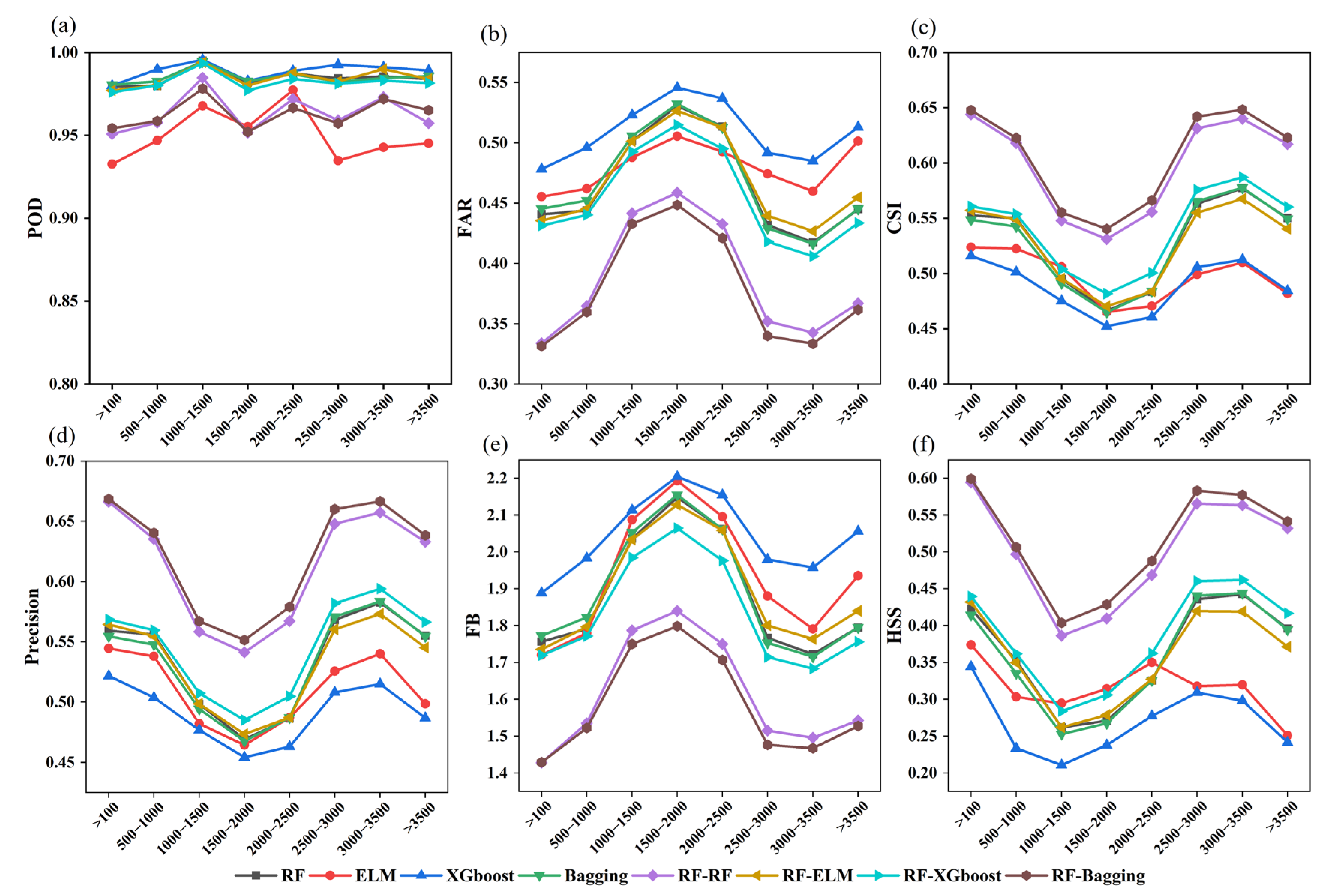
• RF-Bagging and RF-RF models exhibit strong stability: Critical Success Index (CSI) remains stable at ~0.7 under moderate-to-heavy precipitation, and Probability of Detection (POD) approaches 1 in high-altitude areas of the MRB.
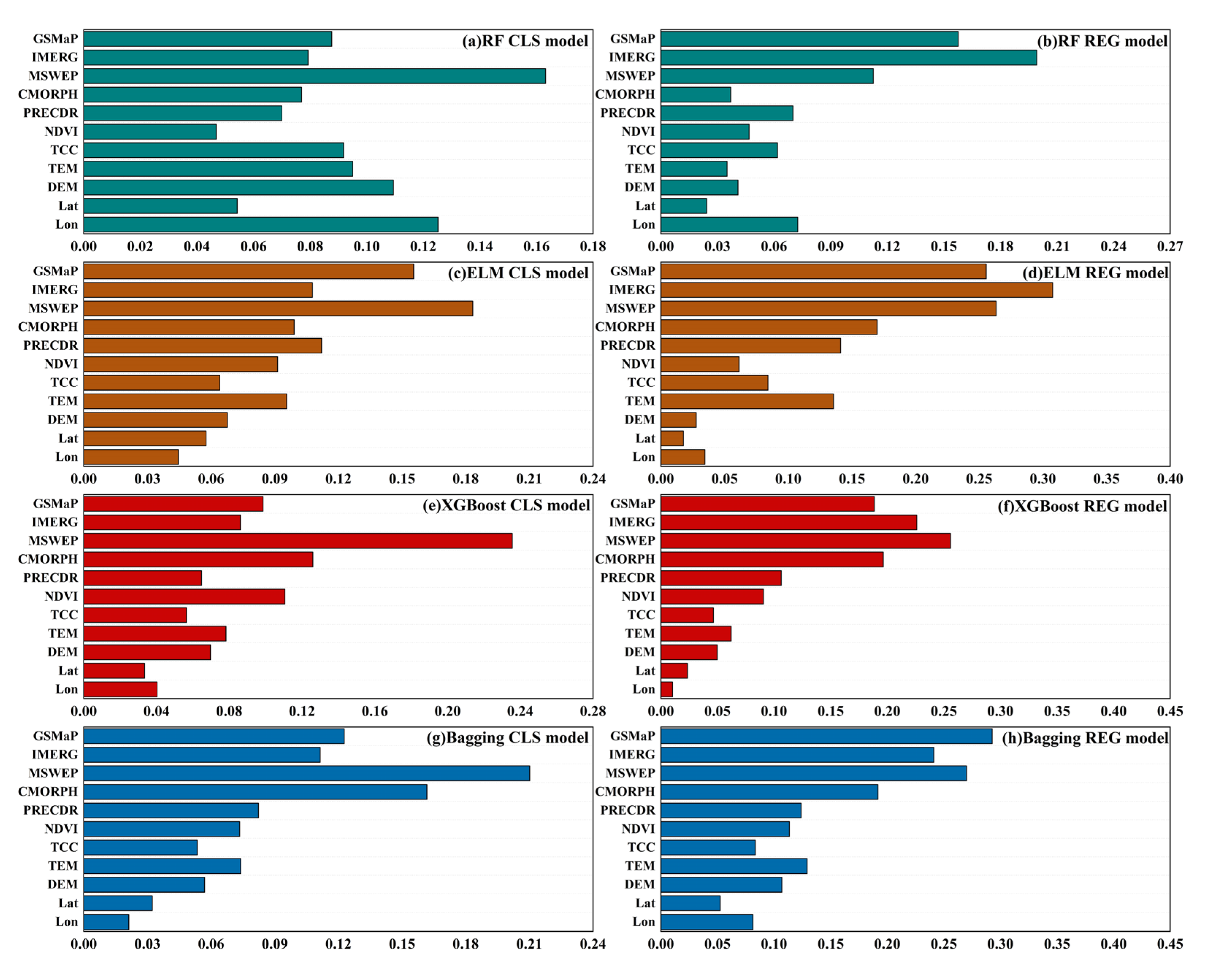
• GSMaP, IMERG, and MSWEP serve as core input variables for all models; RF/ELM rely more on environmental variables (NDVI, TCC, DEM), while XGBoost/Bagging depend more on satellite precipitation data, reflecting distinct variable sensitivity characteristics.

Abstract

Against the backdrop of insufficient accuracy and adaptability of satellite precipitation products in complex terrain areas, this study focused on the Min River Basin (MRB) on the eastern edge of the Qinghai–Tibet Plateau. A two-step machine learning fusion framework was established, which integrates precipitation event identification and quantitative intensity estimation in a systematic manner. This framework incorporated 5 precipitation products (PERSIANN-CDR, CMORPH, GSMaP, IMERG, MSWEP), measured data, and environmental variables. The study compared the precipitation estimation performance of Random Forest (RF), Extreme Learning Machine (ELM), eXtreme Gradient Boosting (XGBoost), Bagging, and Double Machine Learning (DML) models, and analyzed the models’ performance under different precipitation intensities and altitudes, as well as their variable sensitivity. The results showed that: (1) DML models outperformed Single Machine Learning (SML) models and original precipitation products, with RF-Bagging being the optimal model. The daily-scale Correlation Coefficient (CC) of RF-Bagging was over 50% higher than that of original products, while the Root Mean Square Error (RMSE) and Mean Absolute Error (MAE) were reduced by more than 40% and 35%, respectively. (2) For moderate-to-heavy precipitation, the RF-Bagging and RF-RF models maintain a stable Critical Success Index (CSI) of 0.7. In high-altitude regions, their Probability of Detection (POD) approaches 1, and the Heidke Skill Score (HSS) is 30–40% higher than that in mid-altitude areas, significantly outperforming other models and demonstrating strong adaptability to complex terrain. For light precipitation, while the POD values of these two models are comparable to those of other models, their False Alarm Rate (FAR) is reduced by 15–20%, effectively mitigating precipitation false alarms. (3) GSMaP, IMERG, and MSWEP were the core input variables for all models. RF and ELM models were more dependent on environmental variables, while XGBoost and Bagging models relied more on satellite data. This framework can provide technical references for precipitation estimation in complex terrain areas and contribute to watershed water resource management as well as flood prevention and mitigation.

1. Introduction

Applications for flood forecasting and water resource management depend heavily on high-precision precipitation forecasting [1,2,3,4]. The main techniques for observing precipitation are weather radar, satellite remote sensing, and ground-based measurements [5,6]. The most precise and widely used technique for measuring precipitation is still ground-based observation, which usually uses rain gauges to determine the amount of precipitation. However, it is challenging to fully capture large-scale precipitation events or provide real-time, dynamic precipitation data due to the constraints of ground-based observation, which include sparse station distribution and limited spatial coverage [7,8]. With the rapid advancement of remote sensing and detection technologies, non-contact observation methods such as satellite remote sensing and meteorological radar have exhibited distinct advantages in acquiring high spatiotemporal resolution precipitation information. Compared with traditional point-based ground station observations, these technologies can provide regional precipitation data with wide coverage and strong continuity, significantly improving the spatial completeness and timeliness of precipitation monitoring [9]. Among them, satellite remote sensing, with the capability of covering large-scale areas, can effectively compensate for the limitations of ground rain gauges, especially in remote regions where ground observations are scarce [10,11]. Numerous global satellite precipitation datasets have been released and used extensively in recent years due to notable advancements in the observation capability, accuracy, and dependability of satellite remote sensing data: The Cloud Classification System for Precipitation Estimation Based on Artificial Neural Networks and Remote Sensing Information—Climate Data Record (PERSIANN-CDR) [12]; the Integrated Multi-Satellite Global Precipitation Measurement Inversion Technology Product (IMERG) [13], which combines multi-satellite microwave and infrared precipitation inversion results and includes rain gauge data for calibration; the Climate Prediction Center Morphological Precipitation Product (CMORPH) [14], which calculates rainfall rates from microwave radiometer and geostationary satellite infrared data; and the Multi-source Weighted Ensemble Precipitation Product (MSWEP) [15].

Satellite remote sensing-based precipitation simulation technology has demonstrated significant application value in the assessment of global and regional climate variability, and has been widely applied in various fields such as hydrological simulation and meteorological forecasting. However, precipitation products still face considerable uncertainties, particularly in terms of spatial resolution, temporal sampling frequency, and light precipitation measurement errors—these uncertainties remain key challenges affecting the accuracy of precipitation prediction [16,17]. Previous researchers have conducted multi-dimensional comparative analyses on satellite precipitation datasets across different spatiotemporal scales [18]. The results confirm that due to differences in the sensing mechanisms of remote sensing platforms and data retrieval algorithms, various products exhibit distinct strengths and limitations in performance. Furthermore, this performance variation shows significant spatial heterogeneity with changes in regional underlying surfaces and climatic backgrounds. Consequently, these products struggle to meet the requirements of refined analysis in diverse scenarios, which greatly restricts their practical application potential in fields such as regional hydrological process simulation and ecological response.

Fusing multi-source satellite precipitation products (MSPs) with in situ precipitation data from meteorological stations serves as a core technical pathway to enhance the estimation accuracy of MSPs. This approach can effectively offset the inherent limitations of a single data source in terms of spatial coverage, observation timeliness, or error characteristics [19]. The academic community has currently developed a variety of classical statistical fusion methods, including quantile mapping (QM), geographically weighted regression (GWR), Bayesian model averaging, and Kriging based methods [20,21,22,23]. While the aforementioned methods have demonstrated performance advantages in applications across certain regions, they generally rely on strict mathematical assumptions. This characteristic imposes significant limitations on their use in practical scenarios, as they fail to accurately capture the nonlinear relationships between precipitation processes and complex environmental variables—ultimately greatly restricting their applicability in regions with strong environmental heterogeneity [24,25].

The advancement of machine learning (ML) techniques has provided a new pathway to overcome the limitations of traditional precipitation data fusion methods [26,27]. ML can accurately capture the complex nonlinear relationships between precipitation processes and environmental variables through a data-driven approach [28]. Meanwhile, it possesses multi-task processing capabilities ranging from classification and regression to prediction, and exhibits outstanding performance in learning and generalizing from massive datasets. These characteristics enable it to demonstrate significant application advantages in the field of MSPs calibration and fusion [29]. Currently, a variety of machine learning algorithms, such as random forest (RF), convolutional neural network (CNN), deep neural network (DNN), and long short-term memory network (LSTM), have been widely applied in this field, providing technical support for improving the accuracy of precipitation estimation [30,31,32]. Despite the fact that ML offers an efficient technical means for precipitation fusion, most existing relevant studies still have obvious limitations: First, the research framework is mostly confined to the fusion within MSPs, failing to break through the restriction of a single data source type and fully explore and integrate complementary information from various data sources such as environmental variables and in situ observation data. This significantly limits the applicability of the constructed models under complex underlying surfaces and climatic backgrounds [33]; Second, MSPs themselves have non-negligible uncertainties, which partially stem from insufficient accuracy in precipitation event detection—this flaw not only directly interferes with the reasonable definition of precipitation statistical durations and the accurate determination of start/end times for rainy/dry days, but also may further lead to systematic overestimation or underestimation of precipitation intensity, becoming a key bottleneck restricting the improvement of precipitation prediction accuracy. In fact, accurately identifying the occurrence of precipitation events is a core prerequisite for fundamentally avoiding the aforementioned cascading errors and optimizing precipitation prediction performance [34]. This study selects the MRB on the eastern edge of the Qinghai–Tibet Plateau as a case study. The upper reaches of this basin not only lack sufficient meteorological observation data, but also exhibit significant spatial heterogeneity in precipitation due to the combined effects of complex terrain and other factors. This characteristic directly increases the frequency and severity of severe periodic floods in the basin [35]. Thus, this study suggests a two-step data fusion strategy focused on two main goals: accurate identification of precipitation events and precise quantitative estimation of precipitation intensity. This approach aims to address the identification biases of traditional models under various precipitation intensities and topographic conditions, as well as the large quantitative estimation errors of MSPs. The first step is increasing the precision of precipitation event identification, with a focus on improving the detection capabilities of moderate-to-heavy precipitation in complicated terrain and addressing the misjudgment issue of light precipitation. The goal of step two is to improve quantitative precipitation estimation accuracy. Through optimizing the model structure, this approach improves the spatiotemporal discrimination capability of precipitation events using a core algorithmic framework that includes RF, ELM, XGBoost, and Bagging ensemble models. Based on this, multi-dimensional environmental variables like spatial autocorrelation are integrated, and an adaptation mechanism of “algorithm-variable-precipitation heterogeneity” is built to further increase the accuracy and stability of precipitation estimation in complex river basins.

2. Materials and Methods

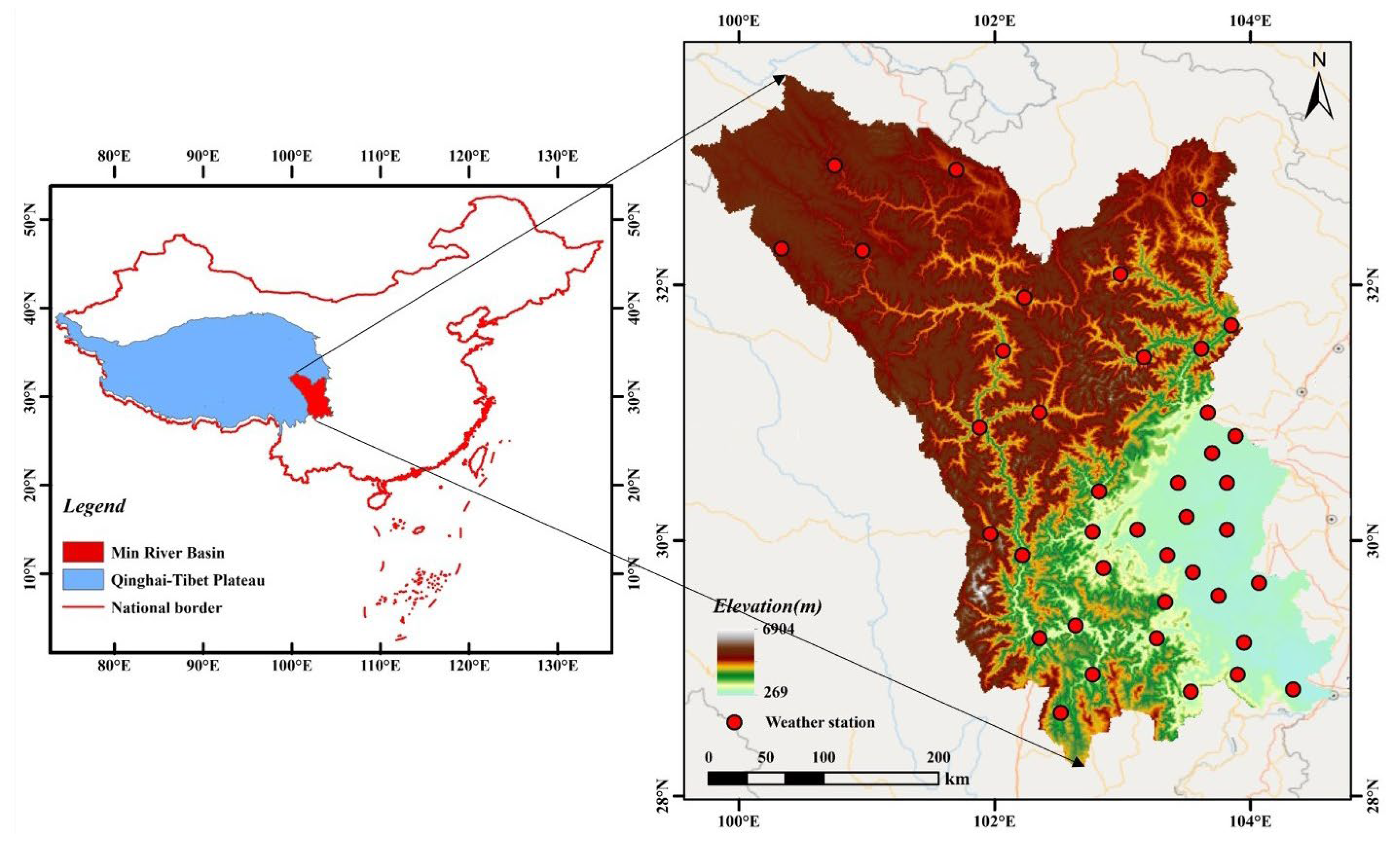
2.1. Materials

The main stream of the MRB originates from the southern foot of the Minshan Mountains in Songpan County, Aba Tibetan and Qiang Autonomous Prefecture, Sichuan Province (Figure 1). Its primary source is situated at an elevation of approximately 4070 m, with a total drainage area of 135,881 km². The terrain displays a distinct “high in the north and low in the south” gradient: the upper reaches are dominated by high-mountain canyons, featuring narrow river channels, large elevation drops, and substantial hydropower potential; the middle reaches extend into the Chengdu Plain, forming an alluvial plain; and the lower reaches—from Leshan to the confluence—transition to hilly terrain, eventually discharging into the Yangtze River [36]. Among its major tributaries, the Dadu River originates from the eastern edge of the Qinghai–Tibet Plateau in northern Kangding City, Ganzi Tibetan Autonomous Prefecture, with a total length of approximately 1062 km and a drainage area of 77,700 km². Its geomorphology is dominated by plateaus and deep valleys: the upper reaches feature steep terrain and a large riverbed gradient; the middle reaches gradually flatten out as they extend to the edge of the basin; and the lower reaches flow into the MRB. Geologically, it is located at the boundary between the Yangtze Block and the Songpan Orogenic Belt, where tectonic activity is intense and glaciers are well-developed in high-altitude areas. The Qingyi River originates from the Qionglai Mountains in Ya’an City, with a total length of approximately 276 km and a drainage area of 13,000 km². Characterized by low-to-moderate mountains and hills, it has a gentle river channel gradient, a well-developed river system, and prominent karst landforms [37]. In terms of precipitation characteristics, precipitation in the MRB is controlled by the East Asian Monsoon, but exhibits significant spatial and seasonal variations: the annual precipitation of the MRB main stream ranges from 600 to 1600 mm, with less precipitation in the northwest and more in the southeast, and over 70% of it concentrates in the period from May to September; the annual mean precipitation of the Dadu River is 700–1500 mm, showing a pattern of less in river valleys and more in high mountains, and the proportion of precipitation in the flood season exceeds 80%; the Qingyi River has an annual mean precipitation of 1000–1800 mm, making it the wettest area among the three sub-basins, with the most uniform seasonal distribution [38].

This study utilizes daily precipitation observation data and mean temperature data from 43 national-level meteorological stations in the MRB spanning 2001–2022, which were provided by the China Meteorological Administration (CMA) [39]. To enhance data reliability and spatiotemporal consistency, systematic data quality control was performed on the meteorological data of each observation station. Specifically, the quality control process included the following steps: (1) Extreme value detection, which was used to eliminate potential outliers; (2) Internal consistency check, which ensured the internal logical rationality of the data by comparing the consistency between precipitation/temperature data and other meteorological variables; (3) Spatial consistency check, which identified potential abnormal observations through cross-validation using observation data from adjacent stations [40]. Furthermore, this study integrated four satellite precipitation products—IMERG, CMORPH, GSMaP, and PERSIANN—and reanalysis precipitation products. During the algorithm improvement process, in situ observational data were further incorporated to enhance the spatiotemporal accuracy and reliability of the data.

PERSIANN-CDR is a high-resolution, long-term global precipitation dataset developed by the University of California, Irvine (UCI), USA [41]. As the climate data record (CDR) contains remote sensing-based precipitation estimation products that rely on artificial neural networks, PERSIANN-CDR integrates infrared (IR) satellite observations and ground-based rain gauge data to estimate precipitation via machine learning algorithms. It also undergoes standardized processing for climate data records to ensure long-term consistency and comparability of the data. PERSIANN-CDR features a spatial resolution of 0.25° × 0.25° and a daily temporal resolution, covering the global region between 60°S and 60°N, with long-term precipitation records available from 1983 to the present. This makes it one of the few satellite products capable of providing precipitation data with a long time series of over 40 years, rendering it suitable for long-term climate analysis and the study of extreme precipitation events [42].

CMORPH is a global satellite remote sensing-based precipitation product developed by the Climate Prediction Center (CPC) of the National Centers for Environmental Prediction (NCEP), USA. It is designed to provide precipitation estimation data with high spatiotemporal resolution. CMORPH uses observational data from passive microwave sensors as its primary input and applies a unique morphing filtering technique for spatiotemporal interpolation, thereby enhancing the continuity and accuracy of precipitation data [43]. The product offers multiple versions, including high-resolution datasets (8 km, 30 min), daily-scale datasets (0.25°, 3 h daily), and reanalysis products such as CMORPH-CRT and CMORPH-BLD, covering the global latitudinal range of 60°S–60°N.

IMERG is a high-resolution precipitation product from the Global Precipitation Measurement (GPM) mission, developed by the NASA Goddard Space Flight Center (GSFC). The IMERG dataset is based on observational data from multiple microwave (MW) satellite sensors and employs optimal interpolation and various bias correction methods to generate high-quality global precipitation estimates [44]. This product covers global precipitation regions between 60°S and 60°N, offering a high spatial resolution of 0.1° × 0.1°, along with temporal resolutions of 30 min, 1 h, 1 day, and 1 month.

The GSMaP dataset is characterized by high spatiotemporal resolution, global coverage, multi-sensor data fusion, and a long-term time series. It achieves a spatial resolution of 0.1° × 0.1° and a temporal resolution of up to 1 h; some products even offer 30 min updates, which can meet the requirements for short-term precipitation monitoring. The dataset covers a latitudinal range of 60°N–60°S [45]. Additionally, GSMaP integrates observational data from multiple passive microwave satellites and incorporates numerical weather prediction (NWP) models for data fusion, thereby effectively improving the accuracy of precipitation estimation.

MSWEP features a spatial resolution of 0.1° × 0.1°, which meets the requirements for small- and medium-scale hydrological simulations. It also has a high temporal resolution of 3 h and provides long-term precipitation data from 1979 to the present, making it suitable for short-term weather monitoring and long-term climate trend analysis [46]. Additionally, MSWEP is unique in that it integrates three types of data sources: (1) Ground-based station data (e.g., data from the Global Weather Data Sharing System and Global Historical Climatology Network), which enhances the ground observation constraints of the dataset; (2) Satellite precipitation data, which improves the spatial coverage of the dataset; (3) Reanalysis dat, which compensates for the spatiotemporal discontinuities of the dataset.

Total Cloud Cover (TCC) data were obtained from the ERA5 dataset released by the European Centre for Medium-Range Weather Forecasts (ECMWF) [47], with a spatial resolution of 0.25° and a temporal resolution of 1 h. The Normalized Difference Vegetation Index (NDVI) was derived from the MODIS product MOD13A1 [48], which has a temporal resolution of 16 days and a spatial resolution of 500 m (available at https://modis.gsfc.nasa.gov; accessed on 18 July 2024).

2.2. Methods

2.2.1. Data Preprocessing

Five mainstream precipitation products were selected in this study to train the precipitation fusion model. Variables considered in the fusion algorithm included DEM, longitude, latitude, air temperature, TCC, and NDVI. The spatial resolution was set to 0.1° to improve the accuracy of precipitation fusion, and bilinear interpolation was applied to resample DEM, PERSIANN-CDR, CMORPH, and NDVI data. Meteorological stations within the study basin were randomly divided into a training set and a testing set, with 70% of the stations allocated to the training set and 30% to the testing set. During the training process, training samples were further randomly split into a training subset and a validation subset to facilitate model tuning and validation.

2.2.2. Fusion Method

In the fusion model, in addition to precipitation products, multiple environmental variables were introduced as feature variables (Figure 2). Based on the geographical locations of meteorological stations, relevant environmental covariates and the pixel values of corresponding precipitation products were extracted as the input features of the model; observed precipitation amounts were used as output variables to construct and train the fusion model. To improve the fusion accuracy of precipitation products, this study adopted a combination of SML models and DML models. The input variables of the framework included in situ station data, environmental variables, and MSPs. Among these, environmental variables covered DEM, latitude (LAT), longitude (LON), temperature (TEM), TCC, and NDVI; precipitation products included multiple datasets, namely PERSIANN-CDR, CMORPH, IMERG, GSMaP, and MSWEP. For the SML model component, the framework employed four distinct machine learning algorithms: RF, ELM, XGBoost, and Bagging. These algorithms were separately used to fuse raw precipitation product data. For the DML model component, four different combined models were formed by integrating SML models with RF: RF-RF, RF-ELM, RF-XGBoost, and RF-Bagging. Overall, fusing multiple precipitation products via machine learning methods can effectively improve the accuracy and reliability of precipitation estimation.

As illustrated in Figure 3, ML algorithms were employed to construct classification models for the preliminary identification of precipitation events. Specifically, samples with observed precipitation greater than zero were defined as “wet days”, while those with observed precipitation equal to zero were designated as “dry days”, and the classification models were utilized to predict these categories. The classified precipitation observation data, together with the input variables, were used to train and optimize the ML classification models, which constitutes the first stage of the DML method. The accuracy of “dry/wet day” classification for each ML algorithm was evaluated using an independent test dataset, and the model with the best performance was selected. In the second stage, regression models for each ML algorithm were trained to estimate the precipitation amount on days classified as “wet days”, a process analogous to the SML method. If a day was predicted as a “dry day” by the classification model, the precipitation prediction value of the corresponding regression model was set to zero. By integrating the prediction results of the classification and regression models, the DML method achieves the fusion and optimization of precipitation data. Compared with the traditional SML regression method, this DML framework significantly improves the comprehensive performance of the model in two dimensions: dry/wet day identification and quantitative precipitation estimation. In the application of multi-source precipitation data fusion, the DML method can effectively suppress systematic errors, reduce spatial heterogeneity, and enhance the spatiotemporal adaptability of fused precipitation products under complex topographic and climatic backgrounds.

2.2.3. RF

Random forest is an ensemble machine learning algorithm based on decision trees, proposed by Breiman. By constructing multiple independent decision trees and aggregating their prediction results, RF enhances the generalization ability and stability of the model [49]. In classification tasks, RF determines the final class via majority voting, while in regression tasks, it employs the mean of predictions from all trees as the final output. This enhances computational efficiency on large-scale datasets, making it particularly suitable for application scenarios requiring large-scale data processing [50]. Even in winter precipitation prediction tasks characterized by a severely imbalanced ratio between wet days and dry days, RF can still maintain stable prediction performance.

2.2.4. ELM

Extreme learning machine is an efficient single-hidden layer feedforward neural network (SLFN) algorithm proposed by Huang [51]. Unlike traditional backpropagation (BP) neural networks, ELM eliminates the need for iterative optimization. Instead, it randomly initializes hidden layer weights and calculates output weights using analytical solutions, which significantly accelerates training speed while maintaining strong generalization ability. Compared with traditional neural networks, ELM boasts a training speed tens to hundreds of times faster, enabling it to train large-scale datasets within milliseconds—making it an ideal choice for large-scale data processing. ELM also exhibits robust generalization capability: by randomly mapping data into a high-dimensional space and solving output layer weights via the least squares method, it can effectively avoid overfitting and underfitting [52].

2.2.5. XGBoost

XGBoost is an efficient, flexible, and scalable gradient boosting decision tree (GBDT) algorithm proposed by Chen and Guestrin. Compared with traditional GBDT, XGBoost enhances computational efficiency through block processing, parallel computing, cache optimization, and weighted split finding, resulting in a more than 10-fold increase in training speed—making it particularly suitable for large-scale datasets [53]. In terms of feature modeling, XGBoost does not rely on linear assumptions and can capture complex nonlinear relationships, making it applicable to remote sensing image classification tasks. It employs a sparsity-aware algorithm and weighted split finding, enabling it to exhibit excellent modeling capabilities on high-dimensional sparse data.

2.2.6. Bagging

Bagging is a method based on bootstrap sampling and ensemble learning, proposed by Breiman [54]. Bagging performs excellently in high-dimensional data processing: by randomly sampling feature subsets, it alleviates the curse of dimensionality, rendering it applicable to tasks such as remote sensing image classification. In terms of computational efficiency, Bagging supports parallel computing, where individual base learners can be trained independently to enhance computational efficiency—making it suitable for large-scale data modeling [55]. Furthermore, Bagging is compatible with various machine learning algorithms; it can be not only applied to decision trees but also combined with support vector machines, neural networks, and logistic regression to further improve model stability and predictive capability.

2.2.7. Model Validation

Comprehensive evaluation of the performance of machine learning-based fused precipitation was conducted using a 10-fold cross-validation approach [56,57]. Seven commonly used statistical metrics were selected for multi-dimensional quantitative analysis, including CC, RMSE, MAE, relative bias (RB), modified Kling-Gupta efficiency (KGE), POD, FAR, and CSI [58]. Each evaluation metric has a well-defined theoretical value range and optimal performance: CC, POD, FAR, and CSI are all constrained between 0 and 1; the optimal value of FAR is 0; KGE ranges from -∞ to 1, with values closer to 1 indicating better performance; RMSE and MAE have an optimal value of 0, with smaller values indicating lower errors [59]. Frequency bias (FB) was used to measure the balance of precipitation products in detecting precipitation events, calculated as the ratio of POD to FAR, indicating the equilibrium of the model in precipitation event detection. Additionally, the Heidke Skill Score (HSS) was employed to compare the actual predictive performance of precipitation products with that of random predictions. A positive HSS value indicates that the model prediction is superior to random forecasting. The theoretical range of HSS is typically -∞ to 1, with values closer to 1 indicating a high degree of consistency between model predictions and actual observations [60]. The specific calculation formulas for each metric are as follows:

$$CC={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n\left(O_i-\overline{O}\right)\left(S_i-\overline{S}\right)}}{\sqrt{{\displaystyle {\sum }_{i=1}^n{\left(O_i-\overline{O}\right)}^2\cdot {\displaystyle {\sum }_{i=1}^n{\left(S_i-\overline{S}\right)}^2}}}}}$$

(1)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n{\left(S_i-O_i\right)}^2}}$$

(2)

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^n\left|S_i-O_i\right|}$$

(3)

$$RB={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n\left(S_i-O_i\right)}}{{\displaystyle {\sum }_{i=1}^n{O}_i}}}$$

(4)

$$KGE=1-\sqrt{{\left(CC-1\right)}^2+{\left(\beta -1\right)}^2+{\left(\gamma -1\right)}^2}$$

(5)

$$POD={\displaystyle \frac{H}{H+M}}$$

(6)

$$FAR={\displaystyle \frac{F}{H+F}}$$

(7)

$$CSI={\displaystyle \frac{H}{H+M+F}}$$

(8)

$$Precision={\displaystyle \frac{H}{H+F}}$$

(9)

$$FB={\displaystyle \frac{H+F}{H+M}}$$

(10)

$$HSS={\displaystyle \frac{2\left(HN-FM\right)}{\left(H+M\right)\cdot \left(M+N\right)+(H+F)\cdot \left(F+N\right)}}$$

(11)

$n$ denotes the total number of samples; $O$ and $S$ represent the estimated value from the precipitation product and the corresponding ground-based observation value, respectively; $\overline{O}$ and $\overline{S}$ denote the mean values of the estimated and observed values, respectively, and are used to measure systematic bias; $\beta$ represents the relative bias between the estimated and observed values, reflecting the direction and magnitude of the estimation error; $\gamma$ is the ratio of the coefficient of variation between the two, which measures the consistency of the estimated values in expressing variability; $H$ denotes the number of precipitation events identified as such by both the observational data and the precipitation product; $M$ represents the number of precipitation events identified by ground-based observations but not detected by the precipitation product; and $F$ denotes the number of false precipitation events detected by the precipitation product but not observed by ground-based measurements.

3. Results

3.1. Applicability Evaluation in Daily Scale Identification and Quantitative Estimation

As shown in Figure 4, calibrated precipitation data based on SML methods exhibited significantly higher CC values than raw precipitation products. Among these SML methods, RF-Bagging and RF outperformed RF-ELM and RF-XGBoost, with the ratio of their predicted values to observed values mainly concentrated between 0.8 and 0.9. DML methods generally achieved higher CC values than SML methods; it is evident that the precipitation estimation accuracy of DML models is significantly superior to both SML models and raw satellite products, with the RF-Bagging model standing out as the optimal performer: its daily-scale CC values range from 0.8 to 0.99, and its RMSE and MAE are reduced to 1.7–2.8 mm and 0.4–1.2 mm, respectively, representing an error reduction of over 40% compared to raw products. In terms of RMSE and MAE, SML methods were distinctly superior to raw precipitation products. Although ELM performed the worst among SML methods, its RMSE and MAE were concentrated in the ranges of 3.5–6.5 mm and 1.2–2.3 mm, respectively. RF showed the best performance among SML methods, with RMSE and MAE ranging from 2.5–3.8 mm and 0.8–1.3 mm, respectively. For DML methods, all models outperformed both SML methods and raw precipitation products. RF-Bagging again demonstrated the optimal performance, with RMSE and MAE ranging from 1.7 mm to 2.8 mm and 0.4 mm to 1.2 mm, respectively. Regarding RB, ELM among SML methods exhibited substantial bias, with fluctuations ranging from −110 to 60 and a primary concentration between −12.7 and −0.67. In contrast, other SML methods showed smaller RB fluctuations, mainly ranging from −11.3 to 0.32, indicating more stable performance. DML models performed better in terms of RB: all DML models had narrow bias fluctuations, primarily concentrated between −10 and 0, reflecting a slight underestimation trend. In terms of KGE, precipitation data fused by machine learning methods outperformed raw precipitation products. RF and ELM showed relatively poor KGE performance: RF had a KGE range of −0.42 to 0.91, with the main concentration between 0.67–0.83, while ELM had a KGE range of −0.39 to 0.82, with the primary distribution in 0.57–0.68. RF-Bagging achieved the best KGE performance, with values ranging from 0.78–0.92, followed by RF-XGBoost, with values in the range of 0.46–0.87.

The accuracy improvement of SML and DML models in precipitation identification was analyzed using six metrics. Figure 5 shows that the RF-Bagging and RF-RF models perform exceptionally well in precipitation event identification, with a POD exceeding 0.95, a FAR controlled within 0.32–0.38, and a CSI reaching 0.52–0.58, which significantly mitigates the rain-dry confusion issue of traditional models. In particular, the RF-RF modeled POD value was below 0.95, whereas all other fused models showed higher accuracy in precipitation detection, with POD values concentrated between 0.93 and 1.0. RF-Bagging and RF-RF models had the best FAR performance, with values ranging from 0.32 to 0.38, whereas the SML models’ values were centered in the range of 0.42 to 0.53. With CSI values ranging from 0.52 to 0.58, the Bagging and RF models performed well; the RF-XGBoost and RF-ELM models fared poorly, with an average CSI value of 0.55, while the RF-Bagging and RF-RF models continued to perform better.

In terms of Precision, machine learning methods significantly improved precision. Bagging and RF performed relatively well, with values primarily ranging from 0.51 to 0.57. RF-Bagging and RF-RF models showed values mainly in the range of 0.61 to 0.67, which were much higher than those of SML models and most precipitation products. For FB, among SML models, XGBoost performed the worst, with values primarily ranging from 1.8 to 2.3. DML models achieved a better balance between hit rate and false alarm rate, with RF-RF and RF-Bagging demonstrating superior performance, their values predominantly ranging from 1.35 to 1.62. Finally, HSS evaluation results indicated that RF and Bagging performed well, with values of 0.38 and 0.39, respectively, while XGBoost and ELM showed relatively poor performance, with median values of only 0.28 and 0.34. RF-Bagging and RF-RF achieved the best performance, with HSS values mainly ranging from 0.47 to 0.63. RF-Bagging and RF-XGBoost exhibited excellent performance across multiple evaluation metrics, particularly in POD, Precision, and CSI, demonstrating high prediction accuracy and consistency.

3.2. Evaluation of Spatial Distribution Identification and Estimation Performance at the Daily Scale

This spatial distributions of CC and MAE for precipitation fused by various machine learning techniques are displayed in Figure 6. The spatial distribution characteristics show that the RF-Bagging and RF-RF models achieve higher estimation accuracy in the upstream and downstream regions of the MRB, with the proportion of stations having a CC > 0.8 exceeding 75%. The MAE is slightly higher in the mid-altitude areas of the middle reaches, indicating the impact of topographic heterogeneity on model performance. In particular, CC values progressively rise from the northwest to the southeast of the basin: the RF and Bagging models perform exceptionally well, with high CC values primarily concentrated in the upstream and downstream regions (ranging from 0.8 to 1.0); the ELM and XGBoost models perform comparatively poorly, particularly in the upstream region where CC values are the lowest (ranging from 0.5 to 0.7). The XGBoost model performs comparatively better, with just 44% of stations displaying CC values below 0.8, while the ELM model has CC values in the range of 0.7 to 0.8 over the majority of the basin, accounting for 63% of the stations. High CC values are still concentrated in the upstream and downstream areas in DML models, which show a notable improvement over SML models. More than 75% of stations have CC values greater than 0.8.

Overall basin’s upstream and midstream areas often have lower MAE values in terms of the geographic distribution. While MAE values were mostly centered between 1.5 mm and 3 mm in the southwest and downstream regions of the basin, 77% of stations in SML models had MAE values for RF in the range of 0–1.5 mm. In the majority of the basin, DML models showed lower MAE values. Notably, the northern area had a rise in MAE values, while the center and southern regions showed greater MAE values. The RF-RF and RF-Bagging models showed improved accuracy and reduced errors in precipitation prediction based on the CC and MAE studies.

The spatial distributions of RMSE and KGE across different machine learning models in the MRB are presented in Figure 7. The RF and Bagging models exhibited superior RMSE performance in precipitation prediction, particularly in the upstream and midstream regions of the basin. In contrast, the ELM and XGBoost models showed poor RMSE performance, with generally higher RMSE values observed in the midstream and downstream regions. For the RF-Bagging model, stations with RMSE values ranging from 0 to 4 accounted for 79% of the total, although only 27% of stations fell within the 0–2 range. Fused precipitation generally showed low RMSE across the MRB, with relatively high values only in the southwestern region. In terms of KGE evaluation, the RF model performed best among SML models, with KGE values predominantly ranging from 0.8 to 0.9. However, its overall performance was poorer in the upstream region of the basin. Across the entire basin, 72% of stations showed KGE values above 0.7 for the RF model, compared to 24%, 63%, and 67% for the ELM, XGBoost, and Bagging models, respectively. DML models demonstrated significant improvements in KGE compared to SML models. The RF-RF and RF-Bagging models were particularly outstanding, with 53% and 63% of stations, respectively, exhibiting KGE values in the 0.9–1 range. In contrast, the RF-XGBoost and RF-ELM models performed poorly, with only 5% and 28% of stations, respectively, falling within this range.

The spatial distributions of FAR and CSI are illustrated in Figure 8. Analysis of SML models reveals that the upstream basin consistently displayed high FAR values, with magnitudes approximately ranging from 0.4 to 0.6. FAR values in the midstream region were comparable to those in the upstream, whereas the heavy rainfall center of the basin was characterized by generally lower FAR values. DML models achieved significant progress in reducing FAR, particularly in the upstream region where RF-RF and RF-Bagging models effectively controlled FAR within 0.1 to 0.4. FAR values in the midstream region were also mainly concentrated in the range of 0.3 to 0.5. In the evaluation of CSI, the RF and Bagging models among SML models had a larger number of stations with high CSI values in the range of 0.6 to 0.7. These stations with high CSI values were primarily distributed in the upstream and midstream regions of the basin. The RF model generally showed high CSI values, with most areas ranging from 0.5 to 0.6, while the Bagging model exhibited a more uniform distribution of CSI values across the basin, mainly concentrated between 0.4 and 0.5. Dual machine learning models performed particularly well in terms of CSI, especially RF-RF and RF-Bagging. Stations with CSI values exceeding 0.7 accounted for 9.3%, while those with CSI values in the range of 0.6 to 0.8 reached 67.5%.

Based on Figure 9, two key metrics (FB and HSS) were evaluated to analyze the accuracy of precipitation data fused by different machine learning models. The RF and Bagging models outperformed other models, particularly in the downstream and upstream regions of the MRB, where their FB values mostly fell within the optimal range of 1.5 to 2. DML models demonstrated significant improvements in FB compared to single models, with the RF-RF and RF-Bagging models in particular achieving 60% and 65% of stations, respectively, with FB values in the 0–1.5 range. Most of these high-precision stations were concentrated in the downstream and northeastern regions of the basin. In contrast, other DML models showed a smaller degree of improvement, with 84% of stations exhibiting FB values between 1.5 and 2.

In the HSS evaluation of SML models, overall performance was suboptimal, with all models exhibiting HSS values concentrated in the lower range of 0 to 0.5. Relatively better HSS values were observed in the upstream and downstream regions of the basin, primarily distributed between 0.3 and 0.5. However, poorer HSS performance was noted in the southwestern region of the basin, where values were mainly confined to the 0 to 0.3 range. DML models demonstrated particularly outstanding performance in terms of HSS, with the RF-RF and RF-Bagging models standing out. Approximately 35% of stations using these models exhibited HSS values in the 0.6 to 0.7 range, predominantly concentrated in the downstream and northeastern regions of the basin. Although HSS values remained relatively low in the southwestern basin, with values primarily ranging from 0.3 to 0.5, marked improvements were still observed compared to SML models.

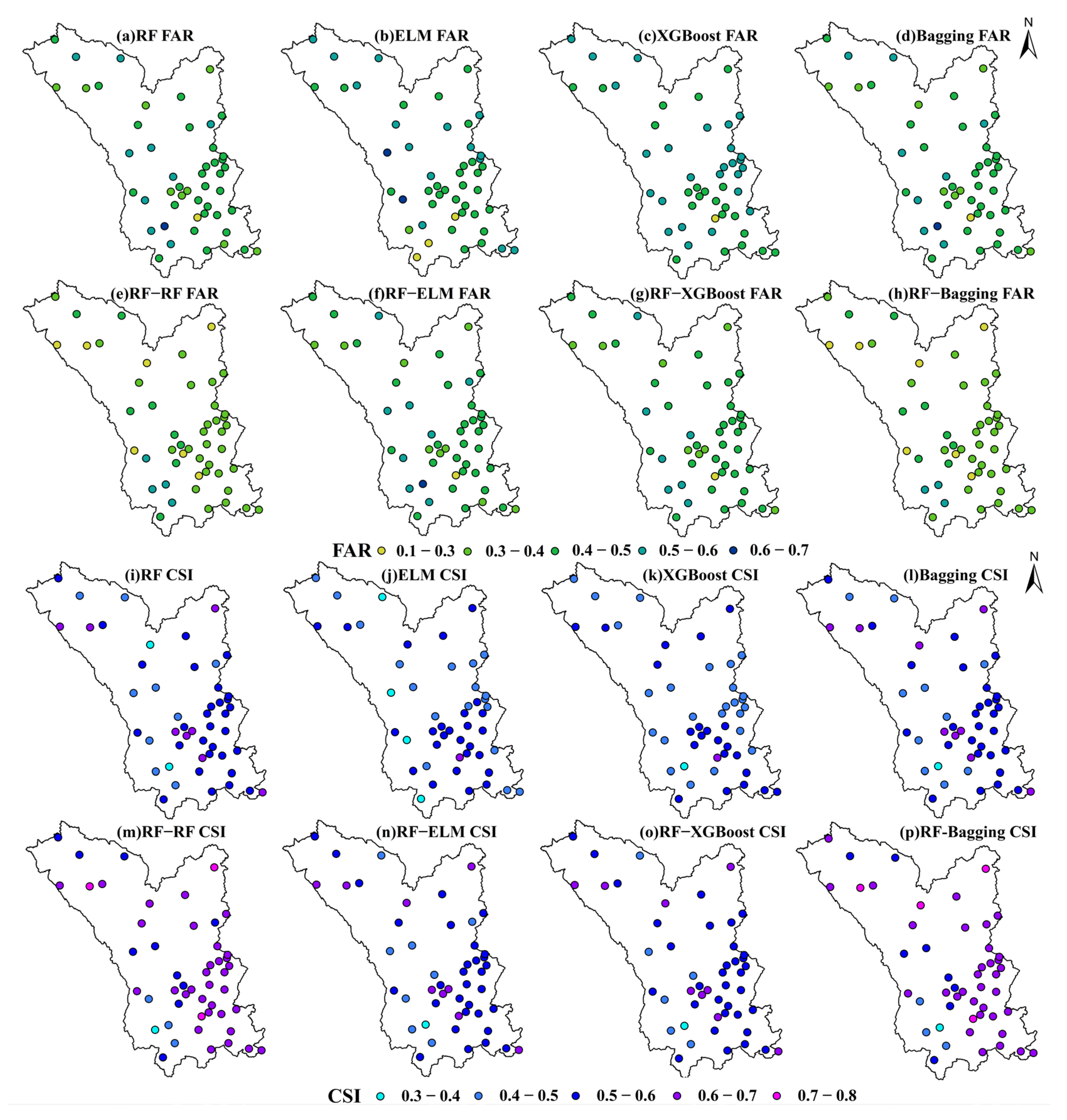
3.3. Performance Characteristics Across Different Precipitation Intensities and Elevation Conditions

Precipitation was categorized based on percentiles: 0–30% for light precipitation, 30–60% for moderate precipitation, 60–90% for moderate-to-heavy precipitation, and 90–100% for heavy precipitation. This study evaluated machine learning-based fused precipitation data across different precipitation intensities, with results presented in Figure 10. Regarding the variation of POD across precipitation intensities, all models exhibited strong detection capabilities for light precipitation (0.1–2 mm), with POD values exceeding 0.8 for all models except ELM. As precipitation intensity increased, POD values gradually decreased. For moderate-to-heavy precipitation (10–40 mm), the RF-RF and RF-Bagging models demonstrated higher hit rates, with POD values approaching 0.8, indicating their advantage in predicting moderate-to-heavy precipitation. For heavy precipitation (>40 mm), hit rates declined significantly across all models; even the RF-RF and RF-Bagging models showed POD values dropping to approximately 0.6. In the evaluation of FAR, all models displayed higher FAR values under light precipitation conditions. Except for RF-RF and RF-Bagging, other models exhibited FAR values around 0.3, reflecting a vulnerability of machine learning methods to higher false alarms in low-precipitation scenarios. As precipitation intensity increased, FAR values gradually decreased, with the RF-RF and RF-Bagging models achieving FAR values below 0.2, demonstrating the greater reliability of machine learning methods in predicting high-intensity precipitation. For CSI, the RF-RF and RF-Bagging models consistently outperformed other models across all precipitation intensities. Particularly in moderate and moderate-to-heavy precipitation ranges, their CSI values stabilized around 0.7, indicating strong comprehensive predictive capabilities.

For the Precision metric, the RF-RF and RF-Bagging models achieved Precision values approaching 0.8 for moderate and moderate-to-heavy precipitation, indicating their favorable predictive stability. For FB values, all models exhibited overprediction under light precipitation conditions, with FB values exceeding 1. However, as precipitation intensity increased, FB values gradually approached 1. Particularly in the moderate-to-heavy precipitation range, the RF-RF and RF-Bagging models displayed FB values closest to 1, demonstrating their greater accuracy in predicting precipitation intensity. In the case of heavy precipitation, specific models such as ELM and XGBoost exhibited a certain degree of underestimation. HSS comprehensively evaluates the predictive skill of models. Under light precipitation conditions, all models yielded relatively low HSS values. In the moderate-to-heavy precipitation range, however, both RF-RF and RF-Bagging achieved HSS values exceeding 0.8, indicating their enhanced stability and skill for such precipitation intensities. Overall, under light precipitation conditions, despite high POD values, the elevated FAR values suggest room for improvement in model performance. For moderate-to-heavy precipitation, the RF-RF and RF-Bagging models performed optimally, outperforming other models across multiple metrics. For heavy precipitation, all models exhibited some degree of decline in hit rates and underestimation.

An investigation into the impact of elevation on fused precipitation in the MRB is presented in Figure 11, which analyzes identification results across different elevation zones. Under varying elevation conditions, POD remained generally stable. All models maintained POD values above 0.9 in areas with elevations exceeding 2500 m, with the RF-RF and RF-Bagging models performing most excellently, achieving POD values close to 1. However, in regions with elevations below 1000 m, POD values decreased slightly, which may be attributed to the more complex precipitation characteristics in low-elevation areas limiting the models’ identification capabilities. FAR exhibited a certain fluctuating trend with changing elevation, reaching the highest values in the mid-elevation zone (1000–2500 m). The XGBoost model performed worst in this range, with FAR values peaking at approximately 0.55, indicating a higher tendency for false alarms of precipitation events in this region. In terms of CSI, better performance was observed in low- and high-elevation regions, while a decline was noted in mid-elevation areas. Nevertheless, the RF-Bagging and RF-RF models maintained CSI values between 0.5 and 0.55 in mid-elevation zones, demonstrating their strong adaptability across different elevation conditions.

Precision values were relatively high in low- and high-elevation regions but decreased significantly in mid-elevation areas, ranging primarily from 0.45 to 0.55. This phenomenon may be attributed to the higher uncertainty in precipitation characteristics within mid-elevation zones, which reduces the reliability of model identification in these areas. The RF-Bagging model maintained superior Precision values across all elevation regions. FB metrics peaked in mid-elevation areas, reaching a maximum of 2.2, indicating overestimation of precipitation event frequencies in these regions. In contrast, in high-elevation areas above 3000 m, the RF-RF and RF-Bagging models yielded FB values close to 1, demonstrating their ability to better reflect the actual distribution of precipitation frequencies in this zone. HSS performance was favorable in low- and high-elevation regions but lowest in mid-elevation areas, with the XGBoost model exhibiting an HSS value of only approximately 0.2. Notably, the RF-Bagging and RF-RF models outperformed other models significantly in high-elevation regions, with minimum HSS values around 0.4, highlighting their predictive advantages under complex topographic conditions.

3.4. Variable Importance of Precipitation Fusion Algorithms

As illustrated in Figure 12, significant discrepancies exist in the variable importance rankings among different machine learning models for precipitation estimation in the MRB, both for classification (CLS) and regression (REG) tasks. This observation reflects the varying sensitivities of individual models to input variables. GSMaP exhibited the highest importance across all models, indicating its core role in precipitation identification and estimation. Meanwhile, IMERG and MSWEP also held high weights in multiple models, suggesting their substantial influence on improving precipitation predictions. In contrast, PERCDR and CMORPH ranked lower in importance across all models, indicating their limited contribution to precipitation estimation. Furthermore, environmental variables achieved high rankings in RF and ELM tasks, highlighting the significant impact of surface vegetation indices and topographic features on precipitation patterns. Variable importance rankings varied somewhat among models: RF and ELM showed greater reliance on environmental variables, particularly NDVI, TCC, and DEM, indicating their higher susceptibility to surface and meteorological conditions in precipitation estimation. In contrast, XGBoost and Bagging primarily depended on satellite precipitation data with lower sensitivity to topographic variables, reflecting their focus on data-driven precipitation estimation. Additionally, the Bagging method displayed high sensitivity to Lon and Lat, particularly in classification tasks, indicating its certain advantages in learning spatial distribution characteristics of precipitation. This study reveals the variable dependence characteristics of different machine learning models in precipitation fusion prediction. GSMaP, IMERG, and MSWEP contributed most significantly to fused precipitation, while environmental variables such as NDVI, TCC, and DEM played key roles in RF and ELM. Models demonstrated varying adaptabilities in variable dependence for precipitation estimation: RF and ELM showed greater reliance on geographical environmental features, whereas XGBoost and Bagging tended to predict directly based on precipitation products.

4. Discussion

4.1. Advantages of Machine Learning Based Multi-Source Precipitation Fusion Frameworks

In recent years, multi-source data synergy has emerged as a core technical direction to break through the accuracy bottleneck of satellite precipitation products, with a growing body of research focusing on obtaining high-resolution and high-precision precipitation data through fusion methods [61]. From a technical perspective, machine learning has become the mainstream approach for multi-source precipitation fusion due to its robust capabilities in nonlinear fitting and multi-feature learning. However, existing schemes have key limitations: first, weight parameters are highly dependent on empirical settings; second, weight allocation lacks spatiotemporal dynamic adaptability, mostly adopting a globally uniform weight strategy that ignores the spatiotemporal heterogeneity of precipitation fields. For instance, weight requirements for satellite products and covariates differ between plain and mountainous areas, and such static weight strategies significantly restrict the generalization ability of models in complex regions [62,63].

Machine learning methods based on classification and regression have demonstrated unique advantages in the field of precipitation fusion, with their core lying in the precise handling of complex characteristics of precipitation data through task decoupling and collaborative optimization [64]. This study shares both commonalities and differences with the research by Ghosh et al. [65] and Yao et al. [66]: all three acknowledge the core value of multi-source data fusion and algorithm optimization in enhancing satellite precipitation estimation accuracy. The former study, conducted in Kenya’s tropical savanna climate zone, aligns with this research by employing dual machine learning to integrate multi-satellite products and ground observation data. The latter study’s approach of combining machine learning with auxiliary data augmentation also shares technical logic with this research, collectively reflecting the field’s developmental trends. In terms of scenario adaptability, the former focuses on drought monitoring and emphasizes the spatiotemporal continuity of precipitation, while this study targets complex high-altitude basins to address estimation errors caused by terrain heterogeneity. Regarding technical approaches, the latter employs a single model combined with meteorological simulation correction without phased decoupling, whereas this study achieves superior error control through a two-step framework of wet/dry classification and intensity estimation. Additionally, unlike the equalized fusion of multiple satellite products adopted in existing studies, this study enhances regional adaptability by explicitly defining core product weights through variable importance analysis—with PERCDR and CMORPH contributing relatively little—indicating inherent differences in the regional applicability of various satellite precipitation products, which stems from the varying adaptability of their data sources and retrieval algorithms to specific regional environments. The two-step machine learning fusion framework constructed in this study embodies this advantage, showing significantly better performance than original satellite precipitation products in precipitation estimation in the MRB. This superiority stems from the decoupling and collaborative optimization of the two-stage tasks of “precipitation event identification—quantitative intensity estimation”. From the daily-scale evaluation, the correlation coefficient of the RF-Bagging model in the DML framework has reduced the error by more than 50% compared with the original products. By first implementing dry-wet day discrimination through classification models and then estimating precipitation intensity via regression models, it effectively addresses the issues of overestimation of light precipitation and underestimation of heavy precipitation caused by rain-dry confusion in traditional single regression models. Furthermore, the integration of environmental covariates has further enhanced adaptability in regions with complex terrain. Variable importance analysis reveals that GSMaP, IMERG, and MSWEP occupy core weights, while PERCDR and CMORPH contribute relatively little, indicating differences in regional applicability among various satellite precipitation products. This discrepancy arises from the varying adaptability of different products’ data sources and retrieval methods to regional environments. This combined classification and regression approach not only retains the classification model’s ability to accurately capture rain-dry boundaries but also leverages the regression model’s advantages in nonlinear fusion of multi-source data, providing an efficient technical pathway for constructing high-precision precipitation fields over complex underlying surfaces. Its value has been verified in empirical studies in related regions [67].

4.2. Spatial Heterogeneity of Model Performance Under Different Scenarios and Driving Mechanisms

The topographic gradient with higher elevation in the north and lower in the south, coupled with the climatic differentiation featuring wetter conditions in the east and drier in the west, results in significant spatial heterogeneity in the performance of the fusion model within the MRB. Regarding the spatial distribution of CC and MAE, the RF-Bagging model achieves optimal performance in both the upper and lower reaches of the basin, whereas errors increase significantly in the middle reaches. This discrepancy is closely associated with altitude-related mechanisms of precipitation formation. In the high-altitude areas of the upper reaches, precipitation is dominated by solid forms and influenced by glacial meltwater recharge, leading to relatively stable precipitation processes. The model can readily capture these patterns through DEM and temperature variables. In the plain regions of the lower reaches, precipitation primarily consists of frontal rainfall with uniform spatial distribution, and the retrieval accuracy of satellite products is inherently high. However, in the middle reaches, the model performance declines, primarily due to the synergistic effects of topographic lifting and cloud interference. Topographic barriers force air masses to ascend, triggering localized convective precipitation characterized by small spatial scales and short durations—features that satellite sensors struggle to fully capture, as seen in the concentrated heavy rainfall centers in the Qingyi River sub-basin. Meanwhile, extensive cloud and fog in this mid-altitude zone attenuate satellite microwave signals; for products like IMERG and GSMaP, which rely on microwave-infrared joint inversion, complex terrain distorts the correlation between microwave brightness temperature and precipitation intensity, while infrared sensors lack the ability to distinguish thin clouds from light precipitation. This dual constraint reduces the retrieval accuracy of satellite precipitation products, degrades the quality of model input data, and ultimately exacerbates uncertainties in precipitation event identification [68]. This phenomenon aligns with the “error peak of precipitation estimation in the mid-altitude zone” observed by Lyu et al. on the Qinghai–Tibet Plateau, further confirming that topographic complexity is a critical factor limiting the accuracy of satellite-based precipitation fusion [69].

The scenario dependence of model performance is further highlighted by stratified analysis across different precipitation intensities and altitudes. Under weak precipitation conditions, all models exhibit high POD and FAR values, attributed to the fact that weak precipitation signals are easily confused with interference signals such as cloud-top radiation and surface moisture, leading to misclassification by the models. Under moderate to heavy precipitation conditions, the CSI of the RF-Bagging model remains stable at approximately 0.7, significantly outperforming other models. This advantage stems from the robustness of ensemble learning against extreme values, which effectively reduces the overfitting of single decision trees to heavy precipitation outliers [70]. Along the altitude gradient, the HSS values of the models in high-altitude areas are significantly higher than those in mid-altitude regions. In addition to the topographically driven stability of precipitation, this phenomenon is related to the quality of ground observation data in high-altitude areas: meteorological stations in the upper reaches are mostly distributed in open river valleys with minimal interference from the observation environment, whereas stations in the middle reaches are often affected by topographic occlusion, resulting in higher data uncertainty that indirectly reduces the accuracy of model training [71]. Notably, all models show a sharp decline in POD under heavy precipitation conditions, which is consistent with the globally prevalent issue of underestimation of heavy precipitation in satellite precipitation products. Regarding sensor performance, the inversion algorithm of microwave sensors relies on the statistical relationship of raindrop size distribution (RSD). When precipitation intensity exceeds 40 mm/day, the RSD deviates from conventional characteristics, resulting in inversion values lower than the actual precipitation. Additionally, the strong convective cloud systems associated with heavy precipitation block the observation view of satellites, causing missing observations in the core areas of precipitation [72].

4.3. Limitations and Future Research Directions

Although the fusion framework developed in this study has achieved satisfactory results in the MRB, there are still three limitations that require further optimization. First, the model has insufficient adaptability to heavy precipitation and complex terrain in mid-altitude areas. As mentioned earlier, the scarcity of heavy precipitation samples and the topography-induced locality of precipitation are the main sources of current errors. Future improvements can be made through two approaches: one is to introduce radar precipitation data, utilizing radar’s high sensitivity to heavy precipitation to supplement satellite data; the other is to adopt spatiotemporal augmentation techniques, synthesizing heavy precipitation samples via Generative Adversarial Networks (GAN) to enhance the model’s ability to learn extreme events [73]. Second, the existing framework does not consider the temporal autocorrelation of precipitation. The daily-scale model only relies on the environmental variables of the current day and ignores the impact of antecedent precipitation on soil moisture, which may lead to deviations in precipitation estimation in seasonally arid regions. In subsequent work, we can draw on time-series models such as LSTM, incorporate antecedent precipitation and evapotranspiration data into input features, and construct a spatiotemporal fusion model [74].

From the perspective of disciplinary development, the two-step fusion framework proposed in this study provides a promotable technical paradigm for the synergistic retrieval of multi-source remote sensing data. Compared with traditional statistical fusion methods, machine learning models do not require preset mathematical assumptions, making them more suitable for complex underlying surfaces such as those in the MRB. In contrast to purely data-driven deep learning models, this study enhances the interpretability of the model by introducing environmental variables with clear physical meanings, thus avoiding the limitations of black box models. This fusion approach, which combines data-driven methods with physical constraints, can serve as a reference for precipitation estimation in other ecologically fragile regions. It holds particular application value in remote areas where ground observations are scarce. With the popularization of high-resolution satellites and IoT rain gauges in the future, the fusion dimension of multi-source data will be further expanded. This is expected to realize high-precision precipitation monitoring from point to surface and from static to dynamic, providing more solid technical support for watershed water resource management and flood disaster prevention and mitigation [75,76].

5. Conclusions

This study developed a fusion framework based on multiple machine learning models, which integrates multi-source precipitation products, ground meteorological observations, geographical environment and other multi-dimensional data to obtain a fused precipitation dataset with better spatiotemporal consistency and higher estimation accuracy. Meanwhile, a variety of evaluation metrics were adopted to analyze the daily-scale precipitation estimation and identification performance of different models, and the main conclusions are as follows:

• Significant application impacts have been attained by the suggested two-step fusion architecture of precipitation event identification-intensity quantitative estimate. The DML models stand out among them, with the RF-Bagging model exhibiting the best estimation accuracy—the daily-scale CC is more than 50% higher than the original precipitation products, and the RMSE and MAE are reduced by more than 40% and 35%, respectively, indicating notable improvements in accuracy and error control.
• The performance of DML models varies significantly in space. The higher and lower reaches of the basin are where the RF-Bagging and RF-RF models function best; however, mid-altitude regions see a minor decline in model performance due to complicated topography and cloud interference. For better estimation stability in the future, targeted optimization for this area’s features is needed.
• The CSI for moderate-to-heavy rainfall is consistently maintained at about 0.7, demonstrating the RF-Bagging and RF-RF models’ high flexibility in precipitation estimate by intensity. The FAR and CSI of these two models are still better than those of other models such as ELM and single XGBoost, making them more dependable in heavy precipitation event estimation even if underestimating still occurs in heavy precipitation situations.
• Forecasting models perform most effectively in high-altitude regions, where the precipitation frequency forecast accuracy is high and the POD is close to 1. Additionally, the HSS is 30–40% greater than that in the middle altitude regions, which has exceptional application in complicated high altitude settings and can effectively adapt to the precipitation estimate requirements of the high altitude terrain on the eastern side of the Qinghai–Tibet Plateau.
• Three categories of satellite precipitation data are essential input variables that significantly affect the estimation outcomes of all models, according to variable importance analysis. From the standpoint of individual models, there are clear differences in the features of variable dependence: XGBoost and Bagging models rely more on satellite precipitation data, whilst RF and ELM models are more dependent on environmental factors like NDVI and DEM.