A Machine Learning-Based Quality Control Algorithm for Heavy Rainfall Using Multi-Source Data

Highlights

What are the main findings?

• Machine learning-based algorithm significantly outperforms conventional methods in heavy rainfall quality control.
• The remote sensing and minute-level data are identified as dominant contributors to model predictions.

What is the implication of the main finding?

• The traditional quality control algorithm will be replaced gradually by the machine learning-based one in operational service, resulting in a substantial enhancement of heavy rainfall data quality.
• The advantages of multi-source data are leveraged by a machine learning model for heavy rainfall quality control.

Abstract

In this study, a machine learning-based quality control algorithm for heavy rainfall was developed by integrating automatic weather station observations with remote sensing data, minute-level data, and metadata. Based on heavy rainfall samples from 1 June 2022 to 31 December 2024, the performances of four gradient boosting models—eXtreme Gradient Boosting (XGBoost), Light Gradient Boosting Machine (LightGBM), Categorical Boosting (CatBoost), and Gradient Boosted Regression Trees (GBRT)—significantly outperformed precipitation-threshold-based conventional methods, including regional extreme value checks, temporal consistency checks, and others. Specifically, the XGBoost in particular achieves an increase in precision by 0.110 and recall by 0.162. This translates to a substantial reduction in both false alarms (higher precision) and missed detections (higher recall) of anomalous heavy rainfall events, thereby significantly enhancing the reliability of the quality-controlled data. The radar composite reflectivity, satellite cloud-top temperature, and minute-level precipitation were identified as dominant contributors to model predictions. The integration of multi-sensor observations effectively addressed limitations inherent in conventional threshold-based approaches. Through SHapley Additive exPlanations (SHAP)-based interpretability analysis, the model’s decision logic was shown to align with meteorological physical principles. Characteristic patterns such as combinations of low radar reflectivity and elevated cloud-top temperatures were flagged as anomalous rainfall events, typically corresponding to manual operational errors. Moreover, the model identified anomalous minute-level precipitation extremes to be critical signals for detecting instrument malfunctions, data encoding and transmission errors. The physical consistency of the model’s reasoning enhances its trustworthiness and supports its potential for operational implementation in heavy rainfall quality control.

1. Introduction

In surface meteorological observation, precipitation data are regarded as one of the most frequently utilized and critically supportive datasets [1,2,3]. The utilization of accurate precipitation data extends across weather forecasting, climate change studies, and numerical model assimilation [3,4,5], with heavy rainfall observations being particularly valuable for understanding extreme weather events and their hydrological impacts [6,7,8]. These data also serve as essential decision-making bases for key societal sectors such as agricultural production, water resource management, and ecological security [9,10,11].

With the continuous construction and expansion of the Chinese surface observation network, the number of automatic weather stations (AWSs) has exceeded 70,000, significantly improving observational coverage and density [12]. However, more than 95% of them are unmanned. Without dedicated on-site maintenance or backup precipitation observation devices, these unmanned stations often suffer from operational instability and non-standard installation, making them prone to various data quality anomalies [13,14,15].

Currently, the quality control (QC) of surface precipitation data in China primarily relies on precipitation-threshold-based traditional methods, such as regional extreme value checks, temporal consistency checks, and spatial consistency comparisons between stations [16,17,18,19]. For instance, the Meteorological Data Operation System (MDOS) of the China Meteorological Administration (CMA) employs a combination of file-level rapid QC, hourly batch QC, and daily data QC to achieve automated processing [20]. However, these methods still exhibit high rates of missed detections and false alarms in cases such as isolated heavy rainfall caused by human operational errors or continuous large precipitation values resulting from equipment malfunctions [21,22,23,24,25]. Although manual review can serve as an effective supplement to automated QC, it is typically conducted several hours after data arrival, making it difficult to meet the timeliness requirements for real-time heavy rainfall monitoring and emergency response [20,26].

With the advancement of ground- and satellite-based observation technologies and the explosive growth of meteorological data, multi-source data collaborative QC for precipitation has demonstrated significant advantages [27,28,29,30,31]. Compared with traditional approaches, these methods integrate various observational data, including Doppler weather radar, geostationary meteorological satellite, and weather detector, effectively reducing the false alarm rate in anomaly detection [27,28,29]. Furthermore, multi-source collaborative QC also contributes positively to the quality improvement of hydrological precipitation data [30,31]. However, multi-source collaborative QC methods rely mainly on statistically based static thresholds and have not yet fully exploited the complementary potential of multi-source data. Therefore, their optimization and fusion mechanisms require further exploration.

The machine learning-based QC algorithm enables the establishment of non-linear relationships between multi-source data and QC outcomes, facilitating the identification of potentially effective features [24,32,33]. This approach effectively mitigates the limitations associated with single-data-source dependency inherent in precipitation threshold-based QC algorithms. Additionally, through built-in libraries, the contribution weights of input features can be optimally configured, thereby leveraging the distinct advantages of features derived from diverse data sources [34,35]. For example, machine learning algorithms such as decision trees, K-nearest neighbors, and isolation forests have been applied to classify outliers, significantly improving the detection accuracy of anomalous precipitation data [36,37,38,39]. Neural networks have been used to construct real-time precipitation confidence intervals, enabling model adaptation across spatial and seasonal variations [40,41]. By incorporating topographic elevation data through deep neural networks and multi-scale ensemble learning techniques, the capability to detect precipitation quality anomalies in data-sparse regions such as coastal and mountainous areas has been enhanced [42].

The practical objective of this research is to enhance the operational capability of the Chinese meteorological service in automatically and accurately identifying heavy rainfall anomalies. This is critical for improving the reliability of input data for numerical weather prediction models and flash flood early warning systems, which are highly sensitive to spurious precipitation extremes. To this end, we have developed a machine learning-based QC algorithm by integrating multi-source data, including AWS observations, Doppler weather radar data, satellite data, and minute-level precipitation records, covering the period from June 2022 to December 2024. This algorithm is designed to address the high rates of missed detections and false alarms inherent in the current threshold-based method, particularly those caused by manual operational errors and instrument malfunctions. Furthermore, the interpretability analysis is employed to verify that the model’s decision logic is physically consistent with established meteorological principles. This validation is crucial for ensuring the reliability and operational adoption of the automated QC algorithm.

2. Data and Methods

2.1. Data and Workflow

The data employed in this study were drawn from a two-and-a-half-year period, from 1 June 2022 to 31 December 2024, and encompassed the entirety of China. The dataset was categorized into three primary types: (1) surface observational data, including both hour-level and minute-level records; (2) remote sensing data; and (3) metadata. For the development of the heavy rainfall QC algorithm, a focus was placed on surface observational data where the hourly precipitation exceeded 40 mm. The corresponding remote sensing data and metadata from these events were selectively extracted, resulting in a total dataset of 127,889 samples. For model development and evaluation, the entire dataset was partitioned into training, validation, and testing sets with a ratio of 5.8:1.7:2.5, corresponding to 74,176, 21,741, and 31,972 samples, respectively.

2.1.1. Surface Observational Data

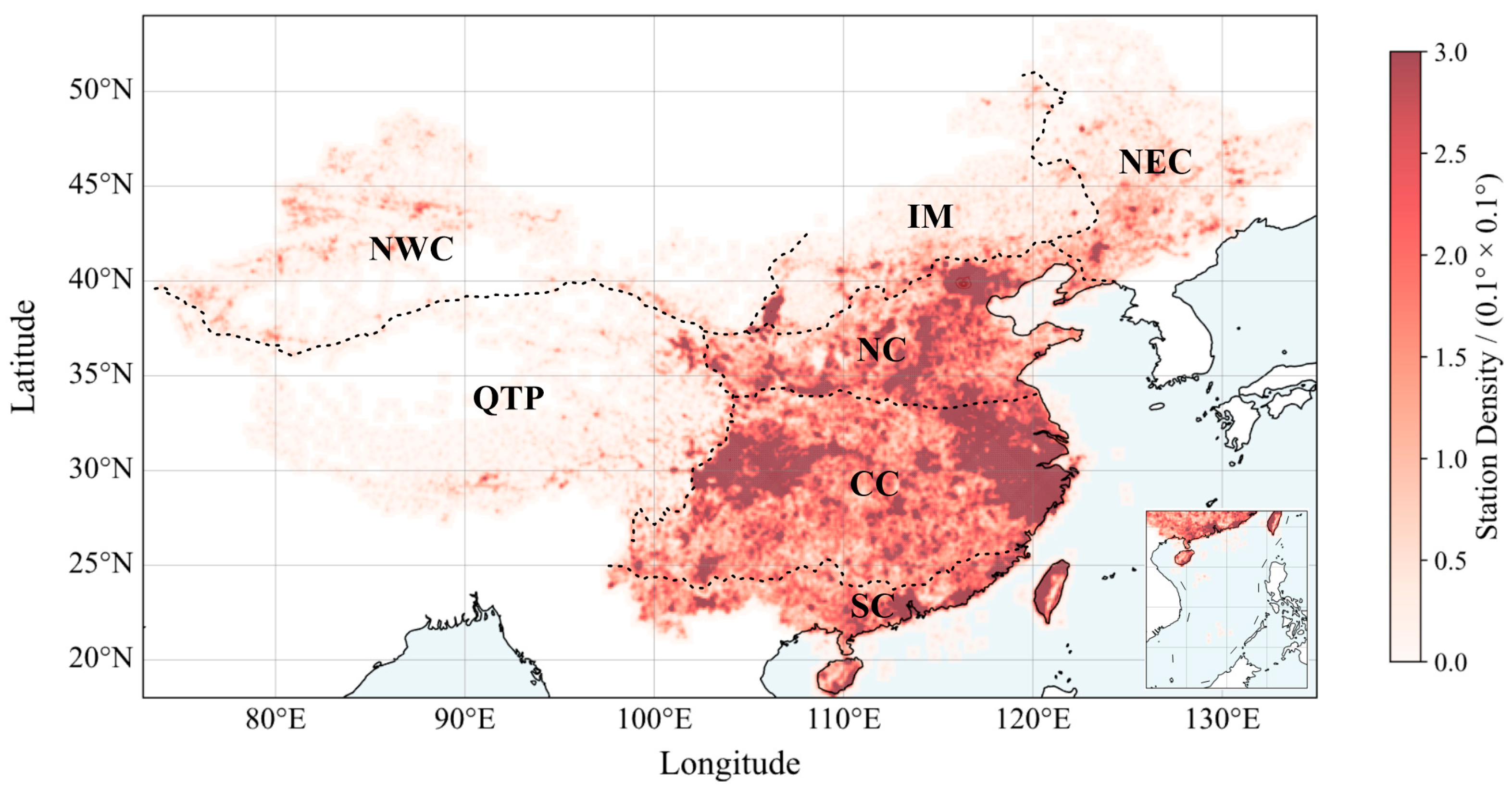
The surface observational data were obtained from a CMA-maintained network comprising national and provincial AWSs [9,12,20], with a station density higher in the eastern and southern regions than in the western and northern areas (Figure 1). Thirteen hour-level parameters, including hourly precipitation (PRE_1h), temperature (TEM), dew point temperature (DPT), atmospheric pressure (PRS), 3 h atmospheric pressure change (PRS_Change_3h), 24 h atmospheric pressure change (PRS_Change_24h), relative humidity (RHU), instantaneous wind speed (WIN_S_INST), maximum instantaneous wind speed in 1 h (WIN_S_INST_Max), 10 min average wind speed (WIN_S_Avg_10mi), instantaneous wind direction (WIN_D_INST), direction of maximum instantaneous wind speed in 1 h (WIN_D_INST_Max), and 10 min average wind direction (WIN_D_Avg_10mi), were extracted as input features for the models.

In addition to the hour-level surface observational data, minute-level precipitation data were also incorporated in this study. Due to the substantial volume of the minute-level data, feature extraction processes were performed to characterize its mean, extremums, and degree of dispersion. The average (PRE_1m_Ave), maximum (PRE_1m_Max), minimum (PRE_1m_Min), and standard deviation (PRE_1m_Std) of all minute-level values in each hour were calculated and used as input features for the models. The average and standard deviation of minute-level precipitation were defined by Equations (1) and (2), respectively.

$$PRE\_1m\_Ave={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{PRE}_i$$

(1)

$$PRE\_1m\_Std=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{({PRE}_i-PRE\_1m\_Ave)}^2}$$

(2)

where ${PRE}_i$ represents the minute-level precipitation value of the i-th sample, and N indicates the record number of minute-level precipitation in this hour.

2.1.2. Remote Sensing Data

The remote sensing data utilized in this study comprised the composite reflectivity (CR) mapping product from Doppler weather radars and the cloud-top temperature (CTT) product retrieved from the Fengyun-4B (FY-4B) geostationary meteorological satellite. Both products were quality-controlled data [43,44].

The CR mapping product is generated through periodic volume scans conducted by individual radar stations [45]. Base data, such as reflectivity, are transmitted in real time to processing centers, where they undergo rigorous QC algorithms to remove ground clutter and electromagnetic interference. The polar coordinate data from every single radar are then interpolated onto a unified latitude–longitude grid. Finally, a “maximum reflectivity” fusion algorithm is applied to produce the composite reflectivity mapping product. This mapping product is built upon a foundation of unified calibration across all radars in China, ensuring consistency and comparability of data from different stations. It provides complete coverage of China at high spatiotemporal resolutions of 6 min and 0.01°.

The FY-4B satellite-derived cloud-top temperature product is retrieved via multi-channel remote sensing detection [46]. The satellite employs an Advanced Geosynchronous Radiation Imager to observe specific infrared channels, such as the long-wave infrared window channels at 10.3–11.3 μm and 11.5–12.5 μm. The raw radiance emitted from cloud tops is acquired and radiometrically calibrated to obtain accurate top-of-atmosphere radiance values [47]. Based on Planck’s blackbody radiation law, these radiance values are subsequently inverted into cloud-top temperatures. The geographic projection coordinates from the satellite data are computed based on the World Geodetic System-1984 Coordinate System [48], and the row and column numbers of the detection products are thereby converted into geographical latitude and longitude values. This product covers East Asia with temporal and spatial resolutions of 15 min and ~4 km, respectively.

Radar and satellite data exhibit strong complementary characteristics. Radar observations provide high spatiotemporal resolution, enabling effective monitoring of the initiation and evolution of meso- and micro-scale severe convective systems, thereby compensating for the limitations of satellites in detailed monitoring. Satellite observations are not constrained by topography and can cover regions such as oceans, plateaus, and mountains, where radar deployment is challenging, thus mitigating radar blind zones in areas with complex topography. By integrating radar and satellite data, the technical advantages of both ground-based and satellite-based remote sensing can be leveraged, enhancing the reliability of heavy rainfall QC.

2.1.3. Metadata

Metadata are defined as “data about data”, which describe the context and provenance of the data and are essential for their correct interpretation and use. Key components include station location, instrument specifications, measurement method, etc. [49]

The acquisition of metadata is a systematic process. During station construction, geographical and instrumental information are surveyed and recorded. Subsequently, identifiers and timestamps are embedded by the data loggers during data collection and transmission. Finally, processing logs are integrated through standardized formats in processing and archiving. In this study, altitude (Alti), station level, and measurement method were selected as the input features for the models.

2.1.4. Overall Workflow

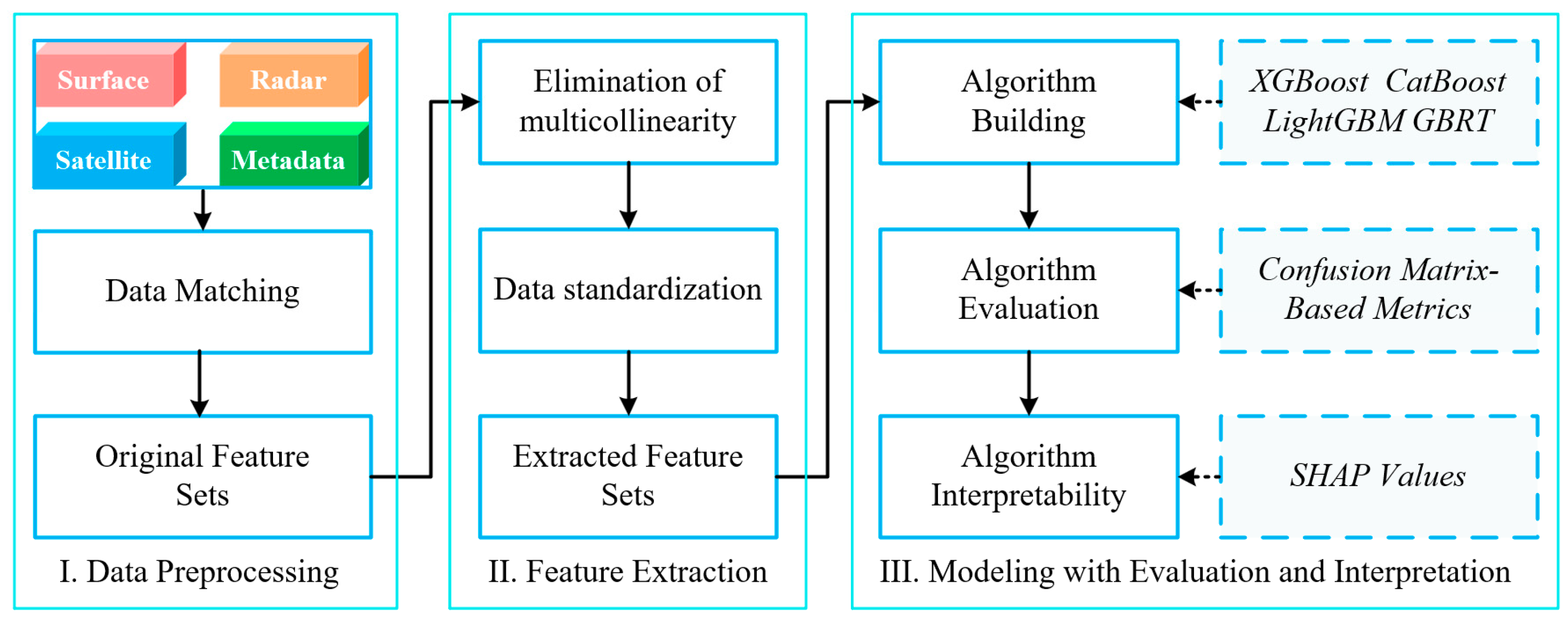
The machine learning-based QC process algorithm is structured into three consecutive stages (Figure 2): data preprocessing, feature extraction, and modeling with evaluation and interpretation.

The first stage focuses on data integration and preparation, beginning with the data matching of multi-source inputs (surface, radar, satellite, and metadata) to form a unified set of original features. In the second stage, this initial feature set undergoes a refinement process through the elimination of multicollinearity to remove redundancy and data standardization to ensure numerical stability, resulting in refined and effective extracted features. The final stage encompasses the core modeling and analysis, including algorithm building with multiple models, rigorous algorithm evaluation using confusion matrix-based metrics, and algorithm interpretability analysis. This analysis examines the consistency between the model’s decision logic and established meteorological principles.

2.2. Feature Engineering

2.2.1. Data Matching

Hourly precipitation data represent the cumulative rainfall during the one-hour period immediately preceding each hour (e.g., the precipitation recorded at 06:00 corresponds to the accumulated rainfall between 05:00 and 06:00). However, remote sensing data sources—with temporal resolutions of 6 min for radar and 15 min for satellite—exhibit significantly higher temporal resolution than hourly precipitation data. This discrepancy in temporal scale leads to fundamental inconsistencies when directly performing grid-to-grid matching in these heterogeneous datasets.

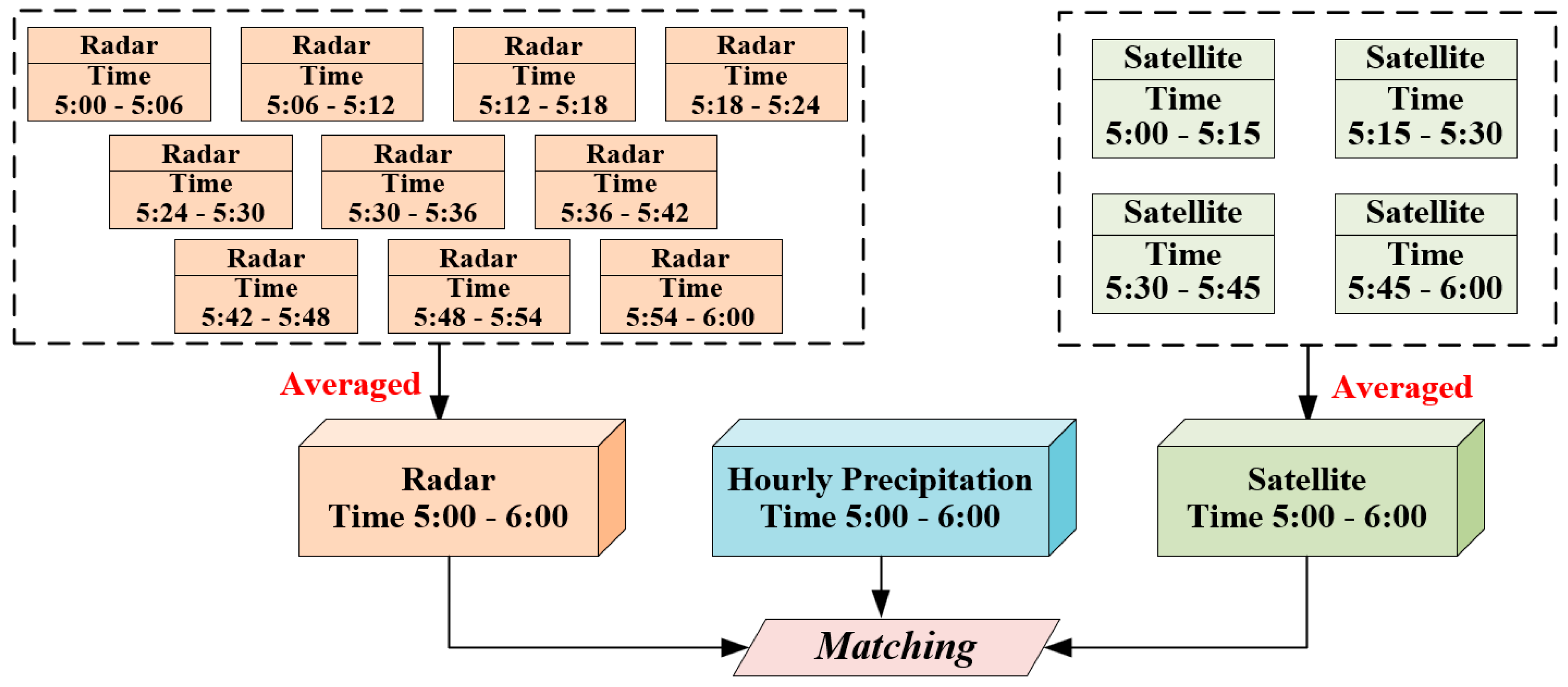
A sliding average temporal window method was applied to process the remote sensing data [50]. For each hourly precipitation value, all available radar or satellite gridded observations within the preceding one-hour window were extracted. The average of these high-resolution values was then computed (A schematic diagram is shown in Figure 3) and matched with the hourly precipitation data. This method effectively aligns the high-frequency remote sensing data with the hourly precipitation observations on a consistent temporal scale, thus achieving temporal consistency for multi-source data matching.

For spatial matching, a spatial nearest-neighbor averaging method was employed in this study [51]. Centered on the latitude and longitude coordinates of each AWS, the CR and CTT gridded data within the surrounding area were searched. The arithmetic mean of the five nearest grid points was then calculated and used as the remote sensing observation values matched to the hourly precipitation data.

The utilization of multiple grid points within a defined spatial domain for averaging is motivated by practical considerations regarding spatial representation and error minimization. During heavy rainfall events, accompanying strong low-level winds can induce horizontal advection of hydrometeors, resulting in a displacement between the precipitation measured at ground stations and the cloud properties observed directly overhead via remote sensing. Relying solely on the single grid value immediately above one AWS may introduce significant mismatches. This method reduced small-scale spatial inconsistencies, thereby providing a more reliable representation of the remote sensing data within the vicinity of the station.

2.2.2. Feature Selection

In high-dimensional datasets, redundancy and multicollinearity among input features are frequently observed [52]. These issues can increase computational complexity, prolong training time, and potentially lead to overfitting, thus reducing model generalization capability and interpretability. Therefore, feature selection is a critical preprocessing step in machine learning. It aims to construct a low-dimensional and efficient feature subset while preserving essential information from the original data. This process enhances model performance and computational efficiency.

This study adopted a strategy based on correlation analysis to systematically eliminate redundant features [53]. The Pearson correlation coefficient matrix was calculated for all pairwise combinations of the input features and a threshold was set to identify highly correlated feature pairs. For each such pair, one of the features was retained while the other was eliminated. This process effectively removed redundant information, ensuring that the final feature subset consists of features with low mutual correlation.

Based on absolute Pearson correlation coefficient analysis (Figure 4) with a threshold of |r| > 0.5, a systematic elimination of redundant features from the initial 22 input features was conducted. This process resulted in the removal of 7 redundant features (

Table 1. Input features before and after selection.

	Original Features	Features After Selection
MetaData	Alti, Station_Level, Measurement_Method	Station_Level, Measurement_Method
Surface	PRE_1h, TEM, DPT, PRS, PRS_Change_3h, PRS_Change_24h, RHU, WIN_S_INST, WIN_S_INST_Max, WIN_S_Avg_10mi, WIN_D_INST, WIN_D_INST_Max, WIN_D_Avg_10mi	PRE_1h, TEM, PRS, PRS_Change_3h, RHU, WIN_S_INST_Max, WIN_S_Avg_10mi, WIN_D_INST_Max, WIN_D_Avg_10mi
Remote Sensing	CR, CTT	CR, CTT
Minute precipitation	PRE_1m_Ave, PRE_1m_Min, PRE_1m_Max, PRE_1m_Std	PRE_1m_Min, PRE_1m_Max
Total	22 features	15 features

), including altitude (Alti), dew point temperature (DPT), 24 h pressure change (PRS_Change_24h), instantaneous wind speed (WIN_S_INST), instantaneous wind direction (WIN_D_INST), minute-level precipitation mean (PRE_1m_Ave) and standard deviation (PRE_1m_Std) in an hour. The refined feature set retained 15 core features, achieving a 31.8% reduction in feature dimensionality while fully preserving critical precipitation-related information encompassing dynamic, thermodynamic, moisture, and cloud microphysical characteristics.

2.3. Machine Learning Models

The Gradient boosting machine (GBM) was adopted in this study due to its strong capability in modeling complex non-linear relationships and handling heterogeneous, multi-source datasets commonly found in meteorological applications [54,55]. As an ensemble learning method, GBM iteratively combines multiple base learners (typically decision trees) to progressively improve prediction performance, making it highly effective for both classification and regression tasks.

Within this framework, four state-of-the-art GBM variants were selected for a comprehensive comparative analysis: eXtreme Gradient Boosting (XGBoost) [56,57], Light Gradient Boosting Machine (LightGBM) [58], Categorical Boosting (CatBoost) [59,60], and Gradient Boosted Regression Trees (GBRT) [61]. Each model brings distinct algorithmic advantages: XGBoost is known for its regularization mechanisms and robustness, LightGBM offers high training efficiency through histogram-based learning, CatBoost effectively handles categorical features and reduces prediction bias, while GBRT represents a classical and interpretable implementation of the boosting paradigm.

To ensure these models achieve their designed performance, the hyperparameters of all models were optimized using the Optuna library, which employed a 5-fold cross-validation strategy on the training data to select the most robust parameter set [62].

Since the input data are derived from multiple heterogeneous sources, significant differences are observed in their measurement principles, accuracy, and acquisition environments. Considerable variations are exhibited in the value ranges, distribution characteristics, and systematic biases among different inputs [63]. Therefore, Z-score normalization was applied to preprocess each type of input feature separately, by using the formula given in Equation (3).

$$z_i^j={\displaystyle \frac{X_i^j-{\mu }_i}{{\sigma }_i}}$$

(3)

where $z_i^j$ denotes the Z-score of the j-th sample in the i-th feature, $X_i^j$ represents the observed value of the j-th sample in the i-th feature, ${\mu }_i$ is the mean value of the i-th feature, and ${\sigma }_i$ is the standard deviation of the i-th feature.

By transforming features into a unified scale through mean subtraction and standard deviation division, Z-score normalization effectively reduces distributional discrepancies and prevents numerically dominant features from exerting disproportionate influence during model training. While it is recognized that precipitation data often follow skewed distributions, the primary purpose of applying Z-score normalization to tree-based models (which are invariant to linear scaling) is not to achieve normality in feature distributions, but rather to stabilize gradient-based optimization and enhance numerical convergence, thereby contributing to accelerated training and improved generalization capability.

2.4. Model Performance Metrics

To evaluate model performance, a confusion matrix-based performance metric was employed in this study, utilizing accuracy, precision, recall, and F1-Score as key metrics. These metrics are defined by Equations (4)–(7), respectively [64,65].

$$\mathrm{a}\mathrm{c}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{y}={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}}$$

(4)

$$\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{TP}{TP+FP}}$$

(5)

$$\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}={\displaystyle \frac{TP}{TP+FN}}$$

(6)

$$F_1 \mathrm{S}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=2\times {\displaystyle \frac{Pre\times Rec}{Pre+Rec}}$$

(7)

where TP (true positive) denotes the number of samples that are positive and correctly predicted as positive; FN (false negative) refers to the number of samples that are positive but incorrectly predicted as negative; FP (false positive) is the number of samples that are negative but incorrectly predicted as positive; and TN (true negative) represents the number of samples that are negative and correctly predicted as negative.

The “actual value” in the confusion matrix is obtained from manually corrected hourly precipitation QC results, which are currently regarded as the most accurate benchmark (although its timeliness is relatively poor). Furthermore, by comparing the metrics calculated between the model’s outputs and the actual value against those derived from traditional MDOS results and the same actual value, the proposed GBM learning models effectively demonstrate their superiority over current operational QC methods.

2.5. Model Interpretation

The interpretability of the machine learning model is crucial for establishing trust in its operational application. In this study, the model’s decision logic was interpreted using SHapley Additive exPlanations (SHAP) [66,67], a method grounded in cooperative game theory that provides a unified framework for explaining the output of any machine learning model. The prediction of the black-box model is decomposed into the sum of individual feature effects by calculating each feature’s contribution, and renders the final prediction clear and interpretable. A lower SHAP value indicates a lower feature contribution, whereas a higher value corresponds to a greater contribution. The SHAP value is mathematically defined by Equation (8).

$$g(x^{\prime })={\varnothing }_0+{\sum }_{i=1}^M{\varnothing }_i{x}_i^{\prime }$$

(8)

where $g\left(x^{\prime }\right)$ represents the explanation model, x denotes the input features, and M indicates the number of input features. ${\varnothing }_i$ represents the Shapely values for feature i and ${\varnothing }_0$ denotes the constant output value when all inputs are absent. For each feature, the term ${\varnothing }_i$ is computed using Equations (9) and (10).

$${\varnothing }_i(f, x)={\sum }_{z^{\prime }\subseteq x^{\prime }}{\displaystyle \frac{\left|z^{\prime }\right|!(M-|z^{\prime }|-1)!}{M!}}[f_x(z^{\prime })-f_x(z^{\prime }\backslash i)]$$

(9)

$$f_x\left(z^{\prime }\right)=E\left[f\right(x\left)\right|x_S]$$

(10)

where f represents the black box model. $z^{\prime }$ denotes a subset of input features, and $\left|z^{\prime }\right|$ is the number of non-zero entries in $z^{\prime }$. $E\left[f\right(x\left)\right|x_S]$ represents the expected value of the function and S is the set of non-zero indices in $z^{\prime }$.

SHAP values can be approximated using various methods, such as Kernel SHAP, Deep SHAP, and Tree SHAP. In this study, the Tree SHAP-based approach was employed and implemented via the SHAP library in Python 3.12.7.

Globally, the mean absolute SHAP value for each feature was analyzed to assess its overall importance to the model. Locally, the individual SHAP values were investigated to understand the reasoning behind specific predictions. This two-level analysis was visualized using summary plots and dependence plots, which collectively illustrate how different feature values and their interactions push the model’s prediction towards a classification of “anomalous” or “normal” precipitation. The primary objective of this interpretability analysis was to validate whether the model’s decision-making aligns with meteorological physical principles, thereby verifying the physical consistency and enhancing the reliability of the QC algorithm.

3. Results

3.1. Importance Analysis

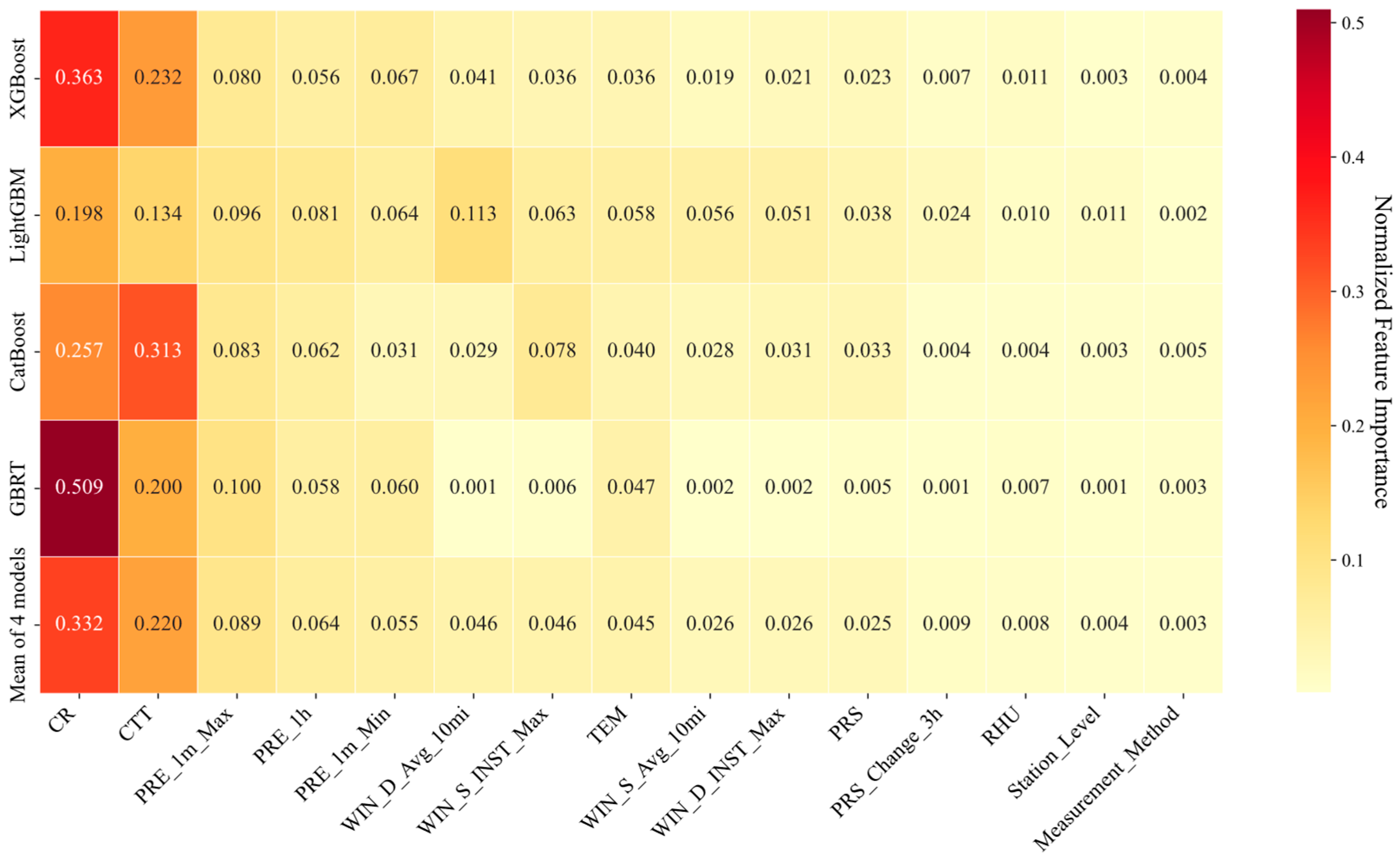
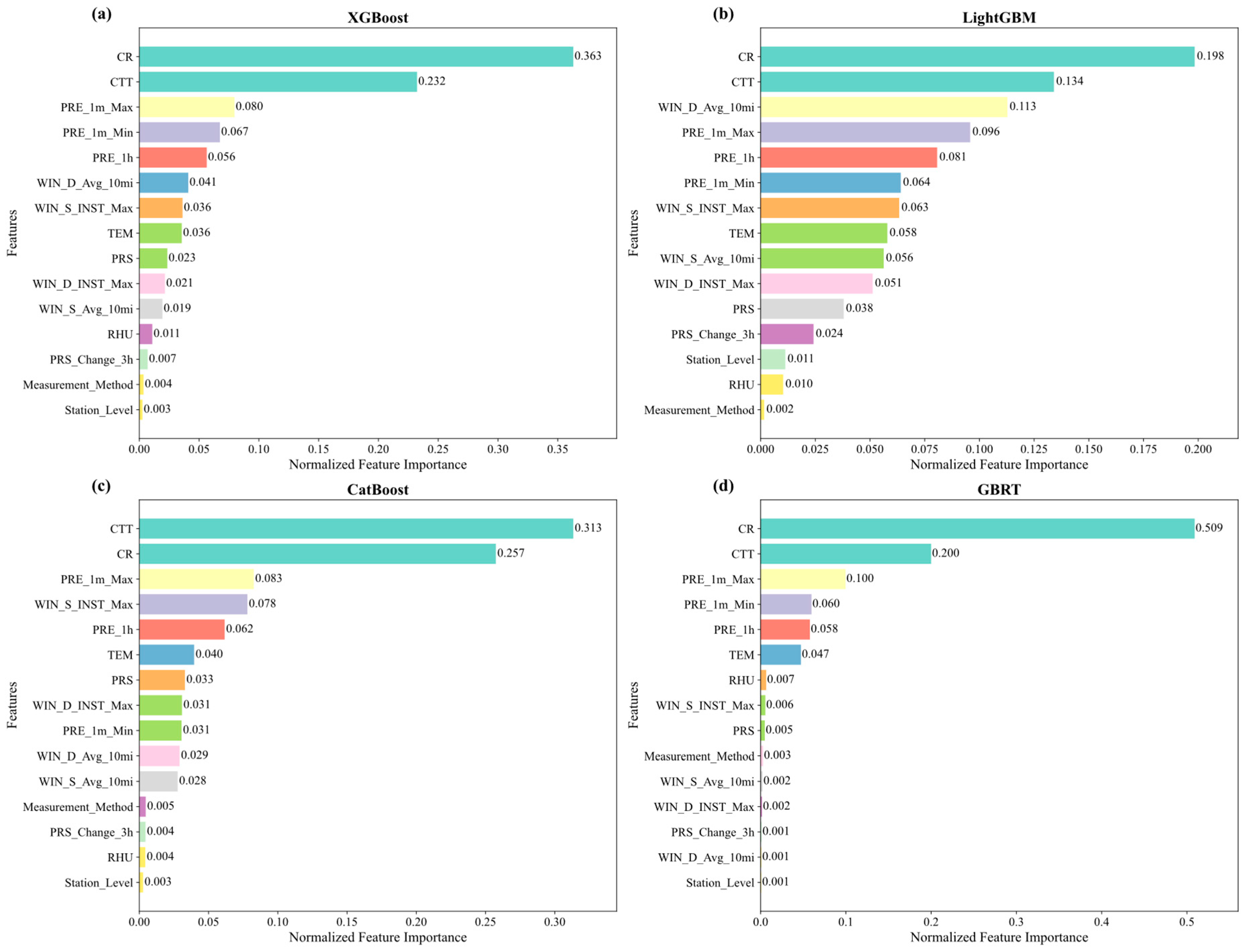
The analysis of normalized feature importance in the four models for the 15 features revealed that remote sensing data played a dominant role in the predictions, with mean normalized feature importance values of 0.332 for CR and 0.220 for CTT, respectively (Figure 5). Precipitation-related features were consistently identified as stable predictors, where the PRE_1m_Max, PRE_1h, and PRE_1m_Min were identified as subdominant predictive factors, with mean normalized feature importance values of 0.089, 0.064, and 0.055. Moderate contributions were observed from wind speed, wind direction, PRS, and TEM, with mean normalized feature importance values ranging from 0.025 to 0.046. In contrast, the importance of PRS_Change_3h, RHU, and metadata features was relatively low, with normalized feature importance values all below 0.01.

However, distinct model-specific characteristics were observed in the feature weighting in the four models (Figure 6). In the XGBoost model, the ranking of feature importance was observed to be similar to the average of the four models, with remote sensing data identified as the most significant (CR, 0.363; CTT, 0.232), followed by precipitation-related features (PRE_1m_Max, 0.080; PRE_1m_Min, 0.067; PRE_1h, 0.056). Greater sensitivity to wind direction (WIN_S_Avg_10mi, 0.113; WIN_D_INST_Max, 0.051) and wind speed (WIN_S_INST_Max, 0.063; WIN_S_Avg_10mi, 0.056) features were exhibited by the LightGBM model, with these values being significantly elevated compared to other models. A unique pattern was presented by CatBoost, which was identified as the only model where a higher importance was allocated to CTT (0.313) than to CR (0.257). This model was also characterized by a considerably greater emphasis being placed on the WIN_S_INST_Max (0.078). In contrast, an extreme dependence on CR was displayed by the GBRT model, which was attributed a normalized feature importance value of 0.509, accounting for over half of the total feature importance. Concurrently, wind-related features were largely disregarded (normalized feature importance value ≤ 0.006). These discrepancies highlighted the inherent biases of different models in capturing complex feature-target relationships, underscoring that the selection of an appropriate model is critical for the accurate interpretation of feature influences in practical applications.

During the modeling process, feature elimination was performed based on feature importance. Only features whose cumulative contribution exceeded 99.5% after sorting in descending order were retained. This procedure further streamlined the model architecture and improved interpretability, following the initial feature selection outlined in Section 2.2.2.

3.2. Comparison of Performance in Different Models

The performances of the four models in heavy rainfall QC were systematically evaluated by the metrics outlined in Section 2.4. The accuracy measures the overall proportion of correct predictions. The precision quantifies the proportion of predicted anomalous events that are truly anomalous, where a higher value directly translates to fewer false alarms. In contrast, the recall quantifies the proportion of actual anomalous events that are correctly identified, with a higher value signifying a lower rate of missed detections. The F1-score, as the harmonic mean of precision and recall, provides a single metric to evaluate the model’s balanced performance.

Comparative analysis of two sets revealed that the performance degradation of the four models was not significant, with observed decreases in F1-scores of 0.045, 0.049, 0.047, and 0.044, respectively, thus indicating no substantial overfitting was detected (

Table 2. Performance metrics of the four models with control experiment on the training set.

	Accuracy	Precision	Recall	F1-Score
MDOS (control experiment)	0.986	0.709	0.619	0.661
XGBoost	0.994	0.89	0.834	0.861
LightGBM	0.994	0.894	0.828	0.860
CatBoost	0.992	0.885	0.804	0.843
GBRT	0.992	0.881	0.811	0.845

and

Table 3. Performance metrics of the four models with control experiment on the testing set.

	Accuracy	Precision	Recall	F1-Score
MDOS (control experiment)	0.986	0.734	0.627	0.676
XGBoost	0.992	0.844	0.789	0.816
LightGBM	0.991	0.845	0.78	0.811
CatBoost	0.991	0.843	0.753	0.796
GBRT	0.991	0.849	0.758	0.801

).

High accuracies (accuracy > 0.99) were observed by all models in the testing set (Table 3). However, it could be attributed to the significant class imbalance in the precipitation dataset employed, where normal precipitation events (negative samples) substantially outnumbered anomalous precipitation events (positive samples). The identification of true negative samples by the models was relatively easy, resulting in the TN value in Equation (2) being considerably larger than TP, FP, and FN. Consequently, the accuracies were universally inflated, failing to adequately reflect the capability to detect the critical minority class of anomalous precipitation. In comparison, the precision, recall, and F1-score demonstrated greater diagnostic value in identifying such imbalanced datasets.

According to the results, all evaluated metrics of the four models outperformed those of the MDOS QC (Table 3). The superiority of applying machine learning techniques to multi-source data, particularly remote sensing data, for heavy rainfall QC was effectively highlighted. The highest F1-score (0.816) and recall (0.789) were achieved by XGBoost, indicating its superior comprehensive performance in identifying anomalous precipitation. LightGBM was observed to closely follow, with its F1-score (0.811) nearly matching that of XGBoost, while a slightly higher precision (0.845) was attained. The highest precision (0.849) was recorded by the GBRT model, though its recall was found to be relatively lower. All metrics obtained by the CatBoost model on the test set were noted to be slightly inferior to those of the other three comparative models.

The precision-recall (PR) and receiver operating characteristic (ROC) curves [68] of the four models were observed to be similar (Figure 7). The highest average precisions (APs) of 0.777 were achieved by both XGBoost and CatBoost. Meanwhile, the highest two areas under the curves (AUCs) were exhibited by LightGBM and XGBoost, with values of 0.942 and 0.941, respectively. Therefore, through a synthesis of metrics, PR and ROC curves assessment, the XGBoost model was regarded as the preferred high-quality model and was chosen for further study (Section 3.4). Compared to the MDOS, the XGBoost model achieved an increase in precision by 0.110, recall by 0.162, and F1-score by 0.140 in the heavy rainfall QC.

The XGBoost model was implemented with its hyperparameters optimized using the Optuna library. The final architecture comprised 268 estimators and a maximum tree depth of 7. The learning process was configured with a learning rate of 0.0236 and substantial regularization, where L1 and L2 regularization terms were set to 0.9621 and 0.0527, respectively. Additionally, stochasticity was introduced through column subsampling at a ratio of 0.9166 and instance subsampling at a ratio of 0.8266.

3.3. Model Validation

An independent validation set of 21,741 samples was used to calculate the model performance metrics, which are summarized in

Table 4. Performance metrics of the four models with control experiment on the validation set.

	Accuracy	Precision	Recall	F1-Score
XGBoost	0.993	0.838	0.727	0.779
LightGBM	0.993	0.823	0.727	0.772
CatBoost	0.992	0.833	0.687	0.753
GBRT	0.992	0.824	0.702	0.758

. All models exhibited only marginal performance degradation on the validation set. Specifically, precision decreased by merely 0.006, 0.022, 0.010, and 0.025 for XGBoost, LightGBM, CatBoost, and GBRT, respectively. Recall also showed reduction, ranging from 0.053 to 0.066, while the F1-score experienced declines between 0.037 and 0.043. These limited decreases confirm that the models maintain strong generalization capability in validation.

3.4. Feature Contribution

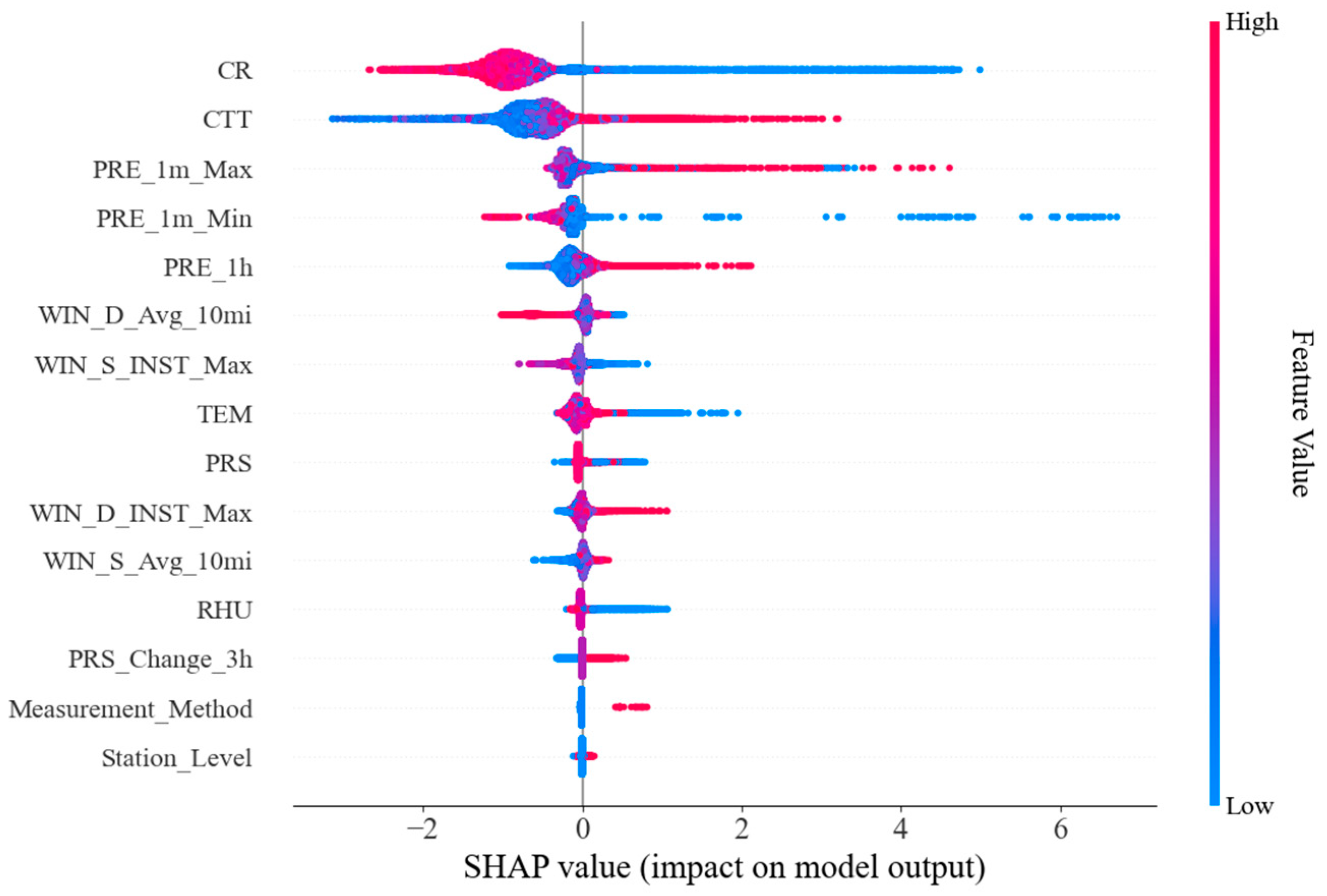
Rooted in an individualized model interpretation method, SHAP values allow a distinct explanation to be provided for each feature. Figure 8 presents how a feature modulates its own contribution to the model output. In this figure, the color of the dot represents the value of that feature for the review (red: high, blue: low), and the position of the dot is the contribution of the feature to the review’s helpfulness. Positive SHAP values signify that the feature’s value contributes to the model’s prediction of “anomalous precipitation”, and a larger value indicates a stronger contribution. Conversely, negative SHAP values signify a contribution to the prediction of “normal precipitation”, with a smaller (more negative) value corresponding to a stronger contribution.

CR was regarded as the most discriminative feature in the model (Figure 6a and Figure 8). The SHAP summary plot demonstrated that lower CR values were significantly positively correlated with the probability of a record being classified by the model as “abnormal precipitation” (Figure 8). Additionally, CR SHAP values exhibited a dependence on CTT and PRE_1h (Figure 9a,d). The samples with CR values below 20 dBZ, combined with either hourly precipitation greater than 70 mm or CTT exceeding 260 K, were strongly classified as “anomalous precipitation” by the model. These phenomena were highly consistent with the physical mechanisms governing heavy rainfall formation. Weak radar echoes imply underdeveloped convective systems and weaker processes of water vapor condensation and hydrometeor growth, which are theoretically insufficient to support a precipitation rate greater than 40 mm/h. Consequently, when an observed hourly precipitation with a lower CR, the record is highly likely to be attributed to manual operational errors, such as garden watering, cleaning the gauge without disconnecting communication [23,28,29].

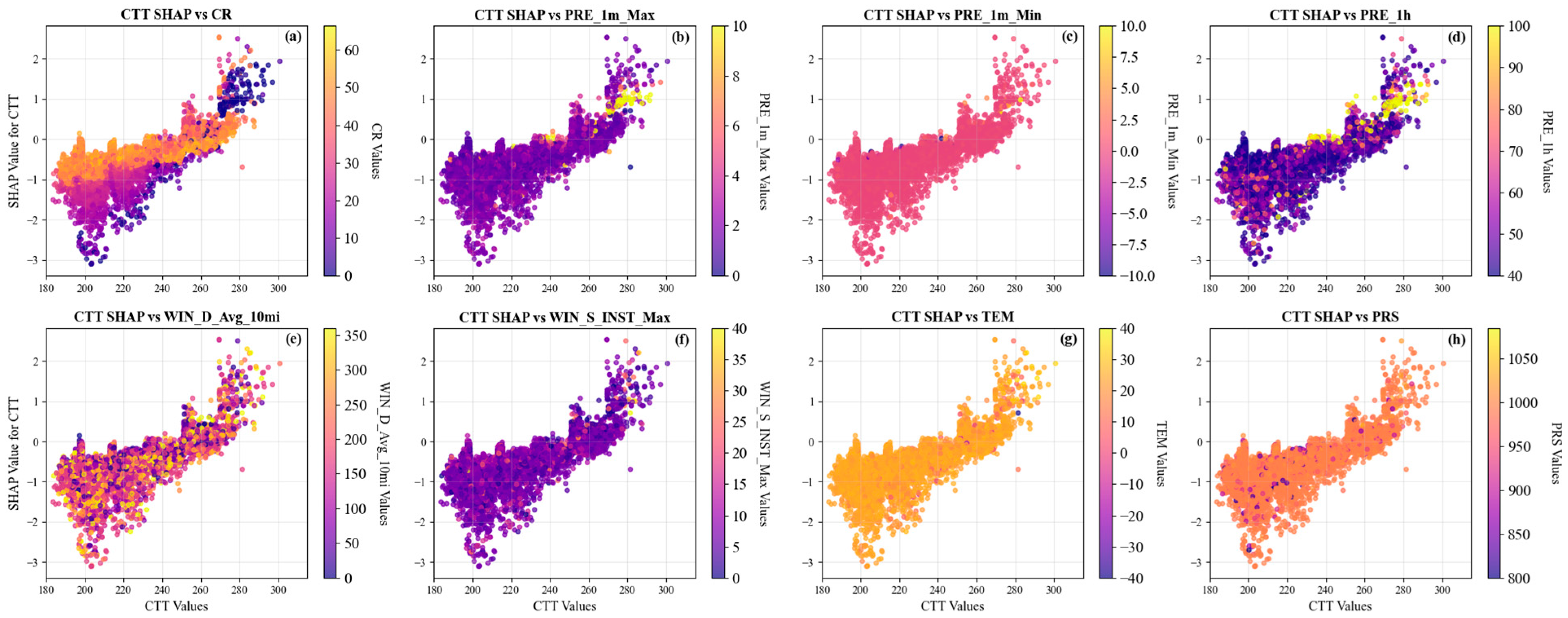
CTT was established as a key indicator in the model (Figure 6a and Figure 8). It showed that samples with elevated CTT (i.e., warmer cloud tops), particularly when combined with either a CR below 20 dBZ or hourly precipitation exceeding 70 mm, were readily classified as anomalous precipitation (Figure 10a,d). From a meteorological perspective, cloud systems capable of generating intense convection are typically characterized by high cloud top heights and low cloud top temperatures. A heavy rainfall event accompanied by a high CTT value is considered suspicious. Such events may be associated with shallow or warm-cloud-dominated systems, which typically lack the dynamic and microphysical conditions necessary for producing substantial rainfall. Similar to the CR SHAP analysis, these phenomena may also be attributed to non-meteorological factors.

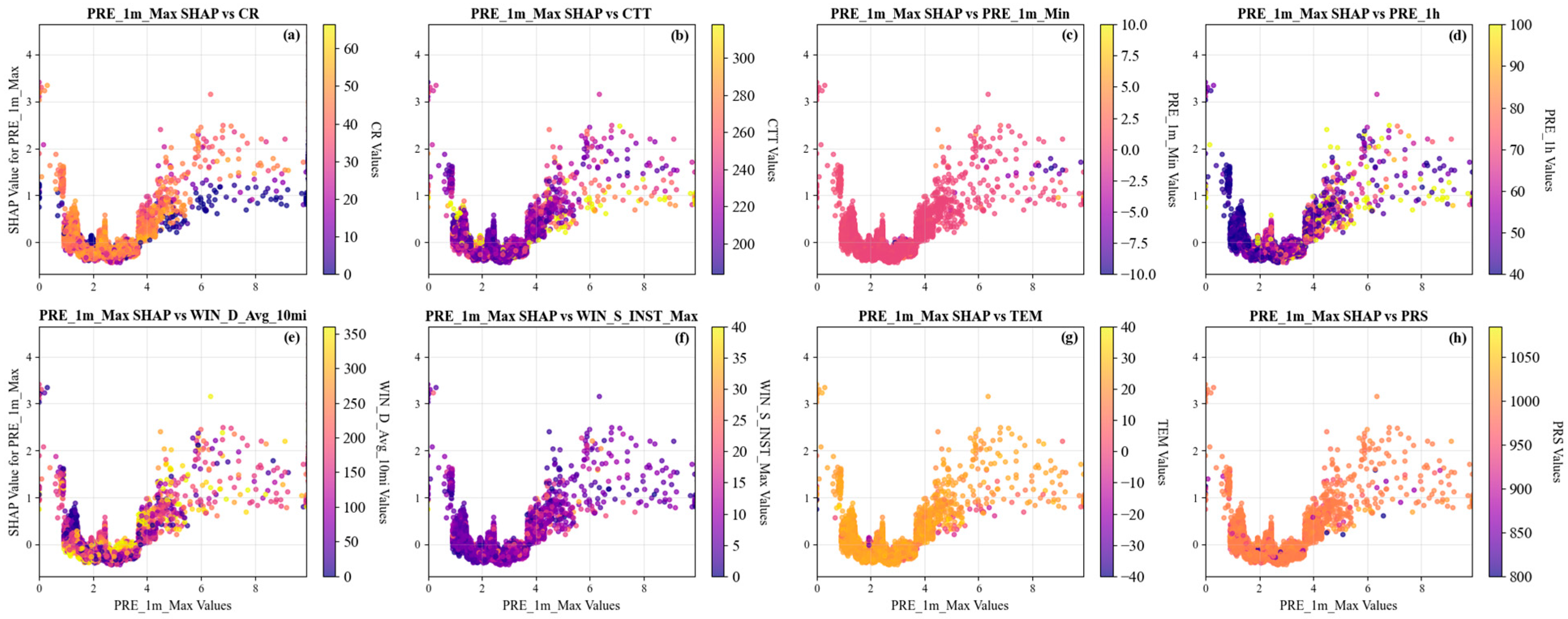
The PRE_1m_Max was identified as a critical feature utilized for the model (Figure 6a and Figure 8). SHAP analysis indicated that the model was more likely to classify a precipitation event as anomalous under two scenarios: (1) the PRE_1m_Max was less than 0.5 mm (Figure 8 and Figure 11). This was primarily attributed to a logical inconsistency in the data, as such a low precipitation rate was physically implausible to support the observed hourly precipitation greater than 40 mm. This discrepancy is likely caused by data encoding or transmission errors [25,29]; (2) the PRE_1m_Max exceeded 3.5 mm, particularly when accompanied by either a CR of less than 20 dBZ or a CTT greater than 260 K (Figure 11a,b). An actual heavy rainfall event is composed of several high-intensity minute-scale segments, yet its maximum value usually falls within a reasonable physical range. These anomalously high minute values were likely to be induced by instrumental malfunctions [14,21,25,29], such as the persistent false triggering of a reed switch in a tipping-bucket rain gauge due to metal fatigue or foreign object adhesion, leading to an abnormally high count within a single minute. Additionally, occasional strong electromagnetic interference can also produce such physically implausible extreme peaks [23].

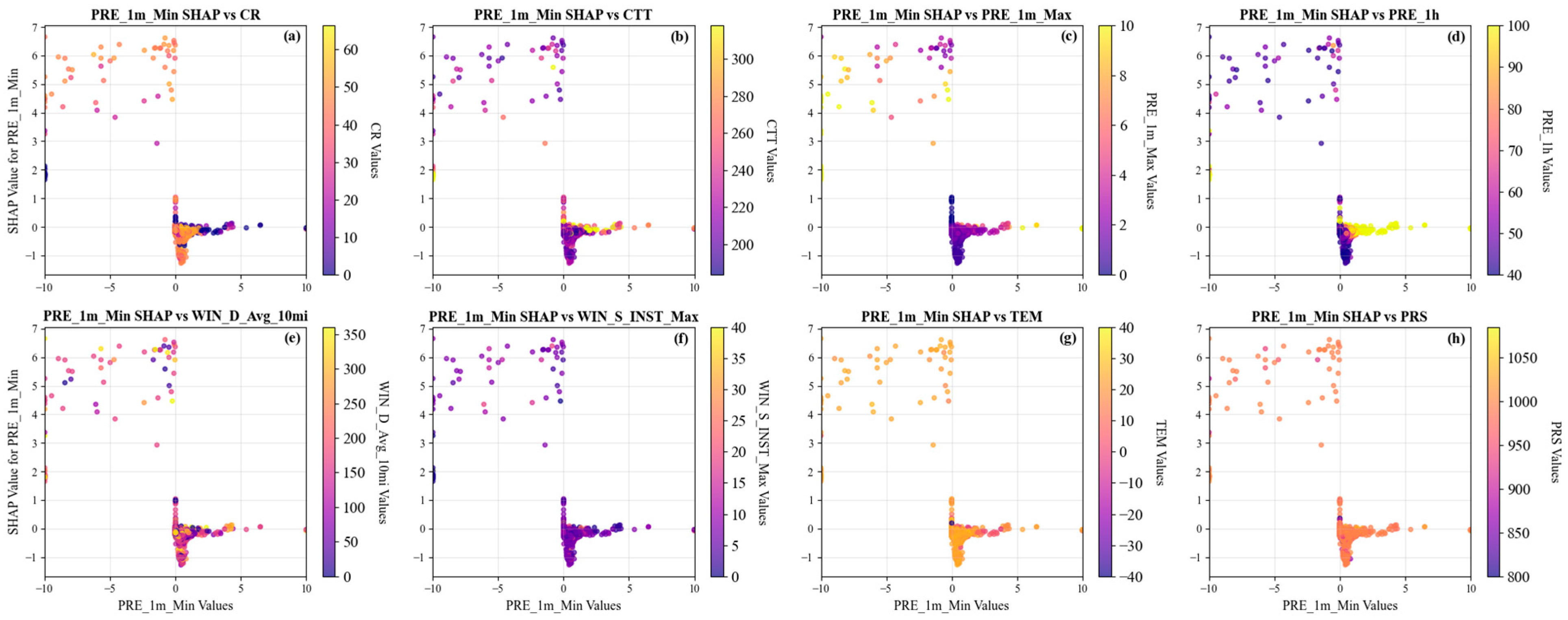
The PRE_1m_Min played a distinctive role in this model (Figure 6a and Figure 8). The SHAP analysis revealed that PRE_1m_Min did not heavily depend on other features (Figure 12). But anomalously low values (particularly negative values) of this feature served as a strong indicator for the model to classify a record as “abnormal precipitation”. As minute precipitation represents an accumulated quantity over a period, its value is inherently non-negative. Therefore, the occurrence of negative values exposes errors in the data encoding or transmission, such as improper sign bit handling or data type conversion errors [25,29]. Thus, it is also established as a sensitive indicator for heavy rainfall QC.

4. Discussion

This study demonstrates the superior performance of machine learning-based algorithms over traditional threshold-based methods for heavy rainfall QC. By effectively integrating multi-source data, the algorithm significantly reduces both false alarms and missed detections. However, before operational deployment, a comprehensive analysis is essential to enhance the algorithm’s robustness and interpretability.

4.1. Seasonal Variations in Algorithm Performance

To investigate seasonal variations in algorithm performance, monthly performance metrics from January to December were calculated using the XGBoost-based QC algorithm based on 31,972 samples from the testing set (

Table 5. Monthly performance metrics of the XGBoost-based QC algorithm in testing set.

Month	Accuracy	Precision	Recall	F1-Score	Sample Count
January	0.990	0.845	0.932	0.886	103
February	0.992	0.856	0.930	0.891	243
March	0.991	0.866	0.923	0.894	336
April	0.993	0.853	0.832	0.842	2541
May	0.993	0.843	0.829	0.836	3236
June	0.996	0.842	0.772	0.805	6396
July	0.997	0.856	0.763	0.807	8594
August	0.997	0.839	0.769	0.802	6871
September	0.994	0.842	0.825	0.833	2604
October	0.992	0.849	0.924	0.885	630
November	0.991	0.859	0.947	0.901	227
December	0.990	0.859	0.932	0.894	191

).

The results revealed a clear and meteorologically consistent seasonal distribution in sample counts, characterized by a pronounced peak during summer months and a distinct minimum in winter [69]. Meanwhile, the monthly performance metrics indicated that accuracy and precision showed minimal seasonal variation, with values ranging from 0.990–0.997 and 0.839–0.866, respectively.

In contrast, recall and F1-scores showed distinct seasonal fluctuations. Although sample counts were at their highest during summer months, recall and F1-scores were comparatively lower, with values ranging from 0.763–0.772 and 0.802–0.807, respectively. This performance pattern is likely consistent with the more complex, localized, and microphysically diverse nature of warm-season convective rainfall [69,70,71], which presents a greater challenge for the QC algorithm. In the winter months, the algorithm exhibited higher recall and F1-scores (0.932–0.947 and 0.886–0.901) despite lower sample sizes. This can be attributed to the more organized and systemic nature of cool-season weather patterns [71,72], which leads to more spatially and temporally consistent signatures in the remote sensing and surface data, making events easier to classify.

4.2. Spatial Variations in Algorithm Performance

To evaluate the spatial generalization capability of the algorithm under different climatic backgrounds, a detailed regional performance assessment was conducted. China was divided into seven climatic regions based on multiple-year mean values of temperature, precipitation and altitude [73] (Figure 1): arid desert of Northwest China (NWC), semi-arid steppe of Inner Mongolia (IM), Qinghai-Tibetan Plateau (QTP), (semi-) humid cold-temperate Northeast China (NEC), semi-humid warm-temperate North China (NC), humid subtropical Central China (CC), and humid tropical South China (SC). The testing set was partitioned according to these seven regions, and performance metrics for the XGBoost-based QC algorithm were subsequently calculated (

Table 6. Regional performance metrics of the XGBoost-based QC algorithm in testing set in different climatic regions.

Climatic Region	Accuracy	Precision	Recall	F1-Score	Sample Count
NWC	0.991	0.945	0.940	0.942	235
IM	0.989	0.955	0.950	0.952	179
QTP	0.985	0.955	0.970	0.962	67
NEC	0.990	0.931	0.937	0.934	798
NC	0.992	0.841	0.811	0.826	4116
CC	0.993	0.849	0.807	0.827	16,641
SC	0.992	0.843	0.737	0.786	9936

).

The results demonstrated a spatial variation in sample counts consistent with the station distribution, with the highest density observed in NC, CC and SC. The regional performance metrics revealed that the accuracy exhibited minimal spatial variation, with values ranging from 0.985 to 0.993.

Notably, the northwestern and high-latitude regions (NWC, IM, QTP, and NEC) achieved superior performance in multiple metrics, characterized by high precision (0.931–0.955), recall (0.937–0.970), and F1-scores (all above 0.93). This consistently strong performance may be attributed to the dominant heavy rainfall mechanisms in these regions, which are primarily driven by large-scale synoptic systems [74,75,76]. These systems typically produce organized precipitation cloud structures with well-defined spatial patterns, leading to clearer physical relationships between remote sensing features and surface precipitation.

In contrast, the eastern and southern regions (NC, CC, and SC) exhibited notably degraded performance in both recall (0.737–0.811) and F1-scores (0.786–0.827). This was compounded by substantially lower precision values (0.841–0.849) compared to those in the northwestern and high-latitude regions. This performance pattern reflects the greater algorithmic challenges posed by complex terrain and heterogeneous precipitation mechanisms prevalent in these regions [74,77,78]. Particularly in SC, which presented the most challenging scenario with the lowest recall (0.737) and F1-score (0.786), the frequent occurrence of highly localized warm-sector convective rainfall introduces substantial variability in remote sensing signatures and creates non-linear relationships with surface rain rates. These factors collectively contribute to the increased difficulty in accurate heavy rainfall identification by the algorithm.

The analysis reveals notable spatiotemporal variations in algorithm performance, particularly during the warm season and in regions with complex terrain or heterogeneous precipitation mechanisms, which indicates substantial room for improvement. The future work will prioritize the development of spatiotemporally adaptive algorithms capable of addressing distinct precipitation mechanisms in seasons and regions, thereby enhancing performance stability throughout annual cycles and diverse climatic regions. To support this goal, the temporal coverage of datasets will be expanded by continuously incorporating observational data from additional years, with particular emphasis on periods marked by strong climate anomaly events (e.g., strong ENSO). This systematic data diversification is expected to significantly improve the algorithm’s generalization capability under evolving climatic conditions.

Beyond these spatiotemporal considerations, the current specialization in heavy rainfall events (≥40 mm/h) will be extended to develop a unified, multi-class QC algorithm. This expansion addresses the critical need for a comprehensive QC system capable of handling the full spectrum of precipitation intensities, including light rain and snowfall. These types exhibit distinct physical signatures and error modes that require specialized detection approaches.

Additionally, false alarm cases will be systematically analyzed to identify specific causes (such as precipitation phase changes, radar beam blockage, or shallow warm-rain processes) that violate the typical relationship. Feature refinement and the creation of a specialized edge-case training library will then be guided by these insights, with the ultimate goal of enhancing the algorithm’s discriminative capability and reducing false alarms in operations.

5. Summary and Conclusions

In this study, a machine learning-based QC algorithm for heavy rainfall was developed by integrating AWS observations with radar, satellite, and metadata inputs. Based on heavy rainfall samples from 1 June 2022 to 31 December 2024, performance metrics and interpretability were analyzed on the model outputs. The main conclusions are summarized as follows:

In heavy rainfall QC, the four gradient boosting models (XGBoost, LightGBM, CatBoost, and GBRT) demonstrated a marked improvement over the conventional MDOS method, achieving consistently superior performance in precision, recall, and F1-score. Through a comprehensive evaluation of the performance metrics, PR and ROC curves, the XGBoost model achieved the best overall performance, with precision, recall, and F1-score reaching 0.844, 0.789, and 0.816 on the testing set. Compared to the MDOS, the XGBoost model achieved an increase in precision by 0.110, recall by 0.162, and F1-score by 0.140 in heavy rainfall QC. This finding indicates that by effectively learning the non-linear relationships from complex multi-source data, gradient boosting-based machine learning algorithms significantly improve heavy rainfall QC, yielding a substantial reduction in both false alarms (higher precision) and missed detections (higher recall). These algorithms significantly improved the identification of challenging QC issues like isolated anomalies and continuous heavy rainfall.

The radar, satellite, and minute-level precipitation data were found to play dominant roles in the model’s feature importance. The inclusion of these high-value features overcame the limitations of traditional QC methods that rely on static thresholds and single data sources. Moreover, radar data compensated for the spatiotemporal resolution limitations of satellite observations, while satellite data effectively covered the observational gaps of radar in complex terrain. Through the adaptive learning strategy of the machine learning model, these two data sources achieved complementary advantages and synergistic effects.

Interpretability analysis based on the SHAP method demonstrated that the model’s decision logic was highly consistent with meteorological physical mechanisms. For example, low CR or high CTT generally indicated weak precipitation or underdeveloped convective clouds. Heavy rainfall records associated with such features were accurately identified as anomalous by the model, which corresponds to manual operational errors (e.g., garden watering, cleaning the gauge without disconnecting communication) or other non-meteorological factors. Furthermore, anomalous minute-level precipitation extremes were confirmed by the model as key indicators for identifying instrument malfunctions (e.g., the persistent false triggering of a reed switch in a tipping-bucket rain gauge due to metal fatigue or foreign object adhesion), data encoding and transmission errors. This alignment between the decision logic mechanism and physical principles enhances the reliability of the model results and makes the decision process transparent and interpretable for forecasters, demonstrating strong potential for operational application.

Future work will be directed along three primary dimensions. First, spatiotemporally adaptive algorithms will be developed to better represent precipitation mechanisms in seasons and regions, supported by a continuous expansion of observational data. Second, the framework will be extended to establish a unified, multi-class QC system capable of handling all precipitation types and intensities. Finally, false alarm cases will be systematically analyzed to identify root causes. These developments are expected to collectively enhance the algorithm’s stability, generalization capability, and operational applicability.