Correction of Refraction Effects on Unmanned Aerial Vehicle Structure-from-Motion Bathymetric Survey for Coral Reef Roughness Characterisation
Highlights
- Both analytical (Snell’s law) and empirical (regression) methods for correcting refraction at the water/air interface drastically improve the quality of UAV-derived bathymetry.
- Empirical (regression) methods are more efficient to reduce roughness errors and are fairly robust in terms of the choice of calibration points, as long as they cover a range of depths that is representative of the area.
- Refraction corrections enable accurate, low-cost and large-scale coral reef mapping by UAV over shallow areas—reducing the need for extensive in-water measurements and supporting better assessments of wave dissipation, habitat complexity and reef health.
- Even after correction, the 2.5D raster format of UAV DEM tends to smooth the bed 3D complexity, altering the roughness metrics. Three-dimensional mapping formats should be considered.
Abstract
1. Introduction
- through artificial intelligence (AI) methods, generally used to optimise radiometric regression models [40,43,46] by improving the consideration of non-linearities in radiometric models or to empirically correct refraction [47,48]. Some studies use AI by combining radiometric and geometric (photogrammetry) approaches [31,49].
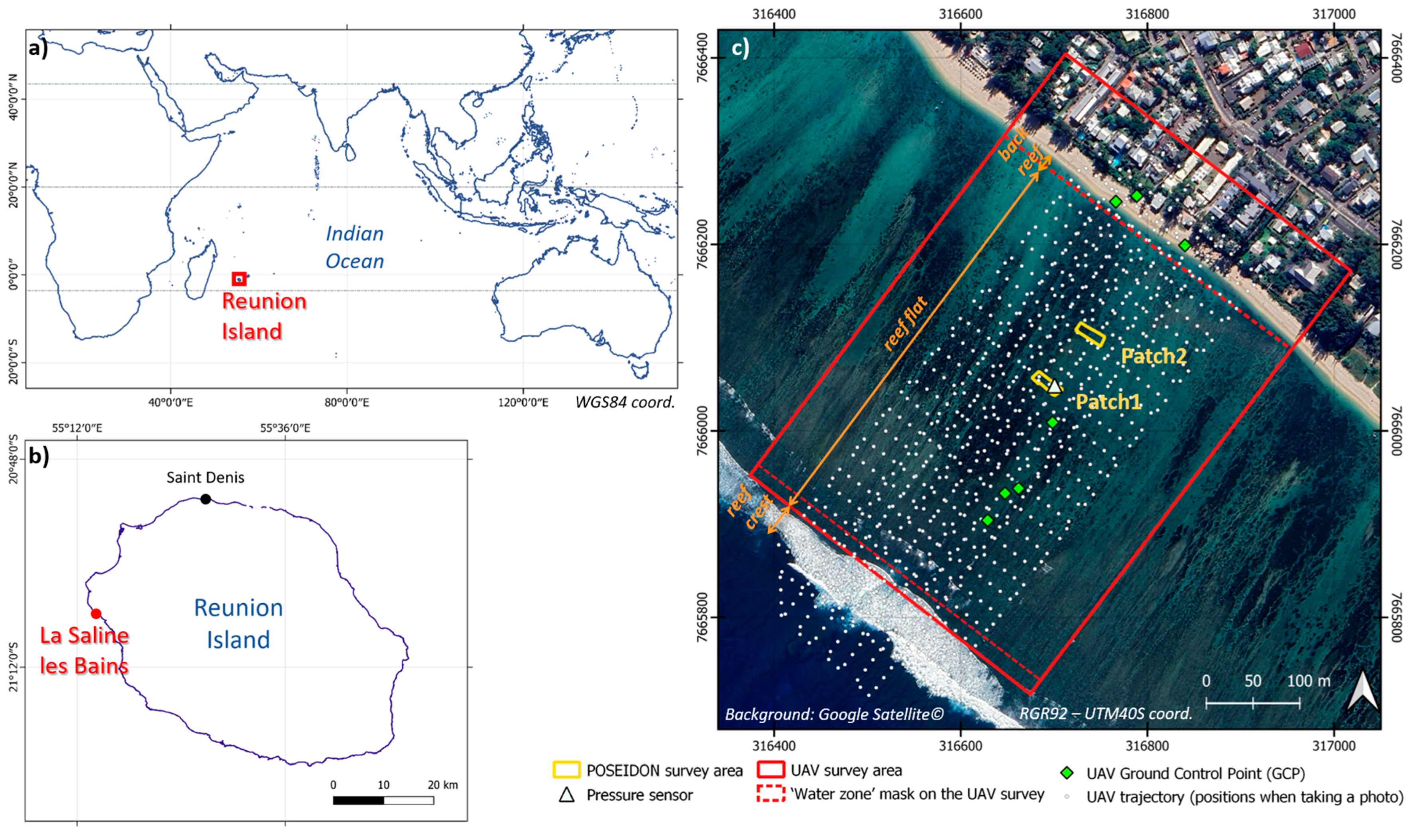
2. Study Area
3. Material and Methods for Data Collection
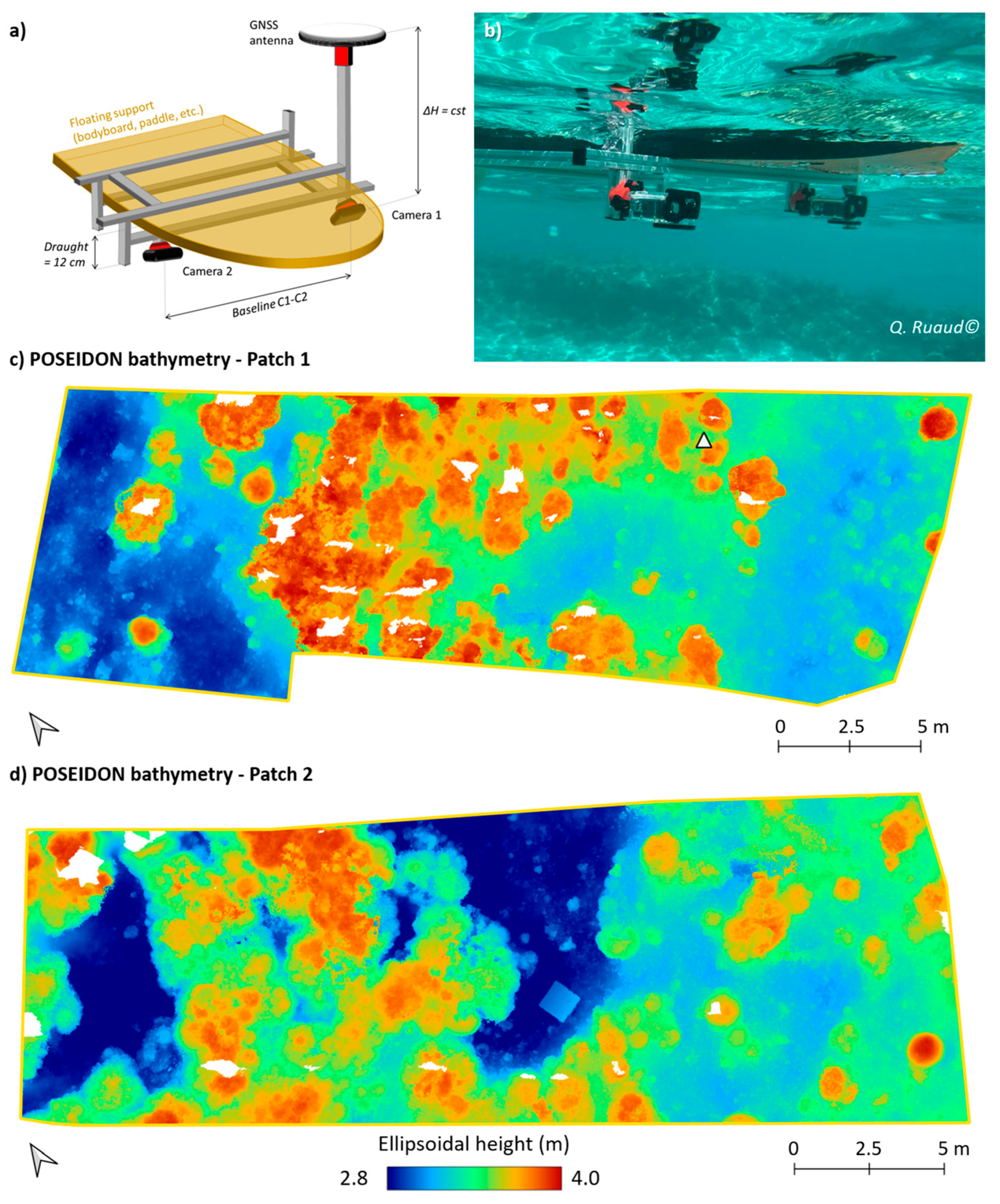
3.1. POSEIDON Survey
3.2. UAV Survey
3.3. Pressure Sensor
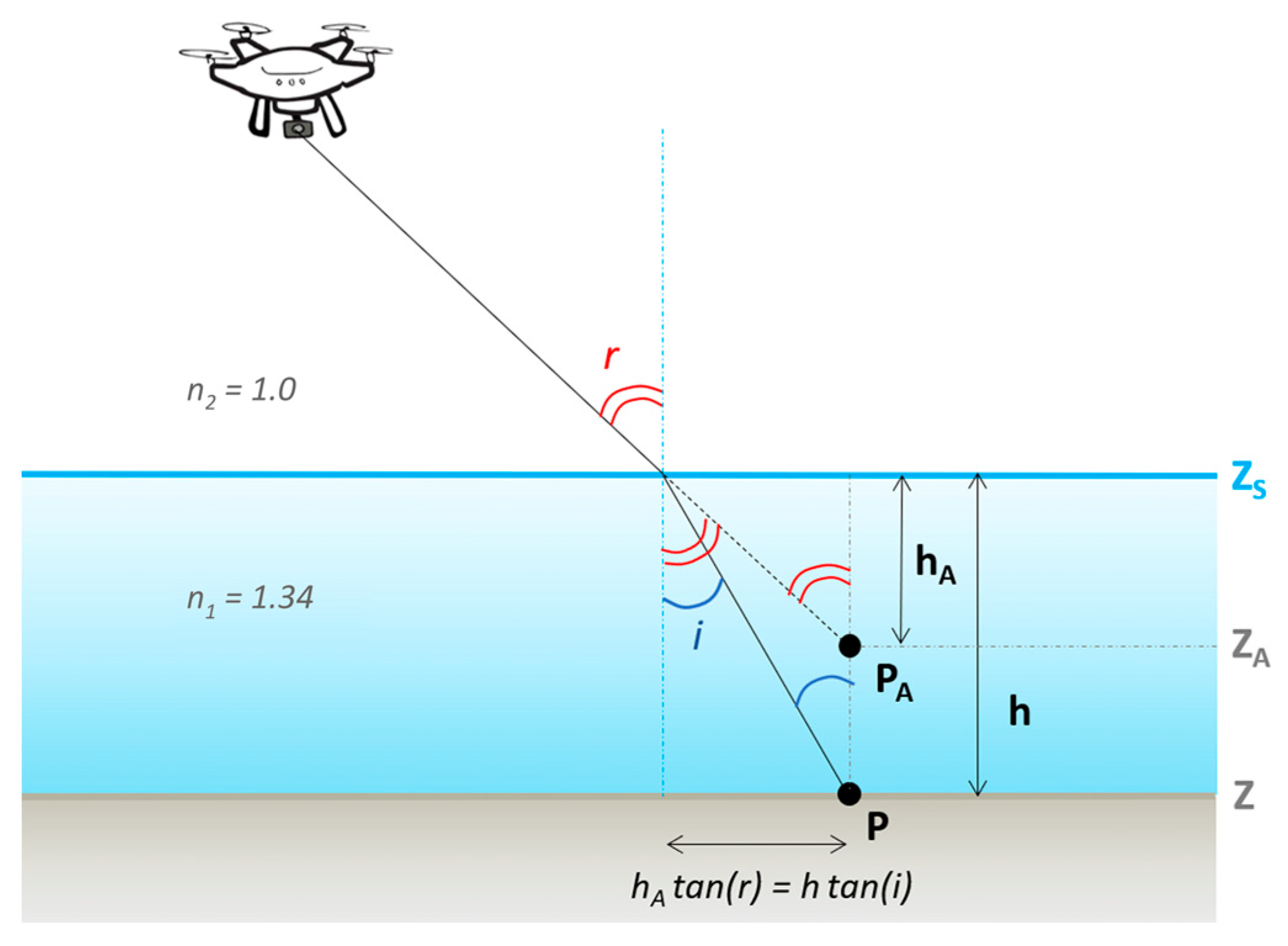
4. Methods for Correction of Refraction Effects
4.1. Analytical Approach
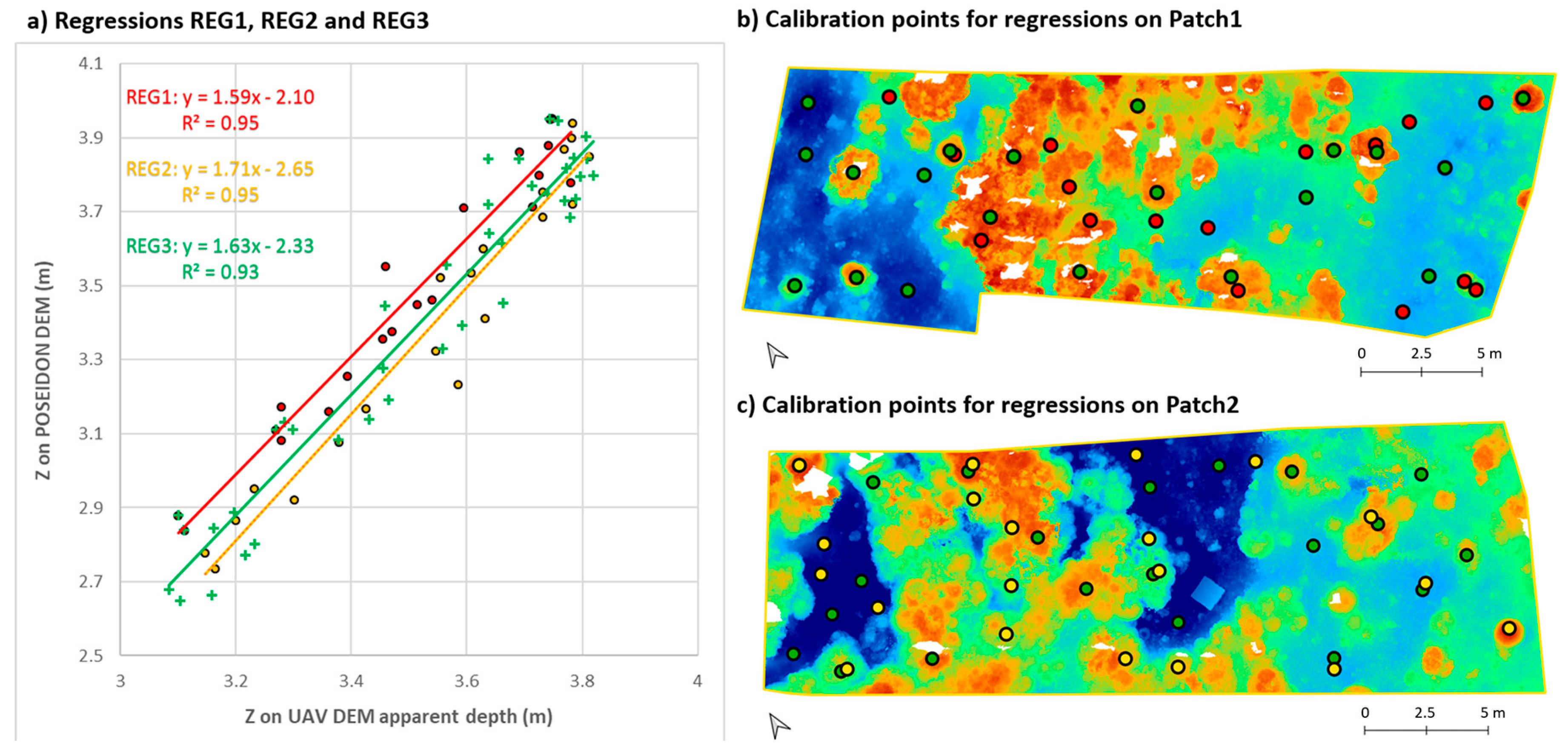
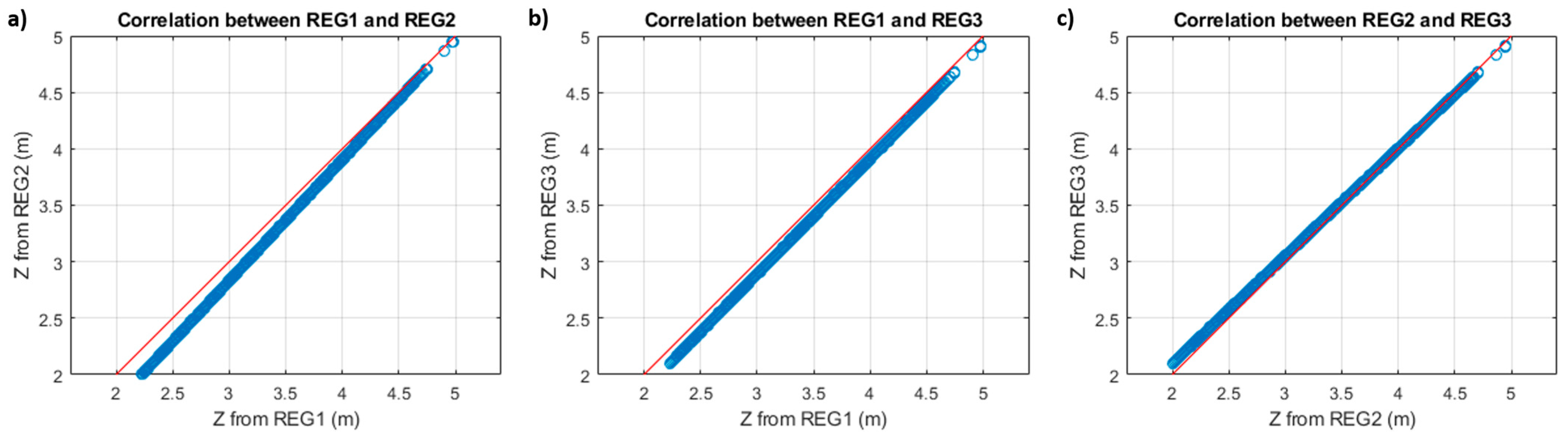
4.2. Empirical Approach Based on Regression
- Regression 1 (REG1): using a batch of 20 calibration points distributed at different depths on Patch 1 (in red colour on Figure 5);
- Regression 2 (REG2): using a batch of 20 calibration points distributed at different depths on Patch 2 (in yellow colour on Figure 5);
- Regression 3 (REG3): using a batch of 40 calibration points distributed at different depths on Patches 1 and 2 (in green colour on Figure 5).
4.3. Assessment of Refraction Correction
5. Results
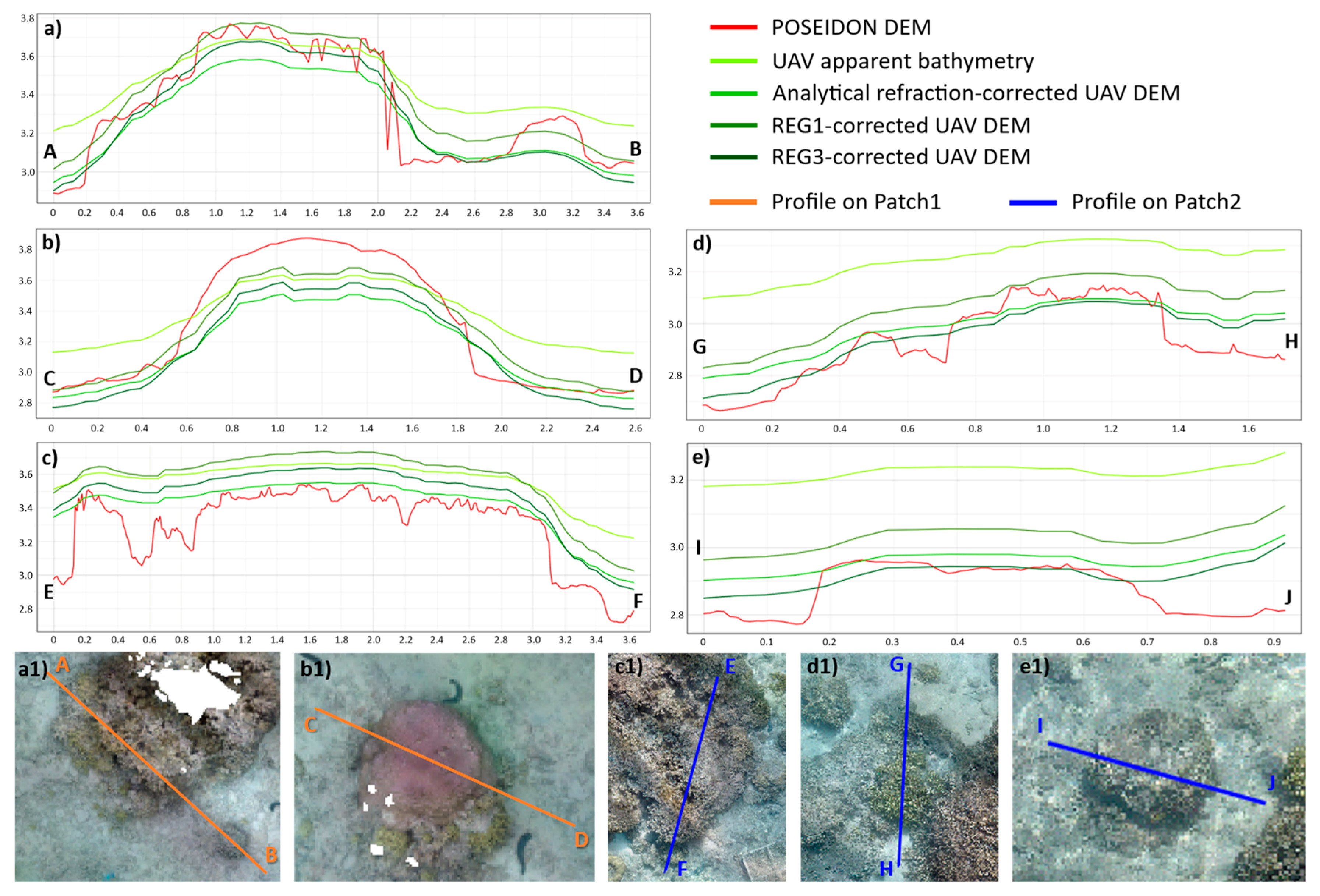
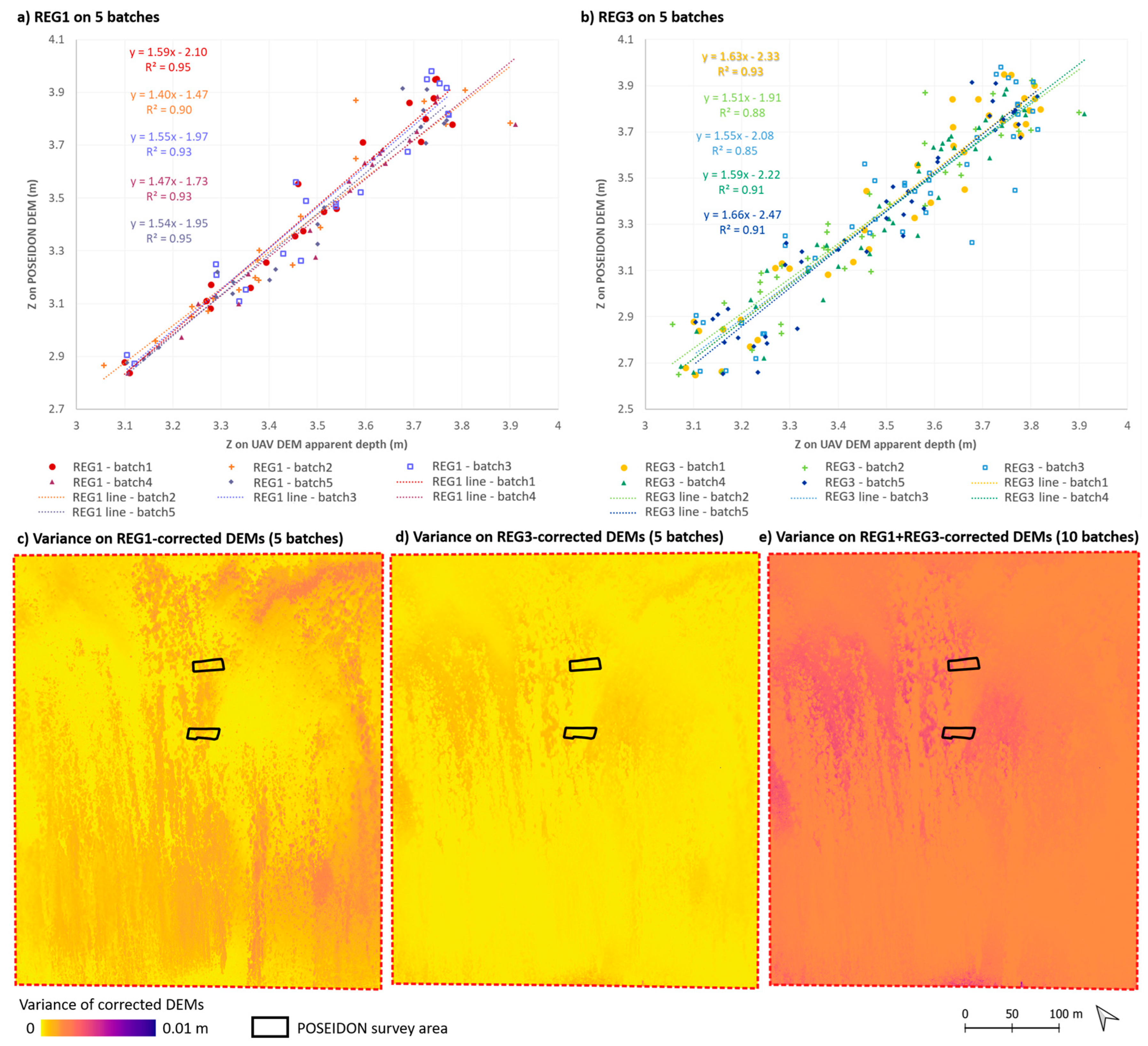
5.1. Impact of Refraction Corrections on DEM Quality
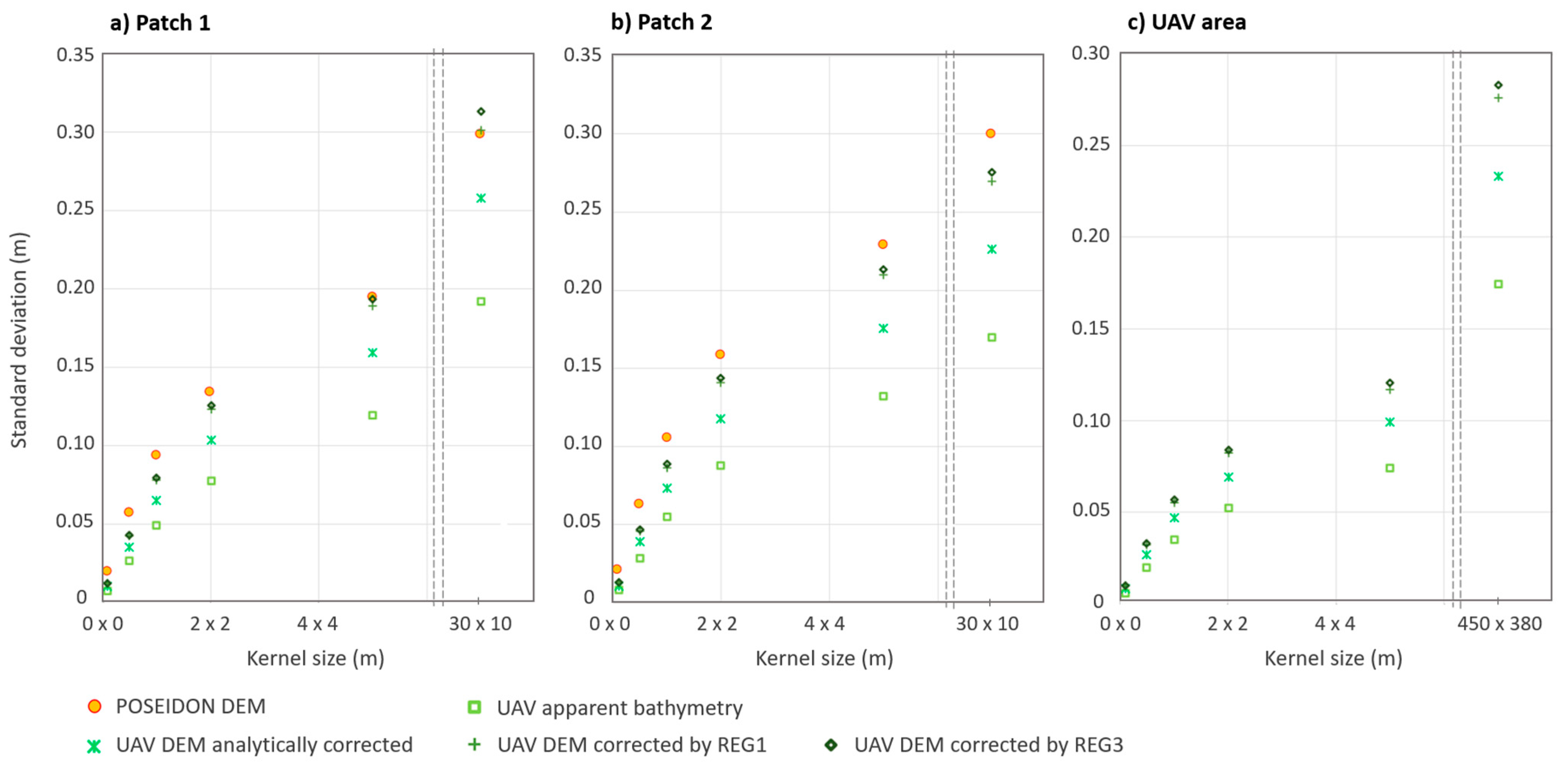
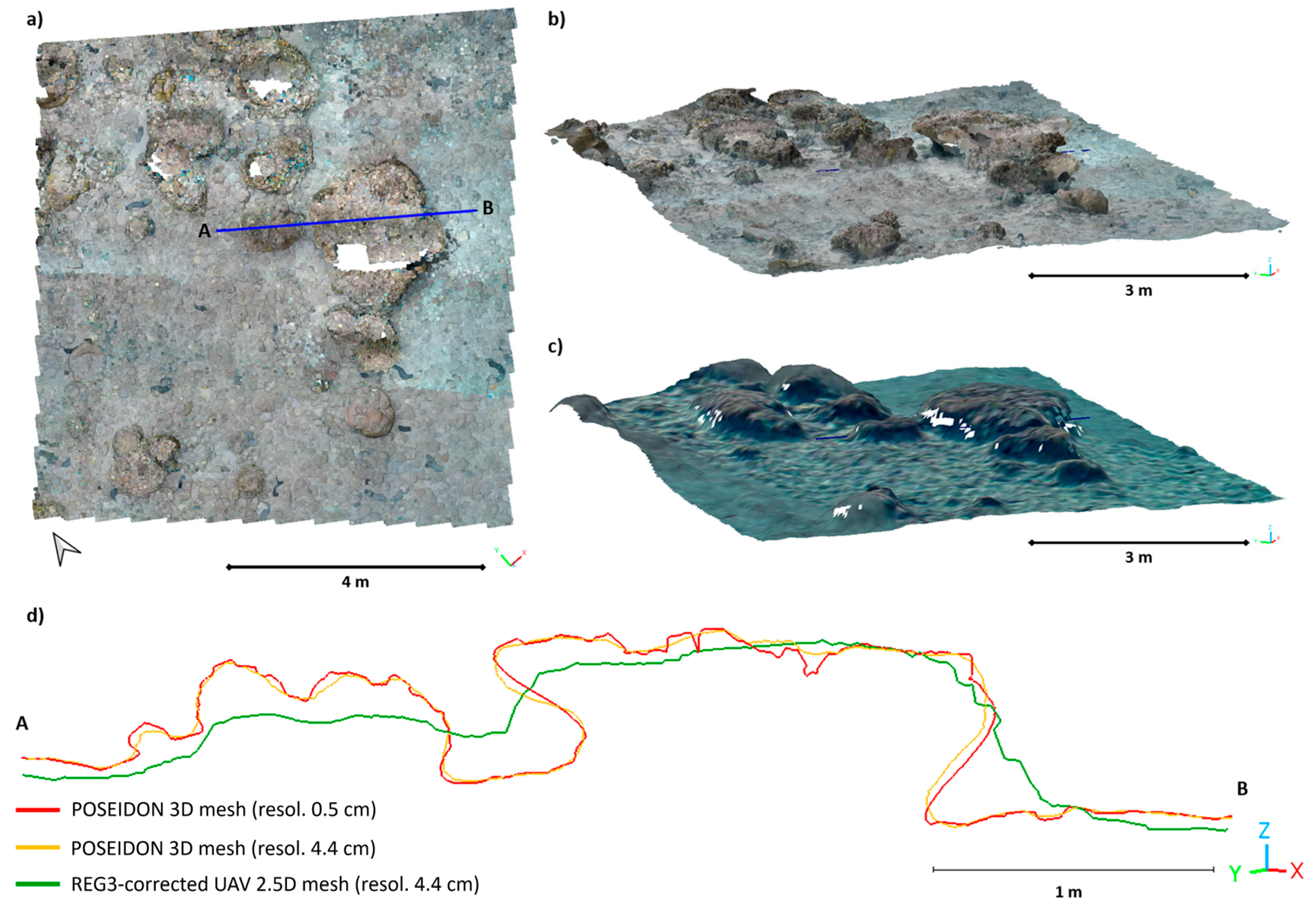
5.2. Impact of Refraction Corrections on Seabed Roughness Calculations
6. Discussion
6.1. Potential and Limitations of Refraction Correction Methods
6.2. Analytical Approach vs. Regression Method
- Five batches of ‘REG1 type’, i.e., with 20 points on Patch1;
- Five batches of ‘REG3 type’, i.e., with 20 points on Patch1 and 20 points on Patch2.
6.3. Limits of the Raster Format and Standard Deviation for Estimating Seabed Roughness
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cordier, E. Dynamique Hydrosédimentaire du Récif Frangeant de l’Hermitage/La Saline (La Réunion): Processus Physiques et Flux Sédimentaires; Université de la Réunion: Saint-Denis, France, 2007. [Google Scholar]
- Frihy, O.E.; El Ganaini, M.A.; El Sayed, W.R.; Iskander, M.M. The Role of Fringing Coral Reef in Beach Protection of Hurghada, Gulf of Suez, Red Sea of Egypt. Ecol. Eng. 2004, 22, 17–25. [Google Scholar] [CrossRef]
- Lowe, R.J.; Falter, J.L.; Bandet, M.D.; Pawlak, G.; Atkinson, M.J.; Monismith, S.G.; Koseff, J.R. Spectral Wave Dissipation over a Barrier Reef. J. Geophys. Res. 2005, 110, 2004JC002711. [Google Scholar] [CrossRef]
- Viehman, T.; Hench, J.; Griffin, S.; Malhotra, A.; Egan, K.; Halpin, P. Understanding Differential Patterns in Coral Reef Recovery: Chronic Hydrodynamic Disturbance as a Limiting Mechanism for Coral Colonization. Mar. Ecol. Prog. Ser. 2018, 605, 135–150. [Google Scholar] [CrossRef]
- Baldock, T.E.; Shabani, B.; Callaghan, D.P.; Hu, Z.; Mumby, P.J. Two-Dimensional Modelling of Wave Dynamics and Wave Forces on Fringing Coral Reefs. Coast. Eng. 2020, 155, 103594. [Google Scholar] [CrossRef]
- Bruch, W.; Cordier, E.; Floc’h, F.; Pearson, S.G. Water Level Modulation of Wave Transformation, Setup and Runup over La Saline Fringing Reef. JGR Oceans 2022, 127, e2022JC018570. [Google Scholar] [CrossRef]
- Masselink, G.; Tuck, M.; McCall, R.; Van Dongeren, A.; Ford, M.; Kench, P. Physical and Numerical Modeling of Infragravity Wave Generation and Transformation on Coral Reef Platforms. JGR Oceans 2019, 124, 1410–1433. [Google Scholar] [CrossRef]
- Nelson, R.C. Hydraulic Roughness of Coral Reef Platforms. Appl. Ocean Res. 1996, 18, 265–274. [Google Scholar] [CrossRef]
- Pomeroy, A.W.M.; Lowe, R.J.; Ghisalberti, M.; Storlazzi, C.; Symonds, G.; Roelvink, D. Sediment Transport in the Presence of Large Reef Bottom Roughness. J. Geophys. Res. Oceans 2017, 122, 1347–1368. [Google Scholar] [CrossRef]
- Madsen, O.S. Spectral Wave-Current Bottom Boundary Layer Flows. Int. Conf. Coastal. Eng. 1994, 1994, 384–398. [Google Scholar] [CrossRef]
- Geindre, M.; Sous, D.; Michaud, H.; Floc’h, F.; Bertin, X.; Aubry, A.; Jeanson, M.; Pezerat, M. Wave Friction Factor and Roughness Definition in 2 Multi-Scale Coral Barrier Reef. JGR Oceans 2025. submitted. [Google Scholar]
- Gon, C.J.; MacMahan, J.H.; Thornton, E.B.; Denny, M. Wave Dissipation by Bottom Friction on the Inner Shelf of a Rocky Shore. JGR Oceans 2020, 125, e2019JC015963. [Google Scholar] [CrossRef]
- Marques, O.B.; MacMahan, J.H.; Feddersen, F.; Conlin, M.P.; Wilson, G.W.; Malila, M.; Rosman, J.H.; Acevedo-Ramirez, C.; Suanda, S.H. Observations of Wave Dissipation by Bottom Friction on a Rough Rocky Shore. In Proceedings of the American Geophysical Union, Ocean Sciences Meeting, New Orlean, LA, USA, 18–23 February 2024; p. CP23B–01. [Google Scholar]
- Sous, D.; Martins, K.; Tissier, M.; Bouchette, F.; Meulé, S. Spectral Wave Dissipation over a Roughness-Varying Barrier Reef. Geophys. Res. Lett. 2023, 50, e2022GL102104. [Google Scholar] [CrossRef]
- Bertin, S.; Groom, J.; Friedrich, H. Isolating Roughness Scales of Gravel-bed Patches. Water Resour. Res. 2017, 53, 6841–6856. [Google Scholar] [CrossRef]
- Groom, J.; Bertin, S.; Friedrich, H. Evaluation of DEM Size and Grid Spacing for Fluvial Patch-Scale Roughness Parameterisation. Geomorphology 2018, 320, 98–110. [Google Scholar] [CrossRef]
- Knudby, A.; LeDrew, E. Measuring Structural Complexity on Coral Reefs. In Proceedings of the American Academy of Underwater Sciences 26th Symposium, Dauphin Island, AL, USA, 19–24 March 2007; Available online: https://www.semanticscholar.org/paper/Measuring-Structural-Complexity-on-Coral-Reefs-Knudby-LeDrew/942441117a2ccc58b4bcb192853da0151630a1f3 (accessed on 20 October 2025).
- McCormick, M. Comparison of Field Methods for Measuring Surface Topography and Their Associations with a Tropical Reef Fish Assemblage. Mar. Ecol. Prog. Ser. 1994, 112, 87–96. [Google Scholar] [CrossRef]
- Risk, M.J. Fish Diversity on a Coral Reef in the Virgin Islands. Atoll Res. Bull. 1972, 153, 1–6. Available online: https://repository.si.edu/server/api/core/bitstreams/8a70c2cc-4c5d-42b0-9a35-7524ac79534e/content (accessed on 20 October 2025). [CrossRef]
- Allouis, T.; Bailly, J.-S.; Pastol, Y.; Le Roux, C. Comparison of LiDAR Waveform Processing Methods for Very Shallow Water Bathymetry Using Raman, near-Infrared and Green Signals. Earth Surf. Process. Landf. 2010, 35, 640–650. [Google Scholar] [CrossRef]
- Yang, F.; Qi, C.; Su, D.; Ding, S.; He, Y.; Ma, Y. An Airborne LiDAR Bathymetric Waveform Decomposition Method in Very Shallow Water: A Case Study around Yuanzhi Island in the South China Sea. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102788. [Google Scholar] [CrossRef]
- Wright, A.E.; Conlin, D.L.; Shope, S.M. Assessing the Accuracy of Underwater Photogrammetry for Archaeology: A Comparison of Structure from Motion Photogrammetry and Real Time Kinematic Survey at the East Key Construction Wreck. JMSE 2020, 8, 849. [Google Scholar] [CrossRef]
- Menna, F.; Nocerino, E.; Nawaf, M.M.; Seinturier, J.; Torresani, A.; Drap, P.; Remondino, F.; Chemisky, B. Towards Real-Time Underwater Photogrammetry for Subsea Metrology Applications. In Proceedings of the OCEANS 2019, Marseille, France, 17–20 June 2019; IEEE: Marseille, France, 2019; pp. 1–10. [Google Scholar]
- Storlazzi, C.D.; Dartnell, P.; Hatcher, G.A.; Gibbs, A.E. End of the Chain? Rugosity and Fine-Scale Bathymetry from Existing Underwater Digital Imagery Using Structure-from-Motion (SfM) Technology. Coral Reefs 2016, 35, 889–894. [Google Scholar] [CrossRef]
- Urbina-Barreto, I.; Garnier, R.; Elise, S.; Pinel, R.; Dumas, P.; Mahamadaly, V.; Facon, M.; Bureau, S.; Peignon, C.; Quod, J.-P.; et al. Which Method for Which Purpose? A Comparison of Line Intercept Transect and Underwater Photogrammetry Methods for Coral Reef Surveys. Front. Mar. Sci. 2021, 8, 636902. [Google Scholar] [CrossRef]
- Ventura, D.; Mancini, G.; Casoli, E.; Pace, D.S.; Lasinio, G.J.; Belluscio, A.; Ardizzone, G. Seagrass Restoration Monitoring and Shallow-Water Benthic Habitat Mapping through a Photogrammetry-Based Protocol. J. Environ. Manag. 2022, 304, 114262. [Google Scholar] [CrossRef]
- Jaud, M.; Delsol, S.; Urbina-Barreto, I.; Augereau, E.; Cordier, E.; Guilhaumon, F.; Le Dantec, N.; Floc’h, F.; Delacourt, C. Low-Tech and Low-Cost System for High-Resolution Underwater RTK Photogrammetry in Coastal Shallow Waters. Remote Sens. 2023, 16, 20. [Google Scholar] [CrossRef]
- Casella, E.; Lewin, P.; Ghilardi, M.; Rovere, A.; Bejarano, S. Assessing the Relative Accuracy of Coral Heights Reconstructed from Drones and Structure from Motion Photogrammetry on Coral Reefs. Coral Reefs 2022, 41, 869–875. [Google Scholar] [CrossRef]
- Casella, E.; Collin, A.; Harris, D.; Ferse, S.; Bejarano, S.; Parravicini, V.; Hench, J.L.; Rovere, A. Mapping Coral Reefs Using Consumer-Grade Drones and Structure from Motion Photogrammetry Techniques. Coral Reefs 2017, 36, 269–275. [Google Scholar] [CrossRef]
- David, C.G.; Kohl, N.; Casella, E.; Rovere, A.; Ballesteros, P.; Schlurmann, T. Structure-from-Motion on Shallow Reefs and Beaches: Potential and Limitations of Consumer-Grade Drones to Reconstruct Topography and Bathymetry. Coral Reefs 2021, 40, 835–851. [Google Scholar] [CrossRef]
- Slocum, R.K.; Parrish, C.E.; Simpson, C.H. Combined Geometric-Radiometric and Neural Network Approach to Shallow Bathymetric Mapping with UAS Imagery. ISPRS J. Photogramm. Remote Sens. 2020, 169, 351–363. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; Melo De Almeida, L.P.; Sall, M. On the Operational Use of UAVs for Video-Derived Bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Holman, R.; Plant, N.; Holland, T. cBathy: A Robust Algorithm for Estimating Nearshore Bathymetry. JGR Oceans 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Lange, A.M.Z.; Fiedler, J.W.; Merrifield, M.A.; Guza, R.T. UAV Video-Based Estimates of Nearshore Bathymetry. Coast. Eng. 2023, 185, 104375. [Google Scholar] [CrossRef]
- Matsuba, Y.; Sato, S. Nearshore Bathymetry Estimation Using UAV. Coast. Eng. J. 2018, 60, 51–59. [Google Scholar] [CrossRef]
- Plant, N.G.; Holland, K.T.; Haller, M.C. Ocean Wavenumber Estimation from Wave-Resolving Time Series Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2644–2658. [Google Scholar] [CrossRef]
- Sun, S.-H.; Chuang, W.-L.; Chang, K.-A.; Young Kim, J.; Kaihatu, J.; Huff, T.; Feagin, R. Imaging-Based Nearshore Bathymetry Measurement Using an Unmanned Aircraft System. J. Waterw. Port Coast. Ocean Eng. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Feurer, D.; Bailly, J.-S.; Puech, C.; Le Coarer, Y.; Viau, A.A. Very-High-Resolution Mapping of River-Immersed Topography by Remote Sensing. Prog. Phys. Geogr. Earth Environ. 2008, 32, 403–419. [Google Scholar] [CrossRef]
- He, J.; Lin, J.; Ma, M.; Liao, X. Mapping Topo-Bathymetry of Transparent Tufa Lakes Using UAV-Based Photogrammetry and RGB Imagery. Geomorphology 2021, 389, 107832. [Google Scholar] [CrossRef]
- Kim, J.S.; Baek, D.; Seo, I.W.; Shin, J. Retrieving Shallow Stream Bathymetry from UAV-Assisted RGB Imagery Using a Geospatial Regression Method. Geomorphology 2019, 341, 102–114. [Google Scholar] [CrossRef]
- Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting Shallow Stream Bathymetry from Multi-View Stereo Photogrammetry. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying Submerged Fluvial Topography Using Hyperspatial Resolution UAS Imagery and Structure from Motion Photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef]
- Tamminga, A.D.; Eaton, B.C.; Hugenholtz, C.H. UAS-Based Remote Sensing of Fluvial Change Following an Extreme Flood Event. Earth Surf. Process. Landf. 2015, 40, 1464–1476. [Google Scholar] [CrossRef]
- Bagheri, O.; Ghodsian, M.; Saadatseresht, M. Reach Scale Application Of UAV+SFM Method In Shallow Rivers Hyperspatial Bathymetry. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2015, XL-1/W5, 77–81. [Google Scholar] [CrossRef]
- Partama, I.G.Y.; Kanno, A.; Ueda, M.; Akamatsu, Y.; Inui, R.; Sekine, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Removal of Water-surface Reflection Effects with a Temporal Minimum Filter for UAV-based Shallow-water Photogrammetry. Earth Surf. Process. Landf. 2018, 43, 2673–2682. [Google Scholar] [CrossRef]
- Collin, A.; James, D.; Lamontagne, N.; Hardy, R.; Monpert, C.; Feunteun, E. Ultra-High-Resolution Bathymetry Estimation Using a Visible Airborne Drone, Photogrammetry and Neural Network. In Proceedings of the XVIIIèmes Journées, Anglet, France, 25–27 June 2024; Editions Paralia: Nantes, France, 2024; pp. 477–484. [Google Scholar]
- Agrafiotis, P.; Karantzalos, K.; Georgopoulos, A.; Skarlatos, D. Correcting Image Refraction: Towards Accurate Aerial Image-Based Bathymetry Mapping in Shallow Waters. Remote Sens. 2020, 12, 322. [Google Scholar] [CrossRef]
- Szostak, B.; Specht, M.; Burdziakowski, P.; Stateczny, A.; Specht, C.; Lewicka, O. Methodology for Performing Bathymetric Measurements of Shallow Waterbodies Using an UAV, and Their Processing Based on the SVR Algorithm. Measurement 2023, 223, 113720. [Google Scholar] [CrossRef]
- Alevizos, E.; Nicodemou, V.C.; Makris, A.; Oikonomidis, I.; Roussos, A.; Alexakis, D.D. Integration of Photogrammetric and Spectral Techniques for Advanced Drone-Based Bathymetry Retrieval Using a Deep Learning Approach. Remote Sens. 2022, 14, 4160. [Google Scholar] [CrossRef]
- Specht, M.; Szostak, B.; Lewicka, O.; Stateczny, A.; Specht, C. Method for Determining of Shallow Water Depths Based on Data Recorded by UAV/USV Vehicles and Processed Using the SVR Algorithm. Measurement 2023, 221, 113437. [Google Scholar] [CrossRef]
- Cordier, E.; Lézé, J.; Join, J.-L. Natural Tidal Processes Modified by the Existence of Fringing Reef on La Reunion Island (Western Indian Ocean): Impact on the Relative Sea Level Variations. Cont. Shelf Res. 2013, 55, 119–128. [Google Scholar] [CrossRef]
- Camoin, G.F.; Colonna, M.; Montaggioni, L.F.; Casanova, J.; Faure, G.; Thomassin, B.A. Holocene Sea Level Changes and Reef Development in the Southwestern Indian Ocean. Coral Reefs 1997, 16, 247–259. [Google Scholar] [CrossRef]
- Soler, O. Atlas Climatique de La Réunion; Météo France: Toulouse, France, 1997; p. 79. [Google Scholar]
- Butler, J.; Lane, S.; Chandler, J.; Porfiri, E. Through-Water Close Range Digital Photogrammetry in Flume and Field Environments. Photogramm. Rec. 2002, 17, 419–439. [Google Scholar] [CrossRef]
- Jerlov, N. Preface to the Second Edition. In Marine Optics; Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 1976; Volume 14, p. vii. ISBN 978-0-444-41490-8. [Google Scholar]
- Westaway, R.M.; Lane, S.N.; Hicks, D.M. Remote Sensing of Clear-Water, Shallow, Gravel-Bed Rivers Using Digital Photogrammetry. Photogramm. Eng. Remote Sens. 2001, 67, 1271–1281. [Google Scholar]
- Westaway, R.M.; Lane, S.N.; Hicks, D.M. The Development of an Automated Correction Procedure for Digital Photogrammetry for the Study of Wide, Shallow, Gravel-Bed Rivers. Earth Surf. Process. Landf. 2000, 25, 209–226. [Google Scholar] [CrossRef]
- Carbonneau, P.E.; Dietrich, J.T. Cost-effective Non-metric Photogrammetry from Consumer-grade sUAS: Implications for Direct Georeferencing of Structure from Motion Photogrammetry. Earth Surf. Process. Landf. 2017, 42, 473–486. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating Systematic Error in Topographic Models Derived from UAV and Ground-Based Image Networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Jaud, M.; Passot, S.; Allemand, P.; Le Dantec, N.; Grandjean, P.; Delacourt, C. Suggestions to Limit Geometric Distortions in the Reconstruction of Linear Coastal Landforms by SfM Photogrammetry with PhotoScan® and MicMac® for UAV Surveys with Restricted GCPs Pattern. Drones 2018, 3, 2. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; J. Wiley & Sons: New York, NY, USA, 2000; ISBN 978-0-471-32188-0. [Google Scholar]
- Kujawa, P.; Wajs, J.; Pleśniak, K. The Approach to UAV Image Acquisition and Processing for Very Shallow Water Mapping. Int. J. Appl. Earth Obs. Geoinf. 2025, 141, 104604. [Google Scholar] [CrossRef]
- Zhan, Y.; Nobuhara, S.; Nishino, K.; Zheng, Y. NeRFrac: Neural Radiance Fields through Refractive Surface. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 18356–18366. [Google Scholar]
- Günthner, A.; Brezovsky, M.; Schulte, F.; Winiwarter, L.; Mandlburger, G.; Jutzi, B. Exploring the Potential of Refractive NeRFs for Photogrammetric Bathymetry—First Application to UAV-Based Data from the Pielach River. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 3D Underwater Mapping from Above and Below—3rd International Workshop, Vienna, Austria, 8–11 July 2025; Volume XLVIII-2/W10-2025, pp. 107–114. [Google Scholar] [CrossRef]
- Schulte, F.; Brezovsky, M.; Günthner, A.; Jutzi, B.; Mandlburger, G.; Winiwarter, L. Simulation and Validation of Underwater Scenes for Two-Media Optical 3D Reconstruction. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 3D Underwater Mapping from Above and Below—3rd International Workshop, Vienna, Austria, 8–11 July 2025; Volume XLVIII-2/W10-2025, pp. 271–278. [Google Scholar] [CrossRef]
- Skarlatos, D.; Agrafiotis, P. A Novel Iterative Water Refraction Correction Algorithm for Use in Structure from Motion Photogrammetric Pipeline. JMSE 2018, 6, 77. [Google Scholar] [CrossRef]
- Scilla, D.; Lopez, O.A.; Nieuwenhuis, B.O.; Johansen, K.; Elías-Lara, M.; Angulo, V.; Rodríguez, J.L.; Jones, B.H.; McCabe, M.F. Computer Vision Corrections Enhance UAV-Based Retrievals in Shallow Waters. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 18134–18149. [Google Scholar] [CrossRef]
- Murase, T.; Tanaka, M.; Tani, T.; Miyashita, Y.; Ohkawa, N.; Ishiguro, S.; Suzuki, Y.; Kayanne, H.; Yamano, H. A Photogrammetric Correction Procedure for Light Refraction Effects at a Two-Medium Boundary. Photogramm. Eng. Remote Sens. 2008, 74, 1129–1136. [Google Scholar] [CrossRef]
- Del Savio, A.A.; Luna Torres, A.; Vergara Olivera, M.A.; Llimpe Rojas, S.R.; Urday Ibarra, G.T.; Neckel, A. Using UAVs and Photogrammetry in Bathymetric Surveys in Shallow Waters. Appl. Sci. 2023, 13, 3420. [Google Scholar] [CrossRef]
- You, Y.; Stramski, D.; Darecki, M.; Kattawar, G.W. Modeling of Wave-Induced Irradiance Fluctuations at near-Surface Depths in the Ocean: A Comparison with Measurements. Appl. Opt. 2010, 49, 1041. [Google Scholar] [CrossRef] [PubMed]
- Darecki, M.; Stramski, D.; Sokólski, M. Measurements of High-frequency Light Fluctuations Induced by Sea Surface Waves with an Underwater Porcupine Radiometer System. J. Geophys. Res. 2011, 116, 2011JC007338. [Google Scholar] [CrossRef]
- Yanovski, R.; Nelson, P.A.; Abelson, A. Structural Complexity in Coral Reefs: Examination of a Novel Evaluation Tool on Different Spatial Scales. Front. Ecol. Evol. 2017, 5, 27. [Google Scholar] [CrossRef]
- Fukunaga, A.; Burns, J.H.R.; Craig, B.K.; Kosaki, R.K. Integrating Three-Dimensional Benthic Habitat Characterization Techniques into Ecological Monitoring of Coral Reefs. J. Mar. Sci. Eng. 2019, 7, 27. [Google Scholar] [CrossRef]
- Young, G.C.; Dey, S.; Rogers, A.D.; Exton, D. Cost and Time-Effective Method for Multi-Scale Measures of Rugosity, Fractal Dimension, and Vector Dispersion from Coral Reef 3D Models. PLoS ONE 2017, 12, e0175341. [Google Scholar] [CrossRef] [PubMed]
- Chung, D.; Hutchins, N.; Schultz, M.P.; Flack, K.A. Predicting the Drag of Rough Surfaces. Annu. Rev. Fluid Mech. 2021, 53, 439–471. [Google Scholar] [CrossRef]
- Dealbera, S.; Sous, D.; Morichon, D.; Michaud, H. The Role of Roughness Geometry in Frictional Wave Dissipation. Coast. Eng. 2024, 189, 104478. [Google Scholar] [CrossRef]
- Patil, A.; García-Sánchez, C. A Comparative Hydrodynamic Characterization of the Flow Through Regular and Stochastically Generated Synthetic Coral Reefs over Flat Topography. arXiv 2025, arXiv:2501.15237. [Google Scholar] [CrossRef]
- Sous, D.; Meulé, S.; Dealbera, S.; Michaud, H.; Gassier, G.; Pezerat, M.; Bouchette, F. Quantifying the Topographical Structure of Rocky and Coral Seabeds. PLoS ONE 2024, 19, e0303422. [Google Scholar] [CrossRef]

| Methods | DEM of Differences (DoD) | |
|---|---|---|
| Patch 1 | Patch 2 | |
| POSEIDON—UAV apparent bathymetry | ME = 0.09 m σ = 0.13 m RMSE = 0.16 m | ME = 0.19 m σ =0.15 m RMSE = 0.24 m |
| POSEIDON—Analytical refraction-corrected UAV DEM | ME = 0.08 m σ = 0.09 m RMSE = 0.13 m | ME = 0.03 m σ = 0.11 m RMSE = 0.11 m |
| POSEIDON—REG1-corrected UAV DEM | ME = −0.04 m σ = 0.09 m RMSE = 0.10 m | ME = −0.17 m σ = 0.08 m RMSE = 0.20 m |
| POSEIDON—REG2-corrected UAV DEM | ME = 0.10 m σ = 0.10 m RMSE = 0.14 m | ME = −0.04 m σ = 0.09 m RMSE = 0.09 m |
| POSEIDON—REG3-corrected UAV DEM | ME = 0.06 m σ = 0.09 m RMSE = 0.11 m | ME = −0.07 m σ = 0.08 m RMSE = 0.11 m |
| Kernel Size (m × m) | Subsamp. POSEIDON DEM | UAV Apparent Bathymetry | UAV DEM Analytically Corrected | UAV DEM Corrected by REG1 | UAV DEM Corrected by REG3 | ||
|---|---|---|---|---|---|---|---|
| Standard deviation of bed elevations (bottom roughness) (m) | Patch 1 | 0.13 × 0.13 | 0.019 | 0.007 | 0.010 | 0.012 | 0.012 |
| 0.48 × 0.48 | 0.057 | 0.026 | 0.035 | 0.042 | 0.043 | ||
| 1.01 × 1.01 | 0.093 | 0.049 | 0.065 | 0.078 | 0.079 | ||
| 1.98 × 1.98 | 0.134 | 0.077 | 0.103 | 0.123 | 0.125 | ||
| 4.97 × 4.97 | 0.194 | 0.119 | 0.159 | 0.189 | 0.193 | ||
| 30 × 10 | 0.298 | 0.192 | 0.258 | 0.301 | 0.313 | ||
| Patch 2 | 0.13 × 0.13 | 0.021 | 0.008 | 0.011 | 0.013 | 0.013 | |
| 0.48 × 0.48 | 0.063 | 0.029 | 0.039 | 0.046 | 0.047 | ||
| 1.01 × 1.01 | 0.106 | 0.055 | 0.074 | 0.087 | 0.089 | ||
| 1.98 × 1.98 | 0.159 | 0.088 | 0.118 | 0.141 | 0.144 | ||
| 4.97 × 4.97 | 0.229 | 0.132 | 0.176 | 0.210 | 0.214 | ||
| 30 × 10 | 0.300 | 0.170 | 0.227 | 0.270 | 0.276 | ||
| UAV area | 0.13 × 0.13 | 0.006 | 0.008 | 0.010 | 0.010 | ||
| 0.48 × 0.48 | 0.020 | 0.027 | 0.032 | 0.033 | |||
| 1.01 × 1.01 | 0.035 | 0.047 | 0.055 | 0.057 | |||
| 1.98 × 1.98 | 0.052 | 0.069 | 0.082 | 0.084 | |||
| 4.97 × 4.97 | 0.074 | 0.099 | 0.117 | 0.120 | |||
| 450 × 380 | 0.174 | 0.233 | 0.276 | 0.283 | |||
| POSEIDON DEM vs. UAV Apparent Bathymetry | POSEIDON DEM vs. Analytically Corr. UAV DEM | POSEIDON DEM vs. REG1-Corrected UAV DEM | POSEIDON DEM vs. REG3-Corrected UAV DEM | |
|---|---|---|---|---|
| Mean error on roughness | 48.0% | 30.0% | 16.8% | 15.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaud, M.; Geindre, M.; Bertin, S.; Benoit, Y.; Cordier, E.; Floc’h, F.; Augereau, E.; Martins, K. Correction of Refraction Effects on Unmanned Aerial Vehicle Structure-from-Motion Bathymetric Survey for Coral Reef Roughness Characterisation. Remote Sens. 2025, 17, 3846. https://doi.org/10.3390/rs17233846
Jaud M, Geindre M, Bertin S, Benoit Y, Cordier E, Floc’h F, Augereau E, Martins K. Correction of Refraction Effects on Unmanned Aerial Vehicle Structure-from-Motion Bathymetric Survey for Coral Reef Roughness Characterisation. Remote Sensing. 2025; 17(23):3846. https://doi.org/10.3390/rs17233846
Chicago/Turabian StyleJaud, Marion, Mila Geindre, Stéphane Bertin, Yoan Benoit, Emmanuel Cordier, France Floc’h, Emmanuel Augereau, and Kévin Martins. 2025. "Correction of Refraction Effects on Unmanned Aerial Vehicle Structure-from-Motion Bathymetric Survey for Coral Reef Roughness Characterisation" Remote Sensing 17, no. 23: 3846. https://doi.org/10.3390/rs17233846
APA StyleJaud, M., Geindre, M., Bertin, S., Benoit, Y., Cordier, E., Floc’h, F., Augereau, E., & Martins, K. (2025). Correction of Refraction Effects on Unmanned Aerial Vehicle Structure-from-Motion Bathymetric Survey for Coral Reef Roughness Characterisation. Remote Sensing, 17(23), 3846. https://doi.org/10.3390/rs17233846








