Reconstructed SWHs Based on a Deep Learning Method and the Revealed Long-Term SWH Variance Characteristics During 1993–2024
Highlights
- This study reconstructed daily long-term high-resolution 0.25° × 0.25° SWHs for 1993–2024 using a partial convolutional U-Net model with attention and residual blocks, altimeter swath-derived SWHs, and ERA5 SWHs.
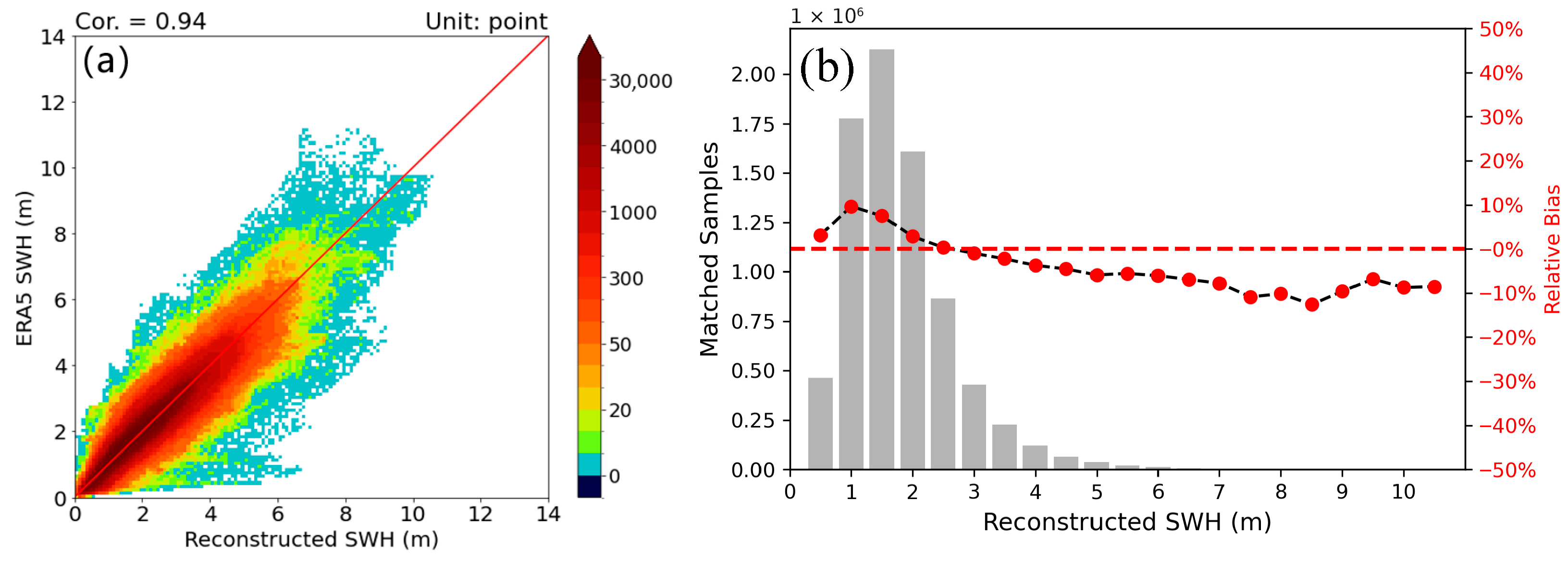
- Comparison between the daily reconstructed SWHs and ERA5 SWHs demonstrated enhanced accuracy for SWHs of >2.5 m (a range systematically underestimated in ERA5 SWHs).
- ERA5 reanalysis data exhibit systematic underestimation of SWH in geographically complex straits and under high sea state conditions, but swath-derived SWH measurements from satellite altimeters can substantially enhance SWH accuracy in these regions.
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. ERA5 Significant Wave Height (SWH) Data
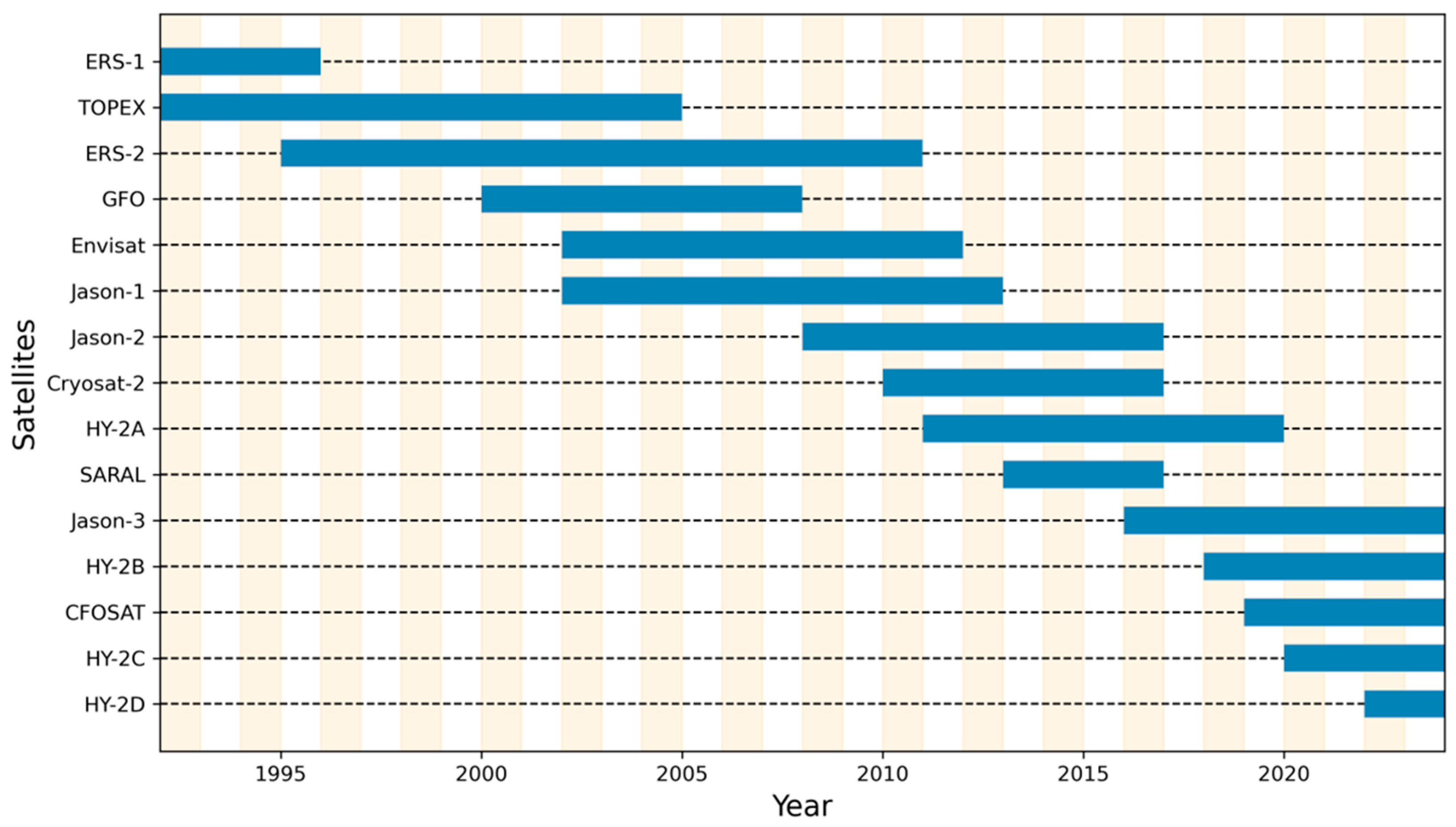
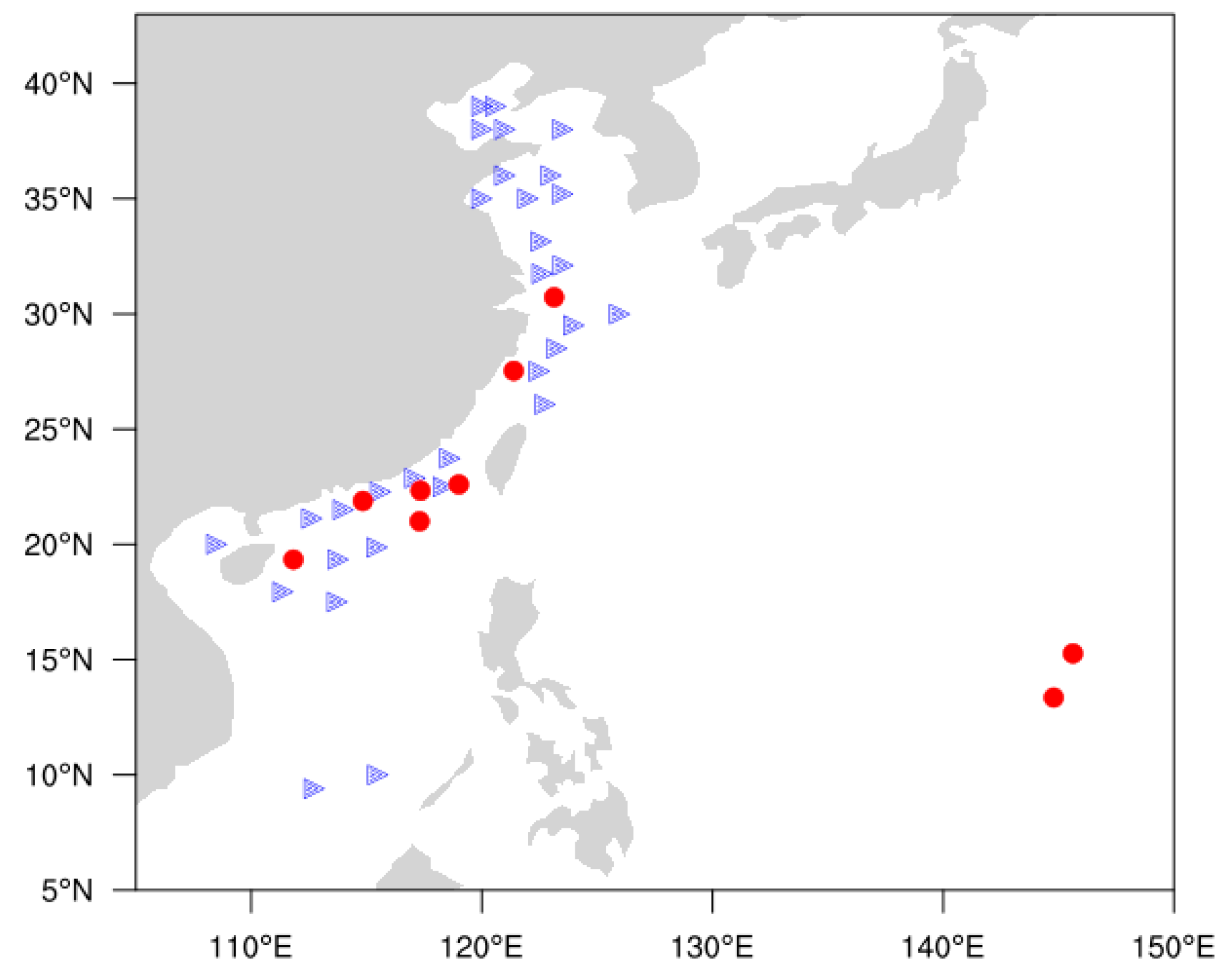
2.1.2. Applied Multisource Altimeter SWHs and Buoy Observations
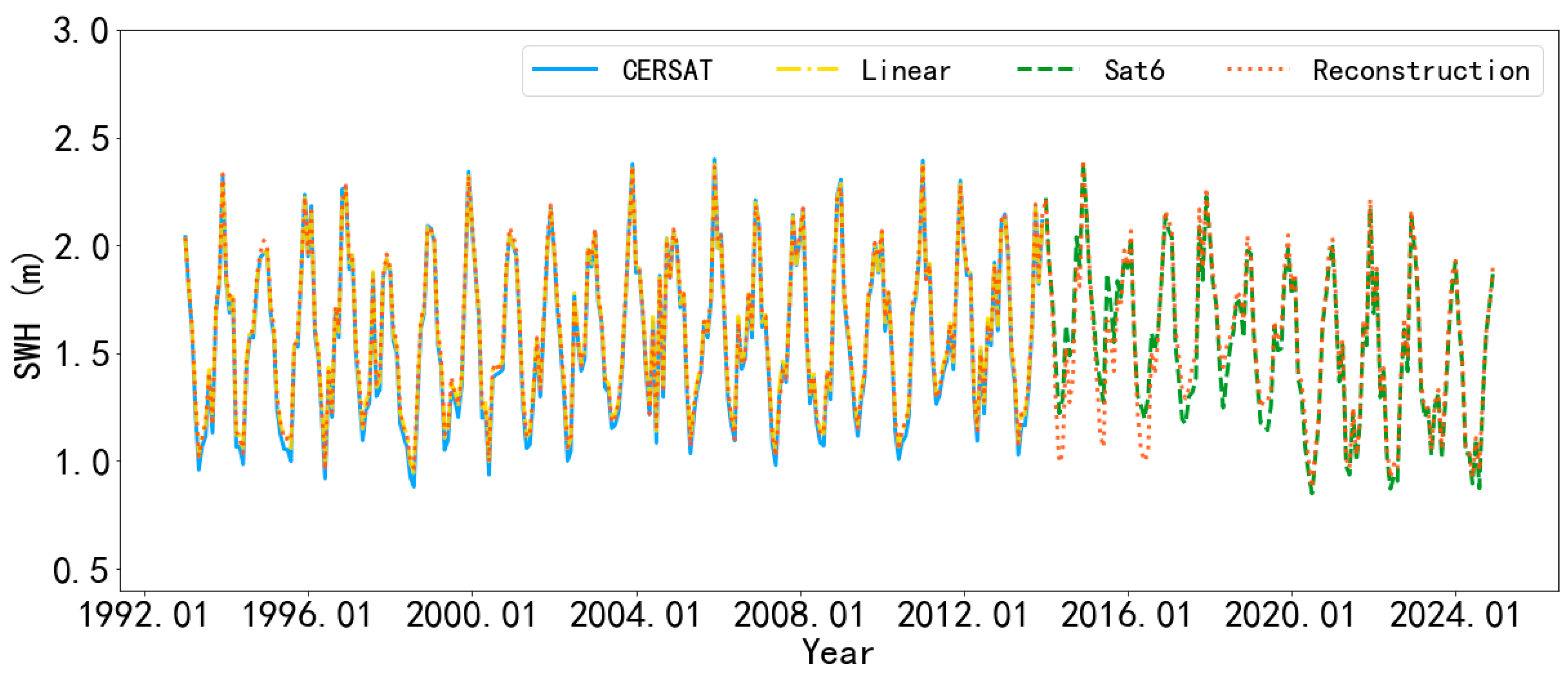
2.1.3. Merging of the Two Main Multisource Altimeter SWHs Datasets
2.2. Method
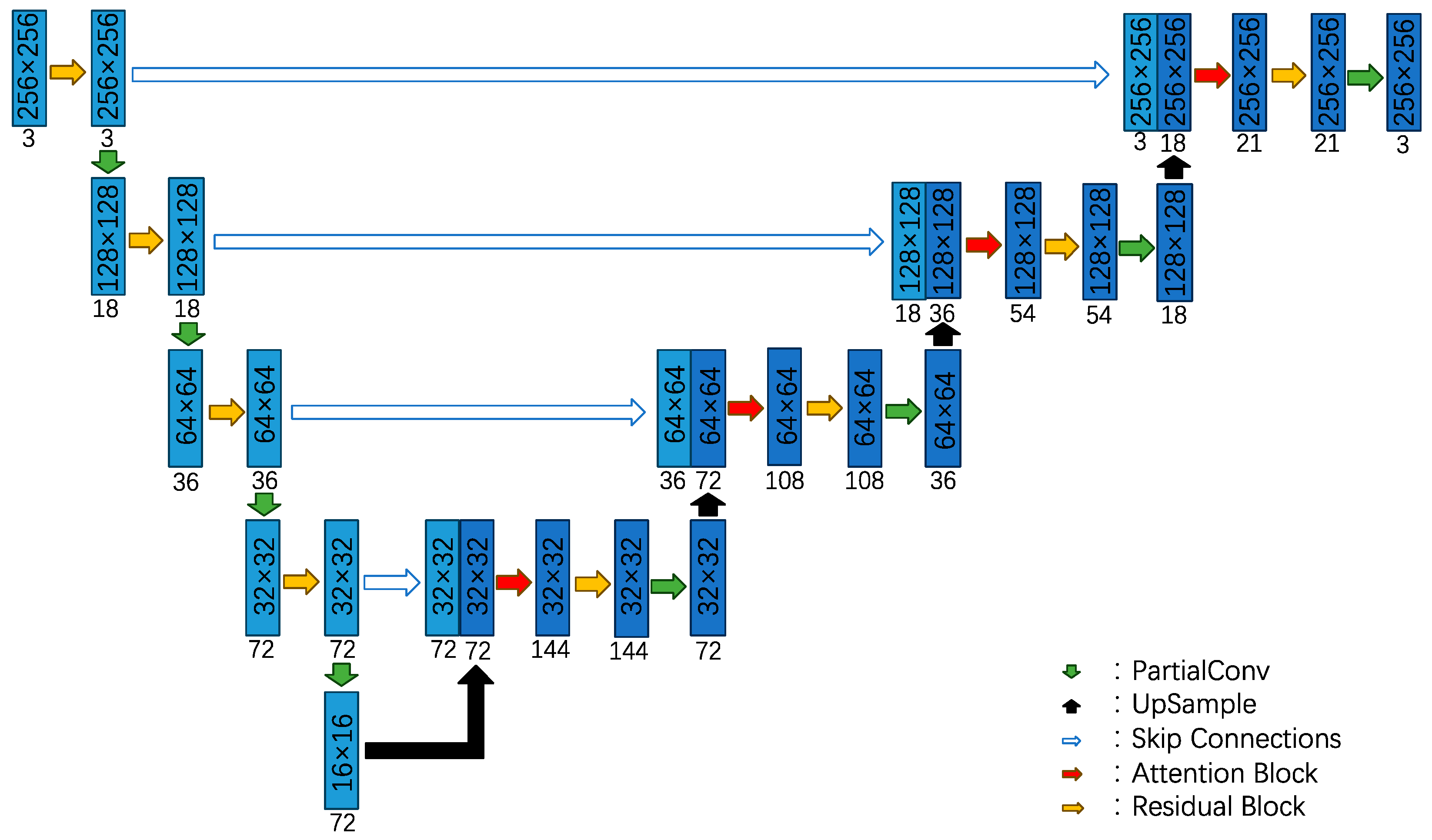
2.2.1. Residual Attention CNN
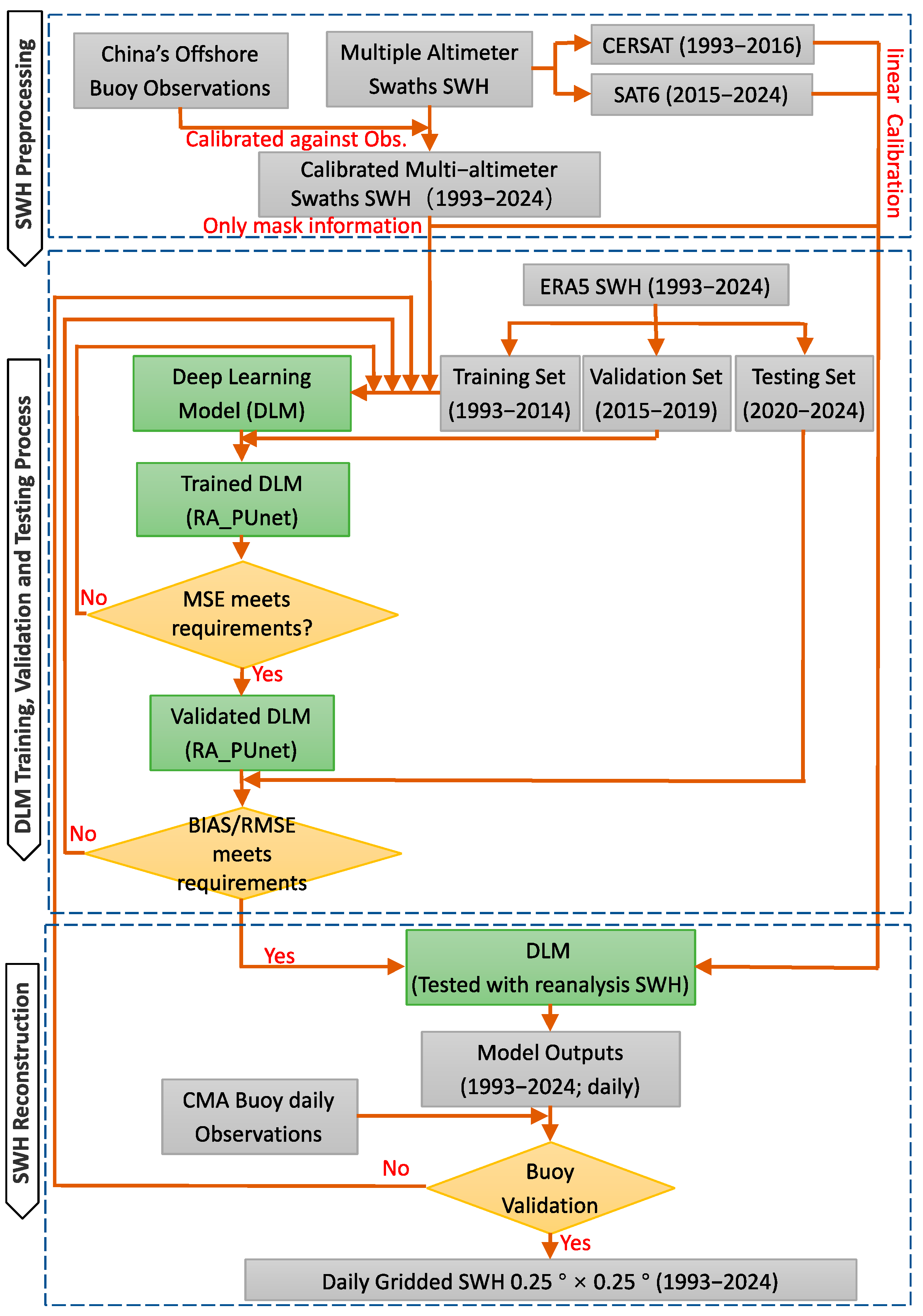
2.2.2. SWH Reconstruction Process
3. Results
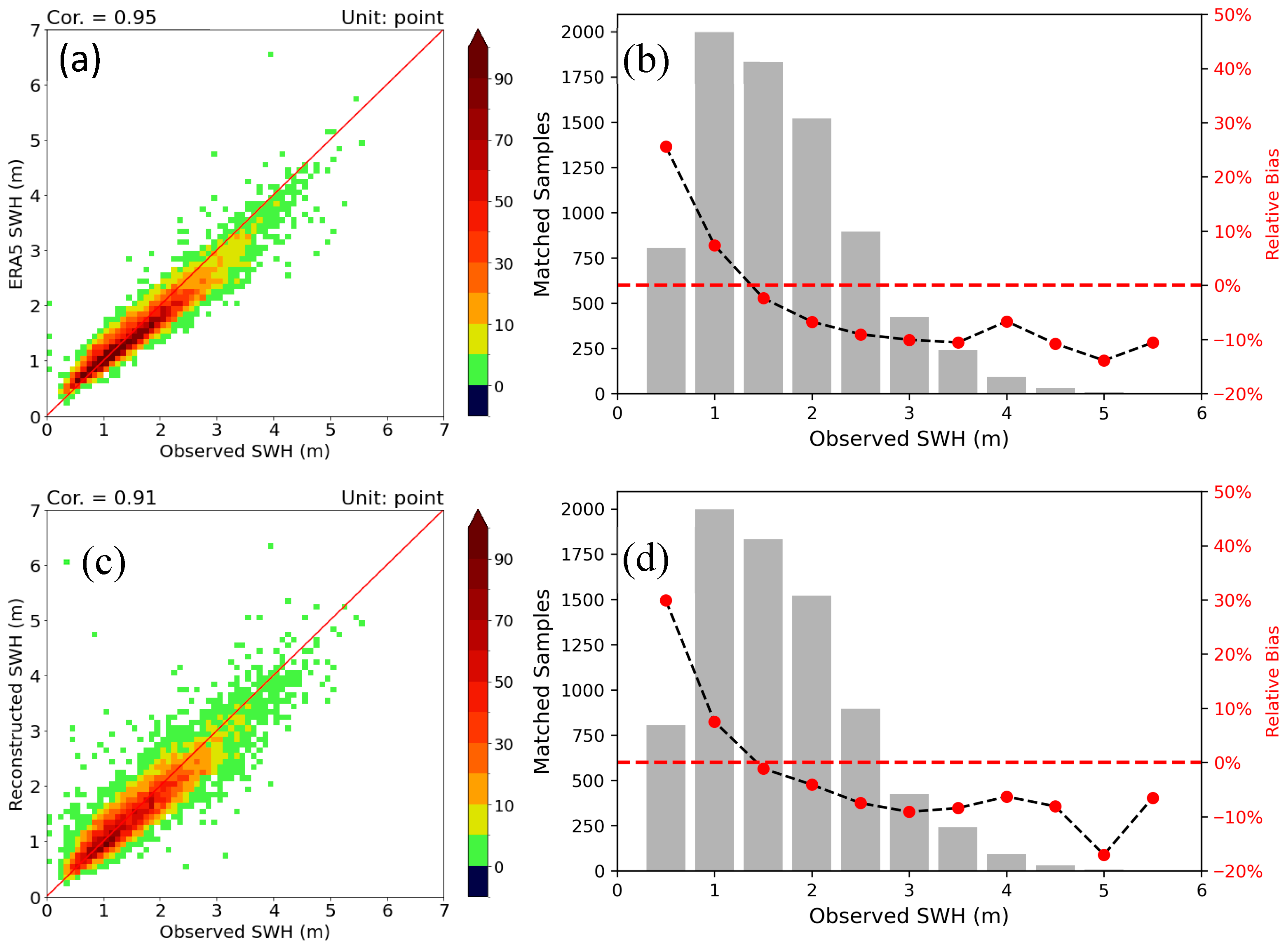
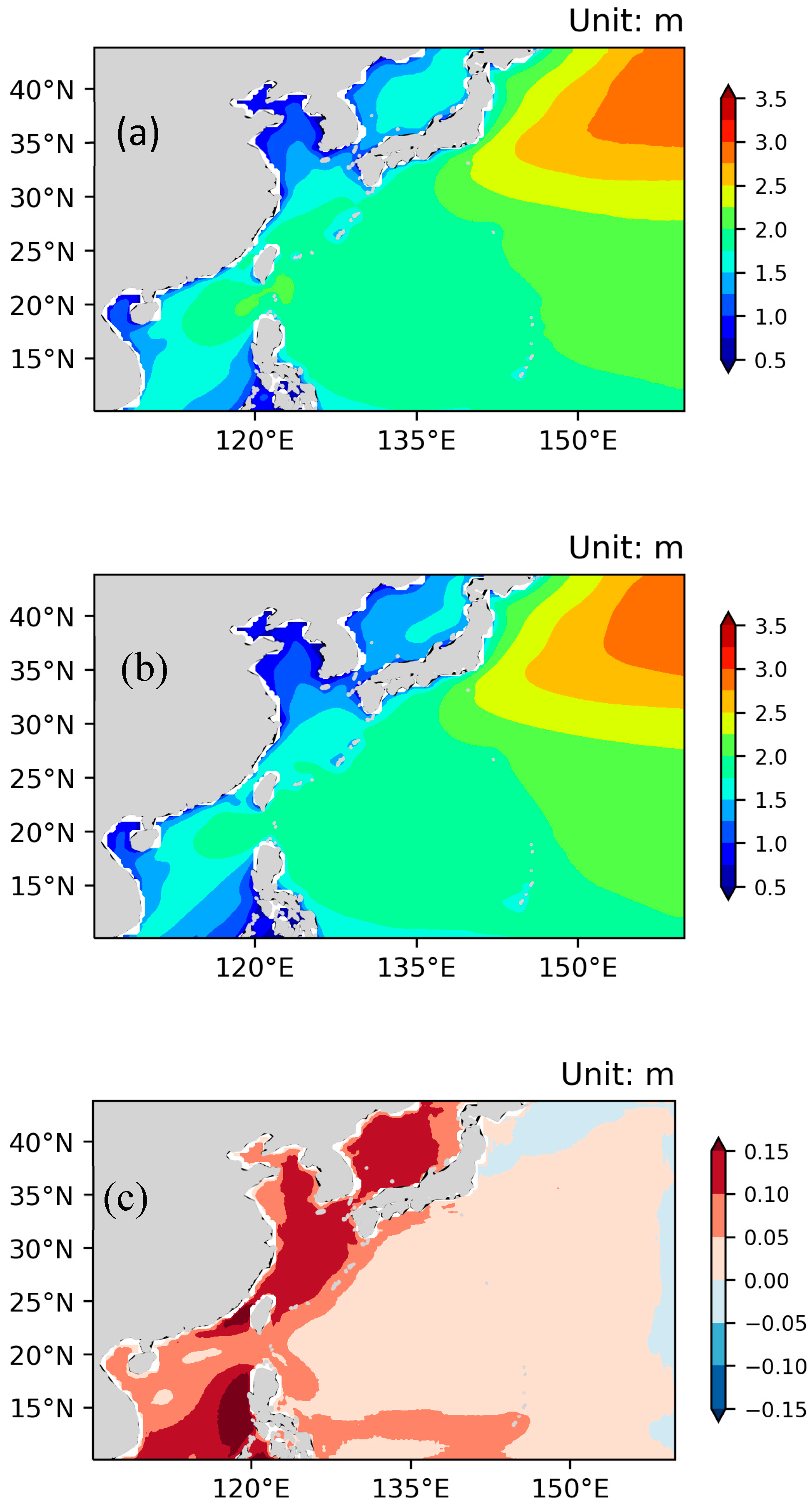
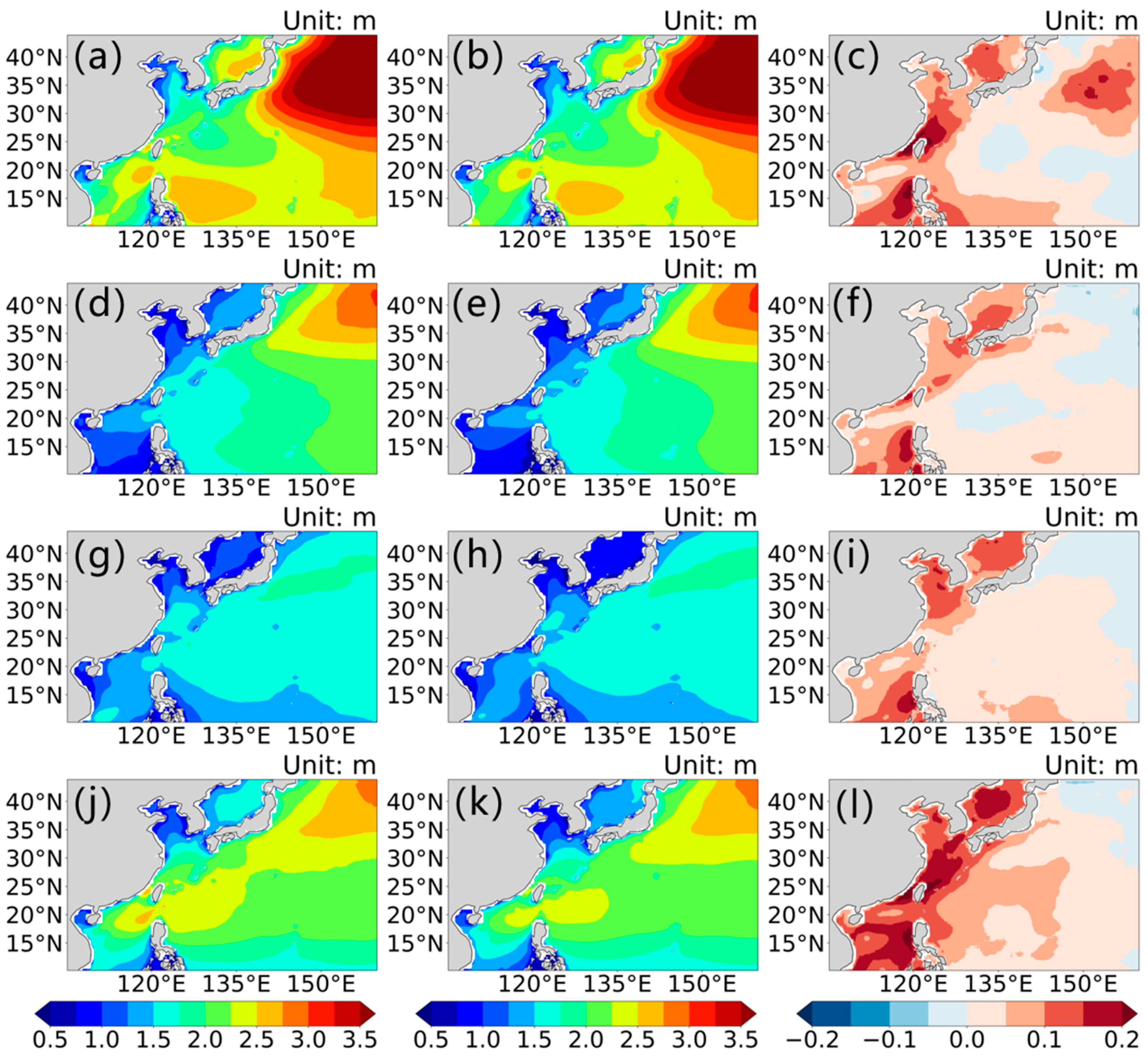
3.1. Validation of the Reconstructed SWHs and Their Comparison with ERA5 SWHs
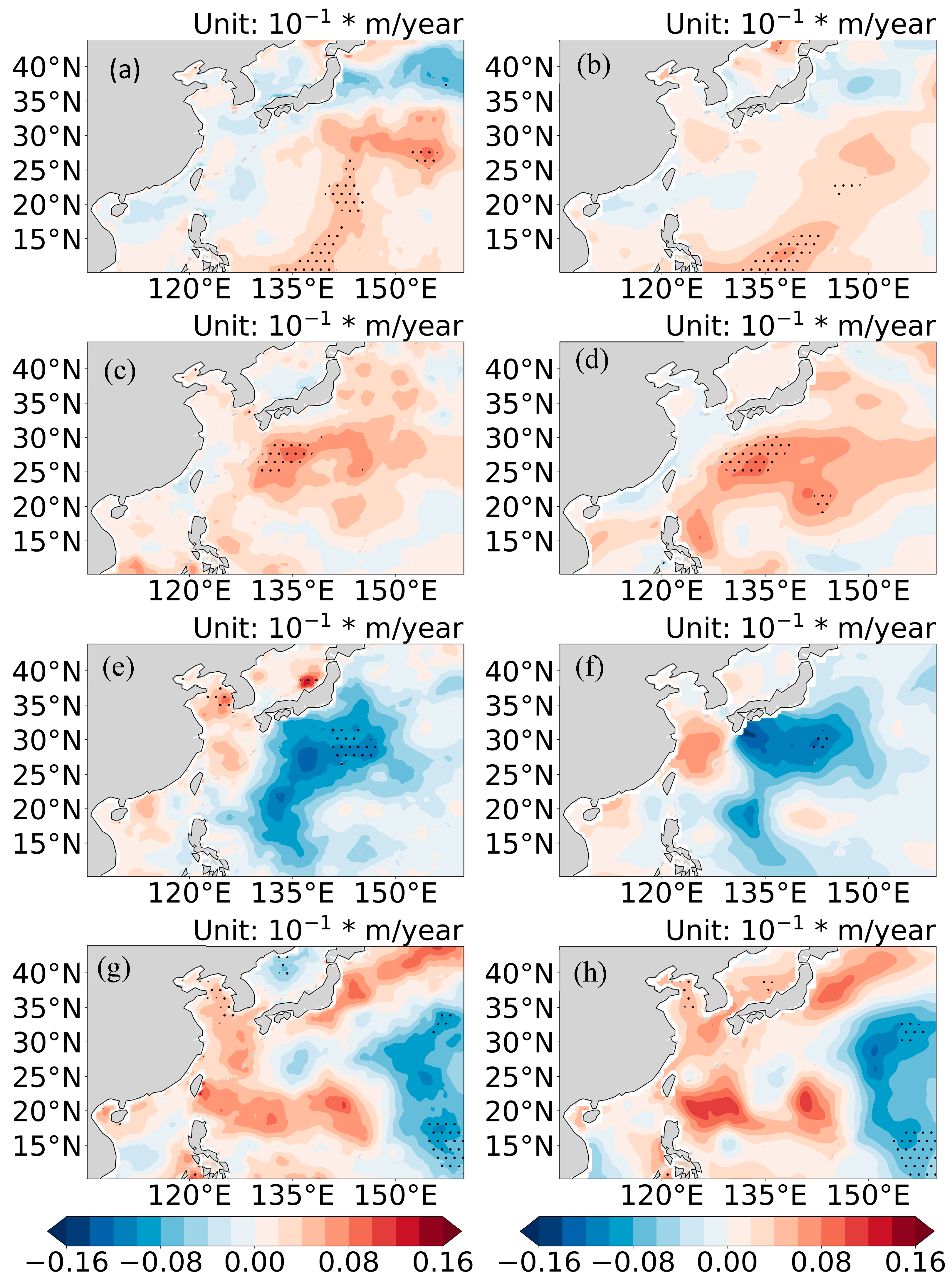
3.2. Differences in Spatial Distribution Between ERA5 SWHs and Reconstructed SWHs
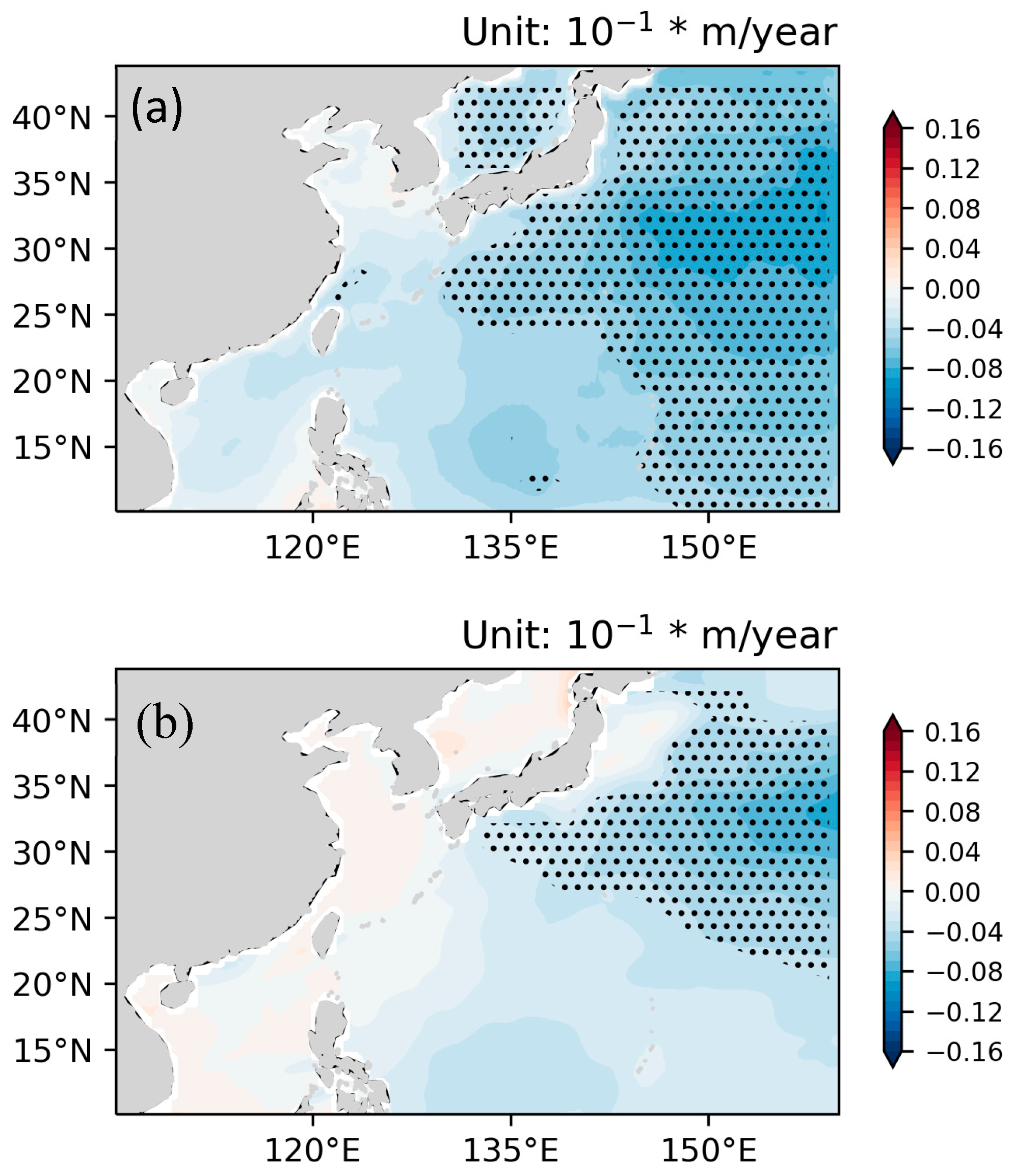
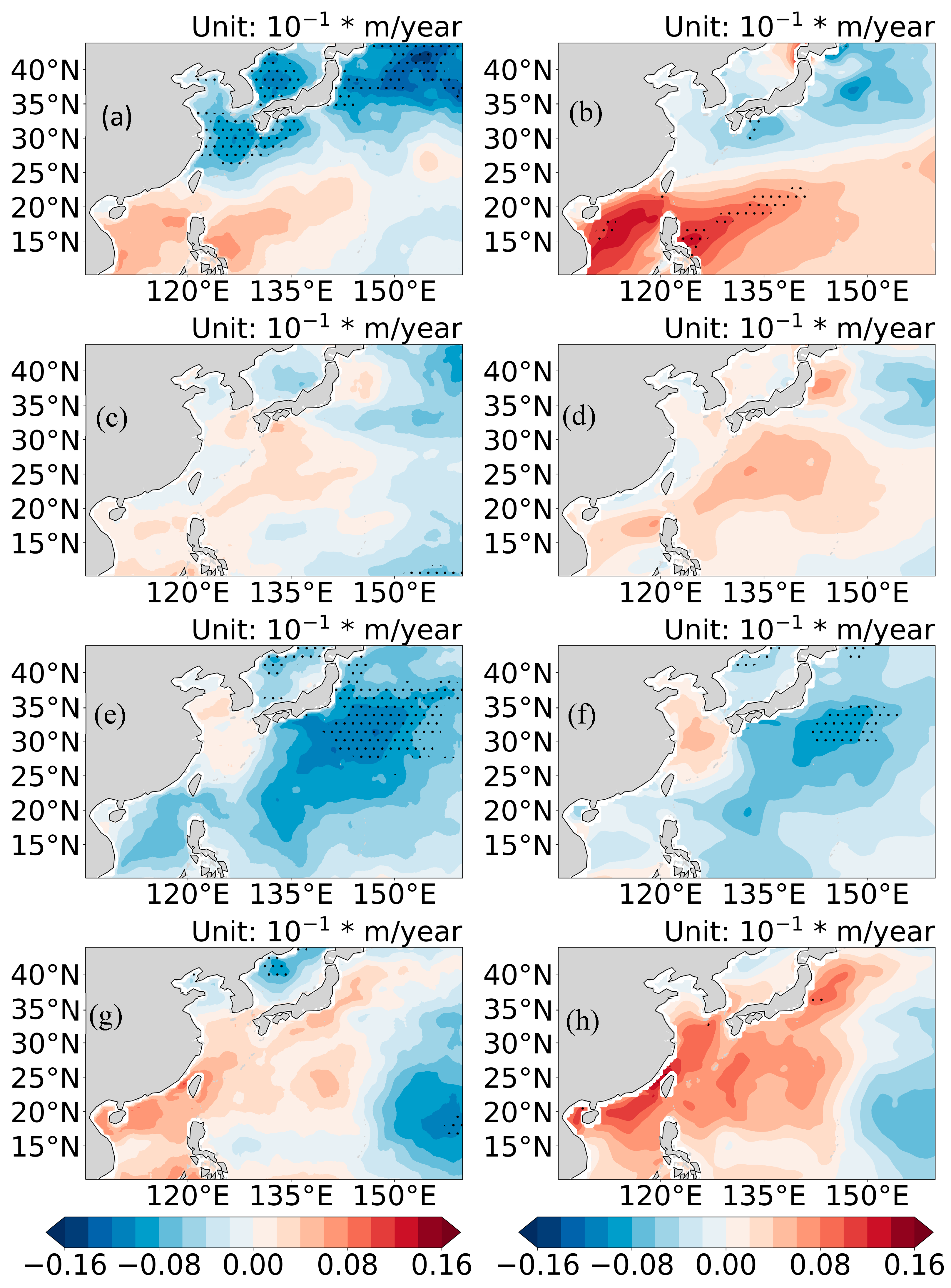
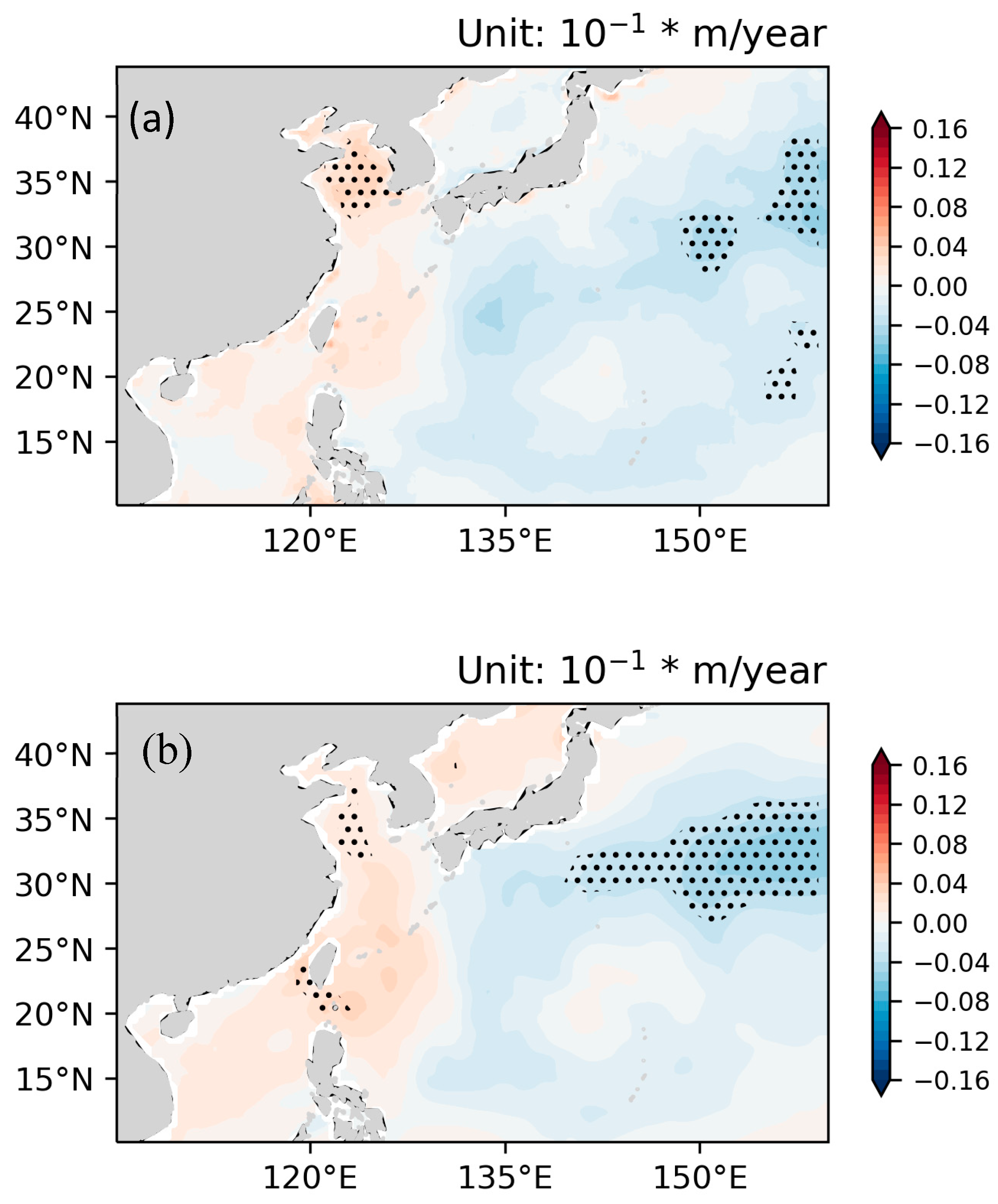
3.3. Differences in Linear Trends Between ERA5 SWHs and Reconstructed SWHs
4. Discussion
5. Conclusions
- (1)
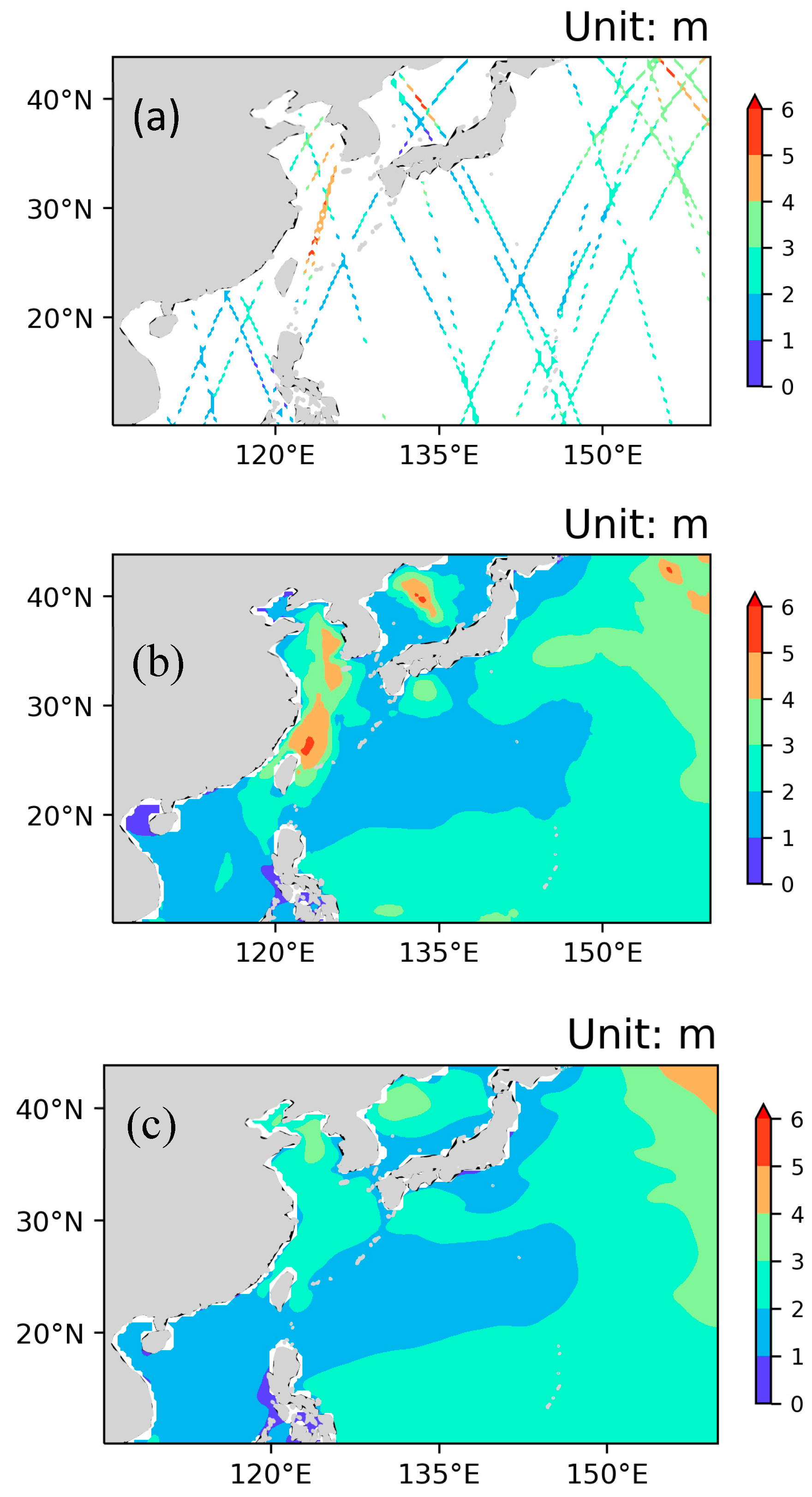
- The proposed partial convolutional U-Net model with attention and residual blocks can effectively extract the spatial features of ERA5 SWHs and fill missing values around the daily altimeter swaths. Consideration of the results for a single day, as an example, revealed that the spatial features of the ERA5 and reconstructed SWHs are similar. Furthermore, in the original swath position, the SWH values can control the values in the reconstruction results in the same position.
- (2)
- The reconstructed daily SWHs are lower than the observations, with relative bias of approximately −10% for SWHs between 1.25 and 4.25 m, the quality of which is as good as that of 10-day mean SWHs, but with dramatic improvement in temporal resolution. The reconstructed SWHs improve accuracy for SWHs of >2.5 m, which are usually underestimated in the ERA5 data.
- (3)
- Although the spatial distribution of the reconstructed SWHs is similar to that of the ERA5 SWHs, the greatest differences are found in China’s offshore waters, especially in straits and waters influenced by robust air–sea interactions, e.g., the Taiwan Strait and the region affected by the Huanghai Warm Current. This indicates that ERA5 underestimates both the intensity of wind in straits and the strength of air–sea interactions.
- (4)
- For the period 1993–2024, the negative trend of SWHs from the reconstruction is greater than that of SWHs from ERA5, especially in waters to the east of 150°E. Moreover, the reconstructed SWHs revealed an obvious positive trend in STDs over northern parts of China’s offshore waters, indicating that the magnitude of abnormal SWHs has increased during the study period.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, X.; Wang, X.; He, Z.; Wu, J. Significant Wave Height Retrieval in Tropical Cyclone Conditions Using CYGNSS Data. Remote Sens. 2024, 16, 4782. [Google Scholar] [CrossRef]
- Xu, J.; Zhi, X.; Sein, D.V.; Cabos, W.; Luo, Y.; Zhang, L.; Dong, F.; Fraedrich, K.; Jacob, D. Predictability of Coastal Boundary Layer Jets in South China Using Atmosphere–Ocean Coupling. J. Geophys. Res. Atmos. 2023, 128, e2023JD039184. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, R.; Jia, Y.; Jin, T.; Kong, X. Performance of HaiYang-2 Altimetric Data in Marine Gravity Research and a New Global Marine Gravity Model NSOAS22. Remote Sens. 2022, 14, 4322. [Google Scholar] [CrossRef]
- Aboobacker, V.M.; Shanas, P.R.; Al-Ansari, E.M.A.S.; Sanil Kumar, V.; Vethamony, P. The maxima in northerly wind speeds and wave heights over the Arabian Sea, the Arabian/Persian Gulf and the Red Sea derived from 40 years of ERA5 data. Clim. Dyn. 2021, 56, 1037–1052. [Google Scholar] [CrossRef]
- Wang, J.; Yu, T.; Deng, F.; Ruan, Z.; Jia, Y. Acquisition of the Wide Swath Significant Wave Height from HY-2C through Deep Learning. Remote Sens. 2021, 13, 4425. [Google Scholar] [CrossRef]
- Bué, I.; Lemos, G.; Semedo, Á.; Catalão, J. Assessment of satellite altimetry SWH measurements by in situ observations within 25 km from the coast. Ocean Dyn. 2024, 74, 183–210. [Google Scholar] [CrossRef]
- Grigorieva, V.G.; Badulin, S.I.; Gulev, S.K. Global Validation of SWIM/CFOSAT Wind Waves Against Voluntary Observing Ship Data. Earth Space Sci. 2022, 9, e2021EA002008. [Google Scholar] [CrossRef]
- Kang, J.; Mao, R.; Chang, Y.; Fu, H. Comparative analysis of significant wave height between a new Southern Ocean buoy and satellite altimeter. Atmos. Ocean. Sci. Lett. 2021, 14, 100044. [Google Scholar] [CrossRef]
- Müller, M.; Knol-Kauffman, M.; Jeuring, J.; Palerme, C. Arctic shipping trends during hazardous weather and sea-ice conditions and the Polar Code’s effectiveness. NPJ Ocean Sustain. 2023, 2, 12. [Google Scholar] [CrossRef]
- Woo, H.-J.; Park, K.-A. Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016). Remote Sens. 2021, 13, 1063. [Google Scholar] [CrossRef]
- Quartly, G.D.; Chen, G.; Nencioli, F.; Morrow, R.; Picot, N. An Overview of Requirements, Procedures and Current Advances in the Calibration/Validation of Radar Altimeters. Remote Sens. 2021, 13, 125. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 77. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef]
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47, e2019GL086880. [Google Scholar] [CrossRef]
- Dodet, G.; Piolle, J.F.; Quilfen, Y.; Abdalla, S.; Accensi, M.; Ardhuin, F.; Ash, E.; Bidlot, J.R.; Gommenginger, C.; Marechal, G.; et al. The Sea State CCI dataset v1: Towards a sea state climate data record based on satellite observations. Earth Syst. Sci. Data 2020, 12, 1929–1951. [Google Scholar] [CrossRef]
- Xu, J.; Wu, H.; Zhi, X.; Koldunov, N.V.; Zhang, X.; Xu, Y.; Zhang, Y.; Guo, M.; Kong, L.; Fraedrich, K. Validation of Multisource Altimeter SWH Measurements for Climate Data Analysis in China’s Offshore Waters. Remote Sens. 2024, 16, 2162. [Google Scholar] [CrossRef]
- Xu, J.; Wu, H.; Xu, Y.; Koldunov, N.V.; Zhang, X.; Kong, L.; Xu, M.; Fraedrich, K.; Zhi, X. Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters. Remote Sens. 2023, 15, 1005. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y. Evaluation of the ERA5 Significant Wave Height against NDBC Buoy Data from 1979 to 2019. Mar. Geod. 2022, 45, 151–165. [Google Scholar] [CrossRef]
- Yang, Y.; Qi, J.; Yan, Q.; Fan, C.; Zhang, R.; Zhang, J. Reconstruction of Wide Swath Significant Wave Height From Quasi-Synchronous Observations of Multisource Satellite Sensors. Earth Space Sci. 2024, 11, e2023EA003162. [Google Scholar] [CrossRef]
- Qiao, X.; Zhang, K.; Huang, W. Impacts of Climate Change on Oceans and Ocean-Based Solutions: A Comprehensive Review from the Deep Learning Perspective. Remote Sens. 2025, 17, 2306. [Google Scholar] [CrossRef]
- Sardana, D.; Kumar, P.; Bhaskaran, P.K.; Nair, T.M.B. The projected changes in extreme wave height indices over the Indian Ocean using COWCLIP2.0 datasets. Clim. Dyn. 2023, 61, 255–269. [Google Scholar] [CrossRef]
- Queffeulou, P. Long-Term Validation of Wave Height Measurements from Altimeters. Mar. Geod. 2004, 27, 495–510. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Xie, L.; Sun, C.; Liu, J.; Li, J.; Xian, D. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields. Acta Oceanol. Sin. 2019, 38, 158–161. [Google Scholar] [CrossRef]
- Haifeng, Z.; Qing, W.U.; Ge, C. Validation of HY-2A Remotely Sensed Wave Heights against Buoy Data and Jason-2 Altimeter Measurements. J. Atmos. Ocean. Technol. 2015, 32, 150402094232008. [Google Scholar]
- Jia, Y.; Yang, J.; Lin, M.; Zhang, Y.; Ma, C.; Fan, C. Global assessments of the HY-2B measurements and cross-calibrations with Jason-3. Remote Sens. 2020, 12, 2470. [Google Scholar] [CrossRef]
- Ye, X.; Lin, M.; Xu, Y. Validation of Chinese HY-2 satellite radar altimeter significant wave height. Acta Oceanol. Sin. 2015, 34, 60–67. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C. The global monitoring for environment and security (GMES) sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J. Validation of Sentinel-3A/3B satellite altimetry wave heights with buoy and Jason-3 data. Sensors 2019, 19, 2914. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, J.; Zhang, X.; Luo, Y.; Ding, M.; Wen, J.; Jin, W.; Qiao, C.; Yin, Y. Newly reconstructed Arctic surface air temperatures for 1979–2021 with deep learning method. Sci. Data 2023, 10, 140. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, R.; Ghanshala, K.K.; Joshi, R.C. Convolutional Neural Network (CNN) for Image Detection and Recognition. In Proceedings of the 2018 First International Conference on Secure Cyber Computing and Communication (ICSCCC), Jalandhar, India, 15–17 December 2018; pp. 278–282. [Google Scholar]
- Liu, D.; Han, G.; Liu, P.; Yang, H.; Sun, X.; Li, Q.; Wu, J. A Novel 2D-3D CNN with Spectral-Spatial Multi-Scale Feature Fusion for Hyperspectral Image Classification. Remote Sens. 2021, 13, 4621. [Google Scholar] [CrossRef]
- Du, G.; Cao, X.; Liang, J.; Chen, X.; Zhan, Y. Medical image segmentation based on U-net: A review. J. Imaging Sci. Technol. 2020, 64, 1. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, Q.; Duan, M.; Liu, H.; Huo, J.; Han, C. Deep Learning Model for Precipitation Nowcasting Based on Residual and Attention Mechanisms. Remote Sens. 2025, 17, 1123. [Google Scholar] [CrossRef]
- Ma, Z.; Huang, J.; Zhang, X.; Luo, Y.; Dou, T.; Ding, M. Deep learning-based reconstruction of monthly Antarctic surface air temperatures from 1979 to 2023. Sci. Data 2025, 12, 847. [Google Scholar] [CrossRef]
- Liu, G.; Dundar, A.; Shih, K.J.; Wang, T.-C.; Reda, F.A.; Sapra, K.; Yu, Z.; Yang, X.; Tao, A.; Catanzaro, B. Partial convolution for padding, inpainting, and image synthesis. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 6096–6110. [Google Scholar] [CrossRef] [PubMed]
- Bochow, N.; Poltronieri, A.; Rypdal, M.; Boers, N. Reconstructing historical climate fields with deep learning. Sci. Adv. 2025, 11, eadp0558. [Google Scholar] [CrossRef]
- Zhai, R.; Huang, C.; Yang, W.; Tang, L.; Zhang, W. Applicability evaluation of ERA5 wind and wave reanalysis data in the South China Sea. J. Oceanol. Limnol. 2023, 41, 495–517. [Google Scholar] [CrossRef]
- Hauser, D.; Tison, C.; Amiot, T.; Delaye, L.; Corcoral, N.; Castillan, P. SWIM: The First Spaceborne Wave Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3000–3014. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on pressure levels from 1940 to present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2023. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-pressure-levels?tab=overview (accessed on 20 November 2025). [CrossRef]
| Model | BIAS | RMSE | Wall Clock Time (h) |
|---|---|---|---|
| RA-PUnet 1 | 0.0001 | 0.4692 | 65 |
| R-PUnet | −0.0405 | 0.4732 | 53.5 |
| A-PUnet | −0.0233 | 0.5025 | 68 |
| PU-net | −0.0482 | 0.5069 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhang, Y.; Zhi, X.; Ma, Z.; Zhang, X.; Xu, Y.; Luo, Y.; Kong, L.; Yi, L. Reconstructed SWHs Based on a Deep Learning Method and the Revealed Long-Term SWH Variance Characteristics During 1993–2024. Remote Sens. 2025, 17, 3802. https://doi.org/10.3390/rs17233802
Xu J, Zhang Y, Zhi X, Ma Z, Zhang X, Xu Y, Luo Y, Kong L, Yi L. Reconstructed SWHs Based on a Deep Learning Method and the Revealed Long-Term SWH Variance Characteristics During 1993–2024. Remote Sensing. 2025; 17(23):3802. https://doi.org/10.3390/rs17233802
Chicago/Turabian StyleXu, Jingwei, Yangyang Zhang, Xiefei Zhi, Ziqi Ma, Xiuzhi Zhang, Ying Xu, Yong Luo, Lisha Kong, and Lin Yi. 2025. "Reconstructed SWHs Based on a Deep Learning Method and the Revealed Long-Term SWH Variance Characteristics During 1993–2024" Remote Sensing 17, no. 23: 3802. https://doi.org/10.3390/rs17233802
APA StyleXu, J., Zhang, Y., Zhi, X., Ma, Z., Zhang, X., Xu, Y., Luo, Y., Kong, L., & Yi, L. (2025). Reconstructed SWHs Based on a Deep Learning Method and the Revealed Long-Term SWH Variance Characteristics During 1993–2024. Remote Sensing, 17(23), 3802. https://doi.org/10.3390/rs17233802






