High-Resolution Mapping and Spatiotemporal Dynamics of Cropland Soil Temperature in the Huang-Huai-Hai Plain, China (2003–2020)
Highlights
- Monthly two-depth (0–5, 5–15 cm) cropland soil temperature mapping with RF + RFE-CV.
- Seasonally adaptive feature selection reveals a monthly driver hierarchy.
- There is a 1 km cropland soil temperature dataset for the Huang-Huai-Hai Plain (2003–2020).
- There is spatiotemporal heterogeneity driven by latitude, elevation, and soil type.
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.2.1. In Situ Soil Temperature Measurements
2.2.2. Predictor Variables
2.2.3. Auxiliary Variables
2.3. Methods
2.3.1. Soil Temperature Prediction
2.3.2. Spatiotemporal Variation Analysis of Soil Temperature
3. Results
3.1. Model Predictive Performance
3.1.1. Model Performance
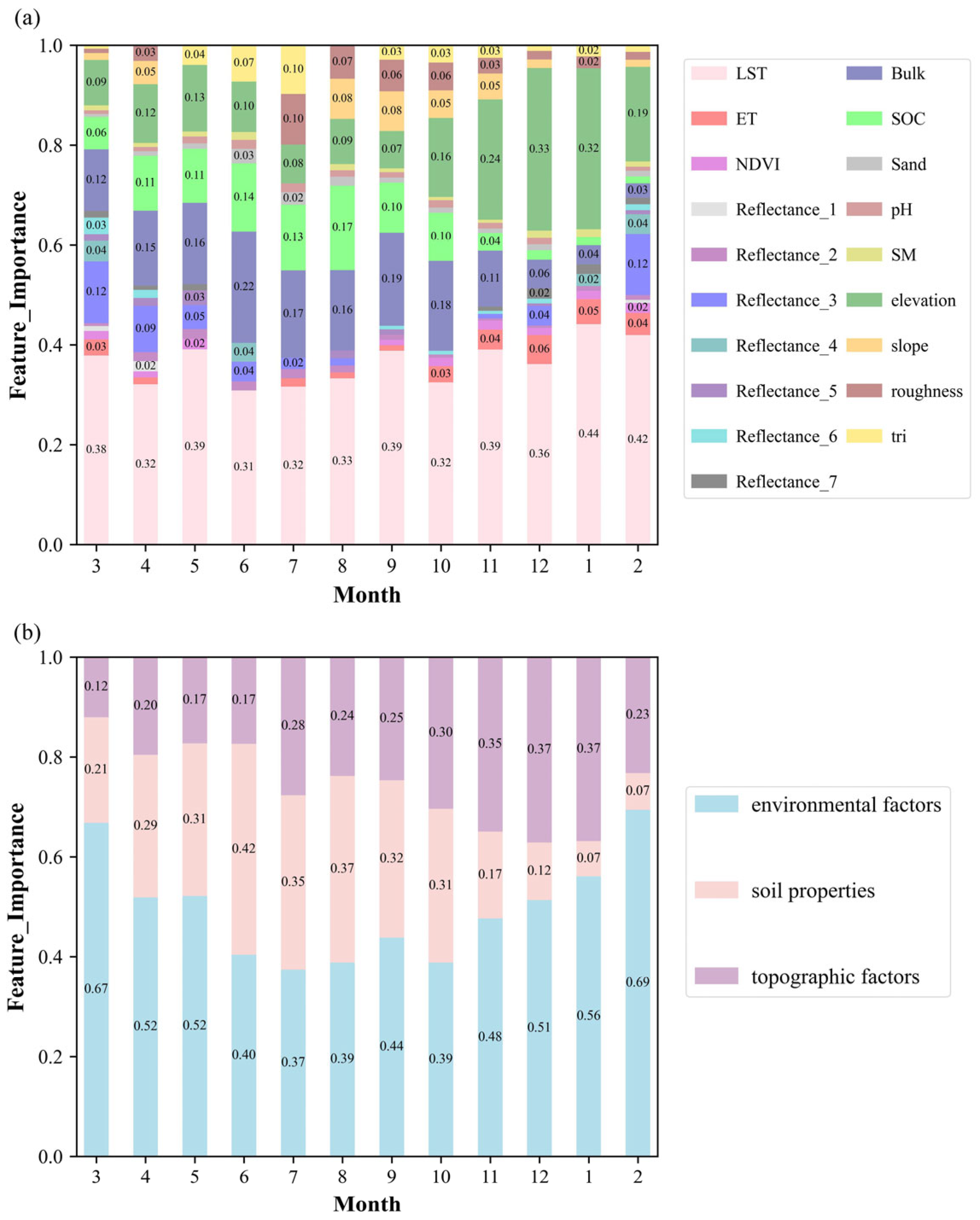
3.1.2. Feature Importance
3.2. Spatiotemporal Patterns of Soil Temperature
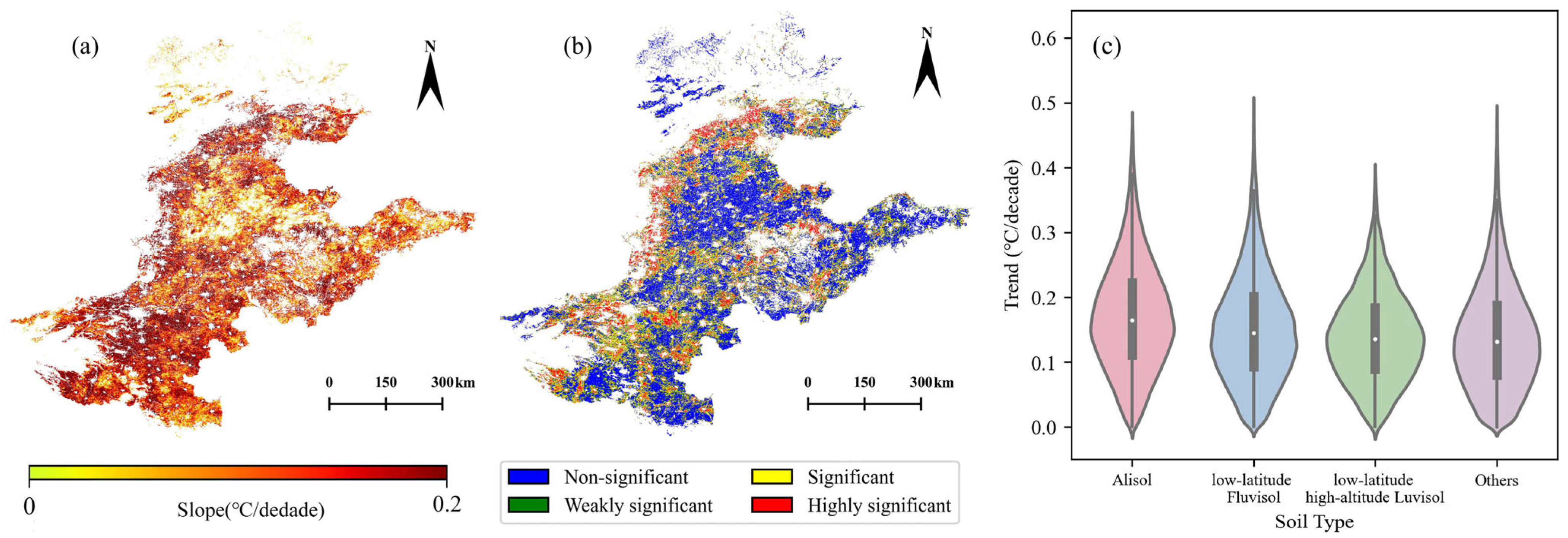
3.2.1. Long-Term Trend Analysis
3.2.2. Seasonal Characteristics Analysis
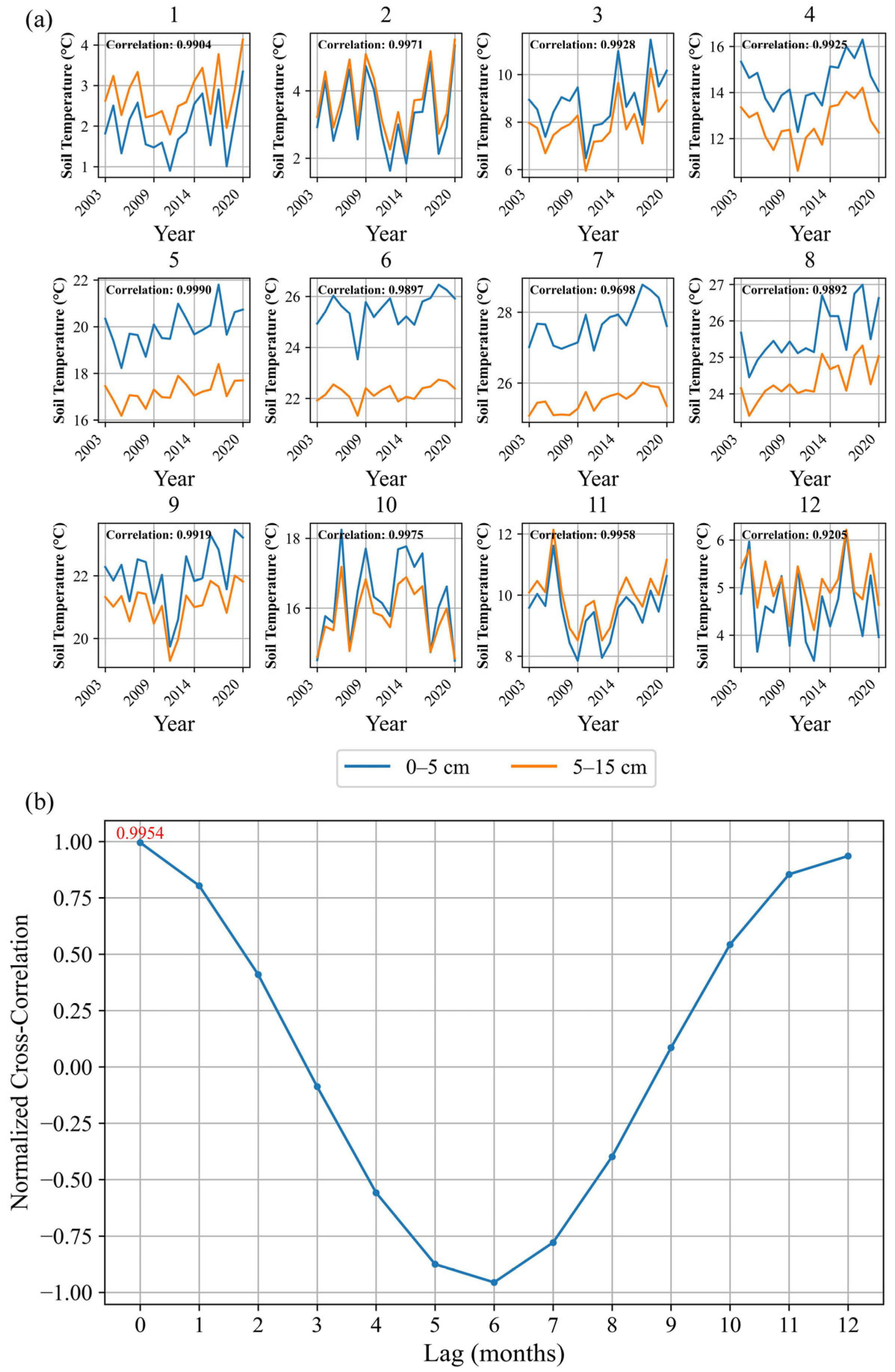
3.2.3. Depth Variation Analysis
4. Discussion
4.1. Model Development and Feature Selection Strategy
4.2. Seasonal Mechanisms of Predictive Factors
4.3. Spatial Variation in Soil Temperature Dynamics and Contributing Factors
4.4. Impact of Soil Temperature on Crop Growth Stages
4.5. Limitations and Future Directions
5. Conclusions
- (1)
- The proposed method accurately estimates soil temperature, with Mean_R2 values of 0.8–1.0 (0.9–1.0), Mean_RMSE values of 1.0–1.9 °C (1.1–1.6 °C), Mean_MAE values of 0.7–1.0 °C (0.8–1.1 °C), Mean_NSE values of 0.8–1.0 (0.9–1.0), and Mean_Bias values of 0.0–0.3 °C (0.0 °C throughout) for the 0–5 cm (5–15 cm) layer.
- (2)
- Environmental variables have the greatest overall impact, particularly in the shallow layer (0.40–0.88) compared to the deep layer (0.37–0.69). Soil properties (0–0.42 in the shallow layer; 0.07–0.42 in the deep layer) and topographic factors (0.08–0.34 in the shallow layer; 0.12–0.37 in the deep layer) show greater sensitivity at deeper depths. Seasonally, environmental influence decreases and then increases (U-shaped); soil properties are more influential in spring–summer, while topography becomes comparatively more influential in autumn–winter.
- (3)
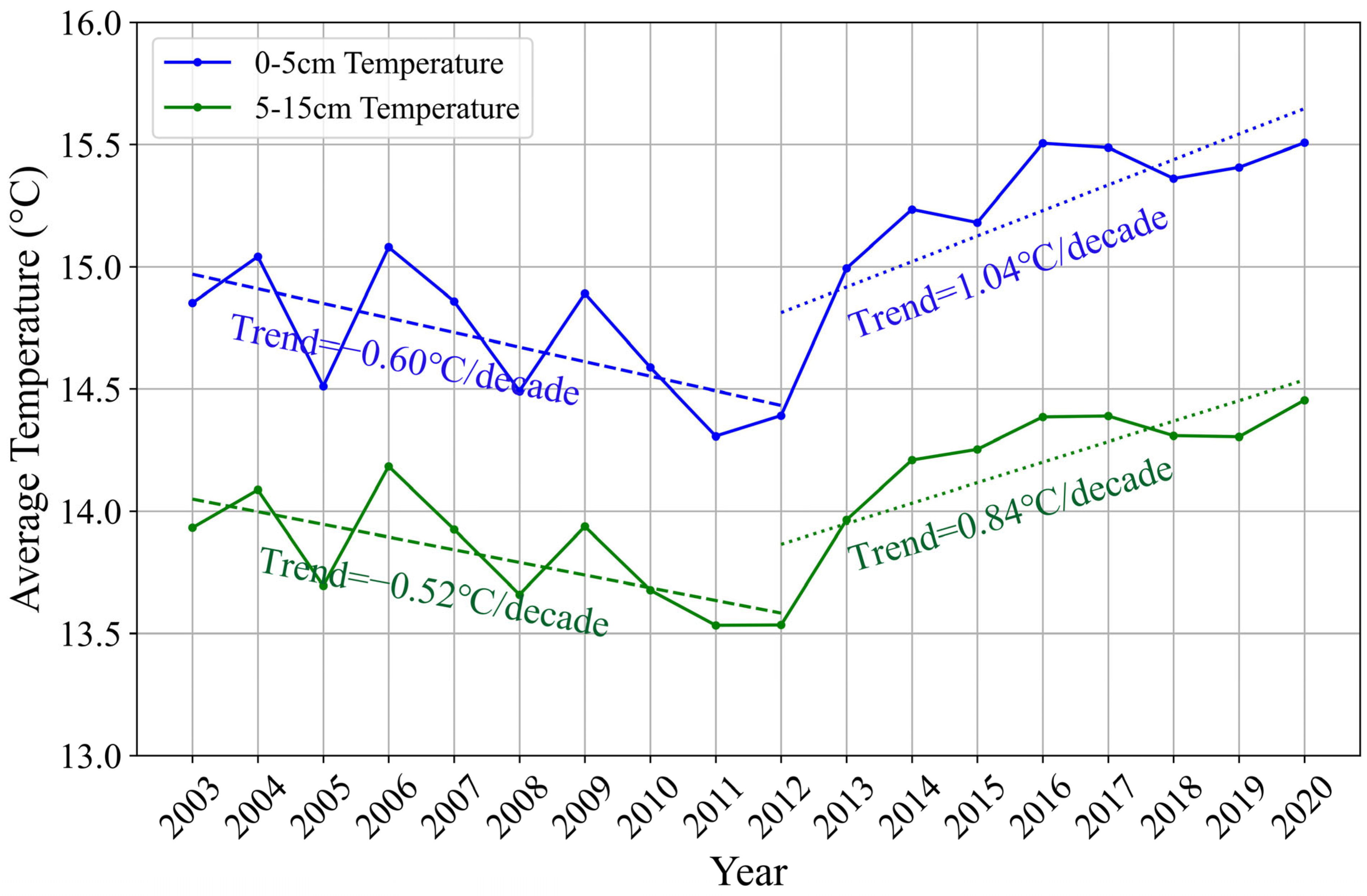
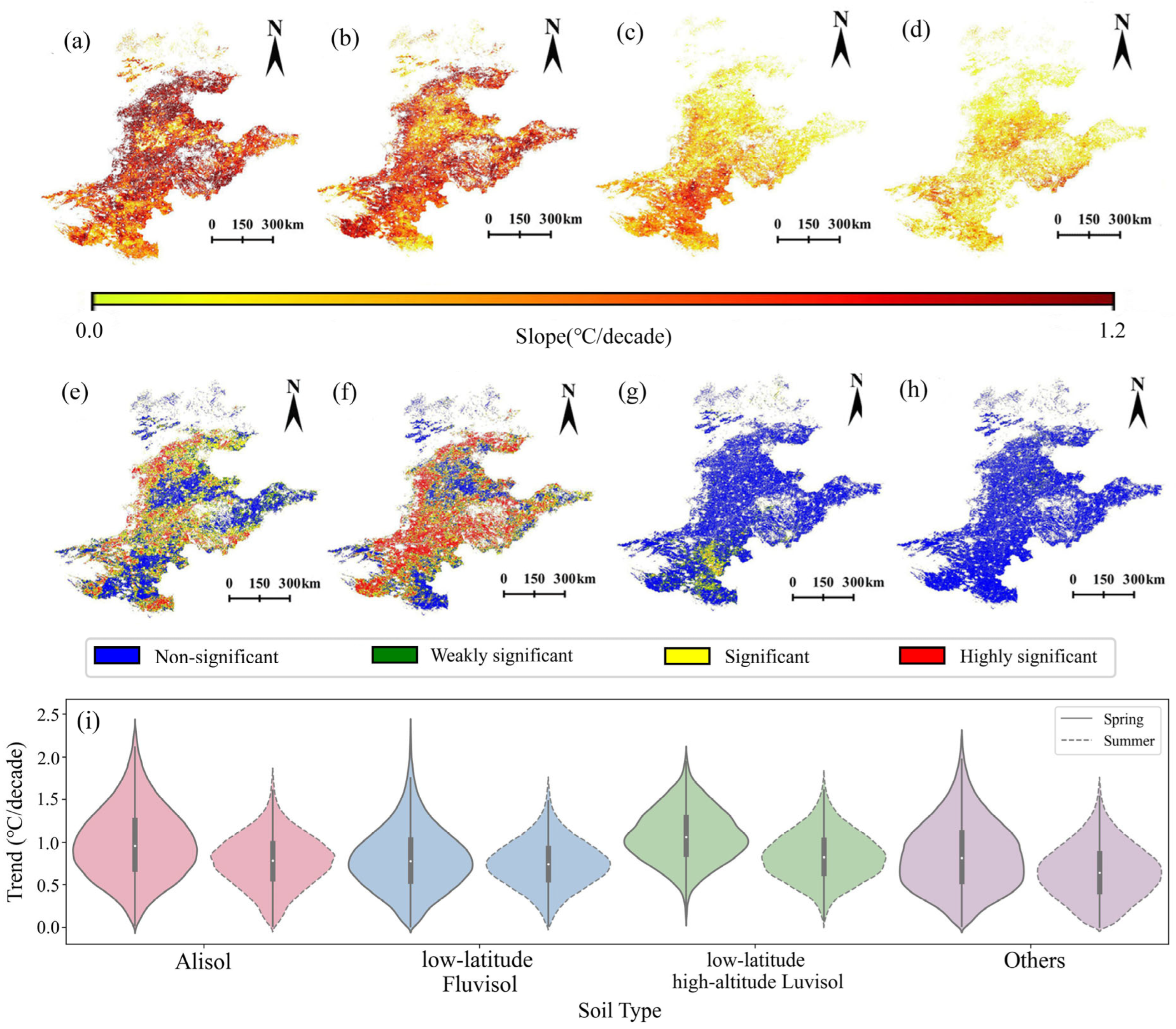
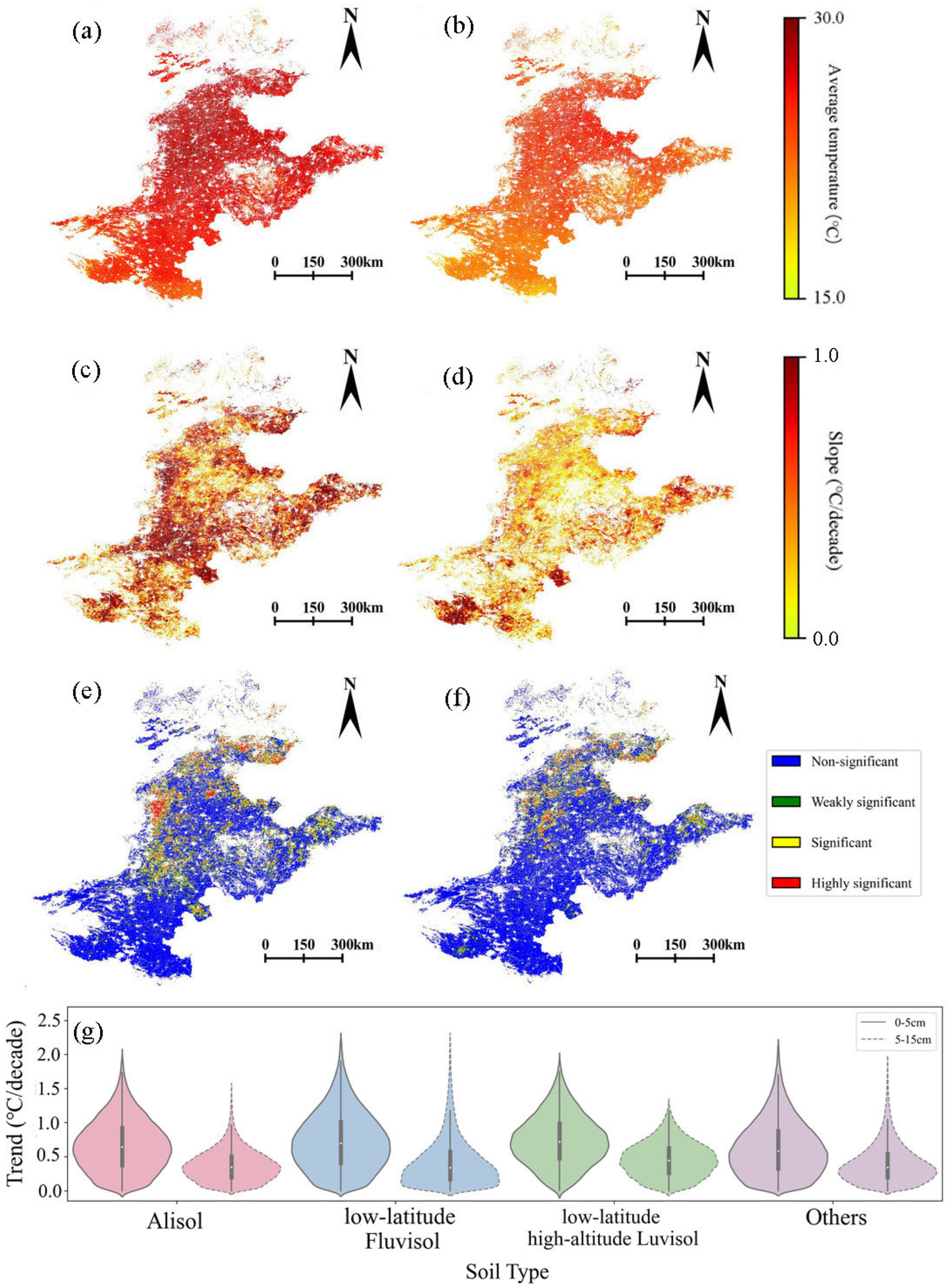
- Cropland soil temperature exhibited a cooling trend from 2003 to 2012 (shallow: −0.6 °C/decade; deep: −0.52 °C/decade), shifting to a warming trend from 2012 to 2020 (shallow: 1.04 °C/decade; deep: 0.84 °C/decade). Seasonally, warming is pronounced in spring (shallow from −0.5 °C to 0.5 °C; deep from −0.4 °C to 0.4 °C) and summer (shallow from −0.4 °C to 0.4 °C; deep from −0.2 °C to 0.2 °C), with it being milder in autumn (shallow and deep both from −0.1 °C to 0.1 °C) and negligible in winter (shallow and deep both stable at 0 °C).
- (4)
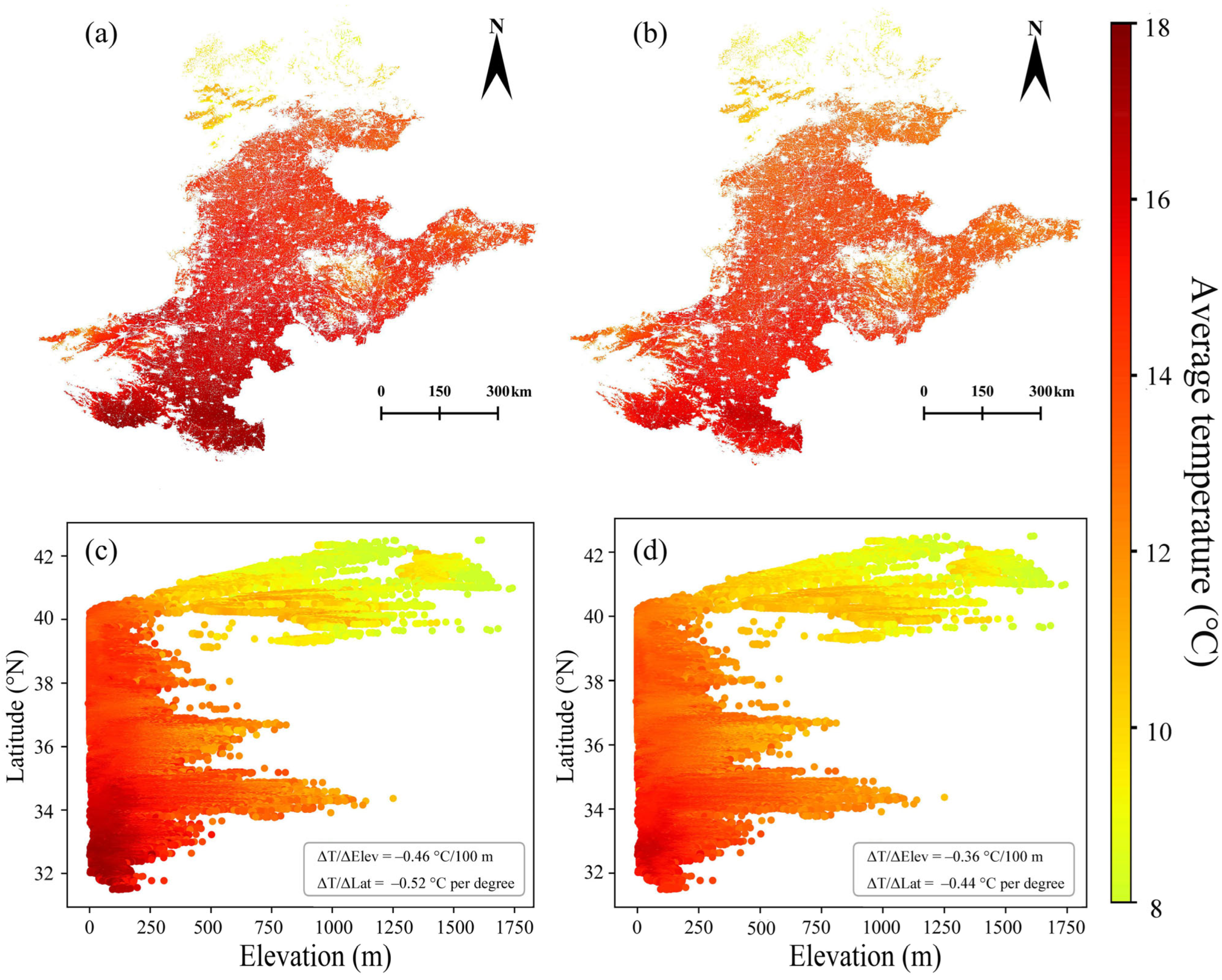
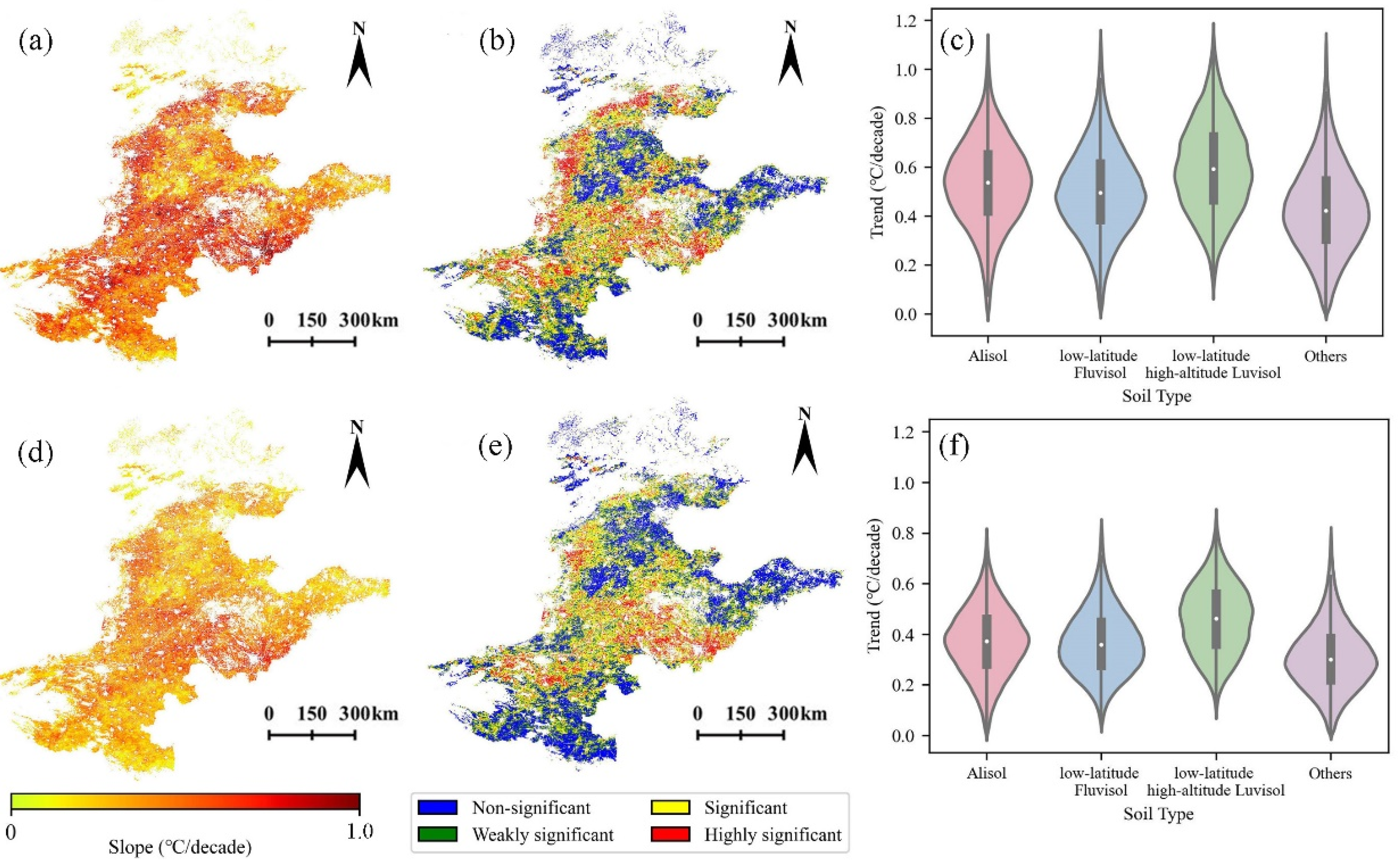
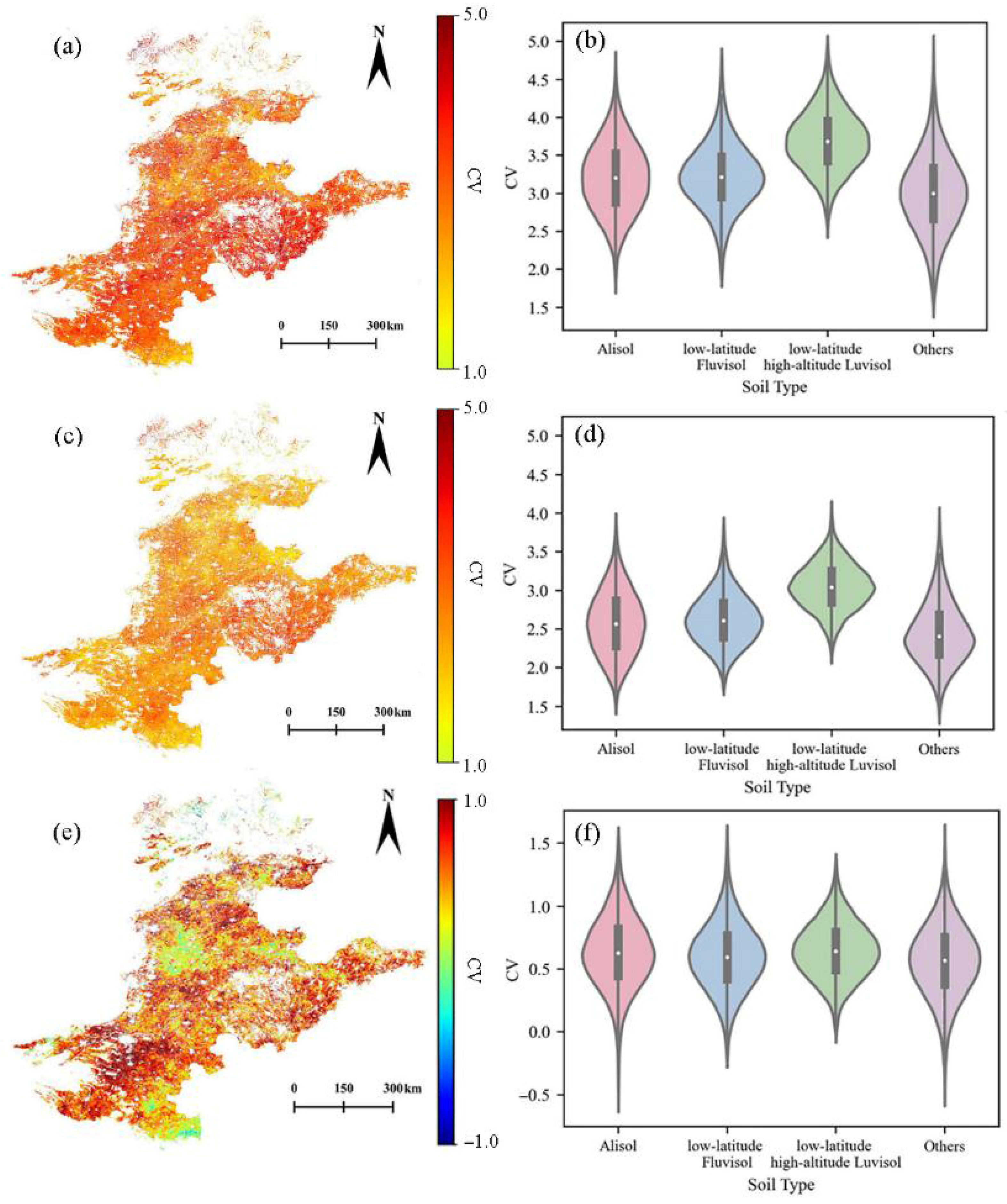
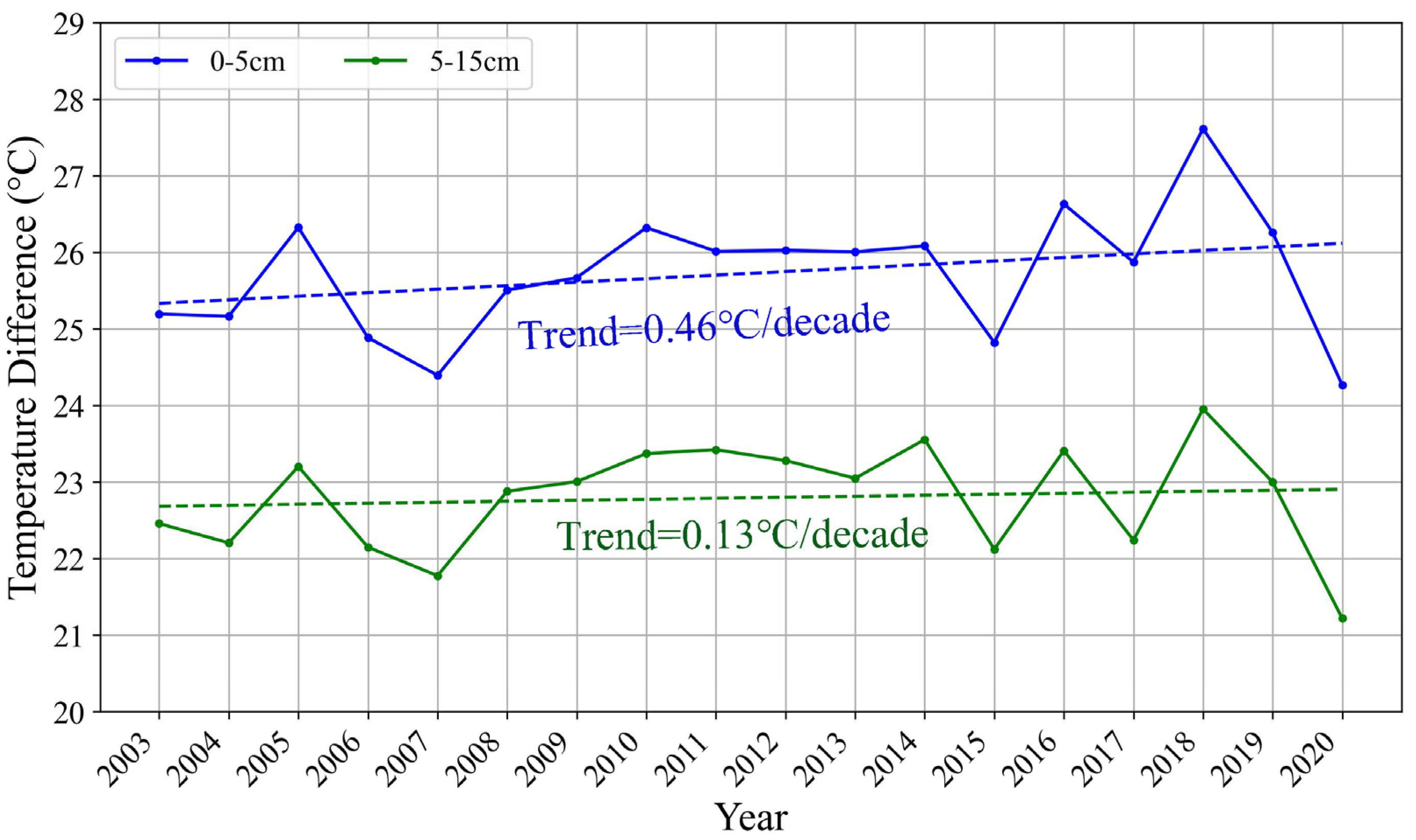
- Latitude, elevation, soil type, and soil depth jointly influence the spatial and temporal patterns of soil temperature. A distinct temperature gradient exists, with warmer conditions in low-latitude, low-elevation areas. Soil types such as Alisol, low-latitude Fluvisol, and high-altitude Luvisol show stronger trends and higher statistical significance. Compared to shallow soil, deep soil exhibits more stable trends, lower variability, and weaker seasonality, though both layers remain highly synchronized (correlation = 0.9954). The growing difference in interlayer trends suggests a decline in soil thermal inertia.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Araghi, A.; Adamowski, J.; Martinez, C.J.; Olesen, J.E. Projections of Future Soil Temperature in Northeast Iran. Geoderma 2019, 349, 11–24. [Google Scholar] [CrossRef]
- Pitombeira De Figueirêdo, L.; Athayde, D.B.; Daam, M.A.; Van Gestel, C.A.M.; Guerra, G.D.S.; Duarte-Neto, P.J.; Espíndola, E.L.G. Impact of Temperature on the Toxicity of Kraft 36 EC® (a.s. Abamectin) and Score 250 EC® (a.s. Difenoconazole) to Soil Organisms under Realistic Environmental Exposure Scenarios. Ecotoxicol. Environ. Saf. 2020, 194, 110446. [Google Scholar] [CrossRef] [PubMed]
- Costa, J.M.; Egipto, R.; Aguiar, F.C.; Marques, P.; Nogales, A.; Madeira, M. The Role of Soil Temperature in Mediterranean Vineyards in a Climate Change Context. Front. Plant Sci. 2023, 14, 1145137. [Google Scholar] [CrossRef] [PubMed]
- Sabri, N.S.A.; Zakaria, Z.; Mohamad, S.E.; Jaafar, A.B.; Hara, H. Importance of Soil Temperature for the Growth of Temperate Crops under a Tropical Climate and Functional Role of Soil Microbial Diversity. Microbes Environ. 2018, 33, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Onwuka, B. Effects of Soil Temperature on Some Soil Properties and Plant Growth. Adv. Plants Agric. Res. 2018, 8, 34–37. [Google Scholar] [CrossRef]
- Poll, C.; Marhan, S.; Back, F.; Niklaus, P.A.; Kandeler, E. Field-Scale Manipulation of Soil Temperature and Precipitation Change Soil CO2 Flux in a Temperate Agricultural Ecosystem. Agric. Ecosyst. Environ. 2013, 165, 88–97. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhang, M.; Jin, H.; Ren, Y. Spatiotemporal Variation Characteristics of Hourly Soil Temperature in Different Layers in the Low-Latitude Plateau of China. Front. Environ. Sci. 2022, 10, 1091985. [Google Scholar] [CrossRef]
- Huang, R.; Huang, J.; Zhang, C.; Ma, H.; Zhuo, W.; Chen, Y.; Zhu, D.; Wu, Q.; Mansaray, L.R. Soil Temperature Estimation at Different Depths, Using Remotely-Sensed Data. J. Integr. Agric. 2020, 19, 277–290. [Google Scholar] [CrossRef]
- O’Brien, P.L.; Hatfield, J.L. Extreme Soil Surface Temperatures Reflect Need to Rethink Agronomic Management. Agric. Env. Lett. 2020, 5, e20002. [Google Scholar] [CrossRef]
- Tsai, Y.-Z.; Hsu, K.-S.; Wu, H.-Y.; Lin, S.-I.; Yu, H.-L.; Huang, K.-T.; Hu, M.-C.; Hsu, S.-Y. Application of Random Forest and ICON Models Combined with Weather Forecasts to Predict Soil Temperature and Water Content in a Greenhouse. Water 2020, 12, 1176. [Google Scholar] [CrossRef]
- Alizamir, M.; Kisi, O.; Ahmed, A.N.; Mert, C.; Fai, C.M.; Kim, S.; Kim, N.W.; El-Shafie, A. Advanced Machine Learning Model for Better Prediction Accuracy of Soil Temperature at Different Depths. PLoS ONE 2020, 15, e0231055. [Google Scholar] [CrossRef]
- Kamyab, M.; Liu, G.; Adjeisah, M. Attention-Based CNN and Bi-LSTM Model Based on TF-IDF and GloVe Word Embedding for Sentiment Analysis. Appl. Sci. 2021, 11, 11255. [Google Scholar] [CrossRef]
- Zhao, E.; Qu, N.; Wang, Y.; Gao, C.; Zeng, J. Tebs: Temperature–Emissivity–Driven Band Selection for Thermal Infrared Hyperspectral Image Classification with Structured State-Space Model and Gated Attention. Int. J. Appl. Earth Obs. Geoinf. 2025, 142, 104710. [Google Scholar] [CrossRef]
- Petitjean, M.; Randoux, Y.; Jordens, A.; Saadaoui, H.; Haemers, J. Low-Complexity Mapping of Soil Temperature for Thermal Treatment Follow-Up. J. Contam. Hydrol. 2022, 250, 104056. [Google Scholar] [CrossRef] [PubMed]
- Trask, J.C.; Devine, S.M.; Fogg, G.E. Soil Temperature Survey in a Mountain Basin. Geoderma 2020, 367, 114202. [Google Scholar] [CrossRef]
- Li, Z.; Wu, H.; Duan, S.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite Remote Sensing of Global Land Surface Temperature: Definition, Methods, Products, and Applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.-L.; Duan, S.-B.; Leng, P.; Si, M. Retrieval of Global Surface Soil and Vegetation Temperatures Based on Multisource Data Fusion. Remote Sens. Environ. 2025, 318, 114564. [Google Scholar] [CrossRef]
- Zhang, R.; Tian, J.; Su, H.; Sun, X.; Chen, S.; Xia, J. Two Improvements of an Operational Two-Layer Model for Terrestrial Surface Heat Flux Retrieval. Sensors 2008, 8, 6165–6187. [Google Scholar] [CrossRef]
- Taheri, M.; Schreiner, H.K.; Mohammadian, A.; Shirkhani, H.; Payeur, P.; Imanian, H.; Cobo, J.H. A Review of Machine Learning Approaches to Soil Temperature Estimation. Sustainability 2023, 15, 7677. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Ahmadi, F.; Kozekalani Sales, A. Modelling Daily Soil Temperature at Different Depths via the Classical and Hybrid Models. Meteorol. Appl. 2020, 27, e1941. [Google Scholar] [CrossRef]
- Xu, C.; Liao, S.; Huang, L.; Xia, J. Soil Temperature Estimation at Different Depths over the Central Tibetan Plateau Integrating Multiple Digital Earth Observations and Geo-Computing. Int. J. Digit. Earth 2023, 16, 4023–4043. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, N.; Ma, Z.; Huang, Y. Understanding the Soil Temperature Variability at Different Depths: Effects of Surface Air Temperature, Snow Cover, and the Soil Memory. Adv. Atmos. Sci. 2021, 38, 493–503. [Google Scholar] [CrossRef]
- Geng, Q.; Wang, L.; Li, Q. Soil Temperature Prediction Based on Explainable Artificial Intelligence and LSTM. Front. Environ. Sci. 2024, 12, 1426942. [Google Scholar] [CrossRef]
- Mampitiya, L.; Rozumbetov, K.; Rathnayake, N.; Erkudov, V.; Esimbetov, A.; Arachchi, S.; Kantamaneni, K.; Hoshino, Y.; Rathnayake, U. Artificial Intelligence to Predict Soil Temperatures by Development of Novel Model. Sci. Rep. 2024, 14, 9889. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; Li, L.; Gong, J.; Ren, C.; Liu, J.; Chen, H. Daily Soil Temperatures Predictions for Various Climates in United States Using Data-Driven Model. Energy 2018, 160, 430–440. [Google Scholar] [CrossRef]
- Belouz, K.; Zereg, S. Extreme Learning Machine for Soil Temperature Prediction Using Only Air Temperature as Input. Env. Monit. Assess. 2023, 195, 962. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Hao, W.; Gao, L.; Gong, D. Estimation of Soil Temperature from Meteorological Data Using Different Machine Learning Models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Hatamiafkoueieh, J.; Heddam, S.; Khoshtinat, S.; Khazaei, S.; Osmani, A.-B.; Nohani, E.; Kiomarzi, M.; Sharafi, E.; Tiefenbacher, J. Enhanced Forecasting of Multi-Step Ahead Daily Soil Temperature Using Advanced Hybrid Vote Algorithm-Based Tree Models. J. Hydroinformatics 2023, 25, 2643–2659. [Google Scholar] [CrossRef]
- Lembrechts, J.J.; Van Den Hoogen, J.; Aalto, J.; Ashcroft, M.B.; De Frenne, P.; Kemppinen, J.; Kopecký, M.; Luoto, M.; Maclean, I.M.D.; Crowther, T.W.; et al. Global Maps of Soil Temperature. Glob. Change Biol. 2022, 28, 3110–3144. [Google Scholar] [CrossRef]
- Pan, Y.; Lin, Y.; Yang, R. Agricultural Production Space Suitability in China: Spatial Pattern, Influencing Factors and Optimization Strategies. Int. J. Environ. Res. Public Health 2022, 19, 13812. [Google Scholar] [CrossRef]
- Ishola, K.A.; Mills, G.; Fealy, R.M.; Choncubhair, Ó.N.; Fealy, R. Improving a Land Surface Scheme for Estimating Sensible and Latent Heat Fluxes above Grasslands with Contrasting Soil Moisture Zones. Agric. For. Meteorol. 2020, 294, 108151. [Google Scholar] [CrossRef]
- Feldman, A.F.; Short Gianotti, D.J.; Trigo, I.F.; Salvucci, G.D.; Entekhabi, D. Satellite—Based Assessment of Land Surface Energy Partitioning–Soil Moisture Relationships and Effects of Confounding Variables. Water Resour. Res. 2019, 55, 10657–10677. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.-L.; Li, J.-H.; Leng, P.; Liu, M.; Gao, M. Global 1-Km Monthly Mean Land Surface Temperature Product (2003–2020); Zenodo: Geneva, Switzerland, 2022. [Google Scholar]
- Gan, R.; Zhang, Y.; Shi, H.; Yang, Y.; Eamus, D.; Cheng, L.; Chiew, F.H.S.; Yu, Q. Use of Satellite Leaf Area Index Estimating Evapotranspiration and Gross Assimilation for Australian Ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-Decadal Trends in Global Terrestrial Evapotranspiration and Its Components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef]
- Didan, K. MODIS/Aqua Vegetation Indices 16-Day L3 Global 250m SIN Grid V061; NASA EOSDIS Land Processes Distributed Active Archive Center (DAAC) data set: Sioux Falls, South Dakota, 2021. [Google Scholar]
- Schaaf, C.; Wang, Z. MODIS/Terra+Aqua BRDF/Albedo Nadir BRDF Adjusted Ref Daily L3 Global—500m V061; NASA EOSDIS Land Processes Distributed Active Archive Center (DAAC) data set: Sioux Falls, South Dakota, 2021. [Google Scholar]
- Zheng, C.; Jia, L.; Zhao, T. A 21-Year Dataset (2000–2020) of Gap-Free Global Daily Surface Soil Moisture at 1-Km Grid Resolution. Sci. Data 2023, 10, 139. [Google Scholar] [CrossRef]
- Batjes, N.H.; Ribeiro, E.; Van Oostrum, A. Standardised Soil Profile Data to Support Global Mapping and Modelling (WoSIS Snapshot 2019). Earth Syst. Sci. Data 2020, 12, 299–320. [Google Scholar] [CrossRef]
- Amatulli, G.; Domisch, S.; Tuanmu, M.-N.; Parmentier, B.; Ranipeta, A.; Malczyk, J.; Jetz, W. A Suite of Global, Cross-Scale Topographic Variables for Environmental and Biodiversity Modeling. Sci. Data 2018, 5, 180040. [Google Scholar] [CrossRef]
- Jie, Y.; Xin, H. The 30 m Annual Land Cover Datasets and Its Dynamics in China from 1985 to 2023. Earth Syst. Sci. Data 2024, 13, 3907–3925. [Google Scholar]
- Liu, X.; Li, Z.-L.; Li, Y.; Wu, H.; Zhou, C.; Si, M.; Leng, P.; Duan, S.-B.; Yang, P.; Wu, W.; et al. Local Temperature Responses to Actual Land Cover Changes Present Significant Latitudinal Variability and Asymmetry. Sci. Bull. 2023, 68, 2849–2861. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H. Thermal Properties of Soils as Affected by Density and Water Content. Biosyst. Eng. 2003, 86, 97–102. [Google Scholar] [CrossRef]
- Hengl, T.; Nussbaum, M.; Wright, M.N.; Heuvelink, G.B.M.; Gräler, B. Random Forest as a Generic Framework for Predictive Modeling of Spatial and Spatio-Temporal Variables. PeerJ 2018, 6, e5518. [Google Scholar] [CrossRef]
- Du, W.; Liu, X.; Li, Z.-L.; Qin, Z.; Fan, J. An Improved Integrated Model for Temporal Normalization of Satellite-Derived Land Surface Temperature. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–9. [Google Scholar] [CrossRef]
- Zhao, W.; Duan, S.-B.; Li, A.; Yin, G. A Practical Method for Reducing Terrain Effect on Land Surface Temperature Using Random Forest Regression. Remote Sens. Environ. 2019, 221, 635–649. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Ye, Y.; Liu, L.; Chen, F.; Huang, L. An Improved Soil Moisture Retrieval Method Considering Azimuth Angle Changes for Spaceborne GNSS-R. Adv. Space Res. 2025, 75, 178–189. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Moran, P.A.P.; Kendall, M.G. Rank Correlation Methods. Int. Stat. Rev. 1973, 41, 399. [Google Scholar] [CrossRef]
- Pearson, K. Mathematical Contributions to the Theory of Evolution—III. Regression, Heredity, and Panmixia. Proc. R. Soc. Lond. 1895, 59, 69–71. [Google Scholar]
- Lewis, J.P. Fast Template Matching. Vis. Interface 1995, 95, 15–19. [Google Scholar]
- Feng, Z.; Wang, L.; Peng, Q.; Li, J.; Liang, T. Effect of Environmental Factors on Soil Properties under Different Land Use Types in a Typical Basin of the North China Plain. J. Clean. Prod. 2022, 344, 131084. [Google Scholar] [CrossRef]
- García-García, A.; Cuesta-Valero, F.J.; Miralles, D.G.; Mahecha, M.D.; Quaas, J.; Reichstein, M.; Zscheischler, J.; Peng, J. Soil Heat Extremes Can Outpace Air Temperature Extremes. Nat. Clim. Change 2023, 13, 1237–1241. [Google Scholar] [CrossRef]
- Liu, X.; Li, Z.-L.; Li, J.-H.; Leng, P.; Liu, M.; Gao, M. Temporal Upscaling of MODIS 1-Km Instantaneous Land Surface Temperature to Monthly Mean Value: Method Evaluation and Product Generation. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Perkins-Kirkpatrick, S.; Barriopedro, D.; Jha, R.; Wang, L.; Mondal, A.; Libonati, R.; Kornhuber, K. Extreme Terrestrial Heat in 2023. Nat. Rev. Earth Env. 2024, 5, 244–246. [Google Scholar] [CrossRef]
- Cohen, J.L.; Furtado, J.C.; Barlow, M.; Alexeev, V.A.; Cherry, J.E. Asymmetric Seasonal Temperature Trends. Geophys. Res. Lett. 2012, 39, 2011GL050582. [Google Scholar] [CrossRef]
- Matiu, M.; Ankerst, D.P.; Menzel, A. Asymmetric Trends in Seasonal Temperature Variability in Instrumental Records from Ten Stations in Switzerland, Germany and the UK from 1864 to 2012. Int. J. Climatol. 2016, 36, 13–27. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, G. Differences in Temperature Variation Between Winter and Summer Across China in Recent Decades. Int. J. Climatol. 2025, 45, e8828. [Google Scholar] [CrossRef]
- Hao, H.; Yu, F.; Li, Q. Soil Temperature Prediction Using Convolutional Neural Network Based on Ensemble Empirical Mode Decomposition. IEEE Access 2021, 9, 4084–4096. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Y.; Li, Q.; Zhao, H.; Zhu, J.; Zhang, C. Interpretable Spatio-Temporal Modeling for Soil Temperature Prediction. Front. For. Glob. Change 2023, 6, 1295731. [Google Scholar] [CrossRef]
- Jiang, K.; Pan, Z.; Pan, F.; Teuling, A.J.; Han, G.; An, P.; Chen, X.; Wang, J.; Song, Y.; Cheng, L.; et al. Combined Influence of Soil Moisture and Atmospheric Humidity on Land Surface Temperature under Different Climatic Background. iScience 2023, 26, 106837. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, X.; Jiang, Y.; Li, J.; Fu, Q.; Qiu, Y.; Fu, X.; Yao, Z.; Dai, Z.; Qiu, Y.; et al. Effects of Simulated Warming on Soil Microbial Community Diversity and Composition across Diverse Ecosystems. Sci. Total Environ. 2024, 911, 168793. [Google Scholar] [CrossRef]
- Li, F.; Hao, D.; Zhu, Q.; Yuan, K.; Braghiere, R.K.; He, L. Global Impacts of Vegetation Clumping on Regulating Land Surface Heat Fluxes. Agric. For. Meteorol. 2024, 345, 109820. [Google Scholar] [CrossRef]
- Estevo, C.A.; Stralberg, D.; Nielsen, S.E.; Bayne, E. Topographic and Vegetation Drivers of Thermal Heterogeneity along the Boreal–Grassland Transition Zone in Western Canada: Implications for Climate Change Refugia. Ecol. Evol. 2022, 12, e9008. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Xue, Y.; Liu, Y. Impact of Frozen Soil Processes on Soil Thermal Characteristics at Seasonal to Decadal Scales over the Tibetan Plateau and North China. Hydrol. Earth Syst. Sci. 2021, 25, 2089–2107. [Google Scholar] [CrossRef]
- Brito, W.B.M.; Campos, M.C.C.; Souza, F.G.D.; Silva, L.S.; Lima, H.N.; Lima, A.F.L.D.; Cunha, J.M.D. Magnetic Susceptibility and Properties of Alisols under Forest and Crops in South Amazonas. J. South Am. Earth Sci. 2024, 144, 105023. [Google Scholar] [CrossRef]
- Wang, X.; Chen, R.; Han, C.; Yang, Y.; Liu, J.; Liu, Z.; Guo, S.; Song, Y. Soil Temperature Change and Its Regional Differences under Different Vegetation Regions across China. Int. J. Climatol. 2021, 41, E2310–E2320. [Google Scholar] [CrossRef]
- Sharma, S.; Singh, V.; Tanwar, H.; Mor, V.S.; Kumar, M.; Punia, R.C.; Dalal, M.S.; Khan, M.; Sangwan, S.; Bhuker, A.; et al. Impact of High Temperature on Germination, Seedling Growth and Enzymatic Activity of Wheat. Agriculture 2022, 12, 1500. [Google Scholar] [CrossRef]
- Khaeim, H.; Kende, Z.; Jolánkai, M.; Kovács, G.P.; Gyuricza, C.; Tarnawa, Á. Impact of Temperature and Water on Seed Germination and Seedling Growth of Maize (Zea Mays L.). Agronomy 2022, 12, 397. [Google Scholar] [CrossRef]
- Takoutsing, B.; Heuvelink, G.B.M. Comparing the Prediction Performance, Uncertainty Quantification and Extrapolation Potential of Regression Kriging and Random Forest While Accounting for Soil Measurement Errors. Geoderma 2022, 428, 116192. [Google Scholar] [CrossRef]
- Deng, W.; Liu, D.; Guo, F.; Zhang, L.; Ma, L.; Huang, Q.; Li, Q.; Ming, G.; Meng, X. Evaluation of the Potential of Using Machine Learning and the Savitzky–Golay Filter to Estimate the Daily Soil Temperature in Gully Regions of the Chinese Loess Plateau. Agronomy 2024, 14, 703. [Google Scholar] [CrossRef]
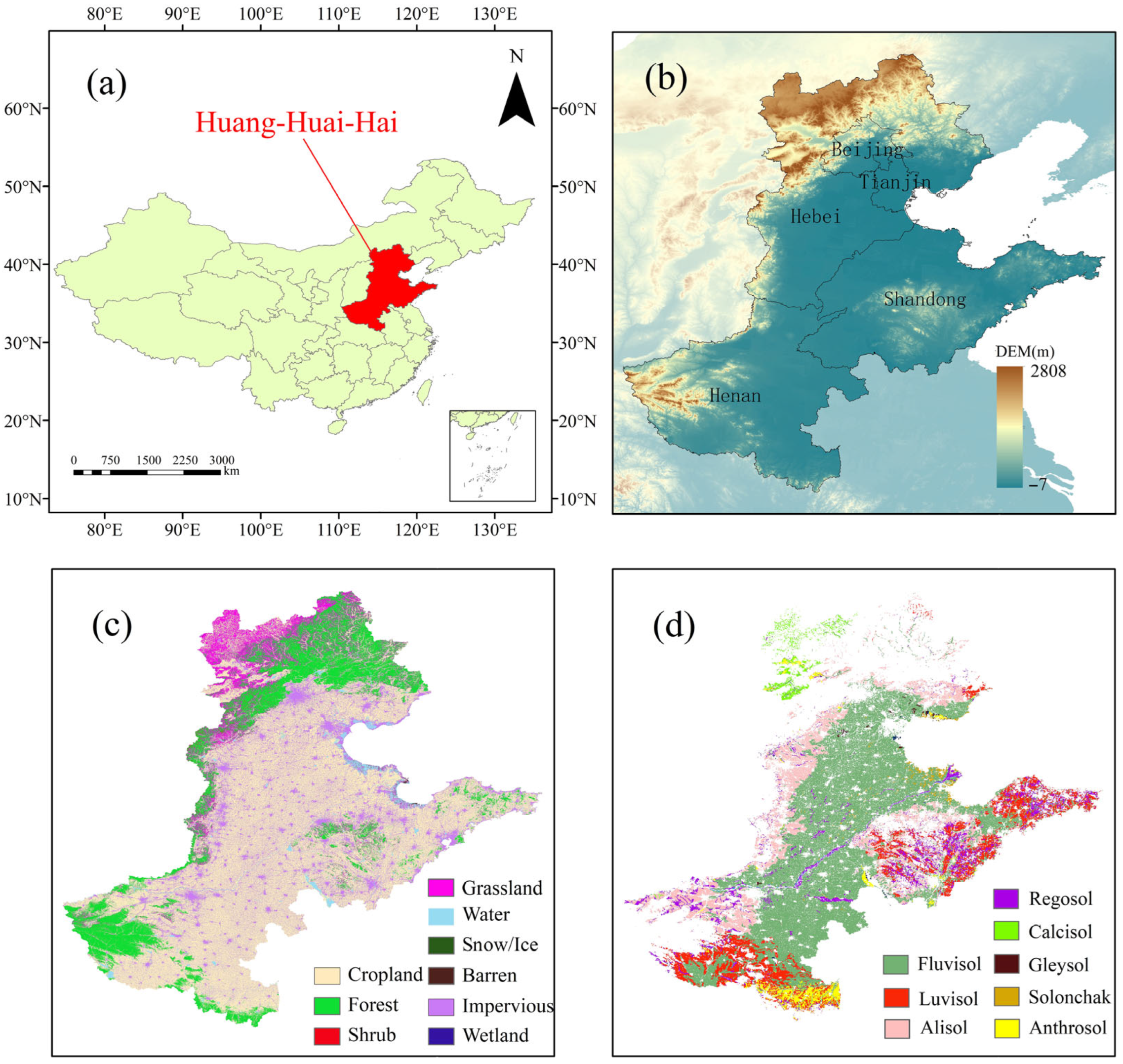
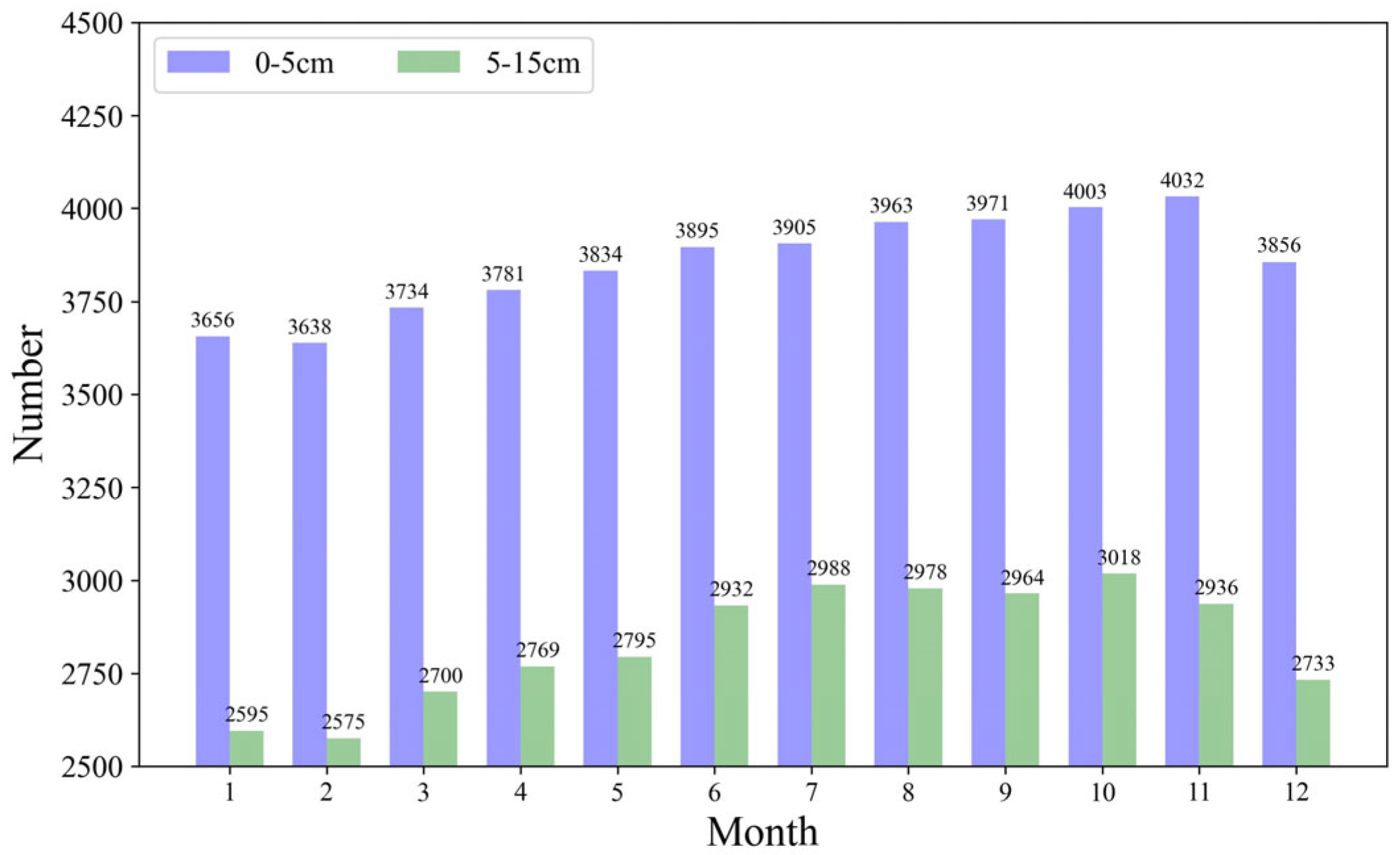
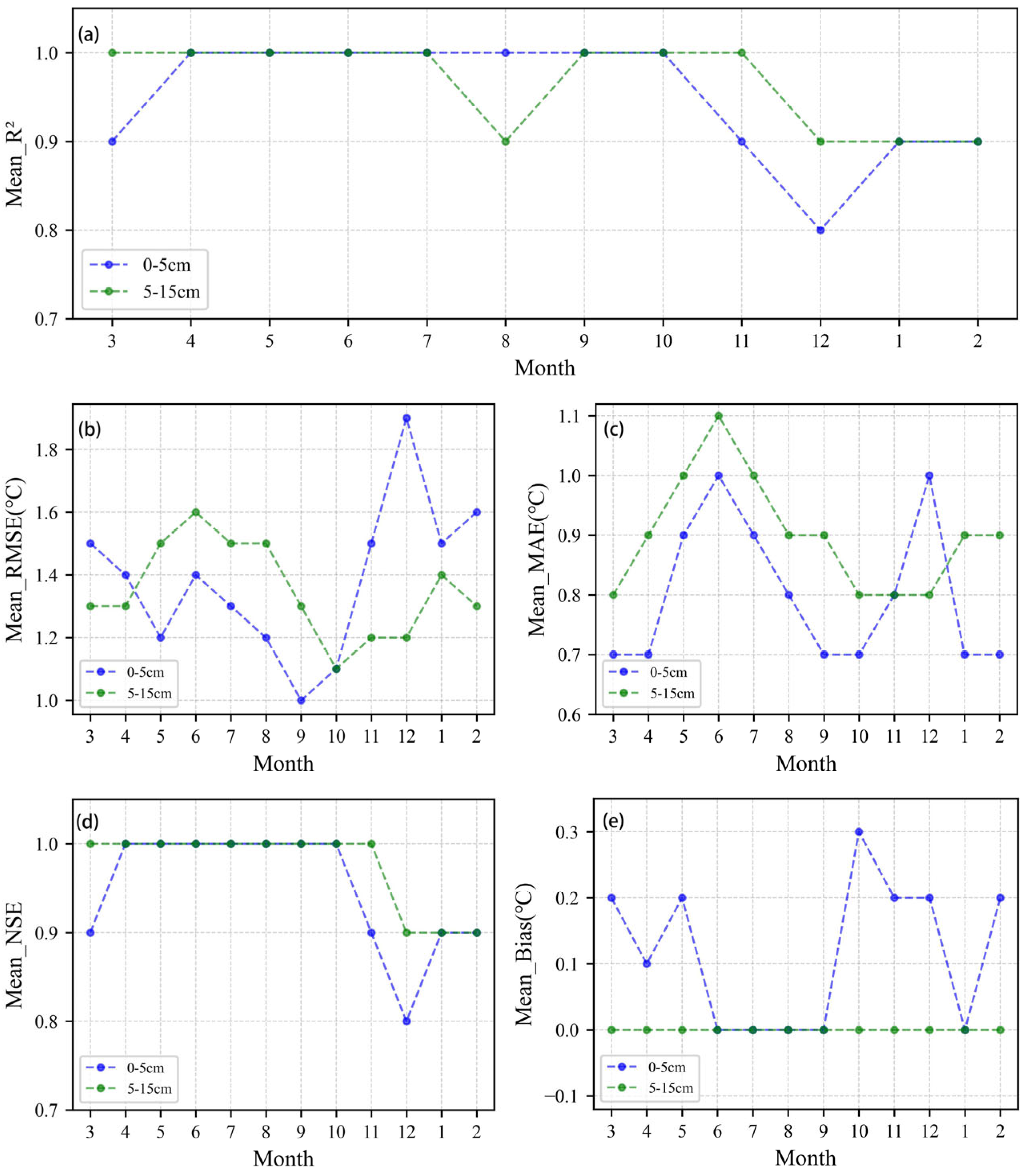
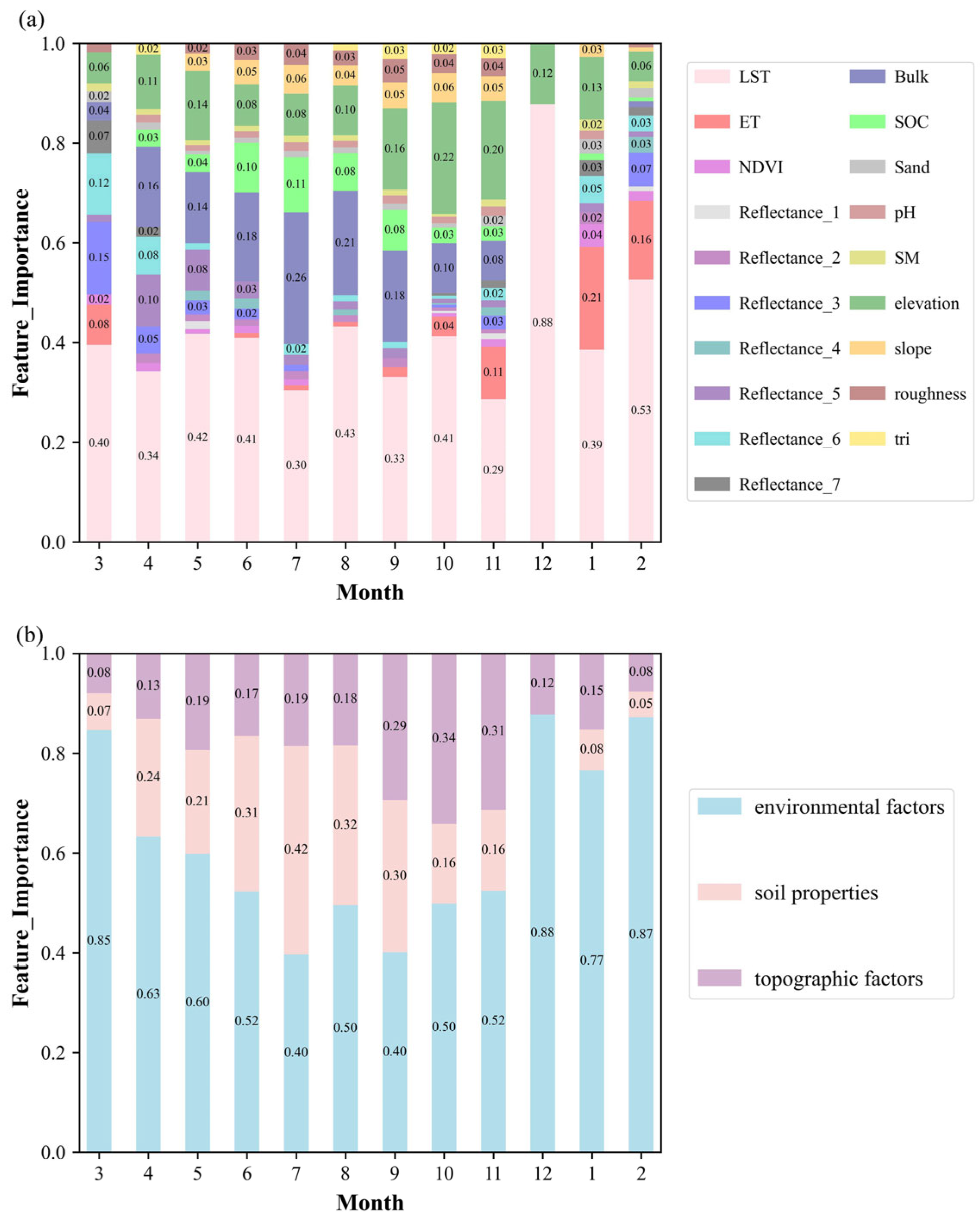


| Attribute | Variable | Variation Characteristics | Temporal Resolution | Spatial Resolution | Source |
|---|---|---|---|---|---|
| Environmental variables | land surface temperature (LST) | dynamically | monthly | 1 km | Zenodo [33] |
| evapotranspiration (ET) | dynamically | monthly | 1 km | Google Earth Engine [34,35] | |
| normalized difference vegetation index (NDVI) | dynamically | monthly | 1 km | Google Earth Engine [36] | |
| radiation (Reflectance_1 Reflectance_2 Reflectance_3 Reflectance_4 Reflectance_5 Reflectance_6 Reflectance_7) | dynamically | monthly | 1 km | Google Earth Engine [37] | |
| Soil properties | soil moisture (SM) | dynamically | monthly | 1 km | Tibetan Plateau Data Center [38] |
| Bulk density | statically | 250 m | SoilGrids [39] | ||
| Sand | statically | 250 m | SoilGrids [39] | ||
| soil organic carbon (SOC) | statically | 250 m | SoilGrids [39] | ||
| soil pH (pH) | statically | 250 m | SoilGrids [39] | ||
| Topographic factors | elevation | statically | 1 km | EarthEnv Topography [40] | |
| slope | statically | 1 km | EarthEnv Topography [40] | ||
| roughness | statically | 1 km | EarthEnv Topography [40] | ||
| terrain ruggedness index (tri) | statically | 1 km | EarthEnv Topography [40] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, G.; Tian, Y.; Liu, X.; Zhang, X.; Li, Z.; An, S. High-Resolution Mapping and Spatiotemporal Dynamics of Cropland Soil Temperature in the Huang-Huai-Hai Plain, China (2003–2020). Remote Sens. 2025, 17, 3765. https://doi.org/10.3390/rs17223765
Shang G, Tian Y, Liu X, Zhang X, Li Z, An S. High-Resolution Mapping and Spatiotemporal Dynamics of Cropland Soil Temperature in the Huang-Huai-Hai Plain, China (2003–2020). Remote Sensing. 2025; 17(22):3765. https://doi.org/10.3390/rs17223765
Chicago/Turabian StyleShang, Guofei, Yiran Tian, Xiangyang Liu, Xia Zhang, Zhe Li, and Shixin An. 2025. "High-Resolution Mapping and Spatiotemporal Dynamics of Cropland Soil Temperature in the Huang-Huai-Hai Plain, China (2003–2020)" Remote Sensing 17, no. 22: 3765. https://doi.org/10.3390/rs17223765
APA StyleShang, G., Tian, Y., Liu, X., Zhang, X., Li, Z., & An, S. (2025). High-Resolution Mapping and Spatiotemporal Dynamics of Cropland Soil Temperature in the Huang-Huai-Hai Plain, China (2003–2020). Remote Sensing, 17(22), 3765. https://doi.org/10.3390/rs17223765





