The Impact on Triple/N-Way Collocation-Based Validation of Remote Sensing Products Due to Non-Ideal Error Statistics

Highlights

This study evaluates the impact of some of the real-world scenarios on the triple/N-way collocation (TC/NWC) method using the proposed numerical simulator. By perturbing statistical parameters and input distributions, it identifies which assumptions critically affect performance and provides empirical corrections to improve real-world applicability in satellite data validation.

What are the main findings?

• TC/NWC remains robust to changes in true signal distribution (e.g., Rayleigh, Weibull, or empirical) and to moderate levels of bias or reference noise, with estimated error variances typically within a few percent of true values.
• Introducing correlated errors between systems and scaling deviations in the reference—cause large biases or algorithmic instability, which the simulator quantitatively characterizes.

What are the implications of the main findings?

• The developed simulator enables users to derive empirical correction factors for bias, scaling, and correlated-error effects, improving accuracy of TC/NWC-based error variance estimation for their remote sensing systems.
• The ideas proposed here enhance the realism and reliability of collocation analysis for operational remote sensing applications.

Abstract

Triple/N-way collocation is a statistical analysis tool used to estimate the individual error variances of simultaneous observations of a physical quantity by three or more distinct systems. The tool is widely used to validate remote sensing data products such as ocean surface winds and soil moisture retrieved by satellite sensors, where simultaneous observations by different systems are common. However, the method relies on several assumptions about the statistical properties of the observations that are not always valid in a real-world scenario. We test the validity of these assumptions using a numerical simulator and assess their impact on error variance estimates. Some of these assumptions, that the errors are uncorrelated between observing systems or the reference system having a non-unity scaling factor, etc., are found to have a large impact on estimates of error variance when violated. The violation of some other assumptions is found to be less impactful. The simulator also provides corrections to the erroneous estimates of error variances that result when the underlying assumptions are violated. Additionally, we present a new, more general version of the collocation analysis tool that accommodates cases where the error variance in an observing system has a dependence on the true signal.

1. Introduction

With the continuous expansion of global observation networks, remotely sensed and reanalysis modeled geophysical variables are becoming increasingly available on a global scale. However, validating these datasets remains a challenge [1]. No single observing system can be assumed to represent the true state of the geophysical variable, making the interpretation of differences between any pair of systems problematic. Traditional validation approaches rely on performance metrics such as the mean difference (bias) and Root Mean Square Difference (RMSD) between an observation under test and a reference observation. This implicitly assumes that the reference provides an accurate representation of the truth. It has been shown that this approach can lead to significant errors in the estimate of the true bias of the observation under test—the so-called pseudo-bias problem [2]. The RMSD statistic will also generally overestimate the true Root Mean Square Error (RMSE) in the observation under test since the RMSD also includes contributions from the error in the reference observation [3]. Triple/N-way collocation analysis offers a means to circumvent these problems. It formulates the problem in terms of a joint probability distribution between the errors in each observing system, makes certain assumptions about the statistical properties of the errors to simplify the problem, and then deconstructs the joint distribution into individual components for each observing system. When three or more collocated products are included, this framework allows their individual biases and RMSEs to be estimated [4].

Triple collocation (TC) analysis is a well-established and widely utilized technique for assessing various geophysical products derived from diverse sensor types and numerical models, over both land and oceans. For example, over land, it has been applied to soil moisture measurements from scatterometers, radiometers, ground-based observations, and GNSS-R sensors [5,6,7,8]; leaf area index retrievals from optical and radiometric sensors [9]; and precipitation estimates from rain gauges, satellite observations, and reanalysis model outputs [10]. Over the oceans, TC has been employed to evaluate ocean vector winds from scatterometers; ocean surface wind speed measurements from GNSS-R, scatterometers, radiometers, altimeters, and models; significant wave height estimates from altimeters, in situ buoys, and models; ocean current assessments from drifters and models; and sea surface temperature retrievals from radiometers and buoy observations, among others [4,11,12,13,14,15]. This list is not exhaustive, and readers may consult the references for further details. Given its widespread application, it is crucial to understand both the strengths and limitations of TC analysis to ensure well-informed scientific conclusions when interpreting its error variance estimations. While TC analysis is a valuable tool for evaluating multiple geophysical properties, it relies on several underlying assumptions about the nature of errors that may not always hold in real-world scenarios. The key assumptions of TC analysis are: (1) The reference system is free of errors; (2) Errors in all products are mutually independent; (3) The statistical properties of errors in a product do not depend on the true signal; and (4) Each product is related to the true signal by a linear transformation. However, these assumptions are often violated in practice. For example, the first assumption does not hold in the case of global ocean surface winds, which exhibit a non-Gaussian distribution. The second assumption is violated by reanalysis models, which are often used as the reference system but are not perfect. The third assumption can be violated when collocated remote sensing systems use retrieval algorithms trained against the same or similar numerical models. The fourth assumption is violated if, for example, a soil moisture product performs worse in dry soil conditions or an ocean wind product performs worse in high wind conditions. The fifth assumption may not hold if a retrieval algorithm does not properly account for non-linearities in the relationship between the engineering measurement and the geophysical variable.

The objective of this study is to evaluate the validity of these assumptions and assess their impact on error variance estimation in TC analysis. Specifically, we investigate three primary ways in which the assumptions may be violated: (1) Varying the statistical distribution of the true signal; (2) Adding noise to the reference system; (3) Introducing partial error correlation between two systems. To achieve this, we develop a numerical simulator that generates synthetic collocated measurements with controlled distributions, noise levels, and error correlations. By applying the TC algorithm to these simulated datasets, we examine how these non-ideal statistical properties, representative of real-world conditions, can influence the error variance estimation. Additionally, we explore an important aspect often overlooked in triple/N-way collocation analysis: the dependence of observation system errors on the true signal. The standard assumption that observation errors are orthogonal to the true state is frequently violated, particularly in ocean wind measurements. For instance, scatterometers operate based on backscattering principles, where an increase in ocean surface wind speed enhances backscattered power, thereby strengthening the received signal. In contrast, GNSS-R sensors rely on bistatic scattering, meaning that higher wind speeds reduce forward-scattered power, leading to a weaker received signal. In both cases, wind speed retrieval errors are inherently dependent on wind speed itself. To account for such dependencies, we introduce a simple linear model that relates observation errors to the true signal. Furthermore, we derive an analytical solution that corrects error variance estimates in scenarios where observation errors exhibit such signal dependence.

The remainder of this paper is structured as follows. In the next section, we review the TC equations based on Stoffelen’s [4] formulation, explicitly identifying where key assumptions are applied and how error variance estimation depends on these assumptions. Section 3 presents the application of the TC algorithm to real-world triplets derived from four global ocean surface wind products, including a GNSS-R instrument, a scatterometer, a radiometer, and a numerical weather model. Using these datasets, we demonstrate how real-world geophysical variables often exhibit non-Gaussian distributions and cross-correlated errors. In subsequent sections, we evaluate correction factors for error variance estimates obtained through TC, leveraging the simulator developed in this study. In Section 4, we introduce the simulator, which generates synthetic triplet datasets mimicking real-world scenarios. We use this tool to systematically assess how violations of TC assumptions affect error variance estimates. Section 5 presents an analytical solution to determine the minimum number of observation systems required to account for dependencies between an observation system’s error variance and the true signal. In Section 6, we discuss the key findings of this study, emphasizing their implications for improving error variance estimation in triple/N-way collocation andonclude by summarizing the major takeaways and outlining directions for future research in remote sensing data product validation.

2. Assumptions in Triple/N-Way Collocation

We begin by briefly reviewing the derivation of the original TC algorithm as formulated by Stoffelen in [2,4]. The primary objective of this review is to identify the underlying assumptions and examine their implications for real-world datasets. Stoffelen proposes a simple linear error model, which is expressed as

$$x_i=a_i\left(t+{\epsilon }_i\right)+b_i$$

(1)

where x_i is the measurement by the ith observing system (i = 1…n), $t$ is the true signal observed by the different systems, $a_i$ and $b_i$ are the scaling and bias terms for the ith observing system, and ${\epsilon }_i$ is the measurement error of the ith observing system (assumed to be a random error with symmetric variance ${\sigma }_i^2$).

The first moment, or expected value, of Equation (1) is given by

$$M_i=<x_i>=a_i<t>+b_i$$

(2)

The first observing system is the calibration reference. In this case, $a_1$ and $b_1$ are assumed to be 1 and 0, respectively, or at least assumed to be well calibrated. However, in remote sensing datasets, especially airborne and space-borne, model winds are empirical and do not have absolute calibration. Therefore this is one of the sections to be tested in this work. The purpose of this assumption is to derive the first moment of Equation (1) as a function of the true signal and eliminate the other terms in the expression. The first moment of Equation (1) for i = 1 then yields $M_1= <t>$. Now the bias terms can be replaced as

$$b_i=M_i-a_i{M}_1.$$

(3)

Next, the second moments can be represented as $M_{ij}= <x_i{x}_j>$, which can be expanded as

$$<x_i{x}_j>=<\left(a_i\left(t+{\epsilon }_i\right)+b_i\right)\left(a_j\left(t+{\epsilon }_j\right)+b_j\right)>$$

(4)

To simplify the second moment equations, a key assumption made here is that the random errors in all observing systems are independent of the true signal. Mathematically, this assumption can be expressed as $<t{\epsilon }_i>=<t><{\epsilon }_i>=0$. However, in many remote sensing systems this assumption is not valid since the sensitivity and noise characteristics of the estimate of the geophysical variable are dependent on the true signal. For example, global ocean-surface wind speed measurements obtained from scatterometers, radiometers, and GNSS-R systems exhibit signal sensitivity that is a function of wind speed. This dependency arises directly from the underlying physical principles governing their operation. 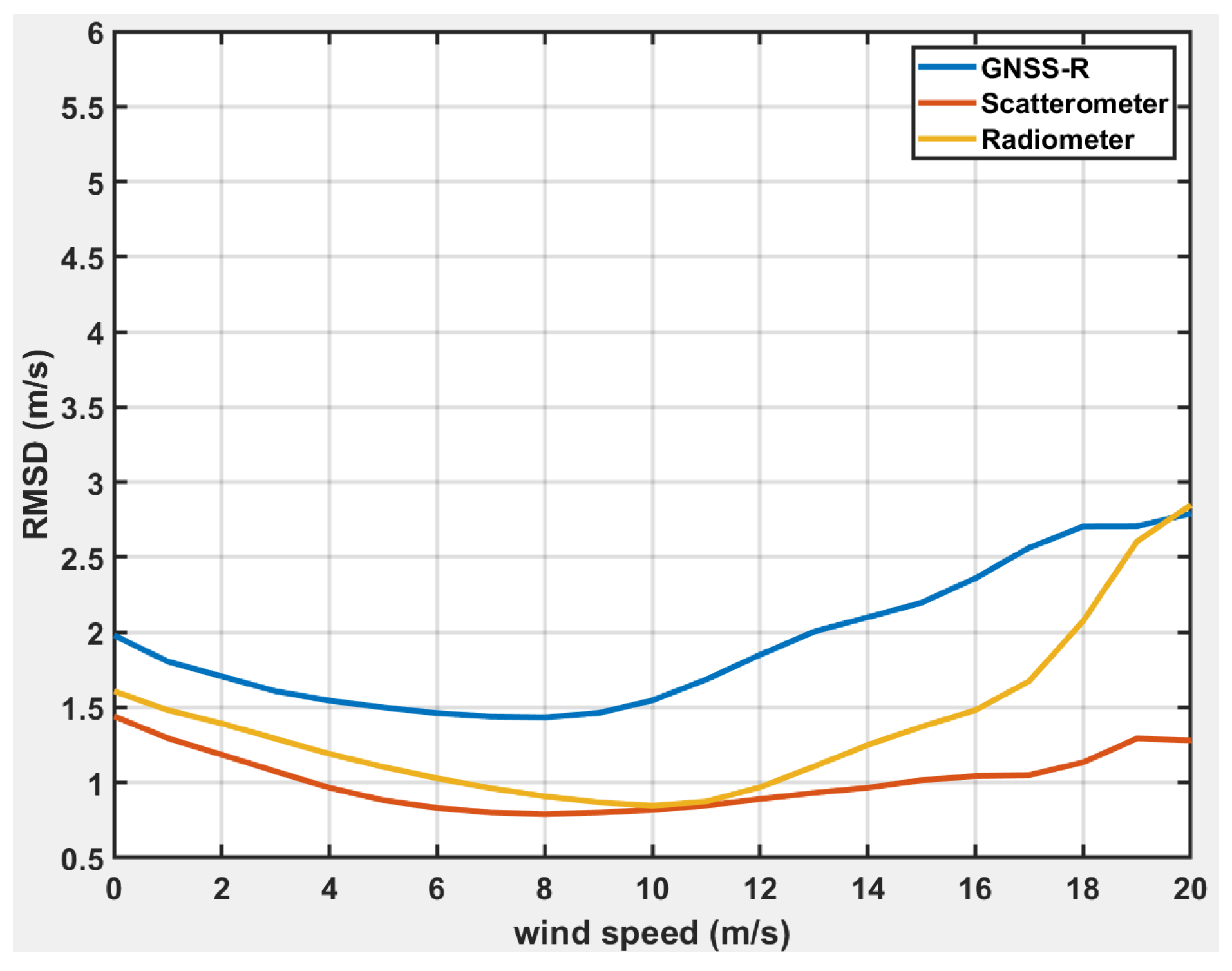Figure 1 illustrates this effect by showing the Root Mean Square Difference (RMSD) of a GNSS-R sensor (Cyclone Global Navigation Satellite System, CYGNSS), a scatterometer (The Advanced Scatterometer, ASCAT which is onboard the MetOp-B/C satellites launched by the European Space Agency), and a radiometer (GPM Microwave Imager, GMI) evaluated against ERA-5 reanalysis winds. The RMSD values exhibit a clear dependence on wind speed (stronger for CYGNSS, weaker for ASCAT and GMI, but in all cases not independent of the true wind speed), demonstrating that the RMSD is dependent on the true signal.

The second moment term in Equation (4) can then be simplified as

$$M_{ij}=a_i{a}_j\left(<t^2>-M_1^2+<{\epsilon }_i{\epsilon }_j>\right)+M_i{M}_j$$

(5)

The expression for covariance can be written as

$$C_{ij}=M_{ij}-M_i{M}_j.$$

(6)

If a new term, T, is used to denote the true signal parameter and the error correlation term is represented by $e_{ij}$ then the covariance equation can be rewritten as

$$C_{ij}=a_i{a}_j(T+e_{ij})$$

(7)

Equations (3) and (7) together define the N-way collocation system of equations.

In the case of TC (n = 3), one additional assumption is made that the errors in the different systems are uncorrelated, i.e., $<{\epsilon }_i{\epsilon }_j>$ = 0. This assumption reduces the collocation system of equations to a closed form with 3 equations and 3 unknowns. However, this assumption may not be valid in practice, where different systems can exhibit correlated errors for various reasons. For instance, remote sensing systems may rely on similar retrieval algorithms, or their model functions may be trained using the same reference wind datasets, as is often the case with satellite sensors. Similarly, numerical models frequently employ similar physical parameterization, leading to shared error structures. Additionally, satellite observations are sometimes assimilated into numerical models, and conversely, model outputs may be used to calibrate satellite retrievals, further increasing the potential for correlated errors. A well-calibrated reference should ideally represent the true geophysical variable and therefore, when used for retrieval models of other systems, should not introduce a correlation in the errors. However, in real-world systems the uncertainties in the reference system do introduce correlation in the errors of the other systems that use it as a reference.

In summary, we have identified a few important assumptions in TC analysis that are important to consider in real-world datasets. The objective of this study is to assess the impact of these assumptions on error variance estimation and propose corrections that enable the application of TC analysis under real-world conditions. The key ideas that are tested in this work are:

1.

The need for an ideal/well-calibrated reference system in the collocated dataset

2.

What if the random errors are correlated with each other.

3.

The probability distribution of the true signal.

4.

The dependence of mean observation error on the true signal.

By systematically evaluating these assumptions, this study aims to improve the robustness and applicability of TC analysis for geophysical data validation.

3. Triple Collocation Analysis of Global Ocean Winds Datasets

For this study, we utilized four different datasets of global ocean surface wind measurements collected over 6.5 years from fall 2018 to the end of 2024. The collocated datasets include:

• GNSS-R -derived wind speed from CYGNSS satellites.
• Scatterometer-derived wind speed from ASCAT.
• Radiometer-derived wind speed from the GMI instrument onboard the Global Precipitation Measurement (GPM) mission.
• Numerical model estimates of wind speed from ERA-5 reanalysis.

These datasets provide a diverse representation of ocean surface wind measurements, incorporating different sensing principles and retrieval methodologies, which allows for a comprehensive evaluation of error variance estimation using TC analysis. The CYGNSS data product used for this analysis is the CYGNSS SDR v3.2 L2 wind speed. ASCAT B and C that are used here are the Level 2, 25 km ocean surface wind vector product from MetOp-B/C. GMI datasets are produced by the Remote Sensing Systems (REMSS) using data from the Global Precipitation Measurement (GPM) Microwave Imager (GMI), data product version 8.2. ERA-5 reanalysis winds from ECMWF, produced as a part of the Copernicus Climate Change Service (C3S), are used as the numerical model estimate. The temporal and spatial collocation criterion used for this 4-way matchup are ±30 min and ±25 km, respectively. The matchups are quality filtered and a specific GNSS-R parameter referred to as the RCG [16] is set to a value of 50 or higher to obtain the highest quality matchups with GNSS-R. This dataset contains about 2 million globally collocated measurements for these above-mentioned 4 global ocean wind speed estimates, available over a wind speed range of 0–25 m/s. Despite using stringent quality filters, the 2 million samples in this matchup dataset are sufficient to perform robust statistical analysis.

In the case of global ocean winds under “non-extreme weather” conditions, ERA-5 is considered to be a consistent and robust dataset and is therefore often assumed as a reference. Therefore, in this study we consider the ERA-5 reanalysis winds as our reference. Figure 2 shows density scatter plots comparing the different wind speeds with the reference ERA-5 winds and with the reference as the scatterometer—ASCAT winds. It is important to note here that the ERA-5 reanalysis winds assimilate GMI and ASCAT winds and the CYGNSS Fully Developed Sea (FDS) data product in-turn uses ERA-5 to develop its Geophysical Model Function (GMF). It is common for many of the remote sensing and model reanalysis datasets to be used to calibrate one another, which makes this study particularly important for accurately evaluating the individual errors of the different datasets despite real-world correlations. Figure 3 shows the distribution of winds in this collocated dataset.

To estimate the correlation between errors in estimates of the wind speed made by different satellite sensors, we estimate the error as the difference between each satellite measurement and the reference numerical model. We then evaluate the correlation between the errors for different sensor pairs. This approach provides insights into the degree of error dependence among satellite observations, with the objective to assess the validity of the common assumption made during collocation analysis that observational errors are uncorrelated. Figure 4 is a density scatterplot showing the correlation between ERA-5 differences for different pairs of sensors on the top row and ASCAT differences in the bottom row and Figure 5 shows the distribution of errors for the different systems.

Figure 4 shows how these datasets are correlated. One of the reasons we use this matchup dataset is to understand how these correlations affect the estimation of error variances using Triple Collocation. These plots reveal a noteworthy observation regarding the error correlation for different pairs of systems. Despite operating on entirely different physical principles and being deployed on separate satellite platforms, we observe a non-negligible correlation of errors across all systems. This correlation varies as we change the reference system from ERA5 to ASCAT. It is known from previous studies that the accuracy of ASCAT is higher than ERA-5 and that ERA5 reanalysis assimilates ASCAT to estimate winds. In particular, there is a notably strong error correlation between ASCAT and GMI measurements when ERA-5 is used as a reference versus when ASCAT is used as a reference. The cause of the observed correlation differences may be two-fold: (1) due to ERA-5 assimilating ASCAT and GMI into its model; and (2) the finer spatial resolutions of the satellites having more correlation with the coarser model winds. However, spatial representation error is not addressed in this work.

This finding suggests the potential for underlying root causes of the correlation, such as the possibility that the satellites’ empirical retrieval algorithms are trained using the same (or at least highly correlated) reference datasets. Investigating the precise cause or causes of these correlations is beyond the scope of this study. Nevertheless, our observations reinforce the necessity of studies like this one, which assess how the error variance estimated using TC is affected by such inter-sensor error correlations.

To establish a baseline for error variance estimation, we apply the TC algorithm to different triplets selected from our quadruple-collocated dataset. One principal estimate made by the TC algorithm is the absolute error variance, which represents the error statistics of the individual systems. We have computed the standard deviation of the error from the error variance estimated by the TC algorithm.

Table 1. Error standard deviation of the different datasets based on triple collocation.

Triplet	ERA-5	FDS	ASCAT	GMI
ERA-5, FDS, ASCAT	0.75	1.44	0.43
ERA-5, FDS, GMI	0.89	1.32		0.45
ASCAT, FDS, GMI		1.40	0.58	0.34
ERA-5, ASCAT, GMI	0.81		0.30	0.59
Mean absolute error standard dev	0.82	1.39	0.44	0.46

presents the absolute error standard deviation estimates for each dataset, as computed from the respective triplets using TC analysis. These estimates serve as a reference for evaluating the impact on error variance estimation of the violation of assumed error independence.

4. Numerical Simulator and Results

We developed a simulation framework to evaluate the robustness of the TC algorithm given various non-ideal statistical properties. The simulator first generates synthetic ocean surface wind speed triplets based on user-defined statistical characteristics. The following properties can be specified: the true distribution; the error variances to be introduced in the simulated observation probability density functions (PDFs); the functional relationships between true and observed values (e.g., linear or non-linear); and the degree of error correlation among the different observation systems.

This approach enables the generation of synthetic datasets that emulate complex real-world error characteristics. The simulated observations are then processed using the triple (or N-way) collocation algorithm to estimate the absolute error variances of each input dataset. By systematically varying the input conditions, we assess the ability of TC to recover true error statistics even when its underlying assumptions are violated. A block diagram of the simulator methodology is depicted in Figure 6.

These simulated observations are processed by the triple/N-way collocation algorithm to estimate their absolute error variance. Here, we manipulate various combinations of input variations to assess how accurately the TC algorithm estimates the absolute error variance/standard deviations of individual datasets, even when many of its underlying assumptions are violated. Note that standard deviation represents a physical unit of wind speed (m/s), this is the reason we represent this parameter wherever we can to show how much physical variation occurs. The performance metric used in this study to assess the TC estimation is the relative error, defined as the ratio of the difference between the estimated and actual absolute error variance, divided by the actual absolute error variance. Our primary objective is to violate different underlying assumptions in TC analysis and evaluate how well the algorithm estimates the absolute error variance under these complex, real-world scenarios. The following block diagram summarizes the simulator’s approach.

The TC method, originally proposed by Ad Stoffelen, is based on a linear error model as described in Equation (1). Accordingly, the primary input parameters to our simulator are the three components of the model: the scaling factor $a$, the additive bias $b$, and the random error term $\epsilon$. Additional user-defined inputs include the nature of the true wind speed distribution (e.g., Rayleigh, Weibull, or other) and the pairwise error correlations among the three observation systems.

Using these inputs, the simulator generates four datasets—one representing the true wind speed and three representing independent observation systems—each comprising 100,000 samples. These datasets are constructed to satisfy the specified statistical characteristics.

For each set of input parameters, the TC algorithm is executed 1000 times and the results averaged. This reduces standard errors in the estimates of relevant statistics. The mean relative error is computed and recorded for each configuration. The relative error is defined as:

$$R.E \left(\%\right)={\displaystyle \frac{{\epsilon }_{est }-{ \epsilon }_{true}}{{\epsilon }_{true}}}\ast 100$$

(8)

To demonstrate the functionality of the simulator, we present two example input configurations. The true wind field is assumed to follow a distribution similar to the distribution of real observation of winds from the real-world matchup dataset. The first observation system—treated as the reference—is modeled as ideal, with a scaling factor of 1, a bias of 0 m/s, and zero error variance. The second observation system is configured with a scaling factor of 0.8, an additive bias of 2 m/s, and an error standard deviation of 5 m/s. The third observation system is defined with a scaling factor of 1.1, a bias of 4 m/s, and an error standard deviation of 2 m/s. The correlation between errors in systems 2 and 3 are assumed to be either uncorrelated or correlated with a partial correlation of 10%. It should be noted that the values selected here are for illustrative purposes only and are, in general, greater than real world scenarios. When this parameterization is processed through the simulator, the resulting synthetic datasets are fed to the TC algorithm, and the estimated absolute error variances and relative errors for each system are computed. The results of this example are summarized in

Table 2. Example case to show the Numerical simulator operation.

System	Scaling Factor	Bias (m/s)	True Error Std. Dev. (m/s)	Estimated Error Std. Dev. with No Error Correlation (m/s)	Estimated Error Std. Dev. with 10% Error Correlation (m/s)
System 1 (Ref.)	1	0	0	0.00	0.94
System 2	0.8	2	5	5.00	4.37
System 3	1.1	4	2	2.00	1.54

, illustrating the simulator’s ability to reproduce and assess known error statistics under controlled, non-ideal conditions.

From the results in Table 2, it is evident that the TC algorithm works properly when errors are uncorrelated but exhibits significant estimation error when error correlation is present. This deviation arises from the non-ideal, real-world conditions introduced through the simulator. The primary objective of this study is to systematically evaluate the performance of the TC algorithm in estimating absolute error variances when the underlying assumptions are relaxed to reflect practical observational scenarios.

In the following subsections, we present a detailed analysis of how key input parameters—such as scaling factors, biases, error variances, distribution shapes, and inter-sensor error correlations—influence the accuracy and robustness of the TC method.

4.1. Impact of Non Ideal Reference System Characteristics on Estimation

As discussed in Section 2, one of the key assumptions used to simplify the first-order moment equation (Equation (2)) is the existence of an ideal reference observation system—one that exhibits zero bias, and unity scaling factor. However, such ideal conditions are rarely met in practical scenarios, where no observation system can perfectly capture the true state. In this subsection, we investigate how deviations from this ideal reference condition impact the performance of the TC algorithm. Specifically, we examine the sensitivity of the absolute error variance estimation to variations in the reference system’s scaling factor, additive bias, and noise level.

To inform the input parameters for this analysis, we estimate representative values for the scaling factor and bias using the available matchup dataset. Specifically, we treat ERA5 as a quasi-ideal reference system and perform linear regressions on scatter plots between ERA5 and each of the other observation systems: FDS, ASCAT, and GMI. These linear fits, shown in Figure 7, yield empirical estimates for the scaling factor and bias for each system pair. The derived values are then used as input parameters in the simulator to assess how the performance of the TC algorithm varies with respect to the scaling factor, a.

Table 3. Input parameterization for scaling factor, bias and noise dependence analysis.

Observation Systems	Input Parameterization For Ref. Scaling Factor Dependence [a, b, Std. Dev.]	Input Parameterization For Ref. Bias Dependence [a, b, Std. Dev.]	Input Parameterization For Ref. Noise Dependence [a, b, Std. Dev.]
System 1 (Ref)	[a, 0, 0]	[1, b, 0]	[1, 0, n]
System 2 (FDS)	[0.83, 1.57, 1.39]	[0.83, 1.57, 1.39]	[0.83, 1.57, 1.39]
System 3 (ASCAT)	[0.95, 0.58, 0.44]	[0.95, 0.58, 0.44]	[0.95, 0.58, 0.44]

summarizes the parameter configurations used for this sensitivity analysis.

As shown in Table 3, System 1 is configured to evaluate the impact of varying the scaling factor, denoted as $a$, while keeping both the bias and noise level fixed at zero. The scaling factor is varied systematically from 0.8 to 1.2 in increments of 0.05 to assess its influence on TC performance.

System 2 incorporates information from FDS wind data. Its scaling factor and bias are obtained from the linear regression fit against ERA5, as shown in Figure 7a. The error variance (noise level) for FDS is derived as the mean value from the TC results presented earlier in Table 1, column 3.

System 3 utilizes the ASCAT wind measurements. Similarly to System 2, the scaling factor and bias for ASCAT are determined from the linear fit to ERA5 shown in Figure 7b, and the associated noise level is extracted from the corresponding column in Table 1, column 4. Figure 8 shows the performance of the TC algorithm as a function of reference system scaling factor.

Figure 8 represents how the relative error varies as a function of the scaling factor–a. If we look at the linear error model used in TC, the error variance ($\epsilon$) and calibration scaling factor (a) are independent terms as seen from Equation1. This is the reason the true error variance in the denominator of Equation (8) remains independent of the change in scaling factor. However, in the estimation of error variance by the TC algorithm, an assumption is made that the scaling factor of the reference system is 1 in order to have a closed set of equations to solve. This assumption of unity scaling factor is applied to the covariance equation (Equation (7)). When we violate this assumption and introduce a non-unity reference system scaling factor, we then notice the systematic linear variation in the estimated error variance in the numerator of Equation (8). This results in an overall linear increase in the relative error with increasing reference system scaling factor, which is depicted in Figure 8. Interestingly, the introduction of a reference system scaling factor impacts all of the individual estimations identically which is seen from the overlap of the three lines in the figure. Figure 8 also illustrates the sensitivity of the TC algorithm to variations in the scaling factor of the reference system. The results clearly indicate that the relative error in the estimated absolute error variance exhibits a near-linear dependence on the scaling factor. Specifically, a deviation of ±20% from the ideal scaling factor of unity (i.e., values of 0.8 or 1.2) leads to approximately ±20% relative error in the estimation. This finding underscores a critical limitation of the TC method: its reliance on an accurate reference system. In practical applications, the absolute relationship between the reference and the true state is often unknown or difficult to characterize precisely. Consequently, diagnostic plots such as Figure 8 can serve as calibration tools to account for scaling errors in the reference system and improve the robustness of TC–based error variance estimates.

Next, we evaluate the impact of non-zero bias and error variance in the reference observation system. Following a methodology similar to that used for analyzing the effect of the scaling factor, we define two new variable parameters: reference bias b, varied from 0 to 10 m/s, and reference noise level n, varied from 0 to 5 m/s. Systems 2 and 3 retain the same parameter settings as previously described.

For each configuration, we assess the relative error in the estimated error variances of all systems using the TC algorithm. The results of these experiments are presented in Figure 9, where the relative error is plotted as a function of both reference bias and noise level. The corresponding input parameterizations used for these tests are summarized in Table 3. The selected ranges for the scaling factor, bias, and noise were chosen to represent realistic variability observed in operational wind datasets. Analysis of the results reveals that, unlike the scaling factor, the reference bias and noise level have negligible influence on the accuracy of TC–based error variance estimates. This finding highlights a key insight: while precise knowledge of the scaling relationship between the reference system and the true state is essential, uncertainties in the reference system’s bias or noise characteristics do not substantially degrade the estimation performance. This has important practical implications. In many real-world applications, the noise characteristics of a reference system are poorly understood or not quantified. However, scaling factors can often be reliably determined through inter-comparisons with multiple measurement sources. Thus, even reference systems with significant bias or noise can still be used effectively in TC, provided the scaling relationship is well-characterized.

4.2. Impact of Error Correlation Between the Systems on Estimation

Another critical assumption in the TC framework is the mutual independence of error terms across the observation systems. As described in Section 2, Equation (7), this assumption enables the system of covariance equations to be reduced to a closed-form solution comprising three equations and three unknowns.

These findings emphasize the importance of systematically evaluating how such inter-sensor error correlations impact the performance of the TC algorithm. To assess the impact of inter-sensor error correlations on the performance of the TC algorithm, we conduct a step-by-step analysis through a series of controlled case studies using the simulator. Each case incrementally introduces different correlation structures while keeping other parameters fixed, allowing us to isolate the effects of error correlation on absolute error variance estimation. The following is the step-by-step procedure as to how correlation is introduced between the noise in different systems:

• Step1: Provide a 3 × 3 diagonal matrix with standard deviation required for each system (D).
• Step2: Provide a correlation matrix with the required correlation between the different systems (rho).
• Step3: Provide the number of samples needed (N). Covariance (Cov) = D × rho × D. Generate an N × 3 matrix of random vectors from a multivariate normal distribution. Each column in this N × 3 matrix is the random noise (ei) of the individual systems in the triplet that satisfies the standard deviation requirement as well as the correlation requirement with the other systems’ random noise.
• Step4: xi = (ai(t + ei)) + bi. Here xi is the simulated wind measurement generated from the system calibration parameters (ai, bi and ei) and a simulated true winds ‘t’. The true winds can be derived from any desired distribution (gaussian, Rayleigh, Weibull or custom distribution).

Xi ‘s form the simulated wind measurements that satisfy the statistical requirements of the desired calibration parameters. Following are different case studies to analyze the impact of various combinations of these correlations.

• Case Study 1: We assume an ideal reference system with zero bias, unity scaling factor, and non-zero random noise. The other two systems also have unity scaling and zero bias and both contain non-zero error variances to be estimated. In this scenario, only one of the two systems (System 2) is configured to have a correlated error with the reference system.
• Case Study 2: The setup remains the same as in Case Study 1, but both non-reference systems now have error components that are correlated with each other.
• Case Study 3: We extend the previous configuration by introducing pairwise error correlations between all three systems—thereby creating a fully interconnected (and more realistic) error structure.

These case studies are designed to quantify the degradation in TC accuracy as error correlations increase, and to provide insight into the algorithm’s limitations under realistic, non-ideal observational conditions. The mean error standard deviation of FDS from Table 1 is chosen for System 2 and that of ASCAT for System 3.

Figure 10 illustrates the performance of the TC algorithm under two distinct scenarios involving inter-sensor error correlations:

(a)

error correlation between the reference system and one of the other observation systems, and

(b)

error correlation between the two non-reference systems.

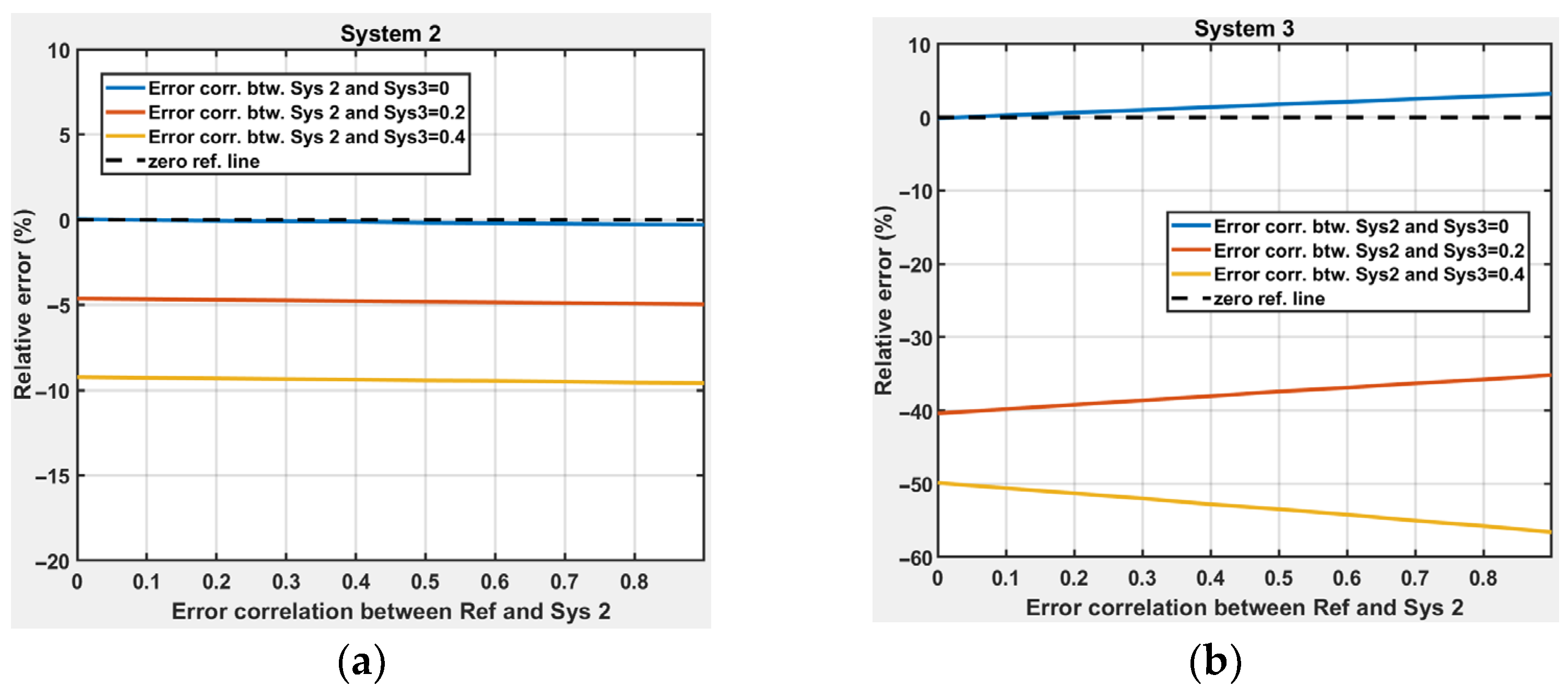
From Figure 10a, two key insights emerge. First, the presence of error correlation between the reference system and another observation system has only a modest impact on the algorithm’s performance. Even at 100% correlation, the induced relative error in the estimated variance remains below 5%. Second, when System 2 is correlated with the reference system, the estimation error in System 3 is higher than that of System 2 itself (i.e., the TC algorithm overestimates the error variance). This highlights a non-local propagation effect in the estimation error due to the correlation structure. Another factor to keep in mind is when systems 1 and 2 are higher resolution than system 3, or, indeed, have ancillary correlation. In this case, the TC method takes the correlated variance of systems 1 and 2 as the truth. Since system 3 lacks the resolution or the correlation, the TC method addresses the missing variance by adding estimated error variance to system 3.

Case Study 2, corresponding to Figure 10b, reveals more severe limitations. As the error correlation between the two non-reference systems increases, the performance of the TC algorithm degrades sharply. Notably, the TC algorithm can be seen to underestimate the true error variance. Beyond a critical threshold (approximately 30% correlation), the covariance matrix becomes ill-conditioned, causing the matrix inversion step in the TC solution to break down. This is evident in the rapidly increasing relative error for System 3 as correlation levels rise.

These results highlight a fundamental constraint in the application of TC: the algorithm assumes mutually uncorrelated errors between systems, and violation of this assumption—especially between the two non-reference systems—can severely compromise estimation accuracy or render the method unusable. Therefore, careful assessment of inter-sensor error correlation is essential before applying TC-based error variance estimation in practical settings.

In the next case study, we generate a family of curves to visualize the impact of various combinations of pairwise error correlations on the performance of the TC algorithm as shown in Figure 11. To simplify the analysis and reduce dimensionality, we fix the error correlation between the reference system and System 3 at 10%. We then vary the remaining pairwise correlations—specifically, the correlation between the reference and System 2, and between Systems 2 and 3—across a defined range (0–90%). This approach allows us to generate a set of performance curves that illustrate how combinations of error correlations influence the relative error in estimated error variances. The resulting visualization helps identify safe operational zones for applying TC and highlights combinations of correlations that lead to unstable or biased estimates.

The results from this experiment further confirm that error correlation between System 2 and System 3 exerts a substantial influence on the accuracy of error variance estimation using the TC algorithm. Among all pairwise correlations examined, this particular correlation consistently demonstrated the strongest degradation in performance.

These findings underscore the critical role that inter-sensor error correlation plays in determining the reliability of TC estimates. In particular, our results suggest that the algorithm’s assumptions begin to break down when the correlation between System 2 and System 3 exceeds approximately 50%. Beyond this threshold, the estimation becomes increasingly unstable and inaccurate, indicating that TC should not be applied in such scenarios without correction or adjustment mechanisms.

4.3. Impact of Nature of True Distribution on Estimation

Thus far, we have examined how sensor-specific calibration parameters—namely the scaling factor a, bias b, and random noise—as well as inter-sensor error correlations influence the accuracy of TC–based error variance estimation. In this subsection, we extend the analysis further by investigating the influence of the underlying true state distribution on algorithm performance. Ocean surface wind speeds are well-documented to follow distributions such as Rayleigh or Weibull, typically peaking around 7 m/s in global climatologies. To evaluate the robustness of the TC algorithm under these conditions, we systematically vary the assumed distribution of the true wind field and examine how it affects the accuracy of error variance estimates.

To evaluate the impact of the true state distribution on TC performance, we design an experiment that compares five distinct distribution types: Gaussian, Uniform, Rayleigh, Weibull, and an observation-based empirical distribution. All other calibration parameters are held at ideal values—unity scaling factor, zero bias, and zero inter-sensor error correlations. The mean error standard deviations for the three observation systems are set using the values previously obtained from ERA5, FDS, and ASCAT, as reported in Table 1. The goal of this experiment is to isolate the effect of ground truth distribution on the accuracy of absolute error variance estimates, under otherwise idealized conditions. Of particular interest is the inclusion of an observation-based distribution, which is constructed from the full match-up dataset used in this study. While it is commonly assumed that ocean surface winds follow Rayleigh or Weibull distributions, our extensive multi-platform observational dataset reveals a different empirical distribution. As illustrated in Figure 12, wind speed PDFs from four independent global wind observations exhibit strong mutual agreement, yet diverge significantly from the canonical Rayleigh and Weibull models. Although the causes behind this deviation are beyond the scope of the current study, we highlight this discrepancy as an important observation. We encourage further research to revisit and refine the statistical characterization of global ocean surface wind distributions using long-term, multi-sensor datasets. Therefore, throughout this study we have used an empirical distribution derived from these various observations. The results of this analysis are summarized in

Table 4. Performance assessment with varying true distributions.

Type of Distribution	System 1 (True Error Std. Dev. = 0.82 m/s)	System 2 (True Error Std. Dev. = 1.39 m/s)	System 3 (True Error Std. Dev. = 0.44 m/s)
Gaussian	0.8200	1.3900	0.4401
Uniform	0.8200	1.3899	0.4401
Rayleigh	0.8201	1.3899	0.4397
Weibull	0.8197	1.3900	0.4403
Empirical	0.8199	1.3900	0.4402

.

The results in Table 4 highlight the robustness of the TC algorithm. Despite substantial variation in the underlying true distribution—from Gaussian to Uniform to observation-based—the algorithm consistently yields highly accurate error variance estimates. This demonstrates a key strength of the method: its robustness across a broad range of distributions.

This robustness is particularly valuable in geophysical applications, where the assumption of Gaussianity is often violated. The findings suggest that TC can be confidently applied to a wide variety of geophysical variables, provided their distributions are unimodal. In this study, we limit our analysis to unimodal distributions, reflecting our focus on global ocean surface wind speeds, which are known to follow such distributions.

5. Analytical Solution for Dependence of Observation Error on True Signal

Up to this point, we have evaluated the importance of various foundational assumptions related to sensor calibration and the statistical characteristics of the true state. These investigations reaffirm that triple and N-way collocation are powerful and robust techniques for estimating the absolute error variances of individual observation systems. When appropriately corrected for scaling errors and inter-sensor error correlations, no alternative method currently offers comparable reliability and versatility in quantifying system-level uncertainties.

To further enhance the capabilities of this framework, we now introduce a critical yet often overlooked consideration: the dependence of sensor error variance on the magnitude of the geophysical variable being measured. Most remote sensing instruments exhibit variable sensitivity across different ranges of the target variable due to their underlying physical principles. Consequently, assuming that error variance is constant across the entire domain of the geophysical signal—as is typically done in conventional TC (see Section 2, Equation (4))—can lead to biased or incomplete characterizations of measurement uncertainty.

For example, radiometers estimate surface wind speed based on brightness temperature, which is influenced by fractional foam coverage. Sensitivity is higher at wind speeds above ~7 m/s, where foam coverage and, consequently, brightness temperature increase more rapidly. At lower wind speeds, the slope of the geophysical model function (GMF) flattens, resulting in reduced sensitivity and increased measurement noise. Scatterometers have a more uniform sensitivity to wind speed changes and tend to perform well except at the highest levels, e.g., in tropical cyclones. GNSS reflectometry (GNSS-R) systems operate on the principle of forward scattering by wind-driven surface roughness. These systems exhibit the opposite behavior: lower wind speeds produce stronger forward-scattered signals and higher sensitivity, while higher wind speeds flatten the GMF slope, reducing sensitivity and increasing noise.

These examples collectively underscore that the error variance of remote sensing systems may not be constant but can depend on the underlying geophysical conditions. Ignoring this dependency may limit the applicability of TC in operational contexts where measurement sensitivity is non-uniform.

To address this, we extend the conventional N-way collocation formulation by explicitly accounting for the dependence of sensor error variance on the true geophysical signal. We re-derive the relevant equations to incorporate this functional relationship, thereby laying the groundwork for a more physically realistic and generalizable validation framework.

The second moment described in Equation (4) from Section 2 can be expanded further as:

$$\begin{array}{c}<x_i{x}_j> = <a_i{a}_j{t}^2+a_i{a}_{j}t{\epsilon }_j+a_i{b}_{j}t+a_i{a}_{j}t{\epsilon }_i+a_i{a}_j{\epsilon }_i{\epsilon }_j+a_i{b}_j{\epsilon }_i+a_j{b}_{i}t+a_j{b}_i{\epsilon }_j+b_i{b}_j>\\ =a_i{a}_j<t^2>+a_i{a}_j<t{\epsilon }_j>+a_i{b}_j<t>+a_i{a}_j<t{\epsilon }_i>+a_i{a}_j {<\epsilon }_i{\epsilon }_j>+{\mathit{a}}_{\mathit{i}}{\mathit{b}}_{\mathit{j}} {<\mathit{\epsilon }}_{\mathit{i}}>+a_j{b}_i<t>+{\mathit{a}}_{\mathit{j}}{\mathit{b}}_{\mathit{i}}<{\mathit{\epsilon }}_{\mathit{j}}>+<b_i{b}_j>\end{array}$$

(9)

The highlighted terms in Equation (9) become zero. Using Equations (3) and (5), the equation can be further simplified, while retaining the error and true signal dependence terms:

$$\begin{array}{l}{M}_{ij}= a_i{a}_j\left(<t^2>-M_1^2+{<\epsilon }_i{\epsilon }_j>\right)+M_i{M}_j+a_i{a}_j(<t{\epsilon }_i>+<t{\epsilon }_j>)\\ =a_i{a}_j\left(T+{<\epsilon }_i{\epsilon }_j>\right)+M_i{M}_j+a_i{a}_j(<t{\epsilon }_i>+<t{\epsilon }_j>)\end{array}$$

(10)

$$\begin{array}{l}{C}_{ij}=M_{ij}-M_i{M}_j=a_i{a}_j(T+{<\epsilon }_i{\epsilon }_j>+<t{\epsilon }_i>+<t{\epsilon }_j>)\\ =a_i{a}_j(T+e_{ij}+e_{ti}+e_{tj})\end{array}$$

(11)

The terms $e_{ti}$ and $e_{tj}$ represent the dependence of the error variance of individual observation systems on the true signal.

Let the covariance matrix C be an N × N matrix representing N observation systems with N unknown error variances. Then there are N − 1 scaling factor terms, $a_2\dots a_N$ and one common variance, T. The covariance matrix yields ${\displaystyle \frac{N(N + 1)}{2}}$ independent equations. Now, depending on how many of the system error variances are to be solved for, we can include as many true signal dependent terms, $e_{ti}$. For instance, if we are interested in just retrieving the error variance of CYGNSS FDS measurements amongst the four existing matchups in our case study, we can assume other terms to be zero, though this may not be true, and retain only the $e_{tCYG}$ term in Equation (11). This will lead to a total of 2N + 1 unknowns and ${\displaystyle \frac{N(N + 1)}{2}}$ independent equations. This results in a closed form solution to this system of equations for which we require a minimum of 4 observation systems in the matchup dataset. This solution is more generic, accounting for the error variance dependence on the true signal. While this derivation of true signal dependence is straightforward, it is noteworthy because many remote sensing platforms exhibit this true signal error dependence but do not correct for it while using TC. Thus Equation (11) forms the more general form of N-way collocation that takes into account dependency of error variance on true signal.

6. Discussion and Conclusions

This study presents a comprehensive examination of the core assumptions underlying the triple/N-way collocation (TC/NWC) method and evaluates their validity and limitations using a newly developed numerical simulator. By systematically perturbing individual parameters and statistical properties—such as scaling, bias, noise, inter-sensor correlations, and the distribution of the true geophysical variable—we characterize the robustness and reliability of the method across a range of realistic scenarios.

A. 

Validity and Limitations of Assumptions

TC is built on several simplifying assumptions: (1) at least one system is ideal (zero bias, unity scaling), (2) measurement errors are uncorrelated across systems, (3) error variance is independent of the true signal. Our analysis shows that many of these assumptions are routinely violated in practical remote sensing applications, yet the algorithm still performs remarkably well under many conditions. We find in particular that the TC function well with different kinds of true distribution. With Rayleigh, Weibull, or observation-based empirical distributions, the relative error in estimated error variances remains within a few percent of the true value, demonstrating the robustness of the method to distributional changes.

The assumption of uncorrelated measurement errors, however, proves to be far more consequential. Particularly, correlations between the non-reference systems (e.g., System 2 and System 3) can introduce significant bias and instability in the solution. Our experiments indicate that TC should not be used if such correlations exceed approximately 30–50%, as the error variances become significantly inaccurate and the matrix inversion process becomes ill-conditioned or fails entirely.

The assumption of an ideal reference system also has measurable effects. While biases and noise in the reference have only a minor impact on the algorithm’s estimates, deviations in the scaling factor are much more detrimental. A 20% deviation in scaling factor leads to an approximately 20% relative error in estimated variances. This highlights the importance of ensuring proper scaling or applying correction factors when the reference system is non-ideal.

The often-overlooked assumption that error variance is independent of the true signal can also be problematic. Many sensor systems exhibit signal-dependent sensitivity based on their physical measurement principles, such as radiometers being more accurate at high winds and GNSS-R systems performing better at low winds. Incorporating this dependency into the TC formulation—as we propose through a simple modification to the derivation—can significantly improve estimation realism and reliability.

B. 

Relative Impact of Assumptions

Among all the tested assumptions, error correlation between non-reference systems and reference scaling errors have the most significant impact on TC performance. These two factors can fundamentally alter or invalidate the results. In contrast, bias, reference noise, and true state distributions are shown to have a relatively low impact, making the algorithm robust in those dimensions.

C. 

Estimating Correction Factors Using the Simulator

A key contribution of this work is the development of a flexible simulation framework that allows controlled experimentation with all TC input variables. This simulator can be used not only to evaluate algorithmic robustness but also to estimate correction factors for RMSE or error variance estimates derived under non-ideal conditions.

For example, by generating synthetic datasets with known error statistics and controlled violations (e.g., scaling deviation or correlated errors), the simulator allows the estimation of empirical relationships between input assumptions and TC outputs. These relationships can then be encoded into lookup tables or parametric models that serve as post-estimation correction tools. As demonstrated in our scaling factor experiments, correction curves can be created to adjust for known deviations from ideal conditions, significantly improving the accuracy of the final error variance estimates.

D. 

Conclusions

In summary, triple and N-way collocation remain among the most powerful and practical tools available for estimating absolute error variances in remote sensing systems. However, the method’s applicability hinges on the validity of its underlying assumptions. Through targeted simulation-based testing, we have identified which assumptions are critical, which are benign, and how violations can be mitigated through empirical correction. Future extensions of this work may focus on incorporating spatial and temporal error structures, as well as refining signal-dependent noise modeling to further improve TC/NWC performance in operational Earth observation.