Automatic Ghost Noise Labeling for 4D mmWave Radar Data in Underground Mine Environments Using LiDAR as Reference
Highlights
- Proposes a LiDAR-assisted two-stage ghost noise automatic labeling method for 4D mmWave radar data, combining distance threshold filtering and density-based clustering analysis (DBSCAN), which demonstrates superior performance compared to single-method approaches.
- Designs a complete automated labeling workflow tailored for underground mining environments, significantly reducing the cost and complexity of manual labeling while addressing current data annotation bottlenecks in research.
- Validates the proposed method’s efficiency and robustness in ghost noise detection across three typical underground mining scenarios (straight tunnels, straight tunnels with side tunnels, and cross-tunnel turns), providing a practical solution for optimizing radar data quality in complex confined environments.
- Lays an important foundation for the application of 4D mmWave radar in underground mining environments and provides new technical means for studying ghost noise labeling issues, with potential applications in similar industrial settings.
Abstract
1. Introduction
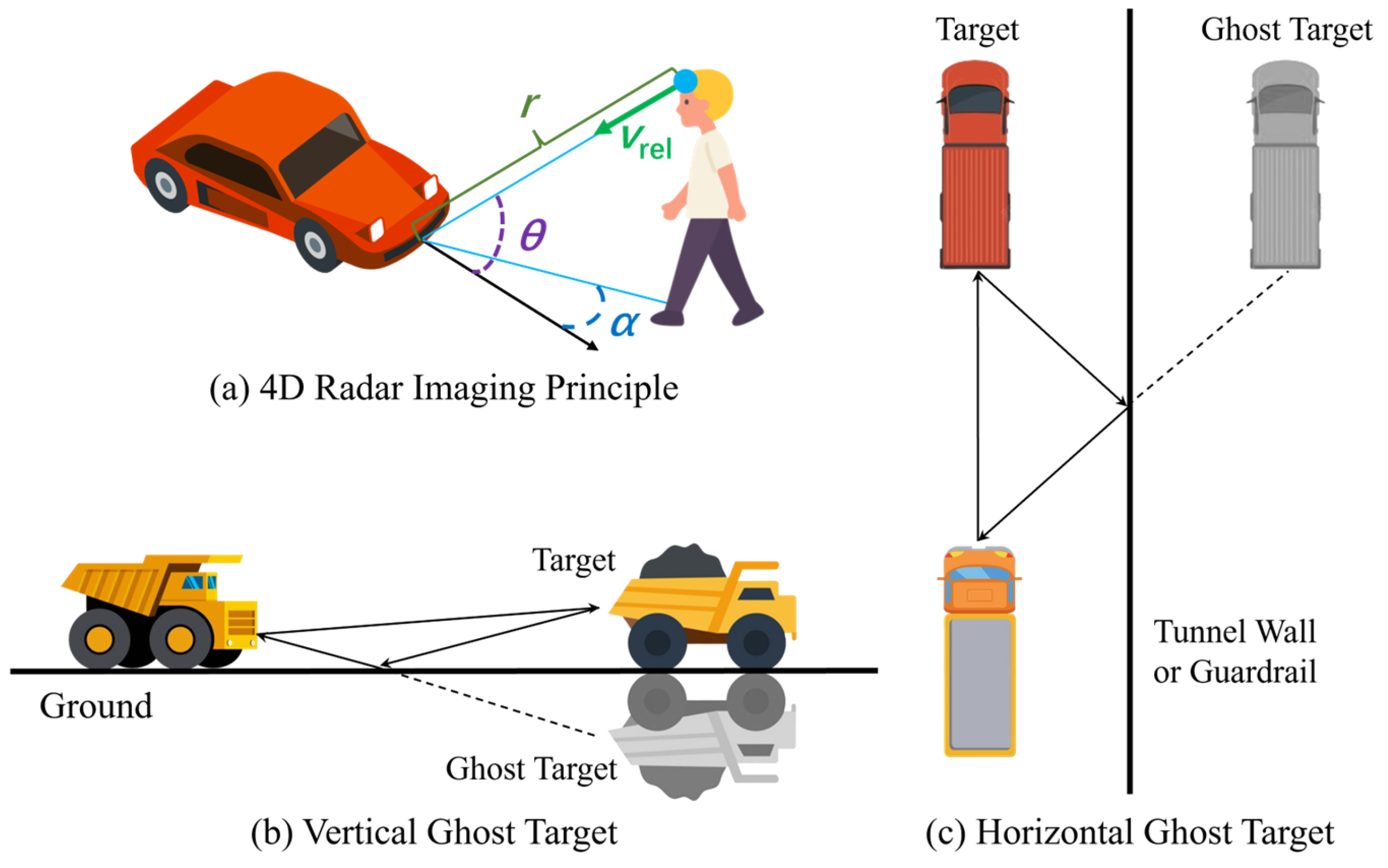
1.1. Background and Motivation
1.2. Related Work
1.2.1. Ghost Noise Detection at the Signal Processing Stage
1.2.2. Automated Point Cloud Labeling Techniques
1.2.3. Research Gaps
1.3. Contributions
- (1)
- A lightweight two-stage ghost noise detection method is proposed, combining the distance threshold method with clustering analysis, which breaks the dependency on traditional signal processing and achieves efficient detection at the point cloud level: first using the distance threshold method to quickly screen candidate noise points, then further verifying through clustering analysis, thereby enhancing the accuracy and robustness of ghost noise point detection.
- (2)
- An automatic labeling workflow tailored for underground mining environments is designed: from data preprocessing to noise detection and labeling, to validation, this paper designs a complete automated workflow that significantly reduces the cost and complexity of manual labeling.
2. Methodology
2.1. Data Preprocessing
2.1.1. Time Synchronization
2.1.2. Spatial Alignment
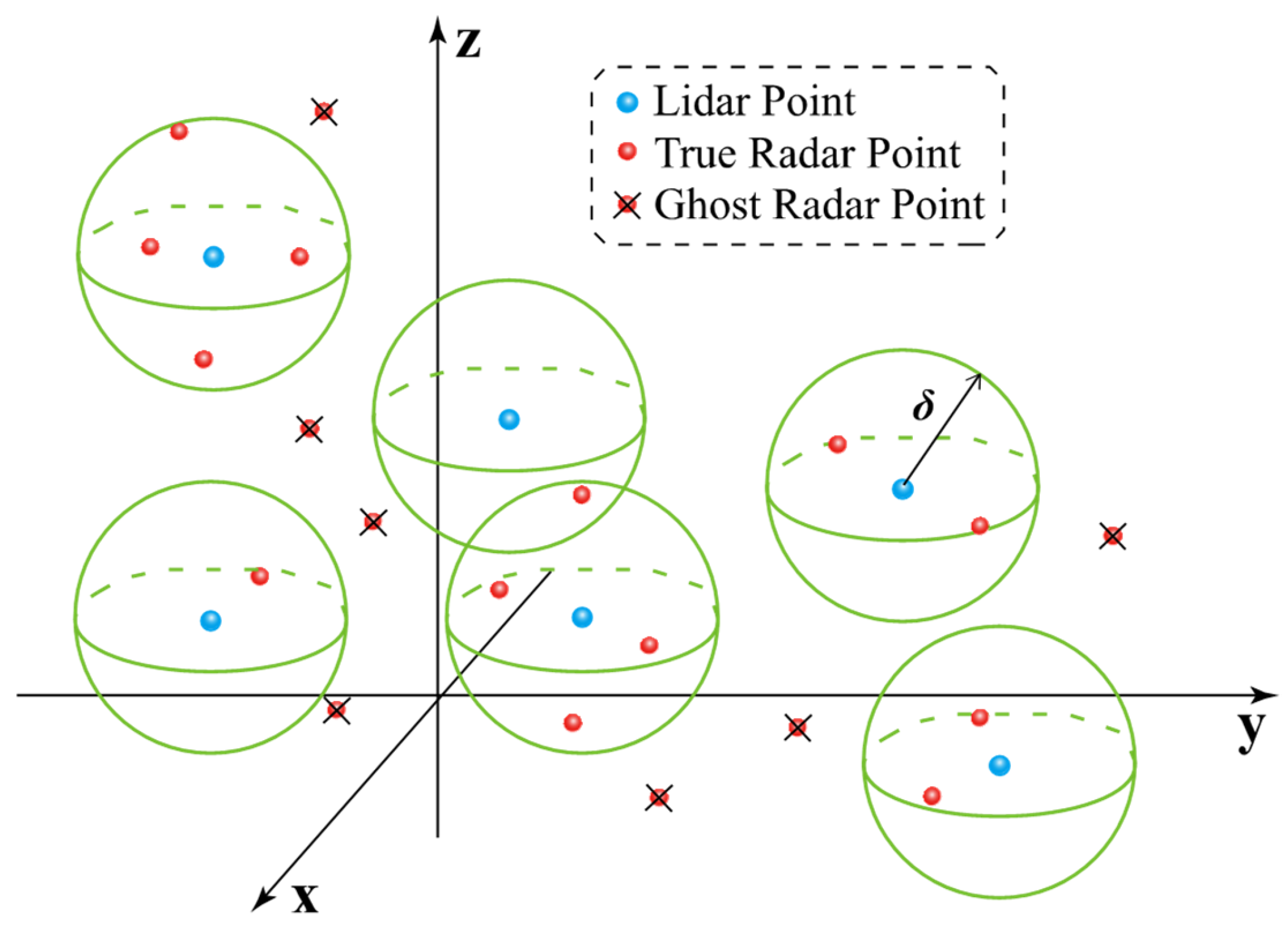
2.2. Ghost Noise Detection
2.2.1. Distance Threshold Method
2.2.2. Clustering Analysis Method
2.2.3. Two-Stage Method
- Stage 1: Preliminary filtering
- Stage 2: Clustering verification
3. Experimental Results
3.1. Dataset Description
3.2. Evaluation Metrics
3.2.1. Precision
3.2.2. Recall
3.2.3. F1 Score
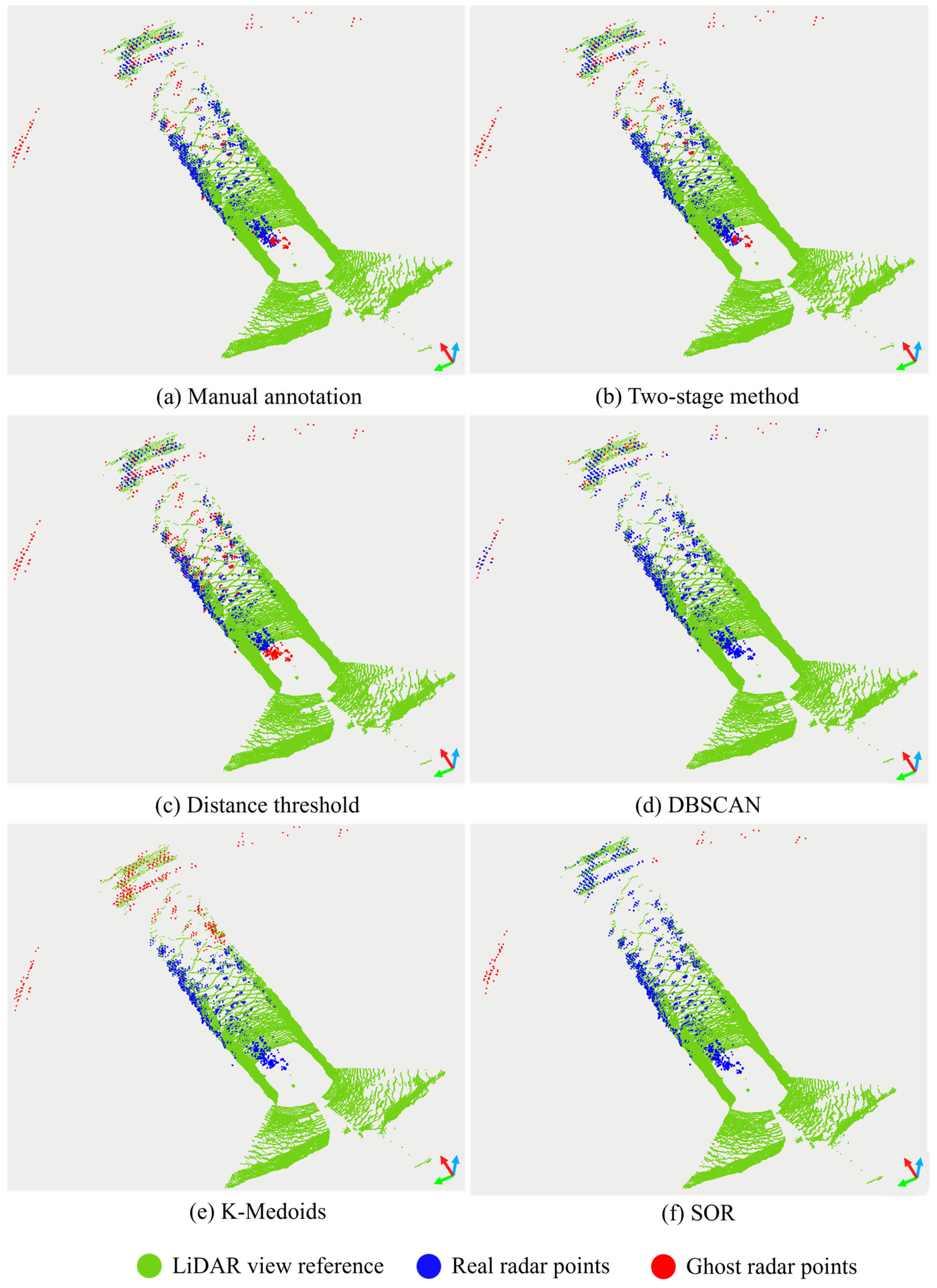
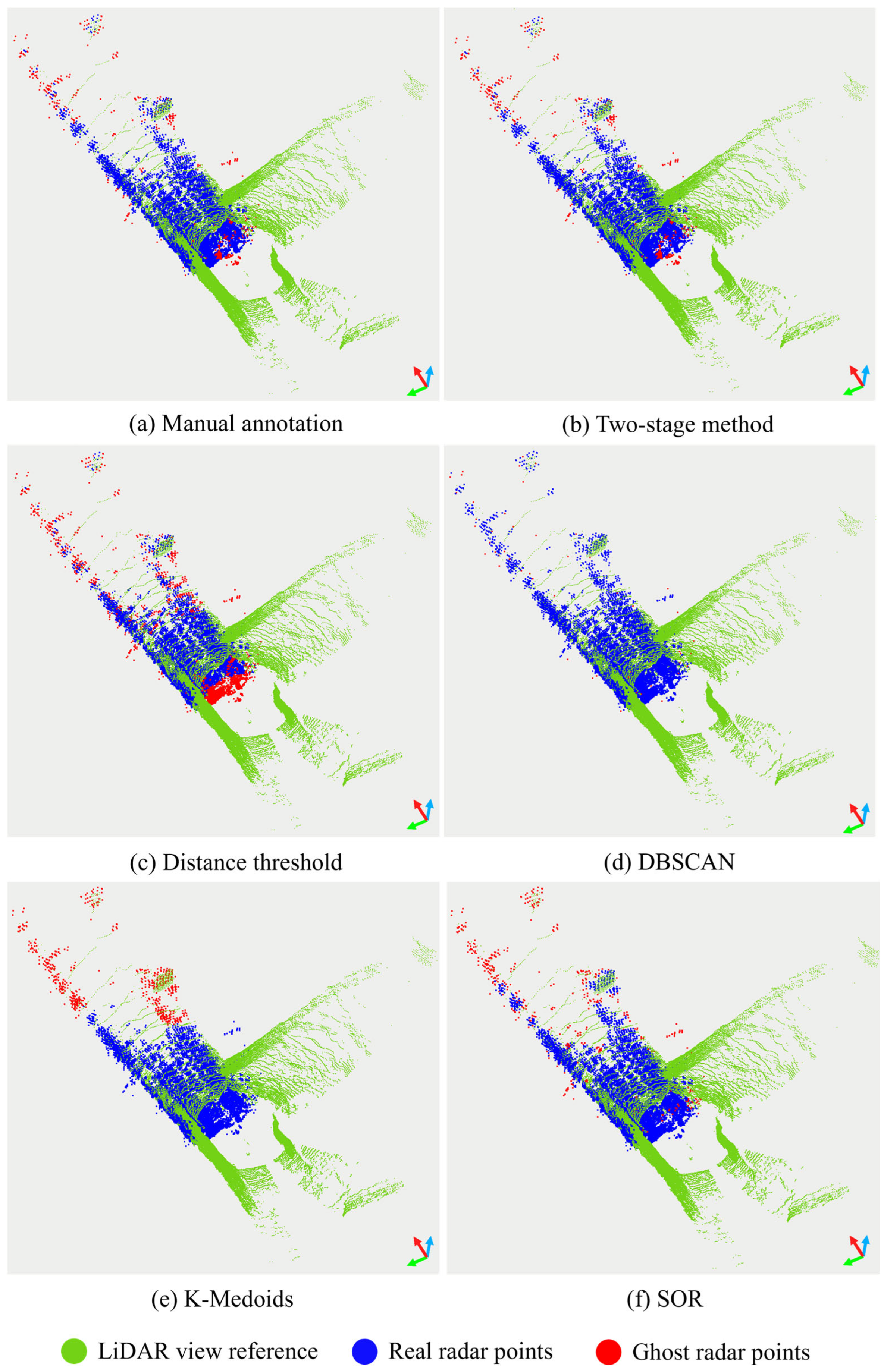
3.3. Results
4. Discussion
4.1. Performance Comparison and Analysis of Different Methods
4.2. Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paluchamy, B.; Mishra, D.P. Measurement and analysis of airborne dust generation and dispersion from low-profile dump truck haulage in underground metalliferous mines. Measurement 2024, 227, 114252. [Google Scholar] [CrossRef]
- Luo, Y.; Hu, Q.; Wang, L.; Cheng, Y.; Li, S. Reconfigurable intelligent surface in underground mines radio localization: A review. Measurement 2025, 251, 117312. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Kanellakis, C.; Kominiak, D.; Nikolakopoulos, G. Deploying MAVs for autonomous navigation in dark underground mine environments. Rob. Auton. Syst. 2020, 126, 103472. [Google Scholar] [CrossRef]
- Jin, H.; Ren, S.; Li, S.; Liu, W. Research on mine personnel target detection method based on improved YOLOv8. Measurement 2025, 245, 116624. [Google Scholar] [CrossRef]
- Imam, M.; Baïna, K.; Tabii, Y.; Ressami, E.M.; Adlaoui, Y.; Benzakour, I.; Abdelwahed, E.H. The Future of Mine Safety: A Comprehensive Review of Anti-Collision Systems Based on Computer Vision in Underground Mines. Sensors 2023, 23, 4294. [Google Scholar] [CrossRef]
- Ralston, J.; Reid, D.; Hargrave, C.; Hainsworth, D. Sensing for advancing mining automation capability: A review of underground automation technology development. Int. J. Min. Sci. Technol. 2014, 24, 305–310. [Google Scholar] [CrossRef]
- Shi, W.; Tong, P.; Bi, X. Moving-Least-Squares-Enhanced 3D Object Detection for 4D Millimeter-Wave Radar. Remote Sens. 2025, 17, 1465. [Google Scholar] [CrossRef]
- Gong, B.; Sun, J.; Lin, C.; Liu, H. Space occupancy rectangle-based multivehicle localization and tracking using roadside 4D millimeter-wave radar. Measurement 2025, 247, 116859. [Google Scholar] [CrossRef]
- Wan, Q.; Peng, H.; Liao, X.; Li, W.; Liu, K.; Mao, J. A Point Cloud Improvement Method for High-Resolution 4D mmWave Radar Imagery. Remote Sens. 2024, 16, 2856. [Google Scholar] [CrossRef]
- Zheng, L.; Long, J.; Lops, M.; Liu, F.; Hu, X.; Zhao, C. Detection of Ghost Targets for Automotive Radar in the Presence of Multipath. IEEE Trans. Signal Process. 2024, 72, 2204–2220. [Google Scholar] [CrossRef]
- Jin, F.; Cao, S. Automotive Radar Interference Mitigation Using Adaptive Noise Canceller. IEEE Trans. Veh. Technol. 2019, 68, 3747–3754. [Google Scholar] [CrossRef]
- Hu, Q.; Luo, Y.; Wang, L.; Cheng, Y.; Yuan, S.; Zhang, Y. A NLOS position estimation method for T-shaped tunnel based on corrected ghost point. Measurement 2025, 253, 117428. [Google Scholar] [CrossRef]
- Luo, H.; Zhu, Z.; Jiang, M.; Guo, S.; Cui, G. An Effective Multipath Ghost Recognition Method for Sparse MIMO Radar. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5111611. [Google Scholar] [CrossRef]
- Liu, C.; Liu, S.; Zhang, C.; Huang, Y.; Wang, H. Multipath propagation analysis and ghost target removal for FMCW automotive radars. In Proceedings of the IET International Radar Conference (IET IRC 2020), Online, 4–6 November 2020; pp. 330–334. [Google Scholar] [CrossRef]
- Cheng, Y.; Su, J.; Jiang, M.; Liu, Y. A Novel Radar Point Cloud Generation Method for Robot Environment Perception. IEEE Trans. Rob. 2022, 38, 3754–3773. [Google Scholar] [CrossRef]
- Huang, H.; Brenner, C. Rule-based roof plane detection and segmentation from laser point clouds. In Proceedings of the 2011 Joint Urban Remote Sensing Event, Munich, Germany, 11–13 April 2011; pp. 293–296. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, H.; Hu, Q.; Liu, H.; Liu, L.; Bennamoun, M. Deep Learning for 3D Point Clouds: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 4338–4364. [Google Scholar] [CrossRef]
- Kramer, A.; Harlow, K.; Williams, C.; Heckman, C. ColoRadar: The direct 3D millimeter wave radar dataset. Int. J. Rob. Res. 2022, 41, 351–360. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, Z.; Zhu, X.; Tan, B.; Li, S.; Long, K.; Sun, W.; Chen, S.; Zhang, L.; Wan, M.; et al. TJ4DRadSet: A 4D Radar Dataset for Autonomous Driving. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 493–498. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, L.; Chen, J.; Fang, C.; Yang, G.; Wang, Y.; Yang, L.; Song, Z.; Liu, L.; Zhang, X.; et al. Dual Radar: A Multi-modal Dataset with Dual 4D Radar for Autononous Driving. Sci. Data 2025, 12, 439. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Peng, P.; Jiang, Y.; Wu, J.; Liu, Y. Efficient and accurate mapping method of underground metal mines using mobile mining equipment and solid-state lidar. Measurement 2023, 221, 113581. [Google Scholar] [CrossRef]
- Park, J.I.; Jo, S.; Seo, H.T.; Park, J. LiDAR Denoising Methods in Adverse Environments: A Review. IEEE Sens. J. 2025, 25, 7916–7932. [Google Scholar] [CrossRef]
- Song, P.; Jin, F.; Ji, M.; Liang, T.; Li, Q. Denoising algorithm for inclined tunnel point cloud data based on irregular contour features. Meas. Sci. Technol. 2024, 35, 095203. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Zhou, F.; Gao, Y.; Li, A.; Xing, M. Indoor personnel detection and tracking of millimeter-wave radar based on improved DBSCAN algorithm. Eng. Res. Express 2025, 7, 025220. [Google Scholar] [CrossRef]
- Khan, K.; Rehman, S.U.; Aziz, K.; Fong, S.; Sarasvady, S. DBSCAN: Past, present and future. In Proceedings of the Fifth International Conference on the Applications of Digital Information and Web Technologies (ICADIWT 2014), Bangalore, India, 17–19 February 2014; pp. 232–238. [Google Scholar] [CrossRef]
- Kubelka, V.; Fritz, E.; Magnusson, M. Do we need scan-matching in radar odometry? In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 13710–13716. [Google Scholar] [CrossRef]
- Magnusson, M.; Lilienthal, A.; Duckett, T. Scan registration for autonomous mining vehicles using 3D-NDT. J. Field Rob. 2007, 24, 803–827. [Google Scholar] [CrossRef]
- Hand, D.J. Assessing the Performance of Classification Methods. Int. Stat. Rev. 2012, 80, 400–414. [Google Scholar] [CrossRef]
- Park, H.-S.; Jun, C.-H. A simple and fast algorithm for K-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Balta, H.; Velagic, J.; Bosschaerts, W.; De Cubber, G.; Siciliano, B. Fast Statistical Outlier Removal Based Method for Large 3D Point Clouds of Outdoor Environments. IFAC-PapersOnLine 2018, 51, 348–353. [Google Scholar] [CrossRef]




| Sensors | Model | Main Parameters | Sampling Frequency |
|---|---|---|---|
| 4D Radar | Sensrad Hugin A3-Sample | HFoV, VFoV 80° × 30°, the horizontal and vertical resolution is 1.25° and 1.7°, the highest range resolution of 0.1 m | 16 Hz |
| LiDAR | Ouster OS1-64 | HFoV 360°, VFoV 45°, range 120 m | 10 Hz |
| IMU | Xsens MTi-30 | Roll (0.5°), Pitch (0.5°), Yaw (2°) | 400 Hz |
| Scenarios | Methods | Precision | Recall | F1 Score |
|---|---|---|---|---|
| Straight tunnels | Distance threshold [22,23] | 57.55% | 97.44% | 72.37% |
| DBSCAN clustering [25] | 53.85% | 14.65% | 23.03% | |
| K-Medoids [30] | 37.95% | 38.84% | 38.39% | |
| SOR [31] | 94.12% | 14.88% | 25.70% | |
| Two-stage method (we propose) | 95.15% | 95.81% | 95.48% | |
| Straight tunnels with side tunnels | Distance threshold [22,23] | 24.56% | 92.65% | 38.83% |
| DBSCAN clustering [25] | 89.06% | 7.22% | 13.36% | |
| K-Medoids [30] | 36.08% | 32.70% | 34.31% | |
| SOR [31] | 60.93% | 43.09% | 50.48% | |
| Two-stage method (we propose) | 98.81% | 94.68% | 96.70% | |
| Cross-tunnel turns | Distance threshold [22,23] | 28.59% | 98.03% | 44.27% |
| DBSCAN clustering [25] | 78.57% | 3.10% | 5.96% | |
| K-Medoids [30] | 2.74% | 2.54% | 2.63% | |
| SOR [31] | 45.19% | 13.24% | 20.48% | |
| Two-stage method (we propose) | 98.85% | 97.18% | 98.01% |
| Scenarios | Methods | Total Points | Processing Time (s) | Speed (points/s) |
|---|---|---|---|---|
| Straight tunnels | Distance threshold | 2531 | 0.018 | 140,611 |
| DBSCAN clustering | 2531 | 0.011 | 230,090 | |
| K-Medoids | 2531 | 0.069 | 36,681 | |
| SOR | 2531 | 0.044 | 57,522 | |
| Two-stage method (we propose) | 2531 | 0.070 | 36,157 | |
| Straight tunnels with side tunnels | Distance threshold | 15,011 | 0.043 | 349,093 |
| DBSCAN clustering | 15,011 | 0.108 | 138,990 | |
| K-Medoids | 15,011 | 0.091 | 164,956 | |
| SOR | 15,011 | 0.241 | 62,286 | |
| Two-stage method (we propose) | 15,011 | 0.920 | 16,316 | |
| Cross-tunnel turns | Distance threshold | 4028 | 0.036 | 111,889 |
| DBSCAN clustering | 4028 | 0.017 | 236,941 | |
| K-Medoids | 4028 | 0.050 | 80,560 | |
| SOR | 4028 | 0.064 | 62,938 | |
| Two-stage method (we propose) | 4028 | 0.189 | 21,312 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, Z.; Chen, G.; Benndorf, J.; Yang, J. Automatic Ghost Noise Labeling for 4D mmWave Radar Data in Underground Mine Environments Using LiDAR as Reference. Remote Sens. 2025, 17, 3732. https://doi.org/10.3390/rs17223732
Liu H, Zhang Z, Chen G, Benndorf J, Yang J. Automatic Ghost Noise Labeling for 4D mmWave Radar Data in Underground Mine Environments Using LiDAR as Reference. Remote Sensing. 2025; 17(22):3732. https://doi.org/10.3390/rs17223732
Chicago/Turabian StyleLiu, Hu, Zhenghua Zhang, Guoliang Chen, Jörg Benndorf, and Jing Yang. 2025. "Automatic Ghost Noise Labeling for 4D mmWave Radar Data in Underground Mine Environments Using LiDAR as Reference" Remote Sensing 17, no. 22: 3732. https://doi.org/10.3390/rs17223732
APA StyleLiu, H., Zhang, Z., Chen, G., Benndorf, J., & Yang, J. (2025). Automatic Ghost Noise Labeling for 4D mmWave Radar Data in Underground Mine Environments Using LiDAR as Reference. Remote Sensing, 17(22), 3732. https://doi.org/10.3390/rs17223732





