Exploiting Diffusion Priors for Generalizable Few-Shot Satellite Image Semantic Segmentation
Highlights
- We propose DiffSatSeg, a diffusion-based framework that combines parameter-efficient fine-tuning, distributional similarity-based segmentation, and consistency learning to tackle few-shot satellite component segmentation, while also enabling fine-grained, reference-guided predictions.
- The proposed method delivers state-of-the-art performance across one-, three-, and ten-shot settings, maintains high effectiveness under low-light and backlit conditions, robustly handles substantial morphological variations—particularly in antennas—and achieves significant gains over previous methods, reaching up to +33.6% mIoU in the one-shot scenario.
- This work opens a new direction for leveraging the prior knowledge of diffusion models to achieve fine-grained perception of satellite targets, bridging a critical research gap. To the best of our knowledge, it is the first attempt to employ diffusion models for few-shot satellite segmentation, establishing a solid foundation for future exploration in this field.
- DiffSatSeg addresses the scarcity of annotated data and substantial morphological differences across satellite types, enabling reliable generalization to unseen targets and fine-grained, reference-guided segmentation, which holds tremendous value for practical space applications such as structural analysis, fault detection, and on-orbit servicing.
Abstract
1. Introduction
- 1.
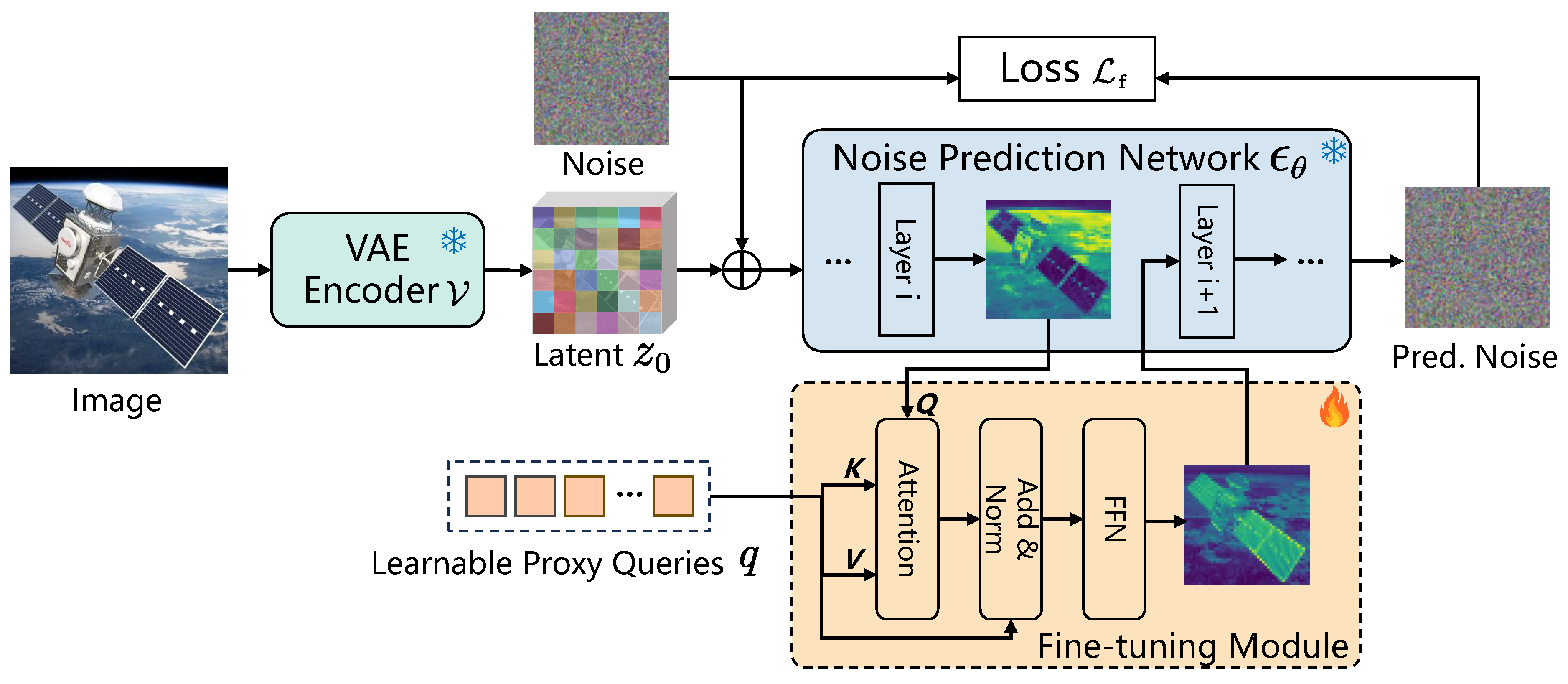
- We propose a novel diffusion-based framework for few-shot satellite segmentation, named DiffSatSeg, which employs a set of learnable proxy queries for parameter-efficient fine-tuning, retaining the rich priors of diffusion models while enabling flexible adaptation to diverse satellite structures.
- 2.
- We propose a segmentation mechanism guided by distributional similarity, which extracts the principal components of a metric similarity matrix constructed from proxy queries to perform discriminative analysis, thereby enabling strong generalization to unseen satellite targets with substantial intra-class variations.
- 3.
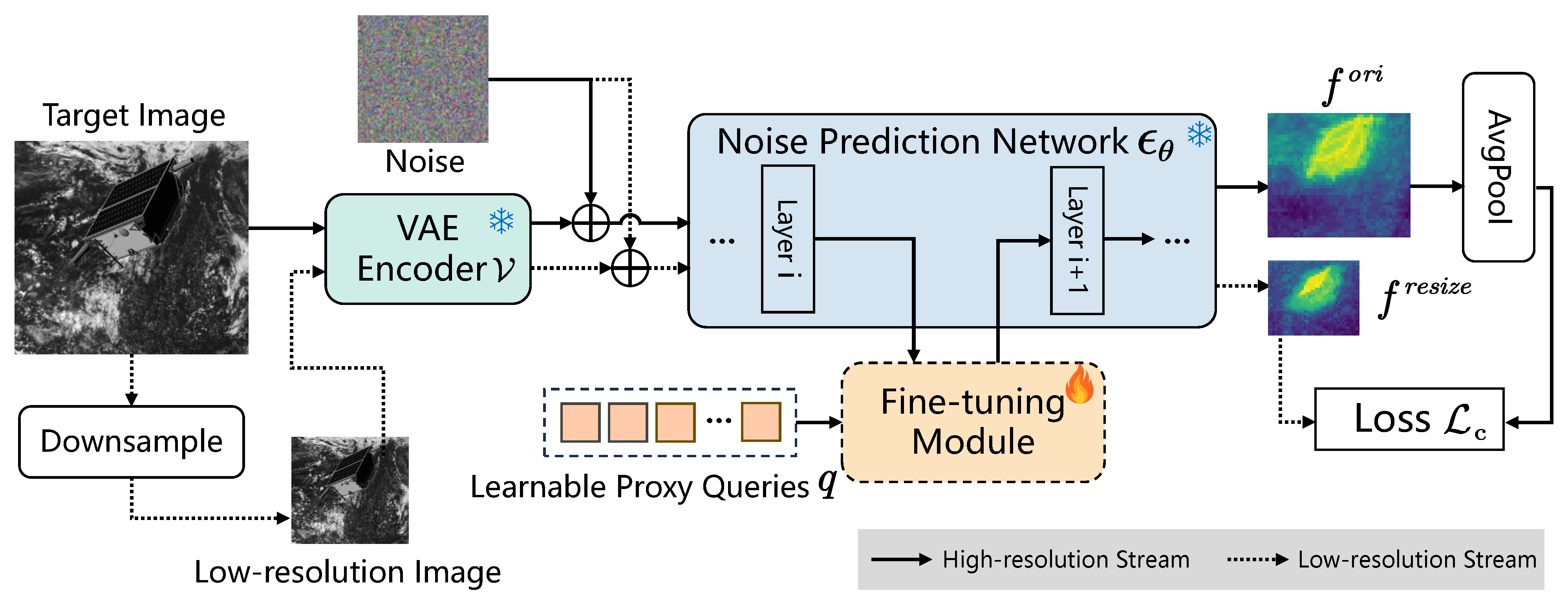
- We design a consistency learning strategy that suppresses redundant texture details in diffusion features, guiding the proxy queries to concentrate on structural semantics and enhancing the reliability of feature representations for segmentation.
- 4.
- Extensive experiments conducted on four benchmark datasets comprehensively validate the effectiveness of the proposed framework, achieving state-of-the-art performance across diverse satellite segmentation scenarios. Furthermore, our method supports reference-based fine-grained segmentation, demonstrating strong practicality and adaptability for real-world satellite applications.
2. Related Work
2.1. Semantic Segmentation
2.2. Few-Shot Segmentation
2.3. Diffusion Model
3. Methods
3.1. Parameter-Efficient Adaptation of Diffusion Models to Rare Targets
3.2. Few-Shot Segmentation via Proxy-Driven Similarity Modeling
3.3. Consistency Learning for Texture Suppression
4. Results
4.1. Experimental Setup
4.1.1. Datasets
4.1.2. Implementation Details
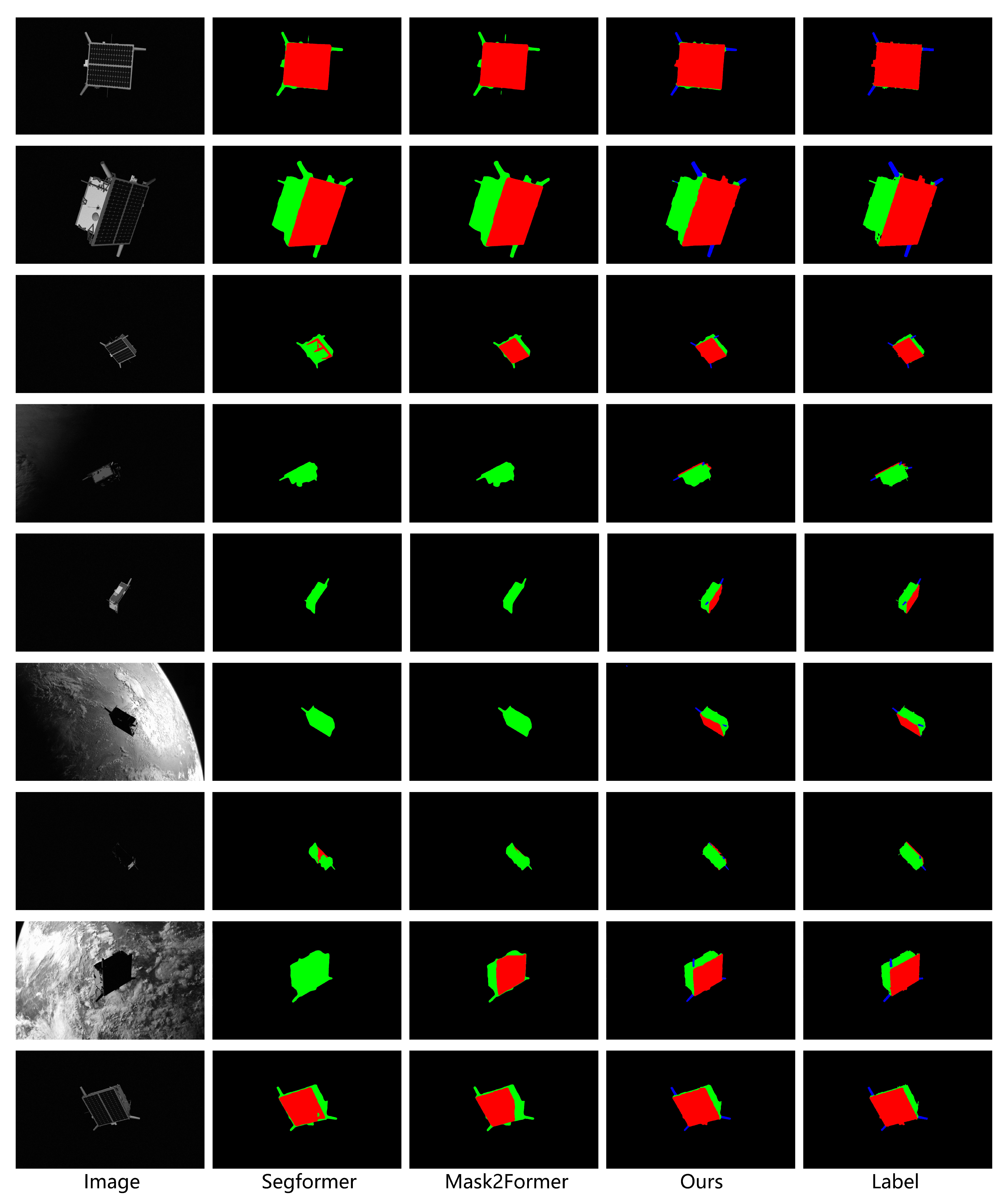
4.2. Main Results
4.2.1. Comparisons with Previous Methods on the Speed+ Dataset
| Method | Training Samples | mIoU | ||||
|---|---|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | |||
| DeepLabV3+ [52] | Semantic Segmentation | Speed+ (One-shot) | 50.3 | 59.6 | 0.0 | 36.6 |
| HRNet+ [53] | 53.6 | 60.3 | 1.9 | 38.6 | ||
| GroupViT [54] | 60.9 | 62.7 | 2.8 | 42.1 | ||
| Segformer [9] | 57.1 | 62.4 | 2.1 | 40.5 | ||
| Maskformer [24] | 63.7 | 63.8 | 3.6 | 43.7 | ||
| Mask2former [25] | 64.1 | 63.2 | 5.7 | 44.3 | ||
| BCM [55] | Few-shot Segmentation | 69.7 | 68.6 | 28.6 | 55.6 | |
| PI-CLIP [56] | 72.3 | 71.9 | 33.8 | 59.3 | ||
| LLaFS [57] | 74.5 | 73.1 | 35.9 | 61.2 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 76.6 | 72.3 | 35.1 | 61.3 | |
| DiffewS [58] | 78.9 | 74.8 | 40.7 | 64.8 | ||
| DeFSS [59] | 81.7 | 75.2 | 42.4 | 66.4 | ||
| Ours | 86.5 | 77.5 | 69.8 | 77.9 | ||
| DeepLabV3+ [52] | Semantic Segmentation | Speed+ (Three-shot) | 50.5 | 59.7 | 0.0 | 36.7 |
| HRNet+ [53] | 53.3 | 61.2 | 1.7 | 38.7 | ||
| GroupViT [54] | 61.4 | 63.5 | 3.0 | 42.6 | ||
| Segformer [9] | 56.9 | 63.1 | 2.8 | 40.9 | ||
| Maskformer [24] | 64.1 | 63.7 | 5.8 | 44.5 | ||
| Mask2former [25] | 64.0 | 63.9 | 6.0 | 44.6 | ||
| BCM [55] | Few-shot Segmentation | 71.3 | 70.7 | 38.5 | 60.2 | |
| PI-CLIP [56] | 74.7 | 74.2 | 41.0 | 63.3 | ||
| LLaFS [57] | 77.1 | 75.0 | 42.1 | 64.7 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 77.9 | 73.8 | 38.9 | 63.5 | |
| DiffewS [58] | 80.3 | 75.6 | 42.1 | 66.0 | ||
| DeFSS [59] | 82.1 | 76.4 | 44.3 | 67.6 | ||
| Ours | 89.7 | 80.6 | 71.5 | 80.6 | ||
| DeepLabV3+ [52] | Semantic Segmentation | Speed+ (Ten-shot) | 52.1 | 60.9 | 1.7 | 38.2 |
| HRNet+ [53] | 55.6 | 61.3 | 2.2 | 39.7 | ||
| GroupViT [54] | 65.6 | 66.8 | 4.5 | 45.6 | ||
| Segformer [9] | 60.1 | 65.7 | 3.9 | 43.2 | ||
| Maskformer [24] | 69.8 | 68.5 | 7.9 | 48.7 | ||
| Mask2former [25] | 71.6 | 70.8 | 8.7 | 50.4 | ||
| BCM [55] | Few-shot Segmentation | 81.6 | 80.0 | 53.2 | 71.6 | |
| PI-CLIP [56] | 82.3 | 81.5 | 51.7 | 71.8 | ||
| LLaFS [57] | 81.9 | 80.7 | 55.8 | 72.8 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 83.6 | 78.9 | 52.0 | 71.5 | |
| DiffewS [58] | 85.0 | 81.7 | 54.6 | 73.8 | ||
| DeFSS [59] | 86.5 | 82.1 | 58.5 | 75.7 | ||
| Ours | 93.6 | 86.7 | 77.6 | 86.0 | ||
4.2.2. Comparisons with Previous Methods on the UESD Dataset
| Method | Training Samples | mIoU | ||||||
|---|---|---|---|---|---|---|---|---|
| Solar Panel | Antenna | Instrument | Thruster | Optical Payload | Avg. | |||
| DeepLabV3+ [52] | Semantic Segmentation | UESD (One-shot) | 67.3 | 48.4 | 22.9 | 13.4 | 17.2 | 33.8 |
| HRNet+ [53] | 68.7 | 52.7 | 25.8 | 13.3 | 18.9 | 35.9 | ||
| GroupViT [54] | 70.7 | 58.0 | 31.2 | 15.2 | 21.0 | 39.2 | ||
| Segformer [9] | 70.9 | 60.5 | 33.1 | 18.7 | 27.8 | 42.2 | ||
| Maskformer [24] | 71.1 | 61.5 | 36.1 | 22.1 | 39.6 | 46.1 | ||
| Mask2former [25] | 72.6 | 63.8 | 37.4 | 23.6 | 41.6 | 47.8 | ||
| BCM [55] | Few-shot Segmentation | 75.2 | 68.5 | 46.4 | 37.9 | 57.1 | 57.0 | |
| PI-CLIP [56] | 76.4 | 70.9 | 48.3 | 40.2 | 62.5 | 59.7 | ||
| LLaFS [57] | 76.1 | 70.6 | 51.5 | 43.1 | 63.3 | 60.9 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 76.3 | 73.4 | 56.8 | 48.9 | 64.2 | 63.9 | |
| DiffewS [58] | 77.3 | 75.3 | 59.3 | 53.0 | 67.3 | 66.4 | ||
| DeFSS [59] | 77.5 | 76.3 | 61.2 | 56.9 | 69.5 | 68.3 | ||
| Ours | 78.4 | 79.7 | 65.3 | 60.1 | 77.6 | 72.2 | ||
| DeepLabV3+ [52] | Semantic Segmentation | UESD (Three-shot) | 69.1 | 53.8 | 26.9 | 25.2 | 20.5 | 39.1 |
| HRNet+ [53] | 70.2 | 60.0 | 31.2 | 20.1 | 28.8 | 42.1 | ||
| GroupViT [54] | 71.7 | 63.7 | 38.7 | 28.3 | 39.9 | 48.5 | ||
| Segformer [9] | 71.3 | 67.4 | 41.7 | 32.3 | 41.2 | 50.8 | ||
| Maskformer [24] | 72.4 | 66.6 | 50.2 | 39.0 | 52.1 | 56.1 | ||
| Mask2former [25] | 73.2 | 69.0 | 43.6 | 37.3 | 53.2 | 55.3 | ||
| BCM [55] | Few-shot Segmentation | 75.6 | 70.3 | 57.0 | 49.4 | 59.4 | 62.3 | |
| PI-CLIP [56] | 77.4 | 72.6 | 61.6 | 59.9 | 65.4 | 67.4 | ||
| LLaFS [57] | 79.6 | 74.4 | 65.5 | 58.9 | 64.6 | 68.6 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 79.4 | 76.7 | 63.3 | 51.5 | 68.4 | 67.9 | |
| DiffewS [58] | 81.7 | 77.4 | 65.7 | 59.9 | 70.3 | 71.0 | ||
| DeFSS [59] | 81.4 | 78.6 | 64.4 | 58.1 | 72.5 | 71.0 | ||
| Ours | 82.3 | 81.1 | 70.7 | 64.9 | 78.5 | 75.5 | ||
| DeepLabV3+ [52] | Semantic Segmentation | UESD (Ten-shot) | 72.4 | 67.7 | 40.8 | 43.7 | 41.1 | 53.1 |
| HRNet+ [53] | 73.9 | 70.1 | 42.7 | 45.0 | 44.3 | 55.2 | ||
| GroupViT [54] | 74.6 | 72.1 | 45.1 | 47.9 | 51.6 | 58.3 | ||
| Segformer [9] | 74.9 | 71.2 | 53.8 | 54.0 | 54.5 | 61.7 | ||
| Maskformer [24] | 76.4 | 73.0 | 52.3 | 55.8 | 57.1 | 62.9 | ||
| Mask2former [25] | 77.1 | 73.3 | 54.5 | 56.2 | 60.8 | 64.4 | ||
| BCM [55] | Few-shot Segmentation | 80.7 | 77.9 | 63.2 | 59.9 | 68.8 | 70.1 | |
| PI-CLIP [56] | 83.9 | 76.9 | 65.3 | 61.7 | 72.0 | 72.0 | ||
| LLaFS [57] | 83.1 | 79.1 | 68.5 | 63.2 | 76.0 | 74.0 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 82.5 | 81.3 | 67.7 | 62.3 | 75.5 | 73.9 | |
| DiffewS [58] | 84.7 | 83.6 | 69.4 | 66.5 | 72.2 | 75.3 | ||
| DeFSS [59] | 85.8 | 83.4 | 68.3 | 65.4 | 76.7 | 75.9 | ||
| Ours | 87.1 | 86.2 | 75.6 | 70.2 | 83.4 | 80.5 | ||
4.2.3. Comparisons with Previous Methods on the SSP Dataset
| Method | Training Samples | mIoU | |||||
|---|---|---|---|---|---|---|---|
| Spacecraft | Solar Panel | Radar | Thruster | Avg. | |||
| DeepLabV3+ [52] | Semantic Segmentation | SSP (One-shot) | 63.0 | 64.7 | 39.7 | 25.4 | 48.2 |
| HRNet+ [53] | 65.0 | 66.3 | 39.8 | 32.8 | 51.0 | ||
| GroupViT [54] | 69.2 | 68.8 | 42.3 | 39.7 | 55.0 | ||
| Segformer [9] | 68.0 | 68.2 | 42.1 | 46.5 | 56.2 | ||
| Maskformer [24] | 69.3 | 69.6 | 45.0 | 43.7 | 56.9 | ||
| Mask2former [25] | 70.9 | 71.8 | 44.7 | 45.1 | 58.1 | ||
| BCM [55] | Few-shot Segmentation | 71.7 | 70.6 | 53.9 | 52.6 | 62.2 | |
| PI-CLIP [56] | 73.4 | 72.5 | 53.8 | 55.0 | 63.7 | ||
| LLaFS [57] | 75.9 | 75.9 | 57.4 | 59.3 | 67.1 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 76.1 | 76.0 | 61.6 | 59.9 | 68.4 | |
| DiffewS [58] | 77.8 | 78.9 | 63.6 | 58.4 | 69.7 | ||
| DeFSS [59] | 78.0 | 79.8 | 66.9 | 59.4 | 71.0 | ||
| Ours | 81.2 | 81.8 | 70.9 | 63.1 | 74.3 | ||
| DeepLabV3+ [52] | Semantic Segmentation | SSP (Three-shot) | 68.5 | 67.5 | 42.6 | 29.4 | 52.0 |
| HRNet+ [53] | 69.8 | 68.1 | 43.4 | 35.6 | 54.2 | ||
| GroupViT [54] | 71.4 | 70.6 | 49.2 | 43.8 | 58.8 | ||
| Segformer [9] | 71.1 | 71.4 | 47.0 | 47.3 | 59.2 | ||
| Maskformer [24] | 73.5 | 73.4 | 50.3 | 48.8 | 61.5 | ||
| Mask2former [25] | 74.4 | 75.6 | 51.7 | 50.9 | 63.2 | ||
| BCM [55] | Few-shot Segmentation | 75.2 | 77.4 | 56.4 | 53.6 | 65.7 | |
| PI-CLIP [56] | 78.3 | 78.1 | 61.3 | 58.3 | 69.0 | ||
| LLaFS [57] | 77.8 | 78.7 | 64.7 | 60.4 | 70.4 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 78.9 | 79.7 | 65.1 | 61.6 | 71.3 | |
| DiffewS [58] | 80.3 | 81.8 | 68.0 | 63.8 | 73.5 | ||
| DeFSS [59] | 81.1 | 83.2 | 71.4 | 65.1 | 75.2 | ||
| Ours | 83.3 | 85.4 | 74.7 | 67.6 | 77.8 | ||
| DeepLabV3+ [52] | Semantic Segmentation | SSP (Ten-shot) | 71.0 | 71.5 | 49.2 | 43.5 | 58.8 |
| HRNet+ [53] | 73.3 | 72.7 | 51.8 | 47.4 | 61.3 | ||
| GroupViT [54] | 74.8 | 72.8 | 56.7 | 55.6 | 65.0 | ||
| Segformer [9] | 76.5 | 74.4 | 59.4 | 55.1 | 66.4 | ||
| Maskformer [24] | 76.6 | 77.2 | 59.0 | 57.5 | 67.6 | ||
| Mask2former [25] | 78.5 | 77.4 | 59.9 | 56.1 | 68.0 | ||
| BCM [55] | Few-shot Segmentation | 80.8 | 79.8 | 63.5 | 60.7 | 71.2 | |
| PI-CLIP [56] | 82.7 | 81.5 | 67.6 | 66.9 | 74.7 | ||
| LLaFS [57] | 81.9 | 81.7 | 69.0 | 65.4 | 74.5 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 83.7 | 84.7 | 71.7 | 67.3 | 76.9 | |
| DiffewS [58] | 85.7 | 87.0 | 72.5 | 68.5 | 78.4 | ||
| DeFSS [59] | 86.1 | 87.9 | 74.1 | 69.0 | 79.3 | ||
| Ours | 87.6 | 88.9 | 79.9 | 73.1 | 82.4 | ||
4.2.4. Comparisons with Previous Methods on the MIAS Dataset
| Method | Training Samples | mIoU | ||||
|---|---|---|---|---|---|---|
| Solar Panel | Antenna | Body | Avg. | |||
| DeepLabV3+ [52] | Semantic Segmentation | MIAS (One-shot) | 58.0 | 33.5 | 57.5 | 49.7 |
| HRNet+ [53] | 59.4 | 35.2 | 59.8 | 51.5 | ||
| GroupViT [54] | 62.4 | 46.1 | 62.3 | 56.9 | ||
| Segformer [9] | 63.6 | 47.1 | 64.5 | 58.4 | ||
| Maskformer [24] | 65.3 | 50.9 | 63.7 | 60.0 | ||
| Mask2former [25] | 66.0 | 52.7 | 67.0 | 61.9 | ||
| BCM [55] | Few-shot Segmentation | 68.4 | 53.3 | 69.1 | 63.6 | |
| PI-CLIP [56] | 71.4 | 56.8 | 71.8 | 66.7 | ||
| LLaFS [57] | 72.5 | 59.5 | 72.2 | 68.1 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 73.4 | 62.4 | 72.6 | 69.5 | |
| DiffewS [58] | 75.5 | 66.7 | 74.2 | 72.1 | ||
| DeFSS [59] | 75.9 | 67.2 | 74.8 | 72.6 | ||
| Ours | 79.7 | 72.9 | 78.2 | 76.9 | ||
| DeepLabV3+ [52] | Semantic Segmentation | MIAS (Three-shot) | 60.4 | 42.9 | 59.6 | 54.3 |
| HRNet+ [53] | 62.0 | 41.4 | 61.8 | 55.1 | ||
| GroupViT [54] | 65.3 | 55.2 | 65.7 | 62.1 | ||
| Segformer [9] | 65.7 | 57.1 | 67.4 | 63.4 | ||
| Maskformer [24] | 68.9 | 55.8 | 69.4 | 64.7 | ||
| Mask2former [25] | 68.8 | 56.5 | 70.8 | 65.4 | ||
| BCM [55] | Few-shot Segmentation | 71.9 | 61.6 | 73.7 | 69.1 | |
| PI-CLIP [56] | 73.8 | 63.6 | 74.4 | 70.6 | ||
| LLaFS [57] | 75.9 | 64.6 | 74.6 | 71.7 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 77.2 | 68.4 | 77.4 | 74.3 | |
| DiffewS [58] | 80.8 | 72.1 | 77.7 | 76.9 | ||
| DeFSS [59] | 81.2 | 71.9 | 78.6 | 77.2 | ||
| Ours | 84.1 | 77.2 | 82.9 | 81.4 | ||
| DeepLabV3+ [52] | Semantic Segmentation | MIAS (Ten-shot) | 64.8 | 51.7 | 63.9 | 60.1 |
| HRNet+ [53] | 66.7 | 52.2 | 65.7 | 61.5 | ||
| GroupViT [54] | 68.6 | 60.1 | 68.5 | 65.7 | ||
| Segformer [9] | 71.9 | 62.9 | 70.1 | 68.3 | ||
| Maskformer [24] | 74.0 | 65.7 | 73.7 | 71.1 | ||
| Mask2former [25] | 75.3 | 63.9 | 76.5 | 71.9 | ||
| BCM [55] | Few-shot Segmentation | 77.4 | 67.9 | 79.5 | 74.9 | |
| PI-CLIP [56] | 78.6 | 70.6 | 79.8 | 76.3 | ||
| LLaFS [57] | 80.7 | 71.5 | 81.1 | 77.8 | ||
| DICEPTION [60] | Diffusion-based Segmentation | 80.2 | 73.1 | 82.4 | 78.6 | |
| DiffewS [58] | 82.8 | 78.2 | 84.8 | 81.9 | ||
| DeFSS [59] | 83.9 | 78.0 | 85.7 | 82.5 | ||
| Ours | 87.6 | 82.7 | 88.1 | 86.1 | ||
4.2.5. Fine-Grained Segmentation of Satellite Components
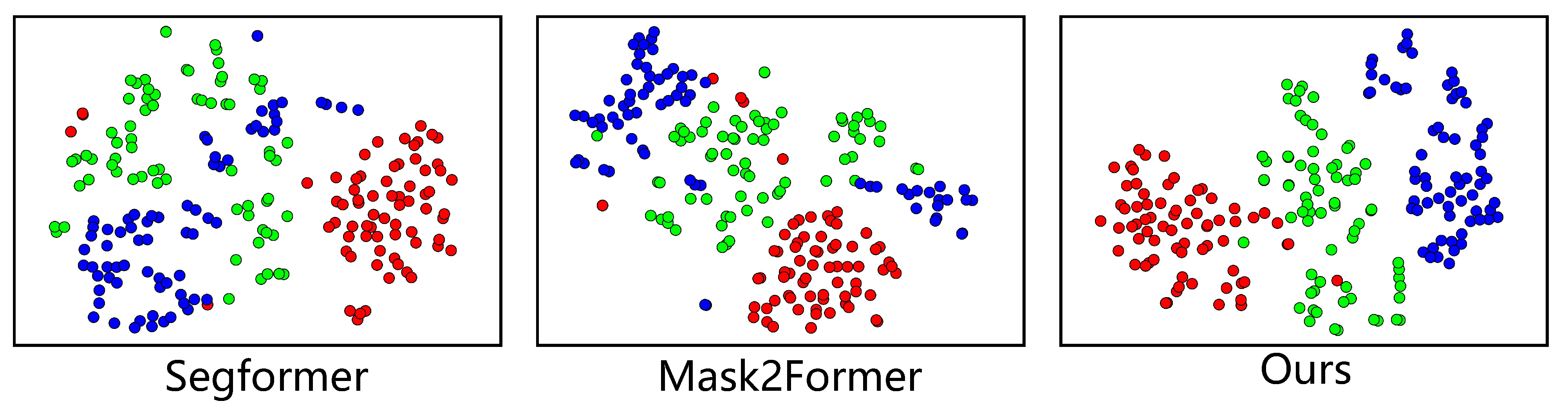
4.3. Ablation Studies and Further Analysis
4.3.1. Ablation Study on Primary Components
4.3.2. Effect of Diffusion Models and Feature Layers
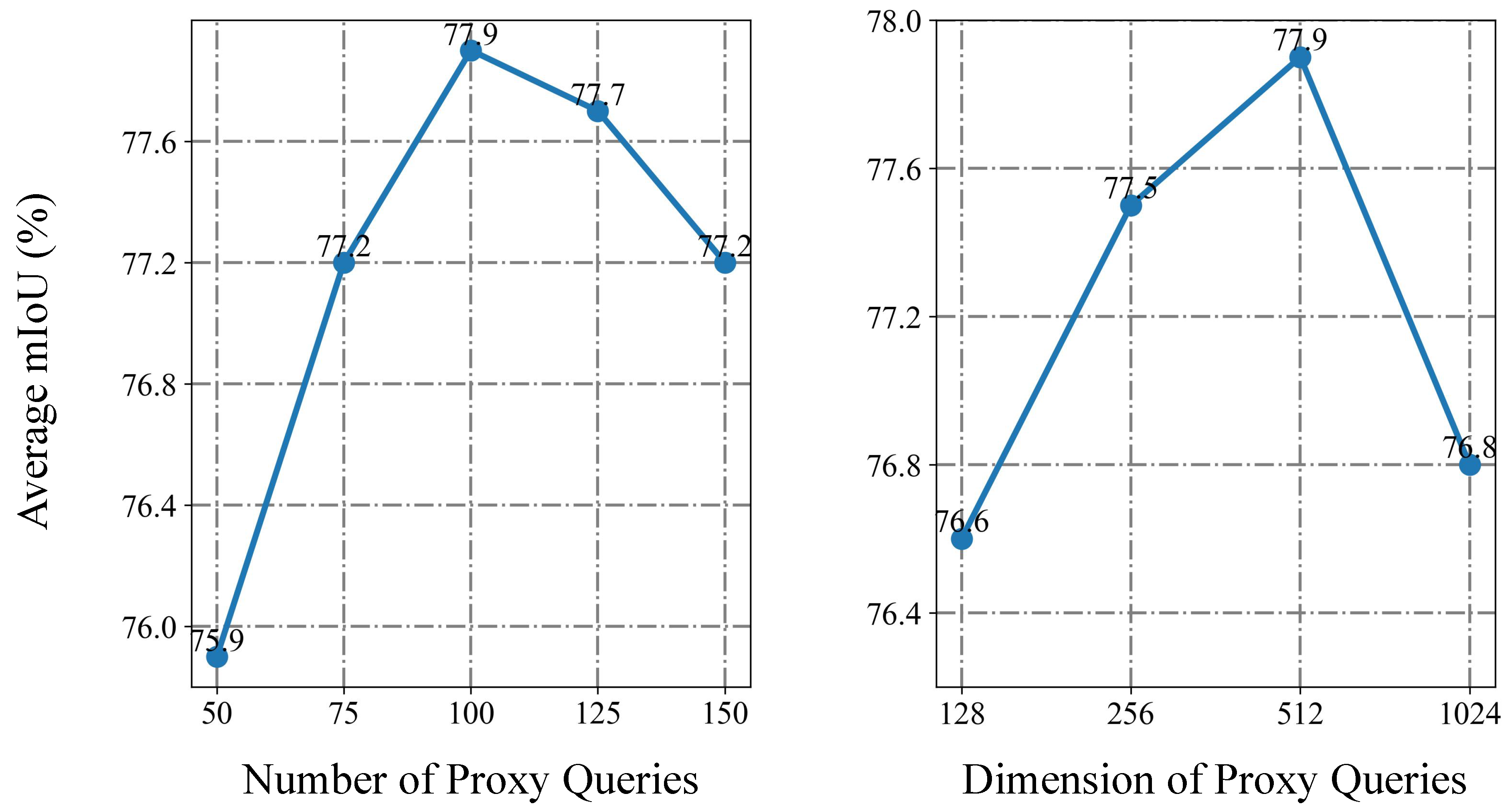
4.3.3. Effect of Proxy Query Length and Dimension
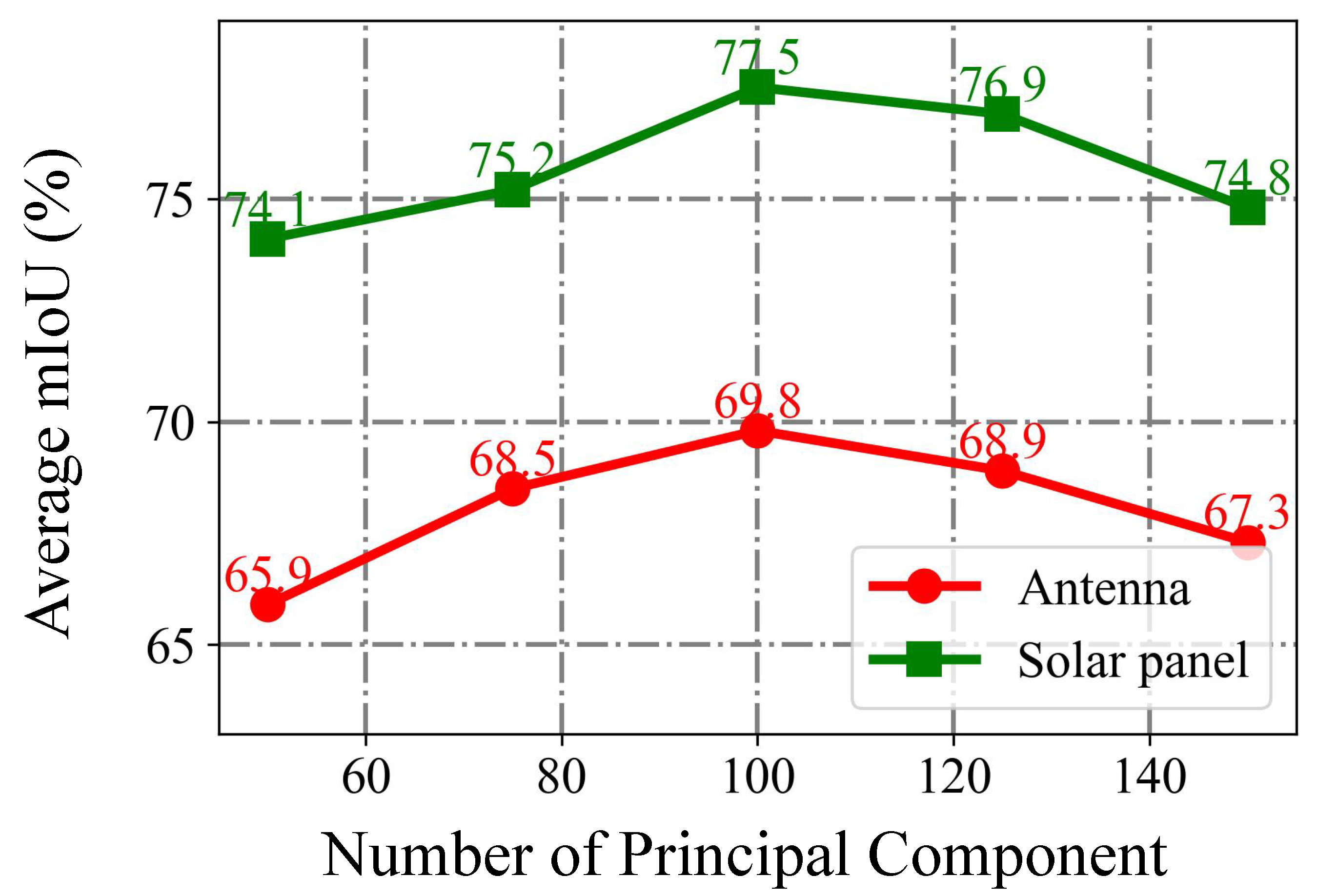
4.3.4. Effect of the Number of Principal Components
4.3.5. Effect of Downsampling Scale in Consistency Learning
4.3.6. Effect of Loss Weights
4.3.7. Fine-Tuning Strategy Analysis
4.3.8. The Choice of Timestep t
4.3.9. Analysis of Computational Efficiency
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Wu, T.; Wang, N.; Huang, Y.; Song, B.; Gao, X. HCNN-PSI: A hybrid CNN with partial semantic information for space target recognition. Pattern Recognit. 2020, 108, 107531. [Google Scholar] [CrossRef]
- Dung, H.A.; Chen, B.; Chin, T.J. A spacecraft dataset for detection, segmentation and parts recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 2012–2019. [Google Scholar]
- Qu, Z.; Wei, C. A spatial non-cooperative target image semantic segmentation algorithm with improved deeplab V3+. In Proceedings of the 2022 IEEE 22nd International Conference on Communication Technology (ICCT), Nanjing, China, 11–14 November 2022; pp. 1633–1638. [Google Scholar]
- Zhao, Y.; Zhong, R.; Cui, L. Intelligent recognition of spacecraft components from photorealistic images based on Unreal Engine 4. Adv. Space Res. 2023, 71, 3761–3774. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 4015–4026. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Shao, Y.; Wu, A.; Li, S.; Shu, L.; Wan, X.; Shao, Y.; Huo, J. Satellite component semantic segmentation: Video dataset and real-time pyramid attention and decoupled attention network. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 7315–7333. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Hu, Y.; Yang, Y.; Cao, X.; Zhen, X. Few-shot semantic segmentation with democratic attention networks. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XIII 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 730–746. [Google Scholar]
- Zhang, B.; Xiao, J.; Qin, T. Self-guided and cross-guided learning for few-shot segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8312–8321. [Google Scholar]
- Yang, B.; Liu, C.; Li, B.; Jiao, J.; Ye, Q. Prototype mixture models for few-shot semantic segmentation. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 763–778. [Google Scholar]
- Li, G.; Jampani, V.; Sevilla-Lara, L.; Sun, D.; Kim, J.; Kim, J. Adaptive prototype learning and allocation for few-shot segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 8334–8343. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Niemeijer, J.; Schwonberg, M.; Termöhlen, J.A.; Schmidt, N.M.; Fingscheidt, T. Generalization by adaptation: Diffusion-based domain extension for domain-generalized semantic segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–10 January 2024; pp. 2830–2840. [Google Scholar]
- Kawano, Y.; Aoki, Y. Maskdiffusion: Exploiting pre-trained diffusion models for semantic segmentation. IEEE Access 2024, 12, 127283–127293. [Google Scholar] [CrossRef]
- Xing, Z.; Wan, L.; Fu, H.; Yang, G.; Zhu, L. Diff-unet: A diffusion embedded network for volumetric segmentation. arXiv 2023, arXiv:2303.10326. [Google Scholar] [CrossRef]
- Ma, C.; Yang, Y.; Ju, C.; Zhang, F.; Liu, J.; Wang, Y.; Zhang, Y.; Wang, Y. Diffusionseg: Adapting diffusion towards unsupervised object discovery. arXiv 2023, arXiv:2303.09813. [Google Scholar] [CrossRef]
- Ke, B.; Obukhov, A.; Huang, S.; Metzger, N.; Daudt, R.C.; Schindler, K. Repurposing diffusion-based image generators for monocular depth estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Waikoloa, HI, USA, 1–10 January 2024; pp. 9492–9502. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Zheng, S.; Lu, J.; Zhao, H.; Zhu, X.; Luo, Z.; Wang, Y.; Fu, Y.; Feng, J.; Xiang, T.; Torr, P.H.; et al. Rethinking semantic segmentation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 6881–6890. [Google Scholar]
- Cheng, B.; Schwing, A.; Kirillov, A. Per-pixel classification is not all you need for semantic segmentation. Adv. Neural Inf. Process. Syst. 2021, 34, 17864–17875. [Google Scholar]
- Cheng, B.; Misra, I.; Schwing, A.G.; Kirillov, A.; Girdhar, R. Masked-attention mask transformer for universal image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 1290–1299. [Google Scholar]
- Hoyer, L.; Dai, D.; Van Gool, L. Daformer: Improving network architectures and training strategies for domain-adaptive semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 9924–9935. [Google Scholar]
- Wei, Z.; Chen, L.; Jin, Y.; Ma, X.; Liu, T.; Ling, P.; Wang, B.; Chen, H.; Zheng, J. Stronger Fewer & Superior Harnessing Vision Foundation Models for Domain Generalized Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; Waikoloa, HI, USA, 1-10 January 2024, pp. 28619–28630.
- Chen, Y.; Gao, J.; Zhang, Y.; Duan, Z.; Zhang, K. Satellite components detection from optical images based on instance segmentation networks. J. Aerosp. Inf. Syst. 2021, 18, 355–365. [Google Scholar] [CrossRef]
- Xiang, A.; Zhang, L.; Fan, L. Shadow removal of spacecraft images with multi-illumination angles image fusion. Aerosp. Sci. Technol. 2023, 140, 108453. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, M.; Wang, J.; Guo, X.; Yang, Y.; Wang, J. Multi-scale deep neural network based on dilated convolution for spacecraft image segmentation. Sensors 2022, 22, 4222. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Lin, G.; Liu, F.; Yao, R.; Shen, C. Canet: Class-agnostic segmentation networks with iterative refinement and attentive few-shot learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 5217–5226. [Google Scholar]
- Liu, Y.; Zhang, X.; Zhang, S.; He, X. Part-aware prototype network for few-shot semantic segmentation. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part IX 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 142–158. [Google Scholar]
- Min, J.; Kang, D.; Cho, M. Hypercorrelation squeeze for few-shot segmentation. In Proceedings of the the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 6941–6952. [Google Scholar]
- Tian, Z.; Zhao, H.; Shu, M.; Yang, Z.; Li, R.; Jia, J. Prior guided feature enrichment network for few-shot segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1050–1065. [Google Scholar] [CrossRef]
- Zhang, G.; Kang, G.; Yang, Y.; Wei, Y. Few-shot segmentation via cycle-consistent transformer. Adv. Neural Inf. Process. Syst. 2021, 34, 21984–21996. [Google Scholar]
- Dhariwal, P.; Nichol, A. Diffusion models beat gans on image synthesis. Adv. Neural Inf. Process. Syst. 2021, 34, 8780–8794. [Google Scholar]
- Zhang, L.; Rao, A.; Agrawala, M. Adding conditional control to text-to-image diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 3836–3847. [Google Scholar]
- Chen, M.; Laina, I.; Vedaldi, A. Training-free layout control with cross-attention guidance. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–10 January 2024; pp. 5343–5353. [Google Scholar]
- Epstein, D.; Jabri, A.; Poole, B.; Efros, A.; Holynski, A. Diffusion self-guidance for controllable image generation. Adv. Neural Inf. Process. Syst. 2023, 36, 16222–16239. [Google Scholar]
- Wu, W.; Zhao, Y.; Shou, M.Z.; Zhou, H.; Shen, C. Diffumask: Synthesizing images with pixel-level annotations for semantic segmentation using diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 1206–1217. [Google Scholar]
- Wu, W.; Zhao, Y.; Chen, H.; Gu, Y.; Zhao, R.; He, Y.; Zhou, H.; Shou, M.Z.; Shen, C. Datasetdm: Synthesizing data with perception annotations using diffusion models. Adv. Neural Inf. Process. Syst. 2023, 36, 54683–54695. [Google Scholar]
- Lee, H.Y.; Tseng, H.Y.; Yang, M.H. Exploiting diffusion prior for generalizable dense prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Waikoloa, HI, USA, 1–10 January 2024; pp. 7861–7871. [Google Scholar]
- Chen, S.; Sun, P.; Song, Y.; Luo, P. Diffusiondet: Diffusion model for object detection. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–3 October 2023; pp. 19830–19843. [Google Scholar]
- Tosi, F.; Ramirez, P.Z.; Poggi, M. Diffusion models for monocular depth estimation: Overcoming challenging conditions. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; Springer: Berlin/Heidelberg, Germany, 2024; pp. 236–257. [Google Scholar]
- Esser, P.; Rombach, R.; Ommer, B. Taming transformers for high-resolution image synthesis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12873–12883. [Google Scholar]
- Park, T.H.; Märtens, M.; Lecuyer, G.; Izzo, D.; D’Amico, S. SPEED+: Next-generation dataset for spacecraft pose estimation across domain gap. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–15. [Google Scholar]
- Guo, Y.; Feng, Z.; Song, B.; Li, X. SSP: A large-scale semi-real dataset for semantic segmentation of spacecraft payloads. In Proceedings of the 2023 8th International Conference on Image, Vision and Computing (ICIVC), Dalian, China, 27–29 July 2023; pp. 831–836. [Google Scholar]
- Wang, Z.; Zhang, Z.; Sun, X.; Li, Z.; Yu, Q. Revisiting Monocular Satellite Pose Estimation With Transformer. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4279–4294. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, M.; Guo, Y.; Li, Z.; Yu, Q. Bridging the Domain Gap in Satellite Pose Estimation: A Self-Training Approach Based on Geometrical Constraints. IEEE Trans. Aerosp. Electron. Syst. 2023, 60, 2500–2514. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Tranheden, W.; Olsson, V.; Pinto, J.; Svensson, L. Dacs: Domain adaptation via cross-domain mixed sampling. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 1379–1389. [Google Scholar]
- Pissas, T.; Ravasio, C.S.; Cruz, L.D.; Bergeles, C. Multi-scale and cross-scale contrastive learning for semantic segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 413–429. [Google Scholar]
- Wang, W.; Zhou, T.; Yu, F.; Dai, J.; Konukoglu, E.; Van Gool, L. Exploring cross-image pixel contrast for semantic segmentation. In Proceedings of the of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 20–25 June 2021; pp. 7303–7313. [Google Scholar]
- Xu, J.; De Mello, S.; Liu, S.; Byeon, W.; Breuel, T.; Kautz, J.; Wang, X. Groupvit: Semantic segmentation emerges from text supervision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 18134–18144. [Google Scholar]
- Sakai, T.; Qiu, H.; Katsuki, T.; Kimura, D.; Osogami, T.; Inoue, T. A surprisingly simple approach to generalized few-shot semantic segmentation. Adv. Neural Inf. Process. Syst. 2024, 37, 27005–27023. [Google Scholar]
- Wang, J.; Zhang, B.; Pang, J.; Chen, H.; Liu, W. Rethinking prior information generation with clip for few-shot segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Waikoloa, HI, USA, 1–10 January 2024; pp. 3941–3951. [Google Scholar]
- Zhu, L.; Chen, T.; Ji, D.; Ye, J.; Liu, J. Llafs: When large language models meet few-shot segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Waikoloa, HI, USA, 1–10 January 2024; pp. 3065–3075. [Google Scholar]
- Zhu, M.; Liu, Y.; Luo, Z.; Jing, C.; Chen, H.; Xu, G.; Wang, X.; Shen, C. Unleashing the potential of the diffusion model in few-shot semantic segmentation. Adv. Neural Inf. Process. Syst. 2024, 37, 42672–42695. [Google Scholar]
- Qin, Z.; Xu, J.; Ge, W. DeFSS: Image-to-Mask Denoising Learning for Few-shot Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Nashville, TN, USA, 11–15 June 2025; pp. 22232–22240. [Google Scholar]
- Zhao, C.; Sun, Y.; Liu, M.; Zheng, H.; Zhu, M.; Zhao, Z.; Chen, H.; He, T.; Shen, C. Diception: A generalist diffusion model for visual perceptual tasks. arXiv 2025, arXiv:2502.17157. [Google Scholar] [CrossRef]
- Xu, J.; Liu, S.; Vahdat, A.; Byeon, W.; Wang, X.; De Mello, S. Open-vocabulary panoptic segmentation with text-to-image diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Paris, France, 2–3 October 2023; pp. 2955–2966. [Google Scholar]
- Baranchuk, D.; Voynov, A.; Rubachev, I.; Khrulkov, V.; Babenko, A. Label-Efficient Semantic Segmentation with Diffusion Models. In Proceedings of the International Conference on Learning Representations, Virtual, 25–29 April 2022. [Google Scholar]




| Dataset | Link | Number of Categories | Classes |
|---|---|---|---|
| SatelliteDataset [2] | https://github.com/Yurushia1998/SatelliteDataset (accessed on 18 September 2025) | 3 | [Body; Solar panel; Antenna] |
| Speed+ [46] | https://github.com/willer94/lava1302 (accessed on 18 September 2025) | 3 | [Body; Solar panel; Antenna] |
| UESD [4] | https://github.com/zhaoyunpeng57/BUAA-UESD33 (accessed on 18 September 2025) | 5 | [Solar panel; Antenna; Instrument; Thruster; Optical Payload] |
| SSP [47] | https://github.com/Dr-zfeng/SPSNet (accessed on 18 September 2025) | 4 | [Body (Spacecraft); Solar panels; Radar; Thruster] |
| MIAS [29] | https://github.com/xiang-ao-data/Spacefuse-shadow-removal/tree/master (accessed on 18 September 2025) | 3 | [Body; Solar panel; Antenna] |
| Training Samples | mIoU | |||
|---|---|---|---|---|
| Antenna1 | Antenna2 | Antenna3 | Avg. | |
| SatelliteDataset & Speed+ (One-shot) | 44.9 | 42.6 | 53.7 | 47.1 |
| SatelliteDataset & Speed+ (Three-shot) | 50.8 | 49.5 | 60.1 | 53.5 |
| SatelliteDataset & Speed+ (Ten-shot) | 57.2 | 55.7 | 68.5 | 60.5 |
| mIoU | |||||||
|---|---|---|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | ||||
| 1 | 65.7 | 64.6 | 5.6 | 45.3 | |||
| 2 | ✓ | 77.5 | 70.9 | 60.7 | 69.7 | ||
| 3 | ✓ | ✓ | 81.1 | 72.2 | 64.7 | 72.7 | |
| 4 | ✓ | ✓ | 82.9 | 73.5 | 65.3 | 73.9 | |
| 5 | ✓ | ✓ | ✓ | 86.5 | 77.5 | 69.8 | 77.9 |
| Diffusion Model | Stable Diffusion v1.4 | Stable Diffusion v1.5 | Stable Diffusion v2.1 |
|---|---|---|---|
| mIoU | 77.8 | 77.8 | 77.9 |
| Layer-i of Diffusion Feature | mIoU | |||
|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | |
| 3 | 82.7 | 73.9 | 65.7 | 74.1 |
| 6 | 82.4 | 73.2 | 66.3 | 74.0 |
| 12 | 82.4 | 73.9 | 66.5 | 74.3 |
| 3, 6 | 83.3 | 74.9 | 67.6 | 75.3 |
| 6, 9 | 83.5 | 74.2 | 67.4 | 75.0 |
| 9, 12 | 84.1 | 74.0 | 67.7 | 75.3 |
| 3, 6, 9 | 85.7 | 75.8 | 68.1 | 76.5 |
| 6, 9, 12 | 85.9 | 76.1 | 68.8 | 76.9 |
| 3, 6, 9, 12 | 86.5 | 77.5 | 69.8 | 77.9 |
| All | 86.4 | 77.2 | 69.5 | 77.7 |
| Downsampling Scale | mIoU | |||
|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | |
| 2× | 85.2 | 75.7 | 67.5 | 76.1 |
| 4× | 86.5 | 77.5 | 69.8 | 77.9 |
| 8× | 84.3 | 74.9 | 66.7 | 75.3 |
| 0.5 | 1 | 1.5 | 2 | |
|---|---|---|---|---|
| mIoU | 76.8 | 77.9 | 77.1 | 76.2 |
| 0.5 | 1 | 1.5 | 2 | |
|---|---|---|---|---|
| mIoU | 76.3 | 77.9 | 76.9 | 76.0 |
| Fine-Tune Method | Trainable Parameters | mIoU | |||
|---|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | ||
| Full | 368M | 78.3 | 68.9 | 61.2 | 69.5 |
| Ours | 5.9M | 86.5 | 77.5 | 69.8 | 77.9 |
| t | mIoU | |||
|---|---|---|---|---|
| Body | Solar Panel | Antenna | Avg. | |
| 0 | 85.0 | 76.4 | 68.7 | 76.7 |
| 25 | 85.2 | 76.5 | 69.1 | 76.9 |
| 50 | 85.5 | 77.0 | 69.5 | 77.3 |
| 75 | 86.1 | 77.3 | 69.7 | 77.7 |
| 100 | 86.5 | 77.5 | 69.8 | 77.9 |
| 150 | 85.9 | 77.2 | 69.4 | 77.5 |
| 200 | 85.8 | 77.0 | 68.3 | 77.0 |
| 300 | 85.1 | 76.4 | 67.8 | 76.4 |
| 500 | 84.0 | 74.9 | 66.9 | 75.3 |
| Method | Training Time (h) | Trainable Parameters (M) | Inference Time (s) |
|---|---|---|---|
| DeepLabV3+ | 3.8 | 62 | 0.10 |
| Mask2Former | 4.2 | 89 | 0.13 |
| PI-CLIP | 6.1 | 63 | 0.26 |
| DeFSS | 8.6 | 97 | 0.35 |
| Ours | 4.3 | 21 | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhang, Z.; Wang, X.; Wang, X.; Xu, Y. Exploiting Diffusion Priors for Generalizable Few-Shot Satellite Image Semantic Segmentation. Remote Sens. 2025, 17, 3706. https://doi.org/10.3390/rs17223706
Li F, Zhang Z, Wang X, Wang X, Xu Y. Exploiting Diffusion Priors for Generalizable Few-Shot Satellite Image Semantic Segmentation. Remote Sensing. 2025; 17(22):3706. https://doi.org/10.3390/rs17223706
Chicago/Turabian StyleLi, Fan, Zhaoxiang Zhang, Xuan Wang, Xuanbin Wang, and Yuelei Xu. 2025. "Exploiting Diffusion Priors for Generalizable Few-Shot Satellite Image Semantic Segmentation" Remote Sensing 17, no. 22: 3706. https://doi.org/10.3390/rs17223706
APA StyleLi, F., Zhang, Z., Wang, X., Wang, X., & Xu, Y. (2025). Exploiting Diffusion Priors for Generalizable Few-Shot Satellite Image Semantic Segmentation. Remote Sensing, 17(22), 3706. https://doi.org/10.3390/rs17223706





