Hyperspectral Object Tracking via Band and Context Refinement Network

Highlights

What are the main findings?

• Developed a hyperspectral tracker with band-importance modeling and contextual feature refinement.
• Uses importance-guided spectral grouping to enhance tracking accuracy.

What is the implication of the main finding?

• Its spectral and contextual design helps track objects more accurately in complex scenes.
• Improves robustness of target localization in challenging hyperspectral videos.

Abstract

The scarcity of labeled hyperspectral video samples has motivated existing methods to leverage RGB-pretrained networks; however, many existing methods of hyperspectral object tracking (HOT) select only three representative spectral bands from hyperspectral images, leading to spectral information loss and weakened target discrimination. To address this issue, we propose the Band and Context Refinement Network (BCR-Net) for HOT. Firstly, we design a band importance learning module to partition hyperspectral images into multiple false-color images for pre-trained backbone network. Specifically, each hyperspectral band is expressed as a non-negative linear combination of other bands to form a correlation matrix. This correlation matrix is used to guide an importance ranking of the bands, enabling the grouping of bands into false-color images that supply informative spectral features for the multi-branch tracking framework. Furthermore, to exploit spectral–spatial relationships and contextual information, we design a Contextual Feature Refinement Module, which integrates multi-scale fusion and context-aware optimization to improve feature discrimination. Finally, to adaptively fuse multi-branch features according to band importance, we employ a correlation matrix-guided fusion strategy. Extensive experiments on two public hyperspectral video datasets show that BCR-Net achieves competitive performance compared with existing classical tracking methods.

1. Introduction

Hyperspectral object tracking (HOT) constitutes a key problem in computer vision, with broad applications in intelligent surveillance [1], traffic monitoring [2], and medical imaging analysis [3]. Given an initial target annotation in the first frame, a tracker must localize the target throughout subsequent frames despite appearance variation, motion dynamics, partial occlusion, illumination changes, and background clutter. While deep RGB-based trackers have achieved notable advances  [4,5,6], their reliance on only three broad spectral channels inherently limits discriminability, especially in low-contrast scenes, camouflage settings, and spectrally ambiguous backgrounds frequently encountered in remote sensing and geoscience monitoring.

Hyperspectral imaging (HSI) acquires contiguous narrow-band reflectance measurements, often spanning on the order of tens to over one hundred bands, providing rich joint spatial–spectral information capable of distinguishing targets with similar spatial texture but differing spectral signatures [7]. This fine-grained spectral resolution is particularly advantageous in scenarios involving small or partially occluded objects embedded in spectrally heterogeneous or cluttered environments. Consequently, HOT has emerged as a promising extension of traditional RGB tracking for improved robustness and semantic discrimination in complex environments.

A central challenge in hyperspectral object tracking is obtaining features that reliably distinguish the target from its background under varying conditions. Early HOT methods (such as references [8,9,10]) mainly rely on manually designed features to construct the spectral or spatial expression of the target, such as material abundance, spectral gradient histogram or specific convolution kernel. While these feature representation strategies achieved successes, they lack adaptability, and it is  difficult for them to handle rapid target appearance changes or severe occlusions. In contrast, deep learning has transformed RGB tracking by leveraging large-scale annotated datasets [11,12] to learn hierarchical, discriminative representations.

Due to the scarcity of large labeled hyperspectral video datasets, directly training deep HOT architectures end-to-end often leads to overfitting and unstable optimization. To mitigate this data limitation, a prevalent line of work transfers RGB-pretrained backbones (e.g., GOT-10K [13], TrackingNet [14], LaSOT [15]) to hyperspectral scenarios by first converting the high-dimensional hyperspectral data into one or more three-channel false-color composites [16]. Single-composite methods usually follow two paradigms: (i) selecting three key bands using conventional techniques for dimensionality reduction, such as PCA, or via learning-based selection networks [17], and (ii) constructing a three-channel surrogate image by replicating existing bands. Specifically, band selection is sensitive and may exclude narrow yet discriminative spectral responses critical for small or low-contrast targets. Replication yields zero inter-channel diversity, preventing the pretrained filters from exploiting cross-channel interactions. Adjacent or sequential grouping preserves high local spectral correlation, causing redundant channel responses and underutilizing potential complementary cues. PCA emphasizes directions of maximal global variance; thus, minority-band features with high target–background discriminability but low energy risk being attenuated or entangled in principal components dominated by background structure. However, the above methods collectively reduce spectral separability, distort the statistical assumptions underlying RGB pretraining, and constrain downstream feature discrimination.

Alternatively, hyperspectral bands can be randomly grouped to form false-color composites, with the intention of reducing inter-channel correlation. However, this strategy treats all bands as equally important. In reality, different wavelengths vary significantly in their contribution to hyperspectral image formation and downstream tasks, as demonstrated by band selection studies [18]. Consequently, random grouping often mixes weakly informative or noisy bands with discriminative ones, which negatively impacts hyperspectral tracking and increases training difficulty. To mitigate this problem, Li et al. introduced the Band Attention Ensemble Network (BAE-Net) [19], which employs a band attention module to estimate spectral importance and groups bands accordingly before constructing false-color images. This line of work highlights that incorporating band importance into grouping leads to more reliable representations than purely random partitioning.

Building on the idea of leveraging multiple spectral views, recent multi-branch trackers such as SST-Net [20] and BRRF-Net [21] extend this paradigm by generating several composites and processing them in parallel. Although methods like BAE-Net already consider band importance during grouping, most of these trackers still fuse the outputs of different branches through uniform averaging, effectively assuming equal reliability across composites. In practice, a branch dominated by weak or interference-prone bands can produce an outlier response map; equal weighting then propagates this error and increases the risk of drift. Compounding the issue, adverse imaging factors (e.g., motion blur, defocus, low illumination) erode high-level spatial structure and channel discriminability. Existing refinement modules rarely perform coupled spatial–channel enhancement, limiting their ability to recover degraded details. Although adaptive update mechanisms alleviate gradual appearance evolution, they do not explicitly quantify band importance or implement reliability-aware suppression of low-quality branches.

Despite these advances, hyperspectral tracking still faces two key challenges. First, severe spectral redundancy can cause the tracker to overemphasize noisy or weakly discriminative bands, thereby diluting target–background contrast and increasing false responses. Second, spatial degradation from factors such as blur or low resolution weakens high-level structural integrity, raising the risk of localization drift. We tackle these issues with a Band and Context Refinement Network (BCR-Net), which unifies explicit spectral importance estimation, contextual feature enhancement, and reliability-aware fusion. Specifically, the Band Importance Modeling Module (BIMM) leverages the linear self-representation property of hyperspectral imagery: a U-Net-based unrolled gradient descent solver produces a sparse band coefficient matrix that captures complementary relations while suppressing redundancy. This matrix is then used to (i) quantify per-band importance and (ii) construct multiple complementary false-color composites, allowing an RGB-pretrained backbone to harvest transferable semantic and spatial priors. Building upon the resulting high-level features, the Contextual Feature Refinement Module (CFRM) applies cross-dimensional attention to jointly enhance spatial detail fidelity and channel-wise discriminability. Finally, we perform dynamic reliability-aware fusion: branch-level tracking outputs are adaptively weighted by importance scores derived from the coefficient matrix, effectively attenuating unstable predictions from low-importance or interference-prone composites.

The main contributions of this study can be summarized as follows:

• We propose a unified hyperspectral tracking framework that integrates spectral band importance modeling with RGB-pretrained backbones. By selectively emphasizing informative bands and guiding feature construction, the framework achieves stable representations, efficient adaptation, and enhanced discriminative power during tracking.
• We reformulate the spectral self-expression prior into a parameterized module that learns band-wise importance and guides feature construction, explicitly addressing spectral redundancy and improving the discriminative power of the features.
• We employ a Contextual Feature Refinement Module to enhance multi-scale feature representations, improving discriminative power for target–background separation.
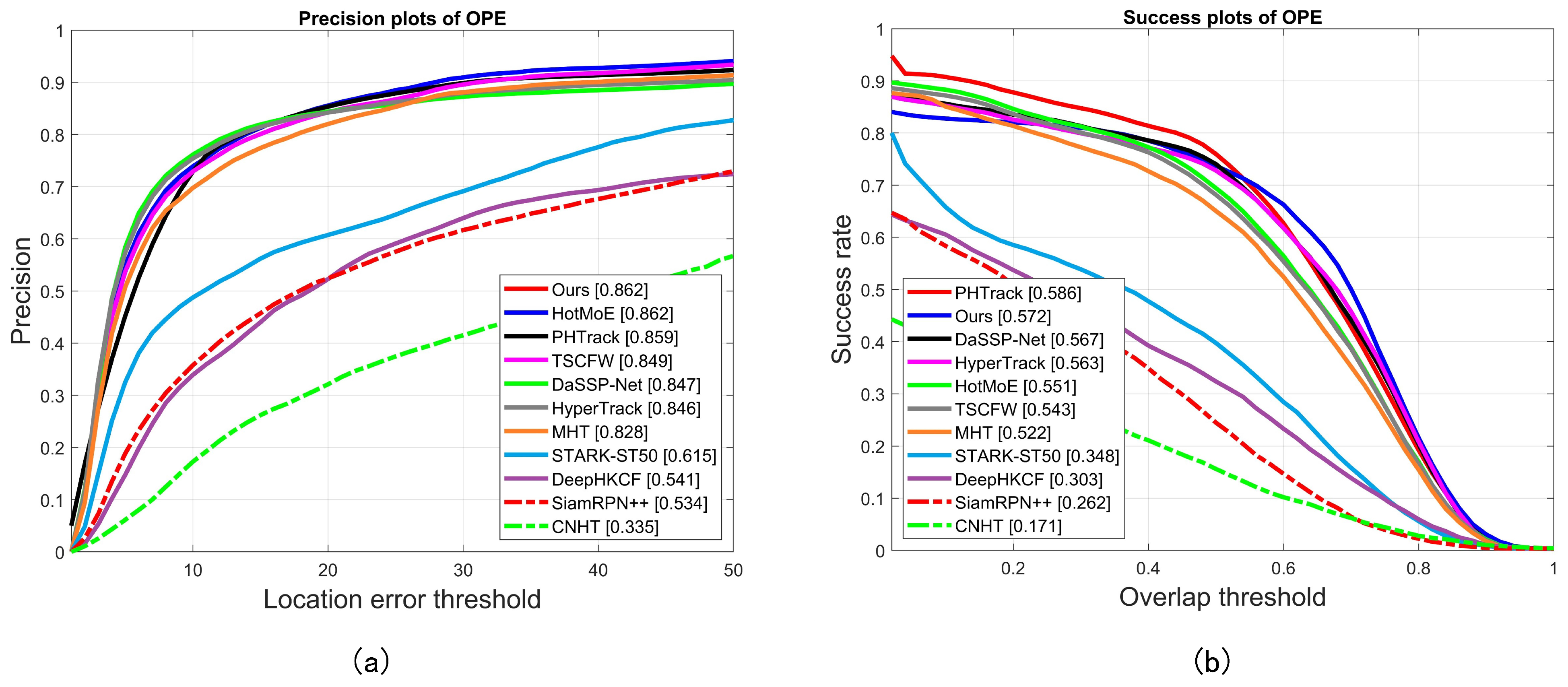
• Extensive experiments on two public hyperspectral video datasets demonstrate that BCR-Net is competitive with existing methods, achieving strong performance in both tracking accuracy and robustness.

The remainder of this paper is organized as follows. Section 2 reviews related work, Section 3 describes the proposed tracker architecture, Section 4 presents comparative analyses with other trackers and includes ablation studies, and Section 5 concludes the paper.

2. Related Works

Current hyperspectral object tracking (HOT) methods have primarily evolved along two directions: correlation filter-based (CF) approaches and deep learning-based (DL) approaches. In the following, we review each category, highlighting their key techniques, advantages, and limitations.

2.1. Correlation Filter-Based HOT

CF methods constitute one of the earliest and most widely adopted strategies for HOT. These methods track targets by learning correlation filters that model the relationship between the target’s spectral–spatial characteristics and its surrounding context. Qian et al. [22] proposed using normalized 3D spectral–spatial cubes as convolution filters to capture local spectral–spatial patterns for hyperspectral object tracking. Zhang et al. [8] introduced a method that combines convolutional features from VGGNet with HOG descriptors and fuses their responses through correlation filters to improve tracking robustness under complex backgrounds. To address occlusions and illumination variations, Guo et al. [23] developed a method that incorporates adaptive weighting and background-aware correlation filters to suppress anomalies in response maps.

To enhance feature extraction efficiency, Chen et al. [24] proposed using fast spatial–spectral convolution kernels with closed-form solutions in the Fourier domain for real-time spectral–spatial feature learning. A tensor-based sparse correlation filter incorporating spatial–spectral weighted regularization was proposed by Hou et al. [10] to reduce background interference and enhance spectral discriminability. Building on these approaches, Lou et al. [25] proposed combining deep and spatial–spectral features by extracting 3D gradient-based spatial features through tensor singular spectrum analysis and convolutional features from a VGGNet pretrained on RGB images, thereby improving tracking accuracy by exploiting the complementarity of deep and enhanced spectral–spatial representations.

Overall, CF methods for HOT provide advantages such as low computational overhead, ease of implementation, and effective use of spectral–spatial priors. Nevertheless, their heavy reliance on handcrafted or predefined features limits adaptability in challenging scenarios, including occlusions, rapid appearance variations, and cluttered environments.

2.2. Deep Learning-Based HOT

DL methods have recently emerged as a major direction in HOT, offering the ability to learn adaptive spectral–spatial representations. The critical challenge, however, lies in the scarcity of labeled hyperspectral video data, which makes it impractical to train large-scale backbone networks tailored specifically for HOT. To mitigate this limitation, many studies transfer knowledge from RGB-pretrained models by dividing hyperspectral bands into groups and generating false-color images for training. Uzkent et al. [26] proposed reducing hyperspectral data to three channels and applying an RGB-pretrained VGGNet to extract robust features for target representation. Wang et al. [27] proposed a strategy that selects representative bands using joint entropy and utilizes RGB-pretrained Siamese networks to achieve effective semantic feature extraction under constrained training conditions.

Building upon RGB-pretrained backbones, many existing methods have specifically utilized spectral–spatial correlations to enhance feature discrimination. Specifically, Wu et al. [21] reorganized hyperspectral bands into groups based on learned correlations and fused them for robust representation, but the final fusion relied on uniform averaging without fully exploiting learned band importance. Liu et al. [16] designed a dual Siamese framework with a hyperspectral target-aware module and spatial–spectral cross-attention for adaptive fusion, yet lacked reliability-aware weighting and coupled spatial–channel refinement. Zhao et al. [28] developed a transformer-based fusion network to capture intra- and inter-band interactions across modalities, effectively integrating hyperspectral and RGB information. Chen et al. [29] proposed a spectral awareness module with feature interaction to model band dependencies and strengthen fusion, but did not incorporate importance learning into a unified fusion strategy. Jiang et al. [30] introduced a channel-adaptive dual Siamese architecture to flexibly handle sequences with varied spectral channels. Xiong et al. [31] introduced SSTCF, which employs spatial–spectral features and a low-rank constraint to enhance global spectral structure, while incorporating temporal consistency to maintain filter stability across consecutive frames. Gao et al. [32] proposed SP-HST, a parameter-efficient method that freezes a pre-trained RGB network and trains only a lightweight branch to generate spectral prompts, which provide complementary HSI information fused with the frozen RGB features for the final tracking decision. Wang et al. [33] presented SSF-Net, which employs spectral angle awareness to capture region-level spectral relationships, achieving more robust spatial–spectral representations for hyperspectral tracking.

Overall, DL-based HOT methods have demonstrated strong effectiveness in leveraging spectral–spatial fusion and knowledge transfer from pre-trained RGB models. Although the above-mentioned methods adopt band regrouping to improve hyperspectral tracking, they often fail to fully exploit the varying importance of spectral bands and suffer from degraded feature discrimination under complex conditions, which limits their efficiency and robustness. Therefore, in this paper, we propose BCR-Net to address these limitations through BIMM and CFRM, enabling adaptive band grouping and contextual refinement.

3. Proposed Method

Here, we describe the Band and Context Refinement Network (BCR-Net), which combines the Band Importance Modeling Module (BIMM) with the Contextual Feature Refinement Module (CFRM).

3.1. Overall Architecture

Since hyperspectral images contain high-dimensional spectral information that cannot be directly processed by conventional RGB-based object trackers, we propose the BCR-Net for hyperspectral tracking. It first learns the importance of each spectral channel and groups the hyperspectral data into multiple false-color images accordingly. Semantic features at a high level are extracted from the grouped images using a pretrained RGB backbone. Finally, the features from different groups are adaptively fused using importance-guided weighting, enabling robust spectral–spatial representation and accurate target localization.

Figure 1 illustrates the overall framework, which adopts a Siamese network architecture and includes three main components: (i) a dynamic spectral feature learning module, (ii) a backbone network for feature extraction, and (iii) an integrated prediction module. Input data is fed into two parallel branches: the template branch representing the initial target patch, and the search branch containing candidate regions from later frames.

The dynamic spectral feature learning module first analyzes inter-band relationships and channel importance through an auxiliary reconstruction task. This step projects the original C-dimensional spectral cube into multiple three-channel false-color images that preserve discriminative information while reducing redundancy. These false-color groups are then fed into a pretrained RGB backbone (e.g., ResNet-50), shared by both template and search branches, to obtain deep semantic features. On top of the backbone output, a context-aware feature refinement module further processes the features to capture fine-grained spatial details and inter-channel correlations, ensuring the extracted representations remain robust for subsequent tracking.

Finally, the integrated prediction module aggregates the similarity maps produced by different false-color branches. To balance their contributions, each branch is adaptively weighted according to the spectral importance scores estimated in the dynamic spectral feature learning stage. The response map guides target localization, complemented by a dynamic template update that adjusts for temporal appearance changes.

3.2. Band Importance Modeling Module

Hyperspectral data are usually converted into three-channel composites to fit RGB-pretrained CNNs, but sequential grouping produces highly correlated channels, and independent processing overlooks spectral structure, both of which weaken discriminability. To overcome these issues, we adopt an importance-guided grouping strategy that ranks bands by significance and assembles them into complementary composites, reducing redundancy while preserving informative cues for robust multi-branch tracking.

For a hyperspectral image $\mathit{X}$, we model intrinsic dependencies between spectral bands by leveraging the prior that each band can be roughly represented as a linear combination of the others. Accordingly, we learn a band correlation matrix via a spectral self-expression model, expressed as a non-negative reconstruction coefficient matrix $\mathit{W}\in {\mathbb{R}}^{B\times B}$. Each row of $\mathit{W}$ indicates how a band is reconstructed from the others, capturing inter-band dependencies, and summing the coefficients provides a quantitative measure of band importance, with larger values highlighting more discriminative spectral channels. Mathematically, the spectral self-expression model is formulated as

$$\underset{\mathit{W}}{min}{\displaystyle \frac{1}{2}}{\parallel \mathit{X}-\mathit{X}\mathit{W}\parallel }_F^2,\mathrm{s}.\mathrm{t}.\mathit{W}\ge 0,diag\left(\mathit{W}\right)=0$$

(1)

where ${\parallel ·\parallel }_F$ denotes the Frobenius norm. The non-negativity constraint $\mathit{W}\ge 0$ ensures physically meaningful importance values, while the zero-diagonal constraint $diag\left(\mathit{W}\right)=0$ prevents self-reconstruction and stabilizes the estimated band importance.

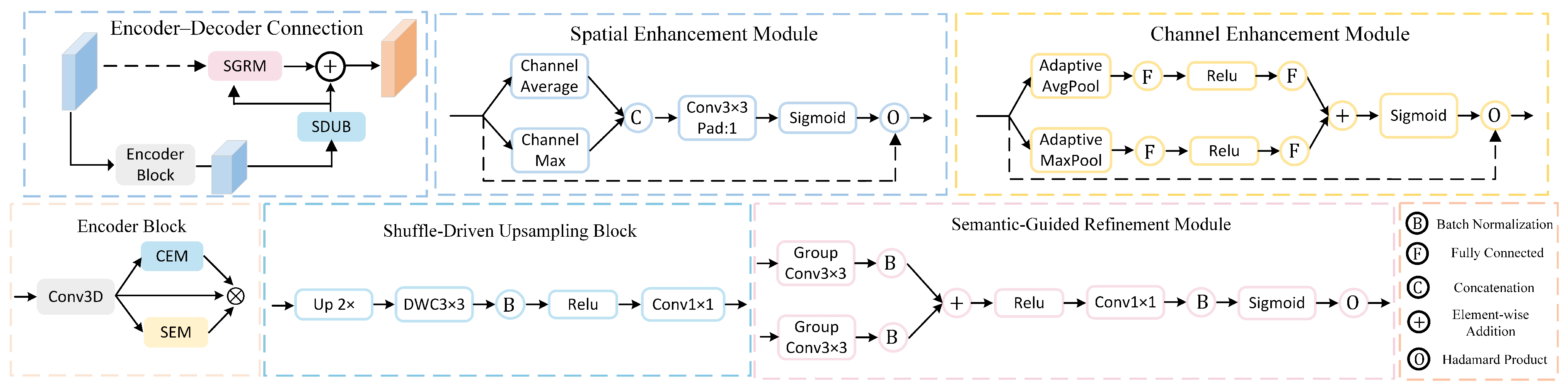
To implement the spectral self-expression problem in Equation (1), we employ an encoder–decoder architecture based on U-Net. Figure 2 depicts the connection between the last encoder block and the first decoder block, as well as the internal structure of each submodule. The reconstruction coefficient matrix $\mathit{W}$ is approximated by aggregating learned spectral–spatial features in a differentiable, end-to-end manner. The encoder captures multi-scale spectral–spatial representations, encoding both local patterns and global inter-band dependencies, while channel and spatial enhancement modules emphasize informative features. The decoder restores spatial resolution and fuses multi-scale features via a Semantic-Guided Refinement Module, where high-level features guide adaptive weighting of low-level features. From the decoder output, a global pooling operation aggregates feature correlations to produce an initial channel weight matrix ${\mathit{W}}_0$, providing a coarse approximation of the reconstruction coefficients $\mathit{W}$. Non-negativity and zero-diagonal constraints are enforced via simple activation and masking, and a lightweight Channel Weight Refinement module further optimizes ${\mathit{W}}_0$ to emphasize informative bands while suppressing redundancies.

3.2.1. Encoder of BIMM

In hyperspectral image reconstruction, the encoder must model both spectral and spatial correlations to extract discriminative features that distinguish the object from its background. We integrate two complementary modules: the Channel Enhancement Module (CEM) for modeling spectral dependencies and alleviating inter-band redundancy, and the spatial enhancement module (SEM) for identifying important spatial regions and enhancing structural details. This design adaptively enhances informative features while suppressing redundancy, improving discrimination and robustness.

Given an input feature map $\mathbf{X}$, CEM first applies adaptive average pooling ${\mathrm{P}}_{\mathrm{a}}(·)$ and max pooling ${\mathrm{P}}_{\mathrm{m}}(·)$ to obtain global channel descriptors $f_{avg}$ and $f_{max}$. Each descriptor is then passed through two fully connected layers: the first reduces the channel dimension to $C/r$ (with $r=2$), and the second restores it, with a ReLU activation in between. The outputs are summed and passed through a Softplus activation to generate the channel weight matrix $\mathit{W}\in {\mathbb{R}}^{B\times C}$, which is broadcasted to match the original feature dimensions and multiplied element-wise (⊙) with $\mathbf{X}$:

$$\mathrm{CEM}\left(\mathbf{X}\right)=\mathrm{Softplus}\left({\mathrm{fc}}_2\left(\mathrm{ReLU}\left({\mathrm{fc}}_1\left({\mathrm{P}}_{\mathrm{m}}\left(\mathbf{X}\right)\right)\right)\right)+{\mathrm{fc}}_2\left(\mathrm{ReLU}\left({\mathrm{fc}}_1\left({\mathrm{P}}_{\mathrm{a}}\left(\mathbf{X}\right)\right)\right)\right)\right)\odot \mathbf{X}$$

(2)

While CEM captures spectral relationships, it does not directly model spatial structures. To address this, the SEM module enhances spatial saliency by highlighting important positions and suppressing irrelevant regions. For an input $\mathbf{X}$, SEM computes channel-wise max and average maps, $m_{max}$ and $m_{avg}$, concatenates them, and applies a $3\times 3$ convolution with padding, followed by a Sigmoid activation ($\sigma$) to generate the spatial weight map $\mathit{W}\in {\mathbb{R}}^{B\times 1\times H\times W}$. The output is then obtained via element-wise multiplication (⊙) with $\mathbf{X}$:

$$\mathrm{SEM}\left(\mathbf{X}\right)=\sigma \left({\mathrm{Conv}}_{3\times 3}\left([m_{max},m_{avg}]\right)\right)\odot \mathbf{X}$$

(3)

where $[·,·]$ denotes concatenation along the channel dimension.

By stacking multiple 3D convolution layers, each followed by SEM and CEM, the encoder progressively captures and enhances spectral–spatial features. Specifically, SEM strengthens important spatial structures, while CEM emphasizes discriminative spectral channels. The output of the l-th encoder layer is expressed as

$$F_E^{\left(l\right)}={\mathrm{CEM}}^{\left(l\right)}\left({\mathrm{SEM}}^{\left(l\right)}\left(\mathrm{Conv}3{\mathrm{D}}^{\left(l\right)}\left({\mathbf{X}}_E^{(l-1)}\right)\right)\right)$$

(4)

This design combines convolution with spectral–spatial enhancement in a complementary way, leading to more discriminative feature representations and laying a strong foundation for decoding and reconstruction.

3.2.2. Decoder of BIMM

A high-quality decoder is essential for restoring spatial resolution, reconstructing boundary details, and maintaining semantic consistency. In this work, the decoder addresses both feature reconstruction and semantic refinement by integrating two complementary modules. The Shuffle-Driven Upsampling Block (SDUB) progressively upsamples features while preserving fine-grained spatial–spectral information, ensuring accurate reconstruction of target details. The Semantic-Guided Refinement Module (SGRM) captures global spectral–spatial dependencies and enhances salient semantic features, thereby improving the overall discriminability of the reconstructed output. This design effectively recovers feature scales, fuses cross-level information, and enhances salient regions.

The SDUB is designed to efficiently enhance spatial resolution while preserving feature quality. It takes either the last encoder output (for the first decoder layer) or the previous decoder feature map (for subsequent layers) and first performs bilinear interpolation to double the spatial size. Local channel features are then extracted via a depthwise separable convolution ($groups=C_{in}$), followed by a channel rearrangement to promote cross-channel fusion, and finally a $1\times 1$ convolution adjusts the output to the target channel dimension $C_{out}$. Formally, the operation on $F_E^{\left(l\right)}$ is expressed as

$$\mathrm{SDUB}\left(F_E^{\left(l\right)}\right)={\mathrm{Conv}}_{1\times 1}\left(\mathrm{ReLU}\left(\mathrm{BN}\left(\mathrm{DWC}\left(\mathrm{Up}\left(F_E^{\left(l\right)}\right)\right)\right)\right)\right)$$

(5)

While SDUB efficiently upsamples feature maps, effectively fusing multi-level features remains challenging. Low-level decoder features contain fine-grained details but are noisy and semantically weak, whereas high-level encoder features provide rich semantic context but suffer from reduced spatial resolution and blurred boundaries. Simple concatenation or addition often preserves noise and dilutes semantics, resulting in suboptimal reconstruction.

In response, we introduce the Semantic-Guided Refinement Module (SGRM) to refine low-level decoder features using high-level encoder information. Specifically, for the l-th decoding layer, let $F_E^{\left(l\right)}$ and $F_D^{(l-1)}$ denote the encoder and previous decoder features after SDUB upsampling. Both are processed by $3\times 3$ grouped convolutions with batch normalization, spatially aligned via bilinear interpolation if needed, and fused through element-wise addition followed by ReLU to form the intermediate attention tensor $q_{att}(F_E^{\left(l\right)},F_D^{(l-1)})$:

$$q_{att}(F_E^{\left(l\right)},F_D^{(l-1)})=\mathrm{ReLU}\left(\mathrm{BN}({\mathrm{GC}}_{\mathrm{E}}\left(F_E^{\left(l\right)}\right)+\mathrm{BN}\left({\mathrm{GC}}_{\mathrm{D}}\left(F_D^{(l-1)}\right)\right))\right)$$

(6)

where $G{C}_E$/$G{C}_D$ are $3\times 3$ grouped convolutions.

The intermediate tensor $q_{att}(F_E^{\left(l\right)},F_D^{(l-1)})$ passes through a $1\times 1$ convolution with batch normalization and Sigmoid activation, and the resulting spatial attention map modulates $F_D^{(l-1)}$ via element-wise multiplication to produce the fused decoder feature:

$$\mathrm{SGRM}(F_E^{\left(l\right)},F_D^{(l-1)})=F_D^{(l-1)}\odot \sigma \left(\mathrm{BN}\left(\mathbf{C}\left(q_{att}(F_E^{\left(l\right)},F_D^{(l-1)})\right)\right)\right)$$

(7)

The decoder reconstructs multi-level semantic information by applying SDUB and SGRM in a nested manner:

$$F_D^{\left(l\right)}=\mathrm{SGRM}\left(F_E^{\left(l\right)},\mathrm{SDUB}\left(F_D^{(l-1)}\right)\right)$$

(8)

In this structure, SDUB upsamples the previous decoder output, while SGRM fuses it with the corresponding encoder features, enabling efficient multi-scale feature reconstruction with enhanced spatial details and semantic consistency.

3.2.3. Channel Weight Refinement of BIMM

To capture inter-channel dependencies in the decoder features, we apply global average pooling ($\mathrm{avg}(·)$) to the decoder output $F_D$ to obtain a channel-wise summary. The correlation matrix of these pooled features is then mapped through a Softplus function to produce the initial channel weight matrix ${\mathit{W}}_0$:

$${\mathit{W}}_0=\mathrm{Softplus}\left(\mathrm{avg}\left(F_D\right)·\mathrm{avg}{\left(F_D\right)}^{\top }\right)$$

(9)

where ${\mathit{W}}_0\in {\mathbb{R}}^{C\times C}$ captures the similarity between different feature channels.

However, ${\mathit{W}}_0$ is a heuristic estimate that may contain noisy or suboptimal correlations, limiting its ability to highlight discriminative channels. To address this, we propose a single-step structural optimization module that refines ${\mathit{W}}_0$ while preserving its non-negativity and zero-diagonal constraints. A lightweight MLP ($G(·)$) predicts a gradient-like update for each element, simulating conventional gradient descent in a learnable, end-to-end manner. The refined weight matrix is computed as

$$\mathit{W}=\zeta \left({\mathit{W}}_0-G\left({\mathit{W}}_0\right)\right)$$

(10)

where $\zeta (·)$ is a diagonal suppression function that explicitly zeros out the diagonal elements of the matrix.

This single-step optimization captures the main structural patterns in channel correlations, promoting sparsity and highlighting important channels. By refining ${\mathit{W}}_0$ into a task-aligned, discriminative $\mathit{W}$, the decoder emphasizes informative channels and suppresses irrelevant ones, enhancing both feature discrimination and robustness while remaining consistent with the initial estimation.

3.3. Contextual Feature Refinement Module

Previous studies by Chen et al. [34] show that different backbone layers capture complementary information: shallow layers (e.g., conv3 in $ResNet$-50) retain high spatial resolution and encode local structures, aiding precise target localization, while deeper layers (e.g., conv4 and conv5) provide strong semantic abstraction, capturing high-level concepts and appearance variations. Accordingly, we select conv3, conv4, and conv5 for multi-scale feature fusion, forming a hierarchically complementary framework. To enhance context perception without increasing parameters, dilated convolutions with rates 2 and 4 are applied in conv4 and conv5, respectively. Spatial downsampling is removed in these stages to maintain consistent spatial sizes, ensuring alignment for multi-layer fusion and preserving both fine-grained details and semantic richness.

We further introduce a context-aware feature optimization module to enhance separability between template and search features. Channel-wise semantics are captured via global average and max pooling, while spatial dependencies are modeled by compressing the feature map into query and key matrices to compute a correlation score. A learnable $1\times 1$ convolution propagates contextual information, and the resulting channel and spatial cues are combined via element-wise Hadamard product to highlight salient regions and suppress background noise. Formally, this process is expressed as

$$\begin{array}{c}\hfill Q^j=P^j+a^j\sum _{j=1}^N\left[{\displaystyle \frac{exp\left({\omega }_{qk}{P}^j\right)}{{\sum }_{n=1}^{N}exp\left({\omega }_{qk}{P}^n\right)}}·{\omega }_v{P}^j\right],\\ \hfill a^j={\displaystyle \frac{exp\left([\mathrm{avg}\left(P\right);\max \left(P\right)]P^j\right)}{{\sum }_{n=1}^{N}exp\left([\mathrm{avg}\left(P\right);\max \left(P\right)]P^n\right)}}·{\omega }_v\end{array}$$

(11)

where $P^j$ and $Q^j$ are the input and output at the j-th pixel, N denotes the total number of pixels, ${\omega }_{qk}$ and ${\omega }_v$ are learnable $1\times 1$ convolution layers, $\mathrm{avg}(·)$ and $\max (·)$ compute global average and maximum pooling, $exp(·)$ is applied element-wise, and $\left[\mathrm{avg}\right(P);\max (P\left)\right]$ indicates concatenation along the channel dimension.

By jointly modeling channel semantics and spatial dependencies in this integrated manner, the Contextual Feature Refinement Module strengthens salient target representations and suppresses redundant background responses, providing robust, contextually enriched features for subsequent multi-branch tracking and prediction.

3.4. Training and Tracking

3.4.1. Offline Training

During training, the backbone $ResNet$-50 remains frozen, while the upstream modules—including the dynamic spectral feature learning module and multiple Box-Adaptive prediction heads—are optimized jointly in an end-to-end manner. Training pairs are constructed by sampling template and search regions from hyperspectral videos. The template and search regions are cropped from the original images and resized to $127\times 127\times B$ and $255\times 255\times B$, respectively, before being fed into the network.

To exploit multi-scale information from different backbone stages, a hierarchical fusion strategy is applied. Feature maps from conv3, conv4, and conv5 are extracted for classification and regression, and their outputs are combined using learnable weights ${\alpha }_k$ and ${\delta }_k$ to produce the final multi-level response maps:

$$Q_n^{cl{s}^{\prime }}=\sum _{k=3}^5{\alpha }_k{\left(Q_n^{cls}\right)}_k,Q_n^{bo{x}^{\prime }}=\sum _{k=3}^5{\delta }_k{\left(Q_n^{box}\right)}_k$$

(12)

where ${\left(Q_n^{cls}\right)}_k$ and ${\left(Q_n^{box}\right)}_k$ denote the classification and regression outputs from the k-th convolutional block, and the weights ${\alpha }_k$ and ${\delta }_k$ (initialized to 1) control each layer’s contribution.

For label assignment, we follow the ellipse sampling strategy [34]. In the search frame, the target is represented by a bounding box with top-left $(u_l,v_l)$, center $(u_c,v_c)$, and bottom-right $(u_r,v_r)$ coordinates, having width $w_b$ and height $h_b$. Two ellipses are generated at the box center: $E_1$ with semi-axes $w_b/2$ and $h_b/2$, and $E_2$ with semi-axes $w_b/4$ and $h_b/4$:

$$\begin{array}{c}\hfill {\left({\displaystyle \frac{q_i-u_c}{w_b/2}}\right)}^2+{\left({\displaystyle \frac{q_j-v_c}{h_b/2}}\right)}^2=1,\\ \hfill {\left({\displaystyle \frac{q_i-u_c}{w_b/4}}\right)}^2+{\left({\displaystyle \frac{q_j-v_c}{h_b/4}}\right)}^2=1\end{array}$$

(13)

where $(q_i,q_j)$ represents a candidate position. Points within $E_2$ are labeled positive, points outside $E_1$ negative, and those in between are ignored to prevent ambiguous supervision.

For each positive point, the regression target encodes its horizontal and vertical offsets relative to the left, top, right, and bottom boundaries of the ground-truth box:

$$\begin{array}{cc}\hfill d_l& =q_i-u_l,d_t=q_j-v_l\hfill \\ \hfill d_r& =u_r-q_i,d_b=v_r-q_j\hfill \end{array}$$

(14)

Here, $d_l$ and $d_r$ indicate the horizontal distances to the left and right edges of the ground-truth box, while $d_t$ and $d_b$ correspond to the vertical distances to the top and bottom edges, respectively.

To jointly capture hyperspectral characteristics and dynamic target behavior, a multi-task loss function is adopted, combining spectral reconstruction, classification, and regression objectives:

$$\mathcal{L}={\displaystyle \frac{\lambda }{2}}\left(\Vert Z-Z{W}_Z{\Vert }_F^2+{\Vert X-X{W}_X\Vert }_F^2\right)+\sum _{n=1}^N{\omega }_n\left({\rho }_1{\mathcal{L}}_n^{cls}+{\rho }_2{\mathcal{L}}_n^{box}\right)$$

(15)

where Z and X correspond to the features extracted from the template and search regions, respectively. $W_Z$ and $W_X$ denote the band correlation matrices for the template and search regions, respectively. ${\omega }_n$ represents the importance weight of the n-th sample, ${\rho }_1$ and ${\rho }_2$ balance the classification and regression losses, and $\lambda$ controls the influence of spectral reconstruction. The first term in the loss guides the dynamic spectral feature learning module to capture physically meaningful band relationships, while the second and third terms supervise classification and precise bounding box regression.

3.4.2. Online Tracking

The initial target template is extracted from the first frame to initialize the tracking process. Using the weights provided by the dynamic spectral feature learning module, the spectral bands are ordered and grouped to generate multiple false-color images. Subsequently, these template images are fed into the contextual feature module to extract multi-scale target features, which serve as references for tracking in the following frames.

For each new frame, the search region is extracted based on the previous target state. Its spectral bands are similarly ranked and grouped into false-color search images $x_1,x_2,...,x_N$. The feature extraction network generates feature maps for each search image, which are paired with the corresponding template feature maps $z_n$. Each pair is fed into the Box-Adaptive Head to produce classification scores $Q_n^{cls}$ and regression offsets $Q_n^{box}$:

$$Q_n^{cls}=\varphi {\left(x_n\right)}^{cls}\star \varphi {\left(z_n\right)}^{cls},Q_n^{box}=\varphi {\left(x_n\right)}^{box}\star \varphi {\left(z_n\right)}^{box}$$

(16)

where $\varphi (·)$ denotes a $1\times 1$ convolution, and ⋆ is cross-correlation operation. Each response map provides an independent target estimate, and the final position is determined by fusing these estimates based on the relative importance of each spectral band.

Target localization is achieved by finding the location with the highest response in the classification map $Q^{cls}$, and reconstructing the bounding box using the corresponding regression values $Q^{box}$. To avoid unstable predictions, a cosine window is applied to discourage large positional shifts, and a scale regularization is introduced to prevent abrupt size fluctuations. These strategies collectively improve robustness and maintain tracking accuracy across frames.

4. Experiments

This section evaluates the proposed hyperspectral tracker against existing mainstream methods to demonstrate its effectiveness. Furthermore, we perform a detailed ablation study to assess the impact of each proposed module on overall tracking performance.

4.1. Experimental Setup

4.1.1. Dataset Description

To comprehensively assess performance across diverse scenarios, we employ two benchmark datasets.

The hyperspectral object tracking Competition (HOTC) benchmark [35] comprises 75 video sequences, split into 40 for training and 35 for testing. Each sequence averages 390 frames at 25 FPS, providing three data modalities: hyperspectral (16 bands), false-color (3 bands), and RGB (3 bands). The dataset includes attribute annotations for 11 tracking challenges: fast motion, background clutter, illumination variation, out-of-plane rotation, occlusion, motion blur, low resolution, scale variation, in-plane rotation, out-of-view, and deformation.

The Multispectral UAV-based Spatio-temporal Tracking Dataset (MUST) [36] features eight spectral channels (390–950 nm) captured at 1280 × 960 resolution and 5 FPS. This UAV-focused dataset balances spectral richness with temporal consistency, incorporating 12 challenging attributes: partial occlusion, background clutter, low resolution, similar object interference, scale variation, motion blur, fast motion, similar color, out-of-view, illumination variation, full occlusion, and camera motion.

4.1.2. Network Implementation

The tracking framework is implemented in Python 3.7.16 and evaluated on a machine with an Intel^® Xeon^® Silver 4310 CPU and NVIDIA RTX A6000 GPU. We adopt the optimizer configuration from SiamBAN [37], setting the implicit momentum coefficient $\lambda$ to 0.028. Training proceeds for 60 epochs using batch size 56, with learning rate initialized at 0.003 and decayed via standard scheduling for stable convergence.

4.1.3. Evaluation Indexes

We evaluate tracking performance using the One Pass Evaluation (OPE) protocol with two key metrics: area under the success rate curve (AUC), which measures average bounding box overlap across all frames, and distance precision (DP) at 20-pixel threshold, representing the percentage of frames where predicted centers fall within 20 pixels of ground truth. Additionally, we include frames per second (FPS), floating point operations (FLOPs), and model size as extra indicators to analyze the computational complexity of the algorithms. FPS reflects the computational efficiency of the tracker and indicates its practical suitability for real-time applications; FLOPs quantify the amount of computation required by the model; model size measures the memory footprint of the model, which is important for deployment efficiency.

4.2. Experimental Results Comparison

4.2.1. Experiments with the HOTC Dataset

To comprehensively assess the effectiveness of BCR-Net, we conduct evaluations on the HOTC dataset and compare its performance against a set of representative hyperspectral and RGB-based tracking methods. From the perspective of network architecture, these methods can be broadly categorized into three groups. The first group comprises hand-crafted feature-based trackers, including CNHT [22] and MHT [35], which rely on manually designed features for object representation. The second group consists of CNN-based methods, including DeepHKCF [26], SiamRPN++ [5], TSCFW [10], and PHTrack [38]. Specifically, DeepHKCF leverages deep features while compressing spectral bands, SiamRPN++ uses a Siamese region proposal network to correlate template and search features, TSCFW utilizes tensor representations with context modeling to capture spectral–spatial dependencies, and PHTrack leverages prompt learning to adapt foundation models for hyperspectral tracking. The third group consists of transformer-based frameworks, including HOTMoE [39], DASSP-Net [40], and HyperTrack [41]. Specifically, HOTMoE models cross-spectral interactions through a modality mixture of experts, DASSP-Net employs dual attention to jointly learn spatial–spectral dependencies, and HyperTrack incorporates spectral reconstruction and a multi-branch framework to strengthen hyperspectral video representation.

Table 1. Comparison of tracking results across various algorithms on the HOTC dataset.

Algorithm	DP	AUC	FPS	FLOPs(G)	Model Size(M)
CNHT	0.335	0.171	2.52	-	-
STARK-ST50	0.615	0.348	41	4.00	110
SiamRPN++	0.534	0.262	35	10.00	225
DeepHKCF	0.541	0.303	1.12	N/A	N/A
MHT	0.828	0.522	2.13	N/A	N/A
TSCFW	0.849	0.543	3.40	N/A	N/A
DaSSP-Net	0.847	0.566	25.3	56.3	104.1
HotMoE	0.862	0.550	36.1	31.13	432.7
HyperTrack	0.845	0.563	21.6	36.8	98.4
PHTrack	0.859	0.586	15.16	58.5	159.7
BCR-Net (Ours)	0.862	0.572	8.27	49.2	186.1

The two best results are highlighted in red and blue for clarity.

reports the tracking results of BCR-Net and the compared approaches. As shown in Table 1, correlation filter-based trackers demonstrate limited capability in modeling the complex spatial–spectral representation of hyperspectral data, leading to poor adaptability in cluttered or dynamic scenes. CNN-based methods achieve improved accuracy by learning hierarchical feature representations, thereby enhancing spatial discrimination and robustness. Specifically, PHTrack attains the highest AUC value of 0.586 owing to its foundation model adaptation via prompt learning, which strengthens overlap accuracy. Transformer-based frameworks further enhance the representation of spectral–spatial dependencies through attention mechanisms. In particular, HyperTrack integrates band embedding and multi-branch attention modules to capture both inter-band and spatial correlations, achieving an AUC of 0.845 and a DP of 0.563. Although the band embedding and multi-branch attention improve overall spectral–spatial feature representation compared with most CNN-based trackers, the limited interaction across branches and the additional structural complexity reduce localization stability. Compared with ViT-based frameworks, BCR-Net attains a higher DP score of 0.862, demonstrating that its explicit spectral–spatial interaction combined with adaptive channel refinement provides more stable and accurate target tracking under challenging conditions.

To evaluate the Inference speed of the compared methods and the proposed BCR-Net, we report FPS, FLOPs, and model size on the HOTC dataset (Table 1). Among this, “N/A” indicates that the method does not involve a complete end-to-end deep learning framework. STARK-ST50 and SiamRPN++ achieve high FPS by directly operating on false-color images, thereby avoiding the computational overhead. PHTrack and HotMoE exhibit moderate FPS, benefiting from prompt learning and selective expert activation, respectively, which reduce unnecessary spectral computations. DaSSP-Net and HyperTrack show slightly lower FPS due to the inclusion of spatial–spectral attention and multi-branch ViT modules. BCR-Net processes frames at 8.27 FPS, reflecting the additional computations introduced by the Dual Enhancement Module and adaptive band grouping, which contribute to improved tracking accuracy. Regarding computational complexity, PHTrack requires moderate FLOPs and model size since only its lightweight prompt branch is trained, whereas HotMoE’s multiple expert modules increase both FLOPs and memory consumption. DaSSP-Net and HyperTrack demand larger FLOPs and parameters owing to the ViT backbone and attention-based fusion. In conlusion, BCR-Net incurs slightly higher computational cost but achieves a deliberate balance between tracking precision and efficiency.

From Figure 3, our method achieves the highest DP score of 0.862, while PHTrack attains the highest AUC of 0.586. This indicates that our approach excels in localization stability, whereas PHTrack is more effective in overlap accuracy.

To evaluate model robustness, we selected four representative sequences: $coke$ (fast motion), $kangaroo$ (background clutter), $rider2$ (target rotation and scale variation), and $card$ (occlusion and low resolution). As shown in Figure 4, our approach accurately tracks targets under these conditions, substantially outperforming other methods.

4.2.2. Experiments with the MUST Dataset

To further evaluate the practical performance of our proposed tracker in UAV video scenarios, we conducted systematic comparative experiments on the MUST dataset. A set of representative RGB object tracking algorithms was included for comparison, including SiamRPN [42], SiamMask [43], TaMOs [44], ToMP [45], SGDViT [46], and OSTrack256 [47]. All methods were run using their officially published models and parameter settings on a unified experimental platform to ensure fairness and to minimize the influence of implementation or environmental differences.

Performance evaluation on the MUST dataset is presented in

Table 2. Comparison of tracking results across various algorithms on the MUST dataset.

Algorithm	DP	AUC
SiamMask	0.548	0.369
SGDViT	0.539	0.375
TaMOs	0.316	0.177
OSTrack256	0.549	0.385
ToMP	0.461	0.318
SiamRPN	0.552	0.374
BCR-Net (Ours)	0.595	0.388

The two best results are highlighted in red and blue for clarity.

, where trackers are assessed using AUC and DP metrics. Our approach delivers superior results with AUC of 0.595 and DP of 0.388, highlighting its effectiveness and robustness in UAV aerial object tracking scenarios. Among the compared methods, TaMOs and ToMP perform relatively poorly, with AUCs of 0.316 and 0.461 and DPs of 0.177 and 0.318, respectively. Their limited modeling mechanisms reduce the ability to fully exploit spectral information, resulting in lower discrimination and tracking accuracy under complex conditions. In contrast, SiamRPN, SiamMask, SGDViT, and OSTrack256 maintain relatively stable performance, achieving AUCs around 0.539–0.552 and DPs around 0.369–0.385. These RGB-based deep models benefit from effective spatial and temporal feature extraction, yet they still lack comprehensive spectral modeling, which constrains their precision in scenarios with complex spectral variations. Our proposed method effectively leverages full spectral information through channel refinement and spectral–spatial correlation modules. By explicitly modeling inter-band relationships and enhancing deep feature representation, our tracker achieves superior accuracy and stability, surpassing both traditional and RGB-based deep models, and demonstrating enhanced cross-modal adaptability for UAV tracking.

To evaluate model robustness, we selected four representative sequences: $Bicycle$ (fast motion), $Bus$ (scale variation), $Person$ (partial occlusion), and $car$ (Similar Object). As shown in Figure 5, our approach accurately tracks targets under these conditions, substantially outperforming other methods.

In summary, while existing RGB tracking algorithms demonstrate strong performance under standard visible light conditions, their performance generally degrades to varying degrees when faced with UAV videos, which present greater spectral complexity and perceptual challenges. By contrast, our method leverages spectral information and structural optimization, achieving a favorable balance between tracking accuracy and stability. This demonstrates its strong cross-modal adaptability and practical application potential in aerial tracking scenarios.

4.3. Ablation Study

The following presents a systematic ablation study on the HOTC dataset to evaluate the impact of each module and design choice on tracking performance.

4.3.1. Comparison of Tracking Performance with Proposed Modules

In the following, a systematic ablation evaluation is performed to quantify the effect of each key component. Specifically, a baseline tracker is first established, in which hyperspectral images are converted into false-color representations before being fed into the model for prediction. Building on this baseline, the Band Importance Modeling Module (BIMM) and the Contextual Feature Refinement Module (CFRM) are subsequently incorporated, and their effects are assessed on the HOTC dataset.

Table 3. Comparison of tracking performance under different module combinations.

Method	AUC	DP
Baseline	0.534	0.831
Baseline + BIMM	0.549	0.852
Baseline + BIMM + CFRM	0.572	0.862

illustrates the AUC and DP achieved by different module configurations. When BIMM is incorporated into the baseline, the AUC increases from 0.534 to 0.549 and the DP rises from 0.831 to 0.852, indicating that this module improves the selection of key spectral channels. Adding CFRM further increases the AUC to 0.572 and the DP to 0.862, suggesting that contextual information modeling contributes positively to hyperspectral target representation. Taken together, the inclusion of these two modules enhances both tracking accuracy and robustness while maintaining a simple model structure.

Secondly, we investigated how different initialization strategies affect the performance of the BIMM module. Specifically, we initialized the weight matrix ${\mathit{W}}_0$ to a mean matrix with all elements equal to ${\displaystyle \frac{1}{B-1}}$, and compared this with a learned attention-based initialization. As shown in

Table 4. Comparison of tracking performance under different BIMM initialization strategies.

Methods	AUC	DP
Learned Attention	0.572	0.862
Mean Initialization	0.544	0.837

, using the learned attention initialization yields tracking results of 0.572 and 0.862 in terms of AUC and distance precision (DP), respectively, outperforming the mean initialization results of 0.544 and 0.837. These findings indicate that learning-based initialization provides a more effective starting point for band importance modeling, facilitating better feature selection and improving overall tracking accuracy.

4.3.2. Comparison of BIMM Component Configurations

To evaluate the effectiveness of each component in BIMM, we conduct ablation experiments by selectively removing one module at a time while keeping the others unchanged. The complete BIMM serves as the baseline.

Table 5. Comparison of tracking performance under different BIMM component configurations.

SEM	CEM	SDUB	SGRM	AUC	DP
✓				0.541	0.801
	✓			0.547	0.803
		✓		0.538	0.802
			✓	0.549	0.810
✓			✓	0.551	0.819
	✓	✓		0.554	0.834
	✓	✓	✓	0.563	0.846
✓		✓	✓	0.557	0.831
✓	✓		✓	0.566	0.847
✓	✓	✓		0.563	0.844
✓	✓	✓	✓	0.572	0.862

reports the performance under different configurations.

Table 5 reports the performance of BIMM under different component configurations. The results reveal that each component—SEM, CEM, SDUB, and SGRM—contributes distinctly to the overall tracking capability. Removing any single component consistently degrades both AUC and DP, demonstrating the necessity of each module. SEM enhances semantic feature representation, improving discrimination and robustness. CEM provides crucial contextual information that strengthens feature correlation. SDUB facilitates effective spatial-depth feature integration, contributing to improved spatial representation. SGRM captures global spectral relationships, which is vital for handling hyperspectral data. Configurations combining multiple components achieve higher performance, confirming their complementary nature. The full BIMM configuration delivers the highest performance, validating that the integrated design of these modules effectively synergizes semantic, contextual, spatial, and spectral information to maximize tracking accuracy and robustness.

4.3.3. Comparison of Ensemble Prediction Methods

To evaluate the ensemble strategy’s effectiveness in hyperspectral tracking, we compared different prediction fusion methods and weighting mechanisms, analyzing their performance impact from two perspectives.

First, to investigate the differences between fusion mechanisms, the weighted ensemble was replaced by a simple average ensemble. As shown in

Table 6. Comparison of tracking performance under different ensemble prediction methods.

Ensemble Prediction Method	AUC	DP
Weighted ensemble (ours)	0.572	0.862
Average ensemble	0.551	0.859

, while average ensemble improves the ability to fuse multi-channel information to some extent, it slightly underperforms our proposed weighted ensemble scheme (AUC 0.572, DP 0.862) in both AUC (0.551) and DP (0.859). These findings suggest that weighting the influence of each false-color image during prediction improves feature integration and enhances overall tracking performance.

Further, to investigate the effect of different weight generation strategies within the Band Importance Modeling Module, we compare our Integrated Prediction Module, which dynamically adjusts fusion weights, with a baseline that uses learnable fixed weights. In the baseline, all weights are learned during training but remain constant during testing, while all other settings are kept identical. As shown in

Table 7. Comparison of tracking performance under different weighted settings.

Methods	AUC	DP
Integrated Prediction Module	0.572	0.862
Learnable Fixed Weights	0.549	0.846

, the fixed-weight strategy produces an AUC of 0.549 and a DP of 0.846, corresponding to decreases of 0.023 and 0.016 relative to the Integrated Prediction Module. This performance drop indicates that static weights cannot adapt to distribution shifts caused by changes in the target’s appearance or spectral properties across frames, thereby limiting effective feature fusion. In contrast, the Integrated Prediction Module leverages the BIMM to dynamically adjust fusion weights based on the input content of each frame, improving both generalization and robustness.

4.3.4. Comparison of Band Grouping and Branch Number Strategies

In order to evaluate the band grouping design, four baseline strategies were considered in addition to our approach: sequential partitioning, which groups bands into equal intervals; single-band replication, which replicates each band three times to form a false-color image; PCA-based grouping, which projects hyperspectral bands into three principal components; and random grouping, which assigns bands arbitrarily to the RGB channels. All methods use the same tracking framework to ensure fairness.

As shown in

Table 8. Comparison of tracking performance under different band grouping strategies.

Methods	AUC	DP
ours	0.572	0.862
Sequential	0.56	0.857
Bandwise	0.527	0.804
PCA-based	0.534	0.831
Random	0.549	0.852

, our strategy reaches 0.572 in AUC and 0.862 in DP, outperforming all other grouping approaches. Sequential partitioning fails to fully exploit complementary spectral relationships, while single-band replication introduces redundancy that limits feature discriminability. PCA-based grouping captures global variance but may overlook task-specific band importance, and random grouping arbitrarily assigns bands, disrupting natural spectral correlations. In contrast, our method selects bands based on learned importance, forming more informative false-color images that enhance feature representation and improve overall tracking performance.

4.4. Parameter Analysis

To further investigate the impact of key hyper-parameters in the experiments, we conduct experiments on two factors: the depth of the MLP layers and the number of false-color images.

Firstly, as shown in

Table 9. Comparison of tracking performance under different MLP layer configurations.

MLP Depth	AUC	DP
1	0.572	0.862
3	0.528	0.830
5	0.549	0.846

, varying the MLP depth produces notable differences in tracking performance. The single-layer configuration achieves the highest performance. Increasing the depth to three or five layers leads to performance degradation, with AUC values of 0.528 and 0.549, respectively. This suggests that deeper MLP structures may lead to overfitting and reduced generalization ability.

Secondly, the results in

Table 10. Comparison of tracking performance under different numbers of false-color images.

Methods	AUC	DP
1	0.505	0.761
3	0.541	0.801
5	0.572	0.862

clearly demonstrate the effect of the number of false-color images on tracking performance. In our experiments, the input consists of 16-band hyperspectral images, and each false-color image is formed by grouping three bands, which allows a maximum of five images. The configuration with five images achieves the highest performance, with an AUC of 0.572 and a DP of 0.862. Reducing the number of images to three or one results in notable performance degradation, with AUC values of 0.541 and 0.505, respectively, accompanied by corresponding decreases in DP. This indicates that increasing the number of false-color images provides more diverse feature information, thereby enhancing tracking robustness.

5. Discussion

While the comprehensive experiments and analyses have validated the effectiveness of the proposed BCR-Net in hyperspectral video tracking, several important challenges remain that open avenues for future research.

• The shortage of high-quality hyperspectral video datasets with precise annotations presents a challenge for robust feature learning. Future research could focus on weakly supervised or semi-supervised learning, leveraging partial or noisy annotations. Additionally, knowledge transfer from well-labeled datasets in related domains could be explored to bootstrap hyperspectral trackers with minimal hyperspectral-specific annotations.
• Although the current fusion design improves feature representation, the interaction between spectral and spatial information remains insufficiently explored. In our earlier attempts, spectral attention mechanisms were employed to capture inter-band dependencies, but the resulting improvements were marginal. By contrast, the U-Net-based design adopted in this work yielded more substantial performance gains, highlighting the importance of structural modeling. Looking ahead, we plan to investigate adaptive fusion strategies that can adaptively integrate spectral and spatial features under varying scene conditions, with the goal of further improving both accuracy and computational efficiency in hyperspectral tracking.
• Our experiments demonstrate that explicit modeling of spectral information substantially improves target discrimination in challenging scenarios. Building upon this insight, future work will explore end-to-end network architectures that directly process raw multi-dimensional hyperspectral inputs, enabling more comprehensive utilization of spectral cues and potentially improving robustness in complex tracking environments.

6. Conclusions

A tracking algorithm for hyperspectral videos is proposed in this work, which benefits from spectral–spatial feature fusion and an improved network design. Based on the above experiments and analyses, the main conclusions are as follows:

• The band selection module ranks spectral bands by importance and groups them into complementary composites, improving feature discrimination and computational efficiency without compromising accuracy.
• By adaptively fusing results based on feature importance, our method achieves superior performance compared to uniform averaging, demonstrating more effective utilization of hyperspectral information for target discrimination.
• The proposed spectral–spatial fusion design, based on a U-Net architecture, demonstrates notable gains compared to earlier attempts with spectral attention mechanisms, validating its effectiveness in hyperspectral tracking.
• The method achieves a good balance between accuracy and efficiency, showing competitive performance on the HOTC dataset (with a DP of 0.862 and an AUC of 0.572), demonstrating its potential for real-world applications.
• Future work will further explore adaptive fusion strategies that dynamically balance spectral and spatial information to further improve robustness and generalization in challenging tracking scenarios.