1. Introduction
Inverse Synthetic Aperture Radar (ISAR) plays a pivotal role in
non-cooperative target imaging [
1,
2], especially for maritime surveillance where long-range, high-resolution sensing is required under complex motion and environmental conditions [
3]. However, conventional ISAR imaging is severely challenged by resolution degradation due to limited observation time (restricted aspect coverage), complex target maneuvers, and sea-induced clutter (e.g., wave returns) in addition to thermal noise. These challenges limit the system’s ability to perform reliable classification, identification, and recognition.
To address these issues, much research has focused on super-resolution [
4,
5] and noise/clutter suppression. Classical spectral-estimation and subspace methods (e.g., Root-MUSIC [
6] and RELAX [
7]) can enhance Doppler/cross-range resolution, yet they remain sensitive to limited apertures and non-ideal motion. Likewise, techniques derived from ESPRIT [
8] offer fine parameter estimation but often require stringent model assumptions and may generalize poorly in dynamic maritime environments.
Recently, data-driven approaches have gained traction. Generative Adversarial Networks (GANs) have reported notable improvements in ISAR resolution enhancement [
9], producing visually plausible outputs from low-resolution inputs; nevertheless, adversarial objectives may introduce hallucinations and do not guarantee phase fidelity, which is crucial in radar applications. To better capture radar-specific structure, complex-valued convolutional neural networks tailored to complex data have been explored [
10], achieving gains in magnitude and phase consistency. Integrated models that combine denoising with super-resolution have also been proposed [
11], showing promising artifact suppression and quality improvements.
Despite these advances, many existing solutions still struggle in the presence of strong sea clutter (e.g., sea spikes) and
non-Gaussian clutter statistics, particularly at low signal-to-noise ratios (SNRs). In parallel, several works target highly specific scenarios [
12,
13]. For instance, Shao et al. [
14] proposed an integrated framework that couples super-resolution with fine motion compensation for maneuvering ship targets under high-sea-state conditions. While this approach improves resolution and robustness, it relies on precise motion modeling and is tailored to severe sea states. Similarly, Yang et al. [
15] investigated high-resolution ISAR in the terahertz band for complex motions; however, practical maritime deployment remains limited by atmospheric attenuation, hardware constraints, and lack of standardization. These contributions are important yet narrow in applicability, constraining generalization across broader maritime ISAR tasks. Practical ISAR pipelines often include range-profile alignment, translational motion compensation, and—when required—polar-to-Cartesian reformatting. In this work, we adopt a complementary strategy: we first map the frequency-aspect data to a coarse complex image via a two-dimensional inverse FFT (IFFT2) and then perform
learned restoration in the image domain using a deep residual network. This design is appropriate under
small aspect sweeps with
cross range alignment and
moderate residual phase errors, conditions under which remaining artifacts behave as image-domain degradations (defocus, blur, and clutter) that a CNN can remove while preserving the complex structure. Later sections quantify magnitude–phase fidelity to verify that enhancement does not compromise the physical integrity of returns. In this work, we propose a deep residual learning framework [
16,
17] specifically tailored to maritime ISAR imaging, with synthetic training under cluttered and noisy conditions (wave interference, platform drift, low SNR). Our method preserves both magnitude and phase, enhancing spatial (cross-range) resolution while maintaining physical consistency in complex ISAR images. Extensive validation against benchmarked synthetic datasets demonstrates state-of-the-art performance, particularly in cluttered and low-SNR regimes.
A direct IFFT2 → deep restoration paradigm for ISAR that operates in the complex image domain, appropriate under small-sweep, coarsely aligned conditions common in maritime surveillance.
A residual CNN tailored to complex ISAR imagery that jointly denoises, suppresses clutter, and refocuses/enhances cross-range structure while preserving magnitude and phase.
A synthetic maritime dataset with realistic degradations (SNR/SWR sweeps, wave-like clutter, platform drift) for training and evaluation.
This paper is organized as follows.
Section 2 presents the ISAR signal model, simulation setup, and data generation.
Section 3 describes the architecture of the proposed residual network.
Section 4 reports experimental results and comparisons.
Section 5 and
Section 6 conclude the paper and outline future directions.
2. Dataset and Methods
In this work, we developed a comprehensive simulation framework to generate synthetic Inverse Synthetic Aperture Radar (ISAR) data for training and evaluating the proposed resolution enhancement method. Because public ISAR datasets that reflect high-resolution
maritime scenarios are scarce—especially with controlled noise levels, target geometries, and environmental complexity—existing resources are either proprietary, limited in diversity, or lack paired low-/high-resolution examples required for supervised learning. We therefore designed a simulation pipeline that affords full control over target structure, motion models, radar parameters, and noise/clutter levels, ensuring a diverse dataset tailored to our goals. The simulations assume a stepped-frequency continuous-wave (SFCW) radar [
18] operating at a center frequency
with a total bandwidth
This configuration yields the theoretical range resolution
where
c is the speed of light in free space.
2.1. Target and Reflector Modeling
Synthetic maritime targets were modeled as collections of isotropic point scatterers that represent structural features of naval vessels. To emulate realistic variability, vessel geometries were generated with different overall dimensions and varying numbers of scatterers, distributed non-uniformly to capture structural asymmetries. For each configuration, we synthesized the two-dimensional
frequency-aspect scattering matrix using the standard narrow-band ISAR model [
19]:
where
is the total number of scatterers;
is the complex radar cross section (RCS) of the n-th scatterer;
is the k-th transmitted frequency;
is the m-th aspect angle;
is the instantaneous slant range to the n-th scatterer.
2.2. Clutter Model
Sea-surface backscatter (
clutter) is modeled as the coherent superposition of
traveling-wave components that evolve over slow time (aspect). For each simulation,
is drawn from a prescribed range to reflect moderate sea states. The
i-th component is specified by a nonnegative amplitude
, wavenumber
, temporal frequency
, and phase
. The surface elevation at position
x and slow time
t is
Parameters are sampled
per scene as
where
and
are physically plausible 1D spectra chosen according to the assumed sea state and grazing geometry.
Slow-Time Correlation
Let aspect samples be
with increment
. We relate slow time to aspect via
where
is the nominal yaw rate (rad/s). This induces temporal correlation of clutter across aspect. The raw clutter field is the coherent sum of facet returns:
where
is the instantaneous two-way path length to the
i-th wave facet. To achieve a prescribed signal-to-wave ratio (SWR), defined as
we first compute the mean powers using the
unscaled clutter
and set the scaling
and then define
By construction, the resulting clutter satisfies
to within numerical tolerance, independent of the particular draw of
.
2.3. Thermal Noise Model
Thermal noise was added to the frequency-domain ISAR data as additive white Gaussian noise (AWGN):
where
was determined from the desired signal-to-noise ratio (SNR).
2.4. Radar Data Representation
Let
denote the complex-valued frequency-aspect field matrix collected by the radar, where
is the
k-th transmitted frequency and
is the
m-th aspect-angle sample. In the proposed simulation framework, the measured field consists of three additive components:
where
—the target scattering term, representing coherent returns from isotropic scatterers located on the vessel;
—sea-surface clutter;
—thermal noise (AWGN).
2.4.1. Sampling Grid and Padding Rationale
The high-resolution (HR) field is sampled on a measurement-driven grid with in frequency and aspect, respectively. To standardize FFT sizes and learning I/O without altering the physics, we apply zero-padding from to after apodization and prior to the 2D IFFT. Assembling a native grid would either (i) change the sampling steps (thus changing calibration/FOV), or (ii) require extending the band/aperture beyond the prescribed sensing scenario. Padding preserves the physical resolution (set by band and aperture) while providing computational convenience.
2.4.2. High-Resolution (HR) and Low-Resolution (LR) Construction
Let the full angular span be
and the corresponding cross-range resolution be
under the small-sweep assumption. The HR matrix
uses the full span
.
To synthesize the low-resolution (LR) set, we
reduce the angular span by a factor
while keeping the native angular step the same. Concretely, we define a reduced span
centered at
(typically the mid-aspect) and retain the same sampling increment
. The LR aspect count is therefore
with the
frequency grid unchanged, so range resolution is preserved.
This reduction in aperture directly
degrades cross-range resolution by the same factor:
Equation (
16) makes it explicit that
compromises cross-range resolution by a factor of 2 to 6, exactly reflecting the reduced angular span used to construct
.
2.4.3. High-Resolution vs. Low-Resolution Measurements
The
high-resolution field matrix
is sampled densely over
K frequency points and
M aspect angles, producing an array of size
. This is subsequently zero-padded to
before applying the spatial-domain transformation:
The
low-resolution measurement
is obtained by reducing the number of aspect-angle samples to
while maintaining the same frequency coverage, i.e.,
After zero-padding in the cross-range dimension to match the
grid, the low-resolution image is obtained as follows:
This formulation explicitly characterizes the ISAR simulation as the problem of reconstructing or enhancing towards , given that both originate from the same underlying target but differ due to sampling limitations, clutter contamination, and thermal noise.
2.5. High-Resolution and Low-Resolution Data Generation
The high-resolution frequency-domain matrix was generated on a uniform
frequency-angle grid, corresponding to the collected field matrix
. This matrix was zero-padded to
and transformed to the spatial (image) domain via two-dimensional inverse fast Fourier transform (IFFT):
Low-resolution datasets were obtained by subsampling the frequency-angle domain to different resolutions (e.g.,
, with
). Each low-resolution matrix
was zero-padded along the cross-range dimension to
before applying the same IFFT process:
This ensured that all images (low- and high-resolution) had the same spatial dimensions for network training, while retaining differences in effective resolution.
2.6. Simulation Dataset
To support supervised learning in ISAR super-resolution, we generated a large-scale synthetic dataset tailored to capture the physical and environmental variability typical in maritime surveillance scenarios. The dataset was constructed by systematically varying key parameters:
Vessel size and scatterer distribution: Vessel geometries were randomized with physical dimensions ranging from (representing smaller patrol or cargo vessels) to (representing larger ships). The number and placement of point scatterers were independently sampled for each instance to emulate complex structural layouts, including asymmetric masts, superstructures, and hull shapes.
SNR and SWR levels: Each simulation incorporated additive white Gaussian noise (AWGN) and spatially correlated clutter to generate scenarios spanning a broad range of signal quality. Signal-to-noise ratio (SNR) and signal-to-wave ratio (SWR) were independently sampled from the interval to reflect challenging low-contrast conditions and clutter-dominated environments.
Wave and clutter variability: To further enhance realism, we introduced target modulation effects by applying low-frequency oscillations to scatterer amplitudes. These were governed by wave parameters for each scatterer i, simulating the influence of sea wave-induced fluctuations and platform instability.
This systematic variation yielded a comprehensive collection of synthetic ISAR measurements, encompassing a rich diversity of imaging conditions and target profiles. The simulated data provides a robust foundation for training and evaluating deep learning models for resolution enhancement, autofocus, and feature recovery. The imaging configuration used in our simulation framework is summarized in
Table 1. These settings reflect a stepped-frequency continuous-wave (SFCW) radar system with high resolution in both range and cross-range domains. Specifically, the choice of 250 frequency samples over a
bandwidth allows submeter range resolution.
Table 1.
Imaging parameters.
Table 1.
Imaging parameters.
| Center frequency | 10 GHz |
| Bandwidth | 750 MHz |
| Number of frequency samplings | 250 |
| Number of angle samplings | 250 |
| Region of imaging | |
| Number of pixels in the image | |
These imaging parameters were carefully selected to balance resolution fidelity with computational efficiency, ensuring that the generated dataset effectively captures the nuances of realistic maritime ISAR scenarios. The resulting diversity of samples plays a crucial role in enabling deep learning models to generalize across varied operational conditions, including noise, clutter, and target complexity.
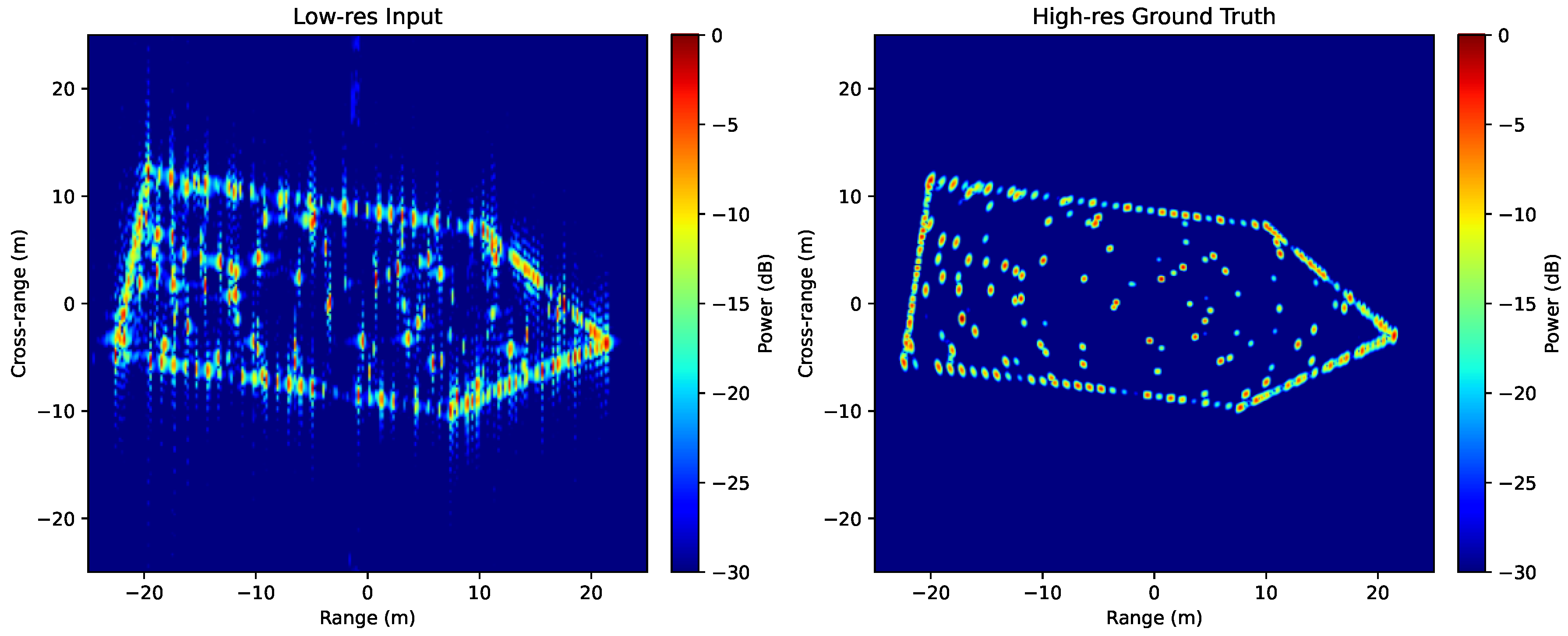
2.7. Visual Examples of Simulated ISAR Samples
To further illustrate the nature of the ISAR dataset used for network training and evaluation,
Figure 1 and
Figure 2 present two representative examples of simulated low-resolution input images alongside their high-resolution ground-truth counterparts. These examples emphasize the distinct characteristics of each case in terms of scene complexity and signal conditions.
As can be seen in
Figure 1, the low-resolution ISAR image retains a reasonably clean profile with clearly distinguishable scatterers. In contrast,
Figure 2 reflects a more severe degradation scenario, where noise and scattering ambiguity increase significantly, underscoring the importance of robust super-resolution approaches under realistic adverse conditions.
3. Architecture of the Deep Residual Network
3.1. Overview
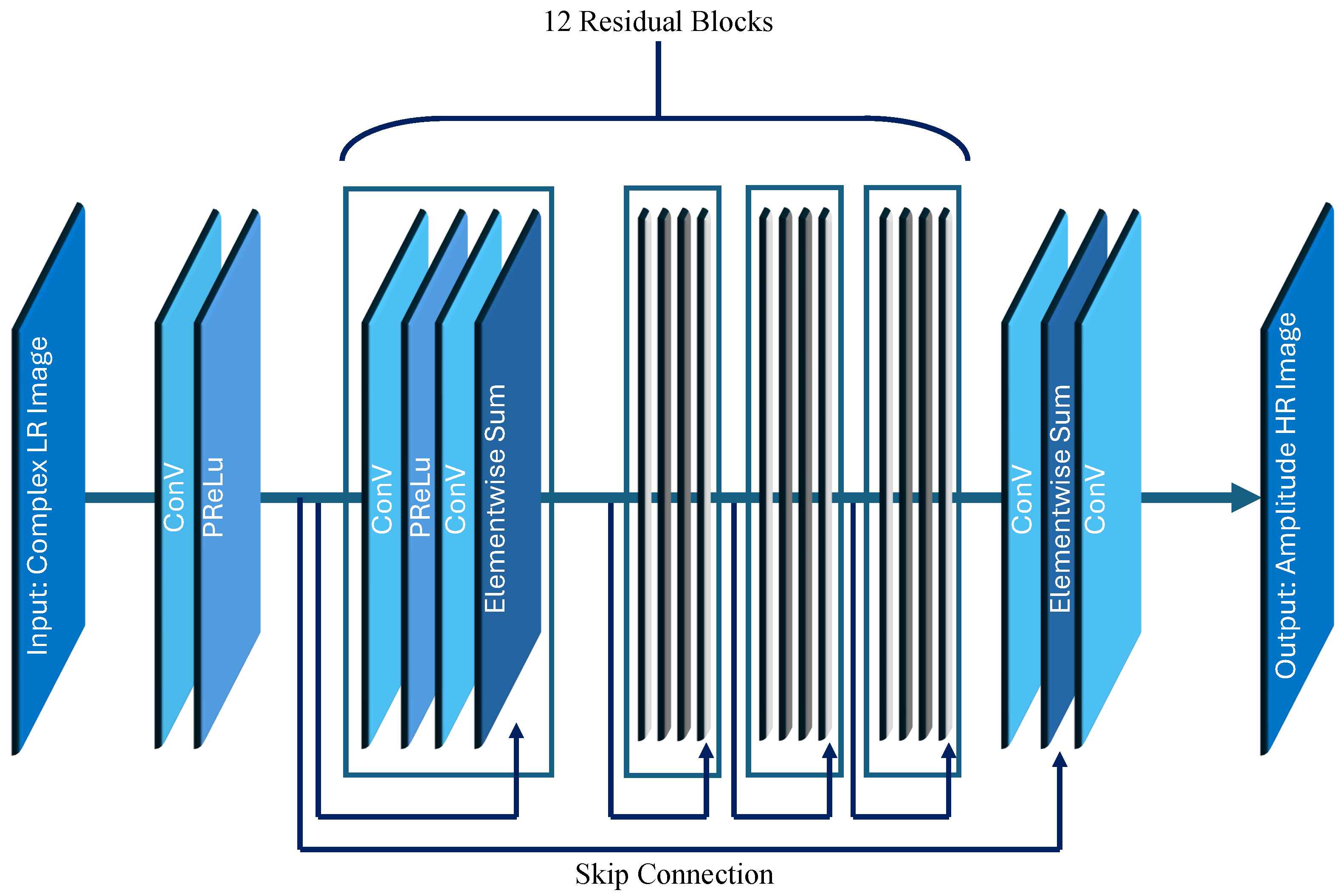
The proposed resolution enhancement model is a deep residual convolutional network specifically designed to operate directly on complex-valued ISAR data. The network is trained to learn a mapping from low-resolution (LR) ISAR images, degraded by limited angular sampling, clutter, and noise, to their corresponding high-resolution (HR) counterparts. The architecture follows a residual learning paradigm, enabling efficient training and better preservation of fine structural details. This architectural design is visually summarized in
Figure 3, which illustrates the proposed residual deep learning network tailored for ISAR image enhancement. The diagram encapsulates the end-to-end structure, including the initial convolutional layer, the residual block cascade with skip connections, and the final reconstruction layers responsible for recovering the real and imaginary parts of the complex-valued ISAR data. This layout emphasizes the balance between depth and parameter efficiency, supporting both representational richness and the preservation of fine radar-specific features throughout the super-resolution process.
3.2. Input Representation
The ISAR images are inherently complex-valued. To process them using standard convolutional operations, each complex image
is decomposed into two real-valued channels:
which yields an input tensor of shape of
. This representation preserves both magnitude and phase information throughout the network.
3.3. Network Structure
The architecture (
Table 2) consists of the following:
An initial convolution layer with 64 feature maps, followed by a Parametric ReLU (PReLU) activation.
A cascade of 12 residual blocks, each containing the following:
convolution with 64 feature maps + PReLU activation.
convolution with 64 feature maps.
Element-wise addition (skip connection) between the block input and output.
A long skip connection from the network input to the output of the last residual block stack.
A final convolution projecting 64 channels back to two channels (real and imaginary parts of the output).
The PReLU activation was chosen for its ability to adaptively learn the negative slope, improving convergence over standard ReLU in regression tasks.
3.4. Loss Function
The training objective combines pixel-wise accuracy with structural fidelity. We use a weighted sum of mean squared error (MSE) and the structural similarity index (SSIM) computed on magnitude images:
where
and
are empirically selected.
3.5. Optimizer and Training Settings
The Adam optimizer is employed with , , and . The training regimen includes the following:
Batch size: 8.
Epochs: Maximum of 50.
Early stopping: Patience of seven epochs.
Learning rate schedule: ReduceLROnPlateau with a factor of and patience of five epochs.
Callbacks: Model checkpointing is used to save the best model weights.
3.6. Dataset and Supervised Learning Framework
The proposed network is trained under a supervised learning paradigm using a dataset comprising a total of 10,000 synthetic ISAR examples. Each sample consists of a low-resolution complex-valued input and its corresponding high-resolution ground-truth target. This extensive dataset is designed to simulate realistic naval imaging scenarios, incorporating various signal-to-noise ratios (SNRs), signal-to-wave ratios (SWRs), and reflector configurations.
To ensure robust model generalization, the dataset is partitioned as follows:
Training set: 8000 examples (80%) used for parameter optimization.
Validation set: 1000 examples (10%) used to monitor performance and guide early stopping.
Test set: 1000 examples (10%) reserved for final quantitative and qualitative evaluation.
This supervised setup enables the network to learn a direct mapping from degraded ISAR input images to their high-resolution counterparts, leveraging ground-truth guidance to optimize pixel-wise and structural fidelity losses.
3.7. Output Reconstruction
The output consists of two channels
and
, recombined into the complex-valued enhanced image,
from which magnitude and phase can be analyzed for resolution improvement assessment.
4. Results and Comparative Analysis
We evaluate the proposed deep learning-based ISAR super-resolution framework against both classical and modern benchmarks: the Estimation of Signal Parameters via Rotational Invariance Techniques (ESPRIT) [
8] and a recent complex-valued convolutional neural network (CNN) baseline [
10]. Performance is assessed under varying settings of signal-to-noise ratio (SNR), signal-to-wave ratio (SWR), and resolution degradation. The objective is to demonstrate the capability of our ResNet-based model to accurately reconstruct high-resolution ISAR imagery under challenging, real-world conditions, and to compare its robustness and fidelity to both parametric and data-driven alternatives.
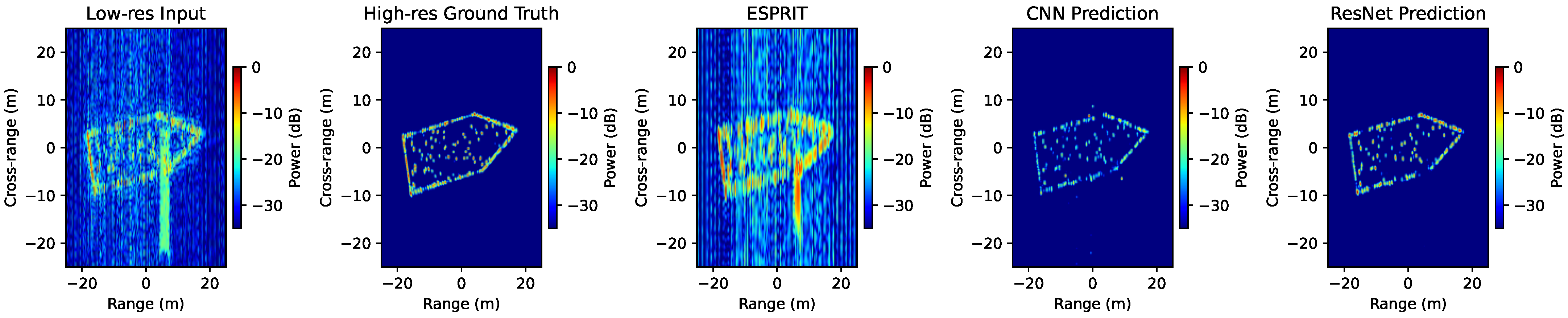
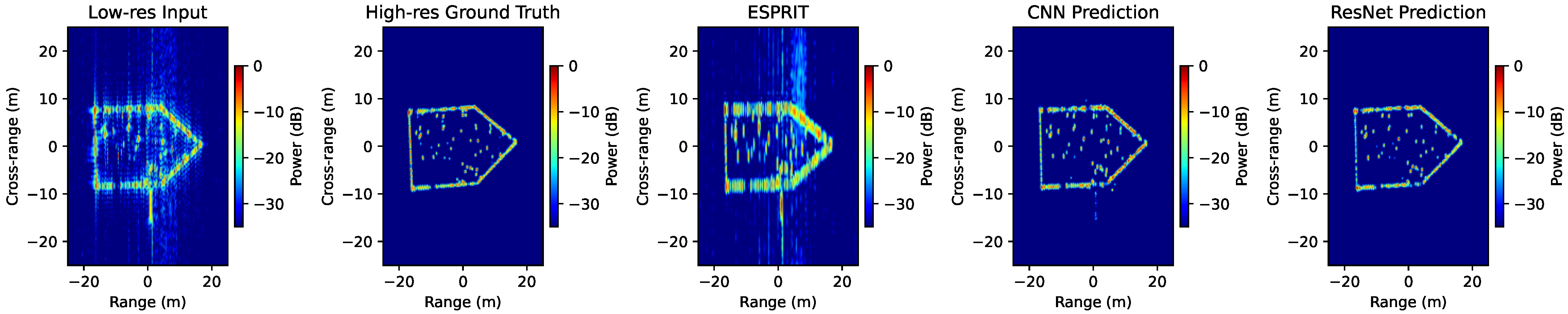
Figure 4 and
Figure 5 illustrate two representative examples under different sensing conditions. The classical ESPRIT method partially reconstructs dominant scatterers but suffers from residual streaking, strong sidelobes, and geometric distortions—especially when noise or wave-induced clutter is present. Its performance degrades significantly in complex scenes with many closely spaced reflectors or low SNR/SWR, leading to fragmented reconstructions and loss of weak targets.
The CNN baseline, trained on complex-valued radar data, produces smoother and cleaner reconstructions with improved noise suppression compared to ESPRIT. It demonstrates the strength of data-driven learning in capturing general structural priors. However, CNN predictions exhibit reduced spatial coherence and intensity imbalances—resulting in fragmented reflector patterns and weakened representation of fine features.
In contrast, our ResNet-based super-resolution framework achieves a high-fidelity reconstruction that best matches the ground truth. It captures both the global geometry and fine-scale reflectors with balanced amplitude and strong spatial consistency. The model successfully reconstructs weak targets that ESPRIT and CNN fail to recover, even in the presence of strong noise and sidelobes. This demonstrates superior generalization to complex, structured, and noisy radar data scenarios.
4.1. Quantitative Evaluation: RMSE Trends vs. SNR and SWR
To complement the qualitative comparisons in
Figure 4 and
Figure 5, we further examine the quantitative performance of the proposed ResNet-based model, the CNN baseline [
10], and the ESPRIT algorithm via the root-mean-square error (RMSE) metric as functions of both SNR and SWR. The RMSE is defined as follows:
where
and
represent the predicted and ground-truth high-resolution complex-valued ISAR images, respectively.
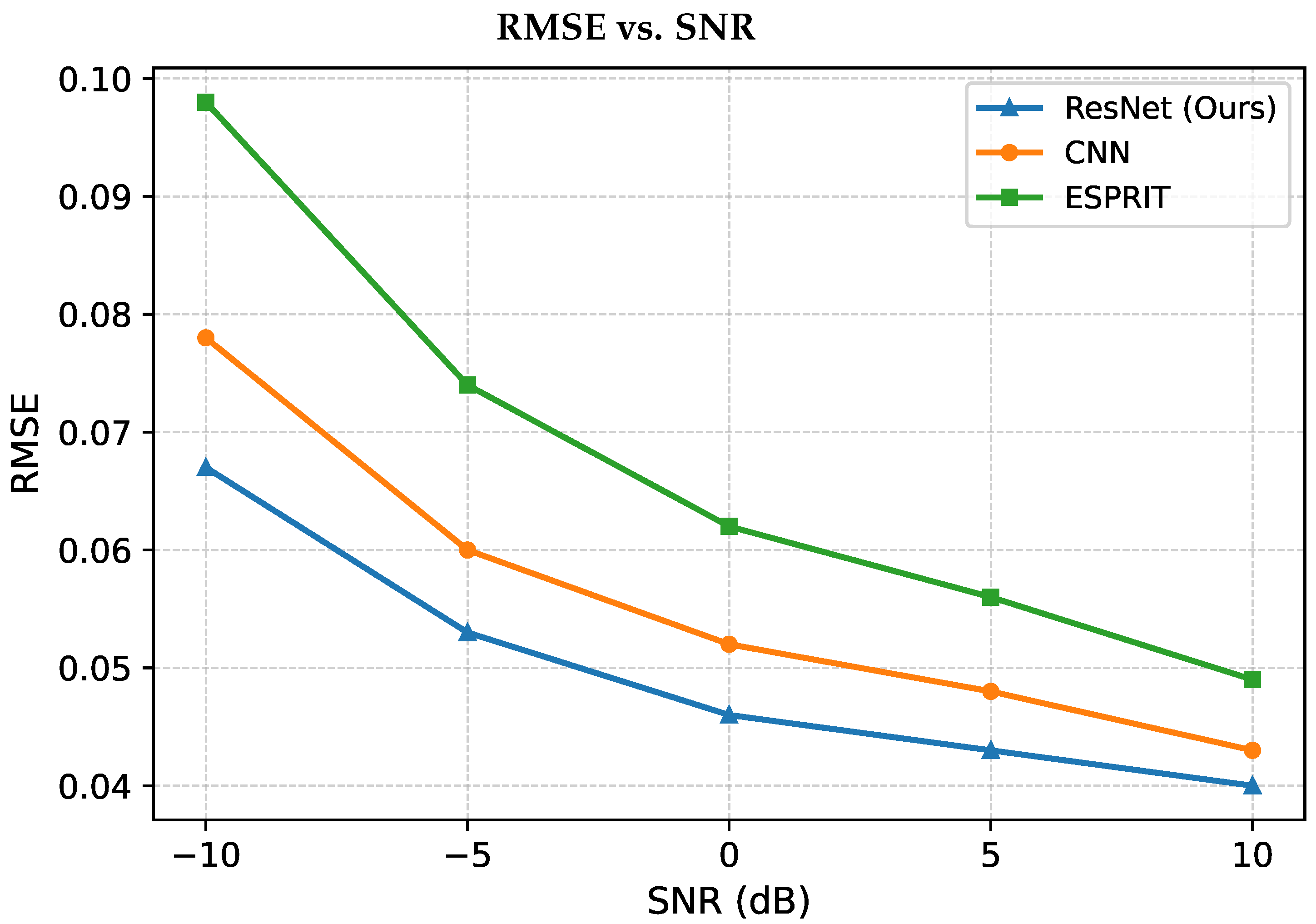
Figure 6 shows RMSE values versus SNR for all evaluated methods. As expected, the RMSE of the low-resolution input increases with decreasing SNR, highlighting the compounded effect of undersampling and measurement noise. The ESPRIT algorithm consistently improves upon this baseline, particularly in high-SNR regimes, but exhibits a steep performance drop under low-SNR conditions due to subspace perturbations. The CNN baseline achieves a more stable reconstruction, outperforming ESPRIT across the SNR range, though it still suffers from moderate degradation in highly noisy scenarios. In contrast, the proposed ResNet-based model consistently achieves the lowest RMSE values across all SNR levels, demonstrating its ability to generalize across both clean and noisy acquisition conditions.
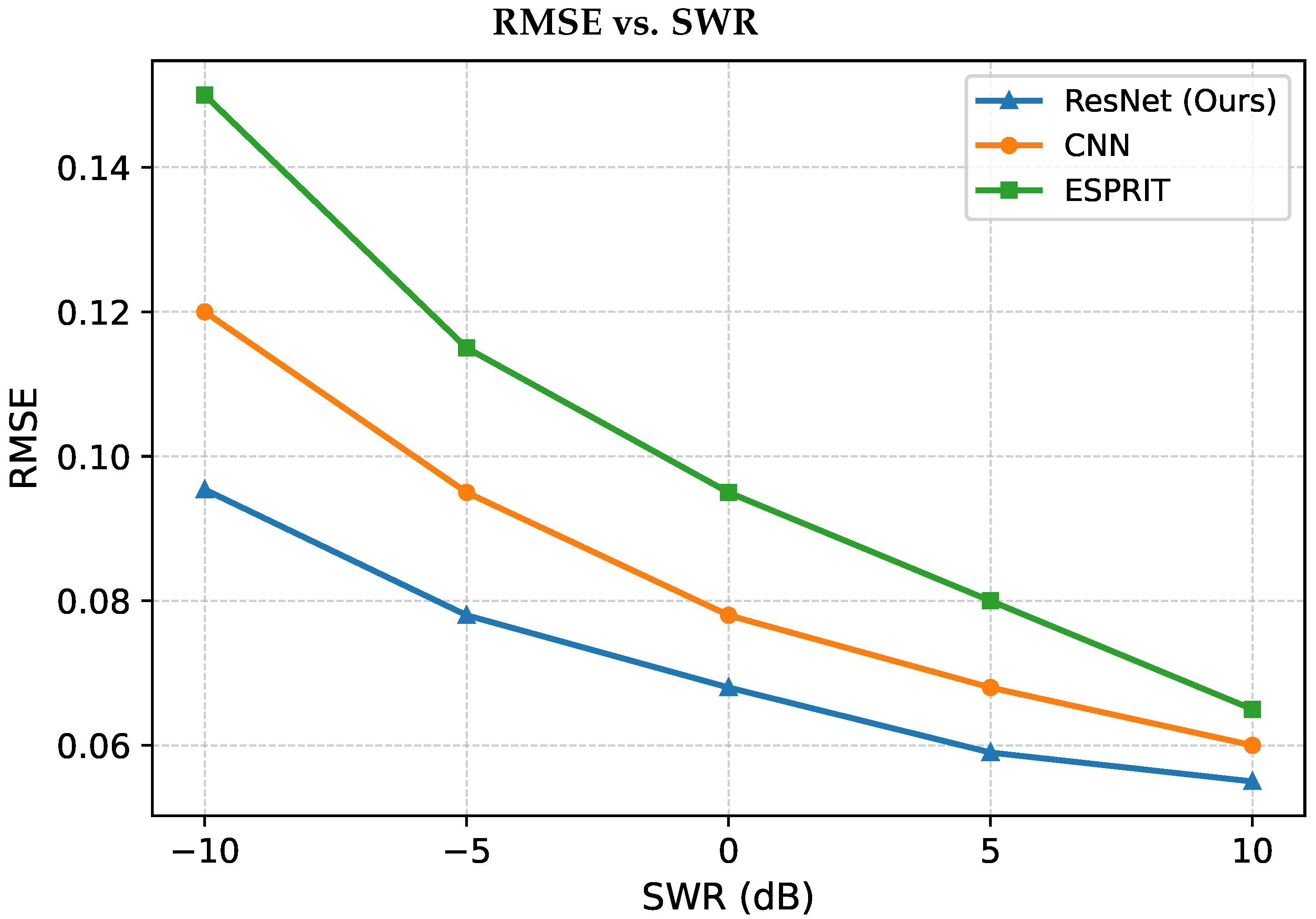
Figure 7 examines performance under increasing SWR degradation, which introduces structured wave interference and multipath-induced sidelobes. In this more challenging regime, all methods experience a higher error floor compared to the SNR case. The ESPRIT algorithm is especially sensitive to these distortions, showing the sharpest increase in RMSE. The CNN model displays improved robustness, yet its spatial consistency deteriorates as SWR drops. Our proposed network once again yields the lowest RMSE across all SWR levels, indicating superior suppression of interference and better preservation of scene geometry under wave-induced distortions.
Summary of Quantitative Findings
The proposed ResNet-based architecture consistently outperforms both CNN and ESPRIT across all tested SNR and SWR conditions. Notably, the performance gap widens under low-SNR and low-SWR scenarios, where classical parametric approaches degrade sharply and conventional CNNs exhibit limited spatial coherence. These results, in conjunction with the qualitative comparisons, affirm the network’s ability to deliver high-fidelity ISAR reconstructions with enhanced robustness to both stochastic noise and structured wave interference.
4.2. Phase Preservation Assessment
In addition to amplitude fidelity, phase consistency plays a crucial role in ISAR imaging, as it directly affects the coherence of scatterer localization, interferometric processing, and subsequent classification tasks. To quantitatively assess phase preservation in the reconstructed complex-valued ISAR images, we evaluated two complementary metrics over the entire test set: the mean phase error (MPE) and the complex phase correlation (CPC).
For each reconstructed sample
and its corresponding high-resolution ground-truth
, the mean phase error was defined as follows:
where
denotes the wrapped phase of each complex-valued pixel and
N is the total number of image elements. Lower MPE values indicate higher phase consistency between the predicted and reference images.
The complex phase correlation was computed as follows:
where
denotes the complex conjugate. This metric measures the global phase alignment and coherence between the predicted and reference complex fields, with values approaching 1 indicating excellent phase preservation.
Figure 8 presents the empirical distributions of these two metrics across 600 test samples. The majority of reconstructed images exhibit low mean phase errors (centered around
–
rad) and high correlation coefficients exceeding
, demonstrating that the proposed ResNet-based framework maintains not only the amplitude structure but also the underlying phase integrity of the original ISAR data. This finding confirms that the learned mapping effectively preserves complex-domain relationships, ensuring that phase-dependent downstream operations such as coherent summation and scatterer tracking remain physically meaningful.
4.3. Computational Complexity and Runtime Analysis
Beyond reconstruction accuracy, practical applicability depends strongly on computational efficiency. To this end, we compared the average runtime of the proposed ResNet, the CNN baseline, and the ESPRIT algorithm when processing single ISAR frames. The experiments were conducted on a modern GPU (NVIDIA RTX series) for the deep learning models and on a CPU for ESPRIT, reflecting their typical operational settings. The proposed ResNet requires approximately 8–12 ms per frame on a modern GPU, compared with about 300 ms for ESPRIT on CPU. The large difference arises because ESPRIT involves covariance-matrix construction and eigenvalue decomposition, which scale cubically with data dimension. In contrast, the ResNet leverages parallel convolutional operations whose computational cost scales linearly with pixel count and benefits from GPU acceleration. These results highlight that the proposed network not only achieves superior reconstruction quality but also operates at real-time speeds suitable for practical maritime ISAR applications.
4.4. CST Ship Model and Realistic ISAR Generation
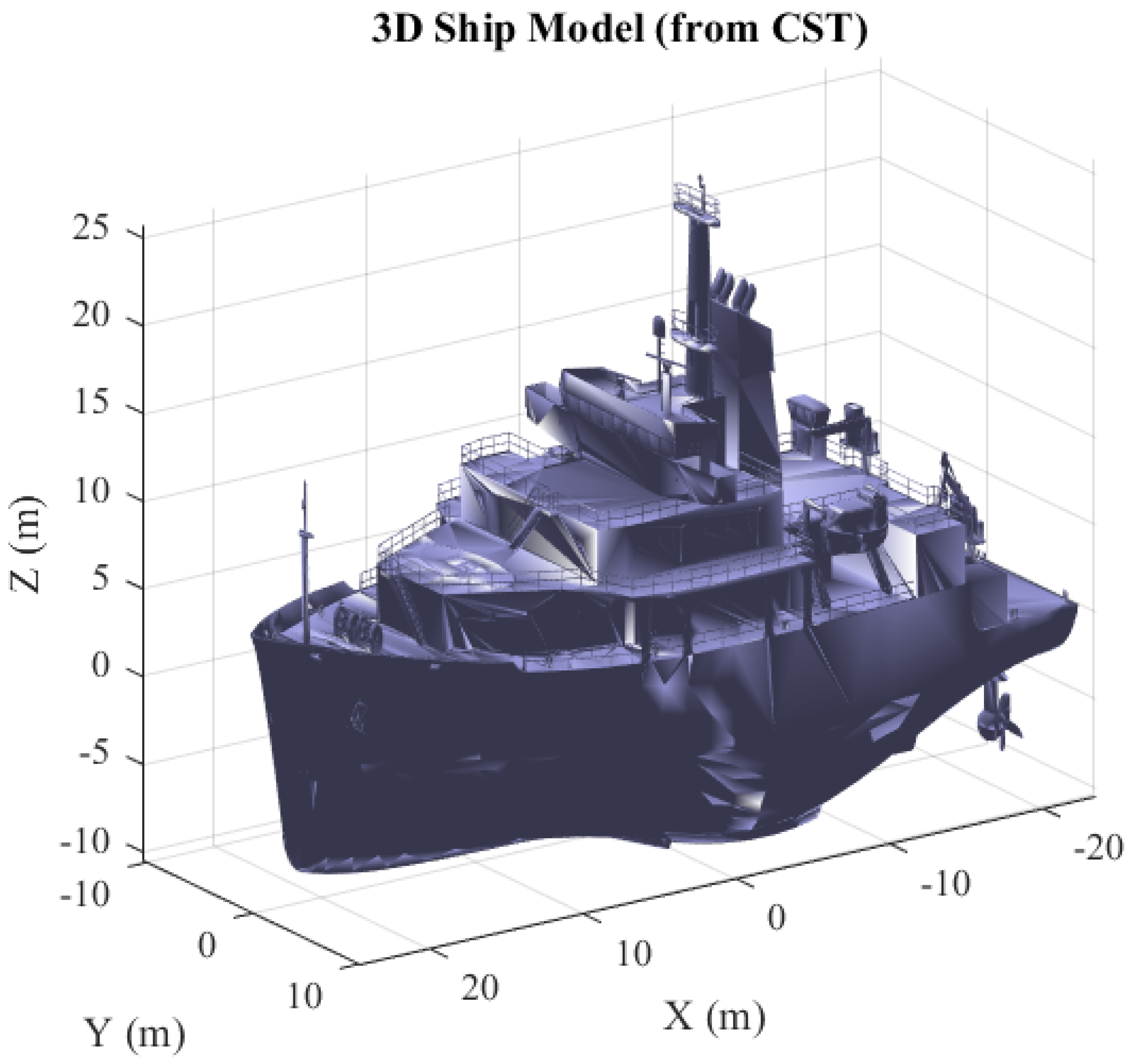
Since publicly available ISAR datasets of maritime targets are extremely limited and rarely include both phase-preserving measurements and realistic sea conditions, we generated our own physically based data using full-wave electromagnetic simulations in CST Studio Suite. To evaluate the method on a physically meaningful geometry, we built a detailed surface mesh model of a ship in CST Studio Suite and exported it for visualization (
Figure 9). The mesh preserves the salient scattering features of the superstructure (masts, deck equipment, and discontinuities along the hull) that dominate X-band monostatic returns.
Using this model, we synthesized ISAR measurements in CST under the same assumptions as our simulation study: a small-aperture, small-bandwidth collection suitable for short coherent dwell, with a sea surface present. To mimic realistic maritime conditions, we enabled a gently undulating sea plane and added measurement impairments consistent with marine radar operation: (i) a controlled thermal noise floor, (ii) low-frequency sea-clutter texture from the wave state, and (iii) mild defocus consistent with platform micro-motion. CST’s ISAR tool then formed a low-resolution magnitude image from the resulting far-field responses. This degraded CST image serves as input to our reconstruction network. The proposed ResNet takes the low-resolution ISAR and predicts a high-resolution reconstruction that restores fine structural detail and attenuates clutter, while preserving the global geometry of the target.
Figure 10 illustrates the end-to-end result on the CST data. The left panel shows the CST
low-res input (dB scale) with sea-state artifacts and reduced cross-range resolution. The right panel shows our
ResNet prediction, which sharpens the dominant scatterers along the superstructure and hull, suppresses background clutter, and recovers edges that are consistent with the 3D model.
5. Discussion
The results obtained in this study underscore the effectiveness of the proposed deep residual network in enhancing the resolution of ISAR images under a wide range of imaging conditions. This section critically analyzes the implications of the results, identifies limitations, and explores avenues for future work.
5.1. Performance Across Degradation Conditions
The network demonstrates strong generalization capabilities across various degradation scenarios characterized by low signal-to-noise ratio (SNR) and severe side-lobe-to-weak-reflector ratio (SWR) imbalances. As depicted in
Figure 4, the model successfully reconstructs fine structural features of the vessel under moderate degradation, yielding a sharp image with well-defined scatterers and suppressed artifacts. This behavior suggests that while the network effectively preserves prominent scatterers and general vessel geometry, its performance can slightly degrade in edge cases dominated by noise and clutter. The robustness to these extreme cases is particularly relevant for maritime applications where weather, motion, and low RCS targets introduce non-Gaussian, non-stationary interference.
5.2. Effectiveness of the Training Strategy
The training strategy employed, which includes a hybrid loss function combining MSE and SSIM, proved essential in balancing pixel-wise accuracy with structural fidelity. The loss function encourages the network not only to minimize reconstruction error but also to preserve spatial correlations and textural patterns. This dual-objective training is particularly effective in preserving the shape of weak reflectors and suppressing high-frequency noise without over-smoothing.
The incorporation of high variability in the training dataset—including a wide span of frequency samplings, angle samplings, and noise levels—contributed significantly to the network’s robustness. The use of synthetic data with controlled reflector positions and geometric patterns allowed for fine-grained learning of underlying scattering physics, enhancing the model’s ability to generalize.
5.3. Insights on Model Design and Limitations
The network’s residual architecture and use of skip connections support stable convergence and preservation of spatial information across scales. This is especially critical in the ISAR domain, where small positional inaccuracies can lead to phase wrapping and range migration errors. However, the reliance on magnitude-only inputs (i.e., ignoring phase) may limit potential performance gains in coherent target enhancement. Incorporating phase information or complex-valued processing is a compelling future direction.
Another notable limitation arises from the synthetic nature of the training data. While the synthetic ISAR simulations were carefully designed to mimic realistic maritime scenarios, the lack of real-world measured data introduces potential domain gaps. Evaluating the network on field-measured ISAR datasets or real sea trials would be a vital next step to validate operational readiness. An additional strength of the proposed architecture lies in its ability to preserve the complex phase structure of the reconstructed ISAR images. Through a dedicated evaluation of phase error and complex correlation metrics over the test set, the network demonstrated a high degree of phase consistency with the ground-truth high-resolution images. This capability is crucial for downstream tasks such as coherent integration, Doppler analysis, and interferometric applications, where phase distortions can undermine interpretability and physical accuracy. The results confirm that the network does not merely learn to approximate image magnitudes but also maintains the integrity of the underlying complex-valued scattering information.
5.4. Broader Implications and Future Work
The proposed framework contributes meaningfully to the growing body of research at the intersection of radar signal processing and deep learning. The demonstrated ability to restore high-resolution ISAR signatures from degraded inputs has direct implications for naval surveillance, automatic target recognition (ATR), motion compensation [
20,
21,
22,
23] and anomaly detection in marine environments.
Future research can pursue several promising directions. First, expanding the architecture to support complex-valued input tensors would allow phase-aware learning, potentially improving performance in coherence-sensitive scenarios. Second, incorporating adversarial loss or attention mechanisms could enhance fidelity, especially for ambiguous or low-SNR inputs. Third, transferring the learned model to different radar bands or geometries (e.g., bistatic ISAR or spotlight SAR) would test its adaptability. Finally, augmenting the dataset with measured data and investigating domain adaptation techniques could bridge the synthetic-to-real gap.
6. Conclusions
This work presented a deep learning-based framework for ISAR image super-resolution and comprehensively compared its performance against the classical ESPRIT algorithm and CNN, under a range of realistic acquisition conditions. The proposed approach, built upon a ResNet-inspired architecture, demonstrated the ability to recover fine structural details, suppress noise, and preserve the geometric integrity of maritime targets, even when the input data suffered from severe resolution degradation and low measurement quality. Qualitative analyses revealed that the network consistently produced sharper, more artifact-free reconstructions than ESPRIT and CNN, with improved localization of both strong and weak scattering centers. Notably, in scenarios characterized by low SNR and SWR, where classical parametric methods exhibited significant artifacts and loss of critical features, the proposed model maintained coherent target shapes and recovered a greater proportion of low-intensity scatterers. These advantages were further validated through quantitative evaluation: RMSE trends across SNR and SWR confirmed that the learned approach outperforms ESPRIT and CNN in all tested regimes, with the largest margins observed under challenging noise and interference conditions. The findings underscore the potential of data-driven models to complement or surpass well-established analytical methods in ISAR processing, particularly in operational scenarios where acquisition imperfections are unavoidable. By jointly learning denoising, de-aliasing, and resolution enhancement within a unified architecture, the proposed framework exhibits resilience to factors that traditionally limit the performance of subspace-based estimators. Future work will focus on extending the methodology to broader target classes, incorporating temporal and multi-aperture coherence, and exploring hybrid model-based and data-driven strategies to further improve interpretability and robustness. Additionally, validation on measured ISAR data from real maritime scenarios will be pursued to assess the generalization capability of the network and to bridge the gap between simulation and operational deployment. In conclusion, this study demonstrates that deep learning can serve as a powerful tool for ISAR image enhancement, offering substantial improvements over classical techniques in both accuracy and robustness, and paving the way for next-generation high-resolution radar imaging systems.