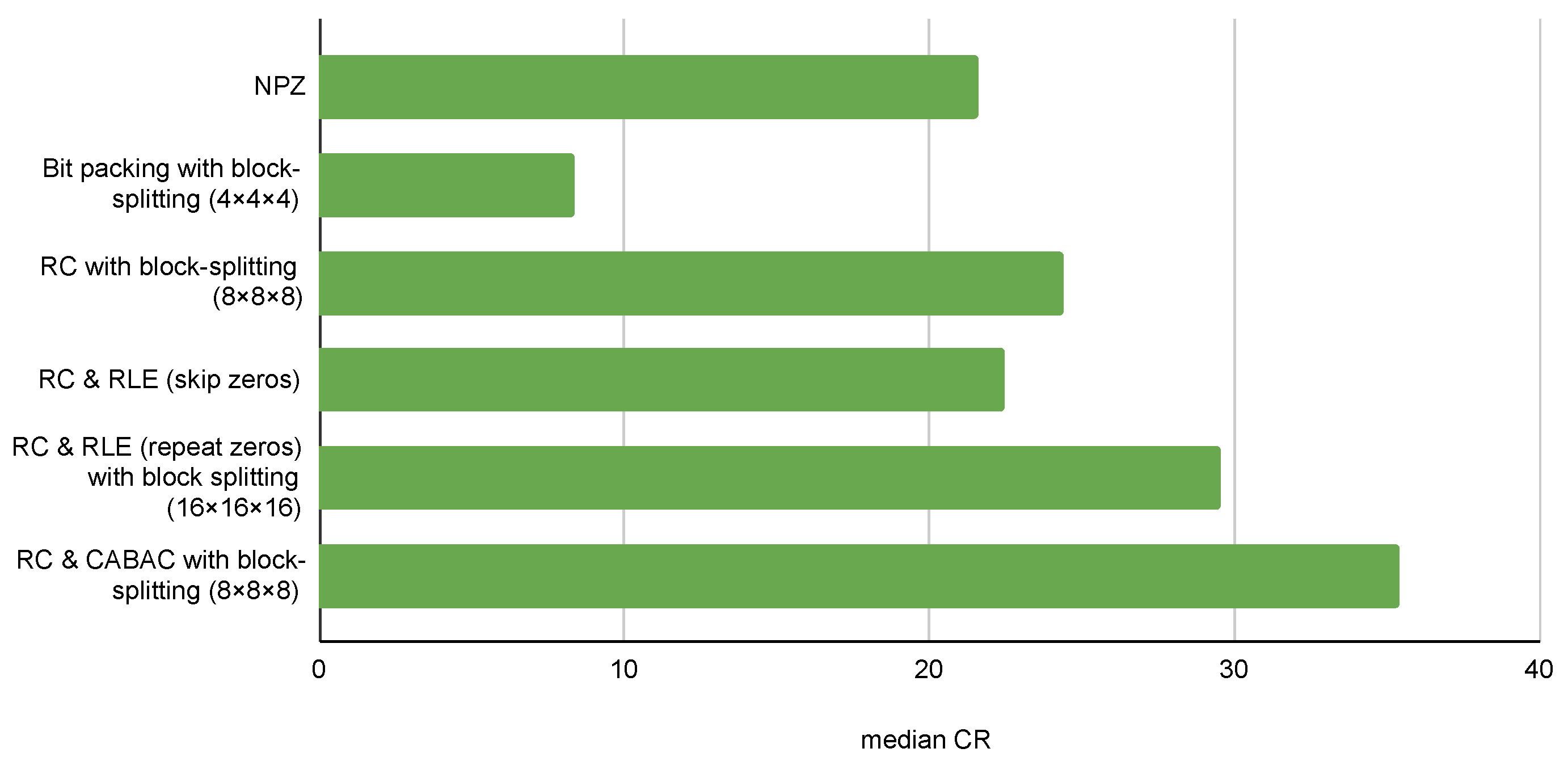On the Lossless Compression of HyperHeight LiDAR Forested Landscape Data

Highlights

What are the main findings?

• The combination of Golomb–Rice coding with run-length encoding and context-adaptive binary arithmetic coding within the developed block-splitting framework provides a median compression ratio above 24 for HyperHeight LiDAR data.
• The proposed methods provide lossless reconstruction and outperform standard NPZ and bit packing when compressing HyperHeight LiDAR data.

What are the implications of the main findings?

• The proposed approach enables efficient, lossless onboard compression of large LiDAR datasets for satellite missions such as NASA CASALS.
• Scalability and data transfer efficiency are improved, supporting real-time environmental monitoring and analysis.

Abstract

Satellite Light Detection and Ranging (LiDAR) systems produce high-resolution data essential for confronting critical environmental challenges like climate change, disaster management, and ecological conservation. A HyperHeight Data Cube (HHDC) is a novel representation of LiDAR data. HHDCs are structured three-dimensional tensors, where each cell captures the number of photons detected at specific spatial and height coordinates. These data structures preserve the detailed vertical and horizontal information essential for ecological and topographical analyses, particularly Digital Terrain Models and canopy height profiles. In this paper, we investigate lossless compression techniques for large volumes of HHDCs to alleviate constraints on onboard storage, processing resources, and downlink bandwidth. We analyze several methods, including bit packing, Rice coding (RC), run-length encoding (RLE), and context-adaptive binary arithmetic coding (CABAC), as well as their combinations. We introduce the block-splitting framework, which is a simplified version of octrees. The combination of RC with RLE and CABAC within this framework achieves a median compression ratio greater than 24, which is confirmed by the results of processing two large sets of HHDCs simulated using the Smithsonian Environmental Research Center NEON data.

1. Introduction

Satellite Light Detection and Ranging (LiDAR) systems provide critical, high-resolution data essential for addressing pressing environmental challenges, including climate change, disaster management, and ecological preservation. These advanced remote sensing platforms capture the planet’s three-dimensional structure with unparalleled precision, providing critical data for applications ranging from global terrain mapping to vegetation monitoring [1,2,3]. Yet, as missions like NASA’s Global Ecosystem Dynamics Investigation (GEDI) and Ice, Cloud, and Land Elevation Satellite-2 (ICESat-2) push the boundaries of resolution and coverage, they generate exponentially increasing data volumes that strain onboard storage, processing power, and downlink capacities [4,5]. The upcoming NASA CASALS mission, leveraging adaptive wavelength scanning and linear-mode single-photon-sensitive technology, exemplifies this trend—promising richer datasets while amplifying the urgency for innovative data management solutions [6,7].

To tackle these data-intensive challenges, a novel representation known as the HyperHeight Data Cube (HHDC) offers a promising approach [8]. HHDCs organize LiDAR photon returns into structured three-dimensional tensors, where each cell captures the number of photons detected at specific spatial and height coordinates [9]. This framework preserves the detailed vertical and horizontal information essential for ecological and topographical analyses, such as Digital Terrain Models (DTMs) and Canopy Height Models (CHMs). Moreover, HHDCs exhibit sparsity and low entropy due to the integer-valued nature of photon counts, making them highly amenable to compression. Beyond traditional products, HHDCs support advanced techniques like compressed sensing, super-resolution, and denoising, enhancing their versatility for next-generation remote sensing applications [10,11,12,13].

Efficient compression of HHDCs is vital, but it must be lossless to maintain scientific integrity. Unlike lossy methods, lossless compression ensures exact reconstruction of photon-counted measurements, a non-negotiable requirement for quantitative analyses—such as forest carbon stock estimation or ice sheet dynamics—that depend on precise photon counts [6]. The inherent redundancy and low entropy of photon-based LiDAR data, particularly from systems like CASALS, make tailored entropy-based coding techniques (e.g., Huffman or arithmetic coding) particularly effective. However, while classical methods provide a foundation, the unique structural properties of HHDCs demand specialized strategies that remain underexplored.

In this paper, we investigate lossless compression techniques tailored for HHDCs, drawing on their inherent sparsity, low entropy, and structural redundancies to enable efficient data management for missions like NASA CASALS. We analyze a suite of entropy-based methods—including bit packing, Rice coding (RC), run-length encoding (RLE), and context-adaptive binary arithmetic coding (CABAC)—along with their synergistic combinations. To further exploit large contiguous regions of zeros in forested landscapes, we introduce a block-splitting framework, a streamlined adaptation of octree structures that partitions HHDCs into manageable blocks, prunes zero-dominated regions, and optimizes subsequent encoding. This approach yields substantial data reduction while preserving exact photon counts, with the optimal combination of RC, RLE, and CABAC within block-splitting achieving a median compression ratio exceeding 24 across diverse datasets.

Our contributions are threefold:

• We propose and refine lossless compression pipelines for HHDCs, integrating classical entropy coders with RLE and a novel block-splitting mechanism to capitalize on data sparsity and geometric distributions.
• We performed a rigorous comparative evaluation of these techniques, quantifying performance through compression ratios, computational complexity, and robustness across varying block sizes and data characteristics.
• We established empirical benchmarks using two extensive sets of simulated HHDCs derived from Smithsonian Environmental Research Center NEON LiDAR data, providing practical recommendations for onboard implementation in future satellite missions.

By fusing insights from remote sensing and information theory, this work paves the way for scalable, resource-efficient handling of high-volume LiDAR data, amplifying the potential for real-time environmental monitoring and scientific discovery.

The remainder of this paper is organized as follows. Section 2 details the structure and properties of HyperHeight Data Cubes, emphasizing their sparsity and suitability for compression. Section 3 presents the proposed lossless compression strategies, including requirements for such methods, the application of Golomb–Rice coding, run-length encoding variants, the block-splitting framework, and metrics for evaluating efficiency. Section 4 evaluates these techniques on two large datasets of simulated HHDCs, comparing compression ratios and performance across configurations. Section 5 discusses the implications of the results, limitations, and avenues for future enhancements. Finally, Section 6 summarizes the key findings and recommendations.

2. HyperHeight Data Cubes

HyperHeight Data Cubes (HHDCs) offer a novel framework for organizing satellite LiDAR data, designed to capture the full three-dimensional structure of landscapes in a compact and structured format [8]. Unlike traditional 2D LiDAR profiles, which provide only cross-sectional views along a satellite’s path, HHDCs integrate horizontal spatial dimensions (length and width) with vertical elevation data, enabling comprehensive ecological and topographic analyses. This representation is particularly valuable for deriving products such as Canopy Height Models (CHMs), Digital Terrain Models (DTMs), Digital Surface Models (DSMs), and Digital Elevation Models (DEMs), which are essential for applications like forest monitoring and terrain mapping.

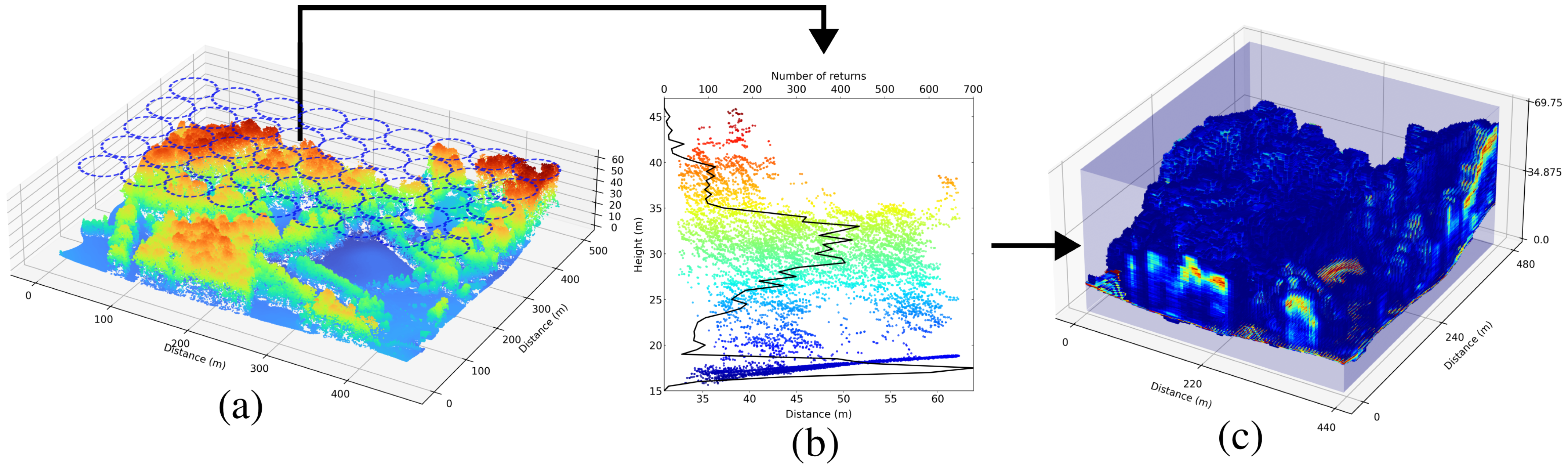
The construction of an HHDC begins with a LiDAR point cloud, as shown in Figure 1a, where each satellite shot illuminates a cylindrical footprint defined by the instrument’s resolution. Photon returns within this footprint are binned into discrete vertical elevation intervals, forming a height-based histogram (Figure 1b) that resembles waveform LiDAR data. These histograms are then spatially aligned across adjacent footprints along and across the satellite swath, merging into a unified 3D tensor, as depicted in Figure 1c. Mathematically, an HHDC is a third-order tensor $\mathcal{X}\in {\mathbb{R}}^{n\times m\times c}$, where n and m represent spatial dimensions (footprints along and across the swath), and c denotes vertical bins. Each element $(i,j,k)$ of $\mathcal{X}$ records the photon count at a specific spatial location $(i,j)$ and elevation $k{\Delta }_z$, where ${\Delta }_z$ is the vertical resolution. For instance, a DTM can be extracted from a 2% percentile slice of the HHDC (Figure 2c), whereas a CHM is derived by subtracting the DTM from the 98% height percentile (Figure 2a), with intermediate slices like the 50% percentile (Figure 2b) aiding biomass estimation.

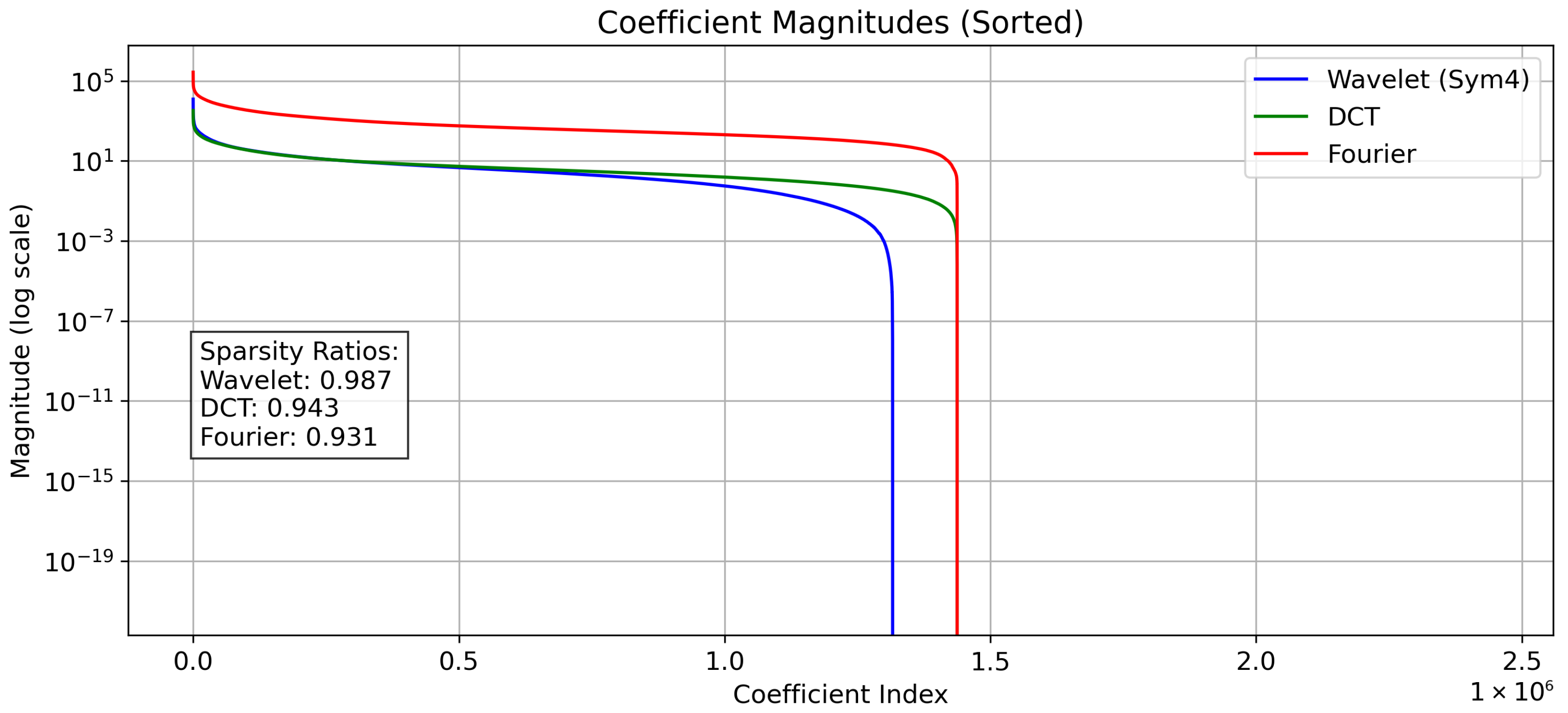
A defining feature of HHDCs is their sparsity, particularly in transform domains like wavelets, where natural landscape data typically exhibit coefficients of less than 1% significance (as shown in Figure 3). This property, combined with the integer-valued, low-entropy nature of photon counts, makes HHDCs ideally suited for lossless compression—a critical requirement for satellite data transmission under bandwidth and energy constraints. Lossless compression preserves the exact photon counts, ensuring the scientific integrity of quantitative analyses such as forest carbon stock estimation or ice sheet dynamics, as emphasized in the Introduction. This capability aligns seamlessly with the needs of the NASA CASALS mission, which will generate dense, high-resolution datasets requiring efficient onboard management and downlink. By leveraging HHDCs’ structural and statistical characteristics, tailored compression strategies can maximize data reduction while maintaining fidelity, supporting the transformative potential of next-generation LiDAR systems for global Earth observation.

3. Lossless Compression of HHDCs

3.1. Requirements for Lossless Compression and Existing Analogs

Classically, lossless methods are defined as data compression algorithms that allow for the reduction in data size without loss of information; therefore, the decompressed file can be restored bit-for-bit, achieving the identical form to the original file. For the considered application, there are a few basic requirements for lossless compression methods and algorithms to be applied.

First, it is desired to have as large a compression ratio (CR) as possible [14,15]. It is defined as follows:

$$CR={\displaystyle \frac{sizeofthesource}{sizeofthecompresseddata}}.$$

This leads to faster data transmission downlink and less memory for temporary saving of compressed data onboard, where resources are usually limited. Here, it is worth stressing that the compression ratio for lossless compression depends on many factors, including coded data properties (complexity, sparsity, and number of channels) and the used compression technique. As a rule, the CR increases for a larger number of image components if component images are correlated, and this fact is exploited by an employed coder. In other words, it is possible (on average) to expect a larger CR for color images than for grayscale ones and for hyperspectral images than for color ones [16]. Meanwhile, the CR might vary in rather wide limits depending on data properties, but usually it cannot be varied for a given image and given coder. This might cause problems since one might run into images for which the CR can be too (inappropriately) small. This means that, characterizing a given method of lossless data compression, one has to operate not only by the mean CR for a set of test data but also by minimal, maximal, and median CR values (or distribution of CR values). Second, a method for lossless compression and the corresponding algorithm should allow fast and lightweight operation. This requirement deals with two factors—the aforementioned limited onboard resources and the possible desire to have information data as soon as possible. Thus, available or new solutions for lossless compression of HHDC have to be analyzed from the viewpoint of computational efficiency.

The considered task of HHDC lossless compression has analogs, the closest of which probably being hyperspectral image (HSI) compression. Numerous papers are devoted to HSI compression (see [17,18,19] and references therein). The paper [17] states that the existing methods can be divided into five main categories: (1) transformed-based; (2) prediction-based; (3) dictionary-based; (4) decomposition-based; and (5) learning-based. Modern lossless techniques [19] often exploit the inherent spectral correlation of component images for multi-band prediction, aiming to increase the CR. On-board systems [16] use simplified adaptive Golomb–Rice encoding to accelerate processing. Neural-based approaches are becoming popular [18]. Meanwhile, standards for lossless and near-lossless multispectral and hyperspectral image compression have been introduced [20,21].

In spite of efforts in the development of lossless techniques for HSI compression, the CR rarely exceeds 5–6 [21,22]. Note that HSIs have specific features [23,24] such the following: (1) they are usually presented as 16-bit data; (2) null-values are rarely met; (3) data ranges in different components vary in rather wide limits; (4) noise is present where input SNR varies in wide limits too. These features distinguish HSI lossless compression from the considered task of HHDC lossless compression, although some aspects can be taken into account, such as the use of correlation in data components.

3.2. Golomb–Rice Coding

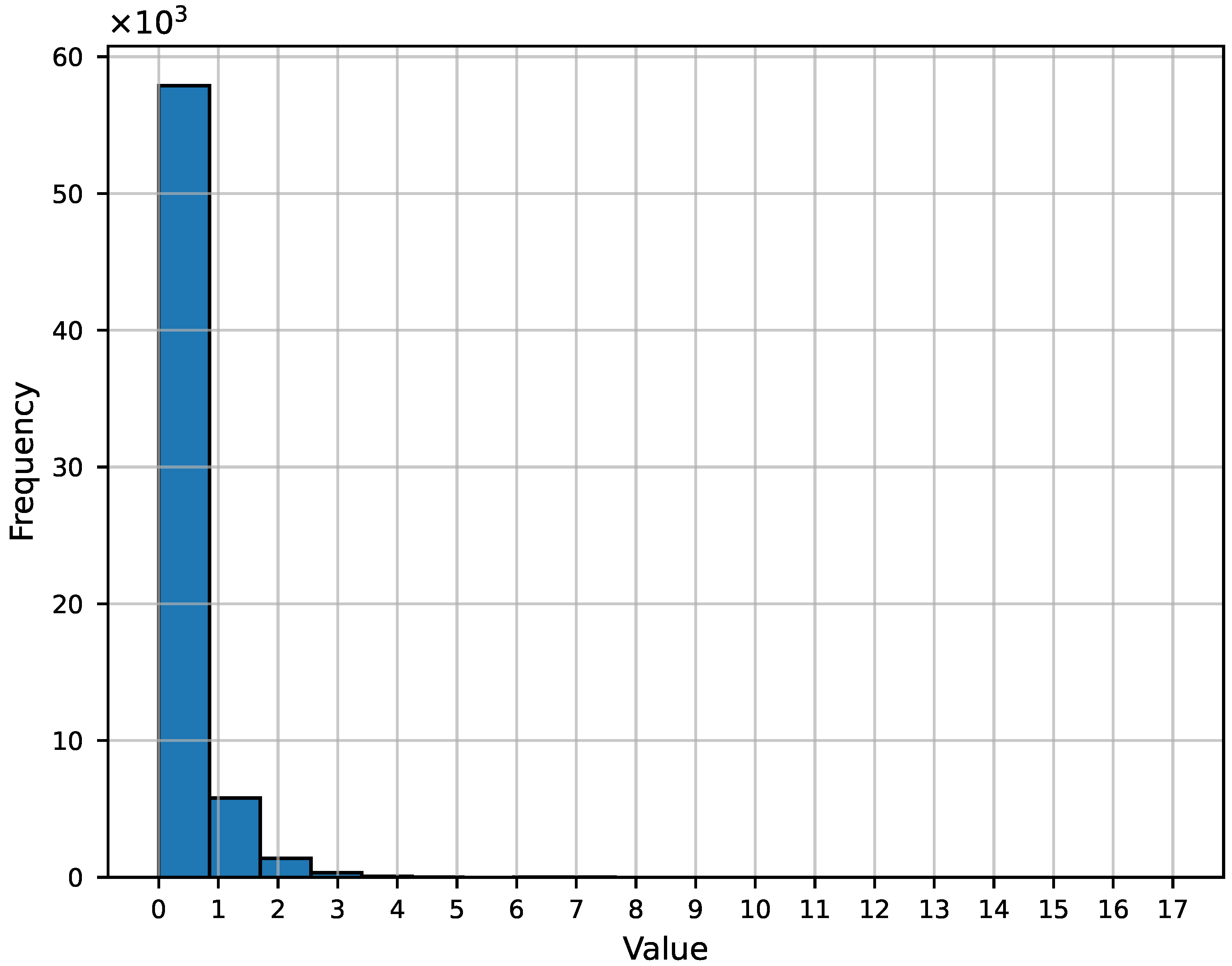
By definition, the entries of HHDCs, which are three-dimensional tensors, are nonnegative integers. Furthermore, in most cases, the set of these values constitutes a highly imbalanced dataset (see Figure 4). Zero is the most frequent value, and its frequency is significantly higher than the total number of all other entries. So, HHDCs are highly sparse. Sparsity can be measured as follows

$$sparsity={\displaystyle \frac{thenumberofzeroelements}{thetotalnumberofelements}}.$$

(1)

Classical lossless algorithms for compressing such data include the following methods: Huffman coding, Golomb coding, arithmetic coding, and prediction by partial matching [25]. Moreover, these techniques are often combined with other methods, in particular, run-length encoding, which is useful if the data being compressed contains long sequences of a single value.

The choice of a compression method is governed by a set of requirements, measured by different performance indicators, including the desired compression ratio, as well as computational complexity limitations, which are of particular relevance when processing large volumes of data on edge devices.

The use of Golomb coding (GC) is optimal if the data follow a geometric distribution:

$$P\left(k\right)=(1-p)p^k,$$

(2)

where p is a parameter of the geometric distribution, and k is an index of encoded value. In general, this method represents each nonnegative integer n with the code $G(n,m)$ that consists of the unary code $U(n,m)$ of $q=[n/m]$ and the truncated remainder $R(n,m)$, where m is a positive integer. Here, $U(n,m)$ is a sequence of q 1s followed by a single 0, and $R(n,m)$ is defined as follows:

• r truncated to $k-1$ bits if $0\le r<c$;
• $r+c$ truncated to k bits otherwise.

where $k={log}_{2}m$, $c=2^k-m$, and $r=nmodm$. In the case of the geometric distribution (2), the parameter m meets the equality $p^m=0.5$. We note that the best correspondence of this distribution to the typical distribution of elements of HHDCs, which represent forestry data, is achieved for the case p = 0.5. This implies that $m=1$, and, therefore, $R(n,m)$ is eliminated. Hence, the following coding scheme is obtained:

$$0\leftrightarrow 0,1\leftrightarrow 10,2\leftrightarrow 110,\dots ,n\leftrightarrow 1\dots 10,\dots .$$

(3)

The scheme (3) is a partial case of GC. It is called Rice coding (RC).

The GC algorithm is computationally more efficient than Huffman coding, arithmetic coding, and the prediction by partial matching approach [25]. Its time and spatial complexities are $T\left(N\right)=O\left(N\right)$ and $S\left(N\right)=O\left(1\right)$, respectively, where N is the size of compressed data. Moreover, the use of the scheme (3) requires only bit shifts, masks, and additions that are particularly effective operations [26]. Furthermore, the development of accurate models, even when restricted to small forestry regions, requires a great number of data samples.

Thus, the application of the GC and RC algorithms to lossless compression of HHDCs is promising. Nevertheless, these methods do not fully exploit the sparsity of the tensors to achieve better compression. In the following, we suggest several approaches that address this feature.

3.3. Run-Length Encoding

Run-length encoding (RLE) is a lossless data compression method [25]. It replaces sequences of similar values with their count, which ensures memory cost reduction. This approach can be implemented in different ways, providing the flexibility feature. The distribution of repeated values is the main factor that specifies the choice of the RLE implementation. If a certain element significantly predominates while consecutive sets of other values occur rarely, the method is applied exclusively to the most frequent element (see Figure 4). Since HHDCs are sparse tensors and zero is a dominant value, it is reasonable to apply the RLE compression exclusively to their sequences. We suggest compressing other values with the RC method given in (3). This approach yields a hybrid compression technique that combines RC and RLE. Further, we denote it with RC & RLE.

The integration of several compression algorithms is frequently utilized to achieve greater reduction in memory costs. The JPEG compression algorithm, which is the de facto standard for digital photos [27], is a classic example [28].

Consider the following ways to perform RC & RLE:

• RC & RLE (skip zeros). This approach compresses a one-dimensional array of non-negative integers by applying two steps. First, it replaces each non-zero element n with the pair $(n,c)$, where c is the number of zeros following this value. For example, the sequence $(12,3),(3,4),(9,7)$ represents the array $12,0,0,0,3,0,0,0,0,9,0,0,0,0,0,0,0$. Next, the first item in each pair is encoded using the modified version of RC:

  $$1\leftrightarrow 0,2\leftrightarrow 10,3\leftrightarrow 110,\dots ,n\leftrightarrow 1\dots 10,\dots .$$
  The second item, which represents the number zeros, is encoded using bit packing. The advantage of this approach is that, compared to (3), it uses one bit less for encoding each positive integer. At the same time, its significant drawback is the need for information about the length of the maximum zero sequence, which determines the number of bits required to represent repetitions of zeros. To compute this value, a single scan of a compressed array is required. The time and spatial complexities of this procedure are $O\left(N\right)$ and $O\left(1\right)$, respectively, where N is the length of the encoded array. In addition, short zero sequences could be encoded with fewer bits, which increases compression efficiency. Below, we consider a more flexible approach.
• RC & RLE (repeat zeros). This technique encodes each positive value of one-dimensional arrays using the scheme (3). Also, it replaces each sequence of zeros with the pair $(0,c)$, where c is the number of zeros following the first zero. For example, the the array $12,0,0,0,3,0,0,0,0,9,0,0,0,0,0,0,0$ is transformed to the sequence $12,(0,2),3,(0,3),9,(0,6)$. After that, this approach encodes the first item of any pair with 0. To compress the second item, bit packing with a fixed number of bits b is applied. If a sequence of zeros is too long, i.e., its length is greater than $2^b-1$, then it is split into k nearly equal-sized parts, where k is the smallest value that guarantees the possibility of encoding with b bits. This technique leads to RC & RLE (repeat zeros), whose performance depends on the parameter b, making it more flexible than the previous approach. Since the best value of b depends on the compressed array, in practice, b can be obtained through an exhaustive search over the range from 0 to $k-1$, where k is a positive integer. The time and spatial complexities of these computations are $O\left(Nk\right)$ and $O\left(k\right)$, respectively, where N is the number of elements of the compressed array.

To apply both RC & RLE (skip zeros) and RC & RLE (repeat zeros) to HHDCs, the transform of three-dimensional tensors into a one-dimensional array is required. This procedure can be performed with respect to the storage order of tensors in memory, which maximizes the efficiency of utilizing the computing system’s memory hierarchy [26]. At the same time, other data scan orders, which ensure better compression, might exist. Indeed, some HHDCs might contain large parts composed exclusively of zeros, and the proper usage of this feature could improve the efficiency. Further, we suggest an approach that exploits particular structural features of HHDCs.

3.4. Block-Splitting

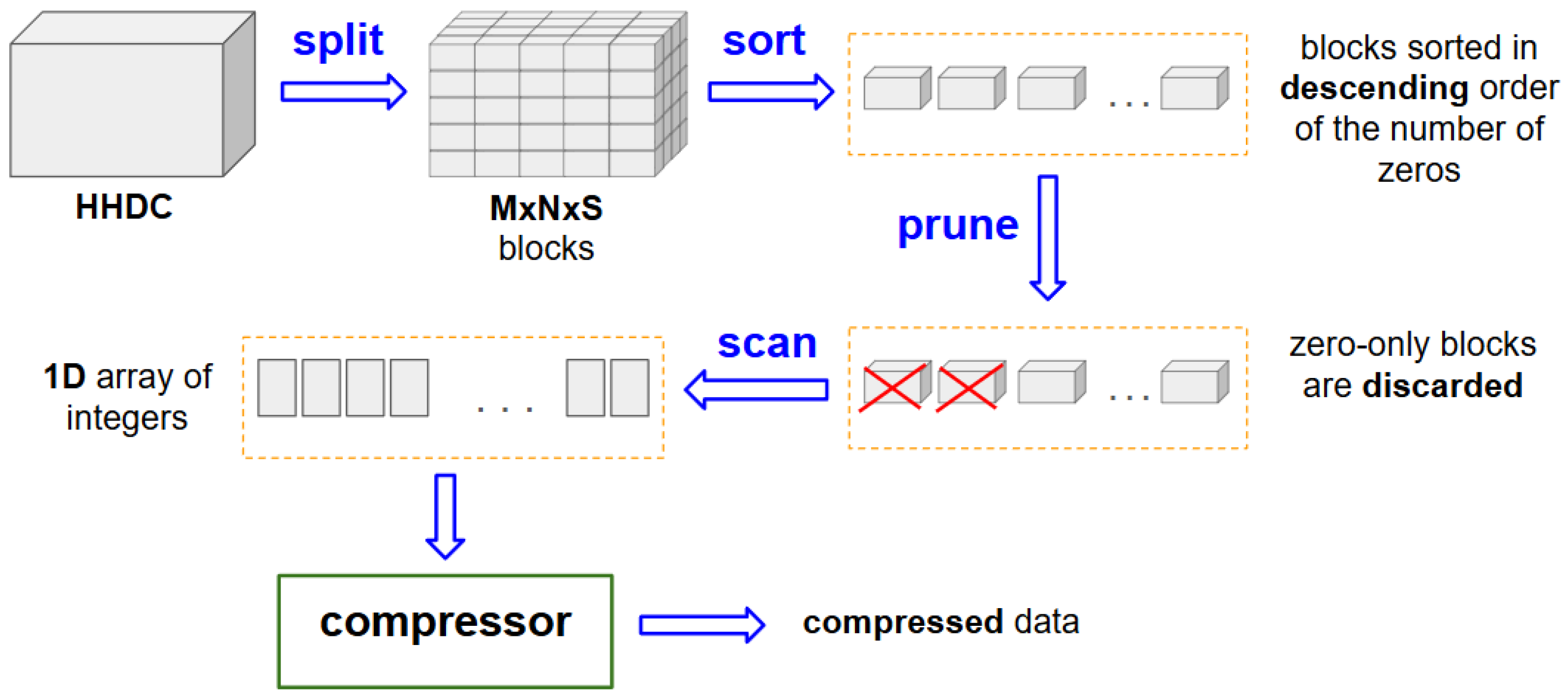
We suggest the following framework for compressing HHDCs (see Figure 5):

• Splitting. The input HHDC of the size $M\times N\times C$ is split into blocks of the size $m\times n\times c$. For software implementation simplicity, the values of m, n, and c are chosen such that they are divisors of M, N, and C, respectively. This guarantees the absence of incomplete blocks. Furthermore, if applicable, m, n, and c should be powers of 2, which ensures the best utilization of the hardware capabilities of the used computational system [26].
• Sorting. The resulting set of blocks is sorted in descending order according to the number of zero elements.
• Pruning. Blocks consisting solely of zeros are eliminated.
• Scanning. The remaining blocks are scanned row by row, and the resulting arrays are concatenated.
• Compression. A lossless compression algorithm is applied to the one-dimensional array obtained above. To provide a correct reconstruction of the input HHDC, the compressed data is appended with two items:
  • A set of integer values specifying the ordering of the blocks;
  • A bitmask indicating whether the corresponding block consisted of zeros and is therefore skipped.

At the final step, any compression method may be employed, including RC, RC & RLE (skip zeros), and RC & RLE (repeat zeros).

We note that the proposed approach requires information on the number of zeros in each block. This data can be obtained with a single pass over the input tensor. This procedure has the following time and spatial complexities: $T=O\left(MNC\right)$ and $S=O\left(K\right)$, where K is the number of blocks. The algorithmic complexity of step 2 is of the order $O(KlogK)$ [29].

It is clear that the compression efficiency of the proposed framework significantly depends on the compressed HHDC, the size of blocks, and the applied coder. Optimal setting selection can be achieved through an exhaustive search, which is feasible for compressing a limited number of tensors. Nevertheless, this single-sample-oriented strategy is impractical for very large sets of HHDCs. For this reason, many algorithms employ settings and components determined based on the analysis of specially selected benchmark data [30]. This approach may not guarantee the best performance; nevertheless, if the number of benchmark samples is sufficiently large, the average outcome is expected to be close to optimal. Further, we evaluate the efficiency of the block-splitting method with the use of the RC method and its extensions.

To make the proposed approach lossless, i.e., to allow exact reconstruction of the original data, two components are required:

• A specification of the block order;
• A specification of which blocks consist entirely of zeros.

To achieve this, we additionally propose using row-wise numbering of the blocks. Next, an array with block indices is added to the header of each compressed data file. Furthermore, an array of bits indicating whether a block consists entirely of zeros is added to the header. This information ensures an exact reconstruction of the original data; however, it increase the size of the compressed file: the more blocks, the larger this additional information. Therefore, in practice, dividing the HHDCs into very small blocks may be inefficient.

3.5. Measuring Compression Efficiency

This research is focused on the application of the RC algorithm and its combinations with RLE. Also, it is suggested to use them as a part of the block-splitting framework. To measure the compression efficiency, we propose to compare these approaches to the following methods:

• Bit packing. This approach is based on the idea that elements within a limited range can be represented using fewer bits than the source [30]. We assume that the evaluation of this method provides a lower-bound estimate for the compression efficiency of other techniques explored in this paper.
• RC & CABAC. This technique is performed as follows. First, each element of the compressed array is encoded using the RC method. Then, context-adaptive binary arithmetic coding (CABAC) is applied to the obtained bitstream. CABAC is a lossless coding method that performs arithmetic coding for binary symbols [25]. It uses context-dependent probability models of the encoded data. These models are continuously updated to capture local statistical correlations. CABAC provides nearly optimal bitstream compression; however, this technique is slower than other methods due to the large number of multiplication operations involved. So, unlike bit packing, its efficiency can be considered an upper-bound estimate.

Further, we use the compression ratio (CR) as the main performance indicator. It is proposed to compute the minimum, maximum, mean, and median of this indicator across the compression of a large dataset of HHDCs. These four parameters are able to quite adequately describe the distributions of CR values that are all non-Gaussian and non-symmetric. Depending on particular conditions and restrictions of compression, each of these four parameters might occur to be the most important. The next section compares the use of RC, RC & RLE (skip zeros), RC & RLE (repeat zeros), RC & CABAC, and bit packing with respect to these metrics.

4. Test Data Compression

Now, we evaluate the compression efficiency of the proposed techniques using two sets of HHDCs denoted as CASALS and 1 × 1. They were retrieved from the Smithsonian Environmental Research Center NEON LiDAR data [31] and represent the same forested area located in the state of Maryland (Latitude 38.88°N, Longitude 76.56°W). Samples of these datasets are tensors of 16-bit unsigned integers, obtained using different simulation parameters that correspond to various data acquisition conditions. CASALS and 1 × 1 HHDCs are tensors with dimensions $16\times 32\times 128$ and $96\times 96\times 256$, respectively. They are available at the following link: https://doi.org/10.34808/2yv1-e686 (accessed on 31 August 2025). Both CASALS and 1 × 1 datasets consist of 13027 compressed NumPy tensors [32] stored in the format NPZ. These files represent the output obtained by applying a combination of the LZ77 algorithm and Huffman coding to the raw tensors [25,30].

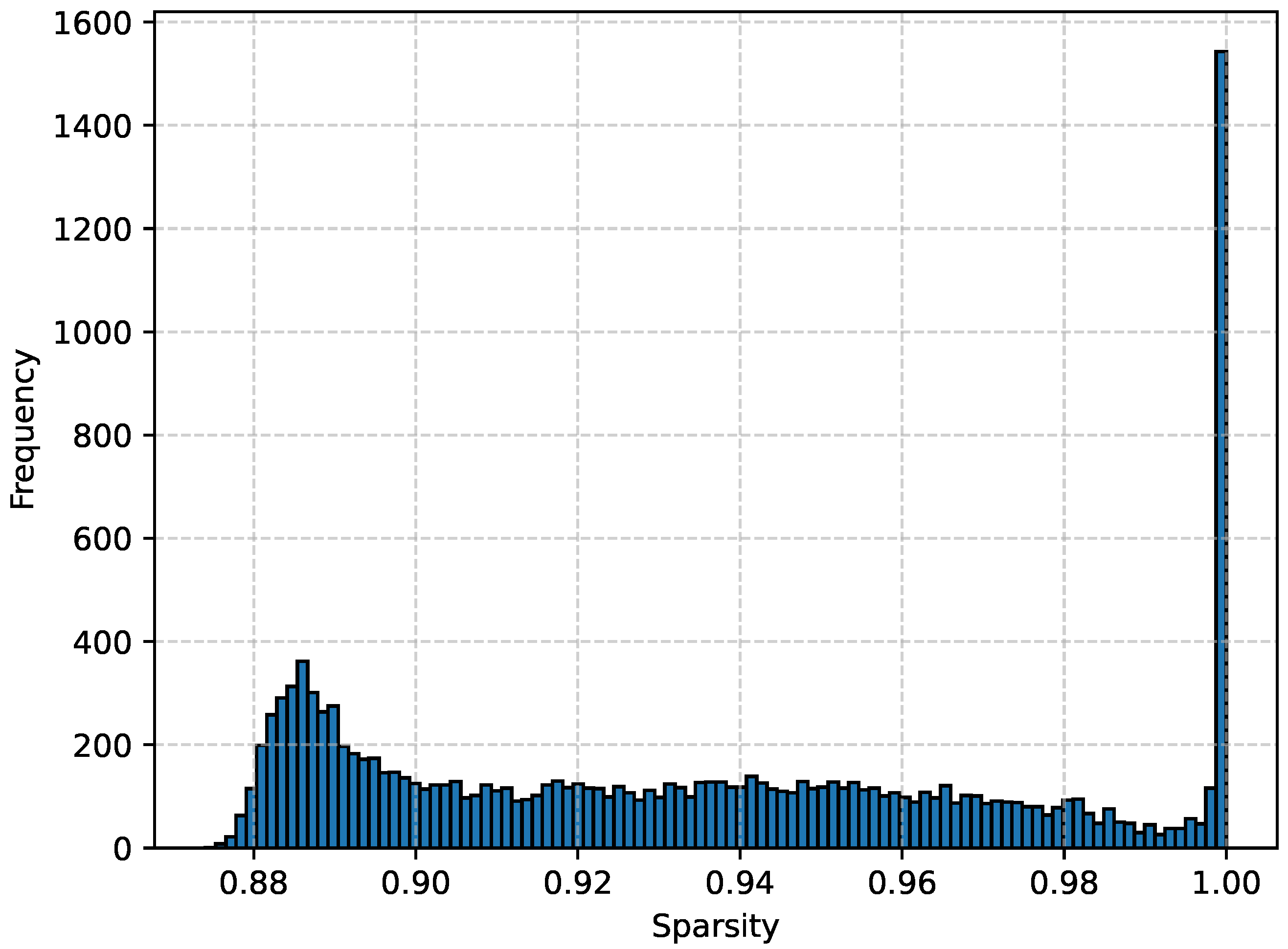
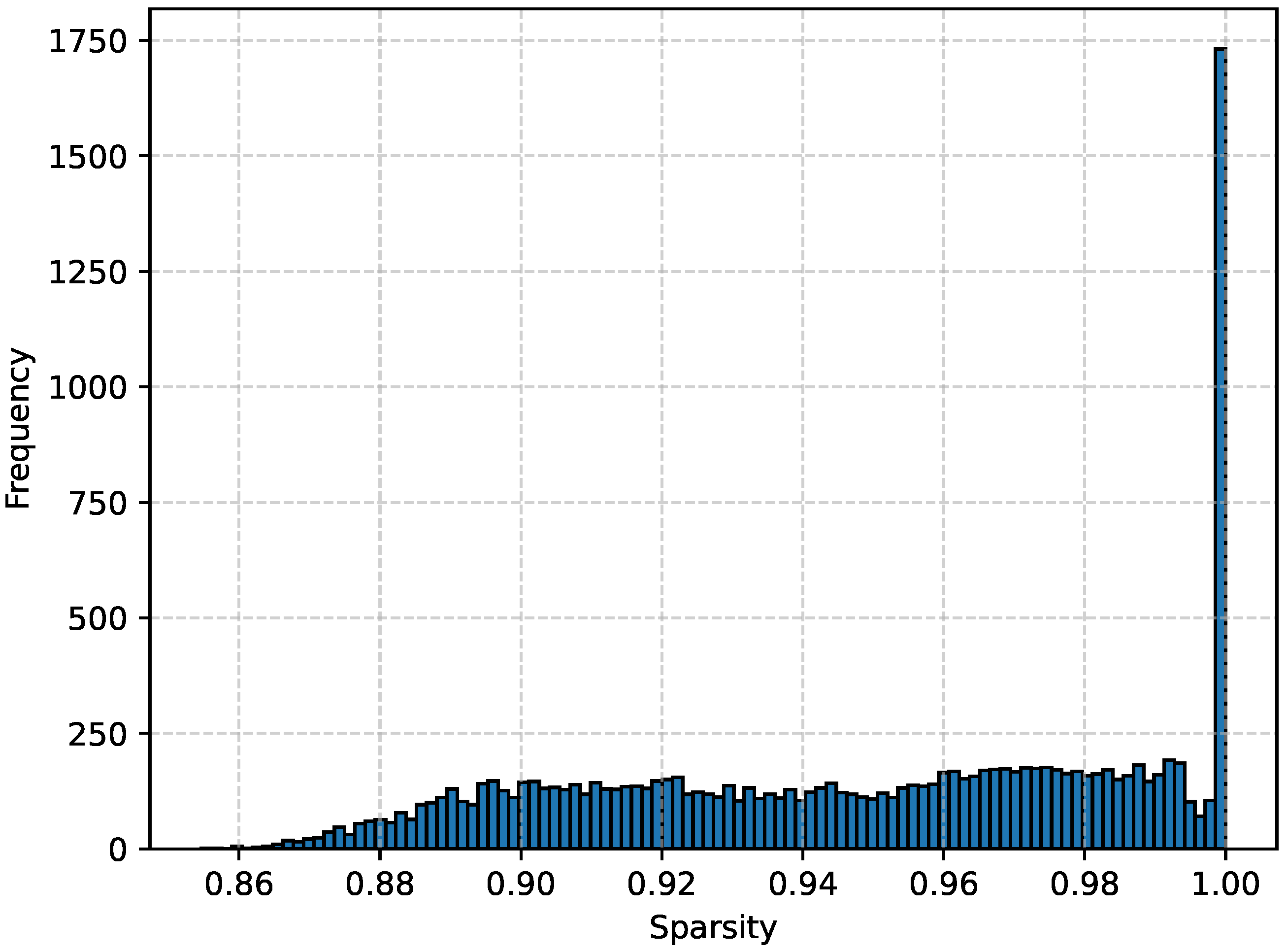
For each tensor of the CASALS and 1 × 1 sets, we evaluate the dominance of zeros over the other elements by calculating $sparsity$ (see Equation (1)). Figure 6 and Figure 7 show the distributions of $sparsity$ for each dataset.

Table 1. Sparsity of CASALS and 1 × 1 HHDCs.

Dataset	Min	Max	Mean	Median
CASALS	0.874	1.000	0.935	0.932
1 × 1	0.855	1.000	0.949	0.954

provides a summary. It follows that the considered data samples are sparse, and therefore, the application of the above-proposed compression methods appears promising.

In this research, we evaluate the compression performance of this approach.

Table 2. The compression efficiency of NPZ.

Dataset	Min	Max	Mean	Median
CASALS	14.24	354.25	50.23	21.62
1 × 1	12.74	976.73	126.65	31.30

compares the minimum, maximum, mean, and median values of the CR provided by NPZ.

Table 3. Bit packing: compression of CASALS HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	3.20	16.00	3.92	3.20
4 × 4 × 4	4.40	92.56	17.28	8.40
8 × 8 × 8	3.78	682.67	33.96	6.99
16 × 16 × 16	3.20	251.10	14.37	5.12

,

Table 4. RC: compression of CASALS HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	13.81	16.00	14.13	13.84
4 × 4 × 4	14.90	92.50	30.88	23.43
8 × 8 × 8	15.41	679.13	62.54	24.37
16 × 16 × 16	13.81	250.62	34.88	20.42

,

Table 5. RC & RLE (skip zeros): compression of CASALS HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	10.38	43,690.67	1010.34	22.43
4 × 4 × 4	13.20	93.02	27.56	19.31
8 × 8 × 8	11.31	1008.25	93.43	18.35
16 × 16 × 16	9.14	10,922.67	445.71	15.83

,

Table 6. RC & RLE (repeat zeros): compression of CASALS HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	18.34	26,214.40	727.56	28.70
4 × 4 × 4	14.27	46.51	22.47	19.47
8 × 8 × 8	19.17	506.07	71.26	29.39
16 × 16 × 16	18.64	5461.33	295.84	29.57

,

Table 7. RC & CABAC: compression of CASALS HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	24.17	16,384.00	608.22	30.73
4 × 4 × 4	21.45	92.89	36.12	27.91
8 × 8 × 8	25.66	985.50	113.86	35.42
16 × 16 × 16	24.71	8738.13	416.09	34.29

,

Table 8. Bit packing: compression of 1 × 1 HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	1.33	16.00	3.01	2.67
4 × 4 × 4	3.71	60.23	17.58	10.28
8 × 8 × 8	2.86	580.54	54.12	8.24
16 × 16 × 16	2.37	3618.55	105.41	6.18
32 × 32 × 32	1.86	1132.10	31.16	4.43

,

Table 9. RC: compression of 1 × 1 HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	10.75	16.00	13.80	13.71
4 × 4 × 4	13.02	60.23	29.43	25.52
8 × 8 × 8	14.04	580.46	87.84	33.06
16 × 16 × 16	13.50	3615.78	176.37	28.31
32 × 32 × 32	12.23	1131.83	67.68	22.19

,

Table 10. RC & RLE (skip zeros): compression of 1 × 1 HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	6.35	1,572,864.00	10,867.03	24.95
4 × 4 × 4	9.19	60.23	25.54	20.67
8 × 8 × 8	8.31	585.00	84.37	23.35
16 × 16 × 16	6.89	5942.81	473.11	19.84
32 × 32 × 32	5.82	63,764.76	2669.51	17.20

,

Table 11. RC & RLE (repeat zeros): compression of 1 × 1 HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	15.94	786,432.00	8593.21	39.56
4 × 4 × 4	10.90	30.12	19.21	18.18
8 × 8 × 8	15.56	292.52	67.97	37.49
16 × 16 × 16	16.37	2971.41	298.81	40.90
32 × 32 × 32	16.37	31,668.40	1688.51	40.23

and

Table 12. RC & CABAC: compression of 1 × 1 HHDCs.

Block-Splitting	Min	Max	Mean	Median
none	15.98	57,543.80	2708.12	39.16
4 × 4 × 4	15.84	60.23	33.69	30.41
8 × 8 × 8	18.82	584.78	114.20	49.12
16 × 16 × 16	18.52	5913.02	536.81	49.11
32 × 32 × 32	18.43	59,729.01	2844.71	47.69

present the results of the evaluation of other considered methods. Furthermore, Figure 8 and Figure 9 provide the comparison of the median values of the CR. We note that, when evaluating the compression ratio, the information required for lossless reconstruction of the original tensor is also taken into account.

From the analysis of the obtained results, the following observations can be made.

First, the difference between the minimum and maximum values of the CR is significant in all cases. Moreover, for the techniques that use RLE, this deviation is drastically high (see Table 5, Table 6, Table 10 and Table 11). This is due to the high sparsity of certain HHDCs, which ensures a high level of compression efficiency for the RLE-based approaches. The mean CR can be relatively high due to the compression of several very sparse arrays. Therefore, we also rely on the median value of the CR in our analysis.

Second, for each of the explored methods, except NPZ, there exists a major dependence on whether block splitting is applied, and, if so, on the chosen block size. Nevertheless, when compressing the CASALS HHDCs using RC & RLE (repeat zeros) combined with block-splitting (see Table 6), the difference between the splitting into 8 × 8 × 8 and 16 × 16 × 16 blocks is insignificant. Another illustration of this feature can be observed in the compression of 1 × 1 HHDCs using RC & RLE (repeat zeros) and RC & CABAC (see Table 7 and Table 12).

Third, in the processing of CASALS HHDCs, the highest and lowest compression efficiency are demonstrated by RC & CABAC with block-splitting (8 × 8 × 8) and bit packing with block splitting (4 × 4 × 4), respectively, (see Figure 8). Also, RC & RLE (skip zeros) is less efficient than RC with block-splitting (8 × 8 × 8) and RC & RLE (repeat zeros) with block-splitting (16 × 16 × 16), yet it outperforms NPZ.

Finally, in compressing the 1 × 1 HHDCs, as in the previous case, the highest and lowest performances are exhibited by RC & CABAC with block-splitting (8 × 8 × 8) and bit packing with block splitting (4 × 4 × 4), respectively. RC & RLE (skip zeros) demonstrates lower efficiency than all other algorithms except bit packing. RC with block splitting (8 × 8 × 8) is outperformed only by RC & RLE (repeat zeros) with block-splitting (16 × 16 × 16) and RC & CABAC with block-splitting (8 × 8 × 8).

In summary, taking into account computational complexity, the following conclusions can be drawn regarding the RC-based approaches:

• RC & CABAC with block-splitting (8 × 8 × 8) is recommended if the primary objective is to achieve the maximum compression ratio.
• RC with block splitting (8 × 8 × 8) is recommended in scenarios with strict constraints on processing time.
• RC & RLE (repeat zeros) with block-splitting (16 × 16 × 16) is recommended when high compression efficiency is desired with comparatively low computational expenses.

These recommendations apply to both CASALs and 1 × 1 HHDCs. Furthermore, they provide greater memory savings compared to NPZ and bit packing.

5. Discussion

The obtained results show that the provided CR values are significantly larger than for HSI compression; hence, the resulting compressed file size is smaller for the same input files compared to the application of the HSI method. We associate this with the following:

• A considerably larger percentage of zero values (see Table 1 and Figure 6 and Figure 7);
• A narrower range of possible values;
• A large probability that there are blocks consisting only of zeros;
• Adaptation of coding techniques to these properties of HHDCs.

In practice, the influence of noise and/or other factors may lead to a smaller sparsity, and, in turn, this will result in smaller CRs. Nevertheless, if sparsity is high (above 0.85), one can expect high efficiency of the proposed methods. However, the question of which method is the best for compressing a tensor with a given sparsity remains, in general, open.

Our approach to compression can be treated as a simplified version of the Octree method [33], although more complex versions might provide better results. This can be one of the directions of future research.

The Octree method has been primarily used in computer graphics for the compression of 3D data, such as voxels, or point clouds. Its operating principle involves dividing a cube into eight equal parts (octants) and then selecting those with a non-zero number of elements for further division using the same principle. In the case of color reduction, these can be cubes that represent the largest clusters of pixels with similar colors. Lossless data compression takes advantage of the fact that for sparse data, such as LiDAR data, many of the sub-octants obtained from subsequent divisions contain no data at all and are therefore highly amenable to lossless compression. Only non-empty or non-uniform regions are further subdivided.

We give our recommendations concerning the computational efficiency based on the fixed sizes of the considered types of data cubes. For other sizes of HHDCs, the recommendations might change. For example, the optimal block size can differ from that obtained in our analysis. Meanwhile, our analysis elucidates the potential bottleneck for each method and proposes some approaches to accelerate data processing.

The complexity analysis of the proposed methods is presented in the form of asymptotic relations. From these results, it is not possible to evaluate performance, including processing time and system load, on a specific hardware platform. Such metrics strongly depend on the software implementation of the algorithms. This implementation should take into account the hardware capabilities. This topic will be addressed in a separate study.

The suggested methods are targeted mainly for forest environments characterized by high sparsity. This design choice may limit their generalizability to other landscape types. The algorithm’s performance is anticipated to deteriorate in densely structured urban areas. Similar degradation may occur in topographically complex terrain.

The proposed approach to skipping the “empty” blocks can be applied on the basis of hybrid compression techniques where lossy compression is applied only to blocks containing non-zero values.

If a lossless compression method contains auxiliary information (for example, about positions of non-empty blocks), it should be passed first to be used at the decompression side.

When comparing two similar compression methods, RC & RLE (skip zeros) and RC & RLE (repeat zeros), we observe that the performance of RC & RLE (skip zeros) is lower than that of RC & RLE (repeat zeros). This difference is mainly due to the design of the algorithms. Both methods use zero-sequence packing. However, RC & RLE (repeat zeros) allows zero chains to be split into segments and compressed separately, while RC & RLE (skip zeros) does not provide such flexibility. In RC & RLE (skip zeros), each nonzero value is represented with fewer bits than in RC & RLE (repeat zeros), but an additional k bits are required to encode subsequent zeros. These k bits must be sufficient to encode the longest possible sequence. In other words, RC & RLE (skip zeros) does not allow k to be adjusted, unlike RC & RLE (repeat zeros). This lack of flexibility is reflected in the compression results on the test data.

The results obtained from compressing two datasets, which consist of more than 13,000 HHDCs, demonstrate that the suggested block-splitting technique improves the efficiency of each considered compression algorithm except RC & RLE (skip zeros). This preprocessing stage requires additional computational resources, primarily associated with determining the appropriate order, i.e., sorting. The algorithmic complexity is $O(BlogB)$, where B is the number of blocks. For the explored datasets and the obtained block size recommendations, the maximum number of blocks does not exceed 5000. Sorting arrays of non-negative integers of this size constitutes a straightforward task for most modern systems [26].

Next, the optimal value of the block size s depends on the sparsity of the compressed HHDC and the applied method. To achieve maximum memory efficiency, this parameter should be determined individually for each object. However, this requires additional computational resources, especially when the size of the compressed data cubes is very large. In cases where processing is performed on a standalone device with limited computational power or when high speed is required, it is reasonable to use a predefined s. The recommended values of this parameter for the considered data were obtained in the previous section. In a more general case, however, it would be more practical to use a trained model that suggests the optimal s for a given sparsity level. The study of such an approach will be the subject of future research.

It follows that both RC and RC & RLE (repeat zeros) combined with block-splitting using an appropriate block size outperform bit packing and NPZ, which serve as baselines. Furthermore, since these methods are computationally efficient, they can be recommended for the compression of large-scale sets of HHDCs. In addition, these techniques exhibited a consistent performance pattern across CASALS and 1 × 1 HHDCs. For this reason, similar behavior may be expected in the general case. Specifically, in terms of the CR, the best block-splitting is achieved for RC with block sizes $8\times 8\times 8$, and for RC & RLE (repeat zeros) with block sizes $16\times 16\times 16$. Nevertheless, RC & CABAC outperforms them, which means that better compression can be obtained. However, this method is computationally more expensive due to the extensive usage of multiplication operations. When compressing a large number of HHDCs, the resulting resource overhead may be unacceptable. To solve this problem, alternative variants of arithmetic coding, in particular, the Q-coder [34] and MQ-coder [35], can be applied. Another approach involves the application of integrated techniques similar to JPEG2000 [27]. Nevertheless, the complexity of software implementation might be an obstacle to further adoption and maintenance.

6. Conclusions

In this paper, we have considered the problem of lossless compression of LiDAR data given in the novel form of three-dimensional tensors called HyperHeight Data Cubes. Specific properties of HHDCs are shown, including high sparsity of data and a limited range of values. This leads to the necessity and possibility to exploit these properties in the design of modified methods of lossy compression that can obtain compression ratios considerably larger than in other typical practical situations when one deals with 3D data compression (such as hyperspectral images). Rice coding, its combinations with run-length encoding and context-adaptive binary arithmetic coding, bit packing, and LZ77 combined with Huffman coding have been explored. The block-splitting method, which transforms an input tensor to a one-dimensional array for further compression by these algorithms, has been introduced. The considered methods have been evaluated in terms of the compression ratio achieved.

The results of the analysis have shown that bit packing demonstrates the lowest efficiency in terms of compression ratio. Our further recommendations are as follows:

• Rice coding combined with context-adaptive binary arithmetic coding and block-splitting (with block size 8 × 8 × 8) ensures the highest compression ratio, with a median value greater than 35. However, this method is computationally more resource-intensive than other techniques. Therefore, it should be used when the number of tensors to be compressed is relatively small or when processing time constraints are not strict.
• Rice coding combined with run-length encoding (the repeat zeros mode) and block-splitting (with block size 16 × 16 × 16) provides the highest efficiency among the methods with low computational costs. The median value of the compression ratio is greater than 29. This approach is recommended when a balance is required between achieving high compression performance and limiting computational expenses.
• Rice coding combined with block-splitting (with block size 8 × 8 × 8) is recommended when low processing time is critical. This method is less effective than the two previous techniques. Nevertheless, it outperforms bit packing and LZ77 combined with Huffman coding, providing a median value of compression ratio not lower than 24.

In general, these methods provide a high compression ratio. Moreover, this value exceeds that achieved by lossless HSI compression methods, rarely exceeding 6. Lossless compression of remote sensing data achieves lower efficiency [36]. The results obtained in this research are primarily attributed to the specific characteristics of the data, especially their sparsity.

The proposed tensor block-splitting method can be considered a simplified analogue of octrees. Modifying this method, including adaptations to specific data patterns, and developing compression techniques within this framework are promising directions. These will be objectives for our future research. In addition, the suggested methods have been explored in the context of comparison with a limited set of techniques. The effectiveness of other approaches, especially those based on constructive tools such as trigonometric polynomials, wavelets, and atomic functions, remains unstudied. In our next study, we will focus on these methods and perform a comparative analysis with existing industry standards, such as CCSDS-123.0.