High-Precision HRWS SAR Phase Error Estimation with Inaccurate Baseline: A Joint-Pixel-Based Image Subspace Approach
Highlights
- An image domain subspace-based phase error estimation method based on joint-pixel selection and vector construction is proposed in this paper; this method has higher accuracy when the baseline error exists.
- Two construction methods of joint-pixel data vectors are compared, and a more effi-cient method is selected through performance analysis; this method is suitable for er-ror estimation scenarios.
- The method proposed in this paper is aimed at the background of the decrease in phase error estimation accuracy caused by inaccurate baseline error. By converting multichannel signals into image domain and constructing joint pixels, more robust and more efficient channel error estimation is achieved.
- The proposed method provides an idea of processing in the image subspace for the robustness estimation of other multichannel errors.
Abstract
1. Introduction
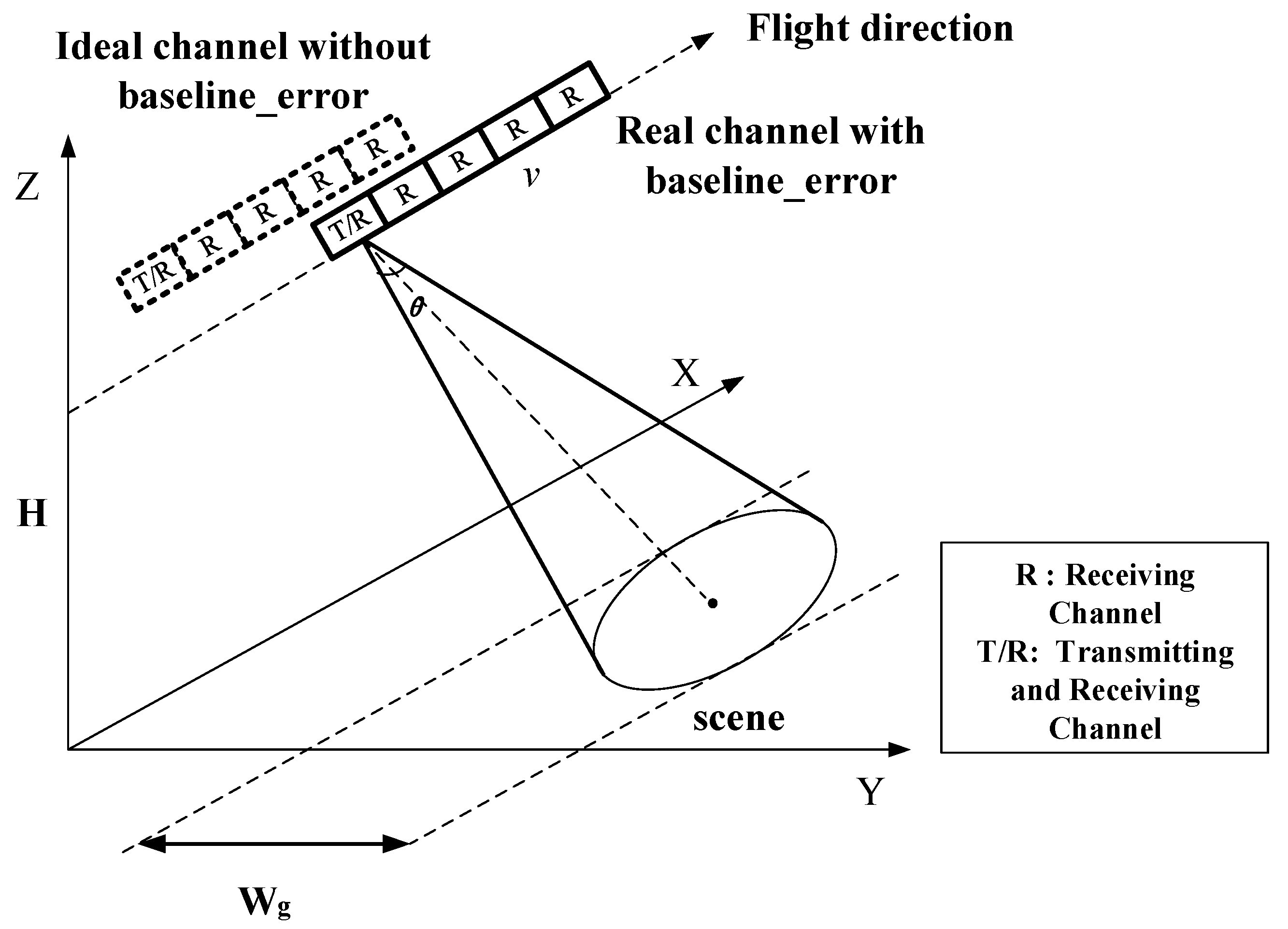
2. Multichannel Signal Model in Image Domain
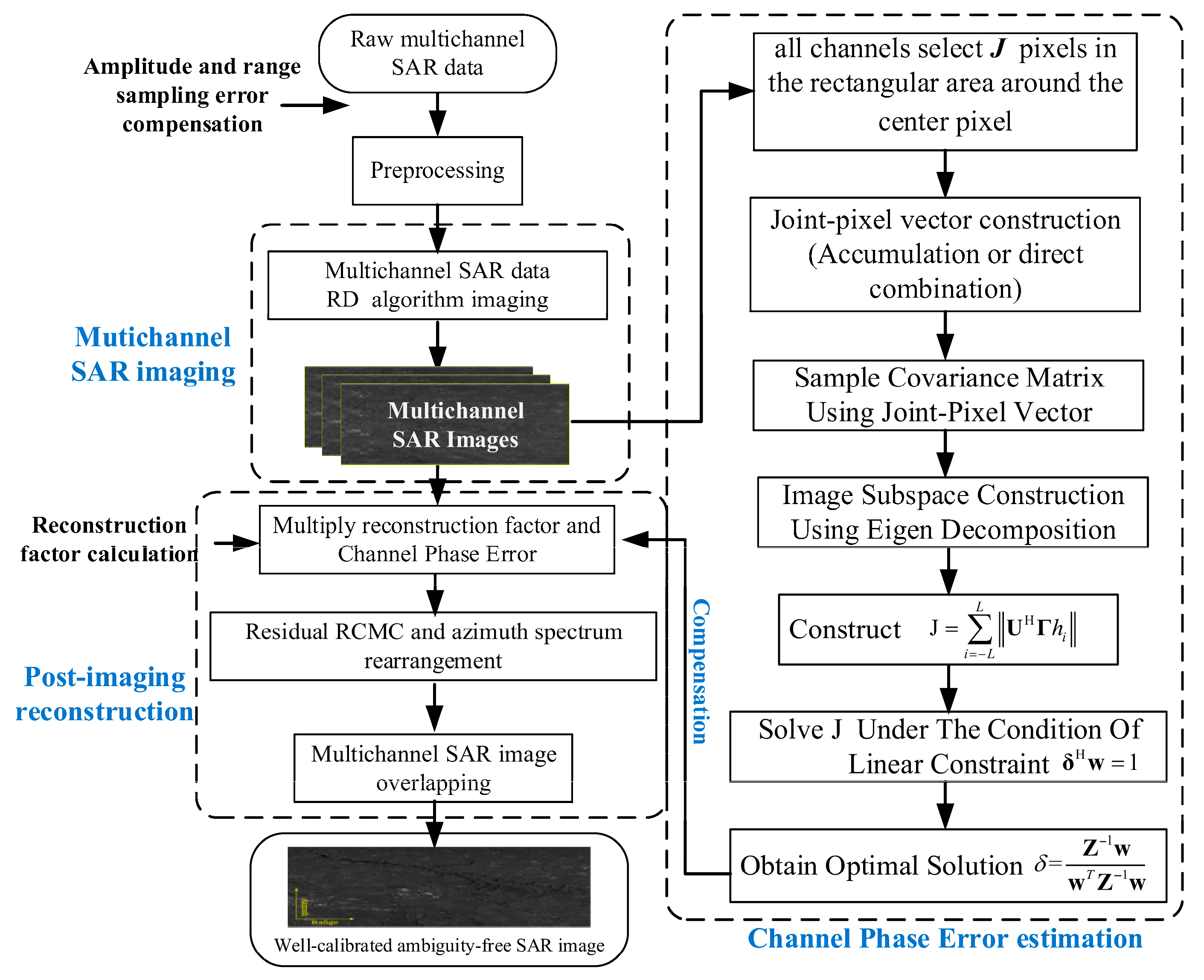
3. Proposed Method
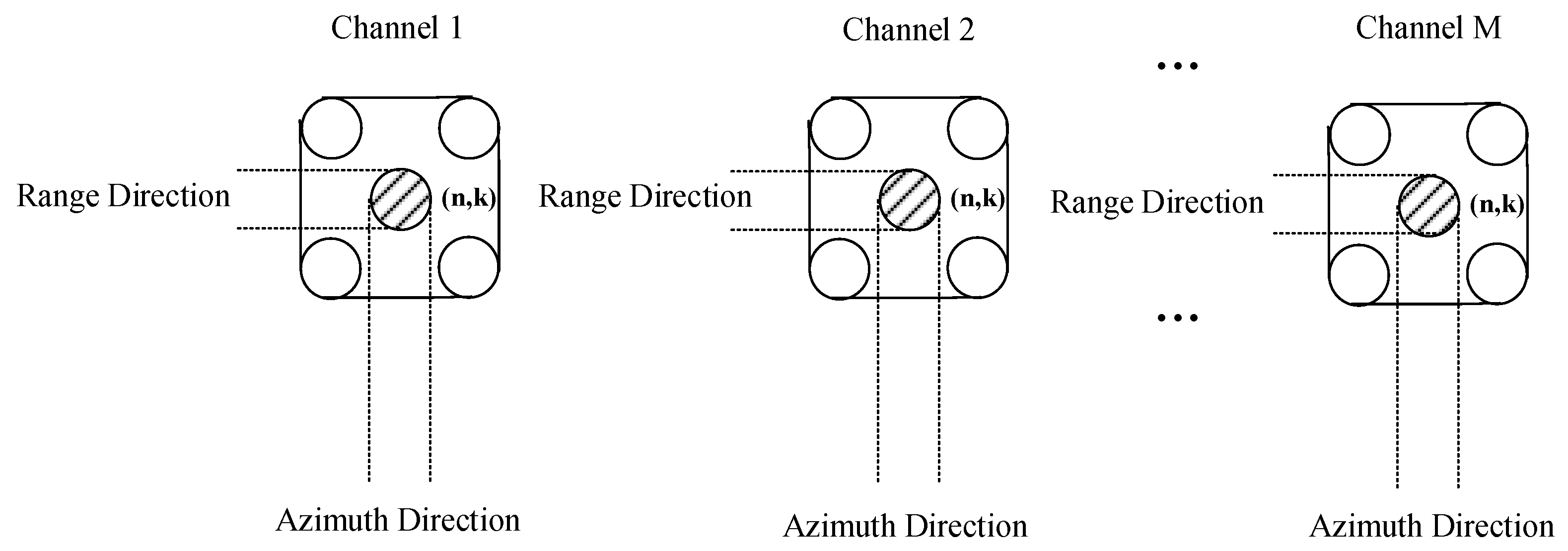
3.1. Image-Domain Channel Phase Error Estimation Method Based on Single Pixel
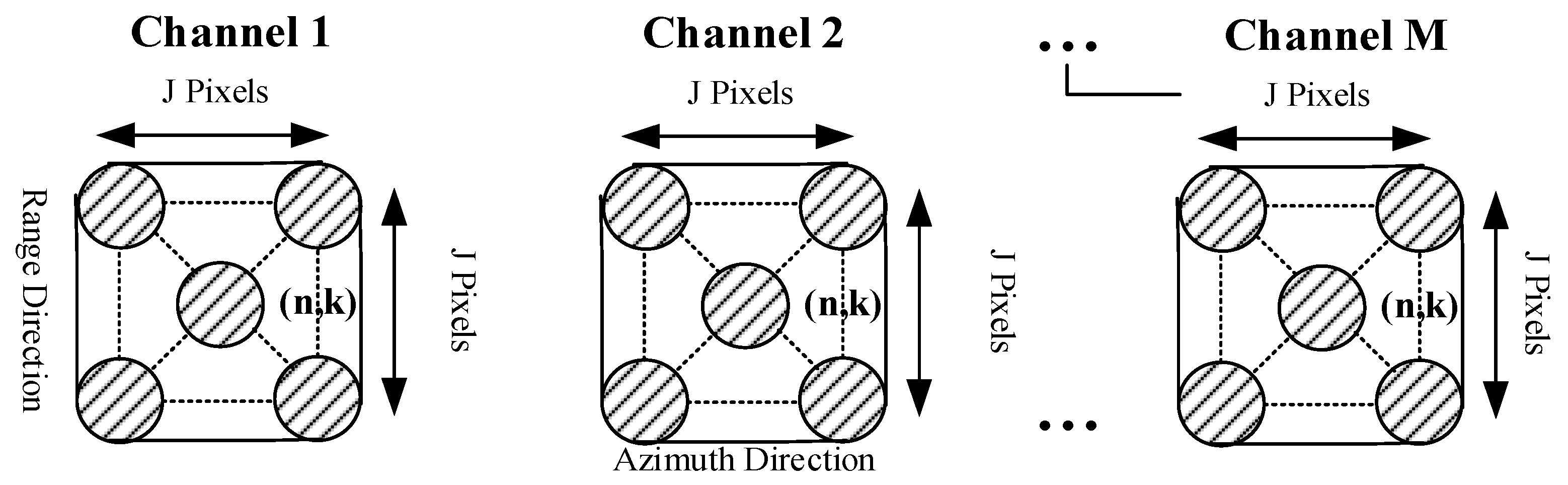
3.2. Image-Domain Channel Phase Error Estimation Method Based on Joint Pixel
4. Results
4.1. Simulated Data Experiment
4.2. Analysis of the Computational Complexity
4.3. Acquired SAR Data Processing
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, G.-C.; Liu, Y.; Xiang, J.; Liu, W.; Xing, M.; Chen, J. Spaceborne Synthetic Aperture Radar Imaging Algorithms: An overview. IEEE Geosci. Remote Sens. Mag. 2022, 10, 161–184. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, G.-C.; Xiang, J.; Xing, M.; Guo, L.; Yang, J. A Imaging Passive Localization Method for Wideband Signal Based on SAR. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019. [Google Scholar]
- Ji, Y.; Dong, Z.; Zhang, Y.; Wang, C.; Hu, C.; Xu, Z. Trans-ionospheric Synthetic Aperture Radar Observation: A Comprehensive Review. IEEE Geosci. Remote Sens. Mag. 2025, 13, 273–313. [Google Scholar] [CrossRef]
- Ji, Y.; Dong, Z.; Zhang, Y.; Tang, F.; Mao, W.; Zhao, H.; Xu, Z.; Zhang, Q.; Zhao, B.; Gao, H. Equatorial Ionospheric Scintillation Measurement in Advanced Land Observing Satellite (ALOS) Phased Array-Type L-Band Synthetic Aperture Radar (PALSAR) Observations. Engineering 2025, 47, 70–85. [Google Scholar] [CrossRef]
- Curlander, J.; Mcdonough, R. Synthetic Aperature Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991; pp. 205–215. [Google Scholar]
- Yang, W.; Li, C.; Chen, J.; Wang, P.B. Effects of time synchronization on image quality of spaceborne multi-channels SAR. Chin. J. Radio Sci. 2011, 26, 636–640. [Google Scholar]
- Xu, W.; Huang, P.; Wang, R.; Deng, Y. Processing of Multichannel Sliding Spotlight and TOPS Synthetic Aperture Radar Data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4417–4429. [Google Scholar] [CrossRef]
- Chen, Q.; Deng, Y.; Wang, R.; Liu, Y. Investigation of Multichannel Sliding Spotlight SAR for Ultrahigh-Resolution and Wide-Swath Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1339–1343. [Google Scholar] [CrossRef]
- Qian, J.; Sun, G.-C.; Li, L.; Xing, M. Multichannel SAR high speed target indication with improved detection probability. Chin. J. Radio Sci. 2011, 26, 354–361. [Google Scholar]
- Liu, Y.; Wang, H.; Liao, G. Calibration and remedy for multichannel imaging satellites. Chin. J. Radio Sci. 2005, 20, 614–618. [Google Scholar]
- Li, X.; Xing, M.; Xia, X.-G.; Sun, G.-C.; Liang, Y.; Bao, Z. Deramp Space–Time Adaptive Processing for Multichannel SAR Systems. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1448–1452. [Google Scholar]
- Zhou, Y.; Wang, W.; Chen, Z.; Zhao, Q.; Zhang, H.; Deng, Y.; Wang, R. High-Resolution and Wide-Swath SAR Imaging Mode Using Frequency Diverse Planar Array. IEEE Geosci. Remote Sens. Lett. 2021, 18, 321–325. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.; Chen, Z.; Wang, P.; Zhang, H.; Qiu, J. Digital Beamforming Synthetic Aperture Radar (DBSAR): Experiments and Performance Analysis in Support of 16-Channel Airborne X-Band SAR Data. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6784–6798. [Google Scholar] [CrossRef]
- Ender, J.; Berens, P.; Brenner, A.R.; Rossing, L.; Skupin, U. Multichannel SAR/MTI system development at FGAN: From AER to PAMIR. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1697–1701. [Google Scholar]
- Baumgartner, S.; Gabele, M.; Gebert, N.; Scheiber, R.; Krieger, G.; Bethke, K.-H.; Moreira, A. Digital beamforming and traffic monitoring using the new FSAR system of DLR. In Proceedings of the International Radar Symposium (IRS), Cologne, Germany, 5–7 September 2007. [Google Scholar]
- Liu, A.; Wang, F.; Xu, H. Nriet-SAR: A new Multichannel Multi-Mode Polarimetric Airborne SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 8, 3155–3166. [Google Scholar]
- Morena, L.; James, K.; Beck, J. An introduction to the RADARSAT-2 mission. Can. J. Remote Sens. 2004, 30, 221–234. [Google Scholar] [CrossRef]
- Kankaku, Y.; Suzuki, S.; Osawa, Y. ALOS-2 mission and development status. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 2396–2399. [Google Scholar]
- Lehner, S.; Schulz-Stellenfleth, J.; Brusch, S.; Li, X.M. Use of TerraSAR-X data for oceanography. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Zhang, Q. System Design and Key Technologies of the GF-3 Satellite. Acta Geod. Cartogr. Sin. 2017, 46, 269–277. [Google Scholar]
- Zhang, S.-X.; Li, S.; Liu, Y.; Xing, M.-D.; Chen, J. A Novel Azimuth Doppler Signal Reconstruction Approach for the GEO-LEO Bi-Static Multichannel HRWS SAR System. IEEE Access 2019, 7, 39539–39546. [Google Scholar] [CrossRef]
- Mapelli, D.; Guccione, P.; Giudici, D.; Stasi, M.; Imbembo, E. Generalization of the Synthetic Aperture Radar Azimuth Multi-Aperture Processing Scheme—MAPS. Remote Sens. 2024, 16, 3170. [Google Scholar] [CrossRef]
- Kim, J.-H.; Younis, M.; Prats-Iraola, P.; Gabele, M.; Krieger, G. First spaceborne demonstration of digital beamforming for azimuth ambiguity suppression. IEEE Trans. Geosci. Remote Sens. 2013, 51, 579–590. [Google Scholar] [CrossRef]
- Younis, M.; Fischer, C.; Wiesbeck, W. Digital beamforming in SAR systems. Remote Sens. 2003, 41, 1735–1739. [Google Scholar] [CrossRef]
- Sun, G.-C.; Xiang, J.; Wang, Y.; Zhang, Z.; Yang, J.; Xing, M. A Postmatched-Filtering Image-Domain Subspace Method for Channel Mismatch Estimation of Multiple Azimuth Channels SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5100614. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, F.; Chen, L.; Wan, Y.; Jiang, T. A Novel Error Correction Method for Airborne HRWS SAR Based on Azimuth-Variant Attitude and Range-Variant Doppler Domain Pattern. Remote Sens. 2025, 17, 2831. [Google Scholar] [CrossRef]
- Xiang, J.; Ding, X.; Sun, G.-C.; Zhang, Z.; Xing, M.; Liu, W. An Efficient Multichannel SAR Channel Phase Error Calibration Method Based on Fine-Focused HRWS SAR Image Entropy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7873–7885. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Xie, J.; Fang, G.; Chen, H.; Shen, Y.; Yang, Z.; Zhang, X. Channel Amplitude and Phase Error Estimation of Fully Polarimetric Airborne SAR with 0.1 m Resolution. Remote Sens. 2025, 17, 2699. [Google Scholar] [CrossRef]
- Li, Z.; Bao, Z.; Wang, H.; Liao, G. Performance improvement for constellation SAR using signal processing techniques. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 436–452. [Google Scholar] [CrossRef]
- Ma, L.; Liao, G.; Li, Z. An Approach for Multichannel SAR Array Error Compensation and Its Verification by Measured Data. J. Electron. Inf. Technol. 2009, 31, 1305–1309. [Google Scholar]
- Xiang, J.; Sun, G.-C.; Zhang, Z.; Zhang, Y.; Ding, X.; Xing, M. A Robust Image-Domain Subspace-Based Channel Error Calibration and Post imaging Reconstruction Algorithm for Multiple Azimuth Channels SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5215818. [Google Scholar] [CrossRef]
- Li, X.; Xing, M.; Xia, X.-G.; Sun, G.-C.; Liang, Y.; Bao, Z. Simultaneous Stationary Scene Imaging and Ground Moving Target Indication for High-Resolution Wide-Swath SAR System. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4224–4239. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Xing, M.; Sun, G.-C.; Zhang, S.; Xiang, J. A Novel Two-Step Scheme Based on Joint GO-DPCA and Local STAP in Image Domain for Multichannel SAR-GMTI. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8259–8272. [Google Scholar] [CrossRef]
- Li, Z.; Bao, Z.; Wang, T. Ground Moving Target Indication for Distributed Small Satellite SAR Systems. Acta Electron. Sin. 2005, 33, 1664–1666. [Google Scholar]
- Li, Z.; Bao, Z.; Suo, Z. A Joint Image Coregistration, Phase Noise Suppression, and Phase Unwrapping Method Based on Subspace Projection for Multibaseline InSAR Systems. IEEE Trans. Geosci. Remote Sens. 2007, 45, 584–591. [Google Scholar] [CrossRef]
- Suo, Z.; Li, Z.; Bao, Z. Multichannel SAR-GMTI Method Robust to Coregistration Error of SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 2035–2043. [Google Scholar] [CrossRef]
- Liu, K.; He, X.; Liao, G.; Yu, Y.; Wang, Q. A Robust Multichannel Moving Target Detection Algorithm for Complex Scenes. J. Electron. Inf. Technol. 2024, 46, 2018–2027. [Google Scholar]
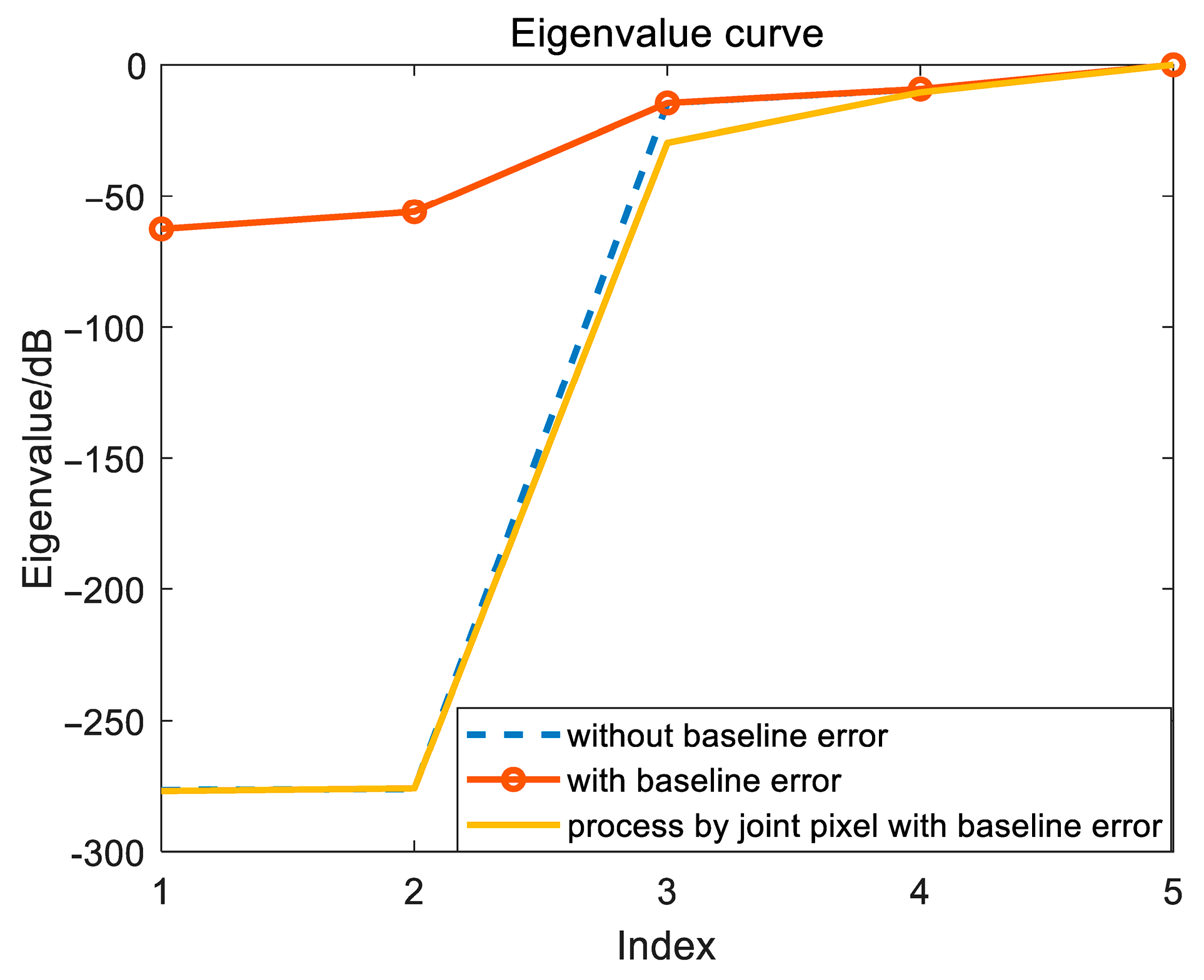
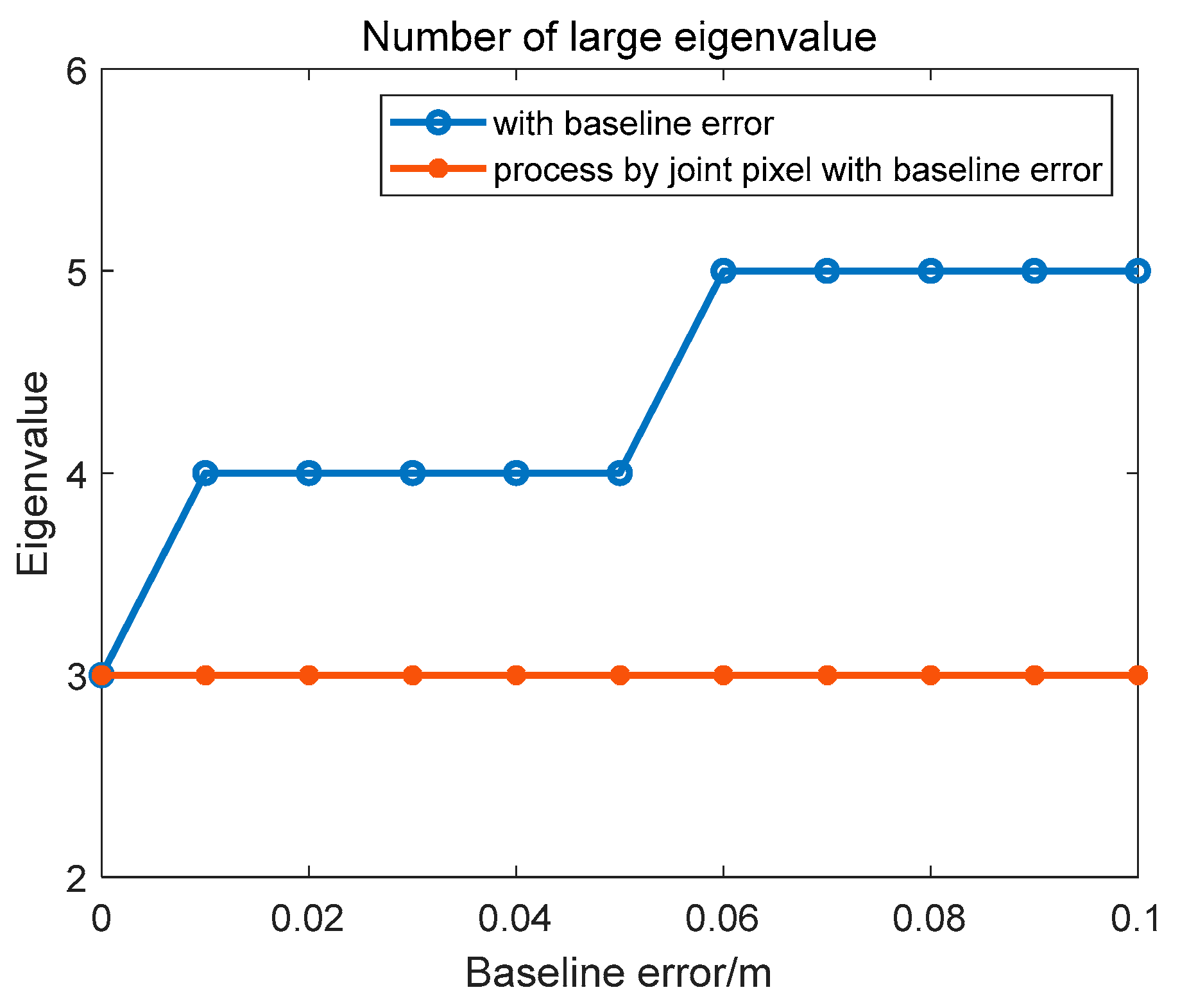
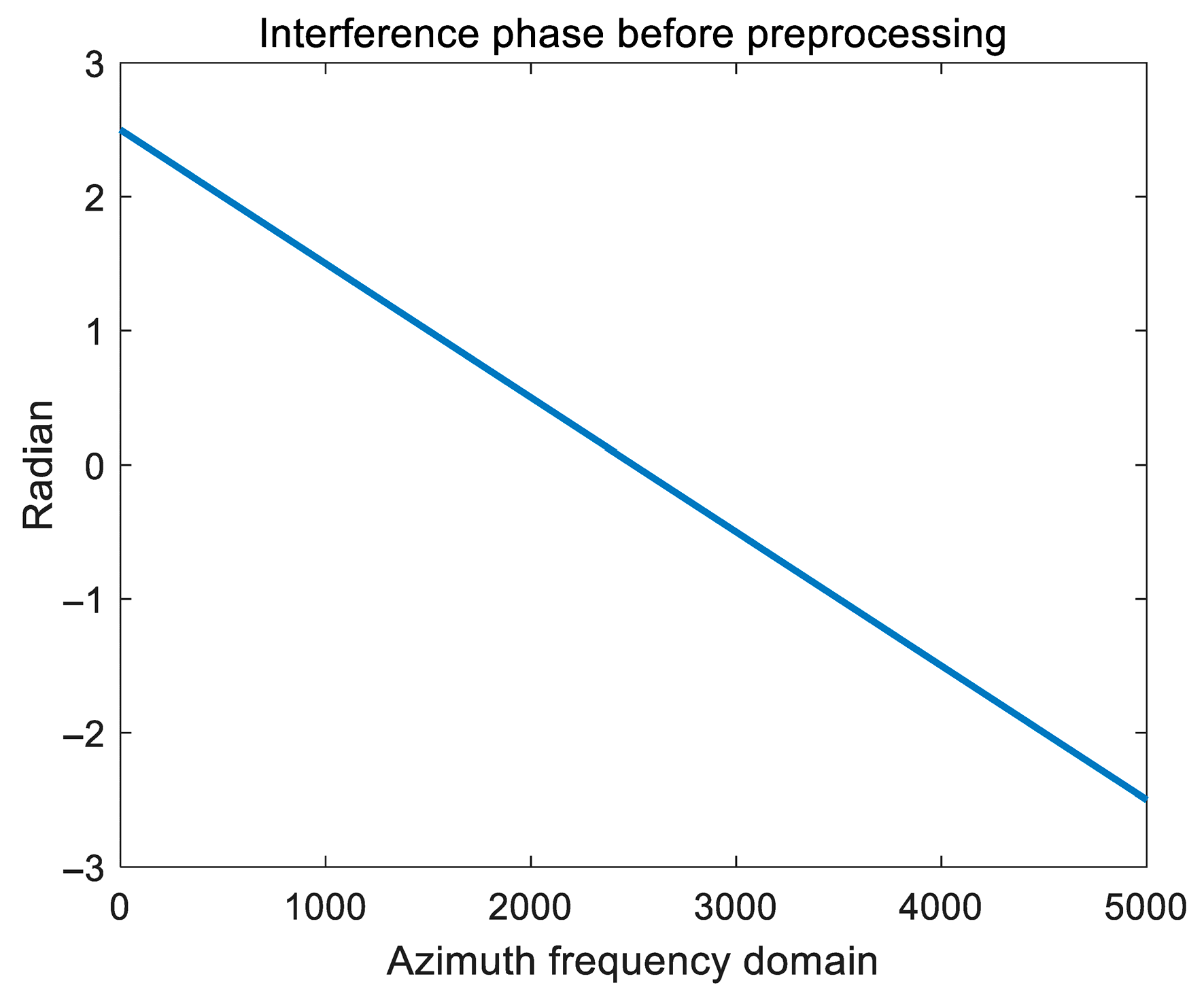
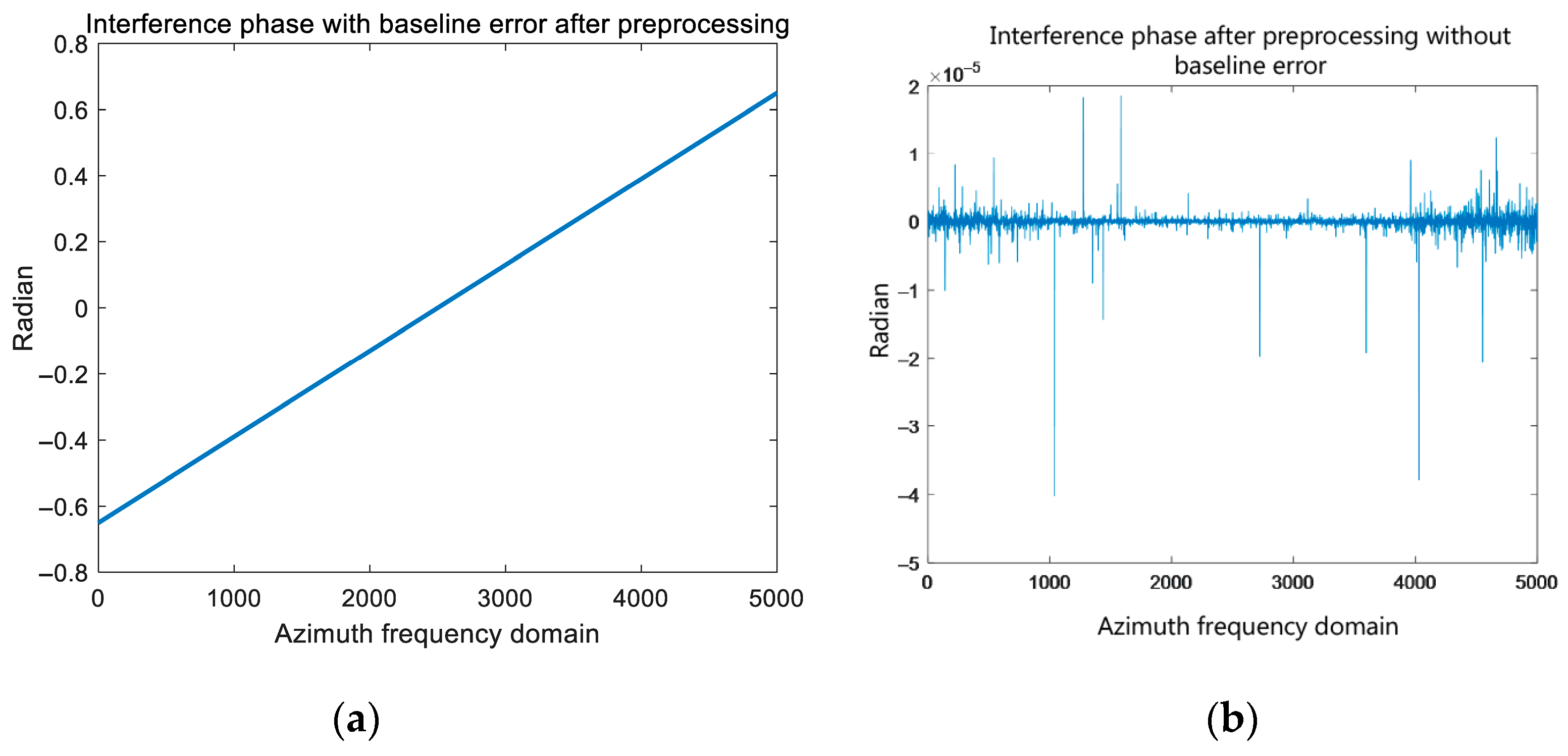

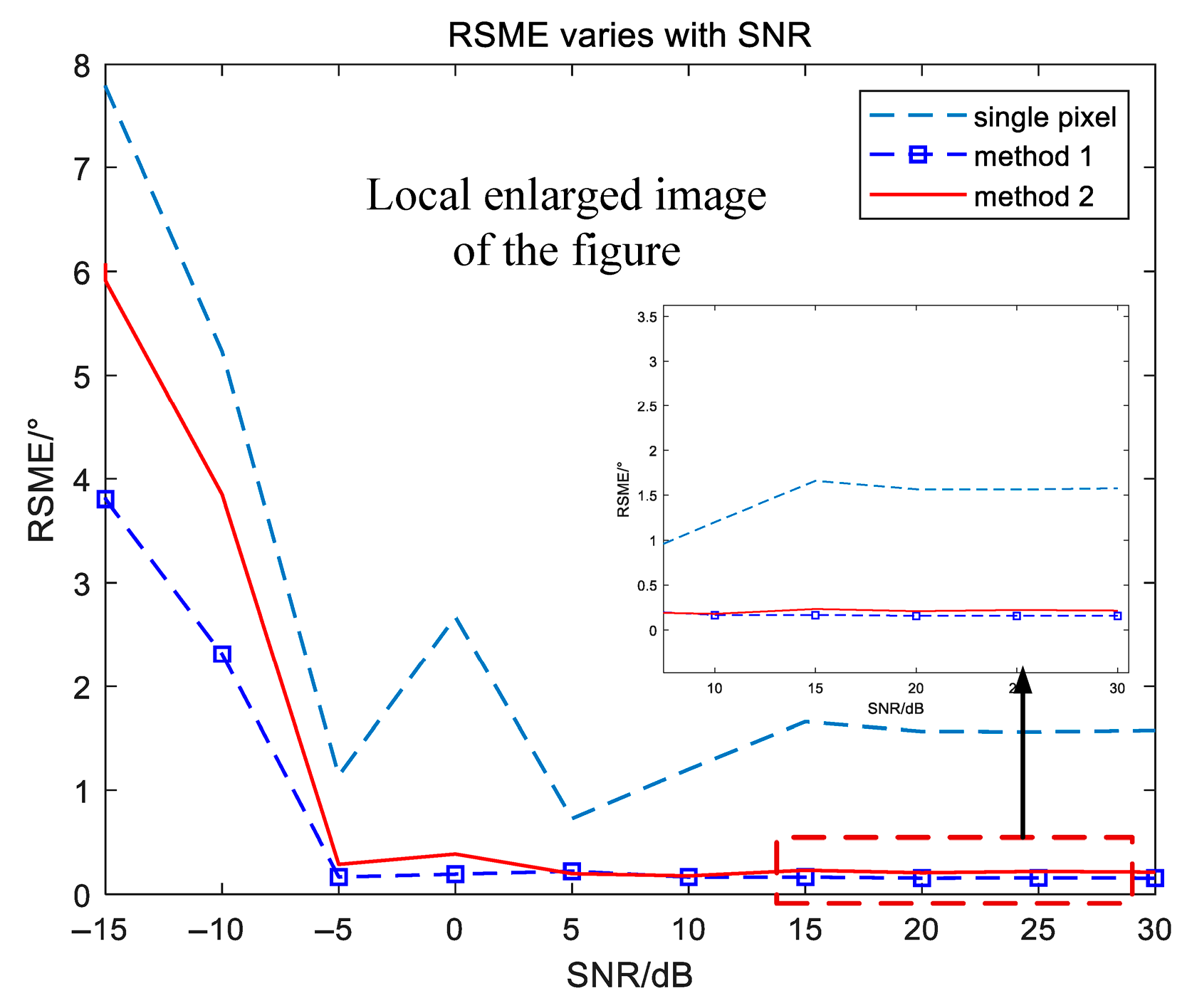
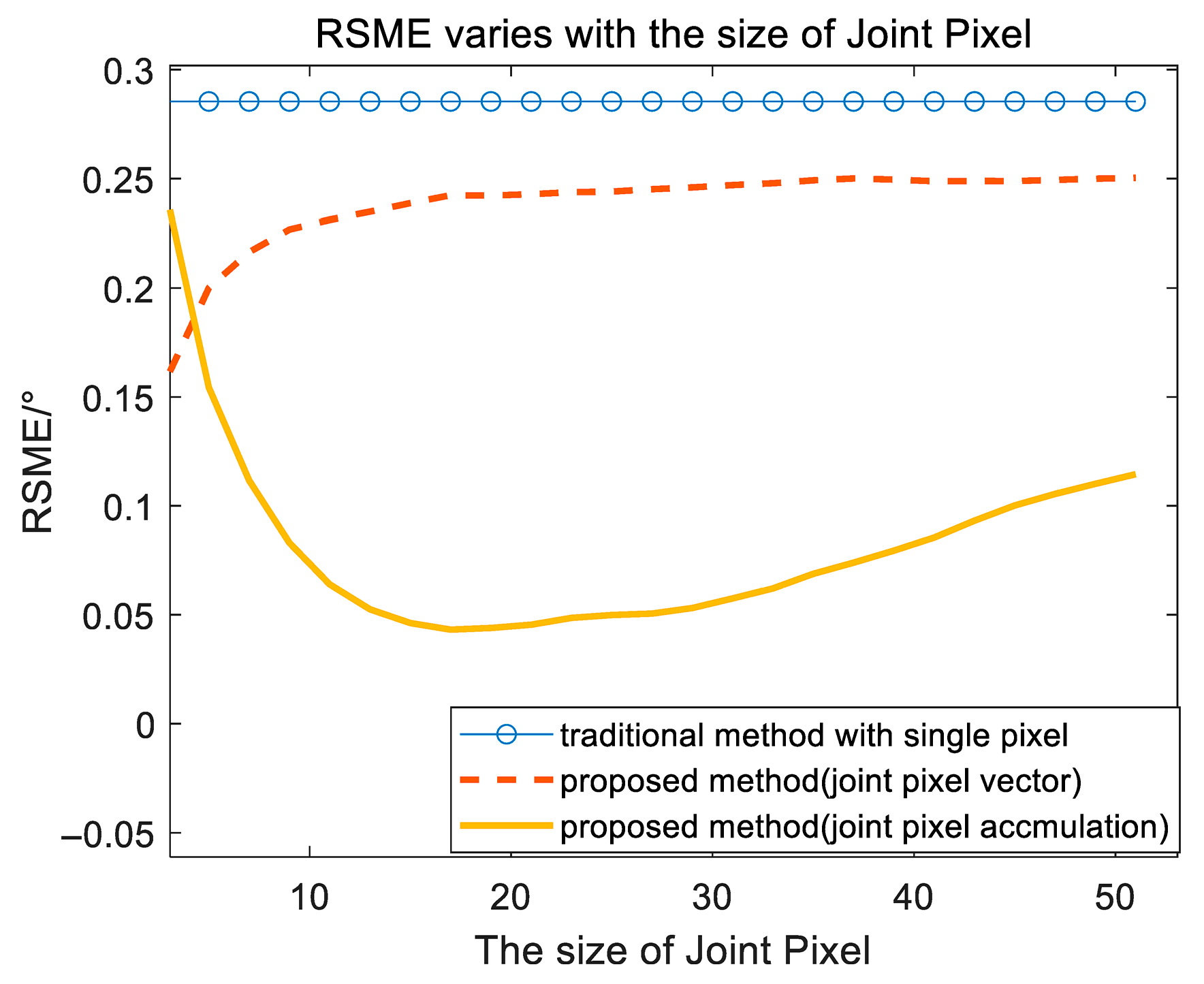
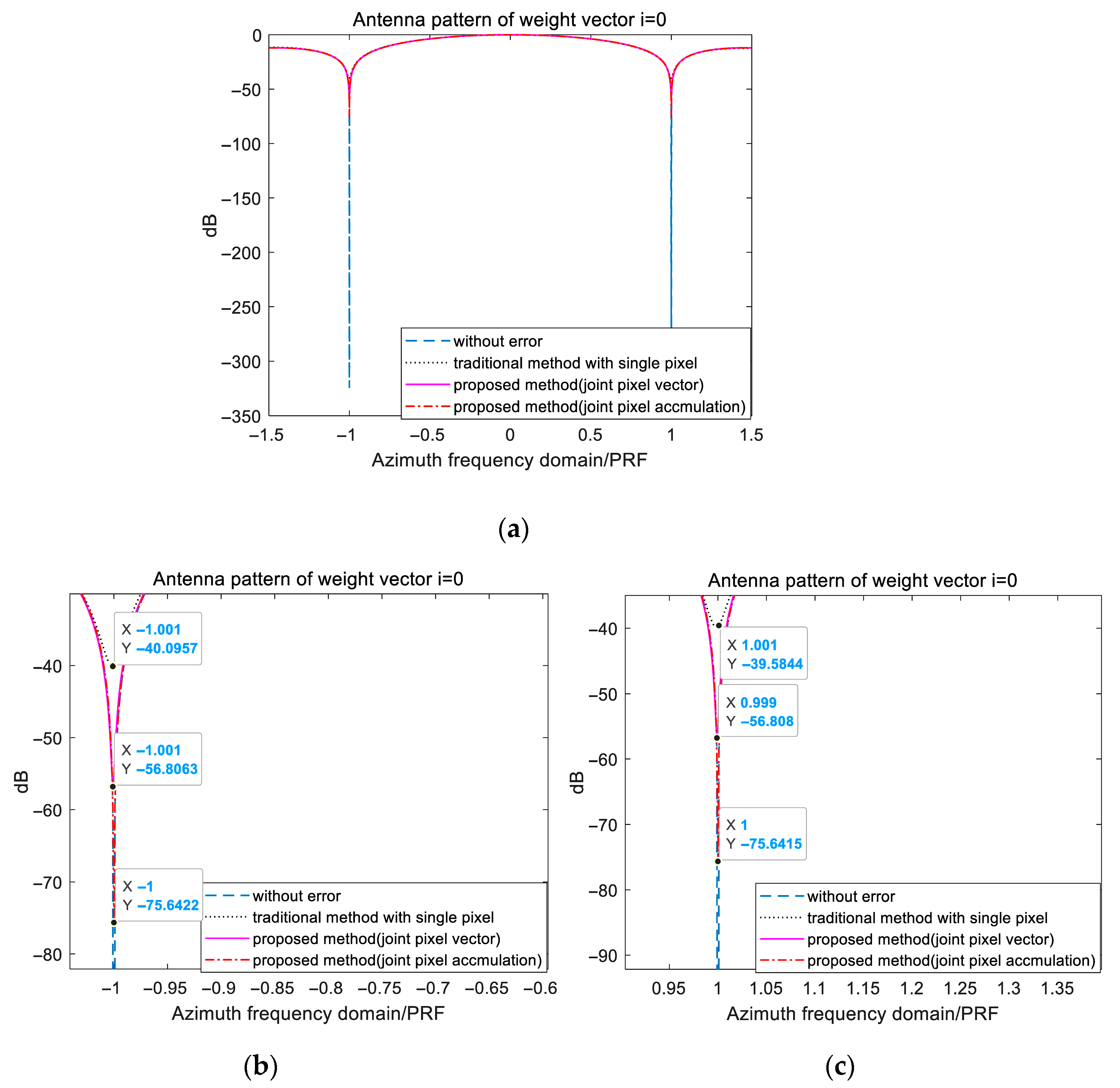

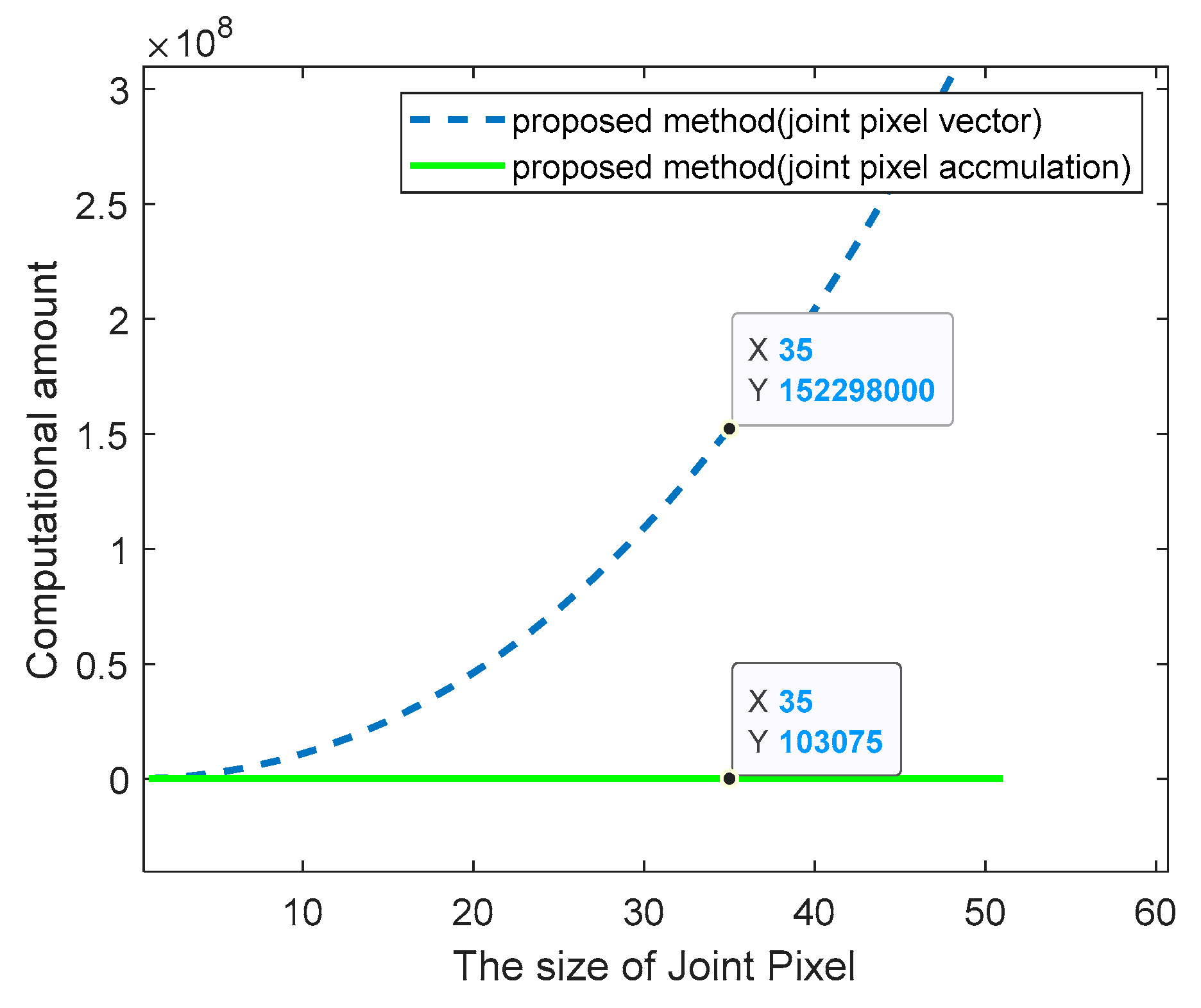


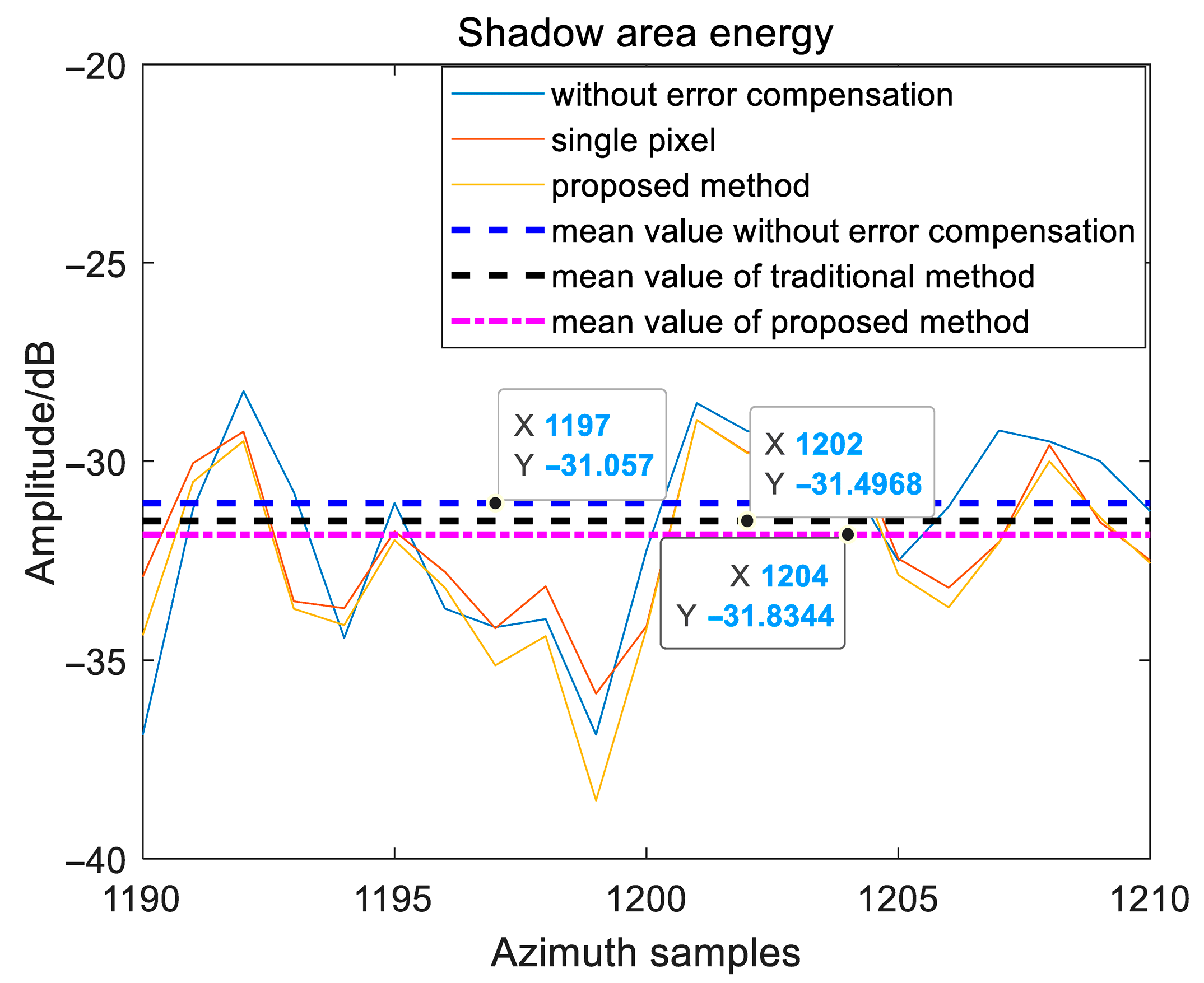
| Parameters | Values |
|---|---|
| Bandwidth | 100 MHz |
| Wave length | 55.5 × 10−3 m |
| PRF | 860 Hz |
| Velocity | 7150 m/s |
| Channel numbers | 5 |
| Azimuth ambiguity number | 3 |
| Pulse width | 24 × 10−6 s |
| Center slant range | 840 km |
| Antenna aperture length | 16.7 m |
| Ch.1 | Ch.2 | Ch.3 | Ch.4 | Ch.5 | |
|---|---|---|---|---|---|
| Phase error (degree) | 0 | −20 | 70 | −45 | 120 |
| Azimuth baseline error (m) | 0.5 | 0.3 | −0.7 | 0.2 | 1.7 |
| Methods | Channel Phase Error Estimation Result (°) | Time Cost (s) | RSME (°) | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||
| Initial error | 0 | −20 | 70 | −45 | 120 | / | / |
| Traditional method | 0 | −20.32 | 69.51 | −44.81 | 119.86 | 1.77 | 0.28 |
| Joint-pixel vector | 0 | −19.80 | 70.12 | −45.21 | 119.61 | 12.58 | 0.23 |
| Joint-pixel accumulation | 0 | −20.06 | 69.92 | −44.98 | 120.10 | 5.84 | 0.06 |
| Methods | Computational Complexity | ||
|---|---|---|---|
| Covariance Estimation | Eigenvalue Decomposition | Optimal Beam Weight | |
| Joint-pixel vector construction | |||
| Joint-pixel accumulation | |||
| Parameters | Values |
|---|---|
| Bandwidth | 180 MHz |
| PRF | 200 Hz |
| Velocity | 110 m/s |
| Channel numbers | 7 |
| Azimuth ambiguity number | 5 |
| Antenna aperture length | 1.785 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Chen, Q.; Xiang, J.; Ding, X.; Zhao, W.; Sun, G. High-Precision HRWS SAR Phase Error Estimation with Inaccurate Baseline: A Joint-Pixel-Based Image Subspace Approach. Remote Sens. 2025, 17, 3554. https://doi.org/10.3390/rs17213554
Fan J, Chen Q, Xiang J, Ding X, Zhao W, Sun G. High-Precision HRWS SAR Phase Error Estimation with Inaccurate Baseline: A Joint-Pixel-Based Image Subspace Approach. Remote Sensing. 2025; 17(21):3554. https://doi.org/10.3390/rs17213554
Chicago/Turabian StyleFan, Jixia, Quan Chen, Jixiang Xiang, Xiaojie Ding, Wenxin Zhao, and Guangcai Sun. 2025. "High-Precision HRWS SAR Phase Error Estimation with Inaccurate Baseline: A Joint-Pixel-Based Image Subspace Approach" Remote Sensing 17, no. 21: 3554. https://doi.org/10.3390/rs17213554
APA StyleFan, J., Chen, Q., Xiang, J., Ding, X., Zhao, W., & Sun, G. (2025). High-Precision HRWS SAR Phase Error Estimation with Inaccurate Baseline: A Joint-Pixel-Based Image Subspace Approach. Remote Sensing, 17(21), 3554. https://doi.org/10.3390/rs17213554






