Comparisons of Differential Code Bias (DCB) Estimates and Low-Earth-Orbit (LEO)-Topside Ionosphere Extraction Based on Two Different Topside Ionosphere Processing Methods
Highlights
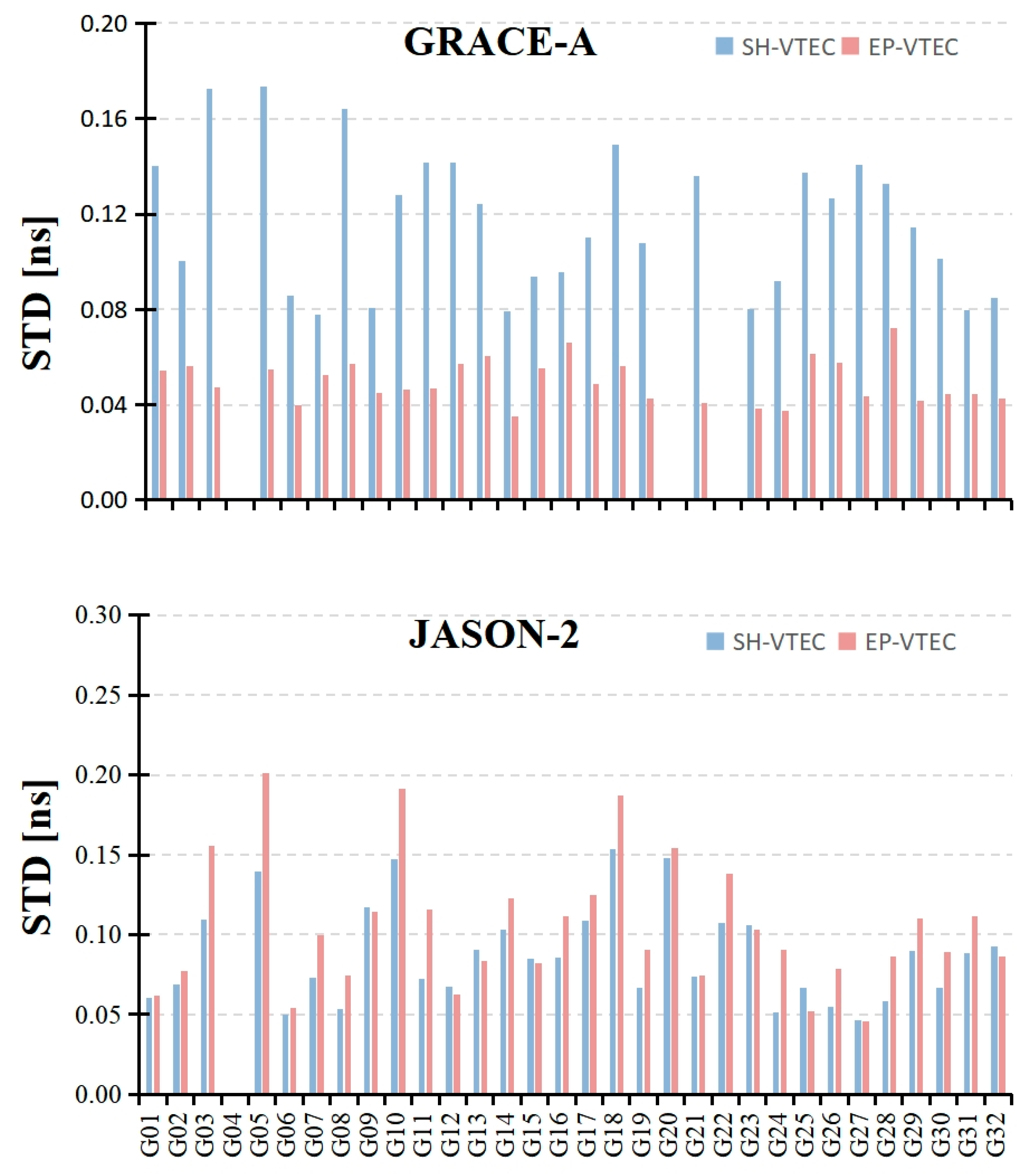
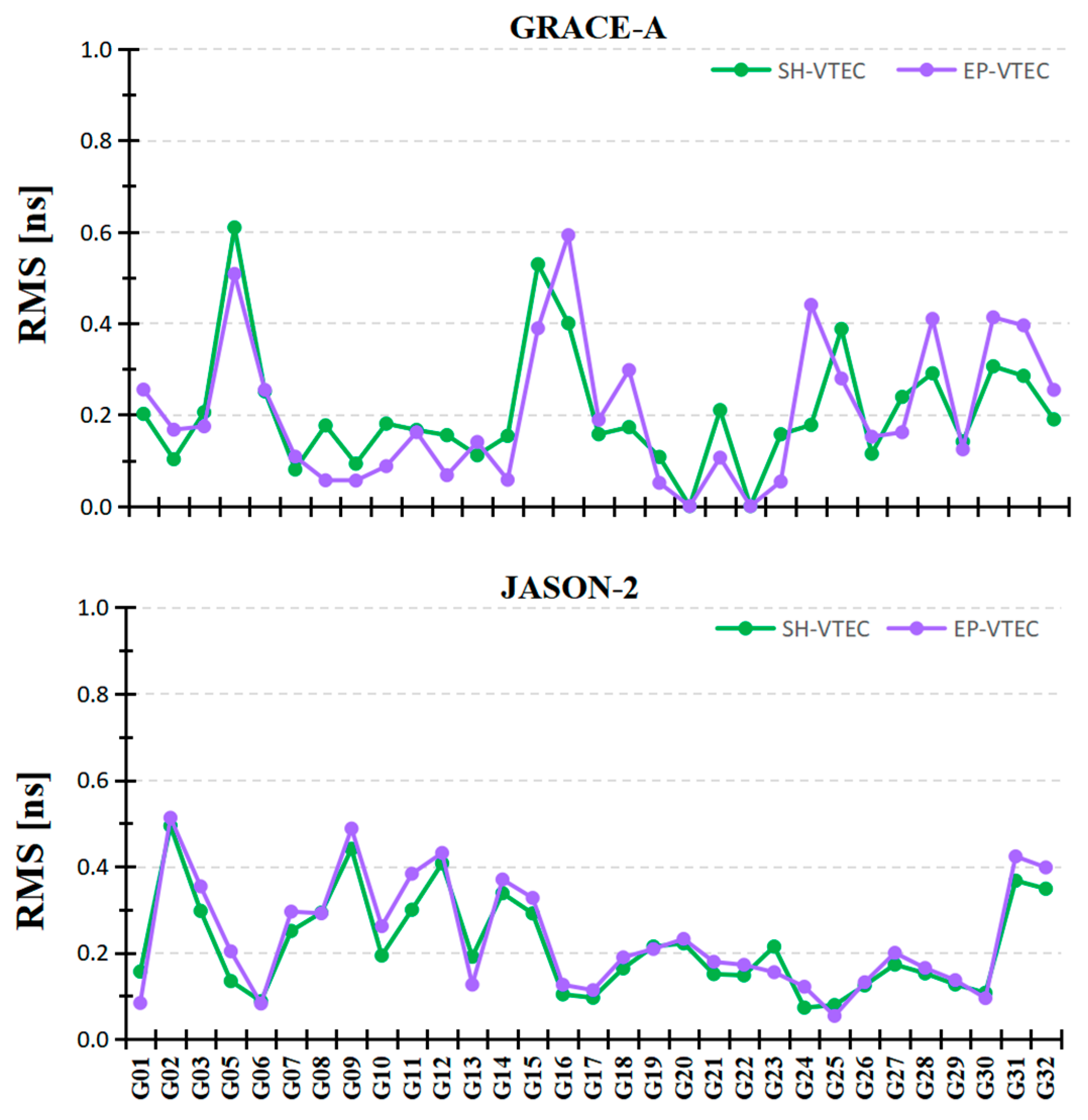
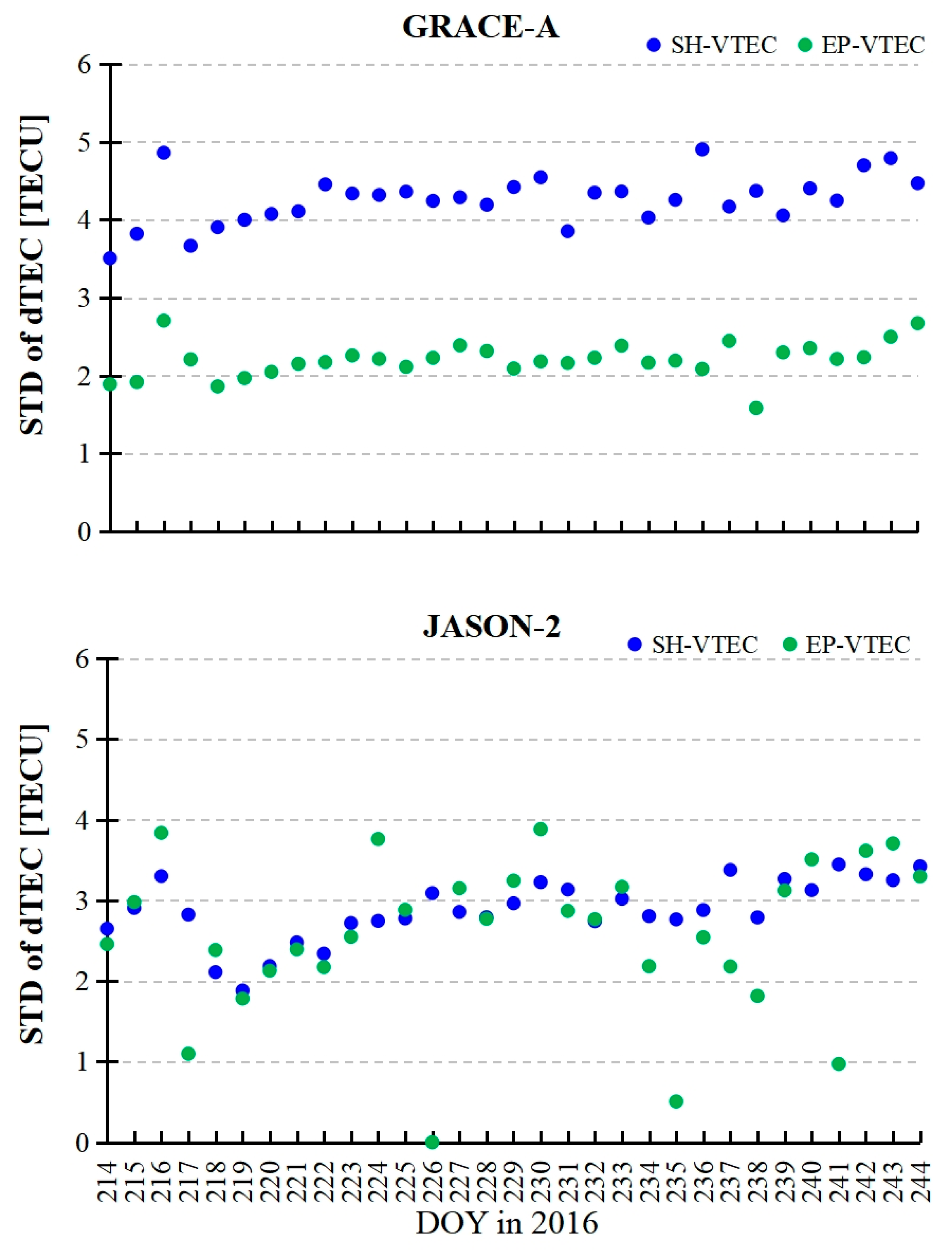
- Using GRACE-A data (400 km in 2016), the monthly stabilities (STDs) of GPS satellite differential code biases (DCBs) and low-earth-orbit (LEO) satellites receiver DCBs using the EP (epoch parameter)-topside vertical electron content (VEC) method are better than those using the SH (spherical harmonic)-topside VEC method. For JASON-2 data (1350 km), the STDs of GPS DCBs using the SH-topside VEC method are slightly superior to those using the EP-topside VEC method, and LEO DCBs using the two methods have similar STD results. However, the root mean square (RMS) results for GPS DCBs using the SH-topside VEC model relative to the Center for Orbit Determination in Europe (CODE) products are slightly superior to those using the EP-topside VEC method.
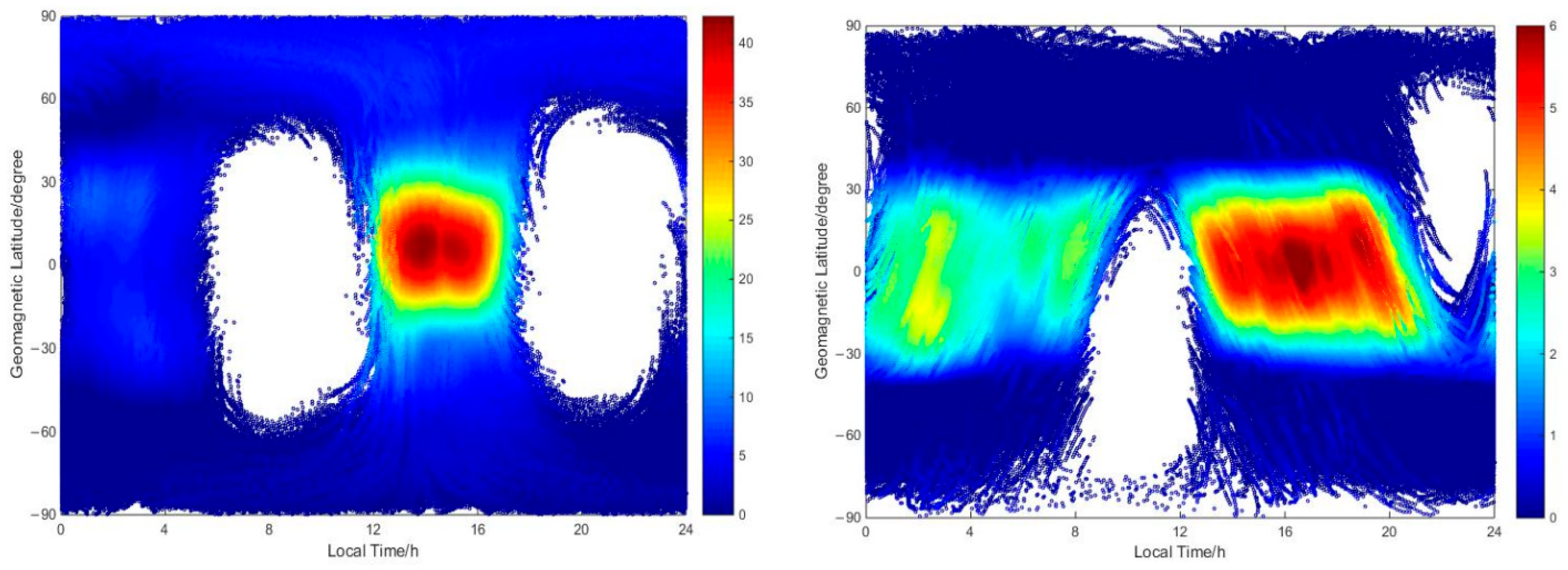
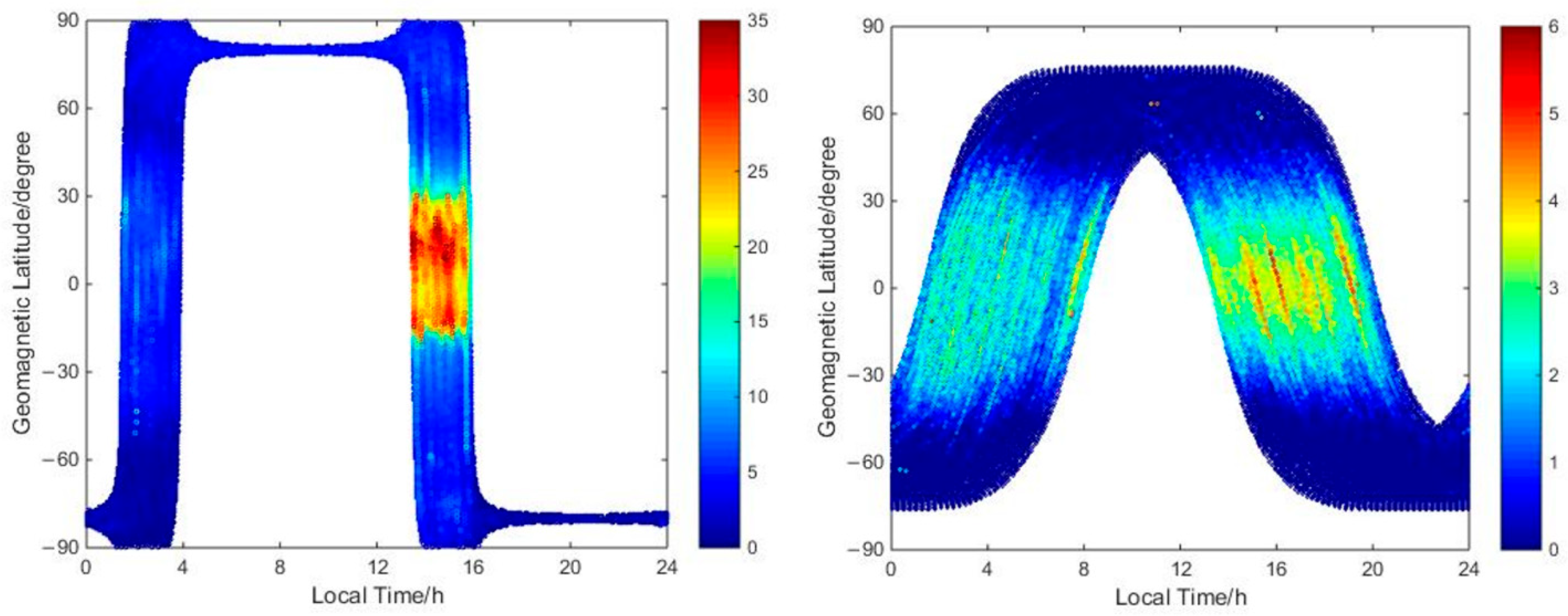
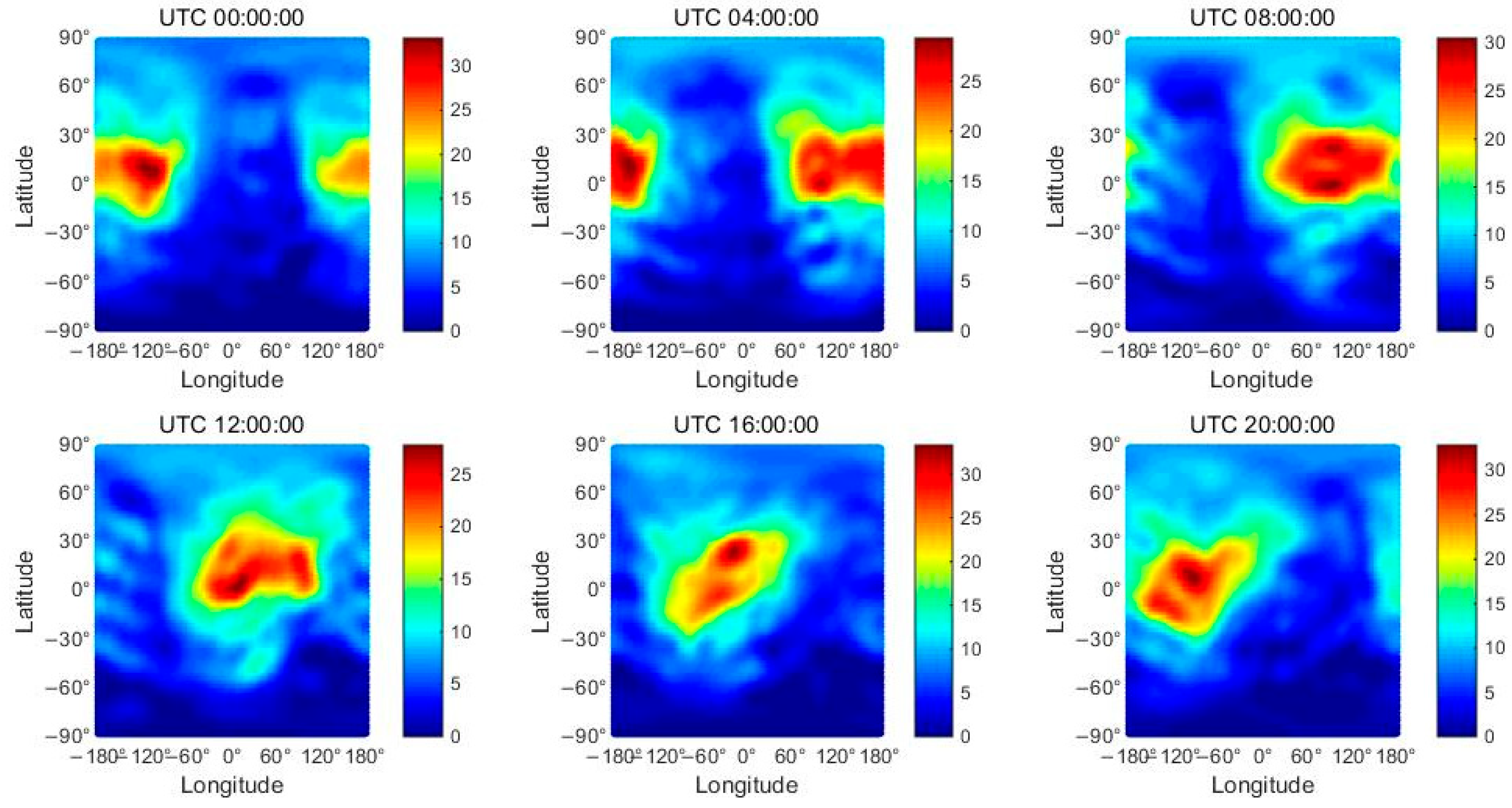
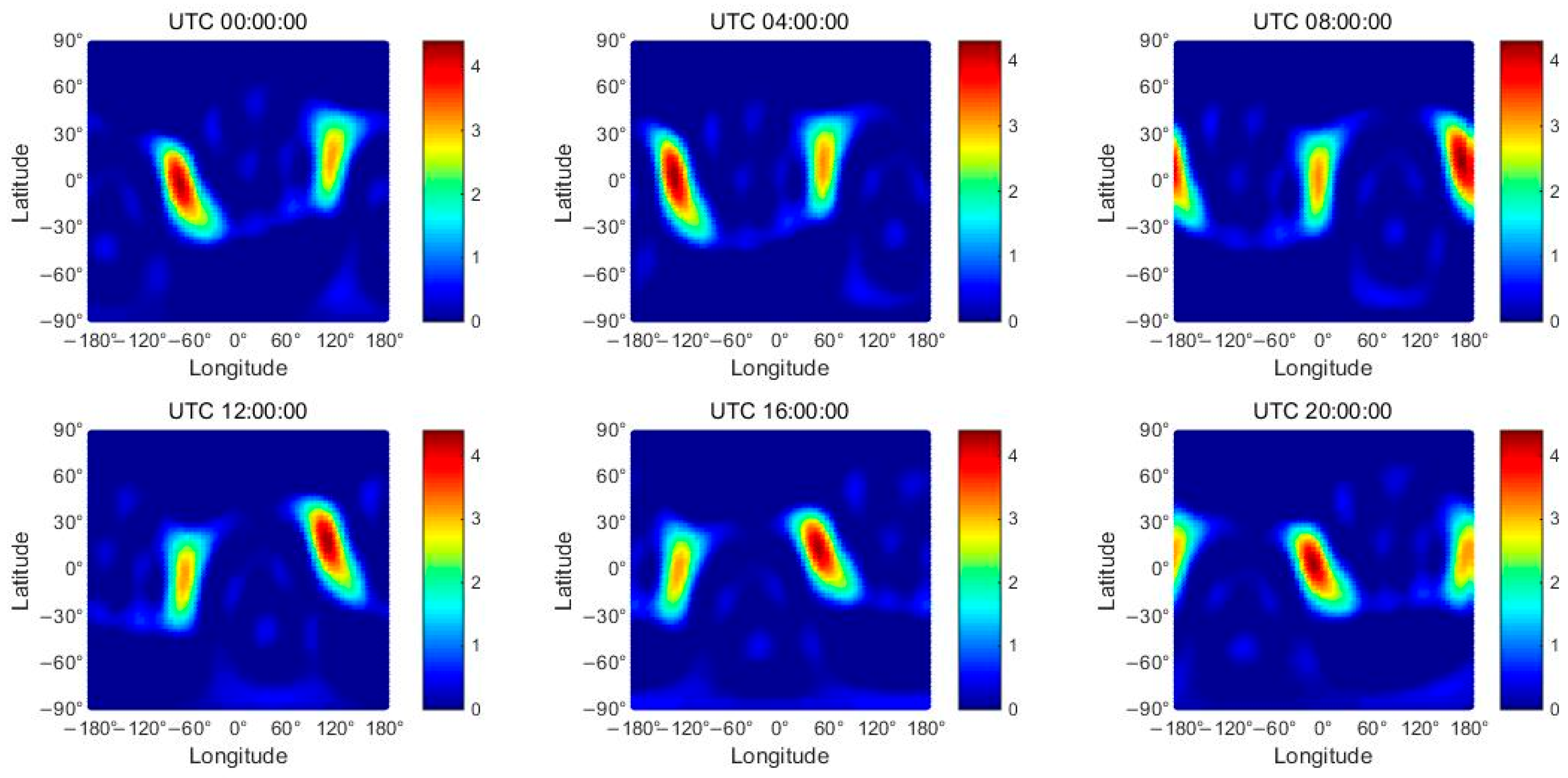
- Due to the difference in orbital altitude, the results and distributions of the GRACE-topside VECs differ from those of the JASON-topside VECs, with the former being more consistent with the ground-based results, indicating that there may be different height structures in the LEO-topside VECs. Meanwhile, we applied the IRI-GIM (International Reference Ionosphere model–Global Ionosphere Map) method to compare the LEO-topside VEC results. The results indicate that the accuracy of GRACE-A-topside VECs using the EP-topside VEC method is better than that using the SH-topside VEC method, whereas for JASON-2, the two methods have similar accuracy. The temporal and spatial resolutions of the SH-topside VEC model are higher than those of the EP-topside VEC method, and the former has a wide range of usability and predictive characteristics.
- At present, there is no research to analyze and compare the effects of the two topside VEC processing methods on DCB estimates and LEO-topside VEC extraction. It is essential to obtain more accurate global navigation satellite system (GNSS)/LEO DCBs and LEO-topside VEC parameters, particularly in future scenarios with an increase in LEO satellites, which can serve next-generation GNSS and LEO positioning.
- For GNSS/LEO DCB estimates, different evaluation criteria yield different results. The STD results are related to the heights of LEO receivers, whereas the RMS results are not. The accuracies of the LEO-topside VEC results are related to the heights of LEO orbits. Meanwhile, the temporal and spatial resolutions of the SH-topside VEC model are higher than those of the EP-topside VECs, and the former have a wide range of usability and predictive characteristics.
Abstract
1. Introduction
2. Methods and Strategies
3. Results
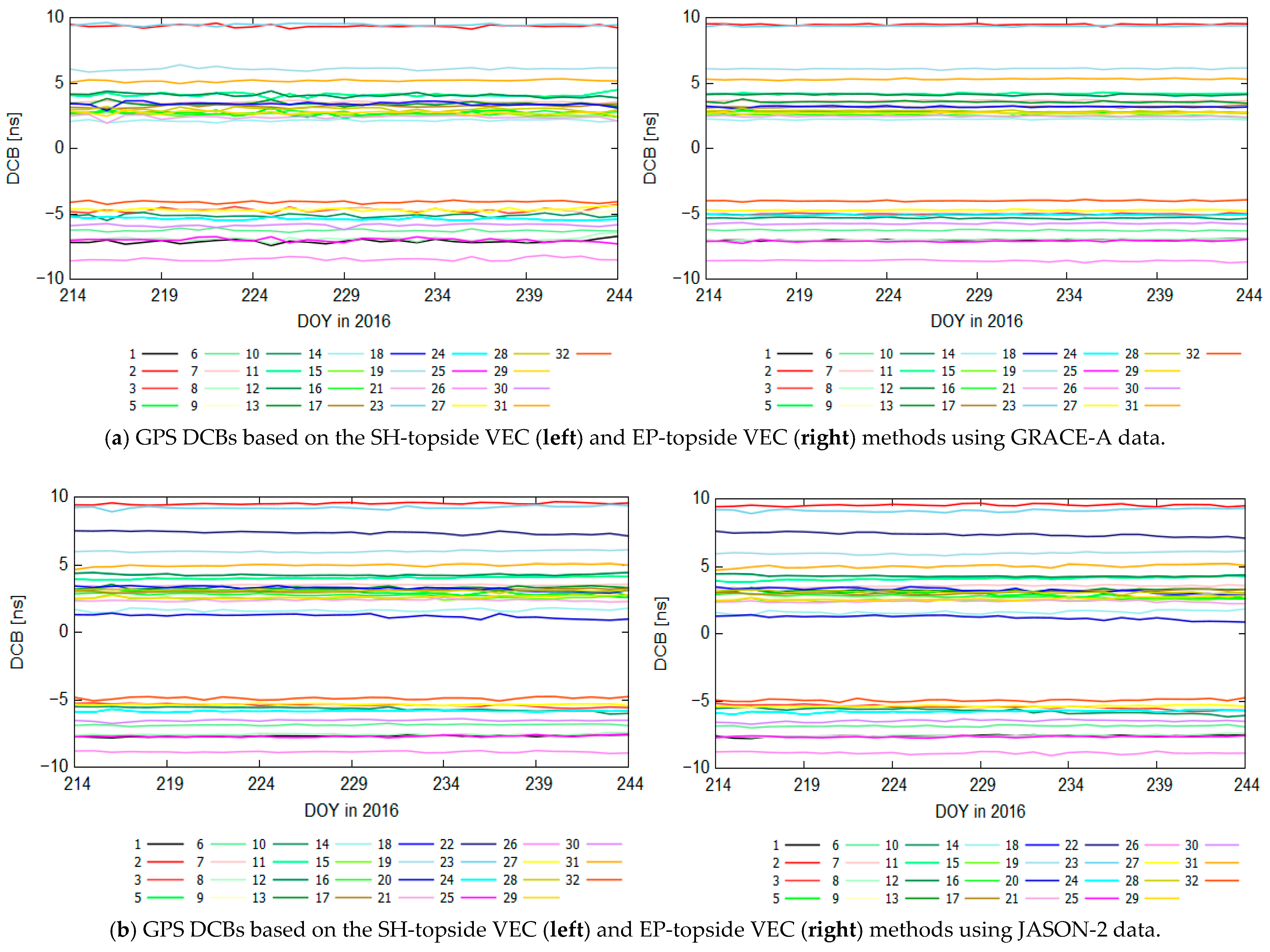
3.1. Comparison and Precision Evaluation of GPS DCB Estimates
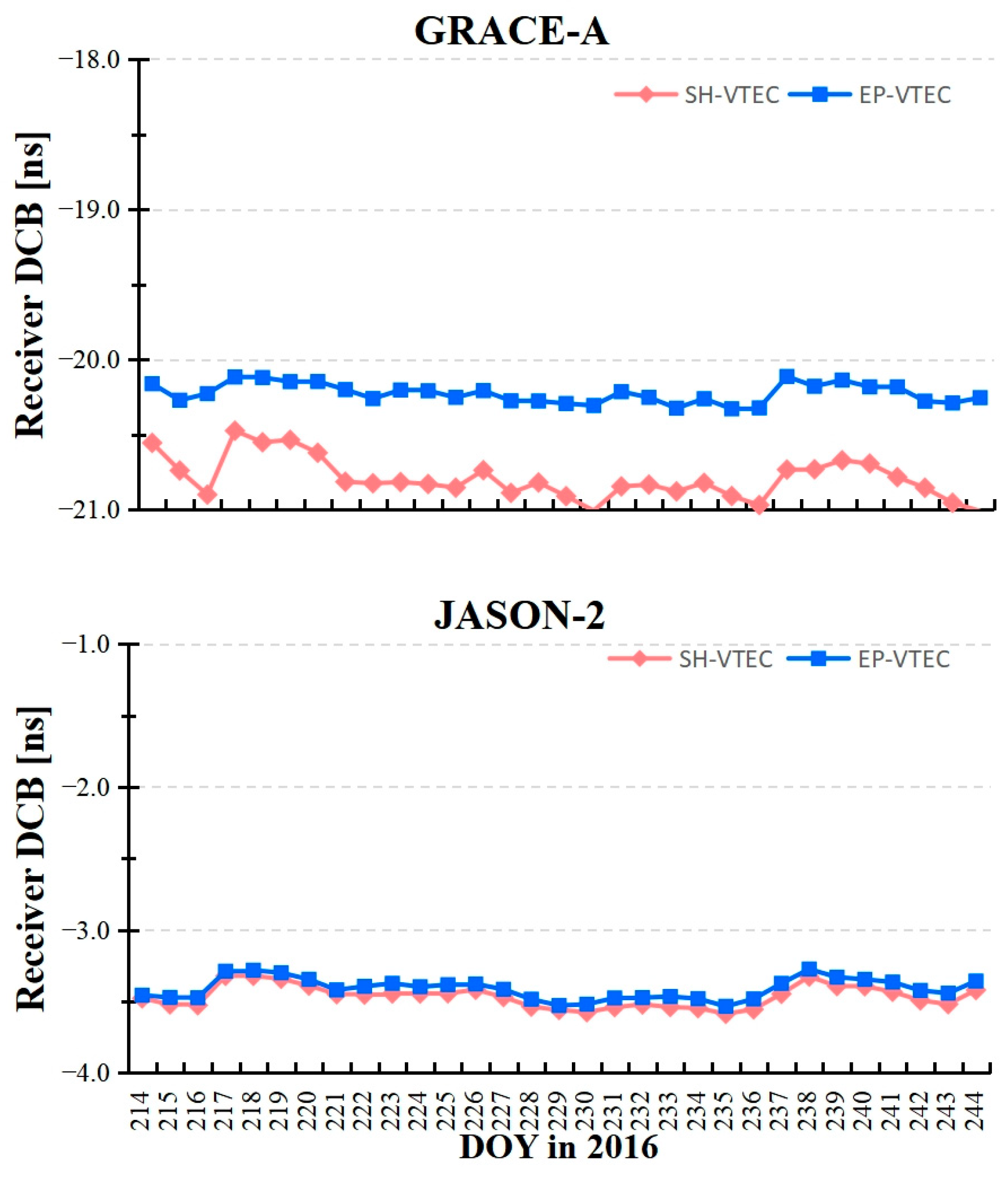
3.2. Comparison Between LEO Receiver DCB Estimates
3.3. Comparison and Evaluation of LEO-Based Topside VEC Modeling Results
3.3.1. Comparison of LEO-Based Topside VEC Results
3.3.2. Evaluation of LEO-Based Topside VEC Results
4. Discussion
5. Conclusions
- (1)
- Using GRACE-A data obtained at an altitude of 400 km, the DCB estimates for GPS satellites and LEO receivers using the EP-topside VEC method are more stable than those using the SH-topside VEC method. In contrast, using the JASON-2 data at a height of 1350 km, the monthly stabilities of estimated GPS DCBs using the SH-topside VEC method are better than those using the EP-topside VEC method, while LEO receiver DCB stabilities derived from the two VEC solutions are similar to each other. The monthly stabilities of GPS and LEO DCB estimates obtained using the EP-topside VEC method are related to LEO receiver altitude. Using both GRACE-A and JASON-2 data, the RMS results of the difference for GPS DCBs using the SH-topside VEC method relative to CODE products are more accurate than those using the EP-topside VEC method. The stability and accuracy of LEO-based DCB estimates are similar to those using ground-based results.
- (2)
- The peak ranges of the GRACE-A-topside VEC results using the SH-topside VEC and EP-topside VEC methods are within 42 and 35 TECU, respectively, while the peak ranges of the JASON-2-topside VEC results using the two models are both within 6 TECU. The study period coincides with summer, and the EIA region moves northward. In contrast, the EIA phenomenon of the GRACE-topside VEC results is more obvious than that of the JASON-topside VEC results due to the lower orbits of the GRACE satellite and closer proximity to the ground. Additionally, the SH-topside VEC model maps are only displayed due to the EP-topside VEC method not modeling VEC. The results and distributions of the GRACE-topside VECs differ from those of the JASON-topside VECs due to the difference in orbital altitude, with the former being more consistent with the ground-based results, indicating that there may be different height structures in the LEO-topside VEC. The LEO-based topside VEC results are validated using the IRI-GIM method. For GRACE-A at an altitude of 400 km (in 2016), the validation results using the EP-topside VEC method for DCB STDs and VEC results are better than those using the SH-topside VEC method, while for JASON-2 at an altitude of 1350 km, the results using the two VEC methods have similar validation results.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, University of Berne, Bern, Switzerland, 1999. [Google Scholar]
- Yuan, Y. Study on Theories and Methods of Correcting Ionospheric Delay and Monitoring Ionosphere Based on GPS. Ph.D. Thesis, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan, China, 2002. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A. Code biases in multi-GNSS point positioning. In Proceedings of the ION ITM 2013, San Diego, CA, USA, 28–30 January 2013. [Google Scholar]
- Liu, T.; Zhang, B. Estimation of code observation-specific biases (OSBs) for the modernized multi-frequency and multi-GNSS signals: An undifferenced and uncombined approach. J. Geod. 2021, 95, 97. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Lyu, H.; Garcia-Fernandez, M.; Orús-Pérez, R. A new way of improving global ionospheric maps by ionospheric tomography: Consistent combination of multi-GNSS and multi-space geodetic dual-frequency measurements gathered from vessel-, LEO-and ground-based receivers. J. Geod. 2020, 94, 73. [Google Scholar] [CrossRef]
- Ren, X.; Zhang, X.; Schmidt, M.; Zhao, Z.; Chen, J.; Zhang, J.; Li, X. Performance of GNSS global ionospheric modeling augmented by LEO constellation. Earth Space Sci. 2019, 7, e2019EA000898. [Google Scholar] [CrossRef]
- Schaer, S. Activities of IGS Bias and Calibration Working Group. In IGS Technical Report 2011; Meindl, M., Dach, R., Jean, Y., Eds.; Astronomical Institute, University of Berne: Berne, Switzerland, 2012; pp. 139–154. [Google Scholar]
- Krankowski, A.; Shagimuratov, I.I.; Ephishov, I.I.; Krypiak-Gregorczyk, A.; Yakimova, G. The occurrence of themid-latitude ionospheric trough in GPS-TEC measurements. Adv. Space Res. 2009, 43, 1721–1731. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Àngel, À.; García-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, H.; Ou, J.; Huo, X. Two-step method for the determination of the differential code biases of COMPASS satellites. J. Geod. 2012, 86, 1059–1076. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2015, 90, 209–228. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Yang, Y. Concepts of comprehensive PNT and related key technologies. Acta Geod. Cartogr. Sin. 2016, 45, 505–510. (In Chinese) [Google Scholar]
- Yang, Y.; Mao, Y.; Ren, X.; Jia, X.; Sun, B. Demand and key technology for a LEO constellation as augmentation of satellite navigation systems. Satell. Navig. 2024, 5, 11. [Google Scholar] [CrossRef]
- Zhang, X.; Ma, F. Review of the development of LEO navigation-augmented GNSS. Acta Geod. Cartogr. Sin. 2019, 48, 1073–1087. [Google Scholar]
- Lin, J.; Yue, X.; Zhao, S. Estimation and analysis of GPS satellite DCB based on LEO observations. GPS Solut. 2014, 20, 251–258. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Dou, X.; Yue, X. Is the long-term variation of the estimated GPS differential code biases associated with ionospheric variability? GPS Solut. 2015, 20, 313–319. [Google Scholar] [CrossRef]
- Wautelet, G.; Loyer, S.; Mercier, F.; Perosanz, F. Computation of GPS P1–P2 Differential Code Biases with JASON-2. GPS Solut. 2017, 21, 1619–1631. [Google Scholar] [CrossRef]
- Li, W.; Li, M.; Shi, C.; Fang, R.; Zhao, Q.; Meng, X.; Bai, W. GPS and BeiDou Differential Code Bias Estimation Using Fengyun-3C Satellite Onboard GNSS Observations. Remote Sens. 2017, 9, 1239. [Google Scholar] [CrossRef]
- Li, X.; Ma, T.; Xie, W.; Zhang, K.; Huang, J.; Ren, X. FY-3D and FY-3C onboard observations for differential code biases estimation. GPS Solut. 2019, 23, 57. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, L. Estimation of COSMIC LEO satellite GPS receiver differential code bias. Chin. J. Geophys. 2014, 57, 377–383. (In Chinese) [Google Scholar]
- Zakharenkova, I.; Cherniak, I. How can GOCE and TerraSAR-X contribute to the topside ionosphere and plasmasphere research? Space Weather 2015, 13, 271–285. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Yue, X.; Dou, X. Determination of differential code bias of GNSS receiver onboard low earth orbit satellite. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4896–4905. [Google Scholar] [CrossRef]
- Chen, P.; Yao, Y.; Li, Q.; Yao, W. Modeling the plasmasphere based on LEO satellites onboard GPS measurements. J. Geophys. Res. Space Phys. 2017, 122, 1221–1233. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Zhang, X.; Schmidt, M.; Li, X.; Zhang, J. Mapping topside ionospheric vertical electron content from multiple LEO satellites at different orbital altitudes. J. Geod. 2020, 94, 86. [Google Scholar] [CrossRef]
- Liu, M.; Yuan, Y.; Huo, X.; Li, M.; Chai, Y. Simultaneous estimation of GPS P1-P2 differential code biases using low earth orbit satellites data from two different orbit heights. J. Geod. 2020, 94, 121. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Dou, X.; Yue, X. Assessment of vertical TEC mapping functions for space-based GNSS observations. GPS Solut. 2015, 20, 353–362. [Google Scholar] [CrossRef]
- Foelsche, U.; Kirchengast, G. A simple “geometric” mapping function for the hydrostatic delay at radio frequencies and assessment of its performance. Geophys. Res. Lett. 2002, 29, 111-1–111-4. [Google Scholar] [CrossRef]
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.; Bettadpur, S.; Ries, J.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Diferential code bias estimation using Multi-GNSS observations and global ionosphere maps. Navigation 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Yue, X.; Schreiner, W.S.; Hunt, D.C.; Rocken, C.; Kuo, Y.H. Quantitative evaluation of the low Earth orbit satellite based slant total electron content determination. Space Weather 2011, 9, S09001. [Google Scholar] [CrossRef]
- Cerri, L.; Berthias, J.P.; Bertiger, W.I.; Haines, B.J.; Lemoine, F.G.; Mercier, F.; Ries, J.C.; Willis, P.; Zelensky, N.P.; Ziebart, M. Precision Orbit Determination Standards for the Jason Series of Altimeter Missions. Mar. Geod. 2010, 33, 379–418. [Google Scholar] [CrossRef]
- Klobuchar, J.A. A First-Order World-Wide Ionospheric Time-Delay Algorithm; Air Force Cambridge Research Labs: Bedford, MA, USA, 1975; No. 324. [Google Scholar]
- IGS. IGS Technical Report 2011; Astronomical Institute, University of Berne: Berne, Switzerland, 2012. [Google Scholar]
- Wang, Y.; Liu, M.; Yuan, Y.; Wang, G.; Geng, H. Effects of topside ionosphere modeling parameters on differential code bias (DCB) estimation using LEO satellite observations. Remote Sens. 2023, 15, 5335. [Google Scholar] [CrossRef]
- Sanz, J.; Miguel-Juan, J.; Rovira-Garcia, A.; Gonza’lez-Casado, G. GPS differential code biases determination: Methodology and analysis. GPS Solut. 2017, 21, 1549–1561. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, I.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Huang, Y.N.; Cheng, K. Solar cycle variations of the equatorial ionospheric anomaly in total electron content in Asian region. J. Geophys. Res. 1996, 101, 24513–24520. [Google Scholar] [CrossRef]
- Zhong, J.; Lei, J.; Wang, W.; Burns, A.G.; Yue, X.; Dou, X. Longitudinal variations of topside ionospheric and plasmaspheric TEC. J. Geophys. Res. 2017, 122, 6737–6760. [Google Scholar] [CrossRef]
- Zhao, X.; Ning, B.; Zhang, M.; Hu, L. Comparison of the Ionospheric F2 Peak Height Between Ionosonde Measurements and IRI2016 Predictions over China. Adv. Space Res. 2017, 60, 1524–1531. [Google Scholar] [CrossRef]


| Option/Parameter | Selection/Description |
|---|---|
| Data preprocessing | |
| Observations | Code and phase observations of the ionosphere-free combination |
| Data interval | 10 s |
| Satellite ephemeris and clock | Center for Orbit Determination in Europe (CODE) precise products |
| Cut-off elevation angle | 7° |
| Attitude GPS antenna phase center (APC) | Attitude files Corrected |
| LEO receiver APC | Corrected |
| LEO receiver clocks | Estimated |
| LEO satellite orbits | Introduced as priori orbits, calculated by reduced dynamic precision orbit determination |
| Screening solutions | Residuals and root mean square (RMS) screening iteratively |
| Differential code bias (DCB) estimation | |
| Observations | Code observations of the geometry-free (GF) combination |
| Cut-off elevation angle Data interval | 15° 30 s |
| GPS satellite DCBs | Daily constants for P1–P2 |
| LEO receiver DCBs | Daily constants for P1–P2 |
| Mapping function+ | F&K + EP-topside VEC: F&K function + epoch parameters in daily solution |
| Vertical electron content (VEC) | F&K + SH-topside VEC: F&K function+ spherical harmonic modeling: degree and order of 8, dynamic parameter spacing of 4 h |
| Datum | Zero-mean condition for all observation satellite DCBs |
| LEO | SH-Topside VEC | EP-Topside VEC |
|---|---|---|
| GRACE-A | 0.117 0.114 | 0.050 0.131 |
| JASON-2 |
| LEO | SH-Topside VEC | EP-Topside VEC |
|---|---|---|
| GRACE-A | 0.219 0.241 | 0.221 0.256 |
| JASON-2 |
| Receiver | SH-Topside VEC | EP-Topside VEC | ||
|---|---|---|---|---|
| Mean | STD | Mean | STD | |
| GRACE-A | −20.793 | 0.138 | −20.226 | 0.065 |
| JASON-2 | −3.446 | 0.078 | −3.412 | 0.075 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Yuan, Y.; Ou, J.; Tan, B. Comparisons of Differential Code Bias (DCB) Estimates and Low-Earth-Orbit (LEO)-Topside Ionosphere Extraction Based on Two Different Topside Ionosphere Processing Methods. Remote Sens. 2025, 17, 3550. https://doi.org/10.3390/rs17213550
Liu M, Yuan Y, Ou J, Tan B. Comparisons of Differential Code Bias (DCB) Estimates and Low-Earth-Orbit (LEO)-Topside Ionosphere Extraction Based on Two Different Topside Ionosphere Processing Methods. Remote Sensing. 2025; 17(21):3550. https://doi.org/10.3390/rs17213550
Chicago/Turabian StyleLiu, Mingming, Yunbin Yuan, Jikun Ou, and Bingfeng Tan. 2025. "Comparisons of Differential Code Bias (DCB) Estimates and Low-Earth-Orbit (LEO)-Topside Ionosphere Extraction Based on Two Different Topside Ionosphere Processing Methods" Remote Sensing 17, no. 21: 3550. https://doi.org/10.3390/rs17213550
APA StyleLiu, M., Yuan, Y., Ou, J., & Tan, B. (2025). Comparisons of Differential Code Bias (DCB) Estimates and Low-Earth-Orbit (LEO)-Topside Ionosphere Extraction Based on Two Different Topside Ionosphere Processing Methods. Remote Sensing, 17(21), 3550. https://doi.org/10.3390/rs17213550







