LEO-Enhanced Multi-GNSS Real-Time PPP Time Transfer
Highlights
- Integrating GNSS and LEO observations can significantly reduce the convergence time and improve the precision of time links.
- Using 1 s observations, the time link errors can converge to 1 ns within 1 min.
- With LEO augmentation, time links can achieve high precision with less time.
- Not only fast, but also high-performance time links can be achieved with LEO augmentation.
Abstract
1. Introduction
2. Methods
2.1. Multi-GNSS-Based PPP Model
2.2. LEO-Enhanced Multi-GNSS PPP Model
2.3. Time Transfer Method
3. Data and Processing Strategies
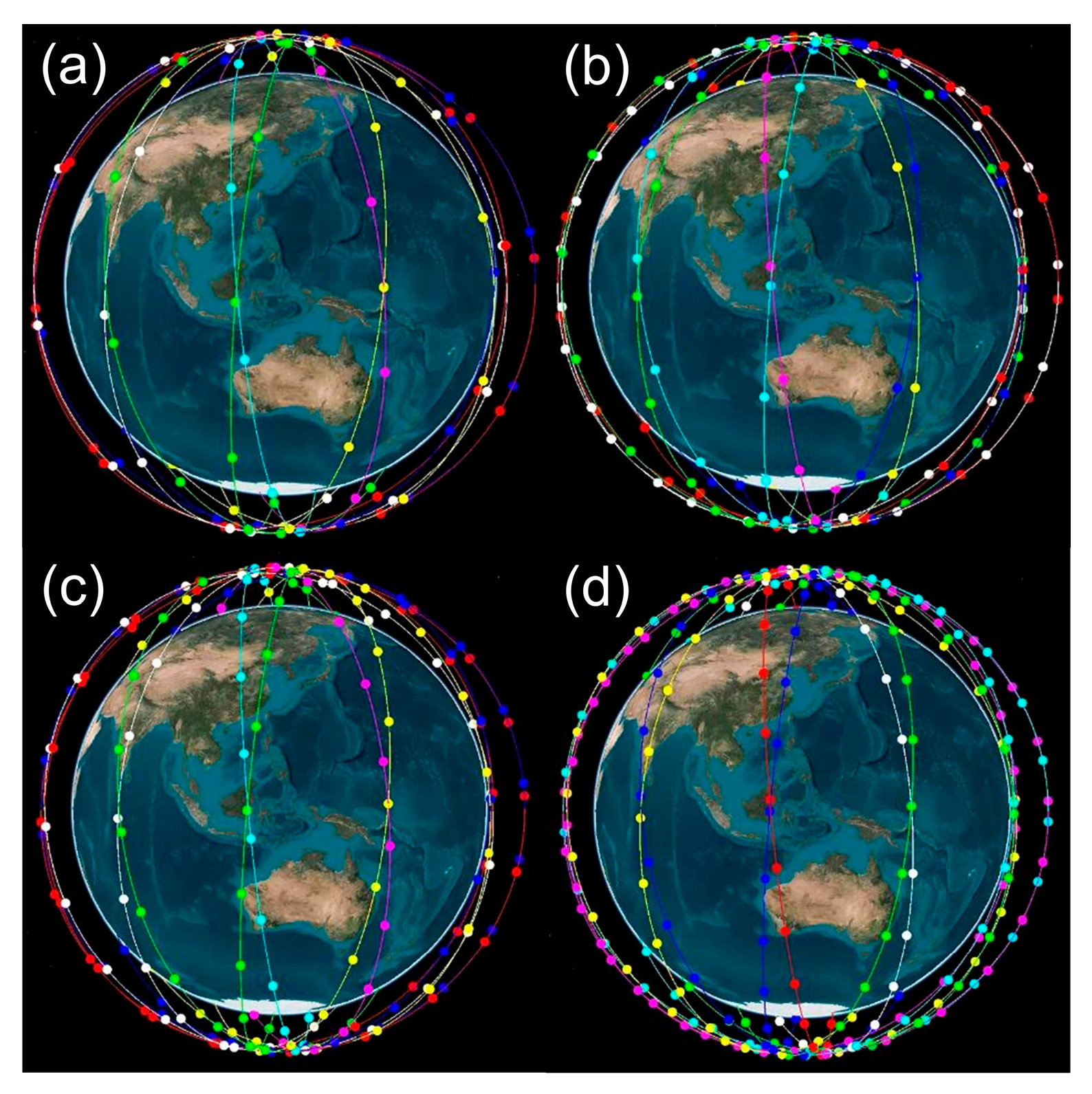
3.1. LEO Satellite Constellations
3.2. Experimental Settings
4. Experimental Results
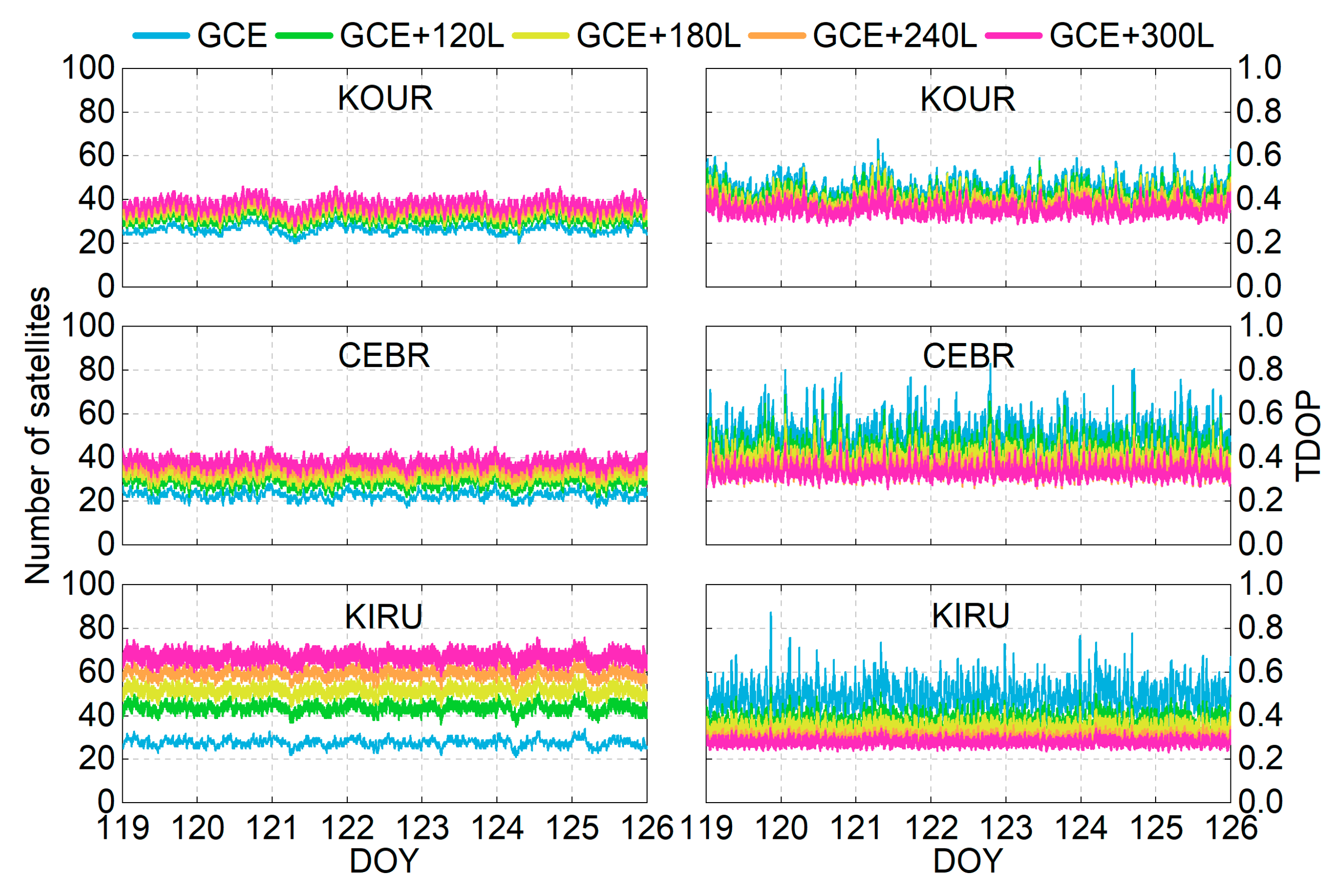
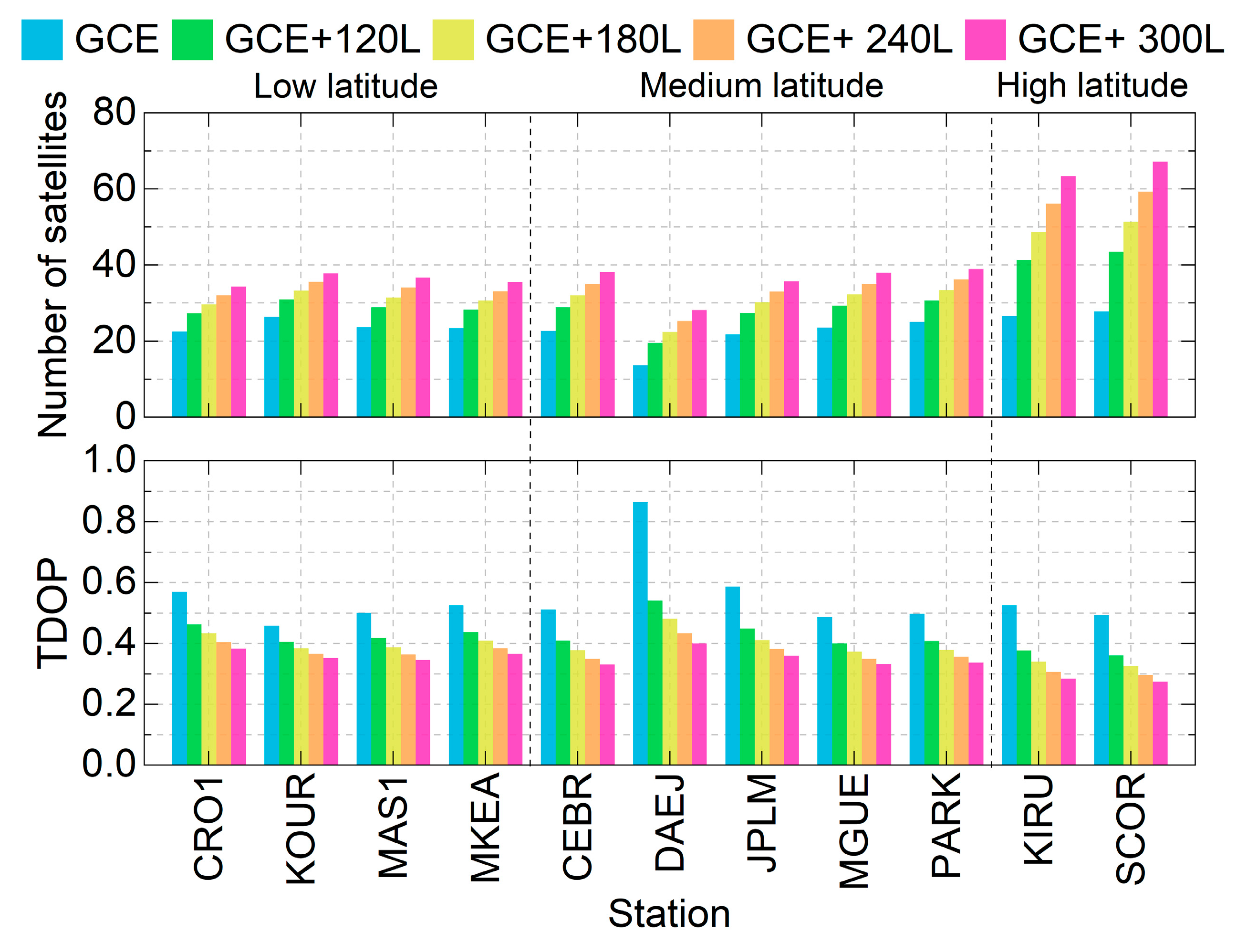
4.1. Number of Satellites and TDOP
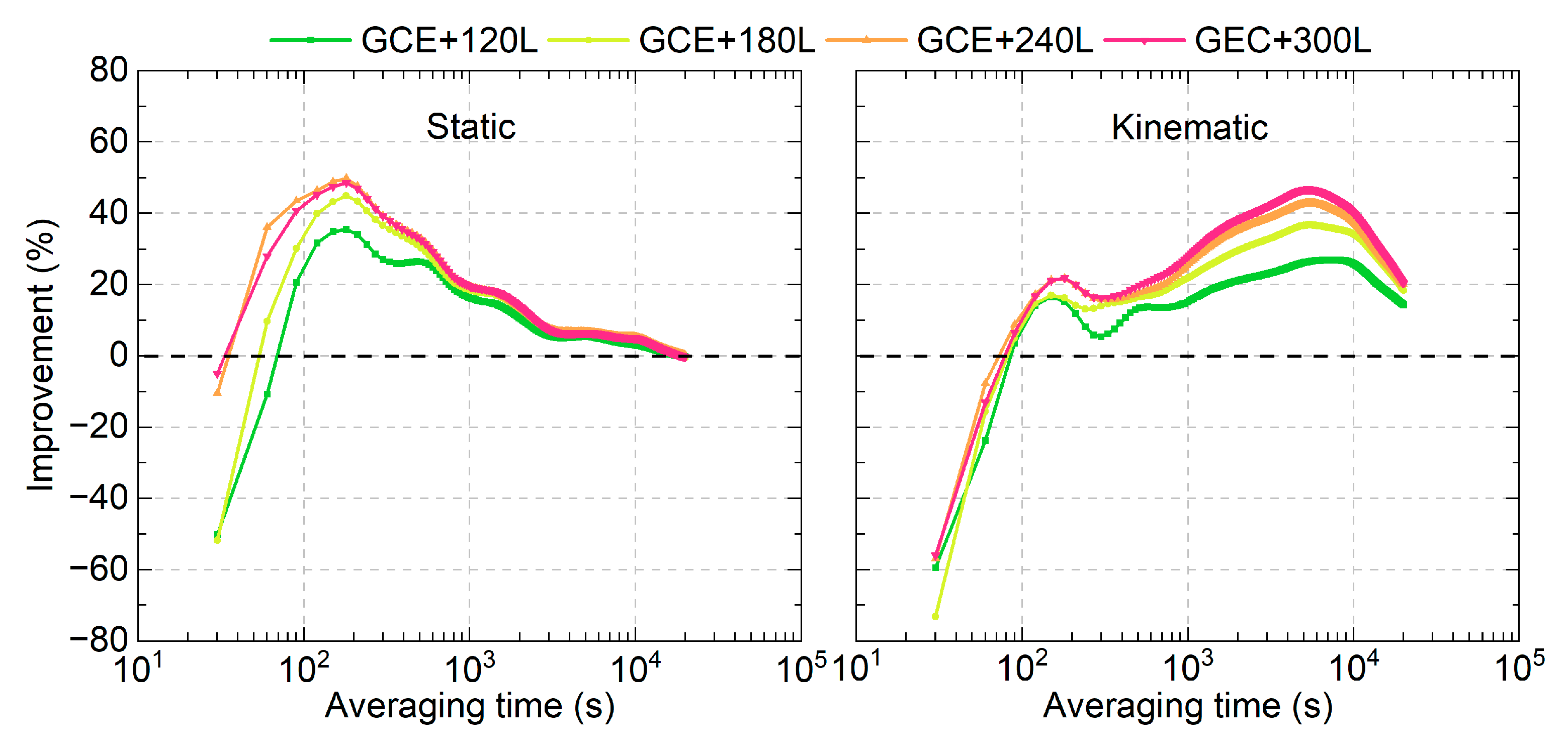
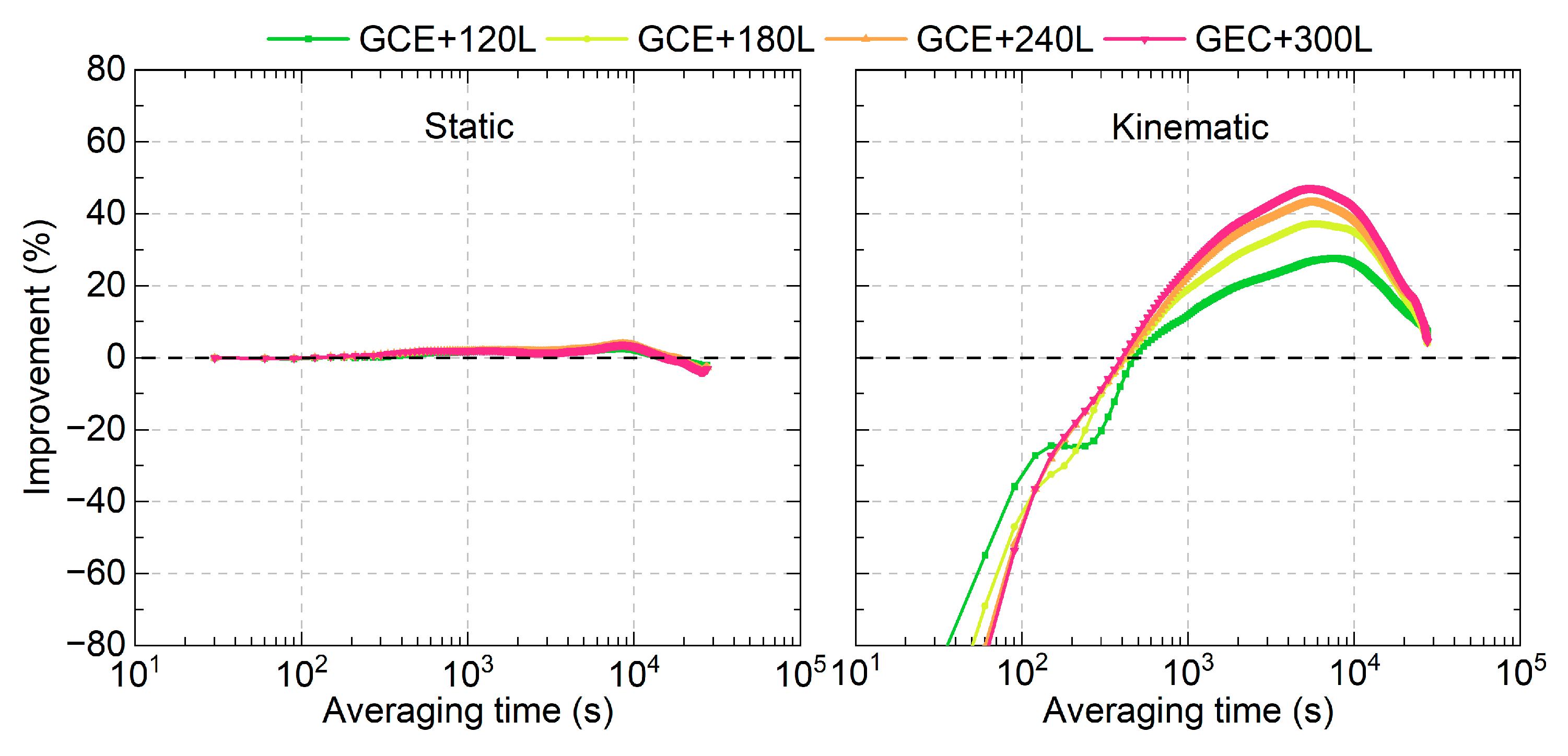
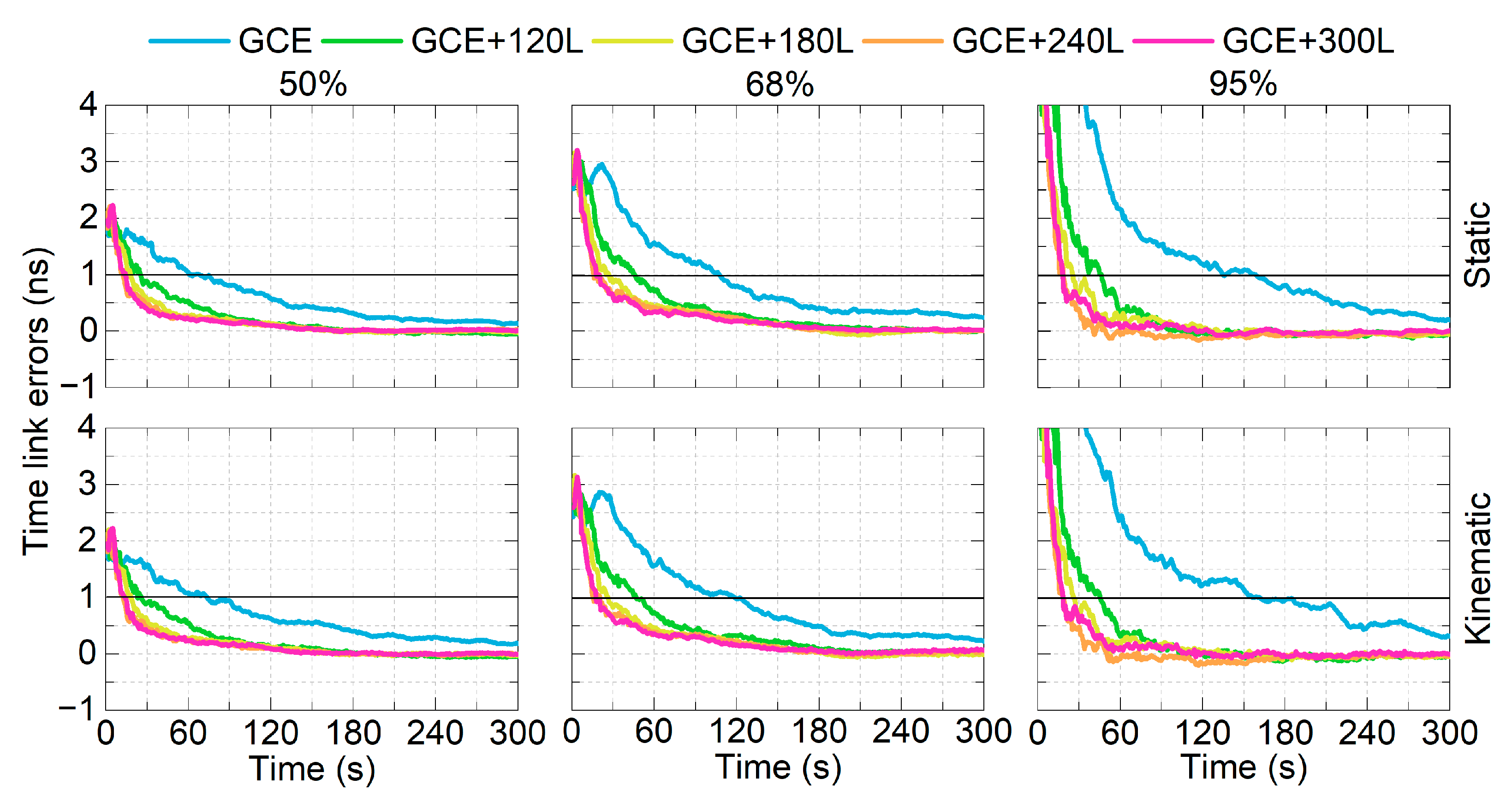
4.2. Convergence Time
4.3. Time Link Precision
4.4. Time Link Stability
5. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ge, Y.; Qin, W.; Su, K.; Yang, X.; Ouyang, M.; Zhou, F.; Zhao, X. A new approach to real-time precise point positioning timing with International GNSS Service real-time service products. Meas. Sci. Technol. 2019, 30, 125104. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and assessment of precise time transfer by using BeiDou navigation satellite system triple-frequency signals. Sensors. 2018, 18, 1017. [Google Scholar] [CrossRef] [PubMed]
- Petit, G.; Jiang, Z. Precise Point Positioning for TAI Computation. Int. J. Navig. Obs. 2008, 2008, 562878. [Google Scholar] [CrossRef]
- Defraigne, P.; Baire, Q. Combining GPS and GLONASS for time and frequency transfer. Adv. Space Res. 2011, 47, 265–275. [Google Scholar] [CrossRef]
- Zhang, P.; Tu, R.; Lu, X.; Fan, L.; Zhang, R. Performance of Multi-GNSS Real-Time UTC(NTSC) Time and Frequency Transfer Service Using Carrier Phase Observations. Remote Sens. 2021, 13, 4184. [Google Scholar] [CrossRef]
- Liu, M.; Tu, R.; Chen, Q.; Li, Q.; Chen, J.; Zhang, P.; Lu, X. Study of fast and reliable time transfer methods using low Earth orbit enhancement. Remote Sens. 2024, 16, 2044. [Google Scholar] [CrossRef]
- Reid, T.G.R.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO constellations for navigation. Navig. J. Inst. Navig. 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Çelikbilek, K.; Saleem, Z.; Ferre, R.M.; Praks, J.; Lohan, S. Survey on Optimization Methods for LEO-Satellite-Based Networks with Applications in Future Autonomous Transportation. Sensors 2022, 22, 1421. [Google Scholar] [CrossRef] [PubMed]
- Yang, L. The CentiSpace-1: A leo satellite-based augmentation system. In Proceedings of the 14th meeting of the international committee on global navigation satellite systems, Beijing, China, 10 December 2019; p. 12. [Google Scholar]
- Yang, Z.; Liu, H.; Qian, C.; Shu, B.; Zhang, L.; Xu, X.; Zhang, Y.; Lou, Y. Real-Time Estimation of Low Earth Orbit (LEO) Satellite Clock Based on Ground Tracking Stations. Remote Sens. 2020, 12, 2050. [Google Scholar] [CrossRef]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2019, 93, 749–764. [Google Scholar] [CrossRef]
- Li, X.; Lv, H.; Ma, F.; Li, X.; Liu, J.; Jiang, Z. GNSS RTK Positioning Augmented with Large LEO Constellation. Remote Sens. 2019, 11, 228. [Google Scholar] [CrossRef]
- Ke, M.; Lv, J.; Chang, J.; Dai, W.; Tong, K.; Zhu, M. Integrating GPS and LEO to accelerate convergence time of precise point positioning. In Proceedings of the 7th international conference on wireless communications and signal, Nanjing, China, 15–17 October 2015; pp. 1–5. [Google Scholar]
- Li, X.; Li, X.; Ma, F.; Yuan, Y.; Zhang, K.; Zhou, F.; Zhang, X. Improved PPP Ambiguity Resolution with the Assistance of Multiple LEO Constellations and Signals. Remote Sens. 2019, 11, 408. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Han, X.; Li, X.; Fu, Y. Toward wide-area and high-precision positioning with LEO constellation augmented PPP-RTK. IEEE Trans. Instrum. Meas. 2024, 73, 5500213. [Google Scholar] [CrossRef]
- Li, W.; Yang, Q.; Du, X.; Li, M.; Zhao, Q.; Yang, L.; Qin, Y.; Chang, C.; Wang, Y.; Qin, G. LEO augmented precise point positioning using real observations from two CENTISPACE™ experimental satellites. GPS Solut. 2024, 28, 44. [Google Scholar] [CrossRef]
- Xu, S.; Yang, Q.; Du, X.; Xu, X.; Zhao, Q.; Yang, L.; Qin, Y.; Guo, J. Multi-GNSS Precise Point Positioning enhanced by the real navigation signals from CENTISPACETM LEO mission. Adv. Space Res. 2024, 73, 4175–4186. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The multi-GNSS experiment (MGEX) of the international GNSS service (IGS)-achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Xie, W.; Huang, G.; Fu, W.; Li, P.; Cui, B. An efficient clock offset datum switching compensation method for BDS real-time satellite clock offset estimation. Adv. Space Res. 2021, 68, 1802–1813. [Google Scholar] [CrossRef]
- Yue, C.; Wang, H.; Xu, C.; Dang, Y. M_FCB: An open-source software for multi-GNSS fractional cycle bias estimation. GPS Solut. 2025, 29, 51. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling performance analysis of precise time transfer based on BDStriple-frequency un-combined observations. J. Geod. 2019, 93, 837–847. [Google Scholar] [CrossRef]
- Ge, Y.; Wang, Q.; Wang, Y.; Lyu, D.; Cao, X.; Shen, F.; Meng, X. A new receiver clock model to enhance BDS-3 real-time PPP time transfer with the PPP-B2b service. Satell. Navig. 2023, 4, 8. [Google Scholar] [CrossRef]
- Lai, W.; Huang, G.; Wang, L.; Qin, Z.; Li, R.; Xie, S.; She, H. Precise orbit determination of integrated BDS-3 and LEO satellites with ambiguity fixing under regional ground stations. Meas. Sci. Technol. 2024, 35, 116305. [Google Scholar] [CrossRef]
- Lai, W.; Huang, G.; Wang, L.; Xie, S.; She, H. Beidou UPD estimation and assessment based on LEO-assisted regional stations observations. GPS Solut. 2025, 29, 110. [Google Scholar] [CrossRef]
- Li, H.; Luojie, D.; Ding, H. Real-time service performances of BDS-3 and Galileo constellations with a linear satellite clock correction models. Satell. Navig. 2023, 4, 23. [Google Scholar] [CrossRef]
- Huang, G.; Zhang, Q.; Xu, G. Real-time clock offset prediction with an improved model. GPS Solut. 2014, 18, 95–104. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, G.; Xie, W.; Xie, S.; Wang, H. Assessment and comparison of satellite clock offset between BeiDou-3 and other GNSSs. Acta Geod. Geophys. 2021, 56, 303–319. [Google Scholar] [CrossRef]
- Wang, J.; Wu, M.; Wang, K.; Zou, M.; Yang, X. Influencing factors on real-time determination of LEO satellite clocks. Meas. Sci. Technol. 2025, 36, 066315. [Google Scholar] [CrossRef]
- Wu, M.; Wang, K.; Wang, J.; Xie, W.; Liu, J.; Chen, B.; Ge, Y.; El-Mowafy, A.; Yang, X. Impact of latency and continuity of GNSS products on filter-based real-tTime LEO satellite clock determination. Remote Sens. 2024, 16, 4315. [Google Scholar] [CrossRef]
- Xie, W.; Su, H.; Wang, K.; Liu, J.; Wu, M.; Zou, M.; El-Mowafy, A.; Yang, X. Real-time LEO satellite clock estimation with predicted LEO satellite orbits constrained. GPS Solut. 2024, 28, 172. [Google Scholar] [CrossRef]
- Xie, W.; Wang, K.; Wang, J.; Chen, B.; Wu, M.; El-Mowafy, A.; Yang, X. Impact of ISB stochastic models on LEO satellite clock estimation with onboard multi-GNSS observations. Meas. Sci. Technol. 2025, 36, 046313. [Google Scholar] [CrossRef]
- Ye, Z.; Wang, K.; Wei, C.; Chen, B.; Wang, J.; Wu, M. The impact of LEO satellite hardware delays on LEO-augmented precise point positioning. GPS Solut. 2025. under review. [Google Scholar]
- Kouba, J. Relativity effects of galileo passive hydrogen maser satellite clocks. GPS Solut. 2019, 23, 117. [Google Scholar] [CrossRef]
- Wu, M.; Wang, K.; Liu, J.; Zhu, Y. Relativistic effects of LEO satellite and its impact on clock prediction. Meas. Sci. Technol. 2023, 34, 095005. [Google Scholar] [CrossRef]
- Wu, J.; Wu, S.; Hajj, G.A.; Bertiger, W.I.; Lichten, S.M. Effects of antenna orientation on GPS carrier phase. Manuscr. Geod. 1993, 18, 91–98. [Google Scholar] [CrossRef]
- Dach, R.; Brockmann, E.; Schaer, S.; Beutler, G.; Meindl, M.; Prange, L.; Bock, H.; Jäggi, A.; Ostini, L. GNSS processing at CODE: Status report. J. Geod. 2009, 83, 353–365. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Saastamoinen, J. Contributions to the theory of atmospheric refraction—Part II Refraction corrections in satellite geodesy. Bull. Géod. 1973, 47, 13–34. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Schoenemann, E.; Gini, F.; Mayer, V.; Springer, T. ESOC MGNSS Processing Strategy. Available online: http://navigation-office.esa.int/products/gnss-products/esm.pdf (accessed on 11 October 2025).
- Laurichesse, D.; Privat, A. An open-source PPP client implementation for the CNES PPP-WIZARD demonstrator. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Jing, C.; Bertolesi, E.; Huang, G.; Li, X.; Zhang, Q.; Zhai, W.; Liu, G.; Li, H. Predicting Accelerometer Baseline Correction and Nondivergent Deformation Velocity Based on Convolutional Neural Network (CNN) During GNSS Downgrade. IEEE Sens. J. 2025, 25, 11982–11994. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Xie, W.; Wang, K.; Cui, B.; Yang, X. Regional multi-station real-time time transfer using an undifferenced multi-GNSS network solution. GPS Solut. 2024, 28, 198. [Google Scholar] [CrossRef]
- Fu, W.; Wang, L.; Chen, R.; Han, Y.; Zhou, H.; Li, T. Combined BDS-2/BDS-3 real-time satellite clock estimation with the overlapping B1I/B3I signals. Adv. Space Res. 2021, 68, 4470–4483. [Google Scholar] [CrossRef]
- Allan, D.W.; Barnes, J.A. A modified ‘Allan variance’ with increased oscillator characterization ability. In Proceedings of the 35th Annual Frequency Control Symposium, Philadelphia, PA, USA, 27–29 May 1981; pp. 470–475. [Google Scholar]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial assessment of precise point positioning with LEO enhanced Global Navigation Satellite Systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef]
- Fu, W.; Huang, G.; Zhang, Q.; Gu, S.; Ge, M.; Schuh, H. Multi-GNSS real-time clock estimation using sequential least square adjustment with online quality control. J. Geod. 2019, 93, 963–976. [Google Scholar] [CrossRef]
- Xie, W.; Huang, G.; Fu, W.; Du, S.; Cui, B.; Li, M.; Tan, Y. Rapid estimation of undifferenced multi-GNSS real-time satellite clock offset using partial observations. Remote Sens. 2023, 15, 1776. [Google Scholar] [CrossRef]
- Xie, W.; Wang, K.; Fu, W.; Xie, S.; Cui, B.; Li, M. Real-time estimation of BDS-3 satellite clock offset with ambiguity resolution using B1C/B2a signals. Remote Sens. 2024, 16, 1666. [Google Scholar] [CrossRef]
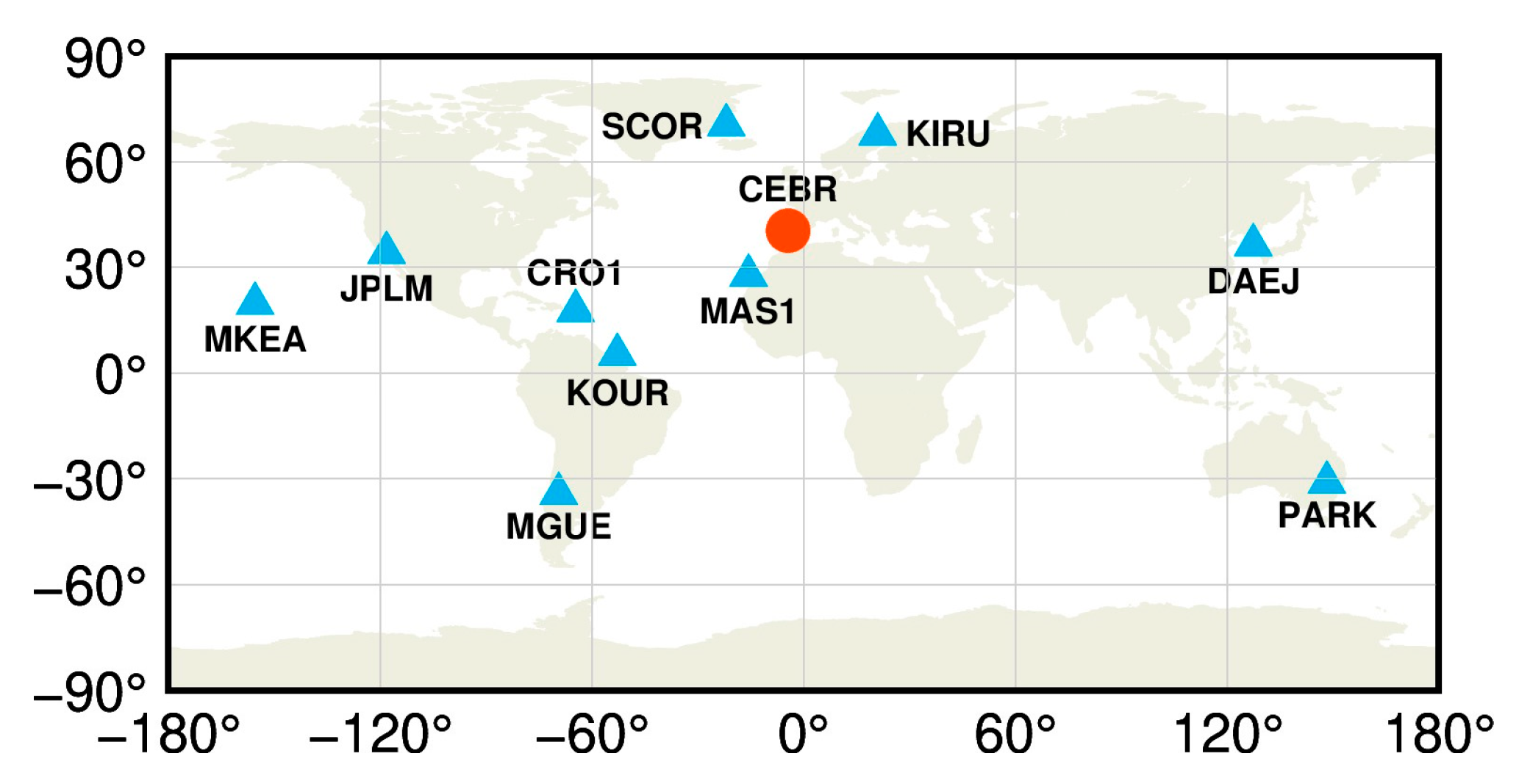
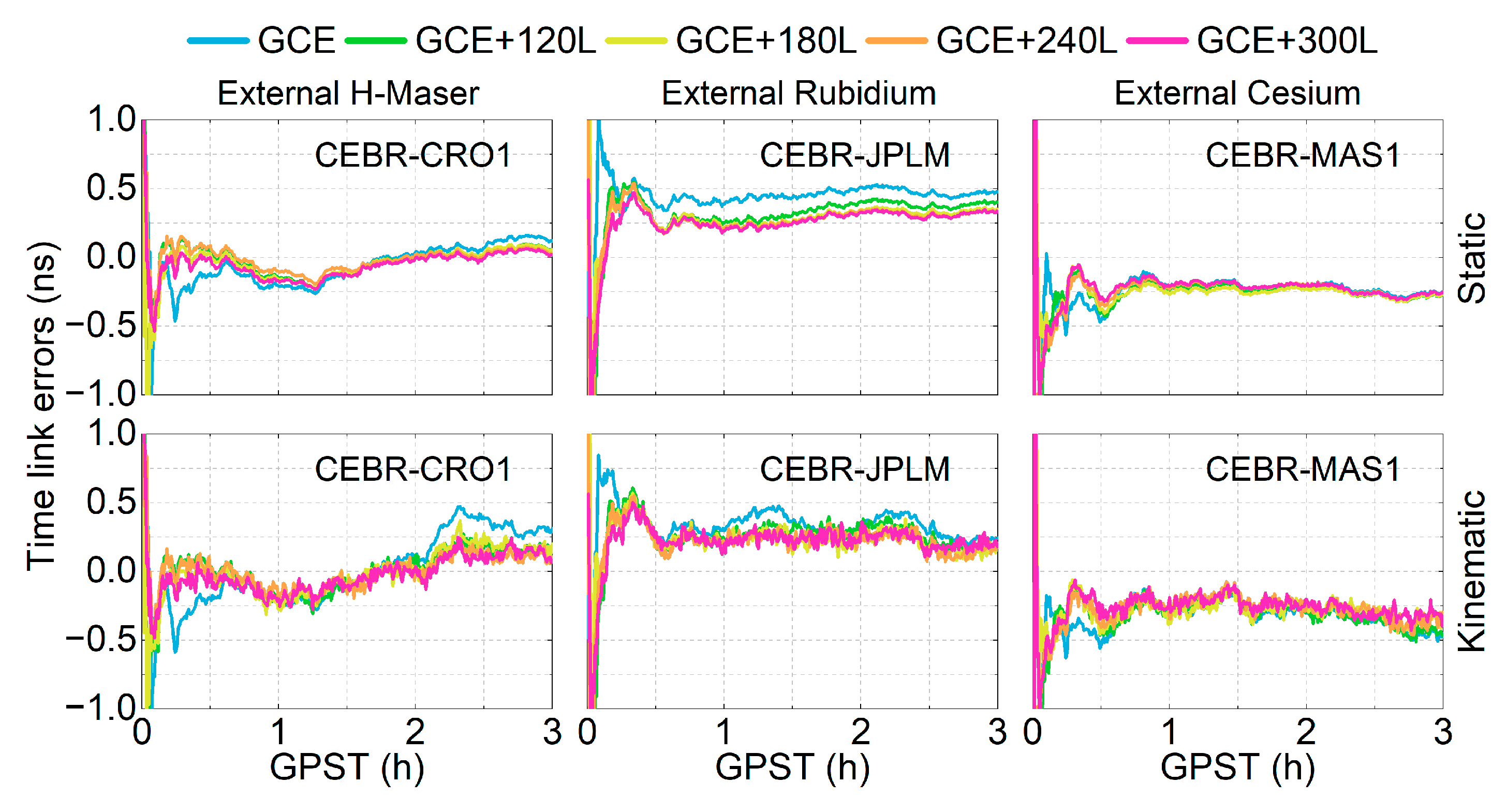

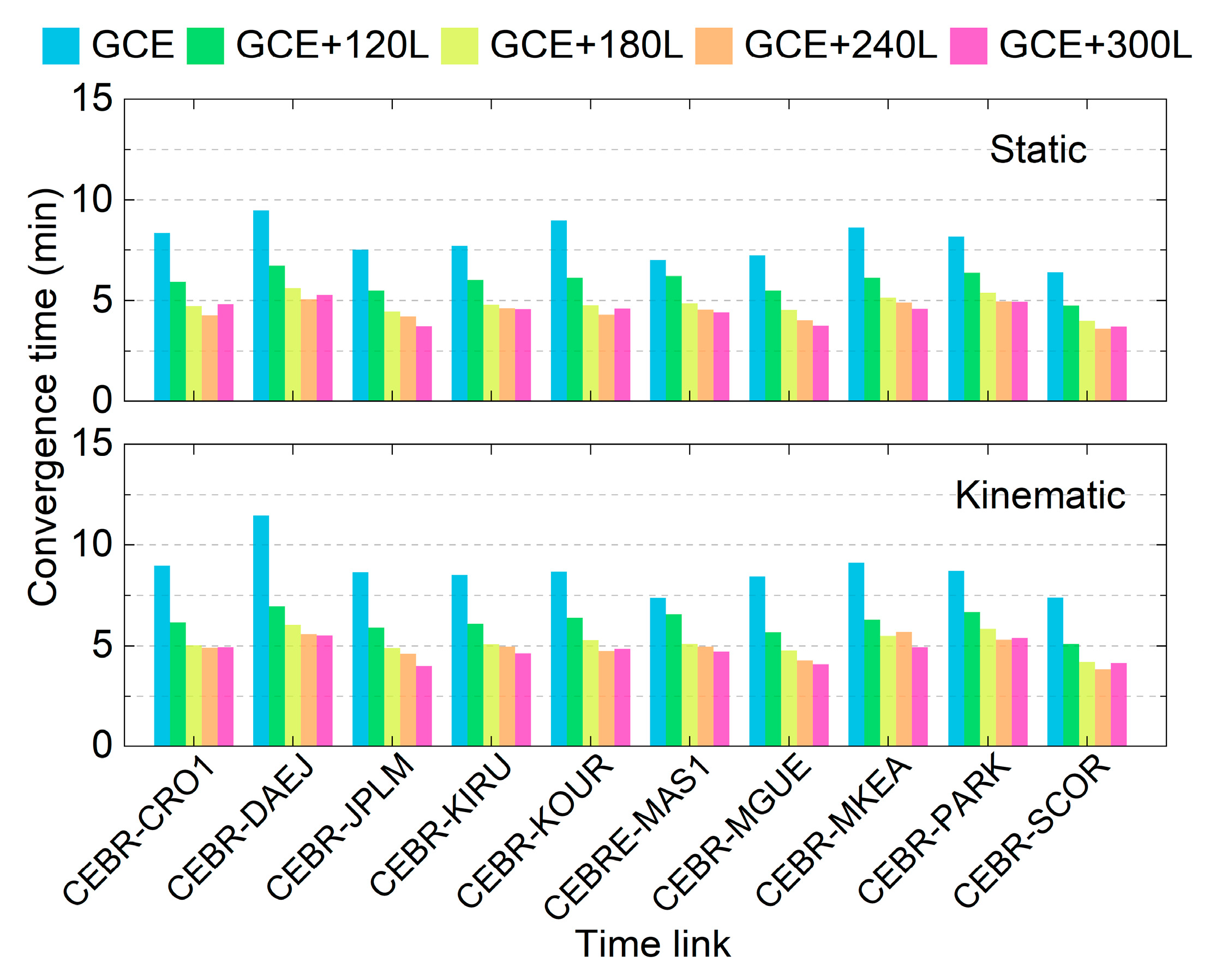
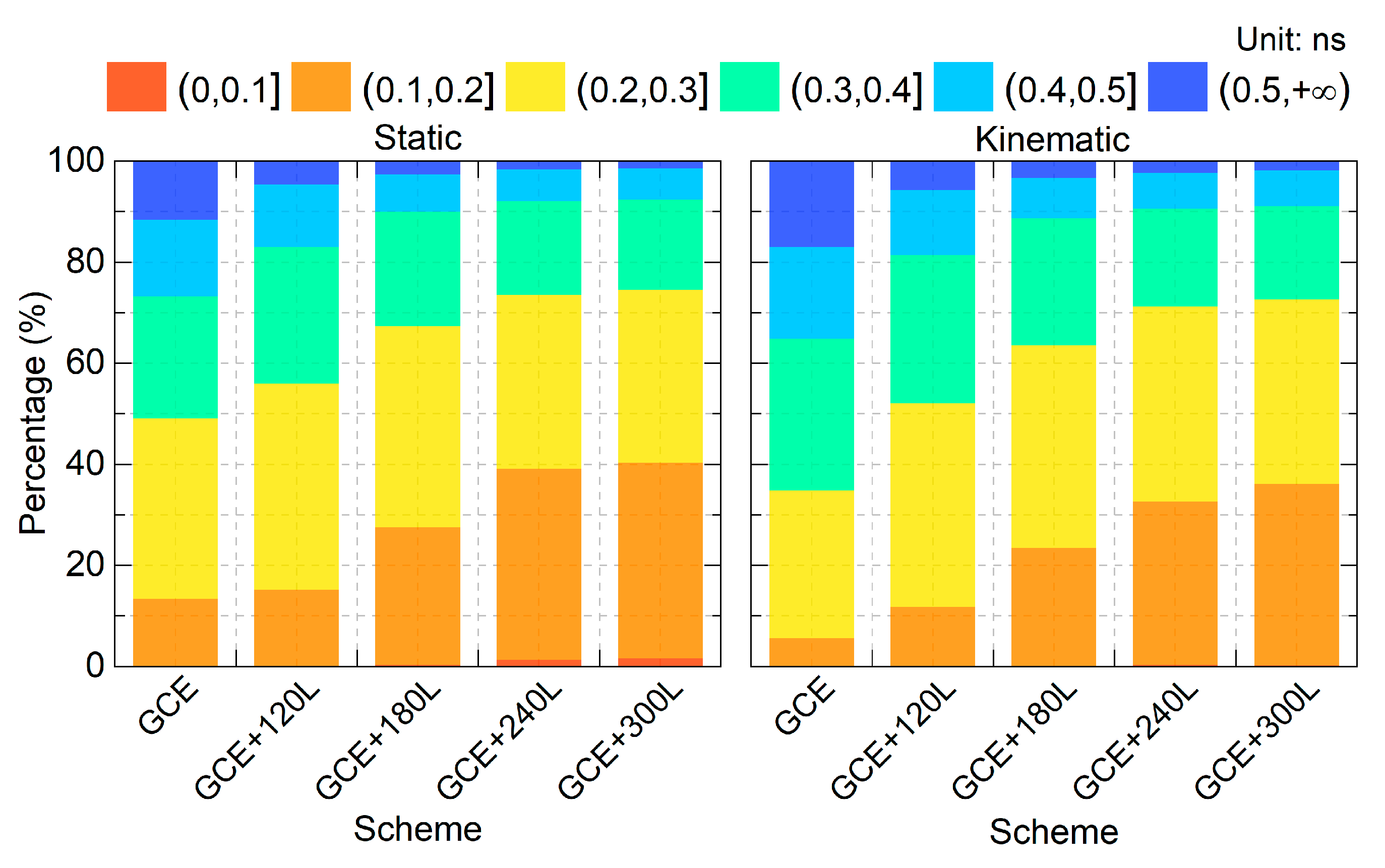
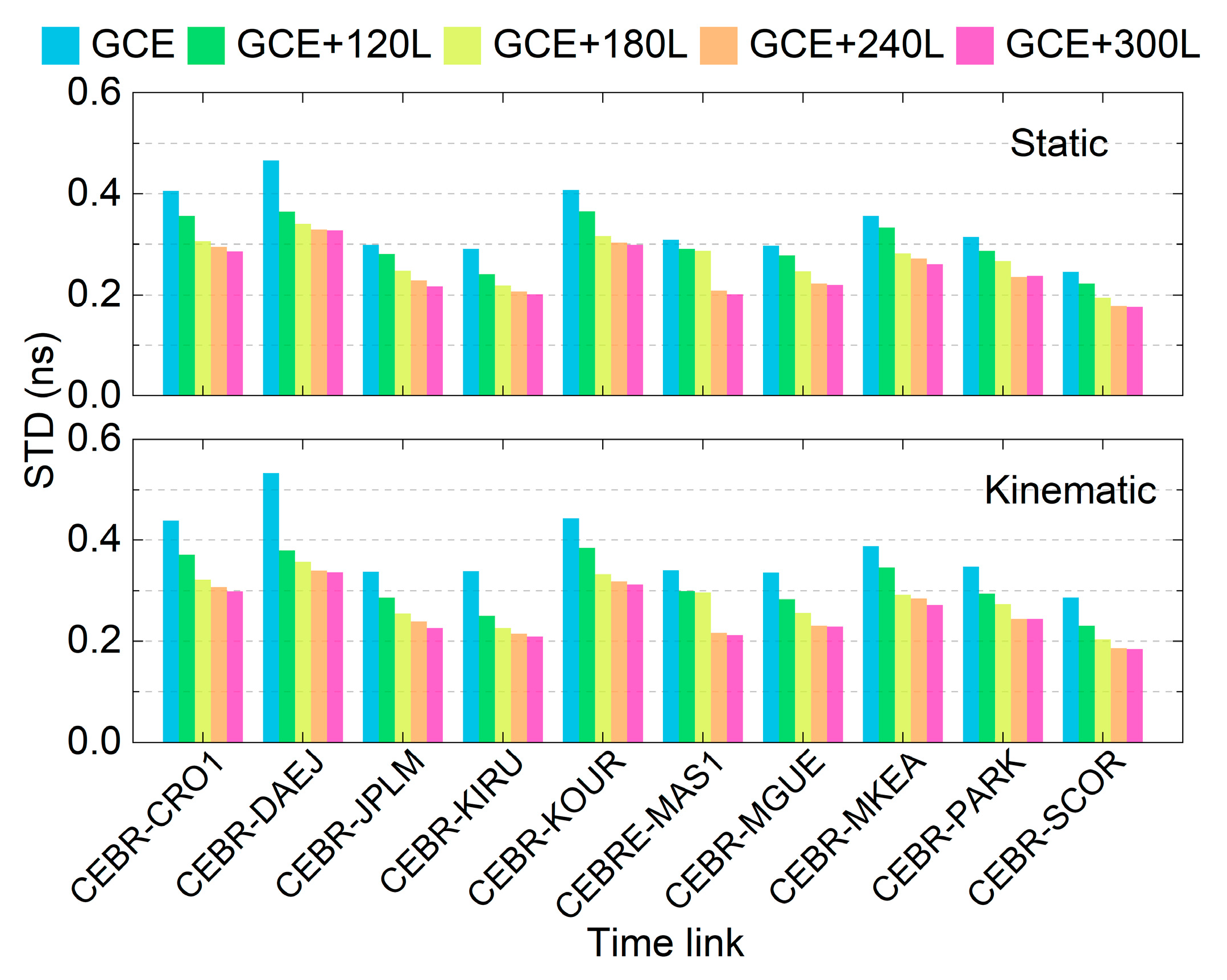

| Station | Receiver Type | Clock | Location | Distance (km) |
|---|---|---|---|---|
| CEBR | SEPT POLARX5TR | External H-Maser | Spain | / |
| CRO1 | SEPT POLARX5TR | External H-Maser | USA | 5998.0 |
| DAEJ | TRIMBLE NETR9 | External Cesium | South Korea | 9134.5 |
| JPLM | SEPT POLARX5 | External Rubidium | USA | 8517.1 |
| KIRU | SEPT POLARX5TR | External Cesium | Sweden | 3373.9 |
| KOUR | SEPT POLARX5TR | External H-Maser | France | 5959.4 |
| MAS1 | SEPT POLARX5 | External Cesium | Spain | 1741.1 |
| MGUE | SEPT POLARX5TR | External H-Maser | Argentina | 9511.0 |
| MKEA | SEPT POLARX5 | External H-Maser | USA | 10,709.9 |
| PARK | SEPT POLARX5TR | External H-Maser | Australia | 12,484.1 |
| SCOR | SEPT POLARX5 | External Rubidium | Denmark | 3449.0 |
| GCE | GCE+120L | GCE+180L | GCE+240L | GCE+300L | |
|---|---|---|---|---|---|
| Number of satellites | 23.4 | 30.6 | 34.1 | 37.7 | 41.3 |
| TDOP | 0.547 | 0.424 | 0.391 | 0.363 | 0.342 |
| GCE | GCE+120L | GCE+180L | GCE+240L | GCE+300L | |
|---|---|---|---|---|---|
| Static | 7.95 | 5.94 | 4.83 | 4.46 | 4.45 |
| Kinematic | 8.74 | 6.18 | 5.17 | 4.89 | 4.72 |
| GCE | GCE+120L | GCE+180L | GCE+240L | GCE+300L | |
|---|---|---|---|---|---|
| Static | 0.337 | 0.302 | 0.266 | 0.248 | 0.243 |
| Static (excl. 0–1 h) | 0.064 | 0.058 | 0.055 | 0.055 | 0.054 |
| Kinematic | 0.377 | 0.313 | 0.277 | 0.259 | 0.253 |
| Kinematic (excl. 0–1 h) | 0.092 | 0.084 | 0.081 | 0.080 | 0.079 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, W.; Wang, K.; Lai, W.; Wu, M.; Li, M.; Yang, X. LEO-Enhanced Multi-GNSS Real-Time PPP Time Transfer. Remote Sens. 2025, 17, 3549. https://doi.org/10.3390/rs17213549
Xie W, Wang K, Lai W, Wu M, Li M, Yang X. LEO-Enhanced Multi-GNSS Real-Time PPP Time Transfer. Remote Sensing. 2025; 17(21):3549. https://doi.org/10.3390/rs17213549
Chicago/Turabian StyleXie, Wei, Kan Wang, Wen Lai, Mengjun Wu, Mengyuan Li, and Xuhai Yang. 2025. "LEO-Enhanced Multi-GNSS Real-Time PPP Time Transfer" Remote Sensing 17, no. 21: 3549. https://doi.org/10.3390/rs17213549
APA StyleXie, W., Wang, K., Lai, W., Wu, M., Li, M., & Yang, X. (2025). LEO-Enhanced Multi-GNSS Real-Time PPP Time Transfer. Remote Sensing, 17(21), 3549. https://doi.org/10.3390/rs17213549






