A Novel MIMO SAR Scheme with Intra–Inter-Pulse Phase Coding and Azimuth–Elevation Joint Processing

Highlights

What are the main findings?

• A novel dual phase-coding MIMO SAR scheme is proposed, which combines intra-pulse and inter-pulse modulation to effectively suppress interference and achieve superior echo separation performance.
• An azimuth–elevation joint digital beamforming (DBF) processing framework is developed, which significantly reduces system complexity, computational burden, and hardware requirements (e.g., fewer elevation channels and lower PRF) compared to conventional methods.

What is the implication of the main finding?

• It provides a practical and cost-effective solution for the implementation of MIMO SAR systems, making it particularly suitable for cost-sensitive missions (e.g., small satellites) and systems with limited hardware resources.
• It enhances system flexibility and paves the way for advanced applications, such as high-precision multi-mode and multi-scene imaging, as well as interferometric measurements, using a reconfigurable hardware platform.

Abstract

Echo separation has long been a challenging and prominent research focus for Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) systems. Digital beamforming (DBF) plays a critical role in achieving effective echo separation, but it often comes at the cost of high system complexity. This paper proposes a novel MIMO SAR scheme based on phase-coded waveforms applied to both inter-pulses and intra-pulses. By introducing phase coding in both dimensions and performing joint azimuth–elevation processing, the proposed method effectively suppresses interference arising during the echo separation process, thereby significantly improving separation performance. Additionally, the approach allows for a significantly simplified array configuration, reducing both hardware requirements and computational burden. The effectiveness and practicality of the proposed scheme are validated through numerical simulations and distributed scene experiments, highlighting its strong potential for application in MIMO SAR systems—particularly in cost-sensitive scenarios and systems with limited elevation channels.

1. Introduction

Synthetic Aperture Radar (SAR) is an advanced radar system that uses microwave technology to achieve high-resolution imaging, characterized by its all-weather and day–night operational capabilities [1]. Traditional SAR systems face inherent limitations in meeting the increasing demands for imaging performance, particularly in balancing high resolution and wide swath coverage. Multiple-Input Multiple-Output (MIMO) SAR enhances the system’s degrees of freedom (DOFs) through the concurrent transmission of diverse orthogonal waveforms and the reception of their respective echoes. In contrast to traditional SAR systems, MIMO SAR provides a potential solution for high-resolution wide-swath imaging [2,3] and multi-mode imaging [4] applications.

However, the system design of MIMO SAR encounters two pivotal challenges: the effective separation of echoes and the design of transmitted waveforms. Orthogonality between transmitted waveforms is crucial for the separation of scattered echoes. Time-division multiplexing (TDM) [5] and frequency-division multiplexing (FDM) [6] waveforms achieve orthogonality by employing distinct time or frequency support sets, but this approach compromises signal coherence.

Consequently, the development of orthogonal waveforms with identical time and frequency support is more pertinent for MIMO SAR applications. To effectively separate echoes, the most straightforward approach is to design fully orthogonal waveforms, enabling signal separation through a set of distinct matched filters. However, this assumption of orthogonality is typically only applicable to radar systems designed for detection purposes and is inadequate for meeting the imaging requirements of SAR in distributed scenes. For aliased echoes received by the antenna, cross-correlation energy after matched filtering does not disappear but disperses across the entire image [7,8,9]. Therefore, researchers have proposed various echo separation schemes to address this issue.

Firstly, there are inter-pulse coding schemes, with the space–time coding (STC) [10] and azimuth phase coding (APC) [11,12] techniques being quite representative. However, these schemes require a high PRF, and as the number of transmitted waveforms increases, the required PRF resources increase proportionally. In fact, these high PRF values do not contribute to an improvement in resolution; they are solely employed to separate aliased echoes. Such high costs are unsustainable, especially for spaceborne MIMO SAR.

To reduce the PRF required for echo separation in MIMO SAR and fully exploit its DOFs, Krieger et al. [13] introduced the concept of multi-dimensional waveform encoding. By elevation digital beamforming (DBF) technology, the received aliased echoes can be separated. Based on this concept, various orthogonal beamforming schemes have been proposed. Notable examples include short-time shift-orthogonal (STSO) waveforms [13,14], orthogonal frequency-division multiplexing (OFDM) waveforms [15,16,17], and segmented phase code (SPC) waveforms [18]. In a sense, these waveforms share common ground: the unique characteristics of each waveform can suppress interference from nearby targets, and digital beamforming (DBF) in elevation handles interference from distant targets.

Specifically, Krieger et al. [13] proposed the STSO waveform and demonstrated the consistency between the STSO and OFDM waveforms for MIMO SAR systems. Kim et al. [15] proposed a MIMO SAR scheme integrating the OFDM chirp waveform with DBF. However, the OFDM signal is susceptible to Doppler leakage, affecting echo separation performance. Moreover, controlling signals to be of equal length during modulation and demodulation poses significant implementation challenges. Jin et al. [18] proposed the SPC waveform scheme that uses a simple time-shift weighting method to separate echoes from close-range scatterers. Subsequently, appropriate bandpass filters and least-squares (LS) beamformers are constructed to differentiate echoes originating from distant scatterers. Additionally, Zhang et al. [16] and Jin et al. [17] proposed a novel OFDM waveform, which, similar to the SPC waveform, consists of multiple sub-pulses encoded by a phase matrix. The primary distinction lies in the different phase encoding matrices used.

The previously mentioned orthogonal beamforming methods can effectively suppress interference. Nevertheless, these techniques usually demand substantial computational resources and complex array configurations. To reduce the demand on computational overhead, some methods have already been proposed [19,20,21]. Wang et al. have conducted studies on MIMO channel estimation [22] and DOA estimation [23], which hold promise for mitigating channel mismatches and the effects of terrain undulation in MIMO SAR systems.

MIMO SAR waveform encoding and echo separation have been extensively studied. The main contributions of this paper, which makes it different from previous works [19,20,21], are as follows:

1.

As the number of transmitted waveforms increases, the interference signal segments generated by multi-dimensional waveform coding schemes also grow linearly [14,15,16,17,18,19,20,21]. The proposed coding scheme employs dual modulation of both inter-pulses and intra-pulses, introducing additional degrees of freedom in the Doppler domain. It enables grouped transmission of waveforms, batch demodulation, and processing at the receiver to reduce the interference signal segments generated in each processing step. Compared with schemes such as MSTS waveforms [21], this modulation approach reduces the number of channels required for the same number of transmitted waveforms, offering particular advantages for low-cost SAR systems with limited channels.

2.

A novel azimuth–elevation joint processing framework is also developed to address the echo separation challenge. This approach significantly enhances separation performance, suppresses interference energy, and simultaneously reduces system complexity and computational overhead. By exploiting the degrees of freedom in both the azimuth and elevation directions, the proposed scheme optimizes resource allocation within MIMO SAR systems.

The remaining sections of this paper are as follows: Section 2 discusses the Transmitting Signal Model and the proposed joint azimuth–elevation processing flow. Section 3 presents the simulation results for point target and distributed scenes. Section 4 discusses the system complexity, computational cost, and echo separation performance of the proposed scheme. Conclusions are given in Section 5 .

2. Materials and Methods

2.1. Transmitting Signal Model

In a MIMO SAR system, an $N\times M$ transmitting antenna array is employed, where each antenna transmits a uniquely coded waveform. These waveforms are grouped into N sets, each utilizing a distinct inter-pulse modulation strategy. As illustrated in Figure 1, for the case of $N=2$, the transmitted signals adopt a dual-layer modulation scheme combining inter-pulse and intra-pulse coding. Inter-pulse phase coding is implemented by alternately transmitting pulse groups with different phase sequences. Within each pulse, orthogonal phase coding is applied to multiple sub-pulses, further enhancing the separability and orthogonality of the intra-pulse signals.

The transmitted waveform of the m-th transmitting channel is denoted as $s_{m,l}\left(t\right)$, where l represents the l-th pulse sequence. Each pulse sequence is accompanied by a different inter-pulse modulation phase ${\phi }_{p,l}$, which can be derived as

$$s_{m,l}\left(t\right)={\phi }_{p,l}{s}_m\left(t\right)={\phi }_{p,l}{\overline{s}}_q\left(t\right)$$

(1)

$$\left\{\begin{array}{c}p=⌊{\displaystyle \frac{m-1}{M}}⌋,p=0,\dots ,N-1\hfill \\ m=1,\dots ,M\times N\hfill \\ q=m-\left(p-1\right)·M,q=1,\dots ,M\hfill \end{array}\right.$$

(2)

where $\lfloor ·\rfloor$ denotes the floor function; t represents fast time; p (p represents the sequence of coding groups, with $p=1,2,\dots ,N$, indicating that there are a total of N groups) represents different inter-pulse modulations; and $s_m\left(t\right)$ is the intra-pulse modulation waveform of the m-th transmitter, which can also be written as ${\overline{s}}_q\left(t\right)$ (q represents the sequence of transmitted OFDM waveforms, with $q=1,2,\dots ,M$, indicating that there are a total of M types of OFDM transmitted waveforms). Additionally, ${\phi }_{p,l}$ represents the inter-pulse phase for the m-th transmitter and the l-th PRI, which is formulated as

$${\phi }_{p,l}=\exp \left(-j{\displaystyle \frac{\pi }{N}}{l}^2+j{\displaystyle \frac{2\pi }{N}}pl\right)$$

(3)

The inter-pulse decoding phases of the l-th PRI received echoes are denoted as

$$\overline{{\phi }_l}=\exp \left(j{\displaystyle \frac{\pi }{N}}{l}^2\right)$$

(4)

Therefore, after inter-pulse decoding, the residual azimuth phase corresponding to the p-th echo cluster signal is

$${\tilde{\phi }}_{p,l}={\phi }_{p,l}·\overline{{\phi }_l}=\exp \left(j{\displaystyle \frac{2\pi }{N}}pl\right)$$

(5)

where the azimuth sampling index l is given by $l=F_a·\eta$, with $F_a$ denoting the azimuth sampling frequency and $\eta$ representing the slow time. This indicates that the p-th echo cluster signal exhibits different frequency shifts in the azimuth frequency domain.

The designed inter-pulse coding can be regarded as an extended form of azimuth phase coding [11,12]. After inter-pulse decoding, the N groups of transmitted waveforms exhibit different Doppler center frequencies. At the receiver side, an LS beamformer can be constructed based on the azimuth array data to decouple the aliased echoes into N independent echo clusters. By maximizing inter-group waveform orthogonality, inter-signal interference is significantly reduced. In addition, echo groups with different Doppler centers can be independently adapted to meet the imaging requirements of multiple modes and diverse scenarios, thereby enabling optimal reuse of transmission resources.

Moreover, ${\overline{s}}_q\left(t\right)$ is the q-th intra-pulse coding signal that consists of M sub-pulses and is designed as

$${\overline{s}}_q\left(t\right)=\sum _{k=1}^M{\varphi }_{q,k}s\left(t-(k-1)T_s\right)={\mathit{\varphi }}_q^{\mathrm{T}}\mathit{s}\left(t\right)$$

(6)

$$\left\{\begin{array}{c}{\mathit{\varphi }}_q={\left[{\varphi }_{q,1},{\varphi }_{q,2},\dots ,{\varphi }_{q,M}\right]}^{\mathrm{T}}\hfill \\ \mathit{s}\left(t\right)={\left[s\left(t\right),s\left(t-T_s\right),\dots ,s\left(t-(M-1)T_s\right)\right]}^{\mathrm{T}}\hfill \end{array}\right.$$

(7)

where $T_s$ is the sub-pulse width, ${[·]}^{\mathrm{T}}$ denotes the matrix transpose, $s\left(t\right)$ is the waveform with a pulse width of $T_s$ (typically a linear or nonlinear frequency modulation waveform), and ${\varphi }_{q,k}$ represents the intra-pulse phase for the m-th transmitting antenna in the k-th sub-pulse segment.

For an M-order matrix ($\mathsf{\Phi }=[{\mathit{\varphi }}_1,{\mathit{\varphi }}_2,\dots ,{\mathit{\varphi }}_M]$) composed of intra-pulse phases, it only needs to satisfy the condition of full column rank, which ensures that part of the echoes can be removed at the receiver through time shifting, weighting, and coherent summation. When the elements of $\mathsf{\Phi }$ satisfy

$${\varphi }_{q,k}=\exp \left(j{\displaystyle \frac{2\pi }{M}}(q-1)(k-1)\right)$$

(8)

the matrix $\mathsf{\Phi }$ becomes orthogonal, i.e.,

$$\mathsf{\Phi }·{\mathsf{\Phi }}^{\mathrm{H}}=M·\mathit{I}$$

(9)

where $\mathit{I}$ represents the M-order identity matrix and ${[·]}^{\mathrm{H}}$ represents the conjugate transpose. The M signals ${\overline{s}}_q\left(t\right)$ thus form an OFDM set [17]. In fact, the signal ${\overline{s}}_q\left(t\right)$ can also be other types of multi-dimensional coded waveforms, such as SPC or STSO waveforms.

After down-conversion, the echoes received by the n-th receiver from the m-th transmitter are denoted as

$$r_{n,m}(t,\eta )=\sum _l\delta \left(\eta -{\displaystyle \frac{l}{F_a}}\right){\phi }_{p,l}{h}_{n,m}(t,\eta ){\otimes }_t{s}_m\left(t\right)$$

(10)

where $\eta$ is the slow time, $\delta (\eta -{\displaystyle \frac{l}{F_a}})$ denotes the l-th azimuth sampling, $F_a$ denotes the azimuth sampling rate, ${\otimes }_t$ is the fast-time convolution, and $h_{n,m}(t,\eta )$ represents the channel response associated with the m-th transmitter and the n-th receiver, which contain information about the target’s location and scattering coefficient.

Because each receiving antenna captures echoes from different transmitting antennas. The aliased echoes received by the n-th receiver are derived as

$$r_n(t,\eta )=\sum _{m=1}^{M\times N}\sum _l\delta \left(\eta -{\displaystyle \frac{l}{F_a}}\right){\phi }_{p,l}{h}_{n,m}(t,\eta ){\otimes }_t{s}_m\left(t\right)$$

(11)

It is noteworthy that this paper discusses a centralized MIMO SAR system, where the MIMO uniform linear array is deployed on the same flight platform.

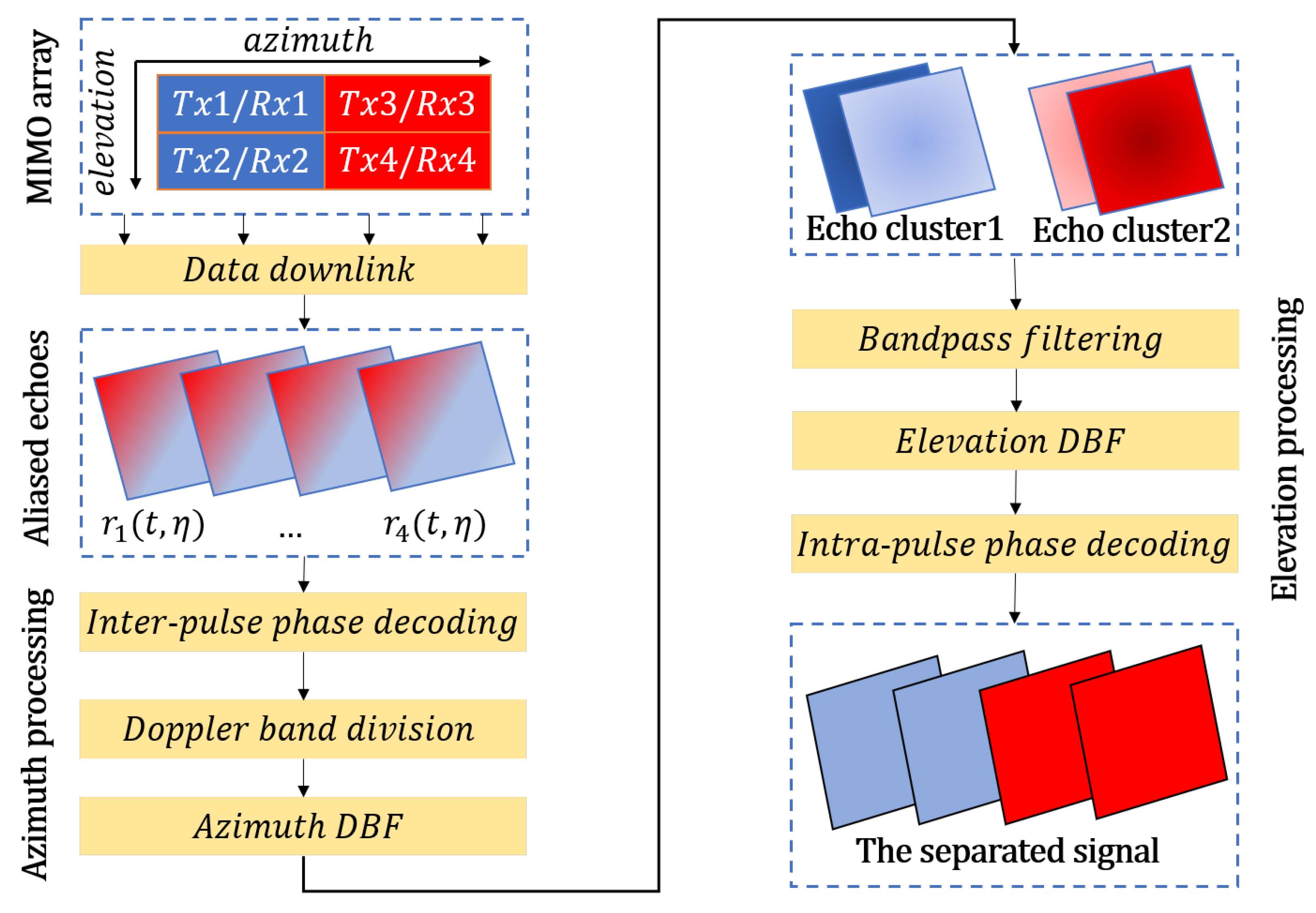
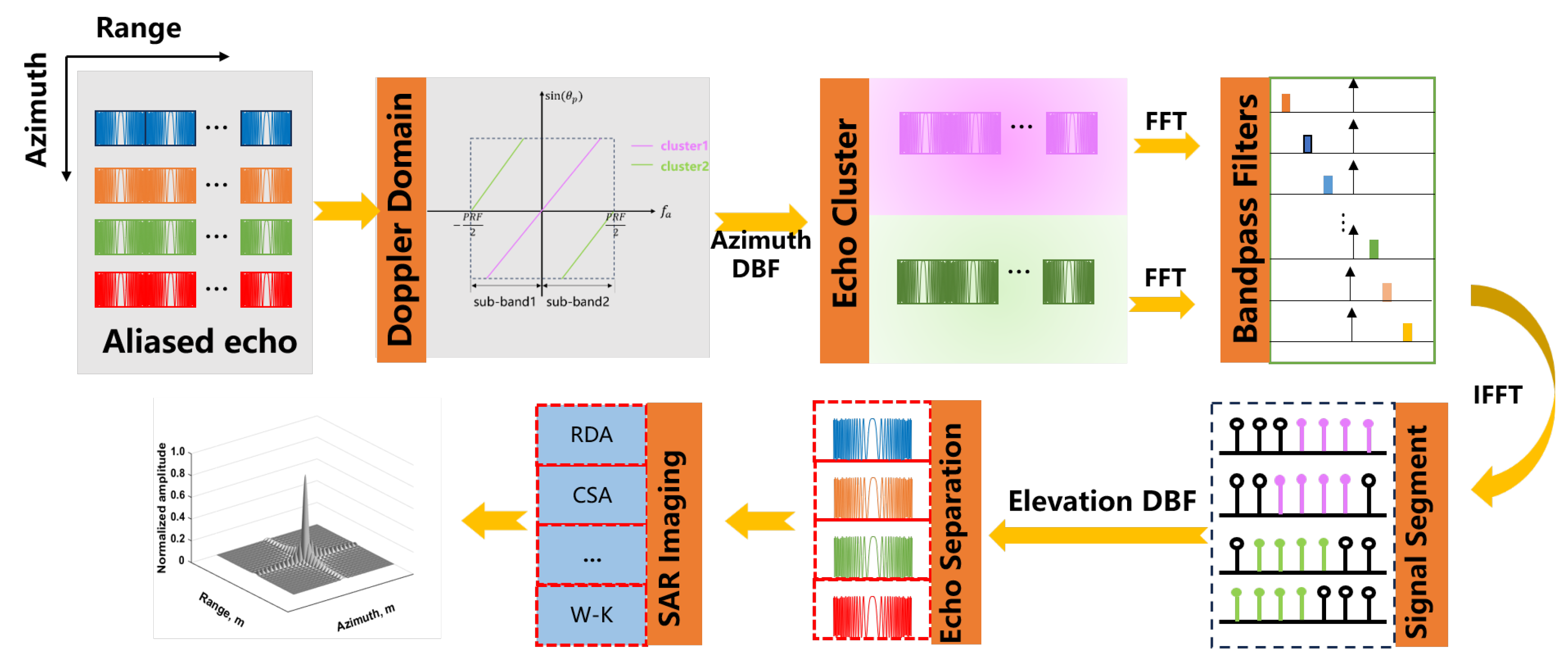
2.2. Processing Scheme

To effectively separate the aliased echoes, the echo separation scheme is mainly divided into two stages: The first stage of processing occurs in the azimuth dimension. After inter-pulse demodulation, the signal is divided into different clusters through azimuth DBF, which only removes part of the aliased echoes. The second stage of processing is in the elevation dimension, where echoes are separated by the bandpass filters and LS beamforming. Finally, complete separation of aliased echoes is achieved through intra-pulse demodulation. The processing scheme ($N=2,M=2$) is illustrated in Figure 2.

The proposed scheme separates the aliased echoes by introducing joint processing. Through joint processing in the azimuth and elevation directions, it significantly reduces the number of channels required when transmitting multiple waveforms. The corresponding signal flow is illustrated in Figure 3.

2.2.1. Operation in the Azimuth Direction

The aliased echoes received by every aperture need to undergo inter-pulse demodulation. Based on Equations (4) and (11), the inter-pulse decoded echoes can be described as

$${\overline{r}}_n(t,\eta )={\overline{\phi }}_l{r}_n(t,\eta )=\sum _{m=1}^{N\times M}{\overline{r}}_{n,m}(t,\eta )$$

(12)

where ${\overline{r}}_{n,m}(t,\eta )$ denotes the inter-pulse decoded echo of the m-th transmitter and the n-th receiver.

For ease of representation, let us assume that there are $N_a$ receiving channels in the azimuth direction and $N_e$ receiving channels in the elevation direction, which implies $n=1,2,\dots ,N_a·N_e$. The inter-pulse demodulated aliased echoes can then be written in the following matrix form:

$$\tilde{\mathit{R}}(t,\eta )=\left(\begin{array}{cccc}{\tilde{r}}_{1,1}(t,\eta )& {\tilde{r}}_{1,2}(t,\eta )& \dots & {\tilde{r}}_{1,N_e}(t,\eta )\\ {\tilde{r}}_{2,1}(t,\eta )& {\tilde{r}}_{2,2}(t,\eta )& \dots & {\tilde{r}}_{2,N_e}(t,\eta )\\ ⋮& ⋮& \ddots & ⋮\\ {\tilde{r}}_{N_a,1}(t,\eta )& {\tilde{r}}_{N_a,2}(t,\eta )& \dots & {\tilde{r}}_{N_a,N_e}(t,\eta )\end{array}\right)$$

(13)

where ${\tilde{r}}_{k,l}(t,\eta )$ denotes the echo data received by the k-th azimuth channel and the l-th elevation channel after inter-pulse demodulation.

After inter-pulse demodulation, the Doppler frequency shift of the signal from the m-th transmitting antenna can be written as

$$▵f_{d,p}={\displaystyle \frac{p}{N}}{F}_a,p=⌊{\displaystyle \frac{m-1}{M}}⌋\in [0,N-1]$$

(14)

In other words, based on the Doppler frequency shifts of the aliased echoes, the aliased echoes can be divided into N different clusters. $\mathit{g}(t,\eta )=\{g_1(t,\eta ),g_2(t,\eta ),\dots ,g_N(t,\eta )\}$, with each cluster consisting of M intra-pulse modulation signals. Furthermore, by transforming the echo data into the Doppler frequency domain, Equation (12) can be written as

$$\tilde{\mathit{R}}(t,f_a)=\mathit{A}·\left(\begin{array}{cccc}{G}_1^1(t,f_a)& G_1^2(t,f_a)& \dots & G_1^{N_e}(t,f_a)\\ G_2^1(t,f_a)& G_2^2(t,f_a)& \dots & G_2^{N_e}(t,f_a)\\ ⋮& ⋮& \ddots & ⋮\\ G_N^1(t,f_a)& G_N^2(t,f_a)& \dots & G_N^{N_e}(t,f_a)\end{array}\right)$$

(15)

where $\mathit{A}$ represents the azimuth steering vector matrix, while $G_p^l(t,f_a)$ denotes the p-th echo signal cluster received by the l-th elevation channel.

Next, to separate the different signal clusters, it is essential to perform Doppler sub-band division. The corresponding k-th bandpass filters are given by

$$H_k\left(f_a\right)=\left\{f_a|-{\displaystyle \frac{F_a}{2}}+{\displaystyle \frac{(k-1)F_a}{N}}\le f_a<-{\displaystyle \frac{F_a}{2}}+{\displaystyle \frac{k}{N}}{F}_a\right\}$$

(16)

The relationship between the Doppler beam pointing angle and Doppler frequency for echo cluster p in the l-th Doppler sub-band is denoted as

$$\sin \left({\theta }_p\left(f_a\right)\right)={\displaystyle \frac{\lambda }{2v}}\left(f_a-\Delta f_{d,p}+M_p\left(l\right)F_a\right)$$

(17)

where $M_p\left(l\right)=\left\{\begin{array}{c}1,p>l-1\hfill \\ 0,p\le l-1\hfill \end{array}\right.$ refers to the ambiguity number [12] , $\theta$ is the azimuth squint angle, $\lambda$ denotes the wavelength of the transmitted signal, and v denotes the velocity of the airborne platform.

Then, the matrix representing the azimuth steering vector for azimuth DBF is denoted as

$$\mathit{A}=\left[{\mathit{a}}_1\left(f_a\right),{\mathit{a}}_2\left(f_a\right),\dots ,{\mathit{a}}_N\left(f_a\right)\right]$$

(18)

where the azimuth steering vector $a_p$ corresponding to echo cluster p can be formulated as

$${\mathit{a}}_p={\left[e^{j{\mu }_0\left({\theta }_p\left(f_a\right)\right)},e^{j{\mu }_1\left({\theta }_p\left(f_a\right)\right)},\dots ,e^{j{\mu }_{N_a-1}\left({\theta }_p\left(f_a\right)\right)}\right]}^{\mathrm{T}}$$

(19)

where ${\mu }_k\left({\theta }_p\left(f_a\right)\right)=2\pi k{d}_a\sin {\theta }_p\left(f_a\right)/\lambda$, while $d_a$ denotes the interval between azimuth sub-apertures. Consequently, the weight vector matrix for azimuth DBF can be calculated as

$${\mathit{W}}^a={\left[{\mathit{w}}_1^a\left(f_a\right),{\mathit{w}}_2^a\left(f_a\right),\dots ,{\mathit{w}}_N^a\left(f_a\right)\right]}^{\mathrm{T}}={\left({\mathit{A}}^{\mathrm{H}}\mathit{A}\right)}^{-1}{\mathit{A}}^{\mathrm{H}}$$

(20)

The division of Doppler sub-bands and the corresponding azimuth DBF are shown in Figure 4. Finally, by merging the sub-bands, different signal clusters can be obtained. Its time-domain form can be written as

$$\begin{array}{cc}\hfill \mathit{G}(t,\eta )& ={\mathcal{F}}_a^{-1}\{{\mathit{W}}_a·\tilde{\mathit{R}}(t,f_a)\}\hfill \\ \hfill & =\left(\begin{array}{cccc}{G}_1^1(t,\eta )& G_1^2(t,\eta )& \dots & G_1^{N_e}(t,\eta )\\ G_2^1(t,\eta )& G_2^2(t,\eta )& \dots & G_2^{N_e}(t,\eta )\\ ⋮& ⋮& \ddots & ⋮\\ G_N^1(t,\eta )& G_N^2(t,\eta )& \dots & G_N^{N_e}(t,\eta )\end{array}\right)\hfill \end{array}$$

(21)

where ${\mathcal{F}}_a^{-1}$ denotes the inverse Fourier transform in the azimuth direction.

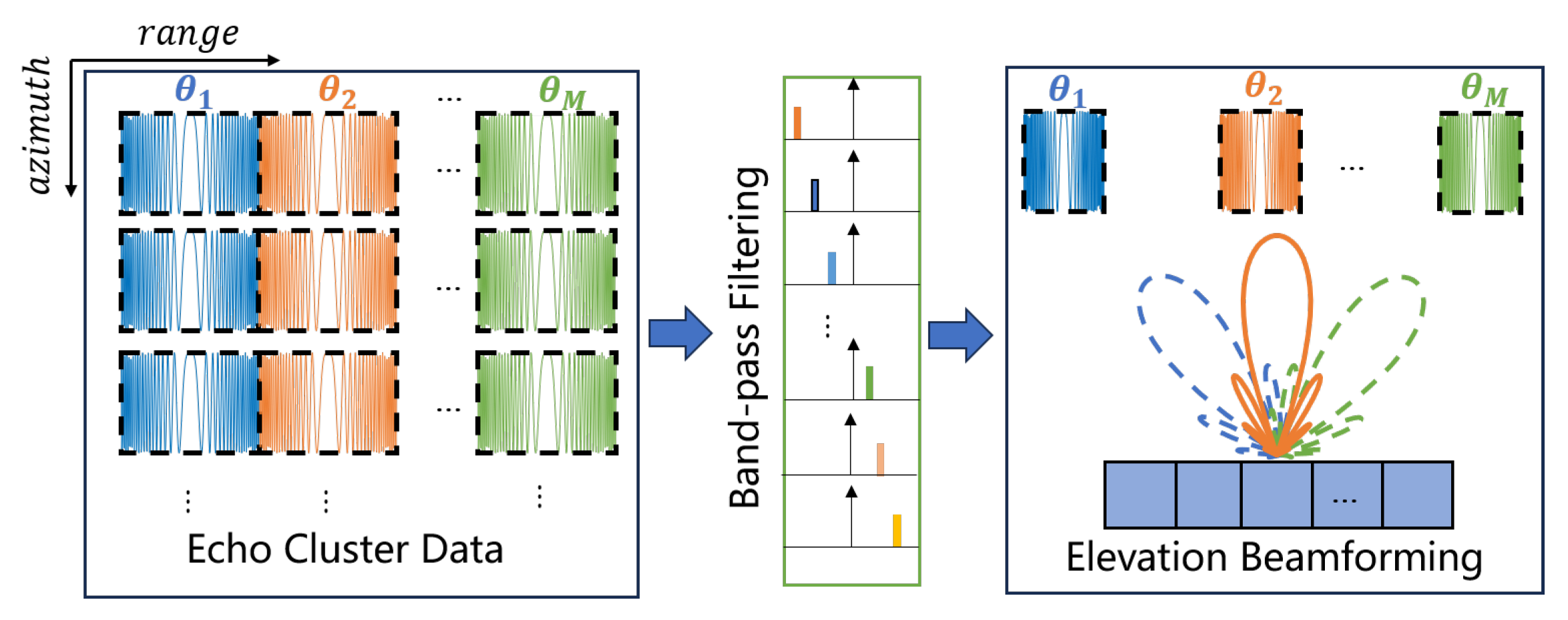
2.2.2. Operation in the Elevation Direction

Subsequently, multiple elevation channels will be utilized to construct corresponding beamformers for further processing of the initially separated echo cluster signals.

The ultimate aim of echo separation is to distinguish the scattered echoes corresponding to different transmitted waveforms. The desired scattered echo for the m-th transmitted waveform can be written as

$${\widehat{r}}_m(t,\eta )={\widehat{h}}_m(t,\eta ){\otimes }_t{s}_m\left(t\right)={\widehat{h}}_m(t,\eta ){\otimes }_t\left({\mathit{\varphi }}_q^{\mathrm{T}}\mathit{s}\left(t\right)\right)$$

(22)

where ${\widehat{h}}_m(t,\eta )={\sigma }_m\delta \left(t-{\tau }_m\right)\exp \left(-j2\pi f_c{\tau }_m\right)$, while ${\sigma }_m$ and ${\tau }_m$ represent the corresponding backscattering coefficient and the round-trip time delay of the waveform, respectively (the correspondence among p, q, and m is given by Equation (2)).

Since each intra-pulse modulation signal consists of M sub-pulses, if the swath is sufficiently wide, there will be M different directions of arrival (DOAs). This implies that a minimum of M channels need to be deployed in the elevation direction to construct an effective beamformer.

According to the correspondence among p, q, and m in (2), the m-th signal represents the q-th intra-pulse modulation signal located in the p-th cluster. Therefore, (22) can be written as

$$\begin{array}{cc}\hfill {\widehat{r}}_m(t,\eta )={\widehat{r}}_q^p(t,\eta )& ={\widehat{h}}_q^p(t,\eta ){\otimes }_t\left({\mathit{\varphi }}_q^{\mathrm{T}}\mathit{s}\left(t\right)\right)\hfill \\ & =\sum _{k=1}^M{\varphi }_{q,k}·{\widehat{h}}_q^p(t,\eta ){\otimes }_{t}s(t-(k-1)T_s)\hfill \\ & =\sum _{k=1}^M{\widehat{r}}_{q,k}^p(t,\eta )\hfill \end{array}$$

(23)

where ${\widehat{r}}_{q,k}^p(t,\eta )={\varphi }_{q,k}·{\widehat{h}}_q^p(t,\eta ){\otimes }_{t}s(t-(k-1)T_s)$, while k denotes the k-th sub-pulse.

Then the p-th echo cluster signal $G_p(t,\eta )={[G_p^1(t,\eta ),G_p^2(t,\eta ),\dots ,G_p^{N_e}(t,\eta )]}^T$ in (21) can be written as

$${\mathit{G}}_p(t,\eta )=\mathit{V}·\left(\begin{array}{cccc}{\widehat{r}}_{1,1}^p(t,\eta )& {\widehat{r}}_{1,2}^p(t,\eta )& \dots & {\widehat{r}}_{1,M}^p(t,\eta )\\ {\widehat{r}}_{2,1}^p(t,\eta )& {\widehat{r}}_{2,2}^p(t,\eta )& \dots & {\widehat{r}}_{2,M}^p(t,\eta )\\ ⋮& ⋮& ⋮& ⋮\\ {\widehat{r}}_{M,1}^p(t,\eta )& {\widehat{r}}_{M,2}^p(t,\eta )& \dots & {\widehat{r}}_{M,M}^p(t,\eta )\end{array}\right)$$

(24)

Given that the look angles corresponding to the M signal segments are $\mathit{\theta }\left(t\right)=\left\{{\theta }_1\left(t\right),{\theta }_2\left(t\right),\dots ,{\theta }_M\left(t\right)\right\}$, the elevation steering vector matrix associated with them can be derived as

$$\left\{\begin{array}{cc}\mathit{V}\hfill & =\left[{\mathit{v}}_1\left(t\right),{\mathit{v}}_2\left(t\right),\dots ,{\mathit{v}}_M\left(t\right)\right]\hfill \\ {\mathit{v}}_l\left(t\right)\hfill & ={\left[e^{j{\mu }_0\left({\theta }_s\left(t\right)\right)},e^{j{\mu }_1\left({\theta }_s\left(t\right)\right)},\dots ,e^{j{\mu }_{N_e-1}\left({\theta }_s\left(t\right)\right)}\right]}^{\mathrm{T}}\hfill \end{array}\right.$$

(25)

where ${\mu }_k\left({\theta }_q\left(t\right)\right)=2\pi k{d}_e\sin \left({\theta }_q\left(t\right)\right)/\lambda$, $d_e$ is the elevation channel spacing, and s and q represent the intended signal and the $M-1$ interference signal segments, respectively.

To ensure the performance of elevation DBF, it is necessary to construct multiple bandpass filters to reduce pulse extension loss (PEL) [18,19,20]. In practice, the bandpass filters can be replaced by matched filters in the range–frequency domain. The i-th constructed bandpass filter can be expressed as

$$H_i\left(f_r\right)=\left\{f_r|-{\displaystyle \frac{B_r}{2}}+{\displaystyle \frac{(i-1)B_r}{L}}\le f_r<-{\displaystyle \frac{B_r}{2}}+{\displaystyle \frac{i}{L}}{B}_r\right\}$$

(26)

where $B_r$ is the signal bandwidth, while L represents the number of bandpass filters. The signal pulse width is reduced after processing by the bandpass filters, thereby enhancing the effectiveness of DBF processing and aiding in the effective suppression of interference signals.

To suppress interference signals from different DOAs, elevation DBF processing is required upon receiving the signal, and the corresponding weighting vector matrix is derived as

$${\mathit{W}}^e=\left[{\mathit{w}}_1^e\left(t\right),{\mathit{w}}_2^e\left(t\right),\dots ,{\mathit{w}}_{M-1}^e\left(t\right)\right]={\left({\mathit{V}}^{\mathrm{H}}\mathit{V}\right)}^{-1}{\mathit{V}}^{\mathrm{H}}$$

(27)

The bandpass filter in the range–frequency domain and the associated elevation DBF are shown in Figure 5. After elevation DBF processing, the sub-pulse signals carrying intra-pulse phases are extracted, and the result can be calculated as

$${\mathit{E}}_p(t,\eta )={\mathit{W}}^e·{\mathit{G}}_p(t,\eta )$$

(28)

Due to the time delays $T_s$ between different sub-pulses, it is necessary to ensure signal alignment in the fast-time domain through time shifting. The corresponding time-shift matrix is

$$\zeta =diag(1,\exp \left(j2\pi f_r{T}_s\right),\dots ,\exp \left(j2\pi (M-1)f_r{T}_s\right))$$

(29)

where $f_r$ represents the range–frequency domain, while $diag(·)$ represents a diagonal matrix.

Typically, the time shift is implemented in the frequency domain, and the result after time shifting is

$$\begin{array}{cc}\hfill {\mathit{E}}_p(t,\eta )& ={\mathcal{F}}_r^{-1}\left\{{\mathit{E}}_p(f_r,\eta )·\zeta \right\}\hfill \\ \hfill & =\mathsf{\Phi }·diag({\widehat{r}}_{1,1}^p,{\widehat{r}}_{2,1}^p,\dots ,{\widehat{r}}_{M,1}^p)\hfill \end{array}$$

(30)

where ${\mathcal{F}}_r^{-1}$ denotes the inverse Fourier transform in the range direction.

Finally, by multiplying with the inverse transform of the intra-pulse phase matrix, the completely separated echo signals within each cluster can be obtained. It can be calculated as

$${\widehat{\mathit{E}}}_p(t,\eta )={\mathsf{\Phi }}^{-1}·{\mathit{E}}_p(t,\eta )=diag({\widehat{r}}_{1,1}^p,{\widehat{r}}_{2,1}^p,\dots ,{\widehat{r}}_{M,1}^p)$$

(31)

3. Results

To comprehensively evaluate the imaging capability and echo separation performance of the proposed scheme, this section provides simulation experiments in accordance with the system parameters detailed in

Table 1. Simulation system parameters.

Parameters	Value
Orbit height	600 Km
Carrier frequency	9.6 GHz
Sub-pulse width $T_s$	20 µ$\mathrm{s}$
Bandwidth $B_r$	40 MHz
PRF	2658 Hz
Antenna length in azimuth	12 m
Antenna length in elevation	0.38 m
Number of channels in azimuth $N_a$	2
Number of channels in elevation $N_e$	2
Number of transmitted waveforms $M_s$	4
Doppler bandwidth $B_a$	2215 Hz
SNR	8 dB

. The simulation was carried out under additive white Gaussian noise (AWGN) with a signal-to-noise ratio (SNR) of 8 dB. The simulations are organized into two distinct parts: (1) a point target simulation, which is used to quantitatively analyze key performance metrics such as the Peak Sidelobe Ratio (PSLR) and the Integrated Sidelobe Ratio (ISLR), and (2) a distributed scene simulation, aimed at verifying the scheme’s adaptability in complex terrain environments. 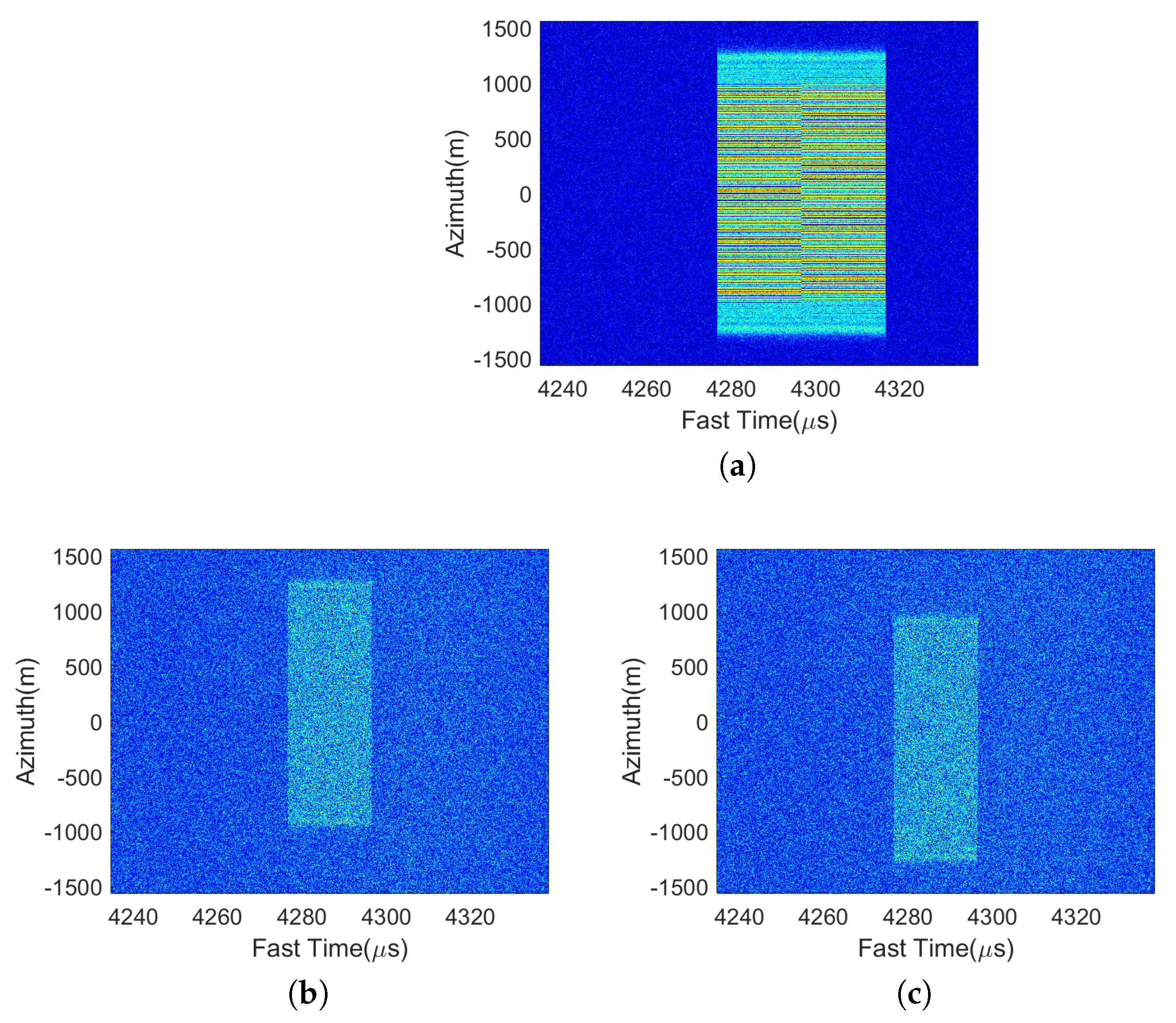Through these experiments, the proposed method is evaluated in depth for its practicality and potential for implementation from multiple perspectives.

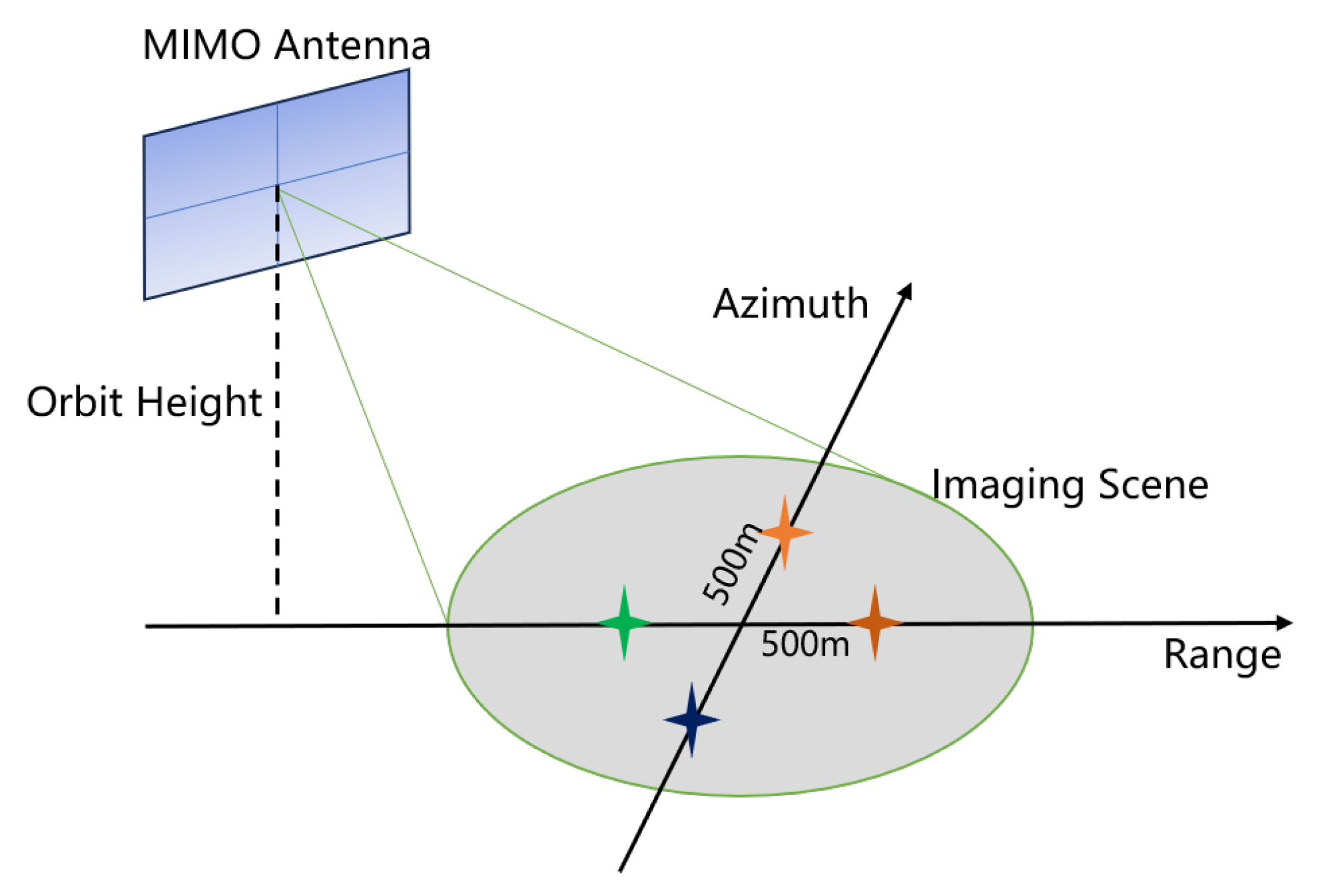
3.1. Point Target Simulation

As shown in Table 1, two channels are arranged in both the elevation and azimuth directions to meet the minimum number of channels required for two-dimensional DBF. Additionally, the intra-pulse coding matrix is a $2\times 2$ matrix, with

$$\mathsf{\Phi }=\left(\begin{array}{cc}\exp \left(j{\displaystyle \frac{7\pi }{12}}\right)\hfill & \exp \left(j{\displaystyle \frac{\pi }{3}}\right)\hfill \\ \exp \left(j{\displaystyle \frac{2\pi }{3}}\right)\hfill & \exp \left(j{\displaystyle \frac{5\pi }{12}}\right)\hfill \end{array}\right)$$

(32)

To more intuitively demonstrate the effect of echo separation, we have set four point-target coordinates, (0, 500 m), (0, −500 m), (500 m, 0), and (−500 m, 0), as shown in Figure 6. Each of the four waveforms is directed toward a different target to simulate signal separation in a multi-waveform transmission scenario.

Figure 7 shows the two-dimensional spectrum of aliased echoes and azimuth-processed echo clusters. In Figure 7a, it can be seen that the spectra of the two echo clusters overlap and cannot be directly separated by simple bandpass filtering. Due to different Doppler centers in the azimuth frequency domain after inter-pulse demodulation, the azimuth DBF technique can be used to effectively separate the aliased echoes. The two-dimensional spectra of the separated echo clusters are shown in Figure 7b and Figure 7c, respectively.

The separated echo clusters after azimuth DBF processing consist of two types of signals, each containing two sub-pulses. Figure 8 displays the results of echo signal cluster 1 and the processing outcomes in the elevation direction. By employing bandpass filtering in the range–frequency domain and further separation using elevation DBF, followed by intra-pulse demodulation, completely separated single-pulse signals can be obtained. Waveforms 1 and 2 are shown in Figure 8b and Figure 8c, respectively.

Next, the Chirp Scaling (CS) imaging algorithm [24] is employed to achieve point target focusing. Figure 9 presents the upsampled results of point targets corresponding to the four waveforms. The clear focusing of the point targets demonstrates the effectiveness of the proposed scheme in echo separation. Additionally, the figure displays the PSLR and ISLR for the four waveforms, providing a quantitative assessment of the imaging performance. The results indicate that in the azimuth direction, the PSLR for all four waveforms is approximately −13.18 dB, aligning with theoretical expectations. Similarly, in the range direction, the PSLR for the four waveforms is around −13.25 dB, which is also consistent with theoretical predictions.

3.2. Distributed Scene Simulation

To further evaluate the effectiveness of the proposed scheme, Figure 10 presents the simulation results of multi-scene imaging. Figure 10a and Figure 10b, respectively, show the scenes illuminated by waveforms 1 and 2, as well as waveforms 3 and 4. Figure 10c and Figure 10d display the imaging results of scene 1 using the OFDM [16,17] and MSTS [21] schemes, respectively. Compared with the original images, the processed images still exhibit noticeable blurring, primarily due to the insufficient number of elevation channels, which prevents the elevation-direction DBF from functioning properly. Figure 10e,f illustrate the multi-scene imaging results of the proposed scheme. The images produced by the proposed scheme demonstrate excellent focusing performance, exhibiting only a minor reduction in contrast relative to the original images.

The imaging results confirm the high fidelity of the proposed scheme to the original scenes, validating its effectiveness. Even under limited system resources, such as a reduced number of elevation channels, the proposed scheme maintains a high interference energy suppression ratio, thereby ensuring superior imaging quality.

4. Discussion

To validate the efficacy of the proposed scheme, this section provides the corresponding analysis and simulation results. The different MIMO SAR systems discussed transmit the same number of waveforms to ensure that the discussion is meaningful and comparable.

4.1. System Cost

The proposed scheme performs joint modulation of the transmitted signals across both the inter-pulse and intra-pulse dimensions. During the data processing stage, the received aliased echoes are demodulated and separated using azimuth DBF. By adopting a three-dimensional waveform co-design in the spatial, temporal, and frequency domains, the scheme ensures effective echo separation while significantly reducing system complexity. A detailed analysis is presented below from both the azimuth and elevation perspectives.

For system complexity in azimuth, the APC-based MIMO SAR schemes [19,21] typically require that $F_a$ satisfies $F_a>M_s{B}_{dop}$, where $M_s$ is the number of transmitted waveforms and $B_{dop}$ is the Doppler bandwidth. This condition ensures the separation of echoes at different Doppler centers using bandpass filters. However, higher PRF results in narrower swath width and higher downlink data rates. Rather than solely relying on bandpass filters, our approach deploys multiple channels in azimuth and uses azimuth DBF to cluster signals into different groups. Therefore, in the proposed scheme, the required PRF only needs to slightly exceed the Doppler bandwidth.

In terms of system complexity in elevation , traditional beamforming schemes [13,14,15,16,17,18] require more elevation channels ($M_e\ge 2M_s-1$) to ensure effective echo separation based on the least-squares algorithm. Additionally, the pulse width $M_s{T}_r$ increases with the number of transmitted waveforms, imposing higher demands on the antenna duty cycle. In contrast, our proposed scheme divides echo separation into azimuth and elevation DBF processing, sequentially handling aliased echoes, thereby reducing the requirement for elevation channels. The number of elevation channels needed is smaller ($M_e^{\prime }\ge M_s/N$), and the pulse width is also shorter ($M_s{T}_s/N$).

In summary, the proposed scheme optimizes resource usage by reducing the required number of channels and the pulse width while maintaining effective echo separation.

4.2. Computational Load

To evaluate the computational complexity of different schemes, the multiplications required for echo separation are a key factor.

In the field of MIMO SAR, for digital beamforming schemes based on orthogonal waveforms, computational complexity mainly arises from the matrix operations involved in digital beamforming and the bandpass filters [18,19]. For the multiplication of two matrices with dimensions of $M\times N$ and $N\times M$, the number of multiplications required is $M·N·M$. In addition, if the Gauss–Jordan method is employed for the inversion of an $M\times M$ matrix, the number of multiplications required is $M^3$. For bandpass filtering, if the number of bandpass filters is $N_B$ and the order of each filter is L, then the required number of multiplications is $N_B·L$.

For the traditional beamforming schemes, such as the OFDM beamforming scheme [16,17], echo separation primarily relies on bandpass filters in the range–frequency domain and elevation DBF. Assuming there are $N_B$ bandpass filters, each of order L, for $M_s$ transmitted waveforms, the lowest computational complexity is

$$T_1=\mathit{O}\left((2M_s-1)N_{B}L+3{\left(2M_s-1\right)}^3{N}_B\right)$$

(33)

where $\mathit{O}\left((2M_s-1)N_{B}L\right)$ is the computational cost required for the bandpass filters in the range–frequency domain, while $\mathit{O}\left(3{\left(2M_s-1\right)}^3{N}_B\right)$ is the computational cost required for the elevation DBF.

For the echo separation scheme based on the MSTS waveform, which is an extension of the STSO waveform, the corresponding computational complexity is reduced through spectral preprocessing and segmented synthesis, and it can be expressed as

$$T_2=\mathit{O}\left(M_s{N}_{B}L+3{M_s}^3{N}_B\right)$$

(34)

where $\mathit{O}\left(M_s{N}_{B}L\right)$ denotes the bandpass filtering operation and $\mathit{O}\left(3{M_s}^3{N}_B\right)$ denotes elevation DBF processing.

In the proposed scheme, echo separation is divided into two parts: the azimuth and elevation operations. During azimuth processing, the number of azimuth channels is N, while the number of bandpass filters in the Doppler frequency domain is N. In the elevation operation, the minimum number of elevation channels is $M_s/N$. Thus, the required minimum computational complexity is

$$T_3=\mathit{O}\left((NL+3N^3)N+\left({\displaystyle \frac{M_s}{N}}L+3{\displaystyle \frac{M_s^3}{N^3}}\right)N_B\right)$$

(35)

where $\mathit{O}\left((NL+3N^3)N\right)$ is the computational cost required for azimuth processing, while $\mathit{O}\left(\left({\displaystyle \frac{M_s}{N}}L+3{\displaystyle \frac{M_s^3}{N^3}}\right)N_B\right)$ is the computational cost required for elevation processing.

The comparison of computational complexity for $T_1,T_2,$ and $T_3$ is shown in Figure 11 and

Table 2. Comparison of computational complexity for different schemes.

Methods	Matrix Inversion	Weighted Vector	Bandpass Filters
OFDM [16,17]	$2{\left(2M_s-1\right)}^3{N}_B$	${\left(2M_s-1\right)}^3{N}_B$	$(2M_s-1)N_{B}L$
MSTS [21]	$2{\left(M_s\right)}^3{N}_B$	${\left(M_s\right)}^3{N}_B$	$M_s{N}_{B}L$
Proposed scheme	$2\left(N^4+{\displaystyle \frac{M_s^3}{N^3}}{N}_B\right)$	$\left(N^4+{\displaystyle \frac{M_s^3}{N^3}}{N}_B\right)$	$\left(N^2+{\displaystyle \frac{M_s}{N}}{N}_B\right)L$

. Table 2 presents the sources of computational complexity corresponding to different schemes. As can be seen, with the increase in the number of transmitted waveforms, the proposed method significantly reduces computational complexity. It is clear that the proposed scheme offers a significant reduction in complexity compared to the OFDM beamforming scheme. With the same number of transmitted waveforms, its computational complexity is also superior to that of the MSTS scheme, which becomes more pronounced when the number of transmitted waveforms is large. This makes it an excellent solution for situations requiring the transmission of multiple distinct waveforms.

4.3. Interference-to-Signal Ratio

The interference-to-signal ratio (ISR) [18] is a crucial indicator for measuring the efficiency of interference energy suppression. It is determined by the ratio of the power of the desired echo between other interfering echoes. The level of the ISR reflects the system’s ability to suppress interference signals and is a key parameter for evaluating echo separation performance.

Since the proposed scheme employs azimuth and elevation DBF to separate echoes, the analysis of the ISR is divided into two distinct parts. For the separation effect of azimuth DBF, processing is implemented in the azimuth–frequency domain, and thus the ISR for the p-th echo cluster can be denoted as

$${\mathrm{ISR}}_p^a\left(f_a\right)={\displaystyle \frac{{\displaystyle \sum _{k=1,k\ne p}^N}{\left|{\mathit{w}}_k^a\left(f_a\right){\mathit{a}}_p\left(f_a\right)\right|}^2}{{\left|{\mathit{w}}_p^a\left(f_a\right){\mathit{a}}_p\left(f_a\right)\right|}^2}}$$

(36)

Unlike azimuth DBF processing, the effectiveness of elevation DBF is influenced by the signal pulse width. Considering the bandpass filter defined in (26), the time corresponding to the filtered signal is

$$t_i=-{\displaystyle \frac{T_s}{2}}+{\displaystyle \frac{T_s}{2L}}+{\displaystyle \frac{(i-1)T_s}{L}}$$

(37)

Since the pulse width of the signal after bandpass filtering affects the entire segment of the echo, the entire segment of the echo after DBF processing will cause interference to the desired echo. Therefore, within each echo cluster, the ISR for the q-th intra-pulse coded signal is

$${\mathrm{ISR}}_q^e\left(t\right)={\displaystyle \frac{{\displaystyle \sum _{i=1}^L}{\displaystyle \sum _{k=1,k\ne q}^M}{\int }_{t_i-\frac{T_s}{2L}}^{t_i+\frac{T_s}{2L}}{\left|{\mathit{w}}_k^e\left(t\right){\mathit{v}}_q\left(t\right)\right|}^{2}dt}{{\displaystyle \sum _{i=1}^L}{\int }_{t_i-\frac{T_s}{2L}}^{t_i+\frac{T_s}{2L}}{\left|{\mathit{w}}_q^e\left(t\right){\mathit{v}}_q\left(t\right)\right|}^{2}dt}}$$

(38)

Taking into account the processing effects of two-dimensional DBF, the ISR for the m-th waveform can be obtained as

$${\mathrm{ISR}}_m\left(t\right)=\mathrm{I}{\mathrm{SR}}_q^e\left(t\right)+{\displaystyle \frac{{\mathrm{ISR}}_p^a·{\displaystyle \sum _{i=1}^L}{\displaystyle \sum _{k=1}^M}{\int }_{t_i-\frac{T_s}{2L}}^{t_i+\frac{T_s}{2L}}{\left|{\mathit{w}}_k^e\left(t\right){\mathit{v}}_q\left(t\right)\right|}^2}{{\displaystyle \sum _{i=1}^L}{\int }_{t_i-\frac{T_s}{2L}}^{t_i+\frac{T_s}{2L}}{\left|{\mathit{w}}_q^e\left(t\right){\mathit{v}}_q\left(t\right)\right|}^{2}dt}}$$

(39)

with the first term being the residual interference arising from the elevation-direction processing, and the second term originating from the joint processing of other echo clusters.

The comparison of the ISR for the two schemes is shown in Figure 12. Notably, the proposed scheme deploys two channels in both the elevation and azimuth directions, whereas the OFDM beamforming scheme deploys four channels in the elevation direction. As seen in Figure 12, the ISR of the proposed scheme is approximately −32 dB, which meets the requirements for spaceborne MIMO SAR imaging and significantly outperforms the OFDM beamforming method [16,17]. In fact, when four waveforms need to be transmitted, the latter scheme requires at least seven channels in the elevation direction; otherwise, the LS beamforming scheme will fail. Clearly, simulations demonstrate that the proposed scheme can maintain effective interference energy suppression even with a limited number of channels.

To more intuitively demonstrate the interference energy suppression capability of the proposed scheme, we compared the one-dimensional echo separation results for a single point target using different schemes when transmitting four types of waveforms. The simulation was conducted under an SNR of 8 dB, and the results are shown in Figure 13.

In Figure 13a, the red box indicates the desired signal segment, while the yellow box highlights the interference signal segment. In the simulation results of the OFDM-based scheme, the interference signal is not effectively suppressed, which would lead to blurring in the SAR image, as shown in Figure 13b. Furthermore, for the MSTS-based scheme, although the interference energy is reduced to some extent, in distributed scenarios, the cumulative effect of blur energy can still degrade image quality, as illustrated in Figure 13c.

In contrast, the proposed scheme reduces the interference signal segment that needs to be processed at each stage through multiple operations in both the azimuth and elevation directions, thereby lowering the requirement for the number of channels. As clearly seen in Figure 13d, the interference suppression performance of the proposed scheme is significantly superior to that of the two aforementioned schemes.

5. Conclusions

This paper designs a novel inter–intra-pulse phase coding scheme and proposes a new azimuth–elevation joint processing method to tackle the echo separation problem in MIMO SAR systems. The designed scheme leverages the degrees of freedom in both the Doppler and spatial domains to ensure effective separation of aliased echoes. Compared to current orthogonal waveform beamforming methods, the primary advantages of proposed scheme are as follows:

1.

Better Interference Suppression: During DBF processing, the number of interference segments to be handled is fewer. This ensures good interference energy suppression even in MIMO SAR systems with limited channels.

2.

Reduced Computational Load: In some cases, the minimum computational resources required are lower, which means less demanding hardware requirements for MIMO SAR systems.

3.

Lower Duty Cycle Requirements: For the same number of transmitted waveforms, the proposed scheme requires fewer sub-pulses, resulting in lower duty cycle requirements for the transmitting antenna.

Simulation results demonstrate that the proposed scheme offers significant advantages in interference suppression, imaging quality, and system flexibility, providing valuable insights for the design and implementation of spaceborne MIMO SAR systems. The proposed scheme is particularly suitable for low-cost SAR systems with multiple modes and scenes [4], which utilize the elevation degree of freedom for interferometric measurements [25]. However, channel phase mismatches [19] and terrain undulation [26] may affect the actual performance of the SAR system. Additionally, the proposed scheme is highly reconfigurable and remains effective for other waveforms, such as the STSO [13,14], OFDM [16,17], or SPC [18] waveforms.