Identification of Non-Photosynthetic Vegetation Fractional Cover via Spectral Data Constrained Unmixing Algorithm Optimization
Abstract
Highlights
- The optimized traditional non-photosynthetic vegetation cover inversion models were setup by incorporating spatial heterogeneity through covariance matrix integration, combined with spectral phenological weights.
- The optimized model implements spectral convolution to align hyperspectral endmembers with multispectral sensor characteristics, and the integration of spatial heterogeneity analysis has significantly improved the accuracy of non-photosynthetic vegetation detection, which has been implemented and validated in the arid regions of northwest China.
- This study addresses the limitation where spectral discrepancies emerge between different regions during the identification of non-photosynthetic vegetation cover.
- The optimized non-photosynthetic vegetation identification model and spectral dataset enable dynamic long-term monitoring of non-photosynthetic vegetation, providing critical insights into the assessment of vegetation ecological health in arid and semi-arid regions under global warming.
Abstract
1. Introduction
2. Datasets and Methods
2.1. Data Source
2.1.1. Satellite Data
2.1.2. UAV Data
2.1.3. Observed Field Data
2.2. Methods
2.2.1. Spectral Indexes
2.2.2. Optimized Spectral Mixture Analysis Model
3. Results
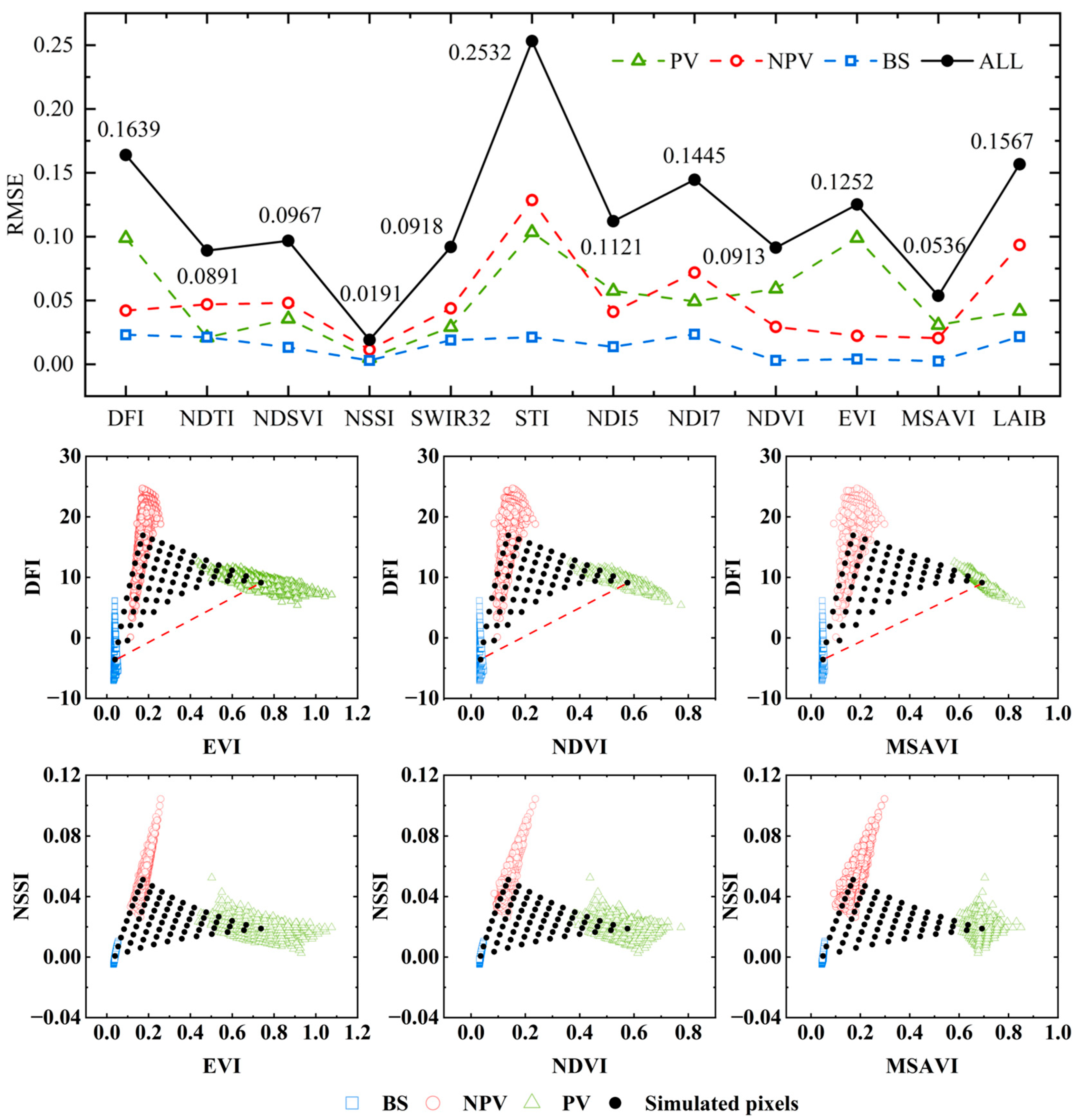
3.1. Optimization of Vegetation Index
3.2. Calibration and Verification
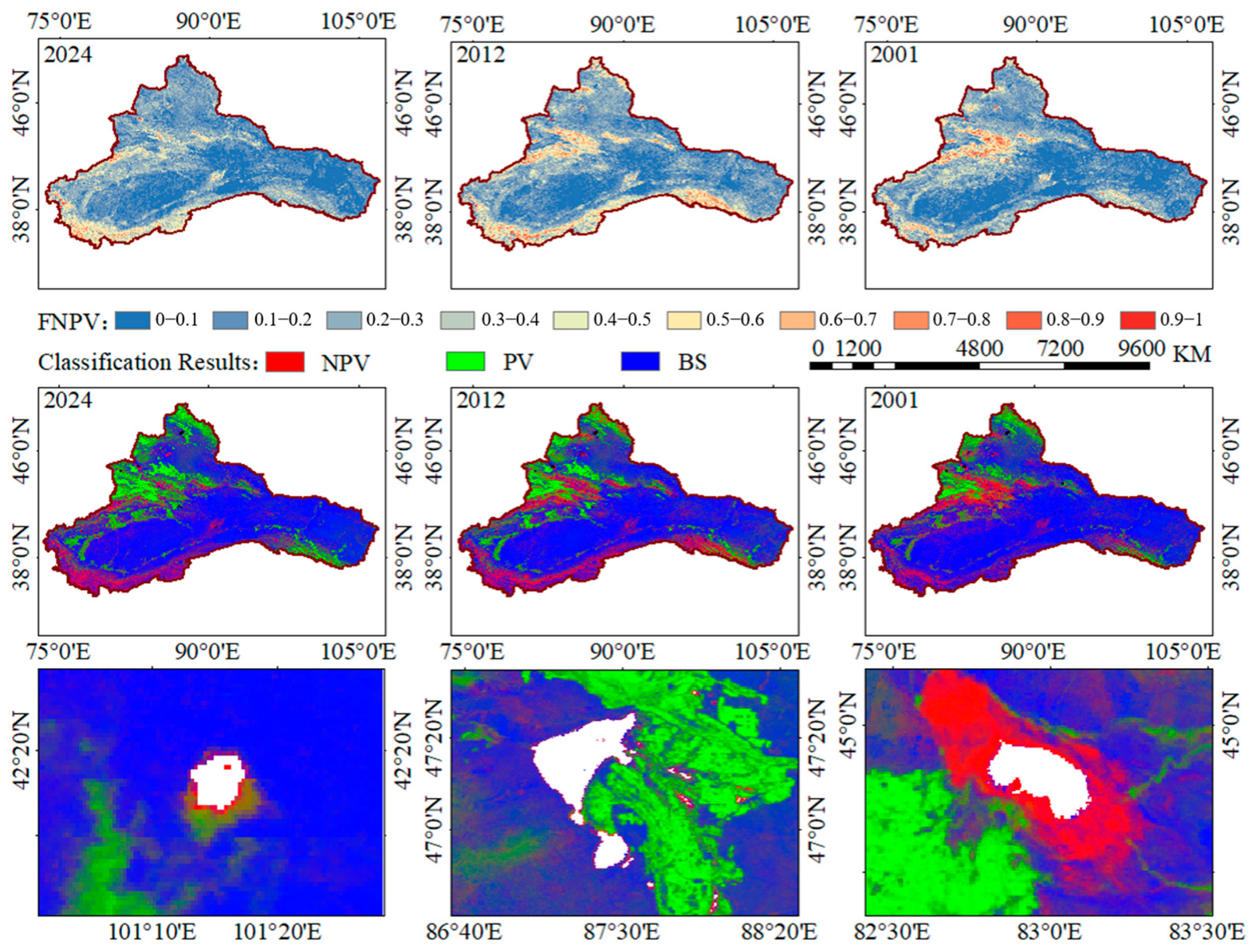
3.3. Inversion Results
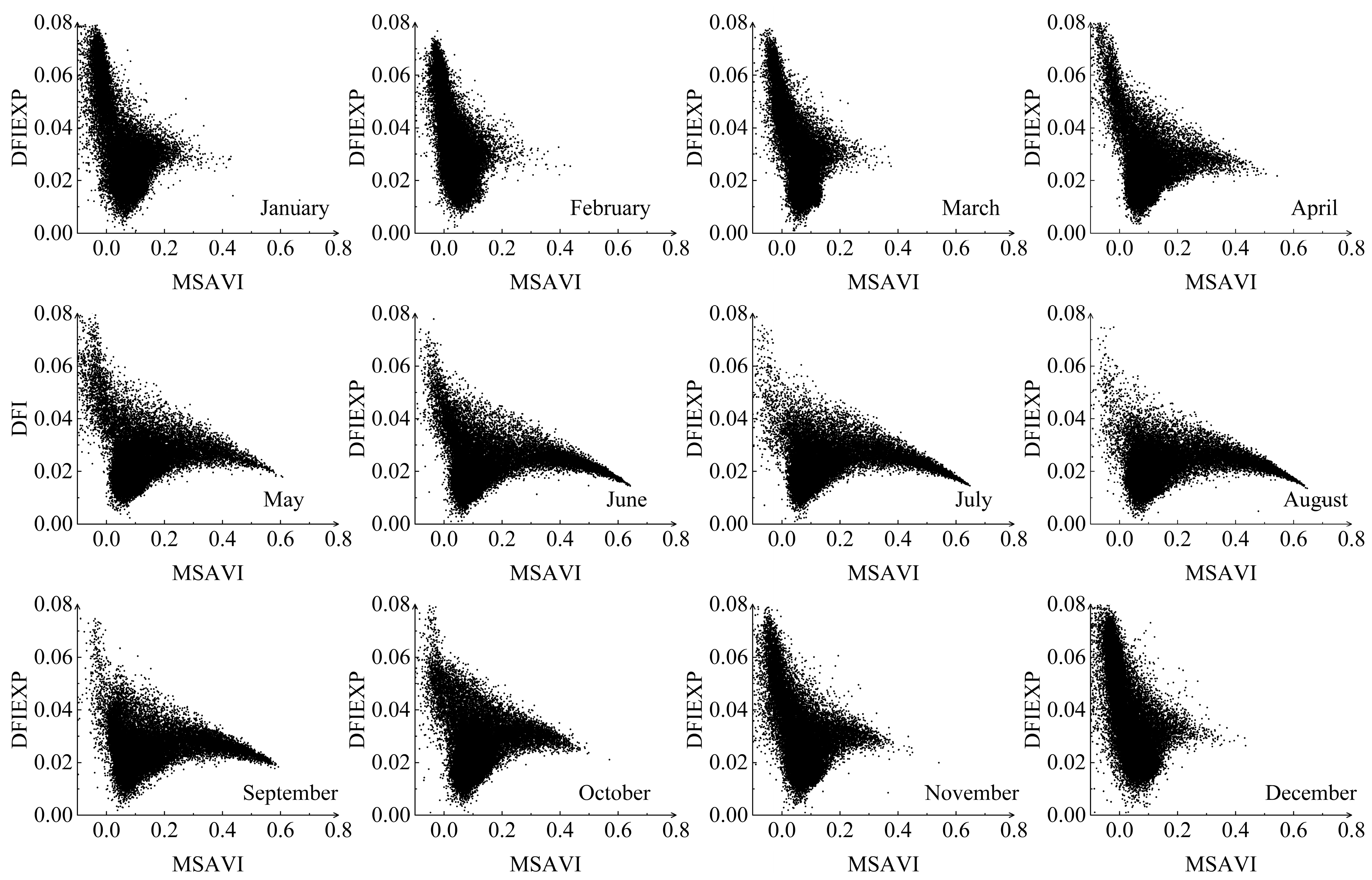
3.4. Optimization of Spectral Constraint Weights for Key Phenological Stages
4. Discussion
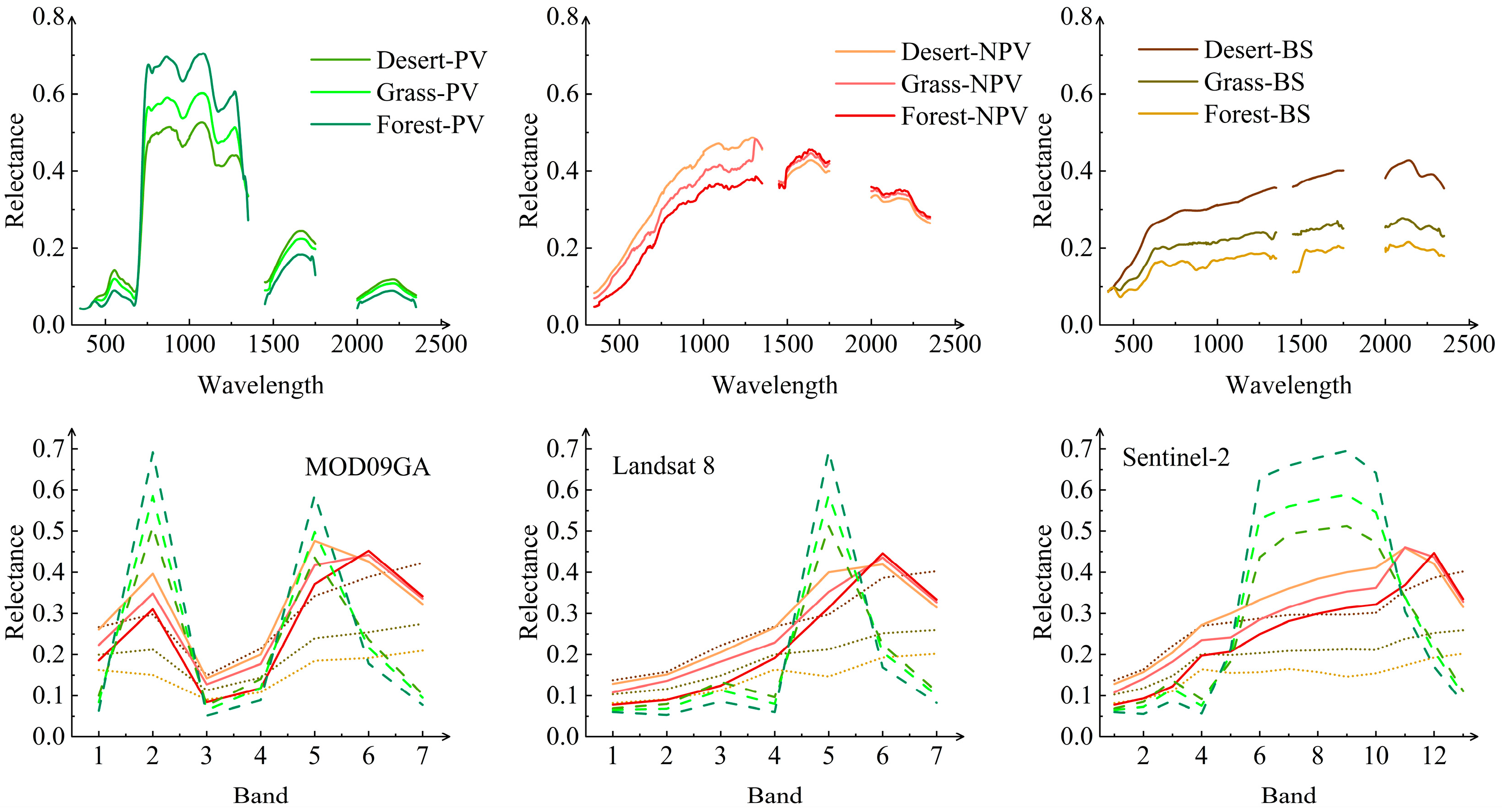
4.1. Development of a Spectral Angle Mapper (SAM) Model Based on Multiple Ecoregions
4.2. Comparison After Model Optimization
4.3. Spatial Block Validation of Model Performance
4.4. Necessity of PV Indices Further Examination
5. Conclusions
- (1)
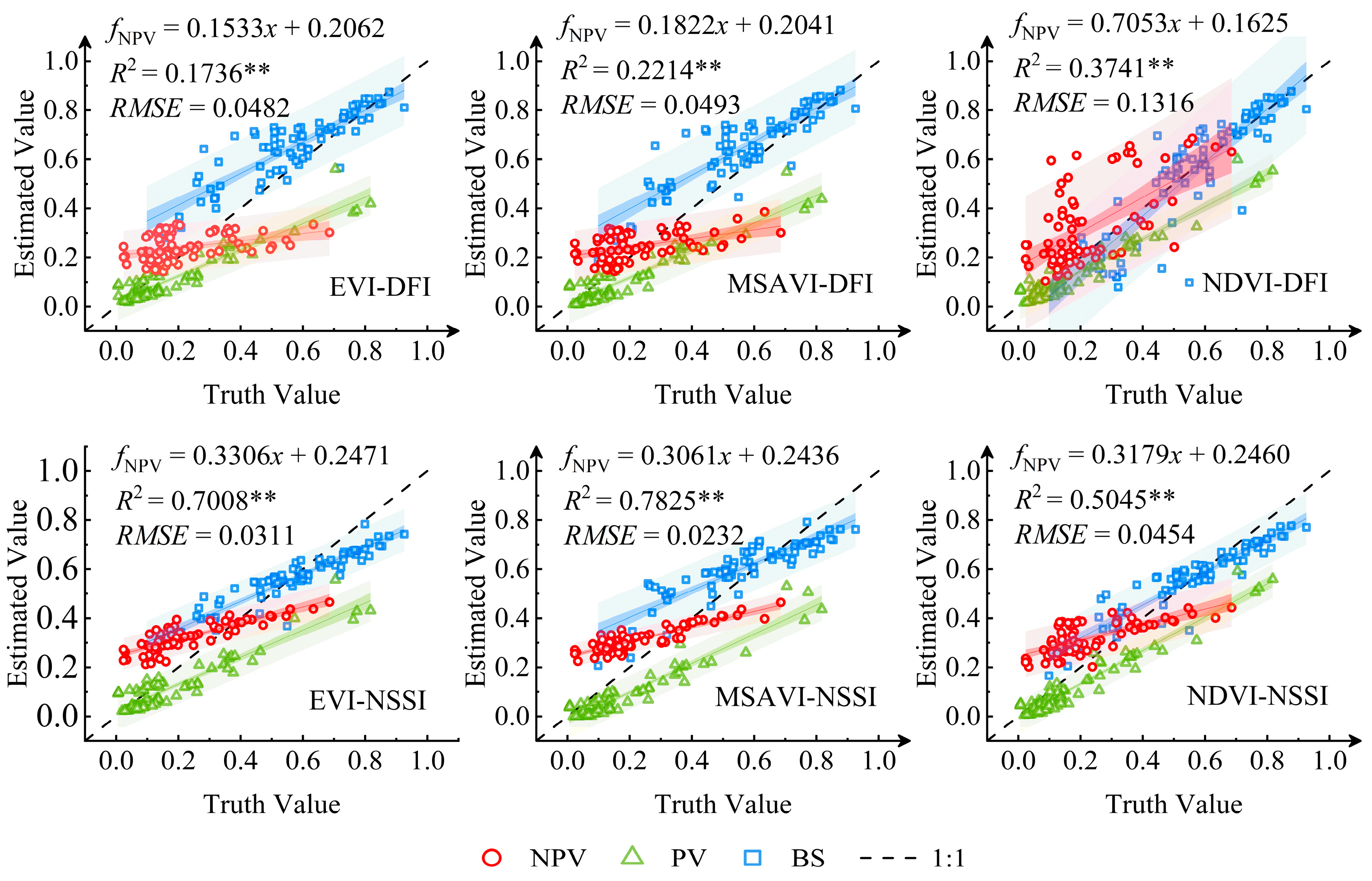
- The incorporation of spatial heterogeneity analysis and additional field spectral matrix information into the traditional model significantly improved inversion accuracy by better aligning with actual conditions. The optimized model demonstrated enhanced performance with an R2 of 0.7825 and RMSE of 0.0232, confirming the effectiveness of the model optimization. Compared to traditional spectral mixture analysis models, the incorporation of spatial heterogeneity analysis significantly enhances NPV detection accuracy, providing guidance for ecological health assessments under climate change in arid and semi-arid area.
- (2)
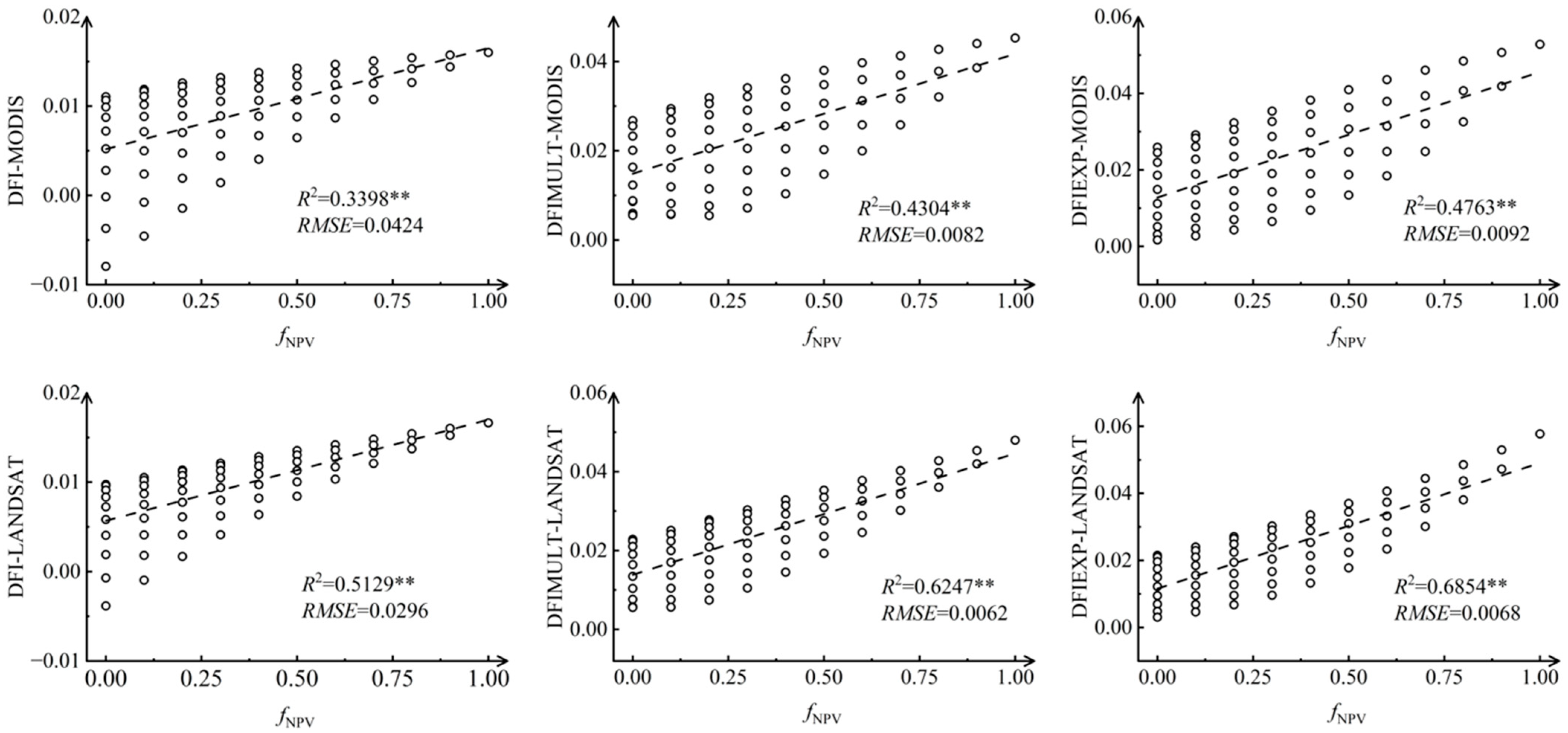
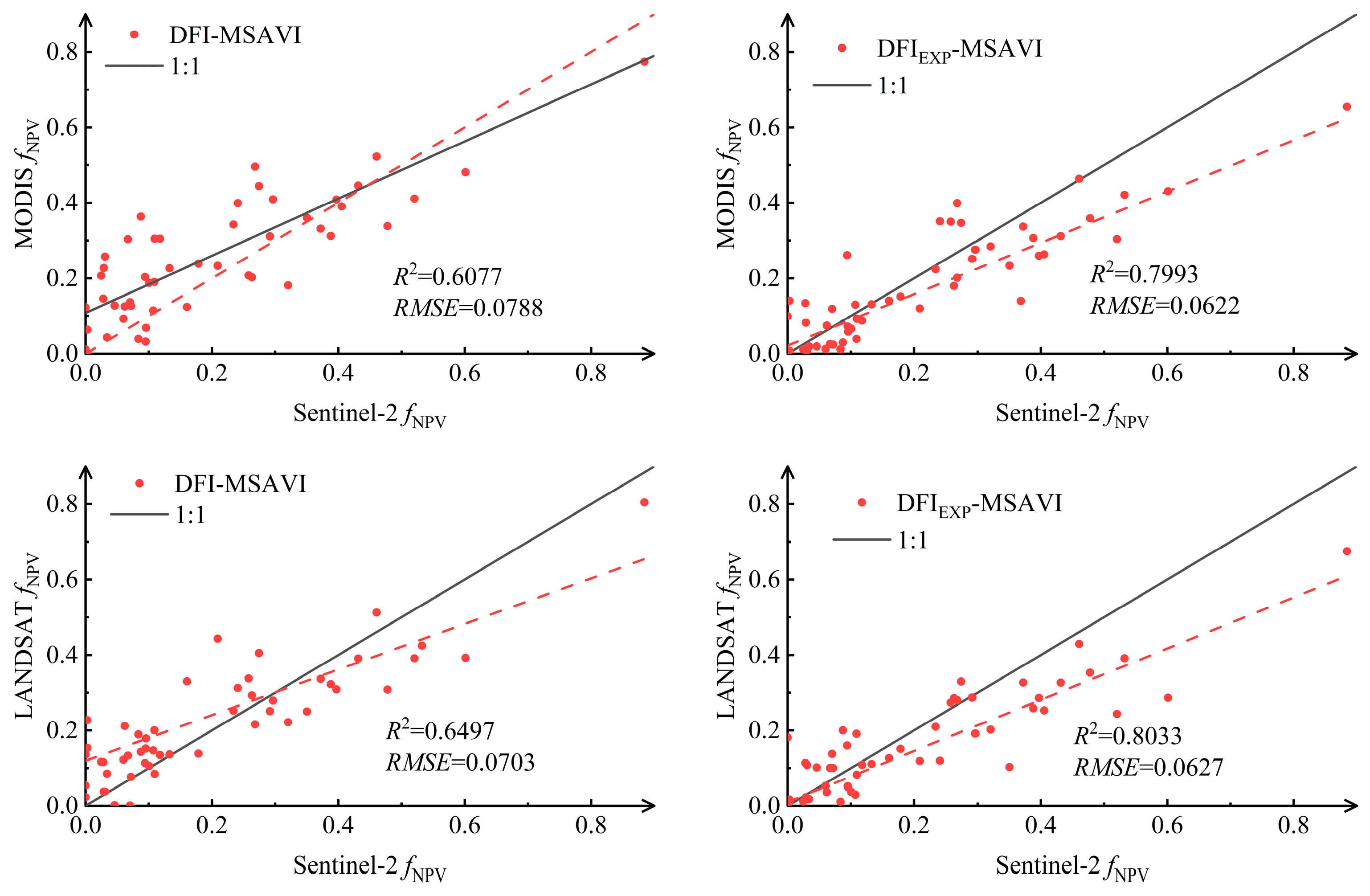
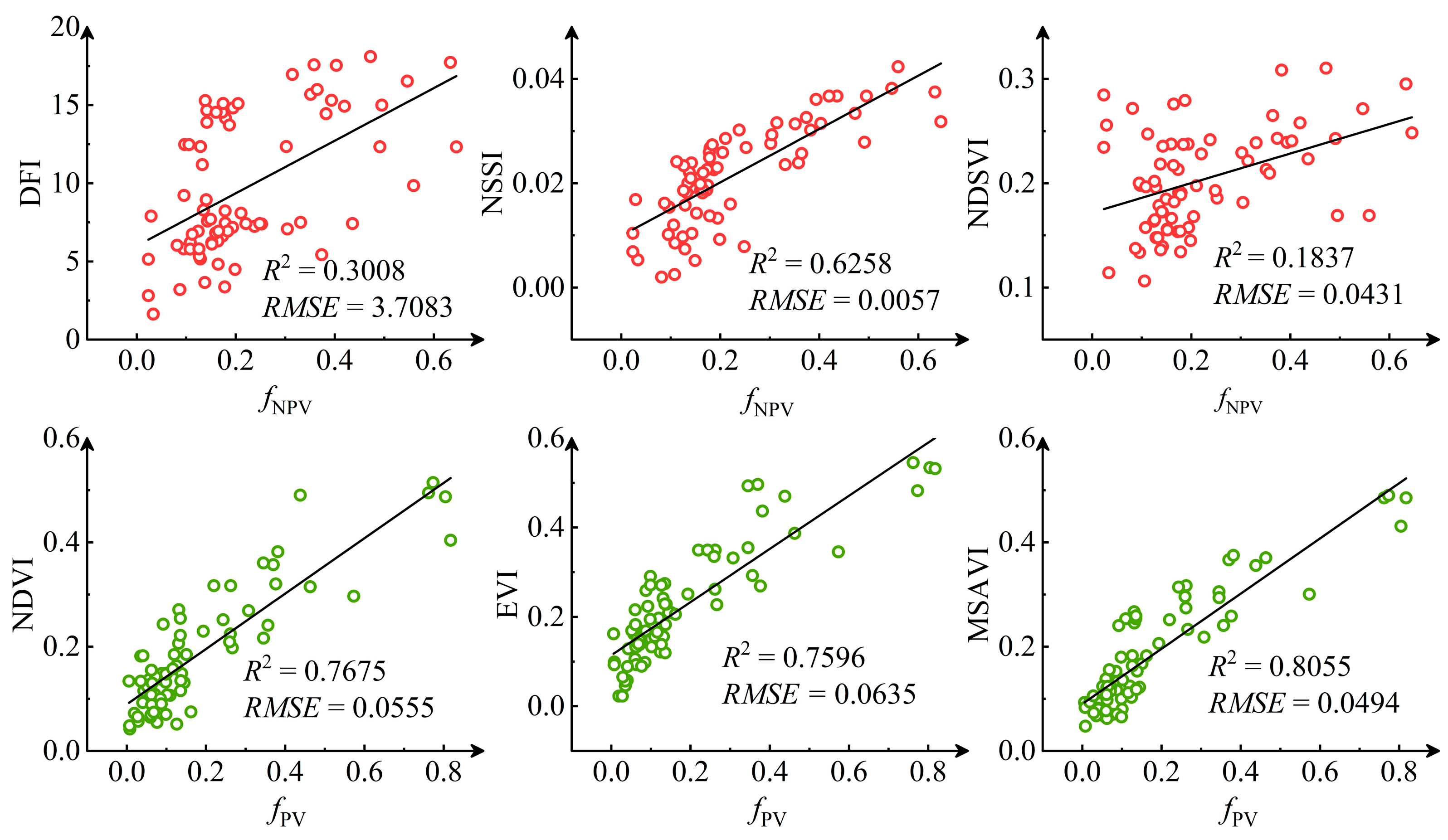
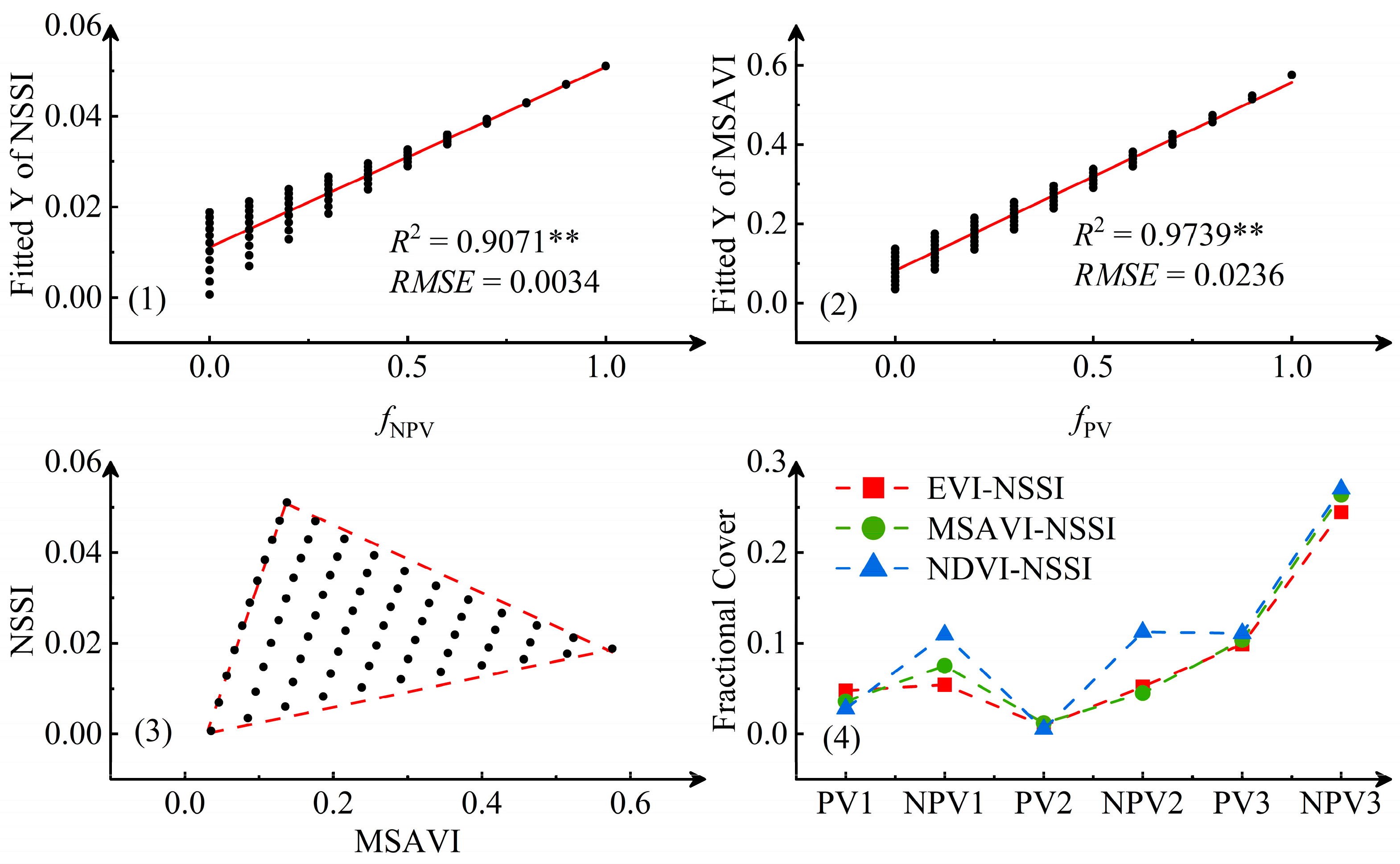
- Vegetation indices exhibit sensor-dependent performance variations due to spectral band differences. For Sentinel-2, the MSAVI and NSSI demonstrated optimal fitting with fNPV, achieving R2 values of 0.9739 and 0.9071, respectively, within the spectral dataset. In contrast, Landsat 8 and MODIS sensors showed improved performance when combining MSAVI with the optimized vegetation index DFIEXP, attributable to their respective band limitations.
- (3)
- By optimizing the spectral constraint weights of endmembers in remote sensing imagery, NPV can be more effectively identified across various phenological conditions, providing a solution for long-term vegetation health monitoring.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPV | Non-photosynthetic vegetation |
| PV | Photosynthetic vegetation |
| BS | Bare soil |
| fNPV | Non-photosynthetic vegetation fractional cover |
| fPV | Photosynthetic vegetation fractional cover |
| fBS | Bare soil fractional cover |
| UAV | Unmanned Aerial Vehicle |
| NDVI | Normalized difference vegetation index |
| EVI | Enhanced vegetation index |
| MSAVI | Modified soil adjusted vegetation index |
| LAIB | Brown leaf area index |
| GBVI | Green brown vegetation index |
| NDTI | Normalized difference tillage index |
| STI | Soil tillage index |
| DFI | Dryness fraction index |
| NSSI | NPV soil separation index |
| NDSVI | Normalized difference senescent vegetation index |
| SWIR32 | Shortwave infrared ratio 3/2 |
| NDI5 | Normalized difference index 5 |
| NDI7 | Normalized difference index 7 |
References
- Verrelst, J.; Halabuk, A.; Atzberger, C.; Hank, T.; Steinhauser, S.; Berger, K. A comprehensive survey on quantifying non-photosynthetic vegetation cover and biomass from imaging spectroscopy. Ecol. Indic. 2023, 155, 110911. [Google Scholar] [CrossRef]
- Guerschman, J.P.; Hill, M.J.; Renzullo, L.J.; Barrett, D.J.; Marks, A.S.; Botha, E.J. Estimating fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil in the australian tropical savanna region upscaling the EO-1 hyperion and MODIS sensors. Remote Sens. Environ. 2009, 113, 928–945. [Google Scholar] [CrossRef]
- Zhu, C.; Tian, J.; Tian, Q.; Wang, X.; Li, Q. Using NDVI-NSSI feature space for simultaneous estimation of fractional cover of non-photosynthetic vegetation and photosynthetic vegetation. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103282. [Google Scholar] [CrossRef]
- Jiapaer, G.; Chen, X.; Bao, A. A comparison of methods for estimating fractional vegetation cover in arid regions. Agric. For. Meteorol. 2011, 151, 1698–1710. [Google Scholar] [CrossRef]
- Byambakhuu, I.; Sugita, M.; Matsushima, D. Spectral unmixing model to assess land cover fractions in Mongolian steppe regions. Remote Sens. Environ. 2010, 114, 2361–2372. [Google Scholar] [CrossRef]
- Mishra, N.B.; Crews, K.A. Estimating fractional land cover in semi-arid central Kalahari: The impact of mapping method (spectral unmixing vs. object-based image analysis) and vegetation morphology. Geocarto Int. 2014, 29, 860–877. [Google Scholar] [CrossRef]
- Zheng, B.; Campbell, J.B.; Serbin, G.; Daughtry, C.S.T. Multitemporal remote sensing of crop residue cover and tillage practices: A validation of the minNDTI strategy in the United States. J. Soil Water Conserv. 2013, 68, 120–131. [Google Scholar] [CrossRef]
- Hou, C.H.; Li, F.P.; Feng, Y.F.; Gu, H.H.; Yuan, X.T.; Song, W.; Liu, H.X. Analysis of differentiation effect of sur-face thermal environment in intensive mining areas based on NDVI-DFI model. Trans. Chin. Soc. Agric. Eng. 2020, 36, 160–168. [Google Scholar] [CrossRef]
- Song, J.; Xia, N.; Hai, W.; Tang, M.Y. Spatial-temporal variation of vegetation in Gobi region of Xinjiang based on NDVI-DFI model. Southwest China J. Agric. Sci. 2022, 35, 2867–2875. [Google Scholar] [CrossRef]
- Tang, M.Y.; Ding, J.L.; Xia, N.; Zhang, Z. Estimation of vegetation in the Boertala mongolian autonomy prefecture based on NDVI-DFI mode. Sci. Surv. Mapp. 2019, 44, 74–81. [Google Scholar] [CrossRef]
- Bai, X.L. Relationship of reflectance spectral and fractional cover of various non-photosynthetic vegetation. Acta Ecol. Sin. 2022, 42, 186–195. [Google Scholar] [CrossRef]
- Chai, G.Q.; Wang, J.P.; Wang, G.Z.; Kang, L.; Wu, M.; Wang, Z. Estimation of fractional cover of non-photosynthetic vegetation in typical steppe based on MODIS data. Remote Sens. Land Resour. 2018, 31, 2836–2844. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Rivera, J.P.; Ruiz-Verdú, A.; Moreno, J. Brown and green LAI mapping through spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 350–358. [Google Scholar] [CrossRef]
- Wang, G.Z.; Wang, J.P.; Zou, X.Y.; Wang, Z.L.; Zong, M. Estimation of fractional cover of photosynthetic and non-photosynthetic vegetation in the xilingol steppe region using the NDVI-DFI model. Acta Ecol. Sin. 2017, 37, 5722–5731. [Google Scholar] [CrossRef]
- Luo, Y.X.; Ji, C.C.; Li, X.S.; Xu, J.H. Vegetation Index Model for Estimating Sparse Photosynthetic/ Non-photosynthetic Vegetation Fractional Cover in Arid Zone. Remote Sens. Inf. 2022, 37, 57–64. [Google Scholar] [CrossRef]
- Xu, M.Z.; Xu, H.; Kong, P.; Wu, Y.L. Remote Sensing Vegetation Classification Method Based on Vegetation Index and Convolution Neural Network. Laser Optoelectron. Prog. 2022, 59, 2428005. [Google Scholar] [CrossRef]
- Han, X. Resaerch data: Measured hyperspectral data of vegetation and soil in northwest China. Mendeley Data 2025. [Google Scholar] [CrossRef]
- Ji, C.; Jia, Y.; Gao, Z.; Wei, H.; Li, X. Nonlinear spectral mixture effects for photosynthetic/non-photosynthetic vegetation cover estimates of typical desert vegetation in western china. PLoS ONE 2017, 12, e0189292. [Google Scholar] [CrossRef]
- Yuan, H.; Ji, C.C.; Yang, X.M.; Chen, M.L.; Pan, J.P.; Cao, Y.M. Construction of sparse non-photosynthetic vegetation index combining sentinel-2 data and spectral features. J. Geo-Inf. Sci. 2023, 25, 1894–1907. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.; Zou, X.; Chai, G.; Wu, M.; Wang, Z. Estimating the fractional cover of photosynthetic vegetation, non-photosynthetic vegetation and bare soil from MODIS data: Assessing the applicability of the NDVI-DFI model in the typical xilingol grasslands. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 154–166. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- van Deventer, A.P.; Ward, A.D.; Gowda, P.H.; Lyon, J.G. Using Thematic Mapper Data to Identify Contrasting Soil Plains and Tillage Practices. Photogramm. Eng. Remote Sens. 1997, 63, 87–93. [Google Scholar]
- Jacques, D.C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Defourny, P. Monitoring dry vegetation masses in semi-arid areas with MODIS SWIR bands. Remote Sens. Environ. 2014, 153, 40–49. [Google Scholar] [CrossRef]
- Cao, X.; Chen, J.; Matsushita, B.; Imura, H. Developing a MODIS-based index to discriminate dead fuel from photosynthetic vegetation and soil background in the Asian steppe area. Int. J. Remote Sens. 2010, 31, 1589–1604. [Google Scholar] [CrossRef]
- Tian, J.; Su, S.; Tian, Q.; Zhan, W.; Xi, Y.; Wang, N. A novel spectral index for estimating fractional cover of non-photosynthetic vegetation using near-infrared bands of sentinel satellite. Int. J. Appl. Earth Obs. Geoinf. 2021, 101, 102361. [Google Scholar] [CrossRef]
- Qi, J.; Marsett, R.; Heilman, P.; Bieden-Bender, S.; Moran, S.; Goodrich, D.; Weltz, M. RANGES improves satellite-based information and land cover assessments in southwest United States. EoS Trans. 2002, 83, 601–606. [Google Scholar] [CrossRef]
- Wang, G.; Wang, J.; Han, L.; Chai, G.; Wang, Z. Estimation of Non-Photosynthetic Vegetation Coverage Using Simulated Landsat-8 OLI Data Based on Measured Spectra. J. Geo-Inf. Sci. 2018, 20, 1667–1678. [Google Scholar]
- Asner, G.P.; Heidebrecht, K.B. Spectral unmixing of vegetation, soil and dry carbon cover in arid regions: Comparing multispectral and hyperspectral observations. Int. J. Remote Sens. 2002, 23, 3939–3958. [Google Scholar] [CrossRef]
- Chai, G. Estimation of Non-Photosynthetic Vegetation Coverage and Its Spatiotemporal Variations in Xilingol Grassland Based on MODIS Data. Master’s Thesis, Ludong University, Yantai, China, 2021. [Google Scholar]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; Driscoll, R.L.; et al. USGS Spectral Library Version 7 Data: U.S. Geological Survey Data Release; USGS: Reston, VA, USA, 2017. [Google Scholar] [CrossRef]
- Boardman, J.W.; Kruse, F.A.; Green, R.O. Mapping Target Signatures via Partial Unmixing of AVIRIS Data (Report No. N95-33); Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 1995. [Google Scholar]
- Ploton, P.; Mortier, F.; Réjou-Méchain, M.; Barbier, N.; Picard, N.; Rossi, V.; Dormann, C.; Cornu, G.; Viennois, G.; Bayol, N.; et al. Spatial validation reveals poor predictive performance of large-scale ecological mapping models. Nat. Commun. 2020, 11, 4540. [Google Scholar] [CrossRef]
- Bahn, V.; McGill, B.J. Testing the predictive performance of distribution models. Oikos 2012, 122, 321–331. [Google Scholar] [CrossRef]
- Lehmann, J.; Kleber, M. The contentious nature of soil organic matter. Nature 2015, 528, 60–68. [Google Scholar] [CrossRef]
- Ji, W.J.; Shi, Z.; Zhou, Q.; Zhou, L.Q. VIS-NIR reflectance spectroscopy of the organic matter in several types of soils: VIS-NIR reflectance spectroscopy of the organic matter in several types of soils. J. Infrared Millim. Waves 2012, 31, 277–282. [Google Scholar] [CrossRef]

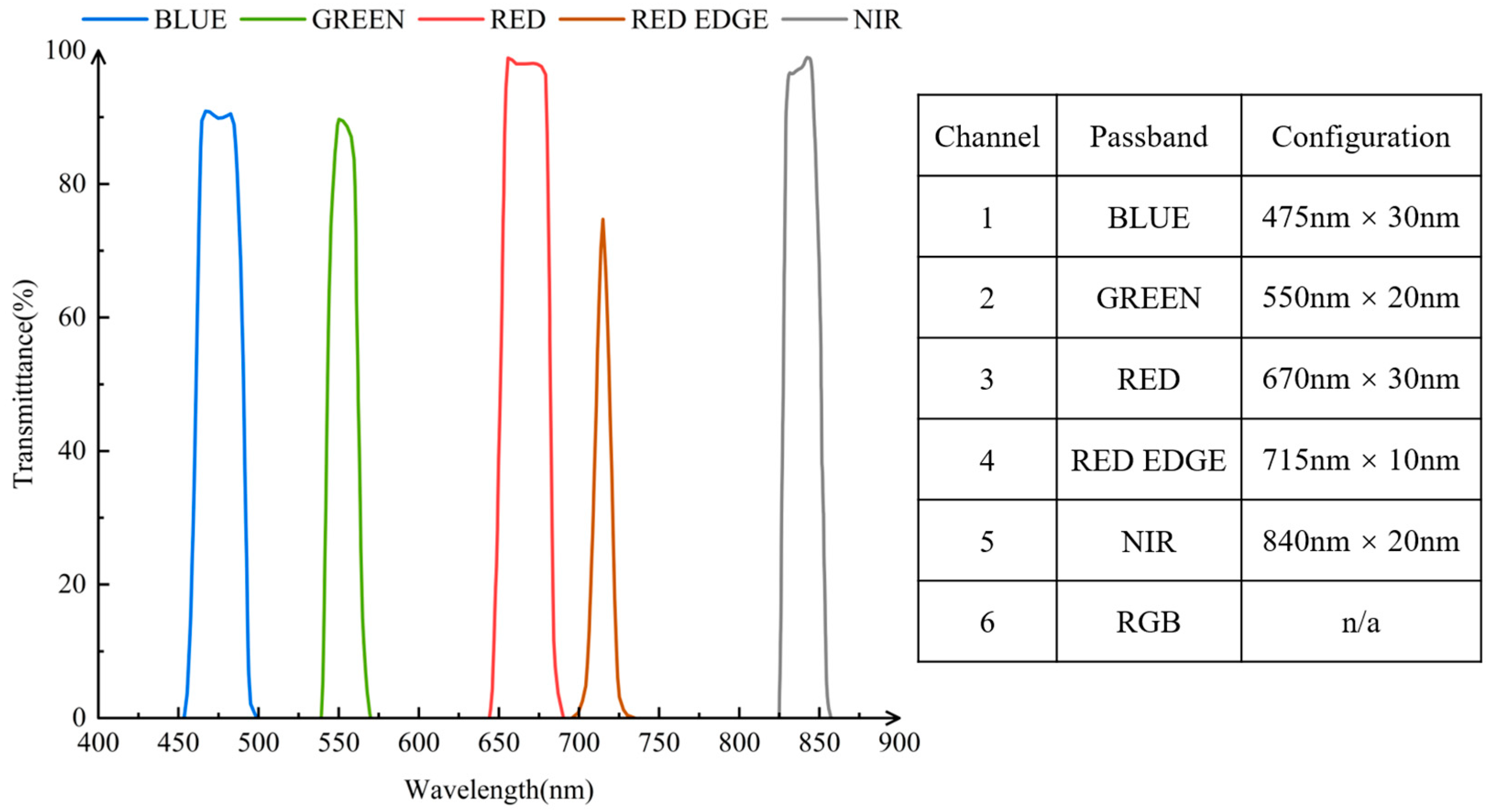

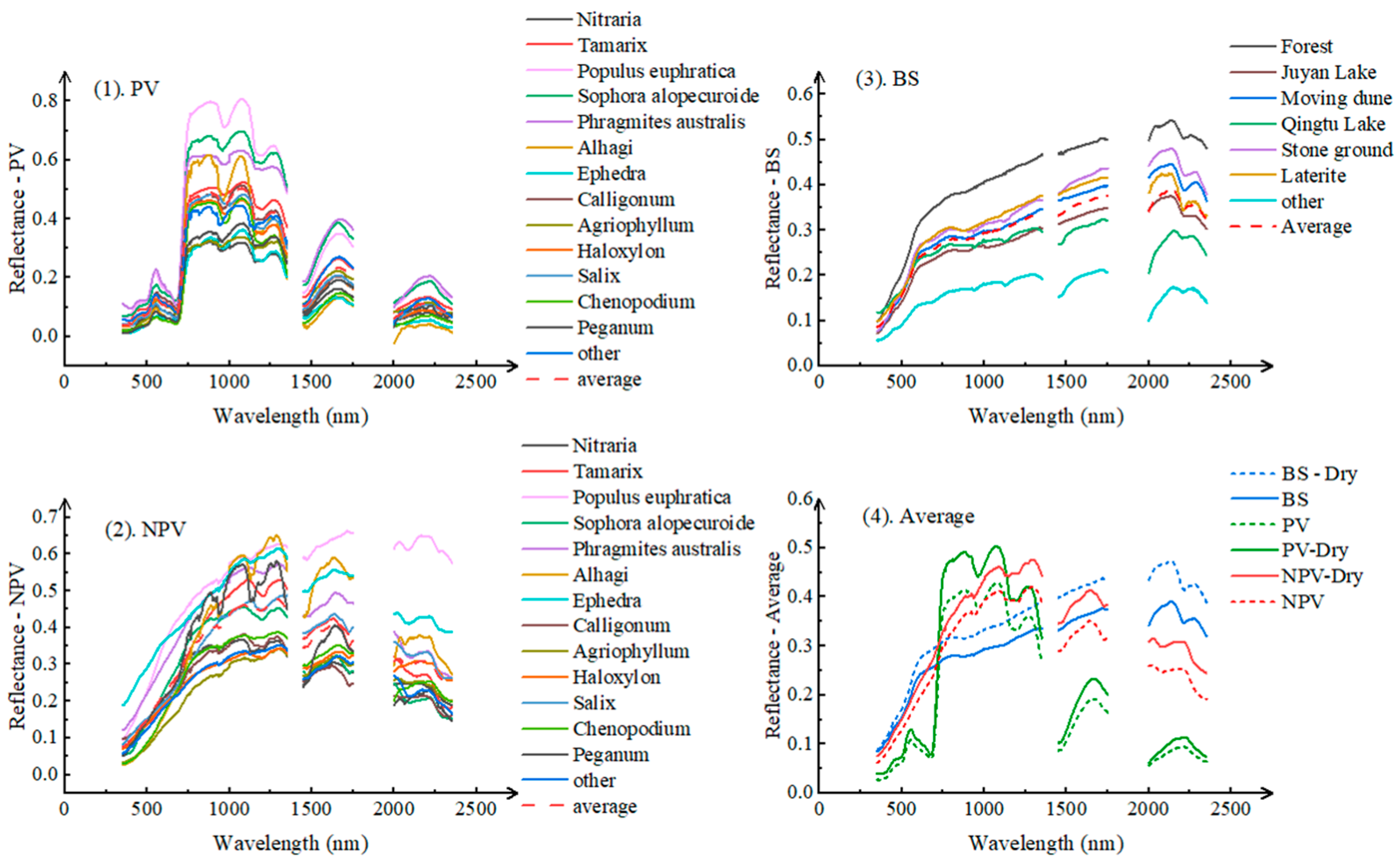
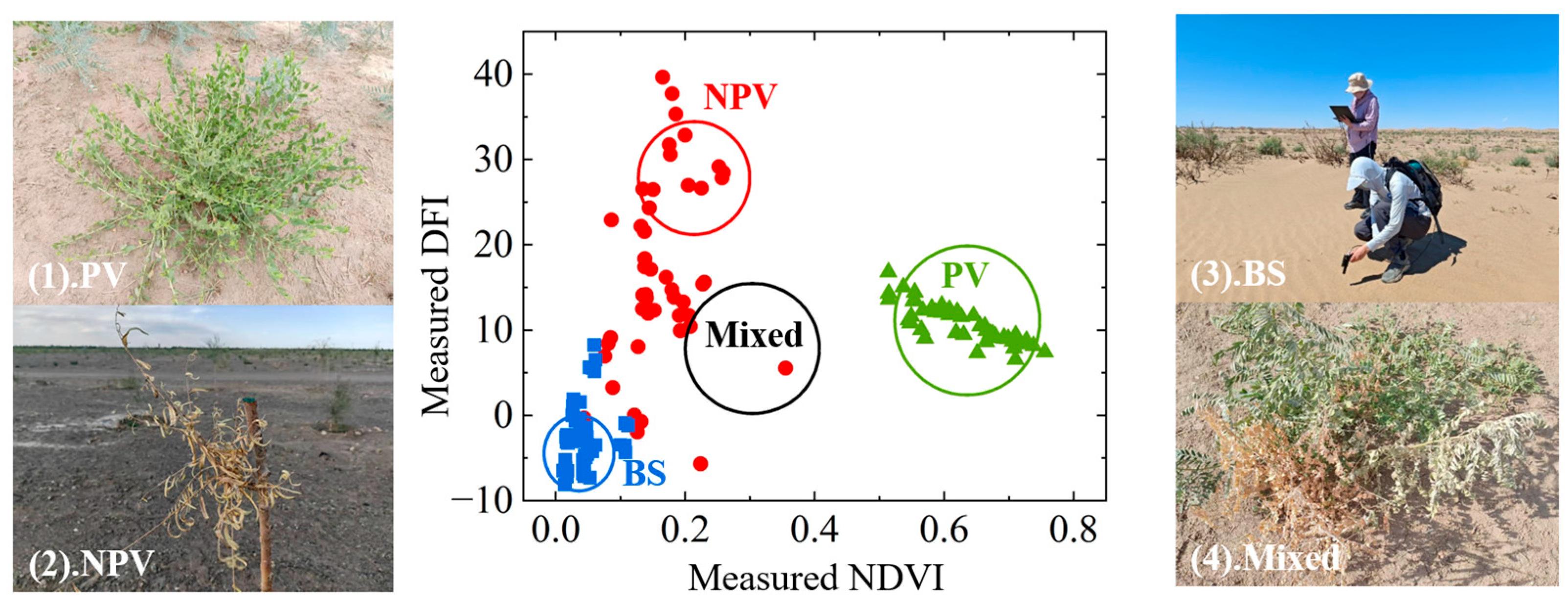



| In Situ | Region | Description | Time | NPV/num | PV/num | BS/num |
|---|---|---|---|---|---|---|
| No.1 | 83°32′52″N, 44°1′43″E | Vegetation: Haloxylon, Nitraria, Calligonum; Soil: forest soil, cultivated soil, salinized soil. | 20 July 2024 | 60 | 120 | 60 |
| No.2 | 88°33′35″N, 44°48′43″E | Vegetation: Tamarix, Haloxylon ammodendro, Nitraria, Reaumuria soongorica; Soil: sandy soil, silty clay. | 22 July 2024 | 45 | 90 | 15 |
| No.3 | 101°18′5″N, 42°9′5″E | Vegetation: Tamarix, P. australis, Sophora alopecuroides; Soil: sandy soil. | 31 July 2024 | 60 | 90 | 60 |
| N0.4 | 100°53′42″N, 41°34′12″E | Vegetation: Populus euphratica, Tamarix, Alhagi, Sophora alopecuroide; Soil: sandy soil. | 31 July 2024 | 100 | 90 | 60 |
| N0.5 | 98°49′8″N, 39°57′43″E | Vegetation: Tamarix, Populus euphratica, Nitraria, Ephedra; Soil: gray-cinnamon soil, meadow soil. | 9 August 2024 | 100 | 100 | 50 |
| N0.6 | 99°40′12″N, 39°33′10″E | Vegetation: Tamarix, Sophora alopecuroides, Populus euphratica, Calligonum, Agriophyllum; Soil: gray-cinnamon soil, meadow soil. | 9 August 2024 | 50 | 50 | 40 |
| N0.7 | 102°54′46″N, 38°35′16″E | Vegetation: Nitraria, Calligonum, Haloxylon; Soil: sandy soil. | 11 August 2024 | 90 | 100 | 60 |
| N0.8 | 103°33′21″N, 39°1′33″E | Vegetation: Tamarix, P. australis, Chenopodium; Soil: moist soil, cinnamon soil. | 11 August 2024 | 60 | 100 | 60 |
| N0.9 | 81°19′33″N, 40°36′33″E | Vegetation: Populus euphratica, P. australis; Soil: aeolian sandy soil, meadow soil. | 31 October 2024 | 30 | 50 | 30 |
| N0.10 | 80°26′50″N, 41°25′52″E | Vegetation: Populus euphratica, Calligonum, Alhagi, Haloxylon; Soil: sandy soil, meadow soil. | 31 October 2024 | 50 | 60 | 10 |
| N0.11 | 86°17′12″N, 41°35′12″E | Vegetation: Populus euphratica, Calligonum, P. australis, Alhagi, Haloxylon; Soil: sandy soil, meadow soil. | 2 November 2024 | 30 | 90 | 30 |
| N0.12 | 92°23′4″N, 40°36′33″E | Vegetation: Populus euphratica, Calligonum, P. australis, Haloxylon; Soil: sandy soil, meadow soil. | 4 November 2024 | 30 | 90 | 30 |
| Index | Formula | References |
|---|---|---|
| NDVI | [21] | |
| EVI | [22] | |
| MSAVI | /2 | [23] |
| LAIB | [13] | |
| NDTI | [24] | |
| STI | [25] |
| Index | Formula | References |
|---|---|---|
| DFI | [26] | |
| NSSI | [27] | |
| NDSVI | [28] | |
| SWIR32 | [2] | |
| NDI5 | [24] | |
| NDI7 | [24] |
| Variables | Definitions | Significance |
|---|---|---|
| R(λ) | The spectral index of a pixel | Used for spectral unmixing, with values varying across different regions. |
| Cx, Cy, Cz | Anomalous pixel values of different land covers | Reduces the impact of anomalous pixels. |
| Spectral mean of the sub-region | Unifies the spectral characteristics within sub-regions. | |
| Endmember | Serves as a critical variable in pixel decomposition, representing the distinctive spectral values of different land cover types. | |
| The fluctuation term of the i-th endmember | Represents spatial heterogeneity. |
| NPV | Regression Formula | R2 | RMSE | PV | Regression Formula | R2 | RMSE |
|---|---|---|---|---|---|---|---|
| DFI | y = 0.1160fNPV + 0.0568 | 0.5443 * | 0.0285 | NDVI | y = 0.5775fPV + 0.1111 | 0.9667 * | 0.0253 |
| SWIR32 | y = 0.0347fNPV + 0.0876 | 0.0098 | 0.0936 | EVI | y = 0.6036fPV + 0.0965 | 0.9638 * | 0.0314 |
| NDSVI | y = 0.0653fNPV + 0.2707 | 0.1092 * | 0.0501 | MSAVI | y = 0.4421fPV + 0.1214 | 0.9739 * | 0.0236 |
| NSSI | y = 0.0398fNPV + 0.0111 | 0.9071 * | 0.0034 | LAIB | y = 0.4582fPV + 0.0451 | 0.6465 * | 0.0911 |
| NDI5 | y = −0.1781fNPV + 0.1273 | 0.1450 * | 0.1162 | NDTI | y = 0.0233fPV + 0.1145 | 0.0066 | 0.0766 |
| NDI7 | y = −0.1349fNPV + 0.2276 | 0.0389 | 0.1802 | STI | y = 0.0145fPV + 1.2924 | 0.0003 | 0.2153 |
| NPV | Regression Formula | R2 | RMSE | PV | Regression Formula | R2 | RMSE |
|---|---|---|---|---|---|---|---|
| DFI | y = 0.1132fNPV + 0.0568 | 0.5129 * | 0.0296 | NDVI | y = 0.5629fNPV + 0.1038 | 0.9562 * | 0.0324 |
| SWIR32 | y = −0.0608fNPV + 0.8117 | 0.0183 | 0.1198 | EVI | y = 0.4595fNPV + 0.0972 | 0.9472 * | 0.0292 |
| NDI5 | y = 0.1634fNPV − 0.1341 | 0.1206 * | 0.1186 | MSAVI | y = 0.5530fNPV + 0.1294 | 0.9571 * | 0.0315 |
| NDSVI | y = 0.1174fNPV − 0.2321 | 0.0291 | 0.1822 | LAIB | y = 0.4575fNPV + 0.0441 | 0.6385 * | 0.0925 |
| NPV | Regression Formula | R2 | RMSE | PV | Regression Formula | R2 | RMSE |
|---|---|---|---|---|---|---|---|
| DFI | y = 0.1132fNPV + 0.0518 | 0.3398 * | 0.0424 | NDVI | y = 0.4484fPV + 0.1001 | 0.9444 * | 0.0292 |
| SWIR32 | y = −0.0526fNPV + 0.8119 | 0.0099 | 0.1417 | EVI | y = 0.5346fPV + 0.1039 | 0.9532 * | 0.0318 |
| NDI5 | y = 0.1625fNPV − 0.1211 | 0.1284 * | 0.1138 | MSAVI | y = 0.5392fPV + 0.1336 | 0.9535 * | 0.0220 |
| NDSVI | y = 0.1253fNPV − 0.2222 | 0.0301 | 0.0301 | LAIB | y = 0.5597fPV + 0.0105 | 0.6772 * | 0.1038 |
| Sensor | Sentinel-2A | Landsat8 OIL | MODIS | |||
|---|---|---|---|---|---|---|
| Index | MSAVI | NSSI | MSAVI | DFIEXP | MSAVI | DFIEXP |
| PV | 0.6183 | 0.0188 | 0.5731 | 0.0209 | 0.5629 | 0.0258 |
| NPV | 0.1836 | 0.0687 | 0.1638 | 0.0717 | 0.1664 | 0.0728 |
| BS | 0.0461 | −0.0024 | 0.0369 | 0.0031 | 0.0821 | 0.0017 |
| Feature Type | Month | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| PVI | PV | 1.9036 | 3.0946 | 2.1194 | 1.2964 | 0.9872 | 0.8782 | 0.8687 | 0.8849 | 0.9634 | 1.1621 | 1.5140 | 1.7791 |
| NPV | −1.2597 | −1.2635 | −1.1358 | −1.3248 | 1.4910 | 1.1954 | 1.2830 | 1.0472 | 1.5923 | −1.4259 | −1.3238 | −1.2208 | |
| BS | 1.4204 | 1.4253 | 1.9138 | 1.6824 | 1.7176 | 1.4058 | 1.8830 | 1.6755 | 1.4034 | 1.4609 | 1.9501 | 2.1105 | |
| PV | 0.8805 | 0.8088 | 0.8459 | 1.0574 | 1.2709 | 1.6863 | 1.7793 | 1.7917 | 1.3368 | 0.9961 | 0.8990 | 0.8012 | |
| NPVI | NPV | 0.9345 | 0.9746 | 0.9455 | 0.9825 | 1.1115 | 1.1357 | 1.1974 | 0.1056 | 1.0882 | 1.0643 | 0.9973 | 0.9467 |
| BS | 0.2982 | 0.3036 | 0.3778 | 0.2742 | 0.3148 | 0.5862 | 0.3542 | 0.5313 | 0.3333 | 0.4146 | 0.3617 | 0.2073 | |
| Site | Sensors | Region | BS | NPV | PV | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Desert | Grass | Forest | Desert | Grass | Forest | Desert | Grass | Forest | |||
| No.1 | Sentinel-2 | 87°55′41″N, 44°22′14″E | 1.3365 | 2.2635 | 3.6115 | 9.5842 | 9.4101 | 10.9228 | 29.6622 | 29.6622 | 37.4339 |
| No.2 | Landsat8 | 88°33′35″N, 44°48′43″E | 8.0471 | 6.8514 | 9.4510 | 7.2022 | 4.6803 | 13.0862 | 29.8591 | 35.2856 | 42.2645 |
| N0.3 | MOD09GA | 92°23′4″N, 40°36′33″E | 28.1599 | 27.5533 | 28.9692 | 16.8658 | 18.9991 | 20.7574 | 19.5427 | 14.3263 | 11.2194 |
| PVI | NPVI | NO. | fNPV | fPV | fBS |
|---|---|---|---|---|---|
| NDVI | NSSI | D. | 39.94% | 19.12% | 40.94% |
| E. | 61.55% | 20.12% | 18.33% | ||
| EVI | NSSI | F. | 38.75% | 13.47% | 47.78% |
| G. | 61.02% | 18.94% | 20.04% | ||
| MSAVI | NSSI | H. | 40.08% | 18.75% | 41.17% |
| I. | 61.42% | 21.12% | 17.46% |
| Method | Validation Area | R2 | RMSE |
|---|---|---|---|
| Global validation | All | 0.7825 ** | 0.0232 |
| Spatial block validation | Average | 0.7017 ** | 0.0279 |
| River | 0.6535 ** | 0.0287 | |
| Oasis | 0.7845 ** | 0.0212 | |
| Desert | 0.8031 ** | 0.0194 | |
| Urban | 0.5373 ** | 0.0376 | |
| Mixed | 0.7299 ** | 0.0324 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, X.; Zhao, C.; Ji, M.; Zhu, J. Identification of Non-Photosynthetic Vegetation Fractional Cover via Spectral Data Constrained Unmixing Algorithm Optimization. Remote Sens. 2025, 17, 3480. https://doi.org/10.3390/rs17203480
Han X, Zhao C, Ji M, Zhu J. Identification of Non-Photosynthetic Vegetation Fractional Cover via Spectral Data Constrained Unmixing Algorithm Optimization. Remote Sensing. 2025; 17(20):3480. https://doi.org/10.3390/rs17203480
Chicago/Turabian StyleHan, Xueting, Chengyi Zhao, Menghao Ji, and Jianting Zhu. 2025. "Identification of Non-Photosynthetic Vegetation Fractional Cover via Spectral Data Constrained Unmixing Algorithm Optimization" Remote Sensing 17, no. 20: 3480. https://doi.org/10.3390/rs17203480
APA StyleHan, X., Zhao, C., Ji, M., & Zhu, J. (2025). Identification of Non-Photosynthetic Vegetation Fractional Cover via Spectral Data Constrained Unmixing Algorithm Optimization. Remote Sensing, 17(20), 3480. https://doi.org/10.3390/rs17203480








